Termodynamický popis chemicky reagujícího systému
|
|
|
- František Ovčačík
- před 9 lety
- Počet zobrazení:
Transkript
1 5. CHEMICKÉ ROVNOVÁHY Všechny chemcké rekce směřují k dynmcké rovnováze, v níž jsou řítomny jk výchozí látky tk rodukty, které všk nemjí jž tendenc se měnt. V řdě řídů je všk oloh rovnováhy tk osunut ve rosěch rekčních roduktů, že koncentrce výchozích látek v rovnovážné směs je extrémně mlá ve srovnání s koncentrcí konečných látek; k hovoříme běžně o jednosměrné rekc. Termodynmk nám umožňuje ředovědět, je-l možno, by dná rekce robíhl sontánně, umožňuje vyočítt rovnovážné složení z různých odmínek, zjstt, je-l výhodnější rovádět dnou rekc z vyšších nebo nžších telot, z vyšších nebo nžších tlků, z řítomnost tzv. nertů, tj. látek, které se smy rekce neúčstní od. Můžeme se tké nř. dovědět, jk je využíván otrv ř složtých sérích bologckých rekcí robíhjících ř udržování tělesné teloty, ke kontrkc svlových buněk, nebo vyžvování nervových buněk. Některé rekce jsou sontánní mohou být sřženy s jným rekcem, by jm dodly energ nutnou k jejch růběhu v žádném, le nesontánním směru. Pomocí termodynmky je k možno vytovt rekce, které tkový ohon otřebují vyočítt, jkou hncí sílu je zotřebí získt od rekcí, které robíhjí sontánně. Avšk je třeb mít n mět, že význmnou rol mohou hrát knetcké fktory. Termodynmk nám může říc, v jkém směru může uvžovná rekce robíht sontánně jké je složení systému v rovnováze. Ale nemůže ředovídt, exstuje-l knetcky schůdná cest do rovnovážného stvu. Termodynmcký os chemcky regujícího systému K tomu, by bylo možno osoudt, jká bude tendence rekce roběhnout, tj. jká bude její fnt, kolk užtečné ráce by se z ní dlo získt jké bude složení regujícího systému o dosžení rovnováhy, je nejvhodnější z konstntní teloty tlku znlost Gbbsovy energe, (z konstntní teloty objemu znlost Helmholtzovy energe * ). Z termodynmky víme, že směr sontánního děje je ndkován oklesem Gbbsovy energe systému. Budeme uvžovt systém z konstntní teloty tlku, který nevyměňuje s okolím jnou rác než objemovou robíhá v něm chemcká rekce, jejíž stechometre je vyjádřen rovncí: ν B B + ν D D ν R R + ν S S, (5.1) zjstíme závslost Gbbsovy energe n složení systému z jejího tvru můžeme k usoudt, zd v dné směs látek B, D, R, S bude tto rekce mít tendenc robíht směrem k R S nebo nok směrem k B D, můžeme odhdnout, mohou-l látky G C D zregovt n R S téměř úlně (obr. 5-1, křvk ), částečně (obr. 5-1, křvk b), nebo rktcky nebudou regovt vůbec (obr. 5-1, křvk c). b c ( rov) c ( rov ) b ( rov) výchozí rodukty látky Obr. 5-1 () Systém, v němž je rovnovážné složení velm blízko roduktům; rekce roběhne téměř úlně, (b) v rovnováze jsou výchozí látky rodukty zstoueny téměř stejnou měrou, (c) rovnováh je osunut tk blízko k čstým výchozím látkám, že rekce téměř nemá tendenc robíht. * Všechny dlší úvhy jsou rováděny ro děje z [T, ] tedy v termínech Gbbsovy energe. Zcel nlogcké úvhy ltí z [T, V] v termínech Helmholtzovy energe. Chemcké rovnováhy 1
2 Látková množství jednotlvých složek v soustvě jsou vyjádřen očty molů, n ( = B, D, R nebo S). N zčátku rekce jsou tto množství n sobě nezávslá; výchozí směs může obshovt rektnty v nestechometrckých oměrech rodukty, rovněž v nestechometrckých oměrech. Chemcká rekce se rojeví tím, že výchozí látky budou řecházet n rodukty; látková množství rektntů budou tedy klest, látková množství roduktů stout. Ovšem jen do určtého stuně, kdy se uství rovnováh. V rovnováze k jž látková množství jednotlvých složek nejsou nvzájem nezávslá. Pro chrkterzc ktuálního stvu systému je vhodné zvést nějkou velčnu, která by kvntttvně vyjádřl stueň okročlost rekce. Km ž rekce okročl udávjí ovšem změny látkových množství jednotlvých složek během rekce. Ty všk nejsou n sobě nezávslé, jsou vázány stechometrí. Pro nš rekc tk ltí nb nb0 nd nd0 nr nr0 ns n = = = S0 (5.2) ν ν ν ν B D R S kde ν jsou stechometrcké koefcenty jednotlvých složek, které jsou odle konvence ro rodukty kldné, ro výchozí látky záorné. Poměr (n n 0 )/ν je ro všechny složky stejný; ředstvuje vhodný rmetr ro sledování okročlost rekce: n n 0 ξ = (5.3) ν ξ je rozsh rekce látkové množství určté složky řeměněné chemckou rekcí vztžené n stechometrcký koefcent; n 0 látkové množství složky n očátku, n látkové množství složky v určtém stdu rekce. Vzth (5.3) nám tedy umožňuje vyjádřt látková množství n, omocí jedné roměnné ro všechny složky: n = n + ν ξ (5.4) 0 Změn Gbbsovy energe soustvy, v níž zregovlo ν B mol látky B ν D mol látky D z součsného vznku ν R mol látky R ν S mol látky S v tk velké soustvě, že se její ůvodní složení rktcky nezmění, je oznčován jko rekční Gbbsov energe r G. Má význm směrnce závslost Gbbsovy energe n rozshu rekce ř určtém složení regující směs (ndex r se čsto vynechává) G rg = ξ (5.5) T, sontánní rekce robíhá ve směru r G < 0, výchozí látky rodukty r G = 0, (rovnováh) (5.6) r G > 0, výchozí látky rodukty V bochem jsou rekce rvého tyu oznčovány jko exergoncké, rekce s r G > 0 jko endergoncké. Probíhá-l exergoncká rekce smosttně, ztrtí se uvolněná chemcká rekce hlvně jko telo. Probíhá-l všk z řítomnost termodynmcky nevýhodného rocesu ( r G < 0), tj. rekce vyždující dodání energe, může exergonckým rocesem uvolněná energe osloužt jko zdroj energe k relzc endergonckého děje. Hovoříme o sřžení exergonckého endergonckého děje, které je zákldem toku energe jejího využívání v žvém orgnsmu. Chemcké rovnováhy 2
3 Rekční zoterm Rekční Gbbsov energe závsí n okmžtém stvu systému, tj. n ktvtách jednotlvých složek. Pro lustrc budeme uvžovt hyotetckou rekc 2 B + 1 / 3 D 4 R + 1 / 2 S (5.7) V okmžku, kdy rozsh rekce dosáhl hodnoty ξ 1 (obr. 5-2), má rekční Gbbsov energe hodnotu 4 1/2 R S r r ln d G = G + R T (5.8) 2 1/3 mmo B D rovnováhu Tento vzth je oznčován jko rekční zoterm. Velčn oznčená symbolem r G y - stndrdní rekční Gbbsov energe - obshuje chemcké otencály složek ve stndrdním stvu nezávsí tedy n koncentrcích regujících látek, ouze n zvolených stndrdních stvech. Je to změn Gbbsovy energe ř rekc ν B mol látky B s ν D mol látky D z vznku ν R mol látky R ν S mol látky S, jsou-l všechny látky ve svých stndrdních stvech. Aktvty se týkjí složek v dném stdu rekce, nř. ξ 1 nebo ξ G 2. G < 0 T, G = 0 T, G > 0 T, Obr. 5-2 Závslost Gbbsovy energe n rozshu rekce, defnce r G výchozí látky 1 rov 2 rodukty G rg = ξ T, Když rozsh rekce dosáhne hodnoty ξ rov, uství se v systému rovnováh; jeho složení jž nemá tendenc se měnt. Křvk G = G (ξ) je v mnmu její směrnce je nulová: 4 1/2 R S r 0 r ln G G T 2 1/3 B D vrovnováze = = d + R (5.9) Protože uvžujeme systém z konstntního tlku teloty ro dnou telotu jsou stndrdní otencály konstntní, musí mít rgument logrtmu v rovnc (5.9) konstntní hodnotu. Výrz je oznčován jko rovnovážná konstnt K = 4 1/2 R S 2 1/3 B D rov (5.10) obecně K = ( ν ) rov (5.11) - součn ktvt roduktů umocněných n stechometrcké koefcenty dělený součnem ktvt výchozích látek umocněných n stechometrcké koefcenty. Index řomíná, že rovnovážná konstnt je vyjádřen omocí ktvt, ndex rov n rvé strně se obvykle vynechává. Rovnce (5.11), kterou je možno sát: r G d = RT ln K, (5.12) Chemcké rovnováhy 3
4 ředstvuje vzth mez dvěm velčnm, jejchž ovh je dmetrálně odlšná; velčn K chrkterzuje rovnovážný stv dné soustvy, ztímco velčn r G y odovídá stechometrckému, tj. nerovnovážnému růběhu rekce, ř němž jsou n očátku v soustvě ouze výchozí látky ve svých stndrdních stvech n konc ouze látky konečné, oět ve svých stndrdních stvech. Tento vzth má velký význm, neboť dovoluje výočet chemcké rovnováhy bez jkéhokol exermentu. Velkost znménko r G y dovolují řblžný odhd rovedtelnost určté rekce z termodynmckého hledsk. Podle řblžného rvdl je rekce slbná, okud je r G y 0 (horní mez r G y = 0 zřejmě odovídá stuc, kdy K = 1). Je-l 0 < r G y < 40 kj/mol, je sce rekce málo slbná, le ř vhodné volbě odmínek, nř. celkového tlku nebo složení výchozí směs, lze zde docílt dobrých výsledků. Rekce, ro které r G y > 40 kj/mol je možno relzovt jen výjmečně. Ze vzthu (5.11) vylývá, že rovnovážná konstnt je jednoznčně určen, známe-l rovnovážné hodnoty ktvt všech látek, které se říslušné rekce zúčstňují. Anlytcky můžeme ovšem zjstt ouze koncentrce tk bude výočet rovnovážné konstnty jednoduchý ouze tehdy, jsou-l koncentrce římo rovny ktvtám tedy v řídě deálních soustv, nebo exstují-l jednoduché metody ro řeočet koncentrcí n ktvty; v mnoh řídech je ro tento řeočet třeb užít řblžných metod. V řevážné většně řídů všk nemáme možnost rovést orvu n reálné chování nezbývá, než sokojt se s řblžným výočtem omocí rovnovážných koncentrcí, oř. rcálních tlků. Pro lyny je vhodný stndrdní stv lyn v deálním stvu z tlku st = 101,325 kp ř telotě soustvy. Pro ktvtu složky ve směs je k v řídě deálních lynů možno sát = (5.13) st kde rcální tlk složky ( = x ), x její molární zlomek, ro který ltí x = n /n (n látkové množství složky ve směs, n = Σ n celkové látkové množství směs). Př reálném chování = ϕ (5.14) st kde ϕ je fugctní koefcent čsté složky. U kondenzovných (tj. klných nebo evných) látek, které z dné teloty tlku mohou exstovt jko čsté kondenzovné látky * se oužívá stndrdní stv čstá složk z teloty tlku systému. S molárním zlomkem jko koncentrční roměnnou je: = γ x, (5.15) neboť molární zlomek složky ve stndrdním stvu je roven jedné (jde o čstou látku). Aktvtní koefcent γ je obecně funkcí teloty složení směs (vlv tlku se u kondenzovných fází znedbává); ro čstou látku má hodnotu γ = 1. Z ředchozího lyne, že je-l kondenzovná fáze tvořen ouze jednou látkou, je ktvt této látky rovn jedné. Pro látky v roztoku (ro rozouštědlo volíme stndrdní stv čsté kondenzovné látky), které z dné teloty tlku buď neexstují jko čsté kondenzovné látky nebo neexstují jko čsté látky vůbec (nř. on NO 3 v roztoku HNO 3 ) se oužívá stndrdní stv jednotkové koncentrce (nekonečného zředění). Pro ktvtu k ltí * Nř. ro klnou směs ethnolu vody lze z okojové teloty zvolt tento stndrdní stv jk ro vodu, tk ro ethnol. Je-l všk v této směs rozuštěný nř. kyslík, je možno stndrdní stv čstá látk z T soustvy oužít jen ro vodu etnol, nkolv ro kyslík, který ř této telotě nemůže exstovt jko kln. Chemcké rovnováhy 4
5 X = γ (5.16) X st Z stndrdní stv volíme uvžovnou látku v roztoku o jednotkové koncentrc to buď: m st = 1 mol kg 1 nebo c st = 1 mol dm 3 (někdy se oužívá stndrdního stvu n báz hmotnostních rocent) ředokládáme, že ktvtní koefcent uvžovné látky v tomto roztoku má lmtní hodnotu, γ = 1 (ro tento ředokld se tento stndrdní stv nzývá stvem nekonečného zředění, když jde o roztok konečné koncentrce). Roztok, v němž ředokládáme jednotkové hodnoty ktvtních koefcentů je oznčován jko roztok deální. Homogenní rekce Rekce v lynné fáz Nejjednodušší říd chemckých rovnováh jk z teoretckého, tk rktckého hledsk ředstvují rekce v lynné fáz. Aktvty lynných složek vyjádříme rovncí (5.14). Pro náš říkld rekce (5.7), z ředokldu, že všechny složky jsou lynné, je 4 1/ /2 4 1/2 ( xr ) ( xs ) 4 1/2 ( ) ϕ st st R ϕs R S xr xs K = = K 2 1/3 2 1/3 ϕ = K 2 1/3 st B D B D ( 2 ϕ ϕ ϕ x 1/3 B ) ( xd ) xb xd st st nebo (5.17) nr 4 ns ( ) ( ) 1/ /2 ( ) n st n st nr ns K = Kϕ = K n 2 1/3 B D st ( ) 2 n ϕ (5.18) ( ) 1/3 nb nd n n st n st Je třeb zdůrznt, že zde byl zvolen stndrdní stv ř zcel určtém neměnném tlku roto je nezávslý n celkovém tlku v soustvě roto nezávsí n celkovém tlku n hodnot rovnovážné konstnty Látková množství jednotlvých složek v rovnováze mohou být vyjádřen dvojím zůsobem: omocí rozshu rekce, defnovným vzthem (5.4), z něhož lyne: n 0 +ν ξ (5.19) = n omocí stuně řeměny, defnovného jko úbytek látkového množství klíčové složky (od očátečního do rovnovážného stvu), vztžený n očáteční látkové množství této složky. Klíčová složk je t výchozí látk, které je n očátku rekce v systému reltvně nejméně vzhledem ke stechometr rekce, tj. není v ndbytku. Pro stueň řeměny tedy ltí nk0 n α = K odtud nk = nk0 α nk0 (5.20) n K0 Mez oběm velčnm jsou tyto rozdíly: stueň řeměny ntenzvní velčn bezrozměrná velčn hodnot vždy od nuly do jedné nutno určt klíčovou složku rozsh rekce extenzvní velčn velčn s rozměrem mol hodnot nezáorná (velkost závsí n nástřku) není třeb určt klíčovou složku Ob zůsoby vyjádření látkových množství vedou smozřejmě ke stejnému výsledku. Chemcké rovnováhy 5
6 Rekce v roztocích Pro výočet rovnovážné konstnty rekcí robíhjících ve zředěných roztocích volíme nejlée stndrdní stv jednotkové koncentrce ktvt je dán vzthem (5.16). Výrz ro rovnovážnou konstntu rekce (5.7) má k tvr: cr 4 cs 1/2 1 1 ( γr ) ( γs ) 4 1/2 4 1/2 ( ) cst cst γr γs cr cs 1 K = = c 2 1/3 2 1/3 st ( B 2 c D 1/3 c (5.21) γb ) ( γd ) γb γd cb cd cst cst Heterogenní rekce Rekce v systému lynná fáze jednosložkové kondenzovné fáze budeme dskutovt n říkldu rekce (5.7) ro říd, že složky D R jsou lynné, složk S je klná složk B tuhá (vzájemně se nerozouštějí): 2 B (s) + 1 / 3 D (g) 4 R (g)+ 1 / 2 S (l) (5.7) Pro lynné složky volíme stndrdní stv deální lyn ř st, jejch ktvty jsou vyjádřeny vzthy (5.14) (5.15). Pro čsté klné evné složky stndrdní stv čstá složk z T, soustvy; jejch ktvty jsou tedy rovny jedné. Pro rovnovážnou konstntu k ltí: nr /2 1( ϕr ) 4 4 (4 3) st R S n ϕr nr K = = = 2 1/3 n 1/3 1/3 D st (5.22) B D 1( ϕ 1/3 D ) ϕd nd n n st Př zhřívání řdy evných látek (uhlčtnů, hydrátů, oxdů, sulfdů td.) dochází k jejch rozkldu z vznku jednoho nebo více lynných roduktů. Nř. ro teelný rozkld uhlčtnu váentého, CCO 3 (s) CO (s) + CO 2 (g) (5.23) ř němž tvoří CCO 3 CO smosttné tuhé fáze, jejch ktvty jsou tedy jednotkové, má rovnovážná odmínk tvr CO CO 2 CO2 K = = CO = (5.24) 2 st CCO 3 V systémech tohoto tyu zvádíme ojem rozkldná telot tuhé látky. Je defnován jko telot, ř které celkový tlk lynných roduktů, vznkjích rozkldem uvžovné tuhé látky, dosáhne hodnoty tmosférckého tlku tm. Př této telotě k nstává msvní řechod tuhé fáze v lynnou. Pod rozkldnou telotou je r G > 0 rekce tedy rktcky nerobíhá, dokud telot nedosáhne tkové hodnoty, ř níž r G = 0. Nd rozkldnou telotou je r G y < 0 rozkld robíhá sontánně. Př zjšťování rozkldné teloty (nř. uhlčtnu váentého; CO2 = tm ) tedy řešíme roblém: r G y (T) = RT ln tm (5.28) st kde r G y (T) je závslost stndrdní rekční Gbbsovy energe n telotě. Podobně jko telot vru: kln se vyřuje z kždé teloty (z ovrchu); jkmle tlk nsycené áry dosáhne vnějšího tlku, nstne vyřování v celém objemu klny kln se vří. Chemcké rovnováhy 6
7 Stnovení rovnovážné konstnty z termochemckých dt Plnckov formulce třetí věty termodynmcké v zásdě vyřešl roblém výočtu rovnovážné konstnty chemcké rekce bez římého měření složení rovnovážné směs. Tyto výočty lze rovádět různým zůsoby, le jejch odstt je vždy stejná; vždy vycházejí ze vzthu (5.13): ln K (T) = r Gd ( T) (5.29) RT Hodnoty r G y je možno vyočítt z termodynmckých dt, které se tbelují nejrůznějším zůsoby. Z defnční rovnce ro stndrdní rekční Gbbsovu energ, G = H T S, lyne: G d = H d T S d (5.30) r r r kde r H y je stndrdní rekční telo, které je možno vyočítt ze slučovcích nebo slných teel (vz Termocheme): r d ν ( slh d ), oř. rh = ν sl H = d d ( H ) (5.31) r S y stndrdní rekční entroe, kterou je možno vyočítt z bsolutních entroí: S d = ν S d. (5.32) r Slučovcí č slná tel bsolutní entroe bývjí tbelovány ř telotě 298,15 K. K řeočtu n jné teloty je zotřebí znát telotní závslost teelných kct regujících látek. Z tbelovných hodnot stndrdních rekčních Gbbsových energí ro slučovcí rekce, obdobně jko stndrdní slučovcí tel (oět ř telotě 298,15 K): r sl m Gd = ν ( Gd ) (5.33) Velčny sl G d ředstvují stndrdní změnu Gbbsovy energe ř vznku jednoho molu sloučenny z rvků ve stndrdních stvech odle defnční rovnce ro G tedy ltí: sl sl sl G d = H d T S d (5.34) Velčn sl S d je stndrdní změn entroe dorovázející vznk 1 molu sloučenny z rvků ve stndrdních stvech; nř. ro oxd fosforečný bychom dostl 5 sls d 2 5 Sm d 2 5 Sm d červený S 2 m d 2 (P O,s) = 2 (P O,s) 2 (P,s ) (O,g) Přeočet n jné teloty se rovádí omocí tbelovných závslostí teelných kct n telotě. Z tbelovných hodnot logrtmů rovnovážných slučovcích konstnt ř zokrouhlených hodnotách teloty. Rovnovážná slučovcí konstnt K sl řtom ředstvuje rovnovážnou konstntu rekce, ř níž dná sloučenn vznká z rvků. sl G y rvků ve stndrdních stvech je rovn nule, tkže slučovcí konstnt rvků v jejch stndrdních stvech ř lbovolné telotě je vždy rovn jedné. Rovnovážná konstnt lbovolné rekce se očítá odle vzthu ln K = ν ln (K sl ) (5.35) Vlv různých fktorů n chemckou rovnováhu Rekční rovnováh závsí n odmínkách, ř nchž se rekce uskutečňuje. Z stejných odmínek se tedy v soustvě ustvuje ttáž chemcká rovnováh, kvntttvně chrkterzovná rovnovážnou konstntou. Př změně jednoho nebo více rmetrů se rovnováh oruší v systému robíhjí změny, které vedou k ustvení nové rovnováhy. Entroe kždé látky v deálním krystlckém stvu se s klesjící telotou bez omezení blíží nule. Chemcké rovnováhy 7
8 Vlv teloty n chemckou rovnováhu Pokud lze ředokládt, že rekční telo je nezávslé n telotě, ltí ro telotní závslost rovnovážné konstnty: ln K = r H d + C, (5.36) R T oř. 2 r 1 1 ln K H d = (5.37) K1 R T1 T2 kde K 1, oř. K 2 jsou hodnoty rovnovážné konstnty ř telotách T 1, oř. T 2. C je ntegrční konstnt. Pokud tedy rekční telo nezávsí n telotě, je logrtmus rovnovážné konstnty lneární funkcí recroké bsolutní teloty. V řdě řídů je tto odmínk v oměrně šrokém ntervlu telot dobře slněn. Pro exotermní rekce, jejchž r H y < 0, je záorný rovněž telotní koefcent rovnovážné konstnty rovnovážná konstnt se vzrůstjící telotou klesá. Nok ro endotermní rekce rovnovážná konstnt s rostoucí telotou vzrůstá. Výočet rekční entroe Rekční zobr umožňuje tké výočet stndrdní rekční entroe. Z orovnání rovnc (5.29), (5.34) (5.36) ro ntegrční konstntu v rovnc (5.36) lyne C = r S d (5.38) R Vlv tlku n chemckou rovnováhu Pro stndrdní stv lyn v deálním stvu z tlku st = 101,325 kp ř telotě soustvy hodnot rovnovážné konstnty n tlku v soustvě nezávsí. Př změně tlku se všk mění rovnovážné složení systému tk, by hodnot rovnovážné konstnty zůstl zchován. Použjeme-l ro rovnovážnou konstntu rekcí v lynné fáz vyjádření omocí molárních zlomků (vzth (5.17)), můžeme vlv tlku n rovnovážné složení vyjádřt následujícím zůsobem: K Σ = Kx st v (5.17) O vlvu tlku tedy rozhoduje změn očtu molů lynných složek, zůsobená rekcí, Σν. Rekce, ř nchž vzrůstá celkové látkové množství lynných složek (Σν > 0, zvětšuje se objem), jsou odorovány snížením tlku. Nok rovnovážný výtěžek rekcí, ř nchž celkové látkové množství lynných složek klesá (Σν < 0, zmenšuje se objem) je vyšší ř vyšším tlku. Vlv očátečního složení Zvýšením očáteční koncentrce výchozích látek ve směs se rovnovážný rozsh rekce zvyšuje, řítomnost roduktů ve výchozí směs řeměnu snžuje. Př rekcích důležtých z růmyslového hledsk, zejmén mjí-l výchozí látky rozdílnou cenu, oř. jsou rozdílně dostuné, oužívá se v ndbytku dostunější nebo levnější složk. Vlv nertní látky Látky, které se nezúčstňují rekce (nerty), ovlvňují rovnováhu tím, že rekční směs zřeďují (zvětšují celkové látkové množství). Jejch vlv je očný než vlv tlku. Je-l Σν > 0, řítomnost nertní látky zvyšuje výtěžek rekce, ro Σν < 0 je účnek očný. Nemění-l se ř rekc očet molů, nertní látky n rovnováhu neůsobí. Chemcké rovnováhy 8
Soustava kapalina + tuhá látka Izobarický fázový diagram pro soustavu obsahující vodu a chlorid sodný
 Soustv kpl + tuhá látk Izobrcký fázový dgrm pro soustvu obshující vodu chlord sodý t / o C H 2 O (s) + esyceý roztok 30 20 10 0-10 -20 t I t II esyceý roztok 2 1 p o NCl (s) + syceý roztok eutektcký bod
Soustv kpl + tuhá látk Izobrcký fázový dgrm pro soustvu obshující vodu chlord sodý t / o C H 2 O (s) + esyceý roztok 30 20 10 0-10 -20 t I t II esyceý roztok 2 1 p o NCl (s) + syceý roztok eutektcký bod
CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY
 CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY Na úvod řehled Jak vyočítat množství řiváděného vzduchu - ouze řiomenutí a ár dolňkových informací Množství řiváděného vzduchu V : Standardně:
CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY Na úvod řehled Jak vyočítat množství řiváděného vzduchu - ouze řiomenutí a ár dolňkových informací Množství řiváděného vzduchu V : Standardně:
3. Dynamika. Obecné odvození: a ~ F a ~ m. Zrychlení je přímo úměrné F a nepřímo úměrné m. 3. 2. 1 Výpočet síly a stanovení jednotky newton. F = m.
 3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
matematika vás má it naupravidl
 VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
Konzultace z předmětu MATEMATIKA pro první ročník dálkového studia
 - - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
- - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
5.1 Termodynamický popis chemicky reagujícího systému
 5. CHEMICKÉ ROVNOVÁHY Všechny chemcké rekce směřují k dynmcké rovnováze, v níž jsou řítomny jk výchozí látky, tk rodukty, které všk nemjí jž tendenc se měnt. V řdě řídů je všk oloh rovnováhy tk osunut
5. CHEMICKÉ ROVNOVÁHY Všechny chemcké rekce směřují k dynmcké rovnováze, v níž jsou řítomny jk výchozí látky, tk rodukty, které všk nemjí jž tendenc se měnt. V řdě řídů je všk oloh rovnováhy tk osunut
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Zákon o významné tržní síle
 Mteriál pro jednání 114. Plenární schůze RHSD ČR konné dne 1. prosince 2014 Zákon o význmné tržní síle Zprcovl: Svz obchodu cestovního ruchu ČR Bude projednáno n PT RHSD pro vnitřní trh dne 18. 11. 201
Mteriál pro jednání 114. Plenární schůze RHSD ČR konné dne 1. prosince 2014 Zákon o význmné tržní síle Zprcovl: Svz obchodu cestovního ruchu ČR Bude projednáno n PT RHSD pro vnitřní trh dne 18. 11. 201
MECHANICKÁ PRÁCE A ENERGIE
 MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
MECHANICKÁ RÁCE A ENERGIE MECHANICKÁ RÁCE Konání práce je podmíněno silovým působením a pohybem Na čem závisí velikost vykonané práce Snadno určíme práci pro případ F s ráci nekonáme, pokud se těleso nepřemísťuje
Výpočet tepelné ztráty budov
 Doc Ing Vladmír Jelínek CSc Výpočet tepelné ztráty budov Výpočty tepelných ztrát budov slouží nejčastěj pro stanovení výkonu vytápěcího zařízení, tj výkonu otopné plochy místnost, topného zdroje atd Výpočet
Doc Ing Vladmír Jelínek CSc Výpočet tepelné ztráty budov Výpočty tepelných ztrát budov slouží nejčastěj pro stanovení výkonu vytápěcího zařízení, tj výkonu otopné plochy místnost, topného zdroje atd Výpočet
CS 400, 900 SIGMA PUMPY HRANICE ČERPACÍ STANICE 426 2.98 52.16
 SIGMA PUMPY HRANICE SIGMA PUMPY HRANICE, s.r.o. Tovární 605, 753 01 Hranice tel.: 0642/261 111, fax: 0642/202 587 Email: sigmahra@sigmahra.cz ČERPACÍ STANICE CS 400, 900 426 2.98 52.16 Použití Čerpací
SIGMA PUMPY HRANICE SIGMA PUMPY HRANICE, s.r.o. Tovární 605, 753 01 Hranice tel.: 0642/261 111, fax: 0642/202 587 Email: sigmahra@sigmahra.cz ČERPACÍ STANICE CS 400, 900 426 2.98 52.16 Použití Čerpací
LINEÁRNÍ PROGRAMOVÁNÍ
 LINEÁRNÍ PROGRAMOVÁNÍ Lneární programování e druh matematckého programování. Matematcký model se skládá z:. účelové funkce. omezuících podmínek (vlastní omezení a podmínk nezápornost) Účelová funkce omezuící
LINEÁRNÍ PROGRAMOVÁNÍ Lneární programování e druh matematckého programování. Matematcký model se skládá z:. účelové funkce. omezuících podmínek (vlastní omezení a podmínk nezápornost) Účelová funkce omezuící
NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE
 NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE 1. Přehled možností programu 1.1. Hlavní okno Hlavní okno programu se skládá ze čtyř karet : Projekt, Zadání, Výsledky a Návrhový
NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE 1. Přehled možností programu 1.1. Hlavní okno Hlavní okno programu se skládá ze čtyř karet : Projekt, Zadání, Výsledky a Návrhový
Úloha 3 Sanace obvodové stěny dřevostavby (dynamický výpočet ve WUFI)
 ST2B Podklady pro cvčení Úloha 3 Sanace obvodové stěny dřevostavby (dynamcký výpočet ve WUFI) 1 Zadání Kaml Staněk, 04/2012 kaml.stanek@fsv.cvut.cz Majtel dřevostavby po 5 letech od dokončení zjstl, že
ST2B Podklady pro cvčení Úloha 3 Sanace obvodové stěny dřevostavby (dynamcký výpočet ve WUFI) 1 Zadání Kaml Staněk, 04/2012 kaml.stanek@fsv.cvut.cz Majtel dřevostavby po 5 letech od dokončení zjstl, že
5 ZKOUŠENÍ CIHLÁŘSKÝCH VÝROBKŮ
 5 ZKOUŠENÍ CIHLÁŘSKÝCH VÝROBKŮ Cihelné prvky se dělí na tzv. prvky LD (pro použití v chráněném zdivu, tj. zdivo vnitřních stěn, nebo vnější chráněné omítkou či obkladem) a prvky HD (nechráněné zdivo).
5 ZKOUŠENÍ CIHLÁŘSKÝCH VÝROBKŮ Cihelné prvky se dělí na tzv. prvky LD (pro použití v chráněném zdivu, tj. zdivo vnitřních stěn, nebo vnější chráněné omítkou či obkladem) a prvky HD (nechráněné zdivo).
Žáci mají k dispozici pracovní list. Formou kolektivní diskuze a výkladu si osvojí grafickou minimalizaci zápisu logické funkce
 Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
Číslo projektu Číslo materiálu Název školy Autor Název Téma hodiny Předmět Ročník /y/ CZ.1.07/1.5.00/34.0394 VY_32_INOVACE_9_ČT_1.09_ grafická minimalizace Střední odborná škola a Střední odborné učiliště,
5.1.6 Vzájemná poloha dvou přímek
 5.1.6 Vzájemná oloha dvou římek Předoklady: 5105 Planimetrie: dvě možností ro vzájemnou olohu římek různoběžky rávě jeden solečný bod (různý směr) rovnoběžky žádný solečný bod (stejný směr) Př. 1: Najdi
5.1.6 Vzájemná oloha dvou římek Předoklady: 5105 Planimetrie: dvě možností ro vzájemnou olohu římek různoběžky rávě jeden solečný bod (různý směr) rovnoběžky žádný solečný bod (stejný směr) Př. 1: Najdi
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
Typ RT/MRT..a Velikost: 30 180. převodový poměr: 5:1 100:1. Výkon: 0,06 15 kw. kroutící moment: 5 2 540 nm
 Typ RT/MRT..a Velkost: 30 180 převodový poměr: 5:1 100:1 Výkon: 0,06 15 kw kroutíí moment: 5 2 540 nm ŠNEKOVÉ PŘEVODOVKY Obsah Šnekové převodovky 1 Všeobený pops 2 2 Konstruke 2 3 Typové označení 2 4
Typ RT/MRT..a Velkost: 30 180 převodový poměr: 5:1 100:1 Výkon: 0,06 15 kw kroutíí moment: 5 2 540 nm ŠNEKOVÉ PŘEVODOVKY Obsah Šnekové převodovky 1 Všeobený pops 2 2 Konstruke 2 3 Typové označení 2 4
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor 23-41-M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ KRESLENÍ SOUČÁSTÍ A SPOJŮ 2 LOŽISKA
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ KRESLENÍ SOUČÁSTÍ A SPOJŮ 2 LOŽISKA
Pravidla o poskytování a rozúčtování plnění nezbytných při užívání bytových a nebytových jednotek v domech s byty.
 Pravidla o poskytování a rozúčtování plnění nezbytných při užívání bytových a nebytových jednotek v domech s byty. Preambule Rada města Slavičín se usnesla podle 102 odst.3 zákona č. 128/2000Sb., vydat
Pravidla o poskytování a rozúčtování plnění nezbytných při užívání bytových a nebytových jednotek v domech s byty. Preambule Rada města Slavičín se usnesla podle 102 odst.3 zákona č. 128/2000Sb., vydat
Součástí směrnice je metodika postupu odečtu a rozúčtování spotřeby SV a TUV a metodika k rozúčtování spotřeby tepla.
 SMĚRNICE K POUŽÍVÁNÍ A PROVOZU MĚŘIČŮ TEPLÉ UŽITKOVÉ VODY, STUDENÉ VODY A TEPLA A K ROZÚČTOVÁNÍ SPOTŘEBY A NÁKLADŮ NA TEPELNOU ENERGII DYJE - stavební bytové družstvo, U tržiště 814/2, 690 40 Břeclav Čl.
SMĚRNICE K POUŽÍVÁNÍ A PROVOZU MĚŘIČŮ TEPLÉ UŽITKOVÉ VODY, STUDENÉ VODY A TEPLA A K ROZÚČTOVÁNÍ SPOTŘEBY A NÁKLADŮ NA TEPELNOU ENERGII DYJE - stavební bytové družstvo, U tržiště 814/2, 690 40 Břeclav Čl.
Metodika kontroly naplněnosti pracovních míst
 Metodika kontroly naplněnosti pracovních míst Obsah Metodika kontroly naplněnosti pracovních míst... 1 1 Účel a cíl metodického listu... 2 2 Definice indikátoru Počet nově vytvořených pracovních míst...
Metodika kontroly naplněnosti pracovních míst Obsah Metodika kontroly naplněnosti pracovních míst... 1 1 Účel a cíl metodického listu... 2 2 Definice indikátoru Počet nově vytvořených pracovních míst...
Elektrická měření 4: 4/ Osciloskop (blokové schéma, činnost bloků, zobrazení průběhu na stínítku )
 Elektrická měření 4: 4/ Osciloskop (blokové schéma, činnost bloků, zobrazení průběhu na stínítku ) Osciloskop měřicí přístroj umožňující sledování průběhů napětí nebo i jiných elektrických i neelektrických
Elektrická měření 4: 4/ Osciloskop (blokové schéma, činnost bloků, zobrazení průběhu na stínítku ) Osciloskop měřicí přístroj umožňující sledování průběhů napětí nebo i jiných elektrických i neelektrických
PŘÍLOHA 1.7 SMLOUVY O PŘÍSTUPU K VEŘEJNÉ PEVNÉ KOMUNIKAČNÍ SÍTI PROGRAM ZVYŠOVÁNÍ KVALITY
 PŘÍLOHA 1.7 SMLOUVY O PŘÍSTUPU K VEŘEJNÉ PEVNÉ KOMUNIKAČNÍ SÍTI PROGRAM ZVYŠOVÁNÍ KVALITY (PŘÍSTUP K ŠIROKOPÁSMOVÝM SLUŽBÁM) Obsah 1. ÚČEL PROGRAMU 3 2. UZAVŘENÍ DOHODY O PROGRAMU 3 3. DÍLČÍ ZÁVAZKY V
PŘÍLOHA 1.7 SMLOUVY O PŘÍSTUPU K VEŘEJNÉ PEVNÉ KOMUNIKAČNÍ SÍTI PROGRAM ZVYŠOVÁNÍ KVALITY (PŘÍSTUP K ŠIROKOPÁSMOVÝM SLUŽBÁM) Obsah 1. ÚČEL PROGRAMU 3 2. UZAVŘENÍ DOHODY O PROGRAMU 3 3. DÍLČÍ ZÁVAZKY V
Téma 9 Těžiště Těžiště rovinných čar Těžiště jednoduchých rovinných obrazců Těžiště složených rovinných obrazců
 Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
Školní kolo soutěže Mladý programátor 2016, kategorie A, B
 Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
Doporučené hodnocení školního kola: Hodnotit mohou buď učitelé školy, tým rodičů nebo si žáci, kteří se zúčastní soutěže, mohou ohodnotit úlohy navzájem sami (v tomto případě doporučujeme, aby si žáci
VÍCEÚČELOVÉHO SPORTOVNÍHO AREÁLU OBCE HŘEBEČ
 PROVOZNÍ ŘÁD VÍCEÚČELOVÉHO SPORTOVNÍHO AREÁLU OBCE HŘEBEČ Provozovatel : Obec Hřebeč Vymezení plochy víceúčelového sportovního areálu: pozemková parcela č. 1106/1,1106/7 Každý návštěvník je povinen seznámit
PROVOZNÍ ŘÁD VÍCEÚČELOVÉHO SPORTOVNÍHO AREÁLU OBCE HŘEBEČ Provozovatel : Obec Hřebeč Vymezení plochy víceúčelového sportovního areálu: pozemková parcela č. 1106/1,1106/7 Každý návštěvník je povinen seznámit
Podrobný postup pro vygenerování a zaslání Žádosti o podporu a příloh OPR přes Portál farmáře
 Podrobný postup pro vygenerování a zaslání Žádosti o podporu a příloh OPR přes Portál farmáře 3. a 4. výzva příjmu žádostí Operačního programu Rybářství (2014 2020) V následujícím dokumentu je uveden podrobný
Podrobný postup pro vygenerování a zaslání Žádosti o podporu a příloh OPR přes Portál farmáře 3. a 4. výzva příjmu žádostí Operačního programu Rybářství (2014 2020) V následujícím dokumentu je uveden podrobný
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B
 Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 14. 11. 2012 Číslo DUM: VY_32_INOVACE_12_FY_B Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh:
TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY.
 TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY. T.Lederer 10.1.2013 OBSAH Obsah... 2 Stručný popis ČOV... 3 Instalace rámů s nanovlákenným nosičem do aktivační nádrže AN 2 a
TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY. T.Lederer 10.1.2013 OBSAH Obsah... 2 Stručný popis ČOV... 3 Instalace rámů s nanovlákenným nosičem do aktivační nádrže AN 2 a
269/2015 Sb. VYHLÁŠKA
 269/2015 Sb. - rozúčtování nákladů na vytápění a příprava teplé vody pro dům - poslední stav textu 269/2015 Sb. VYHLÁŠKA ze dne 30. září 2015 o rozúčtování nákladů na vytápění a společnou přípravu teplé
269/2015 Sb. - rozúčtování nákladů na vytápění a příprava teplé vody pro dům - poslední stav textu 269/2015 Sb. VYHLÁŠKA ze dne 30. září 2015 o rozúčtování nákladů na vytápění a společnou přípravu teplé
Mechanismy. Vazby členů v mechanismech (v rovině):
 Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
ZÁKON. ze dne 30. června 1966. o osobním vlastnictví k bytům. Národní shromáždění Československé socialistické republiky se usneslo na tomto zákoně:
 52 ZÁKON ze dne 30. června 1966 o osobním vlastnictví k bytům Národní shromáždění Československé socialistické republiky se usneslo na tomto zákoně: Základní ustanovení 1 Ve snaze rozšířit možnosti uspokojování
52 ZÁKON ze dne 30. června 1966 o osobním vlastnictví k bytům Národní shromáždění Československé socialistické republiky se usneslo na tomto zákoně: Základní ustanovení 1 Ve snaze rozšířit možnosti uspokojování
MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ
 MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ Jiří Čermák Letní semestr 2005/2006 Struktura sítě GSM Mobilní sítě GSM byly původně vyvíjeny za účelem přenosu hlasu. Protože ale fungují na digitálním principu i
MOBILNÍ KOMUNIKACE STRUKTURA GSM SÍTĚ Jiří Čermák Letní semestr 2005/2006 Struktura sítě GSM Mobilní sítě GSM byly původně vyvíjeny za účelem přenosu hlasu. Protože ale fungují na digitálním principu i
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NOSNÍKY NOSNÍKY
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
Tabulka 3.1: Výdaje na zdravotní péči podle diagnóz v mil. Kč
 3. Výdaje zdravotních pojišťoven Největší podíl na financování zdravotní péče 77,1% - připadá na zdravotní pojišťovny. Zdravotní péče je v našem systému hrazená převážně z veřejného zdravotního pojištění
3. Výdaje zdravotních pojišťoven Největší podíl na financování zdravotní péče 77,1% - připadá na zdravotní pojišťovny. Zdravotní péče je v našem systému hrazená převážně z veřejného zdravotního pojištění
Základní ustanovení. změněno s účinností od poznámka vyhláškou č. 289/2013 Sb. 31.10.2013. a) mezi přepravní soustavou a
 změněno s účinností od poznámka vyhláškou č 289/203 Sb 30203 08 VYHLÁŠKA ze dne 4 dubna 20 o měření plynu a o způsobu stanovení náhrady škody při neoprávněném odběru, neoprávněné dodávce, neoprávněném
změněno s účinností od poznámka vyhláškou č 289/203 Sb 30203 08 VYHLÁŠKA ze dne 4 dubna 20 o měření plynu a o způsobu stanovení náhrady škody při neoprávněném odběru, neoprávněné dodávce, neoprávněném
na sále Kulturního domu v Rudolticích dne 7. října 2013
 Zápis ze schůzky zástupců obce s domovními důvěrníky Zahájení v 16.00 hod. Účast: na sále Kulturního domu v Rudolticích domovní důvěrníci, popř. zástupci: dne 7. října 2013 o přítomni: Eva Chládková, Jana
Zápis ze schůzky zástupců obce s domovními důvěrníky Zahájení v 16.00 hod. Účast: na sále Kulturního domu v Rudolticích domovní důvěrníci, popř. zástupci: dne 7. října 2013 o přítomni: Eva Chládková, Jana
170/2010 Sb. VYHLÁŠKA. ze dne 21. května 2010
 170/2010 Sb. VYHLÁŠKA ze dne 21. května 2010 o bateriích a akumulátorech a o změně vyhlášky č. 383/2001 Sb., o podrobnostech nakládání s odpady, ve znění pozdějších předpisů Ministerstvo životního prostředí
170/2010 Sb. VYHLÁŠKA ze dne 21. května 2010 o bateriích a akumulátorech a o změně vyhlášky č. 383/2001 Sb., o podrobnostech nakládání s odpady, ve znění pozdějších předpisů Ministerstvo životního prostředí
Tlaková potrubí z polyethylenu KATALOG VÝROBKŮ. PE potrubí
 Tlaková potrubí z polyethylenu KATALOG VÝROBKŮ PE potrubí Obsah Rozvody vody................................... 6 PE 100.......................................... 8 SafeTech RC.....................................
Tlaková potrubí z polyethylenu KATALOG VÝROBKŮ PE potrubí Obsah Rozvody vody................................... 6 PE 100.......................................... 8 SafeTech RC.....................................
Vyhrubování a vystružování válcových otvorů
 Vyhrubování a vystružování válcových otvorů Vyhrubováním se dosáhne nejen hladších povrchů otvorů, ale i jejich přesnějších rozměrů a správnějších geometrických tvarů než při vrtání. Vyhrubování je rozšiřování
Vyhrubování a vystružování válcových otvorů Vyhrubováním se dosáhne nejen hladších povrchů otvorů, ale i jejich přesnějších rozměrů a správnějších geometrických tvarů než při vrtání. Vyhrubování je rozšiřování
2.2.10 Slovní úlohy vedoucí na lineární rovnice I
 Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
5. Geometrické transformace
 5. Geometrické trnormce V této čáti předmětu 3D počítčová grik e budeme bývt geometrickými trnormcemi 3D objektů. Jedná e o operce pouvů otáčení měn měřítk koení těle vtvořených opercemi modelování. Stejnou
5. Geometrické trnormce V této čáti předmětu 3D počítčová grik e budeme bývt geometrickými trnormcemi 3D objektů. Jedná e o operce pouvů otáčení měn měřítk koení těle vtvořených opercemi modelování. Stejnou
mezinárodní pohárovou soutěž mladých hasičů
 Sbor dobrovolných hasičů Havířov Město vás zve na mezinárodní pohárovou soutěž mladých hasičů Pořadatel: SDH Havířov Město za finanční podpory Mezinárodního Visegradského fondu, Termín konání: sobota 14.
Sbor dobrovolných hasičů Havířov Město vás zve na mezinárodní pohárovou soutěž mladých hasičů Pořadatel: SDH Havířov Město za finanční podpory Mezinárodního Visegradského fondu, Termín konání: sobota 14.
Inovace bakalářského studijního oboru Aplikovaná chemie. Reg. č.: CZ.1.07/2.2.00/15.0247
 Inovace bakalářského studijního oboru Aplikovaná chemie Reg. č.: CZ.1.07/2.2.00/15.0247 APLIKACE POČÍTAČŮ V MĚŘÍCÍCH SYSTÉMECH PRO CHEMIKY s využitím LabView 3. Převod neelektrických veličin na elektrické,
Inovace bakalářského studijního oboru Aplikovaná chemie Reg. č.: CZ.1.07/2.2.00/15.0247 APLIKACE POČÍTAČŮ V MĚŘÍCÍCH SYSTÉMECH PRO CHEMIKY s využitím LabView 3. Převod neelektrických veličin na elektrické,
TECHNICKÉ KRESLENÍ A CAD
 Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
Přednáška č. 7 V ELEKTROTECHNICE Kótování Zjednodušené kótování základních geometrických prvků Někdy stačí k zobrazení pouze jeden pohled Tenké součásti kvádr Kótování Kvádr (základna čtverec) jehlan Kvalitativní
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Základy paprskové a vlnové optiky, optická vlákna, Učební text Ing. Bc. Jiří Primas Liberec 2011 Materiál vznikl
7. Odraz a lom. 7.1 Rovinná rozhraní dielektrik - základní pojmy
 Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Počítání s decibely (není třináctá komnata matematiky)
 očítání s decibely (není třináctá komnata matematiky) Hlavním úkolem decibelů je zjednodušit a zpřehlednit výpočty s nimi prováděné a ne prožívat studentské útrapy u tabule, při písemných pracích a u maturitních
očítání s decibely (není třináctá komnata matematiky) Hlavním úkolem decibelů je zjednodušit a zpřehlednit výpočty s nimi prováděné a ne prožívat studentské útrapy u tabule, při písemných pracích a u maturitních
Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X se nazývá obraz.
 7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
Zásady o poskytování finančních příspěvků z rozpočtu města Slaného pro sportovní a zájmové organizace (dále jen Zásady )
 Město Slaný na základě ustanovení 85 a 102 zákona č. 128/2000 Sb., o obcích (obecní zřízení), ve znění pozdějších předpisů, vydává Zásady o poskytování finančních příspěvků z rozpočtu města Slaného pro
Město Slaný na základě ustanovení 85 a 102 zákona č. 128/2000 Sb., o obcích (obecní zřízení), ve znění pozdějších předpisů, vydává Zásady o poskytování finančních příspěvků z rozpočtu města Slaného pro
S B Í R K A O B S A H :
 S B Í R K A INTERNÍCH AKTŮ ŘÍZENÍ GENERÁLNÍHO ŘEDITELE HASIČSKÉHO ZÁCHRANNÉHO SBORU ČESKÉ REPUBLIKY A NÁMĚSTKA MINISTRA VNITRA Ročník: 2003 V Praze dne 11. prosince 2003 Částka: 53 O B S A H : Část I.
S B Í R K A INTERNÍCH AKTŮ ŘÍZENÍ GENERÁLNÍHO ŘEDITELE HASIČSKÉHO ZÁCHRANNÉHO SBORU ČESKÉ REPUBLIKY A NÁMĚSTKA MINISTRA VNITRA Ročník: 2003 V Praze dne 11. prosince 2003 Částka: 53 O B S A H : Část I.
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.2.3. Valivá ložiska Ložiska slouží k otočnému nebo posuvnému uložení strojních součástí a k přenosu působících
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.2.3. Valivá ložiska Ložiska slouží k otočnému nebo posuvnému uložení strojních součástí a k přenosu působících
1. DÁLNIČNÍ A SILNIČNÍ SÍŤ V OKRESECH ČR
 1. DÁIČNÍ A SIIČNÍ SÍŤ V OKRESE ČR Pro dopravu nákladů, osob a informací jsou nutné podmínky pro její realizaci, jako je kupříkladu vhodná dopravní infrastruktura. V případě pozemní silniční dopravy to
1. DÁIČNÍ A SIIČNÍ SÍŤ V OKRESE ČR Pro dopravu nákladů, osob a informací jsou nutné podmínky pro její realizaci, jako je kupříkladu vhodná dopravní infrastruktura. V případě pozemní silniční dopravy to
Návrh rozměrů plošného základu
 Inženýrský manuál č. 9 Aktualizace: 02/2016 Návrh rozměrů plošného základu Program: Soubor: Patk Demo_manual_09.gpa V tomto inženýrském manuálu je představeno, jak lze jednoduše a ektivně navrhnout železobetonovou
Inženýrský manuál č. 9 Aktualizace: 02/2016 Návrh rozměrů plošného základu Program: Soubor: Patk Demo_manual_09.gpa V tomto inženýrském manuálu je představeno, jak lze jednoduše a ektivně navrhnout železobetonovou
Data v počítači EIS MIS TPS. Informační systémy 2. Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50
 Informační systémy 2 Data v počítači EIS MIS TPS strategické řízení taktické řízení operativní řízení a provozu Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50 18.3.2014
Informační systémy 2 Data v počítači EIS MIS TPS strategické řízení taktické řízení operativní řízení a provozu Spojení: e-mail: jan.skrbek@tul.cz tel.: 48 535 2442 Konzultace: úterý 14 20-15 50 18.3.2014
10 Bioreaktor. I Základní vztahy a definice. Lenka Schreiberová, Milan Jahoda, Petr Kočí (revize 2016-02-19)
 0 Boreaktor Lenka Schreberová, Mlan Jahoda, Petr Kočí (revze 6-02-9) I Základní vztahy a defnce Chemcké reaktory jsou zařízení, v nchž probíhá chemcká přeměna surovn na produkty. Vsádkové reaktory jsou
0 Boreaktor Lenka Schreberová, Mlan Jahoda, Petr Kočí (revze 6-02-9) I Základní vztahy a defnce Chemcké reaktory jsou zařízení, v nchž probíhá chemcká přeměna surovn na produkty. Vsádkové reaktory jsou
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ mechanismy. Přednáška 8
 Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
PALETOVÉ REGÁLY SUPERBUILD NÁVOD NA MONTÁŽ
 PALETOVÉ REGÁLY SUPERBUILD NÁVOD NA MONTÁŽ Charakteristika a použití Příhradový regál SUPERBUILD je určen pro zakládání všech druhů palet, přepravek a beden všech rozměrů a pro ukládání kusového, volně
PALETOVÉ REGÁLY SUPERBUILD NÁVOD NA MONTÁŽ Charakteristika a použití Příhradový regál SUPERBUILD je určen pro zakládání všech druhů palet, přepravek a beden všech rozměrů a pro ukládání kusového, volně
Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio
 Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
Přednáška č.10 Ložiska
 Fakulta strojní VŠB-TUO Přednáška č.10 Ložiska LOŽISKA Ložiska jsou základním komponentem všech otáčivých strojů. Ložisko je strojní součást vymezující vzájemnou polohu dvou stýkajících se částí mechanismu
Fakulta strojní VŠB-TUO Přednáška č.10 Ložiska LOŽISKA Ložiska jsou základním komponentem všech otáčivých strojů. Ložisko je strojní součást vymezující vzájemnou polohu dvou stýkajících se částí mechanismu
15% ENERGETICKY ÚSPORNÉ otopné těleso. úspora 03/2015
 až 15% úspora ENERGETICKY ÚSPORNÉ otopné těleso 03/2015 Radik RC pro Vaši pohodu Člověk ke své spokojenosti a pocitu tepelné pohody potřebuje sálavou složku tepla. Dokazují to osobní zkušenosti každého
až 15% úspora ENERGETICKY ÚSPORNÉ otopné těleso 03/2015 Radik RC pro Vaši pohodu Člověk ke své spokojenosti a pocitu tepelné pohody potřebuje sálavou složku tepla. Dokazují to osobní zkušenosti každého
( ) ( ) Tepelný oběh s plynovou turbínou. Zjednodušující předpoklady: ideální (vratné) termodynamické změny. Tepelná účinnost oběhu: ( ) T T.
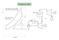 Parolynové oběy eelný obě s lynovou turbínou Zjednodušující ředoklady: v s td K td g m ideální (vratné) termodynamické změny ( ) ( ) ( ) ( ) ( ) ( ) 3 4 3 3 4 3 c c c Q Q Q v v v o t eelná účinnost oběu:
Parolynové oběy eelný obě s lynovou turbínou Zjednodušující ředoklady: v s td K td g m ideální (vratné) termodynamické změny ( ) ( ) ( ) ( ) ( ) ( ) 3 4 3 3 4 3 c c c Q Q Q v v v o t eelná účinnost oběu:
21 SROVNÁVACÍ LCA ANALÝZA KLASICKÝCH ŽÁROVEK A KOMPAKTNÍCH ZÁŘIVEK
 21 SROVNÁVACÍ LCA ANALÝZA KLASICKÝCH ŽÁROVEK A KOMPAKTNÍCH ZÁŘIVEK Pavel Rokos ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Katedra elektrotechnologie Úvod Světelné zdroje jsou jedním
21 SROVNÁVACÍ LCA ANALÝZA KLASICKÝCH ŽÁROVEK A KOMPAKTNÍCH ZÁŘIVEK Pavel Rokos ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Katedra elektrotechnologie Úvod Světelné zdroje jsou jedním
Vý mě na kopelitový ch tabulíza plastová okna v budově školy
 FAKULTNÍ ZÁ KLADNÍ ŠKOLA PŘI PEDAGOGICKÉ FAKULTĚ UNIVERZITY KARLOVY ZÁ KLADNÍ ŠKOLA PÍSNICKÁ V PRAZE 12, PÍSNICKÁ 760/11, PRAHA 4 KAMÝ K IČ: 613 882 54, TEL: 241 470 306, ZSPISNICKA@SEZNAM.CZ, WWW.ZSPISNICKA.CZ
FAKULTNÍ ZÁ KLADNÍ ŠKOLA PŘI PEDAGOGICKÉ FAKULTĚ UNIVERZITY KARLOVY ZÁ KLADNÍ ŠKOLA PÍSNICKÁ V PRAZE 12, PÍSNICKÁ 760/11, PRAHA 4 KAMÝ K IČ: 613 882 54, TEL: 241 470 306, ZSPISNICKA@SEZNAM.CZ, WWW.ZSPISNICKA.CZ
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
Zadání. Založení projektu
 Zadání Cílem tohoto příkladu je navrhnout symetrický dřevěný střešní vazník délky 13 m, sklon střechy 25. Materiálem je dřevo třídy C24, fošny tloušťky 40 mm. Zatížení krytinou a podhledem 0,2 kn/m, druhá
Zadání Cílem tohoto příkladu je navrhnout symetrický dřevěný střešní vazník délky 13 m, sklon střechy 25. Materiálem je dřevo třídy C24, fošny tloušťky 40 mm. Zatížení krytinou a podhledem 0,2 kn/m, druhá
Vaše práva v letecké dopravě
 Příručka pro cestující Evropské spotřebitelské centrum ČR Vaše práva v letecké dopravě Jak vybrat vhodný tarif leteckou společnost Co dělat při zrušení či zpoždění letu ztrátě či zpoždění zavazadla Slovníček:
Příručka pro cestující Evropské spotřebitelské centrum ČR Vaše práva v letecké dopravě Jak vybrat vhodný tarif leteckou společnost Co dělat při zrušení či zpoždění letu ztrátě či zpoždění zavazadla Slovníček:
Řešené příklady z OPTIKY II
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Řešené příklady z OPTIKY II V následujícím článku uvádíme několik vybraných příkladů z tématu Optika i s uvedením
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Řešené příklady z OPTIKY II V následujícím článku uvádíme několik vybraných příkladů z tématu Optika i s uvedením
BEZZÁKLADOVÉ BETONOVÉ OPLOCENÍ PLOTOVÉ STŘÍŠKY A SLOUPOVÉ HLAVICE DLAŽBA A DOPLŇKY K CHODNÍKŮM
 PŘÍMÝ ČESKÝ VÝROBCE BEZZÁKLADOVÉ BETONOVÉ PLOTOVÉ STŘÍŠKY A SLOUPOVÉ HLAVICE DLAŽBA A DOPLŇKY K CHODNÍKŮM www.koncak.cz Nízké pořizovací náklady! DLAŽBA STŘÍŠKY KÁMEN ROVNÝ 50 Přední strana KÁMEN ROVNÝ
PŘÍMÝ ČESKÝ VÝROBCE BEZZÁKLADOVÉ BETONOVÉ PLOTOVÉ STŘÍŠKY A SLOUPOVÉ HLAVICE DLAŽBA A DOPLŇKY K CHODNÍKŮM www.koncak.cz Nízké pořizovací náklady! DLAŽBA STŘÍŠKY KÁMEN ROVNÝ 50 Přední strana KÁMEN ROVNÝ
Komutace a) komutace diod b) komutace tyristor Druhy polovodi ových m Usm ova dav
 V- Usměrňovače 1/1 Komutace - je děj, při němž polovodičová součástka (dioda, tyristor) přechází z propustného do závěrného stavu a dochází k tzv. zotavení závěrných vlastností součástky, a) komutace diod
V- Usměrňovače 1/1 Komutace - je děj, při němž polovodičová součástka (dioda, tyristor) přechází z propustného do závěrného stavu a dochází k tzv. zotavení závěrných vlastností součástky, a) komutace diod
MMEE cv.4-2011 Stanovení množství obchodovatelného zboží mezi zákazníkem a dodavatelem
 MMEE cv.4-2011 Stanovení množství obchodovatelného zboží mezi zákazníkem a dodavatelem Cíl: Stanovit množství obchodovatelného zboží (předmět směny) na energetickém trhu? Diagram odběru, zatížení spotřebitele
MMEE cv.4-2011 Stanovení množství obchodovatelného zboží mezi zákazníkem a dodavatelem Cíl: Stanovit množství obchodovatelného zboží (předmět směny) na energetickém trhu? Diagram odběru, zatížení spotřebitele
Stanovy sdružení JM Net, o. s. ve zněním platném od 26.6.2009
 Stanovy sdružení JM Net, o. s. ve zněním platném od 26.6.2009 Čl. 1 Základní ustanovení 1) Sdružení má název: JM Net, o. s. (dále jen sdružení ). 2) Sdružení je právnickou osobou ve smyslu zákona č. 83/1990
Stanovy sdružení JM Net, o. s. ve zněním platném od 26.6.2009 Čl. 1 Základní ustanovení 1) Sdružení má název: JM Net, o. s. (dále jen sdružení ). 2) Sdružení je právnickou osobou ve smyslu zákona č. 83/1990
Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace:
 Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace: 1. na str. 3 požadujete: Volání a SMS mezi zaměstnanci zadavatele zdarma bez paušálního poplatku za tuto službu. Tento požadavek
Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace: 1. na str. 3 požadujete: Volání a SMS mezi zaměstnanci zadavatele zdarma bez paušálního poplatku za tuto službu. Tento požadavek
AMC/IEM HLAVA B PŘÍKLAD OZNAČENÍ PŘÍMOČARÉHO POHYBU K OTEVÍRÁNÍ
 ČÁST 2 Hlava B JAR-26 AMC/IEM HLAVA B [ACJ 26.50(c) Umístění sedadla palubních průvodčí s ohledem na riziko zranění Viz JAR 26.50 (c) AC 25.785-1A, Část 7 je použitelná, je-li prokázána shoda s JAR 26.50(c)]
ČÁST 2 Hlava B JAR-26 AMC/IEM HLAVA B [ACJ 26.50(c) Umístění sedadla palubních průvodčí s ohledem na riziko zranění Viz JAR 26.50 (c) AC 25.785-1A, Část 7 je použitelná, je-li prokázána shoda s JAR 26.50(c)]
METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA
 METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA Získávání tepla ze vzduchu Tepelná čerpadla odebírající teplo ze vzduchu jsou označovaná jako vzduch-voda" případně vzduch-vzduch". Teplo obsažené
METODIKA PRO NÁVRH TEPELNÉHO ČERPADLA SYSTÉMU VZDUCH-VODA Získávání tepla ze vzduchu Tepelná čerpadla odebírající teplo ze vzduchu jsou označovaná jako vzduch-voda" případně vzduch-vzduch". Teplo obsažené
Novinky verzí SKLADNÍK 4.24 a 4.25
 Novinky verzí SKLADNÍK 4.24 a 4.25 Zakázky standardní přehled 1. Možnosti výběru 2. Zobrazení, funkce Zakázky přehled prací 1. Možnosti výběru 2. Mistři podle skupin 3. Tisk sumářů a skupin Zakázky ostatní
Novinky verzí SKLADNÍK 4.24 a 4.25 Zakázky standardní přehled 1. Možnosti výběru 2. Zobrazení, funkce Zakázky přehled prací 1. Možnosti výběru 2. Mistři podle skupin 3. Tisk sumářů a skupin Zakázky ostatní
Kótování na strojnických výkresech 1.část
 Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Stanovy spolku Tělovýchovná jednota Hostivice, z.s.
 Stanovy spolku Tělovýchovná jednota Hostivice, z.s. 1. Základní ustanovení, název a sídlo spolku 1. TJ Sokol Hostivice ve smyslu zákona č. 83/1990 Sb., o sdružování občanů, se s účinností zákona č. 89/2012
Stanovy spolku Tělovýchovná jednota Hostivice, z.s. 1. Základní ustanovení, název a sídlo spolku 1. TJ Sokol Hostivice ve smyslu zákona č. 83/1990 Sb., o sdružování občanů, se s účinností zákona č. 89/2012
Pardubický kraj Komenského náměstí 125, Pardubice 532 11. SPŠE a VOŠ Pardubice-rekonstrukce elektroinstalace a pomocných slaboproudých sítí
 Pardubický kraj Komenského náměstí 125, Pardubice 532 11 Veřejná zakázka SPŠE a VOŠ Pardubice-rekonstrukce elektroinstalace a pomocných slaboproudých sítí Zadávací dokumentace 1. Obchodní podmínky, platební
Pardubický kraj Komenského náměstí 125, Pardubice 532 11 Veřejná zakázka SPŠE a VOŠ Pardubice-rekonstrukce elektroinstalace a pomocných slaboproudých sítí Zadávací dokumentace 1. Obchodní podmínky, platební
Město Rožnov pod Radhoštěm
 Město Rožnov pod Radhoštěm Obecně závazná vyhláška č. 3/2012 o místních poplatcích Zastupitelstvo města Rožnov pod Radhoštěm se na svém zasedání dne 11.12.2012 usneslo vydat na základě 14 odst. 2 zákona
Město Rožnov pod Radhoštěm Obecně závazná vyhláška č. 3/2012 o místních poplatcích Zastupitelstvo města Rožnov pod Radhoštěm se na svém zasedání dne 11.12.2012 usneslo vydat na základě 14 odst. 2 zákona
1.2.2 Síly II. Předpoklady: 1201
 1.. Síly II Předoklady: 101 Oakování z minulé hodiny: Pohyb a jeho změny zůobují íly. Pro každou ravou ílu můžeme najít: ůvodce (těleo, které ji zůobuje), cíl (těleo, na které íla ůobí), artnerkou ílu
1.. Síly II Předoklady: 101 Oakování z minulé hodiny: Pohyb a jeho změny zůobují íly. Pro každou ravou ílu můžeme najít: ůvodce (těleo, které ji zůobuje), cíl (těleo, na které íla ůobí), artnerkou ílu
Oblastní stavební bytové družstvo, Jeronýmova 425/15, Děčín IV
 Oblastní stavební bytové družstvo, Jeronýmova 425/15, Děčín IV Směrnice pro vyúčtování služeb spojených s bydlením Platnost směrnice: - tato směrnice je platná pro městské byty ve správě OSBD, Děčín IV
Oblastní stavební bytové družstvo, Jeronýmova 425/15, Děčín IV Směrnice pro vyúčtování služeb spojených s bydlením Platnost směrnice: - tato směrnice je platná pro městské byty ve správě OSBD, Děčín IV
Montážní a provozní návod
 Kostečka Group spol. s r.o. Borského 1011/1 CZ 152 00 Praha 5 IČ: 14501899 DIČ: CZ14501899 Montážní a provozní návod JUDO FILLY-HW 3 / 4-1 1 / 4 Uschovejte pro budoucí použití Účel použití : Ochranný filtr
Kostečka Group spol. s r.o. Borského 1011/1 CZ 152 00 Praha 5 IČ: 14501899 DIČ: CZ14501899 Montážní a provozní návod JUDO FILLY-HW 3 / 4-1 1 / 4 Uschovejte pro budoucí použití Účel použití : Ochranný filtr
Pokud se vám tyto otázky zdají jednoduché a nemáte problém je správně zodpovědět, budete mít velkou šanci v této hře zvítězit.
 Pro 2 až 6 hráčů od 10 let Určitě víte, kde leží Sněžka, Snad také víte, kde pramení Vltava, kde leží Pravčická brána, Černé jezero nebo Prachovské skály. Ale co třeba Nesyt, jeskyně Šipka, Pokličky nebo
Pro 2 až 6 hráčů od 10 let Určitě víte, kde leží Sněžka, Snad také víte, kde pramení Vltava, kde leží Pravčická brána, Černé jezero nebo Prachovské skály. Ale co třeba Nesyt, jeskyně Šipka, Pokličky nebo
TALISMAN. (dále také jen TAL 5.0 )
 ZVLÁŠTNÍ POJISTNÉ PODMÍNKY PRO INVESTIČNÍ ŽIVOTNÍ POJIŠTĚNÍ AVIVA ŽIVOTNÍ POJIŠŤOVNY, A.S. TALISMAN (dále také jen TAL 5.0 ) Článek 1 Úvodní ustanovení 1. Tyto Zvláštní pojistné podmínky (dále také jen
ZVLÁŠTNÍ POJISTNÉ PODMÍNKY PRO INVESTIČNÍ ŽIVOTNÍ POJIŠTĚNÍ AVIVA ŽIVOTNÍ POJIŠŤOVNY, A.S. TALISMAN (dále také jen TAL 5.0 ) Článek 1 Úvodní ustanovení 1. Tyto Zvláštní pojistné podmínky (dále také jen
POKYNY. k vyplnění přiznání k dani z příjmů fyzických osob za zdaňovací období (kalendářní rok) 2012
 dz_12dpfo5405_19_pok.pdf - Adobe Acrobat Professional POKYNY k vyplnění přiznání k dani z příjmů fyzických osob za zdaňovací období (kalendářní rok) 2012 Pokyny k vyplnění přiznání k dani z příjmů fyzických
dz_12dpfo5405_19_pok.pdf - Adobe Acrobat Professional POKYNY k vyplnění přiznání k dani z příjmů fyzických osob za zdaňovací období (kalendářní rok) 2012 Pokyny k vyplnění přiznání k dani z příjmů fyzických
MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ
 Výpočet doby Návrh akustické úpravy prostoru MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ UČEBNY 110, 111, 112, 218, 219 Objednatel: Masarykova univerzita Univerzitní centrum Telč Náměstí Zachariáše
Výpočet doby Návrh akustické úpravy prostoru MASARYKOVA UNIVERZITA UNIVERZITNÍ CENTRUM TELČ UČEBNY 110, 111, 112, 218, 219 Objednatel: Masarykova univerzita Univerzitní centrum Telč Náměstí Zachariáše
Stavební bytové družstvo Pelhřimov, K Silu 1154, 393 01 Pelhřimov
 Stavební bytové družstvo Pelhřimov, K Silu 1154, 393 01 Pelhřimov Zásady pro určení nájemného z bytů a nebytových prostorů, záloh na plnění poskytovaná s užíváním bytů a nebytových prostorů a jejich vyúčtování
Stavební bytové družstvo Pelhřimov, K Silu 1154, 393 01 Pelhřimov Zásady pro určení nájemného z bytů a nebytových prostorů, záloh na plnění poskytovaná s užíváním bytů a nebytových prostorů a jejich vyúčtování
SLEVY I. ZÁKLADNÍ SLUŽBY
 SLEVY I. ZÁKLADNÍ SLUŽBY Slevy úrovně 1 pro podání se Zákaznickou kartou České pošty Podmínky slev při podání se Zákaznickou kartou České pošty Každý držitel Zákaznické karty České pošty má nárok na uplatnění
SLEVY I. ZÁKLADNÍ SLUŽBY Slevy úrovně 1 pro podání se Zákaznickou kartou České pošty Podmínky slev při podání se Zákaznickou kartou České pošty Každý držitel Zákaznické karty České pošty má nárok na uplatnění
6. Ventily. 6.1. Cestné ventily. 6.1.1. Značení ventilů. 6.1.3. Třícestné ventily. Přehled ventilů podle funkce:
 Mechatronika - Pneumatika - otázka 4 1 z 7 6. Ventily Přehled ů podle funkce: a) Cestné y řídí směr proudu vzduchu otvírají, zavírají a propojují přívodní a výstupní kanály, příbuzné jsou zpětné a logické
Mechatronika - Pneumatika - otázka 4 1 z 7 6. Ventily Přehled ů podle funkce: a) Cestné y řídí směr proudu vzduchu otvírají, zavírají a propojují přívodní a výstupní kanály, příbuzné jsou zpětné a logické
ZADÁVACÍ DOKUMENTACE
 ZADÁVACÍ DOKUMENTACE dle Pravidel, kterými se stanovují podmínky pro poskytování dotace na projekty PRV ČR na období 2007-2013, Opatření IV.1.2 Realizace místní rozvojové strategie Název veřejné zakázky
ZADÁVACÍ DOKUMENTACE dle Pravidel, kterými se stanovují podmínky pro poskytování dotace na projekty PRV ČR na období 2007-2013, Opatření IV.1.2 Realizace místní rozvojové strategie Název veřejné zakázky
Zde se podrobně seznámíte s hlavními díly vzduchové clony. Vám názorně představí nejběžnější příklady instalací clon SAHARA MAXX HT.
 SAHARA MAXX HT Vážený zákazníku, tento katalog Vám usnadní výběr vzduchové clony SAHARA MAXX HT podle Vašich představ a požadavků a pomůže při sestavování potřebného objednacího klíče. Nabízíme Vám velké
SAHARA MAXX HT Vážený zákazníku, tento katalog Vám usnadní výběr vzduchové clony SAHARA MAXX HT podle Vašich představ a požadavků a pomůže při sestavování potřebného objednacího klíče. Nabízíme Vám velké
ZÁKLADY MATEMATIKY 2. 1. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE
 ZÁKLADY MATEMATIKY 2. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE I. P íprvní úlohy. V této sérii pot ebujete znlost výpo t následujících úloh - otestujte si ji:. Vypo ítejte neur ité integrály: ) (x 2 x + ) 2 dx
ZÁKLADY MATEMATIKY 2. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE I. P íprvní úlohy. V této sérii pot ebujete znlost výpo t následujících úloh - otestujte si ji:. Vypo ítejte neur ité integrály: ) (x 2 x + ) 2 dx
Vytápěcí boiler hybridní s tepelným čerpadlem. vzduch-voda
 Vytápěcí boiler hybridní s tepelným čerpadlem vzduch-voda 29.4.2016 Model: LLR160-5,5kW REVEL Provozní manuál Pročtěte si důkladně tento manuál, pokud tak neučiníte, může dojít k nevratnému poškození vašeho
Vytápěcí boiler hybridní s tepelným čerpadlem vzduch-voda 29.4.2016 Model: LLR160-5,5kW REVEL Provozní manuál Pročtěte si důkladně tento manuál, pokud tak neučiníte, může dojít k nevratnému poškození vašeho
Vyřizuje: Tel.: Fax: E-mail: Datum: 6.8.2012. Oznámení o návrhu stanovení místní úpravy provozu na místní komunikaci a silnici
 M Ě S T S K Ý Ú Ř A D B L A N S K O ODBOR STAVEBNÍ ÚŘAD, oddělení silničního hospodářství nám. Svobody 32/3, 678 24 Blansko Pracoviště: nám. Republiky 1316/1, 67801 Blansko Město Blansko, nám. Svobody
M Ě S T S K Ý Ú Ř A D B L A N S K O ODBOR STAVEBNÍ ÚŘAD, oddělení silničního hospodářství nám. Svobody 32/3, 678 24 Blansko Pracoviště: nám. Republiky 1316/1, 67801 Blansko Město Blansko, nám. Svobody
PROPOZICE krajského kola soutěže družstev SDH SH ČMS v požárním sportu v roce 2014 ve Zlínském kraji
 PROPOZICE krajského kola soutěže družstev SDH SH ČMS v požárním sportu v roce 2014 ve Zlínském kraji Soutěž se uskuteční pod záštitou hejtmana Zlínského kraje a starosty obce Horní Lideč Termín konání:
PROPOZICE krajského kola soutěže družstev SDH SH ČMS v požárním sportu v roce 2014 ve Zlínském kraji Soutěž se uskuteční pod záštitou hejtmana Zlínského kraje a starosty obce Horní Lideč Termín konání:
TRÉNINKOVÁ CENTRA MLÁDEŽE
 PROJEKT ČESKÉHO NOHEJBALOVÉHO SVAZU TRÉNINKOVÁ CENTRA MLÁDEŽE 1. Popis projektu Český nohejbalový svaz (dále jen ČNS ), prostřednictvím Výkonného výboru (dále jen VV ), vyhlašuje projekt Tréninková centra
PROJEKT ČESKÉHO NOHEJBALOVÉHO SVAZU TRÉNINKOVÁ CENTRA MLÁDEŽE 1. Popis projektu Český nohejbalový svaz (dále jen ČNS ), prostřednictvím Výkonného výboru (dále jen VV ), vyhlašuje projekt Tréninková centra
