Datové struktury. Zuzana Majdišová
|
|
|
- Alois Prokop
- před 8 lety
- Počet zobrazení:
Transkript
1 Datové struktury Zuzana Majdišová
2 Datové struktury Numerické datové struktury Efektivní reprezentace velkých řídkých matic Lze využít při výpočtu na GPU Dělení prostoru a binární masky Voxelová datová struktura 2
3 DIA Diagonální formát Definován poli: data (nenulové prvky) a offsets Offset: 0 i > 0 i < 0 Hlavní diagonála super-diagonála sub-diagonála Výhody: row a col definovány implicitně souvislý přístup k paměti Nevýhody: vhodné pouze pro určité uspořádání 3
4 ELL ELLPACK formát Vhodný pro matici s max. nenulovými prvky v řádku Definován poli: data ( ) a indices (sloupcové indexy) Výhody: obecnější než DIA Nevýhody: potřeba přibližně stejný počet nenulových prvků v každém řádku Využití: matice definovaná stencil operací pro síť s téměř stejnou konektivitou vrcholů 4
5 COO Souřadnicový (XY) formát Jednoduché schéma Definován poli: data (nenulové prvky), row (řádkové indexy) a col (sloupcové indexy) Výhody: lze reprezentovat libovolnou řídkou matici Nevýhody: row a col definovány explicitně vyšší výpočetní náročnost 5
6 CSR Compressed Sparse Row formát rozšíření COO formátu aplikace komprese Definován poli: data (nenulové prvky), ptr (pointery) a indices (sloupcové indexy) Výhody: rychlejší zjišťování hodnot matice lze jednoduše zjistit počet nenulových prvků v řádku 6
7 HYB Hybridní formát Kombinace ELL a COO formátu Většina nenulových prvků uložena do ELL formátu, zbytek do COO formátu Nejlepší pro ELL formát určeno z histogramu Plně obsazený ELL formát je přibližně 3 krát rychlejší než COO formát sloupců pro ELL formát pokud má alespoň třetina řádků víc než nenulových prvků 7
8 Experimenty matice vektor Strukturované matice Nestrukturované matice 8
9 Quadtree storage format Předchozí struktury pomalé důsledkem nepřímé adresace Řídké matice často obsahují husté podmatice (bloky) vznik blokových formátů Využití quadtree uzly odpovídají podmaticím Typu uzlů: vnitřní: Mixed Empty NULL pointer listy: Full podíl nenulových prvků větší než práh Sparse podmatice reprezentována COO formátem Výhody: alokováno méně paměti matice uložena jako malé husté bloky lepší výkon jednoduchá konverze z předchozích formátů relativně jednoduchá modifikace quadtree 9
10 Experimenty - matice matice 10
11 Dělení prostoru Jednoduchá technika dělící (rovnoměrně) prostor na menší prostory Paměťová náročnost: počet objektů dimenze počet dělení v jedné ose =,, pravděpodobnost, že průměrný objekt protne podprostor Paměťové nároky prudce rostou s jemností dělení a dimenzí prostoru 11
12 Rezidenční maska Pro každý objekt definován vektor bitů Délka vektoru bitů dána celkovým dělením prostoru Bit nastaven na 1 pokud objekt protíná daný interval Paměťová nároky: = /8 počet objektů dimenze počet dělení v jedné ose Časová složitost: Výhody: rychlá detekce kolize objektů pomocí Nevýhody: při jemném dělení a malé velikosti objektů velmi dlouhé vektory bitů obsahující většinou nuly 12
13 Binární maska Nechť, resp. množina objektů protínajících -tý řádkový řez resp. -tý sloupcový řez, pak všechny objekty protínající buňku na pozici, dány: = Množiny, resp. reprezentovány vektorem bitů ( -tý bit reprezentuje -tý objekt) = Paměťová nároky: = /8 počet objektů dimenze počet dělení v jedné ose Výhody: rychlé nalezení všech objektů protínajících danou oblast jednoduchá kontrola konzistence dat 13
14 Voxelová datová struktura Voxely uložíme pomocí řídkého octree (uzel reprezentuje voxel) Využití ray casting Data dělena do bloků obsahujících: Pole child descriptors Kódování topologie octree Info sekce Adresář dostupných attachments Pointer na první child descriptor Contour data Popis geometrického tvaru voxelů Různé množství attachments Pole ukládající atributy pro stínování pro každý voxel 14
15 Child descriptor (64-bit) Každý odpovídá jednomu nelistovému voxelu (list popsán ve svém rodiči) Rozdělen na dvě 32-bit části: 1. Popis množiny potomků 2. Souvisí s contours Dvě bitové masky (každý potomek má jeden bit) validmask 1 pokud potomek obsahuje voxel leafmask 1 pokud potomek je list Childpointer (15-bit) existuje nelistový potomek pak pointer na child descriptor Far bit pokud nastaven childpointer je nepřímý odkaz na far pointer 15
16 Contours Přímočará vizualizace voxelových dat je aproximace geometrie uvnitř voxelu krychličkou Vznik aproximační chyby Redukce chyby: Voxel oříznut dvojící rovnoběžných rovin (contour) odpovídajících orientaci aproximované plochy Výsledkem kolekce orientovaných slabs Contour mask 1 pokud potomek má přidruženu contour Contourpointer (24-bit) Odkaz na seznam contours (pro každý nastavený bit jedna) Uložení contour (32-bit) 3 krát 6-bit int pro definování normálových vektorů dvou rovin 2 krát 7-bit int definujících jejich pozici uvnitř voxelu 16
17 Budoucí práce Vývoj datových struktur pro meshfree techniky Využití projektivní geometrie Využití geometrické algebry 17
18 DĚKUJI ZA POZORNOST 18
19 Reference Bell,N.,Garland,M.: Efficient Sparse Matrix-Vector Multiplication on CUDA, Nvidia Technical Report NVR , Nvidia Corporation, Vol.2, No.5, Bell,N.,Garland,M.: Implementing Sparse Matrix-Vector Multiplication on Throughput-Oriented Processors, Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, ACM, p.18, Šimeček,I.: Sparse Matrix Computations using the Quadtree Storage Format, Proceedings of 11 th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC 2009), pp , Skala,V.: An Efficient Space Partitioning Method Using Binary Maps, 11 th Conference SIP 2012 conference, pp , ISBN: , St.Malo, WSEAS, France, Laine,S., Tero,K.: Efficient Sparse Voxel Octrees, Visualization and Computer Graphics, IEEE Transactions on, Vol.17, No.8, pp ,
Rastrová reprezentace
 Rastrová reprezentace Zaměřuje se na lokalitu jako na celek Používá se pro reprezentaci jevů, které plošně pokrývají celou oblast, případně se i spojitě mění. Používá se i pro rasterizované vektorové vrstvy,
Rastrová reprezentace Zaměřuje se na lokalitu jako na celek Používá se pro reprezentaci jevů, které plošně pokrývají celou oblast, případně se i spojitě mění. Používá se i pro rasterizované vektorové vrstvy,
Hierarchický model. 1995-2013 Josef Pelikán CGG MFF UK Praha. pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16
 Hierarchický model 1995-2013 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16 Hierarchie v 3D modelování kompozice zdola-nahoru složitější objekty se sestavují
Hierarchický model 1995-2013 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16 Hierarchie v 3D modelování kompozice zdola-nahoru složitější objekty se sestavují
GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 6
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 6 Lubomír Vašek Zlín 2013 Obsah... 3 1. Základní pojmy... 3 2. Princip rastrové reprezentace... 3 2.1 Užívané
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 6 Lubomír Vašek Zlín 2013 Obsah... 3 1. Základní pojmy... 3 2. Princip rastrové reprezentace... 3 2.1 Užívané
Algoritmy výpočetní geometrie
 Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
Hammingovy kódy. dekódování H.kódů. konstrukce. šifrování. Fanova rovina charakteristický vektor. princip generující a prověrková matice
 Hammingovy kódy konstrukce Fanova rovina charakteristický vektor šifrování princip generující a prověrková matice dekódování H.kódů třída lineárních binárních kódů s A n, 3 n = délka kódu, d = distance
Hammingovy kódy konstrukce Fanova rovina charakteristický vektor šifrování princip generující a prověrková matice dekódování H.kódů třída lineárních binárních kódů s A n, 3 n = délka kódu, d = distance
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Jan Březina. 7. března 2017
 TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 7. března 2017 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 7. března 2017 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
Úvod do GIS. Prostorová data II. část. Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium.
 Úvod do GIS Prostorová data II. část Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium. Karel Jedlička Prostorová data Analogová prostorová data Digitální
Úvod do GIS Prostorová data II. část Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium. Karel Jedlička Prostorová data Analogová prostorová data Digitální
Zpracování deklarací a přidělování paměti
 Zpracování deklarací a přidělování paměti Účel deklarací -pojmenování objektů -umístění objektů v paměti Tabulka symbolů -uchovává informace o objektech -umožňuje kontextové kontroly -umožňuje operace
Zpracování deklarací a přidělování paměti Účel deklarací -pojmenování objektů -umístění objektů v paměti Tabulka symbolů -uchovává informace o objektech -umožňuje kontextové kontroly -umožňuje operace
STRUKTURA RASTROVÝCH DAT
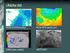 STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Lineární algebra s Matlabem. Přednáška 4
 Lineární algebra s Matlabem Přednáška 4 Import/export dat Matlab podporuje velké množství formátů Matlab data (.mat) Text (.txt,.csv, ) Tabulky (.xls,.xlsx,.ods,...) XML Obrázky (.bmp,.gif,.jpg,.png, )
Lineární algebra s Matlabem Přednáška 4 Import/export dat Matlab podporuje velké množství formátů Matlab data (.mat) Text (.txt,.csv, ) Tabulky (.xls,.xlsx,.ods,...) XML Obrázky (.bmp,.gif,.jpg,.png, )
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
 Úvod do informatiky přednáška čtvrtá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Pojem relace 2 Vztahy a operace s (binárními) relacemi
Úvod do informatiky přednáška čtvrtá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Pojem relace 2 Vztahy a operace s (binárními) relacemi
Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ). Čísla a 1, a 2,..., a n se nazývají složky vektoru
 1 1. Lineární algebra 1.1. Lineární závislost a nezávislost vektorů. Hodnost matice Aritmetické vektory Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ).
1 1. Lineární algebra 1.1. Lineární závislost a nezávislost vektorů. Hodnost matice Aritmetické vektory Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ).
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Static Load Balancing Applied to Time Dependent Mechanical Problems
 Static Load Balancing Applied to Time Dependent Mechanical Problems O. Medek 1, J. Kruis 2, Z. Bittnar 2, P. Tvrdík 1 1 Katedra počítačů České vysoké učení technické, Praha 2 Katedra stavební mechaniky
Static Load Balancing Applied to Time Dependent Mechanical Problems O. Medek 1, J. Kruis 2, Z. Bittnar 2, P. Tvrdík 1 1 Katedra počítačů České vysoké učení technické, Praha 2 Katedra stavební mechaniky
Zdůvodněte, proč funkce n lg(n) roste alespoň stejně rychle nebo rychleji než než funkce lg(n!). Symbolem lg značíme logaritmus o základu 2.
 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
Stromové struktury v relační databázi
 Stromové struktury v relační databázi Stromové struktury a relační databáze Zboží Procesory Intel Pentium IV Celeron Paměti AMD Duron DDR DIMM Athlon http://interval.cz/clanky/metody-ukladani-stromovych-dat-v-relacnich-databazich/
Stromové struktury v relační databázi Stromové struktury a relační databáze Zboží Procesory Intel Pentium IV Celeron Paměti AMD Duron DDR DIMM Athlon http://interval.cz/clanky/metody-ukladani-stromovych-dat-v-relacnich-databazich/
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu geoprvků. Geometrická
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu geoprvků. Geometrická
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí RASTR RASTROVÉ ANALÝZY
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí RASTR RASTROVÉ ANALÝZY TYPY PROSTOROVÝCH OBJEKTŮ Vektorová data geometrie prostorových objektů je vyjádřena za použití geometrických elementů základními
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí RASTR RASTROVÉ ANALÝZY TYPY PROSTOROVÝCH OBJEKTŮ Vektorová data geometrie prostorových objektů je vyjádřena za použití geometrických elementů základními
Toto zadání je podepsané děkanem a vedoucím katedry, po obhajobě).
 Na tomto místě bude oficiální zadání vaší práce Toto zadání je podepsané děkanem a vedoucím katedry, musíte si ho vyzvednout na studiijním oddělení Katedry počítačů na Karlově náměstí, v jedné odevzdané
Na tomto místě bude oficiální zadání vaší práce Toto zadání je podepsané děkanem a vedoucím katedry, musíte si ho vyzvednout na studiijním oddělení Katedry počítačů na Karlově náměstí, v jedné odevzdané
Detekce kolizí v 3D Josef Pelikán KSVI MFF UK Praha
 Detekce kolizí v 3D 2001-2003 Josef Pelikán KSVI MFF UK Praha e-mail: Josef.Pelikan@mff.cuni.cz W W W: http://cgg.ms.mff.cuni.cz/~pepca/ Aplikace CD mobilní robotika plánování cesty robota bez kontaktu
Detekce kolizí v 3D 2001-2003 Josef Pelikán KSVI MFF UK Praha e-mail: Josef.Pelikan@mff.cuni.cz W W W: http://cgg.ms.mff.cuni.cz/~pepca/ Aplikace CD mobilní robotika plánování cesty robota bez kontaktu
Datové typy a struktury
 atové typy a struktury Jednoduché datové typy oolean = logická hodnota (true / false) K uložení stačí 1 bit často celé slovo (1 byte) haracter = znak Pro 8-bitový SII kód stačí 1 byte (256 možností) Pro
atové typy a struktury Jednoduché datové typy oolean = logická hodnota (true / false) K uložení stačí 1 bit často celé slovo (1 byte) haracter = znak Pro 8-bitový SII kód stačí 1 byte (256 možností) Pro
Pokročilé metody fotorealistického zobrazování
 Pokročilé metody fotorealistického zobrazování 14.5.2013 Úvod Motivace Základní informace Shrnutí metod Představení programu RayTracer Reference Motivace Základní informace Motivace snaha o vytvoření realistických
Pokročilé metody fotorealistického zobrazování 14.5.2013 Úvod Motivace Základní informace Shrnutí metod Představení programu RayTracer Reference Motivace Základní informace Motivace snaha o vytvoření realistických
Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy
 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném
1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném
x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b.
![x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b. x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b.](/thumbs/83/87395437.jpg) 1. Afinní podprostory 1.1. Motivace. Uvažujme R 3. Jeho všechny vektorové podprostory jsou počátek, přímky a roviny procházející počátkem a celé R 3. Chceme-li v R 3 dělat geometrii potřebujeme i jiné
1. Afinní podprostory 1.1. Motivace. Uvažujme R 3. Jeho všechny vektorové podprostory jsou počátek, přímky a roviny procházející počátkem a celé R 3. Chceme-li v R 3 dělat geometrii potřebujeme i jiné
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
GPGPU Aplikace GPGPU. Obecné výpočty na grafických procesorech. Jan Vacata
 Obecné výpočty na grafických procesorech Motivace Úvod Motivace Technologie 3 GHz Intel Core 2 Extreme QX9650 Výkon: 96 GFLOPS Propustnost paměti: 21 GB/s Orientační cena: 1300 USD NVIDIA GeForce 9800
Obecné výpočty na grafických procesorech Motivace Úvod Motivace Technologie 3 GHz Intel Core 2 Extreme QX9650 Výkon: 96 GFLOPS Propustnost paměti: 21 GB/s Orientační cena: 1300 USD NVIDIA GeForce 9800
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy
 Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
PA152. Implementace databázových systémů
 PA152 Implementace databázových systémů RAID level 1 zrcadlení disku výpočet MTTF 2 stejné disky, MTTF 3 roky výměna vadného 3,5 dne výpadek oba disky během 3,5 dne p(výpadku disku za rok) = 1/6 p(výp.
PA152 Implementace databázových systémů RAID level 1 zrcadlení disku výpočet MTTF 2 stejné disky, MTTF 3 roky výměna vadného 3,5 dne výpadek oba disky během 3,5 dne p(výpadku disku za rok) = 1/6 p(výp.
Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném rušení ) Muhammada ibn Músá al-chvárizmího (790? - 850?, Chiva, Bagdád),
 1 LINEÁRNÍ ALGEBRA 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci
1 LINEÁRNÍ ALGEBRA 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci
Lineární algebra - I. část (vektory, matice a jejich využití)
 Lineární algebra - I. část (vektory, matice a jejich využití) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 2. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 40 Obsah 1 Vektory
Lineární algebra - I. část (vektory, matice a jejich využití) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 2. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 40 Obsah 1 Vektory
SUPERPOČÍTAČE DANIEL LANGR ČVUT FIT / VZLÚ
 SUPERPOČÍTAČE DANIEL LANGR ČVUT FIT / VZLÚ TITAN / HOPPER / NOTEBOOK TITAN HOPPER NOTEBOOK Počet CPU jader 299 008 153 216 2 Operační paměť [GB] 598 016 217 000 8 Počet GPU (CUDA) jader 50 233 344 0 8
SUPERPOČÍTAČE DANIEL LANGR ČVUT FIT / VZLÚ TITAN / HOPPER / NOTEBOOK TITAN HOPPER NOTEBOOK Počet CPU jader 299 008 153 216 2 Operační paměť [GB] 598 016 217 000 8 Počet GPU (CUDA) jader 50 233 344 0 8
GIS Prostorové modely. Obsah přednášky Rastrový model Pravidelné, nepravidelné buňky Způsoby uložení Komprese dat
 GIS Prostorové modely Obsah přednášky Rastrový model Pravidelné, nepravidelné buňky Způsoby uložení Komprese dat Rastrový model Intuitivně jej chápeme jako množinu elementů obecně různého tvaru a velikosti
GIS Prostorové modely Obsah přednášky Rastrový model Pravidelné, nepravidelné buňky Způsoby uložení Komprese dat Rastrový model Intuitivně jej chápeme jako množinu elementů obecně různého tvaru a velikosti
2. přednáška z předmětu GIS1 Data a datové modely
 2. přednáška z předmětu GIS1 Data a datové modely Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI, autor Ing. K.
2. přednáška z předmětu GIS1 Data a datové modely Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI, autor Ing. K.
Paralelní grafové algoritmy
 Paralelní grafové algoritmy Značení Minimální kostra grafu Nejkratší cesta z jednoho uzlu Nejkratší cesta mezi všemi dvojicemi uzlů Použité značení Definition Bud G = (V, E) graf. Pro libovolný uzel u
Paralelní grafové algoritmy Značení Minimální kostra grafu Nejkratší cesta z jednoho uzlu Nejkratší cesta mezi všemi dvojicemi uzlů Použité značení Definition Bud G = (V, E) graf. Pro libovolný uzel u
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Pohled do nitra mikroprocesoru Josef Horálek
 Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Datové struktury pro prostorové vyhledávání
 Datové struktury pro prostorové vyhledávání 1998-2011 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ SpatialData 2011 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1
Datové struktury pro prostorové vyhledávání 1998-2011 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ SpatialData 2011 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Co je obsahem numerických metod?
 Numerické metody Úvod Úvod Co je obsahem numerických metod? Numerické metody slouží k přibližnému výpočtu věcí, které se přesně vypočítat bud nedají vůbec, nebo by byl výpočet neúměrně pracný. Obsahem
Numerické metody Úvod Úvod Co je obsahem numerických metod? Numerické metody slouží k přibližnému výpočtu věcí, které se přesně vypočítat bud nedají vůbec, nebo by byl výpočet neúměrně pracný. Obsahem
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
Závěrečná zpráva projektu Experimentální výpočetní grid pro numerickou lineární algebru
 Závěrečná zpráva projektu Experimentální výpočetní grid pro numerickou lineární algebru Ing. Ivan Šimeček Ph.D., Zdeněk Buk xsimecek@fit.cvut.cz, bukz1fel.cvut.cz Červen, 2012 1 Zadání Paralelní zpracování
Závěrečná zpráva projektu Experimentální výpočetní grid pro numerickou lineární algebru Ing. Ivan Šimeček Ph.D., Zdeněk Buk xsimecek@fit.cvut.cz, bukz1fel.cvut.cz Červen, 2012 1 Zadání Paralelní zpracování
VYHLEDÁNÍ NEJDELŠÍHO SHODNÉHO PREFIXU V FPGA
 VYHLEDÁNÍ NEJDELŠÍHO SHODNÉHO PREFIXU V FPGA Jiří Tobola Výpočetní technika a informatika, 2. ročník, prezenční studium Školitel: Vladimír Drábek Fakulta informačních technologií, Vysoké učení technické
VYHLEDÁNÍ NEJDELŠÍHO SHODNÉHO PREFIXU V FPGA Jiří Tobola Výpočetní technika a informatika, 2. ročník, prezenční studium Školitel: Vladimír Drábek Fakulta informačních technologií, Vysoké učení technické
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra
 8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Stromy. Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy
 Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
SVD rozklad a pseudoinverse
 SVD rozklad a pseudoinverse Odpřednesenou látku naleznete v kapitole 12 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: Lineární algebra 19.12.2016: SVD rozklad a pseudoinverse 1/21 Cíle
SVD rozklad a pseudoinverse Odpřednesenou látku naleznete v kapitole 12 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: Lineární algebra 19.12.2016: SVD rozklad a pseudoinverse 1/21 Cíle
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
 ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
Jak v Javě primitivní datové typy a jejich reprezentace. BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické
 Jak v Javě primitivní datové typy a jejich reprezentace BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické Obsah Celočíselný datový typ Reálný datový typ Logický datový typ, typ Boolean
Jak v Javě primitivní datové typy a jejich reprezentace BD6B36PJV 002 Fakulta elektrotechnická České vysoké učení technické Obsah Celočíselný datový typ Reálný datový typ Logický datový typ, typ Boolean
Úvod do GIS. Prostorová data I. část. Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium.
 Úvod do GIS Prostorová data I. část Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium. Karel Jedlička Prostorová data Analogová prostorová data Digitální prostorová
Úvod do GIS Prostorová data I. část Pouze podkladová prezentace k přednáškám, nejedná se o studijní materiál pro samostatné studium. Karel Jedlička Prostorová data Analogová prostorová data Digitální prostorová
Numerické metody a programování
 Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.7/2.2./28.157 Numerické metody a programování Lekce 4 Tento projekt je spolufinancován Evropským
Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.7/2.2./28.157 Numerické metody a programování Lekce 4 Tento projekt je spolufinancován Evropským
LabView jako programovací jazyk II
 LabView jako programovací jazyk II - Popis jednotlivých funkcí palety Function II.část - Funkce Numeric, Array, Cluster Ing. Martin Bušek, Ph.D. Práce s daty typu NUMERIC Numerické funkce obsahuje funkce
LabView jako programovací jazyk II - Popis jednotlivých funkcí palety Function II.část - Funkce Numeric, Array, Cluster Ing. Martin Bušek, Ph.D. Práce s daty typu NUMERIC Numerické funkce obsahuje funkce
NOVINKY V DATABÁZÍCH CEDA
 NOVINKY V DATABÁZÍCH CEDA GIS KU květen 2017 Jan Vodňanský Central European Data Agency, a.s. výrobní ředitel vodnansky@ceda.cz StreetNet CrossBorder Vektorové mapové dlaždice Route4All StreetNet CrossBorder
NOVINKY V DATABÁZÍCH CEDA GIS KU květen 2017 Jan Vodňanský Central European Data Agency, a.s. výrobní ředitel vodnansky@ceda.cz StreetNet CrossBorder Vektorové mapové dlaždice Route4All StreetNet CrossBorder
Singulární rozklad. Petr Tichý. 31. října 2013
 Singulární rozklad Petr Tichý 31. října 2013 1 Outline 1 Úvod a motivace 2 Zavedení singulárního rozkladu a jeho vlastnosti 3 Výpočet a náklady na výpočet singulárního rozkladu 4 Moor-Penroseova pseudoinverze
Singulární rozklad Petr Tichý 31. října 2013 1 Outline 1 Úvod a motivace 2 Zavedení singulárního rozkladu a jeho vlastnosti 3 Výpočet a náklady na výpočet singulárního rozkladu 4 Moor-Penroseova pseudoinverze
Odečítání pozadí a sledování lidí z nehybné kamery. Ondřej Šerý
 Odečítání pozadí a sledování lidí z nehybné kamery Ondřej Šerý Plán Motivace a popis úlohy Rozdělení úlohy na tři části Detekce pohybu Detekce objektů Sledování objektů Rozbor každé z částí a nástin několika
Odečítání pozadí a sledování lidí z nehybné kamery Ondřej Šerý Plán Motivace a popis úlohy Rozdělení úlohy na tři části Detekce pohybu Detekce objektů Sledování objektů Rozbor každé z částí a nástin několika
Připomenutí co je to soustava lineárních rovnic
 Připomenutí co je to soustava lineárních rovnic Příklad 2x 3y + z = 5 3x + 5y + 2z = 4 x + 2y z = 1 Soustava lineárních rovnic obecně Maticový tvar: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a
Připomenutí co je to soustava lineárních rovnic Příklad 2x 3y + z = 5 3x + 5y + 2z = 4 x + 2y z = 1 Soustava lineárních rovnic obecně Maticový tvar: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a
[1] samoopravné kódy: terminologie, princip
![[1] samoopravné kódy: terminologie, princip [1] samoopravné kódy: terminologie, princip](/thumbs/51/27813178.jpg) [1] Úvod do kódování samoopravné kódy: terminologie, princip blokové lineární kódy Hammingův kód Samoopravné kódy, k čemu to je [2] Data jsou uložena (nebo posílána do linky) kodérem podle určitého pravidla
[1] Úvod do kódování samoopravné kódy: terminologie, princip blokové lineární kódy Hammingův kód Samoopravné kódy, k čemu to je [2] Data jsou uložena (nebo posílána do linky) kodérem podle určitého pravidla
Elementární datové typy
 Elementární datové typy Celočíselné typy (integers) Mohou nabývat množiny hodnot, která je podmnožinou celých čísel (někdy existuje implementační konstanta maxint). Operace: aritmetické, relační, bitové,
Elementární datové typy Celočíselné typy (integers) Mohou nabývat množiny hodnot, která je podmnožinou celých čísel (někdy existuje implementační konstanta maxint). Operace: aritmetické, relační, bitové,
Reprezentace dat v informačních systémech. Jaroslav Šmarda
 Reprezentace dat v informačních systémech Jaroslav Šmarda Reprezentace dat v informačních systémech Reprezentace dat v počítači Datové typy Proměnná Uživatelské datové typy Datové struktury: pole, zásobník,
Reprezentace dat v informačních systémech Jaroslav Šmarda Reprezentace dat v informačních systémech Reprezentace dat v počítači Datové typy Proměnná Uživatelské datové typy Datové struktury: pole, zásobník,
GIS a DPZ v geologii. Geoinformační systémy. Dálkový průzkum Země. Ondrej Lexa. Karel Martínek
 GIS a DPZ v geologii Geoinformační systémy Ondrej Lexa Dálkový průzkum Země Karel Martínek Cíle získat nejzákladnější teoretické znalosti terminologie a principů GIS a DPZ žijeme v informačním věku postindustriální
GIS a DPZ v geologii Geoinformační systémy Ondrej Lexa Dálkový průzkum Země Karel Martínek Cíle získat nejzákladnější teoretické znalosti terminologie a principů GIS a DPZ žijeme v informačním věku postindustriální
Základy matematiky pro FEK
 Základy matematiky pro FEK 2. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 20 Co nás dneska čeká... Závislé a nezávislé
Základy matematiky pro FEK 2. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 20 Co nás dneska čeká... Závislé a nezávislé
EXTRAKT z mezinárodní normy Extrakt nenahrazuje samotnou technickou normu, je pouze informativním materiálem o normě.
 EXTRAKT z mezinárodní normy Extrakt nenahrazuje samotnou technickou normu, je pouze informativním materiálem o normě. Inteligentní dopravní systémy (ITS) Označení poloh pro geografické databáze Část 3:
EXTRAKT z mezinárodní normy Extrakt nenahrazuje samotnou technickou normu, je pouze informativním materiálem o normě. Inteligentní dopravní systémy (ITS) Označení poloh pro geografické databáze Část 3:
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Zadání semestrálního projektu Algoritmy II. letní semestr 2017/2018
 Zadání semestrálního projektu Algoritmy II. letní semestr 2017/2018 doc. Mgr. Jiří Dvorský, Ph.D. Verze zadání 6. dubna 2018 První verze Obecné pokyny 1. Celkem jsou k dispozici tři zadání příkladů. 2.
Zadání semestrálního projektu Algoritmy II. letní semestr 2017/2018 doc. Mgr. Jiří Dvorský, Ph.D. Verze zadání 6. dubna 2018 První verze Obecné pokyny 1. Celkem jsou k dispozici tři zadání příkladů. 2.
Podobnost matic. Definice 8.6. Dány matice A, B M n (C). Jestliže existuje regulární matice P M n (C) tak,
 Podobnost matic Definice 84 Dány matice A, B M n (C) Jestliže existuje regulární matice P M n (C) tak, že B = P 1 AP, pak říkáme, že matice B je podobná matici A a píšeme A B Takto zavedená binární relace
Podobnost matic Definice 84 Dány matice A, B M n (C) Jestliže existuje regulární matice P M n (C) tak, že B = P 1 AP, pak říkáme, že matice B je podobná matici A a píšeme A B Takto zavedená binární relace
11MAMY LS 2017/2018. Úvod do Matlabu. 21. února Skupina 01. reseni2.m a tak dále + M souborem zadané funkce z příkladu 3 + souborem skupina.
 11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
Přijímací zkouška - matematika
 Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Modelování pevných těles
 Modelování pevných těles Pavel Strachota FJFI ČVUT v Praze 12. března 2015 Obsah 1 Reprezentace pevných těles 2 Objemové reprezentace 3 Tahové reprezentace 4 Hraniční reprezentace 5 Polygonální sítě Obsah
Modelování pevných těles Pavel Strachota FJFI ČVUT v Praze 12. března 2015 Obsah 1 Reprezentace pevných těles 2 Objemové reprezentace 3 Tahové reprezentace 4 Hraniční reprezentace 5 Polygonální sítě Obsah
GIS Geografické informační systémy
 GIS Geografické informační systémy GIS Prostorové modely Rastrový model Pravidelné, nepravidelné buňky Způsoby uložení Komprese dat Rastrový model Intuitivně chápání množina elementů (obecně různého tvaru
GIS Geografické informační systémy GIS Prostorové modely Rastrový model Pravidelné, nepravidelné buňky Způsoby uložení Komprese dat Rastrový model Intuitivně chápání množina elementů (obecně různého tvaru
Zdrojem většiny příkladů je sbírka úloh 1. cvičení ( ) 2. cvičení ( )
 Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Základní pojmy teorie množin Vektorové prostory
 Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
KMA/PDB. Karel Janečka. Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d
 KMA/PDB Prostorové databáze Karel Janečka Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d Sylabus předmětu KMA/PDB Úvodní přednáška Základní terminologie Motivace rozdíl klasické
KMA/PDB Prostorové databáze Karel Janečka Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d Sylabus předmětu KMA/PDB Úvodní přednáška Základní terminologie Motivace rozdíl klasické
Reprezentace 3D scény
 Reprezentace 3D scény 1995-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 36 Metody reprezentace 3D scén objemové reprezentace přímé informace o vnitřních
Reprezentace 3D scény 1995-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 36 Metody reprezentace 3D scén objemové reprezentace přímé informace o vnitřních
Četba: Texty o lineární algebře (odkazy na webových stránkách přednášejícího).
 Předmět: MA 4 Dnešní látka Vektorový (lineární) prostor (připomenutí) Normovaný lineární prostor Normy matic a vektorů Symetrické matice, pozitivně definitní matice Gaussova eliminační metoda, podmíněnost
Předmět: MA 4 Dnešní látka Vektorový (lineární) prostor (připomenutí) Normovaný lineární prostor Normy matic a vektorů Symetrické matice, pozitivně definitní matice Gaussova eliminační metoda, podmíněnost
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
Cvičení z Lineární algebry 1
 Cvičení z Lineární algebry Michael Krbek podzim 2003 2392003 Hodina Jsou dána komplexní čísla z = +2 i a w = 2 i Vyjádřete c algebraickém tvaru (z + w) 3,, (zw), z w 2 Řešte v komplexním oboru rovnice
Cvičení z Lineární algebry Michael Krbek podzim 2003 2392003 Hodina Jsou dána komplexní čísla z = +2 i a w = 2 i Vyjádřete c algebraickém tvaru (z + w) 3,, (zw), z w 2 Řešte v komplexním oboru rovnice
Programování v C++ 2, 4. cvičení
 Programování v C++ 2, 4. cvičení statické atributy a metody, konstruktory 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled Přístupová práva
Programování v C++ 2, 4. cvičení statické atributy a metody, konstruktory 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled Přístupová práva
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague Zjednodušené schéma systému z základ hardware pro mainframe tvoří: operační pamět - MAIN / REAL STORAGE jeden
Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague Zjednodušené schéma systému z základ hardware pro mainframe tvoří: operační pamět - MAIN / REAL STORAGE jeden
GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 4
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 4 Lubomír Vašek Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního fondu (ESF)
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY GEOGRAFICKÉ INFORMAČNÍ SYSTÉMY 4 Lubomír Vašek Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního fondu (ESF)
Základní rutiny pro numerickou lineární algebru. I. Šimeček, M. Šoch
 Základní rutiny pro numerickou lineární algebru I. Šimeček, M. Šoch xsimecek@fit.cvut.cz Katedra počítačových systémů FIT České vysoké učení technické v Praze Ivan Šimeček, 2011 BI-EIA, ZS2011/12, Predn.10
Základní rutiny pro numerickou lineární algebru I. Šimeček, M. Šoch xsimecek@fit.cvut.cz Katedra počítačových systémů FIT České vysoké učení technické v Praze Ivan Šimeček, 2011 BI-EIA, ZS2011/12, Predn.10
Operátory ROLLUP a CUBE
 Operátory ROLLUP a CUBE Dotazovací jazyky, 2009 Marek Polák Martin Chytil Osnova přednášky o Analýza dat o Agregační funkce o GROUP BY a jeho problémy o Speciální hodnotový typ ALL o Operátor CUBE o Operátor
Operátory ROLLUP a CUBE Dotazovací jazyky, 2009 Marek Polák Martin Chytil Osnova přednášky o Analýza dat o Agregační funkce o GROUP BY a jeho problémy o Speciální hodnotový typ ALL o Operátor CUBE o Operátor
Základy programování (IZP)
 Základy programování (IZP) Osmé počítačové cvičení Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 66 Brno - Královo Pole Petr Veigend, iveigend@fit.vutbr.cz 20.11.2017,
Základy programování (IZP) Osmé počítačové cvičení Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 66 Brno - Královo Pole Petr Veigend, iveigend@fit.vutbr.cz 20.11.2017,
Matice. Modifikace matic eliminační metodou. α A = α a 2,1, α a 2,2,..., α a 2,n α a m,1, α a m,2,..., α a m,n
 [1] Základní pojmy [2] Matice mezi sebou sčítáme a násobíme konstantou (lineární prostor) měníme je na jiné matice eliminační metodou násobíme je mezi sebou... Matice je tabulka čísel s konečným počtem
[1] Základní pojmy [2] Matice mezi sebou sčítáme a násobíme konstantou (lineární prostor) měníme je na jiné matice eliminační metodou násobíme je mezi sebou... Matice je tabulka čísel s konečným počtem
Vyplňování souvislé oblasti
 Počítačová grafika Vyplňování souvislé oblasti Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU. Které z následujících tvrzení není pravdivé: a) Princip interpolace je určení
Počítačová grafika Vyplňování souvislé oblasti Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU. Které z následujících tvrzení není pravdivé: a) Princip interpolace je určení
Lineární algebra Operace s vektory a maticemi
 Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Numerické metody a programování. Lekce 4
 Numerické metody a programování Lekce 4 Linarní algebra soustava lineárních algebraických rovnic a 11 a 12 x 2 a 1, N x N = b 1 a 21 a 22 x 2 a 2, N x N = b 2 a M,1 a M,2 x 2 a M,N x N = b M zkráceně A
Numerické metody a programování Lekce 4 Linarní algebra soustava lineárních algebraických rovnic a 11 a 12 x 2 a 1, N x N = b 1 a 21 a 22 x 2 a 2, N x N = b 2 a M,1 a M,2 x 2 a M,N x N = b M zkráceně A
Robust 2014, 19. - 24. ledna 2014, Jetřichovice
 K. Hron 1 C. Mert 2 P. Filzmoser 2 1 Katedra matematické analýzy a aplikací matematiky Přírodovědecká fakulta, Univerzita Palackého, Olomouc 2 Department of Statistics and Probability Theory Vienna University
K. Hron 1 C. Mert 2 P. Filzmoser 2 1 Katedra matematické analýzy a aplikací matematiky Přírodovědecká fakulta, Univerzita Palackého, Olomouc 2 Department of Statistics and Probability Theory Vienna University
LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015
 LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015 1 LBP 1 LBP Tato metoda, publikovaná roku 1996, byla vyvinuta za účelem sestrojení jednoduchého a výpočetně rychlého nástroje pro
LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015 1 LBP 1 LBP Tato metoda, publikovaná roku 1996, byla vyvinuta za účelem sestrojení jednoduchého a výpočetně rychlého nástroje pro
1 Řešení soustav lineárních rovnic
 1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
Kolik existuje různých stromů na pevně dané n-prvkové množině vrcholů?
 Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Část 2 POROVNÁNÍ VÝKONNOSTI A POUŽITELNOSTI ARCHITEKTUR V TYPICKÝCH APLIKACÍCH
 Část 2 POROVNÁNÍ VÝKONNOSTI A POUŽITELNOSTI ARCHITEKTUR V TYPICKÝCH APLIKACÍCH Paralelizace kódu Rozdíl v přístupu k paralelizaci kódu si ukážeme na operaci násobení matice maticí: Mějme tři čtvercové
Část 2 POROVNÁNÍ VÝKONNOSTI A POUŽITELNOSTI ARCHITEKTUR V TYPICKÝCH APLIKACÍCH Paralelizace kódu Rozdíl v přístupu k paralelizaci kódu si ukážeme na operaci násobení matice maticí: Mějme tři čtvercové
Základní datové struktury
 Základní datové struktury Martin Trnečka Katedra informatiky, Přírodovědecká fakulta Univerzita Palackého v Olomouci 4. listopadu 2013 Martin Trnečka (UPOL) Algoritmická matematika 1 4. listopadu 2013
Základní datové struktury Martin Trnečka Katedra informatiky, Přírodovědecká fakulta Univerzita Palackého v Olomouci 4. listopadu 2013 Martin Trnečka (UPOL) Algoritmická matematika 1 4. listopadu 2013
Shapefile. Dalibor Tvrdý GIS 2010/11
 Shapefile Dalibor Tvrdý GIS 2010/11 Co je to shapefile? Shapefile je jednoduchý datový formát pro ukládání prostorových dat Vyvinut společností ESRI (Economic and Social Research Institute) začátkem 90.
Shapefile Dalibor Tvrdý GIS 2010/11 Co je to shapefile? Shapefile je jednoduchý datový formát pro ukládání prostorových dat Vyvinut společností ESRI (Economic and Social Research Institute) začátkem 90.
autorovu srdci... Petr Hliněný, FI MU Brno 1 FI: MA010: Průnikové grafy
 9 Krátké povídání o průnikových grafech Od této lekce teorie grafů se zaměříme lehce na několik vybraných partíı teorie grafů bĺızkých autorovu srdci... Naším prvním výběrem jsou průnikové grafy, což jsou
9 Krátké povídání o průnikových grafech Od této lekce teorie grafů se zaměříme lehce na několik vybraných partíı teorie grafů bĺızkých autorovu srdci... Naším prvním výběrem jsou průnikové grafy, což jsou
