% vyhledání prvku s max. velikostí v jednotlivých sloupcích matice X
|
|
|
- Anežka Machová
- před 6 lety
- Počet zobrazení:
Transkript
1 % % 4. cvičení z předmětu PPEL - MATLAB % % Lenka Šroubová, ZČU, FEL, KTE % lsroubov@kte.zcu.cz % X=round(20.*rand(5,7)) X = sum(x) % součet prvku v jednotlivých % sloupcích matice X sum(sum(x)) % součet prvku v matici X % je to součet součtu prvku ze sloupců matice X, tj. součet % předchozího vektoru ans 357 max(x) % vyhledání prvku s max. velikostí v jednotlivých sloupcích matice X max(max(x)) % vyhledání maxima, tj. prvku s max. velikostí z celé matice X % vyhledání maxima z maxim z jednotlivých sloupců matice X, tj. maximum % z předchozího vektoru ans 19 x=linspace(-pi, pi,100); % zadání vektoru x od -pi do pi ve 100 bodech y=(sin(x)).^2; plot(x,y) % v proměnné y je 100 hodnot funkce (sin(x)).^2 % odpovídá operaci sin(x).*sin(x) % jedná se o umocnění vektoru - nematicová operace.^ % násobí se stejnolehlé prvky ve vektorech s prvky sin(x) % vykreslení dvourozměrného grafu funkce (sin(x)).^2 x=linspace(-pi,pi,100); y=sin(x.^2); plot(x,y) % zadání vektoru x od -pi do pi % v proměnné y je 100 hodnot funkce sin(x.^2) % odpovídá operaci sin(x.*x) % jedná se o umocnění vektoru - nematicová operace.^ % násobí se stejnolehlé prvky ve vektorech x % vykreslení dvourozměrného grafu funkce y=sin(x.^2) % % m-file % skript neobsahuje klíčové slovo function % je to posloupnost příkazů
2 % ukádá se do souboru s příponou.m % spustí se napsáním názvu do příkazového řádku % proměnné vytvořené v rámci provádění skriptu zůstanou zachovány % (viz Workspace po provedeni skriptu) % funkce obsahuje klíčové slovo function, % hlavička je ve tvaru function výstup=nazev(vstup) % vstup, výstup nejsou povinné % hlavička zajišťuje přenos dat z a do funkce % proměnné ve funkci jsou lokální (po skončení posledního příkazu funkce % zaniknou) % výstupní proměnné zůstanou zachovány (viz Workspace) % graf a=5; b=2; c=a+b % skript graf.m % vykreslí průběh funkce sin x 2 % secte hodnoty v proměnných a,b 7 secti % skript secti.m % sečte 2 čísla daná v m-file a=5; b=2; % proměnné vytvořené v rámci provádění skriptu zůstanou zachovány % viz Workspace po provedeni skriptu obsahuje a,b,c 7 whos % vypíše seznam existujících proměnných Name Size Bytes Class a 1x1 8 double array b 1x1 8 double array c 1x1 8 double array Grand total is 3 elements using 24 bytes soucet % funkce soucet.m % sečte 2 čísla daná v m-file a=5; b=2; % hlavička je ve tvaru function nazev % proměnné a,b,c po skončení posledního příkazu funkce zaniknou % viz Workspace po provedeni funkce neobsahuje a,b,c 7 whos % vypíše seznam existujících proměnných % neobjeví se nic, proměnné a,b,c po skončení funkce zanikly a=6; b=-1; soucet_vst(a,b) % funkce soucet_vst.m
3 % hlavička je ve tvaru function nazev(vstup1,vstup2) % funkce se vstupními parametry a,b % sečte zadané proměnné a=6; b=-1; 5 k=3;l=-4; soucet_vst(k,l) % funkce soucet_vst.m % hlavička je ve tvaru function nazev(vstup1,vstup2) % funkce se vstupními parametry k,l % sečte zadané proměnné k=3;l=-4; -1 soucet_vst(3,5) % funkce soucet_vst.m % hlavička je ve tvaru function nazev(vstup1,vstup2) % funkce se vstupními parametry 3,5 % sečte čísla 3,5 8 m=[1,2]; n=[3,4]; soucet_vst(m,n) 4 6 % funkce soucet_vst.m % hlavička je ve tvaru function nazev(vstup1,vstup2) % funkce se vstupními parametry m,n % sečte vektory m=[1,2]; n=[3,4]; soucet_vst_strednik(9,5) % funkce soucet_vst_strednik.m % hlavička je ve tvaru function nazev(vstup1,vstup2) % funkce se vstupními parametry 9,5 % funkce proběhne, ale výsledek se nezobrazí, v m-file % je za proměnnou c středník, zabraňuje výpisu na % obrazovku soucet_vst_vyst(9,5) % funkce soucet_vst_vyst.m % hlavička je ve tvaru function výstup=nazev(vstupy) % funkce se vstupními parametry 9,5 a výstupem % výsledek se uloží do proměnné ans % výstupní proměnná zůstává zachována (viz Workspace) 14
4 whos % vypíše seznam právě existujících proměnných Name Size Bytes Class ans 1x1 8 double array y=soucet_vst_vyst(9,5) y = % funkce soucet_vst_vyst.m % hlavička je ve tvaru function výstup=nazev(vstupy) % funkce se vstupními parametry 9,5 a výstupem y % výsledek se uloží do proměnné y % výstupní proměnná zůstává zachována (viz Workspace) 14 whos % vypíše seznam právě existujících proměnných Name Size Bytes Class ans 1x1 8 double array y 1x1 8 double array u=8; v=-7; y=soucet_vst_vyst(u,v) y = % funkce soucet_vst_vyst.m % hlavička je ve tvaru function výstup=nazev(vstupy) % funkce se vstupními parametry u,v a výstupem y % výsledek se uloží do proměnné y % výstupní proměnná zůstává zachována (viz Workspace) 1 z=soucet_vst_vyst(5,3); % funkce soucet_vst_vyst.m % hlavička je ve tvaru function výstup=nazev(vstupy) % funkce se vstupními parametry 5,3 a výstupem z % výstupní proměnná zůstává zachována (viz Workspace) % výsledek se uloží do proměnné z, ale nezobrazí se na % obrazovku, za příkazem je středník whos % vypíše seznam právě existujících proměnných Name Size Bytes Class z 1x1 8 double array Grand total is 1 element using 8 bytes % % Polynomy % p=[2,-5,4,3,-6,2] % zadání vektoru p % polynom 2*x^5-5*x^4 + 4*x^3 + 3*x^2-6*x + 2*x^0 p = polyval(p,2) % vyčíslení polynomu p pro hodnotu 2 % tj. y=2*2^5-5*2^4 + 4*2^3 + 3*2^2-6*2 + 2 = v=[-2:2] v = % zadání vektoru v
5 w=polyval(p,v) % vyčíslení polynomu p pro všechny hodnoty z vektoru v w = % 2*(-2)^5-5*(-2)^4 + 4*(-2)^3 + 3*(-2)^2-6*(-2) + 2 = -150 % 2*(-1)^5-5*(-1)^4 + 4*(-1)^3 + 3*(-1)^2-6*(-1) + 2 = 0 % 2* 0^5-5* 0^4 + 4* 0^3 + 3* 0^2-6* = 2 % 2* 1^5-5* 1^4 + 4* 1^3 + 3* 1^2-6* = 0 % 2* 2^5-5* 2^4 + 4* 2^3 + 3* 2^2-6* = 18 x=roots(p) % kořeny polynomu p % výpočet rovnice % 2*x^5-5*x^4 + 4*x^3 + 3*x^2-6*x + 2 = 0 x = i i q=poly(x) % zjištění koeficientů polynomu z kořenů q = % polynom pro dané kořeny je 1*x^5-2.5*x^4 + 2*x^ *x^2-3*x + 1 % vynásobením 2 získáme p 2*x^5-5*x^4 + 4*x^3 + 3*x^2-6*x + 2 x=roots(q) % kořeny polynomu q jsou stejné jako kořeny polynomu p x = i i r=[4,0,5,2] % zadání polynomu r, % chybějící člen v polynomu je nahrazen 0 % polynom 4*x^3 + 5*x + 2 = 4*x^3 + 0*x^2 + 5*x + 2*x^0 r = s=conv(q,r) % násobení polynomů q,r s = % (1*x^5-2.5*x^4 + 2*x^ *x^2-3*x + 1)*(4*x^3-5*x + 2)= % =4*x^8-10*x^7 + 13*x^6-4.5*x^5-7*x^ *x^3-12*x^2 - x + 2 t=[1,-5,6] t = % zadání polynomu t % polynom 1*x^2-5*x + 6*x^0 x12=roots(t) % řešení kvadratické rovnice x^2-5*x + 6 = 0 x12 = u=[1,-2,2] u = % zadání polynomu t % polynom 1*x^2-2*x + 2
6 x12=roots(u) % řešení kvadratické rovnice x^2-2*x + 2 = 0 x12 = i i % % Graf - bod se souřadnicemi x,y % plot(3,5) % bod o souřadnicích x=3, y=5 (vykreslen jako modrá tečka) plot(3,5,'*') % bod o souřadnicích x=3, y=5 zobrazen jako hvězdička * plot(3,5,'o') % bod o souřadnicích x=3, y=5 zobrazen jako kolečko o plot(3,5,'x') % bod o souřadnicích x=3, y=5 zobrazen jako křížek x plot(3,5,'^') % bod o souřadnicích x=3, y=5 zobrazen jako trojúhelníček % % Proložení dat - bodů se souřadnicemi x,y (interpolace) % x=[1:7] % zadání vektoru x - x-ové souřadníce bodů x = y=[-1,0,2,2,3,1,-2] % zadání vektoru y - y-ové souřadníce bodů y = plot(x,y,'*') % vykreslení dvourozměrného grafu x,y % body se souřadnicmi x,y zobrazeny jako * k=polyfit(x,y,2) % nalezení koeficientů polynomu 2.stupně % pro proložení bodů x,y k = % body budou proloženy polynomem y(x) = *x^ *x % polynom 2.stupně - křivka - parabola xp=[1:0.1:7]; y2=polyval(k,xp); plot(xp,y2) plot(x,y,'*',xp,y2) % zadání bodů, ve kterých bude počítána aproximace % jemnější dělení osy x pro zobrazení křivky % vyčíslení polynomu k pro všechny tyto body % vykreslení dvourozměrného grafu - polynom 2.st. % vykreslení grafu - body (zobrazeny jako *) a jejich % proložení polynomem 2.st. (parabolou)
7 k3=polyfit(x,y,3) % nalezení koeficientů polynomu 3.stupně % pro proložení bodů x,y k3 = % body budou proloženy polynomem % y(x) = *x^ *x^ *x y3=polyval(k3,xp); % vyčíslení polynomu k3 pro všechny body vektoru xp plot(x,y,'*',xp,y2,xp,y3) % vykreslení dvourozměrného grafu % body - zobrazeny jako modré * % proložení polynomem 2.stupně - zobrazeno zeleně % proložení polynomem 3.stupně - zobrazeno červeně k5=polyfit(x,y,5) % nalezení koeficientů polynomu 5.stupně % pro proložení bodů x,y k5 = % body budou proloženy polynomem % y(x) = *x^ *x^ *x^ *x^ *x % první člen polynomu je nulový, v podstatě se jedná o polynom 4.st. y5=polyval(k5,xp); % vyčíslení polynomu k5 pro všechny body vektoru xp plot(x,y,'*',xp,y2,xp,y3,xp,y5) % vykreslení dvourozměrného grafu % body - zobrazeny jako modré * % proložení polynomem 2.stupně - zobrazeno zeleně % proložení polynomem 3.stupně - zobrazeno červeně % proložení polynomem 5.stupně - zobrazeno modrozeleně legend('body','polynom 2.st (parabola)','polynom 3.st','polynom 5.st') % zobrazení legendy ke grafu
8 % křivka daná polynomem 3.stupně téměř splývá % s křivkou 5.stupně => vhodné je proložení bodů % polynomem 3. stupně (5.st. je zbytečný) % % totéž proložení bodů, pokud není potřeba znát koeficienty polynomů, % nezavádí se proměnná, do které by se koeficienty polynomů ukládaly x=[1:7]; % zadání vektoru x - x-ové souřadníce bodů y=[-1,0,2,2,3,1,-2] % zadání vektoru y - y-ové souřadníce bodů xp=[1:0.1:7]; % zadání bodů, ve kterých bude počítána aproximace % jemnější dělení osy x pro zobrazení křivky y2=polyval(polyfit(x,y,2),xp); % vyčíslení polynomu 2.stupně pro všechny body xp y3=polyval(polyfit(x,y,3),xp); % vyčíslení polynomu 3.stupně pro všechny body xp y5=polyval(polyfit(x,y,5),xp); % vyčíslení polynomu 5.stupně pro všechny body xp plot(x,y,'*',xp,y2,xp,y3,xp,y5) % vykreslení dvourozměrného grafu % body - zobrazeny jako modré * % proložení polynomem 2.stupně - zobrazeno zeleně % proložení polynomem 3.stupně - zobrazeno červeně % proložení polynomem 5.stupně - zobrazeno modrozeleně legend('body','polynom 2.st (parabola)','polynom 3.st','polynom 5.st') % zobrazení legendy ke grafu diary off % přeruší ukládání do textového souboru
PPEL_3_cviceni_MATLAB.txt. % zadat 6 hodnot mezi cisly 2 a 8 % linspace (pocatek, konec, pocet bodu)
 %------------------------------------- % 3. cvičení z předmětu PPEL - MATLAB %------------------------------------- % Lenka Šroubová, ZČU, FEL, KTE % e-mail: lsroubov@kte.zcu.cz %-------------------------------------
%------------------------------------- % 3. cvičení z předmětu PPEL - MATLAB %------------------------------------- % Lenka Šroubová, ZČU, FEL, KTE % e-mail: lsroubov@kte.zcu.cz %-------------------------------------
- transpozice (odlišuje se od překlopení pro komplexní čísla) - překlopení matice pole podle hlavní diagonály, např.: A.' ans =
 '.' - transpozice (odlišuje se od překlopení pro komplexní čísla) - překlopení matice pole podle hlavní diagonály, např.: A.' 1 4 2 5 3-6 {} - uzavírají (obklopují) struktury (složené proměnné) - v případě
'.' - transpozice (odlišuje se od překlopení pro komplexní čísla) - překlopení matice pole podle hlavní diagonály, např.: A.' 1 4 2 5 3-6 {} - uzavírají (obklopují) struktury (složené proměnné) - v případě
pi Ludolfovo číslo π = 3,14159 e Eulerovo číslo e = 2,71828 (lze spočítat jako exp(1)), např. je v Octave, v MATLABu tato konstanta e není
 realmax maximální použitelné reálné kladné číslo realmin minimální použitelné reálné kladné číslo (v absolutní hodnotě, tj. číslo nejblíž k nule které lze použít) 0 pi Ludolfovo číslo π = 3,14159 e Eulerovo
realmax maximální použitelné reálné kladné číslo realmin minimální použitelné reálné kladné číslo (v absolutní hodnotě, tj. číslo nejblíž k nule které lze použít) 0 pi Ludolfovo číslo π = 3,14159 e Eulerovo
PPEL_4_cviceni_MATLAB.txt. % 4. cvičení z předmětu PPEL - MATLAB. % Lenka Šroubová, ZČU, FEL, KTE %
 %------------------------------------- % 4. cvičení z předmětu PPEL - MATLAB %------------------------------------- % Lenka Šroubová, ZČU, FEL, KTE % e-mail: lsroubov@kte.zcu.cz %-------------------------------------
%------------------------------------- % 4. cvičení z předmětu PPEL - MATLAB %------------------------------------- % Lenka Šroubová, ZČU, FEL, KTE % e-mail: lsroubov@kte.zcu.cz %-------------------------------------
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Polynomy opakování a pokračování 31. 10. 2012 Příklad: Funkce, která vykreslí
KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Polynomy opakování a pokračování 31. 10. 2012 Příklad: Funkce, která vykreslí
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných
 Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice 2. 11. 2011 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Polynomiální regrese polyfit(x, y, st) proloží množinu bodů
KTE / PPEL Počítačová podpora v elektrotechnice 2. 11. 2011 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Polynomiální regrese polyfit(x, y, st) proloží množinu bodů
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov 3. 10. 2012 Základy práce s výpočetními systémy opakování a pokračování
KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov 3. 10. 2012 Základy práce s výpočetními systémy opakování a pokračování
Stručný návod k programu Octave
 Stručný návod k programu Octave Octave je interaktivní program vhodný pro technické výpočty. Je nápadně podobný programu MATLAB, na rozdíl od něho je zcela zadarmo. Jeho domovská vebová stránka je http://www.octave.org/,
Stručný návod k programu Octave Octave je interaktivní program vhodný pro technické výpočty. Je nápadně podobný programu MATLAB, na rozdíl od něho je zcela zadarmo. Jeho domovská vebová stránka je http://www.octave.org/,
Příklad: Součet náhodných čísel ve vektoru s počtem prvků, které zadá uživatel, pomocí sum() a pomocí cyklu for. Ověříme, že příliš výpisů na
 Příklad: Součet náhodných čísel ve vektoru s počtem prvků, které zadá uživatel, pomocí sum() a pomocí cyklu for. Ověříme, že příliš výpisů na obrazovku zpomaluje tím, že zobrazíme okno (proužek) o stavu
Příklad: Součet náhodných čísel ve vektoru s počtem prvků, které zadá uživatel, pomocí sum() a pomocí cyklu for. Ověříme, že příliš výpisů na obrazovku zpomaluje tím, že zobrazíme okno (proužek) o stavu
Lineární algebra s Matlabem cvičení 3
 Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice 22.12.2010 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Příklad: Obvod RLC v sérii R=200 Ω L=0,5 H C=5. 10-6 F U 0
KTE / PPEL Počítačová podpora v elektrotechnice 22.12.2010 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Příklad: Obvod RLC v sérii R=200 Ω L=0,5 H C=5. 10-6 F U 0
X37SGS Signály a systémy
 X7SGS Signály a systémy Matlab minihelp (poslední změna: 0. září 2008) 1 Základní maticové operace Vytvoření matice (vektoru) a výběr konkrétního prvku matice vytvoření matice (vektoru) oddělovač sloupců
X7SGS Signály a systémy Matlab minihelp (poslední změna: 0. září 2008) 1 Základní maticové operace Vytvoření matice (vektoru) a výběr konkrétního prvku matice vytvoření matice (vektoru) oddělovač sloupců
Kreslení grafů v Matlabu
 Kreslení grafů v Matlabu Pavel Provinský 3. října 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu
Kreslení grafů v Matlabu Pavel Provinský 3. října 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu
Příklad: Řešte soustavu lineárních algebraických rovnic 10x 1 + 5x 2 +70x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 100 8x 1 + 9x 2 +
 Příklad: Řešte soustavu lineárních algebraických rovnic 1x 1 + 5x 2 +7x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 1 A * x = b 8x 1 + 9x 2 + x 3 +45x 4 +22x 5 = 319 3x 1 +12x 2 + 6x 3 + 8x
Příklad: Řešte soustavu lineárních algebraických rovnic 1x 1 + 5x 2 +7x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 1 A * x = b 8x 1 + 9x 2 + x 3 +45x 4 +22x 5 = 319 3x 1 +12x 2 + 6x 3 + 8x
více křivek v jednom grafu hold on přidrží aktuální graf v grafickém okně, lze nakreslit více grafů do jednoho grafického okna postupně hold off
 více křivek v jednom grafu hold on přidrží aktuální graf v grafickém okně, lze nakreslit více grafů do jednoho grafického okna postupně hold off vypnutí, konec možnosti kreslit více grafů do jednoho grafického
více křivek v jednom grafu hold on přidrží aktuální graf v grafickém okně, lze nakreslit více grafů do jednoho grafického okna postupně hold off vypnutí, konec možnosti kreslit více grafů do jednoho grafického
Základy algoritmizace a programování
 Základy algoritmizace a programování Práce se symbolickými proměnnými Práce s grafikou Přednáška 11 7. prosince 2009 Symbolické proměnné Zjednodušení aritmetických výrazů simplify (s) Příklady: >>syms
Základy algoritmizace a programování Práce se symbolickými proměnnými Práce s grafikou Přednáška 11 7. prosince 2009 Symbolické proměnné Zjednodušení aritmetických výrazů simplify (s) Příklady: >>syms
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
plot(c,'o') grid xlabel('re') ylabel('im')
 Vše platí i pro vektory a matice, např: C = [1+2i, -2+i, -3-4i; 4-3i, 1, i] C = 1.00 + 2.00i -2.00 + 1.00i -3.00-4.00i 4.00-3.00i 1.00 0 + 1.00i real(c) reálné části komplexních čísel (prvků matice C)
Vše platí i pro vektory a matice, např: C = [1+2i, -2+i, -3-4i; 4-3i, 1, i] C = 1.00 + 2.00i -2.00 + 1.00i -3.00-4.00i 4.00-3.00i 1.00 0 + 1.00i real(c) reálné části komplexních čísel (prvků matice C)
KTE / PPEL Počítačová podpora v elektrotechnice
 24. 9. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz ICQ: 361057825 http://home.zcu.cz/~lsroubov tel.: +420 377 634 623 Místnost: EK602 Katedra
24. 9. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz ICQ: 361057825 http://home.zcu.cz/~lsroubov tel.: +420 377 634 623 Místnost: EK602 Katedra
výsledek 2209 y (5) (x) y (4) (x) y (3) (x) 7y (x) 20y (x) 12y(x) (horní indexy značí derivaci) pro 1. y(x) = sin2x 2. y(x) = cos2x 3.
 Vypočtěte y (5) (x) y (4) (x) y (3) (x) 7y (x) 20y (x) 12y(x) (horní indexy značí derivaci) pro 1. y(x) = sin2x 2. y(x) = cos2x 3. y(x) = x sin2x 4. y(x) = x cos2x 5. y(x) = e x 1 6. y(x) = xe x 7. y(x)
Vypočtěte y (5) (x) y (4) (x) y (3) (x) 7y (x) 20y (x) 12y(x) (horní indexy značí derivaci) pro 1. y(x) = sin2x 2. y(x) = cos2x 3. y(x) = x sin2x 4. y(x) = x cos2x 5. y(x) = e x 1 6. y(x) = xe x 7. y(x)
Základy algoritmizace a programování
 Základy algoritmizace a programování Práce s maticemi Přednáška 9 23. listopadu 2009 Pole: vektory a matice Vektor (jednorozměrné pole) deklarace statická int v1[5]; dynamická int * v2; + přidělení paměti:
Základy algoritmizace a programování Práce s maticemi Přednáška 9 23. listopadu 2009 Pole: vektory a matice Vektor (jednorozměrné pole) deklarace statická int v1[5]; dynamická int * v2; + přidělení paměti:
Grafické výstupy v Octave/Matlabu a GnuPlotu
 co byste měli umět po dnešní lekci: nakreslit xy graf s popisky os nakreslit graf s více závislostmi, pro každou z nich vybrat symbol/barvu linie nakreslit více grafů do jednoho vykreslit 3D graf v různých
co byste měli umět po dnešní lekci: nakreslit xy graf s popisky os nakreslit graf s více závislostmi, pro každou z nich vybrat symbol/barvu linie nakreslit více grafů do jednoho vykreslit 3D graf v různých
Příklady k prvnímu testu - Matlab
 Příklady k prvnímu testu - Matlab March 13, 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu rozumíte.
Příklady k prvnímu testu - Matlab March 13, 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu rozumíte.
MODAM Popis okna. 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie, VŠB - TU Ostrava
 GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
1. LINEÁRNÍ ALGEBRA Vektory Operace s vektory... 8 Úlohy k samostatnému řešení... 8
 1 Lineární algebra 1 LINEÁRNÍ ALGEBRA 8 11 Vektory 8 111 Operace s vektory 8 8 112 Lineární závislost a nezávislost vektorů 8 8 113 Báze vektorového prostoru 9 9 12 Determinant 9 9 13 Matice 1 131 Operace
1 Lineární algebra 1 LINEÁRNÍ ALGEBRA 8 11 Vektory 8 111 Operace s vektory 8 8 112 Lineární závislost a nezávislost vektorů 8 8 113 Báze vektorového prostoru 9 9 12 Determinant 9 9 13 Matice 1 131 Operace
Úvod do práce s Matlabem
 Úvod do práce s Matlabem 1 Reálná čísla 1.1 Zadávání čísel Reálná čísla zadáváme s desetinnou tečkou (.), čísla lze také zadávat v exponenciálním tvaru například číslo 0.000014 zadáme takto 1.4e-5, číslo
Úvod do práce s Matlabem 1 Reálná čísla 1.1 Zadávání čísel Reálná čísla zadáváme s desetinnou tečkou (.), čísla lze také zadávat v exponenciálním tvaru například číslo 0.000014 zadáme takto 1.4e-5, číslo
KTE / PPEL Počítačová podpora v elektrotechnice
 KTE / PPEL Počítačová podpora v elektrotechnice 3. 12. 2014 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Grafy, úprava, popisky, vizualizace výsledků výpočtů opakování
KTE / PPEL Počítačová podpora v elektrotechnice 3. 12. 2014 Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Grafy, úprava, popisky, vizualizace výsledků výpočtů opakování
při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t =
 při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t = linspace(0,2*pi,5); plot(t,y,'b') y = sin(t); plot(t,y,'c') při
při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t = linspace(0,2*pi,5); plot(t,y,'b') y = sin(t); plot(t,y,'c') při
Seminář z MATLABU. Jiří Krejsa. A2/710 krejsa@fme.vutbr.cz
 Seminář z MATLABU Jiří Krejsa A2/710 krejsa@fme.vutbr.cz Obsah kurzu Posluchači se seznámí se základy systému Matlab, vědeckotechnickými výpočty, programováním v Matlabu včetně pokročilých technik, vizualizací
Seminář z MATLABU Jiří Krejsa A2/710 krejsa@fme.vutbr.cz Obsah kurzu Posluchači se seznámí se základy systému Matlab, vědeckotechnickými výpočty, programováním v Matlabu včetně pokročilých technik, vizualizací
cyklus s daným počtem opakování cyklus s podmínkou na začátku (cyklus bez udání počtu opakování)
 Řídící příkazy: if podmíněný příkaz switch přepínač for while cyklus s daným počtem opakování cyklus s podmínkou na začátku (cyklus bez udání počtu opakování) if logický_výraz příkaz; příkaz; příkaz; Podmínka
Řídící příkazy: if podmíněný příkaz switch přepínač for while cyklus s daným počtem opakování cyklus s podmínkou na začátku (cyklus bez udání počtu opakování) if logický_výraz příkaz; příkaz; příkaz; Podmínka
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
POZOR!!! atan (imag(c)./real(c)) počítá úhel v 1. a 4. kvadrantu, podle vzorce
 angle(c) počítá úhel ve všech 4 kvadrantech, např: angle(1+i)*180/pi ans = 45 angle(-1+i)*180/pi ans = 135 angle(-1-i)*180/pi ans = -135 angle(1-i)*180/pi ans = -45 POZOR!!! atan (imag(c)./real(c)) počítá
angle(c) počítá úhel ve všech 4 kvadrantech, např: angle(1+i)*180/pi ans = 45 angle(-1+i)*180/pi ans = 135 angle(-1-i)*180/pi ans = -135 angle(1-i)*180/pi ans = -45 POZOR!!! atan (imag(c)./real(c)) počítá
SEMESTRÁLNÍ PRÁCE Z X37SAS Zadání č. 7
 SEMESTRÁLNÍ PRÁCE Z X37SAS Zadání č. 7 Daniel Tureček St-lichý týden, 9:15 Zadání Určete periodu signálu s(k), určete stejnosměrnou složku, výkon, autokorelační funkci. Záznam signálu je v souboru persig2.
SEMESTRÁLNÍ PRÁCE Z X37SAS Zadání č. 7 Daniel Tureček St-lichý týden, 9:15 Zadání Určete periodu signálu s(k), určete stejnosměrnou složku, výkon, autokorelační funkci. Záznam signálu je v souboru persig2.
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Linearní algebra příklady
 Linearní algebra příklady 6. listopadu 008 9:56 Značení: E jednotková matice, E ij matice mající v pozici (i, j jedničku a jinak nuly. [...]... lineární obal dané soustavy vektorů. Popište pomocí maticového
Linearní algebra příklady 6. listopadu 008 9:56 Značení: E jednotková matice, E ij matice mající v pozici (i, j jedničku a jinak nuly. [...]... lineární obal dané soustavy vektorů. Popište pomocí maticového
Interpolace a aproximace dat.
 Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
Základy matematiky pracovní listy
 Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Maple. Petr Kundrát. Ústav matematiky, FSI VUT v Brně. Maple a základní znalosti z oblasti obyčejných diferenciálních rovnic.
 Obyčejné diferenciální rovnice s počítačovou podporou - Maple Petr Kundrát Ústav matematiky, FSI VUT v Brně Tento soubor vznikl za účelem ilustrace použití prostředí Maple k řešení a vizualizaci řešení
Obyčejné diferenciální rovnice s počítačovou podporou - Maple Petr Kundrát Ústav matematiky, FSI VUT v Brně Tento soubor vznikl za účelem ilustrace použití prostředí Maple k řešení a vizualizaci řešení
Úvod do Matlabu. Vít Vondrák Katedra aplikované matematiky FEI, VŠB-TU Ostrava
 Úvod do Matlabu Vít Vondrák Katedra aplikované matematiky FEI, VŠB-TU Ostrava Co je Matlab? Interaktivní softwarový balík MathWorks Inc. Matlab=MATrix LABoratory Základním typem proměnné je matice Číslo
Úvod do Matlabu Vít Vondrák Katedra aplikované matematiky FEI, VŠB-TU Ostrava Co je Matlab? Interaktivní softwarový balík MathWorks Inc. Matlab=MATrix LABoratory Základním typem proměnné je matice Číslo
Příklad elektrický obvod se stejnosměrným zdrojem napětí
 Příklad elektrický obvod se stejnosměrným zdrojem napětí Určete proudy 18, 23, 4, 5, 67 v obvodu na obr., je-li dáno: 1 = 1 Ω, 2 = 2 Ω, 3 = 3 Ω, 4 = 5 Ω, 5 = 3 Ω, 6 = 2 Ω, 7 = 4 Ω, 8 = 4,5 Ω, U = 6 V.
Příklad elektrický obvod se stejnosměrným zdrojem napětí Určete proudy 18, 23, 4, 5, 67 v obvodu na obr., je-li dáno: 1 = 1 Ω, 2 = 2 Ω, 3 = 3 Ω, 4 = 5 Ω, 5 = 3 Ω, 6 = 2 Ω, 7 = 4 Ω, 8 = 4,5 Ω, U = 6 V.
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Gymnázium Česká a Olympijských nadějí, České Budějovice, Česká 64, 37021
 Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Circular Harmonics. Tomáš Zámečník
 Circular Harmonics Tomáš Zámečník Úvod Circular Harmonics Reprezentace křivky, která je: podmonožinou RxR uzavřená funkcí úhlu na intervalu Dále budeme hovořit pouze o takovýchto křivkách/funkcích
Circular Harmonics Tomáš Zámečník Úvod Circular Harmonics Reprezentace křivky, která je: podmonožinou RxR uzavřená funkcí úhlu na intervalu Dále budeme hovořit pouze o takovýchto křivkách/funkcích
Programy na PODMÍNĚNÝ příkaz IF a CASE
 Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
y (5) (x) y (4) (x) + 4y (3) (x) 12y (x) 45y (x) 27y(x) (horní indexy značí derivaci) pro 3. y(x) = x sin 3x 4. y(x) = x cos 3x 9.
 Přezdívka: Jméno a příjmení: výsledek 101 Vypočtěte y x y 4 x + 4y x 12y x 4y x 27yx horní indexy značí derivaci pro 1. yx = sin x 2. yx = cos x. yx = x sin x 4. yx = x cos x. yx = e x 1 6. yx = xe x 7.
Přezdívka: Jméno a příjmení: výsledek 101 Vypočtěte y x y 4 x + 4y x 12y x 4y x 27yx horní indexy značí derivaci pro 1. yx = sin x 2. yx = cos x. yx = x sin x 4. yx = x cos x. yx = e x 1 6. yx = xe x 7.
BPC2E_C08 Parametrické 3D grafy v Matlabu
 BPC2E_C08 Parametrické 3D grafy v Matlabu Cílem cvičení je procvičit si práci se soubory a parametrickými 3D grafy v Matlabu. Úloha A. Protože budete řešit transformaci z kartézských do sférických souřadnic,
BPC2E_C08 Parametrické 3D grafy v Matlabu Cílem cvičení je procvičit si práci se soubory a parametrickými 3D grafy v Matlabu. Úloha A. Protože budete řešit transformaci z kartézských do sférických souřadnic,
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Základy programování: Algoritmizace v systému MATLAB
 Základy programování: Algoritmizace v systému MATLAB Magda Francová magda.francova@ujep.cz CN 463 23. února 2010 Úvodní hodina Podmínky pro zápočet 80% účast na hodinách (můžete 3x chybět). Úvodní hodina
Základy programování: Algoritmizace v systému MATLAB Magda Francová magda.francova@ujep.cz CN 463 23. února 2010 Úvodní hodina Podmínky pro zápočet 80% účast na hodinách (můžete 3x chybět). Úvodní hodina
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY
 VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY Vektoru můžeme přisoudit velikost. S vektory také můžeme provádět početní operace, které jsme zvyklí provádět s čísly, tzn. že je možné je sčítat, odčítat a
VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY Vektoru můžeme přisoudit velikost. S vektory také můžeme provádět početní operace, které jsme zvyklí provádět s čísly, tzn. že je možné je sčítat, odčítat a
KTE / PPEL Počítačová podpora v elektrotechnice
 19. 11. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Příklad řešení soustavy rovnic s komplexními čísly Stanovení
19. 11. 2014 KTE / PPEL Počítačová podpora v elektrotechnice Ing. Lenka Šroubová, Ph.D. email: lsroubov@kte.zcu.cz http://home.zcu.cz/~lsroubov Příklad řešení soustavy rovnic s komplexními čísly Stanovení
Základy algoritmizace a programování
 Základy algoritmizace a programování Příklady v MATLABu Přednáška 10 30. listopadu 2009 Řídící instrukce if else C Matlab if ( podmínka ) { } else { } Podmíněný příkaz if podmínka elseif podmínka2... else
Základy algoritmizace a programování Příklady v MATLABu Přednáška 10 30. listopadu 2009 Řídící instrukce if else C Matlab if ( podmínka ) { } else { } Podmíněný příkaz if podmínka elseif podmínka2... else
Lineární zobrazení. 1. A(x y) = A(x) A(y) (vlastnost aditivity) 2. A(α x) = α A(x) (vlastnost homogenity)
 4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
Příklad animace změny prokládané křivky při změně polohy jednoho z bodů
 3. Polynomy p x x x 3 ( ) = 2 5 Polynom je reprezentován řádkovým vektorem koeficientů jednotlivých řádů od nejvyššího dolů p = [1 0-2 -5]; kořeny polynomu r = roots(p) r = 2.0946-1.0473 + 1.1359i -1.0473-1.1359i
3. Polynomy p x x x 3 ( ) = 2 5 Polynom je reprezentován řádkovým vektorem koeficientů jednotlivých řádů od nejvyššího dolů p = [1 0-2 -5]; kořeny polynomu r = roots(p) r = 2.0946-1.0473 + 1.1359i -1.0473-1.1359i
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
Úvod do Matlabu. Praha & EU: Investujeme do vaší budoucnosti. 1 / 24 Úvod do Matlabu
 Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
Vytěžování dat, cvičení 1: Úvod do Matlabu Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Fakulta elektrotechnická, ČVUT 1 / 24 Úvod do Matlabu Proč proboha Matlab? Matlab je SW pro
Velmi stručný návod jak dostat data z Terminálu Bloomberg do R
 Velmi stručný návod jak dostat data z Terminálu Bloomberg do R Ondřej Pokora, PřF MU, Brno 11. března 2013 1 Terminál Bloomberg Klávesou Help získáte nápovědu. Dvojím stisknutím Help Help spustíte online
Velmi stručný návod jak dostat data z Terminálu Bloomberg do R Ondřej Pokora, PřF MU, Brno 11. března 2013 1 Terminál Bloomberg Klávesou Help získáte nápovědu. Dvojím stisknutím Help Help spustíte online
Aplikovaná matematika I
 Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
10. cvičení - LS 2017
 10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
Doňar B., Zaplatílek K.: MATLAB - tvorba uživatelských aplikací, BEN - technická literatura, Praha, (ISBN:
 http://portal.zcu.cz > Portál ZČU > Courseware (sem lze i přímo: http://courseware.zcu.cz) > Předměty po fakultách > Fakulta elektrotechnická > Katedra teoretické elektrotechniky > PPEL Doňar B., Zaplatílek
http://portal.zcu.cz > Portál ZČU > Courseware (sem lze i přímo: http://courseware.zcu.cz) > Předměty po fakultách > Fakulta elektrotechnická > Katedra teoretické elektrotechniky > PPEL Doňar B., Zaplatílek
vysledek = ((1:1:50).*(100-(1:1:50))) *ones(50,1) vysledek = ((1:1:75)./2).*sqrt(1:1:75) *ones(75,1)
 ZKOUŠKA ČÍSLO 1 x=linspace(0,100,20); y=sqrt(x); A=[x;y]'; save('data.txt','a','-ascii'); polyn = polyfit(x,y,3); polyv = polyval(polyn,x); plot(x,y,'r*') plot(x,polyv,'b') p1=[1 0 0 0 0 0 0-1]; k=roots(p1);
ZKOUŠKA ČÍSLO 1 x=linspace(0,100,20); y=sqrt(x); A=[x;y]'; save('data.txt','a','-ascii'); polyn = polyfit(x,y,3); polyv = polyval(polyn,x); plot(x,y,'r*') plot(x,polyv,'b') p1=[1 0 0 0 0 0 0-1]; k=roots(p1);
Martin Flusser. Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague. October 17, 2016
 ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
11MAMY LS 2017/2018. Úvod do Matlabu. 21. února Skupina 01. reseni2.m a tak dále + M souborem zadané funkce z příkladu 3 + souborem skupina.
 11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
11MAMY LS 2017/2018 Cvičení č. 2: 21. 2. 2018 Úvod do Matlabu. Jan Přikryl 21. února 2018 Po skupinách, na které jste se doufám rozdělili samostatně včera, vyřešte tak, jak nejlépe svedete, níže uvedená
Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích. MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista
 Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista Matematický software MAPLE slouží ke zpracování matematických problémů pomocí jednoduchého
Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista Matematický software MAPLE slouží ke zpracování matematických problémů pomocí jednoduchého
Příklady k druhému testu - Matlab
 Příklady k druhému testu - Matlab 20. března 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu
Příklady k druhému testu - Matlab 20. března 2013 Instrukce: Projděte si všechny příklady. Každý příklad se snažte pochopit. Pak vymyslete a naprogramujte příklad podobný. Tím se ujistíte, že příkladu
otočení matice o 180
 A=[,2,3;4,5,6] A = 2 3 4 5 6 rot90(a) 3 6 2 5 4 otočení matice o 90 (proti směru hodinových ručiček) A.' prostá transpozice 4 2 5 3 6 rot90(rot90(a)) 6 5 4 3 2 otočení matice o 80 rot90(rot90(rot90(a)))
A=[,2,3;4,5,6] A = 2 3 4 5 6 rot90(a) 3 6 2 5 4 otočení matice o 90 (proti směru hodinových ručiček) A.' prostá transpozice 4 2 5 3 6 rot90(rot90(a)) 6 5 4 3 2 otočení matice o 80 rot90(rot90(rot90(a)))
Operátory pro maticové operace (operace s celými maticemi) * násobení maticové Pro čísla platí: 2*2
 * násobení maticové Pro čísla platí: Pro matice - násobení inverzní maticí inv inverzní matice A -1 k dané matici A je taková matice, která po vynásobení s původní maticí dá jednotkovou matici. Inverzní
* násobení maticové Pro čísla platí: Pro matice - násobení inverzní maticí inv inverzní matice A -1 k dané matici A je taková matice, která po vynásobení s původní maticí dá jednotkovou matici. Inverzní
Příklady na testy předmětu Seminář z matematiky pro studenty fakulty strojní TUL.
 Příklady na testy předmětu Seminář z matematiky pro studenty fakulty strojní TUL. Jméno a příjmení(čitelně): varianta č. 90 Přezdívka(nepovinné): Zde pište své výsledky Napište rovnici přímky procházející
Příklady na testy předmětu Seminář z matematiky pro studenty fakulty strojní TUL. Jméno a příjmení(čitelně): varianta č. 90 Přezdívka(nepovinné): Zde pište své výsledky Napište rovnici přímky procházející
1 Funkce dvou a tří proměnných
 1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita
 Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita ročník:2 studijní skupina:2 Page 1 Excentrický klikový mechanismus je zadán parametry
Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita ročník:2 studijní skupina:2 Page 1 Excentrický klikový mechanismus je zadán parametry
VI. Maticový počet. VI.1. Základní operace s maticemi. Definice. Tabulku
 VI Maticový počet VI1 Základní operace s maticemi Definice Tabulku a 11 a 12 a 1n a 21 a 22 a 2n, a m1 a m2 a mn kde a ij R, i = 1,, m, j = 1,, n, nazýváme maticí typu m n Zkráceně zapisujeme (a ij i=1m
VI Maticový počet VI1 Základní operace s maticemi Definice Tabulku a 11 a 12 a 1n a 21 a 22 a 2n, a m1 a m2 a mn kde a ij R, i = 1,, m, j = 1,, n, nazýváme maticí typu m n Zkráceně zapisujeme (a ij i=1m
ALGORITMIZACE A PROGRAMOVÁNÍ
 Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU MODELOVÁNÍ MATLABEM
 SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU MODELOVÁNÍ MATLABEM Jméno: Petr Thür Os. číslo: A04236 E-mail: petr.thur@post.cz Zadání: 8-D Datum vypracování: 7. 5. 2005 Zadání: Sestavte program (funkční M-soubor) pro vykreslení
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU MODELOVÁNÍ MATLABEM Jméno: Petr Thür Os. číslo: A04236 E-mail: petr.thur@post.cz Zadání: 8-D Datum vypracování: 7. 5. 2005 Zadání: Sestavte program (funkční M-soubor) pro vykreslení
Numerická integrace a derivace
 co byste měli umět po dnešní lekci: integrovat funkce různými metodami (lichoběžníkové pravidlo, Simpson,..) počítat vícenásobné integrály počítat integrály podél křivky a integrály komplexních funkcí
co byste měli umět po dnešní lekci: integrovat funkce různými metodami (lichoběžníkové pravidlo, Simpson,..) počítat vícenásobné integrály počítat integrály podél křivky a integrály komplexních funkcí
5. cvičení z Matematiky 2
 5. cvičení z Matematiky 2 21.-25. března 2016 5.1 Nalezněte úhel, který v bodě 1, 0, 0 svírají grafy funkcí fx, y ln x 2 + y 2 a gx, y sinxy. Úhel, který svírají grafy funkcí je dán jako úhel mezi jednotlivými
5. cvičení z Matematiky 2 21.-25. března 2016 5.1 Nalezněte úhel, který v bodě 1, 0, 0 svírají grafy funkcí fx, y ln x 2 + y 2 a gx, y sinxy. Úhel, který svírají grafy funkcí je dán jako úhel mezi jednotlivými
MODAM Popis okna. 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie, VŠB - TU Ostrava
 GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
Skriptování aneb funkce a procedury, cykly a vstupy a výstupy
 co byste měli umět po dnešní lekci: napsat skript a spustit jej napsat externí funkci a zpracovat její návratovou hodnotu/y využívat cykly a podmínky používat formátovaný výstup používat help skript posloupnost
co byste měli umět po dnešní lekci: napsat skript a spustit jej napsat externí funkci a zpracovat její návratovou hodnotu/y využívat cykly a podmínky používat formátovaný výstup používat help skript posloupnost
Literatura: Kapitola 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Metoda sítí v 1D. Myšlenka náhrada derivací diferenčními podíly Přibližné řešení okrajových úloh Aproximace vlastních čísel Literatura: Kapitola 2 d) ze skript Karel Rektorys:
Předmět: MA4 Dnešní látka: Metoda sítí v 1D. Myšlenka náhrada derivací diferenčními podíly Přibližné řešení okrajových úloh Aproximace vlastních čísel Literatura: Kapitola 2 d) ze skript Karel Rektorys:
Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10
 Obsah Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10 KAPITOLA 1 Úvod 11 Dostupná rozšíření Matlabu 13 Alternativa zdarma GNU Octave 13 KAPITOLA 2 Popis prostředí
Obsah Předmluva 9 Obsah knihy 9 Typografické konvence 10 Informace o autorovi 10 Poděkování 10 KAPITOLA 1 Úvod 11 Dostupná rozšíření Matlabu 13 Alternativa zdarma GNU Octave 13 KAPITOLA 2 Popis prostředí
smaže n-tý sloupec matice A vybere hodnotu 6.,1.,3.,2.prvku vektoru a a1 =
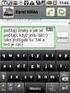 1. Způsoby zadání vektorů, ukládání proměnných >> repmat(a,2,2) ans = 1 2 3 1 2 3 1 2 3 1 2 3 >>M = [ ] uloží prázdnou matici >>A(m,:) = [ ] smaže m-tý řádek matice A >>A(:,n) = [ ] smaže n-tý sloupec
1. Způsoby zadání vektorů, ukládání proměnných >> repmat(a,2,2) ans = 1 2 3 1 2 3 1 2 3 1 2 3 >>M = [ ] uloží prázdnou matici >>A(m,:) = [ ] smaže m-tý řádek matice A >>A(:,n) = [ ] smaže n-tý sloupec
Řešení diferenciálních rovnic v MATLABu
 Řešení diferenciálních rovnic v MATLABu Základy algoritmizace a programování Přednáška 23. listopadu 2011 Co řešíme Obyčejné diferenciální rovnice prvního řádu: separovatelné lineární exaktní druhého řádu,
Řešení diferenciálních rovnic v MATLABu Základy algoritmizace a programování Přednáška 23. listopadu 2011 Co řešíme Obyčejné diferenciální rovnice prvního řádu: separovatelné lineární exaktní druhého řádu,
A0B01LAA Lineární algebra a aplikace (příklady na cvičení- řešení)
 A0B0LAA Lineární algebra a aplikace příklady na cvičení- řešení Martin Hadrava martin@hadrava.eu. ledna 0.týdenod9.9. Řešení soustav lineárních rovnic Gaussovou eliminační metodou diskuse počtu řešení..
A0B0LAA Lineární algebra a aplikace příklady na cvičení- řešení Martin Hadrava martin@hadrava.eu. ledna 0.týdenod9.9. Řešení soustav lineárních rovnic Gaussovou eliminační metodou diskuse počtu řešení..
plot() vytváří dvou-dimenzionální grafy, mnoho různých kombinací vstupních argumentů, nejjednodušší formou je plot(y), plot(x,y).
 plot() vytváří dvou-dimenzionální grafy, mnoho různých kombinací vstupních argumentů, nejjednodušší formou je plot(y), plot(x,y). plot(y) vykreslí hodnoty vektoru y v závislosti na jejich indexu (pořadí
plot() vytváří dvou-dimenzionální grafy, mnoho různých kombinací vstupních argumentů, nejjednodušší formou je plot(y), plot(x,y). plot(y) vykreslí hodnoty vektoru y v závislosti na jejich indexu (pořadí
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Lineární algebra Operace s vektory a maticemi
 Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení
 Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
MATLAB základy. Roman Stanec 27.9.2007 PEF MZLU
 MATLAB základy Roman Stanec 27.9.2007 PEF MZLU Náplň cvičení Matlab představení a motivace Seznámení s prostředím Proměnné a výrazy Řídící struktury Funkce Základní úpravy matic Import dat z tabulkového
MATLAB základy Roman Stanec 27.9.2007 PEF MZLU Náplň cvičení Matlab představení a motivace Seznámení s prostředím Proměnné a výrazy Řídící struktury Funkce Základní úpravy matic Import dat z tabulkového
Vektorový prostor. Př.1. R 2 ; R 3 ; R n Dvě operace v R n : u + v = (u 1 + v 1,...u n + v n ), V (E 3 )...množina vektorů v E 3,
 Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Úvod do programování. Lekce 7
 I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í Inovace a zvýšení atraktivity studia optiky reg. č.: CZ.1.07/2.2.00/07.0289 Úvod do programování Lekce 7 Tento projekt je spolufinancován Evropským
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í Inovace a zvýšení atraktivity studia optiky reg. č.: CZ.1.07/2.2.00/07.0289 Úvod do programování Lekce 7 Tento projekt je spolufinancován Evropským
Téma je podrobně zpracováno ve skriptech [1], kapitola 6, strany
![Téma je podrobně zpracováno ve skriptech [1], kapitola 6, strany Téma je podrobně zpracováno ve skriptech [1], kapitola 6, strany](/thumbs/44/23250842.jpg) 3 Metoda nejmenších čtverců 3 Metoda nejmenších čtverců Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 6, strany 73-80. Jedná se o třetí možnou metodu aproximace,
3 Metoda nejmenších čtverců 3 Metoda nejmenších čtverců Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 6, strany 73-80. Jedná se o třetí možnou metodu aproximace,
Univerzitní licence MATLABu. Pište mail na: se žádostí o nejnovější licenci MATLABu.
 Univerzitní licence MATLABu Pište mail na: operator@service.zcu.cz se žádostí o nejnovější licenci MATLABu. * násobení maticové K = L = 1 2 5 6 3 4 7 8 Příklad: M = K * L N = L * K (2,2) = (2,2) * (2,2)
Univerzitní licence MATLABu Pište mail na: operator@service.zcu.cz se žádostí o nejnovější licenci MATLABu. * násobení maticové K = L = 1 2 5 6 3 4 7 8 Příklad: M = K * L N = L * K (2,2) = (2,2) * (2,2)
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
Rozvinutí funkce do Maclaurinova rozvoje
 Rozvinutí funkce do Maclaurinova rozvoje 1.1 Úvod Na přednáškách z matematické analýzy mě zaujala teorie o mocninných řadách a rozvojích, kde jsem zjistil, že každá vhodná funkce lze rozvinout do nekonečné
Rozvinutí funkce do Maclaurinova rozvoje 1.1 Úvod Na přednáškách z matematické analýzy mě zaujala teorie o mocninných řadách a rozvojích, kde jsem zjistil, že každá vhodná funkce lze rozvinout do nekonečné
Matematické symboly a značky
 Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Nápověda k aplikaci GraphGUI
 Nápověda k aplikaci GraphGUI 1 APLIKACE Aplikace slouží pro zobrazování závislosti několika veličin s různými jednotkami a rozsahy na čase v jednom grafu. Do aplikace lze importovat data ze souborů různých
Nápověda k aplikaci GraphGUI 1 APLIKACE Aplikace slouží pro zobrazování závislosti několika veličin s různými jednotkami a rozsahy na čase v jednom grafu. Do aplikace lze importovat data ze souborů různých
Program SMP pro kombinované studium
 Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
Cvi ení 1. Cvi ení 1. Modelování systém a proces. Mgr. Lucie Kárná, PhD. March 2, 2018
 Cvi ení 1 Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 2, 2018 1 Organizace cvi ení 2 Za ínáme Základní operace Základní funkce 3 Simulink Princip práce v Simulinku Jednoduché
Cvi ení 1 Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 2, 2018 1 Organizace cvi ení 2 Za ínáme Základní operace Základní funkce 3 Simulink Princip práce v Simulinku Jednoduché
DEFINICE,VĚTYADŮKAZYKÚSTNÍZKOUŠCEZMAT.ANALÝZY Ib
 INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
Matematika 3. Úloha 1. Úloha 2. Úloha 3
 Matematika 3 Úloha 1 Co lze říci o funkci imaginární část komplexního čísla která každému komplexnímu číslu q přiřazuje číslo Im(q)? a. Je to funkce mnohoznačná. b. Je to reálná funkce komplexní proměnné.
Matematika 3 Úloha 1 Co lze říci o funkci imaginární část komplexního čísla která každému komplexnímu číslu q přiřazuje číslo Im(q)? a. Je to funkce mnohoznačná. b. Je to reálná funkce komplexní proměnné.
