Návrh Designu: Radek Mařík
|
|
|
- Přemysl Navrátil
- před 6 lety
- Počet zobrazení:
Transkript
1
2 1. 7. Najděte nejdelší rostoucí podposloupnost dané posloupnosti. Použijte metodu dynamického programování, napište tabulku průběžných délek částečných výsledků a tabulku předchůdců. a) b)
3 2. Určete, jak lze využít nebo přizpůsobit metodu hledání nejdelší rostoucí podposloupnosti pro hledání a) nejdelší klesající podposloupnosti, b) nejdelší neklesající podposloupnosti, c) nejdelší konstantní podposloupnosti, d) nejdelší alternující posloupnosti. (V alternující posloupnosti a[1], a[2],... a[n] platí (a[k] a[k1])* (a[k+1] a[k]) < 0, pro k = 2, 3,..., n1.)
4 3. 1. Kolika různými způsoby lze uzávorkovat součin matic? (Různé způsoby závorkování odpovídají různému průběhu výpočtu a obecně různým mezivýsledkům. Závorkování (X) a ((X)) pokládáme za totožné.) a) A B C D b) A B C D E
5 4. Předpokládejme, že na vypočtení součinu matic A B je zapotřebí r s t operací, kde A R rs a B R st. Určete, kolik operací je třeba na výpočet součinu (A B) C a kolik na výpočet součinu A (B C), pokud a) A R n2, B R 23, C R 34 b) A R 5n, B R n4, C R 4n c) A R nn, B R n100, C R 100n
6 5. Určete, pro které hodnoty n je výhodnější vypočítat součin (A B) C než vypočítat součin A (B C). a) A R n2, B R 23, C R 34 b) A R 5n, B R n4, C R 4n c) A R nn, B R n100, C R 100n
7 6. Rozměry matic A, B, C, D, E, jsou po řadě 2 5, 5 3, 3 6, 6 2, 2 4. Určete metodou dynamického programování, jak uzávorkovat součin A B C D E, aby počet operací násobení dvou čísel během výpočtu celého součinu byl co nejmenší. Kolik to bude operací?
8 7. Rozměry matic A, B, C, D, E, jsou stejné jako v předchozí úloze. Z důvodů např. testování HW/SW si přejeme součin uzávorkovat tak, aby počet operací násobení dvou čísel byl co největší. Rozhodněte, zda lze metodu hledání co nejvýhodnějšího uzávorkování přizpůsobit pro řešení této modifikované úlohy. Jaký bude algoritmus řešení?
9 8. Použijte myšlenku výpočtu optimálního uzávorkování v součinu matic pro řešení jednodušší úlohy: Kolika různými způsoby lze uzávorkovat součin n matic? Budete potřebovat 2D nebo 1D tabulku? Ověřte výsledek pro několik malých hodnot n, měl by vyjít
10 9. Optimální binární vyhledávací strom a) minimalizuje hloubku stromu, b) maximalizuje cenu uzlů, c) maximalizuje počet listů, d) minimalizuje dobu vyhledávání ve stromu, e) minimalizuje délku cesty z kořene do libovolného listu.
11 10. Je dáno n klíčů. Společně s každým klíčem je dána také pravděpodobnost dotazu na tento klíč. Nalezení kořene optimálního BVS sestaveného z těchto klíčů má asymptotickou složitost a) O(log(n)) b) (n) c) O(n log(n)) d) (n 2 ) e) (2 n )
12 11a. Pravděpodobnost dotazu na konkrétní klíče daného BVS je uvedena u jednotlivých uzlů. Dlouhodobě je průměrný počet navštívených uzlů při jednom dotazu na klíč ve stromu roven a) 0.5 b) 1.0 c) 1.25 d) 1.5 e) 1.75
13 11b. Pravděpodobnost dotazu na konkrétní klíče daného BVS je uvedena u jednotlivých uzlů. Dlouhodobě je průměrný počet navštívených uzlů při jednom dotazu na klíč ve stromu roven a) 0.2 b) 1.0 c) 2.15 d) 2.2 e) 2.5
14 Pravděpodobnost dotazu na jednotlivé klíče v obou daných BVS je tato: A: 0.10 B: 0.20 C: 0.25 D: 0.05 E: 0.10 F: 0.25 G: 0.05 Vypočtěte, který strom je výhodnější pro operaci FIND. 12. C D E F G B A C D E F G B A C D E F G B A C D E F G B A
15 13. Určete, jak bude vypadat optimální BVS, když jej vybudujeme pro 7 klíčů s frekvencemi: a) E 0.04 F 0.05 G 0.22 H 0.04 I 0.06 J 0.05 K 0.15 b) A 0.10 B 0.10 C 0.25 D 0.35 E 0.10 F 0.05 G 0.05
16 14. V dané matici začneme kdekoli v prvním sloupci a dále vždy postupujeme jen ve směru SV, V, JV až kamkoli do posledního sloupce. Cena cesty je součet hodnot navštívených polí. Jaká může být nejmenší?
17 15. Maticí cestujeme podle stejných pravidel jako v předchozí úloze. Cena za cestu je součet absolutních hodnot rozdílů cen sousedních navštívených polí
18 16. Dva dané řetězce mají oba délku n. Nejdelší společnou podposloupnost těchto řetězců lze nalézt pomocí dynamického programování v čase a) (log(n)) b) (n) c) (n log(n)) d) (n 2 ) e) (n 3 )
19 17. Najděte nejdelší společnou podposloupnost dvojice řetězců a) A: B: (B = A odzadu) b) A: B: c) A: B: (B = doplněk A)
20 18. Řešte neomezenou variantu úlohy batohu pro kapacitu 10 a čtyři předměty, jejichž váhy jsou postupně 1, 3, 4, 6 a ceny jsou ve stejném pořadí předmětů 11, 33, 45, 65. Jaká bude maximální cena předmětů v batohu?
21 19. Řešte 0/1 variantu úlohy batohu pro kapacitu 130 a pět předmětů, jejichž váhy jsou postupně 20, 30, 40, 50, 60 a ceny jsou ve stejném pořadí předmětů 11, 33, 45, 58, 65. Jaká bude maximální cena předmětů v batohu? Uvažte, jak se vyhnout tabulce se cca 130 sloupci a upravte postup řešení tak, aby stačilo řádově méně sloupců.
22 20. Každá zásilka ve skladu má určenou váhu a je nutno všechy zásilky naložit na dvě přistavené dodávky tak, aby se váhy nákladů na obou dodávkách lišily co nejméně. Zdůvodněte, zda lze či nelze metodu DP pro řešení úlohy batohu využít i v této situaci.
23 21. Kryštof staví malé sportovní lodě. Vyrábí jich několik typů a vždy se věnuje stavbě jen jedné lodě, dokud není hotová. Pro každý typ lodě zná počet dní potřebný ke stavbě lodě a zná svůj zisk z jejího prodeje. Ví, kolik dní bude letos v sezóně věnovat své práci. Navrhněte metodu dynamického programování, která bude maximalizovat Kryštofův výdělek za letošní sezónu.
Dynamické programování UIN009 Efektivní algoritmy 1
 Dynamické programování. 10.3.2005 UIN009 Efektivní algoritmy 1 Srovnání metody rozděl a panuj a dynamického programování Rozděl a panuj: top-down Dynamické programování: bottom-up Rozděl a panuj: překrývání
Dynamické programování. 10.3.2005 UIN009 Efektivní algoritmy 1 Srovnání metody rozděl a panuj a dynamického programování Rozděl a panuj: top-down Dynamické programování: bottom-up Rozděl a panuj: překrývání
f(x,y) = max ( f(x 1, y 1)+ f(x 1,y) ) + f(x,y 1) +1 jinak f(x,y,z) = f(x 1, y 1, z 1)+ f(x 1,y,z) + f(x,y 1,z) + f(x,y,z 1)+1 jinak
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Dynamické programování
 Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
bin arn ı vyhled av an ı a bst Karel Hor ak, Petr Ryˇsav y 23. bˇrezna 2016 Katedra poˇ c ıtaˇ c u, FEL, ˇ CVUT
 binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
a) b) c) Radek Mařík
 2012-03-20 Radek Mařík 1. Čísla ze zadané posloupnosti postupně vkládejte do prázdného binárního vyhledávacího stromu (BVS), který nevyvažujte. Jak bude vypadat takto vytvořený BVS? Poté postupně odstraňte
2012-03-20 Radek Mařík 1. Čísla ze zadané posloupnosti postupně vkládejte do prázdného binárního vyhledávacího stromu (BVS), který nevyvažujte. Jak bude vypadat takto vytvořený BVS? Poté postupně odstraňte
Dynamické programování. Optimální binární vyhledávací strom
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamické programování Optimální binární vyhledávací strom Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamické programování Optimální binární vyhledávací strom Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The
Dynamické programování
 ALG 11 Dynamické programování Úloha batohu neomezená Úloha batohu /1 Úloha batohu / Knapsack problem Máme N předmětů, každý s váhou Vi a cenou Ci (i = 1, 2,..., N) a batoh s kapacitou váhy K. Máme naložit
ALG 11 Dynamické programování Úloha batohu neomezená Úloha batohu /1 Úloha batohu / Knapsack problem Máme N předmětů, každý s váhou Vi a cenou Ci (i = 1, 2,..., N) a batoh s kapacitou váhy K. Máme naložit
R zné algoritmy mají r znou složitost
 / / zné algoritmy mají r znou složitost Dynamické programování / / Definice funkce Otázka Program f(x,y) = (x = ) (y = ) f(x, y-) + f(x-,y) (x > ) && (y > ) f(,) =? int f(int x, int y) { if ( (x == ) (y
/ / zné algoritmy mají r znou složitost Dynamické programování / / Definice funkce Otázka Program f(x,y) = (x = ) (y = ) f(x, y-) + f(x-,y) (x > ) && (y > ) f(,) =? int f(int x, int y) { if ( (x == ) (y
Dynamické programování
 ALG 0 Dynamické programování zkratka: DP Zdroje, přehledy, ukázky viz https://cw.fel.cvut.cz/wiki/courses/a4balg/literatura_odkazy 0 Dynamické programování Charakteristika Neřeší jeden konkrétní typ úlohy,
ALG 0 Dynamické programování zkratka: DP Zdroje, přehledy, ukázky viz https://cw.fel.cvut.cz/wiki/courses/a4balg/literatura_odkazy 0 Dynamické programování Charakteristika Neřeší jeden konkrétní typ úlohy,
Vyvažování a rotace v BVS, všude se předpokládá AVL strom
 Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Zdůvodněte, proč funkce n lg(n) roste alespoň stejně rychle nebo rychleji než než funkce lg(n!). Symbolem lg značíme logaritmus o základu 2.
 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 8 9 30 31 3 Zdůvodněte, proč funkce f(n) = n log(n) 1 n 1/ roste rychleji než funkce g(n) = n. Zdůvodněte, proč funkce f(n) = n 3/ log(n) roste
Příklad 1/23. Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) d) g(x) Ω(f(x))
 Příklad 1/23 Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) c) g(x) Θ(f(x)) d) g(x) Ω(f(x)) e) g(x) Ο(f(x)) 1 Příklad 2/23 Pro rostoucí spojité
Příklad 1/23 Pro rostoucí spojité fukce f(x), g(x) platí f(x) Ω(g(x)). Z toho plyne, že: a) f(x) Ο(g(x)) b) f(x) Θ(g(x)) c) g(x) Θ(f(x)) d) g(x) Ω(f(x)) e) g(x) Ο(f(x)) 1 Příklad 2/23 Pro rostoucí spojité
Dynamické programování
 Dynamické programování Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 207 Datové struktury a algoritmy, B6B36DSA 05/207, Lekce 2
Dynamické programování Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 207 Datové struktury a algoritmy, B6B36DSA 05/207, Lekce 2
Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce)
 13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10
 Úlohy- 2.cvičení 1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10 2. Převeďte dané desetinné číslo do dvojkové soustavy (DEC -> BIN): a) 0,8125 10 b) 0,35 10
Úlohy- 2.cvičení 1. Převeďte dané číslo do dvojkové, osmičkové a šestnáctkové soustavy: a) 759 10 b) 2578 10 2. Převeďte dané desetinné číslo do dvojkové soustavy (DEC -> BIN): a) 0,8125 10 b) 0,35 10
NPRG030 Programování I, 2018/19 1 / :03:07
 NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
NEJKRATŠÍ CESTY I. Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze
 NEJKRATŠÍ CESTY I Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 7 Evropský sociální fond Praha & EU: Investujeme do vaší
NEJKRATŠÍ CESTY I Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2010/2011, Lekce 7 Evropský sociální fond Praha & EU: Investujeme do vaší
Binární soubory (datové, typované)
 Binární soubory (datové, typované) - na rozdíl od textových souborů data uložena binárně (ve vnitřním tvaru jako v proměnných programu) není čitelné pro člověka - všechny záznamy téhož typu (může být i
Binární soubory (datové, typované) - na rozdíl od textových souborů data uložena binárně (ve vnitřním tvaru jako v proměnných programu) není čitelné pro člověka - všechny záznamy téhož typu (může být i
Binární vyhledávací stromy pokročilé partie
 Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A
 Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A Každá úloha je hodnocena maximálně 25 body. Všechny své odpovědi zdůvodněte! 1. Postavte na stůl do řady vedle
Informatika navazující magisterské studium Přijímací zkouška z informatiky 2018 varianta A Každá úloha je hodnocena maximálně 25 body. Všechny své odpovědi zdůvodněte! 1. Postavte na stůl do řady vedle
Složitosti základních operací B + stromu
 Složitosti základních operací B + stromu Radim Bača VŠB Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky ŠKOMAM 2010-1- 28/1/2010 Složitosti základních operací B +
Složitosti základních operací B + stromu Radim Bača VŠB Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky ŠKOMAM 2010-1- 28/1/2010 Složitosti základních operací B +
Dynamické programování
 ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
Metody síťové analýzy
 Metody síťové analýzy Řeší problematiku složitých systémů, zejména pak vazby mezi jejich jednotlivými prvky. Vychází z teorie grafů. Základní metody síťové analýzy: CPM (Critical Path Method) deterministický
Metody síťové analýzy Řeší problematiku složitých systémů, zejména pak vazby mezi jejich jednotlivými prvky. Vychází z teorie grafů. Základní metody síťové analýzy: CPM (Critical Path Method) deterministický
Datový typ prioritní fronta Semestrální práce z předmětu 36PT
 Datový typ prioritní fronta Semestrální práce z předmětu 36PT Martin Tůma Cvičení 113, Út 18:00 22. května 2004 Specifikace problému Často potřebujeme přístup k informacím, tak aby tyto byly seřazeny podle
Datový typ prioritní fronta Semestrální práce z předmětu 36PT Martin Tůma Cvičení 113, Út 18:00 22. května 2004 Specifikace problému Často potřebujeme přístup k informacím, tak aby tyto byly seřazeny podle
ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ
 ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2/2, Lekce Evropský sociální fond Praha & EU: Investujeme
ORIENTOVANÉ GRAFY, REPREZENTACE GRAFŮ Doc. RNDr. Josef Kolář, CSc. Katedra teoretické informatiky, FIT České vysoké učení technické v Praze BI-GRA, LS 2/2, Lekce Evropský sociální fond Praha & EU: Investujeme
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_148_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_148_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
5. Dynamické programování
 5. Dynamické programování BI-EP1 Efektivní programování 1 ZS 2011/2012 Ing. Martin Kačer, Ph.D. 2010-11 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické
5. Dynamické programování BI-EP1 Efektivní programování 1 ZS 2011/2012 Ing. Martin Kačer, Ph.D. 2010-11 Martin Kačer Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické
12. Globální metody MI-PAA
 Jan Schmidt 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Zimní semestr 2011/12 MI-PAA EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI
Jan Schmidt 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Zimní semestr 2011/12 MI-PAA EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI
Základy umělé inteligence
 Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
Pracovní listy - programování (algoritmy v jazyce Visual Basic) Algoritmus
 Pracovní listy - programování (algoritmy v jazyce Visual Basic) Předmět: Seminář z informatiky a výpočetní techniky Třída: 3. a 4. ročník vyššího stupně gymnázia Algoritmus Zadání v jazyce českém: 1. Je
Pracovní listy - programování (algoritmy v jazyce Visual Basic) Předmět: Seminář z informatiky a výpočetní techniky Třída: 3. a 4. ročník vyššího stupně gymnázia Algoritmus Zadání v jazyce českém: 1. Je
Vektorový prostor. Př.1. R 2 ; R 3 ; R n Dvě operace v R n : u + v = (u 1 + v 1,...u n + v n ), V (E 3 )...množina vektorů v E 3,
 Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Binární Vyhledávací Stromy, u kterých je. složitost operací v nejhorším. rovná O(log n)
 Stromy Binární Vyhledávací Stromy, u kterých je č asová složitost operací v nejhorším případě rovná O(log n) Vlastnosti Red-Black Stromů Vlastnosti Red-Black stromů Každý uzel stromu je obarven červenou
Stromy Binární Vyhledávací Stromy, u kterých je č asová složitost operací v nejhorším případě rovná O(log n) Vlastnosti Red-Black Stromů Vlastnosti Red-Black stromů Každý uzel stromu je obarven červenou
B) výchovné a vzdělávací strategie jsou totožné se strategiemi vyučovacího předmětu Matematika.
 4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
Dynamické datové struktury IV.
 Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
Datové struktury Úvod
 Datové struktury Úvod Navrhněte co nejjednodušší datovou strukturu, která podporuje následující operace: 1. Insert a Delete v O(n), Search v O(log n); Datové struktury Úvod Navrhněte co nejjednodušší datovou
Datové struktury Úvod Navrhněte co nejjednodušší datovou strukturu, která podporuje následující operace: 1. Insert a Delete v O(n), Search v O(log n); Datové struktury Úvod Navrhněte co nejjednodušší datovou
Prohledávání do šířky = algoritmus vlny
 Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Radek Mařík
 2012-03-20 Radek Mařík 1. Pravá rotace v uzlu U a) v podstromu s kořenem U přemístí pravého syna U.R uzlu U do kořene. Přitom se uzel U stane levým synem uzlu U.R a levý podstrom uzlu U.R se stane pravým
2012-03-20 Radek Mařík 1. Pravá rotace v uzlu U a) v podstromu s kořenem U přemístí pravého syna U.R uzlu U do kořene. Přitom se uzel U stane levým synem uzlu U.R a levý podstrom uzlu U.R se stane pravým
Polynomy. Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1.1 Teorie Zavedení polynomů Operace s polynomy...
 Polynomy Obsah Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1 Základní vlastnosti polynomů 2 1.1 Teorie........................................... 2 1.1.1 Zavedení polynomů................................
Polynomy Obsah Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1 Základní vlastnosti polynomů 2 1.1 Teorie........................................... 2 1.1.1 Zavedení polynomů................................
Řešení: PŘENESVĚŽ (N, A, B, C) = přenes N disků z A na B pomocí C
 Hanojské věže - 3 kolíky A, B, C - na A je N disků různé velikosti, seřazené od největšího (dole) k nejmenšímu (nahoře) - kolíky B a C jsou prázdné - úkol: přenést všechny disky z A na B, mohou se odkládat
Hanojské věže - 3 kolíky A, B, C - na A je N disků různé velikosti, seřazené od největšího (dole) k nejmenšímu (nahoře) - kolíky B a C jsou prázdné - úkol: přenést všechny disky z A na B, mohou se odkládat
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
STACK
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Select sort: krok 1: krok 2: krok 3: atd. celkem porovnání. výběr nejmenšího klíče z n prvků vyžaduje 1 porovnání
 Select sort: krok 1: výběr klíče z n prvků vyžaduje 1 porovnání krok 2: výběr klíče z 1 prvků vyžaduje 2 porovnání krok 3: výběr klíče z 2 prvků vyžaduje 3 porovnání atd. celkem porovnání Zlepšení = použít
Select sort: krok 1: výběr klíče z n prvků vyžaduje 1 porovnání krok 2: výběr klíče z 1 prvků vyžaduje 2 porovnání krok 3: výběr klíče z 2 prvků vyžaduje 3 porovnání atd. celkem porovnání Zlepšení = použít
Graf. Uzly Lokality, servery Osoby fyzické i právní Informatické objekty... atd. Hrany Cesty, propojení Vztahy Informatické závislosti... atd.
 Graf 2 0 3 1 4 5 Uzly Lokality, servery Osoby fyzické i právní Informatické objekty... atd. Hrany Cesty, propojení Vztahy Informatické závislosti... atd. Běžné reprezentace grafu Uzly = indexy Stupně uzlů
Graf 2 0 3 1 4 5 Uzly Lokality, servery Osoby fyzické i právní Informatické objekty... atd. Hrany Cesty, propojení Vztahy Informatické závislosti... atd. Běžné reprezentace grafu Uzly = indexy Stupně uzlů
2.6. VLASTNÍ ČÍSLA A VEKTORY MATIC
 .6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
.6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
1 Zobrazení 1 ZOBRAZENÍ 1. Zobrazení a algebraické struktury. (a) Ukažte, že zobrazení f : x
 1 ZOBRAZENÍ 1 Zobrazení a algebraické struktury 1 Zobrazení Příklad 1.1. (a) Ukažte, že zobrazení f : x na otevřený interval ( 1, 1). x x +1 je bijekce množiny reálných čísel R (b) Necht a, b R, a < b.
1 ZOBRAZENÍ 1 Zobrazení a algebraické struktury 1 Zobrazení Příklad 1.1. (a) Ukažte, že zobrazení f : x na otevřený interval ( 1, 1). x x +1 je bijekce množiny reálných čísel R (b) Necht a, b R, a < b.
Základy algoritmizace. Pattern matching
 Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Algoritmy I, složitost
 A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
Systematizace a prohloubení učiva matematiky. Učebna s dataprojektorem, PC, grafický program, tabulkový procesor. Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Katedra počítačů FEL
 TIS 311 1. Navrhněte KMP vyhledávací stroj pro vzorek v = kakadu, 2. Pro stejný vzorek navrhněte deterministický konečný automat. 3. Simulujte činnost obou strojů na textu T = dukakakaduka, porovnejte
TIS 311 1. Navrhněte KMP vyhledávací stroj pro vzorek v = kakadu, 2. Pro stejný vzorek navrhněte deterministický konečný automat. 3. Simulujte činnost obou strojů na textu T = dukakakaduka, porovnejte
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
Cykly a pole 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 115. 116.
 Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
07 Základní pojmy teorie grafů
 07 Základní pojmy teorie grafů (definice grafu, vlastnosti grafu, charakteristiky uzlů, ohodnocené grafy) Definice grafu množina objektů, mezi kterými existují určité vazby spojující tyto objekty. Uspořádaná
07 Základní pojmy teorie grafů (definice grafu, vlastnosti grafu, charakteristiky uzlů, ohodnocené grafy) Definice grafu množina objektů, mezi kterými existují určité vazby spojující tyto objekty. Uspořádaná
63. ročník Matematické olympiády 2013/2014
 63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
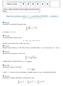 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
4EK213 Lineární modely. 12. Dopravní problém výchozí řešení
 4EK213 Lineární modely 12. Dopravní problém výchozí řešení 12. Distribuční úlohy LP Úlohy výrobního plánování (alokace zdrojů) Úlohy finančního plánování (optimalizace portfolia) Úlohy reklamního plánování
4EK213 Lineární modely 12. Dopravní problém výchozí řešení 12. Distribuční úlohy LP Úlohy výrobního plánování (alokace zdrojů) Úlohy finančního plánování (optimalizace portfolia) Úlohy reklamního plánování
Datové struktury 2: Rozptylovací tabulky
 Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach fronta
 STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 11 Katedra ekonometrie FEM UO Brno Jedná se o speciální případ dopravních úloh, řeší např. problematiku optimálního přiřazení strojů na pracoviště. Příklad Podnik má k dispozici 3 jeřáby,
Přednáška č. 11 Katedra ekonometrie FEM UO Brno Jedná se o speciální případ dopravních úloh, řeší např. problematiku optimálního přiřazení strojů na pracoviště. Příklad Podnik má k dispozici 3 jeřáby,
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Grafové úlohy Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Grafové úlohy Daniela Szturcová Tento
Determinanty. Obsah. Aplikovaná matematika I. Pierre Simon de Laplace. Definice determinantu. Laplaceův rozvoj Vlastnosti determinantu.
 Determinanty Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Determinanty Definice determinantu Sarrusovo a křížové pravidlo Laplaceův rozvoj Vlastnosti determinantu Výpočet determinantů 2 Inverzní
Determinanty Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Determinanty Definice determinantu Sarrusovo a křížové pravidlo Laplaceův rozvoj Vlastnosti determinantu Výpočet determinantů 2 Inverzní
Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT
 PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
PEF ČZU Modely teorie grafů, min.kostra, max.tok, CPM, MPM, PERT Okruhy SZB č. 5 Zdroje: Demel, J., Operační výzkum Jablonský J., Operační výzkum Šubrt, T., Langrová, P., Projektové řízení I. a různá internetová
TGH12 - Problém za milion dolarů
 TGH12 - Problém za milion dolarů Jan Březina Technical University of Liberec 7. května 2013 Složitost problému Co je to problém? Složitost problému Co je to problém? K daným vstupním datům (velkému binárnímu
TGH12 - Problém za milion dolarů Jan Březina Technical University of Liberec 7. května 2013 Složitost problému Co je to problém? Složitost problému Co je to problém? K daným vstupním datům (velkému binárnímu
Interpolace Lagrangeovy polynomy. 29. října 2012
 Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
STROMY A KOSTRY. Stromy a kostry TI 6.1
 STROMY A KOSTRY Stromy a kostry TI 6.1 Stromy a kostry Seznámíme se s následujícími pojmy: kostra rafu, cyklomatické číslo rafu, hodnost rafu (kořenový strom, hloubka stromu, kořenová kostra orientovaného
STROMY A KOSTRY Stromy a kostry TI 6.1 Stromy a kostry Seznámíme se s následujícími pojmy: kostra rafu, cyklomatické číslo rafu, hodnost rafu (kořenový strom, hloubka stromu, kořenová kostra orientovaného
Lineární algebra : Násobení matic a inverzní matice
 Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. března 2014, 12:42 1 2 0.1 Násobení matic Definice 1. Buďte m, n, p N, A
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. března 2014, 12:42 1 2 0.1 Násobení matic Definice 1. Buďte m, n, p N, A
Různé algoritmy mají různou složitost
 / 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
/ 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
Cílem kapitoly je seznámit studenta se seznamem a stromem. Jejich konstrukci, užití a základní vlastnosti.
 Seznamy a stromy Cílem kapitoly je seznámit studenta se seznamem a stromem. Jejich konstrukci, užití a základní vlastnosti. Klíčové pojmy: Seznam, spojový seznam, lineární seznam, strom, list, uzel. Úvod
Seznamy a stromy Cílem kapitoly je seznámit studenta se seznamem a stromem. Jejich konstrukci, užití a základní vlastnosti. Klíčové pojmy: Seznam, spojový seznam, lineární seznam, strom, list, uzel. Úvod
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2014
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Binární vyhledávací stromy II
 Binární vyhledávací stromy II doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 19. března 2019 Jiří Dvorský (VŠB TUO) Binární vyhledávací
Binární vyhledávací stromy II doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 19. března 2019 Jiří Dvorský (VŠB TUO) Binární vyhledávací
Posloupnosti a řady. 28. listopadu 2015
 Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Grafové algoritmy. Programovací techniky
 Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy. Programovací techniky
 Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Lineární algebra : Násobení matic a inverzní matice
 Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Drsná matematika III 10. demonstrovaná cvičení Kostry grafů
 Drsná matematika III 10. demonstrovaná cvičení Kostry grafů Martin Panák Masarykova univerzita Fakulta informatiky 21.11. 2006 1 Domácí úlohy z minulého týdne Příklad 1 Příklad 2 Příklad 3 2 Borůvkův algoritmus
Drsná matematika III 10. demonstrovaná cvičení Kostry grafů Martin Panák Masarykova univerzita Fakulta informatiky 21.11. 2006 1 Domácí úlohy z minulého týdne Příklad 1 Příklad 2 Příklad 3 2 Borůvkův algoritmus
Obecná informatika. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Podzim 2012
 Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Složitost algoritmů. Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol.
 Složitost algoritmů Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2017 Datové struktury a algoritmy, B6B36DSA 02/2017, Lekce 3
Složitost algoritmů Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2017 Datové struktury a algoritmy, B6B36DSA 02/2017, Lekce 3
PŘEDNÁŠKA 2 POSLOUPNOSTI
 PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
IB111 Úvod do programování skrze Python
 Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
Paralelní grafové algoritmy
 Paralelní grafové algoritmy Značení Minimální kostra grafu Nejkratší cesta z jednoho uzlu Nejkratší cesta mezi všemi dvojicemi uzlů Použité značení Definition Bud G = (V, E) graf. Pro libovolný uzel u
Paralelní grafové algoritmy Značení Minimální kostra grafu Nejkratší cesta z jednoho uzlu Nejkratší cesta mezi všemi dvojicemi uzlů Použité značení Definition Bud G = (V, E) graf. Pro libovolný uzel u
II. Úlohy na vložené cykly a podprogramy
 II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
Programy na PODMÍNĚNÝ příkaz IF a CASE
 Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Vstupy a výstupy budou vždy upraveny tak, aby bylo zřejmé, co zadáváme a co se zobrazuje. Není-li určeno, zadáváme přirozená čísla. Je-li to možné, používej generátor náhodných čísel vysvětli, co a jak
Stromy. Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy
 Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
Stromy úvod Stromy Strom: souvislý graf bez kružnic využití: počítačová grafika seznam objektů efektivní vyhledávání výpočetní stromy rozhodovací stromy Neorientovaný strom Orientovaný strom Kořenový orientovaný
3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem
 ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
3. Matice a determinanty
 . Matice a determinanty Teorie matic a determinantů představuje úvod do lineární algebry. Nejrozsáhlejší aplikace mají matice a determinanty při řešení systémů lineárních rovnic. Pojem determinantu zavedl
. Matice a determinanty Teorie matic a determinantů představuje úvod do lineární algebry. Nejrozsáhlejší aplikace mají matice a determinanty při řešení systémů lineárních rovnic. Pojem determinantu zavedl
Úvod. Úvod do programování. Úvod. Hashovací tabulky
 do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava do programování, 2004/2005 Mnohé aplikace nepotřebují ke svému provozu celou škálu operací podporovaných
do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava do programování, 2004/2005 Mnohé aplikace nepotřebují ke svému provozu celou škálu operací podporovaných
Test prvočíselnosti. Úkol: otestovat dané číslo N, zda je prvočíslem
 Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Dynamické datové struktury III.
 Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Matematický seminář. OVO ŠVP Tématický celek Učivo ŠVP Integrace Mezipředmětové vztahy. jejich soustavy. Spojitost funkce v bodě. Limita funkce v bodě
 Řeší s porozumněním rovnice s parametrem Rovnice, nerovnice a jejich soustavy Řovnice, nerovnice a jejich soustavy Třetí, 24 hodin Zvolí vhodnou metodu řešení rovnice nebo nerovnice Vysvětlí zvolený způsob
Řeší s porozumněním rovnice s parametrem Rovnice, nerovnice a jejich soustavy Řovnice, nerovnice a jejich soustavy Třetí, 24 hodin Zvolí vhodnou metodu řešení rovnice nebo nerovnice Vysvětlí zvolený způsob
Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz
 Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz (2 + 5) * (13-4) * + - 2 5 13 4 - listy stromu obsahují operandy (čísla) - vnitřní uzly obsahují operátory (znaménka)
Reprezentace aritmetického výrazu - binární strom reprezentující aritmetický výraz (2 + 5) * (13-4) * + - 2 5 13 4 - listy stromu obsahují operandy (čísla) - vnitřní uzly obsahují operátory (znaménka)
Numerická stabilita algoritmů
 Numerická stabilita algoritmů Petr Tichý 9. října 2013 1 Numerická stabilita algoritmů Pravidla v konečné aritmetice Pro počítání v konečné aritmetice počítače platí určitá pravidla, která jsou důležitá
Numerická stabilita algoritmů Petr Tichý 9. října 2013 1 Numerická stabilita algoritmů Pravidla v konečné aritmetice Pro počítání v konečné aritmetice počítače platí určitá pravidla, která jsou důležitá
Poznámky k ekonomickému ukazateli IRR. výnos do splatnosti...
 Poznámky k ekonomickému ukazateli IRR (Remarks on the economic criterion the Internal Rate of Return ) Carmen Simerská IRR... vnitřní míra výnosnosti, vnitřní výnosové procento, výnos do splatnosti...
Poznámky k ekonomickému ukazateli IRR (Remarks on the economic criterion the Internal Rate of Return ) Carmen Simerská IRR... vnitřní míra výnosnosti, vnitřní výnosové procento, výnos do splatnosti...
Teorie grafů. zadání úloh. letní semestr 2008/2009. Poslední aktualizace: 19. května 2009. First Prev Next Last Go Back Full Screen Close Quit
 Teorie grafů zadání úloh letní semestr 2008/2009 Poslední aktualizace: 19. května 2009 Obsah Úloha číslo 1 5 Úloha číslo 2 6 Úloha číslo 3 7 Úloha číslo 4 8 Úloha číslo 5 9 Úloha číslo 6 10 Úloha číslo
Teorie grafů zadání úloh letní semestr 2008/2009 Poslední aktualizace: 19. května 2009 Obsah Úloha číslo 1 5 Úloha číslo 2 6 Úloha číslo 3 7 Úloha číslo 4 8 Úloha číslo 5 9 Úloha číslo 6 10 Úloha číslo
Jednoduché cykly 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.
 Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
ČVUT FEL X36PAA - Problémy a algoritmy. 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu
 ČVUT FEL X36PAA - Problémy a algoritmy 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu Jméno: Marek Handl Datum: 3. 2. 29 Cvičení: Pondělí 9: Zadání Prozkoumejte citlivost metod
ČVUT FEL X36PAA - Problémy a algoritmy 4. úloha - Experimentální hodnocení algoritmů pro řešení problému batohu Jméno: Marek Handl Datum: 3. 2. 29 Cvičení: Pondělí 9: Zadání Prozkoumejte citlivost metod
Algoritmy I. Číselné soustavy přečíst!!! ALGI 2018/19
 Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
68. ročník Matematické olympiády 2018/2019
 68. ročník Matematické olympiády 2018/2019 Řešení úloh ústředního kola kategorie P 2. soutěžní den P-III-4 Výlet Abychom našli požadovaný výlet délky 4, stačí najít dvě hvězdy a a b, které mají dva společné
68. ročník Matematické olympiády 2018/2019 Řešení úloh ústředního kola kategorie P 2. soutěžní den P-III-4 Výlet Abychom našli požadovaný výlet délky 4, stačí najít dvě hvězdy a a b, které mají dva společné
