Generovanie 3D modelu z vektorového výkresu súčiastky. Doc. Ing. Jozef Vaský CSc.
|
|
|
- Rostislav Vratislav Beran
- před 8 lety
- Počet zobrazení:
Transkript
1 Generovanie 3D modelu z vektorového výkresu súčiastky Doktorand: Školiteľ: Ing. Michal Eliáš Doc. Ing. Jozef Vaský CSc.
2 Celkový pohľad papierový výkres 3D model Kroky konverzie: Zoskenovanie výkresu do rastrovej podoby. Vektorizácia rastrového obrazu. Identifikácia a sémantická analýza objektov. Generovanie 3D modelu.
3 Cieľ dizertačnej práce Návrh metodiky a algoritmov pre riešenie procesu generovania 3D modelu z 2D reprezentácie jednoduchého hranolovitého telesa a následné vytvorenie kompletného dátového modelu.
4 Teoretické podklady Technické výkresy, normalizácia. Zobrazovanie na výkresoch. Geometrické transformácie. Vektorová a maticová matematika. Analytické nástroje. Reprezentácia telies. Súborové formáty.
5 Technické výkresy Podliehajú normalizácii (ISO, EN, STN). Charakteristické údaje výkresov: rozmery a formálne prvky, čiary na výkresoch, popisovanie výkresov, zobrazovanie na výkresoch, mierky zobrazovania, kótovanie, ostatné prvky. Glézl, Š. a kol.: Základy strojníctva. 2. vydanie Bratislava: Alfa Veselovký, J. a kol.: Technické kreslenie. 1. vydanie Bratislava: Alfa Drastík, F.: Technické kreslení podle mezinárodních norem I. Pravidla tvorby výkresů ve strojírenství. Ostrava: Montanex 1994.
6 Zobrazovanie na výkresoch Pravouhlé premietanie na niekoľko priemetní Glézl, Š. a kol.: Základy strojníctva. 2. vydanie Bratislava: Alfa Veselovký, J. a kol.: Technické kreslenie. 1. vydanie Bratislava: Alfa 1986.
7 Premietanie Mongeova projekcia (pravouhlé premietanie na dve navzájom kolmé priemetne) Urban, A.: Deskriptivní geometrie. 3. vydanie Praha: SNTL/Alfa Velichová, D.: Konštrukčná geometria. 1.vydanie Bratislava: Vydavateľstvo STU 1996.
8 Tézy dizertačnej práce Definovanie kritérií pre výber vhodných vektorových výkresov. Transformácia pravouhlých priemetov na 3D drôtený model. Rekonštrukcia objemového modelu výrobku. Výber vhodného súborového formátu pre vstup a výstup.
9 Obmedzujúce kritériá hranaté telesá bez kruhových/valcových prvkov, stupeň zložitosti telies, zobrazenie len v priemetoch (2 až 3), formálne spracovanie vektorového výkresu (hladiny, farba a typ čiar,...).
10 Generovanie 3D drôteného modelu dátové štruktúry pre 2D a 3D dáta, analýza a spracovanie dát priemetov, spätný proces Mongeovej projekcie. Velichová, Zárezová D.: Konštrukčná metóda geometria. a šikmá 1.vydanie axonometria Bratislava: Vydavateľstvo STU 1996.
11 Prvé výsledky Nedostatky: veľké množstvo generovaných čiar, exponenciálny rast času generovania, pracuje systémom hrubej sily, analýza len na úrovni čiar, problémy s niektorými prvkami. chýbajúca hrana prebytočné hrany
12 Možné riešenia konzistencia 3D modelu (manifold) lepšie využitie nástrojov analýzy plôšková reprezentácia korektnosť topológie Eulerov vzťah f e + v = Žára, J., a kol.: Počítačová grafika principy a algoritmy. 1. vydanie Praha: Grada Euler-Poincarého vzťah f e + v r = 2( s h) Vaský, J., Klačo, M., Nemlaha, E.: Grafické spracovanie údajov. 1. vydanie Bratislava: Vydavateľstvo STU
13 Rekonštrukcia objemového modelu identifikácia primitívneho telesa, pridávanie a uberanie materiálu, overenie Mongeovou projekciou. Vaský, J., Nemlaha, E., Masár, L.: CAD/CAM systémy. 1. vydanie Bratislava: Vydavateľstvo STU Konštruktívna geometria telies (CSG) Žára, J., a kol.: Počítačová grafika principy a algoritmy. 1. vydanie Praha: Grada 1992.
14 Súborový formát návrh natívneho formátu, rozhranie pre vstup a výstup dát DXF, IGES, DWG, 3DS,... nezávislosť na súborovom formáte, prenositeľnosť.
15 Výsledný model
16 Ďakujem za pozornosť
17 Významné osobnosti James D. Foley, Andries van Dam Computer Graphics: Principles and Practice Introduction to Computer Graphics Andrej Ferko Počítačová grafika a spracovanie obrazu Jiří Žára Moderní počítačová grafika Počítačová grafika principy a algoritmy Börje Langefors Teoretická analýza informačných systémov
UČEBNÉ TEXTY. I. ročník. Strojnícke zobrazovanie. Ing.Jaroslava Šufliarska
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Strojnícke zobrazovanie Ing.Jaroslava
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Strojnícke zobrazovanie Ing.Jaroslava
ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA
 ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA Pri kolmom premietaní môžeme zvoliť šesť smerov premietania, ale ich priemety nemajú rovnakú dôležitosť: A. hlavné priemety v smere: N - pohľad z predu (nárys),
ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA Pri kolmom premietaní môžeme zvoliť šesť smerov premietania, ale ich priemety nemajú rovnakú dôležitosť: A. hlavné priemety v smere: N - pohľad z predu (nárys),
.-.- Štefan KRÁL František LACKO Jarmila ORAVCOVÁ Eva RIEČIČIAROVÁ Stanislav TOMANíČEK SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE 2007.
 ,..-. ZÁKLADY TECHNICKA KONŠTRUOVANIA a.-.- DOKUMENTACIA Štefan KRÁL František LACKO Jarmila ORAVCOVÁ Eva RIEČIČIAROVÁ Stanislav TOMANíČEK SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE 2007 i I OBSAH Pred
,..-. ZÁKLADY TECHNICKA KONŠTRUOVANIA a.-.- DOKUMENTACIA Štefan KRÁL František LACKO Jarmila ORAVCOVÁ Eva RIEČIČIAROVÁ Stanislav TOMANíČEK SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE 2007 i I OBSAH Pred
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
UČEBNÉ TEXTY. Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Dátum: 2015
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Normalizácia v technickom kreslení
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Normalizácia v technickom kreslení
Počítačová grafika 1 (POGR 1)
 Počítačová grafika 1 (POGR 1) Pavel Strachota FJFI ČVUT v Praze 8. října 2015 Kontakt Ing. Pavel Strachota, Ph.D. Katedra matematiky Trojanova 13, místnost 033a E-mail: WWW: pavel.strachota@fjfi.cvut.cz
Počítačová grafika 1 (POGR 1) Pavel Strachota FJFI ČVUT v Praze 8. října 2015 Kontakt Ing. Pavel Strachota, Ph.D. Katedra matematiky Trojanova 13, místnost 033a E-mail: WWW: pavel.strachota@fjfi.cvut.cz
Počítačová geometrie I
 0 I RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Osnova předmětu Pojem výpočetní geometrie, oblasti
0 I RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Osnova předmětu Pojem výpočetní geometrie, oblasti
Elektronické služby katastra nehnuteľnosti Mapový klient ZBGIS a možnosti jeho konfigurácie
 Mapový klient ZBGIS a možnosti jeho konfigurácie Jaroslav AMBRÓZ Head of analytics department Dátum 14. 11. 2013 Miesto prezentácie: Kongresové centrum Praha Národný projekt: Elektronické služby katastra
Mapový klient ZBGIS a možnosti jeho konfigurácie Jaroslav AMBRÓZ Head of analytics department Dátum 14. 11. 2013 Miesto prezentácie: Kongresové centrum Praha Národný projekt: Elektronické služby katastra
Speciální numerické metody 4. ročník bakalářského studia. Cvičení: Ing. Petr Lehner Přednášky: doc. Ing. Martin Krejsa, Ph.D.
 Speciální numerické metody 4. ročník bakalářského studia Cvičení: Ing. Petr Lehner Přednášky: doc. Ing. Martin Krejsa, Ph.D. 1 Základní informace o cvičení Předmět: 228-0210/01 Speciální numerické metody
Speciální numerické metody 4. ročník bakalářského studia Cvičení: Ing. Petr Lehner Přednášky: doc. Ing. Martin Krejsa, Ph.D. 1 Základní informace o cvičení Předmět: 228-0210/01 Speciální numerické metody
UČEBNÉ TEXTY. Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Dátum: 2015
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Kótovanie Ing.Jaroslava Šufliarska
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Kótovanie Ing.Jaroslava Šufliarska
Malířův algoritmus. 1995-2015 Josef Pelikán CGG MFF UK Praha. pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 15
 Malířův algoritmus 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 15 Malířův algoritmus kreslení do bufferu video-ram, rastrová tiskárna s bufferem vyplňování
Malířův algoritmus 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 15 Malířův algoritmus kreslení do bufferu video-ram, rastrová tiskárna s bufferem vyplňování
FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY
 FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VEKTOROVÁ GRAFIKA Obraz reprezentován pomocí geometrických objektů (body, přímky, křivky, polygony).
FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VEKTOROVÁ GRAFIKA Obraz reprezentován pomocí geometrických objektů (body, přímky, křivky, polygony).
Možnosti analýz obrazových informácií ich reálne využitie dnes a očakávané trendy
 Možnosti analýz obrazových informácií ich reálne využitie dnes a očakávané trendy Kriminalistický e expertízny ústav PZ Ján Kuljovský, odvetvie kriminalistickej fotografie a videa Obsah prezentácie Čím
Možnosti analýz obrazových informácií ich reálne využitie dnes a očakávané trendy Kriminalistický e expertízny ústav PZ Ján Kuljovský, odvetvie kriminalistickej fotografie a videa Obsah prezentácie Čím
Počítačová grafika 2 (POGR2)
 Počítačová grafika 2 (POGR2) Pavel Strachota FJFI ČVUT v Praze 19. února 2015 Kontakt Ing. Pavel Strachota, Ph.D. Katedra matematiky Trojanova 13, místnost 033a E-mail: pavel.strachota@fjfi.cvut.cz WWW:
Počítačová grafika 2 (POGR2) Pavel Strachota FJFI ČVUT v Praze 19. února 2015 Kontakt Ing. Pavel Strachota, Ph.D. Katedra matematiky Trojanova 13, místnost 033a E-mail: pavel.strachota@fjfi.cvut.cz WWW:
3D MODELY MIEST V URBÁNNOM PLÁNOVANÍ
 3D MODELY MIEST V URBÁNNOM PLÁNOVANÍ PAUDITŠOVÁ Eva SLABECIUSOVÁ Barbora AKTUÁLNE VÝZVY V KARTOGRAFII 26. november 2015 SvF STU Bratislava ÚZEMNÉ PLÁNOVANIE rieši komplexne priestorové usporiadanie a funkčné
3D MODELY MIEST V URBÁNNOM PLÁNOVANÍ PAUDITŠOVÁ Eva SLABECIUSOVÁ Barbora AKTUÁLNE VÝZVY V KARTOGRAFII 26. november 2015 SvF STU Bratislava ÚZEMNÉ PLÁNOVANIE rieši komplexne priestorové usporiadanie a funkčné
Princip a vlastnosti promítání. Konstruktivní geometrie a technické kresleni - L
 Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů ve dvojrozměrné rovině. Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů
Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů ve dvojrozměrné rovině. Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
EG Informácie okolo nás 2. ročník
 D29. Vektorová grafika 1. Popis prostredia Inkscape. Grafika rastrová verzus vektorová. Tvary. Farby. Rastrová (bitmapová grafika) V prípade bitmapovej grafiky je každý bod na obrázku označený ako pixel
D29. Vektorová grafika 1. Popis prostredia Inkscape. Grafika rastrová verzus vektorová. Tvary. Farby. Rastrová (bitmapová grafika) V prípade bitmapovej grafiky je každý bod na obrázku označený ako pixel
Watkinsův algoritmus řádkového rozkladu
 Watkinsův algoritmus řádkového rozkladu 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 15 Watkinsův algoritmus nepotřebuje výstupní buffer rastrový výstup
Watkinsův algoritmus řádkového rozkladu 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 15 Watkinsův algoritmus nepotřebuje výstupní buffer rastrový výstup
Výpočet vržených stínů
 Výpočet vržených stínů 1996-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Shadows 2016 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Metody vícenásobný
Výpočet vržených stínů 1996-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Shadows 2016 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Metody vícenásobný
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor 23-41-M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ ÚVOD A DESKRIPTIVNÍ GEOMETRIE
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ ÚVOD A DESKRIPTIVNÍ GEOMETRIE
4) Vztah mezi ČSN, EN a ISO
 Obsah: VÝZNAM TEK A NORMALIZACE 1. Co je to technické kreslení? 2. Cíle výuky TEK. 3. Druhy platných norem v ČR 4. Vztah mezi ČSN, EN a ISO 5. Druhy technických výkresů 6. Formáty výkresů 7. Povinná výbava
Obsah: VÝZNAM TEK A NORMALIZACE 1. Co je to technické kreslení? 2. Cíle výuky TEK. 3. Druhy platných norem v ČR 4. Vztah mezi ČSN, EN a ISO 5. Druhy technických výkresů 6. Formáty výkresů 7. Povinná výbava
7 Transformace 2D. 7.1 Transformace objektů obecně. Studijní cíl. Doba nutná k nastudování. Průvodce studiem
 7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
BA008 Konstruktivní geometrie pro kombinované studium
 BA008 Konstruktivní geometrie pro kombinované studium Jana Slaběňáková Jan Šafařík Ústav matematiky a deskriptivní geometrie Vysoké učení technické v Brně 10. února 2017 Kontakt RNDr. Jana Slaběňáková
BA008 Konstruktivní geometrie pro kombinované studium Jana Slaběňáková Jan Šafařík Ústav matematiky a deskriptivní geometrie Vysoké učení technické v Brně 10. února 2017 Kontakt RNDr. Jana Slaběňáková
Reprezentace bodu, zobrazení
 Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Technická dokumentace
 Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI10 : Zásady kreslení průřezů a průniků Datum vypracování: 26.11.2012 Vypracoval: Ing. Bohumil Freisleben Motto: průřez
Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI10 : Zásady kreslení průřezů a průniků Datum vypracování: 26.11.2012 Vypracoval: Ing. Bohumil Freisleben Motto: průřez
Bitmapové a vektorové grafické editory. Grafické editory používame na kresbu, resp. editovanie obrázkov. Obrázky sa dajú kresliť dvoma spôsobmi.
 Bitmapové a vektorové grafické editory Grafické editory používame na kresbu, resp. editovanie obrázkov. Obrázky sa dajú kresliť dvoma spôsobmi. Menu 1. Bitmapový editor (rastrový) Farebné palety Príklad:
Bitmapové a vektorové grafické editory Grafické editory používame na kresbu, resp. editovanie obrázkov. Obrázky sa dajú kresliť dvoma spôsobmi. Menu 1. Bitmapový editor (rastrový) Farebné palety Príklad:
Technická dokumentace
 Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI18 : Předepisování jakosti povrchu (drsnost, vlnitost) Datum vypracování: 27.01.2013 Vypracoval: Ing. Bohumil Freisleben
Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI18 : Předepisování jakosti povrchu (drsnost, vlnitost) Datum vypracování: 27.01.2013 Vypracoval: Ing. Bohumil Freisleben
ZOBRAZOVÁNÍ Doc. Ing. Jan Brandejs Ing. Jiří Dvořáček VUT FSI Ústav konstruování
 ZOBRAZOVÁNÍ Doc. Ing. Jan Brandejs Ing. Jiří Dvořáček VUT FSI Ústav konstruování Technické kreslení slouží k vyjadřování a sdělování představ a myšlenek techniků, je řečí techniků příslušného oboru. Str.
ZOBRAZOVÁNÍ Doc. Ing. Jan Brandejs Ing. Jiří Dvořáček VUT FSI Ústav konstruování Technické kreslení slouží k vyjadřování a sdělování představ a myšlenek techniků, je řečí techniků příslušného oboru. Str.
Hierarchický model. 1995-2013 Josef Pelikán CGG MFF UK Praha. pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16
 Hierarchický model 1995-2013 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16 Hierarchie v 3D modelování kompozice zdola-nahoru složitější objekty se sestavují
Hierarchický model 1995-2013 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 16 Hierarchie v 3D modelování kompozice zdola-nahoru složitější objekty se sestavují
OBSAH. Úvod Mezinárodní technická normalizace
 OBSAH Úvod... 8 1 Mezinárodní technická normalizace 1.1 Mezinárodní normalizační organizace... 9 1.2 Technické komise ISO... 9 1.3 Návrhy mezinárodních norem... 9 1.4 Regionální technická normalizace v
OBSAH Úvod... 8 1 Mezinárodní technická normalizace 1.1 Mezinárodní normalizační organizace... 9 1.2 Technické komise ISO... 9 1.3 Návrhy mezinárodních norem... 9 1.4 Regionální technická normalizace v
Študijný program: Manažérstvo kvality produkcie
 1 Študijný program: Manažérstvo kvality produkcie 442P102 Aplikovaná chémia 2 2 s 5 345E102 Manažment podniku 2 1 s 4 422A204 Ochrana a tvorba životného prostredia 1 2 s 4 523M118 Základy informatiky 0
1 Študijný program: Manažérstvo kvality produkcie 442P102 Aplikovaná chémia 2 2 s 5 345E102 Manažment podniku 2 1 s 4 422A204 Ochrana a tvorba životného prostredia 1 2 s 4 523M118 Základy informatiky 0
Ing. Jan Buriánek. Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Jan Buriánek, 2010
 Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Geometrické transformace pomocí matic
 Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Lucie Zrůstová HISTORIE DESKRIPTIVNÍ GEOMETRIE NA VUT V BRNĚ. 1 Deskriptivní geometrie na VUT do 2. světové války
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Lucie Zrůstová HISTORIE DESKRIPTIVNÍ GEOMETRIE NA VUT V BRNĚ Abstrakt Příspěvek se zabývá historií výuky deskriptivní geometrie na Vysokém učení technickém.
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Lucie Zrůstová HISTORIE DESKRIPTIVNÍ GEOMETRIE NA VUT V BRNĚ Abstrakt Příspěvek se zabývá historií výuky deskriptivní geometrie na Vysokém učení technickém.
Singularity rotačních obalových ploch
 Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
OSNOVA PRO PŘEDMĚT TECHNICKÁ GRAFIKA
 CZ.1.07/2.2.00/07.0002 Modernizace oboru technická a informační výchova OSNOVA PRO PŘEDMĚT TECHNICKÁ GRAFIKA (CVIČENÍ) 2009 PaedDr. PhDr. Jiří Dostál, Ph.D. Název studijního předmětu: Technická grafika
CZ.1.07/2.2.00/07.0002 Modernizace oboru technická a informační výchova OSNOVA PRO PŘEDMĚT TECHNICKÁ GRAFIKA (CVIČENÍ) 2009 PaedDr. PhDr. Jiří Dostál, Ph.D. Název studijního předmětu: Technická grafika
UČEBNÉ TEXTY. Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Dátum: 2015
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Použitie technického kreslenia
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Použitie technického kreslenia
Základy 3D modelování a animace v CGI systémech Cinema 4D C4D
 EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
Reprezentace 3D scény
 Reprezentace 3D scény 1995-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 36 Metody reprezentace 3D scén objemové reprezentace přímé informace o vnitřních
Reprezentace 3D scény 1995-2016 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ 1 / 36 Metody reprezentace 3D scén objemové reprezentace přímé informace o vnitřních
Pravoúhlá axonometrie - řezy hranatých těles
 Pravoúhlá axonometrie - řezy hranatých těles KG - L MENDELU KG - L (MENDELU) Pravoúhlá axonometrie - řezy hranatých těles 1 / 1 Příklad (Řez šikmého hranolu) Sestrojte řez šikmého čtyřbokého hranolu ABCDA
Pravoúhlá axonometrie - řezy hranatých těles KG - L MENDELU KG - L (MENDELU) Pravoúhlá axonometrie - řezy hranatých těles 1 / 1 Příklad (Řez šikmého hranolu) Sestrojte řez šikmého čtyřbokého hranolu ABCDA
Zachovanie mentálnej mapy pri interakcií s grafom. RNDr. Jana Katreniaková PhD.
 Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
ŠTATISTIKA V EXCELI 2007
 Jozef Chajdiak ŠTATISTIKA V EXCELI 2007 STATIS, Bratislava 2009, ISBN 978-80-85659-49-8, 304 strán A5,väzba V4. Excel sa stal každodenným nástrojom práce mnohých z nás. Jeho verzia 2007, okrem čiastkových
Jozef Chajdiak ŠTATISTIKA V EXCELI 2007 STATIS, Bratislava 2009, ISBN 978-80-85659-49-8, 304 strán A5,väzba V4. Excel sa stal každodenným nástrojom práce mnohých z nás. Jeho verzia 2007, okrem čiastkových
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika AA01. Cvičení, zimní semestr DOMÁCÍ ÚLOHY. Jan Šafařík
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika AA0 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2005 () Jsou dány matice A = AB BA. [ AB BA
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika AA0 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2005 () Jsou dány matice A = AB BA. [ AB BA
Výpočet průsečíků paprsku se scénou
 Výpočet průsečíků paprsku se scénou 1996-2018 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Intersection 2018 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 26 Průsečík
Výpočet průsečíků paprsku se scénou 1996-2018 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Intersection 2018 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 26 Průsečík
TECHNICKÁ DOKUMENTACE
 VŠB-TU Ostrava, Fakulta elektrotechniky a informatiky Katedra elektrických strojů a přístrojů KAT 453 TECHNICKÁ DOKUMENTACE (přednášky pro hodiny cvičení) Zobrazování Petr Šňupárek, Martin Marek 1 Co je
VŠB-TU Ostrava, Fakulta elektrotechniky a informatiky Katedra elektrických strojů a přístrojů KAT 453 TECHNICKÁ DOKUMENTACE (přednášky pro hodiny cvičení) Zobrazování Petr Šňupárek, Martin Marek 1 Co je
Technické kreslení. Konstruktivní geometrie a technické kresleni - L ZS 2009
 ZS 2009 technické kreslení - souhrnný název pro všechny druhy grafického vyjadřování v různých vědních, technických a výrobních oborech úkolem technického kreslení je zobrazení trojrozměrných předmětů
ZS 2009 technické kreslení - souhrnný název pro všechny druhy grafického vyjadřování v různých vědních, technických a výrobních oborech úkolem technického kreslení je zobrazení trojrozměrných předmětů
MAT I. Logika, množiny 6. Finančná matematika 4. Geometria 8. Planimetria 14. Výrazy 18. Funkcie Függvények 4
 MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
Výpočet průsečíků paprsku se scénou
 Výpočet průsečíků paprsku se scénou 1996-2008 Josef Pelikán, MFF UK Praha http://cgg.ms.mff.cuni.cz/~pepca/ Josef.Pelikan@mff.cuni.cz NPGR004, intersection.pdf 2008 Josef Pelikán, http://cgg.ms.mff.cuni.cz/~pepca
Výpočet průsečíků paprsku se scénou 1996-2008 Josef Pelikán, MFF UK Praha http://cgg.ms.mff.cuni.cz/~pepca/ Josef.Pelikan@mff.cuni.cz NPGR004, intersection.pdf 2008 Josef Pelikán, http://cgg.ms.mff.cuni.cz/~pepca
Produktové Dokumenty (Datum 28.11.2014) Srovnání verzí: pcon.planner 7.0 Rozdíly mezi verzemi Standard-, ME a PRO
 Produktové Dokumenty (Datum 28.11.2014) Srovnání verzí: pcon.planner 7.0 Rozdíly mezi verzemi Standard-, ME a PRO Základní formáty STD ME PRO Nahrávání a ukládání souborů DWG a DWT Převod a podpora starších
Produktové Dokumenty (Datum 28.11.2014) Srovnání verzí: pcon.planner 7.0 Rozdíly mezi verzemi Standard-, ME a PRO Základní formáty STD ME PRO Nahrávání a ukládání souborů DWG a DWT Převod a podpora starších
Technická dokumentace:
 Technická dokumentace Technickou dokumentací myslíme veškeré podklady nutné pro převedení technické myšlenky v hotový výrobek. Technická dokumentace: konstrukční dokumentace, technologická dokumentace.
Technická dokumentace Technickou dokumentací myslíme veškeré podklady nutné pro převedení technické myšlenky v hotový výrobek. Technická dokumentace: konstrukční dokumentace, technologická dokumentace.
Téma cvičení. Zadání úloh. XZK Obsah cvičení: ZS 2014/15. č. cv.
 XZK Obsah cvičení: ZS 2014/15 č. cv. Téma cvičení 1. Výkresy pozemních staveb- požadavky, způsoby kreslení. Plocha výkresového listu, orientace výkresů,měřítka, formáty Zobrazovací prostředky- druhy čar,
XZK Obsah cvičení: ZS 2014/15 č. cv. Téma cvičení 1. Výkresy pozemních staveb- požadavky, způsoby kreslení. Plocha výkresového listu, orientace výkresů,měřítka, formáty Zobrazovací prostředky- druhy čar,
Přednáška 1 Úvod do předmětu
 Přednáška 1 Úvod do předmětu Miroslav Lávička 1 Email: lavicka@kma.zcu.cz 1 Katedra matematiky, Fakulta aplikovaných věd Západočeská univerzita v Plzni Geometrické vidění světa KMA/GVS ak. rok 2013/2014
Přednáška 1 Úvod do předmětu Miroslav Lávička 1 Email: lavicka@kma.zcu.cz 1 Katedra matematiky, Fakulta aplikovaných věd Západočeská univerzita v Plzni Geometrické vidění světa KMA/GVS ak. rok 2013/2014
11 Zobrazování objektů 3D grafiky
 11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Ladislav Drs Použití samočinných počítačů a automatického kreslení v deskriptivní geometrii Pokroky matematiky, fyziky a astronomie, Vol. 17 (1972), No. 4, 199--203
Pokroky matematiky, fyziky a astronomie Ladislav Drs Použití samočinných počítačů a automatického kreslení v deskriptivní geometrii Pokroky matematiky, fyziky a astronomie, Vol. 17 (1972), No. 4, 199--203
TECHNICKÉ DOKUMENTY VY_32_INOVACE_TD_2_04. OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/ Modernizace výuky na učilišti
 TECHNICKÉ DOKUMENTY VY_32_INOVACE_TD_2_04 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek Téma Klíčová slova Druh
TECHNICKÉ DOKUMENTY VY_32_INOVACE_TD_2_04 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek Téma Klíčová slova Druh
Multimediální systémy. 11 3d grafika
 Multimediální systémy 11 3d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Princip 3d objekty a jejich reprezentace Scéna a její osvětlení Promítání Renderování Oblasti využití
Multimediální systémy 11 3d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Princip 3d objekty a jejich reprezentace Scéna a její osvětlení Promítání Renderování Oblasti využití
Deskriptivní geometrie 0A5
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Deskriptivní geometrie 0A5 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Veronika Roušarová Brno c 2003 Obsah
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Deskriptivní geometrie 0A5 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Veronika Roušarová Brno c 2003 Obsah
E-learning na FCHPT STU v Bratislave. doc. Ing. Monika Bakošová, CSc.
 E-learning na FCHPT STU v Bratislave doc. Ing. Monika Bakošová, CSc. monika.bakosova@stuba.sk 12. 11. 2012 1 E-learning (e-vzdelávanie) E-learning = e-vzdelávanie, elektronické vzdelávanie je systém vzdelávania,
E-learning na FCHPT STU v Bratislave doc. Ing. Monika Bakošová, CSc. monika.bakosova@stuba.sk 12. 11. 2012 1 E-learning (e-vzdelávanie) E-learning = e-vzdelávanie, elektronické vzdelávanie je systém vzdelávania,
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika 0A1. Cvičení, zimní semestr. Samostatné výstupy. Jan Šafařík
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
současně ale zkracoval dosavadní devítiletou základní školu na osm roků (první stupeň byl zkrácen na čtyři roky)
 v roce 1968 dochází k přeměně a rozšíření tříletých SVVŠ (střední všeobecná vzdělávací škola) na čtyřletá gymnázia 1970 čtyřletá gymnázia celkem mají celkem 4 hodiny týdně na přírodovědné větvi a humanitní
v roce 1968 dochází k přeměně a rozšíření tříletých SVVŠ (střední všeobecná vzdělávací škola) na čtyřletá gymnázia 1970 čtyřletá gymnázia celkem mají celkem 4 hodiny týdně na přírodovědné větvi a humanitní
Úvod Typy promítání Matematický popis promítání Implementace promítání Literatura. Promítání. Pavel Strachota. FJFI ČVUT v Praze
 Promítání Pavel Strachota FJFI ČVUT v Praze 30. března 2011 Obsah 1 Úvod 2 Typy promítání 3 Matematický popis promítání 4 Implementace promítání Obsah 1 Úvod 2 Typy promítání 3 Matematický popis promítání
Promítání Pavel Strachota FJFI ČVUT v Praze 30. března 2011 Obsah 1 Úvod 2 Typy promítání 3 Matematický popis promítání 4 Implementace promítání Obsah 1 Úvod 2 Typy promítání 3 Matematický popis promítání
Technická dokumentace
 Technická dokumentace VY_32_inovace_FREI22 : Zásady kreslení šroubů, matic a podložek Datum vypracování: 1.9.2013 Vypracoval: Ing. Bohumil Freisleben Motto: dobrý výkres, tvoří i správně zobrazené normalizované
Technická dokumentace VY_32_inovace_FREI22 : Zásady kreslení šroubů, matic a podložek Datum vypracování: 1.9.2013 Vypracoval: Ing. Bohumil Freisleben Motto: dobrý výkres, tvoří i správně zobrazené normalizované
BA008 Konstruktivní geometrie. Topografické plochy. Spojení objektu s topografickou plochou. pro kombinované studium
 BA008 Konstruktivní geometrie pro kombinované studium Topografické plochy Spojení objektu s topografickou plochou přednášková skupina P-BK1VS1 učebna Z240 letní semestr 2016-2017 3. března 2017 Základní
BA008 Konstruktivní geometrie pro kombinované studium Topografické plochy Spojení objektu s topografickou plochou přednášková skupina P-BK1VS1 učebna Z240 letní semestr 2016-2017 3. března 2017 Základní
Vektorové grafické formáty
 Vektorové grafické formáty Semestrální práce na předmět KAPR Fakulta stavební ČVUT 28.5.2009 Vypracovali: Petr Vejvoda, Ivan Pleskač Obsah Co je to vektorová grafika Typy vektorových formátů Souborový
Vektorové grafické formáty Semestrální práce na předmět KAPR Fakulta stavební ČVUT 28.5.2009 Vypracovali: Petr Vejvoda, Ivan Pleskač Obsah Co je to vektorová grafika Typy vektorových formátů Souborový
Žiadosť o povolenie obhajoby dizertačnej práce
 Žiadosť o povolenie obhajoby dizertačnej práce Doktorand môže podať žiadosť o povolenie obhajoby dizertačnej práce dekanovi, ak získal najmenej 140 kreditov, bez zarátania kreditov prideľovaných za prijatie
Žiadosť o povolenie obhajoby dizertačnej práce Doktorand môže podať žiadosť o povolenie obhajoby dizertačnej práce dekanovi, ak získal najmenej 140 kreditov, bez zarátania kreditov prideľovaných za prijatie
TECHNICKÉ KRESLENÍ. Technické normy. Popisové pole. Zobrazování na technických výkresech
 Technické normy Formáty výkresů Úprava výkresových listů Popisové pole Skládání výkresů TECHNICKÉ KRESLENÍ Čáry na technických výkresech Technické písmo Zobrazování na technických výkresech Kótování Technické
Technické normy Formáty výkresů Úprava výkresových listů Popisové pole Skládání výkresů TECHNICKÉ KRESLENÍ Čáry na technických výkresech Technické písmo Zobrazování na technických výkresech Kótování Technické
MS OFFICE OUTLOOK 2007
 MS OFFICE OUTLOOK 2007 PRÍRUČKA PRE MANAŽÉROV Eleonóra Beňová Michal Greguš 2013 Univerzita Komenského v Bratislave MS Office Outlook 2007 Príručka pre manažérov Mgr. Eleonóra Beňová, PhD., RNDr. Michal
MS OFFICE OUTLOOK 2007 PRÍRUČKA PRE MANAŽÉROV Eleonóra Beňová Michal Greguš 2013 Univerzita Komenského v Bratislave MS Office Outlook 2007 Príručka pre manažérov Mgr. Eleonóra Beňová, PhD., RNDr. Michal
Základy matematiky pracovní listy
 Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Počítačová geometrie. + algoritmy DG
 Pojem výpočetní geometrie (počítačové) analýza a návrh efektivních algoritmů pro určování vlastností a vztahů geometrických objektů řešení geometrických problémů navrženými geometrickými algoritmy hlavním
Pojem výpočetní geometrie (počítačové) analýza a návrh efektivních algoritmů pro určování vlastností a vztahů geometrických objektů řešení geometrických problémů navrženými geometrickými algoritmy hlavním
Projekt IMPLEMENTACE ŠVP. pořadí početních operací, dělitelnost, společný dělitel a násobek, základní početní operace
 Střední škola umělecká a řemeslná Evropský sociální fond "Praha a EU: Investujeme do vaší budoucnosti" Projekt IMPLEMENTACE ŠVP Evaluace a aktualizace metodiky předmětu Matematika Výrazy Obory nástavbového
Střední škola umělecká a řemeslná Evropský sociální fond "Praha a EU: Investujeme do vaší budoucnosti" Projekt IMPLEMENTACE ŠVP Evaluace a aktualizace metodiky předmětu Matematika Výrazy Obory nástavbového
ŠTATISTIKA JEDNODUCHO V EXCELI STATIS, Bratislava 2013, ISBN , 344 strán A5,väzba V4.
 Jozef Chajdiak ŠTATISTIKA JEDNODUCHO V EXCELI STATIS, Bratislava 2013, ISBN 978-80-85659-74-0, 344 strán A5,väzba V4. Excel sa stal každodenným nástrojom práce mnohých z nás.. Predkladaná kniha ponúka
Jozef Chajdiak ŠTATISTIKA JEDNODUCHO V EXCELI STATIS, Bratislava 2013, ISBN 978-80-85659-74-0, 344 strán A5,väzba V4. Excel sa stal každodenným nástrojom práce mnohých z nás.. Predkladaná kniha ponúka
Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11].
![Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11].](/thumbs/52/30469232.jpg) Konstruktivní geometrie Bod Axonometrie Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. VŠB-TU Ostrava 1 Jana Bělohlávková Konstruktivní geometrie
Konstruktivní geometrie Bod Axonometrie Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. VŠB-TU Ostrava 1 Jana Bělohlávková Konstruktivní geometrie
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech."
 Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Techniky tímovej práce a možnosti ich aplikácie v manažérstve kvality
 Techniky tímovej a možnosti ich aplikácie v manažérstve kvality Doc. Ing. Vladimír Konečný, PhD. Žilinská univerzita v Žiline 9-1 Charakteristické črty tímovej : Definovaný konkrétny cieľ Dočasnosť (po
Techniky tímovej a možnosti ich aplikácie v manažérstve kvality Doc. Ing. Vladimír Konečný, PhD. Žilinská univerzita v Žiline 9-1 Charakteristické črty tímovej : Definovaný konkrétny cieľ Dočasnosť (po
VY_32_INOVACE_INF.10. Grafika v IT
 VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
IS ZBGIS kartografia
 Geodetický a kartografický ústav Bratislava IS ZBGIS kartografia Ing. Juraj Celler Ing. Katarína Moravčíková GKÚ BA Prednáškový seriál odborníkov ÚGKK SR v rámci blokovej výučby študentov končiacich ročníkov
Geodetický a kartografický ústav Bratislava IS ZBGIS kartografia Ing. Juraj Celler Ing. Katarína Moravčíková GKÚ BA Prednáškový seriál odborníkov ÚGKK SR v rámci blokovej výučby študentov končiacich ročníkov
Porada OÚPSŘ s ÚÚP ÚAP. 11. listopad Mgr. Tomáš Vaško OÚPSŘ KÚ LK
 Nový nástroj n územního plánov nování Územně analytické podklady ÚAP Pracovní skupina GIS k ÚAP 15. 09. 2006 Mgr. Tomáš Vaško OÚPSŘ KÚLK Porada OÚPSŘ s ÚÚP 11. listopad 2011 ÚZEMNĚ ANALYTICKÉ PODKLADY
Nový nástroj n územního plánov nování Územně analytické podklady ÚAP Pracovní skupina GIS k ÚAP 15. 09. 2006 Mgr. Tomáš Vaško OÚPSŘ KÚLK Porada OÚPSŘ s ÚÚP 11. listopad 2011 ÚZEMNĚ ANALYTICKÉ PODKLADY
ČESKÁ TECHNICKÁ NORMA
 ČESKÁ TECHNICKÁ NORMA ICS 01.040.01; 01.100.20 2005 Technické výkresy - Hrany neurčitých tvarů - Slovník a označování ČSN ISO 13715 01 3205 Červen Technical drawings - Edges of undefined shape - Vocabulary
ČESKÁ TECHNICKÁ NORMA ICS 01.040.01; 01.100.20 2005 Technické výkresy - Hrany neurčitých tvarů - Slovník a označování ČSN ISO 13715 01 3205 Červen Technical drawings - Edges of undefined shape - Vocabulary
5 Algoritmy vyplňování 2D oblastí
 5 Algoritmy vyplňování 2D oblastí Studijní cíl Tento blok je věnován základním algoritmům pro vyplňování plošných objektů. V textu bude vysvětlen rozdíl mezi vyplňováním oblastí, které jsou definovány
5 Algoritmy vyplňování 2D oblastí Studijní cíl Tento blok je věnován základním algoritmům pro vyplňování plošných objektů. V textu bude vysvětlen rozdíl mezi vyplňováním oblastí, které jsou definovány
ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA
 ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA Technická dokumentácia v elektrotechnike Prednáška 4 Zásady kreslenia elektrotechnických schém Pravidlá na kreslenie elektrotechnických schém sú uvedené v normách
ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA Technická dokumentácia v elektrotechnike Prednáška 4 Zásady kreslenia elektrotechnických schém Pravidlá na kreslenie elektrotechnických schém sú uvedené v normách
Konstruktivní geometrie a TK
 Konstruktivní geometrie a TK Úvodní informace Petr Liška Mendelova univerzita 15.2.2016 Petr Liška (Mendelova univerzita) Konstruktivní geometrie a TK 15.2.2016 1 / 26 Podmínky ukončení Přednáška nepovinná
Konstruktivní geometrie a TK Úvodní informace Petr Liška Mendelova univerzita 15.2.2016 Petr Liška (Mendelova univerzita) Konstruktivní geometrie a TK 15.2.2016 1 / 26 Podmínky ukončení Přednáška nepovinná
ŠVP Gymnázium Ostrava-Zábřeh. 4.8.19. Úvod do deskriptivní geometrie
 4.8.19. Úvod do deskriptivní geometrie Vyučovací předmět Úvod do deskriptivní geometrie je na naší škole nabízen v rámci volitelných předmětů v sextě, septimě nebo v oktávě jako jednoletý dvouhodinový
4.8.19. Úvod do deskriptivní geometrie Vyučovací předmět Úvod do deskriptivní geometrie je na naší škole nabízen v rámci volitelných předmětů v sextě, septimě nebo v oktávě jako jednoletý dvouhodinový
Obsah a průběh zkoušky 1PG
 Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
ZRÝCHLENIE EVIDENCIE VO VÝROBE
 ZRÝCHLENIE EVIDENCIE VO VÝROBE Riešenia na mieru s využitím čiarových kódov v logistike Ondrej Galko, SAP konzultant Agenda 1 Automatizovaná evidencia výroby evidencia výroby pomocou čítačiek čiarových
ZRÝCHLENIE EVIDENCIE VO VÝROBE Riešenia na mieru s využitím čiarových kódov v logistike Ondrej Galko, SAP konzultant Agenda 1 Automatizovaná evidencia výroby evidencia výroby pomocou čítačiek čiarových
ZB GIS referenčný základ národnej infraštruktúry priestorových informácií
 Geodetický a kartografický ústav Bratislava Chlumeckého 4, Bratislava ZB GIS referenčný základ národnej infraštruktúry priestorových informácií Mgr. Ľuboslav Michalík 18. Slovenské geodetické dni, Žilina,
Geodetický a kartografický ústav Bratislava Chlumeckého 4, Bratislava ZB GIS referenčný základ národnej infraštruktúry priestorových informácií Mgr. Ľuboslav Michalík 18. Slovenské geodetické dni, Žilina,
TECHNICKÁ DOKUMENTACE (Technické kreslení)
 TECHNICKÁ DOKUMENTACE (Technické kreslení) 1 NEŽ SE ZAČNE Pro úspěšné zvládnutí technického kreslení je nutno spojit : teoretické znalosti, logické myšlení, praktické dovednosti. CÍL STUDIA Cílem předmětu
TECHNICKÁ DOKUMENTACE (Technické kreslení) 1 NEŽ SE ZAČNE Pro úspěšné zvládnutí technického kreslení je nutno spojit : teoretické znalosti, logické myšlení, praktické dovednosti. CÍL STUDIA Cílem předmětu
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
ZADÁNÍ ZMĚNY Č. 1 ÚZEMNÍHO PLÁNU DRÁŽOV NÁVRH ZADÁNÍ K PROJEDNÁNÍ S DOTČENÝMI ORGÁNY A OSTATNÍMI ÚČASTNÍKY
 ZADÁNÍ ZMĚNY Č. 1 ÚZEMNÍHO PLÁNU DRÁŽOV NÁVRH ZADÁNÍ K PROJEDNÁNÍ S DOTČENÝMI ORGÁNY A OSTATNÍMI ÚČASTNÍKY Pořizovatel: Městský úřad Strakonice odbor rozvoje úřad územního plánování Oprávněná úřední osoba
ZADÁNÍ ZMĚNY Č. 1 ÚZEMNÍHO PLÁNU DRÁŽOV NÁVRH ZADÁNÍ K PROJEDNÁNÍ S DOTČENÝMI ORGÁNY A OSTATNÍMI ÚČASTNÍKY Pořizovatel: Městský úřad Strakonice odbor rozvoje úřad územního plánování Oprávněná úřední osoba
REPREZENTACE 3D SCÉNY
 REPREZENTACE 3D SCÉNY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah reprezentace 3D scény objemové reprezentace výčtové reprezentace
REPREZENTACE 3D SCÉNY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah reprezentace 3D scény objemové reprezentace výčtové reprezentace
23-41-M001 Strojírenství. Celkový počet týdenních vyučovacích hodin za studium: 4 Celkový počet vyučovacích hodin: 136 Platnost od: 1.9.
 Učební osnova vyučovacího předmětu technické kreslení Obor vzdělání: 2-41-M001 Strojírenství Délka forma studia: 4 roky, denní Celkový počet týdenních vyučovacích hodin za studium: 4 Celkový počet vyučovacích
Učební osnova vyučovacího předmětu technické kreslení Obor vzdělání: 2-41-M001 Strojírenství Délka forma studia: 4 roky, denní Celkový počet týdenních vyučovacích hodin za studium: 4 Celkový počet vyučovacích
Konstruktivní geometrie a technické kreslení
 Konstruktivní geometrie a technické kreslení Základy technického kreslení Petr Liška Mendelova univerzita 23.11.2015 Petr Liška (Mendelova univerzita) Konstruktivní geometrie a technické kreslení 23.11.2015
Konstruktivní geometrie a technické kreslení Základy technického kreslení Petr Liška Mendelova univerzita 23.11.2015 Petr Liška (Mendelova univerzita) Konstruktivní geometrie a technické kreslení 23.11.2015
Předmět poskytuje základní vědomosti o normalizaci pro zobrazování, kótování, kreslení řezů a detailů, značení materiálů výrobků na výkresech.
 1. ÚVOD DO PŘEDMĚTU Předmět poskytuje základní vědomosti o normalizaci pro zobrazování, kótování, kreslení řezů a detailů, značení materiálů výrobků na výkresech. Cílem je čtení, kreslení jednoduchých
1. ÚVOD DO PŘEDMĚTU Předmět poskytuje základní vědomosti o normalizaci pro zobrazování, kótování, kreslení řezů a detailů, značení materiálů výrobků na výkresech. Cílem je čtení, kreslení jednoduchých
GIS riešenia pre samosprávy
 GIS riešenia pre samosprávy - praktické ukážky a problémy Peter Pavličko 18.6.2008, Bratislava www.corinex.sk OBSAH 1. GIS v samospráve/verejnej správe 2. Koncepčný prístup, technologické trendy 3. GIS
GIS riešenia pre samosprávy - praktické ukážky a problémy Peter Pavličko 18.6.2008, Bratislava www.corinex.sk OBSAH 1. GIS v samospráve/verejnej správe 2. Koncepčný prístup, technologické trendy 3. GIS
Použité zdroje a odkazy: Nápověda Corel Draw X6, J. Švercl: Technické kreslení a deskriptivní geometrie pro školu a praxi
 Označení materiálu: Autor: Mgr. Ludmila Krčmářová VY_32_INOVACE_PoGra1709 Tematický celek: Corel DrawX6 Učivo (téma): Kótování v Corel Draw Stručná Charakteristika: Využití nástrojů CD vhodných na kótování
Označení materiálu: Autor: Mgr. Ludmila Krčmářová VY_32_INOVACE_PoGra1709 Tematický celek: Corel DrawX6 Učivo (téma): Kótování v Corel Draw Stručná Charakteristika: Využití nástrojů CD vhodných na kótování
U N I V E R Z I N S K Á I T A I L V E R E N L N T A S O
 Ž U N I L I N S K Á U N I V E R Z I T A S I S I V E R S I T A S S O E N L N Ing. Monika Václavková, PhD. Ing. Iveta Nedeljaková, PhD. RNDr. Štefan Kovalík, PhD. Ing. Ján Bohá!ik, PhD. Ing. Josef Kopecký
Ž U N I L I N S K Á U N I V E R Z I T A S I S I V E R S I T A S S O E N L N Ing. Monika Václavková, PhD. Ing. Iveta Nedeljaková, PhD. RNDr. Štefan Kovalík, PhD. Ing. Ján Bohá!ik, PhD. Ing. Josef Kopecký
PŘENOS DAT MEZI ESA PT A CAD PROGRAMY (ALLPLAN)
 PŘENOS DAT MEZI ESA PT A CAD PROGRAMY (ALLPLAN) Ing. Martin Novák, CSc. SCIA CZ, s.r.o, Thákurova 3, 160 00 Praha www.scia.cz 1 ÚVOD Kompatibilita systému ESA PT s programy z oblasti CAD je jednou z dlouhodobých
PŘENOS DAT MEZI ESA PT A CAD PROGRAMY (ALLPLAN) Ing. Martin Novák, CSc. SCIA CZ, s.r.o, Thákurova 3, 160 00 Praha www.scia.cz 1 ÚVOD Kompatibilita systému ESA PT s programy z oblasti CAD je jednou z dlouhodobých
Deskriptivní geometrie
 Deskriptivní geometrie Úvodní informace Petr Liška Mendelova univerzita 20.9.2016 Petr Liška (Mendelova univerzita) Deskriptivní geometrie 20.9.2016 1 / 31 Podmínky ukončení Přednáška nepovinná účast méně
Deskriptivní geometrie Úvodní informace Petr Liška Mendelova univerzita 20.9.2016 Petr Liška (Mendelova univerzita) Deskriptivní geometrie 20.9.2016 1 / 31 Podmínky ukončení Přednáška nepovinná účast méně
VYZNAČOVÁNÍ ZMĚN NA VÝKRESECH
 VYZNAČOVÁNÍ ZMĚN NA VÝKRESECH VY_32_INOVACE_TD_2_20 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek Téma Klíčová
VYZNAČOVÁNÍ ZMĚN NA VÝKRESECH VY_32_INOVACE_TD_2_20 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek Téma Klíčová
HISTORICKÉ MAPY. 24. október 2013
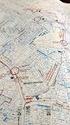 HISTORICKÉ MAPY 24. október 2013 Ing. Renáta KMEŤKOVÁ, Ing. Petra PECHOVÁ GEODETICKÝ A KARTOGRAFICKÝ ÚSTAV BRATISLAVA Katastrálne mapy rezortu geodézie, kartografie a katastra OBSAH A VYUŽITIE KATASTRÁLNYCH
HISTORICKÉ MAPY 24. október 2013 Ing. Renáta KMEŤKOVÁ, Ing. Petra PECHOVÁ GEODETICKÝ A KARTOGRAFICKÝ ÚSTAV BRATISLAVA Katastrálne mapy rezortu geodézie, kartografie a katastra OBSAH A VYUŽITIE KATASTRÁLNYCH
