Interferenční mikroskopie
|
|
|
- Rostislav Esterka
- před 8 lety
- Počet zobrazení:
Transkript
1 Interferenční mikroskopie J. Kuběna ÚFKL Přírodovědecká fakulta Masarykovy University Učební pomůcka ke studiu optiky, verse 6
2 Úvod Následující série obráků je aměřena na objasnění funkce interferenčních mikroskopů, jimiž le vyvolat umělý kontrast struktury preparátu. U mikroskopu na odra (Zeiss -Epival) jde o strukturu povrchového reliéfu, u mikroskopu na průchod (Zeiss -Peraval) může jít i o strukturu indeu lomu v objemu preparátu při jeho konstantní tloušťce. V teoretické části presentace je na ákladě numerických výpočtů interferenční intenity při dvoupaprskové interferenci demonstrován vliv koherenčních vlastností interferujících paprsků na roložení intenity v orném poli mikroskopu. Veperimentální části, jsouna digitálních mikrofotografiích mikroskopu demonstrovány jevy, s nimiž se setkáme ejména při seřiování mikroskopů. Grafy interferenční intenity jsou de výsledkem softwarové analýy digitálního obráku. Tato presentace navauje pojmový aparát užívaný v přednášce Principy moderních optických obraovacích metod a je aměřena na praktickou obsluhu mikroskopů. 2
3 Schéma mikroskopu na odra - Epival preparát P Q body P a Q v rovině meiobrau splynou kondenor Výměnné štěrbiny jako droj objektiv dělič svaku polopropustné rcadlo barevné filtry halogenová žárovka Velikostí a natáčením štěrbin měníme velikost koherenční šířky v rovině meiobrau A B kompenátor dráhového posuvu roštěpení obraů rcadlo Dvou paprskový interferometr P A Q A P A= Q B P B P B roštěpení obrau měna směru paprsku B orné pole (sklon vlnoplochy B) mikroskopu vlnoplochy A a B v rovině meiobrau fáově posunuté o (původně jedna vlnoplocha) r 3
4 Schéma mikroskopu na průchod -Peraval barevný filtr halogenová žárovka štěrbina jako droj preparát kondenor objektiv P Q body P a Q v rovině meiobrau splynou Velikostí a natáčením štěrbiny měníme velikost koherenční šířky v rovině meiobrau dělič svaku A B kompenátor dráhového posuvu roštěpení obraů rcadlo P A Q A P B měna směru paprsku B (sklon vlnoplochy B) vlnoplochy A a B v rovině meiobrau fáově posunuté o (původně jedna vlnoplocha) Dvou paprskový interferometr P A= Q B P B r orné pole mikroskopu roštěpení obrau 4
5 Interferenční intenita Zorné pole vlnoplochy B A Teoretická část: Dvoupaprsková interference 2π I (, α ) = I + I + 2γ γ I I cos( ) P A A y Q A P B Q B r α P A Q B Q A P B B t s A B Vtah dráhového rodílu a souřadnice λ = 2 tan( α / 2) Stupeňčasové koherence γ (, δ ) t = ep( Stupeň prostorové koherence γ s 2 4δ sin( π r β ) ( r, β ) = π r β 2 ) 5
6 Stupeň časovékoherence Závislost stupně časové koherence na dráhovém rodílu měřeném v jednotkách koherenční délky δ δ = λ 2 0 λ 6
7 Stupeň prostorovékoherence Závislost stupně prostorové koherence na roštěpení r měřeném v jednotkách koherenční šířky β β = λ 0 a s 7
8 Úhel vlnoploch α = 10 o Závislost interferenční intenity na souřadnici pro uvedené parametry α Velký úhel působuje rychléstřídání maim intenity, malá koherenční délka (bílé světlo) pak jejich rychlý pokles. 8
9 Úhel vlnoploch α = 3 o Závislost interferenční intenity na souřadnici pro uvedené parametry Malý úhel mei vlnoplochami působí pomaléstřídání maim intenity. Roštěpení obraů je v grafech je vynačeno červenými kroužky u intenitní osy. Jeden kroužek namená, že roštěpení je nulové. 9
10 Úhel vlnoploch α = 0.2 o Závislost interferenční intenity na souřadnici pro uvedené parametry Vlnoplochy jsou téměř rovnoběžné, intenita k okrajům orného pole klesá(v bílém světle nemástejnou barvu). 10
11 Dráhový posuv pro 0 je0.1λ Závislost interferenční intenity na souřadnici pro uvedené parametry Vlnoplochy se protínají mimo střed orného pole. Roštěpení obraů de a na předchoích grafech bylo nulové. Stupeň prostorové koherence byl roven 1. 11
12 α = 10 ο, β = 10 µm, r = 2 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Roštěpení obraů je de 2 mikrometry, stupeň prostorové koherence klesá. V porovnání s grafem na str. 8, maimum intenity kleslo. 12
13 α = 10 ο, β = 10 µm, r = 5 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Roštěpení 5 mikrometrů, maimum intenity dále kleslo, protože stupeň prostorovékoherence se s rostoucím roštěpením dále menšuje. 13
14 α = 10 ο, β = 20 µm, r = 10 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Roložení intenity je stejné, jako na předchoím grafu přes to, že roštěpení se dvojnásobilo. Je to tím, že jsme koherenční šířku takédvojnásobili. 14
15 α = 10 ο, β = 10 µm, r = 9 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Interferenční jev má malou viditelnost. Je to tím, že koherenční šířka je jen o málo větší než roštěpení. Uprostřed orného pole je ale stále maimum interferenčního jevu. 15
16 α = 10 ο, β = 10 µm, r = 11 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Zde je roštěpeníjen o málo větší nežje koherenční šířka. Stupeň prostorové koherence je v tomto případě áporný, a proto je uprostřed minimum. 16
17 α = 10 ο, β = 10 µm, r = 15 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Minimum uprostřed ůstává, interference má lepší viditelnost přes to, že roštěpení dále vrostlo. Stupeň prostorovékoherence je asi
18 δ = 3λ, 0 = 3λ, r = 0 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Maimum interferenčního jevu leží mimo střed orného pole. Posuvem jednévlnoplochy nastavíme maimum opět do středu. 18
19 δ = 10λ, 0 = 3λ, r = 0 µm Závislost interferenční intenity na souřadnici pro uvedené parametry Velký počet maim v orném poli je důsledek velkékoherenční délky (ařaení žlutého filtru). 19
20 Eperimentální část: Hrana tenkévrstvy, malé roštěpeníobrau B A Zeleně je kreslen součet intenit všech barev G+B+R. Červeně intenita po odečtenípoadí. Pás pro analýu intenity digitální fotografie 20
21 Hrana tenkévrstvy, většíroštěpeníobrau, viditelnost interferenčního jevu poklesla Nastal pokles viditelnosti. Větší roštěpení obrau působilo pokles stupně prostorové koherence. 21
22 Hrana tenkévrstvy, většíroštěpeníobrau, užšíštěrbina, viditelnost se lepšila r B A 22
23 Vliv posuvu vlnoplochy B, stejný úhel Vlnoplocha se posunuje B Body nulového fáového rodílu odpovídajíi ma 1 A
24 Bílésvětlo Všimněte si symetrického roloženíbarev kolem nultého interferenčního řádu, který je bílý. Hloubka oubku dobře patrnáv bílém světle je důležitá pro měření tloušťky vrstev větších než λ/2. 24
25 Zelený filtr Trochu větší koherenčnídélka dosažena vložením eleného filtru. Výsledný interferenční jev však určuje nejen propustnost vloženého filtru, ale i filtry ve fotoaparátu. 25
26 Žlutý filtr Koherenční délka je řetelně větší než u eleného filtru. Žlutý filtr má střední vlnovou délku 580nm a spektrální šířku 50nm. 26
27 Zviditelnění reliéfu malým roštěpením nečistota r Velkéroštěpení r, paprsky neinterferují, protože nejsou prostorově koherentní. Reliéf povrchu (hrana) není vidět. Hrana tenkévrstvy Al na povrchu. Roštěpení je malé, oba paprsky interferují, vlnoplochy jsou téměř rovnoběžné. Kromě hrany je viditelněn i jemný reliéf povrchu. 27
28 Růnéobraeníhrany tenkévrstvy Malé roštěpení, dráhový rodíl 0 je asi čtvrtina lambda. Podobně obraí hranu Nomarského kontrast, u něhož je roštěpení konstantní. B A h 2h 0 I( 0 + 2h) I 0 I(- 0-2h) I( 0 ) 28
29 Jiné viditelněníreliéfu povrchu Stejné oblasti povrchů preparátu, malé roštěpení, viditelněný reliéf povrchu Růný dráhový rodíl 0 odpovídá a barvu poadí Maléjamky mají jinou barvu. Hrana povrchového reliéfu překrytávrstvou Al Jak rolišíme jamky od kopečků? 29
30 Vliv růného úhlu vlnoploch α B α A Obra hrany tenké vrstvy při malém roštěpení. Když roštěpení většíme, le pak měřit nenámou tloušťku tenké vrstvy. Vi následující obr. 30
31 Měřenítloušťky tenkévrstvy P1 P2 Pásy obrau pro numerickou analýu intenity Výsledek numerickéanalýy λ 2 intenita B A r Vlnoplocha B, roštěpenío r Vlnoplocha A mápo odrau schodek 2 (otisk reliéfu povrchu) Krycí vrstva, často hliníková, aby měna fáe po odrau byla stejná Tenkávrstva tloušťky Podložka =? 31
Praktikum školních pokusů 2
 Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
Petr Šafařík 21,5. 99,1kPa 61% Astrofyzika Druhý Třetí
 1 Petr Šafařík Astrofyzika Druhý Třetí 1,5 11 99,1kPa 61% Fyzikální praktika 11 Měření tloušt ky tenkých vrstev Tolanského metodou Průchod světla planparalelní deskou a hranolem Petr Šafařík 0. listopadu
1 Petr Šafařík Astrofyzika Druhý Třetí 1,5 11 99,1kPa 61% Fyzikální praktika 11 Měření tloušt ky tenkých vrstev Tolanského metodou Průchod světla planparalelní deskou a hranolem Petr Šafařík 0. listopadu
Mikroskopické metody Přednáška č. 3. Základy mikroskopie. Kontrast ve světelném mikroskopu
 Mikroskopické metody Přednáška č. 3 Základy mikroskopie Kontrast ve světelném mikroskopu Nízký kontrast biologických objektů Nízký kontrast biologických objektů Metodika přípravy objektů pro světelnou
Mikroskopické metody Přednáška č. 3 Základy mikroskopie Kontrast ve světelném mikroskopu Nízký kontrast biologických objektů Nízký kontrast biologických objektů Metodika přípravy objektů pro světelnou
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Podpora rozvoje praktické výchovy ve fyzice a chemii
 VLNOVÁ DÉLKA A FREKVENCE SVĚTLA 1) Vypočítejte frekvenci fialového světla, je-li jeho vlnová délka 390 nm. Rychlost světla ve vakuu je 3 10 8 m s 1. = 390 nm = 390 10 9 m c = 3 10 8 m s 1 f=? (Hz) Pro
VLNOVÁ DÉLKA A FREKVENCE SVĚTLA 1) Vypočítejte frekvenci fialového světla, je-li jeho vlnová délka 390 nm. Rychlost světla ve vakuu je 3 10 8 m s 1. = 390 nm = 390 10 9 m c = 3 10 8 m s 1 f=? (Hz) Pro
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
 Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ
 VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Rovinná a prostorová napjatost
 Rovinná a prostorová napjatost Vdělme v bodě tělesa elementární hranolek o hranách d, d, d Vnitřní síl ve stěnách hranolku se projeví jako napětí na příslušné ploše a le je roložit do směrů souřadnicových
Rovinná a prostorová napjatost Vdělme v bodě tělesa elementární hranolek o hranách d, d, d Vnitřní síl ve stěnách hranolku se projeví jako napětí na příslušné ploše a le je roložit do směrů souřadnicových
Jak vyrobit monochromatické Slunce
 Jak vyrobit monochromatické Slunce Spektroskopie (nejen) ve sluneční fyzice LS 011/01 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Pozorování Slunce ve spektrální čáře Spektroheliogram
Jak vyrobit monochromatické Slunce Spektroskopie (nejen) ve sluneční fyzice LS 011/01 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Pozorování Slunce ve spektrální čáře Spektroheliogram
27. Vlnové vlastnosti světla
 27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako
![Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako](/thumbs/55/36333813.jpg) Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky
 Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky 1. Vysvětlete pojmy kulová a rovinná vlnoplocha. 2. Pomocí Hyugensova principu vysvětlete konstrukci tvaru vlnoplochy v libovolném budoucím
Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky 1. Vysvětlete pojmy kulová a rovinná vlnoplocha. 2. Pomocí Hyugensova principu vysvětlete konstrukci tvaru vlnoplochy v libovolném budoucím
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky
 Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Laboratorní úloha č. 7 Difrakce na mikro-objektech
 Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Fyzikální korespondenční seminář UK MFF 22. II. S
 Fzikální korespondenční seminář UK MFF http://fkosmffcunicz II S ročník, úloha II S Young a vlnová povaha světla (5 bodů; průměr,50; řešilo 6 studentů) a) Jaký tvar interferenčních proužků na stínítku
Fzikální korespondenční seminář UK MFF http://fkosmffcunicz II S ročník, úloha II S Young a vlnová povaha světla (5 bodů; průměr,50; řešilo 6 studentů) a) Jaký tvar interferenčních proužků na stínítku
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie
 Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
Laboratorní práce č. 3: Měření vlnové délky světla
 Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
Digitální učební materiál
 Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Zadání. Pracovní úkol. Pomůcky
 Pracovní úkol Zadání 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chybu měření. 2. Změřte zvětšení a zorná pole
Pracovní úkol Zadání 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chybu měření. 2. Změřte zvětšení a zorná pole
K rozpoznání růstu či klesání dané funkce určitém směru nám pomůže gradient, tj. vektor., ln(1 x2 + y 2 [ = y
 VKM/IM - 204/205 Určete, da funkce f(x, y) ln( x 2 +y 2 ) v bodě A, ve směru vektorů u, 0, u 2 0,, u 3, a u 4, 2 roste či klesá a určete rychlost měny. Řešení: Funkce f(x, y) je definovány pro všechny
VKM/IM - 204/205 Určete, da funkce f(x, y) ln( x 2 +y 2 ) v bodě A, ve směru vektorů u, 0, u 2 0,, u 3, a u 4, 2 roste či klesá a určete rychlost měny. Řešení: Funkce f(x, y) je definovány pro všechny
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
Neživá příroda I. Optické vlastnosti minerálů
 Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Konstrukční varianty systému pro nekoherentní korelační zobrazení
 Konstrukční varianty systému pro nekoherentní korelační zobrazení Technický seminář Centra digitální optiky Vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Zpracoval: Petr Bouchal Řešitelské organizace:
Konstrukční varianty systému pro nekoherentní korelační zobrazení Technický seminář Centra digitální optiky Vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Zpracoval: Petr Bouchal Řešitelské organizace:
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí
 Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
K rozpoznání růstu či klesání dané funkce určitém směru nám pomůže gradient, tj. vektor., ln(1 x2 + y 2 [ = y
 VKM/IM 017/018 Určete da funkce fx y) ln1 x +y ) v bodě A 1 1 ve směru vektorů u 1 1 0 u 0 1 u 3 1 1 a u 4 1 roste či klesá a určete rychlost měny. Řešení: Funkce fx y) je definovány pro všechny body R
VKM/IM 017/018 Určete da funkce fx y) ln1 x +y ) v bodě A 1 1 ve směru vektorů u 1 1 0 u 0 1 u 3 1 1 a u 4 1 roste či klesá a určete rychlost měny. Řešení: Funkce fx y) je definovány pro všechny body R
Jméno a příjmení. Ročník. Měřeno dne Příprava Opravy Učitel Hodnocení. Vlnové vlastnosti světla difrakce, laser
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Spolupracoval Měřeno dne Odevzdáno dne Lukáš Teuer 8.4.2013 22.4.2013 Příprava Opravy
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Spolupracoval Měřeno dne Odevzdáno dne Lukáš Teuer 8.4.2013 22.4.2013 Příprava Opravy
vede sice ke zvýšení kontrastu, zároveň se ale snižuje rozlišení a ostrost obrazu (Obr. 46).
 4. cvičení Metody zvýšení kontrastu obrazu (1. část) 1. Přivření kondenzorové clony nebo snížení kondenzoru vede sice ke zvýšení kontrastu, zároveň se ale snižuje rozlišení a ostrost obrazu (Obr. 46).
4. cvičení Metody zvýšení kontrastu obrazu (1. část) 1. Přivření kondenzorové clony nebo snížení kondenzoru vede sice ke zvýšení kontrastu, zároveň se ale snižuje rozlišení a ostrost obrazu (Obr. 46).
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH
 SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná.
 1 Pracovní úkoly 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
1 Pracovní úkoly 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát
 Michal Veselý, 00 Základní části fotografického aparátu tedy jsou: tělo přístroje objektiv Pochopení funkce běžných objektivů usnadní zjednodušená představa, že objektiv jako celek se chová stejně jako
Michal Veselý, 00 Základní části fotografického aparátu tedy jsou: tělo přístroje objektiv Pochopení funkce běžných objektivů usnadní zjednodušená představa, že objektiv jako celek se chová stejně jako
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Youngův dvouštěrbinový experiment
 Youngův dvouštěrbinový experiment Cíl laboratorní úlohy: Cílem laboratorní úlohy je pochopit princip dvouštěrbinové interference a určit vlnovou délku světla na základě rozteče pozorovaných interferenčních
Youngův dvouštěrbinový experiment Cíl laboratorní úlohy: Cílem laboratorní úlohy je pochopit princip dvouštěrbinové interference a určit vlnovou délku světla na základě rozteče pozorovaných interferenčních
PRINCIPY MODERNÍCH OPTICKÝCH ZOBRAZOVACÍCH METOD PRAKTIKUM
 Ústav fyziky kondenzovaných látek (ÚFKL) Přírodovědecká fakulta, Masarykova univerzita, Brno http://www.physics.muni.cz/ufkl PRINCIPY MODERNÍCH OPTICKÝCH ZOBRAZOVACÍCH METOD PRAKTIKUM jarní semestr 2013
Ústav fyziky kondenzovaných látek (ÚFKL) Přírodovědecká fakulta, Masarykova univerzita, Brno http://www.physics.muni.cz/ufkl PRINCIPY MODERNÍCH OPTICKÝCH ZOBRAZOVACÍCH METOD PRAKTIKUM jarní semestr 2013
(Umělé) osvětlování pro analýzu obrazu
 (Umělé) osvětlování pro analýzu obrazu Václav Hlaváč České vysoké učení technické v Praze Centrum strojového vnímání (přemosťuje skupiny z) Český institut informatiky, robotiky a kybernetiky 166 36 Praha
(Umělé) osvětlování pro analýzu obrazu Václav Hlaváč České vysoké učení technické v Praze Centrum strojového vnímání (přemosťuje skupiny z) Český institut informatiky, robotiky a kybernetiky 166 36 Praha
 é č í é ě í ž ý Ú á í ž ý í ý Á Í ÁŘ É Á áš í ý á ář é í á í ž ý í Ř ú á á č ý š á í š í řá ě č á í í é ář é á é á í í ó á í é č á ú ě ý á í ý žň á í í é ó ó é í á ěř í č í á ů ř ě é ář é á í ář é á á
é č í é ě í ž ý Ú á í ž ý í ý Á Í ÁŘ É Á áš í ý á ář é í á í ž ý í Ř ú á á č ý š á í š í řá ě č á í í é ář é á é á í í ó á í é č á ú ě ý á í ý žň á í í é ó ó é í á ěř í č í á ů ř ě é ář é á í ář é á á
 Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Mikroskop ECLIPSE E200 STUDENTSKÝ NÁVOD K POUŽITÍ. určeno pro studenty ČZU v Praze
 Mikroskop ECLIPSE E200 STUDENTSKÝ NÁVOD K POUŽITÍ určeno pro studenty ČZU v Praze Mikroskop Nikon Eclipse E200 Světelný mikroskop značky Nikon (Eclipse E200) používaný v botanické cvičebně zvětšuje při
Mikroskop ECLIPSE E200 STUDENTSKÝ NÁVOD K POUŽITÍ určeno pro studenty ČZU v Praze Mikroskop Nikon Eclipse E200 Světelný mikroskop značky Nikon (Eclipse E200) používaný v botanické cvičebně zvětšuje při
FYZIKA PRO IV. ROČNÍK GYMNÁZIA - OPTIKA 2. VLNOVÁ OPTIKA
 FYZIKA PRO IV. ROČNÍK GYMNÁZIA - OPTIKA 2. VLNOVÁ OPTIKA Mgr. Monika Bouchalová Gymnázium, Havířov-Město, Komenského 2, p.o. Tento digitální učební materiál (DUM) vznikl na základě řešení projektu OPVK,
FYZIKA PRO IV. ROČNÍK GYMNÁZIA - OPTIKA 2. VLNOVÁ OPTIKA Mgr. Monika Bouchalová Gymnázium, Havířov-Město, Komenského 2, p.o. Tento digitální učební materiál (DUM) vznikl na základě řešení projektu OPVK,
Lom světla na kapce, lom 1., 2. a 3. řádu Lom světla na kapce, jenž je reprezentována kulovou plochou rozhraní, je složitý mechanismus rozptylu dopada
 Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Vlnové vlastnosti světla. Člověk a příroda Fyzika
 Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU
 ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU J. Novák, P. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán software pro počítačovou simulaci
ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU J. Novák, P. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán software pro počítačovou simulaci
Rychlost, zrychlení, tíhové zrychlení
 Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
6.1 Shrnutí základních poznatků
 6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
P5: Optické metody I
 P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
9. Umělé osvětlení. 9.1 Základní veličiny. e. (9.1) I =. (9.6)
 9. Umělé osvětlení Umělé osvětlení vhodně doplňuje nebo cela nahrauje denní osvětlení v případě jeho nedostatku a tím přispívá ke lepšení rakové pohody člověka. Umělé osvětlení ale potřebuje droj energie,
9. Umělé osvětlení Umělé osvětlení vhodně doplňuje nebo cela nahrauje denní osvětlení v případě jeho nedostatku a tím přispívá ke lepšení rakové pohody člověka. Umělé osvětlení ale potřebuje droj energie,
5.3.3 Interference na tenké vrstvě
 5.3.3 Interference na tenké vrstvě Předpoklady: 530 Bublina z bublifuku, slabounká vrstva oleje na vodě, někteří brouci jasné duhové barvy, u bublin se přelévají, barvy se mění s úhlem, pod kterým povrch
5.3.3 Interference na tenké vrstvě Předpoklady: 530 Bublina z bublifuku, slabounká vrstva oleje na vodě, někteří brouci jasné duhové barvy, u bublin se přelévají, barvy se mění s úhlem, pod kterým povrch
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis
 MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
Základní pojmy. Je násobkem zvětšení objektivu a okuláru
 Vznik obrazu v mikroskopu Mikroskop se skládá z mechanické části (podstavec, stojan a stolek s křížovým posunem), osvětlovací části (zdroj světla, kondenzor, clona) a optické části (objektivy a okuláry).
Vznik obrazu v mikroskopu Mikroskop se skládá z mechanické části (podstavec, stojan a stolek s křížovým posunem), osvětlovací části (zdroj světla, kondenzor, clona) a optické části (objektivy a okuláry).
Přímková a rovinná soustava sil
 Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
REALIZACE BAREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚ-FREKVENČNÍ OBLASTI SPEKTRA
 REALIZACE AREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚFREKVENČNÍ OLASTI SPEKTRA. Úvod Antonín Mikš Jiří Novák Fakulta stavební ČVUT katedra fyziky Thákurova 7 66 9 Praha 6 V technické praxi se často vyskytuje
REALIZACE AREVNÉHO KONTRASTU DEFEKTŮ V OPTICKÉ PROSTOVĚFREKVENČNÍ OLASTI SPEKTRA. Úvod Antonín Mikš Jiří Novák Fakulta stavební ČVUT katedra fyziky Thákurova 7 66 9 Praha 6 V technické praxi se často vyskytuje
Základní pojmy a vztahy: Vlnová délka (λ): vzdálenost dvou nejbližších bodů vlnění kmitajících ve stejné fázi
 LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
LRR/BUBCV CVIČENÍ Z BUNĚČNÉ BIOLOGIE 1. SVĚTELNÁ MIKROSKOPIE A PREPARÁTY V MIKROSKOPII TEORETICKÝ ÚVOD: Mikroskopie je základní metoda, která nám umožňuje pozorovat velmi malé biologické objekty. Díky
Fabry Perotův interferometr
 Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Obr. 4 Změna deklinace a vzdálenosti Země od Slunce v průběhu roku
 4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
Tabulka I Měření tloušťky tenké vrstvy
 Pracovní úkol 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
Pracovní úkol 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
VYUŽITÍ MATLABU PRO MODELOVÁNÍ INTERFEROGRAMŮ PROUDÍCÍHO PLYNU S RŮZNÝM INDEXEM LOMU. Jiří Olejníček Pedagogická fakulta, Jihočeská univerzita
 VYUŽITÍ MATLABU PRO MODELOVÁNÍ INTERFEROGRAMŮ PROUDÍCÍHO PLYNU S RŮZNÝM INDEXEM LOMU Jiří Olejníček Pedagogická fakulta, Jihočeská univerzita Abstrakt: Příspěvek se zabývá využitím Matlabu pro modelování
VYUŽITÍ MATLABU PRO MODELOVÁNÍ INTERFEROGRAMŮ PROUDÍCÍHO PLYNU S RŮZNÝM INDEXEM LOMU Jiří Olejníček Pedagogická fakulta, Jihočeská univerzita Abstrakt: Příspěvek se zabývá využitím Matlabu pro modelování
Úloha č. 8 Vlastnosti optických vláken a optické senzory
 Úloha č. 8 Vlastnosti optických vláken a optické senzory Optické vlákna patří k nejmodernějším přenosovým médiím. Jejich vysoká přenosová kapacita a nízký útlum jsou hlavní výhody, které je staví před
Úloha č. 8 Vlastnosti optických vláken a optické senzory Optické vlákna patří k nejmodernějším přenosovým médiím. Jejich vysoká přenosová kapacita a nízký útlum jsou hlavní výhody, které je staví před
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM
 MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
Elektromagnetické vlnění
 Elektromagnetické vlnění kolem vodičů elmag. oscilátoru se vytváří proměnné elektrické i magnetické pole http://www.walter-fendt.de/ph11e/emwave.htm Radiotechnika elmag vlnění vyzářené dipólem můžeme zachytit
Elektromagnetické vlnění kolem vodičů elmag. oscilátoru se vytváří proměnné elektrické i magnetické pole http://www.walter-fendt.de/ph11e/emwave.htm Radiotechnika elmag vlnění vyzářené dipólem můžeme zachytit
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ ANALÝZA PROFILU POVRCHŮ POMOCÍ INTERFEROMETRIE NÍZKÉ KOHERENCE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING ANALÝZA PROFILU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING ANALÝZA PROFILU
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
Optická (světelná) Mikroskopie pro TM I
 Optická (světelná) Mikroskopie pro TM I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Typy klasických biologických a polarizačních mikroskopů Přehled součástí
Optická (světelná) Mikroskopie pro TM I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Typy klasických biologických a polarizačních mikroskopů Přehled součástí
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI
 CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
Mikroskopie a rentgenová strukturní analýza
 Mikroskopie a rentgenová strukturní analýza (1) Světelná mikroskopie (2) Elektronová mikroskopie (3) Mikroskopie skenující sondou (4) Rentgenová strukturní analýza Doporučená literatura (viz STAG): 1.
Mikroskopie a rentgenová strukturní analýza (1) Světelná mikroskopie (2) Elektronová mikroskopie (3) Mikroskopie skenující sondou (4) Rentgenová strukturní analýza Doporučená literatura (viz STAG): 1.
Optické metody a jejich aplikace v kompozitech s polymerní matricí
 Optické metody a jejich aplikace v kompozitech s polymerní matricí Doc. Ing. Eva Nezbedová, CSc. Polymer Institute Brno Ing. Zdeňka Jeníková, Ph.D. Ústav materiálového inženýrství, Fakulta strojní, ČVUT
Optické metody a jejich aplikace v kompozitech s polymerní matricí Doc. Ing. Eva Nezbedová, CSc. Polymer Institute Brno Ing. Zdeňka Jeníková, Ph.D. Ústav materiálového inženýrství, Fakulta strojní, ČVUT
25 A Vypracoval : Zdeněk Žák Pyrometrie υ = -40 C.. +10000 C. Výhody termovize Senzory infračerveného záření Rozdělení tepelné senzory
 25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
Zadání. Goniometrie a trigonometrie
 GONIOMETRIE A TRIGONOMETRIE Zadání Sestrojte graf funkce. Určete definiční obor R, obor hodnot H, určete interval, v němž funkce roste, v němž klesá. Určete souřadnice průsečíků s osou x a s osou y. )
GONIOMETRIE A TRIGONOMETRIE Zadání Sestrojte graf funkce. Určete definiční obor R, obor hodnot H, určete interval, v němž funkce roste, v němž klesá. Určete souřadnice průsečíků s osou x a s osou y. )
EXPERIMENTÁLNÍ METODY I 17. Optické vizualizační metody
 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. EXPERIMENTÁLNÍ METODY I 17. Optické vizualizační metody OSNOVA 17. KAPITOLY Úvod do optických
FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. EXPERIMENTÁLNÍ METODY I 17. Optické vizualizační metody OSNOVA 17. KAPITOLY Úvod do optických
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 10: Interference a ohyb světla
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 8.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 10: Interference a ohyb
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 8.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 10: Interference a ohyb
Maticová optika. Lenka Přibylová. 24. října 2010
 Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
Typy světelných mikroskopů
 Typy světelných mikroskopů Johann a Zacharias Jansenové (16. stol.) Systém dvou čoček délka 1,2 m 17. stol. Typy světelných mikroskopů Jednočočkový mikroskop 17. stol. Typy světelných mikroskopů Italský
Typy světelných mikroskopů Johann a Zacharias Jansenové (16. stol.) Systém dvou čoček délka 1,2 m 17. stol. Typy světelných mikroskopů Jednočočkový mikroskop 17. stol. Typy světelných mikroskopů Italský
POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII. A.Mikš 1, V.Obr 2
 POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII A.Mikš 1, V.Obr 1 Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII A.Mikš 1, V.Obr 1 Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
Filip Hroch. Astronomické pozorování. Filip Hroch. Výpočet polohy planety. Drahové elementy. Soustava souřadnic. Pohyb po elipse
 ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
Cvičení Kmity, vlny, optika Část interference, difrakce, fotometrie
 Cvičení Kmity, vlny, optika Část interference, difrakce, fotometrie přednášející: Zdeněk Bochníček Tento text obsahuje příklady ke cvičení k předmětu F3100 Kmity, vlny, optika. Příklady jsou rozděleny
Cvičení Kmity, vlny, optika Část interference, difrakce, fotometrie přednášející: Zdeněk Bochníček Tento text obsahuje příklady ke cvičení k předmětu F3100 Kmity, vlny, optika. Příklady jsou rozděleny
Světlo v multimódových optických vláknech
 Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
GEOMETRICKÁ OPTIKA. Znáš pojmy A. 1. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci.
 Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
1. Teorie mikroskopových metod
 1. Teorie mikroskopových metod A) Mezi první mikroskopové metody patřilo barvení biologických preparátů vhodnými barvivy, což způsobilo ovlivnění amplitudy světla prošlého preparátem, který pak byl snadno
1. Teorie mikroskopových metod A) Mezi první mikroskopové metody patřilo barvení biologických preparátů vhodnými barvivy, což způsobilo ovlivnění amplitudy světla prošlého preparátem, který pak byl snadno
1 Elektromagnetická vlna
 1 lektromagnetická vlna 1.1 lektromagnetické vlny V nestacionárním případě, ve kterém veličiny elektromagnetického pole mění v ávislosti na čase svoji velikost a případně i směr, eistuje vždy současně
1 lektromagnetická vlna 1.1 lektromagnetické vlny V nestacionárním případě, ve kterém veličiny elektromagnetického pole mění v ávislosti na čase svoji velikost a případně i směr, eistuje vždy současně
Krátká teorie. Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí. Intenzita interferenčního obrazce.
 Interference 1 Krátká teorie Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí Intenzita interferenčního obrazce 2 ), ( ), ( t r E t r I 2 E r E p I r p r p E E E E
Interference 1 Krátká teorie Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí Intenzita interferenčního obrazce 2 ), ( ), ( t r E t r I 2 E r E p I r p r p E E E E
Aplikovaná optika I. Josef Kuběna Učební pomůcka zejména pro studenty optometrie na LF
 Aplikovaná optika I. Josef Kuběna Učební pomůcka zejména pro studenty optometrie na LF Teorie světla Všechny zdroje světla pracují na stejném principu: foton je emitován atomem při přechodu elektronu na
Aplikovaná optika I. Josef Kuběna Učební pomůcka zejména pro studenty optometrie na LF Teorie světla Všechny zdroje světla pracují na stejném principu: foton je emitován atomem při přechodu elektronu na
Interference vlnění
 8 Interference vlnění Umět vysvětlit princip interference Umět vysvětlit pojmy interferenčního maxima a minima 3 Umět vysvětlit vznik stojatého vlnění 4 Znát podobnosti a rozdíly mezi postupnýma stojatým
8 Interference vlnění Umět vysvětlit princip interference Umět vysvětlit pojmy interferenčního maxima a minima 3 Umět vysvětlit vznik stojatého vlnění 4 Znát podobnosti a rozdíly mezi postupnýma stojatým
17. března 2000. Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
 Úloha č. 6 Ohniskové vzdálenosti a vady čoček, zvětšení optických přístrojů Václav Štěpán, sk. 5 17. března 2000 Pomůcky: Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
Úloha č. 6 Ohniskové vzdálenosti a vady čoček, zvětšení optických přístrojů Václav Štěpán, sk. 5 17. března 2000 Pomůcky: Optická lavice s jezdci a držáky čoček, světelný zdroj pro optickou lavici, mikroskopický
Úloha č.3 Interferometry a vlastnosti laserového záření
 Úloha č.3 Interferometry a vlastnosti ového záření Optické interferometry jsou přístroje pro velmi přesná měření, jejiž princip je založen na interferenci světla. Interferometry se dnes používají k měření
Úloha č.3 Interferometry a vlastnosti ového záření Optické interferometry jsou přístroje pro velmi přesná měření, jejiž princip je založen na interferenci světla. Interferometry se dnes používají k měření
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Teorie frézování
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Teorie frézování Geometrie břitu frézy Aby břit mohl odebírat třísky, musí k tomu být náležitě upraven. Každý
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Teorie frézování Geometrie břitu frézy Aby břit mohl odebírat třísky, musí k tomu být náležitě upraven. Každý
Seminář z geoinformatiky
 Seminář z geoinformatiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Délka je definována jako vzdálenost dvou bodů ve smyslu definované metriky. Délka je tedy popsána v jednotkách, tj. v násobcích
Seminář z geoinformatiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Délka je definována jako vzdálenost dvou bodů ve smyslu definované metriky. Délka je tedy popsána v jednotkách, tj. v násobcích
Graf závislosti dráhy s na počtu kyvů n 2 pro h = 0,2 m. Graf závislosti dráhy s na počtu kyvů n 2 pro h = 0,3 m
 Řešení úloh 1. kola 59. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1,, 3, 4, 7), J. Jírů (5), P. Šedivý (6) 1.a) Je-li pohyb kuličky rovnoměrně zrychlený, bude pro uraženou dráhu
Řešení úloh 1. kola 59. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1,, 3, 4, 7), J. Jírů (5), P. Šedivý (6) 1.a) Je-li pohyb kuličky rovnoměrně zrychlený, bude pro uraženou dráhu
(Následující odstavce jsou zde uvedeny jen pro zájemce.) , sin2π, (2)
 Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Úloha 10: Interference a ohyb světla
 Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Modulace vlnoplochy. SLM vytváří prostorově modulovaný koherentní optický signál
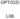 OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
y 10 20 Obrázek 1.26: Průměrová rovina válcové plochy
 36 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ 2 1 2 1 1 y 1 2 Obráek 1.26: Průměrová rovina válcové plochy Věta: Je-li definována průměrová rovina sdružená s asymptotickým směrem, potom je s tímto směrem
36 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ 2 1 2 1 1 y 1 2 Obráek 1.26: Průměrová rovina válcové plochy Věta: Je-li definována průměrová rovina sdružená s asymptotickým směrem, potom je s tímto směrem
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
ZPRACOVÁNÍ OBRAZU přednáška 3
 ZPRACOVÁNÍ OBRAZU přednáška 3 Vít Lédl vit.ledl@tul.cz TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
ZPRACOVÁNÍ OBRAZU přednáška 3 Vít Lédl vit.ledl@tul.cz TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM. F3240 Fyzikální praktikum 2
 Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM F34 Fyzikální praktikum Zpracoval: Dvořák Martin Naměřeno: 1. 11. 9 Obor: B-FIN Ročník: II. Semestr: III. Testováno:
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM F34 Fyzikální praktikum Zpracoval: Dvořák Martin Naměřeno: 1. 11. 9 Obor: B-FIN Ročník: II. Semestr: III. Testováno:
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
