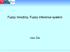
průniku podmnožin, spojení je rovno sjednocení podmnožin a komplement je doplněk Obr. 5: Booleovy algebry

Transkript

1 BOOLEOVY ALGEBRY Připomeňme si, že za Booleovu algebru považujeme každou algebru (B,,, 0, 1, ) s neprázdnou množinou B, binárními operacemi průsek, spojení, s prvky 0, 1 B a unární operací komplement, ve které jsou splněny následující identity: (1) a a = a, a a = a; (2) a b = b a, a b = b a; (3) a (b c) = (a b) c, a (b c) = (a b) c; (4) a (a b) = a, a (a b) = a; (5) a (b c) = (a b) (a c), (a b) (a c) = (a (b c); (6) a 1 = a, a 1 = 1, 0 a = 0, 0 a = a; (7) a a = 0, a a = 1; (8) 0 = 1, 1 = 0, (a ) = a, (a b) = a b, (a b) = a b Uvedený výčet identit není minimální, mnohé identity lze odvodit z platnosti jiných identit Pokuste se odvodit identity (8) z identit (1) až (7) Na množině B lze definovat relaci uspořádání předpisem a b právě tehdy, když je a b = a (což je právě tehdy, když je a b = b) Prvek 0 je nejmenším prvkem uspořádané množiny (B, ) a prvek 1 je největším prvkem (B, ) Nejjednodušší Booleovou algebrou je jednoprvková algebra, kde je největší prvek roven nejmenšímu Tato algebra se nazývá triviální Booleova algebra Nejmenší netriviální Booleova algebra je dvouprvková Booleova algebra, která obsahuje pouze největší prvek 1 a nejmenší prvek 0, další možné Booleovy algebry jsou jsou čtyřprvková, osmiprvková a šestnáctiprvková Booleova algebra Diagramy těchto algeber jsou zobrazeny na Obr 4 Dalším příkladem Booleovy algebry je množina P (M) všech podmnožin (včetně prázdné podmnožiny ) nějaké množiny M Zde je průsek roven průniku podmnožin, spojení je rovno sjednocení podmnožin a komplement je doplněk podmnožiny v množině M Ověřte platnost všech potřebných identit Obr 5: Booleovy algebry Definice Nechť (B,,, 0, 1, ) a (C,,, 0, 1, ) jsou konečné Booleovy algebry Budeme říkat, že zobrazení f z B do C je izomorfizmus, pokud je prosté (tj pro a b je f(a) f(b)), je na (tj pro každé y C existuje x B takové, že f(x) = y), a pokud pro všechny prvky a, b B platí: 1 f(0) je nejmenší a f(1) největší prvek v (C,,, 0, 1, ); 2 je li a b = c v (B,,, 0, 1, ), pak je f(a) f(b) = f(c) v (C,,, 0, 1, ); 3 je li a b = c v (B,,, 0, 1, ), pak je f(a) f(b) = f(c) v (C,,, 0, 1, ); 4 je li a = b v (B,,, 0, 1, ), pak je f(a) = f(b) v (C,,, 0, 1, ) Řekneme, že Booleovy algebry (B,,, 0, 1, ) a (C,,, 0, 1, ) jsou izomorfní, pokud existuje izomorfizmus z (B,,, 0, 1, ) do (C,,, 0, 1, )

2 Existuje li izomorfizmus z f z (B,,, 0, 1, ) do (C,,, 0, 1, ), pak inverzní zobrazení f 1 je izomorfizmus z (C,,, 0, 1, ) do (B,,, 0, 1, ) Dvě navzájem izomorfní Booleovy algebry mají naprosto stejné vlastnosti, které lze formulovat pomocí operací,, 0, 1, Proto jsou z hlediska studia Booleových algeber nerozlišitelné, tedy stejné Uvědomme si, že body 1 až 4 z definice izomorfizmu lze stručně zapsat takto: 1 f(0) = 0 a f(1) = 1; 2 f(a b) = f(a) f(b); 3 f(a b) = f(a) f(b); 4 f(a ) = (f(a)) Pro nás budou důležité zejména Booleovy algebry (B,,, 0, 1, ), kde množina B má konečně mnoho prvků V dalším se proto budeme zabývat již pouze konečnými Booleovými algebrami Konečné Booleovy algebry Atomem Booleovy algebry (B,,, 0, 1, ) budeme rozumět každý prvek, který pokrývá nejmenší prvek z (B,,, 0, 1, ), tj atomem je prvek a B, takový, že je 0 < a a neexistuje prvek x B s vlastností 0 < x < a To, že je prvek a atomem značíme 0 a Duálně můžeme definovat koatom jako prvek, který je pokrýván největším prvkem 1 z (B,,, 0, 1, ), tedy prvek t je koatomen, je li t 1 Je evidentní, že v konečné Booleově algebře je každý nenulový prvek x (tj 0 < x) buďto atomem, nebo existuje atom d pro který je 0 d < x Dále je jasné, že pro každý nenulový prvek x a každý atom a je buďto a x = a (je li a x) nebo a x = 0 (není li a x) Pro největší prvek 1 Booleovy algebry B a libovolný atom a je a 1 Nechť a 1,, a n jsou právě všechny atomy z B Označme d = a 1 a 2 a n K prvku d existuje v B komplement tj prvek d pro který platí: d d = 1 a d d = 0 Kdyby prvek byl prvek d nenulový, pak by existoval atom a v B, pro který by platilo a d Jelikož je a d pro každý atom a, muselo být a d d, což je ve sporu s předpokladem d d = 0 Je tedy d = 0 a odsud ihned plyne, že je d = 1 Největší prvek Booleovy algebry B je tedy sjednocením všech atomů B Toto tvrzení lze zobecnit i pro libovolný prvek b Booleovy algebry B Stačí použít distributivní zákony a vztah b = b 1 = b (a 1 a 2 a n ) Komplementem prvku b je spojení všech atomů, které jsou nesrovnatelné s b Tento důležitý poznatek si formulujme jako větu Věta Nechť B je konečná Booleova algebra, b B, b 0 a nechť a 1, a 2, a k jsou právě všechny atomy v B, které jsou menší nebo rovny prvku b (a i b) a nechť c 1,, c r jsou právě všechny atomy z B, které nejsou menší nebo rovny prvku b (c i b) Potom je b = a 1 a 2 a k a b = c 1 c 2 c k Duálně lze provést stejné úvahy s koatomy Dostaneme, že každý prvek x, který není největší (tj x < 1), je buďto koatomem nebo existuje koatom t, tak, že je x < t 1 a pro každý prvek x, který není největším prvkem, je x t = t (je li x t) nebo x t = 1 (není li x t) Platí i tvrzení, že nejmenší prvek Booleovy algebry B je průnikem všech koatomů B a podobné tvrzení pro každý prvek Věta Nechť B je konečná Booleova algebra, b B, b 1 a nechť t 1, t 2, t k jsou právě všechny koatomy v B, které jsou větší nebo rovny prvku b (t i b) a nechť z 1,, z r jsou právě všechny koatomy z B, které nejsou větší nebo rovny prvku b (z i b) Potom je b = t 1 a 2 t k a b = z 1 c 2 z k Označme symbolem At(B) množinu všech atomů Booleovy algebry (B,,, 0, 1, ) a symbolem P (At(B)) množinu všech podmnožin množiny At(B) (včetně prázdné pod-

3 množiny ) Zobrazení, které přiřazuje prvku 0 z B prázdnou množinu a každému nenulovému prvku x z B množinu všech atomů z B které jsou menší nebo rovny x je, jak si snadno ověříte, izomorfizmus z Booleovy algebry (B,,, 0, 1, ) do Booleovy algebry (P (At(B),,, 0, 1, ), kde 0 =, 1 = At(B) a pro X At(B) je X = At(B) \ X Protože konečná n prvková množina má 2 n podmnožin, je důsledkem předcházejících tvrzení to, že každá Booleova algebra, která má přesně n (n 0) atomů, má 2 n prvků a že každé dvě Booleovy algebry se stejným počtem atomů jsou izomorfní Booleovy algebry, které mají n atomů, budeme obvykle značit symbolem B n Triviální Booleova algebra nemá žádný atom a značíme ji B 0 Poznámka Počet prvků konečné množiny M budeme značit symbolem M a nazývat mohutností množiny M Například to, že Booleova algebra s n atomy má 2 n prvků, můžeme vyjádřit symbolicky zápisem B n = 2 n Další reprezentaci konečné Booleovy algebry s n atomy dostaneme následující úvahou Nechť Booleova algebra (B,,, 0, 1, ) má n atomů, které označíme a 1,, a n Každému prvku x B přiřadíme posloupnost (e 1, e 2,, e n ) složenou z 0 a 1 takto: pro každé přirozené číslo i {1, 2,, n} je e i = 1, je li a i x a e i = 0, není li a i x Prvku 0 je tak např přiřazena posloupnost ze samých 0 (tj 0 (0, 0,, 0)) a prvku 1 je přiřazena posloupnost ze samých 1 (tj 1 (1, 1,, 1)) Je snadné ukázat, že toto přiřazení je izomorfizmus Booleovy algebry (B,,, 0, 1, ) na n tou kartézskou mocninu dvouprvkové Booleovy algebry 2 Booleova algebra 2, která má pouze dva prvky 0 a 1, je tak vlastně v jistém smyslu základní Booleovou algebrou, a to proto, že každá konečná Booleova algebra s n atomy je izomorfní Booleově algebře 2 n Pro úplnost připomeňme, že všechny operace v kartézské mocnině 2 n jsou definovány po složkách, tj je (e 1, e 2,, e n ) (d 1, d 2,, d n ) = (e 1 d 1, e 2 d 2,, e n d n ), (e 1, e 2,, e n ) (d 1, d 2,, d n ) = (e 1 d 1, e 2 d 2,, e n d n ) a pro operaci komplement je (e 1, e 2,, e n ) = (e 1, e 2,, e n) Přitom je 0 0 = 0, 0 1 = 0, 1 1 = 1, 0 0 = 0, 0 1 = 1, 1 1 = 1, 0 = 1 a 1 = 0 Všimněme si nyní, že na Obr 5 jsou postupně zobrazeny diagramy Booleových algeber B 1 = 2, B 2 = 2 2, B 3 = 2 3 a B 4 = 2 4 Booleovy funkce Nyní si uvedeme několik základních informací o tzv Booleových funkcích (nebo též booleovských funkcích), které úzce souvisí s výrokovou logikou a bez jejich znalosti se neobejdou teorie o informatice a programování Začněme příkladem takové funkce Mějme nějakou výrokovou formuli n proměnných, např ϕ(x 1, x 2,, x n ) V závislost na ohodnocení jednotlivých proměnných (vždy 0 nebo 1) je hodnota formule ϕ(x 1, x 2,, x n ) vždy vždy 0 nebo 1, což je dáno tzv pravdivostní tabulkou formule ϕ(x 1, x 2,, x n ) Tato formule tak definuje zobrazení z Booleovy algebry 2 n do Booleovy algebry 2, které budeme nazývat Booleovou funkcí Pojem Booleova funkce si trochu zobecníme i na jiné algebry než dvouprvkovou algebru 2 Definice Nechť (B,,, 0, 1, ) je konečná Booleova algebra Booleovým výrazem v proměnných x 1, x 2,, x n (nad Booleovou algebrou (B,,, 0, 1, )) budeme rozumět každý výraz získaný konečným počtem použití pravidel: 1 libovolný prvek b z B a x 1, x 2,, x n jsou Booleovy výrazy; 2 jsou li p a q Booleovy výrazy, pak jsou p q, p q a p opět Booleovy výrazy Zobrazení f z B n do B, které je definováno předpisem f(x 1, x 2,, x n ) = q(x 1, x 2,, x n ), kde q je nějaký Booleův výraz budeme nazývat Booleovou funkcí n proměnných nad (B,,, 0, 1, )

4 Poznámka Booleovy výrazy nám silně svou definicí připomínají výrokové formule a také spolu velmi úzce souvisí Příkladem Booleových funkcí mohou být např funkce jedné proměnné f 1 (x) = (a x) x, f 2 (x) = a x nebo funkce dvou proměnných g 1 (x, y) = a (x y) (x a ) a g 2 (x, y) = a x nad nějakou Booleovou algebrou obsahující prvek a Snadno zjistíte, že funkce f 1 (x) a f 2 (x) jsou totožné Ověřte, že také funkce g 1 (x, y) a g 2 (x, y) jsou také totožné Vidíme tedy, že je možno tutéž Booleovu funci vyjadřovat více způsoby, což může být nepříjemné pro zjišťování zda dvě takovéto funkce jsou či nejsou totožné Bylo by proto vhodné najít nějaký standardní způsob vyjádřovéní Booleových funkcí, což by umoňovalo snadné rozhodovování o totožnosti dvou funkcí Toto je možno udělat dvěmi navzájem duálními způsoby Jsou to vyjádření Booleovských funkcí v úplné disjunktivní a konjunktivní formě Vyjdem z toho, že každá konečná Booleova algebra s n atomy je izomorfní Booleově algebře 2 n Definice Nechť (B,,, 0, 1, ) je konečná Booleova algebra s n atomy ( tj je izomorfní Booleově algebře 2 n ) Pro každou posloupnost k = (k 1, k 2,, k n ) složenou z nul a jedniček (tj k {0, 1} n ) definujeme elementární průsek nad proměnnými x 1, x 2,, x n jakožto výraz p[k] = x k 1 1 xk 2 2 xk n n, kde x 1 i = x i a x 0 i = x i a elementární spojení nad proměnnými x 1, x 2,, x n jakožto výraz s[k] = x k 1 1 xk 2 2 xk n n, kde k i = 0 je li k i = 1 a k i = 1 je li k i = 0 (tj x k i i = x pro k i = 0 a x k i i = x pro k i = 1) Např pro Booleovu B 1 = 2 a dvě proměnné x a y máme čtyři možnosti pro elementární průseky, a to p[(1, 1)] = x y, p[(1, 0)] = x y, p[(0, 1)] = x y, p[(0, 0)] = x y a čtyři možnosti pro elementární spojení, a to s[(1, 1)] = x y, s[(1, 0)] = x y, s[(0, 1)] = x y, s[(0, 0)] = x y Lze ukázat, že každou Booleovu funkci je možno standardně vyjádřit jako spojení všech možných výrazů f(k) p[k] resp jako průnik všech možných výrazů f(k) s[k], kde k probíhá všechny možné posloupnosti nul a jedniček Toto tvrzení si naformulujme jako větu Věta Každou Booleovu funkci f z B n do B je možno vyjádřit v úplné disjunktivní normální formě, tedy ve tvaru f(x 1, x 2,, x n ) = {f(k 1, k 2,, k n ) x k 1 1 xk 2 2 xk n n, (k 1, k 2,, k n ) {0, 1} n } a každou Booleovu funkci f z B n do B je možno vyjádřit v úplné konjunktivní normální formě, tedy ve tvaru f(x 1, x 2,, x n ) = {f(k 1, k 2,, k n ) x k 1 1 xk 2 2 xk n n, (k 1, k 2,, k n ) {0, 1} n } Důsledkem této věty je, že každá Booleova funkce f z B n do B je jednoznačně určena soustavou 2 n koeficientů f(k 1, k 2,, k n ) a proto jich existuje právě tolik, kolik je různých možností jak zobrazit množinu mající 2 n prvků do B, což je B 2n Obecně je totiž počet možností jak zobrazit k prvkovou množinu do m prvkové množiny m k A protože počet prvků Booleovy algebry B n je B n existuje B B n různých zobrazení z množiny B n do B Z toho ihned plyne, že pro B 1 = 2 je každá funkce z 2 n do 2 Booleova a že pro Booleovy algebry mající více než dva prvky existují i funkce z B n do B, které nejsou Booleovy Ukažme si na třech příkladech vyjádření Booleovy funkce v obou standardních tvarech Nejprve uvažujme dvouprvkovou Booleovu algebru B 1 obsahující prvky 0, 1 a Booleovu funkci dvou proměnných x a y nad B 1 (tj funkci z B 1 B 1 do B 1 ), která je zadána předpisem f(x, y) = x y Utvořme si tabulku hodnot této funkce Dostaneme:

5 x y f(x, y) Hodnoty funkce f(x, y) = x y v bodech (0, 0), (0, 1), (1, 0) a (1, 1) jsou f(0, 0) = 1, f(0, 1) = 0, f(1, 0) = 1 a f(1, 1) = 1 Nyní již snadno vyjádříme funkci f(x, y) v obou normálních formách Úplná disjunktivní normální forma funkce f(x, y) je tvaru f(x, y) = (1 x y ) (0 x y) (1 x y ) (1 x y) a úplná konjunktivní normální forma funkce f(x, y) je tvaru f(x, y) = (1 x y) (0 x y ) (1 x y) (1 x y ) Ověřme si, že úplná disjunktivní normální forma vyjadřuje skutečně stejnou funkci Použijeme li identity Booleovy algebry, dostaneme: f(x, y) = (1 x y ) (0 x y) (1 x y ) (1 x y)= = (x y ) 0 (x y ) (x y) = (x y ) (x (y y)) = (x y ) x = = (x x) (y x) = y x = x y Ověřte, že i úplná konjunktivní normální forma vyjadřuje opět stejnou funkci Nyní mějme Booleovu funkci dvou proměnných x a y nad B 1, která je zadána předpisem g(x, y) = (x y) Utvořme si tabulku hodnot této funkce Dostaneme: x y g(x, y) Protože hodnoty funkce g(x, y) jsou v bodech (0, 0), (0, 1), (1, 0) a (1, 1) stejné jako u funkce f(x, y) z prvního příkladu, budou i jejich úplné disjunktivní a konjunktivní normální formy stejné, tj je: g(x, y) = (1 x y ) (0 x y) (1 x y ) (1 x y), f(x, y) = (1 x y) (0 x y ) (1 x y) (1 x y ) Důsledkem tohoto zjištění je, že funkce f(x, y) a g(x, y) jsou naprosto stejné V dalším příkladě mějme čtyřprvkovou Booleovu algebru B 2 obsahující prvky 0, 1, a, b (viz Obr 6) a Booleovu funkci dvou proměnných x a y nad B 2 (tj funkci z B 2 B 2 do B 2 ), která je zadána předpisem f(x, y) = (a (x y )) (b (x y)) 1 a b 0 Obr 6: Booleova algebra B 2

6 Nyní si utvoříme tabulku hodnot této funkce Dostaneme: x a a a a b b b b y 0 a b 1 0 a b 1 0 a b 1 0 a b 1 f(x, y) 1 b 1 b a 0 1 b 0 a b 1 Pro určení normálních forem Booleovy funkce f(x, y) nemusíme znát její hodnoty ve všech bodech, potřebujeme znát pouze hodnoty funkce f(x, y) v bodech (0, 0), (0, 1), (1, 0) a (1, 1), které jsou f(0, 0) = 1, f(0, 1) = b, f(1, 0) = a a f(1, 1) = 1 Nyní již snadno vyjádříme funkci f(x, y) v obou normálních formách Úplná disjunktivní normální forma funkce f(x, y) je tvaru f(x, y) = (1 x y ) (b x y) (a x y ) (1 x y) a úplná konjunktivní normální forma funkce f(x, y) je tvaru f(x, y) = (1 x y) (b x y ) (a x y) (1 x y ) Ověřte, že při použití normálních forem funkce f(x, y) dostaneme stejné výsledky Normální tvary Booleových funkcí samozřejmě nemusí být nejjednodušším vyjádřením funkce Je zřejmé, že například místo 1 x y můžeme psát x y a proto v úplné disjunktivní normální formě můžeme a obvykle budeme vynechávat koeficienty 1 Jestliže je u elementárního průseku koeficient 0, pak ho opět můžeme vynechat Analogicky v úplné konjunktivní normální formě budeme obvykle vynechávat koeficienty 0 a elementární spojení s koeficientem 1 (např 1 x y) Speciálně u Booleových funkcí nad dvouprvkovou algebrou jsou všechny koeficienty 0 nebo 1 V případě disjunktivní normální formy tak členy s koeficientem 0 vynecháváme a koeficient 1 nepíšeme Obdobně v případě konjunktivní normální formy vynecháváme členy s koeficientem 1 a koeficient 0 nepíšeme Máme li například nějakou Booleovu funkci g(x, y) nad B 2, která splňuje podmínky g(0, 0) = g(0, 1) = g(1, 0) = g(1, 1) = 1, pak její úplná disjunktivní forma je g(x, y) = (1 x y ) (1 x y) (1 x y ) (1 x y) Opakovaným používánín identit 1 x = x a (x y) (x y ) = x (y y ) = x můžeme předpis pro g(x, y) zjednodušit následujícím způsobem: g(x, y) = (x y ) (x y) (x y ) (x y) = (x (y y)) (x (y y)) = x x = 1 Funkce g(x, y) je tedy konstantní funkce, kterou je možno zadat předpisem g(x, y) = 1 Na tomto místě snadno najdeme příklad funkce h z B 2 B 2 do B 2, která není Booleova Stačí aby platilo h(0, 0) = h(0, 1) = h(1, 0) = h(1, 1) = 1 a v jakémkoliv jiném bodě nabývala jinou hodnotu než je 1, například h(0, a) = b, a funkce už nemůže být Booleova Realizace Booleových funkcí klopnými obvody V této části si ukážeme, že lze každou Booleovu funkci nad dvouprvkovou Booleovou algebrou realizovat pomocí elektrických obvodů Vstupní i výstupní hodnoty jsou pouze nuly a jedničky (např záporné a kladné napětí) Základními kameny těchto obvodů jsou tzv logické členy, které se obvykle nazývají invertor, součinový člen a součtový člen V invertoru se vstupní hodnota signálu mění na opačnou hodnotu, výstupní hodnotou součinového členu je 1, právě když všechny vstupní hodnoty mají hodnotu 1 a výstupní

7 hodnotou součtového členu je 0, právě když všechny vstupní hodnoty jsou 0 Všimněme si, že pokud x 1, x 2, x n {0, 1}, pak je x 1 x 2 x n = 1, právě tehdy, když platí: x 1 = x 2 = = x n = 1 a x 1 + x x n = 0, právě, když je x 1 = x 2 = = x n = 0 Víme také, že stejnou vlastnost mají operace a ve dvouprkové Booleově algebře 2 Někdy se také operace v Booleových algebrách pro jednoduchost značí pro průsek a + pro spojení a nazývají se násobení resp sčítání Odtud také plynou názvy součinový a součtový člen Tyto členy se ve schematech obvodů značí obvykle symboly, které jsou zobrazeny na Obr 7 My je v dalším budeme schematicky znázorňovat pomocí trojúhelníků (invertor) a obdélníků s určením typu uvnitř obdélníku pomocí nápisu AND (součinový člen) nebo OR (součtový člen) Součinový člen s n vstupními hodnotami má stejné vlastnosti jako n vypínačů zapojených seriově (proud prochází pouze pokud jsou všechny zapnuty) a součtový člen s n vstupními hodnotami má stejné vlastnosti jako n vypínačů zapojených paralelně (proud prochází je li alespoň jeden vypínač zapnut) x 1 x 1 x 2 x 2 x x NON x n AND x 1 x 2 x n x n OR x 1 x 2 x n invertor součinový člen součtový člen Obr 7: Invertor, součinový a součtový člen Ukažme si na dvou příkladech realizaci Booleových funkcí pomocí klopných obvodů Příklad Realizujme Booleovu funkci f(x, y) = (x y) (x y ) Realizace je uvedena na Obr 8 x y AND AND OR f x,y Obr 8: Realizace funkce f(x, y) = (x y) (x y ) Pokud bychom ve schematu na Obr 8 vynechali invertor pro proměnnou y, dostali bychom realizaci pro Booleovu funkci g(x, y) = (x y) (x y), která je zobrazena na Obr 9 Jelikož, ale je g(x, y) = (x y) (x y) = y, je takovýto obvod zbytečný x y AND AND OR g x,y Obr 9: Realizace funkce g(x, y) = (x y) (x y)

8 Příklad Realizujme Booleovu funkci f(x, y) = x y z Realizace je uvedena na Obr 10 v levé polovině Na její realizace jsou potřeba čtyři logické členy Pokud si uvědomíme, že je f(x, y) = x y z = (x y z), pak je jasné, že na Obr 10 v pravé polovině je znázorněna realizace téže funkce Na tuto realizaci postačí dva logické členy x x y ANDf x,y,z y OR f x,y,z z z Obr 10: Realizace funkce f(x, y, z) = x y z Z uvedených příkladů vidíme, že zejména pro potřeby realizace Booleovských funkcí pomocí klopných obvodů je potřebné umět vyjádřit danou Booleovu funkci nad B 1 = 2 co nejjednodušším způsobem, tedy s použitím co nejmenšího počtu symbolů Zjednodušování výrazů s využitím identit platných v Booleových algebrách je značně pracné a vyžaduje i jistý cvik a intuici Existují ale podstatně jednodušší způsoby Jedna metoda je založena na používání tzv Karnaughových map, což je vhodné pro Booleovy funkce s nejvýše čtyřmi proměnnými Další metoda je tzv Quin-McCluskeyho metoda Její princip spočívá v tom, že vycházíme z nějakého vyjádření ve tvaru spojení průseků a opakovaně předpis zjednodušujeme používáním identity (x y) (x y ) = x Quin-McCluskeyho metoda Mějme Booleovu funkci f(x 1, x 2, x n ) nad ve tvaru spojení průseků Každý průsek je tvaru (x h 1 1 xh 2 2 xh n n ), kde h i {0, 1, } a x 1 i = x i, x 0 i = x i a x znamená, že se proměnná x i ve výrazu nevyskytuje Každému průseku přiřadíme posloupnost (h 1, h 2,, h n ) složenou ze symbolů 0, 1, Vahou průseku budeme rozumět počet 1 v posloupnosti (h 1, h 2,, h n ) Například výrazu (x 1 x 2 x 4 x 5) v pěti proměnných (x 1, x 2, x 3, x 4, x 5 ) přiřadíme posloupnost (1, 0,, 1, 0) Váha tohoto výrazu je 2 Dále budeme postupovat dle následujících dvou pravidel 1 Pokud mezi všemi posloupnostmi, které odpovídají jednotlivým průsekům, najdeme dvě, které jsou stejné, jednu z nich vynecháme 2 Pokud mezi nimi najdem dvě posloupnosti, které se liší na jediném místě, a to na místě i tém, pak obě posloupnosti nahradíme jednou posloupností, ve které dáme na i té místo symbol a ostatní místa necháme beze změn Toto aplikujeme na každou takovou dvojici posloupností, a to i v případě, že se jedna posloupnost objevuje ve více dvojicích Toto opakujeme tak dlouho, až nebudou existovat dvě stejné posloupnosti nebo dvě posloupnosti, které se liší na jediném místě Při porovnávání posloupností se stačí omezit na porovnávání těch posloupností, jejichž váhy se liší nejvýše o 1 Poznámka Pravidlo 1 odpovídá identitě a a = a Pravidlo 2 odpovídá identitě (a b) (a b) = (a a ) b = b, je li na i tém místě jedné posloupností 0 a na i tém místě druhé posloupnosti 1, resp identitě a (a b) = a v případě, že na i tém místě jedné posloupnosti je symbol a na i tém místě druhé posloupnosti je 0 nebo 1 Princip metody si vysvětlíme na jednoduchém příkladě Příklad Zjednodušme předpis pro Booleovu funkci tří proměnných f(x, y, z) = (x y z ) (x y z) (x y z ) (x y z) (x y z)

9 Jednotlivým průsekům odpovídají posloupnosti (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1) a (1, 0, 1) Máme pět dvojic posloupností, které se liší pouze na jednom místě Jsou to dvojice první a druhá, první a třetí, druhá a čtvrtá, druhá a pátá, třetí a čtvrtá Dostaneme nový systém posloupností, a to posloupnosti: (0, 0, ), (0,, 0), (0,, 1), (, 0, 1) a (0, 1, ) V tomto systému existují dvě dvojice posloupností, které se liší pouze na jednom místě Jsou to první a pátá posloupnost a druhá a třetí posloupnost Po aplikaci pravidla 2 dostaneme tři posloupnosti, a to (0,, ), (0,, ) a (, 0, 1) První posloupnost vynecháme podle pravidla 1 Zůstavájí nám dvě posloupnosti (0,, ) a (, 0, 1) a proto funkci f(x, y, z) = (x y z ) (x y z) (x y z ) (x y z) (x y z) lze zjednodušit jako f(x, y, z) = x (y z) Tato metoda ještě není dokonalá Pokud chceme zjednodušit výraz x (x y z), kterému odpovídají posloupnosti (0,, ) a (0, 1, 1), tak nemůžeme použít pravidlo 2, protože se posloupnosti liší na dvou místech Přitom je vidět, že nějaké zjednodušení je možné Je totiž x (x y z) = x podle identity a (a b) = a Toto můžeme zobecnit a identitu a (a b) = a (která říká, že spojení dvou prvků, které jsou srovnatelné v uspořádané množině, je rovno většímu prvku) použít i v dalších případech V námi studovaných případech to je tehdy, jesliže jeden výraz obsahuje méně proměnných a u zbylých proměnných jsou oba výrazy stejné Například x 1 x 3 x 4 je větší nebo roven než x 1 x 2 x 3 x 4 a je větší nebo roven než x 1 x 2 x 3 x 4 a proto je (x 1 x 3 x 4) (x 1 x 2 x 3 x 4) = x 1 x 3 x 4 a také (x 1 x 3 x 4) (x 1 x 2 x 3 x 4) = = x 1 x 3 x 4 V řeči posloupností složených ze symbolů 0, 1, to lze vyjádřit následujícím způsobem Řekneme, že posloupnost (p 1,, p n ) je obsažena v posloupnosti (q 1,, q n ) jestliže platí: kdykoliv je p i, pak je p i = q i, tj posloupnosti se shodují na všech místech, kde posloupnost (p 1,, p n ) nemá Spojením výrazů, které odpovídají těmto posloupnostem je rovno výrazu, který odpovídá posloupnosti (p 1,, p n ) Získali jsme další pravidlo pro zjednodušování Booleových výrazů 3 Pokud je posloupnost (p 1,, p n ) obsažena v posloupnosti (q 1,, q n ), lze posloupnost (q 1,, q n ) vynechat Toto pravidlo ještě neřeší vše Pokud chceme zjednodušit výraz x (x y z), kterému odpovídají posloupnosti (0,, ) a (1, 1, 1), tak nemůžeme použít pravidlo 2 (posloupnosti se liší na třech místech) a ani jedna posloupnost není obsažena v druhé Přitom jisté zjednodušení je možné Je totiž x (x y z) = (x x) (x (y z)) = x (y z) K tomuto zjednodušení výrazu bychom dospěli, pokud bychom při zjednodušování funkce f(x, y) = x (x y z) vycházeli z úplné disjunktivní normální formy funkce f(x, y), která je tvaru f(x, y) = (x y z ) (x y z) (x y z ) (x y z) (x y z) Funkci odpovídají posloupnosti (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1) a (1, 1, 1) Pouze na jednom místě se liší posloupnosti první a druhá, první a třetí, druhá a čtvrtá, třetí a čtvrtá a čtvrtá a pátá Po aplikaci pravidla 2 dostaneme posloupnosti (0, 0, ), (0,, 0), (0,, 1), (0, 1, ) a (, 1, 1) Zde se přesně na jednom místě liší posloupnosti první a čtvrtá a druhá a třetí Použijeme pravidlo 2 a dostaneme posloupnosti (0,, ), (0,, ) a (, 1, 1) První posloupnost vynecháme (dle pravidla 1) a zůstanou nám pouze dvě posloupnosti (0,, ) a (, 1, 1), kterým odpovídá tvar funkce f(x, y) = x (y z) Naformulujme si nyní Quin-McCluskeyho algoritmus pro zminimalizování Booleovy funkce f(x 1, x 2,, x n ) nad Booleovou algebrou B 1 = 2 Budeme postupovat takto: 1) Funkci f(x 1, x 2,, x n ) si vyjádříme v úplné disjunktivní normální formě 2) Používáním pravidel 1, 2 a 3 zjednodušíme disjunktivní tvar funkce f(x 1, x 2,, x n )

10 3) U posloupností odpovídajícím výrazům získaných v bodě 2) otestujeme zda jsou či nejsou obsaženy v posloupnostech, které odpovídají vyjádření funkce f(x 1, x 2,, x n ) v úplné disjunktivní normální formě K tomu si vytvoříme tabulku, kde vodorovně umístíme posloupnosti odpovídající úplné disjunktivní normální formě a svisle umístíme posloupnosti odpovídající vyjádření získanému v bodě 2) Na každém volném místě tabulky otestujeme, zda je posloupnost uvedená v řádku obsažena v posloupnosti uvedené ve sloupci V případě, že ano, příslušné pole tabulky označíme symbolem, není li tomu tak, necháme pole volné 4) Používáním pravidla 3 nalezneme minimální vyjádření funkce f(x 1, x 2,, x n ) pomocí výrazů získaných v bodě 2) Musíme vybrat nějaký minimální systém posloupností umístěných v prvním sloupci tabulky tak, aby každá z posloupností umístěných v prvním řádku tabulky byla obsažena v nějaké posloupnosti z vybraných řádků Toho docílíme takto: je li v nějakém sloupci pouze jeden symbol, pak odpovídající řádek se ve výběru musí vyskytovat Symbolem nahradíme všechny symboly obsažené v tomto řádku a tím máme označeno, které posloupnosti z prvního řádku jsou obsaženy v posloupnosti z prvního sloupce našeho řádku Tento test provedeme pro všechny sloupce a získáme tím neopomenutelné řádky Jestliže je nyní v každém sloupci tabulky (s výjímkou prvního) alespoň jeden symbol, pak posloupnosti v prvním sloupci těchto neopomenutelných řádků určuje hledaný minimální tvar Pokud tomu tak není, pak neopomenutelné řádky doplníme co nejmenším počtem řádků ostatních tak, aby po doplnění každý sloupec obsahoval alespoň jeden ze symbolů nebo Posloupnosti z prvního sloupce těchto řádků (neopomenutelných a doplněných) určují minimální tvar funkce Celý postup si ukážme na následujícím příkladě Příklad Nalezněme minimální tvar Booleovy funkce čtyř proměnných f(x 1, x 2, x 3, x 4 ) = = (x 1 x 2 x 3 x 4) (x 1 x 2 x 3 x 4) (x 1 x 2 x 3 x 4 ) (x 1 x 2 x 3 x 4) (x 1 x 2 x 4) (x 1 x 2 x 3 x 4 ) Funkci odpovídají posloupnosti (0, 0, 1, 0), (0, 1, 0, 0), (0, 1, 1, 1), (1, 0, 1, 0), (1, 1,, 0) a (1, 0, 1, 1) Vyjádření funkce není v úplné disjunktivní normální formě Stačí nahradit posloupnost (1, 1,, 0) posloupnostmi (1, 1, 0, 0) a (1, 1, 1, 0) a tím dostaneme systém posloupností, který odpovídá vyjádření v úplné disjunktivní normální formě Posloupnosti si seřadíme tak, aby jejich váha neklesala Dostaneme posloupnosti (0, 0, 1, 0), (0, 1, 0, 0), (1, 1, 0, 0), (1, 0, 1, 0), (1, 1, 1, 0), (1, 0, 1, 1) a (0, 1, 1, 1) Testujeme, které dvojice posloupností se liší přesně na jednom místě a aplikujeme bod 2 Dostaneme posloupnosti (, 0, 1, 0), (, 1, 0, 0), (1, 0, 1, ), (1,, 1, 0), (1, 1,, 0) a (0, 1, 1, 1) Tyto posloupnosti již nelze více upravit Proto si podle bodu 3) vytvoříme tabulku z těchto posloupností a z posloupností odpovídajících vyjádření funkce v úplné disjunktivní normální formě (, 0, 1, 0) (, 1, 0, 0) (1, 0, 1, ) (1,, 1, 0) (1, 1,, 0) (0, 1, 1, 1) (0, 0, 1, 0) (0, 1, 0, 0) (1, 0, 1, 0) (1, 1, 0, 0) (0, 1, 1, 1) (1, 0, 1, 1) (1, 1, 1, 0)

11 Dále provedeme test, zda posloupnosti z prvního sloupce jsou obsaženy v posloupnostech z prvního řádku (0, 0, 1, 0) (0, 1, 0, 0) (1, 0, 1, 0) (1, 1, 0, 0) (0, 1, 1, 1) (1, 0, 1, 1) (1, 1, 1, 0) (, 0, 1, 0) (, 1, 0, 0) (1, 0, 1, ) (1,, 1, 0) (1, 1,, 0) (0, 1, 1, 1) Výpočet dokončíme podle bodu 4) Symbolem označíme neopomenutelné řádky (0, 0, 1, 0) (0, 1, 0, 0) (1, 0, 1, 0) (1, 1, 0, 0) (0, 1, 1, 1) (1, 0, 1, 1) (1, 1, 1, 0) (, 0, 1, 0) (, 1, 0, 0) (1, 0, 1, ) (1,, 1, 0) (1, 1,, 0) (0, 1, 1, 1) Neopomenutelné řádky neobsahují symbol v posledním sloupci Proto musíme přidat k neopomenutelným řádkům nějaké další, tak, aby obsahovaly symbol v posledním sloupci V našem případě máme dvě možnosti Můžeme přidat pátý nebo šestý řádek Vidíme, že úloha najít minimální tvar Booleovy funkce může mít i více řešení V našem příkladě to jsou dvě následující řešení: f(x 1, x 2, x 3, x 4 ) = = (x 2 x 3 x 4) (x 2 x 3 x 4) (x 1 x 2 x 3 ) (x 1 x 2 x 3 x 4 ) (x 1 x 3 x 4), nebo f(x 1, x 2, x 3, x 4 ) = = (x 2 x 3 x 4) (x 2 x 3 x 4) (x 1 x 2 x 3 ) (x 1 x 2 x 3 x 4 ) (x 1 x 2 x 4) Poznámka Uvědomme si, že Quin-McCluskeyho metoda dává pouze minimální možný tvar vyjádření Booleovy funkce ve tvaru spojení průseků V žádném případě tato metoda nedává nejkratší možné vyjádření Například je li Booleova funkce zadána předpisem f(x 1, x 2, x 3, x 4 ) = x 1 x 2 x 3 x 4, pak její vyjádření je evidentně minimální možné vyjádření ve tvaru spojení průseků Vyjádření předpisu pro tuto funkci ve tvaru f(x 1, x 2, x 3, x 4 ) = (x 1 x 2 x 3 x 4 ) je jednodušší, obsahuje méně (o tři) symbolů pro operaci komplement a také její realizace klopnými obvody by vyžadovala méně prvků Na Quin-McCluskeyho metodě je cenné zejména to, že se jedná o jednoznačný algoritmicky definovaný postup Tento postup, při kterém se pracuje s posloupnostmi, které jsou složeny z nul a jedniček, je možno pochopitelně jednoduše zautomatizovat Příklady k procvičení 1) Nechť a, b, c, d, e jsou prvky Booleovy algebry B, Vyjádřete x pomocí prvků a, b, c, d, e, je li x = a (b (c (d e)))

12 2) Zjednodušte co nejvíce předpis pro Booleovu funkci h(x, y) dvou proměnných, je li h(x, y) = (x y) (x y ) (x y) (x y ) 3) Jaká je úplná disjunktivní normální forma Booleových funkcí jedné proměnné nad Booleovou algebrou B? 4) Jaká je úplná konjunktivní normální forma Booleových funkcí jedné proměnné nad Booleovou algebrou B? 5) Kolik existuje Booleových funkcí jedné proměnné nad Booleovou algebrou B 5 s pěti atomy? 6) Nalezněte všechny funkční hodnoty všech možných Booleových funkcí jedné proměnné nad Booleovou algebrou B 2 = ({0, a, b, 1},,, 0, 1, ) Které z nich jsou prosté? 7) Kolik existuje Booleových funkcí dvou proměnné nad B 2? 8) Které z funkcí f(x, y), g(x, y) a h(x, y) jsou Booleovy funkce? Nalezněte jejich úplné normální formy x a a a a b b b b y 0 a b 1 0 a b 1 0 a b 1 0 a b 1 f(x, y) 1 b a a a 1 b 1 b g(x, y) b 1 b 1 1 a a 1 b a 0 h(x, y) a 0 a 0 0 b b 0 a a 1 9) Nalezněte minimální tvar Booleovy funkce f(x 1, x 2, x 3 ), je li f(x 1, x 2, x 3 ) rovno: a) (x y z ) (x y z ) (x y z) (x y z ) (x y z) (x y z); b) (x y z ) (x y z ) (x y z ) (x y z) (x y z ) (x y z); c) (x y z ) (x y z) (x y z ) (x y z) (x y z ) (x y z); d) (x y z) (x y z ) (x y z) (x y z) (x y z); e) (x y z ) (x y z ) (x y z) (x y z) (x y z) (x y z ); f) (x y z ) (x y z ) (x y z ) (x y z) (x y z) (x y z) Výsledky 1) x = a (b (c (d e ))) 2) h(x, y) = 0 3) f(x) = (f(0) x ) (f(1) x) 4) f(x) = (f(0) x) (f(1) x ) 5) Je jich (2 5 ) 21 = ) Funkční hodnoty všech funkcí jsou uvedeny v následující tabulce Prosté jsou funkce f 4, f 7, f 10 a f 13 f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 f 10 f 11 f 12 f 13 f 14 f 15 f a a a a b b b b a 0 a 0 a 0 a 0 a b 1 b 1 b 1 b 1 b 0 0 b b a a b b a a a b 1 0 a b 1 0 a b 1 0 a b 1 7) 4 22 = 16 8) Funkce f(x, y) a g(x, y) jsou Booleovy a h(x, y) není Booleova (h(1, b) b) Platí: f(x, y) = (x y ) (x y ) (x y) = x y, g(x, y) = (x y ) (x y ) (x y) = x y 9) Minimální tvar pro f(x 1, x 2, x 3 ) je: a) x 1 x 2 ; b) x 2 x 3; c) x 1 x 2; d) (x 1 x 2 ) x 3 ; e) x 1 (x 2 x 3); f) např (x 1 x 3) (x 1 x 2 ) (x 1 x 3 )