Univerzita Karlova v Praze
|
|
|
- Arnošt Brož
- před 6 lety
- Počet zobrazení:
Transkript
1 Univerzita Karlova v Praze Přírodovědecká fakulta Speciální chemicko-biologické obory Molekulární biologie a biochemie organismů Ondřej Kraus Moderní metody predikce sekundární struktury proteinů a jejich srovnání Modern methods for protein secondary structure prediction and their comparison Bakalářská práce Školitel: Mgr. Marian Novotný, Ph.D. Praha, 2011
2 Prohlášení Prohlašuji, ţe jsem závěrečnou práci zpracoval samostatně a ţe jsem uvedl všechny pouţité informační zdroje a literaturu. Tato práce ani její podstatná část nebyla předloţena k získání jiného nebo stejného akademického titulu. V Praze,
3 3 Obsah 1 Abstrakt Zkratky Úvod Sekundární struktura proteinů Torzní úhly Ramachandranův diagram Helix Beta-skládaný list Ohyby a smyčky Predikce sekundární struktury proteinů Historie predikce sekundární struktury proteinů Skryté Markovovy modely Umělé neuronové sítě Feed-Forward umělé neuronové sítě Rekurentní umělé neuronové sítě Metoda nejbliţšího souseda a jiné Porovnání metod Závěr Citace... 31
4 4 1 Abstrakt V současnosti existuje několik nástrojů k predikci sekundární struktury proteinů, většina moderních metod pouţívá algoritmy, jako jsou skryté Markovovy modely nebo umělé neurální sítě. Ve své práci se proto pokusím s nimi čtenáře seznámit a vysvětlit na jakém principu pracují, jaké jsou jejich výhody a nevýhody. Většina moderních metod predikuje tři typy sekundární struktury (helix, list a smyčku) s úspěšností 70%-80%. Nicméně vzhledem k odlišné metodice testování úspěšnosti různých metod lze brát výsledky pouze jako orientační, a uţivatel by se proto měl s metodou a metodikou jejího testování nejprve detailně seznámit. Klíčová slova: predikce proteinové struktury, skrytý Markovův model, umělá neuronová síť, nejbližší soused, sekundární struktura proteinů Abstract Today, there are several protein secondary structure predictors; most of them use algorithms such as hidden Markov models or artificial neural networks. Therefore I will introduce them to a reader in my thesis. I will explain their principles, as well as their advantages and disadvantages. The majority of contemporary predictors have accuracy 70%- 80% for prediction of three types of protein secondary structure. However these results are only approximate, due to different testing methodology. Therefore the user should get familiar with the method and its testing methodology in detail at first. Key-words: protein structure prediction, hidden Markov model, artificial neural network, nearest neighbour, protein secondary structure 2 Zkratky ANN - Artificial neural network HMM - Hidden Markov model MSA - Multiple sequence alignment NN - Nearest neighbour PDB - Protein data bank
5 5 3 Úvod Sekundární struktura říká hodně o vlastnostech a někdy i o funkci proteinů. Jelikoţ je její experimentální získání časově i finančně značně náročné, tak je často vyuţívána predikce sekundární struktury. Dnes existuje celá řada metod pro predikci sekundární struktury proteinů, a je dobré mezi nimi rozlišovat a vybrat tu, která se nejvíce hodí k řešení konkrétního problému. V současnosti se k predikci sekundární struktury proteinů vyuţívají pokročilé matematické modely v podobě umělých neuronových sítí (artificial neural networks, ANN) či skrytých Markovových modelů (hidden Markov models, HMM), které se osvědčili k řešení v řadě jiných bioinformatických úloh (například v tvorbě multiple sequence alignmentu, MSA). Velkou výhodou těchto technik je schopnost učení se ze stále rostoucí databáze experimentálně určených proteinových struktur a díky tomu i stále se zvyšující úspěšnost predikce.
6 6 4 Sekundární struktura proteinů Sekundární struktura proteinů je specifická lokální konformace proteinové kostry. Typickým znakem proteinové struktury je, ţe hydrofobní aminokyseliny bývají uvnitř, zatímco polární se vyskytují na jeho povrchu. Tím vzniká hydrofilní povrch a hydrofobní jádro, které je základem pro správné sbalení proteinu. Nicméně i u hydrofobních aminokyselin jsou hydrofobní pouze jejich postranní řetězce a proteinová kostra obsahuje polární skupiny NH a C=O v kaţdé peptidové jednotce. Aby bylo jádro hydrofobní, je třeba tyto skupiny neutralizovat vodíkovými vazbami mezi těmito polárními skupinami a elegantním řešením je formace pravidelné sekundární struktury, čehoţ lze docílit tak, ţe jsou stupně volnosti peptidického řetězce zúţeny do specifických hodnot torzních úhlů Φ a Ψ (Branden & Tooze, 1999). Sekundární struktura můţe být pravidelná i nepravidelná. Pravidelná sekundární struktura je tvořena a stabilizována vodíkovými můstky, ale bývá definována specifickou kombinací Φ a Ψ úhlů aminokyselin v ní zapojených. Nejčastějšími pravidelnými strukturami jsou alfa-helix a beta-skládaný list (Hancock & Zvelebil, 2004). Avšak existuje mnoho dalších sekundárních struktur: izolovaný β-můstek, 3 10 helix, π-helix, otáčka (turn), ohyb (bend), levotočivý alfa-helix, kolagen, vlásenka atd., jsou však vzácné a vyskytují se ve specifických případech (Voet & Voet, 2004). Beta-skládaný list rozlišujeme na paralelní a antiparalelní, případně smíšený. Oblasti bez pravidelné sekundární struktury jsou označovány jako neuspořádané, v angličtině jako "random coil". 4.1 Torzní úhly Torzní (dihedrální) úhly jsou úhly mezi dvěma rovinami. Podle konvence se jejich velikost pohybuje od -180 po Pokud jsou vázány za sebou čtyři atomy A-B-C-D, pak dihedrální úhel, vzniklý rotací kolem vazby mezi atomy B a C spolu svírá rovina obsahující atomy A, B a C s rovinou obsahující atomy B, C a D. V peptidové kostře jsou tři torzní úhly (viz obr. 1) připadající na kaţdou podjednotku a to: Φ (C i-1 -N i -Cαi-C i ), Ψ (N i -Cαi-C i - N i+1 ) a ω (Cαi-C i -N i+1 -Cαi+1). Úhel omega je definován na peptidové vazbě, která má částečně charakter dvojné vazby, a nabývá proto prakticky jen dvou hodnot. Rozlišujeme peptidovou vazbu cis (ω=0 ) nebo trans (ω=180 ), která se vyskytuje výrazně častěji. Většina úhlů Φ a Ψ není moţných, kvůli sterickým kolizím postranního řetězce s proteinovou kostrou. Úhly Φ a Ψ definují sekundární strukturu a jsou často zaznamenávány do Ramachandranova diagramu (Hancock & Zvelebil, 2004).
7 7 Obrázek 1: Peptidové torzní úhly Část polypeptidu s vyznačenými planárními peptidovými skupinami spojenými atomem Cα. Uvnitř rovin je pohyb atomů velmi omezen, nicméně roviny mohou rotovat podél úhlů Φ (vazba Cα-N) a Ψ (vazba Cα-C), které jsou orientovány podle konvence ve směru hodinových ručiček při pohledu od atomu Cα (obrázek pochází z: Pravidelné sekundární struktury mohou být charakterizovány pomocí specifických kombinací Φ a Ψ úhlů v proteinové kostře. Nejznámější algoritmus pro přiřazení sekundární struktury podle třídimenzionálních souřadnic proteinové struktury je DSSP (zkratka Define Secondary Structure of Proteins). DSSP rozřazuje sekundární strukturu do osmi odlišných tříd: α-helix (H), izolovaný β-můstek (B), β-list (E), 3 10 helix (G), π-helix (I), otáčka (turn, T), ohyb (bend, S) a ostatní (prázdné nebo C) podle vodíkových vazeb (Kabsch & Sandler, 1983). Kromě DSSP existují i další algoritmy pro přiřazování sekundární struktury. Jedním z nich je i STRIDE (Frishman & Argos, 1995). STRIDE je podobný jako DSSP, ale kromě vodíkových vazeb bere v potaz navíc i Φ a Ψ úhly. Existuje vysoká shoda (okolo 95% mezi strukturami přiřazenými algoritmy DSSP a STRIDE (Martin et al., 2005). Tyto algoritmy mohou být vzájemně porovnány například na tomto serveru: navíc je zde lze srovnat i s dalšími podobnými metodami.
8 8 4.2 Ramachandranův diagram Ramachandranův diagram, popsaný G. N. Ramachandranem a jeho spolupracovníky v roce 1963 (Ramachandran et al., 1963), je diagram znázorňující Φ a Ψ úhly proteinové kostry v dvourozměrném grafu, přičemţ na ose x leţí úhel Φ a ose y úhel Ψ. Některé oblasti jsou silně preferovány různými aminokyselinami v proteinu a odpovídají určité sekundární struktuře, zatímco v jiných se aminokyseliny nacházejí jen výjimečně. Jeho vyuţití je primárně posoudit kvalitu zjištěné nebo předpovězené proteinové struktury. Po vynesení kombinací Φ a Ψ úhlů pro všechny peptidové vazby do Rachmandranova diagramu by se měla nacházet většina aminokyselin seskupena v povolených oblastech, přestoţe některé se mohou nacházet i mimo ně. Ačkoli dochází ke sterickým interakcím, které jsou energeticky nevýhodné, můţe to přispět k minimalizaci vnitřní energie proteinu třeba tím, ţe takto nevhodně orientovaná aminokyselina umoţní okolním aminokyselinám zformovat pravidelnou sekundární strukturu (Hancock & Zvelebil, 2004). Na obr. 2 je vidět příklad Rachmandranova diagramu se znázorněním oblastí, kde se nacházejí aminokyseliny podílející se na vytvoření obvyklých sekundárních struktur. Obrázek 2: Ramachandranův diagram - dvourozměrný diagram s vyznačenými oblastmi, kam se vynášejí aminokyseliny v nejčastějších sekundárních strukturách (
9 9 4.3 Helix Alfa-helix (obr. 3) je nejčastější pravidelnou strukturou v globulárních proteinech. Byl popsán Paulingem v roce 1951 (Pauling et al., 1951). Má tvar pravotočivé šroubovice s otáčkou odpovídající 3,6 aminokyselinovým zbytkům. Jeho struktura je stabilizována vodíkovou vazbou mezi C=O skupinou aminokyseliny a NH skupinou vzdálenou čtyři aminokyseliny. Tím se liší od 3 10 helixu a π-helixu, které jsou stabilizovány vazbami mezi třetí, respektive pátou aminokyselinou. Obrázek 3: Schematicky znázorněný alfa-helix s vyznačenými atomy proteinové kostry a vodíkovými vazbami, které jej stabilizují. Karbonylová skupina i-té aminokyseliny (např. C'1) tvoří vodíkovou vazbu s vodíkem aminové skupiny i+4 aminokyseliny (např. C α 5) (Branden & Tooze, 1999). Alfa-helix můţe být popsán také jako helix (podobně jako 3 10 helix). 3.6 je počet aminokyselin na závit a dolní index 13 znamená, kolik atomů se účastní cyklu části spirály uzavřené vodíkovou vazbou, podle obdobného principu můţe být π-helix popsán jako helix. Některé aminokyseliny jako alanin, arginin nebo leucin se v alfa-helixech vyskytují častěji, zatímco jiné jen zřídka, například prolin, jelikoţ není aminokyselinou, ale jedná se o iminokyselinu a nemůţe tak poskytnout volný vodík. Vzhledem ke stejné orientaci všech vodíkových vazeb v alfa-helixu podél osy helixu a skutečnosti, ţe amidové a karbonylové skupiny mají odlišnou polaritu má celý helix dipólový moment (Branden & Tooze, 1999). To vede ke kladnému parciálnímu náboji na N-konci helixu a zápornému parciálnímu náboji na
10 10 C-konci alfa-helixu. Tento fakt vysvětluje přitahování záporně nabitých ligandů, zejména s fosfátovou skupinou k N-konci helixu. Naopak kladně nabité ligandy se jen zřídkakdy váţí k C-konci helixu. Vysvětlením by mohlo být tím, ţe kromě dipólového efektu na N-konci je zde také volná NH skupina v pozici preferující vodíkovou vazbu s fosfátovou skupinou. Sekundární jsou na povrchu proteinu často amfipatické, coţ znamená, ţe obsahují jak hydrofilní, tak hydrofobní aminokyselinové zbytky. V případě amfipatických alfa-helixů bývá zhruba kaţdá třetí či čtvrtá aminokyselina hydrofobní, zatímco zbytek je polárních. To má za následek vytvoření hydrofobní strany helixu, která je pak orientována směrem do jádra proteinu (Martin et al., 2006). Průměrná délka helixu nezáleţí jen na setu analyzovaných proteinů, ale i na metodě určení sekundární struktury. V případě nejčastěji pouţívaných DSSP a STRIDE bylo na setu 126 proteinů určená průměrná délka helixu jako 9, resp. 10, aminokyselin. Nicméně celková délka můţe být i přes 50 aminokyselin (Cuff & Barton, 1999). Kromě pravotočivého alfa-helixu existuje i levotočivý alfa-helix, který je vzácnější, protoţe v případě L-aminokyselin (z kterých se proteiny skládají) jsou postranní řetězce příliš blízko k proteinové kostře, coţ z něj dělá méně stabilní sekundární strukturu neţ je jeho pravotočivá obdoba (Voet & Voet, 2004). V tabulce 1 je porovnání běţně se vyskytujících helixů v proteinech helix a π-helix se vyskytují jen velmi vzácně, je to dáno především jejich malou stabilitou. π-helix (Cooley et al., 2010) vytváří v helixu dutinu, příliš malou pro atomy vody a příliš velkou, aby mohl být stabilizován van der Waalsovými interakcemi, zatímco 3 10 helix (Toniolo & Benedetti, 1991) je svinut příliš těsně, takţe ani jeden není energeticky preferován a tyto konformace se vyskytují především jako krátké úseky na alfahelixech. Helix Počet aminokyselin na závit * n Výška závitu na aminokyselinu* d (Å) Průměr helixu* r (Å) Úhel Φ ** ( ) Úhel Ψ ** ( ) α-helix helix levotočivý α-helix π-helix kolagenový helix Tabulka 1: Rozdíly v helixech - Porovnání parametrů různých typů helixů. Hodnoty pocházejí ze dvou zdrojů: * (Branden & Tooze, 1999), ** (Voet & Voet, 2004). Za zmínku stojí, ţe levotočivý alfa-helix se od pravotočivého liší opačnou orientací, coţ znamená, ţe jeho údaje jsou číselně shodné jako u pravotočivého alfa-helixu, jen mají opačné znaménko úhly Φ a Ψ.
11 Beta-skládaný list Beta-skládaný list byl popsán jiţ v roce 1951 (Pauling & Corey, 1951). Můţe být paralelní, antiparalelní nebo smíšený. Je druhou nejčastěji se vyskytující sekundární strukturou v globulárních proteinech. Beta-skládaný list je stabilizován vodíkovou vazbou mezi amidovými a karbonylovými skupinami sousedních řetězců, které jsou uspořádány paralelně nebo antiparalelně nebo v obou směrech, viz obr. 4, nejčastěji se vyskytují antiparalelní beta-skládané listy, které jsou stabilnější. Délka jednoho listu bývá různá, nejčastěji kolem čtyř aminokyselin, přestoţe mohou být listy i několikanásobně delší (Cuff & Barton, 1999). Obdobně jako alfa-helixy i beta-skládané listy jsou na povrchu proteinu často amfipatické. U beta-listů dochází k tomu, ţe se střídají hydrofilní a hydrofobní aminokyseliny, přičemţ opět vzniká strana listu orientovaná směrem do jádra proteinu a druhá je orientována volně do prostředí (Hancock & Zvelebil, 2004). V globulárních proteinech jsou beta-listy výlučně pravotočivě zkroucené. Skládají se minimálně ze dvou polypeptidových řetězců, nejčastěji však ze šesti. Mohou vytvářet i sloţitější struktury, jako je například betabarel (či beta-soudek), coţ je vlastně jeden velký skládaný list stočený do tvaru soudku (Voet & Voet, 2004). Obrázek 4: Vodíkové vazby v antiparalelním beta-listu (vlevo) jsou těsnější a amidové skupiny s karboxylovými sousedních řetězců jsou přesně proti sobě, zatímco v paralelním beta-listu (vpravo) karbonylové a amidové skupiny nejsou v ideální pozici pro tvorbu vzájemných vodíkových vazeb (Branden & Tooze, 1999).
12 Ohyby a smyčky Kromě helixů a listů je dalším typem pravidelné sekundární struktury beta-ohyb, který je pojmenován podle toho, ţe často spojuje antiparalelní beta-skládané listy. Beta-ohyby se vyskytují téměř výhradně na povrchu proteinů a jsou tvořeny čtyřmi aminokyseliny spojenými vodíkovou vazbou mezi karbonylovou skupinou první a amidovou skupinou čtvrté aminokyseliny. Existují dva typy, které se liší torzními úhly druhé a třetí aminokyseliny v beta-ohybu. Dalším obdobným typem sekundární struktury jsou Ω-smyčky. Nespadají do ţádné z předchozích struktur, vyskytují se ve většině proteinů, bývají 6-16 aminokyselin dlouhé a jejich konce jsou u sebe blíţe neţ 10 Å. Tyto smyčky se nazývají Ω-smyčky podle svého tvaru, připomínajícího velkou omegu. Ω-smyčky jsou rovněţ nejčastěji lokalizovány na povrchu proteinů (Voet & Voet, 2004). Kromě toho u řady proteinů existují zcela neuspořádané úseky. Ty mají často funkční roli a mohou vázat určitou molekulu, přičemţ bez ní jsou neuspořádané a po jejím navázání se stanou uspořádanými a zapříčiní změnu konformace celého proteinu (Dyson & Wright, 2005).
13 13 5 Predikce sekundární struktury proteinů Protoţe je experimentální určení struktury drahé a často i časově náročné, má smysl predikovat sekundární strukturu. Pomocí predikce sekundární struktury lze zpřesnit MSA (Notredame, 2007). Za zmínku nepochybně stojí i vyuţití predikce ke klasifikaci proteinu do proteinové rodiny (alfa, beta ) či k nalezení určitého typu proteinu, jako například u proteinů vnějších membrán (mitochondrií, chloroplastů, gram-negativních bakterií) (Yan et al., 2011) nebo vyuţití v proteinovém inţenýrství pro předpověď, zda nenarušíme jeho sekundární strukturu (Bondugula et al., 2011). Predikce sekundární struktury slouţí často jako základ pro predikci terciární struktury, kdyţ je třeba model vybudovat ab initio a není k dispozici struktura blízkého homologa. Pro ohodnocení přesnosti predikce je nejčastěji pouţívána veličina nazývaná Q 3. Tato hodnota vyjadřuje úspěšnost predikci pouze tří sekundárních struktur (helixu, listu a smyček). Hodnotu Q 3 lze zjistit z následující rovnice: Ke zlepšení predikce je často vyuţíván multiple sequence alignment (MSA), protoţe sekundární struktura je více konzervována a nedochází v ní tak často k delecím, inzercím, případně některým aminokyselinovým záměnám (Bystroff et al., 2000).
14 14 6 Historie predikce sekundární struktury proteinů První automatizované metody pro predikci sekundární struktury se objevily v sedmdesátých letech minulého století. Jednou z prvních a nejznámějších z nich je Chouova- Fashmanova metoda (Chou & Fashman, 1974). Tato metoda bere v potaz pravděpodobnost výskytu dané aminokyseliny v určité sekundární struktuře (helixu, listu nebo coil) a byla odvozena z databáze struktur pouhých 15 proteinů. Základem predikce je nalezení čtyř helixotvorných aminokyselin mezi šesti po sobě jdoucími nebo tří listotvorných mezi pěti. Poté je předpovězená struktura rozšiřována oběma směry, dokud jsou v okně o velikosti čtyř aminokyselin takové, které dohromady nemají tendenci strukturu narušit. Tato metoda dosahovala úspěšnosti predikce (počítáno přes Q 3 skóre) zhruba 50%. Na konci sedmdesátých let byla predikce sekundárních struktur zpřesněna na necelých 60% metodou GOR (Garnierova-Osguthorpeova-Robsonova metoda) (Robson et al., 1974). Patří podobně jako Chouva-Fashmanova metoda k první generaci metod predikujících sekundární strukturu proteinů. Původní metoda (GOR-I) dosahovala přesnosti predikce 55% a byla také zaloţena na preferenci jednotlivých aminokyselin tvořit určitou sekundární strukturu. Nová implementace (GOR-III (Gibrat et al., 1987)) dosahuje přesnosti predikce 58% a je zaloţena na preferenci dvojic určitých aminokyselin vyskytovat se v dané sekundární struktuře (Hancock & Zvelebil, 2004). Navíc na rozdíl od Chouvovy-Fashmanovy metody predikuje metoda GOR kromě helixů, listů a coil také otáčky. První metodou, která měla úspěšnost predikce vyšší neţ 70%, byla PHD. Tato metoda začne vytvořením MSA s podobnými proteiny se známou strukturou, coţ výrazně zlepšuje predikci (o několik procent). Poté je aplikována první neurální síť, která převádí sekvenci na strukturu, čili kaţdé aminokyselině přiřadí pravděpodobnost výskytu v určité sekundární struktuře, tu přiřazuje vţdy prostřední aminokyselině v okně 13 aminokyselin. Poté, několik nezávisle trénovaných neurálních sítí převádí strukturu na strukturu, coţ znamená, ţe na základě sekvence predikované struktury predikují (zpravidla mírně odlišnou) sekvenci sekundárních struktur, přičemţ zpřesňují predikci první neurální sítě. Nakonec jsou výsledky těchto predikcí zprůměrovány, a poskytují tak finální predikci (Rost et al., 1994). Od devadesátých let se pouţívají inteligentní algoritmy jako umělé neurální sítě nebo skryté Markovovy modely a přesnost nejlepších metod se pohybuje blízko 80% (Hancock & Zvelebil, 2004). Protoţe tyto metody jsou stále nejpouţívanější, bude jim věnováno nejvíce pozornosti. Dalším způsobem predikce sekundární struktury je prosté vyuţití ostatních metod a rozhodnutí, které či kterým věřit v predikci sekundární struktury u jednotlivých úseků aminokyselin. Příkladem takové metody můţe být JPred (Cuff et al., 1998), který vyuţívá 6 odlišných metod (DSC, PHD, NNSSP, PREDATOR, ZPRED a MULPRED). Jako výstup se pouţívá konsenzus metod NNSSP, DSC, PREDATOR a PHD, přičemţ pokud je výsledkem remíza pouţije se predikce podle PHD. Přestoţe tento přístup je lepší neţ vyuţití kterékoli z dílčích metod, dnešní prediktory uţ mají větší úspěšnost. Na podobném principu, i kdyţ se sloţitější rozhodovací logikou pro výstup zaloţenou na umělé neurální síti je PROTEUS (Montgomerie et al., 2006), který je zaloţen na třech metodách (PSIPRED, JNET a TRANSSEC) a v současnosti poskytuje zřejmě nejlepší predikce ze všech metod.
15 15 7 Skryté Markovovy modely Skrytý Markovův model (Hidden Markov model, HMM) je pravděpodobnostní metoda slouţící k lineární analýze sekvencí. (Krogh et al., 1994). Metoda je pojmenována podle ruského matematika, Andreje Markova, který zavedl Markovovy řetězce - stochastické procesy, kde záleţí pouze na současném stavu a nikoli stavech předchozích. Je zde definován konečný počet stavů a pravděpodobnost přechodu mezi nimi. Markovův model byl popsán jiţ v roce 1906, i kdyţ pojmenován byl později. Jedná se o rozšíření Markovova řetězce. Markovovy modely mají Markovovu vlastnost - záleţí vţdy na současném stavu, nikoli na stavech předchozích. Skrytý Markovův model se od Markovova řetězce liší tím, ţe stavy jsou jen částečně pozorovatelné, tedy skryté a odtud jeho pojmenování. Nicméně přestoţe stavy nejsou známé, lze pozorovat jejich projevy na výstupní sekvenci. V případě predikce sekundární struktury proteinů to například znamená, ţe jisté aminokyseliny se budou v dané sekundární struktuře objevovat častěji, případně jisté vzory ve střídání například hydrofobních a hydrofilních aminokyselin. HMM jsou pouţívány pro rozpoznávání řeči, kryptoanalýzu (dešifrování šifrovaných dat) atd. V biologii jsou pouţívány pro genovou predikci (Do & Choi, 2006), multiple sequence alignment (MSA) (Eddy, 1995) nebo predikci sekundární struktury. Vyuţívají se i k nalezení transmembránových helixů, příkladem mohou být programy jako HMMTOP (Tusnády & Simon, 2001) nebo TopPred (Claros & von Heijne, 2004). Pouţití HMM má oproti jiným metodám několik podstatných výhod. První je ta, ţe všechny HMM jsou graficky interpretovatelné modely (Martin et al., 2006), to znamená, ţe jejich struktura lze znázornit na obrázku, viz obr. 5 a 7. Druhou je ta, ţe pomocí nich lze určit pravděpodobnost dané predikce (Won et al., 2007). Navíc, oproti starším metodám se dají trénovat a jsou schopny se průběţně učit. Skrytý Markovův model je definován specifikací několika parametrů (Rabiner & Juang, 1986): X = sada n stavů = {x 1, x 2,, x n }, (například sekundární struktury nebo určité části sekundární struktury, počáteční aminokyselina v helixu, hydrofobní aminokyselina v helixu, poslední aminokyselina v helixu ) Y = výstupní abeceda s m hodnotami = {y 1, y 2,, y m }, (například jednotlivé aminokyseliny) π(i) = pravděpodobnost stavu x i v čase t = 0 (to jest v počátečním stavu) A = tranziční pravděpodobnosti (pravděpodobnosti přechodu z jednoho skrytého stavu do jiného, například i změna sekundární struktury) = {a ij }, kde a ij = P[výstupní stav x j v čase t + 1 ze stavu x i v čase t]. Za poznámku stojí, ţe pravděpodobnost přechodu stavu i do stavu j nezáleţí na předchozích stavech, toto je nazýváno Markovova vlastnost.
16 16 B = emisní (nebo také výstupní) pravděpodobnosti = {b jk }, kde b jk = P[ y k v čase t ze stavu x j v čase t] (pravděpodobnost výskytu například dané aminokyseliny v konkrétním skrytém stavu). HMM se stává z pevného počtu stavů (n), které jsou propojeny přímými tranzicemi. Kaţdý stav čte fixní počet znaků (písmen) ze vstupního řetězce (typicky jeden). Stavy, které nečtou ţádný znak, jsou nazývány tiché stavy (silent states) (Durbin, 1998). Součet všech tranzičních pravděpodobností ze stavu x i je roven 1 a emisní pravděpodobnosti pro všechny podřetězce čtené jedním stavem jsou rovněţ rovny 1 (Hancock & Zvelebil, 2004). Uvaţme konkrétní příklad. Podvodník pouţívá dvě mince, jednu zatíţenou (L) a jednu normální (F). Předpokládejme, ţe tuto situaci můţe popsat obr. 5. Zde dva stavy HMM x 1 (F) a x 2 (L) reprezentují mince, výstupní abeceda je tvořena dvěma písmeny {H, T} (head and tail), tranziční pravděpodobnosti odpovídají tomu, jak často jsou mince mezi sebou zaměněny, zatímco emisní pravděpodobnosti předpovídají výstup hodů mincí. Tranziční (a ij ) a emisní (b jk ) pravděpodobnosti nechť jsou takovéto: a 11 =0.75, a 12 =0.25, a 21 =0.4, a 22 =0.6, b 11 =b 12 =0.5, b 21 =0.1 a b 22 =0.9. Fair (x 1 ) Loaded (x 2 ) T: b 11 =0.5 H: b 12 =0.5 a 12 = 0.25 T: b 21 =0.1 H: b 22 =0.9 a 11 = 0.75 a 21 = 0.4 a 22 = 0.6 Obrázek. 5: Skrytý Markovúv model s mincemi - Vlevo je skrytý stav reprezentující nezatíţenou minci, po jejímţ hodu padá panna (H) i orel (T) se stejnou pravděpodobností, vpravo je skrytý stav reprezentující falešnou minci, po jejímţ hodu padá přednostně panna. Šipkami jsou znázorněny tranziční pravděpodobnosti (a ij ) s vyznačenou pravděpodobností ponechání nebo záměny mince mezi jednotlivými hody. Hodnoty b ij reprezentují emisní pravděpodobnosti. Obrázek 6 je příklad moţné tranziční sekvence a výstupní sekvence pro HMM zobrazený na předchozím obrázku, za předpokladu, ţe podvodník začal s pouţitím nezatíţené mince (π(q 1 ) =1 a π(q 2 ) = 0) F F F L L L L F F F T 0.5 T 0.5 H 0.5 H 0.9 H 0.9 H 0.9 H 0.9 T 0.5 H 0.5 H 0.5 Obrázek 6: Příklad tranziční a výstupní sekvence - Tranziční pravděpodobnosti jsou vyznačeny tučně, zatímco emisní pravděpodobnosti kurzivou
17 17 Pravděpodobnost výše uvedené tranziční sekvence můţe být spočtena pomocí následujícího vzorce: P[x 1 x 1 x 1 x 2 x 2 x 2 x 2 x 1 x 1 x 1 ] = π(q 1 )a 11 a 11 a 12 a 22 a 22 a 22 a 21 a 11 a 11 = = ,0068 Pravděpodobnost výše uvedené výstupní sekvence můţe být spočtena pomocí následujícího vzorce: P[(TTHHHHHTHH) (x 1 x 1 x 1 x 2 x 2 x 2 x 2 x 1 x 1 x 1 )] = b 11 b 11 b 12 b 22 b 22 b 22 b 22 b 12 b 11 b 11 = = Pravděpodobnost výše uvedené tranziční a výstupní sekvence lze spočítat jejich vzájemným vynásobením a vychází přibliţně Protoţe násobení mnoha pravděpodobností vede vţdy k velmi malým číslům, které způsobují výpočetní chyby na jakémkoli počítači, tak komplikovanější modely by vţdy měly být počítány v logaritmickém prostoru (například log ( ) -4,15. Obdobně pravděpodobnost 10 je v logaritmickém prostoru jen při základu logaritmu 10) (Durbin, 1998). Protoţe HMM jsou obvykle pouţívány pro analýzu dané sekvence místo generování nejpravděpodobnějších sekvencí, coţ znamená, ţe místo vytvoření pravděpodobné sekvence aminokyselin s danými sekundárními strukturami se zjišťuje, v jaké sekundární struktuře se nachází konkrétní aminokyseliny, je pouţíván Viterbiho algoritmus. Tento algoritmus najde nejpravděpodobnější cestu přes HMM pomocí zpětného vyhledávání (backtracking) (Durbin 1998), coţ znamená, ţe projde modelem obráceně a zjistí, které skryté stavy by nejspíše emitovaly výstupní sekvenci. V případě predikce sekundární struktury proteinů v praxi přiřadí kaţdé aminokyselině skrytý stav s určitou pravděpodobností a je jí pak přiřazena sekundární struktura, kterou nejpravděpodobnější stav (nebo skupina stavů) reprezentuje. Předpovězená cesta udává, který skrytý stav generoval který znak. To je základ pro mnoho aplikací zaloţených na HMM. Na příklad při predikci sekundárních struktur určité skryté stavy reprezentují helixy, a tedy jimi generované znaky (aminokyseliny) jsou dekódovány jako aminokyseliny nacházející se v helixu. K predikci sekundární struktury se skryté Markovovy modely vyuţívají různými způsoby. Mohou slouţit k predikci sekundární struktury jako v případě OSS-HMM (Martin et al., 2006) nebo Block-HMM (Won et al., 2007), přičemţ později můţe být predikce zpřesněna jinou metodou. Na obrázku 7 je grafická reprezentace HMM v OSS-HMM (Optimal Secondary Structure prediction Hidden Markov Model), který se skládá z 36 skrytých stavů, z kterých 15 reprezentuje helixy, 12 neuspořádané struktury a 9 listy. Tento model má 89 tranzicí s pravděpodobností větší neţ 0,1 z celkového počtu 448 nenulových přechodů. Za zmínku stojí, ţe se v něm nevyskytuje ţádná tranzice mezi helixem a listem či listem a helixem s pravděpodobností vyšší neţ 0,1. Červeně je značen stav, který emituje přednostně glycin, ţlutě především hydrofobní aminokyseliny a modře naopak hydrofilní. Fialově označený stav H3 nemá ţádnou silnou preferenci v emitovaných aminokyselinách,
18 coţ znamená, ţe vstupní aminokyselinou v helixu bývají stejně často hydrofilní i hydrofobní aminokyseliny. Celý model je rozdělen na tři části, podle toho jakou sekundární strukturu skryté stavy v něm umístěné reprezentují. H3 je jediný vstupní stav v helixové části modelu. Zajímavé je, ţe se jedná o jediný stav bez silné preference pro určité aminokyseliny. Přechody H3-H10, H2-H9-H1-H8 a H12- H4-H15 jsou silně přednostní a tvoří hlavní trajektorii H3 (vstupní stav), H10, H14, H2, H9, H1, H8, H12, H4, H15, H11, H13 a H5. Stav H7 je jediný helixový stav s přechod na sebe samotného (s pravděpodobností vyšší neţ 0,1). Mnoho 3-stavových a 4-stavových cyklů lze vysvětlit amfipatickým pravidlem. K dispozici je 6 výstupních stavy a 8 vnitřních stavů. Architektura představuje nutnost šroubovice mít délku větší neţ tři aminokyseliny (nejméně jednu otáčku). K dispozici jsou 3 vzájemně propojené vstupní stavy (B3, B5, B7) v listové části, všechny vedou ke stavu b1, jednomu ze tří vnitřních stavů (B1, B6, B8). Dále zde jsou tři výstupní stavy (B2, B4 a B9). Je zde několik dvoustavových cyklů, většina z nich mění hydrofobní a hydrofilní preferenci. Je pozoruhodné, ţe všechny vnitřní stavy listové části mají hydrofobní preferenci. Architektura modelu neuspořádané části je poměrně sloţitá. Jsou zde jen dva "core" stavy (C6 a C8). C7 a C11 stavy jsou napojeny jak na helixovou tak na listovou část. Zbývající stavy jsou rozděleny do dvou skupin, z nichţ kaţdá interaguje s různými sekundárními strukturami (zelená skupina je napojena na helixovou část a červená na listovou část). Je zvláštní, ţe stavy pro neuspořádanou strukturu lze přednostně najít v konkrétních typech smyček. Například stav c1 je zřídka nalezený v β/β nebo α/β smyčkách a slouţí jako výstupní stav tvořící přechod neuspořádané struktury do helixu. 18
19 19 Obrázek 7: Příklad skrytého Markovova modelu použitého k predikci sekundární struktury - Šipkami jsou znázorněny tranziční pravděpodobnosti vyšší neţ 0,1, čím tlustší šipka, tím vyšší pravděpodobnost přechodu do daného stavu. Pro názornost jsou jednotlivé skryté stavy rozděleny do skupin, vlevo skupina helixů, vpravo skupina listů, uprostřed nezařazená skupina. Šestiúhelníkem jsou značeny vstupní stavy, kosočtvercem výstupní stavy dané sekundární struktury a kruhem tzv. "core" skryté stavy. Modrá čísla u kaţdého stavu odpovídají hodnotě Neq, ta můţe nabývat hodnot od jedné po celkový počet skrytých stavů, přičemţ hodnota jedna znamená, ţe z daného skrytého stavu se přechází jen do jediného dalšího s pravděpodobností jedna a hodnota odpovídající všem skrytým stavům znamená, ţe tranziční pravděpodobnosti přechodu do všech skrytých stavů (včetně sebe sama) jsou shodné. Tedy čím niţší hodnota tím spíše po něm následuje určitý skrytý stav. Metoda Block-HMM kombinuje různé predikční metody k dosaţení lepších výsledků. Genetické algoritmy (Won et al., 2004) se pouţívají pro vývoj modelu. Členové populace řešení (rodiče) jsou vybíráni podle genetických operátorů a vyvíjeni k výrobě nové generace řešení (dětí). Fitness je přiřazen k rodině řešení po tomto procesu. Výběrová procedura zvolí rodiče pro další cyklus v závislosti na fitness. Tři genetické operátory byly pouţity v Block- HMM: crossover, mutace a typová-mutace. Ţádný z nich neměnil počet bloků, avšak mohl měnit počet stavů (dokonce aţ na nulu, čímţ se vytvoří nulový blok). Crossover vymění náhodný počet bloků dvou rodičů k vytvoření dvou dětí. Tento genetický operátor je velmi uţitečný, protoţe dobré bloky od různých řešení lze snadno kombinovat. Mutace přidá nebo odebere stav v bloku, nebo můţe přidat či odstranit tranzice (například v dopředném bloku). Typové-mutace mohou změnit bloky vázané (nevázané), na jiný typ bloku, nebo na blok s jinou značkou (sekundární struktura bloku změní). Genetický algoritmus pouţívá také parametrovou metodu učení, takţe výstupní pravděpodobnosti a tranziční pravděpodobnosti se změní také. Počáteční parametry pro vývoj různých HMM byly bloků s 1-4 stavy. Velikost populace byla stanovena na 30 a počet iterací byl 400. Kaţdý genetický operátor byl pouţit dvakrát za iteraci (Won et al., 2007). Architektura modelu Block-HMM je zaloţena, jak název napovídá na blocích stavů, obsahuje 26 nenulových bloků a 52 stavů (22 pro helix, 15 pro list a 15 pro neuspořádanou strukturu). Kaţdý blok představuje jednu ze tří sekundárních struktur (helix, list nebo
20 20 neuspořádaná struktura). Block-HMM vyuţívá čtyři typy bloků: lineární, na sebe navázaný, dopředný a nulový blok. Kaţdý blok obsahuje N stavů (s výjimkou nulového bloku, který neobsahuje ţádné stavy), kde stav n je připojen k stavu n + 1. Stav n je napojen na sebe v na sebe navázaném bloku a dopředný blok je blok, kde první stav je spojen s posledními M stavy, kde 1 M <N. Dopředný a na sebe navázaný blok mohou být vázány, coţ znamená, ţe veškeré emisní a tranziční pravděpodobnosti jsou si uvnitř bloku rovny. Tři nezávisle vytrénované HMM prediktory se pouţívají k ještě většímu zvýšení úspěšnosti predikce. Mají různé struktury, coţ zvyšuje přesnost predikce více neţ stejné struktury s různými parametry. 3-vrstvý perceptron (druh umělé neuronové sítě) je pouţit ke zlepšení výkonnosti predikce. Skládá se ze 3 vstupních uzlů, 3 skrytých uzlů a 3 výstupních uzlů. Tato síť vyuţívá jako vstup pravděpodobnosti toho, ţe se daná aminokyselina bude nacházet v určité sekundární struktuře. (Won et al., 2007). Další metodou s odlišným vyuţitím HMM je YASPIN (Lin et al., 2005). Zde je v prvním kroku predikce pouţita neurální síť k přiřazení sekundární struktury jednotlivým aminokyselinám a následně je predikce vylepšena pomocí HMM. HMM je pouţit k optimalizaci výstupu, protoţe výsledky predikce systému pouze s jedinou neurální sítí mohou být nepřesné. Odlišné vyuţití HMM nabízí SAM-T98, metoda navrţená pro detekci vzdálených homologů. SAM znamená Sequence Alignment and Modelling (Karplus et al., 1998). SAM-T98 má další derivace, jako SAM-T99, SAM-T02 poskytující lepší výsledky, a nejnovější verzi - SAM-T08 (Karplus, 2009). SAM je metoda zaloţená na HMM pro hledání a přiřazování proteinů příbuzných cílové sekvenci (Karplus & Hu, 2001), nikoli jako přímá predikce sekundární struktury. Nejnovější verze SAM-T08 je webový server pro predikci sekundární a terciární struktury proteinů. Vstup je omezena na 700 aminokyselin a primární výstup je 3D model ve formátu PDB. Tento server také nabízí mnoho mezivýsledků jako MSA, predikce kontaktu aminokyselin (interakce) nebo predikci sekundární struktury. Existuje několik abeced pro predikci sekundární struktury: dssp_ehl2 je standardní abeceda, pro predikci se pouţívají jen tři písmena (H pro helix, B pro list a L pro všechno ostatní). Tato metoda začíná tvorbou MSA, které slouţí jako vstup pro umělé neuronové sítě, které předpovídají různé vlastnosti lokálních struktur. Nakonec MSA a místních struktury jsou vyuţity na budování HMM, které se pouţívají k hledání PDB pro potenciální templáty pro predikci proteinové struktury.
21 21 8 Umělé neuronové sítě Umělé neurální sítě (Artificial neural networks, ANN, zkráceně často jen Neural networks) jsou druhem algoritmů, původně vytvořeným jako analogie ke struktuře neuronů v mozku. Rozlišujeme rekurentní neurální sítě (obsahující cykly) a dopředné (feed-forward, acyklické). Speciálním případem feed-forward neurálních sítí jsou vrstvené neurální sítě, organizované do disjunktních tříd (vrstev), příkladem je třívrstvý perceptron (druh dopředné sítě, uspořádané do vrstev) na obrázku 8. ANN jsou vhodné pro predikci sekundární struktury, protoţe umoţňují automatizované učení, podobně jako HMM. Navíc rekurentní ANN, na rozdíl od HMM i dopředných ANN mají paměť, coţ znamená, ţe při zpracování sekvence dokáţí brát v potaz i vzdálené části sekvence. Navíc oproti HMM mají neurální sítě tu výhodu, ţe poskytují predikci přímo a není třeba pouţívat obdobu Viterbiho algoritmu a počítat v logaritmickém prostoru, na druhou stranu jsou výpočetně náročnější a jejich grafické znázornění není zdaleka tak intuitivní. 8.1 Feed-Forward umělé neuronové sítě Nejjednodušším a prvním pouţívaným typem neurálních sítí jsou tzv. feedforward neurální sítě. Vzhledem k jejich struktuře nemají paměť a při predikci sekundární struktury se vyuţívají většinou v kombinaci s jinou metodou. Například u Block-HMM (Won et al., 2007) je pouţit třívrstvý perceptron (obr. 8) ke zlepšení predikce sekundární struktury po přiřazení sekundárních struktur k jednotlivým aminokyselinám pomocí HMM. Naopak například u metody YASPIN (Lin, 2005) je pouţita neurální síť k přiřazení sekundární struktury jednotlivým aminokyselinám a následně je predikce vylepšena pomocí HMM. Dalším příkladem sítě vyuţívající feed-forward architekturu je PSIPRED (Jones, 1999). Tato metoda je navíc zajímavá tím, ţe nevyuţívá multiple sequence alignment ke zvýšení úspěšnosti predikce, ale párový místní alignment (pairwise local alignment) získaný pomocí PSI-BLAST (Position-Specific Iterative Basic Local Alignment Search Tool) (Altschul et al., 1997). PROFsec je upravená verze PHDsec. Pro predikci je pouţita umělá neurální síť, k zpřesnění výsledků je vyuţíván MSA (Rost et al., 2004). 8.2 Rekurentní umělé neuronové sítě Rekurentní neurální sítě obsahují cykly a obousměrné rekurentní sítě se v nich mohou dokonce vracet. Výhodou tohoto typu neurální sítě je, ţe má paměť a predikce do jisté míry záleţí na tom, co síť predikovala dříve. V případě predikce sekundární struktury se tedy bere v potaz, zda například předchozí aminokyseliny byly predikovány v helixu a pak se zvyšuje pravděpodobnost, ţe v něm bude i následující aminokyselina. Příkladem prediktoru vyuţívajícího tento druh sítě je například Porter (Pollastri et al., 2002). Tato metoda je zaloţena na dvou obousměrně rekurentních neuronových sítích a je evolucí SSpro. Porter pouţívá 25 vstupních znaků (20 pro standardní aminokyseliny + B, U, X, Z a. (mezera)). Byla trénována na 2171 struktuře proteinu a aminokyselinách (25% z pdb_select list,
22 22 prosinec 2003). Při predikci je zvaţováno 225 sousedících aminokyselin. Ke zlepšení předpovědí o 1-1.5% při pouţití jedné neurální sítě bylo nakonec pouţito pět nezávisle vytrénovaných neurálních sítí, jejichţ výsledky predikce se zprůměrují (Pollastri & McLysaght, 2005). SSpro8, jiná metoda zaloţená na SSpro, umí predikovat všech osm DSSP struktur (Cheng et al., 2005). Obrázek. 8: Třívrstvý perceptron (druh umělé neuronové sítě) je pouţit ke zlepšení výkonnosti predikce u Block-HMM jako neurální síť zpřesňující predikci sekundárná struktury provedenou HMM. Skládá se ze tří vstupních uzlů, tří skrytých uzlů a tří výstupních uzlů. Tato síť vyuţívá jako vstup pravděpodobnosti toho, ţe se daná aminokyselina bude nacházet v určité sekundární struktuře a výstupem je opět pravděpodobnost výskytu dané aminokyseliny v určité sekundární struktuře. Podobný systém druhého predikčního mechanismu je pouţit u mnoha prediktorů sekundární struktury a v praxi zejména pomáhá odstranit nesmyslně předpovězené sekundární struktury (jako helix nebo beta-list délky jedna) (Won et al., 2007).
23 23 9 Metoda nejbližšího souseda a jiné Nejbliţší soused (nearest neighbour, NN) je klasifikační algoritmus, který při predikci sekundární struktury přiřazuje sekundární strukturu podle nejbliţší homologní sekvence se známou strukturou, úspěch je tedy přímo závislý na dostupnosti a správném odhalení této sekvence. V praxi se pro predikci sekundární struktury můţe pouţít i více homologních sekvencí, přičemţ pro kaţdou aminokyselinu je nalezen homologní podle jejího okolí a je jí přiřazena stejná sekundární struktura, jako má centrální zbytek srovnávaného homologního úseku (Hancock & Zvelebil, 2004). Příkladem této metody je například APSSP2. Tato metoda je zaloţena na dvou modelech umělé inteligence, jednak na metodě nejbliţšího souseda, a také na umělé neuronové síti. APSSP2 můţe předpovídat sekundární struktury pro jednu sekvenci, stejně jako pro MSA. Čtyři kroky jsou potřebné pro předpověď. Přístup nejbliţšího souseda se pouţívá v prvním kroku, ve druhém kroku, je předpovídána sekundární struktura pomocí neuronových sítí. V dalším kroku předpovídá sekundární strukturu ve srovnání s předchozími předpověďmi. Posledním krokem je předpověď struktura-struktura zaloţená na neuronových sítích. Metoda nejbliţšího souseda vyuţívá blízko příbuzné proteiny k testovací sekvenci. Úspěch předpovědi je přímo závislý na blízkosti příbuznosti souvisejících proteinů v databázi proteinových struktur, proto je ve druhém kroku pouţita dopředná (feedforward) neuronová síť k předpovědi sekundární struktury. Tato neuronová síť se skládá ze 75 skrytých jednotek a vstupního okna pro 17 aminokyselin. Tato síť byla vytrénována na všech dostupných proteinech v PDB v době jejího vzniku. Kombinovaná předpověď, pouţitá jako další krok, porovnává předchozí predikce a je to klíčový krok k dosaţení vysoké úspěšnosti predikce, neboť metoda nejbliţšího souseda ostatní metody předčí pouze tehdy, kdyţ jsou nalezeny dostatečně příbuzné sekvence se známou sekundární strukturou. Bez známých příbuzných proteinů jsou ale neuronové sítě přesnější. V posledním kroku je pouţita neuronová síť, která má za cíl především odstranit artefakty z prvního kola predikcí, jako je helix nebo list délky jedna aminokyselina (Raghava, 2000).
24 24 10 Porovnání metod Téměř všechny moderní metody mají společné znaky. K predikci je například pouţíván MSA. I základní struktura většiny metod je podobná. V prvním kroku je převáděna primární sekvence proteinů na sekundární strukturu a ve druhém kroku je tato predikce dále zpřesněna, coţ zvyšuje přesnost predikce a hlavně odstraňuje nesmyslné artefakty z prvního kroku, jakými jsou helixy a listy délky jedna nebo dva. Celá řada metod pouţívá v prvním nebo v druhém, případně v obou krocích více nezávisle trénovaných ANN nebo HMM a pak většinou pouţije průměr jejich dílčích výstupů jako celkovou predikci, neboť to opět umoţňuje zvýšit přesnost predikce. Metod pro predikci sekundární struktury proteinů je mnoho, a proto je dobré je vzájemně porovnávat, aby i neodborník poznal, kterou si má vybrat. Pro ohodnocení přesnosti predikce je pouţívána hodnota nazývaná Q 3. Tato hodnota vyjadřuje úspěšnost predikci pouze tří sekundárních struktur (helixu, listu a smyček). Hodnotu Q 3 lze zjistit z následující rovnice: Přesnost měření na kaţdou jednotlivou aminokyselinu není tou nejlepší metodou, protoţe nepostihuje detaily, v kterých se různé metody liší, ale je to nejjednodušší měření přesnosti predikce proteinové struktury. (Hancock & Zvelebil, 2004). Prediktory sekundární struktury jsou porovnány na serveru EVA. EVA automaticky stahuje nové třídimenzionální struktury z Protein Data Bank (PDB). Kaţdý týden jsou sekvence těchto proteinů rozeslány predikčním serverům, poté jsou shromáţděny výsledky a následně jsou prediktory ohodnoceny (Eyrich et al., 2001). K porovnání metod se nejčastěji pouţívá Q 3 skóre. Nicméně pro přesnější zachycení nuancí mezi jednotlivými metodami se pouţívají i jiné veličiny. Jednou z nich je Q X%y, kde X můţe být H pro helix, E pro list nebo C pro smyčky a y o nebo p, přičemţ o znamená observed (pozorovaných) a p predicted (předpovězených). Tedy například Q H%o = 86% znamená, ţe 86% všech helixů v proteinu bylo předpovězeno jako helixy, zatímco Q H%p = 85% znamená, ţe 85% predikovaných helixů jsou skutečně helixy. Z uvedeného je zřejmé, ţe Q X%o odpovídá senzitivitě, čím vyšší hodnota, tím méně falešně negativních výsledků metoda predikuje. Q X%p odpovídá zase specificitě, tedy čím vyšší hodnota tím méně falešně pozitivních výsledků. Některé metody jsou lepší na predikci proteinů s alfa-helixy nebo betalisty (PROTEUS), jiné zas na predikci proteinů se smyčkami (SSpro). Takto lze získat detailnější informace o silných a slabých stránkách různých metod. Alternativou k hodnocení Q 3 je SOV 3, z anglického Segment OVerlap (Zemla et al., 1999), které zjednodušeně řečeno vyjadřuje, jak moc se predikované struktury shodují s těmi reálnými. Zatímco u Q skóre jde o porovnání sekundární struktury jednotlivých aminokyselin,
25 25 zde se srovnává překryv celých sekundárních struktur (tedy například dvou helixů). Podobně jako u Q skóre i SOV lze měřit zvlášť pro helixy, listy i smyčky. Různé testovací sady proteinů mohou vést k odlišným výsledkům a odlišnému pořadí metod. Například Q 3 skóre u metody PSIPRED je na EVA serveru necelých 78%, nicméně jiní autoři dospěli k odlišným číslům, například lehce přes 80% (Zhang, et al., 2011) nebo téměř 85% (Chatterjee et al., 2011). Tyto rozdíly jsou dány tím, ţe metody se v čase průběţně vyvíjejí a zlepšují díky testování a učení se na nově zjištěných strukturách a také tím, ţe k testování jsou pouţívány různé proteiny, kaţdá metoda totiţ predikuje sekundární strukturu pro různé sekvence s různou úspěšností, proto se často mírně liší i pořadí metod, ke kterému různí autoři dojdou. Moderní metody kombinují tři základní přístupy při predikci sekundární struktury - skryté Markovovy modely, metodu nejbliţšího souseda a umělé neuronové sítě, které se většinou dělí na feed-forward a rekurentní. Kaţdý z těchto přístupů má své výhody i nevýhody, přičemţ ty nejpodstatnější jsou shrnuty v tabulce 2. Ačkoli obecně jsou rekurentní ANN nejúspěšnější v predikci sekundární struktury, pouţívají se i ostatní metody, neboť jsou jednodušší na správnou implementaci, a dokonce za určitých okolností poskytují lepší předpovědi. HMM Metoda Výhody Nevýhody Graficky interpretovatelné modely, ve specifických případech dokáţou překonat umělé neurální sítě (membránové helixy) Feed-forward ANN Rekurentní ANN NN Jednoduché, dobře se trénují, pracují rychle, často se pouţívají ke zlepšení predikce Mají paměť, dosahují nejlepších predikcí Vysoká úspěšnost predikce, pokud existuje homologní protein se známou strukturou Nejsou zatím tak úspěšné jako ANN Většinou mají o něco niţší úspěšnost neţ rekurentní ANN Je náročné je správně vytrénovat Nízká úspěšnost, kdyţ neznáme strukturu příbuzných proteinů. Tabulka 2: Porovnání výhod a nevýhod základních přístupů pouţívaných k predikci sekundární struktury Podrobné srovnání úspěšnosti několika vybraných metod provedli autoři (Zhang et al., 2011) na obrázku 9, včetně porovnání samostatných verzí s verzí dostupnou on-line. Asi nejvýraznější na něm je úspěšnost implementace metody PORTER na webovém serveru, která se pohybuje přes 95%. To je pravděpodobně dáno tím, ţe tento server byl v době testování jiţ trénován na strukturách testovaných proteinů. U metody SSpro jsou serverové výsledky překvapivě o něco horší neţ u samostatné verze, ale není to tak výrazný propad, zbývající metody mají úspěšnost srovnatelnou. Také je třeba upozornit, ţe tato metoda jako jediná na svém serveru neumoţňuje predikovat sekundární strukturu pro sekvence kratší neţ
26 26 25 aminokyselin, proto byly tyto při jejím testování, včetně samostatné verze bez tohoto omezení, vynechány. Při predikci sekundární struktury je dobré zváţit, zda nějaká metoda nemá k dispozici jiţ struktury homologních proteinů, neboť to velmi pomáhá v úspěšné predikci. Kromě toho je vidět, ţe aţ na výjimku u Porteru jsou rozdíly mezi predikcemi prováděné webovým serverem a samostatnou verzí programu relativně malé. Na zpracování malého mnoţství sekvencí je lepší pouţívat serverový prediktor, kvůli jednoduchosti, nicméně z časových důvodů při predikci sekundární struktury velkého mnoţství proteinů a také kvůli řadě omezení, které serverové prediktory mají, se zdá lepší alternativou samostatná verze programu. Obrázek 9: Podrobná úspěšnost predikce sekundární struktury pro vybrané metody. Porovnávány jsou celkem čtyři metody (SSpro černě, PROTEUS modře, PSIPRED červeně a PORTER zeleně), ve dvou verzích, první je samostatná verze (celobarevné sloupce), kterou si můţe kdokoli nainstalovat na svůj počítač, druhá, označená ws, je webový server (barevně ohraničené sloupce) (Zhang, et al., 2011). Při porovnávání metod se nelze zaměřit jen na senzitivitu nebo specificitu, protoţe spolu zpravidla souvisí. Na příkladu metody PROTEUS na obrázku 10 vidíme, jak spolu Q E%p (Q Epre ) a Q E%o (Q Eobs ) skóre souvisí. Zatímco konkurenci překonává v úspěšnosti predikce listů, zaostává ve správnosti jejich predikce, predikuje listy i tam, kde nejsou. Podobný trend se dá pozorovat i u jiných metod, pokud jsou parametry modelu nastavené například k vysoké citlivosti na listy, přibude "false-positive" výsledků a i kdyţ najde (správně) listy i tam, kde ostatní metody selhávají, často je najde i tam, kde ostatní metody správně predikují jinou strukturu. Takový postup se můţe vyplatit u proteinů obsahujících převáţně listy, ale u proteinu, kde je listů málo to naopak kazí úspěšnost predikce. Opačný stav lze pozorovat u OSS-HMM (Martin et al., 2006), kde predikované listy se skutečně velmi často nacházejí v listech, ovšem za cenu mnoha nepředpovězených listů. Také je třeba brát v potaz, na jakých proteinech byla která metoda vytrénována, například pro trénink OSS-HMM nebyly pouţity transmembránové proteiny, coţ znamená, ţe při testech, ve kterých se predikuje i jejich
27 27 struktura za ostatními metodami zaostává. Proto je dobré se seznámit s prediktorem před jeho pouţitím, a pokud máme o proteinu nějakou informaci (třeba, ţe to je membránový protein), vyhnout se prediktorům, které nebyly pro tento typ proteinů trénovány (v tomto případě OSS- HMM), neboť výsledky predikce budou velmi špatné. Naopak, pokud víme, ţe protein není membránový, můţe se OSS-HMM ukázat jako dobrá volba, jelikoţ nebude ovlivněn tréninkem na zcela odlišném typu proteinů. Obrázek 10: Porovnání 12 prediktorů seřazených, podle dosaţeného skóre Q 3. Nutno poznamenat, ţe rozdíly ve skutečnosti nejsou tak velké, neboť grafy nezačínají z prostorových důvodů v nule (Zhang, et al., 2011).
Hemoglobin a jemu podobní... Studijní materiál. Jan Komárek
 Hemoglobin a jemu podobní... Studijní materiál Jan Komárek Bioinformatika Bioinformatika je vědní disciplína, která se zabývá metodami pro shromážďování, analýzu a vizualizaci rozsáhlých souborů biologických
Hemoglobin a jemu podobní... Studijní materiál Jan Komárek Bioinformatika Bioinformatika je vědní disciplína, která se zabývá metodami pro shromážďování, analýzu a vizualizaci rozsáhlých souborů biologických
Blok 2 Sekundární struktura proteinů
 Blok 2 Sekundární struktura proteinů C3211 Aplikovaná bioinformatika Přednášející: Josef Houser Struktura proteinů ADSQTSSNRAGEFSIPPNTDFRAIFFANAAE QQHIKLFIGDSQEPAAYHKLTTRDGPREATL NSGNGKIRFEVSVNGKPSATDARLAPINGKK
Blok 2 Sekundární struktura proteinů C3211 Aplikovaná bioinformatika Přednášející: Josef Houser Struktura proteinů ADSQTSSNRAGEFSIPPNTDFRAIFFANAAE QQHIKLFIGDSQEPAAYHKLTTRDGPREATL NSGNGKIRFEVSVNGKPSATDARLAPINGKK
Genomické databáze. Shlukování proteinových sekvencí. Ivana Rudolfová. školitel: doc. Ing. Jaroslav Zendulka, CSc.
 Genomické databáze Shlukování proteinových sekvencí Ivana Rudolfová školitel: doc. Ing. Jaroslav Zendulka, CSc. Obsah Proteiny Zdroje dat Predikce struktury proteinů Cíle disertační práce Vstupní data
Genomické databáze Shlukování proteinových sekvencí Ivana Rudolfová školitel: doc. Ing. Jaroslav Zendulka, CSc. Obsah Proteiny Zdroje dat Predikce struktury proteinů Cíle disertační práce Vstupní data
Studijní materiály pro bioinformatickou část ViBuChu. úloha II. Jan Komárek, Gabriel Demo
 Studijní materiály pro bioinformatickou část ViBuChu úloha II Jan Komárek, Gabriel Demo Adenin Struktura DNA Thymin 5 konec 3 konec DNA tvořena dvěmi řetězci orientovanými antiparalelně (liší se orientací
Studijní materiály pro bioinformatickou část ViBuChu úloha II Jan Komárek, Gabriel Demo Adenin Struktura DNA Thymin 5 konec 3 konec DNA tvořena dvěmi řetězci orientovanými antiparalelně (liší se orientací
Opakování
 Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
Neuronové časové řady (ANN-TS)
 Neuronové časové řady (ANN-TS) Menu: QCExpert Prediktivní metody Neuronové časové řady Tento modul (Artificial Neural Network Time Series ANN-TS) využívá modelovacího potenciálu neuronové sítě k predikci
Neuronové časové řady (ANN-TS) Menu: QCExpert Prediktivní metody Neuronové časové řady Tento modul (Artificial Neural Network Time Series ANN-TS) využívá modelovacího potenciálu neuronové sítě k predikci
Využití metod strojového učení v bioinformatice David Hoksza
 Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Typy molekul, látek a jejich vazeb v organismech
 Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Markovovy modely v Bioinformatice
 Markovovy modely v Bioinformatice Outline Markovovy modely obecně Profilové HMM Další použití HMM v Bioinformatice Analýza biologických sekvencí Biologické sekvence: DNA,RNA,protein prim.str. Sekvenování
Markovovy modely v Bioinformatice Outline Markovovy modely obecně Profilové HMM Další použití HMM v Bioinformatice Analýza biologických sekvencí Biologické sekvence: DNA,RNA,protein prim.str. Sekvenování
Struktura proteinů. - testík na procvičení. Vladimíra Kvasnicová
 Struktura proteinů - testík na procvičení Vladimíra Kvasnicová Mezi proteinogenní aminokyseliny patří a) kyselina asparagová b) kyselina glutarová c) kyselina acetoctová d) kyselina glutamová Mezi proteinogenní
Struktura proteinů - testík na procvičení Vladimíra Kvasnicová Mezi proteinogenní aminokyseliny patří a) kyselina asparagová b) kyselina glutarová c) kyselina acetoctová d) kyselina glutamová Mezi proteinogenní
Služby pro predikci struktury proteinů. Josef Pihera
 Služby pro predikci struktury proteinů Josef Pihera Struktura proteinů Primární sekvence aminokyselin Sekundární stáčení a spojování vodíkovými vazbami Supersekundární struktura přechod, opakovaná geometrická
Služby pro predikci struktury proteinů Josef Pihera Struktura proteinů Primární sekvence aminokyselin Sekundární stáčení a spojování vodíkovými vazbami Supersekundární struktura přechod, opakovaná geometrická
Využití strojového učení k identifikaci protein-ligand aktivních míst
 Využití strojového učení k identifikaci protein-ligand aktivních míst David Hoksza, Radoslav Krivák SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita
Využití strojového učení k identifikaci protein-ligand aktivních míst David Hoksza, Radoslav Krivák SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita
NUKLEOVÉ KYSELINY. Základ života
 NUKLEOVÉ KYSELINY Základ života HISTORIE 1. H. Braconnot (30. léta 19. století) - Strassburg vinné kvasinky izolace matiére animale. 2. J.F. Meischer - experimenty z hnisem štěpení trypsinem odstředěním
NUKLEOVÉ KYSELINY Základ života HISTORIE 1. H. Braconnot (30. léta 19. století) - Strassburg vinné kvasinky izolace matiére animale. 2. J.F. Meischer - experimenty z hnisem štěpení trypsinem odstředěním
Algoritmy a struktury neuropočítačů ASN - P10. Aplikace UNS v biomedicíně
 Aplikace UNS v biomedicíně aplikace v medicíně postup při zpracování úloh Aplikace UNS v medicíně Důvod: nalezení exaktnějších, levnějších a snadnějších metod určování diagnóz pro lékaře nalezení šetrnějších
Aplikace UNS v biomedicíně aplikace v medicíně postup při zpracování úloh Aplikace UNS v medicíně Důvod: nalezení exaktnějších, levnějších a snadnějších metod určování diagnóz pro lékaře nalezení šetrnějších
7. Rozdělení pravděpodobnosti ve statistice
 7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
OPVK CZ.1.07/2.2.00/
 OPVK CZ.1.07/2.2.00/28.0184 Základní principy vývoje nových léčiv OCH/ZPVNL Mgr. Radim Nencka, Ph.D. ZS 2012/2013 Molekulární interakce SAR Možné interakce jednotlivých funkčních skupin 1. Interakce alkoholů
OPVK CZ.1.07/2.2.00/28.0184 Základní principy vývoje nových léčiv OCH/ZPVNL Mgr. Radim Nencka, Ph.D. ZS 2012/2013 Molekulární interakce SAR Možné interakce jednotlivých funkčních skupin 1. Interakce alkoholů
METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1
 METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1 DOLOVÁNÍ V DATECH (DATA MINING) OBJEVUJE SE JIŽ OD 60. LET 20. ST. S ROZVOJEM POČÍTAČOVÉ TECHNIKY DEFINICE PROCES VÝBĚRU, PROHLEDÁVÁNÍ A MODELOVÁNÍ
METODY DOLOVÁNÍ V DATECH DATOVÉ SKLADY TEREZA HYNČICOVÁ H2IGE1 DOLOVÁNÍ V DATECH (DATA MINING) OBJEVUJE SE JIŽ OD 60. LET 20. ST. S ROZVOJEM POČÍTAČOVÉ TECHNIKY DEFINICE PROCES VÝBĚRU, PROHLEDÁVÁNÍ A MODELOVÁNÍ
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Algoritmy a struktury neuropočítačů ASN - P11
 Aplikace UNS při rozpoznání obrazů Základní úloha segmentace obrazu rozdělení obrazu do několika významných oblastí klasifikační úloha, clusterová analýza target Metody Kohonenova metoda KSOM Kohonenova
Aplikace UNS při rozpoznání obrazů Základní úloha segmentace obrazu rozdělení obrazu do několika významných oblastí klasifikační úloha, clusterová analýza target Metody Kohonenova metoda KSOM Kohonenova
Teorie chemické vazby a molekulární geometrie Molekulární geometrie VSEPR
 Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
 Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Neuronové sítě (11. přednáška)
 Neuronové sítě (11. přednáška) Machine Learning Naučit stroje se učit O co jde? Máme model výpočtu (t.j. výpočetní postup jednoznačně daný vstupy a nějakými parametry), chceme najít vhodné nastavení parametrů,
Neuronové sítě (11. přednáška) Machine Learning Naučit stroje se učit O co jde? Máme model výpočtu (t.j. výpočetní postup jednoznačně daný vstupy a nějakými parametry), chceme najít vhodné nastavení parametrů,
ANALÝZA A KLASIFIKACE BIOMEDICÍNSKÝCH DAT. Institut biostatistiky a analýz
 ANALÝZA A KLASIFIKACE BIOMEDICÍNSKÝCH DAT prof. Ing. Jiří Holčík,, CSc. NEURONOVÉ SÍTĚ otázky a odpovědi 1 AKD_predn4, slide 8: Hodnota výstupu závisí na znaménku funkce net i, tedy na tom, zda bude suma
ANALÝZA A KLASIFIKACE BIOMEDICÍNSKÝCH DAT prof. Ing. Jiří Holčík,, CSc. NEURONOVÉ SÍTĚ otázky a odpovědi 1 AKD_predn4, slide 8: Hodnota výstupu závisí na znaménku funkce net i, tedy na tom, zda bude suma
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Vytěžování znalostí z dat
 Pavel Kordík, Josef Borkovec (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 8 1/26 Vytěžování znalostí z dat Pavel Kordík, Josef Borkovec Department of Computer Systems Faculty of Information
Pavel Kordík, Josef Borkovec (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 8 1/26 Vytěžování znalostí z dat Pavel Kordík, Josef Borkovec Department of Computer Systems Faculty of Information
Operační výzkum. Síťová analýza. Metoda CPM.
 Operační výzkum Síťová analýza. Metoda CPM. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
Operační výzkum Síťová analýza. Metoda CPM. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Pokročilé neparametrické metody. Klára Kubošová
 Klára Kubošová Další typy stromů CHAID, PRIM, MARS CHAID - Chi-squared Automatic Interaction Detector G.V.Kass (1980) nebinární strom pro kategoriální proměnné. Jako kriteriální statistika pro větvení
Klára Kubošová Další typy stromů CHAID, PRIM, MARS CHAID - Chi-squared Automatic Interaction Detector G.V.Kass (1980) nebinární strom pro kategoriální proměnné. Jako kriteriální statistika pro větvení
Algoritmy a struktury neuropočítačů ASN P4. Vícevrstvé sítě dopředné a Elmanovy MLNN s učením zpětného šíření chyby
 Algoritmy a struktury neuropočítačů ASN P4 Vícevrstvé sítě dopředné a Elmanovy MLNN s učením zpětného šíření chyby Vrstevnatá struktura - vícevrstvé NN (Multilayer NN, MLNN) vstupní vrstva (input layer)
Algoritmy a struktury neuropočítačů ASN P4 Vícevrstvé sítě dopředné a Elmanovy MLNN s učením zpětného šíření chyby Vrstevnatá struktura - vícevrstvé NN (Multilayer NN, MLNN) vstupní vrstva (input layer)
Neuronové sítě v DPZ
 Univerzita J. E. Purkyně v Ústí nad Labem Fakulta životního prostředí Neuronové sítě v DPZ Seminární práce z předmětu Dálkový průzkum Země Vypracovali: Jan Lantora Rok: 2006 Zuzana Vašková Neuronové sítě
Univerzita J. E. Purkyně v Ústí nad Labem Fakulta životního prostředí Neuronové sítě v DPZ Seminární práce z předmětu Dálkový průzkum Země Vypracovali: Jan Lantora Rok: 2006 Zuzana Vašková Neuronové sítě
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
1. Statistická analýza dat Jak vznikají informace Rozložení dat
 1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
 28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Automatická detekce anomálií při geofyzikálním průzkumu. Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011
 Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Úloha - rozpoznávání číslic
 Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu odhaduje, jak se svět může vyvíjet.
 Umělá inteligence II Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Dnešní program Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu
Umělá inteligence II Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Dnešní program Agent pracující v částečně pozorovatelném prostředí udržuje na základě senzorického modelu
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Základy fyzikální geodézie 3/19 Legendreovy přidružené funkce
0.1 Úvod do matematické analýzy
 Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Pojem funkce Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Příklady veličin: hmotnost
Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Pojem funkce Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Příklady veličin: hmotnost
Ing. Alena Šafrová Drášilová, Ph.D.
 Rozhodování Ing. Alena Šafrová Drášilová, Ph.D. Rozhodování??? video Obsah typy rozhodování principy rozhodování rozhodovací fáze základní pojmy hodnotícího procesu rozhodovací podmínky rozhodování v podmínkách
Rozhodování Ing. Alena Šafrová Drášilová, Ph.D. Rozhodování??? video Obsah typy rozhodování principy rozhodování rozhodovací fáze základní pojmy hodnotícího procesu rozhodovací podmínky rozhodování v podmínkách
Ambasadoři přírodovědných a technických oborů. Ing. Michal Řepka Březen - duben 2013
 Ambasadoři přírodovědných a technických oborů Ing. Michal Řepka Březen - duben 2013 Umělé neuronové sítě Proč právě Neuronové sítě? K čemu je to dobré? Používá se to někde v praxi? Úvod Umělé neuronové
Ambasadoři přírodovědných a technických oborů Ing. Michal Řepka Březen - duben 2013 Umělé neuronové sítě Proč právě Neuronové sítě? K čemu je to dobré? Používá se to někde v praxi? Úvod Umělé neuronové
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ
 VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0996
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0996 Šablona: III/2 č. materiálu: VY_32_INOVACE_CHE_413 Jméno autora: Mgr. Alena Krejčíková Třída/ročník:
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0996 Šablona: III/2 č. materiálu: VY_32_INOVACE_CHE_413 Jméno autora: Mgr. Alena Krejčíková Třída/ročník:
Rozdělování dat do trénovacích a testovacích množin
 Rozdělování dat do trénovacích a testovacích množin Marcel Jiřina Rozpoznávání je důležitou metodou při zpracování reálných úloh. Rozpoznávání je definováno dvěma kroky a to pořízením dat o reálném rozpoznávaném
Rozdělování dat do trénovacích a testovacích množin Marcel Jiřina Rozpoznávání je důležitou metodou při zpracování reálných úloh. Rozpoznávání je definováno dvěma kroky a to pořízením dat o reálném rozpoznávaném
Struktura elektronového obalu
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Struktura elektronového obalu Představy o modelu atomu se vyvíjely tak, jak se zdokonalovaly možnosti vědy
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Struktura elektronového obalu Představy o modelu atomu se vyvíjely tak, jak se zdokonalovaly možnosti vědy
P ro te i n o vé d a ta b á ze
 Proteinové databáze Osnova Základní stavební jednotky proteinů Hierarchie proteinové struktury Stanovení proteinové struktury Důležitost proteinové struktury Proteinové strukturní databáze Proteinové klasifikační
Proteinové databáze Osnova Základní stavební jednotky proteinů Hierarchie proteinové struktury Stanovení proteinové struktury Důležitost proteinové struktury Proteinové strukturní databáze Proteinové klasifikační
Využití neuronové sítě pro identifikaci realného systému
 1 Portál pre odborné publikovanie ISSN 1338-0087 Využití neuronové sítě pro identifikaci realného systému Pišan Radim Elektrotechnika 20.06.2011 Identifikace systémů je proces, kdy z naměřených dat můžeme
1 Portál pre odborné publikovanie ISSN 1338-0087 Využití neuronové sítě pro identifikaci realného systému Pišan Radim Elektrotechnika 20.06.2011 Identifikace systémů je proces, kdy z naměřených dat můžeme
Bílkoviny - proteiny
 Bílkoviny - proteiny Proteiny jsou složeny z 20 kódovaných aminokyselin L-enantiomery Chemická struktura aminokyselin R představuje jeden z 20 různých typů postranních řetězců R Hlavní řetězec je neměnný
Bílkoviny - proteiny Proteiny jsou složeny z 20 kódovaných aminokyselin L-enantiomery Chemická struktura aminokyselin R představuje jeden z 20 různých typů postranních řetězců R Hlavní řetězec je neměnný
Kybernetika a umělá inteligence, cvičení 10/11
 Kybernetika a umělá inteligence, cvičení 10/11 Program 1. seminární cvičení: základní typy klasifikátorů a jejich princip 2. počítačové cvičení: procvičení na problému rozpoznávání číslic... body za aktivitu
Kybernetika a umělá inteligence, cvičení 10/11 Program 1. seminární cvičení: základní typy klasifikátorů a jejich princip 2. počítačové cvičení: procvičení na problému rozpoznávání číslic... body za aktivitu
II. Úlohy na vložené cykly a podprogramy
 II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky
 Otázka 20 A7B36DBS Zadání... 1 Slovníček pojmů... 1 Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky... 1 Zadání Relační DB struktury sloužící k optimalizaci
Otázka 20 A7B36DBS Zadání... 1 Slovníček pojmů... 1 Relační DB struktury sloužící k optimalizaci dotazů - indexy, clustery, indexem organizované tabulky... 1 Zadání Relační DB struktury sloužící k optimalizaci
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
 ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Algoritmus. Přesné znění definice algoritmu zní: Algoritmus je procedura proveditelná Turingovým strojem.
 Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
Algoritmus Algoritmus je schematický postup pro řešení určitého druhu problémů, který je prováděn pomocí konečného množství přesně definovaných kroků. nebo Algoritmus lze definovat jako jednoznačně určenou
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
Inženýrská statistika pak představuje soubor postupů a aplikací teoretických principů v oblasti inženýrské činnosti.
 Přednáška č. 1 Úvod do statistiky a počtu pravděpodobnosti Statistika Statistika je věda a postup jak rozvíjet lidské znalosti použitím empirických dat. Je založena na matematické statistice, která je
Přednáška č. 1 Úvod do statistiky a počtu pravděpodobnosti Statistika Statistika je věda a postup jak rozvíjet lidské znalosti použitím empirických dat. Je založena na matematické statistice, která je
Bioinformatika a výpočetní biologie KFC/BIN. I. Přehled
 Bioinformatika a výpočetní biologie KFC/BIN I. Přehled RNDr. Karel Berka, Ph.D. Univerzita Palackého v Olomouci Definice bioinformatiky (Molecular) bio informatics: bioinformatics is conceptualising biology
Bioinformatika a výpočetní biologie KFC/BIN I. Přehled RNDr. Karel Berka, Ph.D. Univerzita Palackého v Olomouci Definice bioinformatiky (Molecular) bio informatics: bioinformatics is conceptualising biology
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Základy genomiky. I. Úvod do bioinformatiky. Jan Hejátko
 Základy genomiky I. Úvod do bioinformatiky Jan Hejátko Masarykova univerzita, Oddělení funkční genomiky a proteomiky Laboratoř molekulární fyziologie rostlin Základy genomiky I. Zdrojová literatura ke
Základy genomiky I. Úvod do bioinformatiky Jan Hejátko Masarykova univerzita, Oddělení funkční genomiky a proteomiky Laboratoř molekulární fyziologie rostlin Základy genomiky I. Zdrojová literatura ke
Zákony hromadění chyb.
 Zákony hromadění chyb. Zákon hromadění skutečných chyb. Zákon hromadění středních chyb. Tomáš Bayer bayertom@natur.cuni.cz Přírodovědecká fakulta Univerzity Karlovy v Praze, Katedra aplikované geoinformatiky
Zákony hromadění chyb. Zákon hromadění skutečných chyb. Zákon hromadění středních chyb. Tomáš Bayer bayertom@natur.cuni.cz Přírodovědecká fakulta Univerzity Karlovy v Praze, Katedra aplikované geoinformatiky
Přírodní polymery proteiny
 Přírodní polymery proteiny Funkční úloha bílkovin 1. Funkce dynamická transport kontrola metabolismu interakce (komunikace, kontrakce) katalýza chemických přeměn 2. Funkce strukturální architektura orgánů
Přírodní polymery proteiny Funkční úloha bílkovin 1. Funkce dynamická transport kontrola metabolismu interakce (komunikace, kontrakce) katalýza chemických přeměn 2. Funkce strukturální architektura orgánů
Grafy. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta.
 6 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info množina vrcholů a množina hran hrana vždy spojuje
6 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info množina vrcholů a množina hran hrana vždy spojuje
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
Projekční algoritmus. Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění. Jan Klíma
 Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
Urychlení evolučních algoritmů pomocí regresních stromů a jejich zobecnění Jan Klíma Obsah Motivace & cíle práce Evoluční algoritmy Náhradní modelování Stromové regresní metody Implementace a výsledky
ZÁKLADNÍ NÁSTROJE ŘÍZENÍ JAKOSTI
 ZÁKLADNÍ NÁSTROJE ŘÍZENÍ JAKOSTI SPŠ na Proseku 4-1 Ing. A. Styblíková, Ing. L. Procházka - pevně stanovený soubor grafických technik napomáhajících při řešení problémů s kvalitou - jedná se o 7 nástrojů
ZÁKLADNÍ NÁSTROJE ŘÍZENÍ JAKOSTI SPŠ na Proseku 4-1 Ing. A. Styblíková, Ing. L. Procházka - pevně stanovený soubor grafických technik napomáhajících při řešení problémů s kvalitou - jedná se o 7 nástrojů
COSY + - podmínky měření a zpracování dat ztráta rozlišení ve spektru. inphase dublet, disperzní. antiphase dublet, absorpční
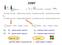 y x COSY 90 y chem. posuv J vazba 90 x : : inphase dublet, disperzní inphase dublet, disperzní antiphase dublet, absorpční antiphase dublet, absorpční diagonální pík krospík + - - + podmínky měření a zpracování
y x COSY 90 y chem. posuv J vazba 90 x : : inphase dublet, disperzní inphase dublet, disperzní antiphase dublet, absorpční antiphase dublet, absorpční diagonální pík krospík + - - + podmínky měření a zpracování
12. Predikce polymorfů. Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253
 12. Predikce polymorfů Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 1 Výpočetní chemie Predikce polymorfů rychle se vyvíjející se oblast růst výkonu počítačů možnost vypočítat
12. Predikce polymorfů Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 1 Výpočetní chemie Predikce polymorfů rychle se vyvíjející se oblast růst výkonu počítačů možnost vypočítat
Analýza dat pomocí systému Weka, Rapid miner a Enterprise miner
 Vysoká škola ekonomická v Praze Analýza dat pomocí systému Weka, Rapid miner a Enterprise miner Dobývání znalostí z databází 4IZ450 XXXXXXXXXXX Přidělená data a jejich popis Data určená pro zpracování
Vysoká škola ekonomická v Praze Analýza dat pomocí systému Weka, Rapid miner a Enterprise miner Dobývání znalostí z databází 4IZ450 XXXXXXXXXXX Přidělená data a jejich popis Data určená pro zpracování
Jednofaktorová analýza rozptylu
 I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
2. RBF neuronové sítě
 2. RBF neuronové sítě Kapitola pojednává o neuronových sítích typu RBF. V kapitole je popsána základní struktura tohoto typu neuronové sítě. Poté následuje definice a charakteristika jednotlivých radiálně
2. RBF neuronové sítě Kapitola pojednává o neuronových sítích typu RBF. V kapitole je popsána základní struktura tohoto typu neuronové sítě. Poté následuje definice a charakteristika jednotlivých radiálně
Vojtěch Hrubý: Esej pro předmět Seminář EVF
 Vojtěch Hrubý: Esej pro předmět Seminář EVF Plazma Pod pojmem plazma většinou myslíme plynné prostředí, které se skládá z neutrálních částic, iontů a elektronů. Poměr množství neutrálních a nabitých částic
Vojtěch Hrubý: Esej pro předmět Seminář EVF Plazma Pod pojmem plazma většinou myslíme plynné prostředí, které se skládá z neutrálních částic, iontů a elektronů. Poměr množství neutrálních a nabitých částic
CHEMIE. Pracovní list č. 10 - žákovská verze Téma: Bílkoviny. Mgr. Lenka Horutová
 www.projektsako.cz CHEMIE Pracovní list č. 10 - žákovská verze Téma: Bílkoviny Lektor: Mgr. Lenka Horutová Projekt: Student a konkurenceschopnost Reg. číslo: CZ.1.07/1.1.07/03.0075 Teorie: Název proteiny
www.projektsako.cz CHEMIE Pracovní list č. 10 - žákovská verze Téma: Bílkoviny Lektor: Mgr. Lenka Horutová Projekt: Student a konkurenceschopnost Reg. číslo: CZ.1.07/1.1.07/03.0075 Teorie: Název proteiny
Základy algoritmizace. Pattern matching
 Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Nauka o materiálu. Přednáška č.2 Poruchy krystalické mřížky
 Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
MULTIKRITERIÁLNÍ ROZHODOVÁNÍ KOMPLEXNÍ HODNOCENÍ ALTERNATIV
 PŘEDNÁŠKA 6 MULTIKRITERIÁLNÍ ROZHODOVÁNÍ KOMPLEXNÍ HODNOCENÍ ALTERNATIV Multikriteriální rozhodování Možnosti řešení podle toho, jaká je množina alternativ pokud množina alternativ X je zadaná implicitně
PŘEDNÁŠKA 6 MULTIKRITERIÁLNÍ ROZHODOVÁNÍ KOMPLEXNÍ HODNOCENÍ ALTERNATIV Multikriteriální rozhodování Možnosti řešení podle toho, jaká je množina alternativ pokud množina alternativ X je zadaná implicitně
Spektra 1 H NMR. Velmi zjednodušeně! Bohumil Dolenský
 Spektra 1 MR Velmi zjednodušeně! Bohumil Dolenský Spektra 1 MR... Počet signálů C 17 18 2 O 2 MeO Počet signálů = počet neekvivalentních skupin OMe = informace o symetrii molekuly Spektrum 1 MR... Počet
Spektra 1 MR Velmi zjednodušeně! Bohumil Dolenský Spektra 1 MR... Počet signálů C 17 18 2 O 2 MeO Počet signálů = počet neekvivalentních skupin OMe = informace o symetrii molekuly Spektrum 1 MR... Počet
OSA. maximalizace minimalizace 1/22
 OSA Systémová analýza metodika používaná k navrhování a racionalizaci systémů v podmínkách neurčitosti vyšší stupeň operační analýzy Operační analýza (výzkum) soubor metod umožňující řešit rozhodovací,
OSA Systémová analýza metodika používaná k navrhování a racionalizaci systémů v podmínkách neurčitosti vyšší stupeň operační analýzy Operační analýza (výzkum) soubor metod umožňující řešit rozhodovací,
Detekce interakčních sil v proudu vozidel
 Detekce interakčních sil v proudu vozidel (ANEB OBECNĚJŠÍ POHLED NA POJEM VZDÁLENOSTI V MATEMATICE) Doc. Mgr. Milan Krbálek, Ph.D. Katedra matematiky Fakulta jaderná a fyzikálně inženýrská České vysoké
Detekce interakčních sil v proudu vozidel (ANEB OBECNĚJŠÍ POHLED NA POJEM VZDÁLENOSTI V MATEMATICE) Doc. Mgr. Milan Krbálek, Ph.D. Katedra matematiky Fakulta jaderná a fyzikálně inženýrská České vysoké
5 Vícerozměrná data - kontingenční tabulky, testy nezávislosti, regresní analýza
 5 Vícerozměrná data - kontingenční tabulky, testy nezávislosti, regresní analýza 5.1 Vícerozměrná data a vícerozměrná rozdělení Při zpracování vícerozměrných dat se hledají souvislosti mezi dvěma, případně
5 Vícerozměrná data - kontingenční tabulky, testy nezávislosti, regresní analýza 5.1 Vícerozměrná data a vícerozměrná rozdělení Při zpracování vícerozměrných dat se hledají souvislosti mezi dvěma, případně
1. Zadání Pracovní úkol Pomůcky
 1. 1. Pracovní úkol 1. Zadání 1. Ověřte měřením, že směry výletu anihilačních fotonů vznikajících po β + rozpadu jader 22 Na svírají úhel 180. 2. Určete pološířku úhlového rozdělení. 3. Vysvětlete tvar
1. 1. Pracovní úkol 1. Zadání 1. Ověřte měřením, že směry výletu anihilačních fotonů vznikajících po β + rozpadu jader 22 Na svírají úhel 180. 2. Určete pološířku úhlového rozdělení. 3. Vysvětlete tvar
Teorie systémů TES 5. Znalostní systémy KMS
 Evropský sociální fond. Praha & EU: Investujeme do vaší budoucnosti. Teorie systémů TES 5. Znalostní systémy KMS ZS 2011/2012 prof. Ing. Petr Moos, CSc. Ústav informatiky a telekomunikací Fakulta dopravní
Evropský sociální fond. Praha & EU: Investujeme do vaší budoucnosti. Teorie systémů TES 5. Znalostní systémy KMS ZS 2011/2012 prof. Ing. Petr Moos, CSc. Ústav informatiky a telekomunikací Fakulta dopravní
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 2017
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Moderní systémy pro získávání znalostí z informací a dat
 Moderní systémy pro získávání znalostí z informací a dat Jan Žižka IBA Institut biostatistiky a analýz PřF & LF, Masarykova universita Kamenice 126/3, 625 00 Brno Email: zizka@iba.muni.cz Bioinformatika:
Moderní systémy pro získávání znalostí z informací a dat Jan Žižka IBA Institut biostatistiky a analýz PřF & LF, Masarykova universita Kamenice 126/3, 625 00 Brno Email: zizka@iba.muni.cz Bioinformatika:
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
12. cvičení z PSI prosince (Test střední hodnoty dvou normálních rozdělení se stejným neznámým rozptylem)
 cvičení z PSI 0-4 prosince 06 Test střední hodnoty dvou normálních rozdělení se stejným neznámým rozptylem) Z realizací náhodných veličin X a Y s normálním rozdělením) jsme z výběrů daného rozsahu obdrželi
cvičení z PSI 0-4 prosince 06 Test střední hodnoty dvou normálních rozdělení se stejným neznámým rozptylem) Z realizací náhodných veličin X a Y s normálním rozdělením) jsme z výběrů daného rozsahu obdrželi
Matematika I (KMI/PMATE)
 Přednáška první aneb Úvod do matematické analýzy Funkce a její vlastnosti Úvod do matematické analýzy Osnova přednášky pojem funkce definice funkce graf funkce definiční obor funkce obor hodnot funkce
Přednáška první aneb Úvod do matematické analýzy Funkce a její vlastnosti Úvod do matematické analýzy Osnova přednášky pojem funkce definice funkce graf funkce definiční obor funkce obor hodnot funkce
Elektřina a magnetismus úlohy na porozumění
 Elektřina a magnetismus úlohy na porozumění 1) Prázdná nenabitá plechovka je umístěna na izolační podložce. V jednu chvíli je do místa A na vnějším povrchu plechovky přivedeno malé množství náboje. Budeme-li
Elektřina a magnetismus úlohy na porozumění 1) Prázdná nenabitá plechovka je umístěna na izolační podložce. V jednu chvíli je do místa A na vnějším povrchu plechovky přivedeno malé množství náboje. Budeme-li
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Úvod do analytické mechaniky
 Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
9. T r a n s f o r m a c e n á h o d n é v e l i č i n y
 9. T r a n s f o r m a c e n á h o d n é v e l i č i n y Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota y závisí nějakým způsobem na vstupní, je její funkcí y = f(x).
9. T r a n s f o r m a c e n á h o d n é v e l i č i n y Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota y závisí nějakým způsobem na vstupní, je její funkcí y = f(x).
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Grafové úlohy Daniela Szturcová Tento
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Grafové úlohy Daniela Szturcová Tento
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
