Speciální aplikace poznatků ze smáčení. Vzlínání do vlákenných materiálů TNT. Eva Kuželová Košťáková KCH, FP, TUL
|
|
|
- Miloš Bílek
- před 5 lety
- Počet zobrazení:
Transkript
1 Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL
2 -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního úhlu u vlákenných bobtnajících materiálů -Perpetuum mobile princip založený na vzlínání kapaliny do vlákenného materiálu -Vzlínání do strukturovaných textilií
3 Jak určit kontaktní úhel u netkaných textilií (či porézních materiálů obecně) pro kontaktní úhly menší než 90? Washburnova metoda Teorie Washburna naznačuje, že pokud se porézní pevná látka (např. netkaná textilie) dostane do styku s kapalinou, takže pevná látka není ponořena do kapaliny, ale spíše se dotýká pouze povrchu kapaliny, potom vzestup kapaliny do pórů pevných látek v důsledku kapilární akce bude řízen následující rovnicí: Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů
4 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů h r cos t 2 Kt 1 2 Co znamená c? Tedy materiálová konstanta? c představuje: strukturu pórů, velikost pórů a počet pórů v pevné porézní látce například v netkané textilii. Jak zjistit velikost hodnoty c? Správně při vynesení čtverce hmotnosti m 2 proti času t ukazuje lineární oblast, jejíž sklon pro známé vlastnosti kapaliny (, ρ a η) obsahuje pouze dvě neznámé c a θ. Vzhledem k tomu, že kontaktní úhel závisí na sklonu křivky ve výše uvedených datech, zvolená část dat pro měření může ovlivnit hodnotu úhlu kontaktu, která je vypočítána z tohoto sklonu. Pokud by byla data blíže počátku experimentu analyzována, sklon by byl větší, než kdyby byla použita data blízká konci experimentu. To by poskytovalo nižší kontaktní úhel pro data vybraná na začátku experimentu než na konci experimentu.
5 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů c představuje: strukturu pórů, velikost pórů a počet pórů v pevné porézní látce například v netkané textilii. Jak zjistit velikost hodnoty c? Použije se nejprve jiná kapalina o známém kontaktním úhlu s pevnou látkou. Typicky se využívá N-hexan, který má velmi nízké povrchové napětí 18,4mN/m a obvykle má s pevnými látkami 0 kontaktní úhel. Následně se dopočítá konstanta c testované netkané textilie. V dalším měření se pak již se známou konstantou c provede měření s požadovanou kapalinou, která nemá nulový kontaktní úhel. Studovaná netkaná textilie musí být co nejrovnoměrnější, což může být problém u nižších plošných hmotností. Je nutné detailní statistické hodnocení získaných dat.
6 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů c představuje: strukturu pórů, velikost pórů a počet pórů v pevné porézní látce například v netkané textilii. Jak zjistit velikost hodnoty c? N-hexan (kontakní úhel 0 ) m 2 = cρ2 γ cosθ y = ax; m 2 = y; t t = x; a = c ρ2 γ cosθ cos θ = a c ρ 2 γ voda
7
8 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů Stejný postup je možné použít i pro práškové materiály. Pro Kruss je nutné použít speciální nádobku, do které je prášek nasypán Kontaktní úhly jsou počítány z lineárních částí grafů v počátcích měření (pro velmi malé h, respektive pro malé m). Nemohou být takto určovány kontaktní úhly větší než 90 - neprobíhá smáčení.
9 Určování kontaktního úhlu na bobtnajících vlákenných materiálech K určení kontaktního úhlu kapalin na pevných látkách je k dispozici celá řada experimentálních metod. Standardní optické či Wilhelmyho metody se ale stávají obtížně aplikovatelnými pokud vzorek při smáčení bobtná. BOBTNÁNÍ X BOTNÁNÍ
10 (a) Schematic of the swelling process of collagen structure consisting of fibers and fibrils. (b) SEM images of the collagen fiber before and after swelling due to water. Kolagenová vlákna v procesu smáčení schematický nákres procesu botnání vláken a SEM obrázek kolagenových vláken předa po smočení vodou. Fig. 1: Pulp fiber with swollen areas marked by the and the corresponding degree of swelling, i.e. the percentage of swollen fiber length. corresponding-degree-of_fig1_ articles/srep20563#f5
11 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH Botnání viskózových dutých vláken ve vodě Různé typy botnání vláken dle geometrických změn - Nárůst průměru vlákna ( D/D) -dial - Nárůst plochy povrchu vlákna ( A/A) - Nárůst délky vlákna ( L/L) - axial - Nárůst objemu vlákna ( V/V)
12 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH
13 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH Při botnání vláken při smáčení není výsledná křivka ve Washburnově metodě lineární ani v počátcích měření. Je nutné přistoupit k nepřímému určení (odhadu) kontaktního úhlu. Viskózová netkaná textilie+voda = není možné měřit přímo === dochází k botnání===křivka není lineární. Experiment se stanovením kontaktního úhlu vody na netkané textilii, která byla používána k výrobě výrobků pro dámskou hygienu. Nepřímý postup měření kontaktního úhlu. 1) Najít kapaliny, které mohou být přímo měřeny, vlákenný materiál v kontaktu s nimi nebotná. Například organická rozpouštědla jako benzylalkohol (benzenmethanol), diodomethan === s viskózovými vlákny nedochází k botnání.
14 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH Nepřímý postup měření kontaktního úhlu: 1) Najít kapaliny, které mohou být přímo měřeny, vlákenný materiál v kontaktu s nimi nebotná. Například organická rozpouštědla jako benzylalkohol (benzenmethanol), diodomethan === s viskózovými vlákny nedochází k botnání. 2) Washburnova metoda přímá závislost křivka m 2 /t při smáčení těmito organickými rozpouštědly 3) Použití Fowkesovy analýzy diodomethane je ideální kandidát neboť má polární složku povrchového napětí nulovou. Tabelované hodnoty polárních a disperzních složek povrchového napětí.
15 Polární a disperzní složky povrchového napětí - Fowkesova rovnice Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH
16 Polární a disperzní složky povrchového napětí - Fowkesova rovnice Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH Základní přístupy k výpočtu povrchové energie Existuje několik přístupů, které se využívají k výpočtu povrchového napětí, respektive povrchové energie pevných látek, rozvíjených řadou vědců. Celková povrchová energie pevných látek a kapalin závisí na různých typech molekulárních interakcí jako jsou disperzní (van der Waals), polární, a acidobazické interakce Metody se liší v počtu komponent, nebo parametrů jimž jsou vybaveny. Nejběžněji používané teorie jsou: - Zismanova teorie - Fowkesova metoda - Owens-Wendt-Rabel-Kaelble (OWRK) metoda - Wu teorie - Acido-bazická Van Oss metoda - Metoda podle Neumanna.
17 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH FOWKESOVA TEORIE Při kontaktu dvou libovolných fází se uplatňuje Lifshitz-van der Waalsova síla, ta je tvořena příspěvky trojího druhu: 1) Coulombickými silami (molekuly s výrazným dipólem voda, alkoholy. 2) Indukční síly indukčním způsobem vyvolané či posílené dipóly se poutají elektrostatickými silami, 3) Disperzními silami těmto silám odpovídá disperzní složka povrchové energie Ve skutečnosti je volná povrchová energie rozdělena pouze do dvou částí: disperzní a nedisperzní (zahrnující všechny nedisperzní složky).
18 FOWKESOVA TEORIE Absence polární složky u diiodomethanu vede k zjednodušení Fowkesovy rovnice Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH P Disperzní podíl povrchové energie je stanoven z měření kontakního úhlu s použitím alespoň jedné čistě disperzní kapaliny. Fowkes předpokládal, že se adheze účastní pouze interakce na rozhraní a z tohoto hlediska jsou proto důležité pouze disperzní síly. Fowkes měřil povrchová napětí mezi vodou a sérií alkanů (od hexanu k tetradekanu) Alkany považoval za modelové tekutiny, protože interagují jen skrz slabé disperzní síly. Jejich molekuly nemají ani polární nebo ionizovatelné funkční skupiny. Následně může být spočítána polární složka povrchové energie s použitím benzylalkoholu, u kterého známe jak polární tak disperzní složku. Použitím rovnice na rozhraní pevná látka kapalina dostaneme Zahrnutím Youngovy rovnice je možné dostat toto:
19 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH FOWKESOVA TEORIE Absence polární složky u diiodomethanu vede k zjednodušení Fowkesovy rovnice Jestliže povrchová energie obou komponent pro pevnou látku byla spočítána, kontaktní úhel s VODOU může být lehce vyřešen následující úpravou Fowkesovy rovnice s použitím standardních hodnot pro povrchové napětí VODY. Následně může být spočítána polární složka povrchové energie s použitím benzylalkoholu, u kterého známe jak polární tak disperzní složku.
20 Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů BOBTNAJÍCÍCH Někdy nelze kontaktní úhel kapaliny vzhledem k bobtnání, rozpustnosti nebo jakémukoli jinému podobnému problému při měření vzorku přímo. Avšak existuje metoda, jak tento úhel určit. Nejprve určete sadu rozpouštědel s různými polárními a disperzními složkami (u jedné z kapalin je jedna ze složek nulová) jejich povrchového napětí, které nevytváří problém se vzorkem (nebotnají, nerozpouští vzorek atd.). (benzylalkohol, diiodomethan) Potom vypočítejte povrchovou energii vzorku pomocí Fowkesovy metody. Botnání viskózových dutých vláken ve vodě c c Jakmile je známá povrchová energie (pevné látky) vzorku mohou být tyto hodnoty společně s hodnotami povrchového napětí problémové kapaliny či rozpouštědla použity v přeuspořádané Fowkesove rovnici v nepřímém určení kontaktního úhlu. c
21 Perpetuum mobile princip založený na vzlínání kapaliny do vlákenného materiálu Capillary motor Perpetuum mobile V utěsněném kontejneru na kaplinu, kapilára vytahuje povrch kapaliny proti gravitaci vzlínání. V místě (ve výšce), kde dochází k ustalování rovnováhy, je otočena kapilára směrem dolů. Kapalina proniklá směrem nahoru do kapiláry pak díky gravitaci opět teče dolů do kontejneru. Délka kapiláry je velmi důležitá.
22 Perpetuum mobile princip založený na vzlínání kapaliny do vlákenného materiálu Rozdíl tlaků v přízích je dán rozdílem kapilární mínus hydrostatický tlak. Kapilární tlak obsahuje materiálový parametr, který je závislý na geometrii pórů a smáčecích vlastnostech páru kapalina/vlákno.
23 Vzlínání do textilií více hierarchická struktura Vzlínání do textilií (netkané textilie, tkanina, pletenina, příze) Existence série rozdílně velkých pórů Kapilární tlak malé kapiláry = vyšší hnací síla; malé kapiláry = menší průchodnost Kapalina se pohybuje rychleji skrze větší póry a zaplňuje menší póry. V určitém okamžiku přichází do hry gravitace a brání průchodu kapaliny přes větší póry. Na konci ve větším póru se meniskus nepohybuje, ale v menším se stále ještě pohybuje.
24 Děkuji za pozornost! :40 Prof. David Lukáš, přednáška Rayleighova nestabilita
Měření povrchového napětí kapalin a kontaktních úhlů
 2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
Úvod do elektrostatického zvlákňování. Eva Košťáková KNT, FT, TUL
 Úvod do elektrostatického zvlákňování Eva Košťáková KNT, FT, TUL Lidský vlas Bavlněné vlákno Jednou v podstatě velmi jednoduchou metodou výroby nanovláken je tak zvané Elektrostatické zvlákňování (anglicky
Úvod do elektrostatického zvlákňování Eva Košťáková KNT, FT, TUL Lidský vlas Bavlněné vlákno Jednou v podstatě velmi jednoduchou metodou výroby nanovláken je tak zvané Elektrostatické zvlákňování (anglicky
Interakce mezi kapalinou a vlákenným materiálem
 5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
Povrchová energie. Povrchová energie je definována jako energie, kterou je třeba dodat k zvětšení mezifází o jednotkovou plochu.
 Povrchová energie Povrchová energie Složky povrchové energie Interakce povrchových energií přes mezifází Predikce mezipovrchové energie Hustota kohezní energie (objemová a povrchová hustota) Parachor Molekulární
Povrchová energie Povrchová energie Složky povrchové energie Interakce povrchových energií přes mezifází Predikce mezipovrchové energie Hustota kohezní energie (objemová a povrchová hustota) Parachor Molekulární
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI. Jaroslav Krucký, PMB 22
 Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Experimentální realizace Buquoyovy úlohy
 Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
TEORETICKÁ PŘÍPRAVA...
 Obsah OBSAH... 7 ÚVOD... 9 1 TEORETICKÁ PŘÍPRAVA... 11 1.1 FÁZOVÁ ROZHRANÍ... 11 1.1.1 Molekuly na mezifázovém rozhraní... 11 1.1.2 Fázové rozhraní z makroskopického hlediska... 13 1.1.3 Fyziologie malých
Obsah OBSAH... 7 ÚVOD... 9 1 TEORETICKÁ PŘÍPRAVA... 11 1.1 FÁZOVÁ ROZHRANÍ... 11 1.1.1 Molekuly na mezifázovém rozhraní... 11 1.1.2 Fázové rozhraní z makroskopického hlediska... 13 1.1.3 Fyziologie malých
Adheze - pokračování
 2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
5. Stavy hmoty Kapaliny a kapalné krystaly
 a kapalné krystaly Vlastnosti kapalin kapalných krystalů jako rozpouštědla Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti kapaliny nestálé atraktivní interakce (kohezní síly) mezi molekulami,
a kapalné krystaly Vlastnosti kapalin kapalných krystalů jako rozpouštědla Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti kapaliny nestálé atraktivní interakce (kohezní síly) mezi molekulami,
3. Měření viskozity, hustoty a povrchového napětí kapalin
 Fyzikální praktikum 1 3. Měření viskozity, hustoty a povrchového napětí kapalin Jméno: Václav GLOS Datum: 12.3.2012 Obor: Astrofyzika Ročník: 1 Laboratorní podmínky: Teplota: 23,5 C Tlak: 1001,0 hpa Vlhkost:
Fyzikální praktikum 1 3. Měření viskozity, hustoty a povrchového napětí kapalin Jméno: Václav GLOS Datum: 12.3.2012 Obor: Astrofyzika Ročník: 1 Laboratorní podmínky: Teplota: 23,5 C Tlak: 1001,0 hpa Vlhkost:
Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma fázemi První ucelená teorie respektující uvedenou skutečnost byla
 Teorie chromatografie - III Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 4.3.3 Teorie dynamická Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma
Teorie chromatografie - III Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 4.3.3 Teorie dynamická Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma
HUSTOTA PEVNÝCH LÁTEK
 HUSTOTA PEVNÝCH LÁTEK Hustota látek je základní informací o studované látce. V případě homogenní látky lze i odhadnout druh materiálu s pomocí známých tabulkovaných údajů (s ohledem na barvu a vzhled materiálu
HUSTOTA PEVNÝCH LÁTEK Hustota látek je základní informací o studované látce. V případě homogenní látky lze i odhadnout druh materiálu s pomocí známých tabulkovaných údajů (s ohledem na barvu a vzhled materiálu
Skupenské stavy látek. Mezimolekulární síly
 Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Kompaktace. Inženýrství chemicko-farmaceutických výrob. Suchá granulace Princip. Vazebné síly. Stlačování sypké hmoty mezi dvěma povrchy
 Zvětšování velikosti částic Kompaktace, extrudace Kompaktace Suchá granulace Princip Stlačování sypké hmoty mezi dvěma povrchy Vazebné síly van der Waalsovy interakce mechanické zaklesnutí částic povrchové
Zvětšování velikosti částic Kompaktace, extrudace Kompaktace Suchá granulace Princip Stlačování sypké hmoty mezi dvěma povrchy Vazebné síly van der Waalsovy interakce mechanické zaklesnutí částic povrchové
Voigtův model kompozitu
 Voigtův model kompozitu Osnova přednášky Směšovací pravidlo použitelnost Princip Voigtova modelu Důsledky Voigtova modelu Specifika vláknových kompozitů Směšovací pravidlo Nejjednoduší vztah pro vlastnost
Voigtův model kompozitu Osnova přednášky Směšovací pravidlo použitelnost Princip Voigtova modelu Důsledky Voigtova modelu Specifika vláknových kompozitů Směšovací pravidlo Nejjednoduší vztah pro vlastnost
Chemie povrchů verze 2013
 Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123MAIN - Základní materiálové parametry
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123MAIN - Základní materiálové parametry Hustota vs. objemová hmotnost - V případě neporézních materiálů (kovy, ) je hustota rovná objemové hmotnosti - V případě
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123MAIN - Základní materiálové parametry Hustota vs. objemová hmotnost - V případě neporézních materiálů (kovy, ) je hustota rovná objemové hmotnosti - V případě
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 345 K metodou bublin.
 1 Pracovní úkoly 1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 35 K metodou bublin. 2. Měřenou závislost znázorněte graficky. Závislost aproximujte kvadratickou
1 Pracovní úkoly 1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 35 K metodou bublin. 2. Měřenou závislost znázorněte graficky. Závislost aproximujte kvadratickou
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
TERMODYNAMIKA Ideální plyn TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY.
 TERMODYNAMIKA Ideální plyn TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Ideální plyn je zjednodušená představa skutečného plynu. Je dokonale stlačitelný
TERMODYNAMIKA Ideální plyn TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Ideální plyn je zjednodušená představa skutečného plynu. Je dokonale stlačitelný
Typy molekul, látek a jejich vazeb v organismech
 Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123TVVM transport kapalné vody
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM transport kapalné vody Transport vody porézním prostředím: Souč. tepelné vodivosti vzduchu: = 0,024-0,031 W/mK Souč. tepelné vodivosti izolantů: = cca
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM transport kapalné vody Transport vody porézním prostředím: Souč. tepelné vodivosti vzduchu: = 0,024-0,031 W/mK Souč. tepelné vodivosti izolantů: = cca
EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU
 EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU Ing. Daniel Koutný Experimental study of lubrication films contaminated by water VYSOKÉ UČENÍ TECHNICKÉ v BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU Ing. Daniel Koutný Experimental study of lubrication films contaminated by water VYSOKÉ UČENÍ TECHNICKÉ v BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška. TNT smáčení úvod. Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL
 2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU
 EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU Ing. Daniel Koutný Experimental study of lubrication films contaminated by water VYSOKÉ UČENÍ TECHNICKÉ v BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
EXPERIMENTÁLNÍ STUDIUM CHOVÁNÍ MAZACÍCH FILMŮ KONTAMINOVANÝCH VODOU Ing. Daniel Koutný Experimental study of lubrication films contaminated by water VYSOKÉ UČENÍ TECHNICKÉ v BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
Opakování
 Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
LOGO. Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123TVVM - Základní materiálové parametry
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM - Základní materiálové parametry Hustota vs. objemová hmotnost - V případě neporézních materiálů (kovy, ) je hustota rovná objemové hmotnosti - V případě
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 123TVVM - Základní materiálové parametry Hustota vs. objemová hmotnost - V případě neporézních materiálů (kovy, ) je hustota rovná objemové hmotnosti - V případě
Autokláv reaktor pro promíchávané vícefázové reakce
 Vysoká škola chemicko technologická v Praze Ústav organické technologie (111) Autokláv reaktor pro promíchávané vícefázové reakce Vypracoval : Bc. Tomáš Sommer Předmět: Vícefázové reaktory (prof. Ing.
Vysoká škola chemicko technologická v Praze Ústav organické technologie (111) Autokláv reaktor pro promíchávané vícefázové reakce Vypracoval : Bc. Tomáš Sommer Předmět: Vícefázové reaktory (prof. Ing.
pracovní list studenta
 Výstup RVP: Klíčová slova: pracovní list studenta Funkce kvadratická funkce Mirek Kubera žák načrtne grafy požadovaných funkcí, formuluje a zdůvodňuje vlastnosti studovaných funkcí, modeluje závislosti
Výstup RVP: Klíčová slova: pracovní list studenta Funkce kvadratická funkce Mirek Kubera žák načrtne grafy požadovaných funkcí, formuluje a zdůvodňuje vlastnosti studovaných funkcí, modeluje závislosti
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
9. Struktura a vlastnosti plynů
 9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
Lineární funkce IV
 .. Lineární funkce IV Předpoklady 0 Pedagogická poznámka Říkám studentům, že cílem hodiny není naučit se něco nového, ale použít to, co už známe (a možná se také přesvědčit o tom, jak se nemůžeme obejít
.. Lineární funkce IV Předpoklady 0 Pedagogická poznámka Říkám studentům, že cílem hodiny není naučit se něco nového, ale použít to, co už známe (a možná se také přesvědčit o tom, jak se nemůžeme obejít
Zahušťování suspenzí v oboru čištění odpadních vod
 Zahušťování suspenzí v oboru čištění odpadních vod Obsah přednášky význam zahušťování suspenzí sedimentační procesy suspenzí s vysokou koncentrací zahušťovací zkoušky návrh a posouzení dosazovací nádrže
Zahušťování suspenzí v oboru čištění odpadních vod Obsah přednášky význam zahušťování suspenzí sedimentační procesy suspenzí s vysokou koncentrací zahušťovací zkoušky návrh a posouzení dosazovací nádrže
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce
 Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE
 HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE Buzgo M. 1,3,4, Vysloužilová L. 2, Míčková A. 1,3,4, Benešová J. 1,3,4, Pokorná H. 1,3,4, Lukáš D. 2, Amler E. 1,3,4 1 Fakulta
HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE Buzgo M. 1,3,4, Vysloužilová L. 2, Míčková A. 1,3,4, Benešová J. 1,3,4, Pokorná H. 1,3,4, Lukáš D. 2, Amler E. 1,3,4 1 Fakulta
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. úloha č. 4 Název: Určení závislosti povrchového napětí na koncentraci povrchově aktivní látky Pracoval: Jakub Michálek
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. úloha č. 4 Název: Určení závislosti povrchového napětí na koncentraci povrchově aktivní látky Pracoval: Jakub Michálek
4. Kolmou tlakovou sílu působící v kapalině na libovolně orientovanou plochu S vyjádříme jako
 1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
15,45 17,90 19,80 21,28. 24,38 28,18 27,92 28,48 dichlormethan trichlormethan tetrachlormethan kys. mravenčí kys. octová kys. propionová kys.
 zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270C vodík 2 mn m při teplotě 253C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m rtuť při 0 o C = 470 mn m organické
zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270C vodík 2 mn m při teplotě 253C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m rtuť při 0 o C = 470 mn m organické
Interní norma č /01 Stupeň kotonizace lýkových vláken
 Předmluva Text vnitřní normy byl vypracován v rámci Výzkumného centra Textil LN00B090 a schválen oponentním řízením dne 7.2.2004. Předmět normy Norma stanoví postup měření a hodnocení stupně kotonizace
Předmluva Text vnitřní normy byl vypracován v rámci Výzkumného centra Textil LN00B090 a schválen oponentním řízením dne 7.2.2004. Předmět normy Norma stanoví postup měření a hodnocení stupně kotonizace
Měření součinitele smykového tření dynamickou metodou
 Měření součinitele smykového tření dynamickou metodou Online: http://www.sclpx.eu/lab1r.php?exp=6 Měření smykového tření na nakloněné rovině pomocí zvukové karty řešil např. Sedláček [76]. Jeho konstrukce
Měření součinitele smykového tření dynamickou metodou Online: http://www.sclpx.eu/lab1r.php?exp=6 Měření smykového tření na nakloněné rovině pomocí zvukové karty řešil např. Sedláček [76]. Jeho konstrukce
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
INDUKTIVNÍ STATISTIKA
 10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
Zařízení: Rotační viskozimetr s příslušenstvím, ohřívadlo s magnetickou míchačkou, teploměr, potřebné nádoby a kapaliny (aspoň 250ml).
 Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Vzdělávací oblast: Člověk a příroda. Vyučovací předmět: fyzika. Třída: sekunda. Očekávané výstupy. Poznámky. Přesahy. Průřezová témata.
 Vzdělávací oblast: Člověk a příroda Vyučovací předmět: fyzika Třída: sekunda Očekávané výstupy Nalezne společné a rozdílné vlastnosti kapalin, plynů a pevných látek Uvede konkrétní příklady jevů dokazujících,
Vzdělávací oblast: Člověk a příroda Vyučovací předmět: fyzika Třída: sekunda Očekávané výstupy Nalezne společné a rozdílné vlastnosti kapalin, plynů a pevných látek Uvede konkrétní příklady jevů dokazujících,
Skupenské stavy. Kapalina Částečně neuspořádané Volný pohyb částic nebo skupin částic Částice blíže u sebe
 Skupenské stavy Plyn Zcela neuspořádané Hodně volného prostoru Zcela volný pohyb částic Částice daleko od sebe Kapalina Částečně neuspořádané Volný pohyb částic nebo skupin částic Částice blíže u sebe
Skupenské stavy Plyn Zcela neuspořádané Hodně volného prostoru Zcela volný pohyb částic Částice daleko od sebe Kapalina Částečně neuspořádané Volný pohyb částic nebo skupin částic Částice blíže u sebe
Interakce mezi kapalinou a vlákenným materiálem
 7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
d p o r o v t e p l o m ě r, t e r m o č l á n k
 d p o r o v t e p l o m ě r, t e r m o č l á n k Ú k o l : a) Proveďte kalibraci odporového teploměru, termočlánku a termistoru b) Určete teplotní koeficienty odporového teploměru, konstanty charakterizující
d p o r o v t e p l o m ě r, t e r m o č l á n k Ú k o l : a) Proveďte kalibraci odporového teploměru, termočlánku a termistoru b) Určete teplotní koeficienty odporového teploměru, konstanty charakterizující
Vlákna a textilie na bázi hyaluronanu
 CETRUM TRANSFERU BIOMEDICÍNSKÝCH TECHNOLOGIÍ HK CZ.1.05/3.1.00/10.0213 Vlákna a textilie na bázi hyaluronanu Seminář JAK VÝZKUMNĚ SPOLUPRACOVAT S FIRMOU CONTIPRO? CENTRUM TRANSFERU BIOMEDICÍNSKÝCH TECHNOLOGIÍ
CETRUM TRANSFERU BIOMEDICÍNSKÝCH TECHNOLOGIÍ HK CZ.1.05/3.1.00/10.0213 Vlákna a textilie na bázi hyaluronanu Seminář JAK VÝZKUMNĚ SPOLUPRACOVAT S FIRMOU CONTIPRO? CENTRUM TRANSFERU BIOMEDICÍNSKÝCH TECHNOLOGIÍ
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT
 VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
Metody separace. přírodních látek
 Metody separace přírodních látek (5) Chromatografie; základní definice a klasifikace ruzných metod; kapalinová chromatografie, plynová chromatografie, přístrojová technika. Chromatografie «F(+)d» 1897
Metody separace přírodních látek (5) Chromatografie; základní definice a klasifikace ruzných metod; kapalinová chromatografie, plynová chromatografie, přístrojová technika. Chromatografie «F(+)d» 1897
Plyn. 11 plynných prvků. Vzácné plyny. He, Ne, Ar, Kr, Xe, Rn Diatomické plynné prvky H 2, N 2, O 2, F 2, Cl 2
 Plyny Plyn T v, K Vzácné plyny 11 plynných prvků He, Ne, Ar, Kr, Xe, Rn 165 Rn 211 N 2 O 2 77 F 2 90 85 Diatomické plynné prvky Cl 2 238 H 2, N 2, O 2, F 2, Cl 2 H 2 He Ne Ar Kr Xe 20 4.4 27 87 120 1 Plyn
Plyny Plyn T v, K Vzácné plyny 11 plynných prvků He, Ne, Ar, Kr, Xe, Rn 165 Rn 211 N 2 O 2 77 F 2 90 85 Diatomické plynné prvky Cl 2 238 H 2, N 2, O 2, F 2, Cl 2 H 2 He Ne Ar Kr Xe 20 4.4 27 87 120 1 Plyn
Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna. Eva Košťáková KNT, FT, TUL
 Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna Eva Košťáková KNT, FT, TUL Rotující válec Řízení orientace vláken Vibrující deska Ostrý disk Rámeček Řízení orientace vláken
Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna Eva Košťáková KNT, FT, TUL Rotující válec Řízení orientace vláken Vibrující deska Ostrý disk Rámeček Řízení orientace vláken
Kritéria porušení laminy
 Kap. 4 Kritéria porušení laminy Inormační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky S ČVU v Praze.. 007-6.. 007 Úvod omové procesy vyvolané v jednosměrovém
Kap. 4 Kritéria porušení laminy Inormační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky S ČVU v Praze.. 007-6.. 007 Úvod omové procesy vyvolané v jednosměrovém
Netkané textilie. Materiály 2
 Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Stanovení účinku vodního paprsku
 Vysoké učení technické v Brně akulta strojního inženýrství Energetický ústav Odbor fluidního inženýrství Victora Kaplana NÁZEV: tanovení účinku vodního paprsku tudijní skupina: 3B/16 Vypracovali: Jméno
Vysoké učení technické v Brně akulta strojního inženýrství Energetický ústav Odbor fluidního inženýrství Victora Kaplana NÁZEV: tanovení účinku vodního paprsku tudijní skupina: 3B/16 Vypracovali: Jméno
Stanovení hustoty pevných a kapalných látek
 55 Kapitola 9 Stanovení hustoty pevných a kapalných látek 9.1 Úvod Hustota látky ρ je hmotnost její objemové jednotky, definované vztahem: ρ = dm dv, kde dm = hmotnost objemového elementu dv. Pro homogenní
55 Kapitola 9 Stanovení hustoty pevných a kapalných látek 9.1 Úvod Hustota látky ρ je hmotnost její objemové jednotky, definované vztahem: ρ = dm dv, kde dm = hmotnost objemového elementu dv. Pro homogenní
Hydromechanické procesy Hydrostatika
 Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
02 Nevazebné interakce
 02 Nevazebné interakce Nevazebné interakce Druh chemické vazby Určují 3D konfiguraci makromolekul, účastní se mnoha biologických procesů, zodpovědné za uspořádání molekul v krystalu Síla nevazebných interakcí
02 Nevazebné interakce Nevazebné interakce Druh chemické vazby Určují 3D konfiguraci makromolekul, účastní se mnoha biologických procesů, zodpovědné za uspořádání molekul v krystalu Síla nevazebných interakcí
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl
 Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Obr. 9.1 Kontakt pohyblivé části s povrchem. Tomuto meznímu stavu za klidu odpovídá maximální síla, která se nezývá adhezní síla,. , = (9.
 9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
34_Mechanické vlastnosti kapalin... 2 Pascalův zákon _Tlak - příklady _Hydraulické stroje _PL: Hydraulické stroje - řešení...
 34_Mechanické vlastnosti kapalin... 2 Pascalův zákon... 2 35_Tlak - příklady... 2 36_Hydraulické stroje... 3 37_PL: Hydraulické stroje - řešení... 4 38_Účinky gravitační síly Země na kapalinu... 6 Hydrostatická
34_Mechanické vlastnosti kapalin... 2 Pascalův zákon... 2 35_Tlak - příklady... 2 36_Hydraulické stroje... 3 37_PL: Hydraulické stroje - řešení... 4 38_Účinky gravitační síly Země na kapalinu... 6 Hydrostatická
Vícefázové reaktory. Probublávaný reaktor plyn kapalina katalyzátor. Zuzana Tomešová
 Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
rtuť při 0 o C = 470 mn m 1 15,45 17,90 19,80 21,28
 zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270 C vodík 2 mn m při teplotě 253 C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m organické látky při teplotě 25
zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270 C vodík 2 mn m při teplotě 253 C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m organické látky při teplotě 25
TEORIE NETKANÝCH TEXTILIÍ. Kapky Kapilární délka. Simulace pomocí Isingova modelu. 7.přednáška
 Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška ÚVOD
 2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
Měření povrchového napětí
 Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
III. STRUKTURA A VLASTNOSTI PLYNŮ
 III. STRUKTURA A VLASTNOSTI PLYNŮ 3.1 Ideální plyn a) ideální plyn model, předpoklady: 1. rozměry molekul malé (ve srovnání se střední vzdáleností molekul). molekuly na sebe navzálem silově nepůsobí (mimo
III. STRUKTURA A VLASTNOSTI PLYNŮ 3.1 Ideální plyn a) ideální plyn model, předpoklady: 1. rozměry molekul malé (ve srovnání se střední vzdáleností molekul). molekuly na sebe navzálem silově nepůsobí (mimo
1 Analytická geometrie
 1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
Kvantitativní fázová analýza
 Kvantitativní fázová analýza Kvantitativní rentgenová (fázová) analýza Založena na měření intenzity charakteristických linií. Intenzita je ovlivněna: strukturou minerálu a interferencemi uspořádáním aparatury
Kvantitativní fázová analýza Kvantitativní rentgenová (fázová) analýza Založena na měření intenzity charakteristických linií. Intenzita je ovlivněna: strukturou minerálu a interferencemi uspořádáním aparatury
Interakce mezi kapalinou a vlákenným materiálem
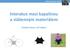 Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Sorpční vlastnosti vláken. Základní pojmy Porózita Sorpční izotermy Sorpce vody Difúze
 Sorpční vlastnosti vláken Základní pojmy Porózita Sorpční izotermy Sorpce vody Difúze Povrchové síly Tělesa-----Molekuly Vzdálenost D r Volná energie interakce W w Síly: 6 W = U * A/ D, U rozměr těles
Sorpční vlastnosti vláken Základní pojmy Porózita Sorpční izotermy Sorpce vody Difúze Povrchové síly Tělesa-----Molekuly Vzdálenost D r Volná energie interakce W w Síly: 6 W = U * A/ D, U rozměr těles
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2 (3) kde S je plocha zdroje. Protože jas zdroje není závislý na směru, lze vztah (5) přepsat do tvaru:
 Pracovní úkol 1. Pomocí fotometrického luxmetru okalibrujte normální žárovku (stanovte její svítivost). Pro určení svítivosti normální žárovky (a její chyby) vyneste do grafu závislost osvětlení na převrácené
Pracovní úkol 1. Pomocí fotometrického luxmetru okalibrujte normální žárovku (stanovte její svítivost). Pro určení svítivosti normální žárovky (a její chyby) vyneste do grafu závislost osvětlení na převrácené
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ.
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ. Protokol o provedeném měření Druh měření Měření vodivosti elektrolytu číslo úlohy 2 Měřený předmět Elektrolyt Měřil Jaroslav ŘEZNÍČEK třída
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ. Protokol o provedeném měření Druh měření Měření vodivosti elektrolytu číslo úlohy 2 Měřený předmět Elektrolyt Měřil Jaroslav ŘEZNÍČEK třída
Samonosné optické kabely teorie a praxe
 Optical Fibre Apparatus Samonosné optické kabely teorie a praxe Brno, 2010 Pavel Dubský OFA s.r.o. pdubsky@ofacom.cz, 603 516 694 1. Úvod Obsah 2. Teorie tahové namáhání, průvěs samonosných optických kabelů
Optical Fibre Apparatus Samonosné optické kabely teorie a praxe Brno, 2010 Pavel Dubský OFA s.r.o. pdubsky@ofacom.cz, 603 516 694 1. Úvod Obsah 2. Teorie tahové namáhání, průvěs samonosných optických kabelů
Mezimolekulové interakce
 Mezimolekulové interakce Interakce molekul reaktivně vzniká či zaniká kovalentní vazba překryv elektronových oblaků, mění se vlastnosti nereaktivně vznikají molekulové komplexy slabá, nekovalentní, nechemická,
Mezimolekulové interakce Interakce molekul reaktivně vzniká či zaniká kovalentní vazba překryv elektronových oblaků, mění se vlastnosti nereaktivně vznikají molekulové komplexy slabá, nekovalentní, nechemická,
1. Určete závislost povrchového napětí σ na objemové koncentraci c roztoku etylalkoholu ve vodě odtrhávací metodou.
 1 Pracovní úkoly 1. Určete závislost povrchového napětí σ na objemové koncentraci c roztoku etylalkoholu ve vodě odtrhávací metodou. 2. Sestrojte graf této závislosti. 2 Teoretický úvod 2.1 Povrchové napětí
1 Pracovní úkoly 1. Určete závislost povrchového napětí σ na objemové koncentraci c roztoku etylalkoholu ve vodě odtrhávací metodou. 2. Sestrojte graf této závislosti. 2 Teoretický úvod 2.1 Povrchové napětí
Struktura a vlastnosti kapalin
 I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Laboratorní práce č. 7 Struktura a vlastnosti kapalin
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Laboratorní práce č. 7 Struktura a vlastnosti kapalin
13. cvičení z Matematické analýzy 2
 . cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
. cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
12. Struktura a vlastnosti pevných látek
 12. Struktura a vlastnosti pevných látek Osnova: 1. Látky krystalické a amorfní 2. Krystalová mřížka, příklady krystalových mřížek 3. Poruchy krystalových mřížek 4. Druhy vazeb mezi atomy 5. Deformace
12. Struktura a vlastnosti pevných látek Osnova: 1. Látky krystalické a amorfní 2. Krystalová mřížka, příklady krystalových mřížek 3. Poruchy krystalových mřížek 4. Druhy vazeb mezi atomy 5. Deformace
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Vysokoúčinná kapalinová chromatografie
 Vysokoúčinná kapalinová chromatografie HPLC High Performance Liquid Chromatography Vysokoúčinná...X... Vysoceúčinná kapalinová chromatografie RRLC Rapid Resolution Liquid Chromatography Rychle rozlišovací
Vysokoúčinná kapalinová chromatografie HPLC High Performance Liquid Chromatography Vysokoúčinná...X... Vysoceúčinná kapalinová chromatografie RRLC Rapid Resolution Liquid Chromatography Rychle rozlišovací
Výměnné pobyty s US vysokými školami
 Výměnné pobyty s US vysokými školami Hlavní řešitel: prof. RNDr. David Lukáš, CSc. Fakulta textilní, Katedra netkaných textilií a nanovlákenných materiálů Závěrečný seminář k rozvojovým programům MŠMT
Výměnné pobyty s US vysokými školami Hlavní řešitel: prof. RNDr. David Lukáš, CSc. Fakulta textilní, Katedra netkaných textilií a nanovlákenných materiálů Závěrečný seminář k rozvojovým programům MŠMT
LOGO. Struktura a vlastnosti plynů Ideální plyn
 Struktura a vlastnosti plynů Ideální plyn Ideální plyn Protože popsat chování plynů je nad naše možnosti, zavádíme zjednodušený model tzv. ideálního plynu, který má tyto vlastnosti: Částice ideálního plynu
Struktura a vlastnosti plynů Ideální plyn Ideální plyn Protože popsat chování plynů je nad naše možnosti, zavádíme zjednodušený model tzv. ideálního plynu, který má tyto vlastnosti: Částice ideálního plynu
Měření tíhového zrychlení matematickým a reverzním kyvadlem
 Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
Adhezní síly. Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008
 Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Karel Lemr. web: Karel Lemr Fotonové páry 1 / 26
 Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází
 2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
2 Tokové chování polymerních tavenin reologické modely
 2 Tokové chování polymerních tavenin reologické modely 2.1 Reologie jako vědní obor Polymerní materiály jsou obvykle zpracovávány v roztaveném stavu, proto se budeme v prvé řadě zabývat jejich tokovým
2 Tokové chování polymerních tavenin reologické modely 2.1 Reologie jako vědní obor Polymerní materiály jsou obvykle zpracovávány v roztaveném stavu, proto se budeme v prvé řadě zabývat jejich tokovým
