Interakce mezi kapalinou a vlákenným materiálem
|
|
|
- Romana Urbanová
- před 6 lety
- Počet zobrazení:
Transkript
1 3. přednáška Interakce mezi kapalinou a vlákenným materiálem
2 Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní umístění strukturní komponenty v celém systému). math.pppst.com
3 Stejný materiál se může ve vztahu ke smáčení chovat drasticky jinak ve formě filmu, vlákna, svazku vláken neo vlákenného materiálu (textilie). Podmínky dokonalého smáčení: ) ovninného povrchu ) Jednoho vlákna 3) Svazku vláken S S 0. e. S > E n γ n
4 KAPALINA NA POVCHU VLÁKNA Povrch kapalinového tělesa - ol VLÁKNO NEKUHOVÉHO PŮŘEZU Povrch vlákna - aol W f W W f = aol P W = aol KP + ol S >((-a)/a) DOKONALÉ SMÁČENÍ nekruhového povrchu vlákna Harkinsonův roztírací koeficient záporný. Čím členitější (větší) je povrch vlákna tím větší ochota ke smáčení existuje.
5 KONTAKTNÍ ÚHEL DSNÝCH POVCHŮ Zdánlivý kontaktní úhel drsných povrchů * závisí na skutečném úhlu smáčení (Youngův kontaktní úhel) a míře drsnosti r cos * = r cos Povrchy kdy <90 ===drsné povrchy smáčí lépe než rovné Povrchy kdy >90 ===drsné povrchy smáčí hůře než rovné
6 Superhydrofóní a superhydrofilní povrchy Supernesmáčivé a supersmáčivé povrchy Jsou toto hraniční hodnoty pro popis smáčení povrchů kapalinou? 0 θ 80 Superhydrofoicita Nano Today (0) 6, θ = 80 Materiály se ale stejně chovají jinak. Jeden je odpudivější než druhý ke stejné kapalině.???? PŘÍODA NEMÁ HANICE NA 0 A 80.
7 Superhydrofóní a superhydrofilní povrchy Supernesmáčivé a supersmáčivé povrchy = S γ +
8 Laplaceův tlak Kapilární tlak odvození
9 Laplaceův tlak Při zakřivení povrchu půsoí povrchová vrstva na kapalinu tlakem, který se přičítá k tlaku, jímž y vrstva na kapalinu půsoila při rovinném povrchu. V literatuře je tlak při rovinném povrchu kapaliny nazýván tlakem kohezním a přídavný tlak, který vzniká zakřivením povrchu je nazýván tlakem kapilárním. Kapilární tlak je ale také často označován jako tlak Laplaceův Pozor změna značení povrchového napětí = Vypočtení Laplaceova tlaku vychází z povrchového napětí. Předpokládejme nejprve, že povrch je válcový a uvažujeme o silách, které půsoí na plošný prvek omezený dvěma površkami délky dl a dvěma křivkami délky dl d= dl d Zavedeme-li poloměr křivosti plochy, pak dl = d
10 Při oecně zakřiveném povrchu můžeme v každém jeho odě vést dva k soě kolmé normálové řezy, v nichž má plocha největší a nejmenší poloměr křivosti a. Platí pak pro každou dvojici rovnoěžných stran plošného prvku stejná úvaha jako u válcové plochy. Tlak p, způsoený zakřivením o poloměru křivosti, je p =/, a tlak p, vzuzený zakřivením o poloměru křivosti, je p =/. Kapilární tlak p, který vzniká u oecně zakřiveného povrchu, je pak součtem oou tlaků p a p Pozor změna značení povrchového napětí = p.
11 Tvarové změny přecházející do povrchových charakteristik je možné ukázat na Laplaceově tlaku (Laplace pressure), kde tlak v kapce (či ulince) je úměrný její charakteristické křivosti. Laplaceův tlak je tlakem přídavným způsoeným zakřivením povrchu. Na rovný povrch kapaliny půsoý tlak kohezní, zakřivením povrchu je k němu potřea připočítat ještě tlak Laplaceův. Jedná se o tlak, kterým povrchová vrstva půsoí na kapalinu pod ní = Kohezní + kapilární.
12 Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna - podmínka dokonalého smáčení při započítání Laplaceova tlaku
13 Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁNÍHO) TLAKU t e =e+ Síly půsoící podél osy vlákna p = P kp = kp t. = (+e)
14 Kapalinové těleso na povrchu vlákna se nachází v rovnováze za následující podmínky rovnováhy sil kp p t Pozn.: Kapalinové těleso se konvexní, znaménko u poloměru křivosti v Laplaceově tlaku je záporné == kapalina má tendenci se rozprostírat po vlákně== t půsoí směrem ven z kapalinového tělesa
15 POZNÁMKA kapilární tlak capillary pressure (synonymum Laplaceův tlak) ozdíl tlaků na konkávní a konvexní straně zakřiveného fázového rozhraní, způsoený mezifázovým napětím (Laplaceova-Youngova rovnice). 00/hesla/laplaceova-youngova_rovnice.html
16 POZNÁMKA kapilární tlak pro konkávní a konvexní tělesa p = ± γ flatworldknowledge.larducket.org Správný zápis pro kapalinová tělesa v kruhových kapilárách A concave meniscus (A) indicated that the molecules of the liquid have a stronger attraction to the material of the container (adhesion) than to each other (cohesion). A convex meniscus (B) indicates the molecules have a stronger attraction to each other than to the material of the container.
17 POZNÁMKA kapilární tlak pro konkávní a konvexní tělesa p = + γ Kapilární deprese Srážení, nasávání kapaliny a srážení vláken k soě p = γ Kapilární elevace ozprostírání kapalina, vzdalování vláken od see
18 POZNÁMKA kapilární tlak pro konkávní a konvexní tělesa ozprostírání kapalina, vzdalování vláken od see Srážení, nasávání kapaliny a srážení vláken k soě
19 Kapalinové těleso na povrchu vlákna se nachází v rovnováze za následující podmínky rovnováhy sil kp p t
20 t p kp p kp S ovnici výše vydělíme výrazem a vyjádříme pomocí Harkinsonova roztíracího koeficientu Vztah udeme dále upravovat za předpokladu, že kapalinové těleso je válcovité. Za tohoto předpokladu ude hodnota nekonečně velká. 0 ) ( ) ( S Z této rovnice je patrné, že hodnota roztíracího koeficientu S je pro studovaný případ kapalinového tělesa vždy kladná.
21 Vyjádříme-li poloměr kapalinového tělesa pomocí poloměru vlákna a tloušťky kapalinového filmu e, dostaneme po řadě matematických úprav podmínku dokonalého smáčení jednoho vlákna ve tvaru S e ( e) Liší o podmínky dokonalého smáčení z minulé přednášky, protože zde se započítává i vliv Laplaceova tlaku. yzikální podstata odlišnosti vztahů podmínky dokonalého smáčení jednoho vlákna: Hodnoty e po započítání kapilárního tlaku mohou naývat větších hodnot než ez započítání Laplaceova tlaku při zachování stejných podmínek pro danou situaci(hodnota, povrchová napětí atd.). Samozřejmě uvažujeme o situaci rovnovážného stavu. STEJNÉ PODMÍNKA == při započítání kapilárních tlaků === e mohou naývat v rovnovážných stavech větších hodnot
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
Měření povrchového napětí kapalin a kontaktních úhlů
 2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
Interakce mezi kapalinou a vlákenným materiálem
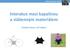 Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška. TNT smáčení úvod. Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL
 2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce
 Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Interakce mezi kapalinou a vlákenným materiálem
 7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
Vlastnosti kapalin. Povrchová vrstva kapaliny
 Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
LOGO. Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází
 2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Adhezní síly. Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008
 Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Adhezní síly v kompozitních materiálech
 Adhezní síly v kompozitních materiálech Obsah přednášky Adhezní síly, jejich původ a velikost. Adheze a smáčivost. Metoty určování adhezních sil. Adhezní síly na rozhraní Mezi fázemi v kompozitu jsou rozhraní
Adhezní síly v kompozitních materiálech Obsah přednášky Adhezní síly, jejich původ a velikost. Adheze a smáčivost. Metoty určování adhezních sil. Adhezní síly na rozhraní Mezi fázemi v kompozitu jsou rozhraní
1. Molekulová stavba kapalin
 1 Molekulová stavba kapalin 11 Vznik kapaliny kondenzací Plyn Vyjdeme z plynu Plyn je soustava molekul pohybujících se neuspořádaně všemi směry Pohybová energie molekul převládá nad energii polohovou Každá
1 Molekulová stavba kapalin 11 Vznik kapaliny kondenzací Plyn Vyjdeme z plynu Plyn je soustava molekul pohybujících se neuspořádaně všemi směry Pohybová energie molekul převládá nad energii polohovou Každá
Chemie povrchů verze 2013
 Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
STRUKTURA A VLASTNOSTI KAPALIN
 STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
Měření povrchového napětí
 Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
TEORIE NETKANÝCH TEXTILIÍ. Kapky Kapilární délka. Simulace pomocí Isingova modelu. 7.přednáška
 Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Adhezní síly v kompozitech
 Adhezní síly v kompozitech Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vazby na rozhraní
Adhezní síly v kompozitech Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vazby na rozhraní
Speciální aplikace poznatků ze smáčení. Vzlínání do vlákenných materiálů TNT. Eva Kuželová Košťáková KCH, FP, TUL
 Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
KVADRATICKÉ FUNKCE. + bx + c, největší hodnotu pro x = a platí,
 KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
STRUKTURA PEVNÝCH LÁTEK A KAPALIN
 STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje
 Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
4. Matematická kartografie
 4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika
 Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
3.3 Částicová stavba látky
 3.3 Částicová stavba látky Malé (nejmenší) částice látky očekávali nejprve filozofové (atomisté) a nazvali je atomy (z řeckého atomos = nedělitelný) starověké Řecko a Řím. Mnohem později chemici zjistili,
3.3 Částicová stavba látky Malé (nejmenší) částice látky očekávali nejprve filozofové (atomisté) a nazvali je atomy (z řeckého atomos = nedělitelný) starověké Řecko a Řím. Mnohem později chemici zjistili,
JEVY NA ROZHRANÍ PEVNÉHO TĚLESA A KAPALINY
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Fázová rozhraní a mezifázová energie
 Fázová ozhaní a mezifázová enegie 1/15 duhy: } l/ g {{ l/ } l mobilní s/g s/l s/s povch koule = 4π 2 Příklad. Kolik % molekul vody je na povchu kapičky mlhy o půměu 200 nm (hanice viditelnosti optickým
Fázová ozhaní a mezifázová enegie 1/15 duhy: } l/ g {{ l/ } l mobilní s/g s/l s/s povch koule = 4π 2 Příklad. Kolik % molekul vody je na povchu kapičky mlhy o půměu 200 nm (hanice viditelnosti optickým
5. Statika poloha střediska sil
 5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
Řešení elektrických sítí pomocí Kirchhoffových zákonů
 4.2.8 Řešení elektrických sítí pomocí Kirchhoffových zákonů Předpoklady: 427 Pedagogická poznámka: Hodina obsahuje čtyři obvody. Fyzikálně mezi nimi není velký rozdíl, druhé dva jsou však podstatně obtížnější
4.2.8 Řešení elektrických sítí pomocí Kirchhoffových zákonů Předpoklady: 427 Pedagogická poznámka: Hodina obsahuje čtyři obvody. Fyzikálně mezi nimi není velký rozdíl, druhé dva jsou však podstatně obtížnější
4. Kolmou tlakovou sílu působící v kapalině na libovolně orientovanou plochu S vyjádříme jako
 1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid
 Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Adheze - pokračování
 2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 R (4.1)
 4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 4.1 Povrchové a mezifázové napětí Mezi nejpoužívanější metody pro stanovení povrchového a mezifázového napětí
4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 4.1 Povrchové a mezifázové napětí Mezi nejpoužívanější metody pro stanovení povrchového a mezifázového napětí
DUM č. 12 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Interakce mezi kapalinou a vlákenným materiálem
 5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
Řešení elektrických sítí pomocí Kirchhoffových zákonů
 4.2.19 Řešení elektrických sítí pomocí Kirchhoffových zákonů Předpoklady: 4218 Pedagogická poznámka: Hodina obsahuje čtyři obvody. Fyzikálně mezi nimi není velký rozdíl, druhé dva jsou však podstatně obtížnější
4.2.19 Řešení elektrických sítí pomocí Kirchhoffových zákonů Předpoklady: 4218 Pedagogická poznámka: Hodina obsahuje čtyři obvody. Fyzikálně mezi nimi není velký rozdíl, druhé dva jsou však podstatně obtížnější
9. Geometrická optika
 9. Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = křivka (často přímka), podél níž se šíří světlo, jeho energie
9. Geometrická optika 1 Popis pomocí světelných paprsků těmi se šíří energie a informace, zanedbává vlnové vlastnosti světla světelný paprsek = křivka (často přímka), podél níž se šíří světlo, jeho energie
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
2 Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost kapalin 7
 Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Nanomateriály a jejich charakterizace (2+0), navazující Mrg. 1 roč. ZS, CN349, Čt 9-11
 Nanomateriály a jejich charakterizace (2+0), navazující Mrg. 1 roč. ZS, CN349, Čt 9-11 2. Přednáška, 1.11.2012 Studium povrchových vlastností nanostrukturovaných materiálů (ablace materiálu, goniometrie,
Nanomateriály a jejich charakterizace (2+0), navazující Mrg. 1 roč. ZS, CN349, Čt 9-11 2. Přednáška, 1.11.2012 Studium povrchových vlastností nanostrukturovaných materiálů (ablace materiálu, goniometrie,
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Kde 1... vzduch (plyn) 2... kapalina 3... stěna
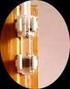 Příčinou povrchového napětí jsou kohezní mezimolekulární síly, které mají velice malý dosah. Uvnitř kapaliny se tyto síly vyrovnají, ale na povrchu se molekulová rovnováha naruší. Síly působí ve směru
Příčinou povrchového napětí jsou kohezní mezimolekulární síly, které mají velice malý dosah. Uvnitř kapaliny se tyto síly vyrovnají, ale na povrchu se molekulová rovnováha naruší. Síly působí ve směru
7 Hallůvjevvkovuapolovodiči
 Zadání 7 Hallůvjevvkovuapolovodiči 1. Změřte Hallův koeficient pro kov a polovodič při laboratorní teplotě. 2. Změřte měrnou vodivost obou vzorků. 3. Pro několik hodnot proudu a magnetické indukce ověřte,
Zadání 7 Hallůvjevvkovuapolovodiči 1. Změřte Hallův koeficient pro kov a polovodič při laboratorní teplotě. 2. Změřte měrnou vodivost obou vzorků. 3. Pro několik hodnot proudu a magnetické indukce ověřte,
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Příklady z teoretické mechaniky pro domácí počítání
 Příklady z teoretické mechaniky pro domácí počítání Doporučujeme spočítat příklady za nejméně 30 bodů. http://www.physics.muni.cz/~tomtyc/mech-prik.ps http://www.physics.muni.cz/~tomtyc/mech-prik.pdf 1.
Příklady z teoretické mechaniky pro domácí počítání Doporučujeme spočítat příklady za nejméně 30 bodů. http://www.physics.muni.cz/~tomtyc/mech-prik.ps http://www.physics.muni.cz/~tomtyc/mech-prik.pdf 1.
Kapka kapaliny na hladině kapaliny
 JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Povrchové napětí KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI
 KATEDRA EXPERIMETÁLÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UIVERZITY PALACKÉHO V OLOMOUCI Fyzikální praktikum z molekulové fyziky a termodynamiky Povrchové napětí Úvod Molekuly kapaliny se vzájemně přitahují kohezními
KATEDRA EXPERIMETÁLÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UIVERZITY PALACKÉHO V OLOMOUCI Fyzikální praktikum z molekulové fyziky a termodynamiky Povrchové napětí Úvod Molekuly kapaliny se vzájemně přitahují kohezními
ρ = 0 (nepřítomnost volných nábojů)
 Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Maticová optika. Lenka Přibylová. 24. října 2010
 Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Zrcadla Zobrazení zrcadlem Zrcadla jistě všichni znáte z každodenního života ráno se do něj v koupelně díváte,
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Zrcadla Zobrazení zrcadlem Zrcadla jistě všichni znáte z každodenního života ráno se do něj v koupelně díváte,
Kvadratické rovnice. Řešení kvadratických rovnic. Kvadratická rovnice bez lineárního členu. Příklad 1:
 Kvadratické rovnice V zadání lineární rovnice se může vyskytovat neznámá ve vyšší než první mocnině. Vždy ale při úpravě tato neznámá ve vyšší než první mocnině zmizí, odečte se, protože se vyskytuje na
Kvadratické rovnice V zadání lineární rovnice se může vyskytovat neznámá ve vyšší než první mocnině. Vždy ale při úpravě tato neznámá ve vyšší než první mocnině zmizí, odečte se, protože se vyskytuje na
Skupenské stavy látek. Mezimolekulární síly
 Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Název: Čočková rovnice
 Název: Čočková rovnice Autor: Mgr. Lucia Klimková Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět (mezipředmětové vztahy) : Fyzika (Matematika) Tematický celek: Optika Ročník: 5. (3.
Název: Čočková rovnice Autor: Mgr. Lucia Klimková Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět (mezipředmětové vztahy) : Fyzika (Matematika) Tematický celek: Optika Ročník: 5. (3.
Teoretické otázky z hydromechaniky
 Teoretické otázky z hydromechaniky 1. Napište vztah pro modul pružnosti kapaliny (+ popis jednotlivých členů a 2. Napište vztah pro Newtonův vztah pro tečné napětí (+ popis jednotlivých členů a 3. Jaká
Teoretické otázky z hydromechaniky 1. Napište vztah pro modul pružnosti kapaliny (+ popis jednotlivých členů a 2. Napište vztah pro Newtonův vztah pro tečné napětí (+ popis jednotlivých členů a 3. Jaká
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno
 Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno JAMES WATT 19.1.1736-19.8.1819 Termodynamika principy, které vládnou přírodě Obsah přednášky Vysvětlení základních
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno JAMES WATT 19.1.1736-19.8.1819 Termodynamika principy, které vládnou přírodě Obsah přednášky Vysvětlení základních
KATEDRA FYZIKY VŠB-TU OSTRAVA
 Stdent Skpina/Osob. číslo KATEDA FYZIKY VŠB-TU OSTAVA NÁZEV PÁCE Měření povrcovéo napětí z kapilární elevace Číslo práce 4 Datm Spolpracoval Podpis stdenta: Cíle měření: Změřit odnoty povrcovéo napětí
Stdent Skpina/Osob. číslo KATEDA FYZIKY VŠB-TU OSTAVA NÁZEV PÁCE Měření povrcovéo napětí z kapilární elevace Číslo práce 4 Datm Spolpracoval Podpis stdenta: Cíle měření: Změřit odnoty povrcovéo napětí
Skořepinové konstrukce. tloušťka stěny h a, b, c
 Skořepinové konstrukce skořepina střední plocha a b tloušťka stěny h a, b, c c Různorodé technické aplikace skořepinových konstrukcí Mezní stavy skořepinových konstrukcí Ztráta stability zhroucení konstrukce
Skořepinové konstrukce skořepina střední plocha a b tloušťka stěny h a, b, c c Různorodé technické aplikace skořepinových konstrukcí Mezní stavy skořepinových konstrukcí Ztráta stability zhroucení konstrukce
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT
 VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
DERIVACE. ln 7. Urči, kdy funkce roste a klesá a dále kdy je konkávní a
 DERIVACE 1. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x 3. Zderivuj funkci y = 3 e sin2 (x 2 ) 4. Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y = cos2 x
DERIVACE 1. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x 3. Zderivuj funkci y = 3 e sin2 (x 2 ) 4. Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y = cos2 x
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
Tvorba perliček (beads) PERLIČKOVÝ EFEKT. Zvýšení koncentrace roztoku vede k odstranění perliček.
 Tvorba perliček (beads) PERLIČKOVÝ EFEKT Zvýšení koncentrace roztoku vede k odstranění perliček. Tvorba perliček (beads) PERLIČKOVÝ EFEKT Snížení rychlosti dodávání roztoku vede ke zmenšení perliček Pouze
Tvorba perliček (beads) PERLIČKOVÝ EFEKT Zvýšení koncentrace roztoku vede k odstranění perliček. Tvorba perliček (beads) PERLIČKOVÝ EFEKT Snížení rychlosti dodávání roztoku vede ke zmenšení perliček Pouze
7. Aplikace derivace 7E. Křivky. 7E. Křivky
 7E. Křivky Derivace nacházejí uplatnění také při studiu křivek. Obrazně řečeno křivka v rovině je množina bodů, která vznikne pohybem pera po papíře. Předpokládáme přitom, že hrot pera je stále v kontaktu
7E. Křivky Derivace nacházejí uplatnění také při studiu křivek. Obrazně řečeno křivka v rovině je množina bodů, která vznikne pohybem pera po papíře. Předpokládáme přitom, že hrot pera je stále v kontaktu
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI
 CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
rtuť při 0 o C = 470 mn m 1 15,45 17,90 19,80 21,28
 zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270 C vodík 2 mn m při teplotě 253 C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m organické látky při teplotě 25
zkapalněné plyny - velmi nízké; např. helium 0354 mn m při teplotě 270 C vodík 2 mn m při teplotě 253 C roztavené kovy - velmi vysoké; např. měď při teplotě tání = 00 mn m organické látky při teplotě 25
9. Je-li cos 2x = 0,5, x 0, π, pak tgx = a) 3. b) 1. c) neexistuje d) a) x ( 4, 4) b) x = 4 c) x R d) x < 4. e) 3 3 b
 008 verze 0A. Řešeními nerovnice x + 4 0 jsou právě všechna x R, pro která je x ( 4, 4) b) x = 4 c) x R x < 4 e) nerovnice nemá řešení b. Rovnice x + y x = je rovnicí přímky b) dvojice přímek c) paraboly
008 verze 0A. Řešeními nerovnice x + 4 0 jsou právě všechna x R, pro která je x ( 4, 4) b) x = 4 c) x R x < 4 e) nerovnice nemá řešení b. Rovnice x + y x = je rovnicí přímky b) dvojice přímek c) paraboly
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Hydromechanické procesy Hydrostatika
 Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Optimalizace vláknového kompozitu
 Optimalizace vláknového kompozitu Bc. Jan Toman Vedoucí práce: doc. Ing. Tomáš Mareš, Ph.D. Abstrakt Optimalizace trubkového profilu z vláknového kompozitu při využití Timošenkovy hypotézy. Hledání optimálního
Optimalizace vláknového kompozitu Bc. Jan Toman Vedoucí práce: doc. Ing. Tomáš Mareš, Ph.D. Abstrakt Optimalizace trubkového profilu z vláknového kompozitu při využití Timošenkovy hypotézy. Hledání optimálního
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI. Jaroslav Krucký, PMB 22
 Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Molekulové jevy Molekula Mezimolekulové síly Koheze a adheze Kapalina Povrchové napětí Povrchová energie Molekulový tlak Kapilární tlak
 Molekulové jevy Molekula Mezimolekulové síly Dosah molekulových sil Lenardův-Jonesův potenciál Druhy mezimolekulových potenciálních energií Koheze a adheze Koheze Adheze Kapalina Struktura kapalin Vlastnosti
Molekulové jevy Molekula Mezimolekulové síly Dosah molekulových sil Lenardův-Jonesův potenciál Druhy mezimolekulových potenciálních energií Koheze a adheze Koheze Adheze Kapalina Struktura kapalin Vlastnosti
GEOMETRICKÁ OPTIKA. Znáš pojmy A. 1. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci.
 Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Přímková a rovinná soustava sil
 Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
ANALÝZA KONSTRUKCÍ. 5. přednáška
 ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů. = 30 s.
 Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
Sestavení pohybové rovnosti jednoduchého mechanismu pomocí Lagrangeových rovností druhého druhu
 Sestavení pohybové rovnosti jednoduchého mechanismu pomocí Lagrangeových rovností druhého druhu Václav Čibera 12. února 2009 1 Motivace Na obrázku 1 máme znázorněný mechanický systém, který může představovat
Sestavení pohybové rovnosti jednoduchého mechanismu pomocí Lagrangeových rovností druhého druhu Václav Čibera 12. února 2009 1 Motivace Na obrázku 1 máme znázorněný mechanický systém, který může představovat
4EK213 LINEÁRNÍ MODELY
 4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 Mgr. Sekničková Jana, Ph.D. 2. PŘEDNÁŠKA MATEMATICKÝ MODEL ÚLOHY LP Mgr. Sekničková Jana, Ph.D. 2 OSNOVA PŘEDNÁŠKY Obecná formulace MM Množina
4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 Mgr. Sekničková Jana, Ph.D. 2. PŘEDNÁŠKA MATEMATICKÝ MODEL ÚLOHY LP Mgr. Sekničková Jana, Ph.D. 2 OSNOVA PŘEDNÁŠKY Obecná formulace MM Množina
