Interakce mezi kapalinou a vlákenným materiálem
|
|
|
- Michaela Tesařová
- před 6 lety
- Počet zobrazení:
Transkript
1 3. přednáška Interakce mezi kapalinou a vlákenným materiálem
2 OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i sekundární (molekulární síly) mají dosah od 0, do nm. Adhezní síly až 00nm == vyjímečnost adhezních sil spočívá kolektivní chování molekul je odlišné od silových projevů izolovaných molekul. Povrchové charakteristiky (povrchové energie) jsou spojeny nejen s pojením vlákenných vrstev při výrobě netkaných textilií.
3 OPAKOVÁNÍ Další příklady spojení povrchových charakteristik materiálů s netkanými textiliemi: Naplavování dispergace vláken v kapalině závisí na povrchových vlastnostech vláken a kapaliny Výroba mokrých kapesníčků povrchové charakteristiky vláken, struktura vlákenného materiálu a povrchové vlastnosti kapaliny ovlivňují dokonalé proniknutí celým objemem. Elektrostatické zvlákňování do kapaliny povrchové napětí vznikajících vláken a kapaliny nad kolektorem Y. Yokoyama et al. / Materials Letters 63 (009)
4 Interakce mezi kapalinou a vlákenným materiálem PODMÍNKY DOKONALÉHO SMÁČENÍ
5 Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní umístění strukturní komponenty v celém systému). math.pppst.com
6 Tvarové změny přecházející do povrchových charakteristik je možné ukázat na Laplaceově tlaku (Laplace pressure), kde tlak v kapce (či bublince) je úměrný její charakteristické křivosti.
7 Stejný materiál se může ve vztahu ke smáčení chovat drasticky jinak ve formě filmu, vlákna, svazku vláken nebo vlákenného materiálu (textilie). Podmínky dokonalého smáčení: ) Rovninného povrchu ) Jednoho vlákna 3) Svazku vláken
8 OPAKOVÁNÍ Povrchová energie připadající na jednotkovou plochu je rovna povrchovému napětí W= Youngova rovnice P cos KP,
9 ) Podmínka dokonalého smáčení ROVINNÉHO POVRCHU Dokonalé smáčení: Kontaktní úhel = 0 O dokonalém smáčení rovinné pevné látky hovoříme v případě, když úhel smáčení je nulový. Z Youngovy rovnice pro tento případ plyne: 0, p kp
10 ) Podmínka dokonalého smáčení ROVINNÉHO POVRCHU Harkinsonův roztírací koeficient S p kp Zápis pomocí Harkinosonova roztíracího koeficientu S p kp 0, S 0.
11 ) Podmínka dokonalého smáčení JEDNOHO VLÁKNA Vlákno o poloměru b pokrývá vrstva kapaliny o tloušťce e a délce L. Obrázek zachycuje případ dokonalého smáčení vlákna. Suché vlákno Smočené vlákno
12 ) Podmínka dokonalého smáčení JEDNOHO VLÁKNA K dokonalému smáčení vlákna dojde tehdy, když celková povrchová energie W vnějšího povrchu filmu kapaliny a povrchu mezi vláknem a kapalinou připadajícím na délku vlákna L bude MENŠÍ než povrchová energie téže délky suchého vlákna W f W f W
13 ) Podmínka dokonalého smáčení JEDNOHO VLÁKNA ; Pro povrchové energie W a W f platí Vlákno o poloměru b pokrývá vrstva kapaliny o tloušťce e a délce L. W f bl p W bl b e L. kp e Wf W Lb p kp 0. b
14 ) Podmínka dokonalého smáčení JEDNOHO VLÁKNA Úpravou nerovnosti využívající Harkinsonova roztíracího koeficientu S získáme podmínku pro dokonalé smáčení vlákna ve tvaru: S e. b
15 Dokonalé smáčení rovného povrchu X Dokonalé smáčení jednoho vlákna S 0. S e. b Porovnáním podmínek pro dokonalé smáčení zjistíme, že jednotlivá vlákna jsou méně ochotna smáčet se kapalinou než rovinné útvary vyrobené z téhož materiálu.???
16 ??? Vynikající savost vlákenné hmoty je výsledkem KOLEKTIVNÍHO CHOVÁNÍ SOUBORŮ VLÁKEN A JEJICH SVAZKŮ. Až toto skupinové uspořádání vláken umožňuje vlákenným materiálům předčít vlastnosti rovinných povrchů ochotně vázat velká množství kapaliny.
17 3) Podmínka dokonalého smáčení SVAZKU VLÁKEN Struktura vlákenných materiálů (reprezentovaná zde počtem a poloměry blízkých a paralelně uspořádaných vláken) silně ovlivňuje jejich vlastnosti v procesu smáčení.
18 3) Podmínka dokonalého smáčení SVAZKU VLÁKEN K dokonalému smáčení svazku vláken dojde tehdy, když celková povrchová energie smočených vláken na rozhraní vlákno kapalina a povrchová energie vnějšího povrchu kapalinového tělesa W je MENŠÍ než povrchová energie suchých vláken W f a to na délce L. W f W
19 3) Podmínka dokonalého smáčení SVAZKU VLÁKEN W f W W f = nbl P W = nbl KP + EL
20
21 Svazek sedmi těsně uspořádaných paralelních vláken může být kapalinou dokonale smáčen i v případě, že rovinný útvar ze stejného materiálu není stejnou kapalinou smáčen dokonale. Pro dokonalé smáčení svazku vláken může být Harkinsonův roztírací koeficient S dokonce záporný.
22 Čím více vláken ve svazku bude a čím těsněji tato vlákna budou uspořádána tím více bude svazek ochotný ke smáčení. 9 vláken kruhového průřezu
23 Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní umístění strukturní komponenty v celém systému). VLIV TVARU VLÁKNA NA SMÁČENÍ
24 KAPALINA NA POVRCHU VLÁKNA Povrch kapalinového tělesa - ol VLÁKNO NEKRUHOVÉHO PRŮŘEZU Povrch vlákna - aol W f W W f = aol P W = aol KP + ol S >((-a)/a) DOKONALÉ SMÁČENÍ nekruhového povrchu vlákna Harkinsonův roztírací koeficient záporný. Čím členitější (větší) je povrch vlákna tím větší ochota ke smáčení existuje.
25 KONTAKTNÍ ÚHEL DRSNÝCH POVRCHŮ Zdánlivý kontaktní úhel drsných povrchů * závisí na skutečném úhlu smáčení (Youngův kontaktní úhel) a míře drsnosti r cos * = r cos Povrchy kdy <90 ===drsné povrchy smáčí lépe než rovné Povrchy kdy >90 ===drsné povrchy smáčí hůře než rovné
26
27 Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna - podmínka dokonalého smáčení při započítání Laplaceova tlaku
28 Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU F t b e R =e+b Síly působící podél osy vlákna F p = b P F kp = b kp F t R R. R b F = (b+e)
29 Kapalinové těleso na povrchu vlákna se nachází v rovnováze za následující podmínky rovnováhy sil F kp F F p F t Pozn.: kapalina má tendenci se rozprostírat po vlákně (=0 ) == F t působí směrem ven z kapalinového tělesa (napomáhá rozprostírání) == tlak působící ven z kapalinového tělesa má záporné znaménko.
30 POZNÁMKA kapilární tlak capillary pressure jiná definice (synonymum Laplaceův tlak) Rozdíl tlaků na konkávní a konvexní straně zakřiveného fázového rozhraní, způsobený mezifázovým napětím (Laplaceova-Youngova rovnice). Má-li povrch kapaliny tvar kulového vrchlíku (resp. Koule) o poloměru R, lze pro kapilární tlak psát p=f/s, kde F je velikost výslednice povrchových sil F p, jejíž nenulová velikost je dána právě zakřiveným povrchem kapaliny. Tato výslednice vzniká F díky zakřivení povrchu a působí na kolmý průmět povrchu kapaliny o obsahu S. S F 00/hesla/laplaceova-youngova_rovnice.html
31 POZNÁMKA kapilární tlak pro konkávní a konvexní tělesa p = ± γ R Správný zápis pro kapalinová tělesa v kruhových kapilárách A concave meniscus (A) indicated that the molecules of the liquid have a stronger attraction to the material of the container (adhesion) than to each other (cohesion). A convex meniscus (B) indicates the molecules have a stronger attraction to each other than to the material of the container. F S S F flatworldknowledge.lardbucket.org
32 POZNÁMKA kapilární tlak pro konkávní a konvexní kapalinová tělesa uvnitř kruhové kapiláry p = + γ R Konvexní tvar povrchu kapaliny Kapilární deprese Kapilární tlak směřuje dovnitř kapalinového tělesa - kladné znaménko Konvexní meniskus ukazuje, že molekuly kapaliny mají silnější přitažlivost k sobě navzájem (koheze) než k materiálu kapiláry (adheze). p = γ R Kapilární elevace Konkávní tvar povrchu kapaliny Kapilární tlak směřuje ven z kapalinového tělesa záporné znaménko Konkávní meniskus ukazuje, že molekuly kapaliny mají silnější přitažlivost k materiálu kapiláry (adheze) než k sobě navzájem (soudržnost - koheze).
33 Kapalinové těleso na povrchu vlákna se nachází v rovnováze za následující podmínky rovnováhy sil F kp F F p F t
34 t p kp F F F F b R R R b R b p kp b R R R b R b S Rovnici výše vydělíme výrazem b a vyjádříme pomocí Harkinsonova roztíracího koeficientu Vztah budeme dále upravovat za předpokladu, že kapalinové těleso je válcovité. Za tohoto předpokladu bude hodnota R nekonečně velká. 0 ) ( ) ( R b b R br b br R br b R S R =e+b b e Z této rovnice je patrné, že hodnota roztíracího koeficientu S je pro studovaný případ kapalinového tělesa vždy kladná.
35 Vyjádříme-li poloměr kapalinového tělesa R pomocí poloměru vlákna b a tloušťky kapalinového filmu e, dostaneme po řadě matematických úprav podmínku dokonalého smáčení jednoho vlákna ve tvaru e b S e b( b e) R =e+b Liší o podmínky dokonalého smáčení z minulé přednášky, protože zde se započítává i vliv Laplaceova tlaku. Fyzikální podstata odlišnosti vztahů podmínky dokonalého smáčení jednoho vlákna: Hodnoty e po započítání kapilárního tlaku mohou nabývat větších hodnot než bez započítání Laplaceova tlaku při zachování stejných podmínek pro danou situaci(hodnota b, povrchová napětí atd.). Samozřejmě uvažujeme o situaci rovnovážného stavu. STEJNÉ PODMÍNKA == při započítání kapilárních tlaků === e mohou nabývat v rovnovážných stavech větších hodnot
36 POZNÁMKA kapilární tlak pro konkávní a konvexní tělesa Rozprostírání kapalina, vzdalování vláken od sebe Srážení, nasávání kapaliny a srážení vláken k sobě
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
Měření povrchového napětí kapalin a kontaktních úhlů
 2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
Vlastnosti kapalin. Povrchová vrstva kapaliny
 Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
LOGO. Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Interakce mezi kapalinou a vlákenným materiálem
 7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
Adheze - pokračování
 2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
Interakce mezi kapalinou a vlákenným materiálem
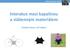 Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška. TNT smáčení úvod. Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL
 2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce
 Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
3.3 Částicová stavba látky
 3.3 Částicová stavba látky Malé (nejmenší) částice látky očekávali nejprve filozofové (atomisté) a nazvali je atomy (z řeckého atomos = nedělitelný) starověké Řecko a Řím. Mnohem později chemici zjistili,
3.3 Částicová stavba látky Malé (nejmenší) částice látky očekávali nejprve filozofové (atomisté) a nazvali je atomy (z řeckého atomos = nedělitelný) starověké Řecko a Řím. Mnohem později chemici zjistili,
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Adhezní síly v kompozitních materiálech
 Adhezní síly v kompozitních materiálech Obsah přednášky Adhezní síly, jejich původ a velikost. Adheze a smáčivost. Metoty určování adhezních sil. Adhezní síly na rozhraní Mezi fázemi v kompozitu jsou rozhraní
Adhezní síly v kompozitních materiálech Obsah přednášky Adhezní síly, jejich původ a velikost. Adheze a smáčivost. Metoty určování adhezních sil. Adhezní síly na rozhraní Mezi fázemi v kompozitu jsou rozhraní
Adhezní síly. Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008
 Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Adhezní síly Technická univerzita v Liberci Kompozitní materiály, 5. MI Doc. Ing. Karel Daďourek 2008 Vazby na rozhraní Mezi fázemi v kompozitu jsou rozhraní mezifázové povrchy. Možné vazby na rozhraní
Měření povrchového napětí
 Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Chemie povrchů verze 2013
 Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
Chemie povrchů verze 2013 Definice povrchu složitá, protože v nanoměřítku (na úrovni velikosti atomů) je elektronový obal atomů difúzní většinou definován fyzikální adsorpcí nereaktivních plynů Vlastnosti
1. Molekulová stavba kapalin
 1 Molekulová stavba kapalin 11 Vznik kapaliny kondenzací Plyn Vyjdeme z plynu Plyn je soustava molekul pohybujících se neuspořádaně všemi směry Pohybová energie molekul převládá nad energii polohovou Každá
1 Molekulová stavba kapalin 11 Vznik kapaliny kondenzací Plyn Vyjdeme z plynu Plyn je soustava molekul pohybujících se neuspořádaně všemi směry Pohybová energie molekul převládá nad energii polohovou Každá
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI
 CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
Speciální aplikace poznatků ze smáčení. Vzlínání do vlákenných materiálů TNT. Eva Kuželová Košťáková KCH, FP, TUL
 Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
STRUKTURA A VLASTNOSTI KAPALIN
 STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT
 VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
2 Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost kapalin 7
 Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
Adhezní síly v kompozitech
 Adhezní síly v kompozitech Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vazby na rozhraní
Adhezní síly v kompozitech Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vazby na rozhraní
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika
 Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška ÚVOD
 2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
Obr. 9.1 Kontakt pohyblivé části s povrchem. Tomuto meznímu stavu za klidu odpovídá maximální síla, která se nezývá adhezní síla,. , = (9.
 9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
STRUKTURA PEVNÝCH LÁTEK A KAPALIN
 STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází
 2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
2.2 Snížení energie systému záměnou fázových rozhraní Rovnováha na rozhraní tří fází Jevy na rozhraní tří stýkajících se fází, z nichž alespoň dvě jsou tekutiny (plyn nebo kapalina), jsou označovány termínem
Práce, energie a další mechanické veličiny
 Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
TEORIE NETKANÝCH TEXTILIÍ. Kapky Kapilární délka. Simulace pomocí Isingova modelu. 7.přednáška
 Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Hydromechanické procesy Hydrostatika
 Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Skupenské stavy látek. Mezimolekulární síly
 Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Úvod. K141 HYAR Úvod 0
 Úvod K141 HYAR Úvod 0 FYZIKA MECHANIKA MECH. TEKUTIN HYDRAULIKA HYDROSTATIKA HYDRODYNAMIKA Mechanika tekutin zabývá se mechanickými vlastnostmi tekutin (tj. silami v tekutinách a prouděním tekutin) poskytuje
Úvod K141 HYAR Úvod 0 FYZIKA MECHANIKA MECH. TEKUTIN HYDRAULIKA HYDROSTATIKA HYDRODYNAMIKA Mechanika tekutin zabývá se mechanickými vlastnostmi tekutin (tj. silami v tekutinách a prouděním tekutin) poskytuje
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Mol. fyz. a termodynamika
 Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
GAUSSŮV ZÁKON ELEKTROSTATIKY
 GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
JEVY NA ROZHRANÍ PEVNÉHO TĚLESA A KAPALINY
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
Molekulové jevy Molekula Mezimolekulové síly Koheze a adheze Kapalina Povrchové napětí Povrchová energie Molekulový tlak Kapilární tlak
 Molekulové jevy Molekula Mezimolekulové síly Dosah molekulových sil Lenardův-Jonesův potenciál Druhy mezimolekulových potenciálních energií Koheze a adheze Koheze Adheze Kapalina Struktura kapalin Vlastnosti
Molekulové jevy Molekula Mezimolekulové síly Dosah molekulových sil Lenardův-Jonesův potenciál Druhy mezimolekulových potenciálních energií Koheze a adheze Koheze Adheze Kapalina Struktura kapalin Vlastnosti
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY
 BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
DUM č. 12 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
Interakce mezi kapalinou a vlákenným materiálem
 5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid
 Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Netkané textilie. Materiály 2
 Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Kinetická teorie ideálního plynu
 Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno
 Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno JAMES WATT 19.1.1736-19.8.1819 Termodynamika principy, které vládnou přírodě Obsah přednášky Vysvětlení základních
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno JAMES WATT 19.1.1736-19.8.1819 Termodynamika principy, které vládnou přírodě Obsah přednášky Vysvětlení základních
FYZIKA I. Gravitační pole. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Vlastnosti molekul kapalin V neustálém pohybu Ve stejných vzdálenostech, nejsou ale vázány Působí na sebe silami: odpudivé x přitažlivé Vlastnosti kapalin
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
4. Kolmou tlakovou sílu působící v kapalině na libovolně orientovanou plochu S vyjádříme jako
 1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 2/7 Gravitační potenciál a jeho derivace
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 2/7 Gravitační potenciál a jeho derivace
Nelineární úlohy při výpočtu konstrukcí s využitím MKP
 Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Pevnost kompozitů obecné zatížení
 Pevnost kompozitů obecné zatížení Osnova Příčná pevnost v tahu Pevnost v tahu pod nenulovým úhlem proti vláknům Podélná pevnost v tlaku Příčná pevnost v tlaku Pevnost vláknových kompozitů - obecně Základní
Pevnost kompozitů obecné zatížení Osnova Příčná pevnost v tahu Pevnost v tahu pod nenulovým úhlem proti vláknům Podélná pevnost v tlaku Příčná pevnost v tlaku Pevnost vláknových kompozitů - obecně Základní
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty.
![a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty. a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty.](/thumbs/88/115052329.jpg) Příklady: 24. Gaussův zákon elektrostatiky 1. Na obrázku je řez dlouhou tenkostěnnou kovovou trubkou o poloměru R, která nese na povrchu náboj s plošnou hustotou σ. Vyjádřete velikost intenzity E jako
Příklady: 24. Gaussův zákon elektrostatiky 1. Na obrázku je řez dlouhou tenkostěnnou kovovou trubkou o poloměru R, která nese na povrchu náboj s plošnou hustotou σ. Vyjádřete velikost intenzity E jako
Voigtův model kompozitu
 Voigtův model kompozitu Osnova přednášky Směšovací pravidlo použitelnost Princip Voigtova modelu Důsledky Voigtova modelu Specifika vláknových kompozitů Směšovací pravidlo Nejjednoduší vztah pro vlastnost
Voigtův model kompozitu Osnova přednášky Směšovací pravidlo použitelnost Princip Voigtova modelu Důsledky Voigtova modelu Specifika vláknových kompozitů Směšovací pravidlo Nejjednoduší vztah pro vlastnost
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
Nauka o materiálu. Přednáška č.2 Poruchy krystalické mřížky
 Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
Nauka o materiálu Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů chemické,
Kapaliny Molekulové vdw síly, vodíkové můstky
 Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje
 Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
10. Energie a její transformace
 10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
1.8. Mechanické vlnění
 1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
Molekulová fyzika a termika. Přehled základních pojmů
 Molekulová fyzika a termika Přehled základních pojmů Kinetická teorie látek Vychází ze tří experimentálně ověřených poznatků: 1) Látky se skládají z částic - molekul, atomů nebo iontů, mezi nimiž jsou
Molekulová fyzika a termika Přehled základních pojmů Kinetická teorie látek Vychází ze tří experimentálně ověřených poznatků: 1) Látky se skládají z částic - molekul, atomů nebo iontů, mezi nimiž jsou
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Vlnění
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Teorie tkaní. Modely vazného bodu. M. Bílek
 Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Náhodné (statistické) chyby přímých měření
 Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
Netkané textilie. Technologická část 1
 Netkané textilie Technologická část 1 Netkané textilie 1 Netkané textilie 2 Příprava vlákenných vrstev Mechanické způsoby přípravy vlákenných vrstev Aerodynamická výroba vlákenné vrstvy Mechanicko-aerodynamické
Netkané textilie Technologická část 1 Netkané textilie 1 Netkané textilie 2 Příprava vlákenných vrstev Mechanické způsoby přípravy vlákenných vrstev Aerodynamická výroba vlákenné vrstvy Mechanicko-aerodynamické
Dynamika. Dynamis = řecké slovo síla
 Dynamika Dynamis = řecké slovo síla Dynamika Dynamika zkoumá příčiny pohybu těles Nejdůležitější pojmem dynamiky je síla Základem dynamiky jsou tři Newtonovy pohybové zákony Síla se projevuje vždy při
Dynamika Dynamis = řecké slovo síla Dynamika Dynamika zkoumá příčiny pohybu těles Nejdůležitější pojmem dynamiky je síla Základem dynamiky jsou tři Newtonovy pohybové zákony Síla se projevuje vždy při
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM. Fyzikální praktikum 2
 Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Fyzikální praktikum 2 Zpracoval: Markéta Kurfürstová Naměřeno: 16. října 2012 Obor: B-FIN Ročník: II Semestr: III
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Fyzikální praktikum 2 Zpracoval: Markéta Kurfürstová Naměřeno: 16. října 2012 Obor: B-FIN Ročník: II Semestr: III
4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 R (4.1)
 4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 4.1 Povrchové a mezifázové napětí Mezi nejpoužívanější metody pro stanovení povrchového a mezifázového napětí
4. Měření některých fyzikálně-chemických charakteristik fázového rozhraní Equation Section 4 4.1 Povrchové a mezifázové napětí Mezi nejpoužívanější metody pro stanovení povrchového a mezifázového napětí
Centrovaná optická soustava
 Centrovaná optická soustava Dvě lámavé kulové ploch: Pojem centrovaná optická soustava znamená, že splývají optické os dvou či více optických prvků. Základním příkladem takové optické soustav jsou dvě
Centrovaná optická soustava Dvě lámavé kulové ploch: Pojem centrovaná optická soustava znamená, že splývají optické os dvou či více optických prvků. Základním příkladem takové optické soustav jsou dvě
Kapka kapaliny na hladině kapaliny
 JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
ANALÝZA KONSTRUKCÍ. 5. přednáška
 ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
Povrchové napětí KATEDRA EXPERIMENTÁLNÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI
 KATEDRA EXPERIMETÁLÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UIVERZITY PALACKÉHO V OLOMOUCI Fyzikální praktikum z molekulové fyziky a termodynamiky Povrchové napětí Úvod Molekuly kapaliny se vzájemně přitahují kohezními
KATEDRA EXPERIMETÁLÍ FYZIKY PŘÍRODOVĚDECKÁ FAKULTA UIVERZITY PALACKÉHO V OLOMOUCI Fyzikální praktikum z molekulové fyziky a termodynamiky Povrchové napětí Úvod Molekuly kapaliny se vzájemně přitahují kohezními
Reologické modely technických materiálů při prostém tahu a tlaku
 . lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
. lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
Adsorpce. molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth Fajans. výměnná iontová adsorpce, protionty v aluminosilikátech
 Adsorpce 1/15 molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth Fajans výměnná iontová adsorpce, protionty v aluminosilikátech Ar na grafitu adsorpce: na povrch/rozhraní absorpce:
Adsorpce 1/15 molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth Fajans výměnná iontová adsorpce, protionty v aluminosilikátech Ar na grafitu adsorpce: na povrch/rozhraní absorpce:
Typy molekul, látek a jejich vazeb v organismech
 Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami
 Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI. Jaroslav Krucký, PMB 22
 Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Kapitola 3.6 Charakterizace keramiky a skla POVRCHOVÉ VLASTNOSTI Jaroslav Krucký, PMB 22 SYMBOLY Řecká písmena θ: kontaktní úhel. σ: napětí. ε: zatížení. ν: Poissonův koeficient. λ: vlnová délka. γ: povrchová
Fáze a fázové přechody
 Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
UČIVO. Termodynamická teplota. První termodynamický zákon Přenos vnitřní energie
 PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
PŘEDMĚT: FYZIKA ROČNÍK: SEXTA VÝSTUP UČIVO MEZIPŘEDM. VZTAHY, PRŮŘEZOVÁ TÉMATA, PROJEKTY, KURZY POZNÁMKY Zná 3 základní poznatky kinetické teorie látek a vysvětlí jejich praktický význam Vysvětlí pojmy
