Interakce mezi kapalinou a vlákenným materiálem
|
|
|
- Nela Kašparová
- před 6 lety
- Počet zobrazení:
Transkript
1 5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h
2 Kapilarita Rostliny transportují vodu z kořenů do listů, houby se dají používat na úklid, textilie sají kapalinu, chromatografie tenké vrstvy separace substancí atd. Dynamika
3 Lucas Washburnův vztah Lucas, R.: Kolloid Zeitschrift, Vol.3, pp.15- (1918) About the time law of the capillary rise of fluids. Washburn, E., W.: Physical Review, Vol. 17, p (191) Dynamics of capillary flow
4
5 Lucas Washburnův vztah Teorie smáčení vlákenných materiálů byla vybudovaná ve dvacátých létech minulého století nezávisle Lucasem a Washburnem. Jejich přístup je založen na silném zjednodušení mnohotvárné struktury vlákenné hmoty do podoby jediné kapiláry. Uvnitř kapiláry je kapalina transportována díky povrchovému napětí. Experimentální výsledky ukazují, že tento silně zjednodušený model dává kvalitativně srovnatelné výsledky s chováním textilií při transportu kapalin.
6 Washburn, E., W.:Physical Review, Vol. 17, p (191) Edward Wight Washburn Edward Wight Washburn was born at Beatrice, Nebraska, on May 10, He died, suddenly, of heart failure February 6, In spite of his all too short life, he has left a record of varied and valuable work which has given him a place of high rank among the chemists of his time.
7 Lucas, R.: Kolloid Zeitschrift, Vol.3, pp.15- (1918) O tři roky dříve napsal stejnou rovnici Richard Lucas.
8 Lucas Washburnův vztah Jejich přístup je založen na silném zjednodušení mnohotvárné struktury vlákenné hmoty do podoby jediné kapiláry. Uvnitř kapiláry je kapalina transportována díky povrchovému napětí. Lucasův - Washburnův vztah odvodíme ze vztahů pro objem V newtonovské viskózní kapaliny o viskozitě, který proteče za čas t trubicí o poloměru r a délce h, mezi jejímiž konci je rozdíl tlaků (p 1 -p ). V,, t, r, h, (p 1 -p ).
9 Lucas Washburnův vztah Tok dv /dt trubicí je dán vztahem odvozovaným v teorii kontinua, označovaným jako Hagenův - Poisseuilleův zákon. dv dt p 1 p 8h r 4. Laminární proudění nepříliš vysoké rychlosti (ne příliš velké tlakové spády) jinak dojde k turbolentnímu proudění a zákon přestává platit. Zmenšením poloměru trubice na polovinu s průtok při zachování stejných tlaků sníží na šestnáctinu. Příklad krevní oběh: Z hlediska krevního oběhu je proto lepší oběh centralizovat, protože při použití tenkých kapilár je nutná velká práce k pohonu krve v oběhu. Viskozita - dynamická viskozita [Pas] - kinematická viskozita [m s -1 ] =/
10 Lucas Washburnův vztah Tok dv /dt trubicí je dán vztahem odvozovaným v teorii kontinua, označovaným jako Hagenův - Poisseuilleův zákon. dv dt p 1 p 8h r 4. V kapiláře vzniká tlak p 1 díky zakřivenému povrchu kapaliny s povrchovým napětím. V případě, že meniskus kapaliny svírá se stěnou kapiláry úhel je p 1 dán výrazem p 1 r cos r cos. r Za meniskus kapaliny označujeme její tvar v blízkosti styku se smáčeným objektem. Tlak p v kapiláře ve výšce odpovídající okolní hladině kapaliny je hydrostatickým tlakem p gh cos.
11 Lucas Washburnův vztah dv dt p 1 p 8h r 4. V r h p 1 cos. r p gh cos. r dh dt 4 r 8 h cos ghcos. r
12 Lucas Washburnův vztah Rychlost postupu tekutiny při vzlínání v kapiláře odhadneme veličinou dh/dt, kterou vyjádříme z předchozí rovnice jako dh dt r cos r 4h g 8 cos. V relaci se předpokládá, že je kapilára dostatečně malá pro to, aby si postupující kapalinový meniskus zachoval tvar kulového vrchlíku neporušeného gravitací. Toho je zpravidla dosaženo za podmínky Malý průměr kapiláry zajistí rychlé vytvoření menisku při vnoření kapiláry do kapaliny. Pro kapaliny podobné vodě jsou výše uvedené požadavky splněny pro kapiláry o poloměru menším než 0.3 mm
13 Následující tabulka udává povrchová napětí vybraných kapalin, jejich hustotu, viskozitu a maximální průměry kapilár které ještě dovolí menisku postupující kapaliny zaujmout tvar kulového vrchlíku. Povrchové napětí, hustota kapalin a jim odpovídající maximální poloměry kapilár r max, ve kterých se ještě vytvoří kapalinový meniskus ve tvaru kulového vrchlíku. Uvedené hodnoty odpovídají teplotě T= 0 o C.
14 Modelová uspořádání jako teoretický úvod do problematiky: Model válcovité kapiláry vnořený do reservoáru s kapalinou 30 5 h 1, 1 h 0 0,8 15 0,6 10 0, t 0, t Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé )
15 Model válcovité kapiláry vnořený do reservoáru s kapalinou Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) dh dt r cos r 4h r cos a 4 b g 8 r cos g cos 8. dh dt a h b
16 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) Úhel = 90. dh dt a h Řešení separace proměnných hdh adt, hdh a dt. 1 h at C, Pro t=0, h=0 je C=0 (integrační konstanta) h r cos at t.
17 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) Úhel = 90. h r cos t Kt 1 Toto řešení platí i pro obecné tehdy, když je možné zanedbat gravitaci (g=0) nebo je výška h velmi malá h0.
18 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) 0,90 ) b je kladné číslo Řešení nelineární diferenciální rovnice s konstantními koeficienty může být řešeno separací proměnných hdh dt; a bh hdh a bh dt t C t h b a b ln a bh
19 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) a b (0,90 t lna bh h b Když t pak ln(a-bh) - a tudíž a-bh=0. Maximální hodnota h tedy je a hmax. b h r cos t Kt 1 Vztah může být řešen i několika jinými cestami za předpokladu, že druhý člen rovnice na pravé straně bude zanedbán z důvodů : (i) zanedbání vlivu gravitace; nebo (ii) velmi malé výšky kdy (h 0).
20 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé ) (90,180 b=-b b je záporné číslo hdh a bh dt t C t h b a b ln a bh Pro velké hodnoty h je možné zapsat B h ln1 h a h a B h a t ln1 h ln1 B a B B B t h B r h B a h g cos t 8 h Kt
21 Model válcovité kapiláry vnořený do reservoáru s kapalinou dh dt a h b Řešení Lucas-Washburnovy rovnice při různých orientacích kapiláry vůči reservoáru s kapalinou (různé )
22 gchr9c
23 zyk7e pjqoi
24 Vztah h=kt 1/ se používá k popisu pronikání kapalin do porézních prostředí. Prostředí se přitom modeluje jako soustava paralelních válcových kapilár. Při kontaktu s kapalinou vlákna porézního textilního prostředí mohou botnat a tím se zmenšuje poloměr pórů myšlených kapilár. Chatterjee v prácích [8,10] navrhl nahradit poloměr kapiláry r výrazem rw / r. Veličina r w je redukovaný poloměr póru za postupujícím kapalinovým meniskem. Rozměry postupujícího kapalinového menisku jsou však stále určovány rozměry suché kapiláry r. [ 8 ] CHATTERJEE, P. K.: Svensk Papperstidning, 74, 503 (1971). [10 ] CHATTERJEE, P. K.: Ed., Absorbency, Textile Science and Tech. Ser., Vol. 7, Elsevier, Amsterdam, Effect of swelling on the cross-section of cotton fibers. Parts (a), (b), and (c) are photos of a native fiber, and that swelled by 1-butanol (b), and water (c), respectively
25 Další korekce vztahu h=kt 1/ se týká zakřivené dráhy, kterou se kapalina v reálném porézním prostředí šíří. Definujeme za tímto účelem faktor T jako poměr skutečné délky kapalinového proudu h ku přímé dráze proudu kapaliny h p (h p = h/t). Tyto korekce upravují konstantu K na tvar K, pro který platí h p = K t 1/. r cos w K rt 1/ r cos e 1/, r e r w je tak zvaný efektivní poloměr póru. rt
26 TEORIE NETKANÝCH TEXTILIÍ
27 Existují tři oblasti faktorů ovlivňující rychlost pronikání kapaliny do vlákenného systému: 1) Viskozita a povrchové napětí smáčející kapaliny ) Strukturní parametry porézního prostředí popsané např. r e 3) Fyzikální interakce kapaliny a vláken, která se projevuje zejména úhlem smáčení. Bez přítomnosti gravitačního pole roste rychlost transportu kapaliny úměrně velikosti pórů a je největší ve směru odpovídajícímu ose pórů.
28 Experimenty pronikání sférických kapek do netkaných textilií Sledování průniku kapek do vlákenné struktury netkaných textilií Použité materiály t Testovací kapaliny a) Epoxidová pryskyřice ( =195 Pas; = 35,8 mnm -1 ; =1,13 gcm -3 ) b) Glycerin ( =1,49 Pas; = 63,4 mnm -1 ; =1,6 gcm -3 ) c) Směs glycerin/voda (7:3) ( =,5 mpas; = 64,8 mnm -1 ; =1, gcm -3 ) Netkané textilie (polyesterová vlákna 6,7dtex, 5m; 80mm) a) Vpichovaná netkaná textilie (190 gm - ; tloušťka 5mm; zaplnění,6%) b) Vpichovaná netkaná textilie (190 gm - ; tloušťka 1mm; zaplnění 16,9%) c) Kolmo kladená termickypojená netkaná textilie struto (56 gm - ; tloušťka po rozříznutí 1,5 mm; zaplnění 1,6%)
29 Experimenty pronikání sférických kapek do netkaných textilií
30 Experimenty pronikání sférických kapek do netkaných textilií Sledování průniku kapek do vlákenné struktury netkaných textilií Výsledky vliv viskozity kapaliny Nižší viskozita kapaliny ukazuje jednoznačně vyšší rychlost pronikání kapek do netkaných textilií. t s
31 Experimenty pronikání sférických kapek do netkaných textilií Sledování průniku kapek do vlákenné struktury netkaných textilií Výsledky vliv orientace vláken Více vláken uspořádaných ve směru pronikání kapaliny způsobuje vyšší rychlost pronikání kapek do netkaných textilií jednoznačně pouze pro kapaliny s vyššími viskozitami. V mm 3 t s
32 velocity mm 3 /s TEORIE NETKANÝCH TEXTILIÍ Experimenty pronikání sférických kapek do netkaných textilií Sledování průniku kapek do vlákenné struktury netkaných textilií Výsledky vliv zaplnění netkané textilie Snižující se hodnota zaplnění netkaných textilií jednoznačně působí zvýšení rychlosti pronikání kapek do netkaných textilií Rychlost pronikání se zvyšuje s použitím vláken s větším průměrem. thickness mm
33 V mm 6 V mm 3 TEORIE NETKANÝCH TEXTILIÍ Experimenty pronikání sférických kapek do netkaných textilií Sledování průniku kapek do vlákenné struktury netkaných textilií Výsledky vliv zaplnění netkané textilie (různé velikosti kapek) V [mm 6 ] Thickness of sample = 1mm Volume fraction = 18,75% Weight of drop (0,01g) (0,06g) (0,038g) (0,065g) V[mm 3 ] Thickness of sample = 3mm Volume fraction = 6,5% Weight of drop (0,031g) (0,050g) (0,058g) (0,071g) time [s] time [s] 15 α=1/ V=kt α V is penetrated volume; k is constant; t is time and α is a scaling exponent. α=1
Interakce mezi kapalinou a vlákenným materiálem
 8. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry 2 dh r Pe. dt 8h Lucas Washburnův vztah Lucas, R.: Kolloid Zeitschrift,
8. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry 2 dh r Pe. dt 8h Lucas Washburnův vztah Lucas, R.: Kolloid Zeitschrift,
TEORIE NETKANÝCH TEXTILIÍ. Kapky Kapilární délka. Simulace pomocí Isingova modelu. 7.přednáška
 Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
Vlastnosti kapalin. Povrchová vrstva kapaliny
 Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
5. Stavy hmoty Kapaliny a kapalné krystaly
 a kapalné krystaly Vlastnosti kapalin kapalných krystalů jako rozpouštědla Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti kapaliny nestálé atraktivní interakce (kohezní síly) mezi molekulami,
a kapalné krystaly Vlastnosti kapalin kapalných krystalů jako rozpouštědla Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti kapaliny nestálé atraktivní interakce (kohezní síly) mezi molekulami,
Speciální aplikace poznatků ze smáčení. Vzlínání do vlákenných materiálů TNT. Eva Kuželová Košťáková KCH, FP, TUL
 Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
STRUKTURA A VLASTNOSTI KAPALIN
 STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
LOGO. Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Proudění viskózní tekutiny. Renata Holubova renata.holubov@upol.cz. Viskózní tok, turbulentní proudění, Poiseuillův zákon, Reynoldsovo číslo.
 PROMOTE MSc POPIS TÉMATU FYZKA 1 Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubov@upol.cz Popis
PROMOTE MSc POPIS TÉMATU FYZKA 1 Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubov@upol.cz Popis
Interakce mezi kapalinou a vlákenným materiálem
 7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
Počítačová dynamika tekutin (CFD) Základní rovnice. - laminární tok -
 Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Měření povrchového napětí kapalin a kontaktních úhlů
 2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT
 VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
BIOMECHANIKA. Studijní program, obor: Tělesná výchovy a sport Vyučující: PhDr. Martin Škopek, Ph.D.
 BIOMECHANIKA 8, Disipativní síly II. (Hydrostatický tlak, hydrostatický vztlak, Archimédův zákon, dynamické veličiny, odporové síly, tvarový odpor, Bernoulliho rovnice, Magnusův jev) Studijní program,
BIOMECHANIKA 8, Disipativní síly II. (Hydrostatický tlak, hydrostatický vztlak, Archimédův zákon, dynamické veličiny, odporové síly, tvarový odpor, Bernoulliho rovnice, Magnusův jev) Studijní program,
Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma fázemi První ucelená teorie respektující uvedenou skutečnost byla
 Teorie chromatografie - III Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 4.3.3 Teorie dynamická Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma
Teorie chromatografie - III Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 4.3.3 Teorie dynamická Při reálném chromatografickém ději nikdy nedojde k ustavení rovnováhy mezi oběma
Teorie měření a regulace
 Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace měření průtoku 17.SPEC-t.4 ZS 2015/2016 2015 - Ing. Václav Rada, CSc. Další pokračování o principech měření Průtok je určen střední
Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace měření průtoku 17.SPEC-t.4 ZS 2015/2016 2015 - Ing. Václav Rada, CSc. Další pokračování o principech měření Průtok je určen střední
Krevní oběh. Helena Uhrová
 Krevní oběh Helena Uhrová Z hydrodynamického hlediska uzavřený systém, složený ze: srdce motorický orgán, zdroj mechanické energie cév rozvodný systém, tvořený elastickými roztažitelnými a kontraktilními
Krevní oběh Helena Uhrová Z hydrodynamického hlediska uzavřený systém, složený ze: srdce motorický orgán, zdroj mechanické energie cév rozvodný systém, tvořený elastickými roztažitelnými a kontraktilními
V i s k o z i t a N e w t o n s k ý c h k a p a l i n
 V i s k o z i t a N e w t o n s k ý c h k a p a l i n Ú k o l : Změřit dynamickou viskozitu destilované vody absolutní metodou a její závislost na teplotě relativní metodou. P o t ř e b y : Viz seznam
V i s k o z i t a N e w t o n s k ý c h k a p a l i n Ú k o l : Změřit dynamickou viskozitu destilované vody absolutní metodou a její závislost na teplotě relativní metodou. P o t ř e b y : Viz seznam
4. Kolmou tlakovou sílu působící v kapalině na libovolně orientovanou plochu S vyjádříme jako
 1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
Základy vakuové techniky
 Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Mechanika tekutin. Hydrostatika Hydrodynamika
 Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
Filtrace 18.9.2008 1
 Výpočtový ý seminář z Procesního inženýrství podzim 2008 Filtrace 18.9.2008 1 Tématické okruhy principy a instrumentace bilance filtru kalolis filtrace za konstantní rychlosti filtrace za konstantního
Výpočtový ý seminář z Procesního inženýrství podzim 2008 Filtrace 18.9.2008 1 Tématické okruhy principy a instrumentace bilance filtru kalolis filtrace za konstantní rychlosti filtrace za konstantního
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov. Modelování termohydraulických jevů 3.hodina. Hydraulika. Ing. Michal Kabrhel, Ph.D.
 ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
STRUKTURA PEVNÝCH LÁTEK A KAPALIN
 STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
STRUKTURA PEVNÝCH LÁTEK A KAPALIN 18. POVRCHOVÁ VRSTVA KAPALIN, KAPILÁRNÍ ELEVACE, DEPRESE Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. POVRCHOVÉ NAPĚTÍ - Povrchové napětí je efekt, při kterém
Zařízení: Rotační viskozimetr s příslušenstvím, ohřívadlo s magnetickou míchačkou, teploměr, potřebné nádoby a kapaliny (aspoň 250ml).
 Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami
 Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
Proudění viskózní tekutiny. Renata Holubova renata.holubova@upol.cz
 Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubova@upol.cz Popis základních zákonitostí v mechanice
Název Tematický celek Jméno a e-mailová adresa autora Cíle Obsah Pomůcky Poznámky Proudění viskózní tekutiny Mechanika kapalin Renata Holubova renata.holubova@upol.cz Popis základních zákonitostí v mechanice
U218 - Ústav procesní a zpracovatelské techniky FS ČVUT v Praze. ! t 2 :! Stacionární děj, bez vnitřního zdroje, se zanedbatelnou viskózní disipací
 VII. cená konvekce Fourier Kirchhoffova rovnice T!! ρ c p + ρ c p u T λ T + µ d t :! (g d + Q" ) (VII 1) Stacionární děj bez vnitřního zdroje se zanedbatelnou viskózní disipací! (VII ) ρ c p u T λ T 1.
VII. cená konvekce Fourier Kirchhoffova rovnice T!! ρ c p + ρ c p u T λ T + µ d t :! (g d + Q" ) (VII 1) Stacionární děj bez vnitřního zdroje se zanedbatelnou viskózní disipací! (VII ) ρ c p u T λ T 1.
2 Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost kapalin 7
 Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
Obsah Obsah 1 Povrchová vrstva 1 2 Jevy na rozhraní 3 2.1 Kapilární tlak........................... 4 2.2 Kapilární jevy........................... 5 3 Objemová roztažnost kapalin 7 1 Povrchová vrstva
MODELOVÁNÍ. Základní pojmy. Obecný postup vytváření induktivních modelů. Měřicí a řídicí technika magisterské studium FTOP - přednášky ZS 2009/10
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
Konstrukce optického mikroviskozimetru
 Ing. Jan Medlík, FSI VUT v Brně, Ústav konstruování Konstrukce optického mikroviskozimetru Školitel: prof. Ing. Martin Hartl, Ph.D. VUT Brno, FSI 2008 Obsah Úvod Shrnutí současného stavu Měření viskozity
Ing. Jan Medlík, FSI VUT v Brně, Ústav konstruování Konstrukce optického mikroviskozimetru Školitel: prof. Ing. Martin Hartl, Ph.D. VUT Brno, FSI 2008 Obsah Úvod Shrnutí současného stavu Měření viskozity
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ
 INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI
 CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
Struktura a vlastnosti kapalin (test version, not revised) Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Povrchová vrstva Jevy na rozhraní Kapilární tlak Kapilární jevy Objemová roztažnost
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
VISKOZITA A POVRCHOVÉ NAPĚTÍ
 VISKOZITA A POVRCHOVÉ NAPĚTÍ TEORETICKÝ ÚVOD V proudící reálné tekutině se projevuje mezi elementy tekutiny vnitřní tření. Síly tření způsobí, že rychlejší vrstva tekutiny se snaží zrychlit vrstvu pomalejší
VISKOZITA A POVRCHOVÉ NAPĚTÍ TEORETICKÝ ÚVOD V proudící reálné tekutině se projevuje mezi elementy tekutiny vnitřní tření. Síly tření způsobí, že rychlejší vrstva tekutiny se snaží zrychlit vrstvu pomalejší
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
Vybrané technologie povrchových úprav. Základy vakuové techniky Doc. Ing. Karel Daďourek 2006
 Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
Vybrané technologie povrchových úprav Základy vakuové techniky Doc. Ing. Karel Daďourek 2006 Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika
 Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Proč funguje Clemův motor
 - 1 - Proč funguje Clemův motor Princip - výpočet - konstrukce (c) Ing. Ladislav Kopecký, 2004 Tento článek si klade za cíl odhalit podstatu funkce Clemova motoru, provést základní výpočty a navrhnout
- 1 - Proč funguje Clemův motor Princip - výpočet - konstrukce (c) Ing. Ladislav Kopecký, 2004 Tento článek si klade za cíl odhalit podstatu funkce Clemova motoru, provést základní výpočty a navrhnout
Dynamická viskozita oleje (Pa.s) Souřadný systém (proč)?
 Viskozimetr kužel-deska S pomocí rotačního viskozimetru s uspořádáním kužel-deska, viz obrázek, byla měřena dynamická viskozita oleje. Při použití kužele o průměru 40 mm, který se otáčel úhlovou rychlostí
Viskozimetr kužel-deska S pomocí rotačního viskozimetru s uspořádáním kužel-deska, viz obrázek, byla měřena dynamická viskozita oleje. Při použití kužele o průměru 40 mm, který se otáčel úhlovou rychlostí
5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY
 Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY 1. TEORIE: Měření viskozity pomocí padající kuličky patří k nejstarším metodám
Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY 1. TEORIE: Měření viskozity pomocí padající kuličky patří k nejstarším metodám
VLASTNOSTI KAPALIN. Část 2. Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič; MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA
 HYDROMECHANIKA LASTNOSTI KAPALIN Část 2 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič; MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA lastnosti kapalin: Molekulární stavba hmoty Příklad
HYDROMECHANIKA LASTNOSTI KAPALIN Část 2 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič; MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA lastnosti kapalin: Molekulární stavba hmoty Příklad
Adheze - pokračování
 2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
CHROMATOGRAFIE ÚVOD Společný rys působením nemísících fází: jedna fáze je nepohyblivá (stacionární), druhá pohyblivá (mobilní).
 CHROMATOGRAFIE ÚOD Existují různé chromatografické metody, viz rozdělení metod níže. Společný rys chromatografických dělení: vzorek jako směs látek - složek se dělí na jednotlivé složky působením dvou
CHROMATOGRAFIE ÚOD Existují různé chromatografické metody, viz rozdělení metod níže. Společný rys chromatografických dělení: vzorek jako směs látek - složek se dělí na jednotlivé složky působením dvou
6. Stavy hmoty - Plyny
 skupenství plynné plyn x pára (pod kritickou teplotou) stavové chování Ideální plyn Reálné plyny Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti skupenství plynné reálný plyn ve stavu
skupenství plynné plyn x pára (pod kritickou teplotou) stavové chování Ideální plyn Reálné plyny Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti skupenství plynné reálný plyn ve stavu
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině.
 Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Kinetická teorie ideálního plynu
 Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
4 STANOVENÍ KINEMATICKÉ A DYNAMICKÉ VISKOZITY OVOCNÉHO DŽUSU
 Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 4 STANOVENÍ KINEMATICKÉ A DYNAMICKÉ VISKOZITY OVOCNÉHO DŽUSU (KAPILÁRNÍ VISKOZIMETR UBBELOHDE) 1. TEORIE: Ve všech kapalných látkách
Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 4 STANOVENÍ KINEMATICKÉ A DYNAMICKÉ VISKOZITY OVOCNÉHO DŽUSU (KAPILÁRNÍ VISKOZIMETR UBBELOHDE) 1. TEORIE: Ve všech kapalných látkách
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid
 Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Praktikum I Mechanika a molekulová fyzika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum I Mechanika a molekulová fyzika Úloha č. XIX Název: Pád koule ve viskózní kapalině Pracoval: Matyáš Řehák stud.sk.: 16 dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum I Mechanika a molekulová fyzika Úloha č. XIX Název: Pád koule ve viskózní kapalině Pracoval: Matyáš Řehák stud.sk.: 16 dne:
Příklady z teoretické mechaniky pro domácí počítání
 Příklady z teoretické mechaniky pro domácí počítání Doporučujeme spočítat příklady za nejméně 30 bodů. http://www.physics.muni.cz/~tomtyc/mech-prik.ps http://www.physics.muni.cz/~tomtyc/mech-prik.pdf 1.
Příklady z teoretické mechaniky pro domácí počítání Doporučujeme spočítat příklady za nejméně 30 bodů. http://www.physics.muni.cz/~tomtyc/mech-prik.ps http://www.physics.muni.cz/~tomtyc/mech-prik.pdf 1.
Mechanika - kinematika
 Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
Úvod. K141 HYAR Úvod 0
 Úvod K141 HYAR Úvod 0 FYZIKA MECHANIKA MECH. TEKUTIN HYDRAULIKA HYDROSTATIKA HYDRODYNAMIKA Mechanika tekutin zabývá se mechanickými vlastnostmi tekutin (tj. silami v tekutinách a prouděním tekutin) poskytuje
Úvod K141 HYAR Úvod 0 FYZIKA MECHANIKA MECH. TEKUTIN HYDRAULIKA HYDROSTATIKA HYDRODYNAMIKA Mechanika tekutin zabývá se mechanickými vlastnostmi tekutin (tj. silami v tekutinách a prouděním tekutin) poskytuje
VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 2
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 2 Přestup tepla nucená konvekce beze změny skupenství v trubkových systémech Hana Charvátová,
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 2 Přestup tepla nucená konvekce beze změny skupenství v trubkových systémech Hana Charvátová,
Základy hydrauliky vodních toků
 Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM
 CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM Místní ztráty, Tlakové ztráty Příklad č. 1: Jistá část potrubí rozvodného systému vody se skládá ze dvou paralelně uspořádaných větví. Obě potrubí mají průřez
CVIČENÍ č. 11 ZTRÁTY PŘI PROUDĚNÍ POTRUBÍM Místní ztráty, Tlakové ztráty Příklad č. 1: Jistá část potrubí rozvodného systému vody se skládá ze dvou paralelně uspořádaných větví. Obě potrubí mají průřez
Neideální plyny. Z e dr dr dr. Integrace přes hybnosti. Neideální chování
 eideální plyny b H Q(, V, T )... e dp 3... dpdr... dr! h Integrace přes hybnosti QVT (,, ) pmkt! h 3 / e dr dr dr /... U kt... eideální chování p kt r B ( T) r B ( T) r 3 3 Vyšší koeficinety velice složité
eideální plyny b H Q(, V, T )... e dp 3... dpdr... dr! h Integrace přes hybnosti QVT (,, ) pmkt! h 3 / e dr dr dr /... U kt... eideální chování p kt r B ( T) r B ( T) r 3 3 Vyšší koeficinety velice složité
Kapaliny Molekulové vdw síly, vodíkové můstky
 Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Termomechanika 12. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 2. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 2. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Řešíme tedy soustavu dvou rovnic o dvou neznámých. 2a + b = 3, 6a + b = 27,
 Přijímací řízení 2015/16 Přírodovědecká fakulta Ostravská univerzita v Ostravě Navazující magisterské studium, obor Aplikovaná matematika (1. červen 2016) Příklad 1 Určete taková a, b R, aby funkce f()
Přijímací řízení 2015/16 Přírodovědecká fakulta Ostravská univerzita v Ostravě Navazující magisterské studium, obor Aplikovaná matematika (1. červen 2016) Příklad 1 Určete taková a, b R, aby funkce f()
Vícefázové reaktory. Probublávaný reaktor plyn kapalina katalyzátor. Zuzana Tomešová
 Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
Mechanika kapalin a plynů
 Mechanika kapalin a plynů Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Tekutiny Tlak Tlak v kapalině vyvolaný vnější silou Tlak v kapalině vyvolaný tíhovou silou Tlak v kapalině vyvolaný
Mechanika kapalin a plynů Petr Pošta pposta@karlin.mff.cuni.cz 24. listopadu 2010 Obsah Tekutiny Tlak Tlak v kapalině vyvolaný vnější silou Tlak v kapalině vyvolaný tíhovou silou Tlak v kapalině vyvolaný
Katedra textilních materiálů ENÍ TEXTILIÍ PŘEDNÁŠKA 5
 PŘEDNÁŠKA 5 π n * ρvk * d 4 n [ ] 6 d + s *0 v m [ mg] [ m] Metody stanovení jemnosti (délkové hmotnosti) vláken: Mikroskopická metoda s výpočtem jemnosti z průměru (tloušťky) vlákna u vláken kruhového
PŘEDNÁŠKA 5 π n * ρvk * d 4 n [ ] 6 d + s *0 v m [ mg] [ m] Metody stanovení jemnosti (délkové hmotnosti) vláken: Mikroskopická metoda s výpočtem jemnosti z průměru (tloušťky) vlákna u vláken kruhového
MECHANIKA KAPALIN A PLYNŮ. Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník
 MECHANIKA KAPALIN A PLYNŮ Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Mechanika kapalin a plynů Hydrostatika - studuje podmínky rovnováhy kapalin. Aerostatika - studuje podmínky rovnováhy
MECHANIKA KAPALIN A PLYNŮ Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Mechanika kapalin a plynů Hydrostatika - studuje podmínky rovnováhy kapalin. Aerostatika - studuje podmínky rovnováhy
Elektrostatické pole Coulombův zákon - síla působící mezi dvěma elektrickými bodovými náboji Definice intenzity elektrického pole Siločáry
 Elektrostatické pole Coulombův zákon - síla působící mezi dvěma elektrickými bodovými náboji Definice intenzity elektrického pole iločáry elektrického pole Intenzita elektrického pole buzená bodovým elektrickým
Elektrostatické pole Coulombův zákon - síla působící mezi dvěma elektrickými bodovými náboji Definice intenzity elektrického pole iločáry elektrického pole Intenzita elektrického pole buzená bodovým elektrickým
MODELOVÁNÍ SHALLOW WATER
 Západočeská univerzita Fakulta aplikovaných věd Matematické metody v aplikovaných vědách a ve vzdělávání MODELOÁNÍ SHLLOW WTER KRISTÝN HDŠOÁ ziraf@students.zcu.cz 1 ÚOD Dostala jsem za úkol namodelovat
Západočeská univerzita Fakulta aplikovaných věd Matematické metody v aplikovaných vědách a ve vzdělávání MODELOÁNÍ SHLLOW WTER KRISTÝN HDŠOÁ ziraf@students.zcu.cz 1 ÚOD Dostala jsem za úkol namodelovat
Základy fyziky + opakovaná výuka Fyziky I
 Ústav fyziky a měřicí techniky Pohodlně se usaďte Přednáška co nevidět začne! Základy fyziky + opakovaná výuka Fyziky I Web ústavu: ufmt.vscht.cz : @ufmt444 1 Otázka 8 Rovinná rotace, valení válce po nakloněné
Ústav fyziky a měřicí techniky Pohodlně se usaďte Přednáška co nevidět začne! Základy fyziky + opakovaná výuka Fyziky I Web ústavu: ufmt.vscht.cz : @ufmt444 1 Otázka 8 Rovinná rotace, valení válce po nakloněné
TERMOMECHANIKA 15. Základy přenosu tepla
 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí Prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 15. Základy přenosu tepla OSNOVA 15. KAPITOLY Tři mechanizmy přenosu tepla Tepelný
FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí Prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 15. Základy přenosu tepla OSNOVA 15. KAPITOLY Tři mechanizmy přenosu tepla Tepelný
Interakce mezi kapalinou a vlákenným materiálem
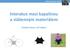 Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl
 Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Mechanika tekutin. Tekutiny = plyny a kapaliny
 Mechanika tekutin Tekutiny = plyny a kapaliny Vlastnosti kapalin Kapaliny mění tvar, ale zachovávají objem jsou velmi málo stlačitelné Ideální kapalina: bez vnitřního tření je zcela nestlačitelná Viskozita
Mechanika tekutin Tekutiny = plyny a kapaliny Vlastnosti kapalin Kapaliny mění tvar, ale zachovávají objem jsou velmi málo stlačitelné Ideální kapalina: bez vnitřního tření je zcela nestlačitelná Viskozita
Snímače hladiny. Učební text VOŠ a SPŠ Kutná Hora. Základní pojmy. měření výšky hladiny kapalných látek a sypkých hmot
 Snímače hladiny Učební text VOŠ a SPŠ Kutná Hora Základní pojmy Použití snímačů hladiny (stavoznaků) měření výšky hladiny kapalných látek a sypkých hmot O výběru vhodného snímače rozhoduje požadovaný rozsah
Snímače hladiny Učební text VOŠ a SPŠ Kutná Hora Základní pojmy Použití snímačů hladiny (stavoznaků) měření výšky hladiny kapalných látek a sypkých hmot O výběru vhodného snímače rozhoduje požadovaný rozsah
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru. Petr Svačina
 Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Kapaliny Molekulové vdw síly, vodíkové můstky
 Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
DUM č. 12 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
JEVY NA ROZHRANÍ PEVNÉHO TĚLESA A KAPALINY
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Dagmar Horká MGV_F_SS_1S3_D17_Z_MOLFYZ_Jevy_na_rozhrani_pevneho_tel esa_a_kapaliny_pl Člověk a příroda Fyzika
Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce
 Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Fázové rozhraní Fázové rozhraní - plocha,na které se vlastnosti systému mění skokem ; fáze o určité tloušťce Homogenní - kapalina/plyn - povrch;kapalina/kapalina Nehomogenní - tuhá látka/plyn - povrch;
Vlny konečné amplitudy vyzařované bublinou vytvořenou jiskrovým výbojem ve vodě
 12. 14. května 2015 Vlny konečné amplitudy vyzařované bublinou vytvořenou jiskrovým výbojem ve vodě Karel Vokurka Technická univerzita v Liberci, katedra fyziky, Studentská 2, 461 17 Liberec karel.vokurka@tul.cz
12. 14. května 2015 Vlny konečné amplitudy vyzařované bublinou vytvořenou jiskrovým výbojem ve vodě Karel Vokurka Technická univerzita v Liberci, katedra fyziky, Studentská 2, 461 17 Liberec karel.vokurka@tul.cz
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
PROCESY V TECHNICE BUDOV cvičení 3, 4
 UNIVERZITA TOMÁŠE ATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE UDOV cvičení 3, 4 část Hana Charvátová, Dagmar Janáčová Zlín 013 Tento studijní materiál vznikl za finanční podpory Evropského
UNIVERZITA TOMÁŠE ATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE UDOV cvičení 3, 4 část Hana Charvátová, Dagmar Janáčová Zlín 013 Tento studijní materiál vznikl za finanční podpory Evropského
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Měření kinematické a dynamické viskozity kapalin
 Úloha č. 2 Měření kinematické a dynamické viskozity kapalin Úkoly měření: 1. Určete dynamickou viskozitu z měření doby pádu kuličky v kapalině (glycerinu, roztoku polysacharidu ve vodě) při laboratorní
Úloha č. 2 Měření kinematické a dynamické viskozity kapalin Úkoly měření: 1. Určete dynamickou viskozitu z měření doby pádu kuličky v kapalině (glycerinu, roztoku polysacharidu ve vodě) při laboratorní
Základem molekulové fyziky je kinetická teorie látek. Vychází ze tří pouček:
 Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Příklady z hydrostatiky
 Příklady z hydrostatiky Poznámka: Při řešení příkladů jsou zaokrouhlovány pouze dílčí a celkové výsledky úloh. Celý vlastní výpočet všech úloh je řešen bez zaokrouhlování dílčích výsledků. Za gravitační
Příklady z hydrostatiky Poznámka: Při řešení příkladů jsou zaokrouhlovány pouze dílčí a celkové výsledky úloh. Celý vlastní výpočet všech úloh je řešen bez zaokrouhlování dílčích výsledků. Za gravitační
Část 3. Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA
 HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 345 K metodou bublin.
 1 Pracovní úkoly 1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 35 K metodou bublin. 2. Měřenou závislost znázorněte graficky. Závislost aproximujte kvadratickou
1 Pracovní úkoly 1. Změřte teplotní závislost povrchového napětí destilované vody σ v rozsahu teplot od 295 do 35 K metodou bublin. 2. Měřenou závislost znázorněte graficky. Závislost aproximujte kvadratickou
Přednáška 2. Martin Kormunda
 Přednáška 2 Objemové procesy Difuze Tepelná transpirace (efuze) Přenos energie Proudění plynů : proud plynu, vakuová vodivost, vodivost otvoru, potrubí. Proudění plynu netěsnostmi Difuze plynu Veškeré
Přednáška 2 Objemové procesy Difuze Tepelná transpirace (efuze) Přenos energie Proudění plynů : proud plynu, vakuová vodivost, vodivost otvoru, potrubí. Proudění plynu netěsnostmi Difuze plynu Veškeré
7 Gaussova věta 7 GAUSSOVA VĚTA. Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro
 7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
F n = F 1 n 1 + F 2 n 2 + F 3 n 3.
 Plošný integrál Několik pojmů Při našich úvahách budeme často vužívat skalární součin dvou vektorů. Platí F n F n cos α, kde α je úhel, který svírají vektor F a n. Vidíme, že pokud je tento úhel ostrý,
Plošný integrál Několik pojmů Při našich úvahách budeme často vužívat skalární součin dvou vektorů. Platí F n F n cos α, kde α je úhel, který svírají vektor F a n. Vidíme, že pokud je tento úhel ostrý,
Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu
 Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu: CZ.1.07/2.2.00/28.0326 PROJEKT
Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu: CZ.1.07/2.2.00/28.0326 PROJEKT
Mechanika tekutin je nauka o rovnováze a makroskopickém pohybu tekutin a o jejich působení na tělesa do ní ponořená či jí obtékaná.
 Mechanika tekutin je nauka o rovnováze a makroskopickém pohybu tekutin a o jejich působení na tělesa do ní ponořená či jí obtékaná. Popisuje chování tekutin makroskopickými veličinami, které jsou definovány
Mechanika tekutin je nauka o rovnováze a makroskopickém pohybu tekutin a o jejich působení na tělesa do ní ponořená či jí obtékaná. Popisuje chování tekutin makroskopickými veličinami, které jsou definovány
Anemometrie - žhavené senzory
 Anemometrie - žhavené senzory Fyzikální princip metody Metoda je založena na ochlazování žhaveného senzoru proudícím médiem. Teplota senzoru: 50 300 C Ochlazování závisí na: Vlastnostech senzoru Fyzikálních
Anemometrie - žhavené senzory Fyzikální princip metody Metoda je založena na ochlazování žhaveného senzoru proudícím médiem. Teplota senzoru: 50 300 C Ochlazování závisí na: Vlastnostech senzoru Fyzikálních
