O BARV Jan Ponec Olomouc, listopad 2005

Transkript

1 O BARV Jan Ponec Olomouc, listopad 2005

2 OBSAH 1) Co je to barva 2) Oko jako fotodetektor 3) Barevné vidní 4) Popis barvy kvalitativní ukazatele 5) Mení barev- kvantitativní ukazatele 6) Zobrazení barev barevné modely 7) Skládání barev

3 1) CO JE TO BARVA Barva je smyslový vjem ( zrakový poitek ), nerozlun spojený se svtlem, vzbuzený dopadem svtelného záení na sítnici oka. Barva rovnž charakterizuje kvalitu svtla. V popisu barvy hovoíme tedy v pojmech ze tí oblastí: - oblast fyzikální (svtelný podnt, jeho spektrální složení, intenzita záení, ) - oblast psychofyzikální ( chromatinost, kolorita, ) - oblast psychosenzorická ( vlastní pojem barva, její vnímání, závislost na stavu recepních orgán, podmínkách pozorování, psychickém stavu pozorovatele, )

4 Chromatinost- vyjaduje barevné vlastnosti prvotních zái ( svtel ) S () F ( ) Zdroj Detektor Barevný podnt : F () = S ()

5 Kolorita vyjaduje barevné vlastnosti druhotných zái ( pedmt ) Zdroj Pedmt Detektor S () τ () ; ( ) F () Barevný podnt : resp. F () = S (). τ () F () = S (). ()

6 2. OKO JAKO FOTODETEKTOR Vidní je fotochemická reakce zpsobená dopadem foton na sítnici oka a pechod na elektrický signál (chemickoelektrická reakce) vedoucí vzruchy do mozkového centra vidní. Oko reaguje na jistou ást elektromagnetického záení o rozsahu vlnových délek asi nm, kterou nazýváme svtlo. Rozsah vnímaných jas je asi 1 : 10 6 Fotocitlivou vrstvou oka je sítnice. Fotocitlivé receptory jsou tyinky a ípky.

7 Prez sítnicí

8 Vidní : denní fotopické : ípky barevné vidní pi jasech > 5 nt úinná látka jodopsyn a 3 druhy pigment poet asi 5 7 milion velikost asi 5 m rozložení: maximum ve žluté skvrn ( úhlov asi 1,5º) a okolí (asi do 40º)

9 za šera (noní) - skotopické : tyinky nebarevné vidní pi jasech < 0,01 nt úinná látka rhodopsyn poet asi 120 milion rozložení : na periferii sítnice * pechodové mezopické :tyinky i ípky

10

11 Spektrální citlivost ípk je maximální pro svtlo o vlnové délce 555 nm. Spektrální citlivost tyinek je maximální pro svtlo o vlnové délce 507 nm. Pomrná svtelná úinnost ípk V () a tyinek V () :

12 3. BAREVNÉ VIDNÍ Rozeznáváme ti druhy ípk dle úinného pigmentu: ípky: resp. L ( Long ), pigment erythrolabe citlivost k ervené barv (max 564 nm) resp. M ( Medium ), pigment chlorolabe citlivost k zelené barv (max 533 nm) resp. S ( Short ), pigment cyanolabe citlivost k modré barv (max 437 nm)

13 Spektrální citlivost ípk:

14 Dv teorie barevného vidní: A) Trichromatická teorie ( Young, Helmholtz, Maxwell, asi 1807) Ti druhy ípk citlivých k ervené, zelené a modré barv a pomr signál tchto jednotlivých fotosenzor uruje barevný vjem. B) Teorie opoziních barev ( Hering ) Signály ze tí rzných skupin ípk nejsou pímo vedeny do mozku, ale jsou pedem zpracovány v neuronech do opoziních signál. Vychází se ze skutenosti, že neexistují ervenozelené, nebo modrožluté tóny barev. ervenozelený signál: Modrožlutý signál: L M + S L + M S Achromatický (jasový) signál: L + M + S

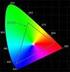
15 4. POPIS BARVY - kvalitativní ukazatele barvy Tón barvy ( Hue ) je to, ím se jednotlivé barvy od sebe liší a co popisujeme pojmy jako ervená, modrá, zelená, žlutá, bílá, erná,. Fyzikálním vzorníkem barev je spektrum, vzniklé rozkladem bílého svtla. (Ve spektru chybí barvy purpurové, tvoící pechod od barvy fialové po barvu ervenou). Rozlišujeme barvy: - pestré, chromatické ( ervená, zelená, jejich smsy a odstíny) - nepestré, achromatické ( šedé,krajní meze jsou bílá a erná ) Nalezneme-li v pírod barvy, které se jeví shodné, ale mají jiné spektrální složení, hovoíme o barvách metamerických.

16 Jas ( Brightness ) uruje množství svtelné energie do oka i jiného detektoru vstupující. Sytost barvy (Saturation,Colourfulness) udává množství (podíl) bílé barvy v základní barv. * Oznaování barev: R - ervená Red G - zelená Green B - modrá Blue C - azurová Cyan M - purpurová Magenta Y - žlutá Yellow K - erná black, resp. Key W- bílá White

17 5. MENÍ BAREV - kvantitativní ukazatele barev Lidské oko údajn rozezná asi barevných odstín.pro toto množství nemáme píslušné pojmenování. Aby bylo možno konkrétní barvu pesn definovat, bylo nutno domluvit njakou barevnou metriku. První standardizace: rok 1931 CIE (Commission Internationale de l Éclairage) a dále pak v létech 1960, 1964, 1976

18 Kolorimetrická mrná soustava Ke kvantitativnímu vyjádení chromatinosti a kolority se zavedla trichromatická soustava. Základem pro kvantitativní vyjádení barvy je definice Standardního kolorimetrického pozorovatele CIE 1931 skládající se ze tí funkcí, tzv. trichromatických lenitel x(λ), y(λ) a z(λ), pro zorný úhel pozorování do 4 o. V roce 1964 rozšíeno pro zorný úhel pozorování 10 o o doplkového pozorovatele leniteli x 10 (λ), y 10 (λ) a z 10 (λ).

19

20 V trichromatické soustav se vychází z pedpokladu, že adiním mísením tí mrných barevných podnt ( základních svtel) lze vzbudit vjem kterékoliv barvy. Za základ byla zvolena svtla o vlnové délce: 700 nm pro ervenou barvu 546,1 nm pro zelenou barvu a 435,8 nm pro modrou barvu. Kolorimetrická množství tchto mrných podnt jsou mítkem charakterizujícím danou barvu. Barvu lze popsat: - množstvím tí barevných podnt, tj.: trichromatickými složkami - jejich pomrem: trichromatickými souadnicemi.

21 Trichromatické složky se vypoítají integrací spektrálního složení barevného podntu F() a trichromatických lenitel v celém rozsahu viditelného spektra. Oznaují se X, Y, Z, resp. X 10, Y 10, Z 10 a jsou dány vztahy: X = k. F(λ). x (λ).dλ, Y = k. F(λ). y(λ). dλ, Z = k. F(λ). z(λ). dλ, resp: X 10 = k. F(λ). x 10 (λ).dλ, Y 10 = k. F(λ). y 10 (λ). dλ, Z 10 = k. F(λ). z 10 (λ). dλ.

22 Grafické prostorové vyjádení, kolorimetrický prostor XYZ, je nepraktické a proto se používá rovinný ez tímto prostorem: - kolorimetrický trojúhelník xy, (diagram chromatinosti xy), používající Trichromatické souadnice x,y,z pro které platí, že: x + y + z = 1 resp: x 10 + y 10 + z 10 = 1, a které se vypotou z trichromatických složek: resp: x = X / X+Y+Z, y = Y / X+Y+Z, z = Z / X+Y+Z, x 10 = X 10 / X 10 +Y 10 +Z 10,

23 Chromatický diagram CIE 1931 V kolorimetrickém prostoru XYZ i v jeho rovinném ezu, diagramu chromatinosti xy, neodpovídají stejné lineární vzdálenosti v rzných místech prostoru nebo trojúhelníku stejn subjektivn vnímaným rozdílm vjemu barvy (viz MacAdamsovy elipsy ).

24 Rovnomrná soustava CIE 1976 (L*u*v*), zkrácen CIELUV, (vychází z CIE UVW 1964, resp. CIE-uv 1960) je v prostoru urena temi vzájemn kolmými osami L*, u*, v*, a je definována rovnicemi pro pepoet z trichromatických složek X, Y, Z. Chromatický diagram CIE 1976

25 Druhá, pibližn rovnomrná soustava CIE 1976 (L*a*b*), resp. CIELAB je urena rovnž pomocí kolmých souadnic L*,a*,b* a je definována rovnicemi pro pepoet z trichromatických složek X,Y a Z.

26 Micí metody íselné údaje urující jednoznan barvu je možno získat rznými metodami, které lze rozdlit do tchto skupin: - mení spektrofotometrická spektrální charakteristika prvotních i druhotných zdroj se mí se mí monochromátorem a následným výpotem se urují trichromatické složky - mení srovnávacími kolorimetry do jedné poloviny zorného pole pístroje se zavádí mený barevný podnt, ve druhé polovin se aditivním nebo subtraktivním skládáním mrných podnt snažíme realizovat stejný barevný vjem - mení fotometrujícími kolorimetry v tomto pístroji se pímo zjistí velikost trichromatických složek pi tíkanálovém mení - srovnání se vzorkovnicí nejjednodušší, ale nejmén pesná metoda porovnání se vzorkovnicí barev

27 6. ZOBRAZENÍ BAREV 2D modely Zde se používají diagramy chromatinosti CIExy 1931, resp. CIEu v Tyto 2D diagramy jsou výhodné pro tídní barev,míchání barev a prakticky pro vtšinu výpot v kolorimetrii. 3D modely patrn nejstarším barevným modelem je z roku 1905 Munsellv model. Systém zohleduje lidské vnímání a souasné modely z nj vycházejí. Pracuje s termíny tón, jas i sytost.

28

29 V technické praxi je nejpoužívanjší na zaízeních nezávislý model CIELAB

30 Další asto užívané modely, hlavn pi skládání barev jsou modely RGB a CMY:

31

32 Pi poítaových barevných úpravách jsou asto používány modely HSB, HSV, HLS a podobné, pracující s pojmy: H Hue Barevný tón S Saturation, Chroma, Sytost B Brightness Jas L Lightness, Jas V Value Jas Model HLS

33 Model HSV V televizní a poítaové technice se užívají modely YUV, YC B C R a jim podobné, mající jasovou složku samostatnou a rozdílové barevné signály.

34 Pojem gamut: Žádné technické zaízení není schopno realizovat všechny reálné barvy obsažené v barevném diagramu, nap. CIE Každý technický prostedek pracuje s omezenou barevnou škálou, má svj gamut.

35

36 7. SKLÁDÁNÍ BAREV Složením tí základních barev lze získat libovolnou barvu. Aditivní, soutové skládání základních barevných svtel R,G,B : Tak jsou generovány barvy nap. v monitorech

37 Subtraktivní, odetové skládání doplkových barev C,M,Y : Na tomto principu pracují nap. tiskárny

38 A to je vše Na shledanou