Základním praktikum z optiky
|
|
|
- Mária Žáková
- před 8 lety
- Počet zobrazení:
Transkript
1 Úloha: Základním praktikum z optiky FJFI ČVUT v Praze #1 Polarizace světelného záření Jméno: Ondřej Finke Datum měření: Spolupracoval: Obor / Skupina: 1. Úvod Alexandr Špaček FE / E Klasifikace: Polarizace je jednou ze základních vlastností světla. Popisuje chování vektoru E v rovině kolmé na šíření vln. Světlo může být i nepolarizované, kdy se vektor E chová v rovině chaoticky. V opačném případě je světlo zcela polarizované a vektor E opisuje uzavřenou křivku, která je nejčastěji reprezentovaná elipsou. Příklady různých druhů polarizace jsou na přiloženém obrázku (Obr.1). Obr. 1 Příklady polarizace optického záření, převzato z [1]. Z obrázku je vidět důležitá vlastnost, kdy si můžeme vektor E rozložit do dvou vzájemně kolmých složek. Výsledná polarizace je závislá na jejich amplitudách a vzájemném fázovém posunu. Záření můžeme polarizovat užitím retardátorů nebo například různé polarizace pomocí polarizačního filtru filtrovat. 2. Měření a výsledky K měření jsme použili tyto pomůcky: Lineárně polarizovaný He-Ne laser (632nm), laserové ukazovátko (632nm), 2 zrcátka, dichroický polarizační filtr, Glan-Thompsonův polarizační hranol, čtvrtvlnná destička pro 632 nm, půlvlnná destička pro 632 nm, klínový depolarizátor, plastová fólie, detektor optického výkonu a stojánky k uchycení prvků. 2.1 Polarizace He-Ne laseru Nejdříve jsme museli zjistit propustnou osu dichroického polarizačního filtru. K tomu jsme využili - 1 -
2 obyčejné stolní lampy a sklíčka. Při Brewsterově úhlu se polarizace p, tedy polarizace rovnoběžná s rovinou dopadu, neodráží a veškeré záření přejde do druhého média [2]. Na optický stůl jsme položili sklíčko a přibližně pod Brewsterovým úhlem jsme sledovali odraz lampičky přes polarizační filtr. Otáčením polarizačního filtru jsme nalezli směr, kdy odraz lampičky na sklíčku zmizel. To je závěrný směr pro s polarizaci a Osa propustnosti je tím pádem kolmá na tento směr. Následně jsme zařadili filtr za již připravenou aparaturu složenou z laseru a zrcátek a hledali jsme jak je laser polarizovaný. Měřením jsme ukázali, že laser má rovinu polarizace kolmou na optický stůl. Polarizace je tedy lineární a vertikální. 2.2 Ověření Malusova zákona Malusův zákon má tvar (1), I=I 0 cos 2 θ (1) a popisuje vztah intenzity prošlého záření a úhlu θ mezi rovinou polarizace vstupního svazku a propustnou osou analyzátoru. I 0 představuje intenzitu vstupujícího svazku. Naměřené i vypočtené hodnoty jsme zanesli do tabulky (Tab. 1). Maximální vstupní intenzitu jsme naměřili I 0 = θ [ ] I měř [ - ] I vyp [ - ] Tab. 1 Hodnoty získané při ověřování Malusova zákona - 2 -
3 Měření jsme provedli pomocí Glan-Thompsonova hranolu a měřáku intenzity světla. Samostatný měřák měřil v neznámých jednotkách ale pro náš výpočet jsme potřebovali pouze absolutní hodnotu a proto jsme ani jednotky nezjišťovali. Pří měření jsme také naměřili větší hodnotu intenzity než I 0. To jsme svedli na špatnou manipulaci a zahřátí hranolu, proto jsme použili při výpočtech původní hodnotu I 0 o které si myslíme, že je přesnější. Intenzita světelného záření bez vloženého hranolu měla hodnotu I max = 128 a s hranolem již známou hodnotu I 0 = Absorpce hranolu je tedy 34% z příchozího záření. Námi naměření hodnoty vykreslíme společně s vypočtenýma hodnotami do grafu (Obr. 2) a porovnáme výsledek. Naměřené hodnoty proložíme křivkou odpovídající Malusově zákonu. Obr. 2 Naměřené a vypočtené hodnoty při měřené Malusova zákonu. Proložená křivka má parametry A = (87.64 ± 1.34), B = (0.979 ± 0.005) a C = (1.7 ± 0.8). Zákon se nám povedlo v rozumné míře dodržet. Naměřené hodnoty se od skutečných pravděpodobně lišily hlavně kvůli temnému proudu a světlu na pozadí měřáku intenzity a také nepravidelností použitého krystalu analyzátoru. 2.3 Změna lineární polarizace na kruhovou Pro převedení lineární polarizace na kruhovou jsme použili λ/4 destičku. Tato destička funguje tak, že fast vektoru E zpozdí fázi vůči druhé o π/2. To v našem případě povede ke kruhové polarizaci. Tu jsme na stůl umístily tak, aby úhel roviny polarizace laserového záření svíral úhel α = 50º vůči ose destičky. Na přiloženém schématu (Obr. 3) je vidět princip tvorby kruhové polarizace z lineární. Při rozboru na nákresu jsme došli k názoru, že v ideálním případě se nám povede vytvořit pravotočivá kruhová polarizace. V tomto případě by se při otáčení analyzátorem neměla měnit intenzita prošlého světla. Otáčeli jsme analyzátorem a hledali největší a nejmenší intenzitu. Naměřili jsme hodnoty I max = 42.3 při úhlu β = 350º na analyzátoru a I min = 39.5 s úhlem γ = 56º. Jelikož se intenzita mění můžeme předpokládat, že jsme nevytvořili dokonalou kruhovou polarizaci ale pouze polarizace eliptickou. To mohlo být způsobeno špatným nastavením úhlu λ/4 destičky, - 3 -
4 nebo také špatnou lineární polarizací vstupního záření. Také jsme změřili absorpci λ/4 retardátoru. Intenzita s retardátorem I sr = 122 a bez je I bez = Jednoduchým výpočtem zjistíme, že λ/4 destička pohlcuje 4% světla. Obr. 3 schéma změny polarizace v λ/4 destičce, které způsobí vytvoření pravotočivě kruhové polarizace z lineární. 2.4 Natočení roviny polarizace svazku Obr. 4 Schéma pootočení roviny polarizace o 40º pomocí λ/2 destičky. Před měřením jsme nalezli maximum intenzity při analyzátoru nastaveném na úhel α = 5º s hodnotou I α = Následně jsme přišli na to, že, aby se lineární svazek pootočil o 40º musíme použít λ/2, která bude vůči rovině polarizaci natočená o 20º. Nastavili jsme tedy λ/2 retardátor na úhel 25º a vložili mezi zdroj a analyzátor. Vzájemná fáze složek vektorů E se posunula o π
5 Otáčením analyzátoru jsme hledali opět největší intenzitu, kterou jsme očekávali kolem úhlu 45º. Tak se i opravdu stalo a největší intenzitu jsme naměřili přesně na úhlu β = 45º s hodnotou I β = 85. Z toho plyne, že se nám podařilo pootočit rovinu polarizace o 40º. Schéma pootočení je na přiloženém obrázku (Obr.4). Intenzita s retardátorem λ/2 I sr = a bez je I bez = 128 z toho plyne, že λ/2 destička pohlcuje 1% světla. 2.5 Depolarizace svazku Depolarizátor jsme vložili do aparatury před lineární polarizační filtr a dokázali jsme ho nastavit tak, že neměl na polarizaci úplně žádný vliv. Poté jsme ho nastavili tak, aby se při otáčení polarizačního filtru měnila intenzita svazku co nejméně. Při bližším pohledu na stínítko za polarizačním filtrem jsme si všimli, že depolarizátor rozložil svazek na dva různé svazky, které při otáčením polarizačního filtru střídavě mizeli a zase se objevovali. Z toho plyne, že depolarizátor rozdělil záření na dvě lineární polarizace, které jsou navzájem na sebe kolmé. Při vložení depolarizátoru za kruhovou polarizaci jsme nepozorovali žádnou změnu intenzit při otáčení polarizátorem. Kruhová polarizace je superpozicí dvou lineárních polarizací a za filtrem jsme neustále pozorovali alespoň jednu polarizaci. 2.6 Určení stupně polarizace světla Stupeň polarizace se určí pomocí Stokesových parametrů. Jejich hodnoty získáme pomocí měření intenzit pod různými úhly analyzátoru a také měřením intenzit kruhových polarizací. Tvar těchto parametrů je (2 5), s 0 =I 0º +I 90 º s 1 =I 0º I 90 º s 2 =I 45 º I 135º s 3 =I CR I CL (2) (3) (4) (5) a výsledný stupeň polarizace má tvar, P= s 1 2 +s 2 2 +s 3 2 s 0 (6) Měření kruhových polarizací jsme provedli pomocí λ/4 destičky. Předpokládali jsme, že když jsme z lineárně polarizovaného světla kolmého na desku stolu pomocí této destičky vytvořili pravotočivě polarizované světlo dostaneme opětovným použitím stejné destičky z pravotočivého světla světlo lineárně polarizované, které bude mít rovinu polarizace rovnoběžnou s deskou stolu. Takže z levotočivě kruhově polarizovaného světla získáme světlo lineárně polarizované s rovinou polarizace kolmou na desku stolu. Pomocí analyzátoru pak můžeme zařídit průchod pouze jedné lineární polarizace a tím pádem měřit intenzity jednotlivých kruhových polarizací. Do tabulky (Tab. 2) jsme zanesly naměřené hodnoty pro všechny měřené situace. Polarizace Laserové ukázovátko He-Ne laser s depolarizátorem He-Ne laser I 0º I 45º He-Ne laser s fólií - 5 -
6 I 90º I 135º I CR I CL P Tab. 2 Naměřené hodnoty a vypočtené stupně polarizace pro jednotlivé případy Podle předchozího měření jsme dosáhli názoru, že k největší depolarizaci svazku dochází je-li na depolarizačním filtru nastavený úhel 0º. Ten jsme pro toto měření použili. Stejně tak při použití fólie jsme použili úhel 220º na nástavci, protože jsme odhadli, že pod tímto úhel dochází k největší depolarizaci laserového záření. Při měření laserového ukazovátka mohl nastat problém u hodnoty intenzity I 135º, neboť tato hodnota se blíží zbytkovému světlu místnosti a temnému proudu měřáku. Tím bylo měření jistě znehodnoceno. Polarizace laserového ukazovátka i He-Ne laseru jsou lineární. Podle výsledku se nám pomocí depolarizátoru povedlo polarizace He-Ne laseru prakticky zrušit a vytvořit nepolarizované světlo. Vložení fólie do svazku naopak na polarizaci mělo pouze minimální vliv. 3. Závěr Na začátku jsme pomocí polarizačního filtru se známou osou propustnosti určili, že He-Ne laser je lineárně polarizován a jeho rovina polarizace je kolmá na desku optického stolu. Následně jsme ověřovali platnost Malusova zákona. Námi naměřené hodnoty se lišili pouze málo od hodnot vypočítaných podle vzorce (1). Lineární polarizaci laserového záření se nám nepovedlo změnit na pravotočivou kruhovou polarizaci ale pouze na polarizaci eliptickou ale podařilo se nám změnit natočení lineární polarizace o 40º. Na závěr jsme depolarizovali světlo, což jsme ukázali měření Stokesových parametrů a výpočtem stupně polarizace. Při tomto měření jsme také ukázali, že obyčejná plastová fólie má na polarizaci světla minimální vliv a laserové ukazovátko je také lineárně polarizované. 4. Použitá literatura [1] Návod k úloze 1 Polarizace světelného záření [online][ ], [2] Základy optiky 12ZAOP, přednášky 2, Marek Škereň [online][ ],
Vypracoval. Jakub Kákona Datum Hodnocení
 Úloha č. 1 - Polarizace světelného záření Název a číslo úlohy Datum měření 4. 5. 2011 Měření provedli Tomáš Zikmund, Jakub Kákona Vypracoval Jakub Kákona Datum Hodnocení 1 Zjištění polarizace LASERu Pro
Úloha č. 1 - Polarizace světelného záření Název a číslo úlohy Datum měření 4. 5. 2011 Měření provedli Tomáš Zikmund, Jakub Kákona Vypracoval Jakub Kákona Datum Hodnocení 1 Zjištění polarizace LASERu Pro
Polarizace čtvrtvlnovou destičkou
 Úkol : 1. Proměřte intenzitu lineárně polarizovaného světla jako funkci pozice analyzátoru. 2. Proměřte napětí na fotorezistoru ozářenou intenzitou světla za analyzátorem jako funkci úhlu mezi optickou
Úkol : 1. Proměřte intenzitu lineárně polarizovaného světla jako funkci pozice analyzátoru. 2. Proměřte napětí na fotorezistoru ozářenou intenzitou světla za analyzátorem jako funkci úhlu mezi optickou
Základním praktikum z laserové techniky
 Úloha: Základním praktikum z laserové techniky FJFI ČVUT v Praze #6 Nelineární transmise saturovatelných absorbérů Jméno: Ondřej Finke Datum měření: 30.3.016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr
Úloha: Základním praktikum z laserové techniky FJFI ČVUT v Praze #6 Nelineární transmise saturovatelných absorbérů Jméno: Ondřej Finke Datum měření: 30.3.016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 1.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Měření s polarizovaným světlem
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 9: Měření s polarizovaným světlem Datum měření: 29. 4. 2016 Doba vypracovávání: 8 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání
Fyzikální praktikum FJFI ČVUT v Praze Úloha 9: Měření s polarizovaným světlem Datum měření: 29. 4. 2016 Doba vypracovávání: 8 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání
Zadání. Pracovní úkol. Pomůcky
 Pracovní úkol Zadání 1. Najděte směr snadného průchodu polarizátoru užívaného v aparatuře. 2. Ověřte, že zdroj světla je polarizován kolmo k vodorovné rovině. 3. Na přiložených vzorcích proměřte závislost
Pracovní úkol Zadání 1. Najděte směr snadného průchodu polarizátoru užívaného v aparatuře. 2. Ověřte, že zdroj světla je polarizován kolmo k vodorovné rovině. 3. Na přiložených vzorcích proměřte závislost
Základním praktikum z optiky
 Úloha: Základním praktikum z optiky FJFI ČVUT v Praze #6 - Zdroje optického záření a jejich vlastnosti Jméno: Ondřej Finke Datum měření: 7.4.2016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr Špaček
Úloha: Základním praktikum z optiky FJFI ČVUT v Praze #6 - Zdroje optického záření a jejich vlastnosti Jméno: Ondřej Finke Datum měření: 7.4.2016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr Špaček
LMF 2. Optická aktivita látek. Postup :
 LMF 2 Optická aktivita látek Úkoly : 1. Určete specifickou otáčivost látky měřením pro známou koncentraci roztoku 2. Měření opakujte pro různé koncentrace a vyneste závislost úhlu stočení polarizační roviny
LMF 2 Optická aktivita látek Úkoly : 1. Určete specifickou otáčivost látky měřením pro známou koncentraci roztoku 2. Měření opakujte pro různé koncentrace a vyneste závislost úhlu stočení polarizační roviny
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Mikrovlny
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 25.3.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Mikrovlny Abstrakt V úloze je
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 25.3.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Mikrovlny Abstrakt V úloze je
18. dubna Fyzikální praktikum FJFI ČVUT v Praze
 9 Měření s polarizovaným světlem 18. dubna 010 Fyzikální praktikum FJFI ČVUT v Praze Jméno: Vojtěch Horný Datum měření: 1.4.010 Pracovní skupina: Ročník a kroužek:. ročník, pondělí 13:30 Spolupracoval
9 Měření s polarizovaným světlem 18. dubna 010 Fyzikální praktikum FJFI ČVUT v Praze Jméno: Vojtěch Horný Datum měření: 1.4.010 Pracovní skupina: Ročník a kroužek:. ročník, pondělí 13:30 Spolupracoval
Úkoly. 1 Teoretický úvod. 1.1 Mikroskop
 Úkoly 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chyby měření. 2. Změřte zvětšení a zorná pole mikroskopu pro
Úkoly 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chyby měření. 2. Změřte zvětšení a zorná pole mikroskopu pro
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Balrmerova série Datum měření: 13. 5. 016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Úloha V.E... nezbedné fotony 1 bodů; (chybí statistiky) Spolu se zadáním úlohy vám přišly polarizační brýle. Máte tedy polarizační filtry. Když je dáte za sebe tak, aby směry jejich polarizace byly na
Měření s polarizovaným světlem
 Fyzikální praktikum FJFI ČVUT v Praze Úloha č. 9 : Měření s polarizovaným světlem Jméno: Ondřej Ticháček Pracovní skupina: 7 Kruh: ZS 7 Datum měření: 18.3.2013 Klasifikace: Měření s polarizovaným světlem
Fyzikální praktikum FJFI ČVUT v Praze Úloha č. 9 : Měření s polarizovaným světlem Jméno: Ondřej Ticháček Pracovní skupina: 7 Kruh: ZS 7 Datum měření: 18.3.2013 Klasifikace: Měření s polarizovaným světlem
Zadání. Pracovní úkol. Pomůcky
 Pracovní úkol Zadání 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chybu měření. 2. Změřte zvětšení a zorná pole
Pracovní úkol Zadání 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. Odhadněte maximální chybu měření. 2. Změřte zvětšení a zorná pole
42 Polarizované světlo Malusův zákon a Brewsterův úhel
 42 Polarizované světlo Malusův zákon a rewsterův úhel ÚKOL 1. Ověřte platnost Malusova 1 zákona. 2. Změřte rewsterův 2 úhel a nalezněte relativní index lomu dvou prostředí. (Výslovnost: rewster ['bru:stər,
42 Polarizované světlo Malusův zákon a rewsterův úhel ÚKOL 1. Ověřte platnost Malusova 1 zákona. 2. Změřte rewsterův 2 úhel a nalezněte relativní index lomu dvou prostředí. (Výslovnost: rewster ['bru:stər,
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí
 Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
Vypracoval Datum Hodnocení. V celé úloze jsme používali He-Ne laser s vlnovou délkou λ = 632, 8 nm. Paprsek jsme nasměrovali
 Název a číslo úlohy - Difrakce světelného záření Datum měření 3.. 011 Měření proveli Tomáš Zikmun, Jakub Kákona Vypracoval Tomáš Zikmun Datum. 3. 011 Honocení 1 Difrakční obrazce V celé úloze jsme používali
Název a číslo úlohy - Difrakce světelného záření Datum měření 3.. 011 Měření proveli Tomáš Zikmun, Jakub Kákona Vypracoval Tomáš Zikmun Datum. 3. 011 Honocení 1 Difrakční obrazce V celé úloze jsme používali
Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí
 Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí Rovinné vlny 1 Při diskusi o řadě jevů je výhodné vycházet z rovinných vln. Vlny musí splňovat Maxwellovy rovnice
Postupné, rovinné, monochromatické vlny v lineárním izotropním nemagnetickém prostředí Rovinné vlny 1 Při diskusi o řadě jevů je výhodné vycházet z rovinných vln. Vlny musí splňovat Maxwellovy rovnice
P o l a r i z a c e s v ě t l a
 Ú k o l : P o l a r i z a c e s v ě t l a 1. Pozorovat různé polarizační stavy světla. 2. Seznámit se s funkcí optického polarizátoru. 3. Experimentálně prověřit zákon Maluse. P o t ř e b y : Viz seznam
Ú k o l : P o l a r i z a c e s v ě t l a 1. Pozorovat různé polarizační stavy světla. 2. Seznámit se s funkcí optického polarizátoru. 3. Experimentálně prověřit zákon Maluse. P o t ř e b y : Viz seznam
Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako
![Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako](/thumbs/55/36333813.jpg) Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Mikrovlny. K. Kopecká*, J. Vondráček**, T. Pokorný***, O. Skowronek****, O. Jelínek*****
 Mikrovlny K. Kopecká*, J. Vondráček**, T. Pokorný***, O. Skowronek****, O. Jelínek***** *Gymnázium Česká Lípa, **,*****Gymnázium Děčín, ***Gymnázium, Brno, tř. Kpt. Jaroše,**** Gymnázium Františka Hajdy,
Mikrovlny K. Kopecká*, J. Vondráček**, T. Pokorný***, O. Skowronek****, O. Jelínek***** *Gymnázium Česká Lípa, **,*****Gymnázium Děčín, ***Gymnázium, Brno, tř. Kpt. Jaroše,**** Gymnázium Františka Hajdy,
Tabulka I Měření tloušťky tenké vrstvy
 Pracovní úkol 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
Pracovní úkol 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
2 Nd:YAG laser buzený laserovou diodou
 2 Nd:YAG laser buzený laserovou diodou 15. května 2011 Základní praktikum laserové techniky Zpracoval: Vojtěch Horný Datum měření: 12. května 2011 Pracovní skupina: 1 Ročník: 3. Naměřili: Vojtěch Horný,
2 Nd:YAG laser buzený laserovou diodou 15. května 2011 Základní praktikum laserové techniky Zpracoval: Vojtěch Horný Datum měření: 12. května 2011 Pracovní skupina: 1 Ročník: 3. Naměřili: Vojtěch Horný,
7 FYZIKÁLNÍ OPTIKA. Interference Ohyb Polarizace. Co je to ohyb? 27.2 Ohyb
 1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
APO seminář 5: OPTICKÉ METODY v APO
 APO seminář 5: OPTICKÉ METODY v APO Princip: fyzikální metody založené na interakci vzorku s elektromagnetickým zářením nebo na sledování vyzařování elektromagnetického záření vzorkem nespektrální metody
APO seminář 5: OPTICKÉ METODY v APO Princip: fyzikální metody založené na interakci vzorku s elektromagnetickým zářením nebo na sledování vyzařování elektromagnetického záření vzorkem nespektrální metody
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou.
 1 Pracovní úkoly 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. 2. Změřte zvětšení a zorná pole mikroskopu pro všechny možné kombinace
1 Pracovní úkoly 1. Z přiložených objektivů vyberte dva, použijte je jako lupy a změřte jejich zvětšení a zorná pole přímou metodou. 2. Změřte zvětšení a zorná pole mikroskopu pro všechny možné kombinace
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE. Úloha 5: Měření tíhového zrychlení
 ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE Datum měření: číslo skupiny: Spolupracovali: 1 Úvod 1.1 Pracovní úkoly [1] Úloha 5: Měření tíhového zrychlení Jméno: Ročník, kruh: Klasifikace: 1. V domácí
ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE Datum měření: číslo skupiny: Spolupracovali: 1 Úvod 1.1 Pracovní úkoly [1] Úloha 5: Měření tíhového zrychlení Jméno: Ročník, kruh: Klasifikace: 1. V domácí
Neživá příroda I. Optické vlastnosti minerálů
 Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
FYZIKA II. Marek Procházka 1. Přednáška
 FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
Fyzikální praktikum FJFI ČVUT v Praze. Úloha č. 8 : Mikrovlny
 Fyzikální praktikum FJFI ČVUT v Praze Úloha č. 8 : Mikrovlny Jméno: Ondřej Ticháček Pracovní skupina: 7 Kruh: ZS 7 Datum měření:.. Klasifikace: Mikrovlny Zadání. Ověřte, že pole před zářičem je lineárně
Fyzikální praktikum FJFI ČVUT v Praze Úloha č. 8 : Mikrovlny Jméno: Ondřej Ticháček Pracovní skupina: 7 Kruh: ZS 7 Datum měření:.. Klasifikace: Mikrovlny Zadání. Ověřte, že pole před zářičem je lineárně
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Úlohač.XI. Název: Měření stočení polarizační roviny
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úlohač.XI Název: Měření stočení polarizační roviny Vypracoval: Petr Škoda Stud. skup.: F14 Dne: 10.3.2006 Odevzdaldne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úlohač.XI Název: Měření stočení polarizační roviny Vypracoval: Petr Škoda Stud. skup.: F14 Dne: 10.3.2006 Odevzdaldne:
Mikrovlny. 1 Úvod. 2 Použité vybavení
 Mikrovlny * P. Spáčil, ** J. Pavelka, *** F. Jareš, **** V. Šopík Gymnázium Vídeňská Brno; ** Gymnázium tř. Kpt. Jaroše; *** Arcibiskupské gymnázium; **** Gymnázium Jeseník; pavelspacil@tiscali.cz; **
Mikrovlny * P. Spáčil, ** J. Pavelka, *** F. Jareš, **** V. Šopík Gymnázium Vídeňská Brno; ** Gymnázium tř. Kpt. Jaroše; *** Arcibiskupské gymnázium; **** Gymnázium Jeseník; pavelspacil@tiscali.cz; **
Balmerova série. F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3
 Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
Fyzikální praktikum 1
 Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #10 Lineární harmonický oscilátor a Pohlovo kyvadlo Jméno: Ondřej Finke Datum měření: 10.11.2014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) Změřte
Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #10 Lineární harmonický oscilátor a Pohlovo kyvadlo Jméno: Ondřej Finke Datum měření: 10.11.2014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) Změřte
Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]
![Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A] Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]](/thumbs/27/10456203.jpg) Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
Jméno a příjmení. Ročník. Měřeno dne. Marek Teuchner Příprava Opravy Učitel Hodnocení. 1 c p. = (ε r
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Lab. skup. Spolupracoval Měřeno dne Odevzdáno dne Marek Teuchner 11. 3. 2013 25. 3.
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Jméno a příjmení Petr Švaňa Ročník 1 Předmět IFY Kroužek 38 ID 155793 Lab. skup. Spolupracoval Měřeno dne Odevzdáno dne Marek Teuchner 11. 3. 2013 25. 3.
Datum měření: 9.3. 2009, skupina: 9. v pondělí 13:30, klasifikace: Abstrakt
 Fyzikální praktikum 9. Měření s polarizovaným světlem Tomáš Odstrčil, Tomáš Markovič Datum měření: 9.3. 2009, skupina: 9. v pondělí 13:30, klasifikace: Abstrakt Pokusíme se změřit stupeň polarizace při
Fyzikální praktikum 9. Měření s polarizovaným světlem Tomáš Odstrčil, Tomáš Markovič Datum měření: 9.3. 2009, skupina: 9. v pondělí 13:30, klasifikace: Abstrakt Pokusíme se změřit stupeň polarizace při
UNIVERZITA PALACKÉHO V OLOMOUCI. Přírodovědecká fakulta. Katedra optiky. Jana Grézlová. Obor: Digitální a přístrojová optika.
 UNIVERZITA PALACKÉHO V OLOMOUCI Přírodovědecká fakulta Katedra optiky Jana Grézlová Obor: Digitální a přístrojová optika Optimalizace podmínek použití širokopásmových zrcadel a dichroických filtrů ve spektrometru
UNIVERZITA PALACKÉHO V OLOMOUCI Přírodovědecká fakulta Katedra optiky Jana Grézlová Obor: Digitální a přístrojová optika Optimalizace podmínek použití širokopásmových zrcadel a dichroických filtrů ve spektrometru
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Cavendishův experiment Datum měření: 3. 1. 015 Skupina: 8, čtvrtek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě odvoďte vztah pro
Fyzikální praktikum FJFI ČVUT v Praze Úloha 4: Cavendishův experiment Datum měření: 3. 1. 015 Skupina: 8, čtvrtek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě odvoďte vztah pro
Abstrakt. fotodioda a fototranzistor) a s jejich základními charakteristikami.
 Název a číslo úlohy: 9 Detekce optického záření Datum měření: 4. května 2 Měření provedli: Vojtěch Horný, Jaroslav Zeman Vypracovali: Vojtěch Horný a Jaroslav Zeman společnými silami Datum: 4. května 2
Název a číslo úlohy: 9 Detekce optického záření Datum měření: 4. května 2 Měření provedli: Vojtěch Horný, Jaroslav Zeman Vypracovali: Vojtěch Horný a Jaroslav Zeman společnými silami Datum: 4. května 2
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 12: Sonar Datum měření: 5. 11. 2015 Skupina: 8, čtvrtek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V domácí přípravě spočítejte úhel prvních
Fyzikální praktikum FJFI ČVUT v Praze Úloha 12: Sonar Datum měření: 5. 11. 2015 Skupina: 8, čtvrtek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V domácí přípravě spočítejte úhel prvních
Úloha 10: Interference a ohyb světla
 Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
2 (3) kde S je plocha zdroje. Protože jas zdroje není závislý na směru, lze vztah (5) přepsat do tvaru:
 Pracovní úkol 1. Pomocí fotometrického luxmetru okalibrujte normální žárovku (stanovte její svítivost). Pro určení svítivosti normální žárovky (a její chyby) vyneste do grafu závislost osvětlení na převrácené
Pracovní úkol 1. Pomocí fotometrického luxmetru okalibrujte normální žárovku (stanovte její svítivost). Pro určení svítivosti normální žárovky (a její chyby) vyneste do grafu závislost osvětlení na převrácené
Fyzikální praktikum 1
 Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #9 Základní experimenty akustiky Jméno: Ondřej Finke Datum měření: 3.11.014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě spočítejte,
Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #9 Základní experimenty akustiky Jméno: Ondřej Finke Datum měření: 3.11.014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě spočítejte,
Měření a analýza mechanických vlastností materiálů a konstrukcí. 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály
 FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 8: Mikrovlny. Abstrakt
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření:. 3. Úloha 8: Mikrovlny Jméno: Jiří Slabý Pracovní skupina: 4 Ročník a kroužek:. ročník,. kroužek, pondělí 3:3 Spolupracovala: Eliška Greplová Hodnocení:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření:. 3. Úloha 8: Mikrovlny Jméno: Jiří Slabý Pracovní skupina: 4 Ročník a kroužek:. ročník,. kroužek, pondělí 3:3 Spolupracovala: Eliška Greplová Hodnocení:
ZJIŠŤOVÁNÍ CUKERNATOSTI VODNÝCH ROZTOKŮ OPTICKÝMI METODAMI
 ZJIŠŤOVÁNÍ CUKERNATOSTI VODNÝCH ROZTOKŮ OPTICKÝMI METODAMI FILÍPEK Josef, ČR DETERMINATION OF SUGAR CONTENT IN WATER SOLUTIONS BY OPTICAL METHODS Abstract The content of saccharose in water solution influences
ZJIŠŤOVÁNÍ CUKERNATOSTI VODNÝCH ROZTOKŮ OPTICKÝMI METODAMI FILÍPEK Josef, ČR DETERMINATION OF SUGAR CONTENT IN WATER SOLUTIONS BY OPTICAL METHODS Abstract The content of saccharose in water solution influences
Úloha 3: Mřížkový spektrometr
 Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Vznik a šíření elektromagnetických vln
 Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
Fyzikální praktikum 1
 Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #11 Dynamika rotačního pohybu Jméno: Ondřej Finke Datum měření: 24.11.2014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě odvoďte
Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #11 Dynamika rotačního pohybu Jméno: Ondřej Finke Datum měření: 24.11.2014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě odvoďte
Úloha 8: Studium ultrazvukových vln
 Úloha 8: Studium ultrazvukových vln FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 30.11.2009 Jméno: František Batysta Pracovní skupina: 11 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovníci:
Úloha 8: Studium ultrazvukových vln FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 30.11.2009 Jméno: František Batysta Pracovní skupina: 11 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovníci:
 Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Jan Fait, Filip Grepl Jan Fait Datum Hodnocení
 Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Digitální učební materiál
 Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úloha 3. Vzduchová dráha - ZZE, srážky, impuls síly Autor David Horák Datum měření 21. 11. 2011 Kruh 1 Skupina 7 Klasifikace 1. PRACOVNÍ ÚKOLY: 1) Elastické srážky:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úloha 3. Vzduchová dráha - ZZE, srážky, impuls síly Autor David Horák Datum měření 21. 11. 2011 Kruh 1 Skupina 7 Klasifikace 1. PRACOVNÍ ÚKOLY: 1) Elastické srážky:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 10: Interference a ohyb světla
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 8.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 10: Interference a ohyb
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 8.4.2011 Jméno: Jakub Kákona Pracovní skupina: 4 Ročník a kroužek: Pa 9:30 Spolupracovníci: Jana Navrátilová Hodnocení: Úloha 10: Interference a ohyb
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
(3) Zvolíme pevné z a sledujme dráhu, kterou opisuje s postupujícím časem koncový bod vektoru E v rovině z = konst. Upravíme vztahy (2) a (3)
 Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. obor (kruh) FMUZV (73) dne
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 11 Název: Stáčení polarizační roviny Pracoval: Lukáš Vejmelka obor (kruh) FMUZV (73) dne 7.4.2014 Odevzdal dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 11 Název: Stáčení polarizační roviny Pracoval: Lukáš Vejmelka obor (kruh) FMUZV (73) dne 7.4.2014 Odevzdal dne:
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie
 Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
Grafické řešení: obvod s fotodiodou
 1.11.2011 2E/95 Grafické řešení: obvod s fotodiodou Zadání: Graficky určete napětí zdroje ε a zatěžovací odpor R, potřebný k dosažení požadovaného efektu změnou osvětlení: a) získání velké proudové citlivosti
1.11.2011 2E/95 Grafické řešení: obvod s fotodiodou Zadání: Graficky určete napětí zdroje ε a zatěžovací odpor R, potřebný k dosažení požadovaného efektu změnou osvětlení: a) získání velké proudové citlivosti
Studium ultrazvukových vln
 Číslo úlohy: 8 Jméno: Vojtěch HORNÝ Spolupracoval: Jaroslav Zeman Datum měření: 12. 10. 2009 Číslo kroužku: pondělí 13:30 Číslo skupiny: 6 Klasifikace: Fyzikální praktikum FJFI ČVUT v Praze Studium ultrazvukových
Číslo úlohy: 8 Jméno: Vojtěch HORNÝ Spolupracoval: Jaroslav Zeman Datum měření: 12. 10. 2009 Číslo kroužku: pondělí 13:30 Číslo skupiny: 6 Klasifikace: Fyzikální praktikum FJFI ČVUT v Praze Studium ultrazvukových
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
METODY BEZ VÝMĚNY ENERGIE MEZI ZÁŘENÍM A VZORKEM
 METODY BEZ VÝMĚNY ENERGIE MEZI ZÁŘENÍM A VZORKEM REFRAKTOMETRIE POLARIMETRIE SPEKTROMETRIE VYUŽÍVAJÍCÍ ROZPTYL MĚŘENÍ VELIKOSTI ČÁSTIC (c) -2012 REFRAKTOMETRIE Metoda založená na měření indexu lomu látek
METODY BEZ VÝMĚNY ENERGIE MEZI ZÁŘENÍM A VZORKEM REFRAKTOMETRIE POLARIMETRIE SPEKTROMETRIE VYUŽÍVAJÍCÍ ROZPTYL MĚŘENÍ VELIKOSTI ČÁSTIC (c) -2012 REFRAKTOMETRIE Metoda založená na měření indexu lomu látek
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Michal Němec Katedra fyzikální elektroniky České vysoké učení technické v Praze michal.nemec@fjfi.cvut.cz Kontakty Ing. Michal Němec,
Úvod do laserové techniky Světlo jako elektromagnetické záření I. část Michal Němec Katedra fyzikální elektroniky České vysoké učení technické v Praze michal.nemec@fjfi.cvut.cz Kontakty Ing. Michal Němec,
Fabry Perotův interferometr
 Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
27. Vlnové vlastnosti světla
 27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
P5: Optické metody I
 P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
8. Anizotropní prostředí
 Trivium z optik 55 8 Anizotropní prostředí Doposud jsme se zabývali šířením světla v izotropních prostředích To jest v takových prostředích, v nichž rchlost světla nezávisí na směru jeho šíření V této
Trivium z optik 55 8 Anizotropní prostředí Doposud jsme se zabývali šířením světla v izotropních prostředích To jest v takových prostředích, v nichž rchlost světla nezávisí na směru jeho šíření V této
Zadání. Pracovní úkol. Pomůcky
 Pracovní úkol Zadání 1. Změřte ohniskovou vzdálenost tenké ploskovypuklé (plankonvexní) čočky jednak Besselovou metodou, jednak metodou dvojího zvětšení. 2. Z následujících možností vyberte jednu: a. Změřte
Pracovní úkol Zadání 1. Změřte ohniskovou vzdálenost tenké ploskovypuklé (plankonvexní) čočky jednak Besselovou metodou, jednak metodou dvojího zvětšení. 2. Z následujících možností vyberte jednu: a. Změřte
Praktikum III - Optika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 1 Název: Studium rotační disperze křemene a Kerrova jevu v kapalině Pracoval: Matyáš Řehák stud.sk.:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 1 Název: Studium rotační disperze křemene a Kerrova jevu v kapalině Pracoval: Matyáš Řehák stud.sk.:
8 b) POLARIMETRIE. nepolarizovaná vlna
 1. TEORETICKÝ ÚVO Rotační polarizace Světlo má zároveň povahu vlnového i korpuskulárního záření. V optických jevech se světlo chová jako příčné vlnění, přičemž světelné kmity probíhají všemi směry a směr
1. TEORETICKÝ ÚVO Rotační polarizace Světlo má zároveň povahu vlnového i korpuskulárního záření. V optických jevech se světlo chová jako příčné vlnění, přičemž světelné kmity probíhají všemi směry a směr
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Obrázek 2: Experimentální zařízení pro E-I. [1] Dřevěná základna [11] Plastové kolíčky [2] Laser s podstavcem a držákem [12] Kulaté černé nálepky [3]
![Obrázek 2: Experimentální zařízení pro E-I. [1] Dřevěná základna [11] Plastové kolíčky [2] Laser s podstavcem a držákem [12] Kulaté černé nálepky [3] Obrázek 2: Experimentální zařízení pro E-I. [1] Dřevěná základna [11] Plastové kolíčky [2] Laser s podstavcem a držákem [12] Kulaté černé nálepky [3]](/thumbs/27/11102316.jpg) Stránka 1 ze 6 Difrakce na šroubovici (Celkový počet bodů: 10) Úvod Rentgenový difrakční obrázek DNA (obr. 1) pořízený v laboratoři Rosalindy Franklinové, známý jako Fotka 51 se stal základem pro objev
Stránka 1 ze 6 Difrakce na šroubovici (Celkový počet bodů: 10) Úvod Rentgenový difrakční obrázek DNA (obr. 1) pořízený v laboratoři Rosalindy Franklinové, známý jako Fotka 51 se stal základem pro objev
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky
 Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Světlo x elmag. záření. základní principy
 Světlo x elmag. záření základní principy Jak vzniká a co je to duha? Spektrum elmag. záření Viditelné 380 760 nm, UV 100 380 nm, IR 760 nm 1mm Spektrum elmag. záření Harmonická vlna Harmonická vlna E =
Světlo x elmag. záření základní principy Jak vzniká a co je to duha? Spektrum elmag. záření Viditelné 380 760 nm, UV 100 380 nm, IR 760 nm 1mm Spektrum elmag. záření Harmonická vlna Harmonická vlna E =
Modulace vlnoplochy. SLM vytváří prostorově modulovaný koherentní optický signál
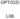 OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
RYCHLOST SVĚTLA PROSEMINÁŘ Z OPTIKY
 RYCHLOST SVĚTLA PROSEMINÁŘ Z OPTIKY JE RYCHLOST SVĚTLA NEKONEČNÁ? Galileo podporuje Aristotelovu (a Descartovu) pozici, Každodenní zkušenost ukazuje, že rychlost světla je nekonečná, protože když uvidíme
RYCHLOST SVĚTLA PROSEMINÁŘ Z OPTIKY JE RYCHLOST SVĚTLA NEKONEČNÁ? Galileo podporuje Aristotelovu (a Descartovu) pozici, Každodenní zkušenost ukazuje, že rychlost světla je nekonečná, protože když uvidíme
Přednáška č.14. Optika
 Přednáška č.14 Optika Obsah základní pojmy odraz a lom světla disperze polarizace geometrická optika elektromagnetické záření Světlo = elektromagnetické vlnění o vlnové délce 390nm (fialové) až 790nm (červené)
Přednáška č.14 Optika Obsah základní pojmy odraz a lom světla disperze polarizace geometrická optika elektromagnetické záření Světlo = elektromagnetické vlnění o vlnové délce 390nm (fialové) až 790nm (červené)
5 Geometrická optika
 5 Geometrická optika 27. března 2010 Fyzikální praktikum FJFI ČVUT v Praze Jméno: Vojtěch Horný Datum měření: 22.března 2010 Pracovní skupina: 2 Ročník a kroužek: 2. ročník, pondělí 13:30 Spolupracoval
5 Geometrická optika 27. března 2010 Fyzikální praktikum FJFI ČVUT v Praze Jméno: Vojtěch Horný Datum měření: 22.března 2010 Pracovní skupina: 2 Ročník a kroužek: 2. ročník, pondělí 13:30 Spolupracoval
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Měření závislosti indexu lomu kapalin na vlnové délce
 Měření závislosti indexu lomu kapalin na vlnové délce TOMÁŠ KŘIVÁNEK Přírodovědecká fakulta Masarykovy univerzity, Brno Abstrakt V příspěvku je popsán jednoduchý experiment pro demonstraci a měření závislosti
Měření závislosti indexu lomu kapalin na vlnové délce TOMÁŠ KŘIVÁNEK Přírodovědecká fakulta Masarykovy univerzity, Brno Abstrakt V příspěvku je popsán jednoduchý experiment pro demonstraci a měření závislosti
Praktikum školních pokusů 2
 Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
Praktikum školních pokusů 2 Optika 3A Interference a difrakce světla Jana Jurmanová Přírodovědecká fakulta Masarykovy univerzity, Brno I Interference na dvojštěrbině Odvod te vztah pro polohu interferenčních
Po stopách Alberta Michelsona, Marina Mersenna a dalších
 Po stopách Alberta Michelsona, Marina Mersenna a dalších J. Dvořák, Gymnázium Botičská, Praha 1, dvorak1430@seznam.cz K. Rydlo, Gymnázium Dobruška, Krystof.Rydlo176@gmail.com V. Mikeska, Gymnázium Františka
Po stopách Alberta Michelsona, Marina Mersenna a dalších J. Dvořák, Gymnázium Botičská, Praha 1, dvorak1430@seznam.cz K. Rydlo, Gymnázium Dobruška, Krystof.Rydlo176@gmail.com V. Mikeska, Gymnázium Františka
Mikroskopické metody Přednáška č. 3. Základy mikroskopie. Kontrast ve světelném mikroskopu
 Mikroskopické metody Přednáška č. 3 Základy mikroskopie Kontrast ve světelném mikroskopu Nízký kontrast biologických objektů Nízký kontrast biologických objektů Metodika přípravy objektů pro světelnou
Mikroskopické metody Přednáška č. 3 Základy mikroskopie Kontrast ve světelném mikroskopu Nízký kontrast biologických objektů Nízký kontrast biologických objektů Metodika přípravy objektů pro světelnou
Úloha 5: Studium rentgenových spekter Mo a Cu anody
 Úloha 5: Studium rentgenových spekter Mo a Cu anody FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 22.2.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník:
Úloha 5: Studium rentgenových spekter Mo a Cu anody FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 22.2.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník:
Lom světla na kapce, lom 1., 2. a 3. řádu Lom světla na kapce, jenž je reprezentována kulovou plochou rozhraní, je složitý mechanismus rozptylu dopada
 Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Modelování blízkého pole soustavy dipólů
 1 Úvod Modelování blízkého pole soustavy dipólů J. Puskely, Z. Nováček Ústav radioelektroniky, Fakulta elektrotechniky a komunikačních technologií, VUT v Brně Purkyňova 118, 612 00 Brno Abstrakt Tento
1 Úvod Modelování blízkého pole soustavy dipólů J. Puskely, Z. Nováček Ústav radioelektroniky, Fakulta elektrotechniky a komunikačních technologií, VUT v Brně Purkyňova 118, 612 00 Brno Abstrakt Tento
Mechanické kmitání a vlnění, Pohlovo kyvadlo
 Fyzikální praktikum FJFI ČVUT v Praze Mechanické kmitání a vlnění, Pohlovo kyvadlo Číslo úlohy: 10 Jméno: Vojtěch HORNÝ Spolupracoval: Jaroslav Zeman Datum : 26. 10. 2009 Číslo kroužku: pondělí 13:30 Číslo
Fyzikální praktikum FJFI ČVUT v Praze Mechanické kmitání a vlnění, Pohlovo kyvadlo Číslo úlohy: 10 Jméno: Vojtěch HORNÝ Spolupracoval: Jaroslav Zeman Datum : 26. 10. 2009 Číslo kroužku: pondělí 13:30 Číslo
3. Diskutujte výsledky měření z hlediska platnosti Biot-Savartova zákona.
 1 Pracovní úkol 1. Změřte závislost výchlk magnetometru na proudu protékajícím cívkou. Měření proveďte pro obě cívk a různé počt závitů (5 a 10). Maximální povolený proud obvodem je 4. 2. Výsledk měření
1 Pracovní úkol 1. Změřte závislost výchlk magnetometru na proudu protékajícím cívkou. Měření proveďte pro obě cívk a různé počt závitů (5 a 10). Maximální povolený proud obvodem je 4. 2. Výsledk měření
