Numerická simulace proudění v hydrostatickém ložisku
|
|
|
- Denis Beránek
- před 9 lety
- Počet zobrazení:
Transkript
1 Numerická simulace proudění v hydrostatickém ložisku Martin Hanek Vedoucí práce prof. RNDr. Pavel Burda, CSc. Školitelé specialisti Ing. Jakub Šístek, PhD., Ing. Eduard Stach Abstrakt Ve své práci se zabývám numerickým řešením Navierových-Stokesových rovnic pro stacionární proudění v hydrostatickém ložisku pomocí metody konečných prvků. Nejprve se věnuji 2D úloze pro rotačně symetrické proudění a poté se zabývám problematikou řešení 3D úlohy, kde využiji rozklad oblasti na nepřekrývající se podoblasti a předpodmiňovač BDDC. Klíčová slova hydrostatické ložisko, Navierovy-Stokesovy rovnice, metoda konečných prvků, BDDC 1 Úvod Ve své práci se zabývám numerickou simulací stacionárního nestlačitelného proudění uvnitř hydrostatického ložiska v hydrostatickém vedení pomocí metody konečných prvků. Problematikou hydrostatického vedení se zabívají na Ústavu výrobních strojů a zařízení fakulty strojní ČVU v Praze (více o této problematice viz Holkup a kol. 3). ato práce vychází z mé bakalářské práce, v níž jsem se zabýval rotačně symetrickou 2D úlohou a jejíž výsledky zde mimo jiné prezentuji (více viz Hanek 4). ato úloha odpovídá vedení v klidu a její výsledky jsem měl možnost ověřit experimentem. Dále se zabývám problematikou řešení 3D úlohy, a tedy i úlohou s pohybem dolním stěny, kde pro numerický výpočet využiji rozklad oblasti a předpodmiňovač BDDC (Ballancing Domain Decomposition by Constraints). Nejprve se v 2. kapitole věnuji slabé formulaci úloh. Ve 3. kapitole se zabývám použitím metody konečných prvků pro oba typy úloh. Kapitola 4. pak ukazuje použití rozkladu oblasti a způsob použití BDDC pro 3D úlohu a v 5. kapitole pak uvádím numerické výsledky jednotlivých úloh. Výpočty provádím pro ložisko s rotačně symetrickou hydrostatickou kapsou, což je oblast, ve které proudí tekutina. Na Obrázku 1 je pro ilustraci fotografie reálné kapsy a 3D model její oblasti řešení. 1
2 Obrázek 1: Hydrostatická kapsa (vlevo) a model 3D oblasti tekutiny (vpravo) 2 Slabá formulace úlohy Ve svých výpočtech uvažuji stacionární nestlačitelné proudění. o odpovídá Navierovým-Stokesovým rovnicím ve tvaru ( např. 1) (u )u ν u + p = f v, (1) u = v, (2) kde u je neznámý vektor rychlosti, p je neznámý tlak, ν je daná kinematická viskozita tekutiny, f je známý vektor objemových sil a je oblast na které úlohu řeším. Při odvození slabé formulace rotačně symetrické 2D úlohy vyjdu ze slabé formulace 3D úlohy a proto jí v této kapitole uvádím jako první D úloha Při slabé formulaci přenásobíme rovnice (1) a (2) testovacími funkcemi v (H 1 ()) 3 a q L 2 () a integrací přes oblast dostáváme (u )u vd ν u vd + p vd = f vd, v ( H 1 () ) 3, q ud =, q L 2 (), a aplikací Greenovi věty získáme výslednou slabou formulaci ve tvaru: 2
3 Hledáme u (H 1 ()) 3 a p L 2 (), tak aby (u )u vd ν Γ ( u)v ndγ + ν + pv ndγ Γ u : vd + (3) p vd = f vd, v ( H 1 () ) 3, (4) q ud =, q L 2 (). (5) 2.2 Rotačně symetrická úloha Slabou formulaci pro rotačně symetrickou 2D úlohu jsem odvodil ze slabé formulace 3D úlohy. o provedu rozepsáním slabé formulace 3D úlohy do jednotlivých složek a následné transformaci do válcových souřadnic. Celé toto odvození a i druhý způsob získání slabé formulace z N-S rovnic pro rotačně symetrické proudění (viz Šístek 5) s následným využitím váhových prostorů je uvedeno v mé bakalářské práci (viz Hanek 4). Výsledná slabá formulace pro rotačně symetrickou 2D úlohu je tedy: Hledáme u r, u a H 1 r () a p L 2 r(), tak aby ( ) ( u a u r r v u a ar + u a w v ua v a ar d + ν r r r + u ) a v a w w r d ( ua ν Γ r v an r r + u ) a w v an w r dγ p v a w rd + pv a n w rdγ = f w v a rd, v a Hr 1 (), (6) Γ ( ) ( u r u r r v u r rr + u a w v ur v r rr d + ν r r r + u r v r w w r + u ) ( r r v ur r d ν Γ r v rn r r + u ) r w v rn w r dγ ( pv r + p v ) r r r d + pv r n r rdγ = f r v r rd, v r Hr 1 (), (7) Γ ( ur r qr + u rq + u ) a w qr d =, q L 2 r(). (8) 3 Metoda konečných prvků Při řešení Navierových-Stokesových rovnic je důležité vhodné zvolení funkčních prostorů pro rychlost a tlak. Metoda konečných prvků využívá k aproximaci polynomy různého stupně. Pro řešení Navierových-Stokesových rovnic aproximujeme na každém prvku rychlost polynomem 2. stupně a tlak polynomem 1. stupně. Následující vlastnosti požadovaného řešení jsou spojeny se slabou formulací Navierových-Stokesových rovnic: každá složka rychlosti je funkce integrovatelná s kvadrátem podle x a má minimálně první zobecněnou derivaci podle libovolné souřadnice integrovatelnou s kvadrátem (prostor H 1 ()) tlak je funkce integrovatelná s kvadrátem podle x (prostor L 2 ()) 3
4 Existuje několik typů konečných prvků, jejichž pomocí lze řešit Navierovy-Stokesovy rovnice. Ve svém výpočtu použivám aylorovy-hoodovy čtyřúhelníkové konečné prvky. yto prvky jsou pro 2D úlohu obecně čtyřúhelníky kde aproximuji tlak v jeho vrcholech a rychlost ve vrcholech, středech stran a uprostřed prvku (viz Obrázek 2). Pro 3D úlohu to jsou šestistěny, kde opět aproximuji tlak v jeho vrcholech a rychlost navíc ještě ve středu každé hrany. Obrázek 2: ylorův-hoodův referenční prvek ve 2D 3.1 Sestavení systému algebraických rovnic Při sestavování sytému algebraických rovnic pro oba typy úloh dosadím do slabé formulace za konečně prvkové funkce rychlosti a tlaku linerní kombinace bázových funkcí a dostanu výslednou nelineární soustavu rovnic ve tvaru νa(u) + N B B u p = f, (9) kde u je vektor neznámých rychlostí, p je vektor nezámých tlaků, A je matice difuze, N je matice advekce, B je matice od rovnice kontinuity a f je diskretní vektor intenzity objemových sil. Matice A, N a B sestavíme takto (viz Elman, Silvester a Wathen 2) A = a ij, a ij = ϕ i : ϕ j, (1) N = n ij, n ij = ( u h ϕ j ) ϕ i, (11) B = b ij, b ij = ψ i ϕ j, (12) kde ϕ i je bázová funkce rychlosti a ψ i je bázová funkce tlaku. 4
5 Soustava (9) je díky matici A nelineární a pro její linerizaci využívám Picardovu iteraci, která vede na systém rovnic ve tvaru νa(u k ) + N B B u k+1 p k+1 = f, (13) kde A(u k ) znamená, že linearizuji matici A pomocí řešení v předchozím kroku. uto, již lineární soustavu, řeším ve 2D přímou metodou (pomocí LU rozkladu pro řídké matice), zatímco ve 3D vzhledem k velikosti úlohy využiji iterační metodu dělení oblasti BDDC. 4 Rozklad oblasti a předpodmiňovač BDDC Pro výpočet 3D úlohy využijeme rozkladu oblasti na několik podoblastí. Použijeme rozklad bez překryvu jednotlivých podoblastí a v systému rovnic (13) si přečíslujeme složky neznámých vektorů u a p tak, že složky odpovídající uzlům na rozhraní očísluji jako poslední. o vede na následující systém rovnic νa 11 + N 11 νa 12 + N 12 B11 B21 νa 21 + N 21 νa 22 + N 22 B12 B22 B 11 B 12 B 21 B 22 u 1 u 2 p 1 = f 1 f 2, (14) kde index 1 značí část týkající se vnitřku oblatí a index 2 část odpovídající uzlům na rozhraní, přečemž každá matice odpovídající prvkům matice z levé strany této rovnice je sestavena z bloků odpovídajících jednolivým podoblastem. Pro použití předpodmiňvače BDDC převedu tento systém na řešení na rozhraní a na řešení uvnitř podoblastí (viz Šístek a kol. 6). Nejprve si přepíšeme systém (14) do následujícího tvaru νa 12 + N 12 B21 B 11 B 12 νa 21 + N 21 B12 νa 22 + N 22 B22 B 21 B 22 u 1 p 1 u 2 = f 1 f 2, a po roznásobení po blocích pro vnitřní neznámé a pro neznámé na rozhraní dostáváme u 1 νa 12 + N 12 B21 u 2 f 1 + =, B 11 p 1 B 12 νa 21 + N 21 B12 u 1 νa 22 + N 22 B22 u 2 f 2 + =. B 21 B 22 Z první rovnice si poté vyjádříme vektor p 1 5
6 u 1 p 1 = B 11 1 f 1 B 11 1 νa 12 + N 12 B21 B 12 u 2, (15) který dosadíme do druhé rovnice a dostaneme systém 1 νa 21 + N 21 B12 B 21 νa 21 + N 21 B12 B 21 B 11 1 B 11 νa 12 + N 12 B21 B 12 u 2 f 1 + νa 22 + N 22 B22 B 22 u 2 = f 2. en odpovídá rovnici S u 2 = g, (16) kde 1 g = f 2 νa 21 + N 21 B12 B 21 B 11 f 1 je redukovaná pravá strana a 1 S = νa 22 + N 22 B22 B 22 νa 21 + N 21 B12 B 21 B 11 νa 12 + N 12 B21 B 12 je tzv. Schurův doplněk. Úlohu (16) řešíme iteračně pomocí metody BiCGstab a jako predpodmiňovač užíváme jeden krok metody BDDC. Po vyřešení systému (16) dosadíme řešení na rozhraní do systému (15) a získáme řešení uvnitř podoblastí. Díky rozdělení na podoblasti lze akci předpodmiňovače BDDC stejně jako násobení maticí S v každém kroku iterační metody paralelizovat a tím urychlit výpočetní čas. 5 Numerické výsledky Prvním krokem při numerické simulaci pro oba typy úloh je vytvoření sítě konečných prvků. K tomu využiji volně dostupný program GMSH 7. Dále je nutno stanovit okrajové podmínky pro naší úlohu a tyto vstupní data zadat do výpočtového programu. Pro výpočet využiji kolekci šablon C++ pro metodu konečných prvků v mechanice tekutin, která mi byla poskytnuta, a kterou jsem pro 2D případ rozšířil o implementaci rotačně symetrické úlohy. Všechny výsledky budou zpracovány ve formě 3D nebo 2D grafů proudnic a 3D grafů průběhu tlaku a rychlosti. 6
7 5.1 2D úloha ímto typem úlohy jsem se zabýval v mé bakalářské práci a zde prezentuji jen některé její výsledky (více viz Hanek 4). Úloha odpovídá vedení v klidu a její výsledky jsem měl možnost ověřit experimentem Okrajové podmínky Vzhledem k rotační symetrii úlohy vypadá oblast následovně: Obrázek 3: Oblast a její hranice s následujícími okrajovými podmínkami na Γ vstup předepisuji vstupní parabolický rychlostní profil pro u a a u r = na Γ stěna předepisuji tzv. no-slip podmínku, t.j. u r = u a = na Γ osa předepisuji vzhledem k symetrii u r = na Γ výstup předepisuji tzv. do-nothing podmínku Eperimentální data Pro možnost kontroly numerické simulace bylo provedeno experimentální měření, jehož schéma je na Obrázku 4. Parametry, které používáme při testovacím výpočtu jsou tyto: Q - je průtok v celém systému z něhož získáme střední vtokovou rychlost tekutiny v stř - je teplota tekutiny díky níž určíme hodnotu dynamické viskozity µ h - je výška škrtící mezery - je vstupní tlak 7
8 Obrázek 4: Schéma měření Naměřené a odvozené hodnoty použité v testovacím výpočtu jsou v abulce 1. Q l/min C h m Pa v stř m/s µ Ns/m 2,576 28,34 7, ,3497,669 abulka 1: Hodnoty pro porovnání s výpočtem estovací výpočet Výsledky testovacího výpočtu jsou na Obrázcích 5-6. Na Obrázku 6 je i pro zajímavost detail singularity tlaku v místě kde tekutina vstupuje do škrtící mezery. Obrázek 5: Průběh tlaku (vlevo) a rychlosti (vpravo) uvnitř kapsy 8
9 Obrázek 6: Proudnice (vlevo) a singularita (vpravo) Kontrolní hodnotou testovacího výpočtu je vstupní tlak. en se od naměřeného liší asi o 1%. Dá se tedy předpokládat, že náš model dobře simuluje proudění uvnitř hydrostatické kapsy. Výpočet se také shoduje s analytickým řešením, které je uvedeno v Holkup a kol. 3. Ve své bakalářské práci jsem se také zabýval vlivem změny některých vstupních parametrů. Konkrétně změnou viskozity, a tedy Reynoldsova čísla, a změnou výšky škrtící mezery. Zde uvedu jen vliv změny Reynoldsova čísla Vliv změny Reynoldsova čísla Parametr, který jsem v těchto výpočtech měnil, je dynamická viskozita µ. Její hodnota se výrazně mění v závistlosti na teplotě (více viz Holkup a kol. 3). o je spojené se změnou Reynoldsova čísla, které je definováno jako bezrozměrné číslo R = LU, kde L označuje charakteristickou délku, ν U označuje charakteristickou rychlost a ν = µ ρ je kinematická viskozita. Pro danou úlohu užívam jako L průměr na vstupu do kapsy a U rovnou střední vtokové rychlosti. V abulce 2 jsou uvedeny hodnoty teplot a jim odpovídající hodnoty dynamické viskozity a Reynoldsova čísla. C , µ Ns/m 2,179,11,669,43,276 Re abulka 2: Závislost dynamické viskozity a Reynoldsova čísla na teplotě Výpočty byly provedeny se stejnými vstupními parametry jako v testovacím výpočtu, kromě hodnoty dynamické viskozity, kterou jsem měnil podle předchozí tabulky. Zde uvádím výsledky pouze pro hodnoty odpovídající 1 C a 5 C. Kompletní výsledky jsou uvedeny v Hanek 4. Výstupem jsou grafy průběhu tlaku a proudnic na Obrázcích
10 Obrázek 7: Průběh tlaku (vlevo) a proudnice (vpravo) uvnitř kapsy, µ =, 179 Ns/m 2, R = 5 Obrázek 8: Průběh tlaku (vlevo) a proudnice (vpravo) uvnitř kapsy, µ =, 276 Ns/m 2, R = 33 Z grafů je vidět, že při snižování hodnoty dynamické viskozity, tedy při zvyšovaní Reynoldsova čísla, nastává menší tlakový spád a zároveň se vytváří větší vír pod horní stranou kapsy D úloha 3D úloha umožňuje simulovat proudění i za pohybu ložiska a tedy s nenulovou rychlostí dolní stěny oblasti řešení. Prvotním cílem 3D výpočtů je ale provést výpočet odpovídající parametrům z testovacího výpočtu 2D úlohy, a už to ssebou nese problémy s konvergencí úlohy. y budou zřejmě způsobeny hodnotou výšky škrtící mezery a tedy špatnou podmíněností některých konečných prvků, což je poměr nejdelší ku nejkratší hraně prvku. Dalšími problémy konvergence může být i reálná hodnota viskozity a případný pohyb dolní stěny. Vzhledem k těmto problémům s konvergencí nejsem zatím schopen spočítat úlohu s reálnými parametry a ve svých výpočtech jsem se k nim zatím snažil co nejvíce přiblížit. Zde pro zajímavost uvedu výsledky s parametry blížícími se úloze s pohybem dolní stěny. 1
11 Oblast řešení je na Obrázku 9. Obrázek 9: Okrajové podmínky 3D úlohy Použiji následující okrajovými podmínkami: na Γ vstup předepisuji vstupní paraboloidový rychlostní profil pro u z a u x = u y = na Γ stěna předepisuji tzv. no-slip podmínku, t.j. u = na Γ stěnadolní předepisuji rychlost posuvu ložiska ve směru osy x t.j. u x = u dolní stěna na Γ výstup předepisuji tzv. do-nothing podmínku Výsledné řešení je potom na Obrázcích 1-11 s parametry uvedenými v abulce 3. v stř m/s h m µ Ns/m 2 v dolní stěna m/s, 3497, 1, 89 1 abulka 3: Hodnoty parametrů pro testovací výpočet Obrázek 1: Proudové trubice se zabarvením podle velikosti rychlosti (zadní pohled) 11
12 6 Závěr Obrázek 11: Proudové trubice se zabarvením podle velikosti rychlosti (přední pohled) V práci jsem se zabýval modelováním proudění v rotačně symetrické hydrostatické buňce pomocí Navierových-Stokesových rovnic. o vede na dva typy úloh - 2D úlohu, která odpovídá vedení za klidu a jíž jsem se zabýval ve své bakalářské práci, a 3D úlohu, která umožnuje simulaci i za pohybu ložiska ve vedení. Z výsledků pro 2D úlohu je vidět, že jsou pro testovací výpočet v dobré shodě s experimentem a tak dávají dobrou představu o proudění uvnitř hydrostatické kapsy za klidu vedení. Dále je vidět z analýzy vlivu změny Reynoldsova čísla, že velký vliv na vznik vírů má dynamická viskozita, která se výrazně mění s teplotou tekutiny. Z presentovaných výsledků pro 3D úlohu je vidět, že zatím nejsem schopen provést výpočty pro reálné parametry jako v případě 2D úlohy, ale pro úlohu s pohybem ložiska ve vedení dostáváme alespoň přibližnou představu o charakteru proudění. 12
13 Literatura 1 Feistauer, M. Mathematical methods in fluid dynamics, John Wiley & Sons Inc., New York, Elman, H. C., Silvester, D. J., Wathen, A. J. Finite elements and fast iterative solvers: with applications in incompressible fluid dynamics, Oxford University Press, New York, 25 3 Holkup,., Sušeň, J., Stach, E., Hudec, J., Mareš, M., Morávek, M. Závěrečná zpráva projektu A za rok 211, ČVU, Praha, Hanek, M. Numerická simulace proudění v hydrostatické buňce, ČVU, Praha, Šístek, J. Stabilization of finite element method for solving incompressible viscous flows, Diplomová práce, ČVU, Praha, 24 6 Šístek, J., Sousedík, B., Burda, P., Mandel, J., Novotný, J. Application of the parallel BDDC preconditioner to Stokes flow, Computers and fluids 46, , Geuzaine, C., Remacle, J. F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities online, dostupné z 13
Stabilizace Galerkin Least Squares pro
 Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Diskrétní řešení vzpěru prutu
 1 z 5 Diskrétní řešení vzpěru prutu Discrete solution of beam buckling Petr Frantík Abstract Here is described discrete method for solution of beam buckling. The beam is divided into a number of tough
1 z 5 Diskrétní řešení vzpěru prutu Discrete solution of beam buckling Petr Frantík Abstract Here is described discrete method for solution of beam buckling. The beam is divided into a number of tough
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami
 Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy
![Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy](/thumbs/97/130835283.jpg) Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aplikace metody BDDC
 Aplikace metody BDDC v problémech pružnosti P. Burda, M. Čertíková, E. Neumanová, J. Šístek A. Damašek, J. Novotný FS ČVUT, ÚT AVČR 14.9.2006 / SAMO 06 (FS ČVUT, ÚT AVČR) 14.9.2006 / SAMO 06 1 / 46 Osnova
Aplikace metody BDDC v problémech pružnosti P. Burda, M. Čertíková, E. Neumanová, J. Šístek A. Damašek, J. Novotný FS ČVUT, ÚT AVČR 14.9.2006 / SAMO 06 (FS ČVUT, ÚT AVČR) 14.9.2006 / SAMO 06 1 / 46 Osnova
l, l 2, l 3, l 4, ω 21 = konst. Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj. analyticky
 Kinematické řešení čtyřkloubového mechanismu Dáno: Cíl: l, l, l 3, l, ω 1 konst Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj analyticky určete úhlovou rychlost ω 1 a úhlové zrychlení
Kinematické řešení čtyřkloubového mechanismu Dáno: Cíl: l, l, l 3, l, ω 1 konst Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj analyticky určete úhlovou rychlost ω 1 a úhlové zrychlení
Numerické řešení modelu proudění v porézní hornině s puklinou
 Numerické řešení modelu proudění v porézní hornině s puklinou Martin Hanek Úvod Vedoucí práce prof. RNDr. Pavel Burda, CSc. Zajímá nás jednofázová tekutina v puklině porézní horniny. Studie je provedena
Numerické řešení modelu proudění v porézní hornině s puklinou Martin Hanek Úvod Vedoucí práce prof. RNDr. Pavel Burda, CSc. Zajímá nás jednofázová tekutina v puklině porézní horniny. Studie je provedena
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Modelování proudění ve vysokém rozlišení
 Modelování proudění ve vysokém rozlišení Vladimír Fuka vedoucí práce: doc. RNDr. Josef Brechler, CSc. Cíle práce Vytvořit základ počítačového modelu proudění. Vyzkoušet některé nové postupy. Ověřit funkčnost
Modelování proudění ve vysokém rozlišení Vladimír Fuka vedoucí práce: doc. RNDr. Josef Brechler, CSc. Cíle práce Vytvořit základ počítačového modelu proudění. Vyzkoušet některé nové postupy. Ověřit funkčnost
Numerická matematika 1
 Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
domain decomposition
 Srovnání některých metod domain decomposition Bedřich Sousedík obor: Matematika ve stavebním inženýrství školitel: Prof. RNDr. Ivo Marek, DrSc. školitel specialista: Professor Jan Mandel Katedra matematiky
Srovnání některých metod domain decomposition Bedřich Sousedík obor: Matematika ve stavebním inženýrství školitel: Prof. RNDr. Ivo Marek, DrSc. školitel specialista: Professor Jan Mandel Katedra matematiky
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Literatura: Kapitola 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Metoda sítí v 1D. Myšlenka náhrada derivací diferenčními podíly Přibližné řešení okrajových úloh Aproximace vlastních čísel Literatura: Kapitola 2 d) ze skript Karel Rektorys:
Předmět: MA4 Dnešní látka: Metoda sítí v 1D. Myšlenka náhrada derivací diferenčními podíly Přibližné řešení okrajových úloh Aproximace vlastních čísel Literatura: Kapitola 2 d) ze skript Karel Rektorys:
Co je obsahem numerických metod?
 Numerické metody Úvod Úvod Co je obsahem numerických metod? Numerické metody slouží k přibližnému výpočtu věcí, které se přesně vypočítat bud nedají vůbec, nebo by byl výpočet neúměrně pracný. Obsahem
Numerické metody Úvod Úvod Co je obsahem numerických metod? Numerické metody slouží k přibližnému výpočtu věcí, které se přesně vypočítat bud nedají vůbec, nebo by byl výpočet neúměrně pracný. Obsahem
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Literatura: Kapitoly 3, 4 a 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
1 0 0 u 22 u 23 l 31. l u11
 LU dekompozice Jedná se o rozklad matice A na dvě trojúhelníkové matice L a U, A=LU. Matice L je dolní trojúhelníková s jedničkami na diagonále a matice U je horní trojúhelníková. a a2 a3 a 2 a 22 a 23
LU dekompozice Jedná se o rozklad matice A na dvě trojúhelníkové matice L a U, A=LU. Matice L je dolní trojúhelníková s jedničkami na diagonále a matice U je horní trojúhelníková. a a2 a3 a 2 a 22 a 23
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Počítačová dynamika tekutin užitečný nástroj pro inženýry
 Počítačová dynamika tekutin užitečný nástroj pro inženýry M. Jahoda Úvod Počítačová dynamika tekutin (Computational Fluid Dynamics, CFD) je moderní metoda, která se zabývá prouděním tekutin, přenosem tepla
Počítačová dynamika tekutin užitečný nástroj pro inženýry M. Jahoda Úvod Počítačová dynamika tekutin (Computational Fluid Dynamics, CFD) je moderní metoda, která se zabývá prouděním tekutin, přenosem tepla
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Dynamika vázaných soustav těles
 Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
CVIČENÍ č. 7 BERNOULLIHO ROVNICE
 CVIČENÍ č. 7 BERNOULLIHO ROVNICE Výtok z nádoby, Průtok potrubím beze ztrát Příklad č. 1: Určete hmotnostní průtok vody (pokud otvor budeme považovat za malý), která vytéká z válcové nádoby s průměrem
CVIČENÍ č. 7 BERNOULLIHO ROVNICE Výtok z nádoby, Průtok potrubím beze ztrát Příklad č. 1: Určete hmotnostní průtok vody (pokud otvor budeme považovat za malý), která vytéká z válcové nádoby s průměrem
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY
 VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
FLUENT přednášky. Metoda konečných objemů (MKO)
 FLUENT přednášky Metoda konečných objemů (MKO) Pavel Zácha zdroj: [Bakker, 2008], [Vodička, 2011], [Runchal, 2008], [Kozubková, 2008] Historie - zřejmě nestarší způsob řešení parciálních diferenciálních
FLUENT přednášky Metoda konečných objemů (MKO) Pavel Zácha zdroj: [Bakker, 2008], [Vodička, 2011], [Runchal, 2008], [Kozubková, 2008] Historie - zřejmě nestarší způsob řešení parciálních diferenciálních
Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace
 Optimalizace systémů tlakových kanalizací pomocí matematického modelování jejich provozních stavů Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace Ing.
Optimalizace systémů tlakových kanalizací pomocí matematického modelování jejich provozních stavů Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace Ing.
Počítačová dynamika tekutin (CFD) Řešení rovnic. - metoda konečných objemů -
 Počítačová dynamika tekutin (CFD) Řešení rovnic - metoda konečných objemů - Rozdělení parciálních diferenciálních rovnic 2 Obecná parciální diferenciální rovnice se dvěma nezávislými proměnnými x a y:
Počítačová dynamika tekutin (CFD) Řešení rovnic - metoda konečných objemů - Rozdělení parciálních diferenciálních rovnic 2 Obecná parciální diferenciální rovnice se dvěma nezávislými proměnnými x a y:
stránkách přednášejícího.
 Předmět: MA 4 Dnešní látka Iterační metoda Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Superrelaxační metoda (metoda SOR) Metoda sdružených gradientů Četba: Text o lineární algebře v Příručce
Předmět: MA 4 Dnešní látka Iterační metoda Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Superrelaxační metoda (metoda SOR) Metoda sdružených gradientů Četba: Text o lineární algebře v Příručce
Simulace (nejen) fyzikálních jevů na počítači
 Simulace (nejen) fyzikálních jevů na počítači V. Kučera Katedra numerické matematiky, MFFUK Praha 7.2.2013 Aerodynamický flutter Tacoma bridge, 1940 Fyzikální model Realita je komplikovaná Navier-Stokesovy
Simulace (nejen) fyzikálních jevů na počítači V. Kučera Katedra numerické matematiky, MFFUK Praha 7.2.2013 Aerodynamický flutter Tacoma bridge, 1940 Fyzikální model Realita je komplikovaná Navier-Stokesovy
2. Schurova věta. Petr Tichý. 3. října 2012
 2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
Připomenutí co je to soustava lineárních rovnic
 Připomenutí co je to soustava lineárních rovnic Příklad 2x 3y + z = 5 3x + 5y + 2z = 4 x + 2y z = 1 Soustava lineárních rovnic obecně Maticový tvar: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a
Připomenutí co je to soustava lineárních rovnic Příklad 2x 3y + z = 5 3x + 5y + 2z = 4 x + 2y z = 1 Soustava lineárních rovnic obecně Maticový tvar: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu a, b : 2 ) y i p i+ 1
 ODR - okrajová úloha Teorie (velmi stručný výběr z přednášek) Okrajová úloha 2. řádu Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu
ODR - okrajová úloha Teorie (velmi stručný výběr z přednášek) Okrajová úloha 2. řádu Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu
Aplikovaná numerická matematika - ANM
 Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Numerická matematika Písemky
 Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ
 INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
a vlastních vektorů Příklad: Stanovte taková čísla λ, pro která má homogenní soustava Av = λv nenulové (A λ i I) v = 0.
 Výpočet vlastních čísel a vlastních vektorů S pojmem vlastního čísla jsme se již setkali například u iteračních metod pro řešení soustavy lineárních algebraických rovnic. Velikosti vlastních čísel iterační
Výpočet vlastních čísel a vlastních vektorů S pojmem vlastního čísla jsme se již setkali například u iteračních metod pro řešení soustavy lineárních algebraických rovnic. Velikosti vlastních čísel iterační
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Řešení "stiff soustav obyčejných diferenciálních rovnic
 Řešení "stiff soustav obyčejných diferenciálních rovnic Jiří Škvára Katedra fyziky, Přírodovědecká fakulta Univerzity J.E. Purkyně v Ústí n.l.. ročník, počítačové metody ve vědě a technice Abstrakt Seminární
Řešení "stiff soustav obyčejných diferenciálních rovnic Jiří Škvára Katedra fyziky, Přírodovědecká fakulta Univerzity J.E. Purkyně v Ústí n.l.. ročník, počítačové metody ve vědě a technice Abstrakt Seminární
Matematické modely a způsoby jejich řešení. Kateřina Růžičková
 Matematické modely a způsoby jejich řešení Kateřina Růžičková Rovnice matematické fyziky Přednáška převzata od Doc. Rapanta Parciální diferencíální rovnice Diferencialní rovnice obsahujcí parcialní derivace
Matematické modely a způsoby jejich řešení Kateřina Růžičková Rovnice matematické fyziky Přednáška převzata od Doc. Rapanta Parciální diferencíální rovnice Diferencialní rovnice obsahujcí parcialní derivace
Rovinný průtokoměr. Diplomová práce Ústav mechaniky tekutin a termodynamiky, 2013. Jakub Filipský
 Rovinný průtokoměr Diplomová práce Ústav mechaniky tekutin a termodynamiky, 2013 Autor: Vedoucí DP: Jakub Filipský Ing. Jan Čížek, Ph.D. Zadání práce 1. Proveďte rešerši aktuálně používaných způsobů a
Rovinný průtokoměr Diplomová práce Ústav mechaniky tekutin a termodynamiky, 2013 Autor: Vedoucí DP: Jakub Filipský Ing. Jan Čížek, Ph.D. Zadání práce 1. Proveďte rešerši aktuálně používaných způsobů a
Počítačová dynamika tekutin (CFD) Základní rovnice. - laminární tok -
 Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Numerické metody a programování
 Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.7/2.2./28.157 Numerické metody a programování Lekce 4 Tento projekt je spolufinancován Evropským
Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.7/2.2./28.157 Numerické metody a programování Lekce 4 Tento projekt je spolufinancován Evropským
Princip řešení soustavy rovnic
 Princip řešení soustavy rovnic Tomáš Kroupa 20. května 2014 Tento studijní materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Obsah Formulace úlohy Metody řešení
Princip řešení soustavy rovnic Tomáš Kroupa 20. května 2014 Tento studijní materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Obsah Formulace úlohy Metody řešení
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině.
 Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
SVOČ FST Bc. Václav Sláma, Zahradní 861, Strakonice Česká republika
 VÝPOČET PROUDĚNÍ V NADBANDÁŽOVÉ UCPÁVCE PRVNÍHO STUPNĚ OBĚŽNÉHO KOLA BUBNOVÉHO ROTORU TURBÍNY SVOČ FST 2011 Bc. Václav Sláma, Zahradní 861, 386 01 Strakonice Česká republika Bc Jan Čulík, Politických vězňů
VÝPOČET PROUDĚNÍ V NADBANDÁŽOVÉ UCPÁVCE PRVNÍHO STUPNĚ OBĚŽNÉHO KOLA BUBNOVÉHO ROTORU TURBÍNY SVOČ FST 2011 Bc. Václav Sláma, Zahradní 861, 386 01 Strakonice Česká republika Bc Jan Čulík, Politických vězňů
2.6. VLASTNÍ ČÍSLA A VEKTORY MATIC
 .6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
.6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
Newtonova metoda. 23. října 2012
 Hledání kořenů rovnic jedné reálné proměnné Newtonova metoda Michal Čihák 23. října 2012 Newtonova metoda (metoda tečen) využívá myšlenku, že tečna v daném bodě grafu funkce nejlépe aproximuje graf funkce
Hledání kořenů rovnic jedné reálné proměnné Newtonova metoda Michal Čihák 23. října 2012 Newtonova metoda (metoda tečen) využívá myšlenku, že tečna v daném bodě grafu funkce nejlépe aproximuje graf funkce
Studentská tvůrčí činnost 2009. 3D modelování vírových struktur v rozváděcí turbínové lopatkové mříži. David Jícha
 Studentská tvůrčí činnost 2009 3D modelování vírových struktur v rozváděcí turbínové lopatkové mříži David Jícha Vedoucí práce : Prof.Ing.P.Šafařík,CSc. a Ing.D.Šimurda 3D modelování vírových struktur
Studentská tvůrčí činnost 2009 3D modelování vírových struktur v rozváděcí turbínové lopatkové mříži David Jícha Vedoucí práce : Prof.Ing.P.Šafařík,CSc. a Ing.D.Šimurda 3D modelování vírových struktur
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ
 APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin. Martin Šourek
 CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin Martin Šourek VŠCHT Praha Ústav matematiky Praha 13. Prosince 2016 Úvod Model Výsledky Závěr Úvod 13.12.2016
CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin Martin Šourek VŠCHT Praha Ústav matematiky Praha 13. Prosince 2016 Úvod Model Výsledky Závěr Úvod 13.12.2016
Numerické metody a programování. Lekce 4
 Numerické metody a programování Lekce 4 Linarní algebra soustava lineárních algebraických rovnic a 11 a 12 x 2 a 1, N x N = b 1 a 21 a 22 x 2 a 2, N x N = b 2 a M,1 a M,2 x 2 a M,N x N = b M zkráceně A
Numerické metody a programování Lekce 4 Linarní algebra soustava lineárních algebraických rovnic a 11 a 12 x 2 a 1, N x N = b 1 a 21 a 22 x 2 a 2, N x N = b 2 a M,1 a M,2 x 2 a M,N x N = b M zkráceně A
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
 Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC
 SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC Pojm: Algebraická rovnice... rovnice obsahující pouze celé nezáporné mocnin neznámé, tj. a n n + a n 1 n 1 +... + a 2 2 + a 1 + a 0 = 0, kde n je přirozené číslo.
SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC Pojm: Algebraická rovnice... rovnice obsahující pouze celé nezáporné mocnin neznámé, tj. a n n + a n 1 n 1 +... + a 2 2 + a 1 + a 0 = 0, kde n je přirozené číslo.
Václav Uruba home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF
 Václav Uruba uruba@fst.zcu.cz home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF 13.10.2014 Mechanika tekutin 1/13 1 Mechanika tekutin - přednášky 1. Úvod, pojmy,
Václav Uruba uruba@fst.zcu.cz home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF 13.10.2014 Mechanika tekutin 1/13 1 Mechanika tekutin - přednášky 1. Úvod, pojmy,
Úlohy nejmenších čtverců
 Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Numerické metody a programování. Lekce 7
 Numerické metody a programování Lekce 7 Řešení nelineárních rovnic hledáme řešení x problému f x = 0 strategie: odhad řešení iterační proces postupného zpřesňování řešení výpočet skončen pokud je splněno
Numerické metody a programování Lekce 7 Řešení nelineárních rovnic hledáme řešení x problému f x = 0 strategie: odhad řešení iterační proces postupného zpřesňování řešení výpočet skončen pokud je splněno
MATEMATIKA V MEDICÍNĚ
 MATEMATIKA V MEDICÍNĚ Tomáš Oberhuber Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Matematika pro život TOMÁŠ OBERHUBER (FAKULTA JADERNÁ A FYZIKÁLNĚ INŽENÝRSKÁ MATEMATIKA
MATEMATIKA V MEDICÍNĚ Tomáš Oberhuber Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Matematika pro život TOMÁŠ OBERHUBER (FAKULTA JADERNÁ A FYZIKÁLNĚ INŽENÝRSKÁ MATEMATIKA
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic
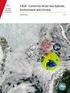 ENumerická analýza transportních procesů - NTP2 Přednáška č. 8 Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic Úvod do přesnosti metody konečných prvků Úvod do přesnosti metody
ENumerická analýza transportních procesů - NTP2 Přednáška č. 8 Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic Úvod do přesnosti metody konečných prvků Úvod do přesnosti metody
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
DIPLOMOVÁ PRÁCE Nelineární řízení magnetického ložiska
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav mechaniky DIPLOMOVÁ PRÁCE Nelineární řízení magnetického ložiska 2004 Jan KRYŠTŮFEK Motivace Účel diplomové práce: Porovnání nelineárního řízení
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav mechaniky DIPLOMOVÁ PRÁCE Nelineární řízení magnetického ložiska 2004 Jan KRYŠTŮFEK Motivace Účel diplomové práce: Porovnání nelineárního řízení
Výpočet stlačitelného proudění metodou konečných objemů
 Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování. vypracovanou úlohu podle níže uvedených zadání. To mimo jiné znamená, že
 Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Podobnostní transformace
 Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
Numerické řešení 2D stlačitelného proudění s kondenzací. Michal Seifert
 Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
Dnešní látka Opakování: normy vektorů a matic, podmíněnost matic Jacobiova iterační metoda Gaussova-Seidelova iterační metoda
 Předmět: MA 4 Dnešní látka Opakování: normy vektorů a matic, podmíněnost matic Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Četba: Text o lineární algebře v Příručce přežití na webových
Předmět: MA 4 Dnešní látka Opakování: normy vektorů a matic, podmíněnost matic Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Četba: Text o lineární algebře v Příručce přežití na webových
Metoda konečných prvků Úvod (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Úvod (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr. Eva Hrubešová, Ph.D.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Úvod (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr. Eva Hrubešová, Ph.D.
Studentská tvůrčí činnost 2009
 Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Iterační metody řešení soustav lineárních rovnic. 27. prosince 2011
 Iterační metody řešení soustav lineárních rovnic Michal Čihák 27. prosince 2011 Přímé metody řešení soustav lineárních rovnic V přednáškách z lineární algebry jste se seznámili s několika metodami řešení
Iterační metody řešení soustav lineárních rovnic Michal Čihák 27. prosince 2011 Přímé metody řešení soustav lineárních rovnic V přednáškách z lineární algebry jste se seznámili s několika metodami řešení
37. PARABOLA V ANALYTICKÉ GEOMETRII
 37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
Numerické řešení soustav lineárních rovnic
 Numerické řešení soustav lineárních rovnic irko Navara Centrum strojového vnímání, katedra kybernetiky elektrotechnická fakulta ČVUT, Praha http://cmpfelkcvutcz/~navara 30 11 2016 Úloha: Hledáme řešení
Numerické řešení soustav lineárních rovnic irko Navara Centrum strojového vnímání, katedra kybernetiky elektrotechnická fakulta ČVUT, Praha http://cmpfelkcvutcz/~navara 30 11 2016 Úloha: Hledáme řešení
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Čebyševovy aproximace
 Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
1.13 Klasifikace kvadrik
 5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda.
 Úvod Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda. Mnoho technických problémů vede na řešení matematických úloh, které se následně převedou na úlohy řešení soustav nelineárních rovnic
Úvod Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda. Mnoho technických problémů vede na řešení matematických úloh, které se následně převedou na úlohy řešení soustav nelineárních rovnic
4. Trojúhelníkový rozklad p. 1/20
 4. Trojúhelníkový rozklad 4. Trojúhelníkový rozklad p. 1/20 4. Trojúhelníkový rozklad p. 2/20 Trojúhelníkový rozklad 1. Permutační matice 2. Trojúhelníkové matice 3. Trojúhelníkový (LU) rozklad 4. Výpočet
4. Trojúhelníkový rozklad 4. Trojúhelníkový rozklad p. 1/20 4. Trojúhelníkový rozklad p. 2/20 Trojúhelníkový rozklad 1. Permutační matice 2. Trojúhelníkové matice 3. Trojúhelníkový (LU) rozklad 4. Výpočet
Propojení matematiky, fyziky a počítačů
 Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
NESTABILITY VYBRANÝCH SYSTÉMŮ. Úvod. Vzpěr prutu. Petr Frantík 1
 NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
Návod k použití programu pro výpočet dynamické odezvy spojitého nosníku
 Návod k použití programu pro výpočet dynamické odezvy spojitého nosníku Obsah. Úvod.... Popis řešené problematiky..... Konstrukce... 3. Výpočet... 3.. Prohlížení výsledků... 4 4. Dodatky... 6 4.. Newmarkova
Návod k použití programu pro výpočet dynamické odezvy spojitého nosníku Obsah. Úvod.... Popis řešené problematiky..... Konstrukce... 3. Výpočet... 3.. Prohlížení výsledků... 4 4. Dodatky... 6 4.. Newmarkova
Arnoldiho a Lanczosova metoda
 Arnoldiho a Lanczosova metoda 1 Částečný problém vlastních čísel Ne vždy je potřeba (a někdy to není ani technicky možné) nalézt celé spektrum dané matice (velké řídké matice). Úloze, ve které chceme aproximovat
Arnoldiho a Lanczosova metoda 1 Částečný problém vlastních čísel Ne vždy je potřeba (a někdy to není ani technicky možné) nalézt celé spektrum dané matice (velké řídké matice). Úloze, ve které chceme aproximovat
0 0 a 2,n. JACOBIOVA ITERAČNÍ METODA. Ax = b (D + L + U)x = b Dx = (L + U)x + b x = D 1 (L + U)x + D 1 b. (i) + T J
 6 Jacobiova a Gaussova-Seidelova iterační metoda pro řešení systémů lin rovnic Kateřina Konečná/ ITERAČNÍ METODY PRO ŘEŠENÍ SYSTÉMŮ LINEÁRNÍCH ROVNIC Budeme se zabývat řešením soustavy lineárních rovnic
6 Jacobiova a Gaussova-Seidelova iterační metoda pro řešení systémů lin rovnic Kateřina Konečná/ ITERAČNÍ METODY PRO ŘEŠENÍ SYSTÉMŮ LINEÁRNÍCH ROVNIC Budeme se zabývat řešením soustavy lineárních rovnic
(Poznámka: V MA 43 je věta formulována trochu odlišně.)
 Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy: zúplnění prostoru funkcí přibližné řešení minim. úlohy metoda konečných prvků jiný pohled na zobecněné řešení stejný způsob numerické aproximace
Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy: zúplnění prostoru funkcí přibližné řešení minim. úlohy metoda konečných prvků jiný pohled na zobecněné řešení stejný způsob numerické aproximace
Derivace funkcí více proměnných
 Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Numerické řešení diferenciálních rovnic
 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni. Abstrakt
 VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni Abstrakt Současný trend snižování počtu kontaktních hodin ve výuce nutí vyučující
VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni Abstrakt Současný trend snižování počtu kontaktních hodin ve výuce nutí vyučující
III. MKP vlastní kmitání
 Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
Měření modulů pružnosti G a E z periody kmitů pružiny
 Měření modulů pružnosti G a E z periody kmitů pružiny Online: http://www.sclpx.eu/lab2r.php?exp=2 V tomto experimentu vycházíme z pojetí klasického pokusu s pružinovým oscilátorem. Z periody kmitů se obvykle
Měření modulů pružnosti G a E z periody kmitů pružiny Online: http://www.sclpx.eu/lab2r.php?exp=2 V tomto experimentu vycházíme z pojetí klasického pokusu s pružinovým oscilátorem. Z periody kmitů se obvykle
