MATEMATIKA. Příklady pro 1. ročník bakalářského studia. II. část Diferenciální počet. II.1. Posloupnosti reálných čísel
|
|
|
- Oldřich Staněk
- před 7 lety
- Počet zobrazení:
Transkript
1 MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní resp. ryze monotónní. 84. a n = 1 + n a n = 5 n 86. a n = 2 n 87. a n = cos n 88. a n = n 89. a n = tg (1/n) 90. a n = n / (n+1) 91. a n = ( 1) n / (n 2 +1) 92. a n = n 2 / (n+1) 93. a n = ( 1) n n 2 / (n+3) Je dána posloupnost a n a čísla L R, 0. Najděte přirozené číslo n 0 takové, že pro všechna n N, n n 0 je a n U (L). 94. a n = 2 / n, L = 0, = a n = 2 + (sin n) / n, L = 2, = a n = 1 / n 3, L = 0, = a n = n, L = 1, = 0.02 Je dána posloupnost a n. Vypočtěte lim a n. n 98. a n = (n 5) / (2n + 3) 99. a n = (n 2 + 2n 4) / (n ) 100. a n = (2n 3 + n 2 50n)/(3n 3 + 4n 2 1) 101. a n = (2n 2 + n 3) / (n 3 + 4n 2 ) 102. a n = (n 3 + 4n 5) / (20n 2 + n + 10) 103. a n = (2n 2 + 3n + 7) / ( 2 n) 104. a n = (n+2) + n / (n+5) 105. a n = (n 3 +1) + 2n / (n 2 + 3) 106. a n = (n+4) n 107. a n = (n 2 +1) n 108. a n = (n 2 +4) 2n 109. a n = n. (n 2 +1) (n 2 1) 110. a n = ( n) / (2n 2 + 1) 111. a n = sin (n 2 +1) / n 112. a n = n cos (2n) / (2n + 5) 113. a n = (n 2 + sin n 2 ) / (3n 2 + n) 114. a n = (n+1) + cos n / (n + 2) 115. a n = (n 2 sin n 3 ) / (5n + 1) 116. a n = ( 1) n.n 2 + 3n / (2n 2 + 1) 117. a n = n.cos (n ) / (3n + 4) II.2. Základní vlastnosti funkcí Určete definiční obory následujících funkcí y = (3x 5) 119. y = (x + 2) / (x 2 4x + 3) 120. y = 1 / (x 2 4x) 121. y = (sin x) + (16 x 2 ) 122. y = ln (2x + 4) / (x 2 5x + 6) 123. y = ln (x + 3) + (10 2x) 124. y = cos (2x) / x. (x + 4) 125. y = arcsin (2x / 3) 126. y = (arcsin x) / (3x 1) 127. y = ln (x 2 3x + 3) 128. y = (2 log 4x) 129. y = (1 ln 2 x) 7
2 Určete supremum a infimum dané funkce f na množině M a rozhodněte, zda f má na M maximum resp. minimum (příp. určete jejich hodnotu). Nakreslete graf funkce y = f(x) pro x M f(x) = 2 + (x 1) 2, M = R 131. f(x) = 2 3x, M = 2, 4) 132. f(x) = 1 / (x 1) 2, M = (1, + ) 133. f(x) = (x + 2), M = 2, + ) 134. f(x) = (5 x), M = 1, 4) 135. f(x) = sin 2x, M = R 136. f(x) = 2 cos x, M = (0, 2 ) 137. f(x) = 2x 3, M = R 138. f(x) = x 1 + 2, M = (0, 5) 139. f(x) = 1 / (x 2 + 2), M = R 140. f(x) = 2 + ln (x 1), M = (1, + ) 141. f(x) = 1 + ln (3 x), M = 0, f(x) = e x+2, M = (, f(x) = 2 arctg x +, M = R 144. f(x) = arcsin (x 3), M = (2, f(x) = 3 (x 2 + 1), M = R Určete maximální intervaly, na kterých je daná funkce f ryze monotónní, a najděte k ní na těchto intervalech inverzní funkce. Určete také definiční obory inverzních funkcí f(x) = x f(x) = (x 2) f(x) = 1 / (x + 3) 149. f(x) = 2 1 / (x 1) 150. f(x) = (3 + e 2x ) 151. f(x) = ln (4 x) II.3. Limita a spojitost funkce Vypočtěte následující limity: 152. lim x 2 sin x 153. lim x cos 2x 154. lim x 2+ (x 2 + 3x 5) 155. lim x 1 (x 2 4x) 156. lim x (1 + 2 x ) 157. lim x 2 / (x + 3) 158. lim x 2 (x 2 + 5) / (x 2 3) 159. lim x 0 (x 3 3x + 4) / (x 2 2) 160. lim x (x 2 + 3x 10) / (2x 2 + 7) 161. lim x (2x 2 + x x) / (x 2 + 5x) 162. lim x (3x + 5) / (x 2 + 2x + 6) 163. lim x (x 3 + 4x 2 + 1) / (2x 2 + 5x) 164. lim x (x 3 + 8x 2) / (3x ) 165. lim x (2x + arctg x) / (x + 100) 166. lim x (x 2 + sin x 2 ) / (2x 2 3) 167. lim x (2x 2 + 1) / (x 5) 168. lim x (1 + x 2 ) 1 / x 169. lim x (x 2 1) x 170. lim x 1 (x 2 1) / (3x + 3) 171. lim x 2 (x 2 x 2) / (x 2 4) 172. lim x 4 (2x 8) / ( x 2) 173. lim x 0+ sin (3x) / x 174. lim x 0 tg (4x) / (2x) 175. lim x 0 sin (4x) / tg x 176. lim x 0 (1 cos 2 x) / (2x 2 ) 177. lim x 0 arctg x / (3x) 178. lim x 0+ (tg x sin x) / x lim x /4 (cos x sin x) / cos 2x 180. lim x 0 (3x 2 5x) / sin 3x 181. lim x 1 (1 x 2 ) / sin ( x) 182. lim x 1 (arctg x /4) / (x 1) 183. lim x 2 tg ( x) / (x + 2) 184. lim x sin x / (x + 1) 185. lim x 0 arctg (1/x 2 ) 186. lim x arcsin x / (x + 2) 187. lim x ln (x 2 5) / (x 2 + 2x) 188. lim x e x / x lim x ln x / x 190. lim x 0 ln (1 + 2x) / x 191. lim x 0+ sin x / x 8
3 Najděte maximální intervaly, v nichž je daná funkce f spojitá. Je-li c R takový bod nespojitosti, že f je definována v jeho některém prstencovém okolí (c, c) (c, c+ ), 0, zjistěte, zda funkci f lze v bodě c spojitě dodefinovat. Pokud ano, najděte odpovídající funkční hodnotu d f(x) = 1 / x 193. f(x) = sin x / x 194. f(x) = (x 2) / (x 2 2x) 195. f(x) = (x + 1) / (x 3 + 1) 196. f(x) = 1 / ln x 197. f(x) = arctg (1/x) 198. f(x) = x. arctg (1/x) 199. f(x) = x / (e x 2) II.4. Derivace funkce a její význam Vypočtěte derivace následujících funkcí. Určete také, pro jaká x je derivace definovaná y = 6x 2 3x y = 7x 5 2x 4 + x y = (x 3 + 2x 2 5x 10) y = (x 2 + 2x + 5) y = (5x 3) 205. y = (x 2 + 4) 206. y = (2x 2 x + 5) 207. y = 3 (x 2 1) 208. y = (x + 1).(2x + 5) y = (x 2). 3 (x 2 4) 210. y = 1 / (x 3) 211. y = (x 2 + 1) / (x + 1) 212. y = 3 (x + 2) / x y = (x + 1)/(x + 3) 214. y = sin 3x 215. y = cos (x 2 + 4x) 216. y = tg 5x 217. y = sin 2 (x 3 + 3x 2 1) 218. y = cotg 2 (3x) 219. y = sin (1/x) 220. y = x. cos 2 x 221. y = (1 + x + sin x) 222. y = arcsin (x 2) 223. y = arccos x y = arctg 2 (5 x) 225. y = arcsin (x + 1) 226. y = arctg x 227. y = arccotg 1 / (x 4) 228. y = e 3x y = exp (5x 2 2x+1) exp z = e z 230. y = exp ( 1/x 2 ) 231. y = (e x 2) 232. y = 2 3x (6x + 1/x) 233. y = y = ln (4x) 235. y = ln (x 2 + 3x 4) 236. y = ln (x + (1+x 2 )) 237. y = ln (ln x) 238. y = (2x) 5x 239. y = (x 2 + 1) 3x 240. y = ln (sin 3x + 2) 241. y = e 3x. (x 2 + 1) y = e 2x. sin 5x 243. y = e x. sin (x 2 + 1) Vypočtěte druhé derivace následujících funkcí. Určete také, pro jaká x je druhá derivace definovaná y = sin (3x + 1) 245. y = cos 2 x 246. y = (1 + x 2 ) 247. y = tg x 248. y = x 2. e x 249. y = (1 + x) / (1 x) 250. y = 1 / (2x + 1) y = arcsin (x/2) 9
4 Najděte rovnici tečny a normály ke grafu funkce f v bodě x 0, f(x 0 ). (Poznámka: Pro směrnice k t resp. k n tečny resp. normály ve společném bodě platí k n. k t = 1.) 252. f(x) = x 2, x 0 = f(x) = sin x, x 0 = 254. f(x) = 8 / (4 + x 2 ), x 0 = f(x) = (3x + 1) / (x + 2), x 0 = f(x) = 1 / (9 x 2 ), x 0 = f(x) = 2 x, x 0 = Najděte tečny ke grafu funkce f(x) = 4x x 2 v bodech jeho průsečíků s osou x a určete úhel, pod jakým se protínají Ve kterém bodě T paraboly y = x 2 2x + 5 je její tečna kolmá k ose prvního kvadrantu? Najděte rovnici tečny Určete koeficienty b, c v rovnici paraboly y = x 2 + bx + c tak, aby se dotýkala přímky o rovnici y = x v bodě x 0, y 0, x 0 = Pod jakým úhlem se protínají grafy funkcí y = sin x a y = cos x? II. 5. Užití derivace, průběh funkce Pro danou funkci najděte lokální extrémy a intervaly, v nichž je funkce ryze monotónní. Určete také, zda je rostoucí nebo klesající f(x) = x 3 6x f(x) = 2x 3 + 3x 2 36x f(x) = x / (x 2 + 1) 265. f(x) = x + x / (x 2 1) 266. f(x) = x. ln x 267. f(x) = x 2 / (x 2 + 1) 268. f(x) = x + e x 269. f(x) = x 2. e x 270. f(x) = e x / (x 2 1) 271. f(x) = x. (1 x) Najděte maximum a minimum funkce f na intervalu I a určete, ve kterých bodech funkce těchto hodnot nabývá f(x) = x 3 3x 2 9x + 35, I = 4, f(x) = (5 4x), I = 1, f(x) = x 2. ln x, I = 1, e 275. f(x) = x / x 16, I = 1, f(x) = x x 2, I = 1, f(x) = x 2. e x, I = 3, 1/ f(x) = x 3 / (x 2 + 1), I = 2, 3 Najděte lokální i absolutní extrémy následujících funkcí (pokud existují) na jejich definičních oborech y = x 2 / (x 2) 280. y = x 3 + x 4 / y = 2x / (x 2 + 1) 282. y = x 3. ln x 283. y = x 2 / 2 3x + 2. ln x 284. y = x. ln x y = 2x + e x 286. y = arctg x x / y = 3x. (1 x) 288. y = x 2. e x 289. y = (2x x 2 ) 290. y = x / 2 + arctg (1/x) 10
5 Určete, na jakých maximálních intervalech jsou následující funkce konvexní nebo konkávní, a najděte jejich inflexní body y = x 3 5x y = 3x 5 40x x y = x / (1 + x 2 ) 294. y = 2x 2 / (1 + x 2 ) 295. y = x 2. e x 296. y = x. ln x y = ln (1+ x 2 ) 298. y = x. (2 x) 299. y = arctg x x / y = e x x 2 Najděte asymptoty následujících funkcí (pokud existují) y = 1 / x y = 3x 1 / (x 2) 303. y = x / (x 2 + 5) 304. y = (x 3 + 2) / (x 2 + 1) 305. y = 2x 1 + e x 306. y = x 3 / (2 x 2 ) 307. y = (4x 2 + x + 3) 308. y = 2x ln (x) / x 309. y = x + ln (x) / (x 2) 310. y = 2x + arctg (x/2) 11
6 Výsledky: 84. omezená zdola, rostoucí 85. omezená shora, klesající 86. omezená, klesající 87. omezená, není monotónní 88. omezená zdola, rostoucí 89. omezená, klesající 90. omezená, rostoucí 91. omezená, není monotónní 92. omezená shora, klesající 93. neomezená, není monotónní 94. n n n n / / / / / neexistuje 117. neexistuje /3, + ) , 1) (1, 3) (3, + ) 120. (, 0) (4, + ) , 0, 122. ( 2, 2) (2, 3) (3, + ) 123. ( 3, ( 4, 0) (0, + ) /2, 3/ , 1/3) (1/3, (, 1 2, + ) 128. (0, /e, e Výsledky k příkladům č : Příklad max M f sup M f min M f inf M f 130. neexistuje neexistuje neexistuje + neexistuje neexistuje neexistuje neexistuje neexistuje neexistuje /2 1/2 neexistuje neexistuje + neexistuje ln ln e 3 e 3 neexistuje neexistuje 2 neexistuje /2 /2 neexistuje / neexistuje a) (, 0, f 1 (y) = (y + 1), D(f 1 ) = 1, + ) b) 0, + ), f 1 (y) = (y + 1), D(f 1 ) = 1, + ) 147. (, + ), f 1 (y) = 2 3 y, D(f 1 ) = (, + ) 148. a) (, 3), f 1 (y) = 1/y 3, D(f 1 ) = (, 0) b) ( 3, + ), f 1 (y) = 1/y 3, D(f 1 ) = (0, + ) 149. a) (, 1), f 1 (y) = 1 + 1/(2 y), D(f 1 ) = (2, + ) b) (1, + ), f 1 (y) = 1 + 1/(2 y), D(f 1 ) = (, 2) 150. (, + ), f 1 (y) = ln (y 2 3) / 2, D(f 1 ) = ( 3, + ) 151. (, 4), f 1 (y) = 4 e y, D(f 1 ) = (, + ) / / / / / / / / / / / / /
7 192. (, 0), (0, + ); c = 0, nelze dodefinovat 193. (, 0), (0, + ); c = 0, d = (, 0), (0, 2), (2, + ); c 1 = 0, nelze dodefinovat, c 2 = 2, d 2 = 1/ (, 1), ( 1, + ); c = 1, d = 1/ (0, 1), (1, + ); c = 1, nelze dodefinovat 197. (, 0), (0, + ); c = 0, nelze dodefinovat 198. (, 0), (0, + ); c = 0, d = (, ln 2), (ln 2, + ); c = ln 2, nelze dodefinovat x 3, x R x 4 8x 3 + 2x, x R (x 3 +2x 2 5x 10).(3x 2 +4x 5), x R (x 2 + 2x + 5).(2x + 2), x R / 2. (5x 3), x (3/5, + ) 205. x / (x 2 + 4), x R 206. (4x 1) / 2. (2x 2 x + 5), x R x / 3.(x 2 1) 2/3, x R 1, (2x + 5) 7.(18x + 21), x R (x 2 4) + (2x 4) / 3.(x 2 4) 2/3, x R 2, / 2.(x 3) 3/2, x (3, + ) 211. (x 1) / (x + 1) 2. (x 2 + 1), x R ( 5x 12) / 3x 3.(x+2) 2/3, x R 2, (x+3)/(x+1) / (x+3) 2, x (, 3) ( 1, + ) cos 3x, x R 215. (2x + 4).sin (x 2 + 4x), x R / cos 2 (5x), x ( /10 + k. /5, /10 + k. /5), k celé 217. (6x x). sin (x 3 + 3x 2 1). cos (x 3 + 3x 2 1), x R cotg 3x / sin 2 (3x), x (k. /3, (k+1). /3), k celé 219. cos (1/x) / x 2, x (, 0) (0, + ) 220. cos 2 x / (2. x) 2. x. cos x. sin x, x (0, + ) 221. (1 + cos x) / 2. (1 + x + sin x), x (x 0, + ), x 0 je řešení rovnice 1 + x + sin x = / (4x x 2 3), x (1, 3) x / (1 x 4 ), x ( 1, 1) arctg (5 x) / (x 2 10x + 26), x R / 2. ( x x 2 ), x ( 1, 0) / 2. x. (1 + x), x (0, + ) / 1 + (x 4) 2, x (, 4) (4, + ) e 3x+1, x R 229. (10x 2). exp (5x 2 2x + 1), x R exp ( 1/x 2 ) / x 3, x R / 2e x. (e x 2), x (, ln 2) x. ln 2, x R 233. (6 1/x 2 ). ln 5. 5 (6x + 1/x), x R / x, x (0, ) 235. (2x + 3) / (x 2 + 3x 4), x (, 4) (1, + ) / (1 + x 2 ), x R / (x. ln x), x (1, + ) 238. (2x) 5x. (5. ln 2x + 5), x (0, + ) 239. (x 2 + 1) 3x. 3. ln (x 2 + 1) + 6x 2 / (x 2 + 1), x R cos 3x / (sin 3x + 2), x R 241. e 3x. (x 2 + 1). (3x 2 + 4x + 3), x R 242. e 2x. (2. sin 5x + 5. cos 5x), x R 243. e x. 2x. cos (x 2 + 1) sin (x 2 + 1), x R sin (3x + 1), x R cos 2x, x R 246. (1 + x 2 ) 3/2, x R sin x / cos 3 x, x /2 + k, k celé 248. (x 2 4x + 2). e x, x R / (1 x) 3, x R / (2x + 1) 4, x R 1/ x / (4 x 2 ) 3/2, x ( 2, 2) 252. t: y = 4x 4, n: y = 9/2 x/ t: y = x, n: y = x 254. t: y = 2 x/2, n: y = 2x t: y = 1/2 + 5x/4, n: y = 1/2 4x/ t: y = 5.x / 8 1/8, n: y = 17/2 8.x / t: y = 1/4 + ln 2. (x + 2) / 4, n: y = 1/4 4. (x + 2) / ln t 1 : y = 4x, t 2 : y = 16 4x, = arccos (15/17) 259. T = 1/2, 17/4, t: y = 19/4 x 260. b = 3, c = = arccos (1/3) 262. rostoucí v (, 2 a 2, + ), klesající v 2, 2, lok. max. y = pro x = 2, lok. min. y = pro x = rostoucí v (, 3 a 2, + ), klesající v 3, 2, lok. max. y = 85 pro x = 3, lok. min. y = 40 pro x = rostoucí v 1, 1, klesající v (, 1 a 1, + ), lok. max. y = 1/2 pro x = 1, lok. min. y = 1/2 pro x = 1 13
8 265. rostoucí v (, 3 a 3, + ), klesající v 3, 1), ( 1, 1) a (1, 3, lok. max. y = 3. 3 / 2 pro x = 3, lok. min. y = 3. 3 / 2 pro x = rostoucí v 1/e, + ), klesající v (0, 1/e, lok. min. y = 1/e pro x = 1/e 267. rostoucí v 0, + ), klesající v (, 0, lok. min. y = 0 pro x = rostoucí v 0, + ), klesající v (, 0, lok. min. y = 1 pro x = rostoucí v (, 2 a 0, + ), klesající v 2, 0, lok. max. y = 4e 2 pro x = 2, lok. min. y = 0 pro x = rostoucí v (, 1), ( 1, 1 2 a 1+ 2, + ), klesající v 1 2, 1) a (1, 1+ 2, lok. max. y = exp(1 2) / (2 2 2) pro x = 1 2, lok. min. y = exp(1+ 2) / (2+2 2) pro x = rostoucí v (, 2/3, klesající v 2/3, 1, lok. max. y = 2. 3 / 9 pro x = 2/3, lok. min. y = 0 pro x = max f = f( 1) = 40, min f = f( 4) = max f = f( 1) = 3, min f = f(1) = max f = f(e) = e 2, min f = f(1) = max f = f(4) = 4, min f = f(2) = max f = f(1) = 4, min f = f(0) = max f = f( 2) = 1/e, min f = f(0) = max f = f(3) = 27/10, min f = f( 2) = 8/ lok. max. y = 0 pro x = 0, lok. min. y = 8 pro x = abs. min. y = 27/4 pro x = abs. max. y = 1 pro x = 1, abs. min. y = 1 pro x = abs. min. y = 3 3. ln 3 pro x = lok. max. y = 5/2 pro x = 1, lok. min. y = 2. ln 2 4 pro x = abs. min. y = 2 1/e pro x = 1/e 285. abs. min. y = 2 2. ln 2 pro x = ln lok. max. y = /4 1/2 pro x = 1, lok. min. y = 1/2 /4 pro x = abs. max. y = 2. 3 / 3 pro x = 2/3, lok. min. y = 0 pro x = lok. max. y = 4.e 2 pro x = 2, abs. min. y = 0 pro x = abs. max. y = 1 pro x = 1, abs. min. y = 0 pro x = 0, x = lok. max. y = /4 1/2 pro x = 1, lok. min. y = /4 + 1/2 pro x = konvexní na 0, + ), konkávní na (, 0, inflexní bod konvexní na 2, 0 a 2, + ), konkávní na (, 2 a 0, 2, inflexní body 2, 0, konvexní na 3, 0 a 3, + ), konkávní na (, 3 a 0, 3, inflexní body 3, 0, konvexní na 3/3, 3/3, konkávní na (, 3/3 a 3/3, + ), inflexní body 3/3, 3/ konvexní na (, 2 2 a 2+ 2, + ), konkávní na 2 2, 2+ 2, inflexní body konvexní na (0, + ), nemá inflexní body 297. konvexní na 1, 1, konkávní na (, 1 a 1, + ), inflexní body 1, konkávní na (, 2, nemá inflexní body 299. konvexní na (, 0, konkávní na 0, + ), inflexní bod konvexní na ln 2, + ), konkávní na (, ln 2, inflexní bod x = ln svislá asymptota x = 0, šikmé asymptoty y = 3 pro x 302. svislá asymptota x = 2, šikmé asymptoty y = 3x pro x 303. šikmé asymptoty y = 0 pro x 304. šikmé asymptoty y = x pro x 305. šikmé asymptoty y = 2x 1 pro x svislé asymptoty x = 2, x = 2, šikmé asymptoty y = x pro x 307. šikmé asymptoty y = 2x 1/4 pro x, y = 2x + 1/4 pro x svislá asymptota x = 0, šikmá asymptota y = 2x + 3 pro x svislé asymptoty x = 0, x = 2, šikmá asymptota y = x pro x šikmé asymptoty y = 2x /2 pro x, y = 2x + /2 pro x + 14
. 1 x. Najděte rovnice tečen k hyperbole 7x 2 2y 2 = 14, které jsou kolmé k přímce 2x+4y 3 = 0. 2x y 1 = 0 nebo 2x y + 1 = 0.
 Diferenciální počet příklad s výsledky ( Najděte definiční obor funkce f() = ln arcsin + ) D f = (, 0 Najděte rovnici tečny ke grafu funkce f() = 3 +, která je rovnoběžná s přímkou y = 4 4 y 4 = 0 nebo
Diferenciální počet příklad s výsledky ( Najděte definiční obor funkce f() = ln arcsin + ) D f = (, 0 Najděte rovnici tečny ke grafu funkce f() = 3 +, která je rovnoběžná s přímkou y = 4 4 y 4 = 0 nebo
1. Písemka skupina A...
 . Písemka skupina A.... jméno a příjmení Načrtněte grafy funkcí (v grafu označte všechny průsečíky funkce s osami a asymptoty). y y sin 4 y y arccos ) Určete, jestli je funkce y ln prostá? ) Je funkce
. Písemka skupina A.... jméno a příjmení Načrtněte grafy funkcí (v grafu označte všechny průsečíky funkce s osami a asymptoty). y y sin 4 y y arccos ) Určete, jestli je funkce y ln prostá? ) Je funkce
Příklady na konvexnost a inflexní body. Funkce f (x) = x 3 9x. Derivace jsou f (x) = 3x 2 9 a f (x) = 6x. Funkce f je konvexní na intervalu (0, )
 Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Matematická analýza 1, příklady na procvičení (Josef Tkadlec, )
 Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
Derivace funkce. existuje limita lim 0 ) xx xx0. Jestliže tato limita neexistuje nebo pokud funkce ff
 Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
IX. Vyšetřování průběhu funkce
 IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
Funkce. RNDR. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Výsledky Př.1. Určete intervaly monotónnosti a lokální extrémy funkce a) ( ) ( ) ( ) Stacionární body:
 Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Příklad 1 ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 6
 Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
MATEMATIKA I - vybrané úlohy ze zkoušek v letech
 MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Funkce jedn e re aln e promˇ enn e Derivace Pˇredn aˇska ˇr ıjna 2015
 Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
1 Množiny, výroky a číselné obory
 1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Přednáška z MA. Michal Tuláček 16. prosince 2004. 1 IV.7 Průběhy funkce 3. 2 Vyšetřování průběhu funkce- KUCHAŘKA 4
 Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
f( x) x x 4.3. Asymptoty funkce Definice lim f( x) =, lim f( x) =, Jestliže nastane alespoň jeden z případů
 3 Výklad Definice 3 Jestliže nastane alespoň jeden z případů lim =, lim =, + + lim =, lim =, kde ( D ), pak říkáme, že přímka = je asymptotou funkce f() v bodě f Jestliže lim ( k q) =, resp lim ( k q)
3 Výklad Definice 3 Jestliže nastane alespoň jeden z případů lim =, lim =, + + lim =, lim =, kde ( D ), pak říkáme, že přímka = je asymptotou funkce f() v bodě f Jestliže lim ( k q) =, resp lim ( k q)
soubor FUNKCÍ příručka pro studenty
 soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
LDF MENDELU. Simona Fišnarová (MENDELU) Průběh funkce ZVMT lesnictví 1 / 21
 Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Pro jakou hodnotu parametru α jsou zadané vektory kolmé? (Návod: Vektory jsou kolmé, je-li jejich skalární součin roven nule.)
 Vybrané příklady ze skript J. Neustupa, S. Kračmar: Sbírka příkladů z Matematiky I I. LINEÁRNÍ ALGEBRA I.. Vektory, vektorové prostory Jsou zadány vektory u, v, w a reálná čísla α, β, γ. Vypočítejte vektor
Vybrané příklady ze skript J. Neustupa, S. Kračmar: Sbírka příkladů z Matematiky I I. LINEÁRNÍ ALGEBRA I.. Vektory, vektorové prostory Jsou zadány vektory u, v, w a reálná čísla α, β, γ. Vypočítejte vektor
7.1 Extrémy a monotonie
 KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
Matematika B 2. Úvodní informace
 Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
Aplikace derivace a průběh funkce
 Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Derivace funkce. Obsah. Aplikovaná matematika I. Isaac Newton. Mendelu Brno. 2 Derivace a její geometrický význam. 3 Definice derivace
 Derivace funkce Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Směrnice přímk Derivace a její geometrický význam 3 Definice derivace 4 Pravidla a vzorce pro derivování 5 Tečna a normála 6 Derivace
Derivace funkce Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Směrnice přímk Derivace a její geometrický význam 3 Definice derivace 4 Pravidla a vzorce pro derivování 5 Tečna a normála 6 Derivace
Funkce. Vlastnosti funkcí
 FUNKCE Funkce zobrazení (na číselných množinách) předpis, který každému prvku z množiny M přiřazuje právě jeden prvek z množiny N zapisujeme ve tvaru y = f () značíme D( f ) Vlastnosti funkcí 1. Definiční
FUNKCE Funkce zobrazení (na číselných množinách) předpis, který každému prvku z množiny M přiřazuje právě jeden prvek z množiny N zapisujeme ve tvaru y = f () značíme D( f ) Vlastnosti funkcí 1. Definiční
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy
 Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Zlín, 23. října 2011
 (. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
(. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
Základy matematiky pro FEK
 Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Přijímací zkouška na navazující magisterské studium 2014
 Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
1. Definiční obor funkce dvou proměnných
 Definiční obor funkce dvou proměnných Řešené příklady 1. Definiční obor funkce dvou proměnných Vyšetřete a v kartézském souřadném systému (O, x, y) zakreslete definiční obory následujících funkcí dvou
Definiční obor funkce dvou proměnných Řešené příklady 1. Definiční obor funkce dvou proměnných Vyšetřete a v kartézském souřadném systému (O, x, y) zakreslete definiční obory následujících funkcí dvou
Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
 Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Derivace a průběh funkce příklady z písemných prací
 Derivace a průběh funkce příklady z písemných prací Vyšetřete průběh následuících funkcí. Příklad. = x +arctg( x ). D(f) =R.. Funkce e spoitá na R. 3. Funkce není lichá, sudá, ani periodická.. lim x ±
Derivace a průběh funkce příklady z písemných prací Vyšetřete průběh následuících funkcí. Příklad. = x +arctg( x ). D(f) =R.. Funkce e spoitá na R. 3. Funkce není lichá, sudá, ani periodická.. lim x ±
Cyklometrické funkce
 4 Cyklometrické funkce V minulé kapitole jsme zkoumali první funkci inverzní ke funkci goniometrické (tyto funkce se nazývají cyklometrické) funkci y = arcsin x (inverzní k funkci y = sin x ) Př: Nakresli
4 Cyklometrické funkce V minulé kapitole jsme zkoumali první funkci inverzní ke funkci goniometrické (tyto funkce se nazývají cyklometrické) funkci y = arcsin x (inverzní k funkci y = sin x ) Př: Nakresli
IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel
 Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Katedra aplikované matematiky, VŠB TU Ostrava.
 SBÍRKA PŘÍKLADŮ Z MATEMATICKÉ ANALÝZY JIŘÍ BOUCHALA Katedra aplikované matematiky, VŠB TU Ostrava jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala 3 Předmluva Cílem této sbírky je poskytnout studentům vhodné
SBÍRKA PŘÍKLADŮ Z MATEMATICKÉ ANALÝZY JIŘÍ BOUCHALA Katedra aplikované matematiky, VŠB TU Ostrava jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala 3 Předmluva Cílem této sbírky je poskytnout studentům vhodné
2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je
![2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je 2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je](/thumbs/102/152847701.jpg) Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15
 Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15 Klíčové pojmy Neznalost některého z klíčových pojmů bude mít za následek ukončení zkoušky se známkou neprospěl(a). supremum infimum limita
Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15 Klíčové pojmy Neznalost některého z klíčových pojmů bude mít za následek ukončení zkoušky se známkou neprospěl(a). supremum infimum limita
Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si zopakovat a orientovat se v pojmech: funkce, D(f), g 2 : y =
 0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
Pavlína Matysová. 5. listopadu 2018
 Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Matematika 1. 1 Derivace. 2 Vlastnosti a použití. 3. přednáška ( ) Matematika 1 1 / 16
 Matematika 1 3. přednáška 1 Derivace 2 Vlastnosti a použití 3. přednáška 6.10.2009) Matematika 1 1 / 16 1. zápočtový test již během 2 týdnů. Je nutné se něj registrovat přes webové rozhraní na https://amos.fsv.cvut.cz.
Matematika 1 3. přednáška 1 Derivace 2 Vlastnosti a použití 3. přednáška 6.10.2009) Matematika 1 1 / 16 1. zápočtový test již během 2 týdnů. Je nutné se něj registrovat přes webové rozhraní na https://amos.fsv.cvut.cz.
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
VIDEOSBÍRKA DERIVACE
 VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x. Zderivuj funkci y = e sin2 (x 2 ). Zderivuj funkci y = x +2x 2 +sin x x 5. Zderivuj funkci y = cos2
VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x. Zderivuj funkci y = e sin2 (x 2 ). Zderivuj funkci y = x +2x 2 +sin x x 5. Zderivuj funkci y = cos2
Definice derivace v bodě
 Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Funkce základní pojmy a vlastnosti
 Funkce základní pojm a vlastnosti Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Pojem funkce Vlastnosti funkcí Inverzní funkce 4 Základní elementární funkce Mocninné Eponenciální Logaritmické
Funkce základní pojm a vlastnosti Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Pojem funkce Vlastnosti funkcí Inverzní funkce 4 Základní elementární funkce Mocninné Eponenciální Logaritmické
FUNKCE A JEJICH VLASTNOSTI
 PŘEDNÁŠKA 3 FUNKCE A JEJICH VLASTNOSTI Pojem zobrazení a funkce Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic
PŘEDNÁŠKA 3 FUNKCE A JEJICH VLASTNOSTI Pojem zobrazení a funkce Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic
I. Úvod. I.1. Množiny. I.2. Výrokový a predikátový počet
 I. Úvod I.1. Množiny Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Značení. Symbol x A značí, že element x je prvkem množiny A. Značení x
I. Úvod I.1. Množiny Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Značení. Symbol x A značí, že element x je prvkem množiny A. Značení x
DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem
Matematika. Obálka ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE MASARYKŮV ÚSTAV VYŠŠÍCH STUDIÍ. Bakalářský program: Ekonomika a management
 Matematika Obálka ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE MASARYKŮV ÚSTAV VYŠŠÍCH STUDIÍ Bakalářský program: Ekonomika a management Matematika doc. RNDr. Stanislav Kračmar, CSc. www.muvs.cvut.cz Evropský
Matematika Obálka ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE MASARYKŮV ÚSTAV VYŠŠÍCH STUDIÍ Bakalářský program: Ekonomika a management Matematika doc. RNDr. Stanislav Kračmar, CSc. www.muvs.cvut.cz Evropský
Matematika I pracovní listy
 Matematika I pracovní listy Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny
Matematika I pracovní listy Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny
Funkce a limita. Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
VIDEOSBÍRKA DERIVACE
 VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos 3x 3. Zderivuj funkci y = 3 e sin2 (x 2 ). Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y
VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos 3x 3. Zderivuj funkci y = 3 e sin2 (x 2 ). Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y
Monotonie a lokální extrémy. Konvexnost, konkávnost a inflexní body. 266 I. Diferenciální počet funkcí jedné proměnné
 66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
1. Písemka skupina A1..
 1. Psemka skupina A1.. Nartněte grafy funkc (v grafu oznate všechny průseky funkce s osami) 3 y y sin( ) y y log ( 1) 1 y 1 y = arccotg - 1) Urete, jestli je funkce y = - + 1 omezená zdola nebo shora?
1. Psemka skupina A1.. Nartněte grafy funkc (v grafu oznate všechny průseky funkce s osami) 3 y y sin( ) y y log ( 1) 1 y 1 y = arccotg - 1) Urete, jestli je funkce y = - + 1 omezená zdola nebo shora?
NMAF 051, ZS Zkoušková písemná práce 4. února 2009
 Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 4 4
Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 4 4
Matematika 1. Matematika 1
 5. přednáška Elementární funkce 24. října 2012 Logaritmus a exponenciální funkce Věta 5.1 Existuje právě jedna funkce (značíme ji ln a nazýváme ji přirozeným logaritmem), s následujícími vlastnostmi: D(ln)
5. přednáška Elementární funkce 24. října 2012 Logaritmus a exponenciální funkce Věta 5.1 Existuje právě jedna funkce (značíme ji ln a nazýváme ji přirozeným logaritmem), s následujícími vlastnostmi: D(ln)
Nalezněte hladiny následujících funkcí. Pro které hodnoty C R jsou hladiny neprázdné
 . Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
. Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
MATEMATIKA I. Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15. I. Základy, lineární algebra a analytická geometrie
 MATEMATIKA I Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
MATEMATIKA I Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
FUNKCE, ZÁKLADNÍ POJMY
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA FUNKCE, ZÁKLADNÍ POJMY Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA FUNKCE, ZÁKLADNÍ POJMY Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného
Matematika 1 pro PEF PaE
 Derivace funkcí jedné proměnné / 9 Matematika pro PEF PaE 4. Derivace funkcí jedné proměnné Přemysl Jedlička Katedra matematiky, TF ČZU Derivace funkcí jedné proměnné Nejjednodušší derivace 2 / 9 Derivace
Derivace funkcí jedné proměnné / 9 Matematika pro PEF PaE 4. Derivace funkcí jedné proměnné Přemysl Jedlička Katedra matematiky, TF ČZU Derivace funkcí jedné proměnné Nejjednodušší derivace 2 / 9 Derivace
Derivace vyšších řádů, aplikace derivací
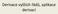 Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
Příklady z matematiky(pro ITS)
 Příklady z matematikypro ITS) František Mošna Definiční obor: Zjistěte maimální definiční obor funkce:. f)=ln 2 8 9 ) + +2 Df= 2, ) 9, ).2 f)=ln 2 4 5 ) 36 2 Df= 6, ) 5,6.3 f)=ln 2 7 8 ) 00 2 Df= 0, 9)
Příklady z matematikypro ITS) František Mošna Definiční obor: Zjistěte maimální definiční obor funkce:. f)=ln 2 8 9 ) + +2 Df= 2, ) 9, ).2 f)=ln 2 4 5 ) 36 2 Df= 6, ) 5,6.3 f)=ln 2 7 8 ) 00 2 Df= 0, 9)
f(x) = ln arcsin 1 + x 1 x. f(x) = (cos x) cosh x + 3x a nalezněte rovnici tečen ke grafu této funkce v bodech f(x) = (sin x) x2 + 3 cos x
 Příkad Nalezněte definiční obor funkce f(x) = ln arcsin + x x Určete definiční obor funkce f(x) = (cos x) cosh x + 3x a nalezněte rovnici tečen ke grafu této funkce v bodech [;?] a Určete definiční obor
Příkad Nalezněte definiční obor funkce f(x) = ln arcsin + x x Určete definiční obor funkce f(x) = (cos x) cosh x + 3x a nalezněte rovnici tečen ke grafu této funkce v bodech [;?] a Určete definiční obor
5. Limita funkce a spojitost strana 1/5 2018/KMA/MA1/přednášky. Definice 5.1. Mějme funkci f : D R a bod x 0 R.
 5. Limita funkce a spojitost strana 1/5 2018/KMA/MA1/přednášky Definice 5.1. Mějme funkci f : D R a bod 0 R. a) Číslo c R je částečná ita funkce f v bodě 0, pokud eistuje posloupnost ( n ) taková, že platí
5. Limita funkce a spojitost strana 1/5 2018/KMA/MA1/přednášky Definice 5.1. Mějme funkci f : D R a bod 0 R. a) Číslo c R je částečná ita funkce f v bodě 0, pokud eistuje posloupnost ( n ) taková, že platí
NMAF 051, ZS Zkoušková písemná práce 26. ledna x. x 1 + x dx. q 1. u = x = 1 u2. = 1 u. u 2 (1 + u 2 ) (1 u 2 du = 2.
 Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
P ˇ REDNÁŠKA 3 FUNKCE
 PŘEDNÁŠKA 3 FUNKCE 3.1 Pojem zobrazení a funkce 2 3 Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic (x, y) A B,
PŘEDNÁŠKA 3 FUNKCE 3.1 Pojem zobrazení a funkce 2 3 Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic (x, y) A B,
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Stručný přehled učiva
 Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
FUNKCE, ZÁKLADNÍ POJMY
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA FUNKCE, ZÁKLADNÍ POJMY Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA FUNKCE, ZÁKLADNÍ POJMY Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného
Přijímací zkouška na navazující magisterské studium 2015
 Přijímací zkouška na navazující magisterské studium 2015 Studijní program: Studijní obory: Matematika MMUI Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 1 (25 bodů Navrhněte deterministický konečný
Přijímací zkouška na navazující magisterské studium 2015 Studijní program: Studijní obory: Matematika MMUI Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 1 (25 bodů Navrhněte deterministický konečný
Funkce jedné proměnné
 Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
D(f) =( 1, 1) [ ( 1, 1) [ (1, 1). 2( x)3 ( x) 2 1 = 2(x) 3. (x) 2 1 = f(x) Funkce je lichá, není periodická
 Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18
 MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
Cyklometrické funkce
 4..7 Cyklometrické funkce Předpoklady: 46 Cyklometrické funkce: funkce inverzní k funkcím goniometrickým z minulé hodiny známe první cyklometrickou funkci y = arcsin x (inverzní k funkci y = sin x ). Př.
4..7 Cyklometrické funkce Předpoklady: 46 Cyklometrické funkce: funkce inverzní k funkcím goniometrickým z minulé hodiny známe první cyklometrickou funkci y = arcsin x (inverzní k funkci y = sin x ). Př.
DERIVACE. ln 7. Urči, kdy funkce roste a klesá a dále kdy je konkávní a
 DERIVACE 1. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x 3. Zderivuj funkci y = 3 e sin2 (x 2 ) 4. Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y = cos2 x
DERIVACE 1. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos x 3. Zderivuj funkci y = 3 e sin2 (x 2 ) 4. Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y = cos2 x
Limita posloupnosti, limita funkce, spojitost. May 26, 2018
 Limita posloupnosti, limita funkce, spojitost May 26, 2018 Definice (Okolí bodu) Okolím bodu a R (také ε- okolím) rozumíme množinu U(a, ε) = {x R; x a < ε} = (a ε, a + ε), bod a se nazývá střed okolí a
Limita posloupnosti, limita funkce, spojitost May 26, 2018 Definice (Okolí bodu) Okolím bodu a R (také ε- okolím) rozumíme množinu U(a, ε) = {x R; x a < ε} = (a ε, a + ε), bod a se nazývá střed okolí a
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika I/1 BA06. Cvičení, zimní semestr
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
22. & 23. & 24. Vlastnosti funkcí a jejich limita a derivace
 22. & 23. & 24. Vlastnosti funkcí a jejich ita a derivace Základní vlastnosti Definiční obor Definiční obor je množina neznámých, pro něž je funkce definována. Obor hodnot Obor hodnot je množina všech
22. & 23. & 24. Vlastnosti funkcí a jejich ita a derivace Základní vlastnosti Definiční obor Definiční obor je množina neznámých, pro něž je funkce definována. Obor hodnot Obor hodnot je množina všech
1. POJMY 1.1. FORMULE VÝROKOVÉHO POČTU
 Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Základy matematiky pro FEK
 Základy matematiky pro FEK 4. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 27 Množiny Zavedení pojmu množina je velice
Základy matematiky pro FEK 4. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 27 Množiny Zavedení pojmu množina je velice
Průběh funkce 1. Průběh funkce. Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:
 Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
WikiSkriptum Ing. Radek Fučík, Ph.D. verze: 4. ledna 2017
 Matematika I - Sbírka příkladů WikiSkriptum Ing. Radek Fučík, Ph.D. verze: 4. ledna 7 Obsah Limity a spojitost. l Hôpitalovo pravidlo zakázáno............................ 4. l Hôpitalovo pravidlo povoleno............................
Matematika I - Sbírka příkladů WikiSkriptum Ing. Radek Fučík, Ph.D. verze: 4. ledna 7 Obsah Limity a spojitost. l Hôpitalovo pravidlo zakázáno............................ 4. l Hôpitalovo pravidlo povoleno............................
3. Derivace funkce Definice 3.1. Nechť f : R R je definována na nějakém okolí U(a) bodu a R. Pokud existuje limita f(a + h) f(a) lim
 3 a b s = (a + b) 2 f(s) 3,46 4,680 3,93-2,9422 3,93 4,680 4,2962-2,034 4,2962 4,680 4,4886-0,0954 4,4886 4,680 4,5848 3,2095 4,4886 4,5848 4,5367,0963 4,4886 4,5367 4,526 0,427 4,4886 4,526 4,5006 0,508
3 a b s = (a + b) 2 f(s) 3,46 4,680 3,93-2,9422 3,93 4,680 4,2962-2,034 4,2962 4,680 4,4886-0,0954 4,4886 4,680 4,5848 3,2095 4,4886 4,5848 4,5367,0963 4,4886 4,5367 4,526 0,427 4,4886 4,526 4,5006 0,508
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí. Definičním oborem kvadratické funkce je množina reálných čísel.
 Kvadratická funkce Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí y = ax 2 + bx + c Číslo a je různé od nuly, b,c jsou libovolná reálná čísla. Definičním oborem kvadratické funkce je
Kvadratická funkce Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí y = ax 2 + bx + c Číslo a je různé od nuly, b,c jsou libovolná reálná čísla. Definičním oborem kvadratické funkce je
c ÚM FSI VUT v Brně 20. srpna 2007
 20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ
 Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
2. Vlastnosti elementárních funkcí, složené, inverzní a cyklometrické funkce,
 . Určete vlastnosti funkcí: (i) f : y = x (ii) f : y = x 4 (iii) f : y = cotgx (iv) f 4 : y = arccosx (v) f 5 : y = 4 x (vi) f 6 : y = ( 4 )x (vii) f 7 : y = lnx (viii) f 8 : y = x. Uveďte příklad: (i)
. Určete vlastnosti funkcí: (i) f : y = x (ii) f : y = x 4 (iii) f : y = cotgx (iv) f 4 : y = arccosx (v) f 5 : y = 4 x (vi) f 6 : y = ( 4 )x (vii) f 7 : y = lnx (viii) f 8 : y = x. Uveďte příklad: (i)
1 LIMITA FUNKCE Definice funkce. Pravidlo f, které každému x z množiny D přiřazuje právě jedno y z množiny H se nazývá funkce proměnné x.
 1 LIMITA FUNKCE 1. 1 Definice funkce Pravidlo f, které každému z množiny D přiřazuje právě jedno y z množiny H se nazývá funkce proměnné. Píšeme y f ( ) Někdy používáme i jiná písmena argument (nezávisle
1 LIMITA FUNKCE 1. 1 Definice funkce Pravidlo f, které každému z množiny D přiřazuje právě jedno y z množiny H se nazývá funkce proměnné. Píšeme y f ( ) Někdy používáme i jiná písmena argument (nezávisle
Matematická analýza I
 Matematická analýza I Cvičení 1 (4. 10. 2016) Definice absolutní hodnoty. Řešení nerovnic s absolutními hodnotami. Geometrická interpretace řešení nerovnice x + 1 < 3. Komplexní čísla a operace s nimi,
Matematická analýza I Cvičení 1 (4. 10. 2016) Definice absolutní hodnoty. Řešení nerovnic s absolutními hodnotami. Geometrická interpretace řešení nerovnice x + 1 < 3. Komplexní čísla a operace s nimi,
Funkce základní pojmy a vlastnosti
 Funkce základní pojm a vlastnosti Základ všší matematik LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplín společného
Funkce základní pojm a vlastnosti Základ všší matematik LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplín společného
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Kapitola 1: Reálné funkce 1/13
 Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
