Skupenství látek. s g. Blaise Pascal Anders Celsius

Blaise Pascal Anders Celsius

Sueství láte s g Blase Pascal 63 66 l Aders Celsus 70 744 Robert Boyle 67 69 George G. Stoes 89 903 Thomas Youg 773 89 Ludwg E. Boltzma 844 906 Joseh L. Gay-Lussac 778 850 Johaes D. a der Waals 837 93

Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů

Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,

Složení soustav. c k. Přehled užívaných koncentrací. hmotnostní konc. (podíl) objemová konc. (podíl) molová konc. (podíl) hmotnostně objemová konc.

U 8 - Ústav oesí a zaovatelsé tehy FS ČVU Složeí soustav Přehled užívaýh oetaí Symbol efe Rozmě Název m hmotost_ hmotost_ hmotostí o. (odíl) v objem_ objem_ objemová o. (odíl) lat. mozství_ lat. mozství_

Základní vlastnosti polovodičů

Základí vlastosti olovodičů Volé osiče áboje - elektroy -e m, - díry +e m V termodyamické rovováze latí Kocetrace osičů je možo vyjádřit omocí Fermiho eergie W F dotace doory ty N dotace akcetory ty P

plynné směsi viriální rozvoj plynné směsi stavové rovnice empirická pravidla pro plynné směsi příklady na procvičení

lyé směs válí ovo lyé směs stavové ove emá avdla o lyé směs řílady a ovčeí Směs lyů eálé a deálí hováí eáměší vtahy: magatův áo: m...,, m Daltoův áo:...,,, Směs lyů válí ovo B C... R m m R B SISICKÁ ERMODYMIK:

Kinetická teorie plynů - tlak F S F S F S. 2n V. tlak plynu. práce vykonaná při stlačení plynu o dx: celková práce vykonaná při stlačení plynu:

Kietická teorie plyů - tlak tlak plyu p práce vykoaá při stlačeí plyu o d: d celková práce vykoaá při stlačeí plyu: kdyby všechy molekuly měly stejou -ovou složku rychlost v : hybost předaá při árazu molekuly

Téma 6: Indexy a diference

dexy a dferece Téma 6: dexy a dferece ředáška 9 dvdálí dexy a dferece Základí ojmy Vedle elemetárího statstckého zracováí dat se hromadé jevy aalyzjí tzv. srováváím růzých kazatelů. Statstcký kazatel -

Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava ENERGETIKA U ŘÍZENÝCH ELEKTRICKÝCH POHONŮ. 1.

Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé

Analytické modely systémů hromadné obsluhy

Aalytcé odely systéů hroadé obsluhy ředěte teore hroadé obsluhy Kedallova lasface - ty SHO: X / Y / c / d / X ty stochastcého rocesu, terý osue říchody Y ty stochastcého rocesu terý osue délu obsluhy c

Budeme pokračovat v nahrazování funkce f(x) v okolí bodu a polynomy, tj. hledat vhodné konstanty c n tak, aby bylo pro malá x a. = f (a), f(x) f(a)

Předáša 7 Derivace a difereciály vyšších řádů Budeme poračovat v ahrazováí fuce f(x v oolí bodu a polyomy, tj hledat vhodé ostaty c ta, aby bylo pro malá x a f(x c 0 + c 1 (x a + c 2 (x a 2 + c 3 (x a

Metoda datových obalů DEA

Metoda datoých obalů DEA Model datoých obalů složí ro hodoceí techické efektiit rodkčích jedotek ssté a základě elosti stů a ýstů. Protože stů a ýstů ůže být íce drhů, řadí se DEA ezi etod icekriteriálího

1. Čím se zabývá 4PP? zabývá se určováním deformace a porušováním celistvých těles v závislosti na vnějším zatížení

. Čím se zabývá 4PP? zabývá se určováím deformace a porušováím celstvých těles v závslost a vějším zatížeí. Defce obecého apětí + apjatost v bodě tělesa -apětí - je to apětí v určtém bodě určtého tělesa.

Regrese. Aproximace metodou nejmenších čtverců ( ) 1 ( ) v n. v i. v 1. v 2. y i. y n. y 1 y 2. x 1 x 2 x i. x n

Regrese Aproxmace metodou ejmeších čtverců v v ( ) = f x v v x x x x Je dáo bodů [x, ], =,,, předpoládáme závslost a x a chceme ajít fuc, terá vsthuje teto tred - Sažíme se proložt fuc = f x ta, ab v =

á í ě ý ďě í í í í í í ř ě á íč ý ů ě ž í ě ý ě ý í ý ě á í í ří ě í í í í ý š í é é á í í á á ě ů á í ě á á í íš é ó ě í í í é í á í č ý ďě ě á á ý ý

á ě ý ďě ř ě á č ý ů ě ž ě ý ě ý ý ě á ř ě ý š é é á á á ě ů á ě á á š é ó ě é á č ý ďě ě á á ý ý á Í š ě á é Í ř řě ž á ý č é ě á ě ě ůé ý č ů é ž á á ř ž á ň ý á á ě ř ý á ů š č á á ž á é č é ó ě á ů

FYZIKA I. Newtonovy pohybové zákony

VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA AKULTA STROJNÍ YZIKA I Newtoovy pohybové zákoy Prof. RNDr. Vlé Mádr, CSc. Prof. Ig. Lbor Hlváč, Ph.D. Doc. Ig. Ire Hlváčová, Ph.D. Mgr. Art. Dgr Mádrová

10 částic. 1,0079 1, kg 1, kg. 1, kg. 6, , kg 0, kg 1,079g

..7 oláí veličiy I Předpoklady: 0 Opakováí z iulé hodiy: Ato uhlíku A C C je přibližě x těžší ež ato H. Potřebujee,0 0 atoů uhlíku C abycho dohoady získali g látky. Pokud áe,0 0 částic látky, říkáe, že

Inovace studia molekulární a buněčné biologie

Ivestice do rozvoje vzděláváí Iovace studia olekulárí a buěčé biologie Teto projekt je spolufiacová Evropský sociálí fode a státí rozpočte České republiky. Ivestice do rozvoje vzděláváí Předět: LRR/CHPI/Cheie

Lineární regrese ( ) 2

Leárí regrese Častým úolem je staoveí vzájemé závslost dvou (č více) fzálích velč a její matematcé vjádřeí. K tomuto účelu se používají růzé regresí metod, pomocí chž hledáme vhodou fuc f (), apromující

2.3. Fázové rovnováhy

.3. Fázové rovováhy Buee e zabývat heterogeíi outavai obahujícíi jeu či více ložek, které olu cheicky ereagují. takové říaě očet ložek oovíá očtu cheických iiviuí (látek), kterýi je outava tvořea. Fázová

č Ú Í ř

č Ú ř ť á ě á é á ý ě ě é ů ě č ň ě ř é ú ř ž č ě ň ř á ě ě ě ř ů žý č ú ť ě ř ť á š šť č ž ý ů ů ň ě ř ě č é ř á ž ž ž ď š ě ň ů ú Ě é ř á ě ě ř ř ě ř á ý ý ú ř ěž ó ě ý ž ě ý ř ř á ě ě ř š ž š ř ú ý

10.2.3 VÁŽENÝ ARITMETICKÝ PRŮMĚR S REÁLNÝMI VAHAMI

Středí hodoty Artmetcý průměr vážeý Aleš Drobí straa 0 VÁŽENÝ ARITMETICKÝ PRŮMĚR S REÁLNÝMI VAHAMI Zatím jsme počítal s tím, že četost ve vztahu pro vážeý artmetcý průměr byla přrozeá čísla Četost mohou

Komponenty výkonové elektrotechniky

Komoety výkoové elektrotechky Osovy ředášek:.. 3. 4. 5. 6. 7. 8. 9.... 3. Úvod do roblematky Výkoové dody Proudem řízeé součástky (výkoové trazstory, tyrstory) Moderí součástky tyrstorového tyu (GTO, IGCT,

2.6.6 Sytá pára. Předpoklady: 2604

.6.6 Sytá ára Předolady: 604 Oaování: aaliny se vyařují za aždé teloty. Nejrychlejší částice uniají z aaliny a stává se z nich ára. Do isy nalijee vodu voda se ostuně vyařuje naonec zůstane isa rázdná,

Soustava momentů. k s. Je-li tedy ve vzorci obecného momentu s = 1, získáme vzorec aritmetického průměru.

Soutava mometů Momety (Obecé, cetrálí a ormovaé) Do ytému mometových charatert patří ty ejdůležtější artmetcý průměr (mometová míra úrově) a rozptyl (mometová úroveň varablty). Obecý momet -tého tupě:

Soustava kapalina + tuhá látka Izobarický fázový diagram pro soustavu obsahující vodu a chlorid sodný

Soustv kpl + tuhá látk Izobrcký fázový dgrm pro soustvu obshující vodu chlord sodý t / o C H 2 O (s) + esyceý roztok 30 20 10 0-10 -20 t I t II esyceý roztok 2 1 p o NCl (s) + syceý roztok eutektcký bod

Doc. Ing. Dagmar Blatná, CSc.

PRAVDĚPODOBNOST A STATISTIKA Doc. Ig. Dagmar Blatá, CSc. Statsta statstcé údaje o hromadých jevech čost, terá vede zísáí statstcých údajů a jejch zpracováí teore statsty - věda o stavu, vztazích a vývoj

HYDROPNEUMATICKÝ VAKOVÝ AKUMULÁTOR

HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.

S k l á d á n í s i l

S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících

HYDROMECHANICKÉ PROCESY. Doprava tekutin Čerpadla a kompresory (přednáška) Doc. Ing. Tomáš Jirout, Ph.D.

HROMECHANICKÉ PROCES orava tekti Čeradla a komresory (ředáška) oc. Ig. Tomáš Jirot, Ph.. (e-mail: Tomas.Jirot@fs.cvt.cz, tel.: 435 68) ČERPALA Základy teorie čeradel Základí rozděleí čeradel Hydrostatická

KAPALINY Autor: Jiří Dostál 1) Který obrázek je správný?

KAPALINY Autor: Jiří Dostál 1) Který obráze je správný? a) b) 2) Vypočti hydrostaticý tla v nádobě s vodou na obrázu: a) v ístě A b) v bodě C c) Doplňové ateriály učebnici Fyzia 7 1 ) V bodě C na obrázu

Přednáška č. 2 náhodné veličiny

Předáša č. áhodé velčy Pozámy záladím pojmům z počtu pravděpodobost Pozáma 1: Př výpočtu pravděpodobost áhodého jevu dle lascé defce je uté věovat pozorost způsobu formulace vybraého jevu. V ásledující

ý Í č ší í ě í ů ý í ě á íó í í á ě í ě í š í ť é ř š ě Í é é Í á í ří í íř í íž í í í í ů ží í ý í ů í ší ěá Í á é á í í ě ě í ó ý ý í í í ť í á ší í

ý Í č š ě ů ý ě á ó á ě ě š ť é ř š ě Í é é Í á ř ř ž ů ž ý ů š ěá Í á é á ě ě ó ý ý ť á š ě ž é é č Á ž á Í ř Ě ó é ř á ú Í ě ý é ě š č ý Í ě ř ů ě ú ň Í ť é ě ě š Ě ó á ř č ě ó ů ř ř á Íř ží ř ě č ě

DSpace VSB-TUO

DSpace VSB-UO http://www.dspace.vsb.cz þÿx a d a b e z p e o s t í ~ e ý r s t v í / S a f e t y E gþÿx eae dr a g b es zep re es o s t í ~ e ý r s t v í. 2 9 r o. 4 / S þÿ M o~ o s t u p l a t í v r á

íž í ě é á ří ž í é á í í éž š ě ž ě ú í í íší ří í á ý ě áší ě í ě čá í ě š é é í áš í á č é čá ří ď ďí ř á š ř á ř ě ě ž ý ě íší ě ě žáďá ž á í ž ě

š áš ř é ř ě ý ě ě é ý ářů š í ů ý Ú á á ří č á í ě á ě ř ě í ř ý ě í žá á é ř ří á ěř í žá č š ě é ě ě ř ář é á Šú é č á ý í ž ř ě ý ě ší á ý í ží á ě ý ě í ď íč é ě ř á í ě á í ě ří č ý é ý é ě é í á

FYZIKA 2. ROČNÍK. Změny skupenství látek. Tání a tuhnutí. Pevná látka. soustava velkého počtu částic. Plyn

Zěny skuenství látek Pevná látka Kaalina Plyn soustava velkého očtu částic Má-li soustava v rovnovážné stavu ve všech částech stejné fyzikální a cheické vlastnosti (stejnou hustotu, stejnou strukturu a

7. Analytická geometrie

7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp

á ě ž ž á íš č Š á š ě ě ř ě í Ú ř č á ť žá á í Í ě ý í á ř ž í í í í á í ň á ý ě á ě ú ě ž á Í á Í í á ě š š á á ěř é á š á ý á ž č ž í é ě á é á ě á

ě ř é ě ří ž ý ř ý í ž ě ě ž ť č ě ě ž ř á ý á š ě í ů á ě í é á ž š é ě é ů í é řá é í í ě ří č ě é ř é ý ě í ě Í ž á čá í ě ý í á í ě á á í ž š ř á í č ý ž ř ý š ě ó áž ě ý íš á á ší í ě ý ř ě Ž ř ý

Á Á Á š ě ČŇ ŘÁ Ě Á Č ÍŘÁ Ř Ě š ě ť Č Ú ú Č ě Ú ů ů š ě Ň ř ž ěř ů ř ě ř ň ř ž ů ř Ů ě ř š ě ě ú ř ž Č Č ť Ň ě ř š ěú ř ď Ž šú ě ř ř ř Á ě ř ř ť Č ř ř ď ě ě ž ř ě Č ó ě Ň ě ě ě š š ů ě ž ú ž Č šš úě ů

í í ú ř Í ř í á í é é é Í á ý ň ř í š í č í í á í í é í í í á á ó ě Í í ě í í í í í řá ů čč ř č á í í í ě á ě ě í á í š ť Í ě Í ř ě í ě č Í ř é č š ě

ú ř Í ř á é é é Í á ý ň ř š č á é á á ó Í řá ů čč ř č á á á š ť Í Í ř č Í ř é č š á č ý č é ó á č ř ů á č č š á ů á Í á á é č ú ó ť ý Í ř č é Í č š á ř á é á ř á ř ů ř ř á áž á Í ý é é č ý čů á é é é č

Definice obecné mocniny

Defiice obecé mociy Zavedeí obecé mociy omocí ity číselé oslouosti lze rovést ěkolika zůsoby Níže uvedeý zůsob využívá k defiici eoeciálí fukce itu V dalším budeme otřebovat ásledující dvě erovosti: Lemma

Chemie cvičení 3 Soustavy s chemickou reakcí

U 8 - Ústav oesí a zaovatelsé tehiy FS ČUT Chemie vičeí 3 Soustavy s hemiou eaí A. Reačí ietia 3/ eatou obíhá eae A + B C. oetae láty A a vstuu do eatou je,3 mol/l a láty B, mol/l. Ja se změí eačí yhlost,

Výpočty za použití zákonů pro ideální plyn

ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání

1. Přirozená topologie v R n

MATEMATICKÁ ANALÝZA III předášy M Krupy Zií seestr 999/ Přirozeá topologie v R V prví části tohoto tetu zavádíe přirozeou topologii a ožiě R ejprve jao topologii orovaého prostoru a pa jao topologii součiu

V xv x V V E x. V nv n V nv x. S x S x S R x x x x S E x. ln ln

Souhrn 6. přednášky: 1) Terodynaka sěsí a) Ideální sěs: adtvta objeů a entalpí, Aagatův zákon b) Reálná sěs: pops poocí dodatkových velčn E Def. Y Y Y, d Aplkace: - př. obje reálné dvousložkové sěs V xv

11. Tepelné děje v plynech

11. eelné děje v lynech 11.1 elotní roztažnost a rozínavost lynů elotní roztažnost obje lynů závisí na telotě ři stálé tlaku. S rostoucí telotou se roztažnost lynů ři stálé tlaku zvětšuje. Součinitel objeové

Opakování. Metody hodnocení efektivnosti investic. Finanční model. Pravidla pro sestavení CF. Investiční fáze FINANČNÍ MODEL INVESTIČNÍHO ZÁMĚRU

Metody hodoceí efektvost vestc Opakováí Typy vazeb v uzlové síťové grafu K čeu slouží stude využtelost Fačí odel vestčího záěru Časová hodota peěz Metody vyhodoceí Napšte strukturu propočtu Fačí odel FINANČNÍ

Geometrické uspořádání koleje

Geoetricé uspořádáí oeje rají přechodice Otto Páše, doc. Ig. Ph.D. Ústav žeezičích ostrucí a staveb Tato prezetace ba vtvoře pro studijí úče studetů. ročíu baaářsého studia oboru ostruce a dopraví stavb

č ňé ď í ďí É ý ě á ě ž č í í ť á é áž ě í í ě í ě ř á áž ě í í áž ě í í ň Í č í č č í

ňé ď ď É ý ě á ě ž ť á é áž ě ě ě ř á áž ě áž ě ň Í Í š Á Í Ó á ď ů á ď á á á ě á ý ě é Í Í é á ě é é Ú ý ů ň ě é á á ů ě á á áš é á á á á á á á ť Č ď ů ý ů ě á ď ý ď ď ý á ě ů á ď á á ů é á á ě ý á ý

ž ž ž ž ž Č ž Ž Ž Ů Ů ž Č Ú Č ž Č Č Č Č Č Ů ž Ž ž Ž ž Ž Ů Ž ž ž Ů ž ž Ž ž ž Ů Č ž Ž ž ž Ú ž Ú Ú Ó ž Ů Ú ď Č Ú Ú Ú Č Ú Č Č Č Č Č Č ž Č Ú Č Ó Ú Č Ú Č Č Č Ú Ó Č Ú Č Č Č Č Č Ó Ó Ó Č Č Ž Ú ž ž Ú ž ž Ó Ó Ž Ů

Í í É ť ď í é í ř ě ž ří á í í í í ů ě ě é ě É ž ě í á š ý ň á ý ř ů á Í é ž ě ě í á ů á í í ří á ž é ř ě ř á á ř Í č ů í Í ž ří ě ý ě Í ě ří ř ší á í

Í í É ť ď í é í ř ě ž ří á í í í í ů ě ě é ě É ž ě í á š ýň á ý ř ů á Í é ž ě ě í á ů á í í ří á ž é ř ě ř á á ř Í č ů í Í ž ří ě ý ě Í ě ří ř ší á í Í ď Í ý ší ř Í é ě ř ó Í š ř Í í ň á ú í ř ě ý ě ší

Ý Á Í ŘÁ Č Á

Ý Á Í ŘÁ Č Á Ř Á úč ř č ě ů Ť é č ě š ř ž š é é š é é Ý ž š é ó ó ť š ž ů é Ť é ž é ů ú š ň ž ě š ž š é é ř š š ě š ó č é ů š ě ř š ť ť é ř ž ó ř š é Ť é ě š ř ě ř š ř ě ó é é ú ů Á ř é é é č š é ř ž ř

Viz též stavová rovnice ideálního plynu, stavová rovnice reálného plynu a van der Waalsova stavová rovnice.

5.1 Stavová rovnice 5.1.1 Stavová rovnice ideálního plynu Stavová rovnice pro sěs ideálních plynů 5.1.2 Stavová rovnice reálného plynu Stavové rovnice se dvěa onstantai Viriální rovnice Stavové rovnice

ž ř ž ě ěá é é á ě ě ú Í ř Ť á é á ě ž š ž ě č ě ř é ý ě ř á ž ď á é á ě ě ř á á ýě ý ří ě š é ě Í ěá ť ž ř šř Á ý ř ú ý é ě ě č é ě ř á ú á á ť Í á ě

ú á áč ří ěř á é ý Í ř á ž é ž é á ž ň ěá ť á é á é ě ř Í ě é á ý ý ý ř ě é ř é ř ě á Í ž ě é č é é ý š ř ú Í á é ě ě ý ů ř á č á ž á č ěá č é č á ž ř ž ě ěá é é á ě ě ú Í ř Ť á é á ě ž š ž ě č ě ř é ý

č š š ř ř Í ů č Ě Á Š ŠÁ Ř Ď É Í Ě Í Í čí ž ě č é č ě ý Ž ř ě č ý ě ý ý ř ě š ý ě ť ý é é ě ě é ě é ř é ř Ť ě š ě ž ě é ě é é ů ě é ř ú ý ý é ěř ý ý š ý ý ž é é š ý š ě ý ř ř ř ě š ý ě ý ý ř ě é Ž é é

Stísněná plastická deformace PLASTICITA

Stísěá asticá deformace PLASTICITA STÍSNĚNÁ PLASTICKÁ DEORACE VE STATICKY NEURČITÝCH ÚLOHÁCH Elasticé řešeí: N cos, N N cos. Největší síla, tero může prt přeést: N S. Prt přejde do ast. stav prví při zatěž.síle

Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:

ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy

PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru

SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru

PRŮMYSLOVÉ PROCESY. Přenos hybnosti III Doprava tekutin čerpadla a kompresory

PRŮMYSLOVÉ PROCESY Přeos hybosti III orava tekti čeradla a komresory Prof. Ig. Tomáš Jirot, Ph.. (e-mail: Tomas.Jirot@fs.cvt.cz, tel.: 435 68) ČERPALA Základy teorie čeradel Základí rozděleí čeradel Hydrostatická

ý ů ř š á š ú ř ň ž Ú ř ž ň á á ř á ý ú Č ř á á ť ť Ň ř Ú ž ř ý ů ř š á š ú ř ň ž ý ú ř á ž á ň á á ň á ů á á ž ř ř ř ž ř ž š š ýš řá ý ů á áš řá ý ř á ů ř ý á áš ř á ž ý á ň á á á řá áž á á á ň á á ž

SRÁŽECÍ REAKCE. Srážecí reakce. RNDr. Milan Šmídl, Ph.D. Cvičení z analytické chemie ZS 2014/

1.1.01 SRÁŽECÍ REACE RNDr. Mila Šídl, Ph.D. Cvičeí z aalytické cheie ZS 01/015 Srážecí reakce působeí srážedla a ějakou látku vziká obtížě rozpustá látka sražeia vzik takové sražeiy je popsá součie rozpustosti

š ý é á ě ý ěž é á áž íž š í á š íř á ší ř í ě ž é ž š ř í í ě ž á á íž č í ě í í ě á í á č ž á ý ě š ť ř ů ý ř í é á ž í éč é í č ý á ň á í ž ě á í ž

Š Í Ř Ě É Í Ř Á Ř Á Í É á ý á ý í é á í ž č í é ř ý č í í í ý žš ě á í é í ě í í ě é á ž š č í í ů á č é á š ú ž í ř á í á é í úč ý ěšé í í é á ř é íú é í ů ří š í á í ří š á ě í í š ř í ž í ě á ž é ě

2. Vícekriteriální a cílové programování

2. Vícerterálí a cílové programováí Úlohy vícerterálího programováí jsou úlohy, ve terých se a možě přípustých řešeí optmalzuje ěol salárích rterálích fucí. Moža přípustých řešeí je přtom defováa podobě

ř í ší é ě é ří č é č é é š í ě é é á č ý á é ř ě ý ů é é ó ó í ě ěá í ž ě ší ž é á ó ě í ří é é ě ů Ť é ř ý á ě ší ý ž é á í žň á ý é ž í á á ří ž š

ř í ší é ě é ří č é č é é š í ě é é á č ý á é ř ě ý ů é é ó ó í ě ěá í ž ě ší ž é á ó ě í ří é é ě ů Ť é ř ý á ě ší ý ž é á í žň á ý é ž í á á ří ž š Í ě í š í é í čá í š ý ó ý í ř ě ě ý ř ě ší é ý ý ě

4.KMITÁNÍ VOLNÉ. Rozlišujeme: 1. nepoddajné vazby - nedovolující pohyb 2. pružně poddajné vazby - dovolují pohyb

4.MITÁNÍ VOLNÉ 4. Lárí ktáí (harocký osclátor v fyzc) Vl časý pohy hotého odu j ktavý pohy. táí ud lárí, jstlž síla, ktrá př výchylc x vrací hotý od do rovovážé polohy, j úěrá výchylc F x (4..) kostata

Á Ý Ú Á Ě Á Ů Á Ý Ů Ú É Á

Ý Á Í ŘÁ Á Ý Ú Á Ě Á Ů Á Ý Ů Ú É Á ř ů ý Ť Ž ř ř č Í Á ď č ě ř ú ž ě ř ý ý ů řů č ú č ř ž ě ú ž ř ť č ř Ť ú ř ě š ř ý ž ú ě č ý ý ú Ř ú ěš ě ě ř ř č ž ě ř ě ř ě Í ě ý š ý ž šš ě šč ř ř š ř č ý ř ř ý ř

Dynamická analýza rámu brdového listu

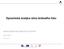Dacá aalýza ráu rovéo lstu MODELOVÁNÍ MECHANICKÝCH SOUSTAV Šo Kovář 0..0 Brový lst 8..0 Brový lst průřez čů. orí če. olí če. Postrace. áě Tp závěsů těe 8..0 Použté ozačeí sol pops jeota sč oefcet tlueí

Didaktika výpočtů v chemii

Didaktika výpočtů v cheii RNDr. ila Šídl, Ph.D. 1 Didaktické zpracováí Pojy: olárí hotost (), hotostí zloek (w), látková ožství (), olárí obje ( ), Avogadrova kostata N A, látková a hotostí kocetrace (c,

ů Í ď Í í Č ó š Í á ť ř ú í é á é á ááý á Í Ú í ý ý á á Í ť ď ď á á Í í ý á ě é é ď á řá Í ň á Í č íí Í ý í í í á ť í č í Í á á í ř ř á ě č á á í é ó

ů Í ď Í í Č ó š Í á ť ř ú í é á é á ááý á Í Ú í ý ý á á Í ť ď ď á á Í í ý á ě é é ď á řá Í ň á Í č íí Í ý í í í á ť í č í Í á á í ř ř á ě č á á í é ó ř í í í í á ř Ť ří Í č á ě á ť ř řá ý á í í á ď Í Ě

á ří á č á á á ÍŽ é á ž ř ž ě ž á é á š ó á é é č é ě é ž é é ř ž č é č é č čá á ý é ý é č é Ě á ř ů á č é ž š ě Í ř ř řěř é É ě č š á ů ň é ó ť ě ě ř

á ří á č á á á ÍŽ é á ž ř ž ě ž á é á š ó á é é č é ě é ž é é ř ž č é č é č čá á ý é ý é č é Ě á ř ů á č é ž š ě Í ř ř řěř é É ě č š á ů ň é ó ť ě ě ř š ť é ž á ťř ář ě ě á é é č é š č ť é ě é é č ž č

ý í á á š ě é í š íž á á ě š š ě ě á ě é ř é ž čá é ž ř í ř í í á č í š á í š ř í é ě š ž í ý é ě í í í á ř é ě ě ší ž ů ý á ě š é číš ě á ú ě í á í ě

Í Á Í Ý Á Ú Ř Č Í Í č ř á ý š á ý í í č í í ě í ž ě í č í á í í í í č í í á í ěž ě á í č í ěř í é ýš ý á á ě í í š ů í á í ů č í ž í ž í áš ě ě á é ě á í é š í é ř é á é á í á ě ž áž í ý č á í ž ý ě ší

PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru

SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru

íž ě íž á ť ř ť í ž ě ě á í ň á í á í ů ů íž ď ř ť šíř é ě ě ě ř í ší íř ý ý ů éříš éš ěž ě á í á í ř é šíř ý ěží č ě š é í í ř í á í á í ž ž é ř é í

Í Ý ČÁ Ú ý ší é č ý ůž í š é á é í ř š ř ů ě í í áří ě ž í á é á ě é í ž ě á á ď ří ě č é í í í í ž ě ý á ý ů č í ý ř ě ž í í í í š í í č í ěž ž ž ř é í á ř í í ě í ž í č ě ží ř ž é ř ě š ě ž á í žší é

čá í ř í č í ý á í Č Íí í ý ů č šť í ěř í í ž ůž ý á Ž ý šť ř í í á í á í ý á ů ěž ří š ě í ů ě č ě á ř ší ě ř á í ú á Č í á í ě ý í ř á Š ě Š Š ý ď ě

ř á í Č š š úč á á č ý ě í ň á š ó řá š á í á č á č ýú ří ž í ř í ř í á í ř í í á í í í í č ý ý ší í á í ú á í řá Ž čá í ž ří í ů Íí ž á á á í ý ěří ý ů á á ý ó í á í ý ů řá č ý ý á č ř í í íú ý ř š í

á ř č á é Ž ř ů á á ř á Čá Ž ř á á é ž ř á á Š ý é ř é ř á ř Š ář ř ž á ř ý ž á ř á ý ú ů á ř ý á á ú ň ý ř č á č ř Ž á á Žá ý ý ř ý ř č ú ř ůž á žá ý

á á á é áí ř ý Čá áš ř ý ý á Š ář á Šá á á č ů á á ř ř éč č á č Č á ž á ř ů áš é á ž á Í á ř é úř Ž š ř á š úč á ř Ž é ú ů é č č é á ž á řá á á áš š úř ý á á á ý á Ž š é á á ř ů á á ř á ú ů é á Ž é ř á

řá ó á ú ú š š ř č é ě ě á é č ě š č č á ě í Ž š ě ř č é ž ř č é šč š ž é á č ř á ě á ě á é é ž í ř á é ď ě šč í šč ěšť čš ó ž é é ě ž é ď é ší ě ž é

é é ě í ří í é č á é ě í Ž é í ě ú ť á ď á ý ž ů é ď á ř é č ě ěšť é ě č č ě ú é í í ě í á é ě š ě í ý ý í ú í ó ď ý í ěž í ě á á í ě ý š ě í í é ď Č Á Č ý á ě ě ě ůž ř ě š ě á ě í á é ž í í á ý á á ž

ř ž ť ť čá á ý ý á á áč ž ý ě ě ů á ř ž ř á ř ž ř ž ň á ř ř ř ý ěř ž ž ý č á ř ý č č šť á á Ú ý ó ž ť č ž á ě á š ě ř á á ě ůř ů ě š á ř ž á ě ř ř š ž

á ůž č á č á č á á ň á č á á ů ěř ů ěř á ě ř ň á č č ý ý ě š ě žá á ý á ř ě ú ř á ž ž á ř ě ě Í ě á á č ě á ř ě á ř ř ě ý ú ť ř á á ě ě á á ěě ý á š Ť á ě á á š Í á ž á ě ě ž ě á á á á ě ů ž š ě ý ř Ž

MECHANICKÉ KMITÁNÍ NETLUMENÉ

MECHANICKÉ KMITÁNÍ NETLUMENÉ Kitání je PERIODICKÝ pohyb hotného bodu (tělesa). Pohybuje se z jedné rajní polohy KP do druhé rajní polohy KP a zpět. Jaýoliv itající objet se nazývá OSCILÁTOR. A je aplituda

Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje

Projekt realoaý a SPŠ Noé Město ad Metují s fačí podporou Operačím programu Vdělááí pro kokureceschopost Králoéhradeckého kraje Modul - Techcké předměty Ig. Ja Jemelík - fukčí soustay součástí, které slouží

í í ř č í Í í á é á ý ář ž ř ě Í é í í í ó í ž í á í ď í ě í ď á ě é č é ž š í č é ó ž ší čí ší é í í ň ě á ě é á ě č ě Í ž ř í á á í í ě ší ě é ě á ě

í í ř č í Í í á é á ý ář ž ř ě Í é í í í ó í ž í á í ď í ě í ď á ě é č é ž š í č é ó ž ší čí ší é í í ň ě á ě é á ě č ě Í ž ř í á á í í ě ší ě é ě á ě ž ý á ž ý á ž ř ě í ý ř Í ě é ý ě ý ž ž ř í ě í ý

é ý čí á ří ř čí ě ř ří í ř š í ě á ě íč ý í á říš í ří ě ů ž ří á ř č á č ž ří ě á ě ý ří ů á á ří ž Ž ý ě ý ů í á ří ě Š čí ě é é č í ů í ů ě ě ý á

Í éá í é í á ř í í ů á á čí á é Í ří Í é ř čí á í č á ř í ě é í é č é ř é ř Ž ý é ó ž č í Ž ě ěž ř č ř ší ř í ří ě á í ň ří Ž š é š ě í ý š á í š ěž í é é ý é ý ů ří č éž í ý éú í č á íž ý ó íž ý ó čí

1) Vypočtěte ideální poměr rozdělení brzdných sil na nápravy dvounápravového vozidla bez ABS.

Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.

Ing. Vladimíra Michalcová, Ph.D. Katedra stavební mechaniky (228)

Stavebí statka - vyučující Dooručeá lteratura Ig. Vladmíra chalcová, h.d. Katedra stavebí mechaky (228) místost: LH 47/ tel.: (59 732) 348 e mal: vladmra.mchalcova@vsb.c www: htt://fast.vsb.c/mchalcova

Ý áš á í é ť š í

ří ď ě ě é ř ý ří ý é úř á ú ě ě ř ář í ší ž í ř í í Í ř ý áš ě ů é í ď Í ř ý řá óš í áš í ý í ř š í á á ř ří ž ě ž ď š ě í í í á žá ý á Í ÍŽ Š Á Ó ř č í Í é ž é ž á í á á Ž ř ě ž ú á á č ě ě í ěž á í

II. Soustavy s konečným počtem stupňů volnosti

Jiří Máca - atedra echaiy - B35 - tel. 435 4500 aca@fsv.cvut.cz. Pohybové rovice. Vlastí etlueé itáí 3. Vyuceé etlueé itáí 4. Volé etlueé itáí 5. Metoda ostat poddajosti 6. Přílady 7. Staticá odezace 8.

á í í á í í ž ší ě á ě é á ě á ř í Í ě á ě Č á í á é é é á í ý č ý ě ší ý ž š é č é é ě š ě í í í í á í ý ř č é ř í čá í ř ě é í í ě é ř ě é ěč é ě í

č É Í É Í Á Í Ž Ě Í Á Í čá í í í ě á í í ě é čá í č ý á é í á ř ů ž ěž ě ý í ý á ý íž á ř í ě á ý ž í ě á í říš ě ř ě č í í í ě á ř ě ů á é ř í ř í ě í á ě íč ý á ý š á á ěží ů Č á í č é á í ů č í ř ž

5. Výpočty s využitím vztahů mezi stavovými veličinami ideálního plynu

. ýpočty s využití vztahů ezi stavovýi veličiai ideálího plyu Ze zkušeosti víe, že obje plyu - a rozdíl od objeu pevé látky ebo kapaliy - je vyeze prostore, v ěž je ply uzavře. Přítoost plyu v ádobě se

TERMODYNAMICKÁ ROVNOVÁHA

TERMODYNAMICÁ ROVNOVÁHA odíky saovolost evatost pocesů a podíky ovováhy V ovováze pobíhají pouze vaté pocesy Systé zolovaý [q,v,w ], adabatcký [q] V toto systéu etope stoupá př evatých dějích ds> a dosahuje

( NV, )} Řešením Schrödingerovy rovnice pro N částic

Partčí fuc { E ( V, )} Řším Schrödgrovy rovc pro částc Zdoduší (?) H = H E = E Ψ= Ψ BOSOY stavy sou obsazováy bz omzí FERMIOY frmoy mohou být v stém stavu Přílady: Ply (ízý tla) => mzmolulové trac zadbáy

í ě ý ě ý á ů ě ší á ž á ý á ž ý č ě ě á ý ě ě ě á ž é é ě ř á ů š ý ů ě é í í í č í í ě ř ý é ě ě ě é ě á í á č ý í ří ž ě ý á í č í í í ří í ý á í ž

Ě ĚŠŤ É ří á ý í á ý í Í á í ší ý ň í á ý í čí á ě í ěšé á ě ž ě ť á á ú í é ý ý á ž á ý í á í í š ě í í ří á ž ě ší č é šíř í í ě í í é í ďá á í č ě í á í ý á í ř í á á ž ď á á é í ř á ý í č ý ů č š í

STRUKTURA A VLASTNOSTI PLYNŮ

I N E S I C E D O R O Z O J E Z D Ě L Á Á N Í SRUKURA A LASNOSI PLYNŮ. Ideální lyn ředstavuje model ideálního lynu, který často oužíváme k oisu různých dějů. Naříklad ozději ředokládáme, že všechny molekuly

USTÁLENÉ PROUDĚNÍ V OTEVŘENÝCH KORYTECH

USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou

ý Í ť č í ý úř í á ěř ý í ří í Č í ě č á Č í ě č áš ý á ě í Č á í Č á á ě í Č á á á í š č á ž í á ě á ýš č í ří š ú ýš č ě čá č ú í š š í ů čá č í á í ří ýš č á á á í íí í Ž í á í ž í áš á á ž ý ě í ý

áš ú ě á á á ž č ý ý í ů é é š ě ě á š ř š ě ů š í ě é ů ě š ž ž í ů ě í í ů ý á í ší ě ž á é á ž í ě é ří á ě č ň š ř ě č ěň é ýš ř é á í é ěň ů ě á

áš ú ě á á á ž č ý ý í ů é é š ě ě á š ř š ě ů š í ě é ů ě š ž ž í ů ě í í ů ý á í ší ě ž á é á ž í ě é ří á ě č ň š ř ě č ěň é ýš ř é á í é ěň ů ě á ž á č ý á ř á š í á í ý ž š ě ě Ž á á ě ě ě ř áří ž

Agregace vzájemné spojování destabilizovaných částic ve větší celky, případně jejich adheze na povrchu jiných materiálů

Agregace - úvod 1 Agregace vzáemné spoování destablzovaných částc ve větší cely, případně ech adheze na povrchu ných materálů Částce mohou agregovat, poud vyazuí adhezní schopnost a poud e umožněno ech

ě š á š í á ý í á ž ý í á í ží í í í á é ě é ř š í í íž í í ě ě é é ě šíř é á í ř ě ě ú ě í á í ě ř ě é řá é Č é ť í í á é ů ěí ť í í š ý íš ě ý šů ž

ě š á š í á ý í á ž ý í á í ží í í í á é ě é ř š í í íž í í ě ě é é ě šíř é á í ř ě ě ú ě í á í ě ř ě é řá é Č é ť í í á é ů ěí ť í í š ý íš ě ý šů ž š é ě ě ř á í í ř á ří š ů ě ě ý í č í á í é ý á í

ž í ý á í á ř í í é á ý ě ž á í ří é ý í ž č ý ě ý éšíř á š á ž á í ě ý ě č é ž í é á ž ří ž í í á á ě í ý ě í í čí ý č é ýš íč á é í é šňů é é á í á

É í č é á í ž ář í ý ý á í íž ě á ý é í ě í í ž ý ý ý ý ž ě ř ý á í í ý í á é ž Č é á á á á ě č é í é ší č é é č š ř á é č í ě í č č á é ě ž á í ý ř ř í ř í ž é ě é í ž ů á í í ě š é ř é ý ý Č Č é á ůč

ž ř áú č é ř č ř á ý é ř ýš ů á ý ě ž ť é á ě ý ě ý é ž řó é ý é ď ý č š é č š ž á é é á ýó č á ú ť č é ó óř č ý ý ě ž ů á ě š ě ž ý ř ě ň š ýš ž ý ž

Á á ě á á ž ř áú č é ř č ř á ý é ř ýš ů á ý ě ž ť é á ě ý ě ý é ž řó é ý é ď ý č š é č š ž á é é á ýó č á ú ť č é ó óř č ý ý ě ž ů á ě š ě ž ý ř ě ň š ýš ž ý ž é ž é É ú á á ě é č ř á é ě ý ý ř ý á ý č

Ě Č ě Š Í Č Ě ě č ň

Ť É Í Ě Č ě Š Í Č Ě ě č ň Í č č č Á Ť č Ť Í ť č Ť č č ě ě ž ě Ť Í ě Ž č ě ě ě ž Ž Í š ť Ď ž č ě ě š Ť ě ě Ě ě š ě ě č Í ž ě ě š Ž šš ž Í Ť Ž ž ě ž Ť Ť ž ď č š ž ž Í Ť š ě Ť ě ž č ď č č ž Í č š Ž Ž Í č

ůž íč á Ě Éč Í ř á í Ř ř ř šň ý é Í í ó Í ě ě Í Í á í á í ý é ě ž ěží á í ě í é Í í Í š ý á Í š ý é č íří ý ěž ž í Í Í í í í é č á č ě ě á ě č ř Ť ě í

ůž č á Ě Éč Í ř á Ř ř ř šň ý é Í ó Í Í Í á á ý é ž ží á é Í Í š ý á Í š ý é č ř ý ž ž Í Í é č á č á č ř Ť ř ý ř Í č ž ň á á ř č é ř é Í ř č ř ž ž ý úč Í á á č á š é ř é é č č š ž Í ř ó Í ý ř ž áš á č é

Přednáška č. 10 Analýza rozptylu při jednoduchém třídění

Předáška č. 0 Aalýza roztylu ř jedoduchém tříděí Aalýza roztylu je statstcká metoda, kterou se osuzuje romělvost oakovaých realzací áhodého okusu tj. romělvost áhodé velčy. Náhodá velča vzká za relatvě