ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ DIPLOMOVÁ PRÁCE
|
|
|
- Marian Havlíček
- před 8 lety
- Počet zobrazení:
Transkript
1 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ DIPLOMOVÁ PRÁCE PRAHA 2014 Pavel RYS
2 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE DIPLOMOVÁ PRÁCE VYHODNOCENÍ POSUNŮ BODŮ VZTAŽNÉ SÍTĚ PRAŽSKÉHO HRADU Vedoucí práce: Ing. Tomáš KUBÍN, Ph.D. Katedra speciální geodézie leden 2014 Pavel RYS
3 ZDE VLOŽIT LIST ZADÁNÍ Z důvodu správného číslování stránek
4 ABSTRAKT Tato diplomová práce se zabývá zpracováním etapových měření ve vztažné polohové síti geodetických bodů na Pražském hradě. V textu je popsán způsob přípravy a zpracování dat měřených v jednotlivých epochách. Podstatná část práce je dále zaměřena na téma robustní transformace, tj. transformace soustavy další etapy do soustavy základní etapy, při níž je transformační klíč určován metodou robustního odhadu. Výsledky práce plynou ze statistického testování vodorovných posunů bodů. KLÍČOVÁ SLOVA etapové měření, robustní transformace, metoda robustního odhadu, L1-norma, vodorovné posuny bodů, statistické testování posunů ABSTRACT This master s thesis deals with the processing of epoch measurements carried out in the local horizontal network of the Prague castle site. There is the process of preparing measured data described in the text. A significant part of work is focused on the method of robust transformation. As a result, horizontal displacements of netpoints have been tested. KEYWORDS epoch measurement, robust transformation, robust parameter estimation, L1-norm estimation, horizontal displacements of netpoints, hypothesis testing
5 PROHLÁŠENÍ Prohlašuji, že jsem diplomovou práci na téma Vyhodnocení posunů bodů vztažné sítě Pražského hradu vypracoval samostatně. Použitou literaturu a podkladové materiály uvádím v seznamu zdrojů. V Praze dne (podpis autora)
6 PODĚKOVÁNÍ Velmi děkuji vedoucímu práce Ing. Tomáši Kubínovi, Ph.D. za neobyčejně ochotný a přátelský přístup, se kterým mi dopomáhal překlenout nejrůznější úskalí, která vznik této práce doprovázela. Dále nemohu opomenout poděkovat doc. Ing. Martinu Štronerovi, Ph.D. za jeho cenné rady a názory k tématu robustního vyrovnání.
7 Obsah Úvod 8 1 Vztažná síť Pražského hradu Polohová síť Výšková síť Příprava vstupních dat Úvaha nad volbou vztažné soustavy Lambertovo konformní kuželové zobrazení Převod GNSS vektorů do roviny zobrazení Transformace mezi (X, Y, Z) a (B, L, H) Zobrazení (B, L) do (x, y) Transformace kovarianční matice Transformace kovarianční matice souřadnic Transformace kovarianční matice GNSS vektoru Vyrovnání sítě GNU Gama Sestavení vstupních dávkových souborů Základní parametry vyrovnání etap Test aposteriorní směrodatné odchylky Robustní transformace O metodách robustního odhadu obecně Robustní M-odhady Huberův M-odhad Odhad pomocí L p -normy Robustní transformace výpočet Verze výpočtu Verze výpočtu Verze výpočtu Zhodnocení výsledků Helmertova transformace Výběr identických bodů
8 5.2 Definitivní transformační klíč Transformace souřadnic Testování posunů bodů Pravděpodobnost uvnitř elipsy chyb Konstrukce testu Výsledky testování Závěr 86 Použité zdroje 90 Seznam příloh 96 A Výsledky verze výpočtu 1 97 B Výsledky verze výpočtu C Výsledky verze výpočtu D Přetransformované souřadnice 118 D.1 Základní etapa E D.2 Základní etapa E E Číselné výsledky testování posunů 127 E.1 Základní etapa E E.2 Základní etapa E F Grafické výsledky testování posunů 134
9 ÚVOD Úvod V této diplomové práci se zabývám zpracováním etapových měření ve vztažné polohové síti bodů na Pražském hradě. Obecně se jedná o lokální prostorovou geodetickou síť, nicméně v této práci se věnuji pouze její polohové složce. Síť vztažných bodů byla vybudována v rámci projektu Grantové agentury České republiky č. 103/07/1522 (Stabilita historických památek) pro sledování předpokládaných prostorových posunů areálu historických objektů jako celku. Hlavními body sítě jsou hloubkové vrty vystrojené pro geotechnická měření a jedna hloubková stabilizace využívající vybetonovaného staršího hydrogeologického vrtu. Síť je doplněna o další geodetické body. Vzhledem k předpokládané nestabilitě zájmového prostoru je však nutné síť bodů vztáhnout k dalším bodům, které leží mimo tento prostor v geologicky stabilním prostředí. Bodem s předpokládanou stabilitou je geotechnický vrt TV01, který byl vybudován před budovou Fakulty stavební ČVUT v Praze ve vzdálenosti cca 1,7 km od Pražského hradu. Zásadní otázkou při zpracování etapových měření a následném výpočtu posunů bodů je, jaké souřadnice mají být vůči sobě porovnávány. Každá z etap měření přesné účelové geodetické sítě je zpravidla zpracována formou vyrovnání volné sítě metodou nejmenších čtverců. Při takovém postupu jsme nutně konfrontováni s řešením singularity systému normálních rovnic, neboť volná síť není umístěna do prostoru a všechny souřadnice jsou považovány za neznámé. Do výpočtu je tak nutné doplnit dodatečné informace, jak má být síť do prostoru umístěna, nebo inverzi singulární matice řešit pomocí pseudoinverze, anebo zvolit dostatečný počet souřadnic, které budou z výpočtu vyrovnání vyřazeny a budou považovány za pevné. Obvyklá řešení jsou založena na umístění sítě do prostoru ve všech etapách vždy stejným způsobem. Po regularizaci systému normálních rovnic a výpočtu vyrovnání jsou vypočtené souřadnice přímo porovnávány. Fixací některých bodů sítě vzniká z hlediska určování posunů zřejmý principiální nedostatek. Obecnější způsob řešení nabízí lineární konformní transformace jednotlivých etap do soustavy etapy základní. Tato metoda nevyžaduje, aby síť byla v jednotlivých etapách umístěna do prostoru vždy stejným způsobem. Zásadním problémem je však zde volba identických bodů. Určujeme-li transformační klíč pomocí nadbytečného počtu identických bodů metodou nejmenších čtverců (tj. Helmertovou transformací), jsou z hlediska vyrovnání souřadnice těchto bodů souborem měření, který díky předpokládaným posunům nepochází ze základního souboru s normálním rozdělením pravděpodobností. 8
10 ÚVOD Původ měřických dat z normálního rozdělení je však důležitým předpokladem pro správnost aplikace metody nejmenších čtverců a zejména souvisejících statistických testů. Je známo, že i mírné odchylky dat od normálního rozdělení způsobují značnou újmu na kvalitě výsledku. I několik málo hrubých chyb tak může zcela znehodnotit jinak kvalitní měření. V případě výskytu odlehlých hodnot je tedy velmi účelné tyto hodnoty detekovat a z výpočtu vyrovnání vyloučit. Malý počet chybných dat lze pro tento účel odhalit statistickými testy odlehlých hodnot. Je-li však kontaminace souboru měření odlehlými hodnotami větší či těžko odhadnutelná, je nutné provést zpracování metodami méně citlivými k výskytu odlehlých hodnot. Takové metody jsou označované jako robustní metody odhadu reálných parametrů. Obecným principem robustních metod je, že v podmínce minimalizace sumy čtverců oprav nahrazují kvadráty nebo celou sumu vhodnějšími funkcemi [15]. V této diplomové práci byla využita nově navržená metoda tzv. robustní transformace. Transformační klíč, který charakterizuje transformaci další etapy do soustavy základní etapy je určován metodou robustního odhadu. Konkrétně je aplikován odhad pomocí L 1 -normy, při které je minimalizována suma absolutních hodnot oprav (chyb). L 1 -norma poskytuje extrémní robustnost odhadu a její užití je tak výhodné zejména v situacích, kdy je předpokládána vysoká míra kontaminace souboru měření odlehlými hodnotami či je tato míra neznámá. V textu práce popisuji 3 verze výpočtu robustní transformace, které se od sebe liší způsobem, jakým jsou měřeným veličinám přisuzovány váhy. Podstatou aplikace robustního odhadu neznámých parametrů (tj. transformačních parametrů) není v této práci zjištění odhadu samotného, nýbrž identifikace takových hodnot (souřadnic identických bodů), které jsou při výpočtu tohoto odhadu označeny za odlehlé. Tyto body z původního souboru identických bodů vyloučíme a vzniklý redukovaný soubor by tak měl splňovat podmínku normality. Definitivní transformační klíč je potom určen metodou nejmenších čtverců pomocí takové sady identických bodů, které nebyly označeny jako odlehlé ani v jedné z robustních transformací. Takto sestavená sada identických bodů poskytuje dostatečnou věrohodnost ve stálosti své polohy v průběhu celého sledovaného období. Z rozdílu souřadnic bodů v základní etapě a přetransformovaných souřadnic v další etapě jsou vypočteny vodorovné posuny, o jejichž průkaznosti je rozhodováno na základě dvourozměrných apriorních testů. 9
11 1. VZTAŽNÁ SÍŤ PRAŽSKÉHO HRADU 1 Vztažná síť Pražského hradu V rámci několika grantových projektů, výzkumných záměrů Fsv ČVUT i zakázek Správy Pražského hradu je již několik let prováděn geodetický a geotechnický monitoring objektů Pražského hradu. Garanty těchto projektů jsou pracovníci kateder speciální geodézie a geotechniky Fsv ČVUT v Praze. V areálu Pražského hradu je prováděna řada velmi přesných měření různého účelu. Sledují se vertikální posuny (poklesy a zdvihy) objektů; k tomu slouží z metod geodetických zejména přesná nivelace a metoda trigonometrická a dále řádově přesnější mikrometrie v hloubkových sondovacích vrtech coby zástupce metod geotechnických. Účelem jiných měření je zjišťování vodorovných posunů a náklonů částí jednotlivých objektů. Zde je využívána především metoda trigonometrická a geotechnická metoda inklinometrie ve vrtech. Ačkoliv poskytují geotechnické metody měření (v porovnání s metodami geodetickými) řádově vyšší přesnost, jsou výstupy metod pozorování obou oborů vzájemně nenahraditelné. Geotechnické metody měření poskytují informace o relativních změnách jednotlivých měřicích značek vystrojeného vrtu vůči jeho patě, která je založena na nezvětralém skalním podloží a je považována za pevnou. Geotechnické vrty tak umoňují vysoce přesně měřit prostorové deformace základů a podloží staveb, odhalit poruchové zóny, degradované horniny v základové spáře či vrstvy stlačitelných zemin. V rámci řešení grantového projektu GAČR č. 103/07/1522 (Stabilita historických památek) byla v areálu Pražského hradu vybudována lokální prostorová geodetická síť. Tato síť propojuje právě zmíněné hloubkové geotechnické vrty a vybrané geodetické body do jednoho souřadnicového a výškového systému. To umožňuje sledování případných změn prostorové polohy objektů a jejich souvislostí s chováním podloží v dané oblasti. Obě složky vztažné sítě Pražského hradu (polohová a výšková) se zaměřují a zpracovávají odděleně. 1.1 Polohová síť Polohová síť je tvořena geotechnickými vrty, jedním hloubkově stabilizovaným bodem (původně hydrogeologický vrt) a vybranými geodetickými body. Hloubkové geotechnické vrty se většinou nacházejí v blízkosti významných nebo ohrožených 10
12 1. VZTAŽNÁ SÍŤ PRAŽSKÉHO HRADU staveb, např. u katedrály sv. Víta, baziliky sv. Jiří, Královského letohrádku aj. Konstrukcí, významem a způsobem měření v těchto vrtech jsem se detailněji zabýval ve své bakalářské práci [1]. Přehled geotechnických vrtů uvádí tabulka 1.1. Tab. 1.1: Geotechnické vrty označení vrtu číslo bodu poloha MPD Vikářská ulice MPD Matheyho pilíř MPD Ludvíkovo křídlo MPD bazilika sv. Jiří - nádvoří MPD04A 1004a bazilika sv. Jiří - věž MPD Královský letohrádek VB Hradčanské náměstí VB zahrada Na Opyši TV Thákurova ulice Z vrtů uvedených v tabulce nejsou do polohové sítě zahrnuty vrty 1004 a 1004a. Naopak součástí sítě je vrt s označením TV01, který se jako jediný nenachází v areálu Pražského hradu, nýbrž před budovou FSv ČVUT v Thákurově ulici. Polohová síť je určována jak klasickou terestrickou metodou přesných polygonových pořadů, tak částečně i metodou družicové geodézie. Aparaturami GNSS se přímo měří na vrtech 1011, 1012, TV01 a dále na několika vybraných geodetických bodech polohové sítě. Ostatní vrty jsou k síti připojeny klasickými polygonovými pořady. Podle možností jsou polygonovými pořady propojena i stanoviska aparatur GNSS. Geotechnický vrt TV01 plní ve vztažné síti Pražského hradu především funkci referenční stanice při GNSS observacích. Zároveň jde o bod s předpokládanou stabilitou, který je využíván pro kontrolu stability vztažné sítě jako celku. Měřický bod je ve zhlaví vrtu realizován speciálním strojírenským přípravkem, viz obr Přípravek se vsouvá do první měřicí značky vrtu a jeho poloha se v uzávěru pažnice vystředí posuvným kuželovým dílcem. Tento způsob realizace vztažného bodu ve zhlaví vrtu zajišťuje vysokou přesnost při přenosu případných vodorovných a svislých posunů. Chyba plynoucí z opakovaných umístění přípravku do pažnice vrtu je považována za zanedbatelnou. Centrační přípravek zároveň umožňuje našroubování trojnožky GNSS přijímače nebo odrazného hranolu. Poloha ostatních bodů sítě je vztažena ke středu otvoru (zápichu) dané stabilizační značky. 11
13 1. VZTAŽNÁ SÍŤ PRAŽSKÉHO HRADU nivelační značka se zápichem pro optickou centraci středící posuvný kužel uzávěr pažnice kulová plocha dosedající do kuželové měřicí značky měřicí značka klouzavého mikrometru jílocementová injektáž vrtu kombinovaná pažnice 1.2 Výšková síť Obr. 1.1: Realizace vztažného bodu ve zhlaví vrtu Výšková síť Pražského hradu je určována převážně přesnou a velmi přesnou nivelací. Při měření jsou tak v maximální možné míře respektovány zásady pro práce v bodových polích III. řádu a II. řádu ČSNS. Tyto zásady jsou popsány v Metodickém návodu pro práce v ZVBP vydaném Zeměměřickým úřadem [2]. Jedinou výjimkou v metodice určování výškových rozdílů v síti je převýšení mezi body 552 a 553. Body jsou oddělené hlubokou přírodní roklí Dolním Jelením příkopem a převýšení je proto určováno trigonometrickou metodou. Zenitové úhly a šikmé délky jsou měřeny oboustranně, což při výpočtu převýšení umožňuje eliminovat vliv zakřivení Země a za určitého předpokladu i vliv vertikální složky refrakce (předpokladem je platnost modelu s konstantním refrakčním koeficientem pro záměru). Komplexní zpracování etapových měření ve vztažné výškové síti Pražského hradu jsem provedl ve své bakalářské práci [1]. Zde jsem se také zabýval statistickou analýzou vertikálních posunů bodů sítě. 12
14 2. PŘÍPRAVA VSTUPNÍCH DAT 2 Příprava vstupních dat Cílem této kapitoly je objasnit postup, který byl použit k převedení všech měření do společné vztažné soustavy pro účel kombinovaného vyrovnání GNSS vektorů a terestrických měření programem GNU Gama. Jedním z předmětů zadání této diplomové práce je provést zpracování všech etap doposud zaměřených ve vztažné polohové síti Pražského hradu. Jak bylo uvedeno v kapitole 1.1, polohová síť je určována kombinací terestrických a družicových metod. Jako nejvhodnější způsob efektivního využití všech dostupných pozorování se proto nabízí společné vyrovnání GNSS vektorů a terestrických dat měřených v polygonových pořadech. Pro tento účel je nutné zvolit vztažnou souřadnicovou soustavu, do níž budou všechny měřené veličiny převedeny. 2.1 Úvaha nad volbou vztažné soustavy Vztažná síť Pražského hradu je lokální prostorová geodetická síť relativně malého rozsahu (řádově několik stovek metrů). Při jejím obecném řešení v prostoru je tak možné učinit různé zjednodušující předpoklady (např. náhrada zemského tělesa koulí a s tím související náhrada tížnic různoběžnými přímkami protínajícími se v geocentru). Tato zjednodušení lze dále ospravedlnit skutečností, že jde o účelovou síť pro zjišťování posunů a přetvoření, kde jsou důležité zejména rozdíly ve vypočtených či měřených hodnotách mezi jednotlivými etapami a nikoliv správnost absolutních souřadnic. Před výpočtem geodetické sítě jsme zpravidla konfrontováni s nutností volby vztažného souřadnicového systému, do něhož musí být všechny měřené veličiny převedeny (redukovány). Kartézský souřadnicový systém E3 (bez redukcí měřených veličin) V sítích velmi malého rozsahu lze provést společné vyrovnání polohové i výškové složky bez zavádění redukcí měřených veličin do vztažného systému. To se týká zejména strojírenských mikrosítí s rozměry několika metrů, maximálně desítek metrů. Výhodnou vtažnou soustavou pro takové sítě je pravoúhlý kartézský souřadnicový systém. Tímto způsobem lze případně řešit i sítě větších rozměrů, avšak s patřičnou újmou na přesnosti výpočtu. Příkladem může být testovací prostorová síť v Mariánské u Jáchymova, kde se každoročně koná výuka v terénu z inženýrské geodézie. 13
15 2. PŘÍPRAVA VSTUPNÍCH DAT Kartézský souřadnicový systém E3 (s redukcemi měřených veličin) Přesnějšího řešení sítí malého rozsahu v pravoúhlém kartézském souřadnicovém systému docílíme umístěním počátku souřadnicového systému do jednoho z bodů sítě a osou z orientovanou do směru tížnice procházející tímto bodem. Do takto umístěného systému lze poté zredukovat měřené veličiny, tj. opravit měřené vodorovné směry (úhly) a zenitové úhly o vliv sbíhavosti tížnic (za předpokladu kulového modelu Země). Tyto redukce vyžadují znalost konfigurace bodů sítě, přibližné souřadnice bodů většinou postačují. Odvození redukcí lze nalézt např. v [3] nebo [4]. Způsob řešení sítě postupem popsaným v předchozím odstavci (tedy v pravoúhlém kartézském systému E3 s redukcí úhlových veličin o vliv tížnicových odchylek) lze teoreticky dobře aplikovat na výpočet vztažné sítě Pražského hradu. Užití tohoto způsobu by však bylo spíše odůvodněné v případě, pokud by»hradní síť«byla řešena jako prostorová. Poměrně pracné redukování úhlových veličin by se stalo nepříliš efektivní prací, pokud bychom síť vypočítanou jako prostorovou (3D) následně degradovali na síť polohovou (2D). Pokud by však hradní síť byla zpracovávána jako prostorová, bylo by velmi výhodné ji dále zpřesnit nivelovanými převýšeními, která jsou z jednotlivých etap k dispozici. V takovém případě ovšem narážíme na komplikaci spočívající v převodu nivelovaných převýšení na převýšení kartézská. Nivelovaná převýšení totiž nelze, na rozdíl od ostatních měřených veličin, do pravoúhlého souřadnicového systému exaktně přímo redukovat. O této problematice a dalších alternativách výpočtu prostorových sítí včetně nivelovaných převýšení pojednává práce [5]. Geocentrický souřadnicový systém (vyrovnání na elipsoidu) Hlavním principem společného vyrovnání polohové i výškové složky sítě je, že díky velmi přesným nivelovaným převýšením dojde ke zpřesnění i polohových souřadnic bodů. Vliv nivelovaných převýšení na přesnost výšek je přímý a zřejmý, vliv na přesnost polohy bodu ovšem závisí na dalších měřených veličinách (zenitové úhly a šikmé délky) a také na vzájemné konfiguraci bodů, jak uvádí [5]. Nejsprávnější způsob kombinovaného vyrovnání GNSS vektorů, terestrických měření a nivelovaných převýšení by měl proto poskytnout matematický model vyrovnání na elipsoidu. Elipsoid je vhodné zvolit jako referenční plochu, protože je ideální pro zavádění tížnicových odchylek a práci s geoidem, resp. kvazigeoidem. Dále také odstraňuje potřebu výpočtů většiny geometrických redukcí klasických měření. 14
16 2. PŘÍPRAVA VSTUPNÍCH DAT Problémem je, že většina dostupných programů pro vyrovnání geodetických sítí neumožňuje vyrovnání na elipsoidu. K tomuto účelu by měla sloužit nová vývojová větev projektu GNU Gama, označovaná jako gama-g3. Dosud však nebyla uvolněna stabilní verze programu. Kartografické zobrazení (vyrovnání v pravoúhlém rovinném systému) Pro vyrovnání pouze polohové složky sítě ideálně postačuje zvolit vhodné kartografické zobrazení a všechny měřené veličiny do něho převést. Volbu kartografického zobrazení lze dále specifikovat požadavkem, aby se v navrženém rovinném souřadnicovém systému vzhledem k rozměru hradní sítě prakticky neprojevovalo délkové zkreslení. Na základě zkušeností pracovníků Katedry vyšší geodézie a některých prací (např. [6]) bylo vybráno Lambertovo konformní kuželové zobrazení s jednou nezkreslenou rovnoběžkou. Jedná se o konformní zobrazení elipsoidu do roviny, kde zobrazovací rovinou je plášť kužele v normální poloze. Tečný kužel se dotýká elipsoidu podél zvolené rovnoběžky, která se zobrazí jako nezkreslená. Varianta zobrazení se dvěma nezkreslenými rovnoběžkami významně snižuje vliv délkového zkreslení v daném pásu a je užívána jako národní zobrazení mnoha států (např. 60 % států USA, Francie, Německo, Rakousko, Belgie a další). Lambertovo konformní kuželové zobrazení, mezinárodně známé pod zkratkou LCC (Lambert Conformal Conic), je na obr Jeho autorem je Johann Heinrich Lambert (1772). 2.2 Lambertovo konformní kuželové zobrazení Jak vyplývá z předchozí kapitoly, pro kombinované vyrovnání GNSS vektorů a terestrických měření bylo vybráno Lambertovo konformní kuželové zobrazení. Toto zobrazení bylo dále specifikováno volbou základní nezkreslené rovnoběžky. Ta má geodetickou šířku φ = a prochází přibližně středem areálu Pražského hradu. Jako základní poledník byl zvolen Greenwichský nultý poledník. Zobrazení užívá referenční elipsoid WGS84. Z této volby zobrazení vyplývá, že počátek rovinného systému je na elipsoidu umístěn do bodu o geodetických souřadnicích λ = 0 a φ = 50,09. Kladná poloosa +x rovinného systému směřuje k severu a poloosa +y k východu. 15
17 2. PŘÍPRAVA VSTUPNÍCH DAT Obr. 2.1: Lambertovo konformní kuželové zobrazení Odvození dále uvedených zobrazovacích rovnic lze nalézt např. v [7]. ρ 0 = a tan φ 0 1 e 2 sin 2 φ (2.1) n = sin φ 0 (2.2) p 2 = p 1 = tan ( φ 0 + ) π 2 4 tan ( φ + ) π 2 4 ( (1 e sin φ0 ) (1 + e sin φ) ) ( n e 2 ) (1 + e sin φ 0 ) (1 e sin φ) n (2.3) (2.4) ρ = ρ 0 p 1 p 2 (2.5) ε = n λ (2.6) x = ρ 0 ρ cos ε (2.7) y = ρ sin ε (2.8) V rovnicích 2.1 až 2.8 jsou ρ 0 a n konstantami zobrazení, p 1 a p 2 pomocné proměnné, ρ a ε polární rovinné souřadnice, x a y pravoúhlé rovinné souřadnice. 16
18 2. PŘÍPRAVA VSTUPNÍCH DAT V rovnicích dále vystupují geodetické souřadnice zobrazovaného bodu φ, λ, geodetická šířka základní nezkreslené rovnoběžky φ 0 a parametry použitého referenčního elipsoidu a, e (hlavní poloosa, numerická excentricita). Zobrazení LCC je součástí knihovny kartografických zobrazení PROJ.4 [8] a lze ji tak využít k výpočtu pravoúhlých rovinných souřadnic. Geodetické souřadnice bodů lze do programu zadat i v podobě vstupního dávkového souboru. Pro převod geodetických souřadnic do pravoúhlých rovinných v zobrazení LCC s výše uvedenými specifikacemi spustíme program PROJ.4 příkazem: proj +proj=lcc +ellps=wgs84 +lat_1=50.09 vstup.txt -f %.4f -V V tomto příkazu parametr +proj specifikuje použité zobrazení, parametrem +ellps je udáván elipsoid, na který je zobrazení aplikováno, parametr +lat_1 určuje geodetickou šířku nezkreslené rovnoběžky, vstup.txt je název dávkového souboru se vstupními souřadnicemi v pořadí geodetická délka λ, geodetická šířka φ. Parametrem -f %.4f se určuje požadovaný počet desetinných míst výstupních rovinných souřadnic. Velice užitečným volitelným parametrem je -V, který za výstupními souřadnicemi vypíše detailně i s popisem hodnoty všech počítaných zkreslení. Níže je uveden příklad detailního výstupu z programu PROJ.4 pro bod point 1011 Hel: Longitude: 14d "E [ ] Latitude: 50d "N [ ] Easting (y): Northing (x): Meridian scale (h)*: ( 1.854e-009 % error ) Parallel scale (k)*: ( 1.854e-009 % error ) Areal scale (s): ( 1.151e-009 % error ) Angular distortion (w): Meridian/Parallel angle: Convergence*: -11d " [ ] Max-min (Tissot axis a-b) scale error: Jak lze z těchto výpisů snadno ověřit, délkové zkreslení se prakticky neprojevuje ani pro nejodlehlejší body sítě. Délkové zkreslení u konformních zobrazení nezávisí na směru uvažovaného délkového elementu a v zobrazení LCC v normální poloze je funkcí pouze zeměpisné šířky. Ekvideformátami jsou potom obrazy zeměpisných rovnoběžek. Pro rozbor vlivu délkového zkreslení je tedy odlehlostí bodu míněna pouze odlehlost od základní nezkreslené rovnoběžky. 17
19 2. PŘÍPRAVA VSTUPNÍCH DAT Redukce měřených délek Délky měřené v polygonových pořadech je nutné před dalším zpracováním převést do roviny použitého kartografického zobrazení. Protože se délkové zkreslení vzhledem k rozměrům sítě prakticky neprojevuje, nebyla tato redukce délek vůbec zaváděna. Přímo měřené délky byly pouze redukovány do nulového horizontu jednotným měřítkem m red = 0, Toto redukční měřítko bylo určeno podle: m red = R R + H, (2.9) kde R je střední poloměr Země a H je průměrná nadmořská výška lokality. Ta byla uvažována hodnotou H = 300 m. Převod GNSS vektorů do roviny zobrazení a s tím spojená transformace charakteristik přesnosti těchto vektorů jsou popsány v následujících kapitolách. 2.3 Převod GNSS vektorů do roviny zobrazení Před samotným popisem převodu měřených GNSS vektorů do roviny Lambertova konformního kuželového zobrazení bude nejprve objasněn původ těchto dat. GNSS vektory měřené v prvních šesti etapách, tj. etapách jaro 2008 až podzim 2010, byly získány ve formě vstupních dávkových souborů pro samostatné vyrovnání vektorů programem GNU Gama. Tyto vstupní soubory jsem, spolu s průvodní technickou zprávou, obdržel od Ing. Tomáše Kubína, Ph.D. Autorem samostatného zpracování GNSS dat ze sítě Pražského hradu je Ing. Michal Seidl, Ph.D. Jelikož byly v roce 2010 ukončeny měřické práce prováděné v rámci zmíněného grantového projektu GAČR č. 103/07/1522, probíhalo zaměření dalších etap pouze nepravidelně. V roce 2011 tak nebylo v hradní síti provedeno žádné měření, jež by poskytlo návaznost na případné další kampaně. Na jaře roku 2012 bylo etapové měření v síti Pražského hradu částečně obnoveno (pouze terestrická měření). Etapa podzim 2012 byla již zaměřena kompletně (terestrická i družicová měření). Měřená GNSS data z etapy podzim 2012 jsem taktéž obdržel od Ing. Tomáše Kubína, Ph.D. a jsou výsledkem zpracování Ing. Michala Glöcknera. Data z této etapy byla k dispozici v podobě protokolů o výpočtu GNSS vektorů ve zpracovatelském programu Trimble Total Control. 18
20 2. PŘÍPRAVA VSTUPNÍCH DAT Všechna zmíněná data z provedených GNSS observací, tj. vstupní dávkové soubory pro samostatné vyrovnání vektorů v etapách jaro 2008 až podzim 2010, výstupní textové soubory a dále protokoly o výpočtu vektorů v etapě podzim 2012, jsou uloženy na přiloženém CD. V souvislosti s provedenými měřeními je vhodné zmínit, že síť Pražského hradu byla od počátku budována s předpokladem nasazení technologie GNSS coby primární metody pro určení polohové složky sítě. Z toho důvodu bylo měření polygonových pořadů v roce 2009 (etapy jaro a podzim 2009) provedeno pouze částečně. V důsledku toho však nebylo možné polygonová měření samostatně zpracovat formou vyrovnání volné sítě. Navázání polygonových měření na GNSS vektory a jejich společné vyrovnání je tak nutnou podmínkou pro vyřešení těchto etap. Od tohoto způsobu zpracování však bylo v dalších etapách upuštěno. Kompletní převod měřených GNSS vektorů do roviny zobrazení byl proveden podle následujícího postupu: ze vstupních dávkových souborů pro samostatné vyrovnání vektorů byly získány přibližné pravoúhlé prostorové souřadnice X, Y, Z všech bodů v systému WGS84 (zadány jako opěrné body), k přibližným souřadnicím počátečního bodu vektoru byl přičten měřený vektor, tím byly určeny souřadnice X, Y, Z koncového bodu vektoru, prostorové pravoúhlé souřadnice X, Y, Z počátečního a koncového bodu vektoru byly převedeny na geodetické zeměpisné souřadnice B, L, H podle vztahů uvedených v kapitole 2.3.1, souřadnice B, L byly pomocí zobrazovacích rovnic 2.1 až 2.8 převedeny na pravoúhlé rovinné souřadnice Lambertova konformního kuželového zobrazení, jako třetí souřadnice bodu byla ponechána elipsoidická výška H, rozdílem zobrazených souřadnic počátečního a koncového bodu byly získány souřadnice vektoru v rovině zobrazení, třetí souřadnicí vektoru je rozdíl elipsoidických výšek plná kovarianční matice vektoru v systému WGS84 byla transformována na kovarianční matici popisující přesnost vektoru v rovině zobrazení, tato transformace je podrobně popsána v kapitole
21 2. PŘÍPRAVA VSTUPNÍCH DAT Transformace mezi (X, Y, Z) a (B, L, H) Souřadnicemi X, Y, Z jsou pro účel této kapitoly míněny prostorové pravoúhlé souřadnice bodu na rotačním elipsoidu. Počátek prostorové pravoúhlé soustavy je ve středu rotačního elipsoidu, osa Z v ose rotace, osa X v průsečíku roviny rovníku s rovinou nultého poledníku a osa Y v rovině rovníku doplňuje systém na pravoúhlý pravotočivý. Souřadnicemi B, L, H jsou potom geodetické zeměpisné souřadnice bodu na elipsoidu, resp. ve výšce H nad elipsoidem. Odvození vztahu mezi prostorovými pravoúhlými souřadnicemi a geodetickými zeměpisnými souřadnicemi lze nalézt např. v [9]. Konečné vztahy mají tvar: X (N + H) cos B cos L Y = (N + H) cos B sin L, (2.10) Z [N (1 e 2 ) + H] sin B kde B je geodetická šířka, L je geodetická délka, H je výška bodu nad elipsoidem (ve směru normály k elipsoidu), N = a/ 1 e 2 sin 2 B je příčný poloměr křivosti (poloměr křivosti v prvním vertikálu 1 ), e = (a 2 b 2 )/a 2 je první excentricita referenčního elipsoidu s hlavní poloosou a a vedlejší poloosou b. V případě transformace z (X, Y, Z) do (B, L, H) je geodetická délka dána výrazem: tan L = Y X (2.11) Zavedeme nyní pomocnou substituci D = X 2 + Y 2. Souřadnice B a H jsou potom obvykle určovány iteračním postupem s volbou počáteční hodnoty B 0, např.: B 0 = arctan ( Z D ) 1 1 e 2 V i-té iteraci jsou souřadnice dále zpřesňovány podle vztahů: N i = (2.12) a 1 e 2 sin 2 B i 1 (2.13) D H i = N i cos B i 1 (2.14) [ ( ) Z B i = arctan D 1 e 2 N 1 ] i N i + H i (2.15) 1 První vertikál je rovina kolmá k rovině poledníku a obsahující normálu elipsoidu v bodě. 20
22 2. PŘÍPRAVA VSTUPNÍCH DAT Zobrazení (B, L) do (x, y) Geodetické zeměpisné souřadnice (B, L) počátečního a koncového bodu vektoru byly dále zobrazeny do pravoúhlého rovinného systému (x, y) Lambertova konformního kuželového zobrazení. Výpočet rovinných souřadnic byl proveden pomocí programu PROJ.4, který byl spolu s příslušnými zobrazovacími rovnicemi podrobněji představen v kapitole 2.2. V detailních výstupech z tohoto programu byly pro jednotlivé body kontrolovány především hodnoty délkových zkreslení. Vzhledem k volbě zobrazení a relativně malému rozměru sítě se však délkové zkreslení neprojevuje ani pro body nejvíce vzdálené od základní nezkreslené rovnoběžky. Rozdílem souřadnic x, y počátečního a koncového bodu vektoru byl získán vektor v rovině zobrazení. Pro účel společného vyrovnání polygonových měření s GNSS vektory programem GNU Gama je nutné zadat vektory obecně jako prostorové. Třetí souřadnicí vektoru je proto rozdíl elipsoidických výšek koncových bodů. Finálním úkolem při přípravě a předzpracování měřených dat bylo provést transformaci kovariančních matic měřených vektorů. Tomuto tématu je věnována následující kapitola. 2.4 Transformace kovarianční matice GNSS vektory (dále jimi budou míněny pouze vektory určené technologií GPS) jsou produktem měření v globálním geocentrickém souřadnicovém systému WGS84. Výsledkem zpracování 2 GNSS observací jsou kromě vektorů samotných i charakteristiky jejich přesnosti. Těmito charakteristikami jsou příslušné kovarianční matice vektorů. V případě prostorového vektoru je kovarianční maticí čtvercová matice rozměru 3 3, symetrická podle diagonály. Diagonální prvky matice (variance) popisují přesnost jednotlivých složek vektoru a kovariance vyjadřují jejich vzájemnou závislost. Kovarianční matice vzešlé ze zpracování GNSS observací přirozeně popisují přesnost vektorů v originálním souřadnicovém systému, tj. systému, v němž bylo měření uskutečněno. S převodem vektoru do jiného souřadnicového systému (např. kartografického zobrazení) je tedy nutně spjata i transformace kovarianční matice vektoru. 2 GNSS observace provedené v rámci etapového měření sítě Pražského hradu byly zpracovány v programu Trimble Total Control. 21
23 2. PŘÍPRAVA VSTUPNÍCH DAT Transformace kovarianční matice souřadnic Uvažujme nyní dva kartézské systémy souřadnic, jejichž vzájemný vztah lze jednoznačně vyjádřit pomocí lineární prostorové transformace. Lineární konformní transformace v třírozměrném prostoru je dle [10] dána rovnicí: X = λ R x + T, (2.16) kde X, x jsou vektory souřadnic v jedné a druhé soustavě, λ je měřítkový koeficient (u konformní transformace je stejný pro všechny osy soustavy), R je matice prostorové rotace a T je vektor translací v jednotlivých osách. Rozepsáním vektorů a matic dostane rovnice 2.16 tvar: X r Y = λ 11 r 12 r 13 x T r 21 r 22 r 23 y + X T Y (2.17) Z r 31 r 32 r 33 z T Z Jednotlivé složky r ij ortogonální rotační matice R získáme součinem tří matic 2.18 až 2.20 pro otočení kolem souřadnicových os o příslušné úhly α, β, γ, přičemž záleží na pořadí, v jakém jsou elementární rotace kolem jednotlivých os aplikovány R X (α) = 0 cos α sin α (2.18) 0 sin α cos α cos β 0 sin β R Y (β) = (2.19) sin β 0 cos β cos γ sin γ 0 R Z (γ) = sin γ cos γ 0 (2.20) Uvažujeme-li dále lineární transformaci shodnostní (λ = 1), zapíšeme transformační rovnice ve tvaru: X = r 11 x + r 12 y + r 13 z + T X Y = r 21 x + r 22 y + r 23 z + T Y (2.21) Z = r 31 x + r 32 y + r 33 z + T Z Lineární transformace nemá vliv na vnitřní vztahy v síti, translaci a otočení lze tedy považovat za bezchybné. Pak za použití transformačních rovnic 2.21 a obecného 22
24 2. PŘÍPRAVA VSTUPNÍCH DAT zákona hromadění směrodatných odchylek můžeme odvodit vztah pro transformaci kovarianční matice M x na M X : M X = A x M x A T x, (2.22) kde M X je výsledná kovarianční matice souřadnic v cílové soustavě, M x je kovarianční matice souřadnic n bodů ve výchozí soustavě: σ x 2 1 C x1 y 1 C x1 z 1 C x1 x n C x1 y n C x1 z n C x1 y 1 σ 2 y 1 C y1 z 1 C y1 x n C y1 y n C y1 z n C x1 z 1 C y1 z 1 σ 2 z 1 C z1 x n C z1 y n C z1 z n M x = C x1 x n C y1 x n C z1 x n σx 2 n C xnyn C xnzn C x1 y n C y1 y n C z1 y n C xnyn σy 2 n C ynzn C x1 z n C y1 z n C z1 z n C xnzn C ynzn σz 2 n (2.23) a A x je matice parciálních derivací transformačních vztahů podle jednotlivých souřadnic: Po provedení derivací dostáváme: X 1 X 1 X 1 X x 1 y 1 z 1 1 X 1 X 1 x n y n z n Y 1 Y 1 Y 1 Y x 1 y 1 z 1 1 Y 1 Y 1 x n y n z n Z 1 Z 1 Z 1 Z x 1 y 1 z 1 1 Z 1 Z 1 x n y n z n A x = X n X n X n X x 1 y 1 z 1 n X n X n x n y n z n Y n Y n Y n Y x 1 y 1 z 1 n Y n Y n x n y n z n Z n Z n Z n Z x 1 y 1 z 1 n Z n Z n x n y n z n r 11 r 12 r r 21 r 22 r r 31 r 32 r R 0 0 A x = R 0 = r 11 r 12 r R r 21 r 22 r r 31 r 32 r 33 (2.24) (2.25) Matice derivací A x vstupující do obecného zákona hromadění směrodatných odchylek je tedy složena z diagonálně řazených rotačních matic a doplněna nulovými čtvercovými maticemi stejného rozměru jako matice R. 23
25 2. PŘÍPRAVA VSTUPNÍCH DAT Vzhledem k tvaru matice derivací A x by se mohla transformace jednotlivých řádků jevit jako nezávislá. Jak je však zdůrazněno v [11], při obecném tvaru kovarianční matice M x původních n bodů tomu tak není a je tedy nutné transformovat celou kovarianční matici jako jeden celek. Odvození lze snadno degradovat i na případnou lineární transformaci v rovině. Výsledné vztahy zůstanou v principu zachovány Transformace kovarianční matice GNSS vektoru Exaktní způsob GNSS vektory byly pro účel společného vyrovnání s terestrickými měřeními převedeny do Lambertova konformního kuželového zobrazení. Protože vztah mezi souřadnicovým systémem WGS84 a systémem kartografického zobrazení obecně nelze vyjádřit lineární transformací, nemůže být použit k exaktnímu řešení transformace kovarianční matice GNSS vektoru postup popsaný v kapitole Jak vyplývá z kapitoly 2.3, provedený postup převodu GNSS vektorů do roviny zobrazení lze schematicky vyjádřit následovně: (X, Y, Z) (B, L, H) (x, y, H) (2.26) Transformaci prostorových pravoúhlých souřadnic (X, Y, Z) do geodetických zeměpisných souřadnic (B, L, H) provedeme iteračním postupem, zatímco opačný převod lze vyjádřit přesně analyticky podle rovnic K zobrazení geodetických souřadnic (B, L) do pravoúhlých rovinných souřadnic (x, y) Lambertova konformního kuželového zobrazení využijeme zobrazovací rovnice. Transformaci kovarianční matice vektoru bychom exaktně řešili postupnou aplikací obecného zákona hromadění směrodatných odchylek. V prvním kroku bychom sestavili matici parciálních derivací přímých analytických vztahů Do zákona hromadění směrodatných odchylek by poté vstupovala inverze této matice. Výsledkem je kovarianční matice vektoru vyjádřeného geodetickými souřadnicemi B, L, H (resp. jejich rozdílem). První krok lze zapsat v maticovém tvaru: Σ BLH = A 1 Σ XYZ (A 1 ) T, (2.27) kde Σ BLH je kovarianční matice vektoru vyjádřeného geodetickými souřadnicemi B, L, H, A je matice parciálních derivací funkčních vztahů 2.10 podle jednotlivých 24
26 2. PŘÍPRAVA VSTUPNÍCH DAT souřadnic B, L, H a Σ XYZ je vstupní kovarianční matice vektoru v systému souřadnic X, Y, Z. V druhém kroku bychom sestavili matici parciálních derivací zobrazovacích rovnic, která by, spolu s výslednou kovarianční maticí Σ BLH z prvního kroku, vstupovala do dalšího zákona hromadění směrodatných odchylek. Výsledkem je nyní požadovaná kovarianční matice vektoru vyjádřeného pravoúhlými rovinnými souřadnicemi x, y a z formálních důvodů zachovanou elipsoidickou výškou H (resp. jejich rozdílem). Tento druhý krok lze opět maticově zapsat: Σ xyh = B Σ BLH B T, (2.28) kde Σ xyh je výsledná kovarianční matice vektoru vyjádřeného souřadnicemi x, y, H, B je matice parciálních derivací zobrazovacích rovnic a Σ BLH je kovarianční matice vektoru vyjádřeného souřadnicemi B, L, H. K oběma krokům je nutné poznamenat, že parciálně derivovanými funkčními vztahy nejsou přímo vztahy mezi jednotlivými souřadnicemi, ale jejich rozdíly. To plyne ze skutečnosti, že transformujeme kovarianční matici vektoru, který je obecně dán rozdílem souřadnic svých koncových bodů. Jak uvádí [11], oba zmíněné kroky lze provést také současně. Se zachováním použitého označení matic bychom kompletní transformaci kovarianční matice vektoru zapsali: Σ xyh = B A 1 Σ XYZ (A 1 ) T B T (2.29) Tento exaktní postup transformace kovarianční matice vektoru bychom měli upřednostnit v případě, pokud by úvahy o reálné vstupní přesnosti byly dobře a spolehlivě známy. Algoritmizace zpracování GNSS observací pomocí některého z dostupných uživatelských programů je však do jisté míry firemním»know-how«a jak již bylo v některých pracích (např. [6]) zaznamenáno, deklarované přesnosti se v dalším zpracování často jeví jako velmi nadhodnocené. O použití přibližného či exaktního způsobu transformace kovarianční matice vektoru by mělo také rozhodovat, jak velký je rozdíl mezi výsledky obou metod. Takové srovnání nebylo v rámci této práce provedeno. Přibližný způsob Přibližný způsob transformace kovarianční matice vektoru je založen na úvaze, že nahradíme-li soustavu kartografického zobrazení (doplněnou údaji o elipsoidických 25
27 2. PŘÍPRAVA VSTUPNÍCH DAT výškách) vhodně zvoleným kartézským pravoúhlým systémem E3, můžeme transformaci charakteristik přesnosti přibližně provést lineární transformací, tj. podle postupu popsaného v kapitole Jak vyplývá z volby kartografického zobrazení (viz kapitola 2.2), počátek rovinného souřadnicového systému je na elipsoidu umístěn do bodu o geodetických souřadnicích λ = 0 a φ = 50,09. Kladná poloosa +x rovinného systému směřuje k severu a poloosa +y k východu. Počátek pravoúhlého kartézského systému E3 však neztotožníme s počátkem pravoúhlého rovinného systému kartografického zobrazení, ale umístíme ho přibližně do středu lokality měření. Jako střed areálu Pražského hradu je uvažován bod 524 s geodetickými souřadnicemi λ 0 = 14,40 a φ 0 = 50,09. Z z x B 0 y X L 0 Y Obr. 2.2: Přibližný způsob transformace kovarianční matice vektoru S odkazem na obr. 2.2 odvodíme matici prostorové rotace následovně. Systém WGS84 nejprve otočíme kolem osy Y o úhel β = π 2 φ 0 v matematicky kladném smyslu. Tím shodně orientujeme osu Z s osou z. Tento krok zapíšeme: Y [ ( ) ] π + 2 φ 0 (2.30) 26
28 2. PŘÍPRAVA VSTUPNÍCH DAT Dále provedeme rotaci kolem osy Z o úhel γ = λ 0 + π, opět v matematicky kladném smyslu (případně můžeme toto otočení provést v matematicky záporném smyslu o úhel γ = λ 0 π). Z [+ (λ 0 + π)] (2.31) Protože systém WGS84 je systém pravotočivý a lokální systém E3 je díky provedené volbě souřadnicových os systémem levotočivým, je posledním krokem zrcadlení osy Y podle roviny XZ. Úpravu zrcadlení vyjádříme následovně: x X y = Y (2.32) z Z Výslednou matici prostorové rotace R zapíšeme pomocí dílčích rotací, avšak v opačném pořadí, než byly jednotlivé kroky aplikovány při odvození: ( π R = R Z (λ 0 + π) R Y 0) 2 φ (2.33) Přibližný způsob transformace kovarianční matice vektoru poté provedeme s využitím vztahu 2.22: Σ xyh Σ E3 = R Σ XYZ R T (2.34) Pro transformaci kovariančních matic GNSS vektorů byl pro účely této práce použit přibližný způsob. 27
29 3. VYROVNÁNÍ SÍTĚ 3 Vyrovnání sítě V předchozí kapitole 2 byl objasněn postup, jakým byla všechna měřená data převedena do společné vztažné soustavy souřadnic. Na základě provedené úvahy nad volbou vztažné soustavy bylo vybráno Lambertovo konformní kuželové zobrazení. Potřebné úpravy dat se tak týkaly zejména GNSS vektorů a jejich kovariančních matic. Tato kapitola si v logické návaznosti klade za cíl popsat sestavení vstupních dávkových souborů pro společné vyrovnání programem GNU Gama a zhodnotit výsledky vyrovnání sítě v jednotlivých etapách. 3.1 GNU Gama K vyrovnání měření byl použit program gama-local. GNU Gama je volně distribuovaný software, který slouží k vyrovnání geodetických sítí. V současné době program plně podporuje vyrovnání sítí v lokálním kartézském systému (tj. program gama-local). Vyrovnání v geocentrické souřadné soustavě je součástí nové vývojové větve a předpokládá užití matematického modelu vyrovnání na elipsoidu (program gama-g3). Na domovských stránkách projektu software/gama/ jsou k dispozici odkazy ke stažení programu a dokumentace. Gama zpracovává příkazy v dávkovém XML souboru, jehož struktura je detailně popsána v dokumentaci k programu [12]. Zde bude zmíněna pouze základní struktura, která se týká vyrovnání vztažné polohové sítě. Kostrou každého vstupního dávkového souboru do programu gama-local je následující základní struktura: <gama-local> <network axes-xy = "ne" angles = "right-handed"> <description>... </description> <parameters sigma-apr = "1" conf-pr = "0.95" tol-abs = "1000" sigma-act = "apriori" /> <points-observations>... </points-observations> </network> </gama-local> 28
30 3. VYROVNÁNÍ SÍTĚ Párový tag <gama-local> obsahuje jediný párový tag <network>, který dále obsahuje údaje definující síť. Definice sítě je uvnitř tagu <network> popisována ve třech různých sekcích: <description> <parameters /> <points-observations> Sekce <description> a <parameters /> jsou volitelné, zatímco povinně uváděnou sekcí je <points-observations>. Tyto tři sekce mohou být v rámci tagu <network> uvedeny v libovolném pořadí. Tag <network> může být dále specifikován dvěma volitelnými atributy, axes-xy a angles. Tyto atributy popisují orientaci os pravoúhlého souřadnicového systému a orientaci měřených úhlů (směrů). V sekci <description> se uvádí pouze údaje informativního významu, které nijak neovlivňují proces vyrovnání, např. popis sítě, komentáře atd. V sekci <parameters /> se nastavují parametry vyrovnání a prováděných statistických analýz, tj. apriorní jednotková směrodatná odchylka, konfidenční pravděpodobnost, tolerance pro identifikování vybočujících absolutních členů v rovnicích oprav, aktuálně používaná jednotková směrodatná odchylka. Do párového tagu <points-observations> se konečně zapisují definice bodů sítě a měřené hodnoty včetně jejich apriorních přesností. Volitelnými atributy lze v tomto tagu definovat implicitní směrodatné odchylky pro jednotlivé typy měřených veličin. Jejich hodnoty se zadávají v mm, resp. desetinách mgon (grádových vteřinách). <direction-stdev=... > směrodatná odchylka vodorovného směru <zenith-angle-stdev=... > směrodatná odchylka zenitového úhlu <distance-stdev=... > směrodatná odchylka délky Body sítě se definují pomocí nepárového tagu <point /> s těmito atributy: id=... číslo bodu x=... y=... z=... souřadnice bodu fix=... specifikuje, které souřadnice jsou při vyrovnání pevné adj=... určuje, které souřadnice mají být vyrovnány (určované neznámé parametry) 29
31 3. VYROVNÁNÍ SÍTĚ Přípustnými hodnotami atributu adj=... jsou xy, XY, z, Z, xyz, XYZ, xyz a XYz. Souřadnice označené velkým písmenem značí tzv. opěrné body (constrained coordinates). V klasických řešeních volných geodetických sítí je sadou opěrných bodů zaváděna regularizující podmínka: (dx 2 i + dyi 2 ) = min. (3.1) kde dx a dy jsou vyrovnané souřadnicové opravy i-tého opěrného bodu. Jinými slovy, sada opěrných bodů udává ve vyrovnání tvar a rozměr sítě, která je současně umístěna na přibližné souřadnice opěrných bodů pomocí Helmertovy transformace. Párový tag <obs> sdružuje již samotná měření a je typicky užíván pro zápis veškerých hodnot měřených v rámci jedné osnovy směrů. Může tedy obsahovat: <direction.../> vodorovný směr <angle.../> vodorovný úhel <distance.../> vodorovná délka <s-distance.../> šikmá délka <z-angle.../> zenitový úhel Požadujeme-li měřeným veličinám stejného typu zadat obecně různou přesnost, je nutné tak učinit explicitně pomocí příkazu stdev=..., který zapíšeme za příslušné měření. Dalším důležitým typem měření, které lze programem GNU Gama zpracovat, jsou vektory (souřadnicové rozdíly). Vektory se zapisují do párového tagu <vectors> a jejich přesnost se vyjadřuje kovarianční maticí. Vektory je nutné zadat vždy jako trojrozměrné. Příkladem může být zápis: <vectors> <vec from="541" to="513" dx=" " dy=" " dz="2.4836" /> <cov-mat dim="3" band="2"> </cov-mat> </vectors> 30
32 3. VYROVNÁNÍ SÍTĚ 3.2 Sestavení vstupních dávkových souborů Pro každou z osmi zaměřených etap byl sestaven vstupní dávkový soubor pro vyrovnání programem GNU Gama. Struktura těchto vstupních souborů se řídí definicí jazyka XML, v němž jsou data zadávána pomocí párových a nepárových tagů, jak bylo podrobněji ukázáno v předchozí kapitole 3.1. V této fázi zpracování jsou již veškeré měřené veličiny převedeny do společné vztažné soustavy souřadnic, tj. Lambertova konformního kuželového zobrazení. Zrekapitulujme nyní, jakými úpravami jednotlivé typy měřených veličin prošly: vodorovné délky redukce délek z kartografického zobrazení nebyla zavedena (vzhledem k volbě zobrazení a rozměru sítě se délkové zkreslení prakticky neprojevuje), všechny délky v síti pouze redukovány do nulového horizontu jednotným měřítkem m red = 0, ; vodorovné směry žádné redukce nebyly zavedeny, vzhledem k vlastnostem zvoleného zobrazení nedochází k úhlovému zkreslení; GNSS vektory geodetické zeměpisné souřadnice B, L koncových bodů vektorů byly převedeny pomocí zobrazovacích rovnic do roviny kartografického zobrazení, třetí souřadnice (elipsoidická výška H) bodů byla zachována; kovarianční matice vektorů transformovány do roviny zobrazení přibližným způsobem. Kovariančním maticím vektorů byla při zpracování obecně věnována vysoká pozornost, neboť jak jsem již v předchozím textu zmínil, v několika pracích bylo zaznamenáno nadhodnocení přesnosti GNSS vektorů. Příkladem může být práce [6] nebo i komplexní zpracování GNSS dat provedené pracovníky Katedry speciální geodézie v rámci řešení grantového projektu. Pro zpracování GNSS observací jsou na Katedře speciální geodézie standardně užívanými nástroji programy Trimble Total Control a Leica Geo Office. Od pana Ing. Tomáše Kubína, Ph.D. jsem obdržel testovací výpočty, v nichž byl zjišťován nejoptimálnější násobek kovarianční matice vektoru podle velikosti aposteriorní jednotkové směrodatné odchylky a podle průměrné polohové chyby na určovaných bodech. Na základě těchto testů bylo empiricky zjištěno, že optimálním násobkem směrodatných odchylek jednotlivých složek vektoru je konstanta 3 (platí pro vektory zpracované programem Trimble Total Control). Při vyšších násobcích aposteriorní jednotková směrodatná odchylka dále klesá a proto je nutné se současně orientovat i podle vývoje průměrné polohové chyby. 31
33 3. VYROVNÁNÍ SÍTĚ Závěrem je, že do společného vyrovnání vstupovaly vektory s přesností třikrát zhoršenou oproti původnímu apriornímu odhadu vzešlému ze zpracování programem Trimble Total Control. Požadujeme-li však směrodatné odchylky zvětšit třikrát, je nutné původní kovarianční matici vynásobit devíti. Finální postup úpravy kovariančních matic tedy zahrnoval jejich transformaci do roviny zobrazení přibližným způsobem a následné vynásobení konstantou 9. Takto upravené kovarianční matice vektorů poté vstupovaly do společného vyrovnání GNSS vektorů s polygonovými měřeními. Přesnosti ostatních měřených veličin byly pro účel vyrovnání uvažovány následovně: směrodatná odchylka vodorovné délky σ d = 1 mm pro etapy 2008j, 2008p, 2010j, 2010p směrodatná odchylka vodorovné délky σ d = 2 mm pro etapy 2009j, 2009p, 2012j, 2012p směrodatná odchylka vodorovné směru σ ψ = 0, 6 mgon pro všechny etapy Tyto směrodatné odchylky jsou chápány a užity ve smyslu normy ČSN ISO (část Elektronické dálkoměry) a ČSN ISO (část Teodolity). Užití různých hodnot směrodatné odchylky délky plyne ze skutečnosti, že příslušné etapy byly zaměřeny různými přístroji, tj. přístrojem Trimble S6 HP s výrobcem udávanou hodnotou σ d = 1 mm+1 ppm, resp. přístrojem Topcon GPT-7501 s hodnotou σ d = 2 mm + 2 ppm. Obousměrně měřené délky stran polygonových pořadů byly do vyrovnání zadávány pouze jednou, a sice svojí průměrnou hodnotou. Apriorní jednotková směrodatná odchylka byla ve všech etapách zvolena σ 0 = 1. Tato směrodatná odchylka byla užita k výpočtu aposteriorních odhadů přesností vyrovnaných neznámých a při statistických testech prováděných programem GNU Gama. Statistické testy byly prováděny na hladině významnosti α = 1 % (tomu odpovídá volba konfidenční pravděpodobnosti 0, 99). Poslední důležitou volbou před samotným vyrovnáním volné geodetické sítě je volba způsobu umístění sítě do prostoru. U volné sítě jsou všechny souřadnice považovány za neznámé, síť tedy není umístěna do prostoru a matice normálních rovnic je singulární. Singularitu systému normálních rovnic lze řešit doplněním dodatečných informací do výpočtu, nebo zvolením dostatečného počtu souřadnic, které budou 32
34 3. VYROVNÁNÍ SÍTĚ z výpočtu vyřazeny a považovány za pevné, a nebo inverzi singulární matice řešit pomocí pseudoinverze. Všechny varianty jsou podrobně popsány v [11]. Obecně platí, že volná geodetická síť musí být do prostoru umístěna minimálním počtem podmínek. V případě nadbytečného počtu by došlo k její deformaci vlivem přizpůsobení se podmínkám umístění. Aby nedošlo ke zkreslení tvaru sítě, je nutné její umístění definovat lineární transformací. U přesných inženýrsko-geodetických sítí tedy připadá v úvahu pouze transformace shodnostní nebo podobnostní. Lineární transformace v rovině je definována maximálně čtyřmi transformačními parametry (změna měřítka, otočení, dva posuny). Z toho vyplývá, že rovinnou síť je možné do prostoru umístit maximálně čtyřmi podmínkami. V závislosti na měřených veličinách v síti se některé transformační parametry nemusejí uplatnit a počet podmínek umístění sítě do prostoru klesá. V našem případě jsou měřenými veličinami v síti vodorovné délky, vodorovné směry a GNSS vektory. Vodorovné délky definují měřítko a tedy rozměr sítě. Měřítkový koeficient se proto neuplatní. Měřenými vektory je navíc udána i orientace sítě, parametr stočení se tedy také neuplatní. Zbývají dvě podmínky umístění takové sítě do prostoru. Jako vhodný způsob dodefinování těchto dvou zbývajících podmínek se nabízí fixace souřadnic právě jednoho bodu sítě. Tím je celá síť jednoznačně umístěna do prostoru a systém normálních rovnic regularizován. Jedná se tedy o volbu umístění pomocí fixování souřadnic podmínkami. Ve všech etapách kromě etapy jaro 2012 byl fixovaným bodem hloubkový geotechnický vrt TV01, který se nachází před budovou FSv ČVUT a je tak značně vzdálen od primárně sledované oblasti. V síti Pražského hradu plní tento bod funkci referenční stanice při GNSS observacích. Fixovanými souřadnicemi jsou lokální rovinné souřadnice x 101 = 5000 m a y 101 = 1000 m. Jedinou etapou, která byla při vyrovnání umístěna do prostoru jiným způsobem, je etapa jaro V této etapě nebylo provedeno žádné GNSS měření a bod TV01 tedy není součástí sítě. Zároveň však bylo požadavkem, aby všechny body sítě v areálu Pražského hradu byly body určovanými. Fixace souřadnic jiného bodu proto neposkytovala uspokojující řešení. Síť byla v této etapě umístěna na 14 opěrných bodů pomocí Helmertovy transformace, při níž je zaváděna regularizující podmínka 3.1. Za přibližné souřadnice sady opěrných bodů byly považovány vyrovnané souřadnice z řešení etapy podzim Všechny vstupní dávkové XML soubory do programu gama-local jsou uloženy na přiloženém CD. 33
35 3. VYROVNÁNÍ SÍTĚ 3.3 Základní parametry vyrovnání etap Základní parametry vyrovnání sítě jsou shrnuty v následujícím seznamu. Zde si lze také snadno udělat přehled o rozsahu provedených měření v jednotlivých etapách. Parametry jsou převzaty z výstupních protokolů o výpočtu vyrovnání programem GNU Gama. Tyto protokoly jsou v podobě textových a XML souborů uloženy na přiloženém CD. Výstup ve formátu XML obsahuje mimo jiné i plné kovarianční matice vyrovnaných neznámých. V úvodní části protokolů je pro každou etapu uvedeno, která měření byla z výpočtu vyrovnání vyloučena. Tutéž informaci lze případně dohledat i v sekci <description> příslušného vstupního XML souboru. Etapa jaro 2008 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 28 Počet osnov : 12 Vodorovné délky : 16 Celkem pozorování : 66 Počet rovnic oprav : 66 Počet neznámých: 50 Počet nadbyt. pozorování: 16 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní: 0.78 Etapa podzim 2008 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 69 Počet osnov : 28 Vodorovné délky : 41 Celkem pozorování : 142 Počet rovnic oprav : 142 Počet neznámých: 102 Počet nadbyt. pozorování: 40 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní:
36 3. VYROVNÁNÍ SÍTĚ Etapa jaro 2009 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 33 Počet osnov : 15 Vodorovné délky : 33 Celkem pozorování : 104 Počet rovnic oprav : 104 Počet neznámých: 59 Počet nadbyt. pozorování: 45 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní: 1.06 Etapa podzim 2009 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 30 Počet osnov : 14 Vodorovné délky : 31 Celkem pozorování : 133 Počet rovnic oprav : 133 Počet neznámých: 62 Počet nadbyt. pozorování: 71 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní: 0.86 Etapa jaro 2010 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 92 Počet osnov : 40 Vodorovné délky : 45 Celkem pozorování : 221 Počet rovnic oprav : 221 Počet neznámých: 124 Počet nadbyt. pozorování: 97 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní:
37 3. VYROVNÁNÍ SÍTĚ Etapa podzim 2010 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 84 Počet osnov : 35 Vodorovné délky : 44 Celkem pozorování : 232 Počet rovnic oprav : 232 Počet neznámých: 107 Počet nadbyt. pozorování: 125 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní: 0.89 Etapa jaro 2012 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 73 Počet osnov : 31 Vodorovné délky : 41 Celkem pozorování : 114 Počet rovnic oprav : 114 Počet neznámých: 103 Počet nadbyt. pozorování: 14 Defekt sítě : 3 m0 apriorní : 1.00 m0 aposteriorní: 0.94 Etapa podzim 2012 Základní parametry vyrovnání Souřadnice xyz xy z Vyrovnané : Opěrné * : Pevné : Celkem : Počet směrů : 86 Počet osnov : 36 Vodorovné délky : 43 Celkem pozorování : 165 Počet rovnic oprav : 165 Počet neznámých: 116 Počet nadbyt. pozorování: 49 Defekt sítě : 0 m0 apriorní : 1.00 m0 aposteriorní:
38 3. VYROVNÁNÍ SÍTĚ 3.4 Test aposteriorní směrodatné odchylky Po výpočtu vyrovnání je vždy důležité provést zhodnocení kvality výsledku a vstupujících hodnot. K tomu slouží zejména testování aposteriorní jednotkové směrodatné odchylky ^σ 0. Ta je základní charakteristikou globální kvality výsledku vyrovnání a je třeba ji vždy posuzovat ve vztahu k apriorní směrodatné odchylce jednotkové σ 0. Testujeme hypotézu, že náhodný výběr s výběrovou směrodatnou odchylkou ^σ 0 je proveden ze základního souboru se směrodatnou odchylkou σ 0. Nulovou hypotézou H 0, resp. alternativní hypotézou H 1 je: H 0 : σ zaklad. = σ 0 (3.2) H 1 : σ zaklad. σ 0 (3.3) Testovací statistikou je veličina: χ 2 = τ σ 2 0 ^σ 2 0, (3.4) která má při platnosti H 0 centrální χ 2 rozdělení pravděpodobností s τ stupni volnosti (při určování ^σ 0 ). Pro zvolenou hladinu významnosti α vyhledáme tabelované kritické hodnoty χ 2 rozdělení. Nulová hypotéza nebude zamítnuta v případě, platí-li nerovnost: χ 2 1 α/2,τ ^σ 0 χ 2 α/2,τ τ σ 0 τ (3.5) Splnění této nerovnosti lze interpretovat tak, že globální kvalita vzájemného souladu měření vyhovuje předpokladům učiněným volbou apriorních přesností (s rizikem odpovídajícím hladině významnosti, na níž byl test proveden). Jak uvádí [11], je-li kvalita podle tohoto testu vyhovující, k výpočtu kovarianční matice vyrovnaných neznámých by měla být užita apriorní směrodatná odchylka jednotková σ 0. Další postupy hodnocení aposteriorní přesnosti vyrovnání MNČ jsou založeny na hodnocení velikosti oprav, hodnocení vlivu každého měření na kvalitu vyrovnání, případně na robustních metodách vyhledání hrubých chyb. V každém případě je však vhodné, bez ohledu na výsledek kritéria 3.5, zkontrolovat i kvalitu jednotlivých měření podle některé z uvedených metod hodnocení. Nejčastěji půjde o využití hodnocení velikosti oprav, kdy jsou hodnoty normovaných oprav porovnávány s příslušnou mezní hodnotou. Hodnocení velikosti normovaných oprav i výše uvedený test aposteriorní jednotkové směrodatné odchylky jsou již standardně obsaženy ve výpočtu vyrovnání programem gama-local. 37
39 3. VYROVNÁNÍ SÍTĚ V tabulce 3.1 jsou uvedeny hodnoty poměrů aposteriorních jednotkových směrodatných odchylek vzešlých z vyrovnání jednotlivých etap vůči apriorním jednotkovým směrodatným odchylkám a jejich příslušné intervaly spolehlivosti, které plynou z výpočtu testovacího kritéria 3.5. Tab. 3.1: Testování aposteriorních jednotkových směrodatných odchylek etapa ^σ 0 /σ 0 99%-ní interval 2008j 0,784 0,567; 1, p 1,052 0,719; 1, j 1,057 0,735; 1, p 0,863 0,788; 1, j 0,937 0,818; 1, p 0,891 0,839; 1, j 0,941 0,539; 1, p 0,804 0,746; 1,264 Z tabulky je zřejmé, že 99%-ní interval spolehlivosti obsahuje hodnotu poměru ^σ 0 /σ 0 ve všech případech vyrovnání etap. Současně platí, že maximální normovaná oprava v žádném řešeném souboru nepřekračuje příslušnou mezní hodnotu. Můžeme tedy učinit závěr, že přesnost měření v jednotlivých etapách lze považovat za odpovídající přesnosti předpokládané a vložené do vah. Z toho dále vyplývá, že kovarianční matice vyrovnaných neznámých budou určeny na základě apriorní směrodatné odchylky jednotkové σ 0. 38
40 4. ROBUSTNÍ TRANSFORMACE 4 Robustní transformace V předchozích kapitolách byl objasněn postup výpočtu a předzpracování dat získaných při etapových měřeních vztažné sítě Pražského hradu. Výsledkem dosavadního zpracování jsou soubory vyrovnaných polohových souřadnic bodů sítě a jejich směrodatné odchylky, resp. úplné kovarianční matice. Cílem dalšího zpracování bude vyhodnotit, zda došlo v jednotlivých etapách k vodorovným posunům bodů sítě. K tomuto úkolu byl navržen následující postup. Z dostupných etap měření zvolíme jednu, která bude dále považována za etapu základní. Základní etapou rozumíme etapu, k níž budou určované posuny vztahovány. Provedeme postupně transformaci všech ostatních etap do soustavy etapy základní, přičemž transformační klíč bude určován robustním vyrovnáním. Ve smyslu vyrovnání je při robustní transformaci sada identických bodů souborem měření, který díky předpokládaným posunům nepochází z normálního rozdělení pravděpodobností. Robustní metoda odhadu aplikovaná na určení transformačního klíče tedy identifikuje ty body, které se při výpočtu transformačních parametrů jeví jako odlehlé. Tyto body z původního souboru identických bodů vyloučíme. Tím pro jednotlivé robustní transformace získáme redukované soubory identických bodů, které mají obecně různý rozsah. K výpočtu definitivního transformačního klíče použijeme pouze ty body, které nejsou označeny jako odlehlé ani v jedné z robustních analýz. Výsledný soubor identických bodů by měl splňovat podmínku normality měřických dat a definitivní transformační klíč tedy určíme metodou nejmenších čtverců. Takto určený transformační klíč použijeme k transformaci všech bodů sítě v dané etapě do soustavy základní etapy. Z rozdílu souřadnic bodů v základní etapě a přetransformovaných souřadnic v dané řešené etapě určíme posuny, o jejichž průkaznosti rozhodneme na základě statistického testování. V následujícím textu budou jednotlivé kroky takto navrženého postupu podrobně popsány. Nejprve však bude stručně objasněna základní podstata metod robustního odhadu reálných parametrů. 4.1 O metodách robustního odhadu obecně Každý proces měření geodetických veličin je přirozeně a nevyhnutelně ovlivňován působením chyb různého původu. Přítomnost těchto chyb má za následek vznik 39
41 4. ROBUSTNÍ TRANSFORMACE nepřesnosti měření. Teoreticky je tedy možné nepřesnost měření vyjádřit rozdílem měřené a skutečné (pravé) hodnoty veličiny. Ačkoliv nelze žádným způsobem chyby z měřického procesu zcela odstranit, lze je kvalitním postupem zpracování efektivně potlačit a získat tak nejpravděpodobnější hodnotu výsledku. V mnoha oblastech inženýrské geodézie je běžné, že hodnoty měřených veličin jsou pořizovány opakovaně, v nadbytečném množství. Klasické postupy zpracování jsou pak zpravidla založeny na aplikaci metody nejmenších čtverců. Pro tu je ideálním (ne však nutným) předpokladem, že soubor měření je náhodným výběrem z normálního rozdělení pravděpodobností. Je-li tento předpoklad splněn, dává metoda nejmenších čtverců identické výsledky jako metoda maximální věrohodnosti a metoda nejlepšího nestranného odhadu [13]. Reálně je však předpoklad původu geodetických dat z normálního rozdělení těžko splnitelný. Měření je neustálým působením chyb kontaminováno odlehlými hodnotami a předpokládaný pravděpodobnostní model není správný. Jak uvádí [11] nebo [14], i malé odchylky od normálního rozdělení pravděpodobností mají značný vliv na kvalitu výsledku. Správná aplikace metody nejmenších čtverců je tedy často problematická právě díky velmi vysoké citlivosti metody na porušení podmínky normality dat. V případě výskytu odlehlých měření je proto nutné před vlastním vyrovnáním odlehlé hodnoty detekovat a z výpočtu vyrovnání vyloučit. Malý počet chybných měření lze pro tento účel odhalit statistickými testy odlehlých měření. Je-li kontaminace souboru měření odlehlými hodnotami vyšší, je nutné provést zpracování metodami méně citlivými k výskytu odlehlých hodnot. Takové metody jsou označovány jako robustní metody odhadu reálných parametrů. Přestávají-li být testy odlehlých hodnot účinné, je tedy nutné aplikovat robustní metody odhadu. To poprvé představil Huber (1964). Obecným principem robustních metod je, že v podmínce minimalizace sumy čtverců oprav nahrazují kvadráty nebo celou sumu vhodnějšími funkcemi [15]. Podle [11] nebo [16] existuje několik nejrozšířenějších tříd odhadů robustní statistiky a to M-odhady, L-odhady a R-odhady. M-odhady jsou odvozeny z metody maximální věrohodnosti (maximum-likelihood method) a pro praktické využití v řešení úloh geodézie mají největší význam. Odvození robustních metod odhadu reálného parametru jsou komplexně teoreticky podána zejména v zahraniční literatuře. Z nejznámějších autorů a jejich prací uvádím především Huber [17] a Koch [15]. 40
42 4. ROBUSTNÍ TRANSFORMACE 4.2 Robustní M-odhady Zde prezentované odvození lze nalézt v [11]. V principu se jedná o řešení minimalizační úlohy, kde základním vztahem je požadavek na maximální věrohodnost řešení daný výrazem: ^x = arg sup x L(l; x), (4.1) kde l je náhodný vektor měření, L(l; x) je pravděpodobnostní funkce a ^x je odhad neznámých parametrů. Má-li náhodný vektor pozorování l hustotu pravděpodobnosti f(x), která závisí na neznámých a fixních parametrech x, pak pro pravděpodobnostní (věrohodnostní) funkci platí: L(l; x) = f(x) (4.2) Lineární model úlohy zapíšeme ve tvaru: A x = l + ε, (4.3) a T 1 x 1 a T 2 x 2 A =, x =, (4.4).. a T n x u kde x je vektor neznámých parametrů, l je vektor měření, ε je vektor skutečných chyb, A je matice lineárních (linearizovaných) vztahů mezi měřením a neznámými parametry. Aby šlo o úlohu s vyrovnáním, musí platit, že počet měření n je větší než počet neznámých u. Měření jsou vzájemně nezávislá. Rovnice pozorování pro měření l i má tvar: l i + ε i = a T i x (4.5) Neznámé parametry ve vektoru x jsou určovány metodou maximální věrohodnosti, jestliže hustota pravděpodobnosti p(l i ) pozorování l i je úměrná funkci f(l i, x), tedy platí: p(l i ) f(l i, x) (4.6) Hustota pravděpodobnosti p(l) pro nezávislá měření je pak: n p(l) f(l i, x) = f(l 1, x) f(l 2, x)... f(l n, x) (4.7) i=1 41
43 4. ROBUSTNÍ TRANSFORMACE Nutným předpokladem pro aplikaci metody maximální věrohodnosti je znalost rozdělení pravděpodobností. Předpokládáme dále, že měření mají normální rozdělení N(A x, σ 2 E). Pro pravděpodobnostní funkci potom platí: L(l; x, σ 2 ) = 1 (2πσ 2 ) ε T ε e n/2 2σ 2 (4.8) Požadujeme maximalizovat věrohodnost (pravděpodobnost) odhadu. Úloha se tedy dále řeší diferenciací výrazu 4.8 podle neznámých x a směrodatných odchylek σ 2 a položením získaných výrazů rovných nule. Vzhledem k vlastnostem funkce normálního rozdělení i věrohodnostní funkce se však častěji derivuje logaritmus této funkce, což je z hlediska analytických výpočtů jednodušší. ln L(l; x, σ 2 ) = n 2 ln (2π) n 2 σ2 1 2σ 2 εt ε (4.9) Pro obdržení nejvěrohodnějšího odhadu tedy musíme maximalizovat výraz: n ln f(l i, x) (4.10) i=1 nebo minimalizovat n ln f(l i, x) (4.11) i=1 Jsou-li měření náhodným výběrem z normálního rozdělení pravděpodobností, obdržíme řešení metody nejmenších čtverců, resp. nejlepšího nestranného odhadu. Neznámé parametry chceme určit metodou robustního odhadu, předpoklad normálního rozdělení měření tedy není splněn a odhadová funkce 4.11 musí být proto nahrazena funkcí vhodnější. Huber [17] pro výpočet tzv. M-odhadů zavádí odhadovou funkci ρ(l i, g i (x)), kde g i (x) je funkce neznámých parametrů. Robustní odhad poté obdržíme minimalizací výrazu: Derivace ψ(l i, x) odhadové funkce ρ(l i, g i (x)): ψ(l i, x) = Odhad ^x neznámých parametrů x získáme z výrazu: n i=1 n ρ(l i, g i (x)) (4.12) i=1 g i (x) ρ(l i, g i (x)) (4.13) ψ(l i, ^x) g i(^x) ^x k = 0 pro k {1,..., u} (4.14) Robustní M-odhad nalezneme pomocí funkce ψ(l i, x). Nutnou a postačující podmínkou pro robustnost odhadu je, aby funkce ψ(l i, x) byla ohraničená, neboť tato funkce 42
44 4. ROBUSTNÍ TRANSFORMACE je úměrná influenční funkci [18]. Influenční funkce popisuje efekt dalšího pozorování na odhad. Dále zavedeme pojem normované chyby, tj. podíl chyby a příslušné směrodatné odchylky měření: ^ε i = at i x l i = ε i (4.15) σ i σ i Odhadem skutečných chyb ε i jsou opravy v i, normované opravy jsou poté definovány: Z toho plyne odhadová funkce: i=1 ^v i = at i ^x l i σ i = v i σ i (4.16) ρ(l i, g i (x) = ρ(^ε i ) (4.17) Protože platí g i (^x) = a T i ^x, můžeme výpočet odhadu upravit na tvar: ( ) n a T ψ i ^x l i aik = 0 pro k {1,..., u} (4.18) σ i σ i a dále: n ( ) vi ψ i=1 σ i aik σ i = 0 pro k {1,..., u} (4.19) Pro metodu MNČ zapíšeme hustotu pravděpodobnosti normálního rozdělení: φ(x) = 1 σ 2π (x E(x)) 2 e 2σ 2, φ(ε) = 1 σ 2π ε 2 e 2σ 2 (4.20) Funkce ρ (bez konstant, po aplikaci logaritmu): Po derivaci: ( ) ε ψ = σ ( ρ(ε) = ln e 2( 1 σ) 2) ε = 1 ( ) ε 2 (4.21) 2 σ ( ( ) ) 2 1 ε 2 σ ( ) ε σ Minimalizační podmínku potom zapíšeme: n i=1 ε i σ i aik σ i = = ε σ = ε σ n i=1 (4.22) ε i σ i aik σ i = 0 (4.23) Skutečné chyby nejsou známy a musí být tedy nahrazeny jejich odhadem opravami. Řešení systému normálních rovnic metodou nejmenších čtverců je výpočetně jednoduché. Aby však bylo možné tento výpočet použít, je nutné normované opravy ^v i formálně vynásobit korekčním koeficientem w i. Platí tedy: n ( ) vi ψ i=1 σ i aik σ i = n i=1 w i vi σ i aik σ i = 0 (4.24) 43
45 4. ROBUSTNÍ TRANSFORMACE a odtud: ( ) vi ψ aik (4.25) σ i σ i σ i σ i Korekční člen w i představuje určitou váhu měření l i a jeho velikost je závislá na = w i vi σ i aik σ i w i = ψ velikosti normované opravy ^v i, tedy w i = w i (v i, σ i ). Po zavedení korekčního členu můžeme psát: 1 σ 2 ( vi ) / ( ) vi n w i v i a ik = 0 pro k {1,..., u} (4.26) i=1 Dále lze definovat diagonální váhovou matici W : a řešit normální rovnice ve tvaru: W = diag(w 1,..., w n ) (4.27) A T W A ^x = A T W l (4.28) Váhy w i závisí na opravách v i a tedy i na odhadu ^x neznámých parametrů x. Z toho plyne, že odhad musí být určován iterativně. Jako první aproximace ^x (0) je zpravidla volen výsledek metody nejmenších čtverců. Řešení v (m + 1)-ní iteraci: ^x (0) = (A T A) 1 A T l (4.29) ^x (m+1) = (A T W (m+1) A) 1 A T W (m+1) l, (4.30) kde a W (m+1) = diag(w (m+1) 1,..., w n (m+1) ), w (m+1) i = ψ v(m) i σ i / v(m) i (4.31) σ i v (m) = A T ^x (m) l (4.32) Konvergence robustního odhadu 4.30 je dokázána v [17]. 4.3 Huberův M-odhad Jestliže jsou pozorování l i normálně rozdělena, lze funkci rozdělení pravděpodobnosti zapsat (bez uvážení konstantních členů): f(ε) = e ε2 2 (4.33) 44
46 4. ROBUSTNÍ TRANSFORMACE a odhadovou funkci: ρ(ε) = ε2 2 Pro derivaci ψ(ε) odhadové funkce platí: a tedy váha ψ(ε) = ρ(ε) ε (4.34) = ε (4.35) w i = ψ(ε) = 1 (4.36) ε Místo výrazu 4.12 se pak minimalizuje: 1 n ε 2 2σ 2 i (4.37) i=1 Minimalizací tohoto výrazu obdržíme řešení nejlepšího nestranného odhadu, resp. metody nejmenších čtverců, resp. metody maximální věrohodnosti. Nejedná se o odhad robustní, neboť funkce funkce ψ(ε) = ε neohraničeně roste s rostoucím ε. Váha w i = 1 je konstantní a odhad tedy získáme bez iterací, přímo ze vztahu Obr. 4.1: Odhad metodou nejmenších čtverců tvar funkce ψ Při odvození robustního odhadu vychází Huber [17] z normálního rozdělení náhodné veličiny. Jeho řešení je založeno na nahrazení okrajových částí funkce normálního rozdělení pravděpodobností Laplaceovým rozdělením (speciální formou exponenciálního rozdělení). Tím dojde k ohraničení vlivové funkce ψ(ε) a dosažení robustnosti odhadu. Takové řešení předpokládá větší pravděpodobnost výskytu odlehlých měření na okrajích rozdělení. Funkce hustoty pravděpodobnosti pro Huberův M-odhad je: f(ε) = e ε2 2 pro ε c (4.38) f(ε) = e c ε +c2 /2 pro ε > c, (4.39) 45
47 4. ROBUSTNÍ TRANSFORMACE kde c je konstanta závisející na předpokládaném množství kontaminace měřených dat odlehlými hodnotami. Podle [17] se pro přibližně 4 % odlehlých měření volí c = 1,5, pro méně než 1 % je stanoveno c = 2,0. V obecném případě je konstanta c zpravidla volena v tomto intervalu. Odhadová funkce má tvar: Pro vlivovou funkci ψ platí: ρ(ε) = ε2 2 ρ(ε) = c ε c2 2 pro ε c (4.40) pro ε > c (4.41) ψ(ε) = ε pro ε c (4.42) ψ(ε) = c ε ε pro ε > c (4.43) Obr. 4.2: Huberův robustní M-odhad tvar funkce ψ Jak je zřejmé z obrázku 4.2, funkce ψ je ohraničená, neboť pro ε > c nabývá konstantní hodnoty. Huberův M-odhad je tedy robustním odhadem. Váhy se volí podle předpisu: w (m) i = 1 pro v (m 1) i c σ (4.44) c σ w (m) i = v (m 1) i pro v (m 1) i > c σ (4.45) Toto odvození platí pouze pro případ, kdy jsou všechna měření stejně přesná. Jsouli zavedeny váhy měření, jak je v geodetických úlohách běžné, je zde uvedená váha w (m) i násobný koeficient (tzv. robustní změna váhy), kterým se původní váha změní. 46
48 4. ROBUSTNÍ TRANSFORMACE Koeficient c v takovém případě slouží k hodnocení velikosti normované opravy ^v i (viz 4.16), nikoliv opravy s libovolnou variancí. V tabulce 4.1 je uveden přehled funkcí užitých v Huberově M-odhadu, tj. odhadová funkce ρ(^v), vlivová funkce ψ(^v) a váhová funkce w(^v). Funkce jsou již vyjádřeny v závislosti na normované opravě měření ^v i 4.16 a jsou proto zobecněním jim odpovídajících vztahů odvozených výše. Tab. 4.1: Huberův M-odhad přehled funkcí (odhadová, vlivová, váhová) ρ(^v) ψ(^v) w(^v) velikost ^v 1 2 ^v2 ^v 1 ^v c c ^v 1 2 c2 c sign(^v) c/ ^v ^v > c Z tvaru váhové funkce w(^v) lze vyvodit, že nepřesáhne-li hodnota normované opravy ^v stanovený interval c, +c, není vliv příslušného měření na stanovení odhadu nijak redukován a toto měření se ve výpočtu uplatní svou plnou vahou. Překročí-li normovaná oprava stanovený interval, váha měření s takovou opravou hyperbolicky klesá. 4.4 Odhad pomocí L p -normy Odvození tohoto typu robustního odhadu vychází z Huberova odvození. Jako funkce hustoty pravděpodobnosti pro pozorování je však nyní volena: f(ε) = e ε p pro p 1, (4.46) která pro p = 1 popisuje Laplaceovo rozdělení a pro p = 2 normální rozdělení (s ohledem na vztah 4.6 nejsou uvažovány konstantní členy funkce). Odtud plyne odhadová funkce: ρ(ε) = ε p (4.47) Derivací odhadové funkce ρ(ε) získáme vlivovou funkci ψ(ε), kterou opět zapíšeme bez uvážení konstant: ψ(ε) = ε p 2 ε (4.48) Ze vztahu 4.25 určíme váhu: w i = ε p 2 (4.49) 47
49 4. ROBUSTNÍ TRANSFORMACE Funkce hustoty pravděpodobnosti 4.46 vede k odhadu pomocí L p -normy s odhadovou funkcí: ( n ) 1/p v p = v i p, (4.50) i=1 která musí být minimalizována. Pro p = 1 se jedná o L 1 -normu, kde je minimalizována suma absolutních hodnot chyb (oprav). Vlivová funkce ψ(ε) je ohraničená, jedná se tedy o robustní odhad. Váhy v m-té iteraci mají tvar: w (m) i = 1 v (m 1) i (4.51) Obr. 4.3: Odhad pomocí L 1 -normy tvar funkce ψ Jak uvádí [15], tento odhad je extrémně robustní. V souboru o sudém počtu měření n lze L 1 -normou odhalit až n 1 chyb (odlehlých hodnot). Obsahuje-li soubor 2 lichý počet měření, dosahuje počet detekovaných chyb až maximální možné hodnoty n 2 (zaokrouhleno dolů). Je-li počet odlehlých hodnot v souboru vyšší (nadpoloviční), nelze již z principu odlišit správná měření od odlehlých. Odhad pomocí L 2 -normy vede k metodě nejmenších čtverců, která, stejně jako další odhady plynoucí z volby p 2, není robustní. Aby byl tedy odhad pomocí L p -normy robustní, musí být splněna podmínka 1 p < 2. Stejně jako pro Huberův M-odhad bude i zde uveden přehled funkcí užitých L 1 -normou. Další druhy užívaných M-odhadů lze nalézt v [11] nebo [15]. 48
50 4. ROBUSTNÍ TRANSFORMACE Tab. 4.2: L 1 -norma přehled funkcí (odhadová, vlivová, váhová) ρ(^v) ψ(^v) w(^v) ^v sign(^v) 1/ ^v 4.5 Robustní transformace výpočet V této kapitole budou představeny variantní metody výpočtu robustní transformace jednotlivých etap do soustavy etapy základní. V popisu navržené metody bylo předesláno, že transformační klíč bude určen metodou robustního odhadu. Konkrétně byl zvolen odhad pomocí L 1 -normy, který poskytuje extrémní robustnost a dokáže tak detekovat až maximální možný počet odlehlých hodnot v souboru měření [15]. Jelikož vyhodnocujeme posuny v polohové síti, užijeme rovinnou lineární transformaci, která je obecně definována čtyřmi transformačními parametry (2 posuny, úhel otočení, změna měřítka). Rozměr sítě je však v každé etapě definován měřením a požadujeme proto jeho zachování. Rovinnou lineární transformaci tedy dále specifikujeme jako shodnostní. Úkolem je nyní robustním odhadem pomocí L 1 -normy určit pouze tři transformační parametry shodnostní rovinné transformace (2 posuny, úhel otočení). Jak bude v dalším zpracování ukázáno, podstatou naší aplikace robustního odhadu nebude zjištění odhadu samotného (tj. robustní odhad transformačních parametrů), nýbrž identifikace těch bodů (souřadnic), které jsou při určení tohoto odhadu vyhodnoceny jako odlehlé. Tyto body ze souboru identických bodů vyloučíme. Tím pro každou robustní transformaci obdržíme redukovaný (očištěný) soubor identických bodů. Cílem je však vyhledat sadu takových bodů, které jsou považovány za stabilní při všech robustních transformacích. Z takto vybrané sady následně určíme definitivní transformační klíč metodou nejmenších čtverců. Věnujme se nyní počtu identických bodů. Obecným problémem etapových měření provedených ve vztažné polohové síti Pražského hradu je, že metodika měření nebyla v jednotlivých etapách důsledně dodržována. Jedná se především o podstatně různé rozsahy provedených měření (viz kapitola 3.3), upřednostnění jednoho typu měření před druhým (z toho plyne neúplné zaměření polygonových pořadů v etapách jaro 2009 a podzim 2009) a užití různé přístrojové techniky. Dosavadními výsledky jsou soubory souřadnic bodů a jejich směrodatné odchylky (resp. úplné kovarianční matice) plynoucí z vyrovnání sítě v jednotlivých etapách. 49
51 4. ROBUSTNÍ TRANSFORMACE V těchto souborech je nutné vyhledat v ideálním případě ty body, které byly součástí zaměření ve všech etapách. Při selekci těchto bodů se různost rozsahu zaměření sítě v jednotlivých etapách stává limitujícím faktorem. Výsledkem selekce bodů je následující: 11 bodů zaměřených ve všech osmi etapách, tj. body 501, 506, 507, 512, 524, 552, 553, 1003, 1005, 1011, body zaměřené právě v sedmi etapách (od 2008p včetně), tj. body 513, 531, 1001, body zaměřené právě v šesti etapách (do 2010p včetně), tj. body 504, 505, 541 Body zaměřené v méně než šesti etapách nebyly při selekci identických bodů uvažovány. Z tohoto výčtu vyplývá, že souvislé vyhodnocení je možné provést pro 11 identických bodů. V takovém případě je vhodné za základní etapu zvolit tzv. nultou etapu, tj. etapu 2008j. Pokud bychom však za základní etapu zvolili etapu 2008p, soubor identických bodů by se tím pro většinu transformací výrazně rozšířil. K robustní transformaci 2008p do soustavy etapy 2008j bychom tak využili dostupných 11 identických bodů a k transformaci všech ostatních etap do soustavy 2008p by bylo k dispozici již 15 identických bodů. Na základě výše zmíněných informací byly zvoleny dvě základní etapy, 2008j a 2008p. Robustní transformaci etapy 2008p do soustavy první základní etapy 2008j provedeme z důvodu menšího rozsahu zaměření nulté etapy pomocí 11 identických bodů (501, 506, 507, 512, 524, 552, 553, 1003, 1005, 1011, 1012). K robustní transformaci všech následných etap do soustavy druhé základní etapy bude využito 15 identických bodů (501, 506, 507, 512, 513, 524, 531, 552, 553, 1001, 1002, 1003, 1005, 1011, 1012). Podle způsobu volby vah měření (souřadnic identických bodů) budou v následujících kapitolách představeny 3 varianty výpočtu robustní transformace Verze výpočtu 1 V první variantě výpočtu jsou váhy měření přisuzovány na základě jednoduchého předpokladu, že všechny identické body (resp. všechny body sítě) jsou v rámci jedné etapy určeny s přibližně stejnou přesností. 50
52 4. ROBUSTNÍ TRANSFORMACE Rovnice rovinné shodnostní lineární transformace má tvar: X = R(ω) x + T (4.52) a po rozepsání jednotlivých členů: X cos ω = Y sin ω sin ω x + T x, (4.53) cos ω y T y kde X je vektor souřadnic identického bodu ve výstupní soustavě, tj. v soustavě základní etapy, x je vektor souřadnic identického bodu ve vstupní soustavě, tj. v soustavě transformované etapy, R(ω) je matice rovinné rotace o úhel ω a T je vektor translací ve směru jednotlivých os. K dispozici je nadbytečný počet identických bodů (15, resp. 11), transformační klíč bude určen metodou robustního odhadu pomocí L 1 -normy. Ve smyslu vyrovnání jsou souřadnice X identických bodů ve výstupní soustavě měřením, souřadnice x identických bodů ve vstupní soustavě konstantami a vektor Φ = (T x, T y, ω) T obsahuje určované neznámé parametry. Při vyrovnání jednotlivých etap byla síť umístěna do prostoru vždy stejným způsobem. Můžeme tedy odůvodněně předpokládat, že transformační parametry nabývají velmi malých hodnot. Za přibližné hodnoty neznámých parametrů proto pokládáme: Φ 0 = (T x, T y, ω) T 0 = 0 (4.54) Matice plánu A, tj. matice parciálních derivací funkčních vztahů 4.53 podle jednotlivých neznámých parametrů Φ: X 1 X 1 X 1 T x T y ω 1 0 ( x 1 sin ω 0 y 1 cos ω 0 ) Y 1 Y 1 Y 1 T x T y ω 0 1 (x 1 cos ω 0 y 1 sin ω 0 ) X 2 X 2 X 2 T x T y ω 1 0 ( x 2 sin ω 0 y 2 cos ω 0 ) Y A = 2 Y 2 Y 2 T x T y ω = 0 1 (x 2 cos ω 0 y 2 sin ω 0 ) X n X n X n T x T y ω 1 0 ( x n sin ω 0 y n cos ω 0 ) Y n Y n Y n 0 1 (x T x T y ω n cos ω 0 y n sin ω 0 ) (4.55) 51
53 4. ROBUSTNÍ TRANSFORMACE Vektor redukovaných měření l : x 1 cos ω 0 y 1 sin ω 0 + T x0 x 1 sin ω 0 + y 1 cos ω 0 + T y0 x 2 cos ω 0 y 2 sin ω 0 + T x0 l = X(Φ 0 ) l = x 2 sin ω 0 + y 2 cos ω 0 + T y0. x n cos ω 0 y n sin ω 0 + T x0 x n sin ω 0 + y n cos ω 0 + T y0 X 1 Y 1 X 2 Y 2. X n Y n (4.56) S ohledem na přibližné hodnoty Φ 0 neznámých parametrů můžeme pro matici plánu A a vektor redukovaných měření l konkrétně psát: 1 0 y 1 x 1 X x 1 y 1 Y y 2 x 2 X 2 A = 0 1 x 2, l = y 2 Y 2 (4.57) y n x n X n 0 1 x n y n Y n Nyní již k volbě vah měření. V úvodu kapitoly bylo předesláno, že tato varianta výpočtu uvažuje stejnou přesnost všech identických bodů v rámci dané etapy. Označme kovarianční matici sady identických bodů ve výstupní soustavě Σ X a kovarianční matici sady identických bodů ve vstupní soustavě Σ x. Z vyrovnání jednotlivých etap jsou k dispozici směrodatné odchylky souřadnic bodů, resp. jejich plné kovarianční matice. Přesnost bodů unifikujeme výpočtem aritmetického průměru známých směrodatných odchylek souřadnic. Tím pro diagonální kovarianční matice Σ X a Σ x dostáváme: Σ X = σ X 2 E, Σ x = σ x 2 E, (4.58) kde E je jednotková matice a průměrné směrodatné odchylky souřadnic n identických bodů vypočteme: σ 2 X = ni=1 (σ Xi + σ Yi ), σ x 2 = 2n ni=1 (σ xi + σ yi ) 2n (4.59) 52
54 4. ROBUSTNÍ TRANSFORMACE Měřením l jsou souřadnice X bodů ve výstupní soustavě s diagonální kovarianční maticí Σ X. Souřadnice x bodů ve vstupní soustavě ovšem nejsou bezchybné, nýbrž určené s průměrnou přesností vyjádřenou diagonální kovarianční maticí Σ x. Abychom uvážili přesnost obou soustav, kovarianční matice sečteme 1. Celkovou přesnost měření l vyjádříme diagonální kovarianční maticí Σ ll, pro kterou platí: Σ ll = Σ X + Σ x = ( σ X 2 + σ x) 2 E (4.60) Měření l i má tedy směrodatnou odchylku σ i = σ X 2 + σ x. 2 Požadujeme dále, aby váha p i každého měření l i byla rovna jedné, tedy aby matice vah P byla maticí jednotkovou: p i = σ2 0 σ 2 i = 1 P = E (4.61) Odtud pro každou transformaci odvodíme volbu apriorní jednotkové směrodatné odchylky σ 0. p i = σ2 0 = 1 σ σi 2 0 = σ i = σ X 2 + σ x 2 (4.62) Takto stanovená apriorní jednotková směrodatná odchylka bude použita k pozdějšímu výpočtu směrodatných odchylek oprav pro účel vyhledání odlehlých měření (viz dále). Robustní odhad neznámých parametrů probíhá iteračně. První aproximaci přírůstků k neznámým určíme metodou nejmenších čtverců: dφ (0) = (A T A) 1 A T l (4.63) Následně se vypočtou opravy v i měřených veličin l i a z nich normované opravy ^v i. V obecné m-té iteraci platí: v (m) = A dφ (m) + l (4.64) Řešení v (m + 1)-ní iteraci: ^v (m) i = v(m) i (4.65) σ i dφ (m+1) = (A T W (m+1) A) 1 A T W (m+1) l, (4.66) 1 Součet kovariančních matic souřadnic dvou obecně různých soustav nelze provést paušálně. Tato úprava a podmínky její správné aplikace budou blíže objasněny ve verzi výpočtu 2, viz kapitola
55 4. ROBUSTNÍ TRANSFORMACE kde W je matice robustních změn vah, kterou v (m + 1)-ní iteraci určíme: W (m+1) = diag(w (m+1) 1,..., w (m+1) 2n ), w (m+1) i = 1 ^v (m) i (4.67) Ukončení iteračního cyklu je podmíněno dostatečnou stabilizací výpočtu. Podmínku je možné vyjádřit více způsoby. Např. podle [19] lze dostatečné ustálení výpočtu vyjádřit splněním nerovnosti: max( w (m+1) w (m) ) Δ, (4.68) kde Δ je maximální tolerovaná změna robustní váhy. Konvergenci výpočtu je možné názorněji sledovat podle vývoje aposteriorní jednotkové směrodatné odchylky ^σ 0. Tu v každé iteraci vypočteme: vt W v ^σ 0 =, (4.69) n kde n je počet nadbytečných měření. Je-li při transformaci počet identických bodů n = 15 a počet neznámých parametrů u = 3, je počet stupňů volnosti n = 2n u = 27. Při transformaci s 11 identickými body je n = 19. Pomocí ^σ 0 můžeme potom podmínku ukončení cyklu vyjádřit: ^σ (m+1) 0 ^σ (m) 0 Δ, (4.70) kde Δ je maximální tolerovaná změna aposteriorní jednotkové směrodatné odchylky. V našem případě byl počet iterací nastaven manuálně na hodnotu 20. Stabilizace výpočtu byla posuzována procentuálním poklesem aposteriorní jednotkové směrodatné odchylky ^σ (m+1) 0 vůči hodnotě ^σ (m) 0 z předchozí iterace. Vývoj ^σ 0 v jednotlivých iteracích byl současně graficky vizualizován. Grafy vývoje hodnoty ^σ 0 jsou uvedeny v příloze A. Pro vyhledání odlehlých měření na základě testování velikosti oprav určíme kovarianční matici oprav Σ vv. Její odvození vychází z dosazení rovnice 4.63 pro výpočet vyrovnaných neznámých (resp. přírůstků) do rovnice 4.64 pro výpočet oprav měření a následné aplikaci obecného zákona hromadění směrodatných odchylek: v = A dφ + l (4.71) = A(A T P A) 1 A T P l + l (4.72) = [ A(A T P A) 1 A T P E ] l (4.73) ε v = [ A(A T P A) 1 A T P E ] ε l (4.74) Σ vv = [ A(A T P A) 1 A T P E ] Σ l l [ A(A T P A) 1 A T P E ] T (4.75) 54
56 4. ROBUSTNÍ TRANSFORMACE Protože dále platí: Σ l l = Σ ll = σ 2 0 P 1, (4.76) obdržíme po roznásobení a úpravě kovarianční matici oprav ve tvaru: Σ vv = σ 2 0 [ P 1 A(A T P A) 1 A T ], (4.77) kde σ 0 je apriorní jednotková směrodatná odchylka, v této konkrétní verzi výpočtu určená podle Směrodatná odchylka opravy σ vi měřené veličiny l i je: σ vi = kde Σ vi v i jsou diagonální prvky matice Σ vv. Následně jsou stanoveny mezní hodnoty oprav: Σ vi v i, (4.78) v Mi = u p σ vi, (4.79) kde u p je normovaná hodnota náhodné veličiny s normálním rozdělením pravděpodobností stanovená pro hladinu významnosti α. V oboustranných testech jednorozměrné veličiny prováděných při tomto výpočtu je voleno u p = 2,57 pro hladinu významnosti α = 1 %. Dále se provede porovnání a platí-li: v i v Mi, (4.80) je měření l i považováno za odlehlé a ze souboru měřených hodnot vyloučeno. Po vyloučení všech takto identifikovaných odlehlých hodnot by měl soubor splňovat podmínku normality. Kompletní výpočet robustní transformace byl proveden pomocí vlastního programu v jazyku GNU Octave. Zdrojové kódy programu a jím užívaných funkcí jsou uloženy na přiloženém CD. V příloze A jsou v tabulkách A.1 až A.7 uvedeny podstatné výsledky robustní transformace jednotlivých etap E i do soustavy etapy základní, tj. E 0 nebo E 1. Těmito výsledky jsou hodnoty oprav měření ze stabilizovaného výpočtu robustního vyrovnání (opravy v Xi, v Yi souřadnic bodů ve výstupní soustavě), jejich směrodatné odchylky σ vxi, σ vy i a příslušné mezní hodnoty oprav v MXi, v MYi. V posledních dvou sloupcích tabulek A.1 až A.7 (test v Xi, test v Yi ) je booleovskou algebrou vyjádřeno splnění kritéria v i v Mi. Je-li výsledkem porovnání 0, 55
57 4. ROBUSTNÍ TRANSFORMACE je souřadnice považována za odlehlou a příslušný bod ze souboru identických bodů vyloučen. Nutnou a postačující podmínkou pro vyloučení identického bodu tedy je, aby alespoň jedna jeho souřadnice byla na základě kritéria 4.80 považována za odlehlou hodnotu. V tabulce 4.3 je uvedeno užívané označení etap. Tab. 4.3: Označení jednotlivých etap měření sítě etapa 2008j 2008p 2009j 2009p 2010j 2010p 2012j 2012p označení E 0 E 1 E 2 E 3 E 4 E 5 E 6 E 7 transf. do E 0 E Verze výpočtu 2 Výpočetní model druhé verze je v principu velmi podobný verzi první. Váhy měření však nejsou unifikovány výpočtem aritmetického průměru směrodatných odchylek souřadnic. Souřadnicím je ponechána původní přesnost vzešlá z vyrovnání jednotlivých etap. Odvození robustních M-odhadů provedené v kapitole 4.2 je provedeno s předpokladem nezávislosti jednotlivých měření; uvažovány jsou tedy opět pouze diagonální kovarianční matice souřadnic identických bodů. Užití plných kovariančních matic souřadnic bodů by vyžadovalo aplikaci podstatně složitějšího modelu robustního odhadu se závislými pozorováními. O tomto tématu pojednává např. [20] nebo [21]. Měřením l jsou nyní souřadnice X bodů ve výstupní soustavě (soustava základní etapy E 0 nebo E 1 ) s diagonální kovarianční maticí Σ X. Přesnost souřadnic x bodů ve vstupní soustavě (soustava transformované etapy) je charakterizována diagonální kovarianční maticí Σ x. Kovarianční matice mají tvar: σx σx σy σ 2 y Σ X = , Σ x = σ 2 X n σ 2 x n 0 (4.81) σ 2 Y n σ 2 y n Výpočetní model však umožňuje přisoudit přesnost pouze jedné sadě souřadnic, tj. té sadě, jejíž souřadnice jsou při vyrovnání měřením l. Abychom uvážili přesnost obou soustav, obě známé kovarianční matice sečteme. 56
58 4. ROBUSTNÍ TRANSFORMACE V našem případě jsme oprávněni tento krok udělat přímo, bez jakýchkoliv předchozích úprav. Při vyrovnání jednotlivých etap byla síť umístěna do prostoru vždy stejným způsobem a systémy jsou tedy ve všech etapách shodně orientovány. Jak plyne z odvození transformace kovarianční matice souřadnic (viz kapitola 2.4.1), je tento úkon závislý pouze na vzájemném stočení systémů. Závěrem lze říci, že pokud by jednotlivé etapy byly řešeny (vyrovnány) s obecně různým umístěním sítě do prostoru (resp. různou orientací), bylo by nutné nejprve kovarianční matici Σ x souřadnic x transformovat do systému souřadnic X podle postupu popsaného v kapitole a teprve poté kovarianční matice sečíst. Výsledná matice vah P vstupující do robustního vyrovnání má tvar: P = σ 2 0 (Σ X + Σ x ) 1, (4.82) kde σ 0 je apriorní jednotková směrodatná odchylka. Její hodnota byla v této verzi výpočtu zvolena σ 0 = 0,001. První aproximaci přírůstků k neznámým určíme metodou nejmenších čtverců: dφ (0) = (A T P A) 1 A T P l (4.83) Opravy v i měřených veličin l i a normované opravy ^v i v obecné m-té iteraci: v (m) = A dφ (m) + l (4.84) ^v (m) i = v(m) i (4.85) σ i Matice robustních změn vah W je diagonální maticí, jejíž členy w i jsou násobnými koeficienty vah původních, resp. vah z předchozí iterace výpočtu. Řešení robustního odhadu v (m + 1)-ní iteraci je tedy: dφ (m+1) = (A T W (m+1) P A) 1 A T W (m+1) P l, (4.86) kde korekční členy w i matice robustních změn vah W určíme jako funkci normovaných oprav ^v i z předchozí iterace výpočtu: W (m+1) = diag(w (m+1) 1,..., w (m+1) 2n ), w (m+1) i = 1 ^v (m) i (4.87) Dále v každé iteraci určíme aposteriorní jednotkovou směrodatnou odchylku ^σ 0 : ^σ 0 = vt W P v n, (4.88) 57
59 4. ROBUSTNÍ TRANSFORMACE kde n je počet nadbytečných měření. Posouzení dostatečné stabilizace výpočtu provedeme stejně jako v první verzi, tj. podle procentuálního poklesu aposteriorní jednotkové směrodatné odchylky ^σ (m+1) 0 vůči hodnotě ^σ (m) 0 z předchozí iterace a dále také podle grafické vizualizace vývoje hodnoty ^σ 0. Grafy vývoje hodnoty ^σ 0 jsou uvedeny v příloze B. Posledním krokem je testování velikosti oprav pomocí jejich mezních hodnot a z toho plynoucí identifikace odlehlých měření. Testování provedeme stejným způsobem jako v první verzi výpočtu, pomocí vztahů 4.77 až Tato verze výpočtu byla taktéž provedena pomocí vlastního programu v jazyku GNU Octave. Zdrojové kódy jsou uloženy na přiloženém CD. V příloze B jsou v tabulkách B.1 až B.7 uvedeny výsledky robustní transformace jednotlivých etap do soustavy etapy základní Verze výpočtu 3 Ve třetí a nejobecnější verzi výpočtu je použit exaktní model transformace s uvážením přesností obou soustav. Princip tohoto výpočetního modelu je následující. Měřením jsou nyní ve vyrovnání souřadnice identických bodů v obou soustavách. Souřadnice jedné ze soustav jsou přitom současně neznámými parametry. Rovnice pozorování jsou proto dvojího typu: 1 x i 1 y i = 2 x i 2 y i = X i (4.89) Y i T x + R(ω) X i, (4.90) T y Y i kde ( 1 x i, 1 y i ) T jsou souřadnice ve vstupní soustavě, tedy soustavě, ze které je transformováno do soustavy základní etapy. Souřadnice ( 2 x i, 2 y i ) T jsou souřadnice ve výstupní soustavě, tj. v soustavě základní etapy, do které je transformováno. Souřadnice (X i, Y i ) T jsou spolu s prvky transformačního klíče dalšími neznámými parametry. Vektor všech neznámých Φ a vektor měření l proto zapíšeme následovně: Φ = (T x, T y, ω, X 1, Y 1, X 2, Y 2,..., X n, Y n ) T (4.91) l = ( 1 ) x 1, 1 y 1,..., 1 x n, 1 y n, 2 x 1, 2 y 1,..., 2 x n, 2 T y n (4.92) 58
60 4. ROBUSTNÍ TRANSFORMACE Matici plánu A sestavíme standardním způsobem. Její submatice A 1 pro funkční vztahy 4.89 má tvar (již po provedení parciálních derivací): A (2n u) 1 = T x T y ω X 1 Y 1 X 2 Y 2 X n Y n 1 x y x y , (4.93) x n y n kde v rozměru (2n u) matice A 1 je n počet identických bodů a u je počet neznámých parametrů ve vektoru Φ. Pro zjednodušení zápisu submatice A 2 zavedeme pro prvky rotační matice R následující označení: cos ω R = sin ω sin ω = r 11 r 12 (4.94) cos ω r 21 r 22 Dále vyjádříme parciální derivace funkčních vztahů 4.90 podle úhlu otočení ω: ( 2 x i ) ω ( 2 y i ) ω = X i sin ω Y i cos ω (4.95) = X i cos ω Y i sin ω (4.96) Submatice A 2 pro funkční vztahy 4.90 má potom tvar (již po provedení parciálních derivací): A (2n u) 2 = T x T y ω X 1 Y 1 X 2 Y 2 X n Y n 2 ( x x 1 ) r ω 11 r ( y y 1 ) r ω 21 r ( x x 2 ) 0 0 r ω 11 r y 2 ( y 2 ) 0 0 r ω 21 r , (4.97) ( x n x n) r ω 11 r 12 2 ( y n y n) r ω 21 r 22 kde rozměr (2n u) submatice A 2 odpovídá rozměru submatice A 1. Výsledná matice plánu je: A (4n u) = A 1 (4.98) A 2 59
61 4. ROBUSTNÍ TRANSFORMACE Transformační klíč bude určován metodou robustního odhadu s předpokladem nezávislosti měření. Uvažujeme proto dále pouze diagonální kovarianční matice souřadnic identických bodů. Kovarianční matice Σ1 x souřadnic vstupní soustavy a Σ2 x souřadnic výstupní soustavy mají tvar: σ 21 x σ 22 x σ 21 y σ 22 y Σ1 x = , Σ2 x = (4.99) 0 0 σ 21 x n σ 22 x n σ 21 y n σ 22 y n Výslednou kovarianční matici všech měření zapíšeme: Σ ll = diag (Σ1 x, Σ2 x) (4.100) Jelikož měřením l jsou ve vyrovnání souřadnice identických bodů v obou soustavách, zapíšeme váhovou matici následovně: 1 P (4n 4n) = σ0 2 Σll 1 = σ0 2 Σ1 x 0, (4.101) 0 Σ2 x kde σ 0 je apriorní jednotková směrodatná odchylka a 0 je nulová matice stejného rozměru jako matice Σ1 x a Σ2 x, tedy (2n 2n). Apriorní jednotková směrodatná odchylka je v této verzi výpočtu volena σ 0 = 0,001. Jak již bylo zmíněno v předchozích verzích výpočtu, síť byla při vyrovnání jednotlivých etap umístěna do prostoru vždy stejným způsobem a lze tedy předpokládat, že transformační parametry nabývají velmi malých hodnot. Přibližné hodnoty neznámých proto volíme následovně: Φ 0 = (T x, T y, ω, X 1, Y 1, X 2, Y 2,..., X n, Y n ) T 0 (4.102) = ( 0, 0, 0, 1 x 1, 1 y 1, 1 x 2, 1 y 2,..., 1 x n, 1 y n ) T (4.103) Vektor redukovaných měření je z důvodu dvojího typu rovnic pozorování složen ze dvou subvektorů: 1 l l 1 x(φ = = 0 ) 1 l (4.104) 2 l 2 x(φ 0 ) 2 l Výpočet robustního odhadu neznámých parametrů probíhá stejně jako v předchozích verzích. První aproximaci přírůstků k neznámým určíme metodou nejmenších čtverců: dφ (0) = (A T P A) 1 A T P l (4.105) 60
62 4. ROBUSTNÍ TRANSFORMACE Opravy v i měřených veličin l i a normované opravy ^v i v obecné m-té iteraci: v (m) = A dφ (m) + l (4.106) ^v (m) i = v(m) i, (4.107) σ i kde směrodatnou odchylku měření l i určíme z i-tého diagonálního prvku kovarianční matice Σ ll jako: σ i = Σ li l i (4.108) Matice robustních změn vah W je diagonální maticí, jejíž členy w i jsou násobnými koeficienty vah původních, resp. vah z předchozí iterace výpočtu. Řešení robustního odhadu v (m + 1)-ní iteraci je tedy: dφ (m+1) = (A T W (m+1) P A) 1 A T W (m+1) P l, (4.109) kde korekční členy w i matice robustních změn vah W určíme jako funkci normovaných oprav ^v i z předchozí iterace výpočtu: W (m+1) = diag(w (m+1) 1,..., w (m+1) 2n ), w (m+1) i = 1 ^v (m) i (4.110) Dále v každé iteraci určíme aposteriorní jednotkovou směrodatnou odchylku ^σ 0 : vt W P v ^σ 0 =, (4.111) n kde n je počet nadbytečných měření. Ten určíme následovně. Počet identických bodů při transformaci je obecně n a tedy počet všech měření ve vektoru l je 4n. Počet neznámých parametrů ve vektoru Φ je nyní u = 3 + 2n (počet určovaných prvků transformačního klíče je 3). Z toho plyne, že počet nadbytečných měření je n = 4n (3 + 2n) = 2n 3. Porovnáme-li tedy tento výpočetní model transformace (tj. transformace s uvážením přesností obou soustav) s modelem uplatněným v předchozích verzích výpočtu, je zřejmé, že počet nadbytečných měření zůstává zachován. Tab. 4.4: Srovnání počtů nadbytečných měření v jednotlivých verzích výpočtu počet Verze 1 Verze 2 Verze 3 měření 2n 2n 4n neznámých n n 2n 3 2n 3 2n 3 61
63 4. ROBUSTNÍ TRANSFORMACE Posouzení dostatečné stabilizace výpočtu opět provedeme podle procentuálního poklesu aposteriorní jednotkové směrodatné odchylky ^σ (m+1) 0 vůči hodnotě ^σ (m) 0 z předchozí iterace a dále také podle grafické vizualizace vývoje hodnoty ^σ 0. Robustní odhad neznámých parametrů Φ je tímto stanoven. Zbývá ovšem identifikovat odlehlá měření na základě testování velikosti oprav měřených veličin. V tomto výpočetním modelu jde o úkon mírně komplikovanější než v předchozích verzích výpočtu, neboť vyrovnávanými měřeními jsou souřadnice identických bodů v obou soustavách. Jako odlehlá měření tak mohou být identifikována i měření ze základní etapy, neboli souřadnice identických bodů v soustavě, kterou z hlediska určování relativních změn polohy bodů považujeme za fixní. Takové řešení je velmi nevýhodné; jednotlivé identické souřadnice jsou ve výpočetním modelu nezávislými měřeními a souřadnice identifikované při robustní transformaci jako odlehlé v jedné soustavě nejsou či nemusí být odlehlými v soustavě druhé. Abychom vyjádřili požadovanou relativní změnu polohy bodu vůči fixní poloze v základní etapě, je nutné dílčí opravy pro identickou souřadnici odečíst a testovat tak rozdíl oprav s příslušnou mezní hodnotou. Po stabilizaci výpočtu robustního vyrovnání tedy máme k dispozici opravy v i měřených veličin, tj. souřadnic identických bodů v obou soustavách. Pro každou identickou souřadnici provedeme porovnání podle: v2 x i v1 x i > v M, (4.112) kde mezní hodnotu v M určíme aplikací obecného zákona hromadění směrodatných odchylek. Opravy měřených veličin vzešlé z vyrovnání jsou vzájemně závislé. Závislosti jsou spolu se směrodatnými odchylkami, resp. variancemi oprav vyjádřeny kovarianční maticí: Σ vv = σ 2 0 [ P 1 A(A T P A) 1 A T ] (4.113) Z této kovarianční matice vyselektujeme prvky takové submatice, která popisuje přesnost»identických oprav«, tj.: σv 2 1xi Σ sub = cov cov (4.114) Funkčním vztahem pro modifikovanou opravu (rozdíl dílčích oprav pro identickou souřadnici) je: σ 2 v 2xi v xi = v2 x i v1 x i (4.115) a tedy vektor f T jeho parciálních derivací: ( ) f T vxi = ( 1 x i ), v xi = ( 1, 1) (4.116) ( 2 x i ) 62
64 4. ROBUSTNÍ TRANSFORMACE Směrodatnou odchylku modifikované opravy (tj. rozdílu oprav) určíme ze vztahu: σv 2 xi = f T Σ sub f (4.117) a poté mezní oprava v M vstupující do je: v M = σ vxi u p, (4.118) kde normovanou hodnotu náhodné veličiny normálního rozdělení volíme stejně jako v předchozích verzích u p = 2,57 (odpovídá oboustrannému testu jednorozměrné veličiny na hladině významnosti α = 1 %). Je-li splněna nerovnost 4.112, souřadnici považujeme v určované etapě za odlehlou a ze souboru identických bodů příslušný bod vyloučíme. Výsledky výše popsaného testování jsou takto porovnatelné s výsledky předchozích verzí výpočtu. Třetí verze výpočtu byla provedena pomocí vlastního programu v jazyku GNU Octave. Zdrojové kódy jsou uloženy na přiloženém CD. V příloze C jsou uvedeny výsledky třetí verze výpočtu. Opravy v xi, v yi uvedené v tabulkách C.1 až C.7 jsou již modifikované opravy určené podle Tyto opravy přisoudíme souřadnicím ( 2 x i, 2 y i ) T a souřadnice ( 1 x i, 1 y i ) T současně ponecháme bez oprav. Touto úpravou lze výsledky třetí verze výpočtu interpretovat stejně jako výsledky předchozích verzí. Relativní vztah mezi identickými souřadnicemi po zavedení oprav je touto úpravou samozřejmě zachován Zhodnocení výsledků V předchozích kapitolách byly představeny tři verze výpočtu robustní transformace. Tyto verze se od sebe liší způsobem, jakým jsou měřeným veličinám ve vyrovnání přisuzovány váhy. V první verzi výpočtu je uvažován standardní model transformace, při níž jsou měřenými veličinami souřadnice bodů ve výstupní soustavě a přesnost všech souřadnic v rámci jedné etapy je považována za shodnou a rovnou aritmetickému průměru směrodatných odchylek souřadnic identických bodů v dané etapě. Druhá verze výpočtu je též založena na standardním modelu transformace, kde měřenými veličinami jsou souřadnice bodů ve výstupní soustavě. Přesnost měřených veličin je dána součtem diagonálních kovariančních matic souřadnic obou soustav. Třetí verze výpočtu je aplikací exaktního modelu transformace s uvážením přesností obou soustav. Měřenými veličinami ve vyrovnání jsou tentokrát souřadnice identických bodů v obou soustavách. 63
65 4. ROBUSTNÍ TRANSFORMACE Neznámé parametry jsou ve všech verzích výpočtu určovány metodou robustního odhadu pomocí L 1 -normy, při níž je minimalizována suma absolutních hodnot oprav měřených veličin, viz kapitola 4.4. Průběh výpočtu lze shrnout následovně. Ve všech verzích výpočtu konverguje řešení robustního odhadu velmi rychle. Zpravidla již v iteraci, ve které je určen první robustní odhad, dochází k největšímu poklesu aposteriorní jednotkové směrodatné odchylky ^σ 0, a to řádově až o desítky procent vůči prvotnímu nerobustnímu odhadu MNČ. V přílohách A, B a C jsou kromě číselných výsledků uvedeny i grafy vývoje hodnoty ^σ 0 ze všech provedených robustních transformací. V těchto grafech je vždy uvedena také hodnota apriorní jednotkové směrodatné odchylky σ 0 a dále počáteční hodnota (1)^σ 0 plynoucí z nerobustního odhadu MNČ a koncová hodnota (20)^σ 0 z robustního odhadu po 20 iteracích. Porovnáme-li libovolnou trojici grafů z jednotlivých verzí výpočtu téže robustní transformace, lze zaznamenat skutečnost, že pokles hodnoty ^σ 0 probíhá rázovitě u prvních dvou verzí výpočtu. Naopak pokles ^σ 0 ve třetí verzi probíhá podstatně plynuleji. Tento jev souvisí s užitím principiálně odlišného modelu transformace, na němž je třetí verze výpočtu založena. Při užití výpočetních postupů popsaných v jednotlivých verzích byla zaznamenána značná numerická nestabilita výpočtu. Vzhledem k předpisu 4.51 pro výpočet robustních změn vah se problematickými stávají zejména opravy, které nabývají velmi malých hodnot. Extrémně nízké opravy způsobují extrémní růst vah vkládaných do další iterace výpočtu. Tím vzniká značná nehomogenita v řádech prvků matice robustních změn vah, která implikuje špatnou podmíněnost celého systému. Reciproká hodnota čísla podmíněnosti matice se tak limitně blíží k nule a výpočet inverze matice selhává. Takto špatně podmíněné matice lze sice řešit pseudoinverzí, nicméně v našem výpočtu byla matice robustních změn vah W určována s dodatečnými podmínkami, které zajišťovaly předejití výskytu extrémně vysokých hodnot robustních změn vah w i. V každé iteraci byly tedy robustní změny vah určovány podle: w (m+1) i = 1 ^v (m) i, ^v(m) i = v(m) i (4.119) σ i Dále byla stanovena maximální tolerovaná hodnota robustní změny váhy: Podmínka pak byla do výpočtu zavedena ve tvaru: w max = 4000 (4.120) w (m+1) i > w max w (m+1) i = w max (4.121) 64
66 4. ROBUSTNÍ TRANSFORMACE Hodnota w max byla stanovena pro hypotetickou situaci, kdy měření l i se směrodatnou odchylkou σ i = 4 mm obdrží ve vyrovnání opravu v i = 0,001 mm. Obdobnou podmínku lze do výpočtu zavést také stanovením hodnoty minimální opravy. V tabulce 4.5 je pro každou transformaci uvedeno, jaké body jsou, na základě testování velikosti oprav souřadnic, považovány za odlehlé. Obecně lze shrnout, že druhá a třetí verze výpočtu si v identifikaci odlehlých hodnot naprosto odpovídají. Jak lze ověřit v tabulkách v přílohách B a C, opravy měření vzešlé ze stabilizovaného výpočtu robustní transformace se ve druhé a třetí verzi liší v řádu setin mm a mezní hodnoty oprav jsou si rovny. Jedinou zaznamenanou odlišností ve výsledcích druhé a třetí verze je plynulost konvergence výpočtu ve třetí verzi konverguje výpočet plynuleji, viz grafy vývoje aposteriorní jednotkové směrodatné odchylky ^σ 0 v přílohách B a C. První verze výpočtu dává z hlediska identifikace odlehlých hodnot mírně odlišné výsledky při robustních transformacích E 2 E 1 a E 3 E 1. To je dáno vstupním, příliš zobecněným předpokladem o shodné přesnosti všech měření v rámci dané etapy. K hodnocení velikosti oprav souřadnic byl použit oboustranný test jednorozměrné náhodné veličiny na hladině významnosti α = 1 %. Při testování oprav na hladině významnosti 5 % jsou rozdíly mezi výsledky první verze a ostatními verzemi výpočtu výraznější. S odkazem na výše provedené zhodnocení byly původní soubory identických bodů pro jednotlivé transformace redukovány o ty body, které byly označeny jako odlehlé ve druhé a třetí verzi výpočtu. Obě tyto verze respektují různou přesnost měření. Z hlediska jednoduchosti interpretace výsledků vyzdvihuji zejména druhou verzi, ve které je přesnost měření dána součtem kovariančních matic souřadnic obou (stejně orientovaných) soustav. V redukovaných souborech identických bodů bude nutné pro účel dalšího zpracování vyhledat sadu takových bodů, které nebyly vyloučeny ani v jedné z robustních analýz. 65
67 4. ROBUSTNÍ TRANSFORMACE Tab. 4.5: Vyloučené identické body při robustních transformacích Robustní transformace E 1 E 0 Verze výpočtu vyloučené identické body Verze Verze Verze Robustní transformace E 2 E 1 Verze výpočtu vyloučené identické body Verze 1 512, 1003 Verze 2 512, 513 Verze 3 512, 513 Robustní transformace E 3 E 1 Verze výpočtu vyloučené identické body Verze 1 507, 512, 513, 1002, 1003 Verze 2 507, 512, 513, 1002, 1003, 1011 Verze 3 507, 512, 513, 1002, 1003, 1011 Robustní transformace E 4 E 1 Verze výpočtu vyloučené identické body Verze Verze Verze Robustní transformace E 5 E 1 Verze výpočtu vyloučené identické body Verze 1 513, 1003 Verze 2 513, 1003 Verze 3 513, 1003 Robustní transformace E 6 E 1 Verze výpočtu vyloučené identické body Verze , 1003 Verze , 1003 Verze , 1003 Robustní transformace E 7 E 1 Verze výpočtu vyloučené identické body Verze Verze Verze
68 5. HELMERTOVA TRANSFORMACE 5 Helmertova transformace 5.1 Výběr identických bodů Na základě statistického testování oprav vzešlých ze stabilizovaného výpočtu robustního vyrovnání byly v souborech identických bodů identifikovány odlehlé hodnoty souřadnic. Identický bod, jehož alespoň jedna souřadnice byla označena za odlehlou, byl ze souboru identických bodů vyloučen. V tabulce 5.1 jsou symbolem označeny identické body, které při jednotlivých robustních transformacích vyhověly testu oprav na hladině významnosti α = 1 % (dle výsledků druhé a třetí verze výpočtu, které jsou ve shodě). Symbolem proškrtnutí jsou v prvním sloupci tabulky označeny 4 body, které pro příslušnou transformaci (E 1 E 0 ) nejsou body identickými, neboť tyto body nebyly předmětem zaměření v etapě E 0. Jednotlivé sloupce tabulky 5.1 s body označenými tedy představují redukované soubory identických bodů, které pro příslušnou transformaci splňují podmínku normality měřických dat. Původ dat z normálního rozdělení pravděpodobností je ideálním předpokladem pro správnost aplikace metody nejmenších čtverců. Účelem je nyní z takto očištěných souborů identických bodů vybrat sadu takových bodů, které nebyly označeny jako odlehlé ani v jedné z robustních analýz. Tyto body poskytnou dostatečnou věrohodnost ve stálosti své polohy v průběhu celého sledovaného období a použijeme je proto k výpočtu definitivního transformačního klíče metodou nejmenších čtverců. Opět s odkazem na tabulku 5.1 je výsledkem výběru 9 identických bodů, které vyhověly testu oprav při všech robustních transformacích. Jedná se o body: 501, 506, 524, 531, 552, 553, 1001, 1005, Na základě porovnání počtů vyloučených bodů při jednotlivých robustních transformacích lze transformaci E 3 E 1 označit v jistém smyslu za podezřelou. Při této robustní transformaci bylo pomocí testů oprav vyloučeno 6 identických bodů, zatímco maximální počet bodů vyloučených při všech ostatních transformacích je 2. Tato informace je nepříznivá zejména z toho důvodu, že vyloučenými body jsou při robustní transformaci E 3 E 1 mimo jiné i body 507 a Jejich hypotetické nevyloučení v etapě E 3 by znamenalo nevyloučení v celé posloupnosti etap a tyto body bychom tak mohli také využít k výpočtu definitivního transformačního klíče. Oba body 507 a 1011 byly při robustní transformaci E 3 E 1 vyloučeny na 67
69 5. HELMERTOVA TRANSFORMACE Tab. 5.1: Identické body vyhovující statistickému testu oprav Helmertova transformace E1 E0 E2 E1 E3 E1 E4 E1 E5 E1 E6 E1 E7 E1 bod použit vylouč celkem základě nevyhovění pouze jedné jejich souřadnice, viz tabulka B.3 nebo C.3. Souřadnice označené jako odlehlé hodnoty proto podrobíme bližšímu zkoumání a testování provedeme ještě pomocí p-hodnoty. P-hodnota kvantifikuje pravděpodobnost realizace hodnoty testovací statistiky, pokud nulová hypotéza H 0 platí. Statistický test oprav pomocí jejich mezních hodnot je konstruován následovně. Testovanou nulovou hypotézou H 0, resp. alternativní hypotézou H 1 je: Testovací statistikou je veličina: H 0 : E(v i ) = 0 (5.1) H 1 : E(v i ) 0 (5.2) t = v i σ vi N(0; 1), (5.3) 68
70 5. HELMERTOVA TRANSFORMACE která má normované normální rozdělení pravděpodobností N(0; 1). Mezní hodnota u p se určí pro danou (zvolenou) pravděpodobnost P z integrálu: u p P = π e t2 2 dt, (5.4) či jako tabelovaný kvantil spojité náhodné veličiny t s rozdělením N(0, 1). V případě oboustranného testu požadujeme splnění podmínky t u p. Není-li toto testovací kritérium splněno, nulovou hypotézu H 0 zamítáme. Pro oboustranný test na hladině významnosti α = 1 % zjistíme příslušný kvantil spojité náhodné veličiny s rozdělením N(0, 1) zadáním příkazu norminv(0.995) v programu Octave. Výsledkem je u p = 2,57. Poté, co byl uveden tvar testovací statistiky 5.3, můžeme p-hodnotu (při oboustranném testu) určit ze vztahu: p = 2 min{f (t); 1 F (t)}, (5.5) kde F je distribuční funkce normovaného normálního rozdělení N(0; 1), pro kterou platí: F (t) = 1 2π t e t2 2 dt (5.6) P-hodnoty testovacích statistik příslušejících vyloučeným souřadnicím identických bodů 507 a 1011 při robustní transformaci E 3 E 1 potom zjistíme pomocí příkazu normcdf(t) v programu Octave. Přesněji řečeno, tímto příkazem zjistíme hodnotu distribuční funkce F v bodě odpovídajícím hodnotě vypočtené testovací statistiky t a po dosazení do 5.5 určíme p-hodnotu. Výpočet p-hodnot je shrnut v následující tabulce. Tab. 5.2: Výpočet p-hodnot bod v i σ vi t F (t) p ,85 1,43 2,69 0, , ,42 2,07 4,07 0, ,00004 Význam výsledků uvedených v tabulce 5.2 je takový, že test opravy bodu 1011 by musel být proveden na hladině významnosti nižší než 0,71 % a bodu 507 na extrémně nízké hladině významnosti α < 0,004 %, aby nulová hypotéza H 0 nebyla zamítnuta. 69
71 5. HELMERTOVA TRANSFORMACE Je zřejmé, že užití takto nízké hladiny významnosti by smazávalo podstatu testu, neboť s klesající hladinou významnosti klesá i síla 1 testu. Zamítnutí H 0 lze tedy v obou případech považovat za jisté. I přes dosavadní zhodnocení bylo rozhodnuto, že body 507 a 1011 budou využity jako identické body k výpočtu definitivního transformačního klíče. Klíčovým argumentem pro toto rozhodnutí je fakt, že etapa E 3, v níž jediné došlo k vyloučení bodů 507 a 1011, byla zaměřena s hrubým porušením metodiky etapových měření. Jedná se o etapu 2009p, ve které nebylo dokončeno zaměření polygonových pořadů. Z toho důvodu nelze terestrická měření v této etapě samostatně vyrovnat formou volné sítě. Nutnou podmínkou pro vyřešení této etapy tedy bylo navázání terestrických měření na GNSS vektory a jejich společné vyrovnání. Vzhledem k úpravám kovariančních matic GNSS vektorů (viz kapitola 3.2) lze předpokládat, že objektivita charakteristik přesnosti bodů plynoucí z vyrovnání etapy 2009p utrpěla jistou újmu. Dalším neopomenutelným důvodem pro použití bodů 507 a 1011 k výpočtu definitivního transformačního klíče je, že tyto body významně přispívají k rovnoměrnosti pokrytí celého sledovaného areálu identickými body, viz obrázek 5.1. Závěr Definitivní transformační klíč Helmertovy rovinné shodnostní transformace jednotlivých etap do soustavy základní etapy E 1 bude vypočten pomocí 11 identických bodů: 501, 506, 507, 524, 531, 552, 553, 1001, 1005, 1011, Tyto body jsou na obrázku 5.1 vyznačeny modře. Helmertovu transformaci E 1 E 0 provedeme pomocí téže sady identických bodů, ovšem bez bodů 531 a 1001, které nebyly předmětem zaměření etapy E 0. 1 Síla testu je pravděpodobnost, že je testem zamítnuta nulová hypotéza, když skutečně neplatí. Vypočte se jako P (H 1 H 1 ) = 1 β, kde β je pravděpodobnost chyby druhého druhu. K chybě druhého druhu dojde, když na základě výběrových hodnot nezamítáme H 0, ačkoliv neplatí. 70
72 5. HELMERTOVA TRANSFORMACE Obr. 5.1: Přehledka bodů polohové sítě Pražského hradu 71
73 5. HELMERTOVA TRANSFORMACE 5.2 Definitivní transformační klíč Definitivní transformační klíč, který charakterizuje transformaci soustavy další etapy do soustavy základní etapy určíme metodou nejmenších čtverců, tj. Helmertovou transformací. Ke všem transformacím užijeme tutéž sadu identických bodů; jejich konkrétní výběr byl proveden a zdůvodněn v předchozí kapitole. Výpočet Helmertovy transformace provedeme podle postupu popsaného v kapitole s tím rozdílem, že ve výpočtu již nefiguruje matice robustních změn vah W a jako váhovou matici P dosadíme: P = σ 2 0 Σ 1 ll = σ 2 0 (Σ X + Σ x ) 1, (5.7) kde σ 0 je apriorní jednotková směrodatná odchylka, Σ X je kovarianční matice souřadnic bodů ve výstupní soustavě (soustava základní etapy) a Σ x je kovarianční matice souřadnic bodů ve vstupní soustavě (soustava transformované etapy). Vypočteme přírůstky k přibližným hodnotám neznámých parametrů: dφ = (A T P A) 1 A T P l (5.8) a z nich vyrovnané neznámé: ^Φ = Φ 0 + dφ (5.9) Dále vypočteme opravy měřených veličin: v = A dφ + l (5.10) a vyrovnané měřené veličiny: ^l = l + v (5.11) Provedeme závěrečnou kontrolu pomocí dvojího výpočtu oprav: v I = A dφ + l (5.12) v II = X(^Φ) l, (5.13) kde X jsou funkční vztahy Závěrem vypočteme charakteristiky přesnosti plynoucí ze zavedení podmínky MNČ. Aposteriorní jednotková směrodatná odchylka Je-li počet polohových identických bodů při Helmertově transformaci n a tedy počet měření ve vyrovnání 2n a dále počet neznámých parametrů u, určíme z daného výběru 2n oprav aposteriorní jednotkovou směrodatnou odchylku podle vztahu: vt P v ^σ 0 =, (5.14) n 72
74 5. HELMERTOVA TRANSFORMACE kde n = 2n u je počet nadbytečných měření. Aposteriorní jednotková směrodatná odchylka ^σ 0 je empirickým odhadem směrodatné odchylky měření o váze p = 1. Její hodnota je náhodná a závislá na náhodném střetnutí hodnot skutečných chyb ε i. Odvození vztahu 5.14 lze nalézt např. v [11]. Směrodatné odchylky vyrovnaných neznámých Směrodatné odchylky vyrovnaných neznámých parametrů, tj. prvků transformačního klíče, se počítají ze vzorce: kde Σ^Φi ^Φi σ^φi = Σ^Φi ^Φi, (5.15) je diagonální prvek kovarianční matice Σ^Φ ^Φ, pro kterou platí: Σ^Φ ^Φ = [ (A T P A) 1 A T P ] Σ ll [ (A T P A) 1 A T P ] T Σ^Φ ^Φ = σ 2 0 ( A T P A ) 1 nebo ^σ 2 0 ( A T P A ) 1 (5.16) (5.17) K výpočtu směrodatných odchylek vyrovnaných neznámých použijeme apriorní jednotkovou směrodatnou odchylku σ 0, pokud při testu aposteriorní jednotkové směrodatné odchylky ^σ 0 podle kapitoly 3.4 není zamítnuta nulová hypotéza 3.2. Směrodatné odchylky vyrovnaných měření Směrodatné odchylky vyrovnaných měření vypočteme ze vzorce: σ^li = Σ^li^li, (5.18) kde Σ^li^li je diagonální prvek kovarianční matice Σ^l^l, pro kterou platí: Σ^l^l = A Σ^Φ ^Φ A T (5.19) Směrodatné odchylky vyrovnaných oprav Odvození kovarianční matice vyrovnaných oprav bylo provedeno v kapitole Pro výslednou matici platí: Σ vv = [ A(A T P A) 1 A T P E ] Σ ll [ A(A T P A) 1 A T P E ] T = ( Σ^l^lΣ 1 ll E ) Σ ll ( Σ^l^lΣ ll 1 E ) T (5.20) (5.21) = Σ ll Σ^l^l (5.22) = [ σ0 2 P 1 A(A T P A) 1 A ] T (5.23) 73
75 5. HELMERTOVA TRANSFORMACE Směrodatné odchylky funkcí vyrovnaných neznámých Jedná se o aplikaci všeobecně známého zákona hromadění směrodatných odchylek v obecném (maticovém) tvaru, resp. zákona hromadění vah pro korelovaná měření. Uvažujeme funkci f = f(^φ T ) korelovaných hodnot ^Φ vzešlých z vyrovnání se známou kovarianční maticí Σ^Φ ^Φ určenou podle Úkolem je určit směrodatnou odchylku uvažované funkce. Vypočteme vektor h T parciálních derivací funkce f podle jednotlivých prvků vektoru ^Φ: h T = f(^φ T ) (5.24) ^Φ V případě jedné funkce je výsledkem pouze skalár: σf 2 = h T Σ^Φ ^Φ h (5.25) Zobecníme-li úlohu na případ, kdy určujeme směrodatné odchylky více funkcí současně, tedy platí: f = f(^φ T ), f = (f 1, f 2,..., f n ) T, (5.26) vypočteme matici parciálních derivací: a výsledkem je poté matice: H = f(^φ T ) ^Φ (5.27) Σ ff = H Σ^Φ ^Φ H T, (5.28) kde přesnost konkrétní funkce f i vyjádříme z diagonálního prvku Σ fi f i matice podle: σ fi = Σ fi f i (5.29) Výpočet definitivních transformačních klíčů Helmertovy transformace jednotlivých etap do soustavy příslušné základní etapy byl proveden pomocí vlastního programu v jazyku GNU Octave. Algoritmus výpočtu odpovídá výše popsanému postupu. Zdrojový kód programu i všechny výstupní soubory jsou uloženy na přiloženém CD. 5.3 Transformace souřadnic V této fázi výpočtu je pro každou transformaci dané etapy do soustavy základní etapy znám definitivní transformační klíč a jeho kovarianční matice plynoucí z výpočtu Helmertovy transformace. Postup výpočtu definitivního transformačního klíče 74
76 5. HELMERTOVA TRANSFORMACE metodou nejmenších čtverců je uveden v kapitole 5.2 a konkrétní výběr identických bodů v kapitole 5.1. Pomocí takto určeného definitivního transformačního klíče byla provedena transformace všech bodů sítě v dané etapě, tedy bodů identických i neidentických. Je zřejmé, že z důvodu různých rozsahů zaměření jednotlivých etap nelze zejména pro některé neidentické body provést kontinuální zhodnocení jejich posunů. To demonstruje tabulka 5.3, v níž jsou symbolem označeny ty body, které byly v dané etapě zaměřeny. Poznámka DIB v tabulce 5.3 znamená»definitivní identický bod«, tj. bod použitý k výpočtu definitivního transformačního klíče. Tab. 5.3: Označení zaměření všech bodů sítě bod E 0 E 1 E 2 E 3 E 4 E 5 E 6 E 7 pozn. 501 DIB DIB 507 DIB IB 513 IB 524 DIB DIB DIB 553 DIB 1001 DIB 1002 IB 1003 IB 1005 DIB 1011 DIB 1012 DIB 75
77 5. HELMERTOVA TRANSFORMACE Přesnost přetransformovaných souřadnic bodů byla určena aplikací obecného zákona hromadění směrodatných odchylek. Funkčními vztahy, na něž je zákon aplikován, jsou již známé transformační rovnice rovinné shodnostní transformace: X i cos ^ω sin ^ω = x i + ^T x (5.30) Y i sin ^ω cos ^ω y i ^T y Pro transformační parametry ^Φ = ( ^T x, ^T y, ^ω) T je známa kovarianční matice Σ^Φ ^Φ z vyrovnání, určená podle Ta byla vypočtena na základě apriorní jednotkové směrodatné odchylky σ 0. Pro vstupní transformované souřadnice x = (x i, y i ) T je známa kovarianční matice Σ xy vzešlá z vyrovnání jednotlivých etap programem GNU Gama. Matice parciálních derivací podle všech parametrů má pro jeden bod tvar: H (2 5) = T x T y ω x i y i X i 1 0 x i sin ω y i cos ω cos ω sin ω (5.31) Y i 0 1 x i cos ω y i sin ω sin ω cos ω Kovarianční matici všech parametrů Σ all uvažujeme v blokově diagonálním tvaru: Σ all = Σ(3 3) ^Φ ^Φ 0 (3 2) 0 (2 3) Σ (2 2) xy (5.32) Kovarianční matice přetransformovaných souřadnic i-tého bodu má tvar: Σ XY = H Σ all H T (5.33) Tímto postupem byly určeny směrodatné odchylky souřadnic a jejich kovariance pro všechny přetransformované body. Toto řešení zanedbává závislosti mezi vstupními transformovanými souřadnicemi různých bodů; exaktní řešení by znamenalo transformovat všechny souřadnice jako jeden celek a jako charakteristiku jejich přesnosti použít plnou kovarianční matici Σ x vzešlou z vyrovnání programem GNU Gama. Výpočet transformace a charakteristik přesnosti přetransformovaných bodů byl proveden vlastním programem v jazyku GNU Octave, resp. byla použita pouze funkce již zmíněného programu vytvořeného k výpočtu Helmertovy transformace, kde definitivní transformační klíč a jeho kovarianční matice jsou vstupními argumenty této funkce. 76
78 5. HELMERTOVA TRANSFORMACE Kompletní program tedy pro každou transformaci generuje 2 výstupní textové soubory, v prvním souboru je uvedena aposteriorní jednotková směrodatná odchylka, výsledný transformační klíč a jeho kovarianční matice. Druhý textový soubor obsahuje přetransformované souřadnice všech identických i neidentických bodů v dané etapě. Pro každý bod jsou uvedeny směrodatné odchylky souřadnic a jejich příslušné kovariance vypočtené podle Tyto textové soubory byly generovány v takovém formátu, který umožňuje jejich následné načtení programem Gizela. V tomto programu byla provedena závěrečná statistická analýza posunů bodů. Všechny seznamy přetransformovaných souřadnic jsou uvedeny v příloze D. 77
79 6. TESTOVÁNÍ POSUNŮ BODŮ 6 Testování posunů bodů 6.1 Pravděpodobnost uvnitř elipsy chyb Posunem bodu je pro účel této práce míněn statisticky prokázaný rozdíl v poloze bodu mezi základní etapou a některou z dalších etap měření. Vodorovný posun bodu mezi základní etapou E 0 a další etapou E j určíme podle vztahů: ΔX (0,j) i = X (j) i X (0) i (6.1) ΔY (0,j) i = Y (j) i Y (0) i (6.2) ( X p (0,j) (j) i = i X (0) ) 2 ( (j) i + Y i Y (0) ) 2 i (6.3) (0,j) α p (0,j) ΔY i i = arctan, (6.4) ΔX (0,j) i kde X i, Y i jsou souřadnice i-tého bodu, p (0,j) i je velikost vodorovného posunu bodu mezi nultou a j-tou etapou a α p (0,j) i je směrník posunu. Cílem statistického testování je provést se zvoleným rizikem rozhodnutí o změně polohy bodu na základě objektivního kritéria. Pro testování vodorovných posunů využijeme metodu testování pomocí konfidenční oblasti. Touto oblastí je tzv. konfidenční elipsa chyb. Předpokladem pro správnou aplikaci testu je, že porovnávané souřadnice v j-té a k-té etapě jsou nezávislé náhodné veličiny s normálním rozdělením pravděpodobností. Pro vektor souřadnic X (j) i X (j) i = ( X (j) i bodu i v etapě j platí (obdobně pro vektor X (k) i ):, Y (j) i ) T N ( E ( X (j) i ) ) (j) ; Σ i, (6.5) kde E ( X (j) ) (j) i je střední hodnota vektoru souřadnic a Σ i je kovarianční matice souřadnic. Předpokládáme-li, že platí 6.5, jsou i souřadnicové rozdíly ΔX (j,k) i, ΔY (j,k) i náhodnými veličinami, jejichž rozdělení pravděpodobností se řídí dvojrozměrným normálním rozdělením. Pro vektor posunu bodu proto platí: p (j,k) i = ΔX(j,k) i ΔY (j,k) i N ( E ( X (k) i ) E ( X (j) i ) ; Σ (j) i Odtud je zřejmé, že kovarianční matice vektoru posunu je dána: Σ p (j,k) = Σ (j) i + Σ (k) ) i (6.6) + Σ (k) i (6.7) 78
80 6. TESTOVÁNÍ POSUNŮ BODŮ Protože jsou souřadnicové rozdíly ΔX (j,k) i, ΔY (j,k) i náhodnými veličinami s dvojrozměrným normálním rozdělením, má i vektor jejich skutečných chyb ε p (j,k) při platnosti H 0 dvojrozměrné normální rozdělení se střední hodnotou: E ( ε p (j,k)) = 0 (6.8) a kovarianční maticí Σ p (j,k), neboli: ε p (j,k) N ( 0; Σ p (j,k) ) (6.9) Hustota pravděpodobnosti náhodného vektoru ε p (j,k) výrazem: f ( ε p (j,k) ) = 1 2π Σ p (j,k) 1 2 { exp 1 } 2 εt p Σ 1 ε (j,k) p (j,k) p (j,k) je např. podle [22] dána, (6.10) kde Σ p (j,k) je determinant kovarianční matice Σ p (j,k). Protože kovarianční matice Σ p (j,k) Σ 1 p (j,k) typu 2 2 je pozitivně definitní, je její determinant kladný a inverzní matice existuje. Průsečnicemi plochy hustoty pravděpodobnosti 6.10 a rovin rovnoběžných s rovinou XY je soustava soustředných a souosých elips chyb, jejichž rovnice lze zapsat: ε T p (j,k) Σ 1 p (j,k) ε p (j,k) = t 2 i, (6.11) kde t i je volitelný parametr. Tyto elipsy se nazývají konfidenční elipsy chyb a jejich velikost vyjadřuje, s jakou pravděpodobností (konfidenční pravděpodobností) leží vektor posunu uvnitř této elipsy, jestliže nedošlo ke skutečné změně polohy bodu. Pro volbu parametru t i = 1 je konfidenční elipsa nazývána střední elipsou chyb. Vztah 6.11 představuje kvadratickou formu dimenze 2, tj. mnohočlen druhého stupně (neobsahuje členy prvního a nultého stupně) a matice Σ 1 p (j,k) je matice kvadratické formy kuželosečky. V [22] lze nalézt odvození, že směry os elipsy chyb splývají s vlastními vektory kovarianční matice Σ p (j,k) jsou odmocniny z vlastních čísel této matice. a velikosti poloos střední elipsy chyb Orientace elipsy chyb vzhledem k původním souřadnicovým osám tedy závisí na kovarianci. Jestliže jsou jsou náhodné proměnné nekorelované, tak osy elipsy jsou rovnoběžné se souřadnicovými osami a takovou elipsu potom můžeme zapsat středovou rovnicí: ( ) X 2 ( ) Y 2 + = 1 (6.12) a t i b t i Pravděpodobnost P, kterou reprezentuje daná chybová elipsa, určíme jako objem eliptického válce ohraničeného plochou normálního rozdělení: { 1 P = 2πab exp 1 [ ( X ) 2 ( ) Y 2 ] } + dx dy (6.13) 2 a b ( X a ) 2 +( Y b ) 2 <t 2 i 79
81 6. TESTOVÁNÍ POSUNŮ BODŮ Řešení dvojného integrálu se provádí s využitím substituce (zavedení polárních souřadnic) a výsledná pravděpodobnost pro zvolenou hodnotu parametru t i je dána výrazem: { ( X ) 2 ( Y P = P + a b ) 2 } t 2 i = 1 e t 2 i 2 (6.14) Úpravou výrazu 6.14 je naopak možné vyjádřit hodnotu parametru t i pro zvolenou pravděpodobnost P : t i = 2 ln(1 P ) (6.15) V tabulce 6.1 jsou uvedeny hodnoty pravděpodobností uvnitř konfidenčních elips chyb pro různé hodnoty parametru t i : Tab. 6.1: Pravděpodobnost uvnitř konfidenční elipsy chyb t i 0 0,5 1 1,5 2 2,5 3 3,5 P % 0 11,8 39,4 67,5 86,5 95,6 98,9 99,8 Parametry konfidenční elipsy chyb Z kovarianční matice vektoru posunu Σ (j,k) p, která má strukturu: i Σ p (j,k) i = σ 2 ΔX (j,k) i cov ( ΔX (j,k) i, ΔY (j,k) i určíme parametry střední elipsy chyb podle vzorců: kde c se určí: a = b = σ2 ΔX (j,k) i σ2 ΔX (j,k) i ) cov ( ΔX (j,k) i + σ 2 ΔY (j,k) i 2 + σ 2 ΔY (j,k) i 2 σ 2 ΔY (j,k) i + c, ΔY (j,k) i ), (6.16) (6.17) c, (6.18) c = ( σ 2 ΔX (j,k) i σ 2 ΔY (j,k) i Směrník hlavní poloosy se vypočte: ) cov 2 tan 2α = 2 cov ( ΔX (j,k) i σ 2 ΔX (j,k) i ( ΔX (j,k) i, ΔY (j,k) ) i σ 2 ΔY (j,k) i, ΔY (j,k) i ) (6.19) (6.20) 80
82 6. TESTOVÁNÍ POSUNŮ BODŮ Pro zvolenou konfidenční pravděpodobnost P vyjádříme hodnotu parametru t i z rovnice 6.15 a velikost hlavní a vedlejší poloosy konfidenční elipsy chyb potom vyjádříme: a ti = a t i, b ti = b t i (6.21) 6.2 Konstrukce testu Testování souřadnicových rozdílů (posunů) provedeme dvourozměrnými apriorními testy. Při testování posunu bodu i mezi etapami j a k mají nulová a alternativní hypotéza tvar: H 0 : E H 1 : E X(k) i Y (k) i X(k) i Y (k) i X (j) i Y (j) i X (j) i Y (j) i = 0 (6.22) 0 0 (6.23) 0 Testovací statistikou apriorního testu je veličina χ 2, pro kterou platí: χ 2 = ( ΔX (j,k) i, ΔY (j,k) ) i Σ 1 ΔX(j,k) i ΔX (j,k) i,δy (j,k) i ΔY (j,k) i, (6.24) kde Σ (j,k) ΔX je kovarianční matice vektoru posunu, kterou určíme pomocí i,δy (j,k) i vztahu 6.7 jako součet kovariančních matic souřadnic porovnávaných bodů: Σ (j,k) ΔX = Σ i,δy (j,k) (j,k) i p = Σ (j) i XY + Σ (k) i XY i (6.25) Testovací statistika χ 2 má při platnosti H 0 centrální χ 2 rozdělení pravděpodobností se dvěma stupni volnosti. Kritická hodnota χ 2 rozdělení pro zvolenou hladinu významnosti α = 5 % a dva stupně volnosti je χ 2 α,2 = 5,99. Testovací kritérium má tvar: χ 2 > χ 2 α,2 (6.26) Je-li podmínka 6.26 splněna, testovanou nulovou hypotézu zamítáme na hladině významnosti α a současně přijímáme hypotézu alternativní. Přijetí alternativní hypotézy dále implikuje přijetí konvenčního závěru, že ve vyhodnocované etapě byl s danou pravděpodobností prokázán posun bodu. Konstrukce testu by se mohla zdát v jistém smyslu matoucí, neboť z formálního hlediska byl díky tvaru alternativní hypotézy H 1 stanoven oboustranný test a testovací kritérium 6.26 současně definuje pouze jednostranný interval spolehlivosti. To 81
83 6. TESTOVÁNÍ POSUNŮ BODŮ je dáno skutečností, že testovací statistika 6.24 je modifikovaným kvadrátem velikosti posunu, resp. kvadrátem posunu, který je pomocí kovarianční matice posunu převeden na kvantil χ 2 rozdělení. Samotný výsledek testu, kterým je rozhodnutí o zamítnutí či nezamítnutí nulové hypotézy H 0, je vhodné doplnit výpočtem p-hodnoty. P-hodnota kvantifikuje pravděpodobnost realizace hodnoty testovací statistiky, pokud nulová hypotéza platí. Podává tak podstatně lepší informaci o výsledku testu než pouhé zamítnutí či nezamítnutí nulové hypotézy. P-hodnota se v tomto případě vypočte podle vztahu: p = 1 F (χ 2 ), (6.27) kde F (χ 2 ) je hodnota distribuční funkce χ 2 rozdělení vypočtená v bodě získané hodnoty testovací statistiky Hodnotu distribuční funkce F rozdělení χ 2 se dvěma stupni volnosti v bodě stat zjistíme např. zadáním příkazu chi2cdf(stat,2) v programu Octave. Pomocí p-hodnoty je též možné provést rozhodnutí o výsledku testu. Platí-li nerovnost: p α, (6.28) testovanou nulovou hypotézu zamítáme na zvolené hladině významnosti α. 6.3 Výsledky testování Výpočet testů posunů bodů byl proveden v programu Gizela. Gizela je volně distribuovaný software, který je primárně vyvinut pro operační systém Linux a slouží ke zpracování a vyhodnocení geodetických etapových měření. Jeho autory jsou Ing. Tomáš Kubín, Ph.D. a Ing. Michal Seidl, Ph.D. Vstupními daty do programu Gizela jsou v našem případě seznamy vyrovnaných souřadnic bodů přetransformovaných do soustavy základní epochy pomocí vybrané sady identických bodů. Ke každému bodu jsou uvedeny směrodatné odchylky přetransformovaných souřadnic a jejich příslušné kovariance. Tyto seznamy souřadnic jsou obsahem přílohy D. Z důvodu volby dvou základních etap je testování posunů mezi jednotlivými etapami provedeno odděleně, tzn. etapa E 1 je hodnocena vůči základní etapě E 0 a etapy E 2 až E 7 jsou hodnoceny vůči základní etapě E 1. Důvody k volbě dvou základních etap byly uvedeny v kapitole
84 6. TESTOVÁNÍ POSUNŮ BODŮ Na základě zpracování vstupních dat program Gizela generuje několik druhů výstupních souborů. Nejdůležitější výsledky obsahuje textový soubor s vypočtenými posuny (souřadnicovými rozdíly), jejich směrodatnými odchylkami, p-hodnotou, výslednou hodnotou testovací statistiky a uvedením výsledku testu. Všechny tyto výsledky jsou formou přehledných tabulek uvedeny v příloze E. Dalším důležitým výstupem z programu Gizela je grafické zobrazení posunů bodů s vykreslením středních elips chyb bodů v jednotlivých etapách a dále grafické zobrazení posunů s vykreslením konfidenčních elips chyb vektorů posunů. Testování posunů bodů bylo provedeno na hladině významnosti α = 5 %. Všechny vstupní i výstupní soubory programu Gizela jsou uloženy na přiloženém CD. Výpočet testování byl také kontrolně proveden pomocí vlastního programu v jazyku Octave. K tomu byly využity stejné vstupní soubory sestavené pro program Gizela, viz příloha D. Algoritmus výpočtu odpovídá konstrukci testu popsané v kapitole 6.2. Výsledkem jsou výstupní textové soubory s vypočtenými posuny, jejich směrodatnými odchylkami, p-hodnotou, výslednou hodnotou testovací statistiky a uvedením výsledku testu. Tyto výsledky se shodují s výsledky testování programem Gizela. Veškerá data související s vlastním výpočtem testování (spustitelný m-soubor, vstupní a výstupní textové soubory) jsou uloženy na přiloženém CD. Kromě samotných výsledků testování posunů plynou velmi důležité závěry z porovnání těchto výsledků s výsledky robustních transformací. Toto porovnání představuje tabulka 6.3. Na základě testování oprav vzešlých ze stabilizovaného výpočtu robustního vyrovnání byly při jednotlivých transformacích identifikovány odlehlé hodnoty souřadnic identických bodů. Obdobně pak byly v jednotlivých etapách označeny body, u nichž byl na základě dvourozměrných apriorních testů prokázán posun. S odkazem na tabulku 6.3 je pak možné učinit závěr, že testy posunů bodů velmi dobře potvrzují výsledky robustních transformací. Jedinou odchylkou v identifikaci»nevyhovujících«bodů je bod 1011 v etapě E 3, resp. robustní transformaci E 3 E 1. U tohoto bodu nebyl na základě testování posun v etapě E 3 prokázán, ačkoliv při robustní transformaci E 3 E 1 jedna jeho souřadnice nevyhověla testu oprav. Současně je však nutné připomenout, že testy oprav byly při robustní analýze prováděny na hladině významnosti 1 %, zatímco testy posunů bodů na hladině významnosti 5 %. Odchylka je tak pravděpodobně vyvolána skutečností, že při robustní transformaci jsou opravy testovány odděleně a identický bod je tak vyloučen při nevyhovění alespoň jedné jeho souřadnice. Při 83
85 6. TESTOVÁNÍ POSUNŮ BODŮ testování posunů je však testován vektor posunu (velikost vektoru souřadnicových rozdílů) a test je tak podstatně komplexnější. Na základě testování posunů všech bodů sítě byla vybrána sada bodů, u nichž nebyl prokázán posun ani v jedné z vyhodnocovaných etap. Jedná se o sadu těchto 15 bodů: 501, 502, 506, 511, 524, 526, 527, 531, 541, 552, 553, 1001, 1005, 1011, Jak je patrné z tabulky 6.2, některé z těchto bodů (502, 511, 526, 527, 531, 541, 1001) nebyly v určitých etapách předmětem zaměření a vyhodnocení posunů těchto bodů proto není možné provést kontinuálně v průběhu všech etap. Na základě dostupných dat však tyto body testům posunů v příslušných etapách vyhověly. Závěrem pokládám tvrzení, že zmíněnou sadu 15 bodů polohové sítě lze podle běžných konvencí považovat za stabilní. Toto tvrzení dokladuji přílohou E s číselnými výsledky testů a přílohou F s grafickými výsledky testů. V tištěné verzi práce doprovázím grafickými přílohami testování etap E 2 až E 7 vůči základní etapě E 1. Grafické přílohy k testování E 1 vůči E 0 jsou uloženy na přiloženém CD. U ostatních bodů sítě byla v nejméně jedné etapě prokázána nestabilita, která byla pravděpodobně způsobena vnějšími vlivy. Nejvýraznější polohovou nestabilitu dlouhodobě vykazuje geotechnický vrt Tab. 6.2: Označení zaměření stabilních bodů sítě bod E 0 E 1 E 2 E 3 E 4 E 5 E 6 E
86 6. TESTOVÁNÍ POSUNŮ BODŮ Tab. 6.3: Porovnání výsledků testování s výsledky robustní transformace Vyloučení bodu při robustní transformaci resp. prokázání posunu při testování Identické body Neidentické body Robustní transformace E1 E Testování posunů E1 vůči E Robustní transformace E2 E1 512, 513 Testování posunů E2 vůči E1 512, 513 Robustní transformace E3 E1 507, 512, 513, 1002, 1003, 1011 Testování posunů E3 vůči E1 507, 512, 513, 1002, , 505 Robustní transformace E4 E Testování posunů E4 vůči E Robustní transformace E5 E1 513, 1003 Testování posunů E5 vůči E1 513, , 505 Robustní transformace E6 E1 1002, 1003 Testování posunů E6 vůči E1 1002, , 510, 525, 532 Robustní transformace E7 E Testování posunů E7 vůči E
87 ZÁVĚR Závěr V této diplomové práci jsem se zabýval komplexním zpracováním etapových měření ve vztažné síti Pražského hradu a statistickým vyhodnocením vodorovných posunů bodů sítě. Ve druhé kapitole popisuji přípravu a postupy zpracování vstupních měřených dat. Cílem této kapitoly je objasnit postup, který byl použit k převedení všech měřených veličin do společné vztažné soustavy pro účel kombinovaného vyrovnání GNSS vektorů a terestrických měření. Uvádím proto úvahu nad volbou vhodného souřadnicového systému, do něhož musí být všechna měření převedena (redukována). Na základě popisované úvahy jsem jako vztažnou souřadnicovou soustavu pro vyrovnání polohové složky sítě zvolil Lambertovo konformní kuželové zobrazení s jednou nezkreslenou rovnoběžkou. Detailně popisuji zejména způsob převodu měřených GNSS vektorů do roviny kartografického zobrazení a s tím související transformaci kovariančních matic těchto vektorů. Ve třetí kapitole se zabývám sestavením vstupních dávkových souborů pro společné vyrovnání programem GNU Gama a hodnotím výsledky vyrovnání sítě v jednotlivých etapách. Při sestavování vstupních dávkových souborů uvádím volbu apriorních přesností měřených veličin a způsobu umístění volné sítě do prostoru. Dále v kapitole shrnuji základní parametry vyrovnání sítě v jednotlivých etapách, tj. zejména počet všech pozorování (počet rovnic oprav), počet neznámých, počet nadbytečných měření a odhad apriorní σ 0 a aposteriorní ^σ 0 jednotkové směrodatné odchylky. Závěrem kapitoly je statistické testování aposteriorních jednotkových směrodatných odchylek. Testována je hypotéza, že náhodný výběr s výběrovou směrodatnou odchylkou ^σ 0 je proveden ze základního souboru se směrodatnou odchylkou σ 0. Pro testovací statistiky byly stanoveny 99%-ní intervaly spolehlivosti. Testovaná nulová hypotéza nebyla zamítnuta ani v jednom případě vyrovnané sítě a lze tedy učinit první důležitý závěr, že přesnost měření v jednotlivých etapách lze považovat za odpovídající přesnosti předpokládané a vložené do vah. Z toho dále vyplývá, že kovarianční matice vyrovnaných neznámých byly vypočteny na základě apriorní směrodatné odchylky jednotkové. Čtvrtá kapitola je v kontextu celé práce naprosto klíčovou. Objasňuje metodu robustní transformace, tj. transformace další etapy do soustavy základní etapy, při níž je transformační klíč určován metodou robustního odhadu. Výpočet robustního 86
88 ZÁVĚR vyrovnání je iterační proces, při kterém jsou váhy měření v každé iteraci modifikovány v závislosti na velikosti oprav z předchozí iterace výpočtu. Konkrétně je aplikován odhad pomocí L 1 -normy, která minimalizuje sumu absolutních hodnot oprav měřených veličin. Měřenými veličinami jsou ve smyslu robustní transformace souřadnice identických bodů. Podstatou určení transformačního klíče metodou robustního odhadu je identifikace těch měřených veličin (souřadnic identických bodů), které jsou na základě testování oprav vzešlých ze stabilizovaného výpočtu robustního vyrovnání označeny jako odlehlé. Tyto identické body byly z původních souborů vyloučeny a takto očištěná data by měla splňovat podmínku normality. Původ dat z normálního rozdělení pravděpodobností je ideálním předpokladem pro správnost aplikace metody nejmenších čtverců. Provedl jsem tři verze výpočtu robustní transformace pomocí L 1 -normy. Tyto verze se od sebe liší způsobem, jakým jsou měřeným veličinám ve vyrovnání (souřadnicím identických bodů) přisuzovány váhy. V první verzi výpočtu je uvažován standardní model transformace, při níž jsou měřenými veličinami souřadnice bodů ve výstupní soustavě a přesnost všech souřadnic v rámci jedné etapy je považována za shodnou a rovnou aritmetickému průměru směrodatných odchylek souřadnic identických bodů v dané etapě. Druhá verze výpočtu je též založena na standardním modelu transformace, kde měřenými veličinami jsou souřadnice bodů ve výstupní soustavě. Přesnost měřených veličin je dána součtem diagonálních kovariančních matic souřadnic obou soustav. Třetí verze výpočtu je aplikací exaktního modelu transformace s uvážením přesností obou soustav. Měřenými veličinami ve vyrovnání jsou tentokrát souřadnice identických bodů v obou soustavách. Průběh výpočtu robustního vyrovnání lze shrnout následovně. Ve všech verzích výpočtu konverguje řešení robustního odhadu velmi rychle. Zpravidla již v iteraci, ve které je určen první robustní odhad, dochází k největšímu poklesu aposteriorní jednotkové směrodatné odchylky ^σ 0, a to řádově až o desítky procent vůči prvotnímu nerobustnímu odhadu MNČ. Vzhledem k předpisu pro výpočet robustních změn vah je výpočet značně numericky nestabilní. Problematickými se stávají zejména opravy, které nabývají velmi malých hodnot. Extrémně nízké opravy způsobují extrémní růst vah vkládaných do další iterace výpočtu. Tím vzniká značná nehomogenita v řádech prvků matice robustních změn vah, která implikuje špatnou podmíněnost celého systému. Reciproká hodnota čísla podmíněnosti matice se tak limitně blíží k nule a výpočet inverze matice selhává. Tato numerická nestabilita byla řešena dodáním dodatečných podmínek, které zajišťovaly předejití výskytu extrémně vysokých hodnot robustních změn vah. 87
89 ZÁVĚR Ke zhodnocení jednotlivých verzí výpočtu lze uvést, že druhá a třetí verze výpočtu si v identifikaci odlehlých hodnot naprosto odpovídají. Opravy měření vzešlé ze stabilizovaného výpočtu robustní transformace se ve druhé a třetí verzi liší v řádu setin mm a mezní hodnoty oprav jsou si rovny. Jedinou zaznamenanou odlišností ve výsledcích druhé a třetí verze je plynulost konvergence výpočtu ve třetí verzi konverguje výpočet plynuleji. První verze výpočtu dává z hlediska identifikace odlehlých hodnot mírně odlišné výsledky. To je dáno vstupním, příliš zobecněným předpokladem o shodné přesnosti souřadnic v rámci dané etapy. V páté kapitole provádím výběr takových identických bodů, které budou využity k výpočtu definitivního transformačního klíče. Výsledkem výše zmíněných robustních transformací jsou očištěné soubory identických bodů, které pro příslušnou transformaci splňují podmínku normality měřických dat. Účelem je však vyhledat sadu takových identických bodů, které nebyly označeny jako odlehlé ani v jedné z robustních transformací. Takové body poskytnou dostatečnou spolehlivost ve stálosti své polohy v průběhu celého sledovaného období a můžeme je tedy využít k výpočtu definitivního transformačního klíče metodou nejmenších čtverců. Výsledkem tohoto výběru je sada 11 identických bodů. Tyto body rovnoměrně pokrývají celý areál Pražského hradu. Definitivní transformační klíč byl využit k transformaci všech bodů sítě v dané etapě do soustavy etapy základní. Aplikací obecného zákona hromadění směrodatných odchylek byly určeny kovarianční matice přetransformovaných bodů. Seznamy přetransformovaných souřadnic bodů a charakteristiky jejich přesnosti jsou vstupními daty pro testování posunů. Šestá kapitola je zaměřena na statistické testování posunů bodů. V této kapitole nejprve odvozuji výpočet parametrů konfidenční elipsy chyb a dále uvádím konstrukci použitého testu. Testovány jsou souřadnicové rozdíly bodů pomocí dvourozměrných apriorních testů. Výpočet testování byl proveden v programu Gizela a kontrolně i pomocí vlastního výpočtu. Na základě použitých testů rozhoduji o zamítnutí či nezamítnutí testované nulové hypotézy. Zamítnutí nulové hypotézy implikuje přijetí konvenčního závěru, že ve vyhodnocované etapě byl s danou pravděpodobností prokázán posun bodu. Číselné výsledky testování doprovázím grafickými přílohami, které jsou automaticky generovány při zpracování programem Gizela. Těmito výstupy je grafické znázornění posunů bodů s vykreslením středních elips chyb bodů a grafické znázornění posunů s vykreslením konfidenčních elips chyb vektorů posunů. Kromě samotných výsledků testování posunů plynou velmi důležité závěry z porovnání těchto výsledků s výsledky robustních transformací. Na základě testování 88
90 ZÁVĚR oprav vzešlých ze stabilizovaného výpočtu robustního vyrovnání byly při jednotlivých transformacích identifikovány odlehlé hodnoty souřadnic identických bodů. Obdobně pak byly v jednotlivých etapách označeny body, u nichž byl na základě dvourozměrných apriorních testů prokázán posun. Z porovnání těchto dvou typů výsledků je pak možné učinit závěr, že testy posunů bodů velmi dobře potvrzují výsledky robustních transformací (ve smyslu identifikace odlehlých hodnot). Na základě testování posunů všech bodů sítě byla vybrána sada 15 bodů, u nichž nebyl prokázán posun ani v jedné z vyhodnocovaných etap. Tyto body lze se známým rizikem považovat za stabilní. U ostatních bodů sítě byla v nejméně jedné etapě prokázána nestabilita, která byla pravděpodobně způsobena vnějšími vlivy. Diplomová práce byla zpracována s použitím výhradně volně distribuovaného software, tj. knihovny kartografických zobrazení PROJ.4, programovacím jazykem pro numerické výpočty GNU Octave, editorem vektorové grafiky Inkscape, programem pro vyrovnání geodetických sítí GNU Gama a programem pro zpracování etapových měření Gizela. Text práce byl vysázen typografickým systémem L A TEX. 89
91 POUŽITÉ ZDROJE Použité zdroje [1] RYS, Pavel. Etapové měření nivelační vztažné sítě Pražského hradu. Praha, Bakalářská práce. FSv ČVUT v Praze. Vedoucí práce Ing. Tomáš Kubín, Ph.D. [2] ZEMĚMĚŘICKÝ ÚŘAD. Metodický návod pro práce v Základním výškovém bodovém poli. [s.l.] : [s.n.], [3] JANDOUREK, Jan. Geodézie IV: Úpravy měřených veličin před výpočty. Geodetická úloha a její kvalitativní hodnocení. Praha: ČVUT, ISBN [4] HRADILEK, Ludvik. Vysokohorská geodézie: trigonometrická nivelace a trojrozměrná terestrická triangulace. První vydání. Praha: Academia, [5] JIŘIKOVSKÝ, Tomáš. Inovace měření v lokálních geodetických sítích. Praha, Disertační práce. FSv ČVUT v Praze. Vedoucí práce Doc. Ing. Jaromír Procházka, CSc. [6] VANĚČEK, Jan. Zpracování měření v lokální prostorové síti na Pražském hradě. Praha, Diplomová práce. FSv ČVUT v Praze. Vedoucí práce Ing. Tomáš Jiřikovský, Ph.D. [7] BUCHAR, Petr. Matematická kartografie. Praha: Nakladatelství ČVUT, ISBN [8] PROJ.4 - Cartographic Projections Library [online] [cit ]. Dostupné z: [9] CIMBÁLNÍK, Miloš, Antonín ZEMAN a Jan KOSTELECKÝ. Základy vyšší a fyzikální geodézie. Praha: ČVUT, ISBN [10] PAVELKA, Karel a Martin ŠTRONER. Lineární prostorová transformace. Geodetický a kartografický obzor. Praha: Vesmír, 2001, roč. 47, č. 5. ISSN [11] HAMPACHER, Miroslav a Martin ŠTRONER. Zpracování a analýza měření v inženýrské geodézii. Praha: ČVUT, ISBN [12] ČEPEK, Aleš. GNU Gama s. Dostupné z: org/software/gama/manual/gama.pdf 90
92 POUŽITÉ ZDROJE [13] MERVART, Leoš a Zdeněk LUKEŠ. Adjustment calculus. Praha: ČVUT, ISBN [14] TŘASÁK, Pavel. Simulace, modelování a statistické zpracování geodetických měření. Praha, Disertační práce. FSv ČVUT v Praze. Vedoucí práce Doc. Ing. Martin Štroner, Ph.D. [15] KOCH, Karl-Rudolf. Parameter Estimation and Hypothesis Testing in Linear Models. Berlin: Springer, ISBN [16] JUREČKOVÁ, Jana. Robustní statistické metody. Praha: Karolinum, ISBN [17] HUBER, Peter J. Robust Statistics. New York: John Wiley & Sons, ISBN [18] HAMPEL, Frank R. Robust Statistics: The Approach Based on Influnce Functions. New York: John Wiley & Sons, ISBN [19] TŘASÁK, Pavel a Martin ŠTRONER. Posouzení robustních metod vyrovnání. Geodetický a kartografický obzor. Praha: Vesmír, 2012, roč. 58, č. 4. ISSN [20] XU, Peiliang. On robust estimation with correlated observations. Bulletin Geodesique. Berlin: Springer, 1989, Vol. 63, No.3, pp ISSN DOI: /BF [21] YANG, Yuan-xi. Robust Estimation for Dependent Observations. Manuscripta Geodaetica. Berlin: Springer, 1994, Vol. 19, No.1, pp ISSN [22] FAN, Huaan. Theory of Errors and Least Squares Adjustment. Stockholm: Universitetsservice AB, ISBN
93 Seznam obrázků 1.1 Realizace vztažného bodu ve zhlaví vrtu Lambertovo konformní kuželové zobrazení Přibližný způsob transformace kovarianční matice vektoru Odhad metodou nejmenších čtverců tvar funkce ψ Huberův robustní M-odhad tvar funkce ψ Odhad pomocí L 1 -normy tvar funkce ψ Přehledka bodů polohové sítě Pražského hradu A.1 Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu A.2 Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu A.3 Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu A.4 Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu A.5 Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu A.6 Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu A.7 Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu B.1 Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu B.2 Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu B.3 Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu B.4 Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu B.5 Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu B.6 Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu B.7 Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu C.1 Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu C.2 Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu C.3 Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu C.4 Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu C.5 Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu C.6 Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu C.7 Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu F.1 Zobrazení a testování posunů bodu F.2 Zobrazení a testování posunů bodu F.3 Zobrazení a testování posunů bodu F.4 Zobrazení a testování posunů bodu F.5 Zobrazení a testování posunů bodu F.6 Zobrazení a testování posunů bodu
94 F.7 Zobrazení a testování posunů bodu F.8 Zobrazení a testování posunů bodu F.9 Zobrazení a testování posunů bodu F.10 Zobrazení a testování posunů bodu F.11 Zobrazení a testování posunů bodu F.12 Zobrazení a testování posunů bodu F.13 Zobrazení a testování posunů bodu F.14 Zobrazení a testování posunů bodu F.15 Zobrazení a testování posunů bodu F.16 Zobrazení a testování posunů bodu F.17 Zobrazení a testování posunů bodu F.18 Zobrazení a testování posunů bodu F.19 Zobrazení a testování posunů bodu F.20 Zobrazení a testování posunů bodu F.21 Zobrazení a testování posunů bodu F.22 Zobrazení a testování posunů bodu F.23 Zobrazení a testování posunů bodu F.24 Zobrazení a testování posunů bodu F.25 Zobrazení a testování posunů bodu F.26 Zobrazení a testování posunů bodu
95 Seznam tabulek 1.1 Geotechnické vrty Testování aposteriorních jednotkových směrodatných odchylek Huberův M-odhad přehled funkcí (odhadová, vlivová, váhová) L 1 -norma přehled funkcí (odhadová, vlivová, váhová) Označení jednotlivých etap měření sítě Srovnání počtů nadbytečných měření v jednotlivých verzích výpočtu Vyloučené identické body při robustních transformacích Identické body vyhovující statistickému testu oprav Výpočet p-hodnot Označení zaměření všech bodů sítě Pravděpodobnost uvnitř konfidenční elipsy chyb Označení zaměření stabilních bodů sítě Porovnání výsledků testování s výsledky robustní transformace A.1 Robustní transformace E 1 do E 0 verze výpočtu A.2 Robustní transformace E 2 do E 1 verze výpočtu A.3 Robustní transformace E 3 do E 1 verze výpočtu A.4 Robustní transformace E 4 do E 1 verze výpočtu A.5 Robustní transformace E 5 do E 1 verze výpočtu A.6 Robustní transformace E 6 do E 1 verze výpočtu A.7 Robustní transformace E 7 do E 1 verze výpočtu B.1 Robustní transformace E 1 do E 0 verze výpočtu B.2 Robustní transformace E 2 do E 1 verze výpočtu B.3 Robustní transformace E 3 do E 1 verze výpočtu B.4 Robustní transformace E 4 do E 1 verze výpočtu B.5 Robustní transformace E 5 do E 1 verze výpočtu B.6 Robustní transformace E 6 do E 1 verze výpočtu B.7 Robustní transformace E 7 do E 1 verze výpočtu C.1 Robustní transformace E 1 do E 0 verze výpočtu C.2 Robustní transformace E 2 do E 1 verze výpočtu C.3 Robustní transformace E 3 do E 1 verze výpočtu C.4 Robustní transformace E 4 do E 1 verze výpočtu C.5 Robustní transformace E 5 do E 1 verze výpočtu C.6 Robustní transformace E 6 do E 1 verze výpočtu C.7 Robustní transformace E 7 do E 1 verze výpočtu
96 D.1 Souřadnice v základní etapě E 0 (2008/04) D.2 Přetransformované souřadnice v etapě E 1 (2008/11) D.3 Souřadnice v základní etapě E 1 (2008/11) D.4 Přetransformované souřadnice v etapě E 2 (2009/05) D.5 Přetransformované souřadnice v etapě E 3 (2009/11) D.6 Přetransformované souřadnice v etapě E 4 (2010/05) D.7 Přetransformované souřadnice v etapě E 5 (2010/10) D.8 Přetransformované souřadnice v etapě E 6 (2012/05) D.9 Přetransformované souřadnice v etapě E 7 (2012/11) E.1 Posuny bodů v etapě E 1 vůči etapě E E.2 Posuny bodů v etapě E 2 vůči etapě E E.3 Posuny bodů v etapě E 3 vůči etapě E E.4 Posuny bodů v etapě E 4 vůči etapě E E.5 Posuny bodů v etapě E 5 vůči etapě E E.6 Posuny bodů v etapě E 6 vůči etapě E E.7 Posuny bodů v etapě E 7 vůči etapě E
97 SEZNAM PŘÍLOH Seznam příloh A Výsledky verze výpočtu 1 97 B Výsledky verze výpočtu C Výsledky verze výpočtu D Přetransformované souřadnice 118 D.1 Základní etapa E D.2 Základní etapa E E Číselné výsledky testování posunů 127 E.1 Základní etapa E E.2 Základní etapa E F Grafické výsledky testování posunů
98 A. VÝSLEDKY VERZE VÝPOČTU 1 A Výsledky verze výpočtu 1 Tab. A.1: Robustní transformace E 1 do E 0 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,24 0,01 2,37 2,33 6,10 6, ,55 1,66 2,36 2,27 6,06 5, ,60 2,19 2,30 2,35 5,91 6, ,83 2,61 2,40 2,42 6,17 6, ,00 0,83 2,42 2,42 6,23 6, ,92 3,59 2,39 2,35 6,15 6, ,46 0,62 2,37 2,40 6,08 6, ,37 3,39 2,42 2,38 6,23 6, ,59 1,34 2,36 2,31 6,07 5, ,04 0,00 2,29 2,29 5,90 5, ,06 3,24 2,34 2,40 6,02 6, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.1: Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu 1 97
99 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.2: Robustní transformace E 2 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,16 0,38 2,43 2,40 6,24 6, ,83 0,11 2,45 2,36 6,29 6, ,69 1,70 2,40 2,43 6,18 6, ,02 7,42 2,48 2,48 6,36 6, ,17 5,01 2,49 2,46 6,39 6, ,33 3,00 2,49 2,48 6,39 6, ,00 1,45 2,48 2,48 6,38 6, ,30 1,29 2,45 2,42 6,30 6, ,39 2,23 2,42 2,46 6,22 6, ,20 0,64 2,48 2,48 6,38 6, ,57 3,24 2,39 2,46 6,14 6, ,71 5,90 2,49 2,46 6,39 6, ,09 0,00 2,41 2,38 6,20 6, ,26 0,05 2,40 2,38 6,17 6, ,47 1,11 2,40 2,47 6,16 6, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.2: Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu 1 98
100 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.3: Robustní transformace E 3 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,48 1,17 2,24 2,22 5,75 5, ,51 0,00 2,26 2,18 5,80 5, ,00 8,52 2,22 2,24 5,70 5, ,33 6,00 2,28 2,29 5,87 5, ,83 3,27 2,29 2,27 5,89 5, ,82 0,62 2,29 2,29 5,89 5, ,37 0,12 2,29 2,29 5,88 5, ,01 1,02 2,26 2,23 5,80 5, ,92 1,20 2,23 2,27 5,73 5, ,10 1,48 2,29 2,29 5,88 5, ,68 15,08 2,20 2,27 5,66 5, ,82 2,93 2,29 2,26 5,89 5, ,65 2,41 2,23 2,20 5,72 5, ,22 4,00 2,21 2,19 5,69 5, ,14 1,03 2,21 2,27 5,68 5, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.3: Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu 1 99
101 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.4: Robustní transformace E 4 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,00 1,11 1,98 1,96 5,08 5, ,27 3,25 1,99 1,92 5,12 4, ,58 1,11 1,96 1,98 5,03 5, ,50 2,93 2,01 2,02 5,18 5, ,64 2,72 2,02 2,00 5,20 5, ,04 1,55 2,02 2,02 5,20 5, ,68 0,93 2,02 2,02 5,19 5, ,47 0,42 1,99 1,97 5,12 5, ,84 0,22 1,97 2,00 5,06 5, ,36 1,17 2,02 2,02 5,19 5, ,01 1,56 1,94 2,00 4,99 5, ,77 0,00 2,02 2,00 5,20 5, ,32 0,00 1,96 1,94 5,05 4, ,14 0,01 1,95 1,94 5,02 4, ,44 0,22 1,95 2,01 5,01 5, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.4: Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu 1 100
102 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.5: Robustní transformace E 5 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,54 0,94 1,96 1,94 5,03 4, ,47 2,33 1,97 1,90 5,07 4, ,60 1,98 1,94 1,96 4,98 5, ,22 1,22 2,00 2,00 5,13 5, ,44 4,77 2,00 1,98 5,15 5, ,29 1,83 2,01 2,00 5,15 5, ,00 1,01 2,00 2,00 5,14 5, ,66 3,05 1,97 1,95 5,08 5, ,38 2,08 1,95 1,98 5,01 5, ,70 0,00 2,00 2,00 5,14 5, ,33 3,05 1,93 1,99 4,95 5, ,25 0,53 2,00 1,98 5,15 5, ,81 0,07 1,95 1,92 5,00 4, ,82 0,82 1,94 1,92 4,97 4, ,49 2,67 1,93 1,99 4,97 5, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.5: Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu 1 101
103 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.6: Robustní transformace E 6 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 1,41 2,78 2,68 2,66 6,90 6, ,34 3,10 2,71 2,61 6,95 6, ,44 0,00 2,66 2,69 6,83 6, ,00 0,32 2,74 2,74 7,04 7, ,19 0,29 2,75 2,72 7,06 6, ,70 1,30 2,75 2,75 7,07 7, ,04 0,09 2,74 2,75 7,05 7, ,59 0,54 2,71 2,67 6,96 6, ,94 2,95 2,68 2,72 6,87 6, ,49 0,02 2,75 2,75 7,06 7, ,75 0,68 2,64 2,72 6,79 7, ,96 1,11 2,75 2,72 7,06 6, ,56 4,83 2,67 2,63 6,86 6, ,94 2,32 2,65 2,63 6,82 6, ,68 3,26 2,65 2,73 6,81 7, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.6: Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu 1 102
104 A. VÝSLEDKY VERZE VÝPOČTU 1 Tab. A.7: Robustní transformace E 7 do E 1 verze výpočtu 1 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,80 0,82 2,86 2,83 7,35 7, ,11 1,93 2,88 2,78 7,40 7, ,56 1,73 2,83 2,86 7,27 7, ,48 1,98 2,92 2,92 7,49 7, ,00 0,20 2,93 2,90 7,52 7, ,58 0,00 2,93 2,93 7,53 7, ,32 1,03 2,92 2,92 7,51 7, ,25 1,90 2,88 2,85 7,41 7, ,74 1,58 2,85 2,90 7,32 7, ,45 1,17 2,92 2,92 7,51 7, ,83 2,43 2,81 2,90 7,23 7, ,47 5,87 2,93 2,89 7,52 7, ,89 2,85 2,84 2,80 7,30 7, ,19 2,56 2,83 2,80 7,27 7, ,97 4,66 2,82 2,90 7,25 7, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. A.7: Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu 1 103
105 B. VÝSLEDKY VERZE VÝPOČTU 2 B Výsledky verze výpočtu 2 Tab. B.1: Robustní transformace E 1 do E 0 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,53 0,78 1,80 1,67 4,62 4, ,28 1,70 2,39 2,19 6,15 5, ,98 2,30 2,18 2,25 5,59 5, ,98 3,12 5,55 3,37 14,26 8, ,00 1,17 2,36 2,23 6,07 5, ,15 2,85 2,06 1,90 5,30 4, ,15 0,01 2,00 2,16 5,13 5, ,39 3,58 4,87 2,87 12,51 7, ,92 0,53 2,21 2,09 5,67 5, ,42 0,00 1,78 1,58 4,58 4, ,70 2,64 1,92 1,98 4,94 5, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. B.1: Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu 2 104
106 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.2: Robustní transformace E 2 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,19 0,28 1,83 1,62 4,70 4, ,84 0,16 2,73 2,45 7,02 6, ,71 1,76 2,12 1,85 5,45 4, ,02 7,33 3,12 2,91 8,02 7, ,16 4,92 2,16 1,82 5,56 4, ,34 3,07 1,93 1,85 4,96 4, ,00 1,52 2,26 2,47 5,80 6, ,33 1,18 1,90 1,95 4,89 5, ,35 2,14 2,03 2,13 5,21 5, ,21 0,71 2,76 2,84 7,10 7, ,60 3,31 2,62 3,52 6,74 9, ,72 5,97 8,11 4,83 20,84 12, ,13 0,11 2,36 2,07 6,07 5, ,28 0,00 1,69 1,51 4,34 3, ,51 1,02 1,85 1,87 4,74 4, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. B.2: Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu 2 105
107 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.3: Robustní transformace E 3 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,82 1,41 1,70 1,62 4,37 4, ,57 0,17 2,22 2,19 5,71 5, ,00 8,42 2,27 2,07 5,83 5, ,21 5,90 3,05 2,92 7,84 7, ,62 3,12 2,07 1,82 5,32 4, ,63 0,64 1,71 1,65 4,39 4, ,51 0,10 2,02 2,34 5,20 6, ,32 0,80 1,81 1,95 4,65 5, ,57 1,36 1,98 2,19 5,09 5, ,95 1,47 2,55 2,77 6,55 7, ,69 15,03 3,08 4,21 7,91 10, ,03 2,87 5,04 2,56 12,96 6, ,01 2,15 2,51 2,20 6,46 5, ,22 3,85 1,55 1,43 3,97 3, ,52 0,89 1,77 1,87 4,55 4, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. B.3: Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu 2 106
108 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.4: Robustní transformace E 4 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,01 1,04 1,68 1,56 4,31 4, ,34 3,23 2,10 2,00 5,40 5, ,50 1,10 1,83 1,58 4,71 4, ,56 2,97 2,35 2,27 6,05 5, ,60 2,78 1,99 1,79 5,12 4, ,01 1,53 1,69 1,60 4,35 4, ,63 0,91 1,85 1,99 4,76 5, ,48 0,49 1,73 1,86 4,46 4, ,84 0,16 1,85 1,98 4,76 5, ,31 1,20 2,08 2,19 5,34 5, ,10 1,55 2,25 2,46 5,78 6, ,81 0,01 4,49 2,40 11,54 6, ,32 0,08 2,03 1,87 5,23 4, ,06 0,02 1,51 1,40 3,88 3, ,44 0,27 1,79 1,85 4,61 4, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. B.4: Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu 2 107
109 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.5: Robustní transformace E 5 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,77 1,00 1,64 1,53 4,23 3, ,62 2,39 2,06 2,00 5,30 5, ,47 1,94 1,84 1,58 4,72 4, ,39 1,20 2,41 2,27 6,18 5, ,25 4,74 1,95 1,71 5,02 4, ,10 1,82 1,69 1,60 4,35 4, ,17 1,01 1,89 1,95 4,87 5, ,88 3,00 1,73 1,76 4,45 4, ,15 2,05 1,90 1,98 4,87 5, ,52 0,01 2,08 2,13 5,34 5, ,20 3,03 2,05 2,30 5,28 5, ,45 0,51 4,46 2,37 11,47 6, ,04 0,01 2,03 1,88 5,23 4, ,68 0,77 1,52 1,40 3,89 3, ,73 2,64 1,88 1,89 4,83 4, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. B.5: Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu 2 108
110 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.6: Robustní transformace E 6 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 1,57 3,03 2,17 2,46 5,59 6, ,29 3,16 2,60 2,47 6,69 6, ,35 0,01 2,81 2,08 7,23 5, ,00 0,17 3,41 2,81 8,76 7, ,13 0,48 2,82 2,27 7,24 5, ,65 1,38 2,45 2,46 6,28 6, ,02 0,00 2,58 2,92 6,63 7, ,73 0,30 2,05 2,07 5,28 5, ,77 2,76 2,04 2,28 5,25 5, ,47 0,10 3,05 3,23 7,83 8, ,85 0,65 4,11 3,50 10,57 8, ,02 1,13 4,97 3,01 12,78 7, ,38 5,10 2,85 3,00 7,32 7, ,84 2,27 2,51 2,03 6,44 5, ,87 3,08 2,22 2,66 5,71 6, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. B.6: Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu 2 109
111 B. VÝSLEDKY VERZE VÝPOČTU 2 Tab. B.7: Robustní transformace E 7 do E 1 verze výpočtu 2 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,66 0,59 2,28 2,02 5,86 5, ,26 2,13 2,68 2,93 6,89 7, ,35 1,85 2,82 2,22 7,24 5, ,39 2,08 3,66 3,44 9,40 8, ,01 0,05 3,21 2,99 8,25 7, ,56 0,00 2,28 2,06 5,86 5, ,25 1,03 2,50 2,74 6,42 7, ,14 2,12 2,47 2,52 6,34 6, ,89 1,73 2,83 2,88 7,27 7, ,52 1,17 2,96 3,13 7,61 8, ,60 2,50 3,41 3,57 8,77 9, ,47 5,95 5,25 3,37 13,48 8, ,73 3,11 3,23 2,97 8,30 7, ,98 2,74 2,17 2,08 5,58 5, ,80 4,79 3,07 3,23 7,88 8, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. B.7: Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu 2 110
112 C. VÝSLEDKY VERZE VÝPOČTU 3 C Výsledky verze výpočtu 3 Tab. C.1: Robustní transformace E 1 do E 0 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,53 0,78 1,80 1,67 4,62 4, ,28 1,70 2,39 2,19 6,15 5, ,98 2,30 2,18 2,25 5,59 5, ,98 3,12 5,55 3,37 14,26 8, ,00 1,17 2,36 2,23 6,07 5, ,15 2,85 2,06 1,90 5,30 4, ,15 0,01 2,00 2,16 5,13 5, ,39 3,58 4,87 2,87 12,51 7, ,92 0,52 2,21 2,09 5,67 5, ,43 0,00 1,78 1,58 4,58 4, ,70 2,64 1,92 1,98 4,94 5, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. C.1: Vývoj ^σ 0 při robustní transformaci E 1 do E 0 verze výpočtu 3 111
113 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.2: Robustní transformace E 2 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,14 0,38 1,83 1,62 4,70 4, ,82 0,16 2,73 2,45 7,02 6, ,67 1,74 2,12 1,85 5,45 4, ,02 7,40 3,12 2,91 8,02 7, ,18 5,00 2,16 1,82 5,56 4, ,33 3,02 1,93 1,85 4,96 4, ,00 1,48 2,26 2,47 5,80 6, ,28 1,28 1,90 1,95 4,89 5, ,41 2,22 2,03 2,13 5,21 5, ,20 0,67 2,76 2,84 7,10 7, ,56 3,28 2,62 3,52 6,74 9, ,70 5,94 8,11 4,83 20,84 12, ,07 0,00 2,36 2,07 6,07 5, ,24 0,00 1,69 1,51 4,34 3, ,44 1,10 1,85 1,87 4,74 4, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. C.2: Vývoj ^σ 0 při robustní transformaci E 2 do E 1 verze výpočtu 3 112
114 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.3: Robustní transformace E 3 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,98 1,62 1,70 1,62 4,37 4, ,59 0,16 2,22 2,19 5,71 5, ,00 8,46 2,27 2,07 5,83 5, ,16 5,75 3,05 2,92 7,84 7, ,53 2,94 2,07 1,82 5,32 4, ,54 0,74 1,71 1,65 4,39 4, ,57 0,00 2,02 2,34 5,20 6, ,47 0,60 1,81 1,95 4,65 5, ,40 1,53 1,98 2,19 5,09 5, ,88 1,37 2,55 2,77 6,55 7, ,70 15,11 3,08 4,21 7,91 10, ,12 2,94 5,04 2,56 12,96 6, ,17 1,93 2,51 2,20 6,46 5, ,22 3,87 1,55 1,43 3,97 3, ,69 0,72 1,77 1,87 4,55 4, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. C.3: Vývoj ^σ 0 při robustní transformaci E 3 do E 1 verze výpočtu 3 113
115 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.4: Robustní transformace E 4 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,00 1,06 1,68 1,56 4,31 4, ,32 3,23 2,10 2,00 5,40 5, ,52 1,11 1,83 1,58 4,71 4, ,54 2,95 2,35 2,27 6,05 5, ,61 2,75 1,99 1,79 5,12 4, ,02 1,54 1,69 1,60 4,35 4, ,65 0,92 1,85 1,99 4,76 5, ,48 0,47 1,73 1,86 4,46 4, ,84 0,19 1,85 1,98 4,76 5, ,32 1,18 2,08 2,19 5,34 5, ,07 1,56 2,25 2,46 5,78 6, ,80 0,00 4,49 2,40 11,54 6, ,32 0,05 2,03 1,87 5,23 4, ,09 0,02 1,51 1,40 3,88 3, ,43 0,25 1,79 1,85 4,61 4, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. C.4: Vývoj ^σ 0 při robustní transformaci E 4 do E 1 verze výpočtu 3 114
116 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.5: Robustní transformace E 5 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 0,60 1,00 1,64 1,53 4,23 3, ,46 2,38 2,06 2,00 5,30 5, ,63 1,95 1,84 1,58 4,72 4, ,22 1,19 2,41 2,27 6,18 5, ,42 4,73 1,95 1,71 5,02 4, ,27 1,83 1,69 1,60 4,35 4, ,01 1,02 1,89 1,95 4,87 5, ,71 3,00 1,73 1,76 4,45 4, ,32 2,04 1,90 1,98 4,87 5, ,69 0,00 2,08 2,13 5,34 5, ,37 3,04 2,05 2,30 5,28 5, ,28 0,52 4,46 2,37 11,47 6, ,87 0,00 2,03 1,88 5,23 4, ,85 0,78 1,52 1,40 3,89 3, ,56 2,64 1,88 1,89 4,83 4, m 0 aposteriori m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = iterace Obr. C.5: Vývoj ^σ 0 při robustní transformaci E 5 do E 1 verze výpočtu 3 115
117 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.6: Robustní transformace E 6 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 1,57 3,03 2,17 2,46 5,59 6, ,30 3,15 2,60 2,47 6,69 6, ,35 0,00 2,81 2,08 7,23 5, ,00 0,17 3,41 2,81 8,76 7, ,13 0,48 2,82 2,27 7,24 5, ,65 1,39 2,45 2,46 6,28 6, ,02 0,00 2,58 2,92 6,63 7, ,73 0,30 2,05 2,07 5,28 5, ,77 2,76 2,04 2,28 5,25 5, ,47 0,10 3,05 3,23 7,83 8, ,85 0,64 4,11 3,50 10,57 8, ,02 1,14 4,97 3,01 12,78 7, ,38 5,10 2,85 3,00 7,32 7, ,85 2,28 2,51 2,03 6,44 5, ,87 3,08 2,22 2,66 5,71 6, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. C.6: Vývoj ^σ 0 při robustní transformaci E 6 do E 1 verze výpočtu 3 116
118 C. VÝSLEDKY VERZE VÝPOČTU 3 Tab. C.7: Robustní transformace E 7 do E 1 verze výpočtu 3 bod v X [mm] v Y [mm] σ vx σ vy v MX v MY test v X test v Y 501 2,60 0,51 2,28 2,02 5,86 5, ,32 2,21 2,68 2,93 6,89 7, ,27 1,90 2,82 2,22 7,24 5, ,36 2,10 3,66 3,44 9,40 8, ,00 0,00 3,21 2,99 8,25 7, ,56 0,00 2,28 2,06 5,86 5, ,23 1,02 2,50 2,74 6,42 7, ,09 2,19 2,47 2,52 6,34 6, ,95 1,77 2,83 2,88 7,27 7, ,54 1,16 2,96 3,13 7,61 8, ,52 2,53 3,41 3,57 8,77 9, ,47 5,98 5,25 3,37 13,48 8, ,67 3,20 3,23 2,97 8,30 7, ,90 2,81 2,17 2,08 5,58 5, ,72 4,84 3,07 3,23 7,88 8, m 0 apriori = (20) m 0 aposteriori = (1) m 0 aposteriori = m 0 aposteriori iterace Obr. C.7: Vývoj ^σ 0 při robustní transformaci E 7 do E 1 verze výpočtu 3 117
119 D. PŘETRANSFORMOVANÉ SOUŘADNICE D Přetransformované souřadnice D.1 Základní etapa E 0 V této příloze jsou uvedeny přetransformované souřadnice všech bodů (identických i neidentických) těch etap, které jsou transformovány do soustavy základní etapy E 0. To se týká pouze jediné etapy E 1. Seznamy souřadnic jsou uvedeny ve formátu, který má podobu vstupního textového souboru do programu Gizela. Tab. D.1: Souřadnice v základní etapě E 0 (2008/04) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9733 0,0010 0,0010 0, , ,2061 0,0015 0,0013 0, , ,3008 0,0023 0,0020 0, , ,1740 0,0020 0,0017 0, , ,8539 0,0016 0,0015 0, , ,9670 0,0016 0,0018 0, , ,8782 0,0052 0,0028 0, , ,6046 0,0018 0,0017 0, , ,7774 0,0024 0,0019 0, , ,1549 0,0014 0,0012 0, , ,6735 0,0012 0,0014 0, , ,7190 0,0024 0,0019 0, , ,2874 0,0014 0,0014 0, , ,0294 0,0013 0,0011 0, , ,7718 0,0011 0,0011 0,
120 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.2: Přetransformované souřadnice v etapě E 1 (2008/11) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9727 0,0019 0,0018 0, , ,2068 0,0025 0,0020 0, , ,2961 0,0044 0,0024 0, , ,1757 0,0030 0,0023 0, , ,8543 0,0022 0,0022 0, , ,9637 0,0021 0,0018 0, , ,6186 0,0022 0,0020 0, , ,4387 0,0024 0,0022 0, , ,8489 0,0023 0,0022 0, , ,8747 0,0023 0,0021 0, , ,5876 0,0020 0,0019 0, , ,6028 0,0019 0,0018 0, , ,3612 0,0021 0,0022 0, , ,4492 0,0021 0,0020 0, , ,8626 0,0021 0,0020 0, , ,7582 0,0020 0,0020 0, , ,6189 0,0022 0,0020 0, , ,7742 0,0024 0,0022 0, , ,1578 0,0019 0,0019 0, , ,6733 0,0020 0,0020 0, , ,5763 0,0021 0,0020 0, , ,2963 0,0024 0,0023 0, , ,7146 0,0044 0,0025 0, , ,2882 0,0021 0,0020 0, , ,0282 0,0019 0,0018 0, , ,7743 0,0020 0,0020 0, D.2 Základní etapa E 1 V této příloze jsou uvedeny přetransformované souřadnice identických i neidentických bodů těch etap, které jsou transformovány do soustavy základní etapy E 1. Důvody k volbě druhé základní etapy jsou uvedeny v kapitole
121 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.3: Souřadnice v základní etapě E 1 (2008/11) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9712 0,0017 0,0016 0, , ,2057 0,0023 0,0019 0, , ,2955 0,0043 0,0022 0, , ,1753 0,0029 0,0020 0, , ,8540 0,0020 0,0019 0, , ,9631 0,0018 0,0016 0, , ,6178 0,0020 0,0018 0, , ,4378 0,0021 0,0021 0, , ,8478 0,0021 0,0021 0, , ,8736 0,0021 0,0020 0, , ,5863 0,0019 0,0017 0, , ,6019 0,0017 0,0016 0, , ,3607 0,0019 0,0020 0, , ,4485 0,0019 0,0018 0, , ,8620 0,0019 0,0018 0, , ,7573 0,0018 0,0018 0, , ,6181 0,0020 0,0018 0, , ,7737 0,0023 0,0020 0, , ,1564 0,0017 0,0017 0, , ,6721 0,0018 0,0018 0, , ,5754 0,0019 0,0019 0, , ,2956 0,0021 0,0021 0, , ,7139 0,0043 0,0023 0, , ,2866 0,0019 0,0018 0, , ,0278 0,0016 0,0015 0, , ,7730 0,0018 0,0018 0,
122 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.4: Přetransformované souřadnice v etapě E 2 (2009/05) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9706 0,0013 0,0012 0, , ,3005 0,0069 0,0040 0, , ,1747 0,0042 0,0024 0, , ,8540 0,0022 0,0020 0, , ,9647 0,0017 0,0014 0, , ,8660 0,0025 0,0023 0, , ,5811 0,0014 0,0011 0, , ,6048 0,0013 0,0013 0, , ,7586 0,0017 0,0019 0, , ,7781 0,0071 0,0034 0, , ,1548 0,0013 0,0014 0, , ,6696 0,0014 0,0015 0, , ,5760 0,0022 0,0023 0, , ,2988 0,0020 0,0030 0, , ,7197 0,0069 0,0044 0, , ,2863 0,0018 0,0016 0, , ,0277 0,0014 0,0013 0, , ,7717 0,0012 0,0011 0,
123 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.5: Přetransformované souřadnice v etapě E 3 (2009/11) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9720 0,0010 0,0012 0, , ,2971 0,0021 0,0012 0, , ,1707 0,0018 0,0017 0, , ,8518 0,0014 0,0017 0, , ,9698 0,0018 0,0017 0, , ,8667 0,0024 0,0023 0, , ,5824 0,0012 0,0011 0, , ,6012 0,0009 0,0009 0, , ,7559 0,0013 0,0017 0, , ,7728 0,0009 0,0010 0, , ,1549 0,0011 0,0014 0, , ,6726 0,0013 0,0016 0, , ,5726 0,0019 0,0022 0, , ,3091 0,0026 0,0038 0, , ,7152 0,0028 0,0015 0, , ,2840 0,0020 0,0017 0, , ,0297 0,0011 0,0011 0, , ,7713 0,0011 0,0011 0,
124 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.6: Přetransformované souřadnice v etapě E 4 (2010/05) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9714 0,0009 0,0010 0, , ,2083 0,0014 0,0013 0, , ,2942 0,0012 0,0010 0, , ,1713 0,0013 0,0014 0, , ,8515 0,0011 0,0013 0, , ,9647 0,0011 0,0009 0, , ,6194 0,0013 0,0011 0, , ,4391 0,0015 0,0013 0, , ,8473 0,0015 0,0014 0, , ,8703 0,0014 0,0013 0, , ,5830 0,0010 0,0010 0, , ,6034 0,0008 0,0008 0, , ,3584 0,0011 0,0011 0, , ,4481 0,0010 0,0010 0, , ,8621 0,0009 0,0009 0, , ,7582 0,0009 0,0012 0, , ,6183 0,0012 0,0010 0, , ,7720 0,0010 0,0010 0, , ,1551 0,0010 0,0012 0, , ,6717 0,0011 0,0012 0, , ,5743 0,0012 0,0013 0, , ,2974 0,0014 0,0015 0, , ,7142 0,0015 0,0011 0, , ,2856 0,0012 0,0012 0, , ,0285 0,0010 0,0009 0, , ,7722 0,0010 0,0009 0,
125 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.7: Přetransformované souřadnice v etapě E 5 (2010/10) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9721 0,0009 0,0009 0, , ,2068 0,0010 0,0008 0, , ,2957 0,0011 0,0009 0, , ,1699 0,0013 0,0013 0, , ,8519 0,0011 0,0013 0, , ,9653 0,0011 0,0009 0, , ,6217 0,0011 0,0010 0, , ,4423 0,0014 0,0013 0, , ,8503 0,0015 0,0015 0, , ,8725 0,0014 0,0013 0, , ,5816 0,0009 0,0009 0, , ,6039 0,0008 0,0008 0, , ,3604 0,0011 0,0011 0, , ,4492 0,0011 0,0009 0, , ,8641 0,0012 0,0010 0, , ,7584 0,0010 0,0011 0, , ,6188 0,0013 0,0010 0, , ,7731 0,0008 0,0009 0, , ,1533 0,0010 0,0011 0, , ,6700 0,0011 0,0012 0, , ,5756 0,0012 0,0012 0, , ,2989 0,0010 0,0013 0, , ,7146 0,0014 0,0010 0, , ,2864 0,0012 0,0012 0, , ,0289 0,0010 0,0009 0, , ,7704 0,0012 0,0010 0,
126 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.8: Přetransformované souřadnice v etapě E 6 (2012/05) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9736 0,0018 0,0024 0, , ,2081 0,0022 0,0021 0, , ,8512 0,0022 0,0022 0, , ,9633 0,0027 0,0019 0, , ,6159 0,0034 0,0023 0, , ,4358 0,0039 0,0023 0, , ,8489 0,0035 0,0024 0, , ,8732 0,0029 0,0023 0, , ,5864 0,0023 0,0019 0, , ,6032 0,0021 0,0022 0, , ,3538 0,0022 0,0023 0, , ,4445 0,0026 0,0021 0, , ,8575 0,0029 0,0024 0, , ,7572 0,0022 0,0025 0, , ,6142 0,0028 0,0021 0, , ,1555 0,0016 0,0018 0, , ,6689 0,0016 0,0018 0, , ,5755 0,0026 0,0028 0, , ,2950 0,0039 0,0030 0, , ,7151 0,0027 0,0023 0, , ,2911 0,0025 0,0028 0, , ,0304 0,0025 0,0020 0, , ,7696 0,0019 0,0023 0,
127 D. PŘETRANSFORMOVANÉ SOUŘADNICE Tab. D.9: Přetransformované souřadnice v etapě E 7 (2012/11) bod X[m] Y [m] σ X σ Y cov(x, Y ) , ,9716 0,0021 0,0019 0, , ,2090 0,0032 0,0027 0, , ,8567 0,0022 0,0028 0, , ,9654 0,0027 0,0021 0, , ,6209 0,0030 0,0025 0, , ,4378 0,0035 0,0027 0, , ,8445 0,0034 0,0029 0, , ,8717 0,0032 0,0030 0, , ,5864 0,0028 0,0028 0, , ,6022 0,0019 0,0017 0, , ,3592 0,0024 0,0024 0, , ,4475 0,0026 0,0022 0, , ,8649 0,0026 0,0022 0, , ,7565 0,0021 0,0023 0, , ,6193 0,0030 0,0022 0, , ,1541 0,0022 0,0024 0, , ,6704 0,0026 0,0026 0, , ,5746 0,0025 0,0027 0, , ,2985 0,0031 0,0031 0, , ,7202 0,0032 0,0028 0, , ,2833 0,0030 0,0029 0, , ,0311 0,0021 0,0021 0, , ,7683 0,0029 0,0029 0,
128 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ E Číselné výsledky testování posunů E.1 Základní etapa E 0 V této příloze jsou uvedeny výsledky testování posunů bodů v etapě E 1 vůči základní etapě E 0. Hodnoty posunů ΔX i, ΔY i a jejich směrodatné odchylky σ ΔX, σ ΔY uvedeny v milimetrech. V dalším sloupci je uvedena p-hodnota, která kvantifikuje pravděpodobnost realizace hodnoty testovací statistiky χ 2, pokud nulová hypotéza H 0 platí. Samotný výsledek testu (passed/failed) je proveden na základě vyhodnocení testovacího kritéria χ 2 > χ 2 α,2. Kritická hodnota χ 2 rozdělení pro zvolenou hladinu významnosti α = 5 % a 2 stupně volnosti je χ 2 α,2 = 5,99. Kritickou hodnotu lze zjistit např. zadáním příkazu chi2inv(0.95,2) v programu Octave. etapa datum E /04 E /11 jsou Tab. E.1: Posuny bodů v etapě E 1 vůči etapě E 0 bod ΔX (0,1) i ΔY (0,1) i σ ΔX σ ΔY p-value χ 2 stat test 501 0,5 0,6 2,1 2,1 0,939 0,127 passed 502 4,1 0,6 2,9 2,4 0,359 2,051 passed ,9 4,7 4,9 3,1 0,008 9,589 failed 505 5,3 1,7 3,6 2,8 0,295 2,440 passed 506 2,2 0,4 2,7 2,6 0,702 0,709 passed 507 2,9 3,3 2,6 2,6 0,200 3,218 passed 512 1,3 3,4 5,7 3,5 0,359 2,050 passed 524 0,5 1,8 2,6 2,4 0,761 0,545 passed 541 0,1 3,2 3,4 2,9 0,516 1,325 passed 552 2,2 2,9 2,3 2,3 0,265 2,654 passed 553 0,2 0,1 2,3 2,4 0,993 0,014 passed ,8 4,4 5,0 3,1 0,011 8,934 failed ,8 0,7 2,5 2,5 0,497 1,400 passed ,3 1,2 2,3 2,1 0,245 2,817 passed ,9 2,5 2,3 2,2 0,528 1,279 passed 127
129 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ E.2 Základní etapa E 1 V této příloze jsou uvedeny výsledky testování posunů bodů v etapách E 2 až E 7 vůči základní etapě E 1. Hodnoty posunů ΔX i, ΔY i a jejich směrodatné odchylky σ ΔX, σ ΔY jsou uvedeny v milimetrech. etapa datum E /11 E /05 E /11 E /05 E /10 E /05 E /11 Tab. E.2: Posuny bodů v etapě E 2 vůči etapě E 1 bod ΔX (1,2) i ΔY (1,2) i σ ΔX σ ΔY p-value χ 2 stat test 501 0,2 0,6 2,1 2,0 0,945 0,113 passed ,9 5,0 8,2 4,5 0,326 2,241 passed 505 6,6 0,5 5,1 3,1 0,433 1,674 passed 506 0,7 0,1 2,9 2,8 0,973 0,055 passed 507 2,5 1,6 2,5 2,2 0,382 1,923 passed ,9 7,6 3,3 3,0 0,000 17,630 failed 513 5,1 5,2 2,3 2,0 0,008 9,756 failed 524 0,4 2,9 2,1 2,0 0,373 1,971 passed 531 0,1 1,3 2,4 2,6 0,879 0,258 passed 541 1,4 4,5 7,5 3,9 0,394 1,865 passed 552 0,3 1,5 2,2 2,2 0,783 0,489 passed 553 0,4 2,4 2,3 2,3 0,580 1,089 passed ,3 0,5 2,9 3,0 0,984 0,033 passed ,4 3,2 2,9 3,7 0,337 2,177 passed ,8 5,8 8,2 4,9 0,335 2,188 passed ,1 0,3 2,6 2,4 0,729 0,633 passed ,1 0,1 2,1 2,0 0,876 0,265 passed ,4 1,3 2,2 2,1 0,632 0,918 passed 128
130 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Tab. E.3: Posuny bodů v etapě E 3 vůči etapě E 1 bod ΔX (1,3) i ΔY (1,3) i σ ΔX σ ΔY p-value χ 2 stat test 501 2,3 0,8 2,0 2,0 0,502 1,378 passed ,8 1,6 4,8 2,5 0,008 9,559 failed 505 7,1 4,6 3,4 2,6 0,046 6,171 failed 506 2,0 2,1 2,5 2,5 0,499 1,389 passed 507 1,7 6,7 2,6 2,3 0,011 9,031 failed ,5 6,9 3,2 3,0 0,000 24,021 failed 513 8,7 4,0 2,2 2,0 0,000 16,790 failed 524 1,7 0,7 1,9 1,9 0,642 0,886 passed 531 0,7 1,4 2,2 2,5 0,801 0,443 passed 541 1,9 0,8 2,5 2,3 0,677 0,781 passed 552 1,7 1,4 2,0 2,2 0,600 1,023 passed 553 1,1 0,5 2,2 2,4 0,846 0,334 passed ,2 2,8 2,7 2,9 0,546 1,209 passed ,5 13,5 3,3 4,3 0,006 10,372 failed ,0 1,3 5,1 2,7 0,002 12,167 failed ,5 2,6 2,7 2,5 0,195 3,271 passed ,9 1,9 2,0 1,9 0,295 2,439 passed ,1 1,8 2,1 2,1 0,695 0,728 passed 129
131 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Tab. E.4: Posuny bodů v etapě E 4 vůči etapě E 1 bod ΔX (1,4) i ΔY (1,4) i σ ΔX σ ΔY p-value χ 2 stat test 501 0,9 0,2 1,9 1,9 0,894 0,225 passed 502 1,3 2,6 2,7 2,3 0,469 1,515 passed ,9 1,3 4,5 2,4 0,003 11,810 failed 505 5,9 4,0 3,2 2,4 0,072 5,271 passed 506 4,6 2,5 2,3 2,3 0,079 5,068 passed 507 2,0 1,6 2,1 1,8 0,416 1,752 passed 509 0,0 1,6 2,4 2,1 0,743 0,595 passed 510 2,2 1,4 2,6 2,5 0,614 0,976 passed 511 4,5 0,6 2,6 2,5 0,196 3,264 passed 512 3,6 3,3 2,5 2,4 0,103 4,545 passed 513 0,9 3,3 2,1 2,0 0,239 2,862 passed 524 0,3 1,5 1,9 1,8 0,678 0,777 passed 525 3,4 2,3 2,2 2,3 0,229 2,951 passed 526 1,0 0,3 2,2 2,1 0,898 0,215 passed 527 2,4 0,1 2,1 2,0 0,519 1,310 passed 531 1,7 0,9 2,0 2,1 0,637 0,903 passed 532 2,6 0,2 2,3 2,1 0,526 1,284 passed 541 0,4 1,6 2,5 2,2 0,763 0,540 passed 552 0,7 1,3 1,9 2,1 0,772 0,518 passed 553 2,8 0,4 2,1 2,2 0,422 1,725 passed ,4 1,2 2,2 2,3 0,763 0,540 passed ,6 1,8 2,5 2,6 0,760 0,550 passed ,5 0,3 4,6 2,6 0,001 13,229 failed ,4 1,0 2,3 2,2 0,295 2,441 passed ,6 0,7 1,9 1,8 0,864 0,294 passed ,4 0,8 2,1 2,0 0,449 1,599 passed 130
132 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Tab. E.5: Posuny bodů v etapě E 5 vůči etapě E 1 bod ΔX (1,5) i ΔY (1,5) i σ ΔX σ ΔY p-value χ 2 stat test 501 0,1 0,9 1,9 1,8 0,886 0,241 passed 502 0,0 1,2 2,5 2,1 0,854 0,315 passed ,6 0,2 4,4 2,4 0,006 10,179 failed 505 6,4 5,3 3,2 2,4 0,020 7,858 failed 506 3,1 2,0 2,3 2,3 0,269 2,624 passed 507 2,9 2,2 2,1 1,8 0,156 3,719 passed 509 2,9 3,8 2,3 2,1 0,052 5,902 passed 510 1,9 4,5 2,6 2,5 0,123 4,192 passed 511 1,5 2,5 2,6 2,6 0,579 1,092 passed 512 0,2 1,2 2,5 2,4 0,890 0,233 passed ,9 4,8 2,1 1,9 0,000 29,986 failed 524 0,8 2,0 1,9 1,8 0,490 1,426 passed 525 1,3 0,3 2,2 2,3 0,839 0,351 passed 526 0,3 0,7 2,2 2,0 0,929 0,148 passed 527 2,4 2,1 2,2 2,0 0,289 2,484 passed 531 0,4 1,2 2,1 2,1 0,840 0,348 passed 532 0,7 0,6 2,4 2,1 0,898 0,215 passed 541 0,8 0,5 2,4 2,2 0,925 0,155 passed 552 0,1 3,1 2,0 2,0 0,305 2,376 passed 553 3,0 2,1 2,1 2,2 0,272 2,604 passed ,1 0,1 2,2 2,3 0,865 0,291 passed ,6 3,2 2,3 2,5 0,121 4,223 passed ,8 0,7 4,5 2,5 0,003 11,883 failed ,2 0,2 2,3 2,2 0,183 3,396 passed ,1 1,1 1,9 1,8 0,642 0,886 passed ,8 2,6 2,1 2,1 0,065 5,457 passed 131
133 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Tab. E.6: Posuny bodů v etapě E 6 vůči etapě E 1 bod ΔX (1,6) i ΔY (1,6) i σ ΔX σ ΔY p-value χ 2 stat test 501 0,7 2,4 2,5 2,8 0,649 0,864 passed 502 5,9 2,4 3,2 2,8 0,152 3,766 passed 506 5,1 2,8 2,9 2,9 0,170 3,542 passed 507 1,2 0,2 3,2 2,5 0,926 0,155 passed 509 9,8 1,9 3,9 2,9 0,046 6,151 failed ,1 2,0 4,4 3,1 0,012 8,783 failed 511 6,8 1,1 4,0 3,2 0,205 3,174 passed 512 0,4 0,4 3,6 3,0 0,985 0,030 passed 513 2,7 0,1 3,0 2,6 0,666 0,813 passed 524 2,2 1,3 2,7 2,7 0,623 0,948 passed 525 4,3 6,9 2,9 3,1 0,050 5,995 failed 526 5,7 4,0 3,2 2,8 0,116 4,311 passed 527 7,5 4,5 3,5 3,0 0,066 5,451 passed 531 6,5 0,1 2,8 3,1 0,072 5,260 passed ,4 3,9 3,4 2,8 0,006 10,311 failed 552 3,9 0,8 2,4 2,5 0,243 2,829 passed 553 3,7 3,2 2,4 2,6 0,166 3,591 passed ,9 0,1 3,3 3,4 0,301 2,401 passed ,9 0,6 4,4 3,7 0,047 6,129 failed ,4 1,2 5,1 3,2 0,004 11,070 failed ,3 4,5 3,1 3,4 0,403 1,817 passed ,7 2,6 3,0 2,5 0,508 1,353 passed ,9 3,4 2,6 2,9 0,104 4,528 passed 132
134 E. ČÍSELNÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Tab. E.7: Posuny bodů v etapě E 7 vůči etapě E 1 bod ΔX (1,7) i ΔY (1,7) i σ ΔX σ ΔY p-value χ 2 stat test 501 2,2 0,5 2,7 2,5 0,706 0,696 passed 502 2,5 3,3 3,9 3,3 0,527 1,282 passed 506 0,3 2,8 3,0 3,4 0,715 0,671 passed 507 5,2 2,3 3,2 2,6 0,167 3,576 passed 509 4,1 3,1 3,6 3,0 0,277 2,564 passed 510 2,8 0,0 4,1 3,4 0,787 0,478 passed 511 1,3 3,4 4,0 3,6 0,618 0,962 passed 512 0,4 2,0 3,9 3,6 0,860 0,301 passed 513 0,2 0,1 3,4 3,2 0,998 0,003 passed 524 3,7 0,3 2,5 2,3 0,339 2,161 passed 525 6,5 1,4 3,0 3,1 0,099 4,624 passed 526 3,6 1,0 3,2 2,8 0,518 1,317 passed 527 5,8 2,8 3,2 2,9 0,114 4,338 passed 531 0,3 0,7 2,8 3,0 0,960 0,081 passed 532 3,8 1,2 3,6 2,8 0,530 1,269 passed 552 5,8 2,2 2,8 2,9 0,097 4,668 passed 553 1,4 1,7 3,2 3,1 0,805 0,434 passed ,4 0,9 3,2 3,3 0,843 0,343 passed ,4 2,9 3,8 3,8 0,495 1,405 passed ,3 6,4 5,4 3,6 0,000 17,633 failed ,3 3,3 3,5 3,4 0,396 1,854 passed ,8 3,3 2,7 2,6 0,211 3,111 passed ,3 4,8 3,4 3,4 0,248 2,788 passed 133
135 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ F Grafické výsledky testování posunů Obr. F.1: Zobrazení a testování posunů bodu
136 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.2: Zobrazení a testování posunů bodu
137 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.3: Zobrazení a testování posunů bodu
138 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.4: Zobrazení a testování posunů bodu
139 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.5: Zobrazení a testování posunů bodu
140 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.6: Zobrazení a testování posunů bodu
141 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.7: Zobrazení a testování posunů bodu
142 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.8: Zobrazení a testování posunů bodu
143 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.9: Zobrazení a testování posunů bodu
144 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.10: Zobrazení a testování posunů bodu
145 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.11: Zobrazení a testování posunů bodu
146 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.12: Zobrazení a testování posunů bodu
147 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.13: Zobrazení a testování posunů bodu
148 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.14: Zobrazení a testování posunů bodu
149 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.15: Zobrazení a testování posunů bodu
150 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.16: Zobrazení a testování posunů bodu
151 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.17: Zobrazení a testování posunů bodu
152 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.18: Zobrazení a testování posunů bodu
153 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.19: Zobrazení a testování posunů bodu
154 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.20: Zobrazení a testování posunů bodu
155 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.21: Zobrazení a testování posunů bodu
156 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.22: Zobrazení a testování posunů bodu
157 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.23: Zobrazení a testování posunů bodu
158 F. GRAFICKÉ VÝSLEDKY TESTOVÁNÍ POSUNŮ Obr. F.24: Zobrazení a testování posunů bodu
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 2 2/6 Transformace souřadnic z ETRF2000 do
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 2 2/6 Transformace souřadnic z ETRF2000 do
Transformace dat mezi různými datovými zdroji
 Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice
 Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Vliv realizace, vliv přesnosti centrace a určení výšky přístroje a cíle na přesnost určovaných veličin
 Vliv realizace, vliv přesnosti centrace a určení výšky přístroje a cíle na přesnost určovaných veličin doc. Ing. Martin Štroner, Ph.D. Fakulta stavební ČVUT v Praze 1 Úvod Při přesných inženýrsko geodetických
Vliv realizace, vliv přesnosti centrace a určení výšky přístroje a cíle na přesnost určovaných veličin doc. Ing. Martin Štroner, Ph.D. Fakulta stavební ČVUT v Praze 1 Úvod Při přesných inženýrsko geodetických
Pro mapování na našem území bylo použito následujících souřadnicových systémů:
 SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
Vytyčení polohy bodu polární metodou
 Obsah Vytyčení polohy bodu polární metodou... 2 1 Vliv měření na přesnost souřadnic... 3 2 Vliv měření na polohovou a souřadnicovou směrodatnou odchylku... 4 3 Vliv podkladu na přesnost souřadnic... 5
Obsah Vytyčení polohy bodu polární metodou... 2 1 Vliv měření na přesnost souřadnic... 3 2 Vliv měření na polohovou a souřadnicovou směrodatnou odchylku... 4 3 Vliv podkladu na přesnost souřadnic... 5
APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY
 APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY Radek Dušek, Jan Mach Katedra fyzické geografie a geoekologie, Přírodovědecká fakulta, Ostravská univerzita, Ostrava Gymnázium Omská, Praha Abstrakt
APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY Radek Dušek, Jan Mach Katedra fyzické geografie a geoekologie, Přírodovědecká fakulta, Ostravská univerzita, Ostrava Gymnázium Omská, Praha Abstrakt
České vysoké učení technické v Praze Fakulta stavební DIPLOMOVÁ PRÁCE
 České vysoké učení technické v Praze Fakulta stavební DIPLOMOVÁ PRÁCE Praha 2009 Jan Vaněček České vysoké učení technické v Praze Fakulta stavební katedra speciální geodézie Zpracování měření v lokální
České vysoké učení technické v Praze Fakulta stavební DIPLOMOVÁ PRÁCE Praha 2009 Jan Vaněček České vysoké učení technické v Praze Fakulta stavební katedra speciální geodézie Zpracování měření v lokální
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY
 GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY VOJENSKÝ GEOGRAFICKÝ A HYDROMETEOROLOGICKÝ ÚŘAD Popis a zásady používání světového geodetického referenčního systému 1984 v AČR POPIS A ZÁSADY POUŽÍVÁNÍ V AČR
GEOGRAFICKÁ SLUŽBA ARMÁDY ČESKÉ REPUBLIKY VOJENSKÝ GEOGRAFICKÝ A HYDROMETEOROLOGICKÝ ÚŘAD Popis a zásady používání světového geodetického referenčního systému 1984 v AČR POPIS A ZÁSADY POUŽÍVÁNÍ V AČR
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 3/3 GPS - výpočet polohy stanice pomocí
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 3/3 GPS - výpočet polohy stanice pomocí
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ. JS pro 3. ročník S3G
 SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu úloha/zadání název úlohy Inženýrská geodézie II 1/5 Určení nepřístupné vzdálenosti
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA SPECIÁLNÍ GEODÉZIE název předmětu úloha/zadání název úlohy Inženýrská geodézie II 1/5 Určení nepřístupné vzdálenosti
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
Zaměření vybraných typů nerovností vozovek metodou laserového skenování
 Zaměření vybraných typů nerovností vozovek metodou laserového skenování 1. Účel experimentů V normě ČSN 73 6175 (736175) Měření a hodnocení nerovnosti povrchů vozovek je uvedena řada metod k určování podélných
Zaměření vybraných typů nerovností vozovek metodou laserového skenování 1. Účel experimentů V normě ČSN 73 6175 (736175) Měření a hodnocení nerovnosti povrchů vozovek je uvedena řada metod k určování podélných
Geodézie a pozemková evidence
 2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.2 - Kartografická zobrazení, souřadnicové soustavy Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.2 - Kartografická zobrazení, souřadnicové soustavy Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
K přesnosti volného stanoviska
 K přesnosti volného stanoviska MDT Doc. Ing. Martin Štroner, Ph.D., ČVUT Fakulta stavební, Praha Abstrakt Článek se zabývá rozborem přesnosti a vyvozením obecnějších závěrů pro přesnost určení souřadnic
K přesnosti volného stanoviska MDT Doc. Ing. Martin Štroner, Ph.D., ČVUT Fakulta stavební, Praha Abstrakt Článek se zabývá rozborem přesnosti a vyvozením obecnějších závěrů pro přesnost určení souřadnic
OBSAH 1 Úvod Fyzikální charakteristiky Zem Referen ní plochy a soustavy... 21
 OBSAH I. ČÁST ZEMĚ A GEODÉZIE 1 Úvod... 1 1.1 Historie měření velikosti a tvaru Země... 1 1.1.1 První určení poloměru Zeměkoule... 1 1.1.2 Středověké měření Země... 1 1.1.3 Nové názory na tvar Země...
OBSAH I. ČÁST ZEMĚ A GEODÉZIE 1 Úvod... 1 1.1 Historie měření velikosti a tvaru Země... 1 1.1.1 První určení poloměru Zeměkoule... 1 1.1.2 Středověké měření Země... 1 1.1.3 Nové názory na tvar Země...
Metodika převodu mezi ETRF2000 a S-JTSK varianta 2
 Výzkumný ústav geodetický topografický a kartografický v.v.i. Stavební fakulta ČVUT v Praze Metodika převodu mezi ETRF a S-JTSK varianta Jan Kostecký Jakub Kostecký Ivan Pešek GO Pecný červen 1 1 Úvod
Výzkumný ústav geodetický topografický a kartografický v.v.i. Stavební fakulta ČVUT v Praze Metodika převodu mezi ETRF a S-JTSK varianta Jan Kostecký Jakub Kostecký Ivan Pešek GO Pecný červen 1 1 Úvod
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 2/3 GPS - Výpočet drah družic školní rok
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 2/3 GPS - Výpočet drah družic školní rok
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
4. Matematická kartografie
 4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ. JS pro 2. ročník S2G 1. ročník G1Z
 SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických
Geodézie pro architekty. Úvod do geodézie
 Geodézie pro architekty Úvod do geodézie Geodézie pro architekty Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek, P. a kol.: Stavební
Geodézie pro architekty Úvod do geodézie Geodézie pro architekty Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek, P. a kol.: Stavební
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Úvod do předmětu geodézie
 1/1 Úvod do předmětu geodézie Ing. Hana Staňková, Ph.D. IGDM, HGF, VŠB-TU Ostrava hana.stankova@vsb.cz A911, 5269 1 Geodézie 1/2 vědní obor o měření části zemského povrchu, o určování vzájemných vztahů
1/1 Úvod do předmětu geodézie Ing. Hana Staňková, Ph.D. IGDM, HGF, VŠB-TU Ostrava hana.stankova@vsb.cz A911, 5269 1 Geodézie 1/2 vědní obor o měření části zemského povrchu, o určování vzájemných vztahů
ZAMĚŘENÍ PŘETVOŘENÍ ŽELEZNIČNÍHO MOSTU V KLÁŠTERCI NAD OHŘÍ
 Komora geodetů a kartografů ZAMĚŘENÍ PŘETVOŘENÍ ŽELEZNIČNÍHO MOSTU V KLÁŠTERCI NAD OHŘÍ Ing. Jaroslav Braun 1 Ing. Martin Lidmila, Ph.D. 2 doc. Ing. Martin Štroner, Ph.D. 1 1 Katedra speciální geodézie,
Komora geodetů a kartografů ZAMĚŘENÍ PŘETVOŘENÍ ŽELEZNIČNÍHO MOSTU V KLÁŠTERCI NAD OHŘÍ Ing. Jaroslav Braun 1 Ing. Martin Lidmila, Ph.D. 2 doc. Ing. Martin Štroner, Ph.D. 1 1 Katedra speciální geodézie,
Úloha č. 1 : TROJÚHELNÍK. Určení prostorových posunů stavebního objektu
 Václav Čech, ČVUT v Praze, Fakulta stavební, 008 Úloha č. 1 : TROJÚHELNÍK Určení prostorových posunů stavebního objektu Zadání : Zjistěte posun bodu P do P, umístěného na horní terase Stavební fakulty.
Václav Čech, ČVUT v Praze, Fakulta stavební, 008 Úloha č. 1 : TROJÚHELNÍK Určení prostorových posunů stavebního objektu Zadání : Zjistěte posun bodu P do P, umístěného na horní terase Stavební fakulty.
Geodézie Přednáška. Souřadnicové systémy Souřadnice na referenčních plochách
 Geodézie Přednáška Souřadnicové systémy Souřadnice na referenčních plochách strana 2 každý stát nebo skupina států si volí pro souvislé zobrazení celého území vhodný souřadnicový systém slouží k lokalizaci
Geodézie Přednáška Souřadnicové systémy Souřadnice na referenčních plochách strana 2 každý stát nebo skupina států si volí pro souvislé zobrazení celého území vhodný souřadnicový systém slouží k lokalizaci
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
Filip Hroch. Astronomické pozorování. Filip Hroch. Výpočet polohy planety. Drahové elementy. Soustava souřadnic. Pohyb po elipse
 ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
Elementární křivky a plochy
 Příloha A Elementární křivky a plochy A.1 Analytický popis geometrických objektů Geometrické vlastnosti, které jsme dosud studovali, se týkaly především základních geometrických objektů bodů, přímek, rovin
Příloha A Elementární křivky a plochy A.1 Analytický popis geometrických objektů Geometrické vlastnosti, které jsme dosud studovali, se týkaly především základních geometrických objektů bodů, přímek, rovin
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
EasyNET Analyser verze 1.1.2
 EasyNET Analyser verze 1.1.2 Komplexní softwarová analýza etapových měření Softwarová dokumentace V Praze dne 20. 06. 2015 Obsah 1 Úvod... 4 2 Základní vlastnosti programu... 4 2.1 Detekce pozorovaných
EasyNET Analyser verze 1.1.2 Komplexní softwarová analýza etapových měření Softwarová dokumentace V Praze dne 20. 06. 2015 Obsah 1 Úvod... 4 2 Základní vlastnosti programu... 4 2.1 Detekce pozorovaných
Triangulace a trilaterace
 Výuka v terénu z vyšší geodézie Triangulace a trilaterace Staré Město pod Sněžníkem 2015 1 Popis úlohy V rámci úlohy Triagulace budou metodami klasické geodézie (triangulace, trilaterace, astronomické
Výuka v terénu z vyšší geodézie Triangulace a trilaterace Staré Město pod Sněžníkem 2015 1 Popis úlohy V rámci úlohy Triagulace budou metodami klasické geodézie (triangulace, trilaterace, astronomické
GIS Geografické informační systémy
 GIS Geografické informační systémy Kartografie Glóbus představuje zmenšený a zjednodušený, 3rozměrný model zemského povrchu; všechny délky na glóbu jsou zmenšeny v určitém poměru; úhly a tvary a velikosti
GIS Geografické informační systémy Kartografie Glóbus představuje zmenšený a zjednodušený, 3rozměrný model zemského povrchu; všechny délky na glóbu jsou zmenšeny v určitém poměru; úhly a tvary a velikosti
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Matematické metody v kartografii. Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.)
 Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Matematická kartografie. Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT. Referenční plochy
 Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
2. Bodové pole a souřadnicové výpočty
 2. Bodové pole a souřadnicové výpočty 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů.
2. Bodové pole a souřadnicové výpočty 2.1 Body 2.2 Bodová pole 2.3 Polohové bodové pole. 2.3.1 Rozdělení polohového bodového pole. 2.3.2 Dokumentace geodetického bodu. 2.3.3 Stabilizace a signalizace bodů.
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
6.1 Základní pojmy - zákonné měřící jednotky
 6. Měření úhlů 6.1 Základní pojmy 6.2 Teodolity 6.3 Totální stanice 6.4 Osové podmínky, konstrukční chyby a chyby při měření 6.5 Měření úhlů 6.6 Postup při měření vodorovného úhlu 6.7 Postup při měření
6. Měření úhlů 6.1 Základní pojmy 6.2 Teodolity 6.3 Totální stanice 6.4 Osové podmínky, konstrukční chyby a chyby při měření 6.5 Měření úhlů 6.6 Postup při měření vodorovného úhlu 6.7 Postup při měření
Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Podpořeno z projektu FRVŠ 584/2011. Křovákovo zobrazení Křovákovo zobrazení
Podpořeno z projektu FRVŠ 584/2011. Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Podpořeno z projektu FRVŠ 584/2011. Křovákovo zobrazení Křovákovo zobrazení
3. Souřadnicové výpočty
 3. Souřadnicové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnic. 3.9 Volné
3. Souřadnicové výpočty 3.1 Délka. 3.2 Směrník. 3.3 Polární metoda. 3.4 Protínání vpřed z úhlů. 3.5 Protínání vpřed z délek. 3.6 Polygonové pořady. 3.7 Protínání zpět. 3.8 Transformace souřadnic. 3.9 Volné
ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN
 Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 1241-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 1241-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE PRAHA 2012 Pavel RYS ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE BAKALÁŘSKÁ PRÁCE ETAPOVÉ MĚŘENÍ
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE PRAHA 2012 Pavel RYS ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE BAKALÁŘSKÁ PRÁCE ETAPOVÉ MĚŘENÍ
MODERNÍ GLOBÁLNÍ GEODETICKÝ REFERENČNÍ GEOCENTRICKÝ SYSTÉM
 WORLD GEODETIC SYSTEM 1984 - WGS 84 MODERNÍ GLOBÁLNÍ GEODETICKÝ REFERENČNÍ GEOCENTRICKÝ SYSTÉM Pro projekt CTU 0513011 (2005) s laskavou pomocí Ing. D. Dušátka, CSc. Soustava základních geometrických a
WORLD GEODETIC SYSTEM 1984 - WGS 84 MODERNÍ GLOBÁLNÍ GEODETICKÝ REFERENČNÍ GEOCENTRICKÝ SYSTÉM Pro projekt CTU 0513011 (2005) s laskavou pomocí Ing. D. Dušátka, CSc. Soustava základních geometrických a
zpřesněná globální transformace mezi ETRS89 a S-JTSK, přetrvávající omyly při využití GNSS
 Setkání geodetů 2014 konference KGK (Beroun, 5. - 6.6.2014) zpřesněná globální transformace mezi ETRS89 a S-JTSK, přetrvávající omyly při využití GNSS Ing. Pavel Taraba Prvotní realizace systému ETRS89
Setkání geodetů 2014 konference KGK (Beroun, 5. - 6.6.2014) zpřesněná globální transformace mezi ETRS89 a S-JTSK, přetrvávající omyly při využití GNSS Ing. Pavel Taraba Prvotní realizace systému ETRS89
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Geometrické transformace pomocí matic
 Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 3/7 Výpočet lokálního geoidu pro body
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Fyzikální geodézie 3/7 Výpočet lokálního geoidu pro body
Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace
 Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace Zeměměřický úřad, Jan Řezníček Praha, 2018 Definice matematická pravidla (rovnice) jednoznačné přidružení souřadnic k prostorovým informacím
Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace Zeměměřický úřad, Jan Řezníček Praha, 2018 Definice matematická pravidla (rovnice) jednoznačné přidružení souřadnic k prostorovým informacím
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 4/003 Průběh geoidu z altimetrických měření
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 4/003 Průběh geoidu z altimetrických měření
PrecisPlanner 3D v2.2
 PrecisPlanner 3D v2.2 Martin Štroner, Doc. Ing., Ph.D., Fakulta stavební ČVUT v Praze, Thákurova 7, 166 29 Praha 6, tel.: +420-2435-4781, e-mail: martin.stroner@fsv.cvut.cz 28.10.2011 Obsah 1 Úvod... 2
PrecisPlanner 3D v2.2 Martin Štroner, Doc. Ing., Ph.D., Fakulta stavební ČVUT v Praze, Thákurova 7, 166 29 Praha 6, tel.: +420-2435-4781, e-mail: martin.stroner@fsv.cvut.cz 28.10.2011 Obsah 1 Úvod... 2
DRUHY VÝŠEK A JEJICH TEORETICKÝ PRINCIP. Hynčicová Tereza, H2IGE1 2014
 DRUHY VÝŠEK A JEJICH TEORETICKÝ PRINCIP Hynčicová Tereza, H2IGE1 2014 ÚVOD o Pro určení výšky bodu na zemském povrchu je nutné definovat vztažnou (nulovou) plochu a jeho výškovou polohu nad touto plochou
DRUHY VÝŠEK A JEJICH TEORETICKÝ PRINCIP Hynčicová Tereza, H2IGE1 2014 ÚVOD o Pro určení výšky bodu na zemském povrchu je nutné definovat vztažnou (nulovou) plochu a jeho výškovou polohu nad touto plochou
PODROBNÉ MĚŘENÍ POLOHOPISNÉ
 Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství MAPOVÉ PODKLADY Ing. Bc. Pavel Voříšek (úředně oprávněný zeměměřický inženýr). Vysoké Mýto 7. 4. 2017 PODROBNÉ MĚŘENÍ POLOHOPISNÉ
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství MAPOVÉ PODKLADY Ing. Bc. Pavel Voříšek (úředně oprávněný zeměměřický inženýr). Vysoké Mýto 7. 4. 2017 PODROBNÉ MĚŘENÍ POLOHOPISNÉ
Souřadnicové výpočty. Geodézie Přednáška
 Souřadnicové výpočt Geodézie Přednáška Souřadnicové výpočt strana 2 Souřadnicové výpočt (souřadnicová geometrie) vchází z analtické geometrie zkoumá geometrické tvar pomocí algebraických a analtických
Souřadnicové výpočt Geodézie Přednáška Souřadnicové výpočt strana 2 Souřadnicové výpočt (souřadnicová geometrie) vchází z analtické geometrie zkoumá geometrické tvar pomocí algebraických a analtických
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
BUDOVÁNÍ PŘESNÉHO BODOVÉHO POLE A GEOMETRICKÉ VLASTNOSTI VIRTUÁLNÍCH REALIZACÍ S-JTSK
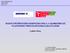 GNSS SEMINÁŘ 2018 BUDOVÁNÍ PŘESNÉHO BODOVÉHO POLE A GEOMETRICKÉ VLASTNOSTI VIRTUÁLNÍCH REALIZACÍ S-JTSK 21. ročník semináře Družicové metody v geodézii a katastru Brno, GNSS SEMINÁŘ 2018 Úvod Problematika:
GNSS SEMINÁŘ 2018 BUDOVÁNÍ PŘESNÉHO BODOVÉHO POLE A GEOMETRICKÉ VLASTNOSTI VIRTUÁLNÍCH REALIZACÍ S-JTSK 21. ročník semináře Družicové metody v geodézii a katastru Brno, GNSS SEMINÁŘ 2018 Úvod Problematika:
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
Přehled vhodných metod georeferencování starých map
 Přehled vhodných metod georeferencování starých map ČVUT v Praze, katedra geomatiky 12. 3. 2015 Praha Georeferencování historická mapa vs. stará mapa georeferencování umístění obrazu mapy do referenčního
Přehled vhodných metod georeferencování starých map ČVUT v Praze, katedra geomatiky 12. 3. 2015 Praha Georeferencování historická mapa vs. stará mapa georeferencování umístění obrazu mapy do referenčního
TECHNICKÁ ZPRÁVA. Geodetické zaměření Neštěmického potoka Geodetické zaměření Neštěmického potoka v úseku 0-3,632 ř. km.
 TECHNICKÁ ZPRÁVA Číslo zakázky: Název zakázky: Název akce: Obec: Katastrální území: Objednatel: Měření zadal: Geodetické zaměření Neštěmického potoka Geodetické zaměření Neštěmického potoka v úseku 0-3,632
TECHNICKÁ ZPRÁVA Číslo zakázky: Název zakázky: Název akce: Obec: Katastrální území: Objednatel: Měření zadal: Geodetické zaměření Neštěmického potoka Geodetické zaměření Neštěmického potoka v úseku 0-3,632
T a c h y m e t r i e
 T a c h y m e t r i e (Podrobné měření výškopisu, okolí NTK) Poslední úprava: 2.10.2018 9:59 Úkolem je vyhotovit digitální model terénu pomocí programového systému Atlas DMT (úloha U_7, vztažné měřítko
T a c h y m e t r i e (Podrobné měření výškopisu, okolí NTK) Poslední úprava: 2.10.2018 9:59 Úkolem je vyhotovit digitální model terénu pomocí programového systému Atlas DMT (úloha U_7, vztažné měřítko
ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN
 Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 510-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 510-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
MAPOVÁNÍ. Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z
 MAPOVÁNÍ Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických základů
MAPOVÁNÍ Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických základů
Dokumentace funkčního vzorku Nástavce pro měření laserovým dálkoměrem na kotevních bodech liniových instalací BOTDA
 Dokumentace funkčního vzorku Nástavce pro měření laserovým dálkoměrem na kotevních bodech liniových instalací BOTDA vyvinutého v rámci řešení projektu FR-TI3/609 Výzkum a vývoj detekce a kontrolního sledování
Dokumentace funkčního vzorku Nástavce pro měření laserovým dálkoměrem na kotevních bodech liniových instalací BOTDA vyvinutého v rámci řešení projektu FR-TI3/609 Výzkum a vývoj detekce a kontrolního sledování
K metodám převodu souřadnic mezi ETRS 89 a S-JTSK na území ČR
 K metodám převodu souřadnic mezi ETRS 89 a S-JTSK na území ČR Vlastimil Kratochvíl * Příspěvek obsahuje popis vlastností některých postupů, využitelných pro transformaci souřadnic mezi geodetickými systémy
K metodám převodu souřadnic mezi ETRS 89 a S-JTSK na území ČR Vlastimil Kratochvíl * Příspěvek obsahuje popis vlastností některých postupů, využitelných pro transformaci souřadnic mezi geodetickými systémy
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 4/3 GPS - oskulační elementy dráhy družice
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 4/3 GPS - oskulační elementy dráhy družice
7.1 Definice délky. kilo- km 10 3 hekto- hm mili- mm 10-3 deka- dam 10 1 mikro- μm 10-6 deci- dm nano- nm 10-9 centi- cm 10-2
 7. Měření délek 7.1 Definice délky, zákonné měřící jednotky 7.2 Měření délek pásmem 7.3 Optické měření délek 7.3.1 Paralaktické měření délek 7.3.2 Ryskový dálkoměr 7.4 Elektrooptické měření délek 7.5 Fyzikální
7. Měření délek 7.1 Definice délky, zákonné měřící jednotky 7.2 Měření délek pásmem 7.3 Optické měření délek 7.3.1 Paralaktické měření délek 7.3.2 Ryskový dálkoměr 7.4 Elektrooptické měření délek 7.5 Fyzikální
EasyNET verze 3.4.2. Komplexní softwarové zpracování měření inženýrské geodézie. Softwarová dokumentace
 EasyNET verze 3.4.2 Komplexní softwarové zpracování měření inženýrské geodézie Softwarová dokumentace V Praze dne 20. 6. 2015 Obsah 1 Úvod... 6 2 Základní vlastnosti programu... 6 2.1 Detekce měřických
EasyNET verze 3.4.2 Komplexní softwarové zpracování měření inženýrské geodézie Softwarová dokumentace V Praze dne 20. 6. 2015 Obsah 1 Úvod... 6 2 Základní vlastnosti programu... 6 2.1 Detekce měřických
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Protokol určení bodů podrobného polohového bodového pole technologií GNSS
 Protokol určení bodů podrobného polohového bodového pole technologií GNSS Lokalita (název): Hosek246 Okres: Rakovník Katastrální území: Velká Buková ZPMZ: Organizace-firma zhotovitele:air Atlas spol. s
Protokol určení bodů podrobného polohového bodového pole technologií GNSS Lokalita (název): Hosek246 Okres: Rakovník Katastrální území: Velká Buková ZPMZ: Organizace-firma zhotovitele:air Atlas spol. s
7 Transformace 2D. 7.1 Transformace objektů obecně. Studijní cíl. Doba nutná k nastudování. Průvodce studiem
 7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
Srovnání konformních kartografických zobrazení pro zvolené
 Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
2 Zpracování naměřených dat. 2.1 Gaussův zákon chyb. 2.2 Náhodná veličina a její rozdělení
 2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
2 Zpracování naměřených dat Důležitou součástí každé experimentální práce je statistické zpracování naměřených dat. V této krátké kapitole se budeme věnovat určení intervalů spolehlivosti získaných výsledků
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
Geodézie 3 (154GD3) doc. Ing. Martin Štroner, Ph.D.
 Geodézie 3 (154GD3) Přednášející: Místnost: Email: www 1: www 2: doc. Ing. Martin Štroner, Ph.D. B912 martin.stroner@fsv.cvut.cz http://k154.fsv.cvut.cz/vyuka/geodezie/gd3.php http://sgeo.fsv.cvut.cz/~stroner/
Geodézie 3 (154GD3) Přednášející: Místnost: Email: www 1: www 2: doc. Ing. Martin Štroner, Ph.D. B912 martin.stroner@fsv.cvut.cz http://k154.fsv.cvut.cz/vyuka/geodezie/gd3.php http://sgeo.fsv.cvut.cz/~stroner/
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Měření vodorovných úhlů Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Základním
Seminář z geoinformatiky Měření vodorovných úhlů Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Základním
Kontrola svislosti montované budovy
 1. Zadání Kontrola svislosti montované budovy Určete skutečné odchylky svislosti panelů na budově ČVUT. Objednatel požaduje kontrolu svislosti štítové stěny objektu. Při konstrukční výšce jednoho podlaží
1. Zadání Kontrola svislosti montované budovy Určete skutečné odchylky svislosti panelů na budově ČVUT. Objednatel požaduje kontrolu svislosti štítové stěny objektu. Při konstrukční výšce jednoho podlaží
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
Úvod do inženýrské geodézie
 Úvod do inženýrské geodézie Úvod do inženýrské geodézie Rozbory přesnosti Vytyčování Čerpáno ze Sylabů přednášek z inženýrské geodézie doc. ing. Jaromíra Procházky, CSc. Úvod do inženýrské geodézie Pod
Úvod do inženýrské geodézie Úvod do inženýrské geodézie Rozbory přesnosti Vytyčování Čerpáno ze Sylabů přednášek z inženýrské geodézie doc. ing. Jaromíra Procházky, CSc. Úvod do inženýrské geodézie Pod
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 1/3 GPS - zpracování kódových měření školní
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 1/3 GPS - zpracování kódových měření školní
Geodetické základy a triangulace Trigonometrické sítě na našem území Stabilizace a signalizace Tachymetrie - úvod Podélné a příčné profily
 Geodetické základy a triangulace Trigonometrické sítě na našem území Stabilizace a signalizace Tachymetrie - úvod Podélné a příčné profily Kartografie přednáška 6 Geodetické základy při měření (mapování)
Geodetické základy a triangulace Trigonometrické sítě na našem území Stabilizace a signalizace Tachymetrie - úvod Podélné a příčné profily Kartografie přednáška 6 Geodetické základy při měření (mapování)
ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN
 Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 506-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
Vyhotovitel Za Kostelem 421, Jedovnice IČO: 75803216, tel.: 603325513 Číslo geometrického plánu (zakázky) 506-5/2017 ZÁZNAM PODROBNÉHO MĚŘENÍ ZMĚN Katastrální úřad pro Katastrální pracoviště Obec Katastrální
Cyklografie. Cyklický průmět bodu
 Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
STANOVENÍ SPOLEHLIVOSTI GEOTECHNICKÝCH KONSTRUKCÍ. J. Pruška, T. Parák
 STANOVENÍ SPOLEHLIVOSTI GEOTECHNICKÝCH KONSTRUKCÍ J. Pruška, T. Parák OBSAH: 1. Co je to spolehlivost, pravděpodobnost poruchy, riziko. 2. Deterministický a pravděpodobnostní přístup k řešení problémů.
STANOVENÍ SPOLEHLIVOSTI GEOTECHNICKÝCH KONSTRUKCÍ J. Pruška, T. Parák OBSAH: 1. Co je to spolehlivost, pravděpodobnost poruchy, riziko. 2. Deterministický a pravděpodobnostní přístup k řešení problémů.
CZEPOS a jeho úloha při zpřesnění systému ETRS v ČR
 CZEPOS a jeho úloha při zpřesnění systému ETRS v ČR Jaroslav Nágl Zeměměřický úřad, Pod sídlištěm 9/1800, 182 11, Praha 8, Česká republika jaroslav.nagl@cuzk.cz Abstrakt. Koncepce rozvoje geodetických
CZEPOS a jeho úloha při zpřesnění systému ETRS v ČR Jaroslav Nágl Zeměměřický úřad, Pod sídlištěm 9/1800, 182 11, Praha 8, Česká republika jaroslav.nagl@cuzk.cz Abstrakt. Koncepce rozvoje geodetických
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004
 System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004 1 Obsah Úvod 3 1 Základní ovládání 4 1.1 Výběr zobrazení a jeho
System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004 1 Obsah Úvod 3 1 Základní ovládání 4 1.1 Výběr zobrazení a jeho
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství. Ing. Pavel Voříšek S-JTSK SYSTÉM JEDNOTNÉ TRIGONOMETRICKÉ SÍTĚ KATASTRÁLNÍ
 Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek S-JTSK SYSTÉM JEDNOTNÉ TRIGONOMETRICKÉ SÍTĚ KATASTRÁLNÍ VOŠ a SŠS Vysoké Mýto leden 2008 Jednotná trigonometrická
Přípravný kurz k vykonání maturitní zkoušky v oboru Dopravní stavitelství Ing. Pavel Voříšek S-JTSK SYSTÉM JEDNOTNÉ TRIGONOMETRICKÉ SÍTĚ KATASTRÁLNÍ VOŠ a SŠS Vysoké Mýto leden 2008 Jednotná trigonometrická
Test k přijímacím zkouškám do Navazujícího magisterského studia oboru Geodézie a kartografie x C)
 Test k přijímacím zkouškám do Navazujícího magisterského studia oboru Geodézie a kartografie - 2015 1. sin 540º = A) B) 1 C) 1 D) 0 2. První derivace funkce tg x je rovna: A) cotg x B) sin cos 2 2 x x
Test k přijímacím zkouškám do Navazujícího magisterského studia oboru Geodézie a kartografie - 2015 1. sin 540º = A) B) 1 C) 1 D) 0 2. První derivace funkce tg x je rovna: A) cotg x B) sin cos 2 2 x x
MOŽNOSTI KOMBINOVANÉHO SLEDOVÁNÍ POKLESŮ TECHNOLOGIÍ GNSS A PŘESNOU NIVELACÍ V PODDOLOVANÝCH ÚZEMÍCH
 Vysoká škola báňská Technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví MOŽNOSTI KOMBINOVANÉHO SLEDOVÁNÍ POKLESŮ TECHNOLOGIÍ GNSS A PŘESNOU NIVELACÍ V PODDOLOVANÝCH
Vysoká škola báňská Technická univerzita Ostrava Hornicko-geologická fakulta Institut geodézie a důlního měřictví MOŽNOSTI KOMBINOVANÉHO SLEDOVÁNÍ POKLESŮ TECHNOLOGIÍ GNSS A PŘESNOU NIVELACÍ V PODDOLOVANÝCH
Klasická měření v geodetických sítích. Poznámka. Klasická měření v polohových sítích
 Klasická měření v geodetických sítích Poznámka Detailněji budou popsány metody, které se používaly v minulosti pro budování polohových, výškových a tíhových základů. Pokud se některé z nich používají i
Klasická měření v geodetických sítích Poznámka Detailněji budou popsány metody, které se používaly v minulosti pro budování polohových, výškových a tíhových základů. Pokud se některé z nich používají i
Základy kartografie. RNDr. Petra Surynková, Ph.D.
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta RNDr., Ph.D. petra.surynkova@mff.cuni.cz www.surynkova.info Kartografie Vědní obor zabývající se znázorněním zemského povrchu a nebeských těles
Univerzita Karlova v Praze Matematicko-fyzikální fakulta RNDr., Ph.D. petra.surynkova@mff.cuni.cz www.surynkova.info Kartografie Vědní obor zabývající se znázorněním zemského povrchu a nebeských těles
