Opiceabanán. Jdeoúlohu,kdysevdanémprostorupohybujeopice,někdejezavěšenýbanánaopicenanějnedosáhne.Vprostorujeovšemtakéžidle,
|
|
|
- David Kovář
- před 8 lety
- Počet zobrazení:
Transkript
1 1 Plánovací systémy Jako další samostatnou kategorii umělé inteligence můžeme vyčlenit oblast plánovacích úloh. Ne vždy jsou úlohy z této třídy řazeny mezi plánování, někdy mohou některé úlohy zapadnout do kategorie hledání řešení, jindy jsou zařazeny mezi speciální expertní systémy. Zde ale bude kategorie plánovacích úloh vyčleněna samostatně. Proč tomu tak je, hned uvidíme. Pokud se podíváme na úlohy hledání řešení, máme obvykle daný problém popsaný docela precizně a jen na základě vlastních kritérií v něm hledáme řešení pro naše zadání. Zkusmesialenastůlvysypatkostkydominaahnedseocitámevezcela jiné pozici. Nemáme graf. Máme krátké spoje pro dvojice čísel, ale jaká bude výsledná cesta se ukáže až během hry. Ataktobudeivtétokapitole.Budemesezabývatstavovýmiveličinami, popisujícími stav našeho problému, nebo modelu(obecněji stavu světa). A pro transformování stavu z aktuálního do cílového budeme používat různé akce, které mohou měnit stav jedné či více stavových veličin současně. 1.1 Příklady plánovacích úloh Než se pustíme do vysvětlování realizace plánovacích systémů, ukažme si několik nejznámějších úloh, pro které se plánovací systémy používají. Jde o takzvané dobřeznámé problémy.jejichpraktickápodobaalebývávelmi odlišná. Opiceabanán. Jdeoúlohu,kdysevdanémprostorupohybujeopice,někdejezavěšenýbanánaopicenanějnedosáhne.Vprostorujeovšemtakéžidle, kterousiopicemůžepřinéstpodbanán,apokudnanivyleze,bude moci banán utrhnout. Tutoúlohusipronašeúčelypřevedemepozdějinaproblémrobotbedna- vypínač. Koza,vlk,zelíapřevozník. V našich krajích úloha známá pro většinu lidí již od základní školy. Převozník má za úkol převézt přes řeku všechny tři uvedené věci, na loďku je však schopen vždy naložit jen jedinou. Na břehu ovšem nesmí zůstatbezdozorukozasezelím,nebovlkskozou. Otecadvasynovésemajípřepravitpřesřeku. Vtomtopřípadějeproblémvtom,želoďkauvezejen100kg.Každý zesynůvážíprávě50kgaotecpřesně100kg.jaksedostanouvšichni přes řeku? 1
2 3misionářia3lidožrouti. Opětsemusívšichnipřepravitpřesřekunalodi,kteráuvezejendvě osoby. Na žádném břehu však nesmí nikdy zůstat lidožrouti v převaze. 15puzzle Známý čtverec rozdělený na 4 4 políčka, vyplněný čísly 1 až 15. Jedno volné políčko dává možnost čísly posouvat a seřadit je vzestupně či sestupně. Hanojské věže. Máme na sobě naskládané kameny dle velikosti. Naším úkolem je přeložit celý sloupec na jiné místo, přičemž smíme vždy přesouvat jen jediný kámen a nesmíme položit kámen větší na menší. K dispozici máme jen jediné pomocné odkládací místo. Nádoby9la4l. Mámedvěnádoby,9la4l.Nádobynemajístupnici,smímejevylévat adolévatdoplna.možnojenádobyipřelévat,alebuďjenvšepřelít, nebo dolít do plna. 3mince. Nastoleleží3mincehlavounahoru.Otáčenímvždydvoumincísoučasně otočte všechny mince hlavou dolů. A ve výčtu bychom mohli pokračovat složitějšími úlohami. 1.2 GPS- General Problem Solver Prvním systémům předcházala celá řada experimentů. Jeden z prvních systémů vznikl tak, že se lidé řešící některé hlavolamy pokusili slovně formulovat své myšlenkové postupy. Vznikly z toho tři základní postupové kroky: Analýza prostředků a cílů. Plánování. Aplikace metody pokus omyl. Podívejme se, co si pod jednotlivými kroky představit. Mějme příklad na obrázku 1. Pokud chceme, aby robot rozsvítil světlo, musí si přesunout bednudomístostim3,vyléztnaniarozsvítit. Máme-li provést první krok pro vytvoření plánovacího systému, musíme tento problém popsat stavovými veličinami a ke každé veličině přiřadit akci, která bude danou veličinu modifikovat. V Prologu bude výsledek analýzy následující: 2
3 % Popis stavovych velicin stav( robot_v, m1 ). stav( robot_na, zemi ). stav( bedna_v, m2 ). stav( svetlo, nesviti ). % Prirazeni dvojic - planovaci akce a promenne akce( robot_v, jdi ). akce( robot_na, vylez ). akce( bedna_v, presun ). akce( svetlo, prepni ). Mámetedyčtyřistavovéveličiny-robotv,robotna,bednav,svetlo. Pro každou veličinu bude jediná akce, která ji bude modifikovat- jdi, vylez, presun, prepni. Možná si položíte otázku, proč jsme nepřiřadili ke každé proměnné a jejímu stavu i akci? V tomto jednoduchém připadě by to asi teoreticky možné bylo,alevpřípadě,kdysedanástavováproměnnásmíměnitvíceakcemi, už bychom se ocitli v problémech. V této chvíli můžeme přistoupit k druhému kroku plánování. Pro každou akci musíme specifikovat, jak bude stav proměnných modifikovat a za jakých podmínek budou jednotlivé akce proveditelné. Naše čtyři akce mohou vypadat asi následovně: % Prechod robota do jine mistnosti jdi( Kam ) :- cil( robot_na, zemi ), retract( stav( robot_v, _ ) ), assert( stav( robot_v, Kam ) ),!. % Vylezeni na bednu vylez( Naco ) :- stav( bedna_v, Kde ), cil( robot_v, Kde ), retract( stav( robot_na, _ ) ), assert( stav( robot_na, Naco ) ),!. % Prepnuti vypinace. 3
4 prepni( S ) :- cil( bedna_v, m3 ), cil( robot_na, bedne ), retract( stav( svetlo, _ ) ), assert( stav( svetlo, S ) ),!. % Presun bedny do jine mistnosti presun( Kam ) :- cil( robot_na, zemi ), stav( bedna_v, Kde ), cil( robot_v, Kde ), retract( stav( bedna_v, _ ) ), retract( stav( robot_v, _ ) ), assert( stav( bedna_v, Kam ) ), assert( stav( robot_v, Kam ) ),!. Všimnětesi,ževakcijdiapresunjsmesizjednodušiliprůchodmezi místnostmi. Jde totiž o hledání řešení a to není v této kapitole podstatné. S takto vytvořenými akcemi se můžeme pustit do posledního bodu, aplikovat jednotlivé akce metodou pokus omyl. Tím se dostáváme k jádru systému GPS, kdy budeme aplikovat jednotlivéakcesicenaslepo,alesamozřejměvpořadí,abysestavsvětaměnil souvisle. Akce na sebe tedy musí navazovat(jako kostky v dominu). Implementace pro náš problém robota je následující: cil( Prom, Stav ) :- stav( Prom, Stav ),!. cil( Prom, Stav ) :- akce( Prom, Akce ), X =.. [ Akce, Stav ], X, write( Akce ), write( => ), write( Prom ), write( - ), write( Stav ), nl, cil( Prom, Stav ),!. Budeme se pokoušet postupně provádět jednotlivé akce, při rekurzi se akce budou řetězit a pokud se dostaneme do cílového stavu, hledání se ukončí. Strom řešení se bude zcela zřejmě rozvíjet do hloubky. Když už máme celý systém sestavený, můžeme ho vyzkoušet. Zadejme mu postupně několik úkolů a sledujme, co se stane. Úkoly mohou být následující: cil(robotv,m4). 4
5 cil(bednav,m1). cil(svetlo,sviti). cil(bednav,m2). cil( svetlo, nesviti). Výpis výsledků plánování bude přímo při komunikaci v příkazovém řádku interpretu Prologu následující:?- cil( robot_v, m4 ). jdi => robot_v - m4?- cil( bedna_v, m1 ). jdi => robot_v - m2 presun => bedna_v - m1?- cil( svetlo, sviti ). presun => bedna_v - m3 vylez => robot_na - bedne prepni => svetlo - sviti?- cil( bedna_v, m2 ). vylez => robot_na - zemi presun => bedna_v - m2?- cil( svetlo, nesviti ). presun => bedna_v - m3 vylez => robot_na - bedne prepni => svetlo - nesviti?- Robot postupně plní naše příkazy a v každém kroku se vypisují provedené akce. Našemu jednoduchému problému odpovídá i snadné řešení jednotlivých úkolů. Možná někoho překvapí univerzální chování akce vylez a prepni. Ale pokud se podíváme na jejich zdrojový kód, zjistíme, že i při této jednoduchosti je možno zachovat dostatečnou univerzalitu. 5
6 m1 m2 vypinac robot bedna m3 m4 Obrázek 1: Popis situace v problému robot bedna vypínač 1.3 STRIPS- Standford Research Institute Problem Solver Metoda STRIPS je výsledkem výzkumného úkolu, jehož záměrem bylo navrhnout univerzálnější plánovací systém, aby nebylo vždy nutno programovat každou plánovací akci pro nově zadaný problém. K jakému závěru autoři dospěli, si můžeme odvodit i sami. Podívámeli se na akce robota v předchozím systému GPS, snadno rozpoznáme tři opakující se kroky. Nejprve podmínky, za jakých může být akce provedena, pak se z modelu světa odeberou již neplatné hodnoty stavových veličin a nahradí se novými. STRIPS bude tedy velmi podobný systému GPS. Jen akce budou definovány jako uspořádaná trojice: akce a =[P a, S a, N a ], kde mají jednotlivé položky následující význam: P a jemnožinapodmíneknutnýchkprovedení akce a, S a obsahujemnožinuhodnotstavovýchveličin,kterébudouzestavusvěta odstraněny, N a obsahujemnožinuhodnotstavovýchveličin,kterésedostavusvěta provedením akce a přidají. V jazyce Prolog bude popis akcí vypadat následovně: akce( název, [ seznam podmínek ], [ seznam hodnot pro odebrání ], [ seznam nových hodnot ] ). 6
7 Popis systému postavíme na příkladu řešení problému robota podle obrázku 1. Akce navrhneme jako trojice seznamů a snadno vyřešíme i korektní průchod mezi místnostmi. Popis problému pro systém STRIPS bude následující: % pocatecni stav stav0 :- retractall( stav( _, _ ) ), assert( stav( robot_v, m1 ) ), assert( stav( robot_na, zemi ) ), assert( stav( bedna_v, m2 ) ), assert( stav( svetlo, nesviti ) ). :-stav0. % pruchody mezi mistnostmi pruchod( m1, m4 ). pruchod( m2, m4 ). pruchod( m3, m4 ). % obousmerne propojeni mistnosti spojeni( X, Y ) :- pruchod( X, Y ). spojeni( X, Y ) :- pruchod( Y, X ). % planovaci akce - ( nazev, [ podminky ], [ odeber ], [ pridej ] ). akce( jdi( X, Y ), [ spojeni( X, Y ), stav( robot_na, zemi ), stav( robot_v, X ) ], [ stav( robot_v, X ) ], [ stav( robot_v, Y ) ] ). akce( presun( X, Y ), [ spojeni( X, Y ), stav( robot_na, zemi ), stav( robot_v, X ), stav( bedna_v, X ) ], [ stav( robot_v, X ), stav( bedna_v, X ) ], [ stav( robot_v, Y ), stav( bedna_v, Y ) ] ). akce( vylez, [ stav( bedna_v, X ), stav( robot_v, X ) ], [ stav( robot_v, X ), stav( robot_na, zemi ) ], [ stav( robot_na, bedne ) ] ). akce( slez, [ stav( bedna_v, X ), stav( robot_na, bedne ) ], [ stav( robot_na, bedne ) ], [ stav( robot_na, zemi ), stav( robot_v, X ) ] ). akce( rozsvit, 7
8 [ stav( bedna_v, m3 ), stav( robot_na, bedne ) ], [ stav( svetlo, nesviti ) ], [ stav( svetlo, sviti ) ] ). akce( zhasni, [ stav( bedna_v, m3 ), stav( robot_na, bedne ) ], [ stav( svetlo, sviti ) ], [ stav( svetlo, nesviti ) ] ). K takto popsaným akcím již můžeme přidat jádro systému STRIPS. Jeho podstatou je vybírat takové akce, které svým provedením dosáhnou cílového stavu(prakticky to znamená, že hodnota stavové veličiny musí být obsažena ve třetím seznamu popisu akce). Tímto krokem se dostaneme do stavu předchozího a od tohoto stavu dále pokračujeme v plánování až do aktuálního stavu. Strom řešení je v tomto případě rozvíjen od stavu cílového k aktuálnímu. Pokud tedy systém nalezne souvislou posloupnost akcí, tak je provede. Implementace tohoto jednoduchého principu je následující: % plneni jednoho cile cil( C ) :- C. % cil je splnen cil( C ) :- rozpracovano( C ),!, fail. % cil je rozpracovan cil( C ) :- assertu( rozpracovano( C ) ), % zaznamename cil jako rozpracovany akce( Akce, Podm, Pryc, Pridat ), % vyber akce member( C, Pridat ), % overeni, zda akce povede k cili cile( Podm ), % splneni podminek odeber_seznam( Pryc ), % odstranime neplatne stavy pridej_seznam( Pridat ), % pridame nove stavy retractu( rozpracovano( C ) ), % splneny cil jiz neni rozpracovan vsechny_stavy( X ), % zaznamename provedenou akci assertu( plan( provedeno( Akce, X ) ) ). start( X ) :- retractall( rozpracovano( _ ) ), retractall( plan( _ ) ), cil( X ), planovani. Vlastní princip systému STRIPS je prakticky zahrnut v pěti řádcíchvýběr akce, ověření, zda akce povede k cíli, splnění podmínek a změna stavu světa. Predikát start použijeme pro spuštění plánování. Nyní už zbývá jen několik pomocných predikátů, kterými si pomůžeme při zpracovávání seznamů stavových veličin a plnění seznamu podmínek. 8
9 % pomocne predikaty % plneni seznamu cilu cile( [] ). cile( [ H T ] ) :- cil( H ), cile( T ). % pridani seznamu stavu pridej_seznam( [] ). pridej_seznam( [ H T ] ) :- assertu( H ), pridej_seznam( T ). % odebrani seznamu stavu odeber_seznam( [] ). odeber_seznam( [ H T ] ) :- retractu( H ), odeber_seznam( T ). % vypis planu planovani :- write( ), nl, stav( X, Y ), write( stav( X, Y ) ), nl, fail. planovani :- nl, write( ), nl, nl, fail. planovani :- plan( provedeno( A, X ) ), write( A ), write( => ), nl, write( ), write( X ), nl, fail. planovani :-!. % stav vsech stavovych velicin do seznamu vsechny_stavy( _ ) :- retractall( svet( _ ) ), assert( svet( [] ) ), fail. vsechny_stavy( _ ) :- stav( X, Y ), retract( svet( S ) ), assert( svet( [ [ X, Y ] S ] ) ), fail. vsechny_stavy( S ) :- retract( svet( S ) ). 9
10 Teď, když máme celý systém pohromadě, můžeme začít s plánováním. Zkusíme systému zadat několik jednoduchých úkolů a podíváme se na nalezená řešení. Zkusíme zadat tyto úkoly: start(stav(robotv,m3)). start(stav(robotna,bedne)). start(stav(svetlo,sviti)). start(stav(robotv,m1)). Chování systému přímo v interpretu Prologu bude následující:?- start( stav( robot_v, m3 ) ). stav(robot_na, zemi) stav(bedna_v, m2) stav(svetlo, nesviti) stav(robot_v, m3) jdi(m1, m4) => [[robot_v, m4], [svetlo, nesviti], [bedna_v, m2], [robot_na, zemi]] jdi(m4, m3) => [[robot_v, m3], [svetlo, nesviti], [bedna_v, m2], [robot_na, zemi]]?- start( stav( robot_na, bedne ) ). stav(bedna_v, m2) stav(svetlo, nesviti) stav(robot_na, bedne) jdi(m3, m4) => [[robot_v, m4], [svetlo, nesviti], [bedna_v, m2], [robot_na, zemi]] jdi(m4, m2) => [[robot_v, m2], [svetlo, nesviti], [bedna_v, m2], [robot_na, zemi]] vylez => [[robot_na, bedne], [svetlo, nesviti], [bedna_v, m2]] 10
11 ?- start( stav( svetlo, sviti ) ). stav(bedna_v, m3) stav(robot_na, bedne) stav(svetlo, sviti) jdi(m4, m1) => [[robot_v, m1], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] jdi(m1, m4) => [[robot_v, m4], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] jdi(m4, m2) => [[robot_v, m2], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] jdi(m2, m4) => [[robot_v, m4], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] slez => [[robot_v, m2], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] vylez => [[robot_na, bedne], [svetlo, nesviti], [bedna_v, m2]] slez => [[robot_v, m2], [robot_na, zemi], [svetlo, nesviti], [bedna_v, m2]] presun(m2, m4) => [[bedna_v, m4], [robot_v, m4], [robot_na, zemi], [svetlo, nesviti]] presun(m4, m1) => [[bedna_v, m1], [robot_v, m1], [robot_na, zemi], [svetlo, nesviti]] presun(m1, m4) => [[bedna_v, m4], [robot_v, m4], [robot_na, zemi], [svetlo, nesviti]] presun(m4, m3) => [[bedna_v, m3], [robot_v, m3], [robot_na, zemi], [svetlo, nesviti]] vylez => [[robot_na, bedne], [bedna_v, m3], [svetlo, nesviti]] rozsvit => [[svetlo, sviti], [robot_na, bedne], [bedna_v, m3]]?- start( stav( robot_v, m1 ) ). stav(svetlo, sviti) stav(bedna_v, m3) stav(robot_na, zemi) stav(robot_v, m1) 11
12 slez => [[robot_v, m3], [robot_na, zemi], [svetlo, sviti], [bedna_v, m3]] jdi(m3, m4) => [[robot_v, m4], [robot_na, zemi], [bedna_v, m3], [svetlo, sviti]] jdi(m4, m1) => [[robot_v, m1], [robot_na, zemi], [bedna_v, m3], [svetlo, sviti]]?- 1.4 Řešeníproblémudvounádob9la4l Podívejme se ještě na řešení jednoho úkolu s použitím systému GPS a STRIPS. Přiklad dvou nádob je výhodný jako praktická ukázka. Má jen dvěstavovéveličiny,ztomůževéstkpředstavě,žecelýproblémbudejednodušší, než příklad s robotem. Analýza však rychle odhalí, že se objevují drobné komplikace. Upozorníme na ně, během realizace GPS-dvěnádoby Stavové veličiny si zjednodušíme jako jedinou dvojici čísel a výsledek analýzy a plánování bude následující: % pocatecni stav sveta stav( 0, 0 ). % 9l, 4l % seznam akci - vsechny akce modifikuji stav % neni proto potreba definovat dvojice (akce - promenna) akce( dolej1 ). akce( dolej2 ). akce( vylej1 ). akce( vylej2 ). akce( prelej12 ). akce( prelej21 ). % preliti z X do Y, kdy YM je maximum Y. % vysledek jde do X1, Y1 prelej( X, Y, YM, X1, Y1 ) :- Z is YM - Y, Z > 0, % volne misto v Y min( X, Z, Z2 ), % ceho je mene? vody nebo mista? X1 is X - Z2, Y1 is Y + Z2,!. % planovaci akce 12
13 % doliti dolej1( _, Y, 9, Y ). dolej2( X, _, X, 4 ). % vyliti vylej1( _, Y, 0, Y ). vylej2( X, _, X, 0 ). % prelivani prelej12( X, Y, X1, Y1 ) :- prelej( X, Y, 4, X1, Y1 ). prelej21( X, Y, X1, Y1 ) :- prelej( Y, X, 9, Y1, X1 ). Zde je asi na místě, objasnit funkci predikátu prelej. Jak jednoduše odpovědět na otázku, kolik vody můžeme přelít z první do druhé nádoby? Záležínatom,čehojeméně:buďkapalinyvprvnínádobě,nebovolného místa v nádobě druhé. Dále narazíme při aplikaci postupu pokus omyl na problém zacyklení. Systém začne nádoby naplňovat a vylévat a k žádnému výsledku nedospěje. Musíme proto rozvoj stromu řešení trochu usměrnit. To lze snadno udělat dvěma způsoby: sledovat stavy světa a nepřipustit stav, který už dříve byl, nebo omezit hloubku stromu řešení. První metoda je efektivnější, druhá jednodušší. Podívejme se na výsledné řešení: % jadro GPS - s omezenim, kdy stav sveta se nesmi opakovat cil( C ) :- C. cil( C ) :- akce( A ), stav( X, Y ), D =.. [ A, X, Y, X1, Y1 ], % vyber akci % vytvoreni volani akce D, % vyvolani akce assertb( bylo( X1, Y1 ) ), % nesmi se opakovat stav sveta % evidence planu akci assertu( plan( provedeno( A, stav( X1, Y1 ) ) ) ), retractu( stav( X, Y ) ), % zmena stavu sveta assertu( stav( X1, Y1 ) ), cil( C ). % navrat do stavu 0 stav0 :- 13
14 retractall( bylo( _, _ ) ), retractall( plan( _ ) ), retractall( stav( _, _ ) ), assert( stav( 0, 0 ) ). % spusteni hledani reseni % Priklad: % start( stav( 5, 0 ) ). % start( stav( 0, 1 ) ). % start( stav( 3, 0 ) ). % start( stav( 7, 0 ) ). start( C ) :- stav0, cil( C ), planovani. % ********************************************************* % jadro GPS s omezenim na pocet kroku rozvoje stromu reseni ciln( C, _ ) :- C. ciln( C, N ) :- N > 0, akce( A ), % vyber akci stav( X, Y ), D =.. [ A, X, Y, X1, Y1 ], % vytvoreni dotazu D, % volani akce assertu( plan( provedeno( [ N, A ], stav( X1, Y1 ) ) ) ), retractu( stav( X, Y ) ), % zmena stavu sveta assertu( stav( X1, Y1 ) ), N1 is N - 1, ciln( C, N1 ). % rekurze % spusteni hledani reseni s omezeni rozvoje stromu reseni % pouziti stejne jako start(...) omezeni( 12 ). startn( C ) :- stav0, omezeni( N ), ciln( C, N ), 14
15 planovani. % ********************************************************* % pomocne predikaty min( A, B, C ) :- A < B,!, C = A;!, C = B. % vypis planu planovani :- stav( X, Y ), write( ), nl, write( stav( X, Y ) ), nl, nl, write( ), nl, fail. planovani :- plan( provedeno( A, X ) ), write( A ), write( => ), write( X ), nl, fail. planovani :-!. Teď systém vyzkoušíme:?- start( stav( 2, 0 ) ). stav(2, 0) dolej1 => stav(9, 0) dolej2 => stav(9, 4) vylej1 => stav(0, 4) prelej21 => stav(4, 0) dolej2 => stav(4, 4) prelej21 => stav(8, 0) dolej2 => stav(8, 4) prelej21 => stav(9, 3) vylej1 => stav(0, 3) prelej21 => stav(3, 0) dolej2 => stav(3, 4) prelej21 => stav(7, 0) dolej2 => stav(7, 4) prelej21 => stav(9, 2) vylej1 => stav(0, 2) prelej21 => stav(2, 0) 15
16 ?- start( stav( 3, 0 ) ). stav(3, 0) dolej1 => stav(9, 0) dolej2 => stav(9, 4) vylej1 => stav(0, 4) prelej21 => stav(4, 0) dolej2 => stav(4, 4) prelej21 => stav(8, 0) dolej2 => stav(8, 4) prelej21 => stav(9, 3) vylej1 => stav(0, 3) prelej21 => stav(3, 0)?- startn( stav( 5, 0 ) ). stav(5, 0) [12, dolej1] => stav(9, 0) [11, dolej1] => stav(9, 0) [10, dolej1] => stav(9, 0) [9, dolej1] => stav(9, 0) [8, dolej1] => stav(9, 0) [7, dolej1] => stav(9, 0) [6, dolej1] => stav(9, 0) [5, dolej1] => stav(9, 0) [4, dolej1] => stav(9, 0) [3, dolej1] => stav(9, 0) [2, prelej12] => stav(5, 4) [1, vylej2] => stav(5, 0)?- startn( stav( 6, 0 ) ). stav(6, 0) [12, dolej1] => stav(9, 0) [11, dolej1] => stav(9, 0) 16
17 [10, dolej1] => stav(9, 0) [9, dolej1] => stav(9, 0) [8, prelej12] => stav(5, 4) [7, vylej2] => stav(5, 0) [6, prelej12] => stav(1, 4) [5, vylej2] => stav(1, 0) [4, prelej12] => stav(0, 1) [3, dolej1] => stav(9, 1) [2, prelej12] => stav(6, 4) [1, vylej2] => stav(6, 0)? STRIPS- dvě nádoby A pro úplnost ještě varianta dvou nádob řešená v systému STRIPS. Popis akcí a jádro systému i s pomocnými predikáty bude následující: % pocatecni stav stav( 0, 0 ). % 9l, 4l % preliti z nadoby Y1 do nadoby X1 - odhad predchoziho stavu % X1, Y1 - pocatecni stav nadob % MX - maximum nadoby X % X, Y - vysledek prelej( X, Y, MX, X1, Y1 ) :- ZX is MX - X1, min( ZX, Y1, M ),!, % mensi je volne misto v X1 % nebo aktualni obsah Y1? M >= 0, % prelit bylo mozno jen kladny pocet X is X1 + M, Y is Y1 - M, X =< MX, % nesmime preplnit X Y >= 0. % a vylit Y vic nez do 0 % planovaci akce % nema smysl vylivat poloprazdne nadoby, viz. trace... akce( vylit1, [ stav( 9, Y ) ], [ stav( 9, Y ) ], 17
18 [ stav( 0, Y ) ] ). akce( vylit2, [ stav( X, 4 ) ], [ stav( X, 4 ) ], [ stav( X, 0 ) ] ). % doliva se vzdy do plna akce( dolit1, [ stav( 0, Y ) ], [ stav( 0, Y ) ], [ stav( 9, Y ) ] ). akce( dolit2, [ stav( X, 0 ) ], [ stav( X, 0 ) ], [ stav( X, 4 ) ] ). % prelivani akce( prelit21( X, Y, X1, Y1 ), [ prelej( Y, X, 4, Y1, X1 ), stav( X, Y ) ], [ stav( X, Y ) ], [ stav( X1, Y1 ) ] ). akce( prelit12( X, Y, X1, Y1 ), [ prelej( X, Y, 9, X1, Y1 ), stav( X, Y ) ], [ stav( X, Y ) ], [ stav( X1, Y1 ) ] ). % plneni jednoho cile cil( C ) :- C. cil( C ) :- rozpracovano( C ),!, fail. cil( C ) :- assertu( rozpracovano( C ) ), akce( Akce, Podm, Pryc, Pridat ), member( C, Pridat ), cile( Podm ), odeber_seznam( Pryc ), pridej_seznam( Pridat ), retractu( rozpracovano( C ) ), stav( X, Y ), assertu( plan( provedeno( Akce, stav( X, Y ) ) ) ). % navrat do stavu 0 stav0 :- retractall( stav( _, _ ) ), 18
19 assert( stav( 0, 0 ) ). % spusteni hledani start( X ) :- stav0, retractall( rozpracovano( _ ) ), retractall( plan( _ ) ), cil( X ), planovani. % ******************************************************* % pomocne predikaty % minimum ze dvou cisel min( X, Y, M ) :- X < Y, M is X,! ; M is Y,!. % plneni seznamu cilu cile( [] ). cile( [ H T ] ) :- cil( H ), cile( T ). % pridani seznamu cilu pridej_seznam( [] ). pridej_seznam( [ H T ] ) :- assertu( H ), pridej_seznam( T ). % odebrani seznamu cilu odeber_seznam( [] ). odeber_seznam( [ H T ] ) :- retractu( H ), odeber_seznam( T ). % vypis planu planovani :- stav( X, Y ), write( ), nl, write( stav( X, Y ) ), nl, nl, write( ), nl, fail. planovani :- plan( provedeno( A, X ) ), write( A ), write( => ), write( X ), nl, fail. planovani :-!. 19
20 A výsledné chování systému:?- start( stav( 5, 0 ) ). stav(5, 0) dolit2 => stav(0, 4) dolit1 => stav(9, 4) vylit2 => stav(9, 0) prelit12(9, 0, 5, 4) => stav(5, 4) vylit2 => stav(5, 0)?- start( stav( 0, 1 ) ). stav(0, 1) dolit1 => stav(9, 0) dolit2 => stav(9, 4) vylit1 => stav(0, 4) prelit21(0, 4, 4, 0) => stav(4, 0) dolit2 => stav(4, 4) prelit21(4, 4, 8, 0) => stav(8, 0) dolit2 => stav(8, 4) prelit21(8, 4, 9, 3) => stav(9, 3) vylit1 => stav(0, 3) prelit21(0, 3, 3, 0) => stav(3, 0) dolit2 => stav(3, 4) prelit21(3, 4, 7, 0) => stav(7, 0) dolit2 => stav(7, 4) prelit21(7, 4, 9, 2) => stav(9, 2) vylit1 => stav(0, 2) prelit21(0, 2, 2, 0) => stav(2, 0) dolit2 => stav(2, 4) prelit21(2, 4, 6, 0) => stav(6, 0) dolit2 => stav(6, 4) prelit21(6, 4, 9, 1) => stav(9, 1) vylit1 => stav(0, 1)?- start( stav( 3, 0 ) ). 20
21 stav(3, 0) dolit2 => stav(0, 4) dolit1 => stav(9, 4) vylit2 => stav(9, 0) prelit12(9, 0, 5, 4) => stav(5, 4) vylit2 => stav(5, 0) prelit12(5, 0, 1, 4) => stav(1, 4) vylit2 => stav(1, 0) prelit12(1, 0, 0, 1) => stav(0, 1) dolit1 => stav(9, 1) prelit12(9, 1, 6, 4) => stav(6, 4) vylit2 => stav(6, 0) prelit12(6, 0, 2, 4) => stav(2, 4) vylit2 => stav(2, 0) prelit12(2, 0, 0, 2) => stav(0, 2) dolit1 => stav(9, 2) prelit12(9, 2, 7, 4) => stav(7, 4) vylit2 => stav(7, 0) prelit12(7, 0, 3, 4) => stav(3, 4) vylit2 => stav(3, 0)?- start( stav( 7, 0 ) ). stav(7, 0) dolit2 => stav(0, 4) dolit1 => stav(9, 4) vylit2 => stav(9, 0) prelit12(9, 0, 5, 4) => stav(5, 4) vylit2 => stav(5, 0) prelit12(5, 0, 1, 4) => stav(1, 4) vylit2 => stav(1, 0) prelit12(1, 0, 0, 1) => stav(0, 1) dolit1 => stav(9, 1) prelit12(9, 1, 6, 4) => stav(6, 4) vylit2 => stav(6, 0) prelit12(6, 0, 2, 4) => stav(2, 4) vylit2 => stav(2, 0) prelit12(2, 0, 0, 2) => stav(0, 2) dolit1 => stav(9, 2) 21
22 prelit12(9, 2, 7, 4) => stav(7, 4) vylit2 => stav(7, 0)?- 2 Cvičení Plánovacím systémům jsou věnována 3 cvičení. Během této doby si každý student nejen ověří fungování prezentovaných příkladů, ale pokusí se algoritmizovat libovolný jednoduchý plánovací problém. 2.1 Ověření plánování s robotem a s dvojicí nádob První z trojice cvičení je věnováno úvodu do problematiky. Seznámení se z oběma plánovacími algoritmy GPS a Strips. Ověření dosažitelnosti všech stavů. Modifikace plánovacích aktivit, testování možných změn chování. 2.2 Výběr vlastního problému Druhé cvičení bude věnováno výběru problému, který si bude každý sám implementovat. Zvážení a konzultace náročnosti daného problému. Výběr vhodnějšího plánovacího systému. Zvážení, zda je lepší postupovat v daném případě od počátečního stavu do cílového, či obráceně, od cíle k počátku. 2.3 Odladění a prezentace plánovacího algoritmu Třetí cvičení věnované plánování bude zaměřeno na doladění, testování a prezentování vlastního systému. 22
Úloha ve stavovém prostoru SP je <s 0, C>, kde s 0 je počáteční stav C je množina požadovaných cílových stavů
 Stavový prostor a jeho prohledávání SP = formalismus k obecnějšímu uchopení a vymezení problému, který spočívá v nalezení posloupnosti akcí vedoucích od počátečního stavu úlohy (zadání) k požadovanému
Stavový prostor a jeho prohledávání SP = formalismus k obecnějšímu uchopení a vymezení problému, který spočívá v nalezení posloupnosti akcí vedoucích od počátečního stavu úlohy (zadání) k požadovanému
1 Hledání řešení. 1.1 Klasické problémy. 1.2 Problém rezervace letenek
 1 Hledání řešení Základem celé řady implementací inteligentních systémů je hledání řešení. Obvykle jsou pro mnoho problémů známé výpočetní metody, které hledají řešení deterministicky podle algoritmu,
1 Hledání řešení Základem celé řady implementací inteligentních systémů je hledání řešení. Obvykle jsou pro mnoho problémů známé výpočetní metody, které hledají řešení deterministicky podle algoritmu,
Typy souborů ve STATISTICA. Tento článek poslouží jako přehled hlavních typů souborů v programu
 StatSoft Typy souborů ve STATISTICA Tento článek poslouží jako přehled hlavních typů souborů v programu STATISTICA, ukáže Vám jejich možnosti a tím Vám dovolí využívat program efektivněji. Jistě jste již
StatSoft Typy souborů ve STATISTICA Tento článek poslouží jako přehled hlavních typů souborů v programu STATISTICA, ukáže Vám jejich možnosti a tím Vám dovolí využívat program efektivněji. Jistě jste již
Algoritmizace. 1. Úvod. Algoritmus
 1. Úvod Algoritmizace V dnešní době již počítače pronikly snad do všech oblastí lidské činnosti, využívají se k řešení nejrůznějších úkolů. Postup, který je v počítači prováděn nějakým programem se nazývá
1. Úvod Algoritmizace V dnešní době již počítače pronikly snad do všech oblastí lidské činnosti, využívají se k řešení nejrůznějších úkolů. Postup, který je v počítači prováděn nějakým programem se nazývá
Obsah prezentace. Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest
 Obsah prezentace Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest 1 Základní pojmy Vrchol grafu: {množina V} Je to styčná vazba v grafu, nazývá se též uzlem, prvkem
Obsah prezentace Základní pojmy v teorii o grafech Úlohy a prohledávání grafů Hledání nejkratších cest 1 Základní pojmy Vrchol grafu: {množina V} Je to styčná vazba v grafu, nazývá se též uzlem, prvkem
Inovace a zkvalitnění výuky prostřednictvím ICT Databázové systémy MS Access propojení relací s formuláři a sestavami Ing.
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Číslo: Anotace: Inovace a zkvalitnění výuky prostřednictvím ICT Databázové systémy MS Access propojení
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Číslo: Anotace: Inovace a zkvalitnění výuky prostřednictvím ICT Databázové systémy MS Access propojení
NP-úplnost problému SAT
 Problém SAT je definován následovně: SAT(splnitelnost booleovských formulí) Vstup: Booleovská formule ϕ. Otázka: Je ϕ splnitelná? Příklad: Formule ϕ 1 =x 1 ( x 2 x 3 )jesplnitelná: např.přiohodnocení ν,kde[x
Problém SAT je definován následovně: SAT(splnitelnost booleovských formulí) Vstup: Booleovská formule ϕ. Otázka: Je ϕ splnitelná? Příklad: Formule ϕ 1 =x 1 ( x 2 x 3 )jesplnitelná: např.přiohodnocení ν,kde[x
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
PŘÍRUČKA PRÁCE SE SYSTÉMEM SLMS CLASS pro učitele
 PŘÍRUČKA PRÁCE SE SYSTÉMEM SLMS CLASS pro učitele Vypracoval : Pavel Žemba Obsah Tvorba vlastních testů... 3 Postup tvorby... 3 Test otázky odpovědi... 3 Zadání otázek testu... 5 Test - cvičení na souboru,
PŘÍRUČKA PRÁCE SE SYSTÉMEM SLMS CLASS pro učitele Vypracoval : Pavel Žemba Obsah Tvorba vlastních testů... 3 Postup tvorby... 3 Test otázky odpovědi... 3 Zadání otázek testu... 5 Test - cvičení na souboru,
6. blok část C Množinové operátory
 6. blok část C Množinové operátory Studijní cíl Tento blok je věnován problematice množinových operátorů a práce s množinovými operátory v jazyce SQL. Čtenáři se seznámí s operátory, UNION, a INTERSECT.
6. blok část C Množinové operátory Studijní cíl Tento blok je věnován problematice množinových operátorů a práce s množinovými operátory v jazyce SQL. Čtenáři se seznámí s operátory, UNION, a INTERSECT.
KIV/ZIS cvičení 5. Tomáš Potužák
 KIV/ZIS cvičení 5 Tomáš Potužák Úvod do SQL (1) SQL (Structured Query Language) je standardizovaný strukturovaný dotazovací jazyk pro práci s databází Veškeré operace v databázi se dají provádět pomocí
KIV/ZIS cvičení 5 Tomáš Potužák Úvod do SQL (1) SQL (Structured Query Language) je standardizovaný strukturovaný dotazovací jazyk pro práci s databází Veškeré operace v databázi se dají provádět pomocí
Metody návrhu algoritmů, příklady. IB111 Programování a algoritmizace
 Metody návrhu algoritmů, příklady IB111 Programování a algoritmizace 2011 Návrhu algoritmů vybrané metody: hladové algoritmy dynamické programování rekurze hrubá síla tato přednáška: především ilustrativní
Metody návrhu algoritmů, příklady IB111 Programování a algoritmizace 2011 Návrhu algoritmů vybrané metody: hladové algoritmy dynamické programování rekurze hrubá síla tato přednáška: především ilustrativní
Hlavolamy a teorie grafů
 Hlavolamy a teorie grafů Petr Kovář 1 petr.kovar@vsb.cz 1 Vysolá škola báňská Technická univerzita Ostrava, Škola matematického modelování, 2009 Přehled přednášky Úloha hanojských věží Část 1. Co není
Hlavolamy a teorie grafů Petr Kovář 1 petr.kovar@vsb.cz 1 Vysolá škola báňská Technická univerzita Ostrava, Škola matematického modelování, 2009 Přehled přednášky Úloha hanojských věží Část 1. Co není
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0637 Šablona III/2 Název VY_32_INOVACE_39_Algoritmizace_teorie Název školy Základní škola a Střední
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0637 Šablona III/2 Název VY_32_INOVACE_39_Algoritmizace_teorie Název školy Základní škola a Střední
Rozklad problému na podproblémy
 Rozklad problému na podproblémy Postupný návrh programu rozkladem problému na podproblémy zadaný problém rozložíme na podproblémy pro řešení podproblémů zavedeme abstraktní příkazy s pomocí abstraktních
Rozklad problému na podproblémy Postupný návrh programu rozkladem problému na podproblémy zadaný problém rozložíme na podproblémy pro řešení podproblémů zavedeme abstraktní příkazy s pomocí abstraktních
MS Excel 2007 Kontingenční tabulky
 MS Excel 2007 Kontingenční tabulky Obsah kapitoly V této kapitole se seznámíme s nástrojem, který se používá k analýze dat rozsáhlých seznamů. Studijní cíle Studenti budou umět pro analýzu dat rozsáhlých
MS Excel 2007 Kontingenční tabulky Obsah kapitoly V této kapitole se seznámíme s nástrojem, který se používá k analýze dat rozsáhlých seznamů. Studijní cíle Studenti budou umět pro analýzu dat rozsáhlých
Hledání správné cesty
 Semestrální práce z předmětu A6M33AST Závěrečná zpráva Hledání správné cesty Nela Grimová, Lenka Houdková 2015/2016 1. Zadání Naším úkolem bylo vytvoření úlohy Hledání cesty, kterou by bylo možné použít
Semestrální práce z předmětu A6M33AST Závěrečná zpráva Hledání správné cesty Nela Grimová, Lenka Houdková 2015/2016 1. Zadání Naším úkolem bylo vytvoření úlohy Hledání cesty, kterou by bylo možné použít
Logika a logické programování
 Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
SimBIm uživatelská dokumentace
 SimBIm uživatelská dokumentace SimBIm (zkratka pro Similarity Between Images) je webová aplikace určená pro sběr uživatelských hodnocení podobnosti mezi obrázky. Tyto nasbíraná hodnocení jsou pak většinou
SimBIm uživatelská dokumentace SimBIm (zkratka pro Similarity Between Images) je webová aplikace určená pro sběr uživatelských hodnocení podobnosti mezi obrázky. Tyto nasbíraná hodnocení jsou pak většinou
Průvodce aplikací FS Karta
 Průvodce aplikací FS Karta Základní informace k Aplikaci Online aplikace FS Karta slouží k bezpečnému ukládání osobních údajů fyzických osob a k jejich zpracování. Osobní údaje jsou uloženy ve formě karty.
Průvodce aplikací FS Karta Základní informace k Aplikaci Online aplikace FS Karta slouží k bezpečnému ukládání osobních údajů fyzických osob a k jejich zpracování. Osobní údaje jsou uloženy ve formě karty.
Základy umělé inteligence
 Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
Základy umělé inteligence Automatické řešení úloh Základy umělé inteligence - prohledávání. Vlasta Radová, ZČU, katedra kybernetiky 1 Formalizace úlohy UI chápe řešení úloh jako proces hledání řešení v
Ovládání Open Office.org Calc Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako.
 Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako. Otevře se tabulka, v které si najdete místo adresář, pomocí malé šedočerné šipky (jako na obrázku), do kterého
Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako. Otevře se tabulka, v které si najdete místo adresář, pomocí malé šedočerné šipky (jako na obrázku), do kterého
Řazení řádků ve vzestupném pořadí (A až Z nebo 0 až 9) nebo sestupném pořadí (Z až A nebo 9 až 0)
 Řazení oblasti Řazení řádků ve vzestupném pořadí (A až Z nebo 0 až 9) nebo sestupném pořadí (Z až A nebo 9 až 0) 1. Klepněte na buňku ve sloupci, podle kterého chcete řádek seřadit. 2. Klepněte na tlačítko
Řazení oblasti Řazení řádků ve vzestupném pořadí (A až Z nebo 0 až 9) nebo sestupném pořadí (Z až A nebo 9 až 0) 1. Klepněte na buňku ve sloupci, podle kterého chcete řádek seřadit. 2. Klepněte na tlačítko
Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe
 Uživatelská příručka Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe Ministerstvo zemědělství České republiky únor
Uživatelská příručka Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe Ministerstvo zemědělství České republiky únor
Základy vytěžování dat
 Základy vytěžování dat předmět A7Bb36vyd Vytěžování dat Filip Železný, Miroslav Čepek, Radomír Černoch, Jan Hrdlička katedra kybernetiky a katedra počítačů ČVUT v Praze, FEL Evropský sociální fond Praha
Základy vytěžování dat předmět A7Bb36vyd Vytěžování dat Filip Železný, Miroslav Čepek, Radomír Černoch, Jan Hrdlička katedra kybernetiky a katedra počítačů ČVUT v Praze, FEL Evropský sociální fond Praha
Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe
 Uživatelská příručka Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe verze pro mobilní zařízení a čtečky elektronických
Uživatelská příručka Elektronické podání žádosti o udělení výjimky pro použití konvenčních osiv v ekologickém zemědělství prostřednictvím Portálu farmáře MZe verze pro mobilní zařízení a čtečky elektronických
Dynamické datové struktury III.
 Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Kontingenční tabulky v MS Excel 2010
 Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Kreslení grafů na plochy Tomáš Novotný
 Kreslení grafů na plochy Tomáš Novotný Úvod Abstrakt. V první části příspěvku si vysvětlíme základní pojmy týkající se ploch. Dále si ukážeme a procvičíme možné způsoby jejich zobrazování do roviny, abychom
Kreslení grafů na plochy Tomáš Novotný Úvod Abstrakt. V první části příspěvku si vysvětlíme základní pojmy týkající se ploch. Dále si ukážeme a procvičíme možné způsoby jejich zobrazování do roviny, abychom
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5
 Rejstřík Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5 Úvod Správcovská aplikace slouží k vytvoření vstupního a zašifrovaného souboru pro odečtovou
Rejstřík Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5 Úvod Správcovská aplikace slouží k vytvoření vstupního a zašifrovaného souboru pro odečtovou
Základy programování (IZP)
 Základy programování (IZP) Osmé počítačové cvičení Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 66 Brno - Královo Pole Petr Veigend, iveigend@fit.vutbr.cz 20.11.2017,
Základy programování (IZP) Osmé počítačové cvičení Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 66 Brno - Královo Pole Petr Veigend, iveigend@fit.vutbr.cz 20.11.2017,
Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. PORTÁL KUDY KAM. Manuál pro administrátory. Verze 1.
 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. PORTÁL KUDY KAM Manuál pro administrátory Verze 1.0 2012 AutoCont CZ a.s. Veškerá práva vyhrazena. Tento
Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. PORTÁL KUDY KAM Manuál pro administrátory Verze 1.0 2012 AutoCont CZ a.s. Veškerá práva vyhrazena. Tento
ALGORITMIZACE A PROGRAMOVÁNÍ
 Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Metodický list č. 1 Algoritmus a jeho implementace počítačovým programem Základním cílem tohoto tematického celku je vysvětlení pojmů algoritmus a programová implementace algoritmu. Dále je cílem seznámení
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Radek Havlík [ÚLOHA 40 PODSESTAVY]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Radek Havlík [ÚLOHA 40 PODSESTAVY] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Radek Havlík [ÚLOHA 40 PODSESTAVY]](/thumbs/26/7519654.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Radek Havlík [ÚLOHA 40 PODSESTAVY] 1 CÍL KAPITOLY Cílem této kapitoly je naučit se tvořit pracovat s podsestavami v CAD softwaru SolidEdge. Podsestavy se
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Radek Havlík [ÚLOHA 40 PODSESTAVY] 1 CÍL KAPITOLY Cílem této kapitoly je naučit se tvořit pracovat s podsestavami v CAD softwaru SolidEdge. Podsestavy se
Identifikátor materiálu: ICT-4-01
 Identifikátor materiálu: ICT-4-01 Předmět Téma sady Informační a komunikační technologie Téma materiálu Počítačové algoritmy Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí Počítačové
Identifikátor materiálu: ICT-4-01 Předmět Téma sady Informační a komunikační technologie Téma materiálu Počítačové algoritmy Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí Počítačové
Vzorová písemka č. 1 (rok 2015/2016) - řešení
 Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
Úvod do logiky (VL): 5. Odvození výrokových spojek z jiných
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 5. Odvození z jiných doc. PhDr. Jiří Raclavský,
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (VL): 5. Odvození z jiných doc. PhDr. Jiří Raclavský,
Cvičení 5 - Průchod stromem a grafem
 Cvičení 5 - Průchod stromem a grafem Radek Mařík Marko Genyk-Berezovskyj ČVUT FEL, K13133 14. března 2013 Cvičení 5 - Průchod stromem a grafem 14. března 2013 1 / 18 Outline 1 Průchod stromem 2 Cvičení
Cvičení 5 - Průchod stromem a grafem Radek Mařík Marko Genyk-Berezovskyj ČVUT FEL, K13133 14. března 2013 Cvičení 5 - Průchod stromem a grafem 14. března 2013 1 / 18 Outline 1 Průchod stromem 2 Cvičení
Postupy práce se šablonami IS MPP
 Postupy práce se šablonami IS MPP Modul plánování a přezkoumávání, verze 1.20 vypracovala společnost ASD Software, s.r.o. dokument ze dne 27. 3. 2013, verze 1.01 Postupy práce se šablonami IS MPP Modul
Postupy práce se šablonami IS MPP Modul plánování a přezkoumávání, verze 1.20 vypracovala společnost ASD Software, s.r.o. dokument ze dne 27. 3. 2013, verze 1.01 Postupy práce se šablonami IS MPP Modul
4 Stromy a les. Definice a základní vlastnosti stromů. Kostry grafů a jejich počet.
 4 Stromy a les Jedním ze základních, a patrně nejjednodušším, typem grafů jsou takzvané stromy. Jedná se o souvislé grafy bez kružnic. Přes svou (zdánlivou) jednoduchost mají stromy bohatou strukturu a
4 Stromy a les Jedním ze základních, a patrně nejjednodušším, typem grafů jsou takzvané stromy. Jedná se o souvislé grafy bez kružnic. Přes svou (zdánlivou) jednoduchost mají stromy bohatou strukturu a
Gymnázium Ostrava Hrabůvka, příspěvková organizace Františka Hajdy 34, Ostrava Hrabůvka
 Gymnázium Ostrava Hrabůvka, příspěvková organizace Františka Hajdy 34, Ostrava Hrabůvka Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 MS Power Point Metodický
Gymnázium Ostrava Hrabůvka, příspěvková organizace Františka Hajdy 34, Ostrava Hrabůvka Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 MS Power Point Metodický
Třídy složitosti P a NP, NP-úplnost
 Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Třídy složitosti P a NP, NP-úplnost Cíle přednášky: 1. Definovat, za jakých okolností můžeme problém považovat za efektivně algoritmicky řešitelný. 2. Charakterizovat určitou skupinu úloh, pro které není
Domény. Petr Štěpánek. S využitím materialu Krysztofa R. Apta
 Domény Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 10 1 Typy programů v čistém Prologu je možné uspořádat podle různých pohledů. Zajímavá je charakteristika podle domén,
Domény Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 10 1 Typy programů v čistém Prologu je možné uspořádat podle různých pohledů. Zajímavá je charakteristika podle domén,
Programování v jazyku LOGO - úvod
 Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
Micro:bit lekce 3. - Konstrukci If Then a If Then Else najdete v kategorii Logic - Podmínky od If (např. porovnání < >= atd.) najdete taktéž v Logic
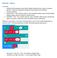 Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
Micro:bit lekce 3. Podmínky - Rozvětvení běhu programu podle splnění nějakých podmínek typu pravda / nepravda - splněno / nesplněno (výsledkem podmínky musí být vždy jen dvě možnosti) - Dva typy podmínek:
6. ROČNÍK ŠKOLNÍ SOUTĚŽE V PROGRAMOVÁNÍ 2013
 6. ROČNÍK ŠKOLNÍ SOUTĚŽE V PROGRAMOVÁNÍ 2013 Pořadí úloh si určujete sami, u každé úlohy je uvedeno její bodové hodnocení. Můžete řešit různé úlohy v různých programovacích jazycích. Každou hotovou úlohu
6. ROČNÍK ŠKOLNÍ SOUTĚŽE V PROGRAMOVÁNÍ 2013 Pořadí úloh si určujete sami, u každé úlohy je uvedeno její bodové hodnocení. Můžete řešit různé úlohy v různých programovacích jazycích. Každou hotovou úlohu
Diskrétní matematika. DiM /01, zimní semestr 2018/2019
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
popel, glum & nepil 16/28
 Lineární rezoluce další způsob zjemnění rezoluce; místo stromu směřujeme k lineární struktuře důkazu Lineární rezoluční odvození (důkaz) z Ë je posloupnost dvojic ¼ ¼ Ò Ò taková, že Ò ½ a 1. ¼ a všechna
Lineární rezoluce další způsob zjemnění rezoluce; místo stromu směřujeme k lineární struktuře důkazu Lineární rezoluční odvození (důkaz) z Ë je posloupnost dvojic ¼ ¼ Ò Ò taková, že Ò ½ a 1. ¼ a všechna
ALGORITMIZACE PRAKTICKÉ
 LOGO IMAGINE Obsah 1. Příkazy 1.1. Základní příkazy 1.2. Vestavěné příkazy Imagine 1.2.1.Příkaz mnohoúhelník 1.2.2.Náhodná procházka 2. Matematické operace 3. Funkce 4. Predikáty 5. Konstruktory 6. Selectory
LOGO IMAGINE Obsah 1. Příkazy 1.1. Základní příkazy 1.2. Vestavěné příkazy Imagine 1.2.1.Příkaz mnohoúhelník 1.2.2.Náhodná procházka 2. Matematické operace 3. Funkce 4. Predikáty 5. Konstruktory 6. Selectory
Obecná informatika. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Podzim 2012
 Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Rektifikace rastrových dat
 Rektifikace rastrových dat Při rektifikaci převádíme rastrová data do příslušného souřadného systému tak, aby byly na svém správném místě a bylo možné tyto data kombinovat s jinými daty. Například letecký
Rektifikace rastrových dat Při rektifikaci převádíme rastrová data do příslušného souřadného systému tak, aby byly na svém správném místě a bylo možné tyto data kombinovat s jinými daty. Například letecký
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
1. D Y N A M I C K É DAT O V É STRUKTUR Y
 1. D Y N A M I C K É DAT O V É STRUKTUR Y Autor: Petr Mik Abychom se mohli pustit do dynamických datových struktur, musíme se nejdřív podívat na datový typ ukazatel. 1. D AT O V Ý TYP U K A Z AT E L Datové
1. D Y N A M I C K É DAT O V É STRUKTUR Y Autor: Petr Mik Abychom se mohli pustit do dynamických datových struktur, musíme se nejdřív podívat na datový typ ukazatel. 1. D AT O V Ý TYP U K A Z AT E L Datové
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
Cvičení Programování I. Stručné poznámky ke cvičení ze
 Cvičení Programování I Cvičící: Pavel urynek, KIM, pavel.surynek@seznam.cz emestr: Zima 2005/2006 Kroužek: Matematika/59 Rozvrh: Pátek 10:40-12:10 (učebna K2) tručné poznámky ke cvičení ze 14.10.2005 1.
Cvičení Programování I Cvičící: Pavel urynek, KIM, pavel.surynek@seznam.cz emestr: Zima 2005/2006 Kroužek: Matematika/59 Rozvrh: Pátek 10:40-12:10 (učebna K2) tručné poznámky ke cvičení ze 14.10.2005 1.
Stromové rozklady. Definice 1. Stromový rozklad grafu G je dvojice (T, β) taková, že T je strom,
 Stromové rozklady Zdeněk Dvořák 25. října 2017 Definice 1. Stromový rozklad grafu G je dvojice (T, β) taková, že T je strom, β je funkce přiřazující každému vrcholu T podmnožinu vrcholů v G, pro každé
Stromové rozklady Zdeněk Dvořák 25. října 2017 Definice 1. Stromový rozklad grafu G je dvojice (T, β) taková, že T je strom, β je funkce přiřazující každému vrcholu T podmnožinu vrcholů v G, pro každé
9.1.6 Permutace I. Předpoklady: 9101, 9102, 9104
 9.1.6 Permutace I Předpoklady: 9101, 9102, 9104 Pedagogická poznámka: První tři příklady jsou opakování, je možné je přeskočit, nebo použít na zkoušení. Př. 1: Vyřeš slovní úlohy. a) Na plese se losuje
9.1.6 Permutace I Předpoklady: 9101, 9102, 9104 Pedagogická poznámka: První tři příklady jsou opakování, je možné je přeskočit, nebo použít na zkoušení. Př. 1: Vyřeš slovní úlohy. a) Na plese se losuje
Programujeme v softwaru Statistica - příklady
 Programujeme v softwaru Statistica - příklady Newsletter Statistica ACADEMY Téma: Programování, makra, skripty Typ článku: Návody, příklady V předchozích článcích bylo vyřčeno mnoho teorie k problematice
Programujeme v softwaru Statistica - příklady Newsletter Statistica ACADEMY Téma: Programování, makra, skripty Typ článku: Návody, příklady V předchozích článcích bylo vyřčeno mnoho teorie k problematice
IMPORT DAT DO DATABÁZE
 Úvod do problematiky IMPORT DAT DO DATABÁZE Databázové tabulky lze naplňovat i již dříve pořízenými údaji. Můžeme tak snadno načíst do databáze data pořízená v textovém editoru WORD nebo v tabulkovém procesoru
Úvod do problematiky IMPORT DAT DO DATABÁZE Databázové tabulky lze naplňovat i již dříve pořízenými údaji. Můžeme tak snadno načíst do databáze data pořízená v textovém editoru WORD nebo v tabulkovém procesoru
BALISTICKÝ MĚŘICÍ SYSTÉM
 BALISTICKÝ MĚŘICÍ SYSTÉM UŽIVATELSKÁ PŘÍRUČKA Verze 2.3 2007 OBSAH 1. ÚVOD... 5 2. HLAVNÍ OKNO... 6 3. MENU... 7 3.1 Soubor... 7 3.2 Měření...11 3.3 Zařízení...16 3.4 Graf...17 3.5 Pohled...17 1. ÚVOD
BALISTICKÝ MĚŘICÍ SYSTÉM UŽIVATELSKÁ PŘÍRUČKA Verze 2.3 2007 OBSAH 1. ÚVOD... 5 2. HLAVNÍ OKNO... 6 3. MENU... 7 3.1 Soubor... 7 3.2 Měření...11 3.3 Zařízení...16 3.4 Graf...17 3.5 Pohled...17 1. ÚVOD
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo projektu: Číslo šablony: Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo projektu: Číslo šablony: Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Grafy. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 13.
 Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Algoritmy a datové struktury
 Algoritmy a datové struktury 1 / 34 Obsah přednášky Základní řídící struktury posloupnost příkazů podmínka cyklus s podmínkou na začátku cyklus s podmínkou na konci cyklus s pevným počtem opakování Jednoduchá
Algoritmy a datové struktury 1 / 34 Obsah přednášky Základní řídící struktury posloupnost příkazů podmínka cyklus s podmínkou na začátku cyklus s podmínkou na konci cyklus s pevným počtem opakování Jednoduchá
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Návod pro práci s aplikací
 Návod pro práci s aplikací NASTAVENÍ FAKTURACÍ...1 NASTAVENÍ FAKTURAČNÍCH ÚDA JŮ...1 Texty - doklady...1 Fakturační řady Ostatní volby...1 Logo Razítko dokladu...2 NASTAVENÍ DALŠÍCH ÚDA JŮ (SEZNAMŮ HODNOT)...2
Návod pro práci s aplikací NASTAVENÍ FAKTURACÍ...1 NASTAVENÍ FAKTURAČNÍCH ÚDA JŮ...1 Texty - doklady...1 Fakturační řady Ostatní volby...1 Logo Razítko dokladu...2 NASTAVENÍ DALŠÍCH ÚDA JŮ (SEZNAMŮ HODNOT)...2
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Optimalizace trasy při revizích elektrospotřebičů
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
1 Expertní systémy. Obrázek 1: Základní moduly experního systému. User Interface. Working Data Base. Interface Engine. Knowledge Base.
 1 Expertní systémy Expertní systémy jsou jednou z komerčně nejúspěšnějších oblastí umělé inteligence. Charakterizovat stručně tuto rozsáhlou oblast není jednoduché. Pokusíme se však o to alespoň následovně:
1 Expertní systémy Expertní systémy jsou jednou z komerčně nejúspěšnějších oblastí umělé inteligence. Charakterizovat stručně tuto rozsáhlou oblast není jednoduché. Pokusíme se však o to alespoň následovně:
Zdokonalování gramotnosti v oblasti ICT. Kurz MS Excel kurz 6. Inovace a modernizace studijních oborů FSpS (IMPACT) CZ.1.07/2.2.00/28.
 Zdokonalování gramotnosti v oblasti ICT Kurz MS Excel kurz 6 1 Obsah Kontingenční tabulky... 3 Zdroj dat... 3 Příprava dat... 3 Vytvoření kontingenční tabulky... 3 Možnosti v poli Hodnoty... 7 Aktualizace
Zdokonalování gramotnosti v oblasti ICT Kurz MS Excel kurz 6 1 Obsah Kontingenční tabulky... 3 Zdroj dat... 3 Příprava dat... 3 Vytvoření kontingenční tabulky... 3 Možnosti v poli Hodnoty... 7 Aktualizace
Hledáme efektivní řešení úloh na grafu
 Hledáme efektivní řešení úloh na grafu Mějme dán graf následující úlohy: G = ( V, E), chceme algoritmicky vyřešit Je daný vrchol t dosažitelný z vrcholu s? Pokud ano, jaká nejkratší cesta tyto vrcholy
Hledáme efektivní řešení úloh na grafu Mějme dán graf následující úlohy: G = ( V, E), chceme algoritmicky vyřešit Je daný vrchol t dosažitelný z vrcholu s? Pokud ano, jaká nejkratší cesta tyto vrcholy
1 Tabulky Příklad 7 Access 2010
 TÉMA: Řazení a filtrace dat Sekretářka společnosti Naše zahrada pracuje s rozsáhlými tabulkami. Pro přehlednější práci s daty používá řazení a filtraci dat na základě různých kritérií. Zadání: Otevřete
TÉMA: Řazení a filtrace dat Sekretářka společnosti Naše zahrada pracuje s rozsáhlými tabulkami. Pro přehlednější práci s daty používá řazení a filtraci dat na základě různých kritérií. Zadání: Otevřete
Práce s programem MPVaK
 Práce s programem MPVaK Tato informace popisuje postup práce s programem "MPVaK Vybrané údaje z majetkové a Vybrané údaje z provozní evidence. Jsou v ní popsány nejdůležitější úlohy, které budete s programem
Práce s programem MPVaK Tato informace popisuje postup práce s programem "MPVaK Vybrané údaje z majetkové a Vybrané údaje z provozní evidence. Jsou v ní popsány nejdůležitější úlohy, které budete s programem
Přihlášení k maturitním zkouškám
 Přihlášení k maturitním zkouškám (v 3.0) Pozn.: Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Slovníček pojmů 2 1. Nutná nastavení 2 Obory a vzdělávací
Přihlášení k maturitním zkouškám (v 3.0) Pozn.: Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Slovníček pojmů 2 1. Nutná nastavení 2 Obory a vzdělávací
MS OFFICE OUTLOOK 2010 - SEZNÁMENÍ
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Petr Koňařík MGV_VT_SS_1S2-D18_Z_OFF_OUT_UVOD.docx Informatika MS Office Outlook MS OFFICE OUTLOOK 2010 - SEZNÁMENÍ
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Petr Koňařík MGV_VT_SS_1S2-D18_Z_OFF_OUT_UVOD.docx Informatika MS Office Outlook MS OFFICE OUTLOOK 2010 - SEZNÁMENÍ
WDLS (BUILDINGDESIGN)
 Vysoká škola báňská Technická univerzita Ostrava Fakulta stavební METODICKÝ POSTUP PRO PRÁCI S PROGRAMEM WDLS (BUILDINGDESIGN) Vypracoval: doc. Ing. Iveta Skotnicová, Ph.D. Ing. Marcela Černíková Ing.
Vysoká škola báňská Technická univerzita Ostrava Fakulta stavební METODICKÝ POSTUP PRO PRÁCI S PROGRAMEM WDLS (BUILDINGDESIGN) Vypracoval: doc. Ing. Iveta Skotnicová, Ph.D. Ing. Marcela Černíková Ing.
Manuál pro NetDOGs práce s administrací
 Manuál pro NetDOGs práce s administrací Po přihlášení se nacházíme v administraci V horní části jsou hlavní ikony značící moduly prezentace - REDAKCE - NOVINKY - OSTATNÍ - ADMINISTRACE (a možná i další
Manuál pro NetDOGs práce s administrací Po přihlášení se nacházíme v administraci V horní části jsou hlavní ikony značící moduly prezentace - REDAKCE - NOVINKY - OSTATNÍ - ADMINISTRACE (a možná i další
Algoritmizace a programování
 Algoritmizace a programování Vyhledávání, vkládání, odstraňování Vyhledání hodnoty v nesetříděném poli Vyhledání hodnoty v setříděném poli Odstranění hodnoty z pole Vkládání hodnoty do pole Verze pro akademický
Algoritmizace a programování Vyhledávání, vkládání, odstraňování Vyhledání hodnoty v nesetříděném poli Vyhledání hodnoty v setříděném poli Odstranění hodnoty z pole Vkládání hodnoty do pole Verze pro akademický
Dokumentace programu piskvorek
 Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
Dokumentace programu piskvorek Zápočtového programu z Programování II PRM045 Ondřej Vostal 20. září 2011, Letní semestr, 2010/2011 1 Stručné zadání Napsat textovou hru piškvorky se soupeřem s umělou inteligencí.
A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h)
 A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h) 2.1 Základy marketingové strategie (2,5h) Učitelé se seznámí se základní marketingovou terminologií a s možnými cestami rozvoje firmy. V
A1 Marketingové minimum pro posílení výchovy k podnikavosti (8h) 2.1 Základy marketingové strategie (2,5h) Učitelé se seznámí se základní marketingovou terminologií a s možnými cestami rozvoje firmy. V
Fakulta informačních technologií. Teoretická informatika
 Vysoké učení technické v Brně Fakulta informačních technologií Teoretická informatika Třetí úkol 2 Jan Trávníček . Tato úloha je řešena Turingovým strojem, který je zobrazen na obrázku, který si můžeme
Vysoké učení technické v Brně Fakulta informačních technologií Teoretická informatika Třetí úkol 2 Jan Trávníček . Tato úloha je řešena Turingovým strojem, který je zobrazen na obrázku, který si můžeme
Obsah. 1.1 Práce se záznamy... 3 1.2 Stránka Dnes... 4. 2.1 Kontakt se zákazníkem... 5
 CRM SYSTÉM KORMORÁN UŽIVATELSKÁ PŘÍRUČKA Obsah 1 Základní práce se systémem 3 1.1 Práce se záznamy................................. 3 1.2 Stránka Dnes.................................... 4 1.3 Kalendář......................................
CRM SYSTÉM KORMORÁN UŽIVATELSKÁ PŘÍRUČKA Obsah 1 Základní práce se systémem 3 1.1 Práce se záznamy................................. 3 1.2 Stránka Dnes.................................... 4 1.3 Kalendář......................................
Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5
 Rejstřík Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5 Úvod Správcovská aplikace slouží k vytvoření vstupního a zašifrovaného souboru pro odečtovou
Rejstřík Úvod...1 Instalace...1 Popis funkcí...2 Hlavní obrazovka...2 Menu...3 Práce s aplikací - příklad...5 Úvod Správcovská aplikace slouží k vytvoření vstupního a zašifrovaného souboru pro odečtovou
V exponenciální rovnici se proměnná vyskytuje v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto:
 Eponenciální rovnice V eponenciální rovnici se proměnná vyskytuje v eponentu. Obecně bychom mohli eponenciální rovnici zapsat takto: a ( ) f ( ) f kde a > 0, b > 0 b Příkladem velmi jednoduché eponenciální
Eponenciální rovnice V eponenciální rovnici se proměnná vyskytuje v eponentu. Obecně bychom mohli eponenciální rovnici zapsat takto: a ( ) f ( ) f kde a > 0, b > 0 b Příkladem velmi jednoduché eponenciální
12. Lineární programování
 . Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
. Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
TransKlim ver.1.13 Uživatelská příručka pro verzi 1.13
 TransKlim v.1.0 Program pro zaznamenávání a vyhodnocování hodnot z měření teplot a vlhkosti v objektech kulturních památek s přenosem po síti nn 230V/50Hz. Uživatelská příručka pro verzi 1.13 Uživatelská
TransKlim v.1.0 Program pro zaznamenávání a vyhodnocování hodnot z měření teplot a vlhkosti v objektech kulturních památek s přenosem po síti nn 230V/50Hz. Uživatelská příručka pro verzi 1.13 Uživatelská
Semestrální z předmětu MM
 Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Společnost pro elektronické aplikace. SEA s.r.o. Dolnoměcholupská 21 CZ-10200 Praha 10
 Společnost pro elektronické aplikace SEA s.r.o. Dolnoměcholupská 21 CZ-10200 Praha 10 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. Výstup 1. Výstup
Společnost pro elektronické aplikace SEA s.r.o. Dolnoměcholupská 21 CZ-10200 Praha 10 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. Výstup 1. Výstup
Slovní úlohy I
 ..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
Přehledový manuál aplikace GABVAR (verze )
 Základní informace: Vývojová skupina Gabvar byla založena v roce 2007. Náplní skupiny je vývoj aplikací pro podporu procesů v oblasti managmentu, údržby a logistiky. Jsme skupinou pracovníků s praxí na
Základní informace: Vývojová skupina Gabvar byla založena v roce 2007. Náplní skupiny je vývoj aplikací pro podporu procesů v oblasti managmentu, údržby a logistiky. Jsme skupinou pracovníků s praxí na
Vzorce. Suma. Tvorba vzorce napsáním. Tvorba vzorců průvodcem
 Vzorce Vzorce v Excelu lze zadávat dvěma způsoby. Buď známe přesný zápis vzorce a přímo ho do buňky napíšeme, nebo použijeme takzvaného průvodce při tvorbě vzorce (zejména u složitějších funkcí). Tvorba
Vzorce Vzorce v Excelu lze zadávat dvěma způsoby. Buď známe přesný zápis vzorce a přímo ho do buňky napíšeme, nebo použijeme takzvaného průvodce při tvorbě vzorce (zejména u složitějších funkcí). Tvorba
Matematika I 2a Konečná pravděpodobnost
 Matematika I 2a Konečná pravděpodobnost Jan Slovák Masarykova univerzita Fakulta informatiky 24. 9. 2012 Obsah přednášky 1 Pravděpodobnost 2 Nezávislé jevy 3 Geometrická pravděpodobnost Viděli jsme už
Matematika I 2a Konečná pravděpodobnost Jan Slovák Masarykova univerzita Fakulta informatiky 24. 9. 2012 Obsah přednášky 1 Pravděpodobnost 2 Nezávislé jevy 3 Geometrická pravděpodobnost Viděli jsme už
Funkce pro studijní obory
 Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují
 Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Školní události. v Pozn.: Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak.
 Školní události v. 2.0 Pozn.: Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Školní událost 2 Záložky události 4 Hodiny třídy / kurzu - nastavení hodin 5
Školní události v. 2.0 Pozn.: Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Školní událost 2 Záložky události 4 Hodiny třídy / kurzu - nastavení hodin 5
Aplikace. vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin
 Aplikace Aplikace se liší tím, k jakému účelu jsou tvořeny. To má vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin s podobnou
Aplikace Aplikace se liší tím, k jakému účelu jsou tvořeny. To má vliv na to, jakou mají strukturu i na to, jak pracné je je vyvinout. Bylo vypozorováno, že aplikace je možné rozdělit do skupin s podobnou
Algoritmizace řazení Bubble Sort
 Algoritmizace řazení Bubble Sort Cílem této kapitoly je seznámit studenta s třídícím algoritmem Bubble Sort, popíšeme zde tuto metodu a porovnáme s jinými algoritmy. Klíčové pojmy: Třídění, Bubble Sort,
Algoritmizace řazení Bubble Sort Cílem této kapitoly je seznámit studenta s třídícím algoritmem Bubble Sort, popíšeme zde tuto metodu a porovnáme s jinými algoritmy. Klíčové pojmy: Třídění, Bubble Sort,
Laboratorní práce: SNMP - Linux snmputils
 Laboratorní práce: SNMP - Linux snmputils Petr Grygárek, VŠB-TU Ostrava, FEI Cílem této laboratorní práce je naučit se pracovat s proměnnými SNMP s použitím PC s OS Linux s a utilit snmputils. Propojte
Laboratorní práce: SNMP - Linux snmputils Petr Grygárek, VŠB-TU Ostrava, FEI Cílem této laboratorní práce je naučit se pracovat s proměnnými SNMP s použitím PC s OS Linux s a utilit snmputils. Propojte
Algoritmy. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna / 39
 Algoritmy Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna 2018 1/ 39 Algoritmy Příklad: Popis algoritmu pomocí pseudokódu: Algoritmus 1: Algoritmus pro nalezení největšího prvku v poli 1 Find-Max(A,n):
Algoritmy Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 15. dubna 2018 1/ 39 Algoritmy Příklad: Popis algoritmu pomocí pseudokódu: Algoritmus 1: Algoritmus pro nalezení největšího prvku v poli 1 Find-Max(A,n):
