3.prednáška Čo je logika? Výroková logika I Logické spojky, tvorba výrokových formúl (syntax) a pravdivostné ohodnotenie formúl (sémantika)
|
|
|
- Blažena Havlíčková
- před 6 lety
- Počet zobrazení:
Transkript
1 3.prednáška Čo je logika? Výroková logika I Logické spojky, tvorba výrokových formúl (syntax) a pravdivostné ohodnotenie formúl (sémantika) priesvitka 1
2 História výrokovej logiky Štúdium logiky ako nezávislej vednej disciplíny bolo zahájené v starom Grécku filozofom Aristotelom ( pr. n. l.). Musíme však poznamenať, že predmetom hlavného záujmu Aristotela boli kvantifikátory každý a niektorý, ktoré nie sú predmetom záujmu výrokovej logiky. Vo svojich rukopisoch o metafyzike Aristoteles diskutuje dva dôležité zákony výrokovej logiky: zákon vylúčenia tretieho a zákon kontradikcie. Oba tieto zákony majú fundamentálny význam pre klasickú výrokovú logiku, menovite špecifikujú dvojhodnotový pravdivostný charakter výrokovej logiky. V jeho spisoch existujú náznaky toho, že rozpoznal dôležitosť zložitých výrokov tvorených pomocou spojok konjunkcie, disjunkcie a implikácie, avšak prienik Aristotela alebo jeho nasledovníkov do tejto nádejnej oblasti bol veľmi malý. priesvitka 2
3 Podstatne úspešnejšie pokusy o využitie logických spojok k vytváraniu zložitejších výrokov pomocou logických spojok konjunkcie, disjunkcie a implikácie boli vykonané stoickou filozofiou (koniec 3. storočia pr. n. l.). Pozitívne vieme, že Diodorus Kronus a jeho žiak Philo navzájom diskutovali o tom, či pravdivostná hodnota implikácie závisí len na pravdivostnej hodnote predpokladu, ale taktiež aj na pravdivostnej hodnote dôsledku. Stoický filozof Chrysippos (približne pr. n. l.) vykonal najväčší krok v rozvoji stoickej výrokovej logiky tým, že zostrojil päť rôznych schém usudzovania, ktoré sú založené na zložených výrokoch: priesvitka 3
4 1 3 ak prvé,tak druhé avšak prvé teda druhé nie je pravda, že aj prvé aj druhé avšak prvé teda nie druhé 5 prvé alebo druhé avšak nie prvé teda druhé ak prvé,tak druhé 2 avšak nie druhé teda nie prvé budˇ prvé alebo druhé 4 avšak prvé teda nie druhé priesvitka 4
5 Galen Boethius Abelard Williamom z Ockhamu Stoická logika bola postupne rozvíjaná v druhom storočí nášho veku rímskym lekárom a logikom Galénom (približne ), v šiestom storočí filozofom Boethiusom (približne ) a neskoršie stredovekými mysliteľmi Petrom Abelardom ( ) and Williamom z Ockhamu ( ) a inými. Ich príspevky väčšinou spočívali v zdokonaľovaní a v lepšej formalizácii základných princípov vytvorených Aristotelom alebo Chrysipposom, menovite v spresnení terminológie a v prehĺbení argumentácie správnosti získaných výsledkov a vzájomných vzťahov medzi logickými spojkami. Tak napríklad, Abelard bol prvý logik, ktorý odlíšil exkluzívnu od inkluzívnej disjunkciu a dôvodil, že inkluzívna disjunkcia je podstatne dôležitejšia ako exkluzívna disjunkcia pre potreby výrokovej logiky. priesvitka 5
6 Veľmi pozitívnu úlohu pre rozvoj modernej logiky zohral nemecký filozof a matematik Gottfried Wilhelm Leibniz ( ). Tento filozof v logike, podobne ako Descartes v geometri (kde nahradil geometrické konštrukcie matematickými manipuláciami s algebraickými výrazmi), pokúsil sa vybudovať formálny systém, ktorý by nahradil verbálne metódy usudzovania manipuláciami s formulami. Postuloval formálny systém s dvoma časťami: (1) jazyk logiky lingua characteristica, pomocou ktorého je možné reprezentovať každý výrok a (2) kalkulus calculus ratiocinator, pomocou ktorého je možné uskutočňovať usudzovanie systematickým a matematicky presným spôsobom. Žiaľ, trvalo ešte ďalších 200 rokov než sa naplnila táto Leibnizova idea, keď v polovici 19 st. anglický matematici A. de Morgan a G. Boole zostrojili kalkulus výrokovú logiku. Pre Descartesovho súčasník anglického filozofa T. Hobbesa myslenie už nebolo nič iné, ako len špeciálny druh výpočtu. Táto hypotéza, ktorá v 17. storočí znela veľmi neobvykle ba až exoticky, bola až v súčasnosti plne akceptovaná a realizovaná pomocou umelej inteligencie a kognitívnej vedy, kde má postavenie centrálnej paradigmy. priesvitka 6
7 Stav výrokovej logiky vo forme vyvinutej v podstate už v starovekom Grécku a Ríme, pretrvával až do začiatku 19. storočia, kedy vďaka rozvoju algebry došlo hlavne zásluhou Augustusa DeMorgana ( ) a Georga Boola ( ) v polovici tohto storočia k algebraizácii stoickej výrokovej logiky Boole zaviedol interperetáciu, kde rovnica "x = 1" sa číta ako "x je pravdivé" a "x = 0" sa číta ako "x je nepravdivé", formuly získané pre jeho logiku tried môžu byť transformované do výrokovej logiky. Napríklad, formula "x + y = 1" je interpretovaná tak, že x alebo y je pravidivé, podobne, formula "xy = 1" je interpretovaná tak, že x a y sú pravdivé. Booleho matematický prístup k formulácii výrokovej logiky zaznamenal veľký záujem u matematikov. Jeho myšlienky boli neskoršie precizované a preformulované do tvaru Boolovej algebry, ktorá v súčasnosti tvorí matematický základ výrokovej logiky a taktiež tvorí jeden z pilierov modernej matematickej logiky s plodnými aplikáciami v informatike a umelej inteligencii. priesvitka 7
8 Koncom 19. storočia nemecký matematik a logik Gottlob Frege ( ) prezentoval logiku ako súčasť systematických snáh jej povýšenia na metavedu pre matematiku, z ktorej sa dajú odvodiť čisto logickými deduktívnymi prostriedkami všetky teorémy matematiky. Frege taktiež navrhol prvý moderný axiomatický systém logiky, ktorá z dnešného pohľadu obsahuje výrokovú logiku a časť predikátovej logiky. Pri formulácii tejto axiomatizácie použil skutočnosť, že výrokové spojky môžu byť redukované na negáciu a implikáciu, spojky konjunkcie, disjunkcie a ekvivalencie sú z nich odvoditeľné. priesvitka 8
9 Až do konca 19. storočia bola logika integrálnou súčasťou filozofie. Hlavné tematické okruhy logiky boli charakteru filozofického a zaoberali sa fundamentálnymi otázkami o podstate ľudského usudzovania. Až na prelome 19. a 20. storočia nastala výrazná matematizácia logiky, pričom sa riešili hlavne problémy formalizácie ľudského usudzovania. Preto vznikal dojem, že v logike existujú problémy, ktoré sú touto matematizáciou nepostihnuteľné a preto sú výlučnou doménou tzv. filozofickej logiky. Tak napr. moment času v usudzovaní (výrok niekedy v minulosti padal sneh ) alebo modalita výrokov ( je možné, že padá sneh ) boli považované za nepostihnuteľné matematickými metódami. Štúdium týchto a podobných aspektov bolo považované za výlučnú doménu filozofickej logiky, ktorá sa týmto pomerne jasne oddelila od matematickej logiky, ktorá akoby sa zaoberala len štúdiom jednoduchých usudzovaní, ktoré nie sú časovo alebo modálne štruktúrované. Postupne sa však ukazovalo, že aj tieto aspekty logiky sú dobre matematicky formalizovateľné a že delenie logiky na,matematickú a filozofickú nemá hlbšieho opodstatnenia. priesvitka 9
10 1. Výroková logika Výroková logika študuje také formy usudzovania, pre ktoré platnosť záverov nezávisí od obsahu a ani od vnútornej štruktúry výrokov, ale výlučne len pravdivosti či nepravdivosti týchto výrokov. Analyzujme tieto jednoduché oznamovacie vety: (1) Atóm je fyzikálna štruktúra (pravdivý výrok). (2) Atóm je sociálna štruktúra. (nepravdivý výrok) (3) Vo vesmíre existuje život aj mimo Zeme. (zatiaľ nerozhodnuteľný) (4) Láska je rádioaktívna. (nezmysel) (5) Rast nášho hospodárstva má neustálu tendenciu. (nesprávny) priesvitka 10
11 Elementárny výrok je jednoduchá oznamovacia veta, pri ktorej má zmysel pýtať sa, či je alebo nie je pravdivá. Elementárne výroky budeme označovať malými písmenami abecedy p, q, r, s, p 1, p 2,.... Pravdivostná hodnota výroku p bude označená val p, pričom, ak výrok p je pravdivý (nepravdivý), potom val p 1 ( val p 0). priesvitka 11
12 Logické spojky Prirodzený jazyk obsahuje spojky (napr. a, alebo, ak..., potom..., je ekvivalentné, nie je pravda, že...) pomocou ktorých z elementárnych výrokov vytvárame zložitejšie výroky (výroky), pričom ich pravdivosť alebo nepravdivosť je určená len pravdivostnými hodnotami ich zložiek (elementárnymi výrokmi). priesvitka 12
13 (1) Negácia Unárna logická spojka, z výroku p vytvára nový výrok nie je pravda, že p čo zapíšeme pomocou symbolu negácie takto: p. Ak je výrok pravdivý p (nepravdivý), potom jeho negácia (pravdivá) 1 val p val p. p je nepravdivá p p priesvitka 13
14 (2) Konjunkcia Binárna symetrická spojka z dvoch výrokov p, q vytvára nový výrok p a q, ktorý je formálne označený pq. Príklad: uvažujme zložený výrok Peter je v škole a Milan je v kine, kde elementárne výroky sú p=(peter je v škole) a q=(milan je v kine). Pravdivostná hodnota zloženého výroku závisí od pravdivostných hodnôt jeho zložiek, pričom nutným predpokladom, aby jeho pravdivostná hodnota bola pravda je pravdivosť oboch jeho zložiek, val p q min val p,val q. p q pq priesvitka 14
15 (3) Disjunkcia Binárna symetrická logická spojka z dvoch výrokov p, q vytvára nový výrok p alebo q, ktorý je formálne označený pq. Príklad: uvažujme zložený výrok Peter je v škole alebo Peter je v divadle, kde elementárne výroky sú p=(peter je v škole) a q=(peter je v divadle). Pravdivosť zloženého výroku pq záleží od toho, či aspoň jedna zložka je pravdivá, ak sú obe nepravdivé, potom pravdivosť zloženého výroku je nepravda val p q max val p,val q. p q pq priesvitka 15
16 (4) Implikácia Binárna logická spojka z dvoch výrokov p a q vytvára nový výrok ak p, potom q, alebo p implikuje q, ktorý je formálne označený p q. Príklad: uvažujme zložený výrok Ak je Peter v škole, potom Tomáš je na výlete, kde elementárne výroky sú p=(peter je v škole) a q=(tomáš je na výlete). Budeme postulovať, že implikácia je nepravdivá len vtedy, ak val(p)=1 a val(q)=0, pre všetky ostatné pravdivostné hodnoty p a q je pravdivá. val p q min 11, val p val q val q 1 val p 0 ináč p q pq priesvitka 16
17 Príklad p=(5+2=8) q=(masaryk bol prvý prezident Československa) Zložený výrok p q ak 5+2=8, potom Masaryk bol prvý prezident Československa je pravdivý výrok, aj keď bežný čitateľ bude pokladať tento výrok za nepravdivý ba až nezmyselný. Jeden zo zakladateľov modernej logiky G. Frege ( ) navrhol riešiť tento problém tak, že v rámci implikácie sa môžu vyskytovať len výroky, ktoré sú v príčinnej súvislosti. Tieto problémy s určením pravdivostných hodnôt implikácie viedli v prvej polovici 20.storočia niektorých logikov k štúdiu tzv. neklasických logík, ktoré majú jemnejšie prostriedky na špecifikáciu implikácie (chápanej ako relácia príčinného vzťahu). priesvitka 17
18 (5) Ekvivalencia Binárna symetrická logická p je ekvivalentné q, formálne p q Príklad: uvažujme zložený výrok číslo n je párne je ekvivalentné číslo n je deliteľné 2, kde elementárne výroky sú p=(číslo n je párne) a q=(číslo n je deliteľné 2). Ekvivalencia dvoch výrokov p q je pravdivá len vtedy, ak jej elementárne výroky p a q sú súčasne buď pravdivé alebo nepravdivé val p q val p val q p q pq priesvitka 18
19 Alternatívna definície ekvivalencie je jej určenie pomocou implikácie a konjunkcie p q p q q p def min 11, val p val q, val p q min min 11, val q val p V matematike sa často používa táto logická spojka v týchto dvoch alternatívnych jazykových formách: (1) p je nutnou a dostatočnou podmienkou q, alebo (2) p práve vtedy a len vtedy (vtt) ak q. Príklady: (1) Nutná a postačujúca podmienka k tomu, aby číslo n bolo párne je, aby bolo deliteľné 2. (2) Číslo n je párne vtedy a len vtedy, ak je deliteľné 2 priesvitka 19
20 Jazyk výrokovej logiky (syntax) Formálny systém pre konštrukciu formúl výrokovej logiky (výrokových formúl), ktoré sú zostrojené pomocou (1) iných výrokov (buď elementárnych alebo zložitých) (2) logických spojok. Nech P p,q,r,..., p, p, je množina elementárnych výrokov (výrokové premenné); výrokové konštanty {0,1} Definícia. Výroková formula nad množinou P výrokových premenných je zostrojená opakovaným použitím týchto dvoch pravidiel: Každá výroková premenná p P je výroková formula alebo výroková konštanta. Ak výrazy a sú výrokové formule, potom aj výrazy,,, a sú výrokové formuly. priesvitka 20
21 Obvykle sa ešte zdôrazňuje, že žiadne iné výrazy, ako tie, ktoré môže vzniknúť opakovaným použitím uvedených pravidiel, nie sú formulami výrokovej logiky. Zátvorky sa používajú ako pomocné symboly, pomocou ktorých môžeme odstrániť prípadnú nejednoznačnosť výrokových formúl. Uvažujme o formule pq r, pomocou zátvoriek môžeme ju interpretovať dvoma rôznymi spôsobmi p q r p q r. a priesvitka 21
22 Príklad. Nech P p,q,r,s sú výrokové formuly, zatiaľ čo nie sú výrokové formuly. je množina výrokových premenných, potom p q p q p q r r s p r s p s p s p priesvitka 22
23 Každá výroková formula je reprezentovaná pomocou grafického útvaru nazývaného syntaktický strom p q p q Koncové vrcholy stromu reprezentujú výrokové premenné p a q, vrcholy z nasledujúcich vrstiev sú priradené spojkám implikácie a konjunkcie. Vyhodnocovanie tohto stromu prebieha postupne zdola nahor. priesvitka 23
24 Každému vrcholu syntaktického stromu môžeme priradiť podformulu p q r p q p r 1 q r p q p r Jednotlivé podformule sú určené takto: 1 p, 2 q 1, 3 r, 4 q r 5 p 4 p q r, 6 p q, 7 p r, p q p r, 5 9 p q r p q p r., priesvitka 24
25 Definícia. Konštrukcia formule nad množinou P je tvorená postupnosťou formúl 1, 2,..., n, pričom posledný prvok n je totožný s formulou, pre každé i 12,,...,n platí jedna s týchto troch možností: (1) i je výroková premenná z P alebo výroková konštanta. (2) i vznikla z niektorého z prvkov množiny 1, 2,..., i 1aplikáciou unárnej, pre j 1, 2,...,i 1. logickej spojky negácie, i j (3) i vznikla z niektorých dvoch prvkov množiny binárnej logickej spojky, napr. i j k,,..., aplikáciou 1 2 i 1, pre j k 1, 2,...,i 1. Prvky postupnosti 1, 2,..., n sa nazývajú podformule formule, i pre i 12,,...,n. priesvitka 25
26 V teórii formálnych jazykov je zvykom špecifikovať ich syntax pomocou Backusovej a Naurovej formy (BNF), použijeme tento prístup aj pre alternatívne určenie syntaxu formúl výrokovej logiky: formula ::= výroková premenná logická konštanta formula formula binárna logická spojka formula výroková premenná ::= p q r... p 1 p 2 p 3... logická konštanta ::=0 1 binárna logická spojka ::= priesvitka 26
27 Pravdivostné ohodnotenie formúl výrokovej logiky (sémantika) Syntax formúl výrokovej logiky je jednoznačne určená spôsobom ich konštrukcie, pomerne ľahko vieme rozhodnúť, či daná formula ma korektnú syntax, alebo nemá. Podobne ako v prirodzenom jazyku, kde syntax špecifikuje tvar vety, nie všetky vety, ktoré môžeme zostrojiť jednoduchým zreťazením slov, sú syntakticky korektné. Podobne aj vo výrokovej logike, nie každé zreťazenie prípustných symbolov nám definuje formulu, existujú formuly, ktoré nie sú syntakticky správne. priesvitka 27
28 Ďalší pojem dôležitý pre výrokovú logiku je sémantika. Pojem pochádza z teórie prirodzených jazykov, kde sémantika špecifikuje význam danej vety (ktorá ma tiež aj svoju syntax). Vo výrokovej logike, ktorá sa zaoberá len pravdivostnými hodnotami premenných a ich formúl, sémantika nie je veľmi bohatá. Sémantika výrokovej formuly je vlastne tabuľka pravdivostných hodnôt formuly pre rôzne hodnoty jej výrokov. priesvitka 28
29 Príklad p q p q ktorá má korektnú syntax (napr. reprezentovaný syntaktickým stromom), je jej sémantika plne určená vyššie uvedenou tabuľkou jej pravdivostných hodnôt pre všetky štyri kombinácie výrokov p a q. Uvažujme formulu výrokovej logiky A, ktorej výrokové premenné p 1, p 2,..., p n sú špecifikované, ktorý určuje pravdivostné hodnoty jej premenných. Táto špecifikácia premenných p 1,q 2,...,r n, kde 1, 2,..., n 01,, spočíva v priradení binárnych pravdivostných hodnôt jednotlivým premenným. Rôznych špecifikácii premenných, ktoré sú priradené n výrokovým premenným je 2 n. Pravdivostná hodnota formule A pre danú špecifikáciu je val A označená výrazom. priesvitka 29
30 val? Ako bude prebiehať výpočet Predpokladajme, že konštrukcia formule je tvorená postupnosťou formúl 1, 2,..., n, pričom n. Pravdivostné vyhodnotenie jednotlivých členov postupnosti pre i 12,,...,n sa vykonáva takto: (1) Ak i je výroková premenná, potom val i je určená priamo špecifikáciou, ktorý špecifikuje pravdivostné hodnoty premenných. (2) Ak i nie je výroková premenná a vznikla z niektorého z prvkov množiny 1, 2,..., i 1aplikáciou unárnej logickej spojky negácie, i j j 1, 2,...,i 1, potom vali 1 val j., pre (3) Ak i nie je výroková premenná a vznikla z niektorýho dvoch prvkov množiny j, k 1, 2,..., i 1aplikáciou binárnej logickej spojky, potom val i je vyhodnotený na základe tabuľky 1.1 pomocou už známych pravdivostných hodnôt, pre j k i, potom j val k. Tak napríklad, nech i j k. val a val val val i j k priesvitka 30
31 Tento rekurentný postup je názorne realizovaný pomocou tabuľkovej metódy, kde postupne počítame pravdivostné hodnoty jednotlivých podformúl pre všetky možné špecifikácie p q p q p q Z tejto tabuľky vyplýva, že existujú také pravdivostné hodnoty premenných p a q (p=0, q=0 a p=0, q=1), pre ktoré je pravdivostná hodnota danej výrokovej formuly nepravda (0). Nevýhoda tabuľkovej metódy výpočtu pravdivostných hodnôt danej formuly: jej zložitosť rastie exponenciálne s počtom premenných, t 2 n. priesvitka 31
32 Vo výrokovej logike majú mimoriadne postavenie také formuly, ktorých pravdivostná hodnota je pravda pre všetky možné kombinácie pravdivostných hodnôt premenných vo všetkých riadkoch. Takéto formuly nazývame tautológie a majú postavenie zákonov výrokovej logiky. Ich používanie pri odvodzovaní nových formúl zabezpečuje, že sú taktiež tautológie. Definícia. Formula sa nazýva tautológia (čo vyjadríme ), ak pre každú špecifikáciu platí val 1; v opačnom prípade, ak pre každú špecifikáciu platí val 0, formula sa nazýva kontradikcia. Ak pre niektorú špecifikáciu platí val 1 a pre inú špecifikáciu platí 0 splniteľná. val, potom formula je priesvitka 32
33 Často používané tautológie (1) Zákon totožnosti p p. (2) Zákon dvojitej negácie p p. (3) Zákon vylúčenia tretieho p p. (4) De Morganov zákon pre konjunkciu p q p q. (5) De Morganov zákon pre disjunkciu p q p q. (6) Zákon ekvivalencie p q p q q p (7) Zákon tranzitívnosti implikácie p r r q p q priesvitka 33
34 (8) Distribúcia konjunkcie p q r p q p r (9) Distribúcia disjunkcie p q r p q p r (10) Zákon kontrapozície p q q p (11) Zákon reductio ad absurdum (12) Zákon nahradenia implikácie p q p q. (13) Zákon modus ponens p q p q (14) Zákon modus tollens p q q p.. p q p q p. priesvitka 34
35 Na záver tejto kapitoly upriamime našu pozornosť na rôzne podmnožiny S z pohľadu podmienky logických spojok z celkovej množiny ich úplnosti, t.j. schopnosti vyjadriť ľubovoľnú výrokovú formulu (Boolovu funkciu) len pomocou niektorých logických spojok tvoriacich podmnožinu S S. Veta 3. (1) Podmnožina S,, je úplná, (2) podmnožiny S, a S, (3) podmnožina S, je úplná a (4) podmnožiny S a sú uplné, S sú uplné. priesvitka 35
36 Dokážte tieto ekvivalencie: Príklad (1) p q p p q q, (2) p q p q p q, (3) p q p q p q, (4) p q p p q q. Pri riešení týchto príkladov použijeme tieto definičné identity p q p q (NOR logická spojka) def priesvitka 36
37 p q def p q (NAND logická spojka) Z týchto dvoch identít odvodíme negácie elementárnych premenných p p p p p (a) p q p p q q def def p p p p p p q p q p q p q p q p q (b) p q p q p q p q p p q q priesvitka 37
38 p q p q p q p q p q p q p q (c) p q p q p q, p q p q p q p q p q p q (d) p q p p q q p q p p q q p q p q p q p q p q p q p q priesvitka 38
39 priesvitka 39
40 The End priesvitka 40
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Matematika pro informatiky KMA/MATA
 Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
8. Implikácia. A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna.
 8. Implikácia Implikáciu B A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna. Implikáciu B' A' nazývame obmenou implikácie A B. Implikácia
8. Implikácia Implikáciu B A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna. Implikáciu B' A' nazývame obmenou implikácie A B. Implikácia
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
OBCHOD MARKETING PSYCHOLÓGIA A ETIKA PREDAJA
 MAAG MAAG - Program na zvýšenie adaptability žiakov stredných škôl pri vstupe na trh práce Projekt je spolufinancovaný Európskou úniou Kód projektu 13120120211 maag.euba.sk maag@euba.sk OBCHOD MARKETING
MAAG MAAG - Program na zvýšenie adaptability žiakov stredných škôl pri vstupe na trh práce Projekt je spolufinancovaný Európskou úniou Kód projektu 13120120211 maag.euba.sk maag@euba.sk OBCHOD MARKETING
Organizačné štruktúry.
 Organizačné štruktúry. (Organizácia práce) Organizácia práce: akým spôsobom sú organizované vzťahy medzi jednotlivými členmi pracovnej skupiny - ich právomoci, povinnosti, zodpovednosti, spôsob komunikácie...
Organizačné štruktúry. (Organizácia práce) Organizácia práce: akým spôsobom sú organizované vzťahy medzi jednotlivými členmi pracovnej skupiny - ich právomoci, povinnosti, zodpovednosti, spôsob komunikácie...
Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od
 A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
Verifikácia a falzifikácia
 Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
ZÁKLADY LOGIKY A METODOLOGIE
 ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Multiplexor a demultiplexor
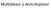 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
Teória grafov. Stromy a kostry 1. časť
 Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Katolícka univerzita v Ružomberku Pedagogická fakulta Katedra matematiky. Diferenciálny počet očami G. W. Leibnitza
 Katolícka univerzita v Ružomberku Pedagogická fakulta Katedra matematiky Diferenciálny počet očami G. W. Leibnitza História matematiky Mária Šuvadová 4. roč. MAT INF Niečo na úvod V rôznych knihách matematiky
Katolícka univerzita v Ružomberku Pedagogická fakulta Katedra matematiky Diferenciálny počet očami G. W. Leibnitza História matematiky Mária Šuvadová 4. roč. MAT INF Niečo na úvod V rôznych knihách matematiky
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL. Algebra a diskrétna matematika
 VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE
 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE júl 2017 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY
OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE júl 2017 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY
Programovanie I. Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM
 Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Dodanie tovaru a reťazové obchody Miesto dodania tovaru - 13/1
 Dodanie u a reťazové obchody Miesto dodania u - 13/1 ak je dodanie u spojené s odoslaním alebo prepravou u - kde sa nachádza v čase, keď sa odoslanie alebo preprava u osobe, ktorej má byť dodaný, začína
Dodanie u a reťazové obchody Miesto dodania u - 13/1 ak je dodanie u spojené s odoslaním alebo prepravou u - kde sa nachádza v čase, keď sa odoslanie alebo preprava u osobe, ktorej má byť dodaný, začína
Úvod do logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 23
 Úvod do logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 23 Co je logika? Čeho se týkají logické zákony? Tři možnosti: (1) světa (2) myšlení (3) jazyka (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216
Úvod do logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 23 Co je logika? Čeho se týkají logické zákony? Tři možnosti: (1) světa (2) myšlení (3) jazyka (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216
VÝUKOVÝ MATERIÁL. Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632 Číslo projektu
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Logický důsledek. Petr Kuchyňka (7765@mail.muni.cz)
 Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Logický důsledek Petr Kuchyňka (7765@mail.muni.cz) Úvod P 1 Logický důsledek je hlavním předmětem zájmu logiky. Je to relace mezi premisami a závěry logicky platných úsudků: v logicky platném úsudku závěr
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
BOOLOVÁ ALGEBRA ZÁKLADNÉ OPERÁCIE
 OOLOVÁ LGER Slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzahy medzi pravdivými a nepravdivými výrokmi. Pravdivému výroku prideujeme logickú hodnotu 1 a nepravidelnému výroku
OOLOVÁ LGER Slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzahy medzi pravdivými a nepravdivými výrokmi. Pravdivému výroku prideujeme logickú hodnotu 1 a nepravidelnému výroku
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Vývoj cien energií vo vybraných krajinách V4
 Vývoj cien energií vo vybraných krajinách V4 Ceny energií majú v krajinách V4 stále výrazný proinflačný vplyv. Je to výsledok významných váh energií a ich podielu na celkovom spotrebnom koši v kombinácii
Vývoj cien energií vo vybraných krajinách V4 Ceny energií majú v krajinách V4 stále výrazný proinflačný vplyv. Je to výsledok významných váh energií a ich podielu na celkovom spotrebnom koši v kombinácii
Pravdepodobnosť. Rozdelenia pravdepodobnosti
 Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Podlimitná zákazka Verejný obstarávateľ
 Finančné limity platné a účinné po 1. marci 2015 Podlimitná zákazka Verejný obstarávateľ BEŽNE DOSTUPNÉ NA TRHU 1 000 eur < 134 000 eur b) bod 3. alebo c)] Stavebné práce 1 000 eur < 5 186 000 eur b) bod.
Finančné limity platné a účinné po 1. marci 2015 Podlimitná zákazka Verejný obstarávateľ BEŽNE DOSTUPNÉ NA TRHU 1 000 eur < 134 000 eur b) bod 3. alebo c)] Stavebné práce 1 000 eur < 5 186 000 eur b) bod.
Všeobecne záväzné nariadenie Mesta Trenčianske Teplice č. x/2016 o používaní pyrotechnických výrobkov na území mesta Trenčianske Teplice
 Dôvodová správa S účinnosťou k 2.12.2015 došlo k zmene zákona č. 58/2014 Z. z. o výbušninách, výbušných predmetoch a munícii a o zmene a doplnení niektorých zákonov v znení neskorších predpisov, ktorý
Dôvodová správa S účinnosťou k 2.12.2015 došlo k zmene zákona č. 58/2014 Z. z. o výbušninách, výbušných predmetoch a munícii a o zmene a doplnení niektorých zákonov v znení neskorších predpisov, ktorý
Starogrécky filozof Demokritos ( pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov
 STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
KURT GÖDEL matematik a logik
 KATOLÍCKA UNIVERZITA V RUŽOMBERKU Pedagogická fakulta Katedra matematiky KURT GÖDEL matematik a logik PRÁCE Z PREDMETU HISTÓRIA MATEMATIKY Meno: Daniel Zahumenický Kombinácia: M IN Ročník: piaty Kurt Gödel
KATOLÍCKA UNIVERZITA V RUŽOMBERKU Pedagogická fakulta Katedra matematiky KURT GÖDEL matematik a logik PRÁCE Z PREDMETU HISTÓRIA MATEMATIKY Meno: Daniel Zahumenický Kombinácia: M IN Ročník: piaty Kurt Gödel
1. Pojem výroku. Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť.
 LOGIKA 1. Pojem výroku Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť. Pravdivosť (správnosť) výroku chápeme aj intuitívne. Príklady výrokov: 1.
LOGIKA 1. Pojem výroku Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť. Pravdivosť (správnosť) výroku chápeme aj intuitívne. Príklady výrokov: 1.
Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov
 Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov D.4 Kontajner XML údajov (XMLDataContainer) Skrátená forma popisu súčastí dátového prvku Kontajner XML údajov (XMLDataContainer)
Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov D.4 Kontajner XML údajov (XMLDataContainer) Skrátená forma popisu súčastí dátového prvku Kontajner XML údajov (XMLDataContainer)
Vysoké školy na Slovensku Prieskum verejnej mienky
 Vysoké školy na Slovensku 201 Prieskum verejnej mienky PRIESKUM VÁCLAV FORST Marketing Research Consultant Metodológia Zber dát bol realizovaný formou internetového dotazníka (CAWI) prostredníctvom internetového
Vysoké školy na Slovensku 201 Prieskum verejnej mienky PRIESKUM VÁCLAV FORST Marketing Research Consultant Metodológia Zber dát bol realizovaný formou internetového dotazníka (CAWI) prostredníctvom internetového
15. Príkazy vetvenia
 Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Kombinačné logické obvody
 Kombinačné logické obvody S polovodičovými prvkami môžeme realizovať ľubovoľne zložité spínacie funkcie vo všetkých zariadeniach na spracovanie informácií, napríklad v počítačoch, riadiacich obvodoch automatizovaných
Kombinačné logické obvody S polovodičovými prvkami môžeme realizovať ľubovoľne zložité spínacie funkcie vo všetkých zariadeniach na spracovanie informácií, napríklad v počítačoch, riadiacich obvodoch automatizovaných
LOGIKA VÝROKOVÁ LOGIKA
 LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Téma : Špecifiká marketingu finančných služieb
 Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
Pracovnoprávny vzťah závislá práca
 časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Autorské práva na softvér a licencie
 Autorské práva na softvér a licencie Všeobecná definícia autorského práva Všeobecne môžeme autorské právo definovať ako súhrn právnych noriem, ktoré sa viažu k vytvoreniu istého diela, a práv, ktoré z
Autorské práva na softvér a licencie Všeobecná definícia autorského práva Všeobecne môžeme autorské právo definovať ako súhrn právnych noriem, ktoré sa viažu k vytvoreniu istého diela, a práv, ktoré z
Operačný systém Úvodná prednáška
 Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
V nej je potrebné skontrolovať správnosť prenesených a prepočítaných zostatkov z roku 2008.
 WinJU ročná uzávierka a prechod na euro Postup prechodu na EURO Vo Win aplikáciách nie je kvôli euru zakladané nové dátové prostredie, ale pokračuje sa v pôvodnej dátovej štruktúre do konca roku 2008 budú
WinJU ročná uzávierka a prechod na euro Postup prechodu na EURO Vo Win aplikáciách nie je kvôli euru zakladané nové dátové prostredie, ale pokračuje sa v pôvodnej dátovej štruktúre do konca roku 2008 budú
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ
 64 1 TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ OBLASŤ PRIJATIA A ZAMIETNUTIA HYPOTÉZY PRI TESTOVANÍ CHYBY I. A II. DRUHU Chyba I. druhu sa vyskytne vtedy, ak je hypotéza správna, ale napriek tomu je zamietnutá,
64 1 TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ OBLASŤ PRIJATIA A ZAMIETNUTIA HYPOTÉZY PRI TESTOVANÍ CHYBY I. A II. DRUHU Chyba I. druhu sa vyskytne vtedy, ak je hypotéza správna, ale napriek tomu je zamietnutá,
Úvod do logiky a logického programování.
 Úvod do logiky a logického programování Luboš Popelínský popel@fi.muni.cz www.fi.muni.cz/~popel Přehled učiva Opakování základů výrokové a predikátové logiky Normální formy ve výrokové a predikátové logice
Úvod do logiky a logického programování Luboš Popelínský popel@fi.muni.cz www.fi.muni.cz/~popel Přehled učiva Opakování základů výrokové a predikátové logiky Normální formy ve výrokové a predikátové logice
Počasie na Slovensku v roku 2008
 Počasie na Slovensku v roku 2008 Rok 2008 patril, podľa výsledkov merania teploty vzduchu na meteorologickej stanici v Hurbanove, spolu s rokmi 2000 a 2007, k trom najtepleším v histórii merania tejto
Počasie na Slovensku v roku 2008 Rok 2008 patril, podľa výsledkov merania teploty vzduchu na meteorologickej stanici v Hurbanove, spolu s rokmi 2000 a 2007, k trom najtepleším v histórii merania tejto
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE
 MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
Technická univerzita v Košiciach
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Súhrnný výkaz v roku Ing. Mgr. Martin Tužinký, PhD.
 v roku 2015 Ing. Mgr. Martin Tužinký, PhD. SV je povinný podať platiteľ DPH, ktorý: Dodal tovar oslobodený od dane z tuzemska do IČŠ osobe, ktorá je identifikovaná pre daň v IČŠ ( 43 ods. 1 ZDPH). Premiestnil
v roku 2015 Ing. Mgr. Martin Tužinký, PhD. SV je povinný podať platiteľ DPH, ktorý: Dodal tovar oslobodený od dane z tuzemska do IČŠ osobe, ktorá je identifikovaná pre daň v IČŠ ( 43 ods. 1 ZDPH). Premiestnil
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
1. Matematická logika
 Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Smernica primátora č. 2/2011 o vykonávaní kontroly požívania alkoholu, omamných látok alebo psychotropných látok
 Smernica primátora č. 2/2011 o vykonávaní kontroly požívania alkoholu, omamných látok alebo psychotropných látok Primátor mesta Svidník podľa 13 odsek 4 písmeno e) zákona SNR č. 369/1990 Zb. o obecnom
Smernica primátora č. 2/2011 o vykonávaní kontroly požívania alkoholu, omamných látok alebo psychotropných látok Primátor mesta Svidník podľa 13 odsek 4 písmeno e) zákona SNR č. 369/1990 Zb. o obecnom
DANE A DAŇOVÝ SYSTÉM V SR
 DANE A DAŇOVÝ SYSTÉM V SR Na tomto svete nie je nič isté, iba dane a smrť. Benjamin Franklin, 1789 DAŇ Povinná, zákonom stanovená platba, ktorú odvádza daňový subjekt, t.j. fyzická alebo právnická osoba,
DANE A DAŇOVÝ SYSTÉM V SR Na tomto svete nie je nič isté, iba dane a smrť. Benjamin Franklin, 1789 DAŇ Povinná, zákonom stanovená platba, ktorú odvádza daňový subjekt, t.j. fyzická alebo právnická osoba,
Fyzika 9. ročník 3. Laboratórna úloha
 Základná škola s materskou školou Chlebnice Fyzika 9. ročník 3. Laboratórna úloha Úloha: Urč pevnú látku, z ktorej je zhotovené teleso, pomocou mernej tepelnej kapacity Príprava: Medzi telesami, ktorých
Základná škola s materskou školou Chlebnice Fyzika 9. ročník 3. Laboratórna úloha Úloha: Urč pevnú látku, z ktorej je zhotovené teleso, pomocou mernej tepelnej kapacity Príprava: Medzi telesami, ktorých
DIZAJN MANUÁL KULT MINOR LOGO MANUÁL. Fond na podporu kultúry národnostných menšín
 LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
Kontrola väzieb výkazu Súvaha a Výkaz ziskov a strát Príručka používateľa
 Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
2. Vyslovte negáciu nasledujúcich výrokov, určte pravdivostnú hodnotu pôvodných výrokov aj negácií: a. Súčin dvoch kladných reálnych čísel je kladný.
 Banka úloh 1 1. ročník 1. Rozhodnite, ktoré z nasledujúcich viet môžeme považovať za výroky. Pri výrokoch uveďte ich pravdivostnú hodnotu: a. Uhlopriečky obdĺžnika nie sú navzájom kolmé. b. Existuje rovnoramenný
Banka úloh 1 1. ročník 1. Rozhodnite, ktoré z nasledujúcich viet môžeme považovať za výroky. Pri výrokoch uveďte ich pravdivostnú hodnotu: a. Uhlopriečky obdĺžnika nie sú navzájom kolmé. b. Existuje rovnoramenný
Model epidemickej choroby (SIR model)
 Slovenská technická univerzita v Bratislave Fakulta elektrotechniky a informatiky Katedra matematiky Študentská Vedecká a Odborná Činnosť Model epidemickej choroby (SIR model) autor: konzultant: Pavol
Slovenská technická univerzita v Bratislave Fakulta elektrotechniky a informatiky Katedra matematiky Študentská Vedecká a Odborná Činnosť Model epidemickej choroby (SIR model) autor: konzultant: Pavol
λογος - LOGOS slovo, smysluplná řeč )
 MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
Telesný vývoj detí a mládeže v SR Výsledky VII. celoštátneho prieskumu v roku 2011
 Telesný vývoj detí a mládeže v SR Výsledky VII. celoštátneho prieskumu v roku 2011 Základným znakom každého živého organizmu je jeho telesný rast a vývin. Telesný rast je definovaný ako rast organizmu
Telesný vývoj detí a mládeže v SR Výsledky VII. celoštátneho prieskumu v roku 2011 Základným znakom každého živého organizmu je jeho telesný rast a vývin. Telesný rast je definovaný ako rast organizmu
Obdobie výrobnej orientácie - D>P, snaha výrobcov vyrobiť čo najviac, lebo všetko sa predalo Potreby zákazníka boli druhoradé Toto obdobie začalo
 MAR filozofiu používali ľudia už dávno bez toho, aby svoje konanie odôvodňovali učením o marketingu Prakticky išlo o živelné úsilie minimalizovať riziko pri podnikaní a maximalizovať zisk z predaja vyrobenej
MAR filozofiu používali ľudia už dávno bez toho, aby svoje konanie odôvodňovali učením o marketingu Prakticky išlo o živelné úsilie minimalizovať riziko pri podnikaní a maximalizovať zisk z predaja vyrobenej
Import Excel Univerzál
 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06)
 C 189/16 Úradný vestník Európskej únie 29.6.2011 Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06) Podľa článku 9 ods. 1 písm. a) druhej zarážky nariadenia Rady (EHS) č. 2658/87 z
C 189/16 Úradný vestník Európskej únie 29.6.2011 Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06) Podľa článku 9 ods. 1 písm. a) druhej zarážky nariadenia Rady (EHS) č. 2658/87 z
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Zápisnica o vyhodnotení ponúk- časť Kritériá
 JA servis, s.r.o. Mestečko 178, 020 52 Mestečko Zápisnica o vyhodnotení ponúk- časť Kritériá v zmysle 42 ods. 8 zákona č. 25/2006 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v
JA servis, s.r.o. Mestečko 178, 020 52 Mestečko Zápisnica o vyhodnotení ponúk- časť Kritériá v zmysle 42 ods. 8 zákona č. 25/2006 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v
Automatický timer pre DX7 návod na inštaláciu a manuál
 Automatický timer pre DX7 návod na inštaláciu a manuál Upozornenie: Aj keď je modul pre DX7 obvodovo takmer totožný s modulom pre DX6i, majú niektoré súčiastky odlišnú hodnotu a v procesore je úplne iný
Automatický timer pre DX7 návod na inštaláciu a manuál Upozornenie: Aj keď je modul pre DX7 obvodovo takmer totožný s modulom pre DX6i, majú niektoré súčiastky odlišnú hodnotu a v procesore je úplne iný
Vedecký prístup ku koncipovaniu ekonomickej teórie. VET Cvičenie 1.2
 Vedecký prístup ku koncipovaniu ekonomickej teórie VET Cvičenie 1.2 Základné funkcie ekonómie ako vedy 1. poznávacia 2. praktická 3. metodologická Ekonómia má nielen svoj predmet skúmania, ale aj svoje
Vedecký prístup ku koncipovaniu ekonomickej teórie VET Cvičenie 1.2 Základné funkcie ekonómie ako vedy 1. poznávacia 2. praktická 3. metodologická Ekonómia má nielen svoj predmet skúmania, ale aj svoje
Špecifikácia testu. z matematiky. pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017
 Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017 Bratislava 2016 Test z matematiky pre celoslovenské testovanie je určený žiakom 5. ročníka základných
Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017 Bratislava 2016 Test z matematiky pre celoslovenské testovanie je určený žiakom 5. ročníka základných
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
HEJNÉHO MATEMATIKA. Vyhodnotenie dotazníka pre rodičov 2018
 HEJNÉHO MATEMATIKA Vyhodnotenie dotazníka pre rodičov 2018 ŠTATISTICKÉ ÚDAJE Vo februári 2018 mali všetci rodičia, ktorých deti pracujú na matematike s Hejného metódou, možnosť vyjadriť svoje názory a
HEJNÉHO MATEMATIKA Vyhodnotenie dotazníka pre rodičov 2018 ŠTATISTICKÉ ÚDAJE Vo februári 2018 mali všetci rodičia, ktorých deti pracujú na matematike s Hejného metódou, možnosť vyjadriť svoje názory a
