Kvadratické funkcie, rovnice, 1
|
|
|
- Monika Jarošová
- před 6 lety
- Počet zobrazení:
Transkript
1 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly, b, c sú ľubovoľné reálne čísla. Jednotlivé členy a koeficienty nazývame: ax... kvadratický člen, a... koeficient kvadratického člena bx... lineárny člen, b... koeficient lineárneho člena c... absolútny člen Grafom kvadratickej funkcie je parabola. Zostrojte graf kvadratickej funkcie f: y = x. Zostavíme tabuľku pre vybrané hodnoty x: x f(x) Zostavíme graf tejto funkcie:
2 Kvadratické funkcie, rovnice,. ročník Z grafu vidíme, že definičným oborom funkcie je množina reálnych čísel. Oborom hodnôt je interval 0 ; ). Funkcia je párna. Je klesajúca na intervale ( ; 0 a rastúca na intervale 0 ; ). Funkcia je zdola ohraničená, nie je zhora ohraničená. V bode x = 0 má ostré minimum. Tento bod sa nazýva vrchol paraboly. Ako vplývajú hodnoty a, b, c na priebeh grafu funkcie? Začneme s hodnotou a. Majme kvadratickú funkciu typu f: y = ax, kde a je reálne číslo rôzne od nuly. Zostrojme grafy funkcií: f 1 : y = x ; f : y =- x ; f 3 : y = x ; f 4 : y = -x ; f 5 : y =3 x ; f 6 : y = -3x ; f 7 : y = 1 x 1 ; f 8 : y = x ; f 9 : y = 3 1 x ; f 10 : y = 4 1 x Zostavíme tabuľku pre vybrané hodnoty x: x f 1 (x) f (x) f 3 (x) f 4 (x) f 5 (x) f 6 (x) f 7 (x) 8 4,5 0,5 0 0,5 4,5 8 f 8 (x) -8-4,5 - -0,5 0-0,5 - -4,5-8 f 9 (x) f 10 (x) Vykreslíme grafy jednotlivých funkcií:
3 Kvadratické funkcie, rovnice, 3. ročník Z grafov funkcií vidíme: Vrchol všetkých parabol je v bode [0, 0]. Ak a > 0, tak graf funkcie má tvar doliny. Ak a < 0, tak graf funkcie má tvar kopca. Ďalej vidíme, že pre kladné hodnoty a čím je hodnota a väčšia, tým sa ramená paraboly viac blížia k osi y; pre záporné hodnoty a čím je hodnota a menšia, tým sa ramená paraboly viac blížia k osi y.
4 Kvadratické funkcie, rovnice, 4. ročník Sledujme priebeh funkcií tvaru f: y = x + e, teda napr. funkcií: f 1 : y = x + 1; f : y = x + ; f 3 : y = x -3; f 4 : y = x -0,5. Sami si zostavte tabuľku hodnôt pre vybrané x, my už priamo vykreslíme grafy jednotlivých funkcií: Vidíme, že vrcholy parabol sa pohybujú po osi y, majú x-ovú súradnicu nula, y-ová súradnica je závislá od hodnoty e, teda vrchol paraboly má súradnice [0, e].
5 Kvadratické funkcie, rovnice, 5. ročník Sledujme priebeh funkcií tvaru f: y = (x + f), teda napr. funkcií f 1 : y = (x + 1) ; f : y = (x + ) ; f 3 : y = (x 1) ; f 4 : y = (x 3). Sami si zostavte tabuľku hodnôt pre vybrané x, my už priamo vykreslíme grafy jednotlivých funkcií: Z grafov vidíme, že vrcholy parabol sa pohybujú po osi x, majú y- ovú súradnicu nula, x-ová súradnica je závislá od hodnoty f, teda vrchol paraboly má súradnice [-f, 0].
6 Kvadratické funkcie, rovnice, 6. ročník Ako bude vyzerať graf funkcie tvaru f: y = (x + f) + e, teda napr. f: y = (x + ) + 1? Z predchádzajúcich skúseností vieme, že graf bude dolina, lebo koeficient kvadratického člena je kladný. Vykreslíme graf funkcie: Vrchol funkcie f: y = (x + ) + 1 má súradnice V[-; 1]. Všeobecne môžeme zapísať, že vrchol funkcie v tvare f: y =(x + f) +e má súradnice V[-f; e]. Budeme však potrebovať zobraziť graf kvadratickej funkcie v tvare f: y = ax + bx + c. Túto funkciu budeme musieť upraviť podobný ako v predchádzajúcej časti. Vyskúšame úpravy na konkrétnych príkladoch:
7 Kvadratické funkcie, rovnice, 7. ročník Určte súradnice vrcholu funkcie f: y = x - x + 3. Predpis funkcie f: y = x - x + 3 budeme upravovať týmto spôsobom: ( x - x) výraz v zátvorke upravíme na štvorec a ab + b = (a b) ( x - x + 1) v skutočnosti sme nič nepridali ( x - x + 1) +... upravíme ( x - 1) + Teda platí f: y = x - x + 3 = ( x - 1) + Z tohto predpisu vieme, že vrchol má súradnice V[1; ]. O správnosti sa presvedčíme zostrojením grafu funkcie f: Určte súradnice vrcholu funkcie f: y =-0,5 x + x +. Z predpisu vidíme, že graf funkcie bude mať tvar kopca, pretože koeficient kvadratického člena je záporný. Musíme upraviť: -0,5 x + x + = -0,5(x - x 4) -0,5[(x x) - 4]
8 Kvadratické funkcie, rovnice, 8. ročník -0,5[(x x +1) -1-4] -0,5[(x x + 1) - 5] -0,5[(x 1) - 5] -0,5 (x - 1) +,5 roznásobíme Teda platí f: y = y =-0,5 x + x + = -0,5 (x - 1) +,5 Z tohto predpisu vieme, že vrchol má súradnice V[1;,5]. O správnosti sa presvedčíme zostrojením grafu funkcie f:
9 Kvadratické funkcie, rovnice, 9. ročník Kvadratická rovnica Rovnica ax + bx + c = 0 Pričom a, b, c sú reálne čísla, a 0, x je neznáma, sa nazýva kvadratická rovnica. Rovnici v takomto tvare často hovoríme kvadratická rovnica v anulovanom tvare, pretože na pravej stne je nula. V kvadratickej rovnici nikdy nesmie chýbať kvadratický člen, teda nikdy nesmie obsahovať člen 0x!!! Jednotlivé členy a koeficienty nazývame: ax... kvadratický člen, a... koeficient kvadratického člena bx... lineárny člen, b... koeficient lineárneho člena c... absolútny člen Určte, či nasledujúce rovnice s neznámou x sú kvadratické rovnice, určte ich jednotlivé členy a koeficienty: a) x + 4x + 7 = 0 b) 7x = 5x + 1 c) 0x 5x + = 0 d) (x 1)(4x + 3) = 0 e) -3x + 5 = 0 f) 4x 9x = 0 a) Rovnica je kvadratická, kvadratický člen je x, koeficient kvadratického člena je, lineárny člen je 4x, koeficient lineárneho člena je 4, absolútny člen je 7. b) Rovnicu upravíme na anulovaný tvar: 7x - 5x 1 = 0. Rovnica je kvadratická, kvadratický člen je 7x, koeficient kvadratického člena je 7, lineárny člen je -5x, koeficient lineárneho člena je -5, absolútny člen je -1. c) Rovnica nie je kvadratická, pretože koeficient kvadratického člena 0x je 0, čo podľa definície kvadratickej rovnice nesmie byť. d) Rovnicu roznásobíme: (x 1)(4x + 3) = 0 4x + 3x 4x 3 = 0 4x x 3 = 0
10 Kvadratické funkcie, rovnice, 10. ročník Rovnica je kvadratická, kvadratický člen je 4x, koeficient kvadratického člena je 4, lineárny člen je x, koeficient lineárneho člena je -1, absolútny člen je -3. e) Rovnica je kvadratická, neobsahuje lineárny člen. Kvadratický člen je -3x, koeficient kvadratického člena je -3, absolútny člen je 5. f) Rovnica je kvadratická, neobsahuje absolútny člen. Kvadratický člen je 4x, koeficient kvadratického člena je 4, lineárny člen je 9x, koeficient lineárneho člena je -9. Grafické riešenie kvadratických rovníc Viem už zostrojiť graf kvadratickej funkcie. Tieto grafy využijeme aj pri riešení kvadratických rovníc. Z grafov kvadratických funkcií určíme približné riešenie rovníc, teda hodnoty premennej x, pre ktoré príslušné funkcie nadobúdajú hodnotu nula. Tieto čísla x sú koreňmi rovníc. Riešte graficky kvadratické rovnice: a) x 5x + 6 = 0 b) x + x + 1 = 0 c) 9x + 6x + 1 = 0 d) 0,1 x,3x + = 0 a) Zostrojíme graf kvadratickej funkcie f:y = x 5x + 6. Zostavíme tabuľku pre vybrané hodnoty x: x f(x)
11 Kvadratické funkcie, rovnice, 11. ročník Zostrojíme graf: Z tabuľky i z grafu je vidieť, že funkcia f nadobúda hodnotu nula pre čísla x 1 = a x = 3. Preto K = {; 3}. b) Zostrojíme graf kvadratickej funkcie g:y = x + x + 1. Zostavíme tabuľku pre vybrané hodnoty x: x g(x) Zostrojíme graf: Z grafu vidíme, že funkcia g nenadobúda hodnotu nula pre nijaké x. Preto K = Ø.
12 Kvadratické funkcie, rovnice, 1. ročník c) Zostrojíme graf kvadratickej funkcie h:y = 9x + 6x + 1. Zostavíme tabuľku pre vybrané hodnoty x: x ,5-0,3 h(x) ,5 0,01 Zostrojíme graf: Z grafu vidíme, že funkcia h nadobúda hodnotu nula pre číslo x väčšie ako -0,3, konkrétne pre 1 = 3 x. Preto K = 1 3 O správnosti riešenia sa presvedčte dosadením hodnoty do kvadratickej rovnice. d) Zostrojíme graf kvadratickej funkcie i:y = 0,1x,3x +. Zostavíme tabuľku pre vybrané hodnoty x: x i(x) 4,4-0, -, -4 7 Zostrojíme graf:.
13 Kvadratické funkcie, rovnice, 13. ročník Z grafu vidíme, že funkcia i nadobúda hodnotu nula pre číslo x z intervalu (0; 1) a pre číslo z intervalu (0; 5) Presné riešenie nám zatiaľ robí problémy. Ako vidíme, grafické riešenie kvadratických rovníc je pomerne náročné a nakoniec nám dáva len približné výsledky. Preto budeme hľadať iné možnosti riešenia kvadratických rovníc. Najprv si uvedieme rôzne typy kvadratických rovníc. Typy kvadratických rovníc Kvadratické rovnice nemusia mať všetky tri členy (teda kvadratický, lineárny a absolútny), v každom prípade musí obsahovať kvadratický člen. Kvadratickú rovnicu, ktorá má tvar ax + bx = 0, nazývame kvadratická rovnica bez absolútneho člena. Kvadratickú rovnicu, ktorá má tvar ax + c = 0, nazývame rýdzokvadratická rovnica. Riešenie kvadratickej rovnice bez absolútneho člena Kvadratickú rovnicu tvaru ax + bx = 0 môžeme riešiť nasledujúcim spôsobom: Rovnicu upravíme na súčinový tvar ax + bx = 0 x(ax + b) = 0 Súčin dvoch čísel je rovný nule práve vtedy, keď aspoň jeden z činiteľov je rovný nule. V našom prípade musí platiť: x = 0 ax + b = 0 Jeden koreň rovnice x 1 = 0, druhý koreň dostávame po úprave b b x =. Preto K = 0, a a.
14 Kvadratické funkcie, rovnice, 14. ročník Riešte kvadratické rovnice: a) 4x x = 0 b) 3x + 5x = 0 a) Rovnicu 4x x = 0 upravíme na súčinový tvar x(x 1) = 0. Rovnica má riešenie práve vtedy, keď x = 0 alebo (x 1) = 0. K = 0;0,5. Potom x 1 = 0 a x = 0,5. Zapíšeme: { } b) Rovnicu 3x + 5x = 0 upravíme na súčinový tvar x(3x + 5) = 0. Rovnica má riešenie práve vtedy, keď x = 0 5 alebo 3x + 5 = 0. Potom x 1 = 0 a x =. Zapíšeme: 3 5 K = 0; 3. Riešenie rýdzokvadratickej rovnice Kvadratickú rovnicu tvaru ax + c = 0 môžeme riešiť nasledujúcim spôsobom (ukážeme na konkrétnych príkladoch): Riešte kvadratické rovnice: a) 4x 1 = 0 b) x + 16 = 0 a) 1. spôsob: Rovnicu 4x 1 = 0 môžeme upraviť na súčinový tvar (x 1) (x + 1) = 0... využili sme vzorec a b = (a b)(a+b) Vieme, že rovnica má riešenie, ak (x 1)=0 alebo (x + 1)=0. Preto x = 1 1 a x = 1. Zapíšeme: 1 1 K = ;
15 Kvadratické funkcie, rovnice, 15. ročník. spôsob: Rovnicu 4x 1 = 0 upravíme na tvar x = 4 1. Hľadáme čísla, ktorých druhá mocnina je rovná 4 1. Je to číslo x = ale aj x =. Je výhodnejšie používať prvý spôsob, pretože často na druhú možnosť (so záporným znamienkom) zabúdame. b) Rovnicu x + 16 = 0 nemôžeme upraviť na súčinový tvar. Preto použijeme druhý spôsob. Dostávame: x = -16. Hľadáme čísla, ktorých druhá mocnina je -16. Také čísla však neexistujú, a tak kvadratická rovnica nemá riešenie. O výsledku sa môžeme presvedčiť z grafu funkcie f: y = x + 16: Z obrázka vidíme, že graf nepretína x-ovú os, preto funkcia pre žiadne x nenadobúda hodnotu nula. Tieto postupy riešení sú vhodné len pre vybrané typy kvadratických funkcií. Ale ako sa riešia kvadratické rovnice so všetkými členmi?
16 Kvadratické funkcie, rovnice, 16. ročník Riešenie kvadratických rovníc Nájdeme algebraické riešenie kvadratickej rovnice ax + bx + c = 0. Vykonáme postupne tieto úpravy: ax + bx + c = 0 rozšírime rovnicu /.a a. ax + a. bx + a. c = 0 necháme na jednej strane členy s x a x + abx = - ac upravíme ľavú stranu na trojčlen (ax) b b +.ax + ax + b = - ac + ax + b = b b 4ac 4 b = - ac + ľavú stanu upravíme na súčin upravíme pravú stranu rovnice Zavedieme označenie D = b 4ac. Keďže ax + b je vždy nezáporné číslo, tak aj D musí byť nezáporné číslo. V prípade, že D<0, rovnica nemá riešenie. Teda dostávame: + b D D ax = pravú stranu rovnice zapíšeme v tvare 4, teda ax + b = D upravíme + b D ax - = 0 ľavú stranu rovnice rozložíme podľa vzťahu a b = (a b)(a + b), teda b D b D ax + = 0 ax + + Musí platiť: b D b D ax + = 0 alebo ax + + = 0, teda b D x a b D alebo x a a a čo môžeme upraviť na tvar
17 Kvadratické funkcie, rovnice, 17. ročník b + D x = alebo a b D x =. a Pre korene kvadratickej rovnice zavedieme označenie x 1, x. Ak D < 0, tak K = Ø. b Ak D = 0, tak K = a. b ± D Ak D > 0, tak K =, D = b 4ac. a Výraz D = b 4ac nazývame diskriminant kvadratickej rovnice ax + bx + c = 0. Už pri grafickom riešení kvadratickej rovnice sme videli, že rovnica môže mať dva, jeden alebo žiadny koreň. Túto skúsenosť sme aj algebraicky overili. Dosadením vypočítaných koreňov do rovnice numericky overíme správnosť výsledku. Riešte rovnicu x + 5x 3 = 0. Využijeme vzorec. Najprv si z rovnice určíme a, b, c. Vidíme, že a =, b = 5, c = -3. Vypočítame hodnotu diskriminantu: D = b 4ac = (-3) = = 49. Keďže D > 0, rovnica má dva korene. Dosadíme do vzorca x 1, = b ± a D = 5 ± 49 = 5 ± 7 4 = 1-3
18 Kvadratické funkcie, rovnice, 18. ročník 1 Zapíšeme K =, 3. Riešenia môžeme overiť dosadením do pôvodnej rovnice. Určte celé čísla, ktoré sú riešením rovnice (x - 4)(4x - 3) + 3 = 0. Najprv rovnicu upravíme na tvar kvadratickej rovnice: (x - 4)(4x - 3) + 3 = 0 4x 3x 16x = 0 4x 19x + 15 = 0 V danej rovnici a = 4, b = -19, c = 15. Vypočítame diskriminant: D = b 4ac = (-19) = = 11, teda úloha má dve riešenia. Dosadíme do vzťahu x 1, b ± = a D 19 ± ± 11 = = = = Podľa zadania musíme určiť celé čísla, takže K = {1}. Vzťahy medzi koreňmi a koeficientmi kvadratickej rovnice Skúsime nájsť vzťahy z algebraického riešenia kvadratickej rovnice ax + bx + c = 0. Vieme, že kvadratická rovnica má najviac dve riešenia, ktorých tvar je b ± D x1, = a Určíme x 1 + x : x 1 + x = b + a D b + a D b = = a b a
19 Kvadratické funkcie, rovnice, 19. ročník Určíme x 1. x : ( b 4ac) b + D b D b D b 4ac c x 1. x = = = = = a a 4a 4a 4a a Tieto vzťahy môžeme využiť pri riešení kvadratických rovníc. Každú kvadratickú rovnicu ax + bx + c = 0 vieme zapísať v tvare a(x x 1 )(x x ) = 0 s koreňmi x 1, x. Dvojčleny x x 1 a x x nazývame koreňové činitele. Výraz ax + bx + c nazývame kvadratický trojčlen. Rozložte kvadratický trojčlen x činiteľov. + x 6 na súčin koreňových Úlohu môžeme riešiť viacerými spôsobmi: 1.spôsob: Kvadratický trojčlen zapíšeme ako kvadratickú rovnicu x + x 6 = 0. Využijeme vzťahy pre určenie koreňov: a = 1, b = 1, c = -6. Vypočítame diskriminant: D = b 4ac = (-6) = = 5, teda úloha má dve riešenia. Dosadíme do vzťahu b ± D 1± 5 1± 5 x 1, = = = = a 1-3 Kvadratický trojčlen x + x 6 = 0 zapíšeme ako súčin koreňových činiteľov a(x x 1 )(x x ) = (x ) (x + 3).
20 Kvadratické funkcie, rovnice, 0. ročník.spôsob: Využijeme vzťahy medzi koreňmi a koeficientmi: b x 1 + x = a c x 1. x = a Po dosadení dostávame: 1 x 1 + x = x x = x 1. x = x1. x 1 = - 6 Určíme dvojice čísel, pre ktoré platí x 1. x = - 6. Vyhovujú dvojice: [1; -6], [-1; 6], [, -3], [-; 3]. Určíme, pre ktoré z nich zároveň platí x 1 + x = - 1. Pre dvojicu [1; -6] platí 1 6 = -5 nevyhovuje. Pre dvojicu [-1; 6] platí = 5 nevyhovuje. Pre dvojicu [; -3] platí 3 = -1 vyhovuje. Pre dvojicu [-; 3] platí = 1 nevyhovuje. Korene rovnice sú a -3, teda kvadratický trojčlen x + x 6 = 0 zapíšeme ako súčin koreňových činiteľov a(x x 1 )(x x ) = (x ) (x + 3). Rozložte kvadratický trojčlen x činiteľov. - 5x 3 na súčin koreňových 5 3 Kvadratický trojčlen najprv upravíme na tvar x x. Budeme upravovať trojčlen v zátvorke, pre ktorý a = 1, b = -,5, c = -1,5. Vypočítame diskriminant: D = b 4ac = (-,5) (-1,5) = 6,5 + 6 = 1,5, teda úloha má dve riešenia. Dosadíme do vzťahu
21 Kvadratické funkcie, rovnice, 1. ročník b ± D,5 ± 1,5,5 ± 3,5 x 1, = = = = 3 a 1-0,5 Kvadratický trojčlen x - 5x 3 upravíme na súčin: (x 3) (x + 0,5). O správnosti sa presvedčíme opätovným roznásobením: (x + 0,5x 3x 1,5) = (x,5x 1,5) =x 5x 3. Kvadratické Všetky tvaru ax + bx + c < 0 ax + bx + c > 0 ax + bx + c 0 ax + bx + c 0 pričom a, b, c sú reálne čísla a a 0, x neznáma, sa nazývajú kvadratické. Kvadratické riešime podobne ako kvadratické rovnice, len pri riešení využívame graf kvadratickej funkcie. Riešte nerovnicu: x + x 6 > 0. Kvadratickú nerovnicu zapíšeme ako kvadratickú rovnicu x + x 6 = 0. Korene tejto rovnice sú a -3. Zakreslíme graf kvadratickej funkcie f: y = x + x 6,
22 Kvadratické funkcie, rovnice,. ročník My potrebuje zistiť, pre ktoré x sú hodnoty funkcie kladné. Z obrázka vidieť, že: Teda riešením x + x 6 > 0 sú intervaly ( ; 3) a ( ; ) Zapíšeme: K = ( ; 3) ( ; )..
23 Kvadratické funkcie, rovnice, 3. ročník Riešte nerovnicu: x + x 6 0. Postupujeme podľa predchádzajúceho príkladu. Dostávame graf: Z grafu vyplýva, že = 3; K.
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
MO-ME-N-T MOderní MEtody s Novými Technologiemi
 Projekt: Reg.č.: Operační program: Škola: Tematický okruh: Jméno autora: MO-ME-N-T MOderní MEtody s Novými Technologiemi CZ.1.7/1.5./34.93 Vzdělávání pro konkurenceschopnost Hotelová škola, Vyšší odborná
Projekt: Reg.č.: Operační program: Škola: Tematický okruh: Jméno autora: MO-ME-N-T MOderní MEtody s Novými Technologiemi CZ.1.7/1.5./34.93 Vzdělávání pro konkurenceschopnost Hotelová škola, Vyšší odborná
M - Kvadratické rovnice a kvadratické nerovnice
 M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Algebraické výrazy - řešené úlohy
 Algebraické výrazy - řešené úlohy Úloha č. 1 Určete jeho hodnotu pro =. Určete, pro kterou hodnotu proměnné je výraz roven nule. Za proměnnou dosadíme: = a vypočteme hodnotu výrazu. Nejprve zapíšeme rovnost,
Algebraické výrazy - řešené úlohy Úloha č. 1 Určete jeho hodnotu pro =. Určete, pro kterou hodnotu proměnné je výraz roven nule. Za proměnnou dosadíme: = a vypočteme hodnotu výrazu. Nejprve zapíšeme rovnost,
Variace. Kvadratická funkce
 Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Funkce pro studijní obory
 Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Praha & EU: investujeme do vaší budoucnosti. Daniel Turzík, Miroslava Dubcová,
 E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
M - Kvadratické rovnice
 M - Kvadratické rovnice Určeno jako učební tet pro studenty denního i dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
M - Kvadratické rovnice Určeno jako učební tet pro studenty denního i dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
M - Kvadratická funkce
 M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Rovnice v oboru komplexních čísel
 Rovnice v oboru komplexních čísel Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu Šablona CZ.1.07/1.5.00/34.0218 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Čerm_01a
Rovnice v oboru komplexních čísel Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu Šablona CZ.1.07/1.5.00/34.0218 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Čerm_01a
VaFu16-T List 1. Kvadratická funkcia. RNDr. Beáta Varinčíková
 VaFu6-T List Kvadratická funkcia RNDr. Beáta Varinčíková U: Vieme, že funkcia predstavuje určitú závislosť medzi dvoma veličinami. V prípade, že jedna veličina závisí od druhej mocnin druhej veličin, hovoríme
VaFu6-T List Kvadratická funkcia RNDr. Beáta Varinčíková U: Vieme, že funkcia predstavuje určitú závislosť medzi dvoma veličinami. V prípade, že jedna veličina závisí od druhej mocnin druhej veličin, hovoríme
M - Příprava na 2. čtvrtletku - třídy 1P, 1VK
 M - Příprava na 2. čtvrtletku - třídy 1P, 1VK Souhrnný studijní materiál k přípravě na 2. čtvrtletní písemnou práci. Obsahuje učivo listopadu až ledna. VARIACE 1 Tento dokument byl kompletně vytvořen,
M - Příprava na 2. čtvrtletku - třídy 1P, 1VK Souhrnný studijní materiál k přípravě na 2. čtvrtletní písemnou práci. Obsahuje učivo listopadu až ledna. VARIACE 1 Tento dokument byl kompletně vytvořen,
4. Určete definiční obor elementární funkce g, jestliže g je definována předpisem
 4 Určete definiční obor elementární funkce g jestliže g je definována předpisem a) g ( x) = x 16 + ln ( x) x 16 ( x + 4 )( x 4) Řešíme-li kvadratickou nerovnice pomocí grafu kvadratické funkce tj paraboly
4 Určete definiční obor elementární funkce g jestliže g je definována předpisem a) g ( x) = x 16 + ln ( x) x 16 ( x + 4 )( x 4) Řešíme-li kvadratickou nerovnice pomocí grafu kvadratické funkce tj paraboly
----- Studijní obory. z matematiky. z matematiky. * Aplikovaná matematika * Matematické metody v ekonomice
 Minimum Maximum Minimum Maximum Studijní obory z matematiky z matematiky z matematiky z matematiky * Aplikovaná matematika * Matematické metody v ekonomice * Obecná matematika Navazující magisterský studijní
Minimum Maximum Minimum Maximum Studijní obory z matematiky z matematiky z matematiky z matematiky * Aplikovaná matematika * Matematické metody v ekonomice * Obecná matematika Navazující magisterský studijní
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Soustavy lineárních a kvadratických rovnic o dvou neznámých
 Soustavy lineárních a kvadratických rovnic o dvou neznámých obsah 1.a) x + y = 5 x 2 + y 2 = 13 3 b) x - y = 7 x 2 + y 2 = 65 5 c) x - y = 3 x 2 + y 2 = 5 6 3. a) x + 2y = 9 x. y = 10 12 b) x - 3y = 1
Soustavy lineárních a kvadratických rovnic o dvou neznámých obsah 1.a) x + y = 5 x 2 + y 2 = 13 3 b) x - y = 7 x 2 + y 2 = 65 5 c) x - y = 3 x 2 + y 2 = 5 6 3. a) x + 2y = 9 x. y = 10 12 b) x - 3y = 1
Matematika Kvadratická rovnice. Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar
 Kvadratická rovnice Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar ax 2 + bx + c = 0. x neznámá; v kvadratické rovnici se vyskytuje umocněná na
Kvadratická rovnice Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar ax 2 + bx + c = 0. x neznámá; v kvadratické rovnici se vyskytuje umocněná na
Ďalší spôsob, akým je možné vygenerovať maticu je použitie zabudovaných funkcií na generovanie elementárnych matíc.
 MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
ROVNICE A NEROVNICE. Kvadratické rovnice Algebraické způsoby řešení I. Mgr. Jakub Němec. VY_32_INOVACE_M1r0108
 ROVNICE A NEROVNICE Kvadratické rovnice Algebraické způsoby řešení I. Mgr. Jakub Němec VY_32_INOVACE_M1r0108 KVADRATICKÁ ROVNICE V rámci našeho poznávání rovnic a jejich řešení jsme narazili pouze na lineární
ROVNICE A NEROVNICE Kvadratické rovnice Algebraické způsoby řešení I. Mgr. Jakub Němec VY_32_INOVACE_M1r0108 KVADRATICKÁ ROVNICE V rámci našeho poznávání rovnic a jejich řešení jsme narazili pouze na lineární
1. Několik základních pojmů ze středoškolské matematiky. Na začátku si připomeneme následující pojmy:
 Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Riešenie nelineárnych rovníc I
 Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice
 Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
VZOROVÝ TEST PRO 1. ROČNÍK (1. A, 3. C)
 VZOROVÝ TEST PRO. ROČNÍK (. A, 3. C) Zjednodušte daný příklad. (a 2 3 b 3 4) 2 (a 2 b 3 8) 3 max. 3 body 2 Ve které z následujících možností je uveden správný postup usměrnění daného zlomku a správný výsledek?
VZOROVÝ TEST PRO. ROČNÍK (. A, 3. C) Zjednodušte daný příklad. (a 2 3 b 3 4) 2 (a 2 b 3 8) 3 max. 3 body 2 Ve které z následujících možností je uveden správný postup usměrnění daného zlomku a správný výsledek?
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
KVADRATICKÉ FUNKCE. + bx + c, největší hodnotu pro x = a platí,
 KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
AR, MA a ARMA procesy
 Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
M - Příprava na 4. zápočtový test - třídy 1DP, 1DVK
 M - Příprava na 4. zápočtový test - třídy 1DP, 1DVK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz VARIACE 1 Tento
M - Příprava na 4. zápočtový test - třídy 1DP, 1DVK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz VARIACE 1 Tento
TC Obsahový štandard - téma Výkonový štandard - výstup
 Mocniny a odmocniny, zápis veľkých čísel Finančná matemati ka UČEBNÉ OSNOVY DEVIATY ROČNÍK TC Obsahový štandard - téma Výkonový štandard - výstup Vklad, úrok, úroková miera Dane zvládnuť základné pojmy
Mocniny a odmocniny, zápis veľkých čísel Finančná matemati ka UČEBNÉ OSNOVY DEVIATY ROČNÍK TC Obsahový štandard - téma Výkonový štandard - výstup Vklad, úrok, úroková miera Dane zvládnuť základné pojmy
CVIČNÝ TEST 9 OBSAH. Mgr. Václav Zemek. I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 9 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Vypočítejte (7,5 10 3 2 10 2 ) 2. Výsledek zapište ve tvaru a 10 n, kde
CVIČNÝ TEST 9 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Vypočítejte (7,5 10 3 2 10 2 ) 2. Výsledek zapište ve tvaru a 10 n, kde
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Rozklad mnohočlenov na súčin
 KrAv05-T List 1 Rozklad mnohočlenov na súčin RNDr. Jana Krajčiová, PhD. U: Teraz si ukážeme, ako môžeme rozložiť mnohočlen na súčin mnohočlenov čo najnižšieho stupňa. Napr. 3x 3xy 3xx y), alebo 3x y )
KrAv05-T List 1 Rozklad mnohočlenov na súčin RNDr. Jana Krajčiová, PhD. U: Teraz si ukážeme, ako môžeme rozložiť mnohočlen na súčin mnohočlenov čo najnižšieho stupňa. Napr. 3x 3xy 3xx y), alebo 3x y )
MOCNINY A ODMOCNINY Eva Zummerová
 MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
4C. Polynomy a racionální lomené funkce. Patří mezi tzv. algebraické funkce, ke kterým patří také funkce s odmocninami. Polynomy
 4C. Polynomy a racionální lomené funkce Polynomy a racionální funkce mají zvláštní význam zejména v numerické a aplikované matematice. Patří mezi tzv. algebraické funkce, ke kterým patří také funkce s
4C. Polynomy a racionální lomené funkce Polynomy a racionální funkce mají zvláštní význam zejména v numerické a aplikované matematice. Patří mezi tzv. algebraické funkce, ke kterým patří také funkce s
Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí. Definičním oborem kvadratické funkce je množina reálných čísel.
 Kvadratická funkce Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí y = ax 2 + bx + c Číslo a je různé od nuly, b,c jsou libovolná reálná čísla. Definičním oborem kvadratické funkce je
Kvadratická funkce Kvadratickou funkcí se nazývá každá funkce, která je daná rovnicí y = ax 2 + bx + c Číslo a je různé od nuly, b,c jsou libovolná reálná čísla. Definičním oborem kvadratické funkce je
2.7.6 Rovnice vyšších řádů
 6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
Ak stlačíme OK, prebehne výpočet a v bunke B1 je výsledok.
 Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
1 Optimization toolbox
 1 Optimization toolbox Optimalizačný toolbox poskytuje používateľom štandardné algoritmy a algoritmy "veľkého rozsahu" large scale na riešenie optimalizačných úloh ako sú: nepodmienená nelineárna minimalizácia,
1 Optimization toolbox Optimalizačný toolbox poskytuje používateľom štandardné algoritmy a algoritmy "veľkého rozsahu" large scale na riešenie optimalizačných úloh ako sú: nepodmienená nelineárna minimalizácia,
M - Příprava na pololetní písemku č. 1
 M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
Nerovnice v součinovém tvaru, kvadratické nerovnice
 Nerovnice v součinovém tvaru, kvadratické nerovnice Příklad: Pro která x R je součin x x 5 kladný? Řešení: Víme, že součin je kladný, mají-li oba činitelé stejné znaménko. Tedy aby platilo x x 5 0, musí
Nerovnice v součinovém tvaru, kvadratické nerovnice Příklad: Pro která x R je součin x x 5 kladný? Řešení: Víme, že součin je kladný, mají-li oba činitelé stejné znaménko. Tedy aby platilo x x 5 0, musí
6. Lineární (ne)rovnice s odmocninou
 @06 6. Lineární (ne)rovnice s odmocninou rovnice Když se řekne s odmocninou, znamená to, že zadaná rovnice obsahuje neznámou pod odmocninou. není (ne)rovnice s odmocninou neznámá x není pod odmocninou
@06 6. Lineární (ne)rovnice s odmocninou rovnice Když se řekne s odmocninou, znamená to, že zadaná rovnice obsahuje neznámou pod odmocninou. není (ne)rovnice s odmocninou neznámá x není pod odmocninou
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
2.7.6 Rovnice vyšších řádů
 6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
Začínam so zadaním z NEPOUŽÍVAME ROZSAH POKIAĽ HO MUSÍME PRESKOČIŤ
 Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Logaritmické funkcie, rovnice a nerovnice. Riešenia. 2. a) 4 = 16, 2 = log 16, b) 3 = log (t. j. 3 = log, 0,064), , 4 = log
 Logaritmické funkcie, rovnice a nerovnice Riešenia 1. Pre definičný obor a obor hodnôt inverznej funkcie ff platí DD ff = HH ff, HH ff = DD ff a pre exponenciálnu funkciu ff sa DD ff = R, HH ff = 0;. 2.
Logaritmické funkcie, rovnice a nerovnice Riešenia 1. Pre definičný obor a obor hodnôt inverznej funkcie ff platí DD ff = HH ff, HH ff = DD ff a pre exponenciálnu funkciu ff sa DD ff = R, HH ff = 0;. 2.
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Funkce s absolutní hodnotou, funkce exponenciální a funkce logaritmická
 Variace 1 Funkce s absolutní hodnotou, funkce exponenciální a funkce logaritmická Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu
Variace 1 Funkce s absolutní hodnotou, funkce exponenciální a funkce logaritmická Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu
M - Příprava na 1. zápočtový test - třída 3SA
 M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
Funkcionální řady. January 13, 2016
 Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
ROVNICE, NEROVNICE A JEJICH SOUSTAVY
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ ÚLOH ROVNICE, NEROVNICE A JEJICH SOUSTAVY CIFRIK C. Úloha 1 [kvadratická rovnice s kořeny y_1=x_1^2+x_2^2, y_2=x_1^3+x_2^3]
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ ÚLOH ROVNICE, NEROVNICE A JEJICH SOUSTAVY CIFRIK C. Úloha 1 [kvadratická rovnice s kořeny y_1=x_1^2+x_2^2, y_2=x_1^3+x_2^3]
Matematika pre tretiakov. Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp
 Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
TEMATICKÝ PLÁN VÝUKY
 TEMATICKÝ PLÁN VÝUKY Studijní obor: 23-41 - M/01 Strojírenství Zaměření: Předmět: Matematika Ročník: 1. Počet hodin 4 Počet hodin celkem: 136 týdně: Tento plán vychází z Rámcového vzdělávacího programu
TEMATICKÝ PLÁN VÝUKY Studijní obor: 23-41 - M/01 Strojírenství Zaměření: Předmět: Matematika Ročník: 1. Počet hodin 4 Počet hodin celkem: 136 týdně: Tento plán vychází z Rámcového vzdělávacího programu
MAT I. Logika, množiny 6. Finančná matematika 4. Geometria 8. Planimetria 14. Výrazy 18. Funkcie Függvények 4
 MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
KrAv02-T List 1. Polynómy. RNDr. Jana Krajčiová, PhD.
 KrAv02-T List 1 Polynómy RNDr. Jana Krajčiová, PhD. U: Povieme si niečo o polynómoch, resp. mnohočlenoch. Ž: A je medzi polynómom a mnohočlenom nejaký rozdiel? U: Práveže žiaden. Slovo polynóm je gréckeho
KrAv02-T List 1 Polynómy RNDr. Jana Krajčiová, PhD. U: Povieme si niečo o polynómoch, resp. mnohočlenoch. Ž: A je medzi polynómom a mnohočlenom nejaký rozdiel? U: Práveže žiaden. Slovo polynóm je gréckeho
Příklad 1. Řešení 1a Máme řešit rovnici ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 1. Řešte v R rovnice: 8 3 5 5 2 8 =20+4 1 = + c) = f) +6 +8=4 g) h)
 Příklad Řešte v R rovnice: a) 8 3 5 5 2 8 =20+4 b) = + c) = d) = e) + =2 f) +6 +8=4 g) + =0 h) = Řešení a Máme řešit rovnici 8 3 5 5 2 8 =20+4 Zjevně jde o lineární rovnici o jedné neznámé. Nejprve roznásobíme
Příklad Řešte v R rovnice: a) 8 3 5 5 2 8 =20+4 b) = + c) = d) = e) + =2 f) +6 +8=4 g) + =0 h) = Řešení a Máme řešit rovnici 8 3 5 5 2 8 =20+4 Zjevně jde o lineární rovnici o jedné neznámé. Nejprve roznásobíme
Obsah. Metodický list Metodický list Metodický list Metodický list
 METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/34.0211. Anotace. Integrální počet VY_32_INOVACE_M0308. Matematika
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 0 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..07/.5.00/3.0 Zlepšení podmínek pro
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 0 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..07/.5.00/3.0 Zlepšení podmínek pro
Soustavy lineárních diferenciálních rovnic I. řádu s konstantními koeficienty
 Soustavy lineárních diferenciálních rovnic I řádu s konstantními koeficienty Definice a) Soustava tvaru x = ax + a y + az + f() t y = ax + a y + az + f () t z = a x + a y + a z + f () t se nazývá soustava
Soustavy lineárních diferenciálních rovnic I řádu s konstantními koeficienty Definice a) Soustava tvaru x = ax + a y + az + f() t y = ax + a y + az + f () t z = a x + a y + a z + f () t se nazývá soustava
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Lineární funkce, rovnice a nerovnice 3 Soustavy lineárních rovnic
 Lineární funkce, rovnice a nerovnice Soustavy lineárních rovnic motivace Využívají se napřklad při analytickém vyšetřování vzájemné polohy dvou přímek v rovině a prostoru. Při řešení některých slovních
Lineární funkce, rovnice a nerovnice Soustavy lineárních rovnic motivace Využívají se napřklad při analytickém vyšetřování vzájemné polohy dvou přímek v rovině a prostoru. Při řešení některých slovních
Beáta Stehlíková Časové rady, FMFI UK, 2013/2014. CvičenievR-kuI.:ARIMAmodely p.1/15
 Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
. je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy platit = 0
 Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Příklad 1 Určete definiční obor funkce: a) = b) = c) = d) = e) = 9 f) = Řešení 1a Máme určit definiční obor funkce =. Výraz je zlomkem. Ten je smysluplný pro jakýkoli jmenovatel různý od nuly. Musí tedy
Jednoduchá exponenciální rovnice
 Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Nerovnice. Vypracovala: Ing. Stanislava Kaděrková
 Nerovnice Vypracovala: Ing. Stanislava Kaděrková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů
Nerovnice Vypracovala: Ing. Stanislava Kaděrková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
a a
 1.. Cíle V této kapitole se naučíme určovat zejména celočíselné kořeny některých polynomů. Výklad Při výpočtu hodnoty polynomu n k p( x) = ak x n-tého stupně n 1 v bodě x 0 C k = 0 musíme provést ( n 1)
1.. Cíle V této kapitole se naučíme určovat zejména celočíselné kořeny některých polynomů. Výklad Při výpočtu hodnoty polynomu n k p( x) = ak x n-tého stupně n 1 v bodě x 0 C k = 0 musíme provést ( n 1)
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV
 CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ MS EXCEL. 1. Zadáme prvky matice A a B do buniek pracovného hárku zošita MS Excel
 RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Lineární funkce, rovnice a nerovnice
 Lineární funkce, rovnice a nerovnice 1. Lineární funkce 1.1 Základní pojmy Pojem lineární funkce Funkce je předpis, který každému číslu x z definičního oboru funkce přiřadí právě jedno číslo y Obecně je
Lineární funkce, rovnice a nerovnice 1. Lineární funkce 1.1 Základní pojmy Pojem lineární funkce Funkce je předpis, který každému číslu x z definičního oboru funkce přiřadí právě jedno číslo y Obecně je
Multiplexor a demultiplexor
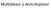 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: geometrická posloupnost, geometrická
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: geometrická posloupnost, geometrická
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
Pravdepodobnosť. Rozdelenia pravdepodobnosti
 Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Využitie programu Derive 6 pri vyučovaní lineárnych funkcií
 Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ RNDr. Mária Kredátusová, PhD. Využitie programu Derive 6 pri vyučovaní lineárnych funkcií Osvedčená pedagogická
Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ RNDr. Mária Kredátusová, PhD. Využitie programu Derive 6 pri vyučovaní lineárnych funkcií Osvedčená pedagogická
Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: =, 0 = 1 = 1. ln = +,
 Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
Lineární rovnice. Rovnice o jedné neznámé. Rovnice o jedné neznámé x je zápis ve tvaru L(x) = P(x), kde obě strany tvoří výrazy s jednou neznámou x.
 Lineární rovnice Rovnice je zápis rovnosti mezi dvěma algebraickými výrazy, které obsahují alespoň jednu proměnnou, kterou nazýváme neznámá. Rovnice má levou stranu L a pravou stranu P. Rovnost pak zapisujeme
Lineární rovnice Rovnice je zápis rovnosti mezi dvěma algebraickými výrazy, které obsahují alespoň jednu proměnnou, kterou nazýváme neznámá. Rovnice má levou stranu L a pravou stranu P. Rovnost pak zapisujeme
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
