Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
|
|
|
- Ludvík Soukup
- před 5 lety
- Počet zobrazení:
Transkript
1 Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
2 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často označuje řeckým písmenem Σ(velké sigma). Definice Slovo v dané abecedě je libovolná konečná posloupnost symbolů z této abecedy. Příklad 1: Σ = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} Slova v abecedě Σ: AHOJ ABRACADABRA ERROR Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
3 Abeceda a slovo Příklad 2: Σ 2 = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z, } Slovovabecedě Σ 2 : HELLO WORLD Příklad 3: Σ 3 = {0,1,2,3,4,5,6,7,8,9} Slovavabecedě Σ 3 : 0, ,65536 Příklad 4: Slovavabecedě Σ 4 = {0,1}: ,111, Příklad 5: Slovavabecedě Σ 5 = {a,b}:aababb,abbabbba,aaab Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
4 Abeceda a slovo Příklad 6: Abeceda Σ 6 jemnožinavšechasciiznaků. Příklad slova: class HelloWorld { public static void main(string[] args) { System.out.println("Hello, world!"); } } class HelloWorld { public static void main(str Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
5 Teorie formálních jazyků motivace Jazyk množina(některých) slov tvořených symboly z dané abecedy Příklady typů problémů, při jejichž řešení se využívá poznatků z teorie formálních jazyků: Tvorba překladačů: lexikální analýza syntaktická analýza Vyhledávání v textu: hledání zadaného vzorku hledání textu zadaného regulárním výrazem Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
6 Práce s formálními jazyky Když chceme nějaký jazyk popsat, máme několik možností: Můžeme vyjmenovat všechna jeho slova(což je ale použitelné jen pro malé konečné jazyky). Příklad: L = {aab, babba, aaaaaa} Můžeme specifikovat nějakou vlastnost, kterou mají právě ta slova, která do tohoto jazyka patří: Příklad: Jazyk nad abecedou {0, 1}, obsahující všechna slova, ve kterých je počet výskytů symbolu 1 sudý. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
7 Práce s formálními jazyky V teorii formálních jazyků se používají především následující dva přístupy: Popsat(idealizovaný) stroj, zařízení, algoritmus, který rozpozná slova patřící do daného jazyka vede k použití tzv. automatů. Popsat nějaký mechanismus umožňující generovat všechna možná slovapatřícídodanéhojazyka vedektzv.gramatikáma regulárním výrazům. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
8 Některé základní pojmy Délkaslovajepočetznakůveslově. Například délka slova abaab je 5. Délkuslovawoznačujeme w. Pokudtedynapř.w =abaab,pak w =5. Početvýskytůznakuaveslověwoznačujeme w a. Proslovow =ababbtedyplatí w a =2a w b =3. Prázdné slovo je slovo délky 0, tj. neobsahující žádné znaky. Prázdné slovo se označuje řeckým písmenem ε(epsilon). (Pozn.: V literatuře se pro označení prázdného slova někdy používá místo symbolu ε řecké písmeno λ(lambda).) ε =0 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
9 Zřetězení slov Se slovy je možné provádět operaci zřetězení: Například zřetězením slov OST a RAVA vznikne slovo OSTRAVA. Operace zřetězení se označuje symbolem (podobně jako násobení). Tento symbol je možné vypouštět. OST RAVA =OSTRAVA Zřetězeníjeasociativní,tj.prolibovolnátřislovau,vawplatí (u v) w =u (v w) což znamená, že při zápisu více zřetězení můžeme vypouštět závorky a psátnapříkladw 1 w 2 w 3 w 4 w 5 místo (w 1 (w 2 w 3 )) (w 4 w 5 ). Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
10 Zřetězení slov Zřetězení není komutativní, tj. obecně pro dvojici slov u a v neplatí rovnost u v =v u Příklad: OST RAVA RAVA OST Zjevněprolibovolnáslovavawplatí: v w = v + w Pro libovolné slovo w také platí: ε w =w ε =w Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
11 Prefixy, sufixy a podslova Definice Slovoxjeprefixemslovay,jestližeexistujeslovovtakové,žey =xv. Slovoxjesufixemslovay,jestližeexistujeslovoutakové,žey =ux. Slovoxjepodslovemslovay,jestližeexistujíslovauavtaková,že y =uxv. Příklad: Prefixyslovaabaabjsou ε,a,ab,aba,abaa,abaab. Sufixyslovaabaabjsou ε,b,ab,aab,baab,abaab. Podslovaslovaabaabjsou ε,a,b,ab,ba,aba,baa,aab,abaa, baab, abaab. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
12 Jazyk Množinuvšechslovtvořenýchsymbolyzabecedy Σoznačujeme Σ. Definice (Formální) jazyk L v abecedě Σ je nějaká libovolná podmnožina množiny Σ,tj.L Σ. Příklad1:Množina {00,01001,1101}jejazykvabecedě {0,1}. Příklad 2: Množina všech syntakticky správných programů v jazyce C je jazyk v abecedě tvořené množinou všech ASCII znaků. Příklad 3: Množina všech textů obsahujících sekvenci znaků ahoj je jazyk v abecedě tvořené množinou všech ASCII znaků. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
13 Množinové operace na jazycích Vzhledem k tomu, že jazyky jsou množiny, můžeme s nimi provádět množinové operace: Sjednocení L 1 L 2 jejazyktvořenýslovy,kterápatříbuďdojazykal 1 nebodojazykal 2 (nebodoobou). Průnik L 1 L 2 jejazyktvořenýslovy,kterápatřísoučasnědojazyka L 1 idojazykal 2. Doplněk L 1 jejazyktvořenýtěmislovyze Σ,kteránepatřídoL 1. Rozdíl L 1 L 2 jejazyktvořenýslovy,kterápatřídol 1,alenepatří dol 2. Poznámka: Při operacích nad jazyky předpokládáme, že jazyky, se kterými operaci provádíme, používají tutéž abecedu Σ. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
14 Množinové operace na jazycích Formálně: Sjednocení:L 1 L 2 = {w Σ w L 1 w L 2 } Průnik:L 1 L 2 = {w Σ w L 1 w L 2 } Doplněk:L 1 = {w Σ w L 1 } Rozdíl:L 1 L 2 = {w Σ w L 1 w L 2 } Poznámka:Předpokládáme,žeL 1,L 2 Σ pronějakoudanouabecedu Σ. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
15 Množinové operace na jazycích Příklad: Uvažujme jazyky nad abecedou {a, b}. Pak L 1 množinavšechslovobsahujícíchpodslovobaa L 2 množinavšechslovsesudýmpočtemvýskytůsymbolub L 1 L 2 množinavšechslovobsahujícíchpodslovobaanebosudý počet symbolů b L 1 L 2 množinavšechslovobsahujícíchpodslovobaaasudý počet symbolů b L 1 množinavšechslov,kteráneobsahujípodslovobaa L 1 L 2 množinavšechslov,vekterýchsevyskytujepodslovobaa, alekdepočetsymbolůbnenísudý Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
16 Zřetězení jazyků Definice ZřetězeníjazykůL 1 al 2,kdeL 1,L 2 Σ,jejazykL Σ takový,že prokaždéw Σ platí w L ( u L 1 )( v L 2 )(w =u v) ZřetězeníjazykůL 1 al 2 označujemel 1 L 2. Příklad: L 1 = {abb,ba} L 2 = {a,ab,bbb} JazykL 1 L 2 obsahujeslova: abba abbab abbbbb baa baab babbb Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
17 Iterace jazyka Definice IteracejazykaL,označovanázápisemL,jejazyktvořenýslovyvzniklými zřetězením libovolného počtu slov z jazyka L. Tj.w L právětehdy,když n N : w 1,w 2,...,w n L:w =w 1 w 2 w n Příklad:L = {aa,b} L = {ε,aa,b,aaaa,aab,baa,bb,aaaaaa,aaaab,aabaa,aabb,...} Poznámka: Počet slov, která zřetězujeme, může být i 0, což znamená, že vždyplatí ε L (bezohledunato,zda ε Lnebone). Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
18 Iterace jazyka alternativní definice NejprvedefinujemeprojazykLačíslok NjazykL k : L 0 = {ε}, L k =L k 1 L prok 1 To znamená L 0 = {ε} L 1 = L L 2 = L L L 3 = L L L L 4 = L L L L L 5 = L L L L L... Příklad:ProL = {aa,b}jazykl 3 obsahujenásledujícíslova: aaaaaa aaaab aabaa aabb baaaa baab bbaa bbb Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
19 Iterace jazyka alternativní definice Alternativní definice Iterace jazyka L je jazyk L = k 0 L k Poznámka: L k =L 0 L 1 L 2 L 3 k 0 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
20 Iterace jazyka Poznámka:PoužívásetakézápisL + jakozkratkaza L L,tj. L + = k 1 L k Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
21 Zrcadlový obraz Zrcadlovýobrazslovawjeslovowzapsané pozpátku. Zrcadlovýobrazslovawznačímew R. Příklad: w =AHOJ w R =JOHA Formálněmůžemedefinovat,žeprow =a 1 a 2 a n (kdea i Σ)je w R =a n a n 1 a 1. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
22 Zrcadlový obraz Zrcadlový obraz jazyka L je jazyk tvořený zrcadlovými obrazy všech slov zjazykal. ZrcadlovýobrazjazykaLznačímeL R. L R = {w R w L} Příklad: L = {ab,baaba,aaab} L R = {ba,abaab,baaa} Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
23 Uspořádání na slovech Předpokládejme určité(lineární) uspořádání < symbolů abecedy Σ, tj.pokud Σ = {a 1,a 2,...,a n },takplatí a 1 <a 2 <... <a n. Příklad: Σ = {a,b,c},přičemža <b <c. Namnožině Σ můžemedefinovatnásledující(lineární)uspořádání < L : x < L yprávětehdy,když: x < y,nebo x = y aexistujíslovau,v,w Σ asymbolya,b Σtakové,že platí x =uav y =ubw a <b Neformálněmůžemeříctvuspořádání < L řadímeslovapodledélkya v rámci stejné délky lexikograficky(podle abecedy). Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
24 Uspořádání na slovech Všechnaslovanadabecedou Σmůžemepomocíuspořádání < L seřaditdo posloupnosti w 0,w 1,w 2,... vekterésekaždéslovow Σ vyskytujeprávějednouakdeprolibovolná i,j Nplatí,žew i < L w j právětehdy,kdyži <j. Příklad:Proabecedu Σ = {a,b,c}(kdea <b <c)budezačátek posloupnosti vypadat následovně: ε,a,b,c,aa,ab,ac,ba,bb,bc,ca,cb,cc,aaa,aab,aac,aba,abb,abc,... PokudbudememluvitnapříkladoprvníchdesetislovechjazykaL Σ, mámetímnamyslidesetslov,kterápatřídojazykalajsoumezivšemi slovyzjazykalnejmenšívzhledemkuspořádání < L. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
25 Regulární výrazy Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
26 Regulární výrazy Regulární výrazy popisující jazyky nad abecedou Σ:, ε,a(kdea Σ)jsouregulárnívýrazy:... označujeprázdnýjazyk ε... označujejazyk {ε} a... označujejazyk {a} Jestliže α, βjsouregulárnívýrazy,paki(α+β), (α β), (α )jsou regulární výrazy: (α+β)... označujesjednoceníjazykůoznačených αaβ (α β)... označujezřetězeníjazykůoznačených αaβ (α )... označujeiteracijazykaoznačeného α Neexistují žádné další regulární výrazy než ty definované podle předchozích dvou bodů. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
27 Regulární výrazy Příklad: abeceda Σ = {0,1} Podledefinicejsou0i1regulárnívýrazy. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
28 Regulární výrazy Příklad: abeceda Σ = {0,1} Podledefinicejsou0i1regulárnívýrazy. Protože0i1jsouregulárnívýrazy,jei(0+1)regulárnívýraz. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
29 Regulární výrazy Příklad: abeceda Σ = {0,1} Podledefinicejsou0i1regulárnívýrazy. Protože0i1jsouregulárnívýrazy,jei(0+1)regulárnívýraz. Protože0jeregulárnívýraz,jei(0 )regulárnívýraz. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
30 Regulární výrazy Příklad: abeceda Σ = {0,1} Podledefinicejsou0i1regulárnívýrazy. Protože0i1jsouregulárnívýrazy,jei(0+1)regulárnívýraz. Protože0jeregulárnívýraz,jei(0 )regulárnívýraz. Protože (0+1)i(0 )jsouregulárnívýrazy,jei((0+1) (0 )) regulární výraz. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
31 Regulární výrazy Příklad: abeceda Σ = {0,1} Podledefinicejsou0i1regulárnívýrazy. Protože0i1jsouregulárnívýrazy,jei(0+1)regulárnívýraz. Protože0jeregulárnívýraz,jei(0 )regulárnívýraz. Protože (0+1)i(0 )jsouregulárnívýrazy,jei((0+1) (0 )) regulární výraz. Poznámka: Jestliže α je regulární výraz, zápisem [α] označujeme jazyk definovaný regulárním výrazem α. [((0+1) (0 ))] = {0,1,00,10,000,100,0000,1000,00000,...} Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
32 Regulární výrazy Strukturu regulárního výrazu si můžeme znázornit abstraktním syntaktickým stromem: (((((0 1) ) 1) (1 1))+(((0 0)+1) )) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
33 Regulární výrazy Popis(abstraktní) syntaxe regulárních výrazů pomocí Backus-Naurovy formy: α ::= ε a α α α α+α Formální definice sémantiky regulárních výrazů: [ ] = [ε] = {ε} [a] = {a} [α ] = [α] [α β] = [α] [β] [α+β] = [α] [β] Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
34 Regulární výrazy Aby byl zápis regulárních výrazů přehlednější a stručnější, používáme následují pravidla: Vynecháváme vnější pár závorek. Vynecháváme závorky, které jsou zbytečné vzhledem k asociativitě operací sjednocení(+) a zřetězení( ). Vynecháváme závorky, které jsou zbytečné vzhledem k prioritě operací (nejvyššíprioritumáiterace( ),menšízřetězení( )anejmenší sjednocení(+)). Nepíšeme tečku pro zřetězení. Příklad: Místo obvykle píšeme (((((0 1) ) 1) (1 1))+(((0 0)+1) )) (01) 111+(00+1) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
35 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem0 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
36 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem01 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
37 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a1 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
38 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a jazyktvořenýslovy ε,0,00,000,... Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
39 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a jazyktvořenýslovy ε,0,00,000,... (01)... jazyktvořenýslovy ε,01,0101,010101,... Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
40 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a jazyktvořenýslovy ε,0,00,000,... (01)... jazyktvořenýslovy ε,01,0101,010101,... (0+1)... jazyktvořenývšemislovynadabecedou {0,1} Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
41 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a jazyktvořenýslovy ε,0,00,000,... (01)... jazyktvořenýslovy ε,01,0101,010101,... (0+1)... jazyktvořenývšemislovynadabecedou {0,1} (0+1) jazyktvořenývšemislovykončícími00 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
42 Regulární výrazy Příklady:Vevšechpřípadech Σ = {0,1} jazyktvořenýjedinýmslovem jazyktvořenýjedinýmslovem jazyktvořenýdvěmaslovy0a jazyktvořenýslovy ε,0,00,000,... (01)... jazyktvořenýslovy ε,01,0101,010101,... (0+1)... jazyktvořenývšemislovynadabecedou {0,1} (0+1) jazyktvořenývšemislovykončícími00 (01) 111(01)... jazyktvořenývšemislovyobsahujícímipodslovo111 předcházené i následované libovolným počtem slov 01 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
43 Regulární výrazy (0+1) 00+(01) 111(01)... jazyktvořenývšemislovy,kterábuď končí 00 nebo obsahují podslovo 111 předcházené i následované libovolným počtem slov 01 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
44 Regulární výrazy (0+1) 00+(01) 111(01)... jazyktvořenývšemislovy,kterábuď končí 00 nebo obsahují podslovo 111 předcházené i následované libovolným počtem slov 01 (0+1) 1(0+1)...jazyktvořenývšemislovyobsahujícímialespoň jeden symbol 1 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
45 Regulární výrazy (0+1) 00+(01) 111(01)... jazyktvořenývšemislovy,kterábuď končí 00 nebo obsahují podslovo 111 předcházené i následované libovolným počtem slov 01 (0+1) 1(0+1)...jazyktvořenývšemislovyobsahujícímialespoň jeden symbol 1 0 (10 10 )... jazyktvořenývšemislovyobsahujícímisudýpočet symbolů 1 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
46 Konečné automaty Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
47 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
48 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
49 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
50 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
51 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
52 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
53 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
54 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
55 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
56 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
57 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
58 Rozpoznávání jazyka Příklad: Uvažujme slova nad abecedou {0, 1}. Chtěli bychom rozpoznávat jazyk L, který je tvořen slovy, ve kterých se vyskytuje sudý počet symbolů 1. Chceme navrhnout zařízení, které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine ANO Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
59 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
60 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
61 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
62 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
63 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
64 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
65 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
66 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
67 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
68 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
69 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
70 Rozpoznávání jazyka První nápad: Počítat počet výskytů symbolů ANO 6jesudéčíslo Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
71 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
72 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
73 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
74 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
75 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
76 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
77 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
78 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
79 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
80 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
81 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
82 Rozpoznávání jazyka Druhý nápad: Ve skutečnosti nás zajímá pouze, zda počet dosud přečtených symbolů 1 je sudý nebo lichý(tj. místo čísla si stačí pamatovat jen jeho poslední bit) S ANO Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
83 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: S L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
84 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
85 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S 1 L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
86 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S 1 0 L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
87 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
88 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
89 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
90 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
91 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
92 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
93 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
94 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
95 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
96 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
97 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
98 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
99 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
100 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L L Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
101 Rozpoznávání jazyka Chovaní tohoto zařízení můžeme popsat grafem: 0 S L S Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
102 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b Deterministický konečný automat se skládá ze stavů a přechodů. Jedenzestavůjeoznačenjakopočátečnístavaněkterézestavůjsou označeny jako přijímající. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
103 Deterministický konečný automat Formálně je deterministický konečný automat(dka) definován jako pětice (Q,Σ,δ,q 0,F) kde: Q je neprázdná konečná množina stavů Σ je abeceda(neprázdná konečná množina symbolů) δ :Q Σ Qjepřechodováfunkce q 0 Qjepočátečnístav F Qjemnožinapřijímajícíchstavů Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
104 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b Q = {1,2,3,4,5} Σ = {a,b} q 0 =1 F = {1,4,5} δ(1,a) =2 δ(1,b) =1 δ(2,a) =4 δ(2,b) =5 δ(3,a) =1 δ(3,b) =4 δ(4,a) =1 δ(4,b) =3 δ(5,a) =4 δ(5,b) =5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
105 Deterministický konečný automat Místo zápisu δ(1,a) =2 δ(1,b) =1 δ(2,a) =4 δ(2,b) =5 δ(3,a) =1 δ(3,b) =4 δ(4,a) =1 δ(4,b) =3 δ(5,a) =4 δ(5,b) =5 budeme raději používat stručnější tabulku nebo grafické znázornění: δ a b Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
106 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 1 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
107 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 a 2 2 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
108 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 a 2 b 5 5 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
109 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 a 2 b 5 a 4 4 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
110 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 a 2 b 5 a 4 b 3 3 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
111 Deterministický konečný automat b a 1 2 b a a a b 3 4 b a 5 b a b a b b 1 a 2 b 5 a 4 b 3 b 4 4 Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
112 Deterministický konečný automat Definice MějmeDKAA = (Q,Σ,δ,q 0,F). Zápisemq w q,kdeq,q Qaw Σ,budemeoznačovatto,že pokudjeautomatvestavuq,takpřečtenímslovawpřejdedostavuq. Poznámka: Q Σ Qjeternárnírelace. Místo (q,w,q ) píšemeq w q. ProDKAplatí,žeprolibovolnýstavqalibovolnéslovowexistujeprávě jedenstavq takový,žeq q w. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
113 Deterministický konečný automat Relaci můžeme formálně definovat následující induktivní definicí: q ε qprolibovolnéq Q Proa Σaw Σ : q aw q w q právětehdy,kdyžexistujeq Qtakové,že δ(q,a) =q a q. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
114 Deterministický konečný automat Slovow Σ jepřijímánodeterministickýmkonečnýmautomatem A = (Q,Σ,δ,q 0,F)právětehdy,kdyžexistujestavq Ftakový,že w q 0 q. Definice Jazyk rozpoznávaný(přijímaný) daným deterministickým konečným automatema = (Q,Σ,δ,q 0,F),označovanýL(A),jemnožinavšechslov přijímaných tímto automatem, tj. L(A) = {w Σ q F :q 0 w q} Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
115 Regulární jazyky Definice Jazyk L je regulární právě tehdy, když existuje nějaký deterministicý konečnýautomata,kterýjejpřijímá,tj.dkaa,takový,žel(a) =L. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
116 Ekvivalence automatů b b b a a a b b b a 1 2 a 3 a b b a 1 2 a Všechny 3 automaty přijímají jazyk všech slov se sudým počtem a. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
117 Ekvivalence automatů Definice OkonečnýchautomatechA 1,A 2 řekneme,žejsouekvivalentní,jestliže L(A 1 ) =L(A 2 ). Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
118 Nedosažitelné stavy automatu b a a a a b b b a b a,b AutomatpřijímájazykL = {w {a,b} wobsahujepodslovoab} Pro žádnou posloupnost vstupních symbolů se automat nedostane do stavů3,4nebo5.. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
119 Nedosažitelné stavy automatu b a a 1 2 b 6 a,b AutomatpřijímájazykL = {w {a,b} wobsahujepodslovoab} Pro žádnou posloupnost vstupních symbolů se automat nedostane do stavů3,4nebo5. Pokud tyto stavy odstraníme, pořád automat přijímá stejný jazyk L. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
120 Nedosažitelné stavy automatu Definice StavqkonečnéhoautomatuA = (Q,Σ,δ,q 0,F)jedosažitelnýpokud existujenějakéslovowtakové,žeq 0 w q. V opačném případě stav nazýváme nedosažitelný. Do nedosažitelných stavů nevede v grafu automatu žádná orientovaná cesta z počátečního stavu. Nedosažitelné stavy můžeme z automatu odstranit(spolu se všemi přechody vedoucími do nich a z nich). Jazyk přijímaný automatem se nezmění. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 2. března / 32
Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 2. března 2017 1/ 32 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často
Regulární výrazy. M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 14. března / 20
Regulární výrazy M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 14. března 2007 1/ 20 Regulární výrazy Jako například v aritmetice můžeme pomocí operátorů + a vytvářet výrazy jako (5+3)
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 7. března / 46
Formální jzyky Z. Sw (VŠB-TUO) Úvod do teoretické informtiky 7. řezn 2012 1/ 46 Teorie formálních jzyků motivce Příkldy typů prolémů, při jejichž řešení se využívá pozntků z teorie formálních jzyků: Tvor
Množinu všech slov nad abecedou Σ značíme Σ * Množinu všech neprázdných slov Σ + Jazyk nad abecedou Σ je libovolná množina slov nad Σ
Abecedou se rozumí libovolná konečná množina Σ. Prvky abecedy nazýváme znaky (symboly) Slovo (řetězec) v nad abecedou Σ je libovolná konečná posloupnost znaků této abecedy. Prázdné posloupnosti znaků odpovídá
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Naproti tomu gramatika je vlastně soupis pravidel, jak
1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
Regulární výrazy. Definice Množina regulárních výrazů nad abecedou Σ, označovaná RE(Σ), je definována induktivně takto:
IB102 Automaty, gramatiky a složitost, 6. 10. 2014 1/29 Regulární výrazy Definice 2.58. Množina regulárních výrazů nad abecedou Σ, označovaná RE(Σ), je definována induktivně takto: 1 ε, a a pro každé a
Z. Sawa (VŠB-TUO) Teoretická informatika 5. listopadu / 43
Zásobníkové automaty Z. Sawa (VŠB-TUO) Teoretická informatika 5. listopadu 2018 1/ 43 Zásobníkový automat Chtěli bychom rozpoznávat jazyk L = {a i b i i 1} Snažíme se navrhnout zařízení (podobné konečným
Predikátová logika 1. řádu shrnutí
Predikátová logika 1. řádu shrnutí Symboly: Syntaxe: Logické symboly: proměnné:x Var,kdeVar = {x 0,x 1,x 2,...} logickéspojky:,,,, kvantifikátory:, závorky: ), ( symbol pro rovnost: = Mimologickésymboly
Automaty a gramatiky(bi-aag) Motivace. 1. Základní pojmy. 2 domácí úkoly po 6 bodech 3 testy za bodů celkem 40 bodů
BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 2/29 Hodnocení předmětu BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 4/29 Automaty a gramatiky(bi-aag) 1. Základní pojmy Jan Holub Katedra teoretické
Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i,
[161014-1204 ] 11 2.1.35 Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i, kde i = 0, 1,..., takto: p 0 q právě tehdy, když bud p, q F nebo p, q F. Dokud i+1 i konstruujeme p
Zásobníkový automat. SlovoaaaabbbbpatřídojazykaL={a i b i i 1} a a a a b b b b
ChtělibychomrozpoznávatjazykL={a i b i i 1} Snažíme se navrhnout zařízení(podobné konečným automatům), které přečte slovo, a sdělí nám, zda toto slovo patřídojazykalčine. Při čtení a-ček si musíme pamatovat
Turingovy stroje. Teoretická informatika Tomáš Foltýnek
Turingovy stroje Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Jaké znáte algebraické struktury s jednou operací? Co je to okruh,
AUTOMATY A GRAMATIKY
AUTOMATY A 1 GRAMATIKY Pavel Surynek Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra teoretické informatiky a matematické logiky Stručný přehled přednášky Automaty Formální jazyky, operace
Pumping lemma - podstata problému. Automaty a gramatiky(bi-aag) Pumping lemma - problem resolution. Pumping lemma - podstata problému
BI-AAG (2011/2012) J. Holub: 10. Vlastnosti regulárních jazyků p. 2/22 Pumping lemma - podstata problému BI-AAG (2011/2012) J. Holub: 10. Vlastnosti regulárních jazyků p. 4/22 Automaty a gramatiky(bi-aag)
/1: Teoretická informatika(ti) přednáška 4
456-330/1: Teoretická informatika(ti) přednáška 4 prof. RNDr Petr Jančar, CSc. katedra informatiky FI VŠB-TUO www.cs.vsb.cz/jancar LS 2009/2010 Petr Jančar (FI VŠB-TU) Teoretická informatika(ti) LS 2009/2010
Minimalizace KA - Úvod
Minimalizace KA - Úvod Tyto dva KA A,A2 jsou jazykově ekvivalentní, tzn. že rozpoznávají tentýž jazyk. L(A) = L(A2) Názorně lze vidět, že automat A2 má menší počet stavů než A, tudíž našim cílem bude ukázat
Teoretická informatika průběh výuky v semestru 1
Teoretická informatika průběh výuky v semestru 1 Týden 1 Po přednášce 14.9. bude text asi mírně modifikován, ale příklady na cvičení se nezmění. (Navíc dodám na web slidy.) Přednáška Na začátku jsme si
Naproti tomu gramatika je vlastně soupis pravidel, jak
1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
Formální jazyky a automaty Petr Šimeček
Formální jazyky a automaty Petr Šimeček Úvod Formální jazyky a automaty jsou základním kamenem teoretické informatiky. Na počátku se zmíníme o Chomského klasifikaci gramatik, nástroje, který lze aplikovat
Výpočetní modely pro rozpoznávání bezkontextových jazyků zásobníkové automaty LL(k) a LR(k) analyzátory
Plán přednášky Výpočetní modely pro rozpoznávání bezkontextových jazyků zásobníkové automaty LL(k) a LR(k) analyzátory Obecný algoritmus pro parsování bezkontextových jazyků dynamické programování 1 Zásobníkový
Formální jazyky a gramatiky Teorie programovacích jazyků
Formální jazyky a gramatiky Teorie programovacích jazyků doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Připomenutí základních pojmů ABECEDA jazyk je libovolná podmnožina
Základy teoretické informatiky Formální jazyky a automaty
Základy teoretické informatiky Formální jazyky a automaty Petr Osička KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI Outline Literatura Obsah J.E. Hopcroft, R. Motwani, J.D. Ullman Introduction to
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
2 Formální jazyky a gramatiky
2 Formální jazyky a gramatiky 2.1 Úvod Teorie formálních gramatik a jazyků je důležitou součástí informatiky. Její využití je hlavně v oblasti tvorby překladačů, kompilátorů. Vznik teorie se datuje přibližně
Množiny. množinové operace jsou mírně odlišné od
Množiny Množina se dá chápat jako soubor prvků. ( Např. lidé na planetě zemi tvoří jednu velkou množinu.) Každá množina tedy obsahuje určitý počet prvků, který může být konečný (lze spočítat) nebo nekonečný
AUTOMATY A GRAMATIKY. Pavel Surynek. Kontextové uzávěrové vlastnosti Turingův stroj Rekurzivně spočetné jazyky Kódování, enumerace
AUTOMATY A 11 GRAMATIKY Pavel Surynek Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra teoretické informatiky a matematické logiky Kontextové uzávěrové vlastnosti Turingův stroj Rekurzivně
/01: Teoretická informatika(ti) přednáška 5
460-4005/01: Teoretická informatika(ti) přednáška 5 prof. RNDr Petr Jančar, CSc. katedra informatiky FEI VŠB-TUO www.cs.vsb.cz/jancar LS 2010/2011 Petr Jančar (FEI VŠB-TU) Teoretická informatika(ti) LS
Úvod do informatiky. Miroslav Kolařík
Úvod do informatiky přednáška desátá Miroslav Kolařík Zpracováno dle R. Bělohlávek, V. Vychodil: Diskrétní matematika 2, http://phoenix.inf.upol.cz/esf/ucebni/dm2.pdf P. Martinek: Základy teoretické informatiky,
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ PŘÍRODOVĚDECKÁ FAKULTA
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ PŘÍRODOVĚDECKÁ FAKULTA BAKALÁŘSKÁ PRÁCE 2002 SEDLÁK MARIAN - 1 - OSTRAVSKÁ UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA KATEDRA INFORMATIKY A POČÍTAČŮ Vizualizace principů výpočtu konečného
Syntaxí řízený překlad
Syntaxí řízený překlad Překladový automat Šárka Vavrečková Ústav informatiky, FPF SU Opava sarka.vavreckova@fpf.slu.cz Poslední aktualizace: 27. listopadu 2008 Zobecněný překladový automat Překladový automat
Bezkontextové jazyky. Bezkontextové jazyky 1 p.1/39
Bezkontextové jazyky Bezkontextové jazyky 1 p.1/39 Jazyky typu 2 Definice 4.1 Gramatika G = (N, Σ, P, S) si nazývá bezkontextovou gramatikou, jestliže všechna pravidla z P mají tvar A α, A N, α (N Σ) Lemma
Bezkontextové gramatiky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 6. května / 49
Bezkontextové gramatiky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 6. května 2018 1/ 49 Bezkontextové gramatiky Příklad: Chtěli bychom popsat jazyk aritmetických výrazů obsahující výrazy jako například:
Vlastnosti regulárních jazyků
Vlastnosti regulárních jazyků Podobně jako u dalších tříd jazyků budeme nyní zkoumat následující vlastnosti regulárních jazyků: vlastnosti strukturální, vlastnosti uzávěrové a rozhodnutelné problémy pro
: Teoretická informatika(ti)
460-4065: Teoretická informatika(ti) prof. RNDr Petr Jančar, CSc. katedra informatiky FEI VŠB-TUO www.cs.vsb.cz/jancar Petr Jančar (FEI VŠB-TU) Teoretická informatika(ti) 460-4065 1/ 25 Základní informace
Vyhledávání v textu. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava
Vyhledávání v textu doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 9. března 209 Jiří Dvorský (VŠB TUO) Vyhledávání v textu 402
0. ÚVOD - matematické symboly, značení,
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Teoretická informatika - Úkol č.1
Teoretická informatika - Úkol č.1 Lukáš Sztefek, xsztef01 18. října 2012 Příklad 1 (a) Gramatika G 1 je čtveřice G 1 = (N, Σ, P, S) kde, N je konečná množina nonterminálních symbolů N = {A, B, C} Σ je
Kapitola 6. LL gramatiky. 6.1 Definice LL(k) gramatik. Definice 6.3. Necht G = (N, Σ, P, S) je CFG, k 1 je celé číslo.
Kapitola 6 LL gramatiky 6.1 Definice LL(k) gramatik Definice 6.1. Necht G = (N, Σ, P, S) je CFG, k 1 je celé číslo. Definujme funkci FIRST G k : (N Σ) + P({w Σ w k}) předpisem FIRST G k (α) = {w Σ (α w
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Formální jazyky. M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 6. března / 48
Formální jzyky M. Kot, Z. Sw (VŠB-TU Ostrv) Úvod do teoretické informtiky 6. březn 2007 1/ 48 Motivce 1: Vyhledávání v textu Potřebujeme řešit následující problém: Máme řdu různých textů(npř. soubory n
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
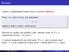Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
LIMITA A SPOJITOST FUNKCE
PŘEDNÁŠKA 5 LIMITA A SPOJITOST FUNKCE 5.1 Spojitost funkce 2 Řekneme, že funkce f(x) je spojitá v bodě a D f, jestliže ke každému ε > 0 existuje δ > 0 takové, že pro každé x (a δ, a + δ) D f platí nerovnost:
Vztah jazyků Chomskeho hierarchie a jazyků TS
Vztah jazyků Chomskeho hierarchie a jazyků TS Jan Konečný; (přednáší Lukáš Havrlant) 15. října 2013 Jan Konečný; (přednáší Lukáš Havrlant) Chomskeho hierarchie a jazyky TS 15. října 2013 1 / 23 Rychlé
Bezkontextové jazyky 2/3. Bezkontextové jazyky 2 p.1/27
Bezkontextové jazyky 2/3 Bezkontextové jazyky 2 p.1/27 Transformace bezkontextových gramatik Bezkontextové jazyky 2 p.2/27 Ekvivalentní gramatiky Definice 6.1 Necht G 1 a G 2 jsou gramatiky libovolného
Úvod do programovacích jazyků (Java)
Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/ Množiny, funkce
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 2. Množiny, funkce MNOŽIN, ZÁKLDNÍ POJMY Pojem množiny patří v matematice ke stěžejním. Nelze jej zavést ve formě definice pomocí
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
Úvod do informatiky přednáška čtvrtá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Pojem relace 2 Vztahy a operace s (binárními) relacemi
Deterministický konečný automat
Deterministický konečný utomt Formálně je deterministický konečný utomt definován jko pětice (Q,Σ,δ,q 0,F) kde: Q je konečná množin stvů Σ je konečná eced δ:q Σ Qjepřechodováfunkce q 0 Qjepočátečnístv
Cvičení 1. Úvod do teoretické informatiky(2014/2015) cvičení 1 1
Úvod do teoretické informatiky(2014/2015) cvičení 1 1 Cvičení 1 Příklad 1: Pro každý z následujících formálních zápisů množin uveďte(svými slovy), jaké prvky daná množina obsahuje: a) {1,3,5,7,...} b)
Automaty a gramatiky(bi-aag) Formální překlady. 5. Překladové konečné automaty. h(ε) = ε, h(xa) = h(x)h(a), x, x T, a T.
BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
Základní pojmy. Úvod do programování. Základní pojmy. Zápis algoritmu. Výraz. Základní pojmy
Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Procesor Procesorem je objekt, který vykonává algoritmem popisovanou
Algoritmizace a programování
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Jednoznačné a nejednoznačné gramatiky
BI-AAG (2011/2012) J. Holub: 11. Bezkontextové gramatiky p. 2/36 Jednoznačné a nejednoznačné gramatiky BI-AAG (2011/2012) J. Holub: 11. Bezkontextové gramatiky p. 4/36 Automaty a gramatiky(bi-aag) 11.
Grafy. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 13.
Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Matice. Předpokládejme, že A = (a ij ) je matice typu m n: diagonálou jsou rovny nule.
Matice Definice. Maticí typu m n nazýváme obdélníkové pole, tvořené z m n reálných čísel (tzv. prvků matice), zapsaných v m řádcích a n sloupcích. Značíme např. A = (a ij ), kde i = 1,..., m, j = 1,...,
Úvod do teoretické informatiky
Úvod do teoretické informatiky Zdeněk Sawa Katedra informatiky, FEI, Vysoká škola báňská Technická universita Ostrava 17. listopadu 15, Ostrava-Poruba 708 33 Česká republika 11. února 2018 Z. Sawa (VŠB-TUO)
Teoretická informatika TIN 2013/2014
Teoretická informatika TIN 2013/2014 prof. RNDr. Milan Češka, CSc. ceska@fit.vutbr.cz doc.ing. Tomáš Vojnar, Ph.D. vojnar@fit.vutbr.cz sazba Ing. A. Smrčka, Ing. P. Erlebach, Ing. P. Novosad Vysoké učení
Teoretická informatika
Teoretická informatika TIN 2017/2018 prof. RNDr. Milan Češka, CSc. ceska@fit.vutbr.cz prof. Ing. Tomáš Vojnar, Ph.D. vojnar@fit.vutbr.cz sazba dr. A. Smrčka, Ing. P. Erlebach, Ing. P. Novosad Vysoké učení
Automaty a gramatiky
Automaty a gramatiky Roman Barták, KTIML bartak@ktiml.mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Co bylo minule Úvod do formálních gramatik produkční systémy generativní gramatika G=(V N,V T,,P) G =
Konečný automat Teorie programovacích jazyků
Konečný automat Teorie programovacích jazyků oc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@menelu.cz Automaty v běžném životě Konečný automat Metoy konstrukce konečného automatu
p 2 q , tj. 2q 2 = p 2. Tedy p 2 je sudé číslo, což ale znamená, že
KAPITOLA 1: Reálná čísla [MA1-18:P1.1] 1.1. Číselné množiny Přirozená čísla... N = {1,, 3,...} nula... 0, N 0 = {0, 1,, 3,...} = N {0} Celá čísla... Z = {0, 1, 1,,, 3,...} Racionální čísla... { p } Q =
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
Konečný automat. Jan Kybic.
Konečný automat Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 33 Konečný automat finite state machine Konečný automat = výpočetní model, primitivní počítač Řídící jednotka s
Fakulta informačních technologií. Teoretická informatika
Vysoké učení technické v Brně Fakulta informačních technologií Teoretická informatika Třetí úkol 2 Jan Trávníček . Tato úloha je řešena Turingovým strojem, který je zobrazen na obrázku, který si můžeme
Algoritmizace prostorových úloh
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
Čísla značí použité pravidlo, šipka směr postupu Analýza shora. Analýza zdola A 2 B 3 B * C 2 C ( A ) 1 a A + B. A Derivace zleva:
1) Syntaktická analýza shora a zdola, derivační strom, kanonická derivace ezkontextová gramatika gramatika typu 2 Nechť G = je gramatika typu 1. Řekneme, že je gramatikou typu 2, platí-li: y
NAIVNÍ TEORIE MNOŽIN, okruh č. 5
NAIVNÍ TEORIE MNOŽIN, okruh č. 5 Definování množiny a jejích prvků Množina je souhrn nějakých věcí. Patří-li věc do množiny X, říkáme, že v ní leží, že je jejím prvkem nebo že množina X tuto věc obsahuje.
Množiny, základní číselné množiny, množinové operace
2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
Lineární algebra : Násobení matic a inverzní matice
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. března 2014, 12:42 1 2 0.1 Násobení matic Definice 1. Buďte m, n, p N, A
V: Pro nulový prvek o lineárního prostoru L platí vlastnosti:
Zpracoval: hypspave@fel.cvut.cz. Základní vlastnosti abstraktních lineárních prostorů. Lineární závislost, nezávislost, báze, souřadnice vzhledem k bázi, matice lineárního zobrazení vzhledem k bázím.skalární
2. Množiny, funkce. Poznámka: Prvky množiny mohou být opět množiny. Takovou množinu, pak nazýváme systém množin, značí se
MNOŽIN, ZÁKLDNÍ POJMY Pojem množiny patří v matematice ke stěžejním. Nelze jej zavést ve formě definice pomocí primitivních pojmů; považuje se totiž rovněž za pojem primitivní. Představa o pojmu množina
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Výroková a predikátová logika - II
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
4.2 Syntaxe predikátové logiky
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Výroková logika. Teoretická informatika Tomáš Foltýnek
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Lineární algebra : Násobení matic a inverzní matice
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Základy maticového počtu Matice, determinant, definitnost
Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
UČEBNÍ TEXTY VYSOKÝCH ŠKOL. Prof. RNDr. Milan Češka, CSc. Gramatiky a jazyky
UČEBNÍ TEXTY VYSOKÝCH ŠKOL Vysoké učení technické v Brně Fakulta elektrotechniky a informatiky Prof. RNDr. Milan Češka, CSc. Gramatiky a jazyky Tato skripta jsou určena pro kurs Základy matematické informatiky
Lineární algebra : Lineární prostor
Lineární algebra : Lineární prostor (3. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. dubna 2014, 14:43 1 2 3.1 Aximotické zavedení lineárního prostoru Číselné těleso Celou lineární
Výroková a predikátová logika - VII
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin.
1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
Úvod do informatiky. Miroslav Kolařík
Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Operační výzkum. Síťová analýza. Metoda CPM.
Operační výzkum Síťová analýza. Metoda CPM. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2014
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 204 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Matematická analýza 1
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická logika. Miroslav Kolařík
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Základy logiky a teorie množin
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Složitost Filip Hlásek
Složitost Filip Hlásek Abstrakt. Příspěvek popisuje dva základní koncepty teoretické informatiky, Turingovy stroje a složitost. Kromě definic důležitých pojmů uvádí také několik souvisejících tvrzení,
Pravděpodobnost a její vlastnosti
Pravděpodobnost a její vlastnosti 1 Pravděpodobnost a její vlastnosti Náhodné jevy Náhodný jev je výsledek pokusu (tj. realizace určitého systému podmínek) a jeho charakteristickým rysem je, že může, ale
Algoritmizace prostorových úloh
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Algoritmus Daniela Szturcová Tento
2. Definice pravděpodobnosti
2. Definice pravděpodobnosti 2.1. Úvod: V přírodě se setkáváme a v přírodních vědách studujeme pomocí matematických struktur a algoritmů procesy dvojího druhu. Jednodušší jsou deterministické procesy,
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Katedra počítačů FEL
TIS 311 1. Navrhněte KMP vyhledávací stroj pro vzorek v = kakadu, 2. Pro stejný vzorek navrhněte deterministický konečný automat. 3. Simulujte činnost obou strojů na textu T = dukakakaduka, porovnejte
Logické operace. Datový typ bool. Relační operátory. Logické operátory. IAJCE Přednáška č. 3. může nabýt hodnot: o true o false
Logické operace Datový typ bool může nabýt hodnot: o true o false Relační operátory pravda, 1, nepravda, 0, hodnoty všech primitivních datových typů (int, double ) jsou uspořádané lze je porovnávat binární
Lexikální analýza. Rozhraní lexikálního analyzátoru. Miroslav Beneš Dušan Kolář. M. Beneš, D. Kolář: Lexikální analýza 1. Lexikální analýza 2
Lexikální analýza Miroslav Beneš Dušan Kolář Rozhraní lexikálního analyzátoru Lexikální analýza 2 M. Beneš, D. Kolář: Lexikální analýza 1 Úkoly Čtení zdrojového textu Sestavování symbolů Odstranění mezer
Programovací jazyk Pascal
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Matematická analýza pro informatiky I.
Matematická analýza pro informatiky I. 1. přednáška Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 14. února 2011 Jan Tomeček, tomecek@inf.upol.cz
Lexikální analýza. Miroslav Beneš Dušan Kolář
Lexikální analýza Miroslav Beneš Dušan Kolář Rozhraní lexikálního analyzátoru Lexikální analýza 2 Úkoly Čtení zdrojového textu Sestavování symbolů Odstranění mezer a poznámek Normalizace symbolů (velká/malá