STŘEDNÍ PRŮMYSLOVÁ ŠKOLA SDĚLOVACÍ TECHNIKY Praha 1, Panská 856/3, , , e mail: sekretariat@panska.
|
|
|
- Roman Mach
- před 9 lety
- Počet zobrazení:
Transkript
1 Autor: STŘEDNÍ PRŮMYSLOVÁ ŠKOLA SDĚLOVACÍ TECHNIKY Praha 1, Panská 856/3, , , e mail: sekretariat@panska.cz HUDEBNÍ AKUSTIKA MATURITNÍ PRÁCE ZE ZKUŠEBNÍHO PŘEDMĚTU aplikovaná informatika Studijní obor: Tomáš Balihar, Adam Auersvald M/001 Obrazová a zvuková technika Školní rok: 2010/2011 Třída: 4. D
2 Anotace Práce je zaměřená na analýzu zvuku a následné porovnání jednoho tónu zahraného pěti různými nástroji pomocí provedení Fourierovy analýzy. V práci jsou též popsány a vysvětleny důležité fyzikální jevy a základní pojmy se zvukem jako takovým spojené. Annotation This work named Music acoustics was made like long term leaving exam work. Work is focused on the analysis and following comparation of one tone played by five different instruments. In the work there are also described and explained important physical phenomena and basic terms with sound itself connected.
3 1. Úvod Naše práce se řadí do tématu hudební akustika. Budeme se tedy především zajímat o hudební nástroje a hlavně o jejich tóny. V teoretické části bude vysvětleno vše podstatné, co do tohoto tématu spadá. Z počátku bude rozdělena akustika, dále bude popsáno, co je to zvuk a budou vysvětleny jeho vlastnosti. V teoretické části si také samozřejmě musíme detailně rozdělit hudební nástroje do jednotlivých skupin, rozebrat Fourierovu transformaci a popsat, jak funguje lidský orgán sluchu ucho, které je pro porovnání tónů velmi podstatné. Dnešní svět by se bez hudby neobešel. Každý poslouchá svůj oblíbený žánr a poslechne si, co se mu líbí. Hudba se stále rozvíjí ve všech směrech, za poslední léta, že se ale, dle našeho názoru rozvíjí zvláště ta moderní, v níž je použito mnoho digitálních prvků, (např.: syntezátorů. Klasickou hudbu hranou na nejstarších hudebních nástrojích poslouchá stále méně lidí. Přitom naučit se hrát na hudební nástroj není vůbec jednoduché, dokonce musí mít daný člověk hodně talentu a hudební sluch. To je právě ten rozdíl od většiny dnešních umělců, kteří spíše dlouhé hodiny sedí ve zvukovém studiu a právě s pomocí digitální techniky tvoří hudbu. Poté většina lidí třeba ani neví, jak znějí staré klasické nástroje, na kterých vlastně začínala tvorba hudebního světa. Setkali jsme se také s hodně lidmi, kteří nepoznají housle od violy. My jsme si dali za úkol vytvořit práci, která by měla zájemcům o dané téma rozšířit obzory, jak jednotlivé nástroje vypadají, znějí a hlavně, v čem se liší. Ukázka bude prezentována na jednotlivých tónech 5 různých nástrojů stejné skupiny. Jako prostředek jsme zvolili výukový software Mathematica od společnosti Wolfram, neboť je studentům naší školy dostupný, má jasnou a jednoduchou syntaxi, takže ho mnoho studentů může začít využívat, pokud tak neučinili. Práce je nám velmi blízká, jelikož hudbu, jako každý z nás, posloucháme rádi a z fyzikálního hlediska je hudba velmi zajímavá. Pevně věříme, že se nám podaří ukázat a objasnit věci, které nám dosud nebyly známy, a že si lidé po přečtení naší práce dále nebudou plést hudební nástroje mezi sebou. 4
4 2. Teoretická část 2.1 Základní pojmy Tato práce se z velké většiny věnuje hudební akustice, která zkoumá zvuky a jejich vzájemné skládání se zřetelem na potřeby hudby, proto nejdříve objasníme základní pojmy a vlastnosti zvuku Akustika a její dělení Akustika, nauka o zvuku, spadá mezi jedny z nejstarších odvětví fyziky. Zabývá se slyšitelným vlněním hmotného prostředí, které se ve fyzice, ale i v běžném životě, nazývá zvuk. Přesná definice dle Úvodu do hudební akustiky pro hudebníky zní: Akustika je obor zabývající se fyzikálními ději, jsou li spojeny se vznikem zvukového vlnění, jeho šíření a vnímání zvuku sluchem. Akustiku je možné dále dělit na podoby podle toho, jakými vlastnostmi zvuku se zabývá. Fyzikální akustika věnuje se způsobu vzniku a šíření zvuku, jeho odrazem od různých materiálů a pohlcování v různých materiálech. Hudební akustika zabývá se zvuky a jejich různými kombinacemi s ohledem na potřeby hudby a zpěvu. Stavební akustika zkoumá dobré a nerušené podmínky poslouchatelnosti hudby a řeči v obytných místnostech a sálech a zároveň možnosti eliminovat nežádoucího šíření hluku z jednoho prostoru do druhého. Fyziologická akustika se zabývá vznikem zvuku v hlasovém orgánu člověka a jeho vnímáním uchem. Elektroakustika věda zabývající se siřením zvuku, jeho záznamem a jeho reprodukci s využitím elektrického proudu. Akustika se dále věnuje vzniku, vlastnostem a účinku mechanického vlnění s velmi vysokou frekvencí pro (f > 16 khz), tj. ultrazvuku, který je slyšitelný pouze pro některé živočichy (netopýr, pes, delfín, ), a vlnění s velmi nízkou frekvencí (f < 16 Hz, tj. infrazvuku, který slyší např.: sloni. Na infrazvuk ani ultrazvuk lidské ucho citlivé není, přesto tato vlnění člověku mohou uškodit. Ultrazvuk se dále používá při lékařském vyšetření, pomocí sonaru ultrazvuk zjišťuje polohu a vzdálenost různých těles a i v technické praxi (např. při rybaření pro zkoumání dna), dále se ultrazvukem čistí filmové materiály ve filmové technice. 5
5 2.1. Hudební nástroje Vzhledem k tomu, že budeme porovnávat zvuky různých hudebních nástrojů, je nutné tyto nástroje lépe rozebrat. Obecně je hudební nástroj zařízení k vydávání tónů a zvuků používaných v hudbě. V dnešní době je hudební nástroj prakticky cokoliv, co vydává nějaký zvuk. Nástroje lze třídit podle různých vlastností, např.: podle: principu vytváření zvuku; materiálu, ze kterého byl daný hudební nástroj vyroben; způsobu použití (jak se vlastně na nástroj hraje). Hudební nástroje lze dělit podle Hornbostelovy a Sachsovy systematiky hudebních nástrojů. Je to nejpoužívanější systém na třídění hudebních nástrojů, který byl zveřejněn roku 1914 a znamenal zásadní změnu v názorech, jak hudební nástroje třídit. Především se tato systematika zabývá hlavně tím, jak daný hudební nástroj zvuk vytvoří nebo jak je hudební nástroj zkonstruován. Tento systém vytvořili muzikologové Erich Moritz von Hornbostel ( ) a Curt Sachs ( ). Původně to měla být systematika určená k třídění nástrojů z celého světa uložených například v muzejních sbírkách, ale zachovala se do dneška. Označování nástrojů vychází z Deweyova desetinného systému, což je systém třídění knih a dalších archiválií podle tématu vynalezený Melvilem Deweyem v roce Systém prodělal dvacet dva revizí a úprav. Vždy jednou za 7 let, naposledy v roce Každý typ hudebního nástroje je vlastně charakterizován číselným kódem. První číslo označuje hlavní skupinu nástroje podle fyzikální podstaty tvoření tónu. Následující čísla označují podskupinu podle způsobu hry na tento nástroj a základních principů jeho stavby. Čísla oddělená tečkou nástroj blíže specifikují. První dvě úrovně třídění ukazuje tabulka: Název: Číselná Popis klasifikace Idofony 1 Materiál nástroje vydává tón díky své pružnosti Úderové 11 Nástroj je rozechvíván úderem Trsaci 12 Nástroj je rozechvíván vychýlením kmitající části Třecí 13 Kmity jsou vybuzovány třením Vzduchové 14 Nástroj je rozezvučen proudem vzduchu 6
6 Membranofony 2 Zvuk je vyluzován membránou Úderové 21 Membrána je rozechvívána úderem Trsací 22 Kmity jsou vybuzovány trsáním Třecí 23 Kmity jsou vybuzovány třením Chordofony 3 Zvuk vzniká kmitáním struny Jednoduché 31 Základem je struna a její upevnění Složené 32 Nedílnou součástí je rezonátor Aerofony 4 Zvuk vznikne kmitáním vzduchu nebo jiného plynu Volné 41 Kmitající vzduch není ohraničen nástrojem Uzavřené 42 Kmitající vzduch je ohraničen nástrojem Elektrotony 5 Zvuk je vytvářen elektronicky Elektroakustické 51 Zvuk vzniká mechanicky a elektricky je zesilován Elektronické 52 Zvuk je vytvářen čistě elektronicky Hydrofony 6 Zvuk vzniká kmitáním vody nebo jiné kapaliny Nástroje jsou rozděleny do 5 skupin: Idiofony jsou to hudební nástroje, které vydávají zvuky a tóny chvěním do nich samotných. Zde nenajdeme žádnou membránu, struny nebo vzduchové sloupce. Většina bicích nástrojů, které nemají membránu, patří právě do této skupiny. Tyto nástroje jsou velmi staré a lidé na ně hráli už v pravěku. Česky nazýváme tyto nástroje jako samozvučné. Patří sem například zvon na obr. 11, gong a triangl na obr. 12. Membranofony jsou to hudební nástroje, u kterých vydává zvuk napjatá membrána. Všechny typy bubnů patří právě do této skupiny. Jako například typický buben na obr. 13. Chordofony jsou to hudební nástroje, u kterých je zdrojem zvuku chvějící se struna, napnutá mezi dvěma body. Chordofony se dále dělí na: smyčcové housle, viola, violoncello a kontrabas; drnkací kytara, citera, harfa a loutna; kolové (či třecí) niněra; klávesové klavír, klavichord a cembalo; úderné cimbál a santur. 7
7 Obr. 13 Buben Chordofony jsou to hudební nástroje, u kterých je zdrojem zvuku chvějící se struna, napnutá mezi dvěma body. Chordofony se dále dělí na: smyčcové housle, viola, violoncello a kontrabas; drnkací kytara, citera, harfa a loutna; kolové (či třecí) niněra; klávesové klavír, klavichord a cembalo; úderné cimbál a santur. Aerofony vzduchozvučné nástroje, u nichž zvuk vzniká kmitáním sloupce vzduchu. Do této skupiny patří všechny druhy fléten (zobcová, příčná, panova), dále pak hoboj, klarinet na obr. 16 a saxofon na obr. 17. V pozdější době, jak se rozvíjela technika a pronikala i do svých hudebních nástrojů, byly přidány další skupiny: Elektrofony jsou všechny nástroje, jehož zvuk je vytvářen elektronicky. V původní klasifikaci Hornbostela a Sachse z roku 1914 ještě nebyly elektrofony obsaženy. Mezi elektrofony řadíme nástroje, které musejí zvuk zesilovat nebo jakkoliv pozměňovat. Elektrofony se dále dělí dle tabulky. Elektromechanické nástroje lze rozdělit podle typu snímání mechanických kmitů. Snímače mohou být elektromagnetické, elektrostatické, piezoelektrické či optické. Elektronické nástroje se dělí na analogové (pracující se spojitými změnami 8
8 elektrických veličin), digitální (pracující se signály v číslicové podobě) a hybridní (kombinující oba principy). Dle způsobu generování zvuku lze elektronické nástroje rozdělit ještě na syntetizéry: Jejich hlavní činnost je přetváření již připravených signálů. Druhá skupina obsahuje samplem, jejichž základem je reprodukce zaznamenaných signálů. Nejznámější elektromechanický nástroj je elektrická kytara. Na obr. 18 a mezi elektrické nástroje patří digitální piano na obr. 19. Obr. 18 Elektrická kytara Kontrabas Obr. 19 Digitální piano V praktické části naší práce budeme některé nástroje blíže zkoumat, proto je nutné o nich vědět základní informace. Kontrabas je strunný smyčcový nástroj se strunami laděnými v čistých kvartách: E 1, A 1, D, G (na rozdíl od většiny moderních smyčcových nástrojů, které jsou laděny v kvintách). Má široké využití v klasické hudbě je nedílnou součástí symfonických i komorních orchestrů a mnoha smyčcových komorních souborů. Velice důležitou roli hraje i v dalších hudebních stylech: jazz, blues, folk. Kontrabas můžeme slyšet také v rock and rollu. Dodnes panuje nejednotnost, zda kontrabas patří do houslové, nebo violové rodiny smyčcových nástrojů (violová rodina je odvozena od středověkého nástroje viola da gamba, moderní viola patří do houslové rodiny). Kontrabas má velmi podobnou stavbu jako viola da gamba (například horní část je výrazně užší než u houslí) a stejně jako ona je laděn v kvartách (housle a příbuzné nástroje jsou laděny v kvintách). Oproti viole da gamba ale nemá na hmatníku pražce, má méně strun a jeho výřezy na horní desce jsou více podobné houslovým. 9
9 Kontrabas zní vždy o oktávu níže, než je uveden v notovém zápisu. Nejčastěji je vyráběn se čtyřmi strunami v kvartovém ladění E 1, A 1, D, G. Pro symfonické účely se používají také pětistrunné kontrabasy s přidanou nejnižší strunou C 1 (kontra C), některé německé varianty mají místo struny C 1 strunu H 2 (subkontra H). Při sólové hře je kontrabas často laděn o dva půltóny výše (tzv. sólové ladění): Fis 1, H 1, E, A, což mu dodá jasnější a brilantnější zvuk. Oproti standardnímu orchestrálnímu ladění se však změní tah strun natolik, že je nutné použít jinou sadu strun. Někteří (zvláště jazzoví) basisté používají kvintové ladění C 1, G 1, D, A, čili o oktávu níže než u violoncella, což má za následek vyšší hlasitost (struny vibrují v přirozenějších intervalech s menšími vyššími harmonickými frekvencemi a snáze se navzájem rozezvučí). Mnohé kontrabasy mají nejnižší strunu laděnou na kontra C (místo kontra E). Toho se může dosáhnout buď prodloužením hmatníku na obr. 20 nebo speciálním mechanickým zařízením vedle hmatníku. Je to velice výhodné zejména pro orchestrální hru, protože violoncellový part je velice často zdvojován s kontrabasovým (přičemž kontrabasy hrají o oktávu níže) a kontrabasy takto získají stejný tónový rozsah jako violoncella. Hráč hrající na kontrabas může buď sedět na speciální stoličce nebo stát. Při hře ve stoje hráč podepírá nástroj levou nohou a nikoliv levou rukou, což mu dovoluje daleko větší volnost při hraní. V případě, že hráč sedí na stoličce, levou nohou se opírá o stoličku a pravou nohou o zem. Podobně jako u violoncella je kontrabas zakončen vysouvatelným bodcem zakončeným gumovou špičkou zabraňující sklouznutí špičky po podlaze. Herní techniky jsou v podstatě stejné jako u ostatních smyčcových nástrojů, stejně jako u violoncella se používá palcová technika, kdy jsou tóny hrány i palcem levé ruky. V jazzu se navíc používá tzv. slapování, což je forma pizzicata, které se zahraje tak, aby se struna dotkla hmatníku (tím se docílí perkusivního bouchnutí struny). Na kontrabas je obecně těžší zahrát rychlé a technicky náročné pasáže než např. na housle, protože basové struny jsou silnější a vzdálenost mezi tóny na hmatníku je větší. 10
10 Obr. 20 Kontrabas 2.3 Fourierova transformace V naší práci je hlavní úkol porovnat jednotlivé tóny hudebních nástrojů. V praxi je výhodné (teoreticky i experimentálně) používat harmonických funkcí, jsou totiž snadno prakticky realizovatelné. Každou funkci jsme schopni vyjádřit jako součet či integraci harmonických funkcí, každá má ale jiný fázový posun a jinou amplitudu. Váhová frekvence nám vlastně udává, jaké frekvence je nutno použít, aby bylo pak možné z harmonických funkcí sestavit zpětně původní funkci. Tato váhová funkce (spektrum) bývá označována jako Fourierova transformace (dále jen FT). Fourierova transformace je matematická metoda, kterou jsme schopni analyzovat periodické signály. Jejím cílem je převést signály časové závislosti na závislost frekvenční. Signál může být vyjádřen ve spojitém nebo diskrétním čase Definice Fourierovy transformace ve spojitém čase Fourierova transformace S (ω) funkce s (t) je definována integrálním vztahem: 11
11 Funkci s (t) vypočteme z S (ω) inverzní Fourierovou transformací: Definice Fourierovy transformace v diskrétním čase Fourierova transformace S (Ω) posloupnosti s(k) je definována vztahem: Posloupnost s(k) vypočteme z S (Ω) inverzní Fourierovou transformací: Tato transformace se označuje: DtFT, aby se tak odlišila od Fourierovy transformace spojitého signálu. Abychom nemuseli značením nijak odlišovat Fourierovu transformaci spojitého a diskrétního signálu, zavedeme vztah mezi spojitým signálem a jeho spektrem: a Spektrum diskrétního signálu se od spektra spojitého signálu liší tím, že je periodické s periodou 2π. Obecně je to vyjádření funkce v jiné bázi. Ve speciálním případě se uvažuje trigonometrická Fourierova transformace, která za hlavní složku pokládá funkce cos(kt) a sinus(kt) nebo v komplexním tvaru exp(kt), kde kt je celé číslo v případě Fourierovy řady nebo reálná proměnná v případě Fourierovy transformace. Fourierovu transformaci lze ve více podobách. Definiční vzorec pro FT je vyjádřen pomocí integrálu, což není pro praktické použití příliš vhodný a to proto, že: 12
12 analytické řešení vzorce existuje jen v omezeném počtu případů a je nutno jej hledat numericky; v případě počítačového zpracování nahraného signálu nemáme spojitou funkci, ale jen její hodnoty v diskrétních vzorkovacích okamžicích. Z tohoto důvodu existuje diskrétní FT, která je již polynomem a jejími vstupy a výstupy jsou posloupnosti hodnot. Použití této metody je nutné v případě, když známe vzorky signálu a potřebujeme nalézt spektrum vzorků signálu, či je nutné nalézt signál ze vzorků spektra Ukázka Fourierovy transformace Nejdříve si uvedeme příklad jednoduchého tónu. Matematický popis je snadný:, kde a f je frekvence daného tónu. Popis složeného tónu je prakticky stejný, ale obsahuje více členů, teoreticky jich může být nekonečně mnoho: složen z mnoha tónů jednoduchých. Složený tón je vlastně V dané rovnici se vyskytuje mnoho členů obsahující frekvenci f 1, která je frekvence základní a určuje výšku složeného tónu, frekvence f 2, f 3, jsou frekvence, které nazýváme vyšší harmonické. Lidské ucho nedokáže rozpoznat jednotlivé tóny, z kterých se složený tón skládá. Vnímá ho jako jeden tón, jenž má specifické zabarvení (barvu). Ta je určena právě vyššími harmonickými frekvencemi. Základní frekvence je vždy nejnižší a vyšší harmonické postupně rostou. Základní tón má ale vetšinou nejvyšší amplitudu (resp. hlasitost). Tón se základní frekvencí je tedy nejdominantnější, a proto určuje právě tento tón se základní frekvencí výšku celého složeného tónu. Tyto jmenované vlastnosti si ukážeme na obrázcích. Na obr. 26, je znázorněno frekvenční spektrum složeného tónu. Spektrum není spojité jasně vidíme, že na obrázku jsou zobrazeny pouze frekvence, které jsou násobkem frekvence základní 13
13 Obr. 26 Nespojité spektrum Spektrum šumu (zobrazené na obr. 27) obsahuje frekvence z určitého intervalu Obr. 27 Šum 14
14 Pomocí funkce dané předpisem, kde f 1,f 2, a y m1, y m2, mají význam popsaný výše, jsme schopni získat vhodnou volbou těchto parametrů různé průběhy signálu např. průběh ve tvaru obdélníku (viz obr. 28)., Graf na obr. 28 není v praxi realizovatelný, je to pouze teoretický průběh. K němu se můžeme přiblížit tak, že ve výše uvedeném vztahu budeme uvažovat jen liché násobky základní frekvence. Obr. 28 Vezme li v úvahu první dva členy, získáme graf zobrazený na obr. 29. Pokud vezmeme v úvahu prvních pět členů, dostaneme graf zobrazený na obr. 30. Tímto způsobem (tj. vhodnou volbou vyšších harmonických frekvencí a započtením vhodného počtu členů do celkového součtu) lze získat průběh libovolného periodického signálu pouze s využitím funkce sinus. A to je pro výrobu i další zpracování takového signálu velmi podstatné, neboť s funkcí sinus se velmi dobře pracuje matematicky a sinusový průběh např. napětí lze relativně snadno realizovatelný v praxi. Obr
15 Obr. 30 Jestliže chceme výpočet koeficientů Y mi pro i = 1,2,3,.n; musíme použít Fourierovu analýzu, jejímž použitím lze zapsat libovolnou periodickou funkci ve tvaru: Definice diskrétní Fourierovy transformace Přímá diskrétní Fourierova transformace má tvar: Zpětná (inverzní) diskrétní Fourierova transformace lze popsat vztahem: Diskrétní Fourierova transformace našla velké uplatnění ve výpočetní technice. Podle definice však potřebujeme k výpočtu N 2 komplexních součinů a N 2 komplexních součtů. Proto je, tento typ FT velice zdlouhavý na výpočet, tak se hledá jednodušší a hlavně rychlejší algoritmus, který by snížil dobu výpočtu. Tento nový algoritmus, založený na exponenciálních diskrétních funkcí, nazýváme rychlá Fourierova transformace, která vyžaduje jen komplexních součinů a komplexních součtů. Díky tomuto algoritmu se stala diskrétní Fourierova transformace nejrozšířenějším prostředkem pro numerický výpočet Fourierovy 16
16 transformace. Tento algoritmus je obsažen v mnoha matematických programech (Mathematica, Maple, Mathcad, Octave a další). 3. Praktická část 3.1. Analýza zvuků V této části práce se budeme zabývat analýzou pěti stejných tónů vycházejících z pěti různých hudebních nástrojů. Použité hudební nástroje se nazývají nástroje smyčcové, jejichž princip jsme již podrobně objasnili v teoretické části naší práce. Smyčcové nástroje, se kterými budeme dále pracovat, jsou: 1. housle 2. violoncello 3. kytara 4. viola 5. kontrabas U všech těchto nástrojů budeme pracovat se stejnou strunou s označením A, která po rozechvění vydává tón a. Jelikož je v naší práci hlavním úkolem analyzovat a následně porovnat již zmíněné tóny hudebních nástrojů, zakládá se celá praktická část na principu Fourierovi transformace, jež je detailně zmapován v teoretické části. Každý tón, který jsme nahráli v hudební škole v Benešově, nejprve v programu Sony soundforge upravíme tak, abychom měli jeho vzorek obsahující jen několik period původního zvuku. Nahraný zvuk má délku několik sekund, což znamená pro následně použitou Fourierovu transformaci zbytečnou zátěž počítače. Zvuk získaný úpravou v programu Sony soundforge je při běžném přehrání neidentifikovatelný, ale pro naše účely vhodný. Sestřihli jsme to tak, aby obsahoval skutečně jen pár period. A i to při vzorkovací frekvenci Hz znamená několik stovek dat (a kdy i několik stovek průchodů cykly v rychlé Fourierově transformaci). Výpočet rychlé Fourierovy transformace jsme realizovali v softwaru Mathematica, který též umožňuje nahraný zvuk v datové podobě načíst. Vypočtená a zobrazená frekvenční spektra jsme pak u všech nástrojů porovnali Housle Prvním nástrojem, který budeme v naší práci analyzovat a následně porovnávat s již zmíněnými nástroji, jsou housle. Je to strunný smyčcový nástroj se 17
17 čtyřmi strunami laděnými v čistých kvintách: g, d¹, a¹, e². Jsou nejmenší z rodiny houslových nástrojů, do které ještě mimo jiné patří viola a violoncello. Podrobnější informace o houslích jsou napsány v teoretické části. Pomocí softwaru Mathematica a nahraného zdrojového tónu a¹, jsme získali graf závislosti intenzity složeného tónu na čase. Průběh tónu zobrazený na obr. 31 udává charakter zvuku, na čemž se podílí fakt, že kromě frekvence základní, tyto zvuky dále obsahují i vyšší harmonické frekvence. Na základě nich jsme schopni jednotlivé zdroje zvuku (v našem případě strunné hudební nástroje) od sebe odlišit a vzájemně porovnávat. V grafu na obr. 31 jsou zobrazeny přesně tři periody průběhu zvuku. Z grafu závislosti intenzity na čase jsme schopni odečíst dobu trvání jedné periody. Jelikož je z grafu zřejmé, že časová osa označuje počet záznamů okamžité intenzity daného zvuku a ne přímo časy jejich záznamů, jsou každé dva po sobě jdoucí záznamy vzdáleny o. Při záznamu zvuku bylo totiž použito záznamové zařízení Edirol se vzorkovací frekvencí Hz. Periodu v sekundách tedy získáme tak, že počet záznamů vynásobíme s. Obr. 31 Průběh složeného tónu houslí 18
18 Jelikož z průběhu složeného tónu houslí nejsme schopni zjistit dost podstatných informací, abychom mohli tento zvuk analyzovat a porovnat s ostatními nástroji, používáme Fourierovi transformaci. Ta převede signál z oblasti časové závislosti (jak tomu bylo u průběhu složeného tónu) do oblasti frekvenční závislosti. Pomocí softwaru Mathematica krátkého notebooku získáme frekvenční spektrum daného tónu houslí (viz obr. 32). Jak jsme již zmínili, složený tón obsahuje frekvenci základní a vyšší harmonické frekvence a právě tyto frekvence jsou spolu se svými amplitudami vidět na (obr. 32). Na základě spektra na obr. 32 můžeme již daný tón dobře analyzovat. Obr. 32 Frekvenční spektrum Podstatné frekvence, které můžeme charakterizovat na základě frekvenčního spektra, jsou:,,,,,. Frekvence je frekvence základní udávající výšku složeného tónu, která je u všech námi porovnávaných nástrojů stejná. Zbývající frekvence se nazývají vyšší harmonické a nesou informaci o barvě zvuku. Nebudeme vypisovat všechny frekvence, které můžeme na grafu vidět. Většina z nich má prakticky nulovou amplitudu a nemají pro nás smysl, charakterizují pouze šum. Můžeme si všimnout, že housle hrají na nejvyšších frekvencích mezi porovnávanými nástroji a na velmi podobných frekvencích jako viola (viz dále). Dále je zde patrné, že housle, oproti všem analyzovaným nástrojům, dosahují nejnižších amplitud neboli nejnižší hlasitosti. V porovnání s violou a violoncellem není rozdíl tak veliký, ale oproti kontrabasu a kytaře je rozdíl mnohem vetší. Tento fakt mohl ovšem ovlivnit i způsob nahrávání 19
19 daného zvuku. Zajímavé také je, že základní frekvence nemá nejvyšší amplitudu, ačkoliv tón o frekvenci 440 Hz slyšíme jasně. To je dáno tím, jak tyto tóny vnímá lidské ucho. Ucho je schopno si tóny o výše uvedených frekvencích spojit dohromady a některé z nich potlačit a jiné naopak zesílit na úkor jiných. Subjektivně (tj. uchem) tedy vnímáme jiné frekvenční spektrum, než jaké spektrum bylo objektivně (tedy přístroji) naměřené. V případě některých hudebních nástrojů (tj. při určité kombinaci vyšších harmonických frekvencí) tyto rozdíly vznikají. 4. Závěr Práci jsme si rozdělili na dvě části. Zpracování první části věnované teorii nebylo tak obtížné. Vzhledem k velkému množství informací na internetu, v encyklopediích, všem znalostem ze školy, se teoretická část práce poměrně dařila. Během psaní této části jsme využili znalostí z fyziky a zvukové techniky a nesetkali jsme se s velkým problémem. Teoretická část je, myslíme si, velmi dobře zpracovaná. Neměly by v ní chybět žádné zásadní informace. Je v ní vysvětleno vše, co potřebujeme znát k vytvoření této práce. U druhé části nebyl průběh tak jednoduchý. Zprvu jsme museli pomocí záznamového zařízení Edirol kvalitně nahrát jednotlivé tóny hudebních nástrojů. Takže první problém byl, sehnat hudební nástroje a člověka, jenž by byl ochotný nám tóny nahrát, jelikož bychom to sami nezvládli. Nakonec se povedlo a tak jsme mohli pokračovat. K rozboru tónů bylo potřeba v Mathematice napsat jednoduchý program; zde jsme se museli obrátit na pomoc k našemu vedoucímu práce, který nám velice pomohl a my mohli konečně začít podrobně jednotlivé tóny analyzovat a porovnávat. Dále žádný problém nenastal a naši práci jsme dokončili. Myslíme si, že se nám podařilo vytvořit kvalitní práci, která může posloužit všem zájemcům o dané téma. Ať už jako výuková práce pro studenty, nebo jen zájemcům z širokého spektra lidí, kteří si potřebují objasnit termíny a fakty z tohoto tématu. Doufáme, že naše práce bude sloužit jako motivace současným, ale i budoucím studentům. Dalším logickým rozšířením této práce by bylo zahrnout do analýzy i další nejen strunné nástroje a směřovat k sestavení celé databáze frekvenčních spekter jednotlivých hudebních nástrojů. Ale to může být téma pro naše pokračovatele. 20
Vybrané oblasti hudební akustiky
 Vybrané oblasti hudební akustiky Adam J. Sporka Katedra počítačů České vysoké učení technické Fakulta elektrotechnická 1 Obsah Definice hudební akustiky Tón Tónové škály Systémy ladění Hudební nástroje
Vybrané oblasti hudební akustiky Adam J. Sporka Katedra počítačů České vysoké učení technické Fakulta elektrotechnická 1 Obsah Definice hudební akustiky Tón Tónové škály Systémy ladění Hudební nástroje
ANALÝZA LIDSKÉHO HLASU
 ANALÝZA LIDSKÉHO HLASU Pomůcky mikrofon MCA-BTA, LabQuest, program LoggerPro (nebo LoggerLite), tabulkový editor Excel, program Mathematica Postup Z každodenní zkušenosti víme, že každý lidský hlas je
ANALÝZA LIDSKÉHO HLASU Pomůcky mikrofon MCA-BTA, LabQuest, program LoggerPro (nebo LoggerLite), tabulkový editor Excel, program Mathematica Postup Z každodenní zkušenosti víme, že každý lidský hlas je
VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY
 VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Zvuk je mechanické vlnění v látkovém prostředí,
VY_32_INOVACE_FY.18 ZVUKOVÉ JEVY Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Zvuk je mechanické vlnění v látkovém prostředí,
Hudební nástroje. Hudební nástroje jsou zařízení k vydávání tónů a zvuků. Používají se v hudbě. Hudební nástroje mají svou barvu tónu.
 Hudební nástroje Hudební nástroje jsou zařízení k vydávání tónů a zvuků. Používají se v hudbě. Hudební nástroje mají svou barvu tónu. Strunné hudební nástroje Lidé si kdysi všimli, že natažený drát může
Hudební nástroje Hudební nástroje jsou zařízení k vydávání tónů a zvuků. Používají se v hudbě. Hudební nástroje mají svou barvu tónu. Strunné hudební nástroje Lidé si kdysi všimli, že natažený drát může
Mechanické kmitání a vlnění
 Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Druh učebního materiálu Anotace (metodický pokyn, časová náročnost, další pomůcky )
 Číslo šablony III/2 Číslo materiálu VY_32_INOVACE_F.6.18 Autor Stanislav Mokrý Vytvořeno 8.12.2013 Předmět, ročník Fyzika, 2. ročník Tematický celek Fyzika 2. - Mechanické kmitání a vlnění Téma Zvuk a
Číslo šablony III/2 Číslo materiálu VY_32_INOVACE_F.6.18 Autor Stanislav Mokrý Vytvořeno 8.12.2013 Předmět, ročník Fyzika, 2. ročník Tematický celek Fyzika 2. - Mechanické kmitání a vlnění Téma Zvuk a
AKUSTIKA. Barva tónu
 AKUSTIKA Barva tónu Tón můžeme objektivně popsat pomocí těchto čtyř vlastností: 1. Výška 2. Délka 3. Barva 4. Hlasitost, hladina intenzity Nyní se budeme zabývat barvou tónu. Barva tónu Barva tónu nám
AKUSTIKA Barva tónu Tón můžeme objektivně popsat pomocí těchto čtyř vlastností: 1. Výška 2. Délka 3. Barva 4. Hlasitost, hladina intenzity Nyní se budeme zabývat barvou tónu. Barva tónu Barva tónu nám
Hudební nástroje se dělí do několika skupin podle způsobu tvoření tónu.
 Hudební nástroje Na celém světě existují stovky hudebních nástrojů. My se budeme zabývat především hudebními nástroji, které jsou běžné v Evropě. Některé z těchto nástrojů můžeme vidět a slyšet v symfonickém
Hudební nástroje Na celém světě existují stovky hudebních nástrojů. My se budeme zabývat především hudebními nástroji, které jsou běžné v Evropě. Některé z těchto nástrojů můžeme vidět a slyšet v symfonickém
AKUSTIKA. Tón a jeho vlastnosti
 AKUSTIKA Tón a jeho vlastnosti Zvuky dělíme na dvě základní skupiny: 1. Tóny vznikají pravidelným chvěním zdroje zvuku, průběh závislosti výchylky na čase je periodický, jsou to např. zvuky hudebních nástrojů,
AKUSTIKA Tón a jeho vlastnosti Zvuky dělíme na dvě základní skupiny: 1. Tóny vznikají pravidelným chvěním zdroje zvuku, průběh závislosti výchylky na čase je periodický, jsou to např. zvuky hudebních nástrojů,
Akustika pro posluchače HF JAMU
 Akustika pro posluchače HF JAMU Zvukové vlny a kmity (1) 2 Vnímání zvuku (3) 2 Akustika hudebního nástroje (2) 2 Akustika při interpretaci (2) 3 Záznam hry na hudební nástroje (2) 4 Seminární a samostatné
Akustika pro posluchače HF JAMU Zvukové vlny a kmity (1) 2 Vnímání zvuku (3) 2 Akustika hudebního nástroje (2) 2 Akustika při interpretaci (2) 3 Záznam hry na hudební nástroje (2) 4 Seminární a samostatné
ZVUKOVÉ JEVY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie
 ZVUKOVÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Odraz zvuku Vznik ozvěny Dozvuk Několikanásobný odraz Ohyb zvuku Zvuk se dostává za překážky Překážka srovnatelná s vlnovou délkou Pružnost Působení
ZVUKOVÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Odraz zvuku Vznik ozvěny Dozvuk Několikanásobný odraz Ohyb zvuku Zvuk se dostává za překážky Překážka srovnatelná s vlnovou délkou Pružnost Působení
Funkce komplexní proměnné a integrální transformace
 Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Akustika. Hudební nástroje. 7. Přednáška
 Akustika Hudební nástroje 7. Přednáška Složky hudebního výkonu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola Časové rozložení tónů I, (N) S, T Dynamika I,
Akustika Hudební nástroje 7. Přednáška Složky hudebního výkonu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola Časové rozložení tónů I, (N) S, T Dynamika I,
Akustika. 3.1 Teorie - spektrum
 Akustika 3.1 Teorie - spektrum Rozklad kmitů do nejjednodušších harmonických Spektrum Spektrum Jedna harmonická vlna = 1 frekvence Dvě vlny = 2 frekvence Spektrum 3 vlny = 3 frekvence Spektrum Další vlny
Akustika 3.1 Teorie - spektrum Rozklad kmitů do nejjednodušších harmonických Spektrum Spektrum Jedna harmonická vlna = 1 frekvence Dvě vlny = 2 frekvence Spektrum 3 vlny = 3 frekvence Spektrum Další vlny
Zvuk a jeho vlastnosti
 Tematická oblast Zvuk a jeho vlastnosti Datum vytvoření 3. prosince 2012 Ročník Stručný obsah Způsob využití Autor Kód Komunikace hudebního umění se znakovými systémy uměleckých a společenských oborů 1.
Tematická oblast Zvuk a jeho vlastnosti Datum vytvoření 3. prosince 2012 Ročník Stručný obsah Způsob využití Autor Kód Komunikace hudebního umění se znakovými systémy uměleckých a společenských oborů 1.
Fyzika_9_zápis_6.notebook June 08, 2015. Akustika = část fyziky, která se zabývá ZVUKEM (vznikem zvuku, vlastnostmi zv., šířením zv., lid.
 AKUSTIKA Akustika = část fyziky, která se zabývá ZVUKEM (vznikem zvuku, vlastnostmi zv., šířením zv., lid.sluchem) Obory akusky Fyzikální a. Hudební a. Fyziologická a. Stavební a. Elektroakuska VZNIK A
AKUSTIKA Akustika = část fyziky, která se zabývá ZVUKEM (vznikem zvuku, vlastnostmi zv., šířením zv., lid.sluchem) Obory akusky Fyzikální a. Hudební a. Fyziologická a. Stavební a. Elektroakuska VZNIK A
Akustika pro posluchače HF JAMU
 Akustika pro posluchače HF JAMU Zvukové vlny a kmity (1)! 2 Vnímání zvuku (3)! 2 Akustika hudebního nástroje (2)! 2 Akustika při interpretaci (2)! 3 Záznam hry na hudební nástroje (2)! 4 Seminární a samostatné
Akustika pro posluchače HF JAMU Zvukové vlny a kmity (1)! 2 Vnímání zvuku (3)! 2 Akustika hudebního nástroje (2)! 2 Akustika při interpretaci (2)! 3 Záznam hry na hudební nástroje (2)! 4 Seminární a samostatné
Václav Syrový: Hudební akustika, Praha 2003, s. 7
 Hudební akustika Mgr. Petr Kalina 30.9.2013 Definice obecné akustiky Předmětem akustiky je zkoumání fyzikální podstaty zvuku a problémů spojených s jeho vznikem, šířením a vnímáním. Zvuk je zvláštní druh
Hudební akustika Mgr. Petr Kalina 30.9.2013 Definice obecné akustiky Předmětem akustiky je zkoumání fyzikální podstaty zvuku a problémů spojených s jeho vznikem, šířením a vnímáním. Zvuk je zvláštní druh
DUM č. 14 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 14 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 04.05.2014 Ročník: 1. ročník Anotace DUMu: Mechanické vlnění, zvuk Materiály
projekt GML Brno Docens DUM č. 14 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 04.05.2014 Ročník: 1. ročník Anotace DUMu: Mechanické vlnění, zvuk Materiály
Akustika. Hudební nástroje. 7. Přednáška
 Akustika Hudební nástroje 7. Přednáška Složky hudebního projevu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola Časové rozložení tónů I, N S, T Dynamika I,
Akustika Hudební nástroje 7. Přednáška Složky hudebního projevu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola Časové rozložení tónů I, N S, T Dynamika I,
Akustika. Hudební nástroje
 Akustika Hudební nástroje Složky hudebního projevu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola časové rozložení tónů I, N S, T Dynamika I, N S, T Intonace
Akustika Hudební nástroje Složky hudebního projevu I - Interpret N - Nástroj P - Akustika prostoru S - Sluch T - Technika Složka Zdroj Kontrola časové rozložení tónů I, N S, T Dynamika I, N S, T Intonace
Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů
 Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů Část 1 - Syntéza orchestrálních nástrojů pro symfonickou báseň B.Smetany "Vltava" Cílem této části práce je syntetizovat symfonickou báseň B.Smetany
Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů Část 1 - Syntéza orchestrálních nástrojů pro symfonickou báseň B.Smetany "Vltava" Cílem této části práce je syntetizovat symfonickou báseň B.Smetany
Úvod do zpracování signálů
 1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
Název: Studium kmitů hudebních nástrojů, barva zvuku
 Název: Studium kmitů hudebních nástrojů, barva zvuku Autor: Mgr. Lucia Klimková Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět (mezipředmětové vztahy) : Fyzika (Hudební výchova) Tematický
Název: Studium kmitů hudebních nástrojů, barva zvuku Autor: Mgr. Lucia Klimková Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět (mezipředmětové vztahy) : Fyzika (Hudební výchova) Tematický
Zvuková karta. Zvuk a zvuková zařízení. Vývoj, typy, vlastnosti
 Zvuk a zvuková zařízení. Vývoj, typy, vlastnosti Zvuková karta Počítač řady PC je ve své standardní konfiguraci vybaven malým reproduktorem označovaným jako PC speaker. Tento reproduktor je součástí skříně
Zvuk a zvuková zařízení. Vývoj, typy, vlastnosti Zvuková karta Počítač řady PC je ve své standardní konfiguraci vybaven malým reproduktorem označovaným jako PC speaker. Tento reproduktor je součástí skříně
VY_32_INOVACE_E 15 03
 Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Taje lidského sluchu
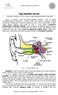 Taje lidského sluchu Markéta Kubánková, ČVUT v Praze, Fakulta biomedicínského inženýrství Sluch je jedním z pěti základních lidských smyslů. Zvuk je signál zprostředkovávající informace o okolním světě,
Taje lidského sluchu Markéta Kubánková, ČVUT v Praze, Fakulta biomedicínského inženýrství Sluch je jedním z pěti základních lidských smyslů. Zvuk je signál zprostředkovávající informace o okolním světě,
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Quantization of acoustic low level signals. David Bursík, Miroslav Lukeš
 KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
Fyzikální podstata zvuku
 Fyzikální podstata zvuku 1. základní kmitání vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění
Fyzikální podstata zvuku 1. základní kmitání vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění
Zvuk. 1. základní kmitání. 2. šíření zvuku
 Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
KTE/TEVS - Rychlá Fourierova transformace. Pavel Karban. Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni
 KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
Hudební nauka. přehled látky pro 1. a 2. ročník DÉLKA VÝŠKA SÍLA BARVA HLAVIČKA NOTY
 Hudební nauka přehled látky pro 1. a 2. ročník Vlastnosti tónu DÉLKA VÝŠKA SÍLA BARVA Prvky notace PŘEDZNAMENÁNÍ NOTA HLAVIČKA NOTY POMOCNÉ LINKY HOUSLOVÝ KLÍČ NOTOVÁ OSNOVA (linky i mezery se číslují
Hudební nauka přehled látky pro 1. a 2. ročník Vlastnosti tónu DÉLKA VÝŠKA SÍLA BARVA Prvky notace PŘEDZNAMENÁNÍ NOTA HLAVIČKA NOTY POMOCNÉ LINKY HOUSLOVÝ KLÍČ NOTOVÁ OSNOVA (linky i mezery se číslují
mel jednotka subjektivní výšky tónu. Výška tónu o frekvenci 1000 Hz a hladině akustického tlaku 40 db se rovná 1000 melům.
 m / Hudební akustika 42 mechanická soustava uspořádání mechanických prvků. Např. u hudebního nástroje představuje soustavu 1D struna houslí, 2D membrána bubnu a 3D zvon. Pro zkoumání vlastností těchto
m / Hudební akustika 42 mechanická soustava uspořádání mechanických prvků. Např. u hudebního nástroje představuje soustavu 1D struna houslí, 2D membrána bubnu a 3D zvon. Pro zkoumání vlastností těchto
Synth challange 2016
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Synth challange 2016 Komentář k práci Jan Dvořák OBSAH ÚVOD... 2 1 Syntéza orchestrálních nástrojů pro symfonickou báseň B. Smetany "Vltava"...
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Synth challange 2016 Komentář k práci Jan Dvořák OBSAH ÚVOD... 2 1 Syntéza orchestrálních nástrojů pro symfonickou báseň B. Smetany "Vltava"...
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cziba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cziba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické
Zvukové rozhraní. Základní pojmy
 Zvukové rozhraní Zvukové rozhraní (zvukový adaptér) je rozšiřující rozhraní počítače, které slouží k počítačovému zpracování zvuku (vstup, výstup). Pro vstup zvuku do počítače je potřeba jeho konverze
Zvukové rozhraní Zvukové rozhraní (zvukový adaptér) je rozšiřující rozhraní počítače, které slouží k počítačovému zpracování zvuku (vstup, výstup). Pro vstup zvuku do počítače je potřeba jeho konverze
Zvukové jevy. Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku
 Zvukové jevy Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku 2. musí existovat látkové prostředí, kterým se zvuk šíří - ve vakuu se zvuk nešíří! 3.
Zvukové jevy Abychom slyšeli jakýkoli zvuk, musí být splněny tři základní podmínky: 1. musí existovat zdroj zvuku 2. musí existovat látkové prostředí, kterým se zvuk šíří - ve vakuu se zvuk nešíří! 3.
Fyzikálními ději, které jsou spojeny se vznikem zvukového vlnění, jeho šířením a vnímáním zvuku sluchem se zabývá akustika.
 Fyzikálními ději, které jsou spojeny se vznikem zvukového vlnění, jeho šířením a vnímáním zvuku sluchem se zabývá akustika. Zvuk je podélné mechanické vlnění, které vnímáme sluchem. Jeho frekvence je v
Fyzikálními ději, které jsou spojeny se vznikem zvukového vlnění, jeho šířením a vnímáním zvuku sluchem se zabývá akustika. Zvuk je podélné mechanické vlnění, které vnímáme sluchem. Jeho frekvence je v
Akustika a hudební nástroje
 Zajímavá fyzika Tomáš Tyc, 2010 Akustika a hudební nástroje Tón časově periodické změny akustického tlaku Je-li p(t) = A cos(ωt + ϕ), jde o jednoduchý tón, jinak je tón složený složený tón: p(t) = A 1
Zajímavá fyzika Tomáš Tyc, 2010 Akustika a hudební nástroje Tón časově periodické změny akustického tlaku Je-li p(t) = A cos(ωt + ϕ), jde o jednoduchý tón, jinak je tón složený složený tón: p(t) = A 1
Akustika. Tónové systémy a ladění
 Akustika Tónové systémy a ladění Harmonická řada Harmonická řada, tónový systém Harmonická řada je nerovnoměrná, záleží na volbě fundamentu, pak se ale nepotkávají alikvoty nižších pořadových čísel, hodně
Akustika Tónové systémy a ladění Harmonická řada Harmonická řada, tónový systém Harmonická řada je nerovnoměrná, záleží na volbě fundamentu, pak se ale nepotkávají alikvoty nižších pořadových čísel, hodně
Číslicové zpracování signálů a Fourierova analýza.
 Číslicové zpracování signálů a Fourierova analýza www.kme.zcu.cz/kmet/exm 1 Obsah prezentace 1. Úvod a motivace 2. Data v časové a frekvenční oblasti 3. Fourierova analýza teoreticky 4. Fourierova analýza
Číslicové zpracování signálů a Fourierova analýza www.kme.zcu.cz/kmet/exm 1 Obsah prezentace 1. Úvod a motivace 2. Data v časové a frekvenční oblasti 3. Fourierova analýza teoreticky 4. Fourierova analýza
Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol:
 Název: Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni robota pro měření hlasitosti
Název: Měření hlasitosti zvuku. Tematický celek: Zvuk. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni robota pro měření hlasitosti
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické či jiné
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické či jiné
Inovace a zkvalitnění výuky prostřednictvím ICT Elektrický proud střídavý Základní pojmy, časový průběh sin. veličin, střední.
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Inovace a zkvalitnění výuky prostřednictvím ICT Elektrický proud střídavý Základní pojmy, časový průběh sin.
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Inovace a zkvalitnění výuky prostřednictvím ICT Elektrický proud střídavý Základní pojmy, časový průběh sin.
25 - Základy sdělovací techniky
 25 - Základy sdělovací techniky a) Zvuk - je mechanické (postupné podélné) vlnění látkového prostředí, které je lidské ucho schopno vnímat. Jeho frekvence je přibližně mezi 16 Hz a 20 khz. Zdroje zvuku
25 - Základy sdělovací techniky a) Zvuk - je mechanické (postupné podélné) vlnění látkového prostředí, které je lidské ucho schopno vnímat. Jeho frekvence je přibližně mezi 16 Hz a 20 khz. Zdroje zvuku
PŘÍTECH. Klarinet Vlastnosti zvuku
 PŘÍTECH Klarinet Vlastnosti zvuku Gymnázium Cheb Vojtěch Müller Nerudova 7 4.E 2014/2015 Čestné prohlášení Prohlašuji, že jsem tuto maturitní práci vypracoval samostatně, pod vedením Mgr. Vítězslava Kubína
PŘÍTECH Klarinet Vlastnosti zvuku Gymnázium Cheb Vojtěch Müller Nerudova 7 4.E 2014/2015 Čestné prohlášení Prohlašuji, že jsem tuto maturitní práci vypracoval samostatně, pod vedením Mgr. Vítězslava Kubína
Mechanické kmitání (oscilace)
 Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Zuzana Štichová. hudební nástroje. Ročník: 6. Datum vytvoření: červen 2012
 Autor: Vzdělávací oblast: Téma: Ročník: 6. Zuzana Štichová Umění a kultura hudební výchova hudební nástroje Datum vytvoření: červen 2012 Materiál: Anotace: Metodické pokyny: Zdroj: VY_32_INOVACE_S2.2_HV.6.05
Autor: Vzdělávací oblast: Téma: Ročník: 6. Zuzana Štichová Umění a kultura hudební výchova hudební nástroje Datum vytvoření: červen 2012 Materiál: Anotace: Metodické pokyny: Zdroj: VY_32_INOVACE_S2.2_HV.6.05
Vlnění. vlnění kmitavý pohyb částic se šíří prostředím. přenos energie bez přenosu látky. druhy vlnění: 1. a. mechanické vlnění (v hmotném prostředí)
 Vlnění vlnění kmitavý pohyb částic se šíří prostředím přenos energie bez přenosu látky Vázané oscilátory druhy vlnění: Druhy vlnění podélné a příčné 1. a. mechanické vlnění (v hmotném prostředí) b. elektromagnetické
Vlnění vlnění kmitavý pohyb částic se šíří prostředím přenos energie bez přenosu látky Vázané oscilátory druhy vlnění: Druhy vlnění podélné a příčné 1. a. mechanické vlnění (v hmotném prostředí) b. elektromagnetické
UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY
 Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ A VÝTVARNÝ OBOR Schválilo Ministerstvo školství, mládeže a tělovýchovy České republiky dne
Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ A VÝTVARNÝ OBOR Schválilo Ministerstvo školství, mládeže a tělovýchovy České republiky dne
Příklady kmitavých pohybů. Mechanické kmitání (oscilace)
 Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Mechanické kmitání (oscilace) pohyb, při kterém se těleso střídavě vychyluje v různých směrech od rovnovážné polohy př. kyvadlo Příklady kmitavých pohybů kyvadlo v pendlovkách struna hudebního nástroje
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454
 Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 5 íé= Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1..00/21.2759 Název DUM: Zvukové jevy -
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 5 íé= Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1..00/21.2759 Název DUM: Zvukové jevy -
B2M31SYN 3. PŘEDNÁŠKA 17. října 2018
 B2M31SYN 3. PŘEDNÁŠKA 17. října 218 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Hudební nástroje Barva zvuku Spektrum Aditivní syntéza a spektrální modelování Parciály Fourierovy
B2M31SYN 3. PŘEDNÁŠKA 17. října 218 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Hudební nástroje Barva zvuku Spektrum Aditivní syntéza a spektrální modelování Parciály Fourierovy
Přednáška 3: Limita a spojitost
 3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
1. KŠPA Kladno, s. r. o., Holandská 2531, Kladno, FYZIKA. Kapitola 8.: Kmitání Vlnění Akustika. Mgr. Lenka Hejduková Ph.D.
 1. KŠPA Kladno, s. r. o., Holandská 2531, 272 01 Kladno, www.1kspa.cz FYZIKA Kapitola 8.: Kmitání Vlnění Akustika Mgr. Lenka Hejduková Ph.D. 1 Kmitání periodický pohyb: pohyb který se pravidelně opakuje
1. KŠPA Kladno, s. r. o., Holandská 2531, 272 01 Kladno, www.1kspa.cz FYZIKA Kapitola 8.: Kmitání Vlnění Akustika Mgr. Lenka Hejduková Ph.D. 1 Kmitání periodický pohyb: pohyb který se pravidelně opakuje
Komplexní analýza. Fourierovy řady. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
Středoškolská technika SCI-Lab
 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY
 Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ, TANEČNÍ, VÝTVARNÝ A LITERÁRNĚ-DRAMATICKÝ OBOR Pozn.: platné učební plány VO viz Vzdělávací
Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ, TANEČNÍ, VÝTVARNÝ A LITERÁRNĚ-DRAMATICKÝ OBOR Pozn.: platné učební plány VO viz Vzdělávací
Vstupní signál protne zvolenou úroveň. Na základě získaných údajů se dá spočítat perioda signálu a kmitočet. Obrázek č.2
 2. Vzorkovací metoda Určení kmitočtu z vzorkovaného průběhu. Tato metoda založena na pozorování vstupního signálu pomocí osciloskopu a nastavení určité úrovně, pro zjednodušování považujeme úroveň nastavenou
2. Vzorkovací metoda Určení kmitočtu z vzorkovaného průběhu. Tato metoda založena na pozorování vstupního signálu pomocí osciloskopu a nastavení určité úrovně, pro zjednodušování považujeme úroveň nastavenou
Jednofaktorová analýza rozptylu
 I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
I I.I Jednofaktorová analýza rozptylu Úvod Jednofaktorová analýza rozptylu (ANOVA) se využívá při porovnání několika středních hodnot. Často se využívá ve vědeckých a lékařských experimentech, při kterých
Syntéza zvuků a hudebních nástrojů v programovém prostředí MATLAB
 Syntéza zvuků a hudebních nástrojů v programovém prostředí MATLAB Úvod Cílem této semestrální práce je syntéza orchestrálních nástrojů pro symfonickou báseň Vltava Bedřicha Smetany a libovolná vlastní
Syntéza zvuků a hudebních nástrojů v programovém prostředí MATLAB Úvod Cílem této semestrální práce je syntéza orchestrálních nástrojů pro symfonickou báseň Vltava Bedřicha Smetany a libovolná vlastní
NOTY A POMLKY - OPAKOVÁNÍ
 NOTY A POMLKY - OPAKOVÁNÍ Doplň názvy not. Napiš půlové noty. e 1 c 1 g 1 h 1 d 1 a 1 c 2 f 1 Zařaď hudební nástroje (smyčcové, dechové plechové-žesťové, dechové dřevěné, bicí). TYMPÁNY POZOUN KONTRABAS
NOTY A POMLKY - OPAKOVÁNÍ Doplň názvy not. Napiš půlové noty. e 1 c 1 g 1 h 1 d 1 a 1 c 2 f 1 Zařaď hudební nástroje (smyčcové, dechové plechové-žesťové, dechové dřevěné, bicí). TYMPÁNY POZOUN KONTRABAS
Měření hlasitosti zvuku. Tematický celek: Světelné a zvukové jevy. Úkol:
 Název: Měření hlasitosti zvuku. Tematický celek: Světelné a zvukové jevy. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni
Název: Měření hlasitosti zvuku. Tematický celek: Světelné a zvukové jevy. Úkol: 1. Zopakuj si, co je to zvuk a ultrazvuk, jaké jsou jednotky hlasitosti zvuku. 2. Jak funguje zvukový senzor. 3. Navrhni
2 Konstrukce houslového nástroje
 Kořenov, 2012 PYTHAGOREJSKÉ LADĚNÍ Jan Hadrava, Jan Sixta, Martin Mirbauer Konzultant: Roman Cach 1 Úvod Púvodním cílem projektu bylo zkonstruovat jednostrunný hudební nástroj podobný houslím, na kterém
Kořenov, 2012 PYTHAGOREJSKÉ LADĚNÍ Jan Hadrava, Jan Sixta, Martin Mirbauer Konzultant: Roman Cach 1 Úvod Púvodním cílem projektu bylo zkonstruovat jednostrunný hudební nástroj podobný houslím, na kterém
Zpráva k semestrální práci
 ČVUT FEL Zpráva k semestrální práci A2B31SMS Jan Vimr 2017/2018 1. Postup Zadáním semestrální práce byla syntéza libovolného hudebního nástroje pro skladbu: Let čmeláka Nikolaj Rimskij Korsakov, dále odevzdat
ČVUT FEL Zpráva k semestrální práci A2B31SMS Jan Vimr 2017/2018 1. Postup Zadáním semestrální práce byla syntéza libovolného hudebního nástroje pro skladbu: Let čmeláka Nikolaj Rimskij Korsakov, dále odevzdat
Náhodné chyby přímých měření
 Náhodné chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně pravděpodobná.
Náhodné chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně pravděpodobná.
Experimentální realizace Buquoyovy úlohy
 Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
Jak na akordové značky
 Jak na akordové značky Cíl článku: Cílem článku je naučit Vás porozumět akordovým značkám a získat schopnost najít si a posléze zahrát na kytaru jakýkoliv akord. V článku rozhodně nenajdete zobrazení všech
Jak na akordové značky Cíl článku: Cílem článku je naučit Vás porozumět akordovým značkám a získat schopnost najít si a posléze zahrát na kytaru jakýkoliv akord. V článku rozhodně nenajdete zobrazení všech
Náhodné (statistické) chyby přímých měření
 Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
Náhodné (statistické) chyby přímých měření Hodnoty náhodných chyb se nedají stanovit předem, ale na základě počtu pravděpodobnosti lze zjistit, která z možných naměřených hodnot je více a která je méně
Ministerstvo školství, mládeže a tělovýchovy České republiky HUDEBNÍ, TANEČNÍ, VÝTVARNÝ A LITERÁRNĚ DRAMATICKÝ OBOR
 Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ, TANEČNÍ, VÝTVARNÝ A LITERÁRNĚ DRAMATICKÝ OBOR 1995 Přípravné studium: pro děti 5 7 leté HUDEBNÍ
Ministerstvo školství, mládeže a tělovýchovy České republiky UČEBNÍ PLÁNY PRO ZÁKLADNÍ UMĚLECKÉ ŠKOLY HUDEBNÍ, TANEČNÍ, VÝTVARNÝ A LITERÁRNĚ DRAMATICKÝ OBOR 1995 Přípravné studium: pro děti 5 7 leté HUDEBNÍ
Základy Hudební Akustiky. 1. Úvod
 Základy Hudební Akustiky 1. Úvod Výuka Bude vás učit: Lubor Přikryl Výuka je za JAMU prikryl@jamu.cz prikryllubor@feec.vutbr.cz lubor@audified.com Zápočty Podmínky pro udělení zápočtu Test - splnění %
Základy Hudební Akustiky 1. Úvod Výuka Bude vás učit: Lubor Přikryl Výuka je za JAMU prikryl@jamu.cz prikryllubor@feec.vutbr.cz lubor@audified.com Zápočty Podmínky pro udělení zápočtu Test - splnění %
Akustické vlnění. Akustická výchylka: - vychýlení objemového elementu prostředí ze střední polohy při vlnění
 Zvukové (akustické) vlny: Akustické vlnění elastické podélné vlny s frekvencí v intervalu 16Hz-kHz objektivní fyzikální příčina (akustická vlna) vyvolá subjektivní vjem (vnímání zvuku) člověk tyto vlny
Zvukové (akustické) vlny: Akustické vlnění elastické podélné vlny s frekvencí v intervalu 16Hz-kHz objektivní fyzikální příčina (akustická vlna) vyvolá subjektivní vjem (vnímání zvuku) člověk tyto vlny
Semestrální práce z předmětu Syntéza audio signálů
 Semestrální práce z předmětu Syntéza audio signálů Téma: Syntéza orchestrálních nástojů ve skladbě Vltava od Bedřicha Smetany a syntéza zvuku mouchy Dominik Šmíd zimní semestr 2016/17 Obsah: 1. Úvod 2.
Semestrální práce z předmětu Syntéza audio signálů Téma: Syntéza orchestrálních nástojů ve skladbě Vltava od Bedřicha Smetany a syntéza zvuku mouchy Dominik Šmíd zimní semestr 2016/17 Obsah: 1. Úvod 2.
B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ
 B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ I. MECHANICKÉ KMITÁNÍ 8.1 Kmitavý pohyb a) mechanické kmitání (kmitavý pohyb) pohyb, při kterém kmitající těleso zůstává stále v okolí určitého bodu tzv. rovnovážné polohy
B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ I. MECHANICKÉ KMITÁNÍ 8.1 Kmitavý pohyb a) mechanické kmitání (kmitavý pohyb) pohyb, při kterém kmitající těleso zůstává stále v okolí určitého bodu tzv. rovnovážné polohy
Dodatek k ŠVP ZUV č. 3. Název školního vzdělávacího programu: Uměním k tvořivosti tvořivostí ke kultuře kulturou k hodnotám lidství
 Dodatek k ŠVP ZUV č. 3 Název školního vzdělávacího programu: Uměním k tvořivosti tvořivostí ke kultuře kulturou k hodnotám lidství Školní vzdělávací program pro základní umělecké vzdělávání Škola: Základní
Dodatek k ŠVP ZUV č. 3 Název školního vzdělávacího programu: Uměním k tvořivosti tvořivostí ke kultuře kulturou k hodnotám lidství Školní vzdělávací program pro základní umělecké vzdělávání Škola: Základní
VLASTNOSTI ZVUKU A ZVUKOVÝCH ZÁZNAMŮ
 VLASTNOSTI ZVUKU A ZVUKOVÝCH ZÁZNAMŮ Hana Hoffmanová, David Krejbich OBSAH PREZENTACE Definice a šíření zvuku Zdroje zvuku Vlastnosti zvuku Dělení zvukových záznamů Zajímavosti DEFINICE ZVUKU Zvuk = mechanické
VLASTNOSTI ZVUKU A ZVUKOVÝCH ZÁZNAMŮ Hana Hoffmanová, David Krejbich OBSAH PREZENTACE Definice a šíření zvuku Zdroje zvuku Vlastnosti zvuku Dělení zvukových záznamů Zajímavosti DEFINICE ZVUKU Zvuk = mechanické
VY_32_INOVACE_04_ Komorní orchestry_38
 VY_32_INOVACE_04_ Komorní orchestry_38 Autor: Jindřiška Čalová Škola : Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu : Zkvalitnění ICT ve slušovské škole Číslo projektu :
VY_32_INOVACE_04_ Komorní orchestry_38 Autor: Jindřiška Čalová Škola : Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu : Zkvalitnění ICT ve slušovské škole Číslo projektu :
Stupnice fis moll má 3 křížky fis, cis, gis
 1 Stupnice fis moll má 3 křížky fis, cis, gis E dur B dur A dur a moll harmonická melodická Crescendo = Decrescendo = Moderato = Allegro = Lento = Adagio = pp = fff = 2 Petr Iljič Čajkovskij Ruský skladatel
1 Stupnice fis moll má 3 křížky fis, cis, gis E dur B dur A dur a moll harmonická melodická Crescendo = Decrescendo = Moderato = Allegro = Lento = Adagio = pp = fff = 2 Petr Iljič Čajkovskij Ruský skladatel
Kapitola 1. Signály a systémy. 1.1 Klasifikace signálů
 Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
Racionální čísla. teorie řešené úlohy cvičení tipy k maturitě výsledky. Víš, že. Naučíš se
 teorie řešené úlohy cvičení tipy k maturitě výsledky Víš, že racionální v matematice znamená poměrový nebo podílový, zatímco v běžné řeči ho užíváme spíše ve významu rozumový? zlomky používali již staří
teorie řešené úlohy cvičení tipy k maturitě výsledky Víš, že racionální v matematice znamená poměrový nebo podílový, zatímco v běžné řeči ho užíváme spíše ve významu rozumový? zlomky používali již staří
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
08 - Optika a Akustika
 08 - Optika a Akustika Zvuk je mechanické vlnění v látkovém prostředí, které je schopno vyvolat sluchový vjem. Člověk je schopen vnímat vlnění o frekvenci 16 Hz až 20000 Hz (20kHz). Frekvenci nižší než
08 - Optika a Akustika Zvuk je mechanické vlnění v látkovém prostředí, které je schopno vyvolat sluchový vjem. Člověk je schopen vnímat vlnění o frekvenci 16 Hz až 20000 Hz (20kHz). Frekvenci nižší než
Direct Digital Synthesis (DDS)
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Ing. Radek Sedláček, Ph.D., katedra měření K13138 Direct Digital Synthesis (DDS) Přímá číslicová syntéza Tyto materiály vznikly za podpory
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická Ing. Radek Sedláček, Ph.D., katedra měření K13138 Direct Digital Synthesis (DDS) Přímá číslicová syntéza Tyto materiály vznikly za podpory
NÁVODNÍK za 5. ročník Co musím umět, abych mohl přestat chodit do nauky! Znám bezpečně kvintový a kvartový kruh:
 NÁVODNÍK za 5. ročník Co musím umět, abych mohl přestat chodit do nauky! Znám bezpečně kvintový a kvartový kruh: Pomůcky pro určování tónin: křížky: Kouknu na poslední křížek (poslední křížek zvyšuje 7.
NÁVODNÍK za 5. ročník Co musím umět, abych mohl přestat chodit do nauky! Znám bezpečně kvintový a kvartový kruh: Pomůcky pro určování tónin: křížky: Kouknu na poslední křížek (poslední křížek zvyšuje 7.
Rezonanční jevy na LC oscilátoru a závaží na pružině
 Rezonanční jevy na LC oscilátoru a závaží na pružině M. Stejskal, K. Záhorová*, J. Řehák** Gymnázium Emila Holuba, Gymnázium J.K.Tyla*, SPŠ Hronov** Abstrakt Zkoumali jsme rezonanční frekvenci závaží na
Rezonanční jevy na LC oscilátoru a závaží na pružině M. Stejskal, K. Záhorová*, J. Řehák** Gymnázium Emila Holuba, Gymnázium J.K.Tyla*, SPŠ Hronov** Abstrakt Zkoumali jsme rezonanční frekvenci závaží na
doc. Dr. Ing. Elias TOMEH Elias Tomeh / Snímek 1
 doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
Výukové texty. pro předmět. Měřící technika (KKS/MT) na téma
 Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D.
Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření akustických projevů (hluk, akustický tlak, šíření v prostředí Autor: Doc. Ing. Josef Formánek, Ph.D.
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují
 Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
Hluk a analýza vibrací stěn krytu klimatizační jednotky
 XXVI. ASR '00 Seminar, Instruments and Control, Ostrava, April 6-7, 00 Paper Hluk a analýza vibrací stěn krytu klimatizační jednotky KOČÍ, Petr Ing., Katedra ATŘ-, VŠB-TU Ostrava, 7. listopadu, Ostrava
XXVI. ASR '00 Seminar, Instruments and Control, Ostrava, April 6-7, 00 Paper Hluk a analýza vibrací stěn krytu klimatizační jednotky KOČÍ, Petr Ing., Katedra ATŘ-, VŠB-TU Ostrava, 7. listopadu, Ostrava
ZÁKLADNÍ STUDIUM HUDEBNÍHO OBORU
 ZÁKLADNÍ STUDIUM HUDEBNÍHO OBORU Vzdělávání na I. stupni základního studia je sedmileté a je určeno žákům, kteří dosáhli věku 7 let. Tato věková hranice platí bez ohledu na skutečnost, zdali žák navštěvoval
ZÁKLADNÍ STUDIUM HUDEBNÍHO OBORU Vzdělávání na I. stupni základního studia je sedmileté a je určeno žákům, kteří dosáhli věku 7 let. Tato věková hranice platí bez ohledu na skutečnost, zdali žák navštěvoval
Příloha č. 1. amplitudová charakteristika filtru fázová charakteristika filtru / frekvence / Hz. 1. Určení proudové hustoty
 Příloha č. 1 Při hodnocení expozice nízkofrekvenčnímu elektromagnetickému poli (0 Hz 10 MHz) je určující veličinou modifikovaná proudová hustota J mod indukovaná v tělesné tkáni. Jak je uvedeno v nařízení
Příloha č. 1 Při hodnocení expozice nízkofrekvenčnímu elektromagnetickému poli (0 Hz 10 MHz) je určující veličinou modifikovaná proudová hustota J mod indukovaná v tělesné tkáni. Jak je uvedeno v nařízení
7. Rozdělení pravděpodobnosti ve statistice
 7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
7. Rozdělení pravděpodobnosti ve statistice Statistika nuda je, má však cenné údaje, neklesejte na mysli, ona nám to vyčíslí Jednou z úloh statistiky je odhad (výpočet) hodnot statistického znaku x i,
9. cvičení z Matematické analýzy 2
 9. cvičení z Matematické analýzy 7. listopadu -. prosince 7 9. Určete Fourierovu řadu periodického rozšíření funkce ft = t na, a její součet. Definice: Necht f je -periodická funkce, která je integrabilní
9. cvičení z Matematické analýzy 7. listopadu -. prosince 7 9. Určete Fourierovu řadu periodického rozšíření funkce ft = t na, a její součet. Definice: Necht f je -periodická funkce, která je integrabilní
ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ 8. týden doc. Ing. Renata WAGNEROVÁ, Ph.D. Ostrava 2013 doc. Ing. Renata WAGNEROVÁ, Ph.D. Vysoká škola báňská
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ 8. týden doc. Ing. Renata WAGNEROVÁ, Ph.D. Ostrava 2013 doc. Ing. Renata WAGNEROVÁ, Ph.D. Vysoká škola báňská
1 Zpracování a analýza tlakové vlny
 1 Zpracování a analýza tlakové vlny 1.1 Cíl úlohy Prostřednictvím této úlohy se naučíte a zopakujete: analýzu biologických signálů v časové oblasti, analýzu biologických signálů ve frekvenční oblasti,
1 Zpracování a analýza tlakové vlny 1.1 Cíl úlohy Prostřednictvím této úlohy se naučíte a zopakujete: analýzu biologických signálů v časové oblasti, analýzu biologických signálů ve frekvenční oblasti,
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ
 VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
VYUŽITÍ PRAVDĚPODOBNOSTNÍ METODY MONTE CARLO V SOUDNÍM INŽENÝRSTVÍ Michal Kořenář 1 Abstrakt Rozvoj výpočetní techniky v poslední době umožnil také rozvoj výpočetních metod, které nejsou založeny na bázi
Pořadové číslo projektu
 Pořadové číslo projektu Nově a lépe s počítači Šablona č.: III/2 Datum vytvoření: 5.12.2012 Pro ročník: VII. Vzdělávací obor - předmět: Hudební výchova Klíčová slova: hudba, klavír, struny, klávesy Název
Pořadové číslo projektu Nově a lépe s počítači Šablona č.: III/2 Datum vytvoření: 5.12.2012 Pro ročník: VII. Vzdělávací obor - předmět: Hudební výchova Klíčová slova: hudba, klavír, struny, klávesy Název
