Sbírka příkladů z matematické analýzy II. Petr Tomiczek

Transkript

1 Sbírka příkladů z matematické analýzy II Petr Tomiczek

2 Obsah Diferenciální rovnice. řádu 3. Separace proměnných Přechod k separaci Variace konstant Bernoulliova rovnice Lineární diferenciální rovnice n-tého řádu 8 3. Systémy funkcí Eulerova rovnice Rovnice s konstantními koeficienty Metoda snižování řádu Nehomogenní rovnice Metoda odhadu tvaru partikulárního řešení Okrajové úlohy Úlohy na vlastní čísla a vlastní funkce Soustavy lineárních diferenciálních rovnic 8 4. Soustavy homogenních diferenciálních rovnic Soustavy nehomogenních diferenciálních rovnic Posloupnosti a řady funkcí 5. Posloupnosti funkcí Funkční řady Mocniné řady Fourierovy řady 7 7 Limity, derivace a diferenciál funkcí více reálných proměnných 30 8 Řešení funkcionálních rovnic, tečná rovina 30 9 Extrémy funkcí více proměnných 3 9. Optimalizační úlohy bez vazeb Optimalizační úlohy s vazbami Vícenásobné integrály 3 0. Dvojné integrály Trojné integrály

3 Diferenciální rovnice. řádu. Separace proměnných Příklad : Najděte obecné řešení (obecný integrál) diferenciální rovnice y = tg x tg y. Separací proměnných převedeme rovnici na tvar dy dx = tg x tg y cos y sin y dy = sin x cos x dx a substitucemi u = sin y, v = cos x dostaneme po integrování ln u = ln v + ln C, neboli sin y = C cos x. (xy + x)dx + (y x y)dy = 0 (obecný integrál). + y = C( x ) 3. xyy = x x + y = ln Cx 4. y tg x y = a y = C sin x a 5. xydx + (x + )dy = 0 y = C(x + )e x 6. y + dx = xydy ln x = C + y + ; x = 0 7. e y ( + x )dy x( + e y )dx = 0 + e y = C( + x ) 8. (x )y + xy = 0, y(0) = y{ln( x ) + } = 9. y sin x = y ln y, y( π ) = e y = e tg x 0. sin y cos xdy = cos y sin xdx, y(0) = π 4 cos x = cos y. y cotg x + y =, y( π 3 ) = 0 y = 4 cos x Řešení pomocí webmathematicy 3

4 . Rovnice umožnující přechod k separaci proměnných. Příklad : Najděte obecné řešení diferenciální rovnice y = 3 + (x + y). Substitucí x + y = u, + y = u převedeme rovnici na tvar u = 3 + u du dx = u u. Separaci proměnných a integrováním dostaneme u u du = dx, neboli u ln u = x C a přejdeme k původním proměnným 3x + y + ln x y = C. Příklad 3 : Najděte obecné řešení diferenciální rovnice (x + y + ) dx + (x + y ) dy = 0. Substitucí x + y = u, dx + dy = du převedeme rovnici na tvar (u + ) dx + (u )(du dx) = 0 (3 u) dx + (u ) du = 0. Separaci proměnných a integrováním dostaneme u 3 u du + dx = C, neboli u 5 ln u 3 + x = C a přejdeme k původním proměnným x + y + 5 ln x + y 3 = C. 4. y y = x 3 x + y = Ce x 5. y = sin(x y) 6. y = 4x + y 7. y = cos(x y ) 8. y + x + y = x + y x + C = cotg( y x + π 4 ) 4x + y ln( 4x + y + ) = x + C y = x arcotg( C x ) + kπ; k Z x + C = u + 3 ln u 8 3 ln(u + ) u = + x + y 4

5 Příklad 9 : Najděte obecné řešení diferenciální rovnice y = x + xy xy Substitucí y = ux, y = u x + u převedeme rovnici na tvar. u x + u = x + xux xux Integrováním dostaneme u + du = ln u + + (u + ) u + a přejdeme k původním proměnným 0. y = x+y x y. y = xy x y u du (u + ) = dx x. = ln x + C ln y x + + y = ln x + C ln x + y + x + x x + y = C. arcotg yx = ln C x + y x + y = Cy. xy y = x + y x = C + Cy) 3. (3y + 3xy + x )dx = (x + xy)dy 4. (x + y )y = xy (x + y) = Cx 3 e x x+y y x = Cy, y = 0 5. xy = y cos ln y x ln Cx = cotg( ln y x ) y = xe kπ, k Z 6. y + x + y xy = 0, y() = 0 y = x 7. (xy y) arcotg y x = x, y() = 0 x + y = e y x arcotg y x 8. (y 3x )dy + xydx = 0, y(0) = 9. y = y xy x y +xy x, y() = y 3 = y x y = x 5

6 .3 Variace konstant Příklad 30 : Metodou variace konstanty řešte diferenciální rovnici y cos x + y = tg x. Nejdříve vyřešíme homogenní rovnici metodou separace proměnných y cos x + y = 0 ln y + tg x = ln C y = Ce tgx. Řešení nehomogenní rovnice hledáme ve tvaru y = C(x)e tgx. Po dosazení do původní rovnice dostaneme (C (x)e tgx + C(x)e tgx cos x ) cos x + C(x)e tgx = tg x. tedy C (x)e tgx cos x = tg x C(x) = e tgx (tgx ) + K. Obecné řešení rovnice má tvar y = Ce tgx + tg x =. 3. xy y = x 4 y = Cx + x 4 3. xy + y + = 0 xy = C ln x 33. xy + (x + )y = 3x e x xy = (x 3 + C)e x 34. (xy + e x )dx xdy = 0 y = e x (ln x + C) 35. y = x(y x cos x) y = x(c + sin x) 36. (xy ) ln x = y y = C ln x ln x 37. y sin x + y cos x = y = sin x + C cos x 38. (e y x)y = x = e y + Ce y 39. y = y 3x y x = Cy 3 + y 40. y = x sin y+ sin y x = 8 sin y cos + y Ce 4. y + 3y x = x 3, y() = 4. y xy =, y(0) = 0 y = x + 3 x y = e x x 0 e t dt 43. xy y = sin x cos x, y je omezená pro y = cos x 44. x y xy = x cos x 3 sin x, y 0 pro x y = sin x x 45. ( + x ) ln( + x )y xy = ln( + x ) x arcotg x y = arcotg x y π pro x 6

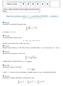
7 .4 Bernoulliova rovnice Příklad 46 : Převodem na lineární diferenciální rovnici vyřešte Substitucí z = y z = yy x y y = x y. dostaneme xy y y = x xz z = x. Vyřešíme lineární rovnici. hom. rovnice. part. řešení xz z = 0 x C e x = x z h = C e x C = e x z p = e x e x = 3. obecné řešení z = C e x + y = C e x y + y = y e x y(e x + Ce x ) =, y = xy x y = 4y y = x 4 ln Cx, y = xy + y + x 5 y 3 e x = 0 y = x 4 (e x + C), y = ( + x )y = xy + x y y = +x (C x + x ln(x + x + )) 7

8 3 Lineární diferenciální rovnice n-tého řádu 3. Systémy funkcí Příklad 5 : Máme rozhodnout o lineární závislosti nebo nezávislosti funkcí, x, x na intervalu I = (, ). Budeme zkoumat, kdy x I nastane rovnost c + c x + c 3 x = 0. Postupně pro x = 0 dostaneme c = 0, pak pro x = a x = dostaneme c + c 3 = 0 a c + c 3 = 0. Odtud plyne c = 0, c 3 = 0. Podle definice jsou funkce, x, x lineárně nezávislé. Wronskián daných funkcí je W (x) = x x 0 x 0 0 = 0. Tedy i podle věty 0.4 jsou funkce, x, x lineárně nezávislé. Rozhodněte o lineární závislosti nebo nezávislosti následujících funkcí 5.,, x, x 53. e x, xe x, x e x 54. 5, cos x, sin x závislé nezávislé závislé 55. cos x, cos(x + ), cos(x ) závislé 56., arcsin x, arccos x závislé 57. cos x, sin x, cos x nezávislé Najděte Wronskián funkcí 58., x 59. e x, xe x 60., cos x, cos x 6. 4, sin x, cos x 6. e 3x sin x, e 3x cos x e x 8 sin 3 x 0 e 6x 8

9 3. Eulerova rovnice Řešení Eulerovy rovnice x n y (n) + a n x n y (n ) + + a x y + a 0 y = 0, kde a 0,..., a n R hledáme ve tvaru y(x) = x λ, (popř. x λ ln x,..., x λ ln k x) λ C. Příklad 63 : Dosazením funkce y(x) = x λ do rovnice x y 4xy + 6y = 0 dostaneme x λ(λ )x λ 4xλx λ + 6x λ = 0, tedy (λ 5λ + 6) x λ = 0. Tato rovnost je splněna (při x 0) pro kořeny λ =, λ = 3, uvedeného polynomu. Funkce y (x) = x, y (x) = x 3 tvoří fundamentální systém dané rovnice a její obecné řešení má tvar y = C x + C x 3. Příklad 64 : Podobně při řešení rovnice x y 3xy + 4y = 0 dostaneme λ 4λ + 4 = 0 λ, = a fundamentální systém rovnice je tvořen funkcemi y (x) = x, y (x) = x ln x. Obecné řešení má tedy tvar y = C x + C x ln x. Příklad 65 : Řešení rovnice x y + 3xy + y = 0 hledáme ve tvaru y(x) = x λ. Po dosazení do rovnice dostaneme λ + λ + = 0 λ = + i, λ = i. Do fundamentálního systému tedy patří funkce y (x) = x +i, y (x) = x i nebo y (x) = x cos(ln x), y (x) = x sin(ln x) a obecné řešení rovnice má tvar y = C x cos(ln x) + C x sin(ln x). 66. x y 3xy y = 0 y = C x C x x 3 y x y = 0 y = C + C x + C 3 x ln x 68. x y + 5xy + 3y = 0 y = C x + C x x y + 7xy + 8y = 0 y = C x + C x x 3 y 6y = 0 y = C x 3 + C cos( ln x) + C 3 sin( ln x) 7. x y xy + y = 0 ; y(0) = 0, y (0) = y = C x 9

10 3.3 Rovnice s konstantními koeficienty Příklad 7 : koeficienty Řešení homogenní lineární diferenciální rovnice s konstantními y y y = 0 hledáme ve tvaru y(x) = e λx (popř. xe λx,..., x k e λx ), kde číselný parametr λ je kořenem charakteristické rovnice (charakteristického polynomu) λ λ + = 0. Tedy λ = 4, λ = 3, fundamentální systém rovnice je tvořen funkcemi e 4x, e 3x a obecné řešení rovnice má tvar Příklad 73 : Rovnice y(x) = C e 4x + C e 3x. y 4y + 4y = 0 má charakteristickou rovnici λ 4λ + 4 = 0 λ, =. Fundamentální systém rovnice je nyní tvořen funkcemi y (x) = e x, y (x) = x e x a obecné řešení rovnice má tvar y = C e x + C x e x. Příklad 74 : K rovnici y + 4y = 0 přísluší charakteristická rovnice λ + 4 = 0 s kořeny λ = i, λ = i. Fundamentální systém je tvořen funkcemi y (x) = e ix, y (x) = e ix nebo y (x) = cos x, y (x) = sin 3x. Obecné řešení má tvar y(x) = C cos x + C sin x. 75. y + y + y y = 0 y = e x ( + x), y(0) =, y (0) =, y (0) = y 4y + 3y = 0; y(0) = 6, y (0) = 0 y = 4e x + e 3x 77. y + 6y + y + 6y = 0 y = C e x + C e x + C 3 e 3x 78. y (6) + y (5) + y (4) = 0 y = C + C x + C 3 x + C 4 x 3 + e x (C 5 + C 6 x) 79. 4y 8y + 5y = 0 y = e x (C cos x + C sin x ) 80. y 8y = 0 y = C e x + e x (C cos 3x + C 3 sin 3x 8. y (4) +4y +0y +y +5y = 0 y = (C + C x)e x + (C 3 cos x + C 4 sin x)e x 8. y y + y = 0; y(0) = 0, y (0) = y = e x sin x 83. y y + 3y = 0; y(0) =, y (0) = 3 y = e x (cos x + sin x) 0

11 3.4 Metoda snižování řádu Pokud známe jedno řešení y (x) homogenní rovnice, pak další partikulární řešení hledáme ve tvaru y(x) = y (x) z(x). Příklad 84 : Rovnice (sin x cos x) y sin x y + (cos x + sin x) y = 0 má jedno řešení y = e x. Pro druhé řešení y(x) = e x z(x), platí y = e x (z + z ), y = e x (z + z + z ) a po dosazení do původní rovnice máme (sin x cos x) e x (z + z + z ) sin x e x (z + z ) + (cos x + sin x) e x z = 0 (sin x cos x) (z + z ) sin x z = 0 (u = z ) (sin x cos x) u cos x u = 0 (sin x cos x) du = cos x u dx u du = cos x sin x cos x dx ; vypočteme integrál vpravo cos x sin x cos x dx = cos x sin x cos x dx = cos x sin x + cos x + sin x dx = sin x cos x { } v = sin x cos x = dx+ dv = (cos x + sin x) dx v dv = x +ln sin x cos x +C ; tedy ln u = x + ln sin x cos x +Ĉ u = Ce x (sin x cos x) (= z ) z = Ce x ( sin x) y = e x Ce x ( sin x) = C sin x a obecné řešení má tvar y = C e x + C sin x. Nalezněte obecné řešení následujících rovnic, jestliže znáte partikulární řešení 85. ( x )y xy + 4 y = 0; y = + x y = C + x + C x 86. x (x + )y y = 0; y = + x y = C ( + x ) + C ( x + x+ x ln x + ) 87. xy + y xy = 0; y = ex x xy = C e x + C e x 88. y ( + tg x)y = 0; y = tg x y = C tg x + C ( + x tg x) 89. (e x + )y y e x y = 0; y = e x y = C (e x ) + C e x x (x )y + (4x 3)xy xy + y = 0 y = C x + C x + C 3(x ln x + ) y = x, y = x 9. (x x + 3)y (x + )y + xy y = 0 y = C x + C e x + C 3 (x ) y = x, y = e x

12 3.5 Nehomogenní rovnice Příklad 9 : Metodou variace konstant vyřešíme rovnici y + 9y = sin 3x.. Určíme obecné řešení homogenní rovnice y + 9y = 0 (viz metoda charakteristické rovnice, příklad (7)) λ + 9 = 0 y h (x) = C cos 3x + C sin 3x.. Partikulární řešení y p nehomogenní rovnice hledáme ve tvaru Funkce y p (x) = C (x) cos 3x + C (x) sin 3x. C (x), C (x) splňují soustavu algebraických rovnic: C cos 3x + C sin 3x = 0 3C cos 3x sin 3x + 3C sin 3x = 0, 3C sin 3x + 3C cos 3x = sin 3x 3C sin 3x cos 3x + 3C cos 3x = cos 3x sin 3x. Odtud po sečtení rovnic dostaneme 3C cos 3x = sin 3x C = 9 ln sin 3x a z první rovnice plyne C cos 3x cos 3x + 3 = 0 C = x 3. Partikulární řešení má tvar y p (x) = x 3 cos x + ln sin 3x sin 3x Obecným řešením úlohy je funkce y(x) = y h (x) + y p (x) = C cos 3x + C sin 3x x 3 cos x + ln sin 3x sin 3x. 9 Řešte rovnice 93. y y + y = ex x y = e x (x ln x + C x + C ) 94. y y + y = ex x + y = e x (C x + C ln x + + x arcotg x) 95. y + 3y + y = e x + y = (e x + e x ) ln(e x + ) + C e x + C e x 96. y + y + cotg x = 0 y = + C cos x + C sin x + cos(x) ln tg x Vyřešte rovnici,y y = f(x), jestliže 97. f(x) = ex +e y = e x (x + C x ) (e x + ) ln(e x + ) + C 98. f(x) = e x e y x = ex (arcsin(e x ) + e x e x + C ) + 3 ( e x ) 3 + C 99. f(x) = e x cos(e x ) y = C e x cos(e x ) + C

13 3.6 Metoda odhadu tvaru partikulárního řešení Příklad 00 : Pomocí odhadu tvaru partikulárníbo řešení vyřešíme rovnici y 5y = (x ).. Charakteristická rovnice λ 5λ = 0, má kořeny λ = 0, λ = 5 a homogenní řešení má tvar y h = C + C e 5x.. Z rovnosti (x ) = e ax (P n (x) cos bx + Q m (x) sin bx) vyplývá a = 0, b = 0, n =, m = 0 k =, R (x) = a x + a x + a 0, kde a, a, a 0 jsou konstanty. Kritické číslo a + i b = 0 je jednonásobný kořen charakteristické rovnice, tedy r =. Partikulární řešení nehomogenní rovnice hledáme ve tvaru y p (x) = x (a x + a x + a 0 ), potom y p(x) = a x + a x + a 0 + x (a x + a ) = 3a x + a x + a 0, y p(x) = 6a x + a. Po dosazení y p, y p do dané rovnice dostaneme: 6a x + a 5 (3a x + a x + a 0 ) = (x ), 5a x + (6a 0a )x + a 5a 0 = x x +, a partikulárním řešením je funkce a = 5, a = 4 5, = a 0 = 7 5, y p (x) = x ( 5 x x ). 3. Obecné řešení má tvar y(x) = C + C xe 5x + x ( 5 x x ). Metodou odhadu řešte rovnice 0. y + y = 4xe x y = C cos x + C sin x + (x + )e x 0. y y = e x x y = C e x + C e x + xe x + x y + y y = 3xe x y = C e x + C e x + ( x x 3 )ex 04. y 3y + y = sin x y = C e x + C e x + sin x cos x y + y = 4 sin x y = C cos x + C sin x x cos x 06. y 3y + y = x cos x y =C e x +C e x +( x 0 00 ) cos x (3x ) sin x 3

14 07. y + 3y 4y = e 4x + xe x y = C e x + C e 4x x 5 e 4x ( x )e x 08. y 9y = e 3x cos x y = C e 3x + C e 3x + e 3x ( 6 37 sin x 37 cos x) 09. y y + y = 6xe x y = (C + C x + x 3 )e x 0. y + y = x sin x y = (C x 4 ) cos x + (C + x 4 ) sin x Řešte rovnice s počáteční podmínkou. y + 9y = 6e 3x ; y(0) = y (0) = 0 y = 3 (cos 3x + sin 3x e3x ). y 4y + 5y = x e x ; y(0) =, y (0) = 3 y =e x (cos x sin x)+(x+) e x 3. y +6y +9y = 0 sin x ; y(0) = y (0) = 0 y = (x+ 3 5 )e 3x + 5 (4 sin x 3 cos x) 4. y + 4y = sin x ; y(0) = y (0) = y = cos x + 3 (sin x + sin x) 5. y + y = cos x ; y(0) =, y (0) = 0 y = cos x + x sin x Odhadněte partikulární řešení následujících rovnic 6. y 7y = (x ) A x 3 + A x + A 3 x 7. y + 7x = e 7x Axe 7x 8. y 8y + 6y = (0 x)e 4x (A x 3 + A x )e 4x 9. y + 5y = cos 5x x(a cos 5x + B sin 5x) 0. y + 4y + 8y = e x (sin x + cos x) (A cos x + B sin x)e x. y 4y + 8y = e x (sin x cos x) x(a cos x + B sin x)e x. y (4) y = 4 Ax 3 3. y + y + y = (x + ) sin x + (x 4x) cos x (Ax + Bx + C) cos x+ +(Dx + Ex + F ) sin x 4. y y = e x sin x + x e x (A cos x + B sin x)+ +x(cx + Dx + E) 5. y (4) 4y + 8y 8y + 4y = e x (x cos x + sin x) x e x {(Ax + B) cos x+ +(Cx + D) sin x} 6. y (5) y (4) +8y 8y +6y 6y = 3 cos x+ x (A cos x + B sin x) + C 4 y = 3 cos x +

15 3.7 Okrajové úlohy Příklad 7 : Pomocí charakteristické rovnice a dosazením okrajových podmínek vyřešíme smíšenou okrajovou úlohu y y 8y = 0, x (0, ), y(0) =, y () = 0. Charakteristická rovnice je λ λ 8 = 0 λ = 4, λ = a obecným řešením úlohy je funkce y(x) = C e 4x + C e x. Z okrajových podmínek dostaneme = C + C, C = +e, 6 0 = 4C e 4 C e, C = e6 +e. 6 Řešením okrajové úlohy je funkce y(x) = +e 6 e 4x + e6 +e 6 e x. Řešte následující okrajové úlohy 8. y y = 0 ; y(0) = 0, y(π) = y = sinh x sinh π 9. y + y = 0 ; y(0) = 0, y(π) = nemá řešení 30. y k y = 0 ; y(0) = v, y(x 0 ) = v y = sinh kx 0 (v sinh k(x 0 x)+v sinh kx) 3. y α y = 0 ; y(0) = v, y (x 0 ) = 0 y = v cosh(x 0 x) cosh αx 0 3. y α sy = 0 ; y(0) = s, y (x 0 ) = 0 s < 0; y = cos α s(x 0 x) s cos α sx 0 pro x 0 = (k+)π α s nemá řešení; s > 0; y = cosh α s(x 0 x) 33. y λ y = 0 ; λ 0, y(0) = 0, y() = λ 34. y λ y = 0 ; λ, y(0) = 0, y () = λ 35. y λ y = 0 ; λ, y (0) = 0, y() = λ pro x 0 (k+)π α s s cosh α sx 0 ; k =,, 3,... y = sinh λx λ sinh λ y = sinh λx λ cosh λ y = cosh λx λ cosh λ 36. xy + y = 0; y() = αy () ; y(x) je omezená pro x y = y (4) λ 4 y = 0; y(0) = y (0) = 0, y(π) = y (π) = 0 y = C sin kx pro λ = k k =,, 3,... y = 0 pro ostatní λ 5

16 3.8 Úlohy na vlastní čísla a vlastní funkce Příklad 38 : Určíme vlastní čísla a vlastní funkce okrajové úlohy y + λy = 0, y (0) = 0, y (π) = 0. Řešení hledáme ve tvaru y(x) = e kx, potom charakteristická rovnice má tvar k + λ = 0 k = ± λ. Pro λ < 0 je k = λ, k = λ a obecné řešení má tvar y(x) = C e λx + C e λx y (x) = λ C e λx λ C e λx. Z okrajových podmínek dostáváme soustavu rovnic pro neznámé konstanty C, C } 0 = C + C, 0 = λ C e λπ λ C e λπ C = 0, C = 0 y = 0., Pro λ = 0 má obecné řešení tvar y(x) = C + C x y (x) = C a z okrajových podmínek dostaneme Pro λ > 0 má obecné řešení tvar C R, C = 0 y = C. y(x) = C cos λx+c sin λx y (x) = λ C sin λx+ λ C cos λx. Z okrajových podmínek plyne 0 = C, 0 = C sin λπ, Dostáváme tak posloupnost vlastních čísel } λπ = nπ, n N. {, 4, 9, 6,...} a posloupnost jim odpovídajících vlastních funkcí je {cos x, cos x, cos 3x,...}. Najděte vlastní čísla a vlastní funkce úlohy y + λy = 0, je-li 39. x < 0, π >, y(0) = y (π) = 0 λ K = (K ) 4, y K = sin K x, K N 6

17 40. x < 0, π >, y (0) = y(π) = 0 4. x <, >, y() = y() = 0 4. x <, >, y() = y () = x <, >, y () = y() = x <, >, y () = y () = x < a, b >, y(a) = y(b) = x < a, b >, y(a) = y (b) = x < a, b >, y (a) = y(b) = 0 λ K = (K ) 4, y K = cos K x, K N λk = K π, y K = sin Kπx, K N λ K = (K ) π 4, y K = cos K πx, K N λ K = (K ) π 4, y K = sin k πx, K N λk = K π, y K = cos Kπx; K = 0,,,... λ K = K π λ K = (K ) π 4(b a) λ K = (K ) π 4(b a) (b a), y K = sin Kπ(x a) b a, K N, y K = sin (K )(x a)π (b a), K N, y K = cos (K )(x a)π (b a), K N Najděte vlastní čísla a vlastní funkce následujících okrajových úloh 48. y + y + λy = 0 ; x < 0, l >, y(0) = y(l) = 0 λ K = + K π ln l yk = l x sin Kπx l, K N 49. x y + xy + λy = 0 ; x <, l >, y() = y(l) = 0 λ K = K π Kπ ln x ln l, y ln l K =sin 50. y + (λ + )y = 0 λk = K π, K N x < 0, >, y(0)=y (0)=0, y() y ()=0 y K =sin(arcotg(kπ)+kπx) 5. y + x y +λy = 0 ; y(l)=0, y je omezená pro x 0 λ K = K π l, y K = Kπx x sin l 7

18 4 Soustavy lineárních diferenciálních rovnic Příklad 5 : 4. Soustavy homogenních diferenciálních rovnic 53. x = x + y y = 3x + 4y 54. x = x y y = y 4x 55. x + x 8y = 0 y x y = x = x + y y = 3y x x = C e t + C e 5t y = C e t + 3C e 5t x = C e t + C e 3t y = C e t C e 3t x = C e 3t 4C e 3t y = C e 3t + C e 3t x = e t (C cos t + C sin t y = e t {(C + C ) cos t + (C C ) sin t} 57. x = x 3y x = e t (C cos 3t + C sin 3t) y = 3x + y y = e t (C sin 3t C cos 3t) 58. x + x + 5y = 0 x = (C C ) cos t (C + C ) sin t y x y = 0 y = C cos t + C sin t 59. x = x + y x = (C + C t)e 3t y = 4y x y = (C + C + C t)e 3t 60. x = 3x y x = (C + C t)e t y = 4x y y = (C C + C t)e t 6. x = x + z y x = C e t + C e t + C 3 e t y = x + y z y = C e t 3C 3 e t z = x y z = C e t + C e t 5C 3 e t 6. x = 3x y + z x = C e t + C e t + C 3 e 5t y = x + y + z y = C e t C e t + C 3 e 5t z = 4x y + 4z z = C e t 3C e t + 3C 3 e 5t 63. x = 4y z 3x x = C e t + C 3 e t y = z + x y = C e t + C e t z = 6x 6y + 5z z = C e t C 3 e t 8

19 64. x = x y z x = e t (C sin t + C 3 cos t) y = x + y y = e t (C C cos t + C 3 sin t) z = 3x + z z = e t ( C 3C 3 cos t + 3C 3 sin t 65. x = 4x y z x = C e t + (C + C 3 )e 3t y = x + y z y = C e t + C e 3t z = x y + z z = C e t + C 3 e 3t 66. x = x y + z x = (C + C t)e t + C 3 e t y = x + y z y = (C C + C t)e t z = z y z = (C C + C t)e t + C 3 e t 67. x = 4x y x = (C + C t + C 3 t )e t y = 3x + y z y = {C C + (C C 3 )t + C 3 t }e t z = x + z z = {C C + C 3 + (C C 3 )t + C 3 t }e t 4. Soustavy nehomogenních diferenciálních rovnic 68. x = y + e t x = C e t + C e t + te t t y + x + t y = C e t C e t + (t )e t t 69. x = y 5 cos t x = C e t + C e t sin t cos t y = x + y y = C e t C e t + sin t + 3 cos t 70. x = 4x + y e t x = C e t + C e 3t + (t + )e t y = y x y = C e t C e 3t te t 7. x = y x + x = (C + C t)e t 3 y = 3y x y = (C + C + C t)e t 7. x = 5x 3y + e 3t x = C e t + 3C e 4t e t 4e 3t y = x + y + 5e t y = C e t + C e 4t e t e 3t 73. x = x 4y x = 4C e t + C e t 4te t y = x 3y + 3e t y = C e t + C e t (t )e t 74. x = x y x = C e 3t + 3t + t + C y = y x + 8t y = C e 3t + 6t t + C 75. x = x + y + 6te t x = C e t + C e 3t (t + 3)e t y = x y y = C e t C e 3t (8t + 6)e t 76. x = x y x = (C + C t t )e t y = x + e t y = {C C + (C + )t t }e t 9

20 77. x = x y + 8t x = C cos t C sin t + t + y = 5x y y = (C + C ) cos t + (C C ) sin t + 0t 78. x = x y x = C e t + C e 3t + e t ( cos t sin t) y = y x 5e t sin t y = C e t C e 3t + e t (3 cos t + sin t) 79. x = y + tg t x = C cos t + C sin t + tg t y = x + tg t y = C sin t + C cos t x = 4x y + e t x = C + C e t + e t ln e t y = 6x + 3y 3 e t y = C 3C e t 3e t ln e t 8. x = x y+ cos t x = C cos t + C sin t + t(cos t + sin t) + (cos t sin t) ln cos t y = x y y = (C C ) cos t + (C + C ) sin t + cos t ln cos t + t sin t 8. x = x + y z t + x = C e t + C sin t + C 3 cos t y = x y = t C e t + C cos t C 3 sin t z = x + y z t + z = + C sin t + C 3 cos t Najděte partikulární řešení následujících soustav diferenciálních rovnic 83. y = y + z ; y(0) = 0, z(0) = y = e t e 3t z = y + 4z z = e t e 3t 84. y = 3y z ; y(0) =, z(0) = 5 y = e t z = 0y 4z z = 5e t 85. x = 3x + 8y ; x(0) = 6, y(0) = x = (e t + e t ) y = 3y x y = e t e t 86. x = e t y 5x ; x(0) = 9 900, y(0) = 900 x = 4 5 et 36 et y = e t + x 3y y = 5 et et 87. x = y ; x(0) = y(0) = x = cos t + sin t y = x y = cos t sin t 88. x = 4x 5y ; x(0) = 0, y(0) = x = ( t)e t y = x y = te t 89. x = x + y + t ; x(0) = 7 9, y(0) = 5 9 x = 4 3 t 7 9 y = x y + t y = 3 t x = x + 5y ; x(0) =, y(0) = x = (sin t cos t)e t y = 3y x y = e t cos t 0

21 9. x = 6x y 6t t + 3 ; x(0) =, y(0) = 3 y = y t x = e t + e 3t + t + t y = e t + t +

22 5 Posloupnosti a řady funkcí Příklad 9 : 5. Posloupnosti funkcí Rozhodněte o stejnoměrné konvergenci posloupnosti {f n (x)}, je-li 93. f n (x) = n n +x x R nestejnoměrně, x <, > stejnoměrně 94. f n (x) = x n x < 0, > nestejnoměrně, x < 0, > stejnoměrně 95. f n (x) = arcotg nx n+x x < 0, + ) stejnoměrně 96. f n (x) = x n x n+ x < 0, > stejnoměrně 97. f n (x) = x n x n x < 0, > nestejnoměrně 98. f n (x) = nx +n x x < 0, > nestejnoměrně 99. f n (x) = x +n x x R stejnoměrně 00. f n (x) = x + n x x < 0, + > stejnoměrně 0. f n (x) = e n(x ) x (0, ) nestejnoměrně 0. f n (x) = arcotg nx x (0, + ) nestejnoměrně 03. f n (x) = x arcotg nx x (0, + ) stejnoměrně 5. Funkční řady Příklad 04 : Najděte obor konvergence řady u n (x), je-li 05. u n (x) = ln n x e < x < e 06. u n (x) = ( )n n+ ( x +x )n < 0, ) 07. u n (x) = +x n x R <, > 08. u n (x) = xn +x n x R {, }

23 09. u n (x) = ( )n+ x n 0. u n (x) = e nx x > x > 0 cos nx e nx. u n (x) = x > 0. u n (x) = (5 x ) n < x < 6 ln x 3. u n (x) = n x > e 4. u n (x) = n e nx x R {0} 5. u n (x) = xn x n Dokažte stejnoměrnou konvergenci 6. f n (x) = x +n 7. f n (x) = ( )n x+ n 8. f n (x) = x +n 4 x 9. f n (x) = sin nx 3 n4 +x 4 f n (x), je-li x < x R x 0 x R x R 0. f n (x) = nx +n 5 x x R. f n (x) = arcotg x x +n 3 x R. f n (x) = cos nx n 3. f n (x) = x sin(n x) +n 3 x 4 x R x 0 4. f n (x) = (arcotg x x +n ) x 0 5. f n (x) = ln( + x ) n, x a, a > 0 n ln n 6. f n (x) = sin( x n ) x x a, a > 0 n+ 7. f n (x) = sin( x n ) sin nx x +4n 8. f n (x) = n n! (x n + x n ) x R x 9. f n (x) = x e nx ε x a, (ε, a > 0, ε < a) 3

24 5.3 Mocniné řady Příklad 30 : Najděte poloměr konvergence řady ( ) n n n x n 5 n x 3n n n! n x n n 3 n (n 3 + )x n Najděte poloměr konvergence řady a n x n, je-li 35. a n = n e a n = n! 37. a n = (+i)n n n 38. a n = α n (0 < α < ) 39. a n = an n + bn n (a, b > 0) n 40. a n = 3 n + 4. a n = a n +b n (a, b > 0) 4. a n = ( ) n { n (n!) (n+)! }p min( a, b ) min(a, b) p 43. a n = ( )n n! ( n e )n 44. a n = a(a+)...(a+n )b(b+)...(b+n ) n!c(c+)...(c+n ) Najděte obor konvergence mocninné řady a n (x x 0 ) n, je-li 45. a n = n n, x 0 = < 0, > 4

25 46. a n = ( n 3n+ )n, x 0 = ( 7, ) 47. a n = ( )n n+, x 0 = 0 (, > 48. a n = 3 n3 n, x 0 = <, 4) n 49. a n = +3 n 3 +4n, x 0 = ( 3, ) 50. a n = 5n +( 3) n n+, x 0 = 0 < 5, 5 ) 5. a n = n+ ln 3n 3n+, x 0 = <, 0 > 5. a n = 3 n+ 3 n n, x 0 = 3 < 4, > 53. a n = n a, x 0 = 0, a > 0, a <, ) n 54. a n = 3, x n +n+ 0 = < 0, > Najděte rozvoj funkce f(x) v mocninou řadu 55. f(x) = e x 56. f(x) = cos x 57. f(x) = sin 3x sin 5x 58. f(x) = sin 3 x 59. f(x) = x (+x) 60. f(x) = 5x 4 x+ 6. f(x) = x x 3 +x 6. f(x) = ln x 5 ( ) n x n n! ; x R + ( ) n n (n)! xn ; x R ( ) n n (n)! ( 4n )x n ; x R ( ) n+ 3(3 n ) 4(n+)! x n+ ; x R ( ) n (n + )x n+ ; x (, ) + 4 7( ) n x n ; x (, ) n +( ) n 3 n+ 3 x n ; x (, ) n+ x n+ n+ ; x (, )

26 63. f(x) = ln 3 x +3x 64. f(x) = x ln 3 + {( 3 )n ( 3 )n } xn n ; x ( 3, 3 > 65. f(x) = + x + x f(x) = ( x ) 3 + n= (n )!! (n)!! x n ; x (, ) ( ) n (n 3)!! (n)!! x n ; x (, ) 67. f(x) = x x x f(x) = ( + x ) arcotg x x + Najděte rozvoj f(x) v mocninnou řadu 69. f(x) = ln(x + + x ) x f(x) = arcsin x 7. f(x) = arcotg x+3 x 3 7. f(x) = x x 73. f(x) = 74. f(x) = 75. f(x) = 4 x + π 4 + (n+)!! (n)!! x n ; x (, ) (n )!! n! x n+ ; x (, ) ( ) n+ 4n xn+ ; x <, > ( ) n (n )!! x n+ (n)!! n+ ; x <, > +x+x 3 x cos α x x cos α+x ln +x x + arcotg x (n )!! x n+ (n)!! n+ ; x <, > ( ) n+ 3 n+ x n+ n+ ; x < 3, 3 > 5 {( 5+ ) n+ + ( ) n ( 5 ) n+ }; x < 5 sin π(n+) 3 x n ; x (, ) x n cos nα; x (, ) x 4n+ 4n+ ; x (, ) 76. f(x) = x arcotg x ln + x ( ) n+ xn n(n ) ; x <, > 77. f(x) = x arcsin x + x + x + 6 (n )!! x n+ (n+)!! n+ ; x <, >

27 78. f(x) = ln(+x) +x 79. f(x) = ex x 80. f(x) = arcotg x 8. f(x) = e x sin x 8. f(x) = e x cos x ( ) n ( n )xn ; x (, ) u k! xn ; x (, ) k=0 ( ) n ( n )xn n ; x <, > n sin( nπ 4 ) n! x n ; x R 83. f(x) = ( arcsin x x ) Vypočtěte integrály x 84. e t dt x 0 x 0 x 0 sin t t dt dt t 4 t dt +t x x + ( ) n (n )!!x n+3 n cos( nπ 4 ) n! x n ; x R n+ (n!) (n+)! x n ; x ( ) n n!(n+) xn+ ; x R ( ) n x n+ (n+)(n+)! ; x R (n )!!x 4n+ (n)!!(4n+) ; x (, ) (n)!!(n+3) ; x <, > 6 Fourierovy řady Příklad 88 : Najděte Fourierovu řadu funkce f(x) na intervalu ( π, π), je-li 89. f(x) = x n+ sin nx ( ) n 7

28 90. f(x) = pro 0 x π f(x) = 0 pro π x 0 9. f(x) = x Výsledku využijte k sečtení řady π (n+) 9. f(x) = π x Výsledku využijte k sečtení řady 3 π f(x) = sign x Výsledku využijte k sečtení řady 94. f(x) = sin ax a Z 95. f(x) = cos ax a Z 96. f(x) = e ax a f(x) = q sin x q cos x+q q < π sinh aπ{ a + Najděte Fourierovu řadu funkce f(x), je-li + π 4 n, ( ) n+ n ( ) n n+ sin πa π sin πa π { ( ) n+ n 4 π a + sin(n )x n cos(n+)x (n+) ; π 8 cos nx; π 6, π sin(n )x n ; π 4 n+ n sin nx ( ) n a n a cos nx ( ) a n } ( ) n a +n (a cos nx n sin nx)} q n sin nx; zaveďte e ix = z 98. f(x) = π x, x (0, π) 99. f(x) = x, x (a, a + l) 300. f(x) = x, x (0, π) 30. f(x) = e ax, x ( h, h) a + l + l π sin nx n nπa π (sin l cos nπx l cos nπa l sin nπx l ) 4π sinh ah{ ah + ( ) f(x) = x cos x, x ( π, π ) π 303. f(x) = e x, x (0, π) 8 e π π { + cos nx n 4π sin nx n nπx nπx n ah cos( h ) n sin( h ) (ah) +(πn) } cos nx ( +n ( ) n+ n (4n ) sin nx n sin nx +n )}

29 Najděte Fourierovu řadu funkcí f n (x) = sin n x a g n (x) = cos n x pro n =, 3, 4, f (x) = cos x g (x) = + cos x 305. f 3 (x) = 3 4 sin x 4 sin 3x g3 (x) = 3 4 cos x + 4 cos 3x 306. f 4 (x) = 3 4 cos x + 8 cos 4x g4 (x) = cos x + 8 cos 4x 307. f 5 (x) = 5 8 sin x sin 3x 6 sin 5x g 5 (x) = 5 8 cos x cos 3x + 6 cos 5x Najděte Fourierovu řadu funkce f(x), je-li 308. f(x) = π 4 x, x (0, π) (kosinová řada) π 309. f(x) = x, x (0, π) (sinová řada) π cos(n+)x (n+) ( ) n+ { π n + n ( ) n } sin nx 30. f(x) = sin ax, a Z, x (0, π) (kosinová řada) 3. f(x) = cos ax, a Z, x (0, π) (sinová řada) cos(n+)x a (n+) pro a sudé a + cos nx a 4n }pro a liché 4a π 4a π { 4 π 8 π sin(n+)x a (n+) n sin nx a 4n pro a sudé pro a liché 3. f(x) = x( π x), x (0, π ) podle soustavy {cos(n )x}, n N (n ) { + 4( )n (n )π } cos(n )x {sin(n )x}, n N { ( )n (n ) + 8 (n ) } sin(n )x 3 Integrací Fourierova rozvoje funkce f(x) = x najděte rozvoj funkcí x, x 3, x 4, x 5 pro x ( π, π) 33. f(x) = x n+ sin nx ( ) 34. f(x) = x π n cos nx n ( ) n 9

30 35. f(x) = x 3 ( ) n 6 π n 36. f(x) = x 4 π ( ) n+ 6 π n n f(x) = x 5 ( ) n+ 0 0π n +π 4 n 4 n 5 n 3 sin nx cos nx sin nx 7 Limity, derivace a diferenciál funkcí více reálných proměnných Příklad 38 : Rozhodněte o spojitosti fce f v bodě 0, 0: 39. f(x, y) = x +y xy, f(0, 0) = 0 není spojitá 30. f(x, y) = ( + sin(x y)) ln x y, f(0, 0) = je spojitá Rozhodněte, zda fce f v bodě 0, 0 a ve směru (, ) roste nebo klesá 3. f(x, y) = (x + y ) sin x, fce roste 3. f(x, y) = tg y e x, fce klesá Najděte diferenciál funkce f v bodech 0, 0 a, 33. f(x, y) = df xy, f(0, 0) = 0 = 0dx + 0dy, df = x +y dx + 3 dy 8 Řešení funkcionálních rovnic, tečná rovina Příklad 34 : Pomocí věty o implicitní funkci zjistěte, jestli existuje jediné, spojité řešení y rovnice F (x, y) = 0 na okolí bodů A, B, C. Případně určete derivaci y v příslušném bodě. 30

31 35. F (x, y) = 3 x + y xy x 3y, A = 0, 3, B =,, C = 3, 0. A : y (0) = 5 3, B : Neex., C : Neex. 36. F (x, y) = x + 4y x + 6y + 3, A =,, B =,, C =, 0. A : Neex, B : y (0) = 0, C : Neex. 37. Určete parciální derivace prvního řádu funkce z = z(x, y) implicitně definované rovnicí z 3 3xyz 8 = 0 v bodě A = 0, 3. A : zx = 3, z y = 0, 38. Ke grafu funkce f najděte tečnou rovinu, která je rovnoběžná s rovinou ϱ. f(x, y) = x + y x, ϱ : 3x + y z = 0. 3(x ) + (y ) (z 3) = K nulové hladině funkce f najděte tečnou rovinu, která je rovnoběžná s rovinou ϱ. f(x, y, z) = x + y + 3z, ϱ : x + 4y + 6z = 0. (x ) + 4(y ) + 6(z ) = 0, (x + ) + 4(y + ) + 6(z + ) = 0 9 Extrémy funkcí více proměnných Příklad 330 : 9. Optimalizační úlohy bez vazeb Najděte lokální extrémy funkce f 33. f(x, y) = x 4 + y 4 x xy y,,, min, 0, 0 sedlo 33. f(x, y) = x + xy + y 4 ln x 0 ln y, min 333. f(x, y) = x + y + z + x + 4y 6z,, 3 min 334. f(x, y) = xy + z(a x y 3z) a 5, a 0, a 0 sedlo 0, ±, ±, 0 sedla,,, (e) (e) 335. f(x, y) = xy ln(x + y ), min,,,, max (e) (e) (e) (e) (e) (e) 3

32 9. Optimalizační úlohy s vazbami Příklad 336 : Najděte lokální extrémy funkce f vzhledem k množině M 337. f(x, y) = x + xy + y, M : 4x + y = 5, 3, 4, 3, 4 max,, 3,, 3 min 338. f(x, y) = x y + z, M : x + y + z =, 3, 3, 3 max, 3, 3, 3 min 339. f(x, y) = xy + yz, M : x + y =, y + z =,,, max Najděte min. a max. hodnoty funkce f vzhledem k množině M 340. f(x, y) = x + y + z, M : x + y z, min, + max 34. f(x, y) = x + y + 3z, M : x + y + z 00, 0 min, 300 max 0 Vícenásobné integrály Příklad 34 : 0. Dvojné integrály 343. y e x dx dy y x y+ x y 6 x x y 4 S 347. S x+y+ x (+y) x y dx dy dx dy e4 + 5 e 0 5 dx dy, kde S je trojúhelník s vrcholy,, 5,, 4, ln ln 6 x dx dy, kde S je dána nerovnostmi x y, 4x + y

33 0. Trojné integrály 348. xy 3 z (+z ) dx dy dz, kde V je dána nerovnostmi, x + y z, 0 V x, 0 y ln x yz 3 dx dy dz, kde V je dána nerovnostmi 0 x, 0 y x, V 0 z xy dx dy dz, kde V je dána nerovnostmi x + y 3, 0 y, 0 x, V x+y 4+z 0 z 4 9 ln 35. xy (4+z) dx dy dz, kde V je dána nerovnostmi x + y 4z 6 0 V 35. V x yz dx dy dz, kde V je dána nerovnostmi 4x + y + z, x 0, y 0, z