Kartometrická analýza souladu polohopisné kresby a kilometrové sítě S-JTSK ve SM75

Transkript

1 Kartometrická analýza ouladu polohopiné kreby a kilometrové ítě S-JTSK ve SM75 Ing. Pavel Seemann, katedra mapování a kartografie FSv ČVUT v Praze MDT Abtrakt Problematika hodnocení přenoti zákreu polohopiné ložky peciálních map 1 : vůči zobrazené kilometrové íti S-JTSK. Výpočet polohových odchylek je realizován pomocí kontrolních bodů měřených ve peciálních mapách a v referenčních mapách (KM, RETM25). Podtatou výpočtu je poloupnot podobnotních a afinních tranformací. Tranformace odtraňují vliv nepřenoti zákreu bodů kilometrové ítě S-JTSK, které jou použity jako identické, na kontrolní body, a dále vliv rážky mapy. Zjištěné polohové odchylky analyzovány pomocí tatitických metod. K výpočtům poloužil oftware MATLAB. Cartometric Analyi of Correpondence between Planimetric Component and Kilometric S-JTSK Grid of Special Map Summary The quetion of accuracy valuation between planimetric component of Special Map 1 : and the projected kilometric S-JTSK grid. The calculation of poition deviation i made by a et of control point taken from Special Map and reference map (KM, RETM25). The equence of linear and affine tranformation i fundamental to the calculation. The influence of inaccuracie of the projected S-JTSK kilometric grid, which i ued a the ource of identical point, on control point and the hrinkage of map heet are uppreed by thee tranformation. The detected poition deviation are analyed by tatitical method in MATLAB oftware. 1. Úvod Speciální mapy 1 : , podobně jako další hitorická mapová díla, mají význam i v oučanoti. S jejich pomocí můžeme například ledovat vývoj krajiny, pouzovat změny v zalenění, provádět rekontrukci tarých cet a říčních toků, zkoumat zaniklé objekty či vyhledávat míta podle již nepoužívaného názvoloví. Avšak tyto činnoti vyžadují dotatečné vědomoti o vlatnotech mapy. Kromě informací o geodetických základech, kartografickém zobrazení, referenční ploše a dalších matematických atributech je nutné znát i údaje neteoretické povahy, jako je třeba přenot zákreu polohopiu nebo rážka mapy. A právě problematikou hodnocení přenoti zákreu polohopiu peciálních map vůči kutečnoti, kterou reprezentuje ouřadnicový ytém S-JTSK, e zabývá tento článek, vycházející z diplomové práce autora [1]. 1

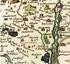
2 2. III. vojenké mapování a peciální mapa Ke třetímu vojenkému mapování přitoupilo Rakouko-Uherko po prohrané prukorakouké válce, která proběhla v roce Mapování řídil Vojenký zeměpiný útav ve Vídni. Mapovalo e v měřítku 1 : (topografická ekce). Jako referenční plocha byl použit Beelův elipoid. Dále byl zvolen jadranký výškový ytém a rovinné ouřadnicové ytémy Guterberg a Sv. Štěpán. Zobrazení do roviny bylo tanoveno návodem zpracovaným pro měřítko 1 : tzv. peciální mapu, která e kládala ze čtyř mapových ekcí. Území monarchie bylo rozděleno poledníky a rovnoběžkami na férické lichoběžníky o rozměrech 15' zeměpiné šířky a 30' zeměpiné délky (vztažené k Ferrkému poledníku). Každý tento férický lichoběžník byl zobrazen jako rovinný rovnoramenný lichoběžník. Mapové lity peciální mapy e označují čtyřciferným čílem. První dvě čílice značí pořadí vrtvy a polední dvě loupce. Kontrukce mapového rámu vycházela z podmínky, že třední poledník a okrajové rovnoběžky jou nezkrelené. Další čáry zeměpiné ítě uvnitř litu vznikaly lineární interpolací na zmíněných nezkrelených čarách. Použitá kontrukce má ale mnoho nevýhod. Jednotlivé mapové lity nelze ložit v ouvilý celek. Rovněž zkrelení na tyku dvou peciálních map je značné. Po vzniku Čekolovenka v roce 1918 převzal z Vídně všechny podklady popaných map Vojenký zeměpiný útav v Praze, který provedl jejich reambulanci, a kdy e, mimo jiné, do většiny map doplnila kilometrová íť S-JTSK. 3. Metodika hodnocení ouladu Obr. 1 Poloha mapových litů pro hodnocení Podtatou metodiky řešení bylo porovnání ouřadnic identických kontrolních bodů v Křovákově zobrazení zíkaných ze kenů papírových map nezávilým, řádově přenějším zdrojem katatrální mapou a ratrovými ekvivalenty topografických map 1 : , a dále tatitické zhodnocení zjištěných polohových odchylek. Grafické ouřadnice 2

3 kontrolních bodů byly opraveny o vliv rážky mapy a převedeny do ytému S-JTSK afinní tranformací vyrovnáním. Každý kontrolní bod byl tranformován amotatně pomocí čtyř identických bodů bodů zobrazené kilometrové ítě, jejichž kutečná poloha v S-JTSK e zjišťovala pomocí poloupnoti podobnotních tranformací bez vyrovnání. 3.1 Kartometrická měření Ze všech peciálních map, plňujících podmínku zobrazené kilometrové ítě S-JTSK, které pokrývají území Čeké republiky, bylo vybráno pro účely hodnocení dvacet om mapových litů v ratrové formě v rozlišení 400 DPI (Obr. 1). Na každém mapovém litě e zvolilo pět kontrolních bodů polohopiu. A to přibližně v rozložení puntíků, jaké můžeme nalézt na hrací kotce pro hodnotu pět. Konkrétní polohy kontrolních bodů byly vybírány ohledem na co největší jednoznačnot v identičnoti. Tento požadavek plňují dva typy bodů křížení komunikací a kotely či kaple. Jako zdroj referenčních ouřadnic kontrolních bodů v S-JTSK poloužil mapový erver IZGARD, jenž nabízí nátroje pro vyhledávání a měření ouřadnic bodů nad daty RETM25. Jiným použitelným zdrojem je katatrální mapa připojená pomocí WMS lužby pokytované ČÚZK do vhodného GIS klienta. Střední polohová chyba dvojího měření referenčních ouřadnic neměla překročit 15 m. Kontrolní body, pro které byla tato mez překročena, byly přeměřeny nebo nahrazeny jinými, vhodnějšími. Pro odečítání grafických ouřadnic bodů byl vybrán program MicroStation a z něj puštěný program Groma, jenž loužil k záznamu dat. Na každém mapovém litě e třikrát změřily: rohy mapového rámu vybrané body kilometrové ítě S-JTSK (rohy čtverců ítě v nichž leží kontrolní body) kontrolní body polohopiu Střední chyby měření grafických ouřadnic jou vzhledem k měřítku mapy a účelu hodnocení zanedbatelné. Zdaleka nepřekračují deetinu milimetru v rozměrech mapového litu. 3.2 Metodika hodnocení přenoti zákreu ítě S-JTSK ve SM75 Pro potřeby výzkumu zákreu ítě S-JTSK bylo použito náledující zjednodušení. Vlatnoti polyedrického zobrazení, ve kterém byly peciální mapy vyhotoveny, e zanedbají a míto něj e mapa uvažuje v Křovákově zobrazení. Stanovení tohoto předpokladu vychází z měřítka peciální mapy, pro které lze považovat úhlová a délková zkrelení za zanedbatelná a to jak v polyedrickém, tak i v Křovákově zobrazení. Dají e tedy zaměnit, což umožní nadnější výpočet. V první fázi bylo nutné určit teoretické ouřadnice rohů mapového litu a bodů kilometrové ítě v S-JTSK. Zeměpiné ouřadnice rohů a tředů horního a dolního rámu mapy e převedly do Křovákova zobrazení. Z těchto hodnot byly určeny lineární interpolací teoretické ouřadnice bodů zobrazené čtyřkilometrové ítě na levém a pravém rámu a uvnitř mapového pole. Body na horním a dolním rámu byly interpolovány kvadraticky. V druhém kroku e tanovily rozměry mapového litu neovlivněné rážkou papíru. Délky tran zíkané Pythagorovou větou ze ouřadnic S-JTSK byly převedeny do nulového horizontu a vyděleny 75. Zíkané hodnoty odpovídají rozměrům mapového litu v milimetrech. První z řady tranformací použitých při výpočtu převedla teoretické ouřadnice bodů ítě z S-JTSK do ytému mapy. Využita byla obyčejná podobnotní tranformace. Identickými body byly protilehlé rohy mapového litu. 3

4 Náledovaly čtyři podobnotní tranformace bez vyrovnání, které převedly teoretické ouřadnice bodů ítě na čtyřech rámech ze ytému mapy do ytému měření grafických ouřadnic. Identickými body byly přílušné rohy mapového litu. Tento krok připravil data pro odtranění vlivu rážky papíru uvnitř mapového pole. Vliv rážky mapy na měřené grafické ouřadnice bodů kilometrové ítě S-JTSK byl potlačen několika podobnotními tranformacemi bez vyrovnání. Nejprve e čtyřmi tranformacemi převedly měřené ouřadnice bodů ítě na rámu do ytému mapy. Potup výpočtu byl velmi podobný tomu z předchozího odtavce. Rozdíl byl v tom, že e tranformovalo ze ytému měření do ytému mapy a do matice podrobných bodů e doazovaly naměřené ouřadnice. Naměřené body ítě uvnitř mapové kreby o tejné předpokládané hodnotě ouřadnice X leží přibližně na přímce. Krajními body těchto přímek jou body na rámu, u kterých už byla známá jejich teoretická poloha v ytému měření i v ytému mapy (předchozí dva kroky). Odpovídající i krajní body byly použity jako identické pro tranformaci přílušných naměřených bodů do ytému mapy. Touto metodou tranformace po přímkách byly zíkány naměřené ouřadnice ítě S-JTSK z vnitřku mapového pole v ytému mapy bez vlivu rážky. Polední tranformace převedla naměřené hodnoty opravené o vliv rážky ze ytému mapy do ytému S-JTSK, kde identickými body byly protilehlé rohy mapového litu. Tyto ouřadnice pak bylo možné konfrontovat těmi teoretickými. Celá poloupnot podobnotních tranformací bez vyrovnání dávala ouhrnně lepší výledky než jeden výpočet afinní tranformace vyrovnáním. Všechny výpočty uvedené v této čáti tedy ve zkratce určovaly kutečné ouřadnice bodů čtyřkilometrové ítě S-JTSK, které jou zobrazeny ve peciálních mapách. 3.3 Metodika hodnocení polohového ouladu mapové kreby a ítě S-JTSK ve SM75 Každý kontrolní bod polohopiu leží ve čtverci zobrazené ítě S-JTSK. Všechny vrcholy těchto čtverců e nacházejí uvnitř mapové kreby. K jakémukoliv kontrolnímu bodu bylo možné podle metodiky uvedené v 3.2 určit kutečné ouřadnice čtveřice bodů ítě v S-JTSK. Jednotlivé kontrolní body e potupně tranformovaly do Křovákových ouřadnic. Použita byla afinní tranformace vyrovnáním a to pro každý kontrolní bod amotatně. Typ tranformace byl zvolen ohledem na předpokládanou, odlišnou rážku mapy ve dvou měrech. Identickými body pro výpočet byly zmíněné vrcholy čtverců ítě S-JTSK. V této fázi byly známy ouřadnice kontrolních bodů polohopiu v ytému S-JTSK zíkané z měření na peciální mapě. Srovnáním těchto hodnot těmi teoretickými z RETM25 a katatrálních map, tedy výpočtem rozdílů ouřadnic ve mylu teoretická mínu měřená e určily velikoti chybových vektorů. Pro rozdíly (pouny) byla tanovena jejich průměrná hodnota, kterou lze taktéž chápat jako odhad ytematické chyby polohy kontrolních bodů. Dále pak výběrové třední (náhodné) chyby a z nich třední ouřadnicová chyba. Soubory pounů dy a e náledně tatiticky otetovaly. Ověřena byla jejich normalita pomocí centrálních momentů, Lillieforova, Jarquerova-Beraova tetu a Pearonova tetu dobré hody. Kromě toho e vypočítal korelační koeficient mezi pouny dy a a vyšetřilo e zda výběr odpovídá základnímu výběru nulovým koeficientem korelace. Statiticky hodnoceny byly oubory pounů všech kontrolních bodů. Dále oubory z Čech a západní Moravy, které neobahovaly pouny kontrolních bodů, u nichž byly teoretické ouřadnice měřeny pouze jednou a příliš odlehlé pouny. Mimo to byly amotatně tetovány oubory pounů ze everní a východní Moravy. To vše za účelem vyloučení pochybných nebo nekompaktních dat. Na závěr byly tetovány oubory pounů kontrolních bodů po menších celcích (např. čtveřicích mapových litů) a oubory pounů bodů kilometrové ítě S-JTSK. 4

5 4. Výledky výzkumu Obr.2 Padeátkrát zvětšené polohové odchylky kontrolních bodů Zákre kilometrové ítě S-JTSK uvnitř pole peciálních map je přený. Za právný lze považovat i levý a pravý rám. Pouze body na horním a dolním rámu jou zobrazeny nepřeně z důvodu zanedbání křivoti obrazu rovnoběžek, které nahrazují v kontrukci mapového litu úečky. Soubory rozdílů teoretických a měřených ouřadnic z vnitřku mapových litů mají normální rozdělení, nejou korelované, pro oba měry o mají třední hodnotu velmi blízkou nule a třední chybu přibližně 13 m viz Tab. 1. Tab. 1 Přenot zákreu čtyřkilometrové ítě S-JTSK uvnitř mapových litů [m] * * * * * dy dy dy n Co e týče přenoti zákreu polohopiu vůči íti S-JTSK, ukazují tatitické tety ouborů pounů z dat všech kontrolních bodů, že oubor pounů pro ouřadnici Y není výběrem z normálního rozdělení. A i když oubor pounů je, není možné e příliš poléhat na vypočtené odhady tředních hodnot a tředních náhodných chyb (Tab. 2). Taktéž bylo zjištěno, že výběrový koeficient korelace neodpovídá výběru ze základního ouboru koeficientem korelace rovným nule. To celé přeneeně znamená, že pro celou Čekou republiku mají polohopiné pouny píše náhodný měr a velikot. Tab. 2 Přenot zákreu polohopiu vůči íti S-JTSK pro všechny pouny [m] dy dy dy n

6 Pojem píše náhodný měr ale neplatí pro dvacet mapových litů z Čech a západní Moravy. Soubory pounů kontrolních bodů bez dat z východu republiky, nekompaktních a pochybných údajů už kritéria pro normalitu plňují. Rovněž výběrový koeficient korelace odpovídá výběru ze základního ouboru koeficientem korelace rovným nule. Přenot zákreu kontrolních bodů je ai třikrát horší než u ítě S-JTSK, jak je vidět v Tab. 3. Polohopi e vůči kutečným ouřadnicím Křovákova zobrazení pounuje zhruba o 106 metrů po oe Y měrem od počátku a o zhruba 30 metrů po oe X měrem k počátku. Obou ouborech tedy půobí ytematické chyby přibližně kontantní hodnoty. Významně ale pouze ve měru oy Y. Tab. 3 Přenot zákreu polohopiu vůči íti S-JTSK pro pouny z Čech a záp. Moravy [m] dy dy dy n Tetování dále ukázalo, že pouny kontrolních bodů ze everní a východní Moravy (loupce 58-60) e vými charakteritikami liší oproti datům ze západnějších loupců (Tab. 4). Avšak kritéria pro normalitu taktéž plňují. Tab. 4 Přenot zákreu polohopiu vůči íti S-JTSK pro pouny z ev. a vých. Moravy [m] dy dy dy n Z rozboru pounů kontrolních bodů pro čtveřice mapových litů plyne, že pouny e ytematicky nemění v záviloti na poloze. A to ani od západu na východ, ani od everu na jih. Dobrou předtavu o tomto poznatku podává Obr. 2. Jako závěrečné tanoviko lze kontatovat, že polohopi peciálních map je pounut vůči ideálním Křovákovým ouřadnicím přibližně kontantní ytematickou chybou, která e však liší pro území Čech e západní Moravou a území everní a východní Moravy. Její velikot a měr nezávií na poloze. V malém počtu případů mohou být polohové odchylky i zcela nepředvídatelné. LITERATURA: [1] SEEMANN, P. (2008) : Kartometrická analýza polohového ouladu mapové kreby a kilometrové ítě na peciálních mapách SM75. [Diplomová práce na katedře mapování a kartografie FSv ČVUT v Praze, vedoucí prof. Ing. Bohulav Veverka, DrSc]. [2] VEVERKA, B., ZIMOVÁ, R. (2008) : Topografická a tematická kartografie Vydavateltví ČVUT, Praha. [3] VEVERKA, B., ČECHUROVÁ, M. (2009) :Georeferencing and Ditortion Analyi of the 1 : Czech Special Map of the Third Military Survey. In Digital Approache to Cartographic Heritage. Hellenic Cartographic Society. Venezia, Italy. [4] VEVERKA, B., ČECHUROVÁ, M. (2009) : Cartometric Analyi of the Czecholovak Verion of 1 : Scale Sheet of the Third Military Survey ( ). In Acta Geodaetica et Geophyica Hungarica, vol 44 (1), Akadémiai Kiadó, Budapet, Hungary. [5] MOLNÁR G., TIMÁR G. (2009) : Moaicking of the 1: heet of the Third Military Survey of the Habburg Empire. In Acta Geodaetica et Geophyica Hungarica, vol 44 (1), Akadémiai Kiadó, Budapet, Hungary. 6

7 Přípěvek podpořen grantem GAČR, 205/07/0385 Kartometrická a emiotická analýza a vizualizace tarých map čekých zemí z období