Tvorba perliček (beads) PERLIČKOVÝ EFEKT. Zvýšení koncentrace roztoku vede k odstranění perliček.
|
|
|
- Zuzana Němcová
- před 6 lety
- Počet zobrazení:
Transkript
1 Tvorba perliček (beads) PERLIČKOVÝ EFEKT Zvýšení koncentrace roztoku vede k odstranění perliček.
2 Tvorba perliček (beads) PERLIČKOVÝ EFEKT Snížení rychlosti dodávání roztoku vede ke zmenšení perliček Pouze u jehlového zvlákňování
3 Hlavní rysy P-R nestability, které se sledují jsou: - Délka rovné trysky - Vzdálenost mezi těmi jednotlivými kapkami (Rayleighova vlnová délka) - Objem kapek (zajímavé spíše pro výrobce inkouskových tiskáren elektricky nabité kapičky)
4 Kapalinová tryska je na počátku válcovitá = má konstantní poloměr. Díky gravitaci padá kapalinová trysky směrem dolů. Jak roste délka kapalinové trysky tak se začíná dosahovat kritické hodnoty. Při kritické hodnotě ztrácí kapalinová tryska svůj válcovitý tvar a začíná se přetvářet do soustavy kapek. Toto je primárně důsledek povrchového napětí.
5 Změny křivostí kapalinového tělesa 3D těleso, křivosti, konstrukce normály a normálových rovin (přednášeno ve Stereologii) K 1 =1/R 1 (R 1 je poloměr válce) K =1/R (R je ) K =0 Kapilární Laplaceovy tlaky v oblasti a a v oblasti b? Který je větší? Která křivost je větší? R je v počátku vývoje nestability stále o mnoho větší než R 1 Přirovnání ke ždímání odkud kam ta kapalina půjde? a b Bude se kapalina snažit ten tvar vyrovnat zpět do válce nebo to bude spíš dělit dál?
6 Jak zastavit P-R nestabilitu? Zvýšit viskozitu = jen delší doba do vývoje nestabilit.,5 wt% PVB in etanol 5 wt% PVB in etanol 10 wt% PVB in etanol Je potřeba převést těleso na pevnou látku, kde viskozita jde k nekonečnu!
7 TEORIE NETKANÝCH TEXTILIÍ
8 TEORIE NETKANÝCH TEXTILIÍ Elspun nanovlákna a zvyšování teploty Macromol. Rapid Commun.01, 33,
9 TEORIE NETKANÝCH TEXTILIÍ Rayleighova nestabilita satelity (existence více velikostí kapek) ciks.cbt.nist.gov cemuseum.ugent.be/nlplat11.html
10 Kvantitativní popis problému Rayleighovy nestability Čerpáno z D. Lukas et al. Textile Progress, 009 Kapalinový válec o charakteristickém poloměru r 0 se rozpadne do sférických kapek o polomeru r d. Vlnová délka odpovídá vzdálenosti středů rozpadlých kapek = r
11 Předpokládá se zachování objemu = objem válce o délce = objemu koule
12 Další rovnice říká, že koule by měla mít menší obsah povrchové energie než válec pak může dojít spontánně k tomuto přetvoření Zachování objemu Zanedbávají se plochy podstav, protože předpokládáme, že se přetváří nekonečný válec na jednotlivé kapičky.
13 Tento výraz se zpřesňuje zavedením tlaků (zavedením tlakových mechanických energií) Celková energie kapalných těles v kulového nebo válcového tvaru se skládá ze dvou složek. Za prvé, jedna je spojena s povrchovým napětím, tj povrchové energie, a druhá z nich je spojena s kapilárním tlakem pv=w Potenciální tlaková energie kapaliny je tlak krát objem
14
15 Rayleigh-Plateau instability on sphere rotating in aqueous glycerol solution Black Hole by Fabian OefnerBlack Hole by Fabian Oefner
16 Black Hole is a series of images, which shows paint modeled by centripetal force. The setup is very simple: various shades of acrylic paint are dripped onto a metallic rod, which is connected to a drill. When switched on, the paint starts to move away from the rod, creating these amazing looking structures. The motion of the paint happens in a blink of an eye, the images you see are taken only millisecond after the drill was turned on. To capture the moment, where the paint forms that distinctive shape, Fabian Oefner has connected a sensor to the drill, which sends an impulse to the flashes. These specialized units are capable of creating flashes as short as a 1/40000 of a second, freezing the motion of the paint.
17 P-R nestabilita na vláknech Rayleigh-Plateau instability on nylon fiber dipped in silicone oil
18 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně Výsledný tvar kapaliny je jiný než u rozpadu jen kapalinového tělesa. Předpokládáme, že vznikne opět kapalná koule o poloměru R, ale také kapalinový válec, který pokrývá vlákno, ovšem bude mít jiný průměr než kapalinový válec původní.
19 TEORIE NETKANÝCH TEXTILIÍ Je třeba zdůraznit, že pro různé poměry R/b se neudržuje konstantní úhel smáčení. Díky Plateau-Rayleighově nestabilitě (Laplaceovým tlakům) vlákno při větších tloušťkách kapalinového filmu nepokryje souvislý film ale dojde k jeho rozpadu na jednotlivé kapky i při úhlu smáčení 0. s=e/b Tvary kapalinových útvarů na vláknech při různých velikostech s. Úhel smáčení je a) =0, b) =45 Ryong Joon Roe, Journal of Colloid and Interface Science, 1975, Vol.50, No.1, 70-79
20 Při dostatečně malých tloušťkách kapalinového filmu nemusí dojít k rozpadu na kapky: Síly od povrchového napětí nepřekonají mezimolekulární síly působící na povrchu kapalina vlákno. Mezimolekulární síly zablokují tvorbu nestabilit. Vlákenný materiál musí být kapalinou dobře smáčen, aby se vytvořil dostatečně tenký film. Mezimolekulární síly: vodíkové můstky, Van der Waalsovy síly, Když chceme potáhnout vlákno kapalinovým filmem: Kosmetický průmysl vlasová kosmetika Lubrikace = sizing textilních vláken
21 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně Z experimentu víme, že jestliže ponoříme vlákno do kapaliny, na vlákně se utvoří kapičky. Tyto kapičky jsou však propojeny mikroskopickým kapalinovým filmem. Jednoduše řečeno, kapalinové těleso umístěné na vlákně je souvislé i potom, co zaujme energeticky nejvýhodnější tvar. V tomto případě pro objemy platí následující rovnost V V c cs
22 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně c V cs V ) ( ) ( ) ( R R a b e b Rovnost objemů kapalinových těles na vlákně ) ( ) ( ) ( 3 b a b e a b R R
23 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně W W c cs Rovnost povrchových energií obou stavů W c ( b e) W cs ( b a)( R) 4R b R Ra Rb ( e a) b
24 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně c W cs W ) ( a e b Rb Ra R c V cs V ) ( ) ( ) ( 3 b a b e a b R R be e b R R e b Rb R 3 a0
25 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně R Rb e b R R b 3 e be Následnými úpravami dojdeme ke zjištění, že pro e/b existuje minimální hodnota, pod kterou neexistuje fyzikálně přípustné řešení. MEZÍ JE HODNOTA e/b = 0,087
26 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně Následnými úpravami dojdeme ke zjištění, že pro e/b existuje minimální hodnota, pod kterou neexistuje fyzikálně přípustné řešení. MEZÍ JE HODNOTA e/b = 0,087 Graf závislosti /b na poměru e/b. Graf je rozdělen do tří oblastí, které zobrazují možnost existence kapalinových těles na vlákně. Zelená křivka je grafickým vyjádřením závislosti podle Rayleigha.
27 TEORIE NETKANÝCH TEXTILIÍ Řešení nestability kapalinového sloupce umístěného na vlákně Následnými úpravami dojdeme ke zjištění, že pro e/b existuje minimální hodnota, pod kterou neexistuje fyzikálně přípustné řešení. MEZÍ JE HODNOTA e/b = 0,087 Graf závislosti /b na poměru e/b. Graf je rozdělen do tří oblastí, které zobrazují možnost existence kapalinových těles na vlákně. Zelená křivka je grafickým vyjádřením závislosti podle Rayleigha. Pro krátká a velké e se nevytvoří kapky, protože se kapky spojí v film
28 TEORIE NETKANÝCH TEXTILIÍ Plateau-Rayleigh Instability De Gennes, Capillarity and Wetting Phenomena Str Doplňky Satelity Journal of Computational Physics Volume 36, 1 March 013, Pages 1 14 Satelity malé kapky mezi velkými Druhotná nestability v kapalinovém plášti mezi dvěma sousedícími velkými kapkami Pro viskózní kapaliny je možné zaznamenat celé hierarchie satelitů DYNAMICKÝ PŘÍSTUP STATICKÝ PŘÍSTUP Odhaluje jen dvojí možnost velikosti kapek. Na vlákně je množství rozvinutí počtu satelitů omezené slejí se do filmu.
29 TEORIE NETKANÝCH TEXTILIÍ Plateau-Rayleigh Instability De Gennes, Capillarity and Wetting Phenomena Str Doplňky Satelity Journal of Computational Physics Volume 36, 1 March 013, Pages 1 14 Satelity malé kapky mezi velkými Druhotná nestability v kapalinovém plášti mezi dvěma sousedícími velkými kapkami Pro viskózní kapaliny je možné zaznamenat celé hierarchie satelitů Time evolution leading to multiple pinch-offs. Viscosity ratio is 0.5, ϵ=0.0, Pe=100/ϵ, Re=0.16, and We= The dimensionless times are shown below each figures. Applied Mathematics and Computation Volume 160, Issue, 14 January 005, Pages
30 TEORIE NETKANÝCH TEXTILIÍ
31 TEORIE NETKANÝCH TEXTILIÍ Plateau-Rayleigh Instability Plateau-Rayleighova nestabilita kapalinového filmu na vlákně De Gennes, Capillarity and Wetting Phenomena Str Hydrodynamický roztor t = 1 b4 γe 0 3 t characteristic growth time of the instability Charakteristický čas pro vznik nestability b poloměr vlákna e 0 počáteční tloušťka kapalinového filmu viskozita kapaliny povrchové napětí kapaliny Změna tloušťky kapalinového filmu e 0 =1m; b=100m; /=0,1 m/s (ordinary cooking oil) === t=10h e 0 =10m; b=100m; /=0,1 m/s (ordinary cooking oil) === t=10s e 0 =10m; b=10m; /=0,1 m/s (ordinary cooking oil) === t=10ms
32
33 TEORIE NETKANÝCH TEXTILIÍ D.H. Reneker, A.L. Yarin / Polymer 49 (008), 387,e 45
34 TEORIE NETKANÝCH TEXTILIÍ
35 s/spinneret/ultra_co-axial.html TEORIE NETKANÝCH TEXTILIÍ
Interakce mezi kapalinou a vlákenným materiálem
 TEORIE NETKANÝCH TEXTILIÍ 9. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita Prof. RNDr. David Lukáš, CSc. Doc. Ing. Eva Kuželová Košťáková, Ph.D. KCH, FP, TUL
TEORIE NETKANÝCH TEXTILIÍ 9. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita Prof. RNDr. David Lukáš, CSc. Doc. Ing. Eva Kuželová Košťáková, Ph.D. KCH, FP, TUL
Interakce mezi kapalinou a vlákenným materiálem
 7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
7. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita - kapalinový film na vlákně Morfologické přechody Lucas Washburnův vztah dynamika průniku kapalin do kruhové
TEORIE NETKANÝCH TEXTILIÍ. Kapky Kapilární délka. Simulace pomocí Isingova modelu. 7.přednáška
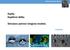 Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Kapky Kapilární délka Simulace pomocí Isingova modelu 7.přednáška Kapaliny vykazují poněkud zvláštní vlastnosti. Mají schopnost porazit gravitaci a vytvořit kapilární mosty, přesouvat se po šikmých rovinách,
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
3. přednáška Interakce mezi kapalinou a vlákenným materiálem OPAKOVÁNÍ Soudržnost dvou spojovaných ploch, tedy vazba mezi pevným povrchem vláken a adhezivem (pojivem) je chápána jako ADHEZE. Primární i
Fyzikální principy tvorby nanovláken. 1. Úvod. D.Lukáš
 Fyzikální principy tvorby nanovláken 1. Úvod D.Lukáš 1 Physical principles of electrospinning (Electrospinning as a nano-scale technology of the twenty-first century) Physical principles of electrospinning
Fyzikální principy tvorby nanovláken 1. Úvod D.Lukáš 1 Physical principles of electrospinning (Electrospinning as a nano-scale technology of the twenty-first century) Physical principles of electrospinning
Úvod do elektrostatického zvlákňování. Eva Košťáková KNT, FT, TUL
 Úvod do elektrostatického zvlákňování Eva Košťáková KNT, FT, TUL Lidský vlas Bavlněné vlákno Jednou v podstatě velmi jednoduchou metodou výroby nanovláken je tak zvané Elektrostatické zvlákňování (anglicky
Úvod do elektrostatického zvlákňování Eva Košťáková KNT, FT, TUL Lidský vlas Bavlněné vlákno Jednou v podstatě velmi jednoduchou metodou výroby nanovláken je tak zvané Elektrostatické zvlákňování (anglicky
Měření povrchového napětí kapalin a kontaktních úhlů
 2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
2. Přednáška Interakce mezi kapalinou a vlákenným materiálem Měření povrchového napětí kapalin a kontaktních úhlů Eva Kuželová Košťáková KCH, FP, TUL 2019 ADHEZE KAPALIN K PEVNÝM LÁTKÁM Povrchové napětí
Parametry ovlivňující proces elektrostatického zvlákňování
 Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Stacionární 3.Přednáška LS 2013/14 Eva Košťáková KNT, FT, TUL NEEDLE-LESS ELECTROSPINNING BEZJEHLOVÉ
Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Stacionární 3.Přednáška LS 2013/14 Eva Košťáková KNT, FT, TUL NEEDLE-LESS ELECTROSPINNING BEZJEHLOVÉ
Interakce mezi kapalinou a vlákenným materiálem
 3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
3. přednáška Interakce mezi kapalinou a vlákenným materiálem Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETIE PEVNÉ LÁTKY (tvar strukturní komponenty a relativní
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Eva Kuželová Košťáková TUL, T KNT Jedním ze základních parametrů, které řídí interakci mezi kapalinou a pevnou látkou je GEOMETRIE PEVNÉ LÁTKY
Interakce mezi kapalinou a vlákenným materiálem
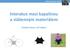 Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Interakce mezi kapalinou a vlákenným materiálem Smáčení dvou a tří vláken Smáčení dvou válců dvou vláken Kapalinová tělesa mezi dvěma pevnými válci (vlákny) v rovnovážném stavu při zanedbání vlivu gravitace.
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl
 Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Elektrostatické zvlákňování: Výroba polymerních nanovláken a jejich využití v kompozitních materiálechl Seminář: KOMPOZITY ŠIROKÝ POJEM, Ústav teoretické a aplikované mechaniky AV ČR Eva Košťáková, Pavel
Interakce mezi kapalinou a vlákenným materiálem
 5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
5. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry dh r Pe. dt 8h Kapilarita Rostliny transportují vodu z kořenů do listů,
Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna. Eva Košťáková KNT, FT, TUL
 Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna Eva Košťáková KNT, FT, TUL Rotující válec Řízení orientace vláken Vibrující deska Ostrý disk Rámeček Řízení orientace vláken
Elektrostatické zvlákňování orientace vláken, výroba nití a bikomponentní vlákna Eva Košťáková KNT, FT, TUL Rotující válec Řízení orientace vláken Vibrující deska Ostrý disk Rámeček Řízení orientace vláken
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT
 VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
VÍTÁM VÁS NA PŘEDNÁŠCE Z PŘEDMĚTU TCT opakování Jeden směr křížem Cros - cros náhodně náhodně náhodně NT ze staplových vláken vlákna pojená pod tryskou Suchá technologie Mokrá technologie vlákna Metody
Interakce mezi kapalinou a vlákenným materiálem
 4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
4. přednáška Interakce mezi kapalinou a vlákenným materiálem Smáčení jednoho vlákna, dvojice a trojice vláken Smáčení vlákna makroskopickým filmem Započítán i vliv LAPLACEOVA (KAPILÁRNÍHO) TLAKU t e b
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid
 Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
Mezi krystalické látky nepatří: a) asfalt b) křemík c) pryskyřice d) polvinylchlorid Mezi krystalické látky patří: a) grafit b) diamant c) jantar d) modrá skalice Mezi krystalické látky patří: a) rubín
STRUKTURA A VLASTNOSTI KAPALIN
 STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
STRUKTURA A VLASTNOSTI KAPALIN Struktura kapalin je něco mezi plynem a pevnou látkou Částice kmitají ale mohou se také přemísťovat Zvýšením teploty se a tím se zvýší tekutost kapaliny Malé vzdálenosti
Netkané textilie. Materiály 2
 Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING
 Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Podmínky ovlivňující proces elektrostatického zvlákňování nanovláken Procesní podmínky -Uspořádání
Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Podmínky ovlivňující proces elektrostatického zvlákňování nanovláken Procesní podmínky -Uspořádání
Vlastnosti kapalin. Povrchová vrstva kapaliny
 Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
Struktura a vlastnosti kapalin Vlastnosti kapalin, Povrchová vrstva kapaliny Jevy na rozhraní pevného tělesa a kapaliny Kapilární jevy, Teplotní objemová roztažnost Vlastnosti kapalin Kapalina - tvoří
4. Kolmou tlakovou sílu působící v kapalině na libovolně orientovanou plochu S vyjádříme jako
 1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
1. Pojem tekutiny je A) synonymem pojmu kapaliny B) pojmem označujícím souhrnně kapaliny a plyny C) synonymem pojmu plyny D) označením kapalin se zanedbatelnou viskozitou 2. Příčinou rozdílné tekutosti
Měření povrchového napětí
 Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Měření povrchového napětí Úkol : 1. Změřte pomocí kapilární elevace povrchové napětí daných kapalin při dané teplotě. 2. Změřte pomocí kapkové metody povrchové napětí daných kapalin při dané teplotě. Pomůcky
Parametry ovlivňující proces elektrostatického zvlákňování
 Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Stacionární, rotační Eva Košťáková KNT, FT, TUL NEEDLE-LESS ELECTROSPINNING BEZJEHLOVÉ ELEKTROSTATICKÉ
Parametry ovlivňující proces elektrostatického zvlákňování ZVLÁKŇOVACÍ ELEKTRODY NEEDLELESS ELECTROSPINNING Stacionární, rotační Eva Košťáková KNT, FT, TUL NEEDLE-LESS ELECTROSPINNING BEZJEHLOVÉ ELEKTROSTATICKÉ
Fyzikální principy tvorby nanovláken. 2. Historie. D.Lukáš 2010
 Fyzikální principy tvorby nanovláken 2. Historie D.Lukáš 2010 1 Objevení fyzikálního jevu spojeného z elektrostatickým zvlákňováním může být datováno až do roku 1600, kdy William Gilbert (*1544 +1603)
Fyzikální principy tvorby nanovláken 2. Historie D.Lukáš 2010 1 Objevení fyzikálního jevu spojeného z elektrostatickým zvlákňováním může být datováno až do roku 1600, kdy William Gilbert (*1544 +1603)
KAPALINY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník
 KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
KAPALINY Mgr. Jan Ptáčník - GJVJ - Fyzika - Termika - 2. ročník Kapaliny Krátkodosahové uspořádání molekul. Molekuly kmitají okolo rovnovážných poloh. Při zvýšení teploty se zmenšuje doba setrvání v rovnovážné
Interakce mezi kapalinou a vlákenným materiálem
 8. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry 2 dh r Pe. dt 8h Lucas Washburnův vztah Lucas, R.: Kolloid Zeitschrift,
8. přednáška Interakce mezi kapalinou a vlákenným materiálem Lucas Washburnův vztah dynamika průniku kapalin do kruhové kapiláry 2 dh r Pe. dt 8h Lucas Washburnův vztah Lucas, R.: Kolloid Zeitschrift,
3. Vypočítejte chybu, které se dopouštíte idealizací reálného kyvadla v rámci modelu kyvadla matematického.
 Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška. TNT smáčení úvod. Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL
 2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
2. přednáška TNT smáčení úvod Eva Kuželová Košťáková Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL OPAKOVÁNÍ z 1.přednášky Cíl předmětu Teorie netkaných textilií: Ukázat, jak struktura
Interakce mezi kapalinou a vlákenným materiálem
 TEORIE NETKANÝCH TEXTILIÍ 6. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita Prof. RNDr. David Lukáš, CSc. Doc. Ing. Eva Košťáková, Ph.D. Plateau-Rayleighova nestabilita
TEORIE NETKANÝCH TEXTILIÍ 6. přednáška Interakce mezi kapalinou a vlákenným materiálem Plateau-Rayleighova nestabilita Prof. RNDr. David Lukáš, CSc. Doc. Ing. Eva Košťáková, Ph.D. Plateau-Rayleighova nestabilita
Zařízení: Rotační viskozimetr s příslušenstvím, ohřívadlo s magnetickou míchačkou, teploměr, potřebné nádoby a kapaliny (aspoň 250ml).
 Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Úvod Pro ideální tekutinu předpokládáme, že v ní neexistují smyková tečná napětí. Pro skutečnou tekutinu to platí pouze v případě, že tekutina se nepohybuje. V případě, že tekutina proudí a její jednotlivé
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Adheze - pokračování
 2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
2. přednáška Adheze - pokračování Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro Podmínky
Flashspinnig, Elecrospinnig, Force spinning
 Vítám vás na dnešní přednášce Flashspinnig, Elecrospinnig, Force spinning a další možné metody výroby vláken Flash-spinning process and solution Bleskové-zvlákňování Číslo publikace US 6638470B2, datum
Vítám vás na dnešní přednášce Flashspinnig, Elecrospinnig, Force spinning a další možné metody výroby vláken Flash-spinning process and solution Bleskové-zvlákňování Číslo publikace US 6638470B2, datum
7 Gaussova věta 7 GAUSSOVA VĚTA. Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro
 7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
DUM č. 12 v sadě. 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia
 projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
projekt GML Brno Docens DUM č. 12 v sadě 10. Fy-1 Učební materiály do fyziky pro 2. ročník gymnázia Autor: Vojtěch Beneš Datum: 03.05.2014 Ročník: 1. ročník Anotace DUMu: Kapaliny, změny skupenství Materiály
1. přednáška. ÚVOD k předmětu TNT
 1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
1. přednáška ÚVOD k předmětu TNT Doc. Ing. Eva Kuželová Košťáková, Ph.D. Katedra netkaných textilií a nanovlákenných materiálů, FT, TUL Eva.kostakova@tul.cz Tel.: 48 535 3233 Budova B, 4. patro https://nanoed.tul.cz/course/vie
Speciální aplikace poznatků ze smáčení. Vzlínání do vlákenných materiálů TNT. Eva Kuželová Košťáková KCH, FP, TUL
 Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
Speciální aplikace poznatků ze smáčení Vzlínání do vlákenných materiálů TNT Eva Kuželová Košťáková KCH, FP, TUL -Určování (odhad) kontaktního úhlu u porézních (vlákenných) materiálů -Určování (odhad) kontaktního
5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY
 Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY 1. TEORIE: Měření viskozity pomocí padající kuličky patří k nejstarším metodám
Laboratorní cvičení z předmětu Reologie potravin a kosmetických prostředků 5b MĚŘENÍ VISKOZITY KAPALIN POMOCÍ PADAJÍCÍ KULIČKY 1. TEORIE: Měření viskozity pomocí padající kuličky patří k nejstarším metodám
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Kapaliny Molekulové vdw síly, vodíkové můstky
 Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
Kapaliny Molekulové vdw síly, vodíkové můstky Metalické roztavené kovy, ionty + elektrony, elektrostatické síly Iontové roztavené soli, FLINAK (LiF + NaF + KF), volně pohyblivé anionty a kationty, iontová
STUDIUM HLADINOVÉHO ELEKTROSTATICKÉHO
 STUDIUM HLADINOVÉHO ELEKTROSTATICKÉHO ZVLÁKŇOVÁNÍ J. Kula, M. Tunák, D. Lukáš, A. Linka Technická Univerzita v Liberci Abstrakt V posledních letech se uplatňuje výroba netkaných, nanovlákenných vrstev,
STUDIUM HLADINOVÉHO ELEKTROSTATICKÉHO ZVLÁKŇOVÁNÍ J. Kula, M. Tunák, D. Lukáš, A. Linka Technická Univerzita v Liberci Abstrakt V posledních letech se uplatňuje výroba netkaných, nanovlákenných vrstev,
Entrance test from mathematics for PhD (with answers)
 Entrance test from mathematics for PhD (with answers) 0 0 3 0 Problem 3x dx x + 5x +. 3 ln 3 ln 4. (4x + 9) dx x 5x 3. 3 ln 4 ln 3. (5 x) dx 3x + 5x. 7 ln. 3 (x 4) dx 6x + x. ln 4 ln 3 ln 5. 3 (x 3) dx
Entrance test from mathematics for PhD (with answers) 0 0 3 0 Problem 3x dx x + 5x +. 3 ln 3 ln 4. (4x + 9) dx x 5x 3. 3 ln 4 ln 3. (5 x) dx 3x + 5x. 7 ln. 3 (x 4) dx 6x + x. ln 4 ln 3 ln 5. 3 (x 3) dx
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
Výroba tablet. Inženýrství chemicko-farmaceutických výrob. Lisování tablet. POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY
 Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE
 HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE Buzgo M. 1,3,4, Vysloužilová L. 2, Míčková A. 1,3,4, Benešová J. 1,3,4, Pokorná H. 1,3,4, Lukáš D. 2, Amler E. 1,3,4 1 Fakulta
HLADINOVÉ KOAXIÁLNÍ ZVLÁKŇOVÁNÍ PRO MASIVNÍ PRODUKCI NANOVLÁKEN DRUHÉ GENERACE Buzgo M. 1,3,4, Vysloužilová L. 2, Míčková A. 1,3,4, Benešová J. 1,3,4, Pokorná H. 1,3,4, Lukáš D. 2, Amler E. 1,3,4 1 Fakulta
Výroba tablet. Lisovací nástroje. Inženýrství chemicko-farmaceutických výrob. Lisování tablet. Horní trn (razidlo) Lisovací matrice (forma, lisovnice)
 Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
Pracovní list slouží k procvičení látky o válci. Žáci si upevní učivo týkající se sítě, povrchu a objemu válce.
 Název projektu: Spokojená škola Číslo projektu: OPVK.CZ.1.07/1.2.33/02.0039 Metodické pokyny k pracovnímu listu č. 8.08 Válec Pracovní list slouží k procvičení látky o válci. Žáci si upevní učivo týkající
Název projektu: Spokojená škola Číslo projektu: OPVK.CZ.1.07/1.2.33/02.0039 Metodické pokyny k pracovnímu listu č. 8.08 Válec Pracovní list slouží k procvičení látky o válci. Žáci si upevní učivo týkající
Maticová optika. Lenka Přibylová. 24. října 2010
 Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
Maticová optika Lenka Přibylová 24. října 2010 Maticová optika Při průchodu světla optickými přístroji dochází k transformaci světelného paprsku, vlnový vektor mění úhel, který svírá s optickou osou, paprsek
1. Měřením na rotačním viskozimetru zjistěte, zda jsou kapaliny připravené pro měření newtonovské.
 1 Pracovní úkol 1. Měřením na rotačním viskozimetru zjistěte, zda jsou kapaliny připravené pro měření newtonovské. 2. Pomocí rotačního viskozimetru určete viskozitu newtonovské kapaliny. 3. Pro nenewtonovskou
1 Pracovní úkol 1. Měřením na rotačním viskozimetru zjistěte, zda jsou kapaliny připravené pro měření newtonovské. 2. Pomocí rotačního viskozimetru určete viskozitu newtonovské kapaliny. 3. Pro nenewtonovskou
Výroba polymerních nanovláken (s výjimkou elektrického zvlákňování)
 Výroba polymerních nanovláken (s výjimkou elektrického zvlákňování) Eva K. Košťáková KNT, FT, TUL Možnosti výroby polymerních nanovláken - Elektrické zvlákňování (electrospinning) - Tažení (Drawing) -
Výroba polymerních nanovláken (s výjimkou elektrického zvlákňování) Eva K. Košťáková KNT, FT, TUL Možnosti výroby polymerních nanovláken - Elektrické zvlákňování (electrospinning) - Tažení (Drawing) -
INDEX. www.proline-tools.pl 217
 www.proline-tools.pl 217 www.proline-tools.pl 218 00001............... 47 00002............... 47 00003............... 47 00006............... 47 00007............... 47 00008............... 47 00009...............
www.proline-tools.pl 217 www.proline-tools.pl 218 00001............... 47 00002............... 47 00003............... 47 00006............... 47 00007............... 47 00008............... 47 00009...............
1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás.
 Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty.
![a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty. a) [0,4 b] r < R, b) [0,4 b] r R c) [0,2 b] Zakreslete obě závislosti do jednoho grafu a vyznačte na osách důležité hodnoty.](/thumbs/88/115052329.jpg) Příklady: 24. Gaussův zákon elektrostatiky 1. Na obrázku je řez dlouhou tenkostěnnou kovovou trubkou o poloměru R, která nese na povrchu náboj s plošnou hustotou σ. Vyjádřete velikost intenzity E jako
Příklady: 24. Gaussův zákon elektrostatiky 1. Na obrázku je řez dlouhou tenkostěnnou kovovou trubkou o poloměru R, která nese na povrchu náboj s plošnou hustotou σ. Vyjádřete velikost intenzity E jako
Klepnutím lze upravit styl předlohy. nadpisů. nadpisů.
 1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika
 Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Připravil: Roman Pavlačka, Markéta Sekaninová Hydrostatika OPVK CZ.1.07/2.2.00/28.0220, "Inovace studijních programů zahradnických oborů s důrazem na jazykové a odborné dovednosti a konkurenceschopnost
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592
 Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Dobrý den vítám vás na dnešní přednášce
 Dobrý den vítám vás na dnešní přednášce Flashspinning Flash = záblesknutí, vyšlehnutí; spinning = zvlákňování Výrobní proces vyvinutý a patentované společností DuPont výrobky pod obchodní značkou Tyvec
Dobrý den vítám vás na dnešní přednášce Flashspinning Flash = záblesknutí, vyšlehnutí; spinning = zvlákňování Výrobní proces vyvinutý a patentované společností DuPont výrobky pod obchodní značkou Tyvec
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Skupenské stavy látek. Mezimolekulární síly
 Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Skupenské stavy látek Mezimolekulární síly 1 Interakce iont-dipól Např. hydratační (solvatační) interakce mezi Na + (iont) a molekulou vody (dipól). Jde o nejsilnější mezimolekulární (nevazebnou) interakci.
Povrchy, objemy. Krychle = = = + =2 = 2 = 2 = 2 = 2 =( 2) + = ( 2) + = 2+ =3 = 3 = 3 = 3 = 3
 y, objemy nám vlastně říká, kolik tapety potřebujeme k polepení daného tělesa. Základní jednotkou jsou metry čtverečné (m 2 ). nám pak říká, kolik vody se do daného tělesa vejde. Základní jednotkou jsou
y, objemy nám vlastně říká, kolik tapety potřebujeme k polepení daného tělesa. Základní jednotkou jsou metry čtverečné (m 2 ). nám pak říká, kolik vody se do daného tělesa vejde. Základní jednotkou jsou
Dynamická viskozita oleje (Pa.s) Souřadný systém (proč)?
 Viskozimetr kužel-deska S pomocí rotačního viskozimetru s uspořádáním kužel-deska, viz obrázek, byla měřena dynamická viskozita oleje. Při použití kužele o průměru 40 mm, který se otáčel úhlovou rychlostí
Viskozimetr kužel-deska S pomocí rotačního viskozimetru s uspořádáním kužel-deska, viz obrázek, byla měřena dynamická viskozita oleje. Při použití kužele o průměru 40 mm, který se otáčel úhlovou rychlostí
Mechanika tekutin. Hydrostatika Hydrodynamika
 Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
Mechanika tekutin Hydrostatika Hydrodynamika Hydrostatika Kapalinu považujeme za kontinuum, můžeme využít předchozí úvahy Studujeme kapalinu, která je v klidu hydrostatika Objem kapaliny bude v klidu,
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
Fáze a fázové přechody
 Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Dobrý den vítám vás na dnešní přednášce. Téma přednášky je Flashspinnig, Elektrospinnig, Force spinning další metody zvlákňování polymerů
 Dobrý den vítám vás na dnešní přednášce Téma přednášky je Flashspinnig, Elektrospinnig, Force spinning další metody zvlákňování polymerů Flashspinning Flash = záblesknutí, vyšlehnutí; sršení spinning =
Dobrý den vítám vás na dnešní přednášce Téma přednášky je Flashspinnig, Elektrospinnig, Force spinning další metody zvlákňování polymerů Flashspinning Flash = záblesknutí, vyšlehnutí; sršení spinning =
Netkané textilie. Technologie 5
 Netkané textilie Technologie 5 Netkané textilie 1 Chemické způsoby zpevňování vlákenných vrstev Základními operacemi při výrobě chemicky pojených textilií jsou: a) příprava vlákenné vrstvy b) nanášení
Netkané textilie Technologie 5 Netkané textilie 1 Chemické způsoby zpevňování vlákenných vrstev Základními operacemi při výrobě chemicky pojených textilií jsou: a) příprava vlákenné vrstvy b) nanášení
5. Duté zrcadlo má ohniskovou vzdálenost 25 cm. Jaký je jeho poloměr křivosti? 1) 0,5 m 2) 0,75 m 3) Žádná odpověď není správná 4) 0,25 m
 1. Vypočítejte šířku jezera, když zvuk šířící se ve vodě se dostane k druhému břehu o 1 s dříve než ve vzduchu. Rychlost zvuku ve vodě je 1 400 m s -1. Rychlost zvuku ve vzduchu je 340 m s -1. 1) 449 m
1. Vypočítejte šířku jezera, když zvuk šířící se ve vodě se dostane k druhému břehu o 1 s dříve než ve vzduchu. Rychlost zvuku ve vodě je 1 400 m s -1. Rychlost zvuku ve vzduchu je 340 m s -1. 1) 449 m
MECHANISMUS TVORBY PORÉZNÍCH NANOVLÁKEN Z POLYKAPROLAKTONU PŘIPRAVENÝCH ELEKTROSTATICKÝM ZVLÁKŇOVÁNÍM
 MECHANISMUS TVORBY PORÉZNÍCH NANOVLÁKEN Z POLYKAPROLAKTONU PŘIPRAVENÝCH ELEKTROSTATICKÝM ZVLÁKŇOVÁNÍM Daniela Lubasová a, Lenka Martinová b a Technická univerzita v Liberci, Katedra netkaných textilií,
MECHANISMUS TVORBY PORÉZNÍCH NANOVLÁKEN Z POLYKAPROLAKTONU PŘIPRAVENÝCH ELEKTROSTATICKÝM ZVLÁKŇOVÁNÍM Daniela Lubasová a, Lenka Martinová b a Technická univerzita v Liberci, Katedra netkaných textilií,
VLIV MLETÍ ÚLETOVÉHO POPÍLKU NA PRŮBĚH ALKALICKÉ AKTIVACE
 VLIV MLETÍ ÚLETOVÉHO POPÍLKU NA PRŮBĚH ALKALICKÉ AKTIVACE INFLUENCE OF GRINDING OF FLY-ASH ON ALKALI ACTIVATION PROCESS Rostislav Šulc 1 Abstract This paper describes influence of grinding of fly - ash
VLIV MLETÍ ÚLETOVÉHO POPÍLKU NA PRŮBĚH ALKALICKÉ AKTIVACE INFLUENCE OF GRINDING OF FLY-ASH ON ALKALI ACTIVATION PROCESS Rostislav Šulc 1 Abstract This paper describes influence of grinding of fly - ash
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
6. Mechanika kapalin a plynů
 6. Mechanika kapalin a plynů 1. Definice tekutin 2. Tlak 3. Pascalův zákon 4. Archimedův zákon 5. Rovnice spojitosti (kontinuity) 6. Bernoulliho rovnice 7. Fyzika letu Tekutiny: jejich rozdělení, jejich
6. Mechanika kapalin a plynů 1. Definice tekutin 2. Tlak 3. Pascalův zákon 4. Archimedův zákon 5. Rovnice spojitosti (kontinuity) 6. Bernoulliho rovnice 7. Fyzika letu Tekutiny: jejich rozdělení, jejich
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
Výroba tablet. Fáze lisování. Lisovací nástroje. Typy tabletovacích lisů. Inženýrství chemicko-farmaceutických výrob
 Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY piva, suchá pojiva, kluzné látky, rozvolňovadla homogenizace homogenizace tabletování z granulátu TABLETOVINA
Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY piva, suchá pojiva, kluzné látky, rozvolňovadla homogenizace homogenizace tabletování z granulátu TABLETOVINA
Otázky PT3 Stroje a zařízení chemického průmyslu
 Otázky PT3 Stroje a zařízení chemického průmyslu 1. Doprava tuhých látek Skluzy, sypný úhel Mechanické dopravníky pásové (tvar pásů, vzduchový polštář, uzavřené, otevřené, trubkový), válečkové, článkové,
Otázky PT3 Stroje a zařízení chemického průmyslu 1. Doprava tuhých látek Skluzy, sypný úhel Mechanické dopravníky pásové (tvar pásů, vzduchový polštář, uzavřené, otevřené, trubkový), válečkové, článkové,
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY
 BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
Složení hvězdy. Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ
 Hvězdy zblízka Složení hvězdy Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ Plazma zcela nebo částečně ionizovaný plyn,
Hvězdy zblízka Složení hvězdy Hvězda - gravitačně vázaný objekt, složený z vysokoteplotního plazmatu; hmotnost 0,08 M ʘ cca 150 M ʘ, ale R136a1 (LMC) má 265 M ʘ Plazma zcela nebo částečně ionizovaný plyn,
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Práce, energie a další mechanické veličiny
 Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Příloha-výpočet motoru
 Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
MOLEKULOVÁ FYZIKA KAPALIN
 MOLEKULOVÁ FYZIKA KAPALIN Struktura kapalin Povrchová vrstva kapaliny Povrchová energie, povrchová síla, povrchové napětí Kapilární tlak Kapilarita Prof. RNDr. Emanuel Svoboda, CSc. STRUKTURA KAPALIN Tvoří
MOLEKULOVÁ FYZIKA KAPALIN Struktura kapalin Povrchová vrstva kapaliny Povrchová energie, povrchová síla, povrchové napětí Kapilární tlak Kapilarita Prof. RNDr. Emanuel Svoboda, CSc. STRUKTURA KAPALIN Tvoří
11. cvičení z Matematické analýzy 2
 11. cvičení z Matematické analýzy 11. - 15. prosince 17 11.1 (trojný integrál - Fubiniho věta) Vypočtěte (i) xyz dv, kde je ohraničeno plochami y x, x y, z xy a z. (ii) y dv, kde je ohraničeno shora rovinou
11. cvičení z Matematické analýzy 11. - 15. prosince 17 11.1 (trojný integrál - Fubiniho věta) Vypočtěte (i) xyz dv, kde je ohraničeno plochami y x, x y, z xy a z. (ii) y dv, kde je ohraničeno shora rovinou
Krevní oběh. Helena Uhrová
 Krevní oběh Helena Uhrová Z hydrodynamického hlediska uzavřený systém, složený ze: srdce motorický orgán, zdroj mechanické energie cév rozvodný systém, tvořený elastickými roztažitelnými a kontraktilními
Krevní oběh Helena Uhrová Z hydrodynamického hlediska uzavřený systém, složený ze: srdce motorický orgán, zdroj mechanické energie cév rozvodný systém, tvořený elastickými roztažitelnými a kontraktilními
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Experimentální realizace Buquoyovy úlohy
 Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
Experimentální realizace Buquoyovy úlohy ČENĚK KODEJŠKA, JAN ŘÍHA Přírodovědecká fakulta Univerzity Palackého, Olomouc Abstrakt Tato práce se zabývá experimentální realizací Buquoyovy úlohy. Jedná se o
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í
 DYNAMIKA SÍLA 1. Úvod dynamos (dynamis) = síla; dynamika vysvětluje, proč se objekty pohybují, vysvětluje změny pohybu. Nepopisuje pohyb, jak to dělá... síly mohou měnit pohybový stav těles nebo mohou
DYNAMIKA SÍLA 1. Úvod dynamos (dynamis) = síla; dynamika vysvětluje, proč se objekty pohybují, vysvětluje změny pohybu. Nepopisuje pohyb, jak to dělá... síly mohou měnit pohybový stav těles nebo mohou
Hmotný bod - model (modelové těleso), který je na dané rozlišovací úrovni přiřazen reálnému objektu (součástce, části stroje);
 Newtonovy pohybové zákony: Hmotný bod - model (modelové těleso), který je na dané rozlišovací úrovni přiřazen reálnému objektu (součástce, části stroje); předpokládáme soustředění hmoty tělesa a všech
Newtonovy pohybové zákony: Hmotný bod - model (modelové těleso), který je na dané rozlišovací úrovni přiřazen reálnému objektu (součástce, části stroje); předpokládáme soustředění hmoty tělesa a všech
OTDR Optical time domain reflection
 OTDR Optical time domain reflection Úvod Co je OTDR Jak měří trasu OTDR Události na trase Nastavení parametrů OTDR Jak vybrat OTDR Co je OTDR? Netopýr vysílá krátké akustické signály a na základě jejich
OTDR Optical time domain reflection Úvod Co je OTDR Jak měří trasu OTDR Události na trase Nastavení parametrů OTDR Jak vybrat OTDR Co je OTDR? Netopýr vysílá krátké akustické signály a na základě jejich
TEORIE NETKANÝCH TEXTILIÍ. 2. přednáška ÚVOD
 2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
2. přednáška ÚVOD https://moodle.fp.tul.cz/nano/ Přihlásit jako host (není možné zkoušet testy) nebo se plnohodnotně přihlásit = vytvořit nový účet. https://moodle.fp.tul.cz/nano/course/view.php?id=63
Skořepinové konstrukce. tloušťka stěny h a, b, c
 Skořepinové konstrukce skořepina střední plocha a b tloušťka stěny h a, b, c c Různorodé technické aplikace skořepinových konstrukcí Mezní stavy skořepinových konstrukcí Ztráta stability zhroucení konstrukce
Skořepinové konstrukce skořepina střední plocha a b tloušťka stěny h a, b, c c Různorodé technické aplikace skořepinových konstrukcí Mezní stavy skořepinových konstrukcí Ztráta stability zhroucení konstrukce
Filtrace stlačeného vzduchu. Nová generace
 Filtrace stlačeného vzduchu Nová generace Filtrace stlačeného vzduchu nová generace Firma Hankison je jedním z předních výrobců zařízení sloužících k sušení a filtraci stlačeného vzduchu. Výrobky Hankison
Filtrace stlačeného vzduchu Nová generace Filtrace stlačeného vzduchu nová generace Firma Hankison je jedním z předních výrobců zařízení sloužících k sušení a filtraci stlačeného vzduchu. Výrobky Hankison
LOGO. Struktura a vlastnosti kapalin
 Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
Struktura a vlastnosti kapalin Povrchová vrstva kapaliny V přírodě velmi často pozorujeme, že se povrch kapaliny, např. vody, chová jako pružná blána, která unese např. hmyz Vysvětlení: Molekuly kapaliny
ZMĚNY SKUPENSTVÍ LÁTEK
 ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
FYZIKA DIDAKTICKÝ TEST
 NOVÁ MATURITNÍ ZKOUŠKA Ilustrační test 2008 FY2VCZMZ08DT FYZIKA DIDAKTICKÝ TEST Testový sešit obsahuje 20 úloh. Na řešení úloh máte 90 minut. Odpovědi pište do záznamového archu. Poznámky si můžete dělat
NOVÁ MATURITNÍ ZKOUŠKA Ilustrační test 2008 FY2VCZMZ08DT FYZIKA DIDAKTICKÝ TEST Testový sešit obsahuje 20 úloh. Na řešení úloh máte 90 minut. Odpovědi pište do záznamového archu. Poznámky si můžete dělat
Atom vodíku. Nejjednodušší soustava: p + e Řešitelná exaktně. Kulová symetrie. Potenciální energie mezi p + e. e =
 Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
