7 Kvantová částice v centrálně symetrickém potenciálu.

Transkript

1 7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří, tak si všimnete, že vna se šíří ve všech směrech stejně a k jejímu popisu stačí funkce závisá pouze na vzdáenosti od počátku f r = f x y. To ceý popis značně zjednoduší. Podobně jsme zvykí pouřívat sférické souřadnice i v jiných případech, aniž bychom si toho expicitně všímai. Popis poohy na Zemi. Orientační běžci. Gravitace, obíhání panet ve suneční soustavě, potenciá eektrického náboje. Mnohé důežité fyzikání systémy je možno popsat pomocí potenciáu vykazujícího sférickou symetrii. Příkadem je částice v Couombově poi, či izotropní harmonický osciátor. Sférické souřadnice D dopředná transf. D dopředná transf. x=r cos sin x=r cos y=r sin sin y=r sin z =r cos D zpětná transformace D zpětná transformace r = x y r = x y z =tan y / x =tan y / x objemový a povrchový eement =cos z / r dv =r dr d objemový a povrchový eement ds=r d dv =r sin dr d d ds=r sin d d Operátor energie pro kvantovou částici v centráně symetrickém potenciáu má tvar ℏ H = V r m, (85) kde r= x y z. (86) Nejprve je nutné napříkad převést operátor energie, ae také operátor kvadrátu momentu hybnosti a jedné kompomenty momentu hybnosti do sférických souřadnic. Uvádím bez 5

2 odvození pouze tvar operátoru energie H ve sférických souřadnicích [ ] ℏ sin V r H = m r r r r sin sin zájemce konkrétní tvary ostatních operátorů ve sfér. souř. odkazuji na QMCA 6.., nebo SKM. Z předchozího pyne, že by možná šo najít vastní funkce tak operátoru energie, aby byy rozožené na radiání a úhovou část, tedy ve tvaru (význam koeficientů N,,m uvidíme záhy) r,, =R N r Y m, (87) (88) Indexy N,,m se týkají vastních číse, jimž tyto funkce přísuší. Takto napsané vnové funkce skutečně naézt ze. Díky možnosti rozděit Hamitonián (85) na radiání a úhovou část (87) je tedy možno řešit úohu na vastní čísa úhové části odděeně od úohy na vastní čísa radiání části. Úhová část vnové funkce (viz QMCA, s. 9) Tato část nezávisí na konkrétním tvaru potenciáu! Úhová část vnové funkce je určena jako vastní funkce operátoru kvadrátu momentu hybnosti. Úhová část vnové funkce tedy vypovídá o otáčení objektu. Dostáváme vastní hodnoty. (89) + a vastní funkce úhové části Hamitoniánu m i m, (9) m m kde P m jsou přidružené Legendrovy funkce definované způsobem m/ m m. (9) m = ℏ, Z, m Z, m Y, :=C P cos e t d t! dt m!, C m = 4 m! P t := Funkce Y m, které jsou spoečnými vastními funkcemi operátorů L, L z s vastními čísy = ℏ, μ=mℏ se nazývají kuové funkce. Y = Y = 4 4 (9) Y = cos Y = cos 4 4 Y ±= sin e±i = sin cos ±isin Y ± = sin Expicitní tvary ostatních kuových funkcí viz např. QMCA, s. 9. (9) 5

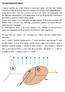
3 Jaká je pravděpodobnost naezení eektronu ve vzdáenosti r od jádra vodíku? r =r Rn r (viz cv. 5.8) * Na násedujícím obrázku jsou vykreseny Y m, =Y m, Y m,. Všiměte si, že tyto funkce nezávisí na úhu! Čísa a m se obvyke nazývají orbitání respektive magnetické kvantové číso stavu. Z kuových funkcí je možno pro částici s daným momentem hybnosti charakterizovaným čísy, m předpovědět pravděpodobnost naezení částice v daném prostorovém úhu Ω (94) m Čím rychejší rotace, tím větší vastní číso (kvadrát momentu hybnosti), tím více uzů vnové funkce mají. Tím má vna (např. eektron) obíhající okoo středu větší rychost pohybupo orbitě. Sožitost výrazů je pouze technickou záežitostí a iustruje obtížnost hedání vastních číse a vastních funkcí operátorů energie, momentu hybnosti a kvadrátu momentu hybnosti. Úpná řešení (88) je možné až tehdy, zadáme-i konkrétní tvar potenciáu V r. dw=, d = Y, d Radiání část vnové funkce: Izotropní harmonický osciátor V předchozí přednášce jsme řešii probém spektra energie třírozměrného harmonického osciátoru a zjistii jsme, že podprostory vastních stavů energie jsou vícerozměrné, což znamená, že (na rozdí od jednorozměrného harmonického osciátoru) jeho stavy nejsou určeny energií jednoznačně. Díky sférické symetrii potenciáu harmonického potenciáu V r = M x y z = M x y z = M r (95) ze jeho stavy jednoznačně popsat úpnou množinou pozorovatených tvořenou energií, kvadrátem momentu hybnosti a průmětem momentu hybnosti do ibovoného směru (voíme standartně směr osy z). Vastní hodnoty operátoru harmonického osciátoru jsou n / ℏ a vastní funkce, které jsou navíc vastními funkcemi operátorů L, L z s vastními hodnotami ℏ a m ℏ, kde n, Z +, m {,..., }, mají tvar / n,, m r,, =K n e / Ln kde 54 Y m,, (96)

4 d n z n L z := e z z n e n! dz n. (97) Zde ξ =r M ω / ħ, L n jsou zobecněné Laguerrovy poynomy. Zvoíme-i / 4 M K n = / 4 ℏ L = / (98) a Y m jsou normaizovány, pak funkce n,, m r,, jsou rovněž normaizovány. Prvních někoik zobecněných Laguerrových poynomů n n! n!! L = 4 r L = L = 8 8r r L =8 6r L = 6 L4= 96 44r 48r 4r L 4=44 96r r L 4= 96 4r 4 L 4=4 (99) Kvantové číso n se obvyke nazývá radiání kvantové číso (udává příspěvek k energii od radiáního pohybu částice) a číso N :=n se nazývá havní kvantové číso, udává cekovou energii částice. Z faktu, že k danému existuje různých stavů, jednouchou kombinatorickou úvahou odvodíme, že degenerace hadiny energie N / ħω harmonického osciátoru, to jest počet stavů s touto energií, je N N /. Tento výsedek jsme již dostai v paragrafu o harmonickém osciátoru, kde N =n n n. N n m E Degenerace E (N+)(N+)/ / ℏ -,, 5/ ℏ -,-,,, 7/ ℏ 6 -,-,-,,,, -,, 9/ ℏ Radiání část vnové funkce: Couombův potenciá Daší vemi důežitý probém je spektrum energie pro potenciá V r = Q,Q r () neboť jej ze použít k popisu hadin energií eektronu v obau atomu vodíku. Uvážímei totiž, že proton je víc než 8 krát těžší než eektron je přirozené očekávat, že vnitřní energie (to jest odhédneme-i od pohybu atomu jako ceku) ceého systému se bude jen máo išit od energie e Ze eektronu v eektrostatickém poi (), kde Q=, (pro obecný atom Q= ) kde 4 4 e je náboj eektronu a je 55

5 permitivita vakua. Vastní hodnoty operátoru energie kvantové částice v Couombickém poi () jsou E = E n, = M eq ℏ n = R, N, n, Z + N () Číso n se opět nazývá radiání kvantové číso. Havní kvantové číso určující hodnotu M eq energie je N = n. Konstanta R= se nazývá Rydbergova energie. R je ℏ e pro každý atom jiná. Hodnota R pro atom vodíku (kde Q= a M e je hmotnost 4 eektronu) je R =.84 8 J =.6 ev. Hadiny energie pro harmonický (vevo) a Couombův (vpravo) potenciá. Vastní funkce operátoru energie kvantové částice v Couombickém poi, odpovídající R vastní hodnotě, která je navíc vastní funkcí operátorů L, L z s vastními N hodnotami ℏ, m ℏ, kde {,..., N }, m {,..., } () má tvar a= ℏ, Q M e () L n jsou zobecněné Laguerrovy poynomy (97) a K N je normaizační N,, m r,, = K N kde r r /Na r e L N Y,, Na Na m konstanta K N = Na / N! N [ N!] (4) a Y m jsou normaizované kuové funkce. Konstanta a, mající fyzikání rozměr déky, se nazývá Bohrův pooměr; vypovídá o veikosti atomu. Pro vodík je a=.5 nm. Radiání části vnové funkce R N pro první tři energetické hadiny atomu vodíku: 56

6 / R r = e r / a a r R r = e r /a a a r r / a R r = e a 6a R r = r r a e r /a a 7a 8 r r r /a 6a e 9 6a a 4 r R r = a e r / a 9 a R r = (5) Funkce mají N-- uzů. Tvary vnových funkcí: pozor, v násedujících obrázcích je n používáno ve smysu havního kvantového čísa (u nás N) 57

7 [ physics_notes/quantum_mechanics/university_phy sics_notes_tabe_of_the_radia_parts_of_wavefunc tions_for_the_hydrogen_atom.htm] Z výrazu () je zřejmé, že všechny stavy (), pro které, m eží v množině () mají tutéž energii. Degenerace hadiny energie N, neboi počet stavů s energií R/ N je N D N = = N. (6) = N n m E Degenerace E N (s) -R/ (s) (p) -,, -R/4 4 (s) (p) -,, -R/9 9 (d) -,-,,, (s) (p) -,, (d) -,-,,, -R/6 6 (f) -,-,-,,,, 4 V předchozí tabuce jsou vypsána jaká kvantová čísa n,,m, které odpovídají kvantovému čísu N pro N=,,,4. Každé takové kombinaci kvantových číse odpovídá unikátní vnová funkce. Hodnoty energie () částice v Couombickém poi předpovězené kvantovou mechanikou ze snadno ověřit experimentáně, neboť je možno tímto systémem popsat vodíkový atom. Jeho záření má (v rozporu s kasickou teorií) čárové spektrum a empiricky byo zjištěno, že frekvence záření spňují tzv. Rydberg Ritzův kombinační princip 58

8 =const n n (7) objevený ještě před vznikem kvantové mechaniky (viz předn. a odvození pomocí Bohrova modeu atomu). V rámci kvantové mechaniky je snadné tuto formui vysvětit předpokadem, že frekvence fotonů emitovaných eektrony v obau atomů je dána rozdíem hadin energií eektronu. Pro vodík pak dostáváme EN EN mq h=e N E N = = ℏ 4 ℏ N N (8) M eq je v tomto 4 ℏ případě. 5 sec a pro N =,,... pak dostáváme frekvence (odpovídající frekvenci emisních čar), jež jsou v dobré shodě s naměřenými hodnotami Lymanovy série N =, Bamerovy série N =, i daších sérií. ℏ jako v případě HO. Nejnižší energie Nejnižší energie pro Couombovský potenciá není je záporná, avšak konečná. To je zajímavé, protože Couombův potenciá je nekonečně huboký. Proč eektrony ihned nespadnou do jádra atomů? Couombovský potenciá má stejný tvar jako gravitační potenciá (ten je ovšem vždy přitaživý). Proč nespadnou panety do Sunce? Ve sférických souřadnicích je stav eektronu jednoznačně popsán třemi z násedujících kvantových číse N havní kvantové číso určuje v. hodnotu operátoru E orbitání kvantové číso určuje v. hodnotu operátoru L (může nabývat hodnot... N-) m magnetické kvantové číso určuje v. hodnotu operátoru L z n radiání kvantové číso spou s určuje v. hodnotu operátoru E Protože hodnota energie stavu často závisí na hodnotě orbitáního kvantového čísa, mají stavy s daným ustáené spektroskopické značení s, p, d, f, g, h,i, k,,... pro =,,,.... ) kde Q=e /4π. Numerická hodnota Rydbergovy frekvence R= Pár upozornění na závěr: Jak uvidíme ve cvičení, v případě harmonického osciátoru úpně jedno, jesti určíme stav HO pomocí kvantových číse (n, n, n), nebo (N,, m). Jde o rozvoj do odišných funkcí, na konci však musí být identická vnová funkce, ať je popsána tou či onou sadou číse. Uvědomme si, že pro jiné prvky než vodík budou vastní stavy vypadat trochu jinak, protože mají odišný počet protonů a eektrony interagují také mezi sebou navzájem. Jaká je pravděpodobnost naezení eektronu ve vzdáenosti r od jádra vodíku? r =r R N r (viz cv. 5.8) * Na násedujícím obrázku jsou vykreseny Y m, =Y m, Y m,. Všiměte si, že tyto funkce nezávisí na úhu! 59

9 [ 6

10 [ 6