Kapitola S4.3. Archimedova serpentína
|
|
|
- Barbora Kučerová
- před 8 lety
- Počet zobrazení:
Transkript
1 Kapitola. Archimedova erpentína
2 Archimedova erpentína V úvode kapitol ú uvedené dva potup vtvorenia Archimedovej erpentín. V tejto kapitole i ich zopakujeme a poukážeme na ich úvi: a) Archimedova erpentína je obalová plocha tému guľových plôch G, ktoré majú konštantný polomer r a ich tred ležia na krutkovici. krutkovica je krutkovica tredu guľovej ploch G. b) Archimedova erpentína vznikne krutkovým pohbom kružnice k. Tvoriaca kružnica k o tredom v bode leží v rovine, ktorá je kolmá na dotčnicu t krutkovice ( je krutkovica bodu ). o o a) b) G p k t t o o G k
3 a) Archimedova erpentína je obalová plocha guľových plôch G ( konštantným polomerom r) o tredmi na krutkovici. krutkovica je krutkovica tredu guľovej ploch G. G polôh krutkovanej guľovej ploch Archimedova erpentína ako obalová plocha DWF
4 b) Archimedova erpentína vznikne krutkovým pohbom kružnice k. Tvoriaca kružnica k o tredom v bode leží v rovine, ktorá je kolmá na dotčnicu t krutkovice ( je krutkovica bodu ). z = o k k o k Mongeova projekcia DWF Kolmá aonometria
5 Obidva potup vtvorenia Archimedovej erpentín úviia tak, že Archimedova erpentína vtvorená ako obalová plocha tému guľových plôch G a dotýka každej guľovej ploch o tredom práve pozdĺž tvoriacej kružnice k o tredom v bode. Kružnica k leží v rovine kolmej na dotčnicu t krutkovice ( je krutkovica bodu ). G k k polôh krutkovanej guľovej ploch G a polôh kružnice k Archimedova erpentína ako obalová plocha a polôh kružnice k DWF
6 v V Mongeovej projekcii zobrazte jeden závit cklickej krutkovej ploch (Archimedovej erpentín), ktorá je obálkou tému krutkovaných guľových plôch G. krutkový pohb je pravotočivý, daný oou o a výškou závitu v. Pre jeden závit zobrazte polôh krutkovanej guľovej ploch. 0 o = z 8 Archimedova erpentína je obalová plocha guľových plôch G konštantným polomerom r a o tredmi na krutkovici. Potup rovania: ) Zobrazíme krutkovicu tredu guľovej ploch G. ) Zobrazíme polôh krutkovanej guľovej ploch. Priemetom guľovej ploch v kolmom premietaní je kruh. ) Pôdorom Archimedovej erpentín je medzikružie. G 0 8 = G o polôh krutkovanej guľovej ploch Archimedova erpentína ako obalová plocha
7 V Mongeovej projekcii zobrazte jeden závit cklickej krutkovej ploch (Archimedovej erpentín), ktorá je obálkou tému krutkovaných guľových plôch G. krutkový pohb je pravotočivý, daný oou o a výškou závitu v. Pre jeden závit zobrazte polôh krutkovanej guľovej ploch. v 0 o = z 8 Potup rovania: ) Obr ploch v náre načrtneme ako obálku kružníc, ktoré ú obrmi guľových plôch. Poznámka: Pri krelení obru ploch v náre môžeme doplniť ľubovoľný počet ďalších polôh krutkovanej guľovej ploch. Ich tred ú ľubovoľné bod na krutkovici. V našom príklade je zobrazených ďalších polôh. Pre úplnoť ú zobrazené aj v pôdore. G 0 8 = G o polôh krutkovanej guľovej ploch Archimedova erpentína ako obalová plocha
8 V kolmej aonometrii zobrazte jeden závit cklickej krutkovej ploch (Archimedovej erpentín), ktorá je obálkou tému krutkovaných guľových plôch G. krutkový pohb je pravotočivý, daný oou o a výškou závitu v. Pre jeden závit zobrazte polôh krutkovanej guľovej ploch. Potup rovania: ) Zobrazíme krutkovicu tredu guľovej ploch G. v 0 8 v O o ) Zobrazíme polôh krutkovanej guľovej ploch. Priemetom guľovej ploch v kolmej aonometrii je kruh. G ) Obr ploch načrtneme ako obálku kružníc, ktoré ú obrmi guľových plôch. Poznámka: Pri krelení obru ploch môžeme doplniť ľubovoľný počet ďalších polôh krutkovanej guľovej ploch. Ich tred ú ľubovoľné bod na krutkovici. V našom príklade je zobrazených ďalších polôh. o O o 8
9 Aproimácia Archimedovej erpentín, ZOO Jihlava k
10 Práca študenta odboru Dizajn Ivan Venkov 008/0 aonometria 0
11 Práca študenta odboru Dizajn Ivan Venkov 008/0 Perpektíva
Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11].
![Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. Konstruktivní geometrie Bod Axonometrie. Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11].](/thumbs/52/30469232.jpg) Konstruktivní geometrie Bod Axonometrie Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. VŠB-TU Ostrava 1 Jana Bělohlávková Konstruktivní geometrie
Konstruktivní geometrie Bod Axonometrie Úloha: V pravoúhlé axonometrii (XY = 10; XZ = 12; YZ = 11) zobrazte bod A[2; 3; 5] a bod V[9; 7.5; 11]. VŠB-TU Ostrava 1 Jana Bělohlávková Konstruktivní geometrie
ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA
 ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA Pri kolmom premietaní môžeme zvoliť šesť smerov premietania, ale ich priemety nemajú rovnakú dôležitosť: A. hlavné priemety v smere: N - pohľad z predu (nárys),
ZOBRAZOVANIE NA VÝKRESOCH - ZÁKLADY PREMIETANIA Pri kolmom premietaní môžeme zvoliť šesť smerov premietania, ale ich priemety nemajú rovnakú dôležitosť: A. hlavné priemety v smere: N - pohľad z predu (nárys),
ŠROUBOVICE. 1) Šroubový pohyb. 2) Základní pojmy a konstrukce
 1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
Základné geometrické telesá a ich styčné, dotykové roviny. Soňa Kudličková, Daniela Hansmanová
 Katedra algebry, geometrie a didaktiky matematiky FMFI UK, oddelenie geometrie Základné geometrické telesá a ich styčné, dotykové roviny Soňa Kudličková, Daniela Hansmanová Úvod... 3 1. Práca v GeoGebre...
Katedra algebry, geometrie a didaktiky matematiky FMFI UK, oddelenie geometrie Základné geometrické telesá a ich styčné, dotykové roviny Soňa Kudličková, Daniela Hansmanová Úvod... 3 1. Práca v GeoGebre...
UČEBNÉ TEXTY. Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Dátum: 2015
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Kótovanie Ing.Jaroslava Šufliarska
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Kótovanie Ing.Jaroslava Šufliarska
Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace. Šroubovice dráha hmotného bodu při šroubovém pohybu
 ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
Rozvinutelné plochy. tvoří jednoparametrickou soustavu rovin a tedy obaluje rozvinutelnou plochu Φ. Necht jsou
 Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura:
 8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
P R O M Í T Á N Í. rovina π - průmětna vektor s r - směr promítání. a // s r, b// s r,
 P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
3.MONGEOVO PROMÍTÁNÍ. Rovnoběžný průmět 3D těles na rovinu není vzájemně jednoznačné zobrazení, k obrazu neumíme jednoznačně určit objekt v prostoru
 3.MONGEOVO PROMÍTÁNÍ A B E 3 E 2 Rovnoběžný průmět 3D těles na rovinu není vzájemně jednoznačné zobrazení, k obrazu neumíme jednoznačně určit objekt v prostoru 3.1.Kartézský souřadnicový systém O počátek
3.MONGEOVO PROMÍTÁNÍ A B E 3 E 2 Rovnoběžný průmět 3D těles na rovinu není vzájemně jednoznačné zobrazení, k obrazu neumíme jednoznačně určit objekt v prostoru 3.1.Kartézský souřadnicový systém O počátek
Na aute vyfarbi celé predné koleso na zeleno a pneumatiku zadného kolesa vyfarbi na červeno.
 Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Šroubovice... 5 Šroubové plochy Stanovte paprsek tak, aby procházel bodem A a po odrazu na rovině ρ procházel bodem
 Geometrie Mongeovo promítání................................ 1 Řezy těles a jejich průniky s přímkou v pravoúhlé axonometrii......... 3 Kuželosečky..................................... 4 Šroubovice......................................
Geometrie Mongeovo promítání................................ 1 Řezy těles a jejich průniky s přímkou v pravoúhlé axonometrii......... 3 Kuželosečky..................................... 4 Šroubovice......................................
tečen a osu o π, V o; plochu omezte hranou vratu a půdorysnou a proved te rozvinutí
 Řešené úlohy Rozvinutelná šroubová plocha v Mongeově promítání Příklad: V Mongeově promítání zobrazte půl závitu rozvinutelné šroubové plochy, jejíž hranou vratu je pravotočivá šroubovice, která prochází
Řešené úlohy Rozvinutelná šroubová plocha v Mongeově promítání Příklad: V Mongeově promítání zobrazte půl závitu rozvinutelné šroubové plochy, jejíž hranou vratu je pravotočivá šroubovice, která prochází
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Animované modely šroubových ploch
 Animované modely šroubových ploch Jaroslav Bušek Abstrakt V příspěvku jsou prezentovány animované prostorové modely přímkových a cyklických šroubových ploch, které byly vytvořeny jako didaktické pomůcky
Animované modely šroubových ploch Jaroslav Bušek Abstrakt V příspěvku jsou prezentovány animované prostorové modely přímkových a cyklických šroubových ploch, které byly vytvořeny jako didaktické pomůcky
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70).
![A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70). A[ 20, 70, 50] a výška v = 70, volte z V > z S ; R[ 40, 20, 80], Q[60, 70, 10]. α(90, 60, 70).](/thumbs/101/151863289.jpg) Úkoly k zápočtu z BA008 Všechny úkoly jsou povinné. Úkoly číslo 4, 7, 12, 14 budou uznány automaticky, pokud poslední den semestru, tj. 3. 5. 2019, budou všechny ostatní úkoly odevzdané a uznané. 1. Je
Úkoly k zápočtu z BA008 Všechny úkoly jsou povinné. Úkoly číslo 4, 7, 12, 14 budou uznány automaticky, pokud poslední den semestru, tj. 3. 5. 2019, budou všechny ostatní úkoly odevzdané a uznané. 1. Je
Singularity rotačních obalových ploch
 Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
UČEBNÉ TEXTY. I. ročník. Strojnícke zobrazovanie. Ing.Jaroslava Šufliarska
 UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Strojnícke zobrazovanie Ing.Jaroslava
UČEBNÉ TEXTY Vzdelávacia oblasť: Predmet: Ročník, triedy: Tematický celok: Vypracoval: Moderné vzdelávanie pre vedomostnú spoločnosť Technické kreslenie cvičenie I. ročník Strojnícke zobrazovanie Ing.Jaroslava
LINEÁRNÍ PERSPEKTIVA. Přednáška DG2*A 6. týden
 LINEÁRNÍ PERSPEKTIVA Přednáška DG*A 6. týden DRY VOLNÉ PERSPEKTIVY Muíme vždy volit ouřadnicový ytém. Souřadné oy pravidla umíťujeme tak, aby byly rovnoběžné ranami obraovanéo objektu. JEDNOÚBĚŽNÍKOVÁ
LINEÁRNÍ PERSPEKTIVA Přednáška DG*A 6. týden DRY VOLNÉ PERSPEKTIVY Muíme vždy volit ouřadnicový ytém. Souřadné oy pravidla umíťujeme tak, aby byly rovnoběžné ranami obraovanéo objektu. JEDNOÚBĚŽNÍKOVÁ
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Další plochy technické praxe
 Další plochy technické praxe Dosud studované plochy mají široké využití jak ve stavební tak ve strojnické praxi. Studovali jsme možnosti jejich konstrukcí, vlastností i využití v praxi. Kromě těchto ploch
Další plochy technické praxe Dosud studované plochy mají široké využití jak ve stavební tak ve strojnické praxi. Studovali jsme možnosti jejich konstrukcí, vlastností i využití v praxi. Kromě těchto ploch
Zachovanie mentálnej mapy pri interakcií s grafom. RNDr. Jana Katreniaková PhD.
 Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
Pracovní listy LINEÁRNÍ PERSPEKTIVA
 Tecnická univerita v Liberci Fakulta přírodovědně-umanitní a pedagogická Katedra matematiky a didaktiky matematiky LINEÁRNÍ PERPEKTIVA Petra Pirklová Liberec, květen 07 . Ve stopníkové metodě obrate stupně
Tecnická univerita v Liberci Fakulta přírodovědně-umanitní a pedagogická Katedra matematiky a didaktiky matematiky LINEÁRNÍ PERPEKTIVA Petra Pirklová Liberec, květen 07 . Ve stopníkové metodě obrate stupně
Interaktivní modely pro Konstruktivní geometrii
 Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI
 KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI Šroubový pohyb vzniká složením otáčení kolem osy o a posunutí ve směru osy o, přičemž oba pohyby jsou spojité a rovnoměrné. Jestliže při pohybu po ose "dolů" je otáčení
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI Šroubový pohyb vzniká složením otáčení kolem osy o a posunutí ve směru osy o, přičemž oba pohyby jsou spojité a rovnoměrné. Jestliže při pohybu po ose "dolů" je otáčení
Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia
 Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia v školskom roku 2014/2015 Skupina A Kód žiaka: dátum: 12. máj 2014 1. Barborka si kupuje v obchode pečivo za centov, dva jogurty
Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia v školskom roku 2014/2015 Skupina A Kód žiaka: dátum: 12. máj 2014 1. Barborka si kupuje v obchode pečivo za centov, dva jogurty
MONGEOVO PROMÍTÁNÍ - 2. část
 MONGEOVO PROMÍTÁNÍ - 2. část ZOBRAZENÍ KRUŽNICE Příklad: V rovině ρ zobrazte kružnici o středu S a poloměru r. kružnice ležící v obecné rovině se v obou průmětech zobrazuje jako elipsa poloměr kružnice
MONGEOVO PROMÍTÁNÍ - 2. část ZOBRAZENÍ KRUŽNICE Příklad: V rovině ρ zobrazte kružnici o středu S a poloměru r. kružnice ležící v obecné rovině se v obou průmětech zobrazuje jako elipsa poloměr kružnice
4.OBECNÁ AXONOMETRIE A KOSOÚHLÉ PROMÍTÁNÍ
 4.BECNÁ AXNMETRIE A KSÚHLÉ PRMÍTÁNÍ Aonometrie kosoúhlé promítání voenská perspektiva pravoúhlá aonometrie Znalost těchto metod e ákladem skicování, které e potřebné i v době CAD sstémů. Kosoúhlé promítání
4.BECNÁ AXNMETRIE A KSÚHLÉ PRMÍTÁNÍ Aonometrie kosoúhlé promítání voenská perspektiva pravoúhlá aonometrie Znalost těchto metod e ákladem skicování, které e potřebné i v době CAD sstémů. Kosoúhlé promítání
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
TC Obsahový štandard - téma Výkonový štandard - výstup
 Mocniny a odmocniny, zápis veľkých čísel Finančná matemati ka UČEBNÉ OSNOVY DEVIATY ROČNÍK TC Obsahový štandard - téma Výkonový štandard - výstup Vklad, úrok, úroková miera Dane zvládnuť základné pojmy
Mocniny a odmocniny, zápis veľkých čísel Finančná matemati ka UČEBNÉ OSNOVY DEVIATY ROČNÍK TC Obsahový štandard - téma Výkonový štandard - výstup Vklad, úrok, úroková miera Dane zvládnuť základné pojmy
MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2]
![MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2] MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2]](/thumbs/55/35543113.jpg) ZOBRAZENÍ BODU - sdružení průměten MONGEOVO PROMÍTÁNÍ π 1... půdorysna π 2... nárysna x... osa x (průsečnice průměten) sdružení průměten A 1... první průmět bodu A A 2... druhý průmět bodu A ZOBRAZENÍ
ZOBRAZENÍ BODU - sdružení průměten MONGEOVO PROMÍTÁNÍ π 1... půdorysna π 2... nárysna x... osa x (průsečnice průměten) sdružení průměten A 1... první průmět bodu A A 2... druhý průmět bodu A ZOBRAZENÍ
A 1. x x. 1.1 V pravoúhlé axonometrii zobrazte průměty bodu A [4, 5, 8].
![A 1. x x. 1.1 V pravoúhlé axonometrii zobrazte průměty bodu A [4, 5, 8]. A 1. x x. 1.1 V pravoúhlé axonometrii zobrazte průměty bodu A [4, 5, 8].](/thumbs/62/46958546.jpg) strana 1 1. onometrie. 1.1 V pravoúhlé aonometrii obrate průmět bodu [4, 5, 8]. 1.2 Zobrate bývající pravoúhlé průmět bodu do souřadnicových rovin. Určete souřadnice bodu, který je obraen v pravoúhlé aonometrii.
strana 1 1. onometrie. 1.1 V pravoúhlé aonometrii obrate průmět bodu [4, 5, 8]. 1.2 Zobrate bývající pravoúhlé průmět bodu do souřadnicových rovin. Určete souřadnice bodu, který je obraen v pravoúhlé aonometrii.
0 x 12. x 12. strana Mongeovo promítání - polohové úlohy.
 strana 9 3.1a Sestrojte sdružené průměty stopníků přímek a = AB, b = CD, c = EF. A [-2, 5, 1], B [3/2, 2, 5], C [3, 7, 4], D [5, 2, 4], E [-5, 3, 3], F [-5, 3, 6]. 3.1b Určete parametrické vyjádření přímek
strana 9 3.1a Sestrojte sdružené průměty stopníků přímek a = AB, b = CD, c = EF. A [-2, 5, 1], B [3/2, 2, 5], C [3, 7, 4], D [5, 2, 4], E [-5, 3, 3], F [-5, 3, 6]. 3.1b Určete parametrické vyjádření přímek
Shodná zobrazení v rovině
 Shodná zobrazení v rovině Zobrazení Z v rovině je předpis, který každému bodu X roviny přiřazuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X jeho obraz. Zapisujeme Z: X X. Množinu obrazů všech
Shodná zobrazení v rovině Zobrazení Z v rovině je předpis, který každému bodu X roviny přiřazuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X jeho obraz. Zapisujeme Z: X X. Množinu obrazů všech
Konstruktivní geometrie
 Konstruktivní geometrie Elipsa Úloha 1: Najděte bod M takový, aby součet jeho vzdáleností od bodů F 1 a F 2 byl 12cm; tj. F 1 M+F 2 M=12. Najděte více takových bodů. Konstruktivní geometrie Elipsa Oskulační
Konstruktivní geometrie Elipsa Úloha 1: Najděte bod M takový, aby součet jeho vzdáleností od bodů F 1 a F 2 byl 12cm; tj. F 1 M+F 2 M=12. Najděte více takových bodů. Konstruktivní geometrie Elipsa Oskulační
s touto válcovou plochou. Tento případ nebudeme dále uvažovat.
 Šroubové plochy Šroubová plocha Φ(k) vzniká šroubovým pohybem křivky k, která není trajektorií daného šroubového pohybu. Je-li pohyb levotočivý, resp. pravotočivý je i plocha Φ levotočivá, resp. pravotočivá.
Šroubové plochy Šroubová plocha Φ(k) vzniká šroubovým pohybem křivky k, která není trajektorií daného šroubového pohybu. Je-li pohyb levotočivý, resp. pravotočivý je i plocha Φ levotočivá, resp. pravotočivá.
-V- novinka. Guľové kohúty VAPB, mechanické ovládanie 5.2. Pripojovací závit podľa DIN Montážna príruba podľa ISO Dĺžka podľa DIN 3202-M3
 -V- novinka Guľové kohúty VAPB, mechanické ovládanie Pripojovací závit podľa DIN 2999 Montážna príruba podľa ISO 5211 Dĺžka podľa DIN 3202-M3 Hriadeľová montáž zvnútra, poistená proti vyfúknutiu Strediaci
-V- novinka Guľové kohúty VAPB, mechanické ovládanie Pripojovací závit podľa DIN 2999 Montážna príruba podľa ISO 5211 Dĺžka podľa DIN 3202-M3 Hriadeľová montáž zvnútra, poistená proti vyfúknutiu Strediaci
5.0 STĚNY PŮDORYSNĚ ZALOMENÉ A ZAKŘIVENÉ
 5.0 STĚNY PŮDORYSNĚ ZALOMENÉ A ZAKŘIVENÉ V některých situacích je potřebné stěnu půdorysně zakřivit, event. vytvořit pravý úhel. V následující kapitole je uveden přehled o možnostech provádění takových
5.0 STĚNY PŮDORYSNĚ ZALOMENÉ A ZAKŘIVENÉ V některých situacích je potřebné stěnu půdorysně zakřivit, event. vytvořit pravý úhel. V následující kapitole je uveden přehled o možnostech provádění takových
ŘEŠENÉ PŘÍKLADY DESKRIPTIVNÍ GEOMETRIE. ONDŘEJ MACHŮ a kol.
 ŘEŠENÉ PŘÍKLADY Z DESKRIPTIVNÍ GEOMETRIE ONDŘEJ MACHŮ a kol. Předmluva Otevíráte sbírku, která vznikla z příkladů zadaných studentům pátého ročníku PřF UP v Olomouci, učitelů matematiky a deskriptivní
ŘEŠENÉ PŘÍKLADY Z DESKRIPTIVNÍ GEOMETRIE ONDŘEJ MACHŮ a kol. Předmluva Otevíráte sbírku, která vznikla z příkladů zadaných studentům pátého ročníku PřF UP v Olomouci, učitelů matematiky a deskriptivní
CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála
 Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 25.5.2013 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála Spirála vrták s válcovou
Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 25.5.2013 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Spirála Spirála vrták s válcovou
17 Kuželosečky a přímky
 17 Kuželosečky a přímky 17.1 Poznámka: Polára bodu M ke kuželosečce Nechť X = [x 0,y 0 ] je bod. Zavedeme následující úpravy: x x 0 x y y 0 y xy (x 0 y + xy 0 )/ x (x 0 + x)/ y (y 0 + y)/ (x m) (x 0 m)(x
17 Kuželosečky a přímky 17.1 Poznámka: Polára bodu M ke kuželosečce Nechť X = [x 0,y 0 ] je bod. Zavedeme následující úpravy: x x 0 x y y 0 y xy (x 0 y + xy 0 )/ x (x 0 + x)/ y (y 0 + y)/ (x m) (x 0 m)(x
8 Podobná (ekviformní) zobrazení v rovině
 Typeset by LATEX2ε 1 8 Podobná (ekviformní) zobrazení v rovině 8.1 Stejnolehlost (homotetie) v rovině Definice 8.1.1. Nechť jsou dány 3 různé kolineární body A, B, C. Dělicím poměrem λ = (ABC) rozumíme
Typeset by LATEX2ε 1 8 Podobná (ekviformní) zobrazení v rovině 8.1 Stejnolehlost (homotetie) v rovině Definice 8.1.1. Nechť jsou dány 3 různé kolineární body A, B, C. Dělicím poměrem λ = (ABC) rozumíme
Definice 3. Kruhová inverze určená kružnicí ω(s, r) (viz Obr. 6) je zobrazení, které každému bodu X S přiřadí bod X tímto způsobem:
 2 Kruhová inverze Definice 3. Kruhová inverze určená kružnicí ω(s, r) (viz Obr. 6) je zobrazení, které každému bodu X S přiřadí bod X tímto způsobem: (1) X SX, (2) SX SX = r 2. Obrázek 6: Kruhová inverze
2 Kruhová inverze Definice 3. Kruhová inverze určená kružnicí ω(s, r) (viz Obr. 6) je zobrazení, které každému bodu X S přiřadí bod X tímto způsobem: (1) X SX, (2) SX SX = r 2. Obrázek 6: Kruhová inverze
ŠROUBOVÉ PLOCHY. 1. Základní úlohy na šroubových plochách.
 ŠROUBOVÉ PLOCHY 1. Základní úlohy na šroubových plochách. Šroubová plocha Φ vzniká šroubovým pohybem křivky k, která není trajektorií daného šroubového pohybu. Je-li pohyb levotočivý (pravotočivý je i
ŠROUBOVÉ PLOCHY 1. Základní úlohy na šroubových plochách. Šroubová plocha Φ vzniká šroubovým pohybem křivky k, která není trajektorií daného šroubového pohybu. Je-li pohyb levotočivý (pravotočivý je i
Deskriptivní geometrie pro střední školy
 Deskriptivní geometrie pro střední školy Mongeovo promítání 1. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Obsah TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY DESKRIPTIVNÍ GEOMETRIE 1. díl
Deskriptivní geometrie pro střední školy Mongeovo promítání 1. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Obsah TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY DESKRIPTIVNÍ GEOMETRIE 1. díl
REKONSTRUKCE ASTROLÁBU POMOCÍ STEREOGRAFICKÉ PROJEKCE
 REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
ZBORCENÉ PŘÍMKOVÉ PLOCHY ŘEŠENÉ PŘÍKLADY
 ZBORCENÉ PŘÍMKOVÉ PLOCHY ŘEŠENÉ PŘÍKLADY Zpracovala: Kristýna Rožánková FA ČVUT 2011 ZBORCENÉ PŘÍMKOVÉ PLOCHY Zborcené přímkové plochy jsou určeny třemi křivkami k, l, m, které neleží na jedné rozvinutelné
ZBORCENÉ PŘÍMKOVÉ PLOCHY ŘEŠENÉ PŘÍKLADY Zpracovala: Kristýna Rožánková FA ČVUT 2011 ZBORCENÉ PŘÍMKOVÉ PLOCHY Zborcené přímkové plochy jsou určeny třemi křivkami k, l, m, které neleží na jedné rozvinutelné
Technická univerzita v Košiciach
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Kontrola väzieb výkazu Súvaha a Výkaz ziskov a strát Príručka používateľa
 Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
DESKRIPTIVNÍ GEOMETRIE PRO STUDENTY GYMNÁZIA CH. DOPPLERA. Mgr. Ondřej Machů. --- Pracovní verze:
 DESKRIPTIVNÍ GEOMETRIE PRO STUDENTY GYMNÁZIA CH. DOPPLERA Mgr. Ondřej Machů --- Pracovní verze: 6. 10. 2014 --- Obsah Úvodní slovo... - 3-1 Základy promítacích metod... - 4-1.1 Rovnoběžné promítání...
DESKRIPTIVNÍ GEOMETRIE PRO STUDENTY GYMNÁZIA CH. DOPPLERA Mgr. Ondřej Machů --- Pracovní verze: 6. 10. 2014 --- Obsah Úvodní slovo... - 3-1 Základy promítacích metod... - 4-1.1 Rovnoběžné promítání...
ŠÍRENIE SIGNÁLU A INŠTALÁCIA RÁDIOVÝCH SYSTÉMOV
 ŠÍRENIE SIGNÁLU A INŠTALÁCIA RÁDIOVÝCH SYSTÉMOV Obsah 1. RÁDIOVÝ SIGNÁL V BUDOVÁCH....3 1.1 Odrazy a prenos...3 1.2. Tienenie signálu...5 1.3. Uhol prieniku...6 2. INŠTALÁCIA ANTÉNY....7 2.1. Inštalácia
ŠÍRENIE SIGNÁLU A INŠTALÁCIA RÁDIOVÝCH SYSTÉMOV Obsah 1. RÁDIOVÝ SIGNÁL V BUDOVÁCH....3 1.1 Odrazy a prenos...3 1.2. Tienenie signálu...5 1.3. Uhol prieniku...6 2. INŠTALÁCIA ANTÉNY....7 2.1. Inštalácia
s.r.o. HelpLine:
 1. Úvod Tento stručný manuál je určený bežnému užívateľovi využívajúcemu služby portálu www.burzabrigad.sk. 1.1 Technické požiadavky na prostredie Technické požiadavky sú nezávislé od operačného systému,
1. Úvod Tento stručný manuál je určený bežnému užívateľovi využívajúcemu služby portálu www.burzabrigad.sk. 1.1 Technické požiadavky na prostredie Technické požiadavky sú nezávislé od operačného systému,
Pracovní listy MONGEOVO PROMÍTÁNÍ
 Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky MONGEOVO PROMÍTÁNÍ Petra Pirklová Liberec, únor 07 . Zobrazte tyto body a určete jejich
Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky MONGEOVO PROMÍTÁNÍ Petra Pirklová Liberec, únor 07 . Zobrazte tyto body a určete jejich
Smysl otáčení. Aplikace. Pravotočivá
 Šroubovice Definice Šroubovice je křivka generovaná bodem A, který se otáčí kolem dané přímky o a zároveň se posouvá podél této přímky, oboje rovnoměrnou rychlostí. Pohyb bodu A šroubový pohyb Přímka o
Šroubovice Definice Šroubovice je křivka generovaná bodem A, který se otáčí kolem dané přímky o a zároveň se posouvá podél této přímky, oboje rovnoměrnou rychlostí. Pohyb bodu A šroubový pohyb Přímka o
1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava A. 2 B. 6 C. 9 D. 14 A. 21 B. 36 C. 24 D. 33
 V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
AXONOMETRIE - 2. část
 AXONOMETRIE - 2. část Průmět přímky K určení přímky stačí její dva libovolné průměty, zpravidla používáme axonometrický průmět a půdorys. Bod ležící na přímce se zobrazí do bodu na přímce v každém průmětu.
AXONOMETRIE - 2. část Průmět přímky K určení přímky stačí její dva libovolné průměty, zpravidla používáme axonometrický průmět a půdorys. Bod ležící na přímce se zobrazí do bodu na přímce v každém průmětu.
Obr. 1 - názov podpísaného súboru/kontajnera v sivej lište
 Zobrazenie dokumentov v elektronickej správe V elektronickej správe sa môžu prenášať autorizované (podpísané/pečatené), ale aj neautorizované súbory, a to buď v hlavnom objekte správy, v prílohách alebo
Zobrazenie dokumentov v elektronickej správe V elektronickej správe sa môžu prenášať autorizované (podpísané/pečatené), ale aj neautorizované súbory, a to buď v hlavnom objekte správy, v prílohách alebo
Evolventní interpolace (INVCW, INVCCW)
 Funkce Evolventa kruhu je křivka, která je popsána koncovým bodem pevného napnutého vlákna odvíjejícího se z kružnice. Evolventní interpolace umožňuje dráhové křivky podél evolventy. Pohyb se uskutečňuje
Funkce Evolventa kruhu je křivka, která je popsána koncovým bodem pevného napnutého vlákna odvíjejícího se z kružnice. Evolventní interpolace umožňuje dráhové křivky podél evolventy. Pohyb se uskutečňuje
DESKRIPTIVNÍ GEOMETRIE ELEKTRONICKÁ SKRIPTA CYKLICKÉ KŘIVKY
 DESKRIPTIVNÍ GEOMETRIE ELEKTRONICKÁ SKRIPTA CYKLICKÉ KŘIVKY Cyklické křivky patří především mezi technické křivky. Mají bohatou historii. První zmínku nacházíme dokonce už u Ptolemáia, konkrétnější studie
DESKRIPTIVNÍ GEOMETRIE ELEKTRONICKÁ SKRIPTA CYKLICKÉ KŘIVKY Cyklické křivky patří především mezi technické křivky. Mají bohatou historii. První zmínku nacházíme dokonce už u Ptolemáia, konkrétnější studie
1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás.
 Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
AXONOMETRIE. Rozměry ve směru os (souřadnice bodů) jsou násobkem příslušné jednotky.
 AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
Šroubovaný přípoj konzoly na sloup
 Šroubovaný přípoj konzoly na sloup Připojení konzoly IPE 180 na sloup HEA 220 je realizováno šroubovým spojem přes čelní desku. Sloup má v místě přípoje vyztuženou stojinu plechy tloušťky 10mm. Pro sloup
Šroubovaný přípoj konzoly na sloup Připojení konzoly IPE 180 na sloup HEA 220 je realizováno šroubovým spojem přes čelní desku. Sloup má v místě přípoje vyztuženou stojinu plechy tloušťky 10mm. Pro sloup
Výstavba jahodovej pyramídy
 Výstavba jahodovej pyramídy Podľa viacerých autorov je najvhodnejší čas na presádzanie jahôd mesiac apríl a máj alebo august a september. Neváhajte a využite tento čas na vybudovanie vlastnej jahodovej
Výstavba jahodovej pyramídy Podľa viacerých autorov je najvhodnejší čas na presádzanie jahôd mesiac apríl a máj alebo august a september. Neváhajte a využite tento čas na vybudovanie vlastnej jahodovej
Úlohy cvičenia z geometrie (Úlohy označené * sú len doplnkové.)
 Kužeľoečk. Elip je dná ohnikmi F 0,, 4, Úloh cvičeni geomerie (Úloh ončené * ú len doplnkové.) G úečkou dĺžkou 6. Zoroje vrchol 8 ďlších odov elip! (odová konšrukci). (Rodielová konšrukci) Elip je dná
Kužeľoečk. Elip je dná ohnikmi F 0,, 4, Úloh cvičeni geomerie (Úloh ončené * ú len doplnkové.) G úečkou dĺžkou 6. Zoroje vrchol 8 ďlších odov elip! (odová konšrukci). (Rodielová konšrukci) Elip je dná
Zobrazení hranolu. Příklad 5: Sestrojte řez pravidelného šestibokého hranolu s podstavou v půdorysně rovinou ρ. Sestrojte síť seříznuté části.
 Zobrazení hranolu Příklad 1: Zobrazte pravidelný pětiboký hranol s podstavou v půdorysně π. Podstava je dána středem S a vrcholem A. Výška hranolu je v. Určete zbývající průmět bodu M pláště hranolu. 1
Zobrazení hranolu Příklad 1: Zobrazte pravidelný pětiboký hranol s podstavou v půdorysně π. Podstava je dána středem S a vrcholem A. Výška hranolu je v. Určete zbývající průmět bodu M pláště hranolu. 1
Naformátuj to. Naformátuj to. pre samoukov
 Naformátuj to pre samoukov PREDHOVOR Publikácia je praktickou príručkou pre každého, kto hľadá jednoduché a ucelené vysvetlenie MS Word z oblasti formátovania dokumentu. Príručka obsahuje jednoduché a
Naformátuj to pre samoukov PREDHOVOR Publikácia je praktickou príručkou pre každého, kto hľadá jednoduché a ucelené vysvetlenie MS Word z oblasti formátovania dokumentu. Príručka obsahuje jednoduché a
Tvorba logického a fyzického dátového modelu relačnej databázy pomocou nástrojov od firmy Oracle výukový tutoriál
 Tvorba logického a fyzického dátového modelu relačnej databázy pomocou nástrojov od firmy Oracle výukový tutoriál Prvým krokom pri vytvorení relačnej databázy je návrh jej štruktúry a realizáciaa logického
Tvorba logického a fyzického dátového modelu relačnej databázy pomocou nástrojov od firmy Oracle výukový tutoriál Prvým krokom pri vytvorení relačnej databázy je návrh jej štruktúry a realizáciaa logického
VNĚJŠÍ ZÁVIT PRAVÝ / VONKAJŠÍ ZÁVIT PRAVÝ VNĚJŠÍ ZÁVIT LEVÝ / VONKAJŠÍ ZÁVIT ĽAVÝ VNITŘNÍ ZÁVIT PRAVÝ / VNÚTORNÝ ZÁVIT PRAVÝ
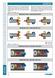 Podle tvaru obrobku a typu soustruhu se zvolí základní metoda soustružení, tj. směr posuvu a smysl otáčení vřetene pro soustružení pravého vnějšího nebo vnitřního závitu resp. levého vnějšího či vnitřního
Podle tvaru obrobku a typu soustruhu se zvolí základní metoda soustružení, tj. směr posuvu a smysl otáčení vřetene pro soustružení pravého vnějšího nebo vnitřního závitu resp. levého vnějšího či vnitřního
1. LABORATÓRNE CVIČENIE
 MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
středové (perspektivní) promítání vytváří obrazy podobné těm, které vidí lidské oko
 tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
1. MONGEOVO PROMÍTÁNÍ
 Mongeovo promítání 1 1. MONGEOVO PROMÍTÁNÍ 1.1 Základní pojmy V Mongeově promítání promítáme na dvě navzájem kolmé průmětny. Vodorovná průmětna se nazývá půdorysna a značí se, svislá průmětna se nazývá
Mongeovo promítání 1 1. MONGEOVO PROMÍTÁNÍ 1.1 Základní pojmy V Mongeově promítání promítáme na dvě navzájem kolmé průmětny. Vodorovná průmětna se nazývá půdorysna a značí se, svislá průmětna se nazývá
Import cenových akcií FRESH
 Návod obsahuje podrobný popis nastavenia a použitia importu cenových akcií reťazca FRESH, druhá časť popisuje ako využiť elektronické faktúry firmy Labaš pre automatické vytvorenie príjemky. Import cenových
Návod obsahuje podrobný popis nastavenia a použitia importu cenových akcií reťazca FRESH, druhá časť popisuje ako využiť elektronické faktúry firmy Labaš pre automatické vytvorenie príjemky. Import cenových
Mat2 - Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků základních škol. Matematické semináře pro 9.
 škola: číslo projektu: název projektu: Základní škola Ivana Olbrachta, Semily CZ.1.07/1.4.00/21.0439 Inovace pro kvalitní výuku Název šablony: číslo šablony: 1 poř.č. označení oblast dle RVP okruh dle
škola: číslo projektu: název projektu: Základní škola Ivana Olbrachta, Semily CZ.1.07/1.4.00/21.0439 Inovace pro kvalitní výuku Název šablony: číslo šablony: 1 poř.č. označení oblast dle RVP okruh dle
Patří mezi tzv. homotetie, tj. afinní zobrazení, která mají všechny směry samodružné.
 11 Stejnolehlost Patří mezi tzv. homotetie, tj. afinní zobrazení, která mají všechny směry samodružné. Definice 26. Budiž dán bod S a reálné číslo κ (různé od 0 a 1). Stejnolehlost H(S; κ) se středem S
11 Stejnolehlost Patří mezi tzv. homotetie, tj. afinní zobrazení, která mají všechny směry samodružné. Definice 26. Budiž dán bod S a reálné číslo κ (různé od 0 a 1). Stejnolehlost H(S; κ) se středem S
Obrázek 101: Podobné útvary
 14 Podobná zobrazení Obrázek 101: Podobné útvary Definice 10. [Podobné zobrazení] Geometrické zobrazení f se nazývá podobné zobrazení, jestliže existuje kladné reálné číslo k tak, že pro každé dva body
14 Podobná zobrazení Obrázek 101: Podobné útvary Definice 10. [Podobné zobrazení] Geometrické zobrazení f se nazývá podobné zobrazení, jestliže existuje kladné reálné číslo k tak, že pro každé dva body
středové (perspektivní) promítání vytváří obrazy podobné těm, které vidí lidské oko
 tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
Zadání domácích úkolů a zápočtových písemek
 Konstruktivní geometrie (KG-L) Zadání domácích úkolů a zápočtových písemek Sestrojte elipsu, je-li dáno a = 5cm a b = 3cm. V libovolném bodě sestrojte její tečnu. Tento úkol je na krásu, tj. udělejte oskulační
Konstruktivní geometrie (KG-L) Zadání domácích úkolů a zápočtových písemek Sestrojte elipsu, je-li dáno a = 5cm a b = 3cm. V libovolném bodě sestrojte její tečnu. Tento úkol je na krásu, tj. udělejte oskulační
Syntetická geometrie I
 Kruhová inverze Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Sférická inverze Autoportrét v kulovém zrcadle M.C.Escher, 1935 Pozor! jen pro ilustraci, inverze a zrcadlení se značně liší Kruhová
Kruhová inverze Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Sférická inverze Autoportrét v kulovém zrcadle M.C.Escher, 1935 Pozor! jen pro ilustraci, inverze a zrcadlení se značně liší Kruhová
Riešené úlohy Testovania 9/ 2011
 Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Súťaž Vráťme knihy do škôl je tu už po 7-krát!
 Súťaž Vráťme knihy do škôl je tu už po 7-krát! O súťaži Občianske združenie Učenie s úsmevom v spolupráci s partnermi internetové kníhkupectvo abcknihy.sk Bratislavským samosprávnym krajom, vydavateľstvom
Súťaž Vráťme knihy do škôl je tu už po 7-krát! O súťaži Občianske združenie Učenie s úsmevom v spolupráci s partnermi internetové kníhkupectvo abcknihy.sk Bratislavským samosprávnym krajom, vydavateľstvom
Mongeovo zobrazení. Bod a přímka v rovině
 Mongeovo zobrazení Bod a přímka v rovině Přímka v rovině Přímka v rovině připomeňme si nejprve větu, která říká, kdy přímka leží v rovině; Přímka v rovině připomeňme si nejprve větu, která říká, kdy přímka
Mongeovo zobrazení Bod a přímka v rovině Přímka v rovině Přímka v rovině připomeňme si nejprve větu, která říká, kdy přímka leží v rovině; Přímka v rovině připomeňme si nejprve větu, která říká, kdy přímka
ZADANIE 1. PDF vytvorené pomocou súšobnej verzie pdffactory
 ZADANIE 1 Navrhnite databázu pre firmu prevádzkujúcu sieť kinosál, jej tabuľky sú uvedené v zozname. Podľa potreby môžete doplniť ďalšie tabuľky a ich stĺpce: prevádzky (názov, mesto, adresa, počet kinosál,
ZADANIE 1 Navrhnite databázu pre firmu prevádzkujúcu sieť kinosál, jej tabuľky sú uvedené v zozname. Podľa potreby môžete doplniť ďalšie tabuľky a ich stĺpce: prevádzky (názov, mesto, adresa, počet kinosál,
Obrázek 34: Vznik středové kolineace
 6 Středová kolineace Jak naznačuje Obr. 34, středová kolineace (se středem S), jako vzájemně jednoznačné zobrazení Ē 2 na sebe, je výsledkem středového průmětu (se středem S ) středového promítání (se
6 Středová kolineace Jak naznačuje Obr. 34, středová kolineace (se středem S), jako vzájemně jednoznačné zobrazení Ē 2 na sebe, je výsledkem středového průmětu (se středem S ) středového promítání (se
Řez jehlanu. Mongeovo promítání. Pravidelný šestiboký jehlan o výšce v má podstavu ABCDEF v půdorysně. Zobrazte řez jehlanu rovinou σ.
 Řez jehlanu Mongeovo promítání Pravidelný šestiboký jehlan o výšce v má podstavu ABCDEF v půdorysně. Zobrazte řez jehlanu rovinou σ. A[ 3; 1; 0], B[0; 2; 0], y C > y B, v = 8cm, σ(4; 7; 3) B 2 A 2 Vyneseme
Řez jehlanu Mongeovo promítání Pravidelný šestiboký jehlan o výšce v má podstavu ABCDEF v půdorysně. Zobrazte řez jehlanu rovinou σ. A[ 3; 1; 0], B[0; 2; 0], y C > y B, v = 8cm, σ(4; 7; 3) B 2 A 2 Vyneseme
Zápis predmetov do AiSu na aktuálny akademický rok
 Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA
 UNIVERZIT PLCKÉHO V OLOMOUCI PŘÍROOVĚECKÁ FKULT KTER LGEBRY GEOMETRIE OSVĚTLENÍ VE STŘEOVÉM PROMÍTÁNÍ LINEÁRNÍ PERSPEKTIVĚ Bakalářká práce Vedoucí práce: RNr. Leka Juklová, Ph.. Rok odevdáí 202 Vypracovala:
UNIVERZIT PLCKÉHO V OLOMOUCI PŘÍROOVĚECKÁ FKULT KTER LGEBRY GEOMETRIE OSVĚTLENÍ VE STŘEOVÉM PROMÍTÁNÍ LINEÁRNÍ PERSPEKTIVĚ Bakalářká práce Vedoucí práce: RNr. Leka Juklová, Ph.. Rok odevdáí 202 Vypracovala:
Gymnázium, Brno, Elgartova 3
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
Cvičení F2070 Elektřina a magnetismus
 Cvičení F2070 Elektřina a magnetismus 20.3.2009 Elektrický potenciál, elektrická potenciální energie, ekvipotenciální plochy, potenciál bodového náboje, soustavy bodových nábojů, elektrického pole dipólu,
Cvičení F2070 Elektřina a magnetismus 20.3.2009 Elektrický potenciál, elektrická potenciální energie, ekvipotenciální plochy, potenciál bodového náboje, soustavy bodových nábojů, elektrického pole dipólu,
půdorysu; pro každý bod X v prostoru je tedy sestrojen pouze jeho nárys X 2 a pro jeho
 Řešené úlohy Rotační paraboloid v kolmém promítání na nárysnu Příklad: V kolmém promítání na nárysnu sestrojte tečnou rovinu τ v bodě A rotačního paraboloidu, který má ohnisko F a svislou osu o, F o, rotace;
Řešené úlohy Rotační paraboloid v kolmém promítání na nárysnu Příklad: V kolmém promítání na nárysnu sestrojte tečnou rovinu τ v bodě A rotačního paraboloidu, který má ohnisko F a svislou osu o, F o, rotace;
Aplikace lineární perspektivy
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Aplikace lineární perspektivy Vypracoval: Jakub Sýkora Třída: 8.M Školní rok: 2015/2016 Seminář : Deskriptivní geometrie Prohlašuji,
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Aplikace lineární perspektivy Vypracoval: Jakub Sýkora Třída: 8.M Školní rok: 2015/2016 Seminář : Deskriptivní geometrie Prohlašuji,
Súťaž Vráťme knihy do škôl je tu už po 5-krát!
 Súťaž Vráťme knihy do škôl je tu už po 5-krát! O súťaži Internetové kníhkupectvo abcknihy.sk v spolupráci s partnermi Bratislavským samosprávnym krajom a vydavateľstvami Ikar, Raabe a vydavateľskou značkou
Súťaž Vráťme knihy do škôl je tu už po 5-krát! O súťaži Internetové kníhkupectvo abcknihy.sk v spolupráci s partnermi Bratislavským samosprávnym krajom a vydavateľstvami Ikar, Raabe a vydavateľskou značkou
Princip a vlastnosti promítání. Konstruktivní geometrie a technické kresleni - L
 Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů ve dvojrozměrné rovině. Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů
Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů ve dvojrozměrné rovině. Vlastnosti promítání Úkolem konstruktivní geometrie je zobrazení trojrozměrných předmětů

