TVORBA 3D MODELU OBJEKTU ZE SNÍMKŮ VÍCE KAMER 3D MODEL FROM MULTIVIEW
|
|
|
- Dalibor Brož
- před 8 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘICÍ TECHNIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF CONTROL AND INSTRUMENTATION TVORBA 3D MODELU OBJEKTU ZE SNÍMKŮ VÍCE KAMER 3D MODEL FROM MULTIVIEW BAKALÁŘSKÁ PRÁCE BACHELOR S THESIS AUTOR PRÁCE AUTHOR VEDOUCÍ PRÁCE SUPERVISOR TOMÁŠ ZEMČÍK Ing. MILOSLAV RICHTER, Ph.D. BRNO 2016
2 2
3 Abstrakt Tvorba 3D modelu objektu ze snímků několika kamer umožňuje bezkontaktní měření reálných objektů. Tato práce popisuje nutné teoretické a matematické zázemí pro pochopení problematiky a navrhuje možné hardwarové a softwarové řešení problému 3D rekonstrukce kukly se senzory EEG přímo na hlavě pacienta. Klíčová slova Počítačové vidění, 3D rekonstrukce, stereoskopické vidění, model kamery, epipolární geometrie, kalibrace kamery, fundamentální matice, zpracování obrazu, více pohledů, OpenCV, Bundle Adjustment Abstract Reconstruction of 3D model from multiple view images allows us to perform a contactless measurement of real world objects. This work contains theoretical and mathematical background necessary for understanding problems of 3D reconstruction. It also proposes possible hardware and software solutions for the task of measuring a hood with EEG sensors while on patients head. Keywords Computer vision, 3D reconstruction, stereoscopic vision, camera model, epipolar geometry, camera calibration, fundamental matrix, image processing, multiple views, multiview, OpenCV, Bundle Adjustment 3
4 Bibliografická citace: ZEMČÍK, T. Tvorba 3D modelu objektu ze snímků více kamer. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, s. Vedoucí bakalářské práce byl Ing. Miloslav Richter, Ph.D. 4
5 Prohlášení Prohlašuji, že svou bakalářskou práci na téma Tvorba 3D modelu objektu ze snímků více kamer jsem vypracoval samostatně pod vedením vedoucího bakalářské práce a s použitím odborné literatury a dalších informačních zdrojů, které jsou všechny citovány v práci a uvedeny v seznamu literatury na konci práce. Jako autor uvedené bakalářské práce dále prohlašuji, že v souvislosti s vytvořením této bakalářské práce jsem neporušil autorská práva třetích osob, zejména jsem nezasáhl nedovoleným způsobem do cizích autorských práv osobnostních a jsem si plně vědom následků porušení ustanovení 11 a následujících autorského zákona č. 121/2000 Sb., včetně možných trestněprávních důsledků vyplývajících z ustanovení části druhé, hlavy VI. díl 4 Trestního zákoníku č. 40/2009 Sb. V Brně dne: 23. května 2016 podpis autora 5
6 Poděkování Děkuji vedoucímu bakalářské práce Ing. Miloslavu Richterovi, Ph.D. za účinnou metodickou, pedagogickou a odbornou pomoc, cenné rady, a nesmírnou vstřícnost a trpělivost při zpracování mé bakalářské práce. 6
7 Obsah Abstrakt... 3 Abstract... 3 Úvod Shrnutí současného stavu Obraz Model kamery Geometrie více pohledů D rekonstrukce Současně používaný software Možné koncepce měření Koncepce měření Koncepce vyhodnocení Požadavky na vybavení Požadované vlastnosti implementace Odhad dosažitelných parametrů implementace Snímání databáze snímků Implementace vyhodnocovacího software Experiment na testovací scéně Experiment na modelu hlavy Závěr Literatura Seznam použitých přístrojů Seznam příloh
8 ÚVOD Lidstvo chtělo vždy zkoumat a měřit své okolí, ale některé jevy a objekty nejsou měřitelné běžnými prostředky, nebo jde o objekty, které již nemusí existovat. Jsou-li ale dostupné fotografie daného předmětu, lze i z nich naměřit mnoho údajů, a někdy i rekonstruovat více či méně kompletní prostorový model. Je-li k tomuto použito výpočetní techniky, dostáváme se do oblasti tzv. počítačového vidění. Tato bakalářská práce se zabývá tvorbou trojrozměrného modelu za pomoci několika dvojrozměrných snímků sledovaného objektu z několika různých pohledů. Rekonstrukce třetího rozměru z dvojrozměrných fotografií je klasickou úlohou v oblasti počítačového vidění s přesahem do fotogrammetrie. Nejde o nikterak novou techniku, úkoly 3D měření a rekonstrukce jsou dávno známé, a některé vyřešené, nicméně i přesto jde o velmi perspektivní oblast. Existuje nespočet aplikací vyžadujících bezkontaktní měření tvarů a rozměrů objektů. 3D rekonstrukce může být levnou a efektivní odpovědí na tyto požadavky. V následujících kapitolách budou představeny základní myšlenky vícepohledové 3D rekonstrukce. Nezbytný teoretický a matematický aparát pro řešení problémů 3D rekonstrukce je shrnut v kapitole 2. Možné koncepce řešení jsou diskutovány v kapitole 3. Kapitola 4 se věnuje praktické části bakalářské práce, a popisuje konkrétní implementaci systému na vícepohledovou rekonstrukci kukly pokryté senzory EEG přímo na hlavě pacienta. 8
9 2 SHRNUTÍ SOUČASNÉHO STAVU Je všeobecně známým faktem, že až 80% vjemů, které vnímáme, vnímáme zrakem. Lidský zrak vnímá celou řadu kvalitativních údajů, jako jsou jas, barva a v neposlední řadě také vzdálenost předmětů. Takto dokonalý smysl nám umožňuje vidět a rozlišovat předměty ve svém okolí, ale také se v něm orientovat zcela přirozeně, aniž bychom si to uvědomovali. Úkolem vědecké disciplíny strojového vidění je napodobit schopnosti lidského zraku za použití technických prostředků snímání a pracování obrazu. Tato práce se bude zabývat právě problematikou 3D vidění, a tedy vnímání vzdálenosti v obraze. Při konvenčním snímání obrazu prostředky jako kamery nebo fotoaparáty je využíváno promítání 3D scény do 2D roviny. Třetí rozměr hloubky obrazu se tak ztrácí. Stejně tak lidské oko získává pouze 2D obraz prostoru, ale lidský mozek využívá následujících jevů k získání informace o hloubce pro potřeby orientace v prostoru. Rozšířeno z [1]: Perspektiva (bližší objekty se jeví větší než vzdálené) Vliv osvětlení a stínů Vliv masy vzduchu mezi pozorovatelem a pozorovaným předmětem (vzdálenější předměty se jeví méně kontrastní) Povědomí o vzdálenosti akomodace oka Povědomí o konvergenčním úhlu očí Stereoskopické vidění Mozek zpracovává tyto obrazové informace na základě zkušenosti tak, že vnímáme prostor kolem nás třírozměrně. Při snímání a zpracování obrazu technickými prostředky nemáme možnost využít těchto vlastností lidského mozku, a proto většina systémů v oblasti 3D počítačového vidění využívá právě poslední jmenované vlastnosti stereoskopického vidění tedy rekonstrukci ze dvou různých pohledů, jen počítače dovedou zpracovávat mnohem více než jen dva pohledy. Stereoskopické vidění se potom mění na vícepohledové. Vícepohledové vidění je podstatným odvětvím počítačového vidění. Jako takovému je mu věnováno mnoho pozornosti, a na téma vícepohledového vidění bylo již mnoho publikováno. Za zvláštní zmínku zde stojí kniha autorů R. Harleye a A. Zissermana ([11]). Následující podkapitoly vznikly rešerší mnoha materiálů a shrnují současný stav oboru. Představují nutný teoretický základ o obraze, snímání obrazu, práci s obrazem a vlastnostech vícepohledové geometrie včetně použitého matematického aparátu, nutného pro porozumění postupů v této práci. Je zde také popsán současně dostupný software k řešení problému vícepohledové 3D rekonstrukce. 9
10 2.1 Obraz Obraz je základním stavebním kamenem počítačového vidění. Jde o dvojrozměrnou reprezentaci trojrozměrného světa prostřednictvím promítání [2] (viz níže). Matematickým popisem obrazu je tzv. obrazová funkce. Obrazová funkce je spojitou funkcí dvou proměnných souřadnic v obraze. Funkční hodnotou obrazové funkce je veličina snímaná obrazovým snímačem, nejčastěji jas [3], nebo v případě barevných snímků vektor jednotlivých barevných složek [3]. V oblasti počítačového vidění pracujeme s obrazem v digitální podobě, který je obvykle snímán kamerou. Digitální obraz je popsán digitální obrazovou funkcí, která je odvozena od obrazové funkce jejím navzorkováním v matici M x N (kde M a N jsou šířka a výška obrazu v pixelech), a kvantováním do K intervalů [2]. Čím je rozlišení a kvantování jemnější, tím je výsledná aproximace obrazové funkce lepší [2]. 2.2 Model kamery V technické praxi je základním prostředkem snímání obrazu kamera [3]. Kamera se obvykle skládá z optické soustavy a snímače. Optickou soustavou se rozumí soustava čoček, zrcadel a clon, které transformují paprsky na vstupu kamery na paprsky dopadající na snímač. Snímač je v dnešní době obvykle maticová struktura světelných detektorů. Mezi nejpoužívanější dnes patří čipy typu CCD nebo CMOS. Historicky byl snímačem světlocitlivý film. Snímače nemusí detekovat jen světlo ve viditelném spektru. Existuje řada kamer, které vidí např. v infračerveném spektru. Kamera snímá informaci o prostoru jako dvojrozměrný signál, který je navíc vzorkovaný na pixely. Pro potřeby rekonstrukce scény je tak nutná transformace 2D informace souřadnice bodu v obrázku, na 3D informaci bod v prostoru. Jedna kamera v prostoru nám však nemůže tuto informaci poskytnout, proto každá kamera poskytuje informaci o přímce paprsku, který prochází bodem x protíná průmětnu v bodě x a směřuje do středu projekce, přičemž x je reálný bod v prostoru, a x je jeho obraz. Tuto skutečnost popisuje náčrt perspektivní projekce: Obr. 2.1 Perspektivní projekce 10
11 Reálný bod je v Obr. 2.1 reprezentován bodem x, jeho obraz je bod x. Přímka r představuje paprsek světla, který vytvoří obraz bodu x na průmětně snímači kamery. Bod O je střed projekce, přímka o optická osa, nebo také někdy osa kamery (anglicky optical axis, nebo camera axis) a bod P představuje hlavní bod (anglicky principal point). Nejjednodušším modelem kamery je takzvaná dírková kamera (pinhole camera) někdy také nazývaná camera obscura nebo dírková komora. Model dírkové kamery představuje čistou perspektivní projekci s tím, že obraz je otočen o 180 obou směrech. Obr. 2.2 Projekce dírkové kamery Obrázek 2.2 je náčrt ideální dírkové kamery se vzdáleností průmětny f (někdy zvětšení nebo ohnisková vzdálenost). Bude-li obraz převrácen zpět do přirozené polohy (tedy zpět do čisté perspektivní projekce), lze transformaci reálného bodu a na obraz a zapsat následovně podle [4]: x a = [ y] (2.1) z a = [ x y ] (2.2) [ x y ] = 1 [f 0 0 x z 0 f 0 ] [ y] (2.3) z Převedeme-li tuto transformaci do homogenních souřadnic, získáme následující vztah, opět podle [4]: x x f [ y ] = 1 [ y 0 f 0 0] [ ] (2.4) z z
12 Matice 3 4 z předcházející rovnice tvoří takzvanou matici kamery, která je obvykle označována jako C nebo K (pro účely této práce budeme užívat označení C pro matici kamery, K bude použito později pro kalibrační matici). Matice kamery je tedy maticí, která popisuje mapování bodu v prostoru do obrazové roviny až na měřítko. Dírková kamera je bohužel díky nízké světelnosti (a tak dlouhému expozičnímu času) prakticky nepoužitelná [1]. Musíme proto použít jiné kamery, která se svými vlastnostmi dírkové kameře alespoň blíží, a její matici kamery sestavit v duchu rovnice 2.4. K tomu je nutné získat takzvané vnitřní parametry kamery Vnitřní parametry kamery Vnitřní (někdy také vlastní nebo intrinsické) parametry kamery (anglicky intrinsic parameters) jsou sadou pěti neměnných vlastností kamery, které ovlivňují její promítání. Vnitřními parametry jsou: Ohnisková vzdálenost (f) Horizontální posun hlavního bodu (Px) Vertikální posun hlavního bodu (Py) Poměr stran snímače (ax:ay) Zkosení (θ) Získání těchto údajů nám umožní sestavit matici dírkové kamery, která bude dobře aproximovat reálnou používanou kameru. Samotný proces získávání vnitřních parametrů se nazývá kalibrace kamery (někdy se jako kalibrace kamery označuje i proces získávání vnitřních, vnějších parametrů a zkreslení kamery - názvosloví v této oblasti je značně nejednoznačné). Kalibrační matice (někdy také označována matice vnitřních parametrů nebo matice kamery opět nejednoznačnost značení) bude mít následující podobu: f a x γ P x K = [ 0 f a y P y ] (2.5) Prvek γ kalibrační matice 2.5 je prvek vycházející ze zkosení θ. Toto zkosení je způsobeno výrobní odchylkou, při které nejsou řádky pixelů přesně nad sebou, a snímač potom není pravoúhlý. U moderních kamer jej lze pokládat za nulový, ale u starších modelů je nutno jej brát v úvahu [5]. Posunutí hlavního bodu o Px v horizontále a p Py ve vertikále je obvykle nula pro situaci, kde počátek souřadnic v obraze leží v hlavním bodě. Někdy se počátek uvádí jako 12
13 levý horní roh obrázku. Další posunutí počátku může být dáno nepřesným umístěním obrazového snímače vůči optice kamery 1. Kalibrační matice kamery K tedy nyní reprezentuje kameru pomocí aproximace na model perspektivní kamery a definuje mapování bodu před objektivem kamery do souřadnic obrazu. Ze souřadnic obrazu ale nevíme zcela nic o souřadnicích pozorovaného bodu ve scéně. Pro ukotvení kamery v souřadnicích scény neboli světových souřadnicích (anglicky world coordinates) je zapotřebí vnějších parametrů kamery Vnější parametry kamery Vnější parametry kamery (anglicky extrinsic, nebo external parameters) jsou soubor šesti proměnných parametrů kamery, které jednoznačně definují polohu a orientaci kamery v souřadnicích scény světových souřadnicích. Vnější parametry kamery se skládají ze dvou komponent, z pozice a orientace. Jak pozice, tak i orientace obsahuje po třech dílčích složkách. Pozici kamery obvykle vyjadřujeme pomocí vektoru posunutí t. Fyzikální význam vektoru t je pozice počátku souřadného systému scény v souřadnicích kamery [6]. t x t = [ t y ] (2.6) t z Orientace, neboli natočení kamery zapíšeme pomocí matice rotace R, která má rozměr 3 3 a obsahuje rotace kamery ve všech směrech. Fyzikální význam jednotlivých sloupců matice rotace jsou směrové vektory os souřadnicového systému scény v souřadnicích kamery [6]. r 11 r 12 r 13 R = [ r 21 r 31 r 22 r 32 r 23 ] r 33 (2.7) Tato obecná rotace se skládá z dílčích rotací, které popisují následující matice rotací podle os x y a z o úhel Θ [7]: R x (Θ) = [ 0 cos (Θ) sin (Θ)] (2.8x) 0 sin (Θ) cos (Θ) 1 SIMEK, Kyle. Dissecting the Camera Matrix je velice dobrý seriál na blogu pana Simka, který ve třetím díle obsahuje interaktivní demonstraci vlivu vnitřních parametrů na projekci kamery. Třetí díl dostupný zde: 13
14 cos (Θ) 0 sin (Θ) R y (Θ) = [ ] (2.8y) sin (Θ) 0 cos (Θ) cos (Θ) sin (Θ) 0 R z (Θ) = [ sin (Θ) cos (Θ) 0] (2.8z) Vnější parametry kamery se souhrnně zapisují v matici externích parametrů, která má podle [6] podobu: Projekční matice r 11 r 12 r 13 t 1 [R t] = [ r 21 r 22 r 23 t 2 ] (2.9) r 31 r 32 r 33 t 3 Známe-li tedy jak kalibrační matici kamery K, tak matici rotace R a vektor posunutí t, známe všech 11 parametrů ideální kamery. Můžeme tak již jednoznačně definovat přímku v souřadnicích scény, na které leží bod x, jehož obraz x máme na obrázku. K mapování reálného bodu do obrazu potom použijeme projekční matici P, která v sobě kombinuje všechny parametry modelu kamery, a má tak 11 stupňů volnosti. Matice P má rozměry 3 4. Vlastní projekční matice P je podle [8] následující: P = K [R t] (2.10) p 11 p 12 p 13 p 14 P = [ p 21 p 31 p 22 p 32 p 23 p 33 p 24 ] p 34 (2.11) f a x γ P x r 11 r 12 r 13 t 1 P = [ 0 f a y P y ] [ r 21 r 22 r 23 t 2 ] (2.12) r 31 r 32 r 33 t 3 Potom platí následující vztah mezi obrazem bodu a skutečným bodem ve scéně: λ x = P x (2.13) Kde x a x jsou vyjádřeny v homogenních souřadnicích, a kde λ je jakékoliv kladné číslo které nahrazuje koeficient 1 z rovnice 2.3. Z 14
15 2.2.4 Zkreslení Až doposud byla kamera pokládána za ideální. Bohužel skutečné kamery touto vlastností obvykle neoplývají, a vykazují celou řadu optických vad. Zkreslení obrazu (anglicky image distortion) mohou být způsobena odchylkami v umístění čoček objektivu, odchylkami v umístění snímače anebo nedokonalým tvarem čoček samotných. V některých případech je dokonce zkreslení žádoucí vlastností kamery. Pro účely fotogrammetrických měření je jakékoliv zkreslení obrazu nežádoucí, protože zavádí další chybu a nejistotu do měření [9]. Neexistuje žádná snadná metoda, jak analyticky řešit korekci zkreslení, ale existují metody, jak zkreslení eliminovat. Pro účely této práce se jimi nebudeme zabývat, a postačí, když budeme předpokládat, že známe zkreslení jako funkci souřadnic bodu v obraze. Úpravou rovnice 2.13 o funkci zkreslení f dostaneme: λ x = f(p x) (2.14) Získáme-li tuto funkci, lze najít korekční funkci g, pomocí které dostaneme korigované body v obraze. g(x ) = x korigované (2.15) Pomocí této korekční funkce lze buďto korigovat celé snímky, nebo ji lze využít ke korigování jednotlivých bodů extrahovaných pro měření. 2.3 Geometrie více pohledů Na základě předchozí kapitoly nyní dovedeme stanovit mapování objektů ve scéně do obrazové roviny. Tato znalost sama ale nepostačuje k rekonstrukci třetího rozměru při použití pouze jedné kamery. Je-li k dispozici více kamer v různých pozicích, jejichž zorná pole se překrývají, máme k dispozici dvě přímky ze dvou obrazů téhož bodu v prostoru, a tak dostatek informací pro jednoznačné zaměření tohoto bodu [10]. Tato kapitola se bude věnovat vlastnostem geometrie pohledu dvou (stereo) a více kamer Epipolární geometrie Epipolární geometrie je vnitřní projektivní geometrií dvou pohledů, je závislá pouze na vnitřních parametrech kamery (viz 2.2.1) a na vzájemné poloze a orientaci [11]. Předmětem zájmu epipolární geometrie jsou vzájemné průměty téhož bodu do obrazových rovin dvou různých kamer. Základem této geometrie je tzv. epipólární rovina. Tato rovina je definována trojúhelníkem, jehož jednou stranou je vždy spojnice středů 15
16 kamer (střed kamery anglicky camera center, spojnice středů kamer baseline), a jehož protilehlým vrcholem je zkoumaný reálný bod ve 3D prostoru. Obr. 2.3 Epipolární rovina Body e1 a e2 na obrázku 2.3 jsou epipóly. Epipól je průsečík spojnice středů kamer a průmětny, nebo alternativně obraz středu kamery v obrazové rovině druhé kamery [11]. Mějme nyní bod x, který se v kameře 1 promítá do obrazu x1 a jeho průmět v do obrazové roviny kamery 2 je neznámý. Obr. 2.4 Epipolární přímka Přestože průmět bodu x do obrazové roviny kamery 2 je neznámý, je z obrázku 2.4 jasné, že musí ležet na přímce, která je tvořena průsečíkem obrazové roviny kamery 2 a epipolární roviny (která je opět definována trojúhelníkem s vrcholy C1, C2 a x). Tato přímka se nazývá epipolární přímka, nebo také epipolára (z kapitoly víme, že epipolára bude přímou jen při ideální projekci. Bude-li projekce zatížena zkreslením, bude epipolára obecnou křivkou). 16
17 Podle [11] se epipolární přímky pro všechny možné body v prostoru protínají v epipólu, stejně tak všechny epipolární roviny mají společnou jen jednu přímku spojnici středů kamer (a také epipólů). Stojí za povšimnutí, že epipolára v obrazové rovině druhé kamery, je vlastně obrazem paprsku, který promítá bod x do bodu x v první kameře [12]. Vlastnosti epipolární geometrie jsou velmi významné například v případě, že známe polohy obou kamer a obraz v jedné z nich, a hledáme korespondující obraz ve druhé. Ze znalostí vnitřních parametrů a vzájemné polohy, tak lze vyjádřit epipoláru pro každý jeden bod na jedné z kamer [13]. Toto značně usnadní hledání této korespondence. Stejně tak funguje úloha, kde je neznámou vzájemná poloha obou kamer, a známými jsou korespondence v jejich obrazech Fundamentální matice Fundamentální matice (anglicky fundamental martix) je algebraickým vyjádření epipolární geometrie [11]. Fundamentální matice je vždy definována nad párem kamer. Mějme proto situaci demonstrovanou v obrázku 2.4, a označme epipoláru v obrazové rovině kamery 2 (zvýrazněna modře) jako l2. Hledáme-li fundamentální matici F pro kamerový pár (1,2), platí podle [11] že: l 2 = F x 1 (2.16) x 2 T F x 1 = 0 (2.17) Fundamentální matice je matice o rozměrech 3 3. Je-li matice F fundamentální maticí kamerového páru (1,2), potom fundamentální matice inverzního páru (2,1) je F T. Proto platí: x 1 T F T x 2 = 0 (2.18) Speciální formou fundamentální matice je esenciální matice (anglicky essential matrix). Esenciální matice E je normalizovanou formou fundamentální matice [11]. Fundamentální matici stanovujeme ze vztahu 2.16, známe-li projekční matice obou kamer. Nejsou-li kamery kalibrované, nebo neznáme-li jejich vzájemnou polohu, lze matici F stanovit na základě korespondencí v obrazech [4]. Nejpopulárnější metodou pro nalezení F na základě minimálně 8 korespondencí je tzv. 8-point algorithm [11]. 17
18 2.4 3D rekonstrukce 3D rekonstrukcí se rozumí proces získávání 3D souřadnic bodu na základě znalosti několika 2D obrazů tohoto bodu, a znalosti projekčních matic kamer, kterými byly tyto obrazy získány Naivní triangulace Triangulace je metoda pro zjišťování souřadnic neznámých bodů na základě známých. Metoda je postavena na vlastnostech trojúhelníka, respektive na větě ÚSÚ o konstrukci trojúhelníka. V počítačovém vidění se triangulací rozumí rekonstrukce souřadnic bodu x ze známě korespondence obrazů bodu x x1 a x2 (které splňují podmínky epipolární geometrie), při známých projekčních maticích obou kamer (platí pro dvě kamery, analogicky lze triangulovat i bod z více než dvou korespondujících obrazů). Triangulovat lze libovolný bod v zorných polích obou kamer, vyjma bodů ležících na spojnici středů promítání kamer (oba paprsky jsou potom reprezentovány tou samou přímkou, a neexistuje tak jeden průsečík) [11]. Situaci popisuje obrázek Obr Bod x se nachází v průsečíku paprsků r1 a r2, které procházejí obrazy bodu x na průmětnách obou kamer. Obr. 2.5 Triangulace v ideálním případě Situace na obrázku 2.5 je ideální a nedosažitelná. Obvykle vlivem nedokonalé kalibrace kamery, distorzí obrazu, nízkého rozlišení kamer, odchylek při hledání korespondencí, vlivem dalších vnesených chyb, anebo kvůli šumu nedojde k protnutí paprsků r1 a r2 v bodě x, viz obrázek
19 Obr. 2.6 Triangulace v reálném případě Na obrázku 2.6 se nachází obecný případ, tedy že r1 a r2 se neprotínají (nebo se pro úplnost protínají mimo bod x, ale pravděpodobnost že se dvě obecné přímky protínají je limitně nulová). V případě že se přímky reprezentující paprsky neprotínají, je rekonstrukce bodu stanovena některou z aproximačních metod. Zde se nabízí naivní metoda určení bodu x jako středu nejkratší kolmice spojující přímky reprezentující paprsky r1 a r2. Tato naivní metoda, známá jako midpoint metoda však není vhodná, protože nejde o metodu invariantní vůči projekci, a její výsledky potom budou závislé na projekci [11]. Nejčastěji používanou metodou je metoda nejmenších čtverců, minimalizující čtverce odchylek, ale nejde o jedinou možnost. Za odchylku se potom považuje tzv. reprojekční chyba, tj. vzdálenost mezi naměřeným obrazem bodu, a jeho reprojekcí získanou ve smyslu rovnice Lineární triangulace pomocí DLT DLT (Direct linear transformation), neboli přímá lineární transformace je algoritmus pro získání transformační matice H, na základě čtyř a více korespondujících obrazů bodů tak, že platí [11]: x i H x i = 0 (2.19) Kde x i a x i jsou korespondující 2D body v homogenních souřadnicích [11]. A kde H je transformační matice o rozměrech 3 3. Popíšeme-li n-tý řádek matice H jako h nt, lze podle [11] zapsat H x i jako: H x i = [ h 1T x i h 2T x i h 3T x i ] (2.20) 19
20 A následně využít zápisu 2.20 k přepsání rovnice 2.19 jako: y i h3t x i w i h 2T x i x i H x i = [ w i h 1T x i x i h 3T x i ] (2.21) x i h 2T x i y i h1t x i Kde x i, y i a w i jsou složky x i. Vyjádření 2.21 lze podle [11] zapsat ve tvaru rovnice A i h = 0, která je lineární v h jako: 0 T [ w T i x i y i x i T w i x i T 0 T x i x i T y i x i T h 1 x T i x i ] [ h 2 ] = 0 (2.22) 0 T h 3 Kde matice A i má rozměry 3 9, ale obsahuje pouze dva lineárně nezávislé řádky, proto se obvykle redukuje na rozměry 2 9 a poslední řádek se vynechává. Vektor h je sloupcový vektor o výšce 9, a jeho jednotlivé prvky představují prvky matice H po řádcích [11]. Každá matice A i pro každý bod x i tedy přidává dvě nezávislé rovnice do soustavy [14]. Výše popsané rovnice tvoří základní verzi algoritmu DLT pro 2D 2D mapování. V oblasti 3D rekonstrukce je ovšem hledáno inverzní mapování k mapování 3D bodu do více 2D obrazů. Podle [14] je možné upravit algoritmus DLT pro hledání mapování 2D 3D prostým zvětšením rozměrů problému, a získat tak následující rovnici opět ve tvaru A i h = 0: 0 T [ w T i X i w i X i T 0 T y i X T i h1 x T i X ] [ h 2 ] = 0 (2.23) i h 3 Kde A i je již ve zmenšené formě bez lineárně závislého třetího řádku, a kde X i představuje bod ve 3D prostoru v homogenních souřadnicích, a jde tak o čtyř-prvkový vektor. Matice A i proto nabývá rozměru 2 12 a vektor h výšky 12 [14]. Analogicky matice H je rozměrů 3 4 a představuje projekční matici P známou z kapitoly [14]. DLT popisovaná výše je variantou DLT algoritmu pro hledání mapování mezi prostory na základě známých korespondencí. V úloze 3D rekonstrukce je ale úkolem nalézt 3D bod na základě několika korespondujících 2D obrazů při známém mapování 3D 2D, tedy při známých projekčních maticích kamer. Předpokládejme nyní, že existují body x a x, které jsou obrazy téhož neznámého 3D bodu X získané přes projekční matice P a P, podle x = P X a x = P X vyjádřených bez měřítka ve tvaru vektorového součinu jako x P X = 0 a x P X = 0. Tyto dvě rovnice lze převést na tvar A X = 0. Podle [14] je potom A: 20
21 x P 3T P 1T y P 3T P 2T A = x P 3T P 1T [ y P 3T P 2T ] (2.24) [14] 2. Vyřešením rovnice A X = 0 jsou potom získány souřadnice bodu X v prostoru 2.5 Současně používaný software Součástí shrnutí současného stavu poznání by měl být zmíněn současně používaný software. Při provádění rešerše bylo nalezeno velké množství software zabývající se vícepohledovou 3D rekonstrukcí. Z nejpoužívanějších nástrojů zde zmíním VisualSFM 3, Autodesk 123D Catch 4, Agisoft PhotoScan 5, a Bundler 6. VisualSFM je software řešící 3D rekonstrukci objektů z databáze nekalibrovaných snímků. Výstupní model je řešen pomocí bodového mračna (point cloud). Software je pro nekomerční a akademické použití zdarma. Dalším zmíněným nástrojem je 123D Catch, který je součástí sbírky nástrojů Autodesk 123D. Jako všechny nástroje Autodesk 123D je i Catch určen spíše pro amatérské 3D modeláře a pro účely 3D tisku. Catch je dostupný jak pro Windows, tak i pro mobilní operační systémy jako Android nebo ios. 123D Catch je založen na centrálním zpracování dat (cloud computing), takže pro jeho běh je nutné internetové připojení. Jediným komerčním produktem v tomto výběru je software PhotoScan firmy Agisoft. Jde o profesionální software s velkým množstvím použití, od spojování panoramatických fotografií až po tvorbu velmi hustých barevných bodových modelů k použití ve filmovém a herním průmyslu. Posledním zmiňovaným nástrojem tohoto výběru je open source nástroj Bundler. Bundler je podobný nástroj jako VisualSFM, i když ne tak dokonalý. Výstupem je opět model formou bodového mračna. 2 Více o triangulaci pomocí DLT v [11] na stranách 88 a 312, a dále v [14] 3 Autor: Changchang Wu, dostupné na: 4 Autor: Autodesk, Inc., dostupné na: 5 Autor: Agisoft LLC, více na: 6 Autor: Noah Snavely, dostupné na: 21
22 3 MOŽNÉ KONCEPCE MĚŘENÍ Cílem této bakalářské práce je rekonstrukce 3D modelu kukly pokryté senzory EEG na hlavě pacienta, resp. vygenerovat 3D mapu EEG senzorů. K vytvoření takového modelu je třeba změřit souřadnice těchto senzorů v prostoru. Obr. 3.1 Kukla se senzory EEG zkoumaný objekt 7 Tato kapitola diskutuje možné koncepce měření a formuluje požadavky na hardware. Dále stanovuje požadavky na implementaci a odhaduje dosažitelné parametry systému. 3.1 Koncepce měření Pro provedení rekonstrukce 3D modelu je nutné nasnímat sadu snímků měřeného objektu. Toto snímání bude probíhat v prostředí, kde je možné si zvolit topologii kamerového systému a scény. Topologie scény může zásadně ovlivnit výsledky měření. Ze zadání vyplývá pouze základní rozložení měřící soustavy. Zkoumané těleso se nachází ve středu koule, a kamery na její ploše. Ostatní parametry jsou ponechány k vlastní volbě. Pro testování a ladění vyhodnocovacího softwaru, je ale model lidské hlavy zcela nevhodný. Pro účely testování bude sloužit rozměrově stejná scéna, kde bude zkoumané těleso zastupovat geometricky lépe popsatelný objekt, například krychle, kvádr nebo koule. Výhodou těchto testovacích scén je, že vstupní sada obrazů pro vyhodnocovací 7 Autorem snímku je Ing. Miloslav Richter, Ph.D. 22
23 program nemusí být pořízena skutečnými kamerami ve skutečném světě, ale data mohou být syntetická. Například vygenerovaná sada korespondujících obrazů bez existujícího snímku, nebo mohou být data renderovaná z 3D modelu scény. Existují renderovací nástroje, které dovedou nasimulovat kameru s danými vnitřními parametry a zkreslením. Výhodou je také snadné ověření funkce vyhodnocovacího programu. Jak vyplývá z kapitoly o triangulaci, tak těleso musí být nasnímáno z různých pohledů tak, aby každý jeden senzor byl viditelný na nejméně dvou různých snímcích. Navíc není lhostejný úhel, pod kterým je objekt snímán. Pod příliš ostrým úhlem by nebylo možné přesně lokalizovat bod na snímku, a navíc při malé odchylce úhlu paprsku (tedy odchylce v souřadnicích obrazu), vzniká velká odchylka v hloubce. Ideální by bylo kolmé snímání. Pro tuto práci budeme uvažovat mezní úhel 45. Následující obrázek představuje základní uspořádání měření. Obr. 3.2 Základní koncepce měření ve vertikále Kamery jsou umístěny ve dvou vrstvách tak, že první nižší vrstva se nachází v rovině tělesa. Druhá vyšší vrstva je skloněna pod úhlem α tak, aby se optické osy (v obrázku 3.2 zvýrazněné červeně) všech kamer protínaly v bodě S, který je reprezentací středu pomyslné koule o poloměru r. Z fotografie 3.1 je patrné, že senzory jsou na hlavě subjektu umístěny pouze po stranách, zezadu a shora, proto je možné použít pouze dvě vrstvy kamer, a přitom zachovat podmínku, že všechny senzory budou viditelné na alespoň dvou snímcích pod úhlem ne ostřejším než 45. Toto rozvržení řeší pouze vertikální rovinu topologie měřící soustavy. Rozdělení v horizontále je komplikovanější. Existuje několik různých možností konstrukce, ze kterých budou v následujících podkapitolách představeny dvě varianta statická a pohyblivá. Dále je možné do scény vložit pouze měřený objekt, a externí kalibraci kamer provádět podle něj, anebo ve scéně použít kalibrační objekt se známou geometrií a kamery externě kalibrovat vůči němu. V takovém případě je důležité, aby byl tento 23
24 kalibrační objekt vůči měřenému nehybný. Při snímání živého pacienta může jít o nějakou formu konstrukce připevněnou pevně k jeho hlavě Statické řešení Statické uspořádání spočívá v pevném umístění kamer do připravené konstrukce. Konstrukce je nepohyblivá, a v provozu nelze uspořádání kamerového systému nijak měnit. Obr. 3.3 Náčrt statického uspořádání kamerového systému o 16 kamerách a) vertikálně b) horizontálně Obrázek 3.3 je náčrtem pevného kamerového systému s kamerami na stěnách pomyslné koule se středem S a poloměrem r, kde α = β = 45. Takový systém bude sestávat ze 16 kamer (pro úsporu lze kameru, která by snímala obličej vynechat na obličeji se senzory nenacházejí). Statické uspořádání s sebou přináší množství výhod, ale také některé nevhodné vlastnosti. Mezi výhody patří: 1. Rychlost - Všechny kamery mohou snímat najednou a urychlit tak pořízení snímků. Toto je obzvláště výhodné, když se subjekt pohybuje 2. Jednoduchost - Pevné uspořádání je mechanicky jednodušší 3. Přesnost - Je-li mechanická část kamerového systému dostatečně přesná a tuhá, lze polohu a orientaci kamer považovat za známou a neměnnou. Je-li toto uspořádání použito v kombinaci s kalibrovanými kamerami, nesmírně zjednodušuje samotné zpracování obrazu Nevýhodami pevného uspořádání jsou: 1. Složitá rekalibrace Změní-li se nastavení kamer (např.: přeostřením), je nutné všechny kamery překalibrovat zvlášť 24
25 2. Těžkopádnost Mechanická konstrukce pro toto uspořádání bude rozměrově náročná a těžká 3. Cena Velké množství použitých kamer povede k vysoké ceně Statické uspořádání je výhodné tam, kde je třeba snímat pohybující se objekty a měření rychle zpracovávat. Snižuje výpočetní a implementační náročnost úlohy Pohyblivé řešení Pohyblivé uspořádání kamerového systému spočívá v tom, že kamery jsou ukotveny v nějaké formě pohyblivého zařízení. Zadání vyžaduje, aby měřené těleso leželo ve středu pomyslné koule, a kamery jej snímaly z její stěny, proto se dobře hodí kamery upevněné na otočném rameni, není to však jediné možné řešení. Systém s otočným ramenem demonstruje obrázek 3.4: Obr. 3.4 Uspořádání kamerového systému s otočným ramenem Výsledná sada fotografií se bude snímat vždy po pootočení ramena podle osy o úhel β. Budou-li úhly α a β, a poloměr r shodné pro systémy na obrázcích 3.3 a 3.4, Měla by být výsledkem stejná sada snímků, která bude ale v případě systému podle 3.3 sejmuta najednou a v případě 3.4 za 360 /β pootočení a snímání. Mezi výhody pohyblivého uspořádání se řadí: 1. Skladnost Systém s otočným ramenem není tak prostorově náročný 2. Cena Otočný mechanismus je sice nákladnější než pevná konstrukce, ale cena mechanismu bude vyvážena menším počtem užitých kamer 3. Snadná kalibrace při přeostření kalibrujeme pouze dvě kamery Nevýhodami jsou: 1. Přesnost mechanismus nemusí mít dobrou přesnost a opakovatelnost 25
26 2. Malá rychlost Snímky se pořizují sekvenčně a ne paralelně 3. Výpočetní složitost Je nepřesná pozice a orientace kamer Pohyblivý systém s otočným ramenem není použitelný pro aplikace probíhající v reálném čase (tzv. real-time aplikace), anebo velice rychlé aplikace, ale při vyhodnocování snímků offline postačí. Kvůli nejistotám v pozici a orientaci kamer je náročnější na zpracování obrazu (toto lze řešit například použitím robotického ramene s velkou přesností a opakovatelností). Přestože snímky jsou pořízeny na pohyblivém zařízení, lze s kamerami na rameni pracovat jako se stereo párem, což v některých situacích může pomoci při následné analýze. Jeho hlavní výhoda ale tkví v potřebě menšího množství kamer a tedy nižší ceně a tedy snadnější kalibraci, a také v možnosti použití menšího úhlu β pro pořízení více snímků na otáčku. 3.2 Koncepce vyhodnocení Algoritmus vyhodnocení pracuje s databází měřících snímků pořízenou některým z postupů popsaných v předešlé kapitole. Skládá se z několika samostatných krocích nutných k 3D rekonstrukci modelu měřeného objektu: Detekce zájmových bodů - Detekcí zájmových bodů se rozumí nalezení souřadnic obrazů měřeného bodu v souřadném systému obrazu Nalezení korespondencí - Nalezení korespondencí je nalezení takových již detekovaných obrazů, které představují obrazy shodného reálného bodu Externí kalibrace kamer - Proces externí kalibrace je hledání vnějších parametrů kamery ve smyslu kapitoly Triangulace bodů - Triangulace bodů je proces samotné 3D rekonstrukce (viz 2.4) Struktura vyhodnocovacího programu se bude odvíjet od použité koncepce snímání měřících snímků. Jak bylo zmíněno v kapitole 3.1, bude se zpracování zásadně odlišovat při použití pevných nebo pohyblivých kamer, a při použití nebo nepoužití kalibračního objektu. V této kapitole jsou popsány možné struktury postupu vyhodnocení v případě použití jednotlivých koncepcí měření zmíněných výše. Popsané postupy předpokládají použití kalibrovaných kamer Struktura pro pevný kamerový systém Pro pevný kamerový systém předpokládáme krom známé kalibrační matice K také známé rotační matice R a translační vektory t. Program potom bude popsán následujícím diagramem: 26
27 R a t Data K Detekce bodů zájmu Hledání korespondencí Triangulace Výstup Obr. 3.5 Diagram programu pro pevný kamerový systém Z diagramu 3.5 je evidentní, že při použití pevného kamerového systému s kalibrovanými kamerami, není vyhodnocení obzvláště složité. Ve skutečnosti je tento způsob vyhodnocování natolik výpočetně jednoduchý, že lze s úspěchem použít v aplikacích běžících v reálném čase Struktura pro pohyblivý kamerový systém Pro pohyblivé kamery je zpracování obtížnější, protože je nutné zjistit vnější parametry kamer na základě korespondencí napříč snímky. Navrhované schéma programu je ne následujícím diagramu: Data Detekce rohů Hledání korespondencí 8-point algorithm/ RANSAC F Detekce bodů zájmu Hledání korespondencí Triangulace Výstup Obr. 3.6 Diagram programu pro pohyblivý kamerový systém Obrázek 3.6 popisuje případ, kdy pro výpočet fundamentální matice F používáme jiný druh zájmových bodů, a tedy i jiný detektor, než který měříme. Toto může zvýšit přesnost určení F, je-li těchto bodů více než měřených. Kamerový systém s neznámou polohou kamer představuje podstatně výpočetně náročnější úlohu, která neumožní rekonstrukci v reálném čase. Při dostatečném počtu vstupních snímků ale může poskytovat přesnější výsledek. V kombinaci s menším potřebným počtem kamer představuje dobře použitelné uspořádání. 27
28 3.2.3 Struktura pro systém s kalibračním objektem Je-li do scény vložen kalibrační objekt o známé geometrii, bude postup struktura programu podobná variantě s pohyblivými kamerami, ale bude se lišit ve způsobu získání externích parametrů kamer: Data Detekce kalibračních bodů Hledání korespondencí K Hledání pozice a orientace K, R a t Detekce bodů zájmu Hledání korespondencí Triangulace Výstup Obr. 3.7 Diagram programu pro systém s kalibračním objektem 3.3 Požadavky na vybavení Nejzásadnější součástí vybavení ke splnění úlohy 3D rekonstrukce jsou kamery. Jejich vlastnosti budou mít vliv na proveditelnost měření a jeho přesnost, a proto je jejich volba důležitým krokem. Je nezbytné formulovat požadavky na vlastnosti kamer a jejich objektivů tak, aby bylo dosaženo žádané rychlosti a přesnosti měření. Požadavky budou výsledkem kompromisu právě mezi rychlostí a přesností. Pro maximální přesnost měření je nutné co možná nejvyšší rozlišení kamery. Parametry jako světelnost objektivu nebo komunikační rozhraní nejsou pro přesnost měření kritické. Pro maximální rychlost je nezbytné obětovat část přesnosti, a zvolit nižší rozlišení pro rychlejší zpracování. Kritická je také světelnost objektivu. Vyšší světelnost objektivu umožní zkrácení expozičního času, a urychlí tak snímání. Komunikační rozhraní kamery může mít také vliv na rychlost měření. Dále existují společné požadavky pro kamery, které vyžadujeme jak pro rychlé, tak pro přesné měření: ideálně žádné nebo malé zkreslení možnost zakázat automatické ostření možnost zakázat automatické úpravy clony nízká cena Požadavek minimálního zkreslení je poněkud problematický, protože objektivy s nízkým zkreslením jsou na běžných komerčních kamerách spíše zvláštností. 28
29 Požadavky ohledně ostření a clonění jsou důležité z důvodu, že jak změna ostření, tak nastavení clony mění vnitřní geometrii objektivu. Dochází proto ke změně vnitřních parametrů kamery ve smyslu kapitoly 2.2.1, a bylo by proto nutné po každém zásahu do nastavení objektivu kameru znovu kalibrovat. Další možností by samozřejmě byla kalibrace při různých nastaveních objektivu potom by bylo možné model kamery parametrizovat a kalibrační matici upravit podle okamžitého nastavení, je-li nastavení známé. Ovšem pouze za předpokladu, že ostření je řízeno servomotoricky, a známe tak jeho okamžitou polohu. Mnohé kamery jsou ale vybaveny pouze clonou ovládanou ručně, nebo používají clonu typu auto-iris (někdy také DC-iris), u které poloha známá není. Až některé novější kamery používají clony p-iris, pro které by bylo možné používat parametrizovaný model clonění. Pro účely této práce je ale možné používat jak fixní ostření, tak i clonu (experiment předpokládá téměř konstantní vzdálenost od zkoumaného objektu, a konstantní osvětlení). Cena je posledním faktorem, který je nutné uvažovat. Obvykle je to nejvíce limitující kritérium, od kterého se ale bude odvíjet kvalita měření. 3.4 Požadované vlastnosti implementace Na základě možných koncepcí měřící soustavy a vyhodnocovacího postupu budou v této kapitole formulovány technické požadavky na hardware a software realizovaný v praktické části této bakalářské práce. Pro značnou materiální náročnost řešení se statickým kamerovým systémem bude implementována varianta pohyblivého kamerového systému. Scéna bude kvůli snadnějšímu vyhodnocování doplněna kalibračním objektem. Softwarovou část úlohy jsem se rozhodl implementovat jako konzolovou aplikaci na platformě PC. Program bude psán v jazyce C++ s použitím velice rozšířené open source knihovny počítačového vidění OpenCV Odhad dosažitelných parametrů Vzhledem k povaze měření s pohyblivým kamerovým systémem není možné provádět měření v reálném čase. Čas měření se tedy bude odvíjet od rychlosti otáčení kamerového systému, a výpočetní čas vyhodnocení pořízených snímků bude pravděpodobně zanedbatelný oproti času potřebnému pro snímání. Dosažitelná přesnost měření je závislá na mnoha faktorech, jako jsou: Kvalita a rozlišení kamer Kvalita kalibrace kamer a popisu zkreslení Tvarová přesnost a definice kalibračního objektu Kvalitní metoda extrakce zájmových bodů 8 Originální článek: BRADSKI, G. The OpenCV Library. Dr. Dobb s Journal of Software Tools,
30 Počet snímků s korespondujícími obrazy Na základě přesnosti podobných metod odhaduji maximální odchylku zaměřeného 3D bodu na menší než 5mm. 30
31 4 IMPLEMENTACE Cílem implementační části práce je vytvoření systému pro tvorbu 3D modelu na základě pohledů více kamer. V práci jde zejména o ověření proveditelnosti metody za daných podmínek, zde prezentovaný systém ale nemusí pracovat obecně. Implementační postup popisuje následující blokové schéma: Kalibrační data Měřící data Kalibrace kamer 1. Kalibrace kamer Matice K Detekce vrcholů kalibrační krychle Detekce senzorů 2. Detekce bodů zájmu 2D data Hledání korespondencí 3. Hledání korespondencí Externí kalibrace 4. Externí kalibrace Matice P 3D rekonstrukce 2D data 5. 3D rekonstrukce Vyhodnocení 3D data Zobrazení Obr. 4.1 Blokové schéma implementace Následující kapitoly popisují jednotlivé fáze implementačního postupu. 31
32 4.1 Snímání databáze snímků V rámci vlastní práce jsem pro měření zvolil koncepci obdobnou topologii s pohyblivým uspořádáním kamer, upravenou tak, že kamery jsou pevně umístěny na stativech, a zkoumaný objekt je umístěn na motoricky ovládaném rotačním stolku. Rotační stolek umožní provádět přesné rotace scény bez nutnosti hýbat s kamerami, nebo sahat na měřený objekt. Scéna byla navíc doplněna geometricky definovaným kalibračním objektem. Pro potřebu této bakalářské práce bohužel nebylo možné zapůjčení skutečné senzorové kukly, a proto bude dále v práci uvažována její maketa vytvořená pomocí polystyrenové hlavy s koupací čepicí, kde jednotlivé senzory jsou představovány kruhovými samolepkami s čísly. Obr. 4.2 Maketa měřeného objektu a rozložení objektů ve scéně Poloměr kulové plochy byl zvolen přibližně 1m. Tato vzdálenost se může měnit podle velikosti měřené scény, a podle zvolených kamer a jejich objektivů. Scéna byla mezi snímky pootočena vždy o 30, a tak celá sada měřících snímků sestává z 24 fotografií. 32
33 4.1.1 Kalibrační objekt Obr. 4.3 Rozložení kamerového systému Volba vhodné geometrie kalibračního objektu je kritickým krokem pro kvalitní externí kalibraci kamer systému. Je nutné zvolit geometrii o dostatečném počtu snadno detekovatelných bodů, která nebude příliš zvětšovat celkové rozměry scény, a zároveň bude umožňovat současnou viditelnost dostatečného počtu bodů pro jednoznačnou kalibraci. Pro tuto bakalářskou práci byla za kalibrační objekt zvolena krychle, nebo přesněji její drátěný model. Při dostatečné velikosti drátěné krychle je možné umístit maketu hlavy do objemu krychle tak, že v každém okamžiku je viditelných alespoň 6 různých vrcholů krychle, což je dostatečný počet pro kvalitní externí kalibraci kamery. Při měření byly použity dvě realizace kalibrační krychle: Krychle z ocelové kulatiny Ø4mm o hraně 175mm, kde za vrcholy jsou považovány průsečíky os kulatiny tvořící její stavbu Obr. 4.4 Kalibrační krychle Krychle z uhlíkové kulatiny Ø3mm o hraně 250mm, jejíž vrcholy jsou ve středu plastových koulí Ø10mm zhotovených 3D tiskem 33
34 4.1.2 Kamery Vzhledem ke zvolené topologii experimentu jsou k nasnímání měřící sady snímků zapotřebí dvě kamery. Z důvodu konzistence měření a snadnější práce s daty je výhodné, aby obě použité kamery byly stejného typu, používaly stejné objektivy, a byly pokud možno i stejně nastaveny. Po dohodě s vedoucím práce mi byly přiděleny dvě kamery typu ImagingSource BFK 31BF03. Základní parametry kamer shrnuje následující tabulka: Tab. 5.1 Základní údaje o kameře ImagingSource BFK 31BF03 IMAGINGSOURCE BFK 31BF03 9 Čip CCD (Sony ICX204AL) Velikost čipu 6 mm Rozlišení 1024 x 768 Velikost pixelu 4,65 µm x 4,65 µm Obraz monochromatický 8-bit Rozhraní FireWire 400 Ke kamerám byla zvolena dvojice TV objektivů s ohniskovou vzdáleností 8mm a clonovým číslem 1,2. Objektivy mají manuální ovládání jak clony, tak i ostření. Snímaný obraz je tedy šedotónový obraz o rozlišení 1024 x 768 s barevnou hloubkou 8 bitů (256 odstínů šedi). Obraz byl snímacím softwarem ukládán v bitmapovém formátu.bmp. 4.2 Implementace vyhodnocovacího software Vyhodnocovací software je koncipován jako modulární, sestavený ze samostatně fungujících programů, které vždy provádějí jednu funkcionalitu. Jednotlivé kroky vyhodnocovacího postupu jsou rozčleněny do modulů tak, jak bylo naznačeno v blokovém schématu výše. Moduly jsou mezi sebou propojeny předáváním vstupně/výstupních XML souborů podporovaných OpenCV třídou cv::filestorage. Pro jejich zápis a čtení byla vytvořena samostatná jednoduchá komunikační knihovna. Následující podkapitoly stručně popisují funkce a implementaci jednotlivých modulů systému. 9 Detailní údaje zde: monochrome/dmk31bf03/ 34
35 4.2.1 Kalibrace kamer Modul kalibrace kamer slouží k získání intrinsických parametrů kamery podle kapitoly 2.2.1, a dále také získává parametry geometrického zkreslení kamery ve formě používané OpenCV. Tento modul je založen na metodách kalibrace implementovaných v knihovně OpenCV. Vstupem modulu je sekvence snímků šachovnicového kalibračního vzoru, který je nasnímán několikrát pokaždé z jiné polohy. Tyto snímky jsou programem postupně načítány, a je v nich detekován šachovnicový vzor. Když je tento vzor nalezen v dostatečném počtu snímků, je provedena kalibrace. Není-li šachovnice nalezena alespoň v deseti snímcích, není program schopen vypočítat vnitřní parametry ani zkreslení. Pokud není dostupný dostatečný počet snímků, lze některé vkládat opakovaně, ale tento postup povede ke snížení kvality výsledných kalibračních parametrů. Obr. 4.5 Kalibrační šachovnice 9x6 10 Při kalibraci kamer je kritické, aby se mezi snímáním jednotlivých kalibračních snímků, a mezi kalibrací a samotným měřením dále neměnily vnitřní parametry kamery. Tedy zejména nastavení objektivu jako jsou ostření a clona. Proto při měření nelze použít kamery s automatickým ostřením ani cloněním, nebo je nutné tyto funkce zakázat. 10 Obrázek převzat z dokumentace OpenCV dostupný na: 35
36 Obr. 4.6 Detekovaný kalibrační obrazec 11 Výsledky kalibrace jsou uloženy v XML souboru pro přenositelnost dat mezi jednotlivými moduly. Kalibrace je potom uložena ve formě kalibrační matice K a parametry zkreslení pomocí vektoru 5 koeficientů popisujících radiální a tangenciální zkreslení Detekce bodů zájmu Ke 3D rekonstrukci je nezbytné ze snímků extrahovat souřadnice zájmových bodů. Druh použitého mechanismu na detekci těchto bodů se odvíjí od charakteru detekovaného objektu. Pro účely této práce je zájmovým bodem střed vrchní strany senzoru ze senzorové kukly, respektive na modelu střed kruhové značky, která senzory zastupuje. Detekovaným objektem je tedy obecný průmět kruhu, který je přibližně eliptický. K detekci elips byla použita modifikace programu z databáze programů OpenCV 12. Tento program tedy v podstatě elipsy nehledá, ale hledá obrysy o daných vlastnostech, následně tyto elipsami aproximuje, a hledá jejich střed. Program načte obraz získaný z kamery, a provede odstranění šumu aplikací mediánového filtru. Dále převede obraz ze stupňů šedi na binární pomocí adaptivního prahování. Následně provede detekci kontur, a tyto poté filtruje podle velikosti a poměru stran. Do kontur odpovídajících podmínkám vepíše elipsu a nalezne její střed, který je potom právě kýženým bodem zájmu. 11 Vykresleno s použitím OpenCV funkce cv::drawchessboardcorners 12 Autor: Denis Burenkov, dostupné na: 36
37 Obr. 4.7 Detekce elips v obraze, postupně: 1) Originální snímek, 2) Snímek po mediánové filtraci, 3) Snímek po vyprahování, 4) Detekce vykreslené v původním obraze Tato metoda vykazuje poměrně velkou úspěšnost při detekci bodů, ale má velké množství falešných detekcí různého původu. Vzhledem k charakteru měření, kde každý jeden senzor musí být změřen, a metody jsou citlivé na hrubé chyby (tzv. outliery), nepovažuji tuto metodu za vhodnou. Protože tvorba dobrého detektoru zájmových bodů a jeho ladění je časově náročná činnost, která není předmětem této bakalářské práce, byla anotace jednotlivých bodů zájmu provedena manuálně Hledání korespondencí Korespondenční problém (anglicky correspondence Problem) spočívá v nalezení obrazů téhož objektu na různých snímcích [15]. V případě 3D rekonstrukce jsou tedy hledány 2D obrazy téhož 3D bodu. Hledání korespondencí představuje velice komplexní problém, který se řeší mnoha různými metodami. Metody jsou obvykle založeny na hledání korelace mezi dvěma a více snímky, nebo na zkoumání rozložení zájmových bodů. Jednou z nejpoužívanějších metod na nalezení korespondencí je metoda Random Sample Consensus (RANSAC), publikovaná M. A. Fischlerem a R. C. Bollesem v roce 37
38 1981 [16]. RANSAC je komplexní iterativní metodou, která se v počítačovém vidění využívá nejen k nalezení korespondencí, ale také například ke zjištění projekčních a fundamentálních matic na základě známých korespondencí. RANSAC se mimo jiné vyznačuje značnou robustností a odolností proti outlierům. Je to ovšem mimořádně výpočetně náročný algoritmus. Vzhledem k použití manuální detekci obrazových bodů byly korespondence určeny už při jejich anotaci, proto pro hledání korespondencí nebyl vytvořen samostatný modul Externí kalibrace Pro zaměření bodu některou z triangulačních metod je potřeba znát polohu a orientaci (externí parametry) všech kamer kamerového systému, aby bylo možno stanovit projekční matice P podle Pozice a orientace kamer záleží na topologii experimentu. Je-li uspořádání experimentu pevné jako v kapitole 3.2.1, jsou matice R a vektory t pro všechny kamery známé a neměnné. V pohyblivém uspořádání jsou R a t neznámé, resp. je možné je odhadnout s relativně velkou chybou. Tento hrubý odhad může sloužit jako výchozí stav pro některou z iterativních metod, a napomoci tak její konvergenci do správného výsledku. Jednou z cest ke zjištění vzájemné polohy a natočení kamer je zjištění fundamentálních matic F systému na základě korespondencí mezi obrazy. Možnou metodou je již výše zmiňovaný osmibodový algoritmus nebo metoda RANSAC. Numerické metody na hledání F jsou výpočetně a implementačně náročné, ale při dostatečně velkém počtu snímků (u pohyblivého uspořádání snímkovacího aparátu je možné nastavit úhel β velmi malý, a nasnímat tak velké množství obrázků) produkují velice dobré výsledky (statisticky se odchylky vyruší). Jednodušší cestu představuje externí kalibrace vůči známému objektu v obraze. Potom lze zjišťovat R a t každé kamery na základě známých 2D 3D korespondencí. V tomto případě je opět použitelná metoda RANSAC, anebo algoritmus DLT popsaný v kapitole Modul externí kalibrace používá k externí kalibraci algoritmus RANSAC prostřednictvím OpenCV funkce cv::solvepnpransac, tato funkce je upřednostněna před funkcí cv::solvepnp, pro svou robustnost. Externí kalibrace probíhá vůči kalibrační krychli prostřednictvím 2D 3D korespondencí, kde 3D geometrie kalibrační krychle je pevně definována se středem souřadné soustavy scény ve středu krychle. Souřadná soustava scény je pravotočivá s orientací podle následujícího obrázku: 38
39 Obr. 4.8 Souřadná soustava scény D rekonstrukce Cílem modulu je naleznutí 3D souřadnic bodu na základě známých 2D korespondencí a projekčních matic z n kamer. Pro triangulaci bodů připadá v úvahu mnoho existujících metod. Zvažoval jsem použití následujících: Sparse Bundle Adjustment 13 prostřednictvím knihovny cvsba 14 Triangulace pomocí DLT prostřednictvím OpenCV funkce cv::sfm::triangulatepoints 15 Bundle Adjustment je komplexní metoda založená na úpravě svazku přímek. Metoda hledá optimální polohu bodů v prostoru na základě minimalizace reprojekční chyby. Nehýbe však jen body, ale všemi parametry soustavy (tedy pozicí kamer, kalibrací kamer a distorzními parametry). Triangulace DLT algoritmem (viz výše) je prostá triangulační metoda na hledání optimální polohy bodu z n korespondencí. Obě metody byly testovány a na základě těchto testů byla zvolena triangulace používající DLT. Výstupní model ve formě bodového mračna je uložen v textovém formátu bod po bodu ve formátu [x, y, z]. Byl také vygenerován soubor typu.m, pro vykreslování modelu v softwarech MatLab nebo Octave. 13 Autor: M. Lourakis, více na: 14 Více na: 15 cv::sfm::triangulatepoints je součástí contrib modulu Structure from Motion OpenCV
40 4.3 Experiment na testovací scéně První měření bylo provedeno na testovací scéně, kde krom kalibrační krychle byla ve scéně další definovaná tělesa pro ověření přesnosti měření. Obr. 4.9 Rozložení testovací scény Do scény byl vložen drátěný model jehlanu, jehož vrcholy byly anotovány jako zájmové body. Dále bylo ve scéně posuvné měřítko pevně nastavené na délku 100mm pro rychlou identifikaci případné hrubé chyby v měření. Obr Výstupní model pro názornost doplněný o hrany 40
Kalibrační proces ve 3D
 Kalibrační proces ve 3D FCC průmyslové systémy společnost byla založena v roce 1995 jako součást holdingu FCC dodávky komponent pro průmyslovou automatizaci integrace systémů kontroly výroby, strojového
Kalibrační proces ve 3D FCC průmyslové systémy společnost byla založena v roce 1995 jako součást holdingu FCC dodávky komponent pro průmyslovou automatizaci integrace systémů kontroly výroby, strojového
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
11 Zobrazování objektů 3D grafiky
 11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník RELATIVNÍ A ABSOLUTNÍ ORIENTACE AAT ANALYTICKÁ AEROTRIANGULACE PŘÍPRAVA STEREODVOJICE PRO VYHODNOCENÍ Příprava stereodvojice pro vyhodnocení
Souřadnicové prostory
 Prostor objektu Tr. objektu Tr. modelu Prostor scény Souřadnicové prostory V V x, y z x, y z z -z x, y Tr. objektu V =V T 1 T n M Tr. modelu Tr. scény x, y Tr. pohledu Tr. scény Tr. pohledu Prostor pozorovatele
Prostor objektu Tr. objektu Tr. modelu Prostor scény Souřadnicové prostory V V x, y z x, y z z -z x, y Tr. objektu V =V T 1 T n M Tr. modelu Tr. scény x, y Tr. pohledu Tr. scény Tr. pohledu Prostor pozorovatele
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MATEMATICKÉ (OPTICKÉ) ZÁKLADY FOTOGRAMMETRIE
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MATEMATICKÉ (OPTICKÉ) ZÁKLADY FOTOGRAMMETRIE MATEMATICKÉ ZÁKLADY FOTOGRAMMETRIE fotogrammetrie využívá ke své práci fotografické snímky, které
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MATEMATICKÉ (OPTICKÉ) ZÁKLADY FOTOGRAMMETRIE MATEMATICKÉ ZÁKLADY FOTOGRAMMETRIE fotogrammetrie využívá ke své práci fotografické snímky, které
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
Úloha - rozpoznávání číslic
 Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Úloha - rozpoznávání číslic Vojtěch Franc, Tomáš Pajdla a Tomáš Svoboda http://cmp.felk.cvut.cz 27. listopadu 26 Abstrakt Podpůrný text pro cvičení předmětu X33KUI. Vysvětluje tři způsoby rozpoznávání
Úvod do mobilní robotiky AIL028
 md at robotika.cz http://robotika.cz/guide/umor07/cs 20. prosince 2007 1 2 3D model světa ProMIS Cvičení hledání domečku Model štěrbinové kamery Idealizovaný jednoduchý model kamery Paprsek světla vychází
md at robotika.cz http://robotika.cz/guide/umor07/cs 20. prosince 2007 1 2 3D model světa ProMIS Cvičení hledání domečku Model štěrbinové kamery Idealizovaný jednoduchý model kamery Paprsek světla vychází
Automatická detekce anomálií při geofyzikálním průzkumu. Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011
 Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
VEKTORY. Obrázek 1: Jediný vektor. Souřadnice vektoru jsou jeho průměty do souřadných os x a y u dvojrozměrného vektoru, AB = B A
 VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
Mechanika
 Mechanika 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Mechanika Kinematika 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Mechanika 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Mechanika Kinematika 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát. Fotografický aparát
 Michal Veselý, 00 Základní části fotografického aparátu tedy jsou: tělo přístroje objektiv Pochopení funkce běžných objektivů usnadní zjednodušená představa, že objektiv jako celek se chová stejně jako
Michal Veselý, 00 Základní části fotografického aparátu tedy jsou: tělo přístroje objektiv Pochopení funkce běžných objektivů usnadní zjednodušená představa, že objektiv jako celek se chová stejně jako
Testování programu PhotoScan pro tvorbu 3D modelů objektů. Ing. Tomáš Jiroušek
 Testování programu PhotoScan pro tvorbu 3D modelů objektů Ing. Tomáš Jiroušek Obsah Rozlišovací schopnost použitých fotoaparátů Kalibrace určení prvků vnitřní orientace Objekty pro testování Testování
Testování programu PhotoScan pro tvorbu 3D modelů objektů Ing. Tomáš Jiroušek Obsah Rozlišovací schopnost použitých fotoaparátů Kalibrace určení prvků vnitřní orientace Objekty pro testování Testování
Stereofotogrammetrie
 Stereootogrammetrie Princip stereoskopického vidění a tzv. yziologické paralaxy Paralaxa je relativní změna v poloze stacionárních objektů způsobená změnou v geometrii pohledu. horizontální yziologická
Stereootogrammetrie Princip stereoskopického vidění a tzv. yziologické paralaxy Paralaxa je relativní změna v poloze stacionárních objektů způsobená změnou v geometrii pohledu. horizontální yziologická
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
 Odstranění geometrických zkreslení obrazu Vstupní obraz pro naše úlohy získáváme pomocí optické soustavy tvořené objektivem a kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
Odstranění geometrických zkreslení obrazu Vstupní obraz pro naše úlohy získáváme pomocí optické soustavy tvořené objektivem a kamerou. Dle optických parametrů objektivu mohou v získaném obraze nastat geometrická
Bezkontaktní měření Fotogrammetrie v automotive
 Bezkontaktní měření Fotogrammetrie v automotive Ing. Jaroslav Kopřiva Konferencia Združenia slovenských laboratórií a skúšobní, Hotel Stupka, Tále I 3.5 5.5. 2017 Využití fotogrammetrie v automotive zkušebnictví
Bezkontaktní měření Fotogrammetrie v automotive Ing. Jaroslav Kopřiva Konferencia Združenia slovenských laboratórií a skúšobní, Hotel Stupka, Tále I 3.5 5.5. 2017 Využití fotogrammetrie v automotive zkušebnictví
Jasové transformace. Karel Horák. Rozvrh přednášky:
 1 / 23 Jasové transformace Karel Horák Rozvrh přednášky: 1. Úvod. 2. Histogram obrazu. 3. Globální jasová transformace. 4. Lokální jasová transformace. 5. Bodová jasová transformace. 2 / 23 Jasové transformace
1 / 23 Jasové transformace Karel Horák Rozvrh přednášky: 1. Úvod. 2. Histogram obrazu. 3. Globální jasová transformace. 4. Lokální jasová transformace. 5. Bodová jasová transformace. 2 / 23 Jasové transformace
Měření průtoku kapaliny s využitím digitální kamery
 Měření průtoku kapaliny s využitím digitální kamery Mareš, J., Vacek, M. Koudela, D. Vysoká škola chemicko-technologická Praha, Ústav počítačové a řídicí techniky, Technická 5, 166 28, Praha 6 e-mail:
Měření průtoku kapaliny s využitím digitální kamery Mareš, J., Vacek, M. Koudela, D. Vysoká škola chemicko-technologická Praha, Ústav počítačové a řídicí techniky, Technická 5, 166 28, Praha 6 e-mail:
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
3.4.2 Rovnováha Rovnováha u centrální rovinné silové soustavy nastává v případě, že výsledná síla nahrazující soustavu je rovna nule. Tedy. Obr.17.
 Obr.17. F F 1x = F.cos α1,..., Fnx = F. cos 1y = F.sin α1,..., Fny = F. sin α α n n. Původní soustava je nyní nahrazena děma soustavami sil ve směru osy x a ve směru osy y. Tutu soustavu nahradíme dvěma
Obr.17. F F 1x = F.cos α1,..., Fnx = F. cos 1y = F.sin α1,..., Fny = F. sin α α n n. Původní soustava je nyní nahrazena děma soustavami sil ve směru osy x a ve směru osy y. Tutu soustavu nahradíme dvěma
V poslední době se v oblasti dokumentace archeologických movitých i nemovitých památek začíná objevovat zcela nová, digitální metoda tzv.
 3D FOTOGRAMMETRIE V poslední době se v oblasti dokumentace archeologických movitých i nemovitých památek začíná objevovat zcela nová, digitální metoda tzv. pozemní 3D fotogrammetrie. Jedná se o tvorbu
3D FOTOGRAMMETRIE V poslední době se v oblasti dokumentace archeologických movitých i nemovitých památek začíná objevovat zcela nová, digitální metoda tzv. pozemní 3D fotogrammetrie. Jedná se o tvorbu
P R O M Í T Á N Í. rovina π - průmětna vektor s r - směr promítání. a // s r, b// s r,
 P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
Laserový skenovací systém LORS vývoj a testování přesnosti
 Laserový skenovací systém LORS vývoj a testování přesnosti Ing. Bronislav Koska Ing. Martin Štroner, Ph.D. Doc. Ing. Jiří Pospíšil, CSc. ČVUT Fakulta stavební Praha Článek popisuje laserový skenovací systém
Laserový skenovací systém LORS vývoj a testování přesnosti Ing. Bronislav Koska Ing. Martin Štroner, Ph.D. Doc. Ing. Jiří Pospíšil, CSc. ČVUT Fakulta stavební Praha Článek popisuje laserový skenovací systém
ZÁKLADNÍ ZOBRAZOVACÍ METODY
 ZÁKLADNÍ ZOBRAZOVACÍ METODY Prostorové útvary zobrazujeme do roviny pomocí promítání, což je jisté zobrazení trojrozměrného prostoru (uvažujme rozšířený Eukleidovský prostor) do roviny, které je zadáno
ZÁKLADNÍ ZOBRAZOVACÍ METODY Prostorové útvary zobrazujeme do roviny pomocí promítání, což je jisté zobrazení trojrozměrného prostoru (uvažujme rozšířený Eukleidovský prostor) do roviny, které je zadáno
ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů
 ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů REGISTRACI OBRAZU (IMAGE REGISTRATION) Více snímků téže scény Odpovídající pixely v těchto snímcích musí mít stejné souřadnice Pokud je nemají
ROZ1 CVIČENÍ VI. Geometrická registrace (matching) obrazů REGISTRACI OBRAZU (IMAGE REGISTRATION) Více snímků téže scény Odpovídající pixely v těchto snímcích musí mít stejné souřadnice Pokud je nemají
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Úvod do zpracování obrazů. Petr Petyovský Miloslav Richter
 Úvod do zpracování obrazů Petr Petyovský Miloslav Richter 1 OBSAH Motivace, prvky a základní problémy počítačového vidění, pojem scéna Terminologie, obraz, zpracování a analýza obrazu, počítačové vidění,
Úvod do zpracování obrazů Petr Petyovský Miloslav Richter 1 OBSAH Motivace, prvky a základní problémy počítačového vidění, pojem scéna Terminologie, obraz, zpracování a analýza obrazu, počítačové vidění,
Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje
 Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
Optické zobrazování Základní pojmy Zobrazení zrcadlem, Zobrazení čočkou Lidské oko, Optické přístroje Základní pojmy Optické zobrazování - pomocí paprskové (geometrické) optiky - využívá model světelného
SIFT: Scale Invariant Feature Transform Automatické nalezení korespondencí mezi dvojicí obrázků
 SIFT: Scale Invariant Feature Transform Automatické nalezení korespondencí mezi dvojicí obrázků lukas.mach@gmail.com Přílohy (videa, zdrojáky, ) ke stažení na: http://mach.matfyz.cz/sift Korespondence
SIFT: Scale Invariant Feature Transform Automatické nalezení korespondencí mezi dvojicí obrázků lukas.mach@gmail.com Přílohy (videa, zdrojáky, ) ke stažení na: http://mach.matfyz.cz/sift Korespondence
Projektivní geometrie. Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni
 Metody Počítačového Vidění (MPV) - 3D počítačové vidění Projektivní geometrie Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Metody Počítačového Vidění
Metody Počítačového Vidění (MPV) - 3D počítačové vidění Projektivní geometrie Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Metody Počítačového Vidění
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy
 Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
Cyklografie. Cyklický průmět bodu
 Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky. Téma Školní výstupy Učivo (pojmy) volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Moderní metody rozpoznávání a zpracování obrazových informací 15
 Moderní metody rozpoznávání a zpracování obrazových informací 15 Hodnocení transparentních materiálů pomocí vizualizační techniky Vlastimil Hotař, Ondřej Matúšek Katedra sklářských strojů a robotiky Fakulta
Moderní metody rozpoznávání a zpracování obrazových informací 15 Hodnocení transparentních materiálů pomocí vizualizační techniky Vlastimil Hotař, Ondřej Matúšek Katedra sklářských strojů a robotiky Fakulta
Základy navrhování průmyslových experimentů DOE
 Základy navrhování průmyslových experimentů DOE cílová hodnota V. Vícefaktoriální experimenty Gejza Dohnal střední hodnota cílová hodnota Vícefaktoriální návrhy experimentů počet faktorů: počet úrovní:
Základy navrhování průmyslových experimentů DOE cílová hodnota V. Vícefaktoriální experimenty Gejza Dohnal střední hodnota cílová hodnota Vícefaktoriální návrhy experimentů počet faktorů: počet úrovní:
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1
 Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1 Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 1 Ing. Jakub Ulmann Zobrazování optickými soustavami 1. Optické
Topografické plochy KG - L MENDELU. KG - L (MENDELU) Topografické plochy 1 / 56
 Topografické plochy KG - L MENDELU KG - L (MENDELU) Topografické plochy 1 / 56 Obsah 1 Úvod 2 Křivky a body na topografické ploše 3 Řez topografické plochy rovinou 4 Příčný a podélný profil KG - L (MENDELU)
Topografické plochy KG - L MENDELU KG - L (MENDELU) Topografické plochy 1 / 56 Obsah 1 Úvod 2 Křivky a body na topografické ploše 3 Řez topografické plochy rovinou 4 Příčný a podélný profil KG - L (MENDELU)
6 Skalární součin. u v = (u 1 v 1 ) 2 +(u 2 v 2 ) 2 +(u 3 v 3 ) 2
 6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
Elementární křivky a plochy
 Příloha A Elementární křivky a plochy A.1 Analytický popis geometrických objektů Geometrické vlastnosti, které jsme dosud studovali, se týkaly především základních geometrických objektů bodů, přímek, rovin
Příloha A Elementární křivky a plochy A.1 Analytický popis geometrických objektů Geometrické vlastnosti, které jsme dosud studovali, se týkaly především základních geometrických objektů bodů, přímek, rovin
Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr
 Geometrické transformace v prostoru Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr Shodné transformace 1 Shodné transformace stejný přístup jako ve 2D shodné transformace (shodnosti,
Geometrické transformace v prostoru Geometrické vidění světa KMA/GVS ak. rok 2013/2014 letní semestr Shodné transformace 1 Shodné transformace stejný přístup jako ve 2D shodné transformace (shodnosti,
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
Analýza a zpracování digitálního obrazu
 Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
Projektivní geometrie dvou pohledů. Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni
 Metody Počítačového Vidění (MPV) - 3D počítačové vidění Projektivní geometrie dvou pohledů Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Metody Počítačového
Metody Počítačového Vidění (MPV) - 3D počítačové vidění Projektivní geometrie dvou pohledů Ing. Zdeněk Krňoul, Ph.D. Katedra Kybernetiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Metody Počítačového
K OZA SE PASE NA POLOVINĚ ZAHRADY Zadání úlohy
 Koza se pase na polovině zahrady, Jaroslav eichl, 011 K OZA E PAE NA POLOVINĚ ZAHADY Zadání úlohy Zahrada kruhového tvaru má poloměr r = 10 m. Do zahrady umístíme kozu, kterou přivážeme provazem ke kolíku
Koza se pase na polovině zahrady, Jaroslav eichl, 011 K OZA E PAE NA POLOVINĚ ZAHADY Zadání úlohy Zahrada kruhového tvaru má poloměr r = 10 m. Do zahrady umístíme kozu, kterou přivážeme provazem ke kolíku
GEOMETRICKÁ OPTIKA. Znáš pojmy A. 1. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci.
 Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Panoramatická fotografie
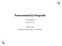 Panoramatická fotografie Jan Hnízdil xhnij08@vse.cz VŠE Praha Fakulta informatiky a statistiky Panoramatická fotografie p.1/37 Osnova Panoramatická fotografie, jak jí vytvořit, programy na tvorbu panoramatických
Panoramatická fotografie Jan Hnízdil xhnij08@vse.cz VŠE Praha Fakulta informatiky a statistiky Panoramatická fotografie p.1/37 Osnova Panoramatická fotografie, jak jí vytvořit, programy na tvorbu panoramatických
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe.
 4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Defektoskopie. 1 Teoretický úvod. Cíl cvičení: Detekce měřicího stavu a lokalizace objektu
 Defektoskopie Cíl cvičení: Detekce měřicího stavu a lokalizace objektu 1 Teoretický úvod Defektoskopie tvoří v počítačovém vidění oblast zpracování snímků, jejímž úkolem je lokalizovat výrobky a detekovat
Defektoskopie Cíl cvičení: Detekce měřicího stavu a lokalizace objektu 1 Teoretický úvod Defektoskopie tvoří v počítačovém vidění oblast zpracování snímků, jejímž úkolem je lokalizovat výrobky a detekovat
b) Po etní ešení Všechny síly soustavy tedy p eložíme do po átku a p ipojíme p íslušné dvojice sil Všechny síly soustavy nahradíme složkami ve sm
 b) Početní řešení Na rozdíl od grafického řešení určíme při početním řešení bod, kterým nositelka výslednice bude procházet. Mějme soustavu sil, která obsahuje n - sil a i - silových dvojic obr.36. Obr.36.
b) Početní řešení Na rozdíl od grafického řešení určíme při početním řešení bod, kterým nositelka výslednice bude procházet. Mějme soustavu sil, která obsahuje n - sil a i - silových dvojic obr.36. Obr.36.
Fotogammetrie. Zpracoval: Jakub Šurab, sur072. Datum:
 Fotogammetrie Zpracoval: Jakub Šurab, sur072 Datum: 7.4.2009 Co je fotogrammetrie Fotogrammetrie je věda, způsob a technologie, která se zabývá získáváním využitelných měření map, digitálních modelů a
Fotogammetrie Zpracoval: Jakub Šurab, sur072 Datum: 7.4.2009 Co je fotogrammetrie Fotogrammetrie je věda, způsob a technologie, která se zabývá získáváním využitelných měření map, digitálních modelů a
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH
 SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
Transformace dat mezi různými datovými zdroji
 Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
Ing. Jakub Ulmann. Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově
 Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 3 Ing. Jakub Ulmann Digitální fotoaparát Jak digitální fotoaparáty
Zavádění inovativních metod a výukových materiálů do přírodovědných předmětů na Gymnáziu v Krnově 07_10_Zobrazování optickými soustavami 3 Ing. Jakub Ulmann Digitální fotoaparát Jak digitální fotoaparáty
DZDDPZ3 Digitální zpracování obrazových dat DPZ. Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava
 DZDDPZ3 Digitální zpracování obrazových dat DPZ Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava Digitální zpracování obrazových dat DPZ Předzpracování (rektifikace a restaurace) Geometrické
DZDDPZ3 Digitální zpracování obrazových dat DPZ Doc. Dr. Ing. Jiří Horák Institut geoinformatiky VŠB-TU Ostrava Digitální zpracování obrazových dat DPZ Předzpracování (rektifikace a restaurace) Geometrické
Geometrické transformace pomocí matic
 Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
III/ 2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Jazyk Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací
Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Jazyk Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací
Využití letecké fotogrammetrie pro sledování historického vývoje krajiny
 Využití letecké fotogrammetrie pro sledování historického vývoje krajiny Jitka Elznicová Katedra informatiky a geoinformatiky Fakulta životního prostředí Univerzita J.E.Purkyně v Ústí nad Labem Letecké
Využití letecké fotogrammetrie pro sledování historického vývoje krajiny Jitka Elznicová Katedra informatiky a geoinformatiky Fakulta životního prostředí Univerzita J.E.Purkyně v Ústí nad Labem Letecké
TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY
 TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY V PROSTŘEDÍ MATLAB K. Nováková, J. Kukal FJFI, ČVUT v Praze ÚPŘT, VŠCHT Praha Abstrakt Při rozpoznávání D binárních objektů z jejich diskrétní realizace se využívají
TSO NEBO A INVARIANTNÍ ROZPOZNÁVACÍ SYSTÉMY V PROSTŘEDÍ MATLAB K. Nováková, J. Kukal FJFI, ČVUT v Praze ÚPŘT, VŠCHT Praha Abstrakt Při rozpoznávání D binárních objektů z jejich diskrétní realizace se využívají
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Trojúhelníky. a jejich různé středy. Součet vnitřních úhlů trojúhelníku = 180 neboli π radiánů.
 Úvod V této knize předkládáme čtenáři základní matematické a fyzikální vzorce v přívětivé a snadno použitelné podobě. Využití čísel a symbolů k modelování, předpovídání a ovládání reality je mocnou zbraní
Úvod V této knize předkládáme čtenáři základní matematické a fyzikální vzorce v přívětivé a snadno použitelné podobě. Využití čísel a symbolů k modelování, předpovídání a ovládání reality je mocnou zbraní
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
6. Vektorový počet Studijní text. 6. Vektorový počet
 6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Zpracování obrazu a fotonika 2006
 Základy zpracování obrazu Zpracování obrazu a fotonika 2006 Reprezentace obrazu Barevný obrázek Na laně rozměry: 1329 x 2000 obrazových bodů 3 barevné RGB kanály 8 bitů na barevný kanál FUJI Superia 400
Základy zpracování obrazu Zpracování obrazu a fotonika 2006 Reprezentace obrazu Barevný obrázek Na laně rozměry: 1329 x 2000 obrazových bodů 3 barevné RGB kanály 8 bitů na barevný kanál FUJI Superia 400
7 Transformace 2D. 7.1 Transformace objektů obecně. Studijní cíl. Doba nutná k nastudování. Průvodce studiem
 7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
7 Transformace 2D Studijní cíl Tento blok je věnován základním principům transformací v rovinné grafice. V následujícím textu bude vysvětlen rozdíl v přístupu k transformacím u vektorového a rastrového
Počítačová geometrie. + algoritmy DG
 Pojem výpočetní geometrie (počítačové) analýza a návrh efektivních algoritmů pro určování vlastností a vztahů geometrických objektů řešení geometrických problémů navrženými geometrickými algoritmy hlavním
Pojem výpočetní geometrie (počítačové) analýza a návrh efektivních algoritmů pro určování vlastností a vztahů geometrických objektů řešení geometrických problémů navrženými geometrickými algoritmy hlavním
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Návod k použití softwaru Solar Viewer 3D
 Návod k použití softwaru Solar Viewer 3D Software byl vyvinut v rámci grantového projektu Technologie a systém určující fyzikální a prostorové charakteristiky pro ochranu a tvorbu životního prostředí a
Návod k použití softwaru Solar Viewer 3D Software byl vyvinut v rámci grantového projektu Technologie a systém určující fyzikální a prostorové charakteristiky pro ochranu a tvorbu životního prostředí a
= cos sin = sin + cos = 1, = 6 = 9. 6 sin 9. = 1 cos 9. = 1 sin 9. + 6 cos 9 = 1 0,939692621 6 ( 0,342020143) = 1 ( 0,342020143) + 6 0,939692621
 ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
ELIMINACE VLIVU DRUHÉ ROTACE PŘI AFINNĚ INVARIANTNÍM 2D ROZPOZNÁVÁNÍ
 ELIMINACE VLIVU DRUHÉ ROTACE PŘI AFINNĚ INVARIANTNÍM 2D ROZPOZNÁVÁNÍ K. Nováková 1, J. Kukal 1,2 1 Fakulta jaderná a fyzikálně inženýrská, ČVUT v Praze 2 Ústav počítačové a řídicí techniky, VŠCHT Praha
ELIMINACE VLIVU DRUHÉ ROTACE PŘI AFINNĚ INVARIANTNÍM 2D ROZPOZNÁVÁNÍ K. Nováková 1, J. Kukal 1,2 1 Fakulta jaderná a fyzikálně inženýrská, ČVUT v Praze 2 Ústav počítačové a řídicí techniky, VŠCHT Praha
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2.5 Rovnováha rovinné soustavy sil
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 2.5 Rovnováha rovinné soustavy sil Rovnováha sil je stav, kdy na těleso působí více sil, ale jejich výslednice
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 2.5 Rovnováha rovinné soustavy sil Rovnováha sil je stav, kdy na těleso působí více sil, ale jejich výslednice
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Rozvinutelné plochy. tvoří jednoparametrickou soustavu rovin a tedy obaluje rozvinutelnou plochu Φ. Necht jsou
 Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
1 3D snímání: Metody a snímače
 1 3D snímání: Metody a snímače Nejprve je potřeba definovat, že se v rámci tohoto předmětu budeme zabývat pouze bezkontaktními metodami zisku hloubkové informace. Metody pro 3D snímání lze dělit v podstatě
1 3D snímání: Metody a snímače Nejprve je potřeba definovat, že se v rámci tohoto předmětu budeme zabývat pouze bezkontaktními metodami zisku hloubkové informace. Metody pro 3D snímání lze dělit v podstatě
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Vytyčení polohy bodu polární metodou
 Obsah Vytyčení polohy bodu polární metodou... 2 1 Vliv měření na přesnost souřadnic... 3 2 Vliv měření na polohovou a souřadnicovou směrodatnou odchylku... 4 3 Vliv podkladu na přesnost souřadnic... 5
Obsah Vytyčení polohy bodu polární metodou... 2 1 Vliv měření na přesnost souřadnic... 3 2 Vliv měření na polohovou a souřadnicovou směrodatnou odchylku... 4 3 Vliv podkladu na přesnost souřadnic... 5
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM. Fyzikální praktikum 2
 Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Fyzikální praktikum 2 Zpracoval: Markéta Kurfürstová Naměřeno: 16. října 2012 Obor: B-FIN Ročník: II Semestr: III
Fyzikální sekce přírodovědecké fakulty Masarykovy univerzity v Brně FYZIKÁLNÍ PRAKTIKUM Fyzikální praktikum 2 Zpracoval: Markéta Kurfürstová Naměřeno: 16. října 2012 Obor: B-FIN Ročník: II Semestr: III
l, l 2, l 3, l 4, ω 21 = konst. Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj. analyticky
 Kinematické řešení čtyřkloubového mechanismu Dáno: Cíl: l, l, l 3, l, ω 1 konst Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj analyticky určete úhlovou rychlost ω 1 a úhlové zrychlení
Kinematické řešení čtyřkloubového mechanismu Dáno: Cíl: l, l, l 3, l, ω 1 konst Proved te kinematické řešení zadaného čtyřkloubového mechanismu, tj analyticky určete úhlovou rychlost ω 1 a úhlové zrychlení
