Modely a metódy lineárneho a celočíselného programovania
|
|
|
- Vít Kovář
- před 6 lety
- Počet zobrazení:
Transkript
1 Modely a metódy lneárneho a celočíselného programovana (Téy prenáše č. 10) Téma prednášy Bvalentné programovane Prof. Dr. Mchal Fende Katedra operačného výsumu a eonometre Eonomcá unverta Bratslava Dolnoemsá Bratslava Katedra operačného výsumu a eonometre, EU v Bratslave
2 Všeobecná formuláca úlohy bvalentného programovana f() = n =1 c et mn; ma (1) Pr ohrančenach n =1 a D {,,=} b = 1,,n =,,m () (3) prčom množna D má nasledovný tvar a) b) 0,1, 1, n D, 0 D 0;1, 1,..., ; D R, 1,..., n 0 D R 0 ;, 1,..., n Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:
3 Oblast eonomcých aplačných problémov bvalentnného programovana Prraďovací problém BP Optmaláca výberu nvesttčne stratége podnu BP Fed Charge Problem - ZmCPaBP Úloha obchodného cestuúceho - BP Optmaláca nvestčného rovoa a výrobne stratége epanducch dvíí oncernu ZmBP Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:3
4 6 (a) 5 (b) *=(3,;,6) 3 (c) *=(3; )Z 1 f() Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:
5 Transformáca úlohy na štandardný tvar f() = n =1 c mn, c 0 N 1,,, n Pr ohrančenach n =1 a s b s M 0,1, 0,, 1,,, m N M Ponáma - Eplctná enumeráca ' V ( n) o počet možných rešení pr = o napr. pre n=3 pr=8, pre n=0 pr= Implctná enumeráca n Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:5
6 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:6 Bvalentné programovane Je daná úloha bvalentného programovana v tvare 0, mn p o f Parcálne rešene J= {3,-1} p = ( 0, _, 1, _ ) má fované premenné 1, 3 Doplno parcálneho rešena J d = (0, 0, 1, 1 ) e množna D={-, } Počet doplnov: a má úloha n premených a parcálne rešene PR má množnu ndeov fovných premenných J = {..} s q ndeam Ta parcálnemu rešenu estue spolu n-q doplnov neobsadené
7 A teda presúmame PR s p fovaným premenným, ta mplctne presúmame n-p doplnov Eplctná enumeráca Implctná enumeráca Egon Balas adtívny algortmus M.A. Geoffron algortmus IE Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:7
8 J(p) J (p) fovaných premenných 1, alebo 0 K ParR J(p) estue n-p dplnov J(p+1) J (p+1) fovaných premenných 1, alebo 0 K ParR J(p+1) estue n-p-1 doplnov J(p+) fovaných premenných 1, alebo 0 J(p+) A sme v onrétnom ule dentfoval tv. Koncový uol, ta alebo Neestue prípustný doplno ParR J(p+), alebo Hodnota účelove funce sa nedá lepšť, alebo ParR J(p+) e prípustným parcálnym rešením Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:8
9 Incalačná etapa Algortmus mplctne enumeráce =0; J =Ø; = 0; H = (pesmstcý odhad) II. Záladná etapa Kro 1 Otáa: Je atuálne ParR J a prípustné rešene úlohy? - Množna ndeov ParR J mplue vetor rešene = [ {0,1}] pre J - Vypočíteme s b J c 0 J a 0 1a) s 0 pre všety M atuálne ParR e prípustné, všety eho doplny sú tým mplctne presúmané a poračueme na ro (a potom Spätný chod) 1b) s ~ 0 pre všety M atuálne ParR e neprípustné, budeme analyovať eho doplny, poračueme na ro (Testovaca procedúra doplnov) Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:9
10 Kro Estue prípustný doplno D parcálnemu rešenu J? Sústava troch elmnačných testov TEST 1 Otáa: Estuú premenné, torých avedene do atuálneho parcaálneho rešena s hodnotou 1 neníža neprípustnosť an edne doplnove premenne s < 0 E N \ J a 0 pre : s 0 T N \ J \ 1 E Potom a) T 1 =Ø ParR J považueme a presúmané, t. neestue an eden anddát (premenná) pre tvorbu doplnu, poračueme na SCH 5 b) T 1 Ø ParR J považueme a nepresúmané, t. estue vhodný anddát (premenná) T 1 pre tvorbu doplnu, poračueme na TEST Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:10
11 TEST Otáa: Estuú vhodný anddát pre doplno (premenná), tore avedene do atuálneho parcaálneho rešene s hodnotou 1 lepší hodnotu účelove funce B T 1 c h T T \ 1 B Potom a) T =Ø ParR J považueme a presúmané, t. neestue an eden anddát (premenná) pre tvorbu doplnu, poračueme na SCH 5 b) T Ø ParR J považueme a nepresúmané, t. estue vhodný anddát (premenná) T 1 pre tvorbu doplnu, poračueme na TEST 3 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:11
12 TEST 3 Otáa: Estuú taá doplnová premenná s, torá po uplatnení aéhooľve vhodného anddáta alebo ch ombnáce pre doplno ostáva naďale neprípustná, t.. platí s < 0 C M s 0 : T mn a,0 s Potom a) C Ø ParR J považueme a presúmané, t. neestue an eden doplno umožňuúc odstránť neprípustnosť doplnove premenne s < 0, poračueme na spätný chod SCH 5 b) C=Ø ParR J považueme a nepresúmané, t. estue prípustný doplno ParR J a platí J " q" T, " q"? 1 J poračueme na Kro 3 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:1
13 Kro 3 Určene nasleduúceho ParR J +1 Vybereme T =q taé, toré mplue nanžšu ostatovú meru neprípustnost doplnových premenných, t.. dpovedá Potom v v q M ma T v mn ma s < 0 0, s a pre T Určíme nové ParR J +1 J 1 J q T položíme = +1 poračueme na Kro 1 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:13
14 Kro Archváca prípustného ParR J s a 0 H M H J, PR nalepšeho doposaľ dentfovaného rešena J * J, * H poračueme na Kro 5 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:1
15 Kro 5 Spätný chod (návrat na ataľ v dôsledu subetívne voľby cesty vetvena nepresúmané rešena) 5a) J =Ø mplctne sme presúmal všety prípustné rešena úlohy a1) H = úloha NEMÁ PRÍPUSTNÉ RIEŠENIE stop a) H úloha MÁ OPTIMÁLNE RIEŠENIE: J*, * stop 5b) J Ø AKTIVNY SPATNY CHOD - Vytvoríme množnu J ndeov množnu J, toré odpovedaú premenným s hodnotou 1 (sú to de facto ndey množny J s ladným namenam) J,, J -potom vybereme množny J nde tae premenne atuálneho rešena J torá po vynulovaní svoe hodnoty spôsobí namenšu neprípustnosť doplnových premenných s <0 0 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:15
16 - vybereme množny J nde tae premenne atuálneho rešena J torá mplue namenšu celovú neprípustnosť všetých doplnových w w q M ma J " mn 0, s a v q J" pre J " potom J 1 J q návrat na Kro 1 Prof. Mchal Fende: Modely a metódy lneárneho a celočíselného programovana Fola č.:16
 ó Šú ž ó ó ó É Ž É Š Ž Š ú ů ó š Š Š Ž ó Š Ž ú ů Š Ž ň š ů É Ž š Ž ó Ž ů ň š š ů š Ú ů Š Ž ž ó Ž ů ú É Ú š É Ť ú ů Š Ž Š š Ť É Š Š Ž Ž Š Š ť ť ť Ž É Š Š Š Ž š Š Ž Ž Ů Š š Ž Ý Ý Š Ž Š Ž Ť Ž É Ý Š Š Ž š
ó Šú ž ó ó ó É Ž É Š Ž Š ú ů ó š Š Š Ž ó Š Ž ú ů Š Ž ň š ů É Ž š Ž ó Ž ů ň š š ů š Ú ů Š Ž ž ó Ž ů ú É Ú š É Ť ú ů Š Ž Š š Ť É Š Š Ž Ž Š Š ť ť ť Ž É Š Š Š Ž š Š Ž Ž Ů Š š Ž Ý Ý Š Ž Š Ž Ť Ž É Ý Š Š Ž š
4EK213 Lineární modely. 10. Celočíselné programování
 4EK213 Lineární modely 10. Celočíselné programování 10.1 Matematický model úlohy ILP Nalézt extrém účelové funkce z = c 1 x 1 + c 2 x 2 + + c n x n na soustavě vlastních omezení a 11 x 1 + a 12 x 2 + a
4EK213 Lineární modely 10. Celočíselné programování 10.1 Matematický model úlohy ILP Nalézt extrém účelové funkce z = c 1 x 1 + c 2 x 2 + + c n x n na soustavě vlastních omezení a 11 x 1 + a 12 x 2 + a
 ů ů ř É ř řřň ů ů ř ř Ú ó ó ó ť ň ó ó ř ř ř š ř ů ů ů ů š ů ů ř ů ů ř ř ř ř ř ů ř ř ó ň ó š ř É ó š řó š ó řó óž ř ř ž ř ž ř ř ř ř Í ř š ů Š ů ř š Š ř ň Š š Š Š ř ž ť ň ň Š š š ň ř Š ň ň ř š Š Š š Í š
ů ů ř É ř řřň ů ů ř ř Ú ó ó ó ť ň ó ó ř ř ř š ř ů ů ů ů š ů ů ř ů ů ř ř ř ř ř ů ř ř ó ň ó š ř É ó š řó š ó řó óž ř ř ž ř ž ř ř ř ř Í ř š ů Š ů ř š Š ř ň Š š Š Š ř ž ť ň ň Š š š ň ř Š ň ň ř š Š Š š Í š
 Ď Ů Ň ž Ů ž ň ž ž ž Č Č Ď Č ž Ě ž ž ž ž ň ž ž ž ž ž ž ž Ě ň ž ž ž ž Ďž ň ž Č Č ň Č Ď Ě Ň Č Ň ž ž ž Ů ň Ň ž ň ň ž ň ň ň ž ň ž Č ž ž Ř ž ž ž ž ň ž ž ž ž Ř ž ň ž ž ž ž ž ž ž Ě Ě Ě Č ž Ď Ř ž ň ň Ř ž ž ž ž
Ď Ů Ň ž Ů ž ň ž ž ž Č Č Ď Č ž Ě ž ž ž ž ň ž ž ž ž ž ž ž Ě ň ž ž ž ž Ďž ň ž Č Č ň Č Ď Ě Ň Č Ň ž ž ž Ů ň Ň ž ň ň ž ň ň ň ž ň ž Č ž ž Ř ž ž ž ž ň ž ž ž ž Ř ž ň ž ž ž ž ž ž ž Ě Ě Ě Č ž Ď Ř ž ň ň Ř ž ž ž ž
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Programovanie I. Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM
 Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
 ú Í ÚŘ Í úř Č Ú Í Ř Á ÁŠ úř ř úř ř š ú ř ú ě é ú Í ř ž Ž ž ě ďě ř š ě šú ě ú ř ř ú ř ě ú é š ě ě ě ř ú é Íé Í é ě é š ě Íř š š ř ř ě š é ě ú é ú é Í ť ú é ř ě ó š é ž š é ě é ě ěř ž é Ž é é ú ř ě ž ť ř
ú Í ÚŘ Í úř Č Ú Í Ř Á ÁŠ úř ř úř ř š ú ř ú ě é ú Í ř ž Ž ž ě ďě ř š ě šú ě ú ř ř ú ř ě ú é š ě ě ě ř ú é Íé Í é ě é š ě Íř š š ř ř ě š é ě ú é ú é Í ť ú é ř ě ó š é ž š é ě é ě ěř ž é Ž é é ú ř ě ž ť ř
KMA/P506 Pravděpodobnost a statistika KMA/P507 Statistika na PC
 Přednáša 04 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Záon velých čísel Lemma Nechť náhodná veličina nabývá pouze nezáporných
Přednáša 04 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Záon velých čísel Lemma Nechť náhodná veličina nabývá pouze nezáporných
1. Nejkratší cesta v grafu
 08. Nekratší cesty. Úloha obchodního cestuícího. Heurstky a aproxmační algortmy. Metoda dynamckého programování. Problém batohu. Pseudopolynomální algortmy 1. Nekratší cesta v grafu - sled e lbovolná posloupnost
08. Nekratší cesty. Úloha obchodního cestuícího. Heurstky a aproxmační algortmy. Metoda dynamckého programování. Problém batohu. Pseudopolynomální algortmy 1. Nekratší cesta v grafu - sled e lbovolná posloupnost
 ě úř ž ž ř ě š ě ž ř ě Í ů Í ř ě ž ř ě ž ž š ě ě ě ě ě ě š ř ů ř Ú š ě ř ř Ř ě ů ř ř ř š ě š ě ň ř š ř ř š ě ř š ě ů ě ě ě ě ů š ů š Č ď š ě Ú š ě ž ó ěř ž ěř ž š ě ž š ě ů Č ě ů ř ě ř ů Í ě ě ě ů ě ďě
ě úř ž ž ř ě š ě ž ř ě Í ů Í ř ě ž ř ě ž ž š ě ě ě ě ě ě š ř ů ř Ú š ě ř ř Ř ě ů ř ř ř š ě š ě ň ř š ř ř š ě ř š ě ů ě ě ě ě ů š ů š Č ď š ě Ú š ě ž ó ěř ž ěř ž š ě ž š ě ů Č ě ů ř ě ř ů Í ě ě ě ů ě ďě
G( x) %, ν%, λ. x, x, N, N nezáporné přídatné proměnné, ( ) 2 Matematické programování
 Matematicé programování Označení a definice veličin. opt i/maimalizace w, Žádaná hodnota,transpozice, relace typu nebo Inde diagonální formy vetoru. Obecná omezovací podmína Γ ( ( = ( Є, R, y podmíny typu
Matematicé programování Označení a definice veličin. opt i/maimalizace w, Žádaná hodnota,transpozice, relace typu nebo Inde diagonální formy vetoru. Obecná omezovací podmína Γ ( ( = ( Є, R, y podmíny typu
GYMNÁZIUM, OLOMOUC, ČAJKOVSKÉHO 9 Kriteria hodnocení pro 1. kolo přijímacích zkoušek pro školní rok 2014/15
 GYMNÁZIUM, OLOMOUC, ČAJKOVSKÉHO 9 Kriteria hodnocení pro 1. kolo přijímacích zkoušek pro školní rok 2014/15 Kriteria hodnocení pro osmileté studium: Všichni uchazeči o osmileté studium budou konat přijímací
GYMNÁZIUM, OLOMOUC, ČAJKOVSKÉHO 9 Kriteria hodnocení pro 1. kolo přijímacích zkoušek pro školní rok 2014/15 Kriteria hodnocení pro osmileté studium: Všichni uchazeči o osmileté studium budou konat přijímací
Teória grafov. Stromy a kostry 1. časť
 Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
13. Lineární programování
 Jan Schmidt 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Zimní semestr 2011/12 MI-PAA EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI
Jan Schmidt 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Zimní semestr 2011/12 MI-PAA EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJENE DO VAŠÍ BUDOUCNOSTI
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Reciprokou funkci znáte ze základní školy pod označením nepřímá úměra.
 @091 7. Reciproá funce Reciproou funci znáte ze záladní šoly pod označením nepřímá úměra. Definice: Reciproá funce je dána předpisem ( 0 je reálné číslo) f : y R \ {0} A) Definiční obor funce: Je třeba
@091 7. Reciproá funce Reciproou funci znáte ze záladní šoly pod označením nepřímá úměra. Definice: Reciproá funce je dána předpisem ( 0 je reálné číslo) f : y R \ {0} A) Definiční obor funce: Je třeba
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
e-mail: RadkaZahradnikova@seznam.cz 1. července 2010
 Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
MULTIKRITERIÁLNÍ ROZHODOVÁNÍ VEKTOROVÁ OPTIMALIZACE
 OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáša 5 PŘEDNÁŠKA 5 MULTIKRITERIÁLNÍ ROZHODOVÁNÍ VEKTOROVÁ OPTIMALIZACE OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáša 5 Multiriteriální rozhodování
OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáša 5 PŘEDNÁŠKA 5 MULTIKRITERIÁLNÍ ROZHODOVÁNÍ VEKTOROVÁ OPTIMALIZACE OPTIMALIZACE A ROZHODOVÁNÍ V DOPRAVĚ část druhá Přednáša 5 Multiriteriální rozhodování
 ÚŘ Á Í Š Í ĚŘ Á Í ĚŘ ě ň ě ý ů ý š ý ů ý š ý ů ý š Č ě ě ý ě ý ý ě ů ý ě ě ýš ť š Ó ě š ý ě ě ě š ů ý ý ý ě ý ě š ý ě ě ě ů ě ý ě ý ý Č ě ě ě ě ě ě ů ý ě ě ů ď ů ě ů ý Č ě Ú š Ú š ě ý ý ě ů ě ě š ě ů š
ÚŘ Á Í Š Í ĚŘ Á Í ĚŘ ě ň ě ý ů ý š ý ů ý š ý ů ý š Č ě ě ý ě ý ý ě ů ý ě ě ýš ť š Ó ě š ý ě ě ě š ů ý ý ý ě ý ě š ý ě ě ě ů ě ý ě ý ý Č ě ě ě ě ě ě ů ý ě ě ů ď ů ě ů ý Č ě Ú š Ú š ě ý ý ě ů ě ě š ě ů š
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
SLOVENSKÁ KOMISIA CHEMICKEJ OLYMPIÁDY CHEMICKÁ OLYMPIÁDA. 51. ročník, školský rok 2014/2015 Kategória C. Krajské kolo
 SLOVENSKÁ KOMISIA CHEMICKEJ OLYMPIÁDY CHEMICKÁ OLYMPIÁDA 51. ročník, školský rok 2014/2015 Kategória C Krajské kolo RIEŠENIE A HODNOTENIE TEORETICKÝCH ÚLOH RIEŠENIE A HODNOTENIE ÚLOH Z ANORGANICKEJ, VŠEOBECNEJ
SLOVENSKÁ KOMISIA CHEMICKEJ OLYMPIÁDY CHEMICKÁ OLYMPIÁDA 51. ročník, školský rok 2014/2015 Kategória C Krajské kolo RIEŠENIE A HODNOTENIE TEORETICKÝCH ÚLOH RIEŠENIE A HODNOTENIE ÚLOH Z ANORGANICKEJ, VŠEOBECNEJ
Úvod do úloh plánování rozvozu (Vehicle Routing Problems)
 Úvod do úloh plánování rozvozu (Vehicle Routing Problems) RNDr. Martin Branda, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Výpočetní
Úvod do úloh plánování rozvozu (Vehicle Routing Problems) RNDr. Martin Branda, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Výpočetní
Otázky ke státní závěrečné zkoušce
 Otázky ke státní závěrečné zkoušce obor Ekonometrie a operační výzkum a) Diskrétní modely, Simulace, Nelineární programování. b) Teorie rozhodování, Teorie her. c) Ekonometrie. Otázka č. 1 a) Úlohy konvexního
Otázky ke státní závěrečné zkoušce obor Ekonometrie a operační výzkum a) Diskrétní modely, Simulace, Nelineární programování. b) Teorie rozhodování, Teorie her. c) Ekonometrie. Otázka č. 1 a) Úlohy konvexního
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
18 OPATRENIE Národnej banky Slovenska z 28. septembra o priemernej výške nákladov na finančné sprostredkovanie v životnom poistení
 častka 33/2010 Vestník NBS opatrene NBS č. 18/2010 369 18 OPATRENIE Národnej banky Slovenska z 28. septembra 2010 o premernej výške nákladov na fnančné sprostredkovane v žvotnom postení Národná banka Slovenska
častka 33/2010 Vestník NBS opatrene NBS č. 18/2010 369 18 OPATRENIE Národnej banky Slovenska z 28. septembra 2010 o premernej výške nákladov na fnančné sprostredkovane v žvotnom postení Národná banka Slovenska
- Pokud máme na množině V zvoleno pevné očíslování vrcholů, můžeme váhovou funkci jednoznačně popsat. Symbolem ( i)
 DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
Obecná úloha lineárního programování
 Obecná úloha lineárního programování Úloha Maximalizovat hodnotu c T x (tzv. účelová funkce) za podmínek Ax b (tzv. omezující podmínky) kde A je daná reálná matice typu m n a c R n, b R m jsou dané reálné
Obecná úloha lineárního programování Úloha Maximalizovat hodnotu c T x (tzv. účelová funkce) za podmínek Ax b (tzv. omezující podmínky) kde A je daná reálná matice typu m n a c R n, b R m jsou dané reálné
 š ě ě ý ř ř ě ě ě ý ů ě ě š ř ů é ě š ř ů ý ů é Í ě ě š ř ů ř ř ú ý ů ý ů ě ě š ř ů ž ě š Í ú ř ž é ú é š ě ě é ě ř Í ř ú š ě š ě ř ř é ř ř é é ř ř š Ř Ě Ř Á Í Ř Í ř ě ř ú ř ř ě ě é ú ě ý ú ů ě ě š ř ů
š ě ě ý ř ř ě ě ě ý ů ě ě š ř ů é ě š ř ů ý ů é Í ě ě š ř ů ř ř ú ý ů ý ů ě ě š ř ů ž ě š Í ú ř ž é ú é š ě ě é ě ř Í ř ú š ě š ě ř ř é ř ř é é ř ř š Ř Ě Ř Á Í Ř Í ř ě ř ú ř ř ě ě é ú ě ý ú ů ě ě š ř ů
P O N D Ě L Í. Te Kr Kn. Ok I. II. Aj - Bl. Vv - Da. Bi - Ja. Hv - Rg Aj - Cs Fy - Mu Jv M - Pk Bi - Ma D - Sh Li - Pa MD - Er Sk Aj - Qu.
 I 0 1 2 3 P O N D Ě L Í Bi - Ma Kek - Ši Čjk - Pa MD - Er Fy - Mu Bi - Ma D - Sh Li - Pa MD - Er Nj-Be MD - Er Nj-Sa U1 Čjk - Rg Ch - Mu If - Ži Ch - Mu Bi - Ma Ov - Sh Aj - Je FjN-Vo Kh La - Lu Re - Pa
I 0 1 2 3 P O N D Ě L Í Bi - Ma Kek - Ši Čjk - Pa MD - Er Fy - Mu Bi - Ma D - Sh Li - Pa MD - Er Nj-Be MD - Er Nj-Sa U1 Čjk - Rg Ch - Mu If - Ži Ch - Mu Bi - Ma Ov - Sh Aj - Je FjN-Vo Kh La - Lu Re - Pa
Rozhodování. s více účastníky. Miroslav. school@utia
 Rozhodování s více účastníky Miroslav Kárný school@utia utia.cas.cz, http://www.utia utia.cas.cz/as Rozhodování Účastník znalosti neúpln plné cíle násobné omezení rozsahů složitostn itostní strategie akce
Rozhodování s více účastníky Miroslav Kárný school@utia utia.cas.cz, http://www.utia utia.cas.cz/as Rozhodování Účastník znalosti neúpln plné cíle násobné omezení rozsahů složitostn itostní strategie akce
 é é é ý š ř é ě ř š ř ě ě Č ě ý ů ř Ů é ř é é é é Č ý Š ř é ě Č é ř Ý ě ě Š ř š ť ě ž Ě Ě Á é é é š ř é ě ř š ř ě ě Č ě ý ů ř ů é ž é ý š é ř š Č ý ř š ě ě š ť ťď ď ě ř š ř ý Č É Á é É é é é ý š ř é ě
é é é ý š ř é ě ř š ř ě ě Č ě ý ů ř Ů é ř é é é é Č ý Š ř é ě Č é ř Ý ě ě Š ř š ť ě ž Ě Ě Á é é é š ř é ě ř š ř ě ě Č ě ý ů ř ů é ž é ý š é ř š Č ý ř š ě ě š ť ťď ď ě ř š ř ý Č É Á é É é é é ý š ř é ě
Matice. Matica typu m x n je tabuľka s m riadkami a n stĺpcami amn. a ij. prvok matice, i j udáva pozíciu prvku
 Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
 š Í Č š Í Í š š š š Ř š ť Ž š ú š ů š Ž š š š ú š Í š ů ý Ž Ž ů ů š ů š š š ó ý š ó š ý ú š ý š Ž ý š ň šú ý Ž ý š ť ň Í ý ý š Í Í ý š ú ú ú ý š š Í š ý ů š š š š ý ý ý š ý š š Ú ů Ž Ž ý š š ý Á š š ů
š Í Č š Í Í š š š š Ř š ť Ž š ú š ů š Ž š š š ú š Í š ů ý Ž Ž ů ů š ů š š š ó ý š ó š ý ú š ý š Ž ý š ň šú ý Ž ý š ť ň Í ý ý š Í Í ý š ú ú ú ý š š Í š ý ů š š š š ý ý ý š ý š š Ú ů Ž Ž ý š š ý Á š š ů
Metody lineární optimalizace Simplexová metoda. Distribuční úlohy
 Metody lineární optimalizace Simplexová metoda Dvoufázová M-úloha Duální úloha jednofázová Post-optimalizační analýza Celočíselné řešení Metoda větví a mezí Distribuční úlohy 1 OÚLP = obecná úloha lineárního
Metody lineární optimalizace Simplexová metoda Dvoufázová M-úloha Duální úloha jednofázová Post-optimalizační analýza Celočíselné řešení Metoda větví a mezí Distribuční úlohy 1 OÚLP = obecná úloha lineárního
UMAKOV ZL180 Z SERIA
 ZL180 Z SERIA , / #+ #! - %, / # + 5., / #+ #! - % 5., / # + Schéma ZL180 1 - Transformátor 2 - Poistka riadiacej jednotky 630mA 3 - Nastavovacie trimre 4 - Programovanie dia¾kového ovládania 5 - Konektor
ZL180 Z SERIA , / #+ #! - %, / # + 5., / #+ #! - % 5., / # + Schéma ZL180 1 - Transformátor 2 - Poistka riadiacej jednotky 630mA 3 - Nastavovacie trimre 4 - Programovanie dia¾kového ovládania 5 - Konektor
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Blokové a prúdové šifry
 Informačná bezpečnosť 2, jar 2015 Blokové a prúdové šifry Ján Karabáš Blokové šifry a dlhé správy Bloková šifra je vhodná pre zašifrovanie iba jedného, relatívne krátkeho bloku Blok je skupina znakov (otvorenej
Informačná bezpečnosť 2, jar 2015 Blokové a prúdové šifry Ján Karabáš Blokové šifry a dlhé správy Bloková šifra je vhodná pre zašifrovanie iba jedného, relatívne krátkeho bloku Blok je skupina znakov (otvorenej
Import Excel Univerzál
 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Přiřazovací problém. Přednáška č. 7
 Přiřazovací problém Přednáška č. 7 Přiřazovací problém je jednou podtřídou logistických úloh. Typickým problémem může být nejkratší převoz materiálu od dodavatelů ke spotřebitelům. spotřebitelé a i dodavatelé
Přiřazovací problém Přednáška č. 7 Přiřazovací problém je jednou podtřídou logistických úloh. Typickým problémem může být nejkratší převoz materiálu od dodavatelů ke spotřebitelům. spotřebitelé a i dodavatelé
 Á ů ů ě Š Č Ú ů Ú ě ů š ě š ě ě ě ů ě ě Ž š š ě ň Č ů ů ň ůž ě ě š ž ě ě Š ů ě Š š š Ú ů ů š ů ě ě Č š ů ě ě ě ě ě ž ě ě ě š ě š ž ě ě ž š ě ž š ě š ů Ý ů ů ě ů š ě ž ě š ě ů š ž ě ě š š ů ň Č ů š ú ů
Á ů ů ě Š Č Ú ů Ú ě ů š ě š ě ě ě ů ě ě Ž š š ě ň Č ů ů ň ůž ě ě š ž ě ě Š ů ě Š š š Ú ů ů š ů ě ě Č š ů ě ě ě ě ě ž ě ě ě š ě š ž ě ě ž š ě ž š ě š ů Ý ů ů ě ů š ě ž ě š ě ů š ž ě ě š š ů ň Č ů š ú ů
U# bolo: Matematika I. Obsah na dnes... Determinanty. Iné ozna!enie: A
 Matematia I Predná'ajúci: prof RNr Igor Podlun$, Sc http://wwwtues/podluny/ # etory a U# olo: etory Aritmetic$ etoro$ priestor Lineárna záislos% a nezáislos% etoro Hodnos% sústay etoro Salárny súin etoro
Matematia I Predná'ajúci: prof RNr Igor Podlun$, Sc http://wwwtues/podluny/ # etory a U# olo: etory Aritmetic$ etoro$ priestor Lineárna záislos% a nezáislos% etoro Hodnos% sústay etoro Salárny súin etoro
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
 ňď Ó Ó Š ť ř ř ř Č ř ť ř Ř Š Ě Č Č ř Č Ý Ě ť Ě ť ř ý ř Ř ť ň Ě Ý ř Ě ř ř ň ť Š Š Š ň ť Ó ť Á ť ř Ů Ú Ě Č ť ň Š ř Ď Č Š ň Ř Ě ň ý řň ř ř ř Č Š ť Š Š Š Ú Š Á Ý Ú Š Š Š Š Š ť Á ť ť Ě ť ť ť ř Ú Ú Ú Š Ů Š ý
ňď Ó Ó Š ť ř ř ř Č ř ť ř Ř Š Ě Č Č ř Č Ý Ě ť Ě ť ř ý ř Ř ť ň Ě Ý ř Ě ř ř ň ť Š Š Š ň ť Ó ť Á ť ř Ů Ú Ě Č ť ň Š ř Ď Č Š ň Ř Ě ň ý řň ř ř ř Č Š ť Š Š Š Ú Š Á Ý Ú Š Š Š Š Š ť Á ť ť Ě ť ť ť ř Ú Ú Ú Š Ů Š ý
ě é ř š á á á á ě š á ž ř š é řž á ý á á ď ú š ú á á ěž ě š é Šř ž ú ě é á ú š š á ů á ú á ů á ů á ů á ů á ů ů á ů á ů á á ý ě ď ý ž ž ě ě ř á é ěř ž
 Ř Ě Š úř š á Ř Á ÁŠ š ý á á ěá ř ě š úř š ý á ě ú á řá ď ě ě š ř ů á á ú ž á Ž á ď ě á ě ě ď ď ú ž é á á úáš ě ě š ú ě ď á ú ř řá ě ď á ú š áů ú á ů á ů á ů á ů ů ů ů á ů ú ť é š ú ě ě á ú š á ů á ú á
Ř Ě Š úř š á Ř Á ÁŠ š ý á á ěá ř ě š úř š ý á ě ú á řá ď ě ě š ř ů á á ú ž á Ž á ď ě á ě ě ď ď ú ž é á á úáš ě ě š ú ě ď á ú ř řá ě ď á ú š áů ú á ů á ů á ů á ů ů ů ů á ů ú ť é š ú ě ě á ú š á ů á ú á
Ako sme postavili Benátky
 Ako sme postavili Benátky alebo Sedem vecí, ktoré sme určite nechceli Tomáš Barbarič, Poštová banka Peter Polák, Softec 7...milión NECHCELI SME polí vo filtri [inteligentné vyhľadávanie] 7 Takto nejak
Ako sme postavili Benátky alebo Sedem vecí, ktoré sme určite nechceli Tomáš Barbarič, Poštová banka Peter Polák, Softec 7...milión NECHCELI SME polí vo filtri [inteligentné vyhľadávanie] 7 Takto nejak
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOS A SAISIKA Regulární systém hustot Vychází se z: -,, P - pravděpodobnostní prostor -, R neprázdná množna parametrů - X X 1,, náhodný vektor s sdruženou hustotou X n nebo s sdruženou pravděpodobnostní
PRAVDĚPODOBNOS A SAISIKA Regulární systém hustot Vychází se z: -,, P - pravděpodobnostní prostor -, R neprázdná množna parametrů - X X 1,, náhodný vektor s sdruženou hustotou X n nebo s sdruženou pravděpodobnostní
Tlač do PDF a odosielanie dokladov cez . OBSAH
 Tlač do PDF a odosielanie dokladov cez e-mail. OBSAH Úvod... 2 Základné podmienky:... 2 Kde nájdem inštalačný program pre PDF tlačiarne?... 2 Pre aký operačný systém ho môžem použiť?... 2 Inštalácia PDF
Tlač do PDF a odosielanie dokladov cez e-mail. OBSAH Úvod... 2 Základné podmienky:... 2 Kde nájdem inštalačný program pre PDF tlačiarne?... 2 Pre aký operačný systém ho môžem použiť?... 2 Inštalácia PDF
Fyzika a as. Vladimír Balek. december u ím ierne diery a ve ký tresk na bratislavskom matfyze
 u ím ierne diery a ve ký tresk na bratislavskom matfyze december 2015 téma fyziky: POHYB koná sa v ase, preto fyzika musí ma POJEM asu (o ase) téma fyziky: POHYB koná sa v ase, preto fyzika musí ma POJEM
u ím ierne diery a ve ký tresk na bratislavskom matfyze december 2015 téma fyziky: POHYB koná sa v ase, preto fyzika musí ma POJEM asu (o ase) téma fyziky: POHYB koná sa v ase, preto fyzika musí ma POJEM
Ružové obrázkové slová skladanie slov z písmen
 Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
1. LABORATÓRNE CVIČENIE
 MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
Úroveň strojového kódu procesor Intel Pentium. Adresovanie pamäte
 Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
 É Ě ů Č ú Č ň ň Č Ť Ý ň ú ň ť ů ú ů ů ů ú ů ň Ě ú ň ů É Ň ú Ť ŤÁŇ ť ť Ť Ý Áň Ť Ý Ď Ď Á Ň Ť ů ň ú Ň ň ů ň ů ú Ý ú ů ú ť ů ů Á ť ú ň ů ů Ů ů Ý Ú ň ť Á Č Č ň É ť Á ť ť ň Ť Č Č Č ú É Ť ť ť Á Ť Ť ů ň Ú ů ť
É Ě ů Č ú Č ň ň Č Ť Ý ň ú ň ť ů ú ů ů ů ú ů ň Ě ú ň ů É Ň ú Ť ŤÁŇ ť ť Ť Ý Áň Ť Ý Ď Ď Á Ň Ť ů ň ú Ň ň ů ň ů ú Ý ú ů ú ť ů ů Á ť ú ň ů ů Ů ů Ý Ú ň ť Á Č Č ň É ť Á ť ť ň Ť Č Č Č ú É Ť ť ť Á Ť Ť ů ň Ú ů ť
Lokace odbavovacího centra nákladní pokladny pro víkendový provoz
 Markéta Brázdová 1 Lokace odbavovacího centra nákladní pokladny pro víkendový provoz Klíčová slova: odbavování záslek, centrum grafu, vážená excentrcta vrcholů sítě, časová náročnost odbavení záslky, vážená
Markéta Brázdová 1 Lokace odbavovacího centra nákladní pokladny pro víkendový provoz Klíčová slova: odbavování záslek, centrum grafu, vážená excentrcta vrcholů sítě, časová náročnost odbavení záslky, vážená
Zmena vo výpočte ceny odchýlky Jesenná konferencia SPX 2017
 Zmena vo výpočte ceny odchýlky Jesenná konferencia SPX 2017 Úvod OBSAH 1. Určenie ceny odchýlky 2. Platby za odchýlky a PRE 3. Príjem zmluvných diagramov Porovnanie Súčasný stav - zúčtovacia cena odchýlky
Zmena vo výpočte ceny odchýlky Jesenná konferencia SPX 2017 Úvod OBSAH 1. Určenie ceny odchýlky 2. Platby za odchýlky a PRE 3. Príjem zmluvných diagramov Porovnanie Súčasný stav - zúčtovacia cena odchýlky
Pψνruθka zaθνnαme Prνruθka zaθνname
 CZ SK Pψνruθka zaθνnαme Prνruθka zaθνname Intuos CZ/SK Intuos Pen & Touch Intuos Pen Vύmμna hrotu pera Vύmena hrotu pera CZ/SK CZ Nastavenν tabletu Intuos 1. Pψipojte se k internetu. 2. Ukonθete v echny
CZ SK Pψνruθka zaθνnαme Prνruθka zaθνname Intuos CZ/SK Intuos Pen & Touch Intuos Pen Vύmμna hrotu pera Vύmena hrotu pera CZ/SK CZ Nastavenν tabletu Intuos 1. Pψipojte se k internetu. 2. Ukonθete v echny
 úř ř Á Ř Í É Á Í é ď ž é Í ř ďé ř ů é ý ř ů ů Íé ý ý ú Í éý ý ů ď ý ý ř é ú ž ř ř ň é ý ň é ý ř ř ř ř ř ř ř é Ž ó é é ř é ů ž ů ž ú Á Ú Ú É ť Ť Ř ÁÉ Ť ň Ý úř Ú Ťř ó ú ú ž ř ý ý Á ú ý ř úť Ě Ě Ť Ť Ý ŘÁ
úř ř Á Ř Í É Á Í é ď ž é Í ř ďé ř ů é ý ř ů ů Íé ý ý ú Í éý ý ů ď ý ý ř é ú ž ř ř ň é ý ň é ý ř ř ř ř ř ř ř é Ž ó é é ř é ů ž ů ž ú Á Ú Ú É ť Ť Ř ÁÉ Ť ň Ý úř Ú Ťř ó ú ú ž ř ý ý Á ú ý ř úť Ě Ě Ť Ť Ý ŘÁ
Modré obrázkové slová skladanie slov z písmen
 Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Teorie her a ekonomické rozhodování. 10. Rozhodování při jistotě, riziku a neurčitosti
 Teore her a ekonomcké rozhodování 10. Rozhodování př stotě, rzku a neurčtost 10.1 Jednokrterální dskrétní model Jednokrterální model rozhodování: f a ) max a Aa, a,..., a ( 1 2 f krterální funkce (zsk,
Teore her a ekonomcké rozhodování 10. Rozhodování př stotě, rzku a neurčtost 10.1 Jednokrterální dskrétní model Jednokrterální model rozhodování: f a ) max a Aa, a,..., a ( 1 2 f krterální funkce (zsk,
OBSAH. strana. Hroty 1, 2. Céčka a eska. strana 2, 3. strana. Šišky. Gule a polgule. strana 5, strana
 OBSAH Hroty 1, 2 Céčka a eska 2, 3 Šišky 3 Gule a polgule 4 Hrozno 5, 6 Lístky 7... 10 Tyčky a stĺpiky 11... 13 Pásoviny a madlá 14, 15 Pätky a krytky 16 Závesy 17 Kľučky 18, 19 Štítky Sortiment pojazdných
OBSAH Hroty 1, 2 Céčka a eska 2, 3 Šišky 3 Gule a polgule 4 Hrozno 5, 6 Lístky 7... 10 Tyčky a stĺpiky 11... 13 Pásoviny a madlá 14, 15 Pätky a krytky 16 Závesy 17 Kľučky 18, 19 Štítky Sortiment pojazdných
Multiplexor a demultiplexor
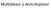 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ MS EXCEL. 1. Zadáme prvky matice A a B do buniek pracovného hárku zošita MS Excel
 RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
TomTom Referenčná príručka
 TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Základním pojmem v kombinatorice je pojem (k-prvková) skupina, nebo také k-tice prvků, kde k je přirozené číslo.
 přednáša KOMBINATORIKA Kombinatoria je obor matematiy, terý se zabývá uspořádáním daných prvů podle určitých pravidel do určitých supin Záladním pojmem v ombinatorice je pojem (-prvová) supina, nebo taé
přednáša KOMBINATORIKA Kombinatoria je obor matematiy, terý se zabývá uspořádáním daných prvů podle určitých pravidel do určitých supin Záladním pojmem v ombinatorice je pojem (-prvová) supina, nebo taé
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0259 Garantující institut: Garant předmětu: Exaktní metody rozhodování Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková,
Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0259 Garantující institut: Garant předmětu: Exaktní metody rozhodování Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková,
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
Plánování projektu. 3. dubna Úvod. 2 Reprezentace projektu. 3 Neomezené zdroje. 4 Variabilní doba trvání. 5 Přidání pracovní síly
 Plánování proektu 3. dubna 2018 1 Úvod 2 Reprezentace proektu 3 Neomezené zdroe 4 Variabilní doba trvání 5 Přidání pracovní síly Problémy plánování proektu Zprostředkování, instalace a testování rozsáhlého
Plánování proektu 3. dubna 2018 1 Úvod 2 Reprezentace proektu 3 Neomezené zdroe 4 Variabilní doba trvání 5 Přidání pracovní síly Problémy plánování proektu Zprostředkování, instalace a testování rozsáhlého
MATLAB (1) - úvod do programovania vedeckých problémov. LS 2017, 8.predn.
 MATLAB (1) - úvod do programovania vedeckých problémov LS 2017, 8.predn. Program predmetu: 1. týždeň: úvod, základné info o Matlabe, pracovné prostredie Matlabu, interaktívny režim, prvé info o písaní
MATLAB (1) - úvod do programovania vedeckých problémov LS 2017, 8.predn. Program predmetu: 1. týždeň: úvod, základné info o Matlabe, pracovné prostredie Matlabu, interaktívny režim, prvé info o písaní
Studentská soutěžní práce
 Univerzita Tomáše Bati Fakulta aplikované informatiky Ústav automatizace a řídicí techniky Studentská soutěžní práce STOČ 2011 Mobilní aplikace celočíselného programování metodou větví a mezí 2011 Adam
Univerzita Tomáše Bati Fakulta aplikované informatiky Ústav automatizace a řídicí techniky Studentská soutěžní práce STOČ 2011 Mobilní aplikace celočíselného programování metodou větví a mezí 2011 Adam
DOTAZNÍK STARÉ MESTO BEZ BARIÉR! kaviareň/pub/bar reštaurácia galéria múzeum kino iné... ulica...
 DOTAZNÍK STARÉ MESTO BEZ BARIÉR! Názov subjektu / prevádzky / / zariadenia......... TYP subjektu (ZAKRÚŽKUJ) kaviareň/pub/bar reštaurácia galéria múzeum kino iné... Subjekt je súčasťou vačšieho objektu......
DOTAZNÍK STARÉ MESTO BEZ BARIÉR! Názov subjektu / prevádzky / / zariadenia......... TYP subjektu (ZAKRÚŽKUJ) kaviareň/pub/bar reštaurácia galéria múzeum kino iné... Subjekt je súčasťou vačšieho objektu......
7.3.9 Směrnicový tvar rovnice přímky
 7.3.9 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme. Vrátíme se obecné rovnici přímy:
7.3.9 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme. Vrátíme se obecné rovnici přímy:
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Modul Kontrolné programy
 Modul Podporné programy str. 1 Modul Kontrolné programy Obsah: 1. Úvod 2 2. Kontrolné programy 3 2.1. Kontrola sklad príjem 4 2.2. Kontrola sklad výdaj 4 2.3. Kontrola sklad korektnosť 5 2.4. Kontrola
Modul Podporné programy str. 1 Modul Kontrolné programy Obsah: 1. Úvod 2 2. Kontrolné programy 3 2.1. Kontrola sklad príjem 4 2.2. Kontrola sklad výdaj 4 2.3. Kontrola sklad korektnosť 5 2.4. Kontrola
 Ž Á Č ČŽ ú ů ů ó ý Ť ý ůž ú ú ň ď ů ň Ř ť ú ú ý ů ý Ď ú ý ů ú ý Ž Á Č Č Ž ů ý ů ň ú ů Ž ú ť ý ý Ž ý ů ý ý ý ý ú ý ú ý ý ý ů ý ů ů Ý ý ý Š ť ů ý ů Č Ž Á Č ČŽ Á ů ý ý ó ů ý ý ň Ž ů ý ť ý ý ú ý ý ý ý ů ů
Ž Á Č ČŽ ú ů ů ó ý Ť ý ůž ú ú ň ď ů ň Ř ť ú ú ý ů ý Ď ú ý ů ú ý Ž Á Č Č Ž ů ý ů ň ú ů Ž ú ť ý ý Ž ý ů ý ý ý ý ú ý ú ý ý ý ů ý ů ů Ý ý ý Š ť ů ý ů Č Ž Á Č ČŽ Á ů ý ý ó ů ý ý ň Ž ů ý ť ý ý ú ý ý ý ý ů ů
Prijímacie skúšky kritériá pre školský rok 2017/2018
 Prijímacie skúšky kritériá pre školský rok 2017/2018 Študijný odbor 4236 M ekonomika pôdohospodárstva Prihlášky na štúdium v tomto študijnom odbore treba doručiť do 20. 4. 2017 Prijímacie skúšky budú v
Prijímacie skúšky kritériá pre školský rok 2017/2018 Študijný odbor 4236 M ekonomika pôdohospodárstva Prihlášky na štúdium v tomto študijnom odbore treba doručiť do 20. 4. 2017 Prijímacie skúšky budú v
 Ž ť ď ť ž ť ťď Ď ž ž ť Ž Č Č ž Ž ž Ď ť ť Ď ž ž ž Ď ž ť ť ž ž ž ž Í É Č ž ž ž ť ž Ď ž Ď ť ž ž ž ž ž ť ť Ď Ú ž ž Š ž ž ž ž ž ž ž ž Í Ž ž Í Č Ú ž Č ž ž Ž ž ž Ž ž Č Č ž ž ž ž ť ž Č Č ž ž ž ž Ř Šť ž Š Ž ž ž
Ž ť ď ť ž ť ťď Ď ž ž ť Ž Č Č ž Ž ž Ď ť ť Ď ž ž ž Ď ž ť ť ž ž ž ž Í É Č ž ž ž ť ž Ď ž Ď ť ž ž ž ž ž ť ť Ď Ú ž ž Š ž ž ž ž ž ž ž ž Í Ž ž Í Č Ú ž Č ž ž Ž ž ž Ž ž Č Č ž ž ž ž ť ž Č Č ž ž ž ž Ř Šť ž Š Ž ž ž
2.5. MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC
 25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ. Metodicko pedagogické centrum.
 Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ Kód ITMS: 26130130051 číslo zmluvy: OPV/24/2011 Metodicko pedagogické centrum Národný projekt VZDELÁVANÍM PEDAGOGICKÝCH
Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ Kód ITMS: 26130130051 číslo zmluvy: OPV/24/2011 Metodicko pedagogické centrum Národný projekt VZDELÁVANÍM PEDAGOGICKÝCH
Dopravní plánování a modelování (11 DOPM )
 Department of Appled Mathematcs Faculty of ransportaton Scences Czech echncal Unversty n Prague Dopravní plánování a modelování (11 DOPM ) Lekce 5: FSM: rp dstrbuton Prof. Ing. Ondře Přbyl, Ph.D. Ing.
Department of Appled Mathematcs Faculty of ransportaton Scences Czech echncal Unversty n Prague Dopravní plánování a modelování (11 DOPM ) Lekce 5: FSM: rp dstrbuton Prof. Ing. Ondře Přbyl, Ph.D. Ing.
rodní konference EUROTRAFFIC 8.3.2006
 Mezinárodn rodní konference EUROTRAFFIC Workshop Letiště Ruzyně 8.3.2006 Prezentace Katedry letecké dopravy FAKULTY DOPRAVNÍ, ČVUT Praha Mgr. Pavel Bíla Ing. Vladimír r NěmecN Adresa a kontakty ČVUT V
Mezinárodn rodní konference EUROTRAFFIC Workshop Letiště Ruzyně 8.3.2006 Prezentace Katedry letecké dopravy FAKULTY DOPRAVNÍ, ČVUT Praha Mgr. Pavel Bíla Ing. Vladimír r NěmecN Adresa a kontakty ČVUT V
 ě Á Á é é ě ě ě ú é é é ě é é ď ď ď š š Č Á ě ú Á ď š ě Č ě š ěž ě é ě ě ě ě ě ě Č Á ě Á é ú Ž é š ě š š é Ž ě é š é Š ť Ž ě Č Á ú Á Ť é ě é š ě ě š š ď ď Č é š š Č ě ě ú ě ú Ť é ě š ě ě š ě š ě ě ú ě
ě Á Á é é ě ě ě ú é é é ě é é ď ď ď š š Č Á ě ú Á ď š ě Č ě š ěž ě é ě ě ě ě ě ě Č Á ě Á é ú Ž é š ě š š é Ž ě é š é Š ť Ž ě Č Á ú Á Ť é ě é š ě ě š š ď ď Č é š š Č ě ě ú ě ú Ť é ě š ě ě š ě š ě ě ú ě
 ú Ú Č š š ó ó ě ě ě ú š ť Í ž ě ť Í Í ž ě ú ž ž š ů Í ů Í Í ú ň š ů ď ú Í ě š ě š ů ú ě Ú ě ě ť ě úě š ě ž š ě Í š Í ě ě ě ě ě ů ž ů ě ů š ž ó ě ú ó Ž Í Í Í ž ž ě Úě ž Í ě ů ú ž Ú ž ž ó Áš ů ů Ž Í ú Ú
ú Ú Č š š ó ó ě ě ě ú š ť Í ž ě ť Í Í ž ě ú ž ž š ů Í ů Í Í ú ň š ů ď ú Í ě š ě š ů ú ě Ú ě ě ť ě úě š ě ž š ě Í š Í ě ě ě ě ě ů ž ů ě ů š ž ó ě ú ó Ž Í Í Í ž ž ě Úě ž Í ě ů ú ž Ú ž ž ó Áš ů ů Ž Í ú Ú
DSS a De Novo programming
 De Novo Programming DSS a De Novo programming DSS navrhují žádoucí budoucnost a cesty k jejímu uskutečnění Optimalizační modely vhodné nástroje pro identifikaci optimálního řešení problému Je ale problém
De Novo Programming DSS a De Novo programming DSS navrhují žádoucí budoucnost a cesty k jejímu uskutečnění Optimalizační modely vhodné nástroje pro identifikaci optimálního řešení problému Je ale problém
INFORMÁCIA Z REZORTU ÚGKK SR
 INFORMÁCIA Z REZORTU ÚGKK SR Ing. Mária Frindrichová 22. slovenské geodetické dni, 6.-7. 11. 2014, Žilina Stav tvorby, aktualizácie a kompletizácie VKM Súhrnný počet súborov máp: 4149 Súbory s vyhlásenou
INFORMÁCIA Z REZORTU ÚGKK SR Ing. Mária Frindrichová 22. slovenské geodetické dni, 6.-7. 11. 2014, Žilina Stav tvorby, aktualizácie a kompletizácie VKM Súhrnný počet súborov máp: 4149 Súbory s vyhlásenou
UHU ČNÝ MANUÁL TALA VOD NA OBSL INŠ NÁ MIRROR SMART
 INŠTALAČNÝ MANUÁL SMART MIRROR NÁVOD NA OBSLUHU SMART MIRROR INŠTALAČNÝ MANUÁL A NÁVOD NA OBSLUHU INŠTALÁCIA SENZOR POHYBU JAS TEPLOTA CHROMATICKOSTI 5 ČASOVAČ VYPNUTIA Riešenie osvetlenia pre skúšobné
INŠTALAČNÝ MANUÁL SMART MIRROR NÁVOD NA OBSLUHU SMART MIRROR INŠTALAČNÝ MANUÁL A NÁVOD NA OBSLUHU INŠTALÁCIA SENZOR POHYBU JAS TEPLOTA CHROMATICKOSTI 5 ČASOVAČ VYPNUTIA Riešenie osvetlenia pre skúšobné
studentská kopie Předběžný odhad profilů: 1. Výpočet zatížení 1.1) Zatížení stálá Materiál: RD S10, LLD SB
 Zadání: Navrhněte a posuďte rozhodujíí nosné prvy (latě, rove, leštiny, vaznie, sloupy) a jejih spoje (vaznie leština, leština-roev, roev-vaznie, vaznie-sloupe) střešní onstrue obytné budovy z materiálů
Zadání: Navrhněte a posuďte rozhodujíí nosné prvy (latě, rove, leštiny, vaznie, sloupy) a jejih spoje (vaznie leština, leština-roev, roev-vaznie, vaznie-sloupe) střešní onstrue obytné budovy z materiálů
Verifikácia a falzifikácia
 Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá
 STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá 1) Lineární i nelineární regrese prostá, korelace Naeditujeme data viz obr. 1. Obr. 1 V menu Statistika zvolíme submenu Pokročilé lineární/nelineární
STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá 1) Lineární i nelineární regrese prostá, korelace Naeditujeme data viz obr. 1. Obr. 1 V menu Statistika zvolíme submenu Pokročilé lineární/nelineární
 š ř č éč é ú ř ě ě ě ý ř ř ý č ě ř ě é ř č ř Ž é ů é ě é ě ě é ě ř é ý ý ť č ď ý ů ůč ě č é Ž é ř ú Ž ý ú ě é ý ý ú ů ý ž ě Ž ř ěď é ě é č ě šč é ě ď č č č š ř ř ě é ě š ů ř č š ě é é ř ě ď ň ř č ý ě Ž
š ř č éč é ú ř ě ě ě ý ř ř ý č ě ř ě é ř č ř Ž é ů é ě é ě ě é ě ř é ý ý ť č ď ý ů ůč ě č é Ž é ř ú Ž ý ú ě é ý ý ú ů ý ž ě Ž ř ěď é ě é č ě šč é ě ď č č č š ř ř ě é ě š ů ř č š ě é é ř ě ď ň ř č ý ě Ž
Zápis schůze výboru klubu
 Zápis schůze výboru klubu Dne 9.11.2008 Přítomní: Fiala, Kracíková, Kůsová, Matějek, Náhlovská, Pavlovský, Svobodová, Vodičková(KRK), Vondráčková Omluveni: Kucková Výbor byl zahájen s 9 členy, schůze je
Zápis schůze výboru klubu Dne 9.11.2008 Přítomní: Fiala, Kracíková, Kůsová, Matějek, Náhlovská, Pavlovský, Svobodová, Vodičková(KRK), Vondráčková Omluveni: Kucková Výbor byl zahájen s 9 členy, schůze je





