PŘEDPODMÍNĚNÍ ALGORITMU SLEDOVÁNÍ CESTY PRO STOKESOVO PROUDĚNÍ SE SKLUZOVOU PODMÍNKOU

Transkript

1 PŘEDPODMÍNĚNÍ ALGORITMU SLEDOVÁNÍ CESTY PRO STOKESOVO PROUDĚNÍ SE SKLUZOVOU PODMÍNKOU Marta JAROŠOVÁ 1, Radek KUČERA 2, Václav ŠÁTEK 1 1 VŠB Technická univerzita Ostrava, IT4Innovations, 2 VŠB Technická univerzita Ostrava 1 ÚVOD Článek pojednává o úloze Stokesova proudění se skluzovou okrajovou podmínkou, která na rozdíl od klasického Navierova zákona [1] umožňuje prokluz tekutiny podél stěně pouze v případě, kdy smykové napětí dosáhne určité dané meze. Matematický model vede na variační nerovnost druhého druhu. Uvažovaná skluzová podmínka má řadu praktických aplikací, jako je modelování průtoků krve, modelování tvářecích procesů, modelování toků polymerů nebo modelování úloh hydrodynamiky [2, 3]. Při řešení úlohy používáme smíšenou metodu konečných prvků s konečně-prvkovou dvojicí P1-bubble/P1 [4]. Matice tuhosti jsou generovány vektorizovaným kódem [5]. Dále používáme TFETI metodou rozložení oblasti [6] umožňující výpočty paralelizovat. Duální algebraická úloha, která vznikne po eliminaci rychlostních i tlakových neznámých, vede na minimalizaci ryze konvexní kvadratické funkce obsahující jako proměnné tři Lagrangeovy multiplikátory. Tyto multiplikátory reprezentují podmínku lepení (včetně Dirichletovy okrajové podmínky), podmínku nepropustnosti stěny a skluzovou podmínku. Třetí z multiplikátorů podléhá jednoduchým oboustranným omezením. Vzhledem k použití TFETI metody musí všechny multiplikátory splňovat také lineární rovnostní vazbu. Řešení duální úlohy je počítáno pomocí metody sledování cesty, což je varianta algoritmu vnitřního bodu [7] upravená pro jednoduchá oboustranná omezení a omezení ve tvaru rovnosti [8]. Slibné výsledky numerických experimentů pro variantu bez dekompozice oblasti byly prezentovány v [9]. Adaptace algoritmu pro TFETI metodu je netriviální. Základem výpočtu je použití tlumené Newtonovy metody, jejíž iterace leží v okolí centrálního cesty směřující k řešení. Vnitřními úlohami jsou soustavy lineárních rovnic s blokovou strukturou, které redukujeme na Schurův doplněk. Redukované soustavy pak řešíme metodou předpodmíněných projektovaných sdružených gradientů (PPCGM). Tato metoda generuje iterace v podprostoru určeném jádrem matice rovnostních vazeb. Vhodným předpodmiňovačem eliminuje špatné podmínění redukované soustavy, které je pro metodu vnitřního bodu typické, jsou-li iterace dostatečně blízko u řešení. Pro předpomínění používáme šikmý projektor. Numerické experimenty jsou počítány na rozložených úlohách převzatých z [9]. První výsledky počítané TFETI metodou pomocí algoritmu aktivních množin a základní popis zjednodušené verze algoritmu sledování cesty pro TFETI

2 metodu jsou uvedeny v práci [1]. Hlavním cílem tohoto článku je provedení experimentálního vyhodnocení kvality různých variant předpodminění [8]. 2 FORMULACE ÚLOHY Nechť Ω je omezená oblast v R 2 s dostatečně hladkou hranicí Ω rozloženou na tři neprázdné disjunktní části: Ω = γ D γ N γ C. Uvažujme model viskózní nestlačitelné Newtonovské kapaliny modelované Stokesovým systémem s Dirichletovou a Neumannovou okrajovou podmínkou na částech hranice γ D, respektive γ N, a s okrajovou podmínkou nepropustnosti stěny a skluzovou podmínkou Trescova typu na γ C : η u + p = f v Ω, u = v Ω, u = u D na γ D, σ = σ N na γ N, σ t (x) < g(x) u t (x) = x γ C, σ t (x) = g(x) κ(x) : σ t (x) = κ(x)u t (x) x γ C, kde σ = η u/ n pn. Zde u = (u 1, u 2 ) je rychlost proudění, p je tlak, f = (f 1, f 2 ) reprezentují síly působící na kapalinu, η > je dynamická viskozita a u D, σ N jsou zadané Dirichletovy a Neumannovy okrajové podmínky. Pro jednotkový vektor vnější normály n = (n 1, n 2 ) k Ω a jednotkový tečný vektor t = ( n 2, n 1 ) definujeme normálovou a tečnou složka u podél Ω jako u n = u n a u t = u t. Smykové napětí podél Ω je definováno předpisem σ t = σ t a g je daná funkce na γ C představující mez skluzu. Dále rozložme Ω na s nepřekrývajících se podoblastí Ω i tak, že Ω = s i=1 Ω i. Duální algebraická úloha má tento tvar: Najdi λ Λ tak, že q(λ) q(µ) µ Λ, (2) kde q : Λ R, q(µ) = 1 2 µt Fµ µ T d, Λ = {µ = (µ T e, µ T n, µ T t ) T : µ t g, Gµ = e}, F = CM + C T, d = CM + f ū D, G = R T C T, e = R T f, a ( ) ( ) A B T B e u D f u M =, f =, C = N, ū D =. B E c T Některé z uvedených objektů mají blokovou strukturu v důsledku použití TFETI metody, kterou lze využít pro paralelní implementaci. Matice tuhosti pro Laplacův operátor je A = diag(a 1,..., A s ) se symetrickými, pozitivně semidefinitními bloky s defektem dvě, f u = (f T u1,..., f T us) T reprezentují uzlové síly, matice tuhosti pro operátor divergence je B = diag(b 1,..., B s ) s bloky s plnou řádkovou hodností. Matice a vektor vznikající eliminací bubble složek jsou E = diag(e 1,..., E s ) se symetrickými, pozitivně semidefinitními bloky a c = (c T 1,..., c T s ) T. Matice B e zajišťuje spojitost řešení a Dirichletovu okrajovou podmínku. Dirichletova data jsou obsažena ve vektoru u D. i-tý řádek N, T je (1)

3 definován normálovým vektorem n(x i ) a tečným vektorem t(x i ), kde x i je uzel ležící na γ C \ γ D. Případné závislé řádky jsou eliminovány, takže matice C má plnou řádkovou hodnost. Vektor g je určen hodnotami meze skluzu uzlech x i γ C \ γ D (vznikající z numerické integrace g). Bázi nulového prostoru matice M lze sestavit takto: ( ) ( ) 1 R A R Ai =, R A = diag(r A1,..., R As ), R =, 1 kde 1 je vektor samých jedniček. Po výpočtu λ z (2) dopočítáme rychlostní a tlakovou složku řešení pomocí w = M + (f C T λ) + Rα, kde α je vedlejší produkt vzniklý při řešení úlohy (2) a w = (u T 1, p T 1,..., u T s, p T s ) T. Akce zobecněné inverze M + se počítá metodou z [11]. 3 ALGORITMUS SLEDOVÁNÍ CESTY Popis algoritmu začneme formulací úlohy která je ekvivalentní s Karush-Kuhn- Tuckerovými podmínkami optimality k (2) [8]: kde H(v) =, ν, z, (3) Fλ d + G T µ + Gλ e H(v) = ( ) λ t g + z λ t g NZ1 ( ν 1 + ν 2 pro v = (λ T, µ T, ν T, z T ) T, ν = (ν T 1, ν T 2 ) T, N = diag(ν), Z = diag(z) a 1 je vektor samých jedniček. Úloha (3) je řešena pomocí newtonovských iterací, takže přitom potřebujeme regulární Jacobiho ( matici ) J = J(v) k H. Jedná se o matici lineárního soustavy (5), kde J 13 = J T I I 31 =. Jelikož z je vždy kladné, J(v) je regulární pro každé ν. Algoritmus sledování cesty využívá tlumící proceduru, která udržuje Newtonovy iterace blízko centrální cesty směřující k řešení úlohy, což umožňuje vytvářet dlouhé kroky [8]. Výpočetní efektivita závisí také na řešení vnitřních lineárních soustav. 4 PŘEDPODMÍNĚNÍ VNITŘNÍCH LINEÁRNÍCH SOUSTAV Vnitřní lineární soustavy mají tvar: F G T J 13 x r 1 G µ J 31 I ν = r 2 r 3, (5) Z N z r 4 ) (4)

4 kde r 1, r 2 =, r 3, r 4 jsou složky vektoru pravé strany. Při řešení (5) používáme redukci na Schurův doplněk. Ze třetí a čtvrté blokové rovnice v (5) dostaneme z = r 3 J 31 x a ν = Z 1 (r 4 Nr 3 ) + Z 1 NJ 31 x. Redukovaný systém pro neznámé x a µ má tvar ( ) ( ) ( ) F G T G x µ = r 1, (6) kde F = F+D, D = diag(z 1 1 N 1 +Z 1 2 N 2, ) je diagonální s N i = diag(ν i ), Z i = diag(z i ), i = 1, 2, z = (z T 1, z T 2 ) T, a r 1 = r 1 + J 13 Z 1 (Nr 3 r 4 ). Matice F a D jsou symetrické, pozitivně semidefinitní, ale mohou být singulární. Druhá rovnice v (6) dává x Ker G. Zaveďme ortogonální projektor na Ker G definovaný předpisem P = I G T (GG T ) 1 G. Přenásobením první rovnice v (6) P, získáme projektovanou rovnici P F x = P r 1, x Ker G. (7) Z invertovatelnosti P F na Ker G [8] vyplývá, že rovnice (7) má jediné řešení, které počítáme projektovanou metodou sdružených gradientů. Neznámou µ z (6) vypočítáme pomocí µ = (GG T ) 1 G( r 1 F x). Diagonální prvky matice D odpovídající složkám vektoru z, které jsou pro řešení úlohy (3) splněny jako rovnosti, rostou nade všechny meze. Rovnice (7) proto vyžaduje efektivní předpodmínění, které provedeme pomocí předpodmiňovače P D, kde D = D F + D a D F je vhodná symetrická pozitivně definitní matice. Předpodmíněnou variantou (7) je projektovaná rovnice [P D] 1 P F x = [P D] 1 P r 1, x Ker G, (8) kde [P D] 1 označuje inverzi k P D na Ker G. Tuto inverzi můžeme počítat podle [P D] 1 = P D 1 D 1, kde P D 1 = I D 1 G T (G D 1 G T ) 1 G je šikmý projektor na Ker G. Rovnice (8) může být řešena algoritmem PPCGM. Rychlost konvergence je určena spektrem opearátoru [P D] 1 P F na Ker G. Nechť f min, f max je nejmenší, respektive největší vlastní číslo F na Ker G a nechť d min, d max je nejmenší, respektive největší vlastní číslo D F na Ker G. Platí následující tvrzení [8]. Věta 4.1 Vlastní čísla λ operátoru [P D] 1 P F na Ker G splňují: (i) jestliže f min < d max a d min < f max, pak λ [f min d 1 max, f max d 1 min]; (ii) jestliže d max f min, pak λ [1, f max d 1 min]; (iii) jestliže f max d min, pak λ [f min d 1 max, 1]. Jako důsledek dostáváme odhad pro spektrální číslo podmíněnosti κ.

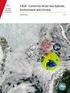
5 Důsledek 4.1 Věta 4.1 implikuje: (i) jestliže f min < d max a d min < f max, pak κ([p D] 1 P F) κ(f)κ(d F ); (ii) jestliže d max f min, pak κ([p D] 1 P F) f max /d min ; (iii) jestliže f max d min, pak κ([p D] 1 P F) d max /f min. Efektivita předpodmínění bude testována experimentálně. 5 NUMERICKÉ EXPERIMENTY Nechť Ω = (, 1) (, 1), γ D = (, 1) {1}, γ Nleft = {} (, 1), γ Nright = {1} (, 1), γ N = γ Nleft γ Nright, a γ C = {(x,.8(x x 2 )) : x (, 1)}. Vstupní data úlohy (1) jsou definována takto: f = ν u exp + p exp, ν = 1, u D =, σ N = σ exp γn a g = 1, kde u exp (x, y) = ( cos(2πx) sin(2πy) + sin(2πy), sin(2πx) cos(2πy) sin(2πx)) a p exp (x, y) = 2π(cos(2πy) cos(2πx)). Poznamenejme, že u exp a p exp neřeší (1). Konečně-prvková síť, rychlostní a tlakové pole jsou znázorněny na obrázku 1. Na γ C předepisujeme různé hodnoty g, abychom ilustrovali třecí efekt, viz obrázek 2. Všechny výpočty jsou počítány s ukončovací přesností tol = 1 5 pro algoritmus sledování cesty. Zdrojové kódy jsou implementovány v Matlabu 213b. Výpočty byly provedeny na superpočítači ANSELM, IT4I VŠB-TU Ostrava. Obr. 1 g = 1: sít (vlevo), rychlostní pole (uprostřed), isobary (vpravo).5.4 g = σ t 1 8 g 4 3 g σ t σ t g 8 1 g 3 4 g Obr. 2 g =.5 (vlevo), g = 1 (uprostřed), g = 4 (vpravo)

6 V tabulkách uvedených níže ukazujeme výpočetní nároky vyjádřené počtem maticových násobení maticí F pro různé počty subdomén (s). Primal značí primární neznámé (3n, kde n je počet konečně-prvkových uzlů přes všechny subdomény) a dual duální neznámé (3n e + 2n d + 2n c, kde n e je počet lepících uzlů, n d je počet uzlů s předepsanou Dirichletovou okrajovou podmínkou a n c je počet trojúhelníků na skluzové části hranice). Symboly h a H označují normu (průměr) konečně-prvkového dělení, respektive průměr subdomén. Příklad 1. Testujeme efektivitu předpodmínění s fixním poměrem H/h = 8. V tabulkách 1 4 používáme D F = I, D F = d I s d = (f max + f + min)/2 (kde f + min je nejmenší kladné vlastní číslo F), D F = abs(diag(f)) a D F = diag(f). Nejlepší výsledky byly dosaženy pro poslední případ. Tab. 1 D F = I s primal/dual g =.5 g = 1 g = 4 4(2 2) 972/ (4 4) 3888/ (6 6) 8748/ (8 8) 15552/ (1 1) 243/ Tab. 2 D F = d I, kde d = (f max + f + min )/2 s primal/dual g =.5 g = 1 g = 4 4(2 2) 972/ (4 4) 3888/ (6 6) 8748/ (8 8) 15552/ (1 1) 243/

7 Tab. 3 D F = abs(diag(f)) s primal/dual g =.5 g = 1 g = 4 4(2 2) 972/ (4 4) 3888/ (6 6) 8748/ (8 8) 15552/ (1 1) 243/ Tab. 4 D F = diag(f) s primal/dual g =.5 g = 1 g = 4 4(2 2) 972/ (4 4) 3888/ (6 6) 8748/ (8 8) 15552/ (1 1) 243/ Příklad 2. V tabulkách 5 8 testujeme efektivitu stejných předpodmiňovačů jako v Příkladě 1 pro pevný počet subdomén s = 16(4 4) a měnící se H/h. Závěr je analogický. Tab. 5 D F = I H/h primal/dual g =.5 g = 1 g = / / / / Tab. 6 D F = d I, kde d = (f max + f + min )/2 H/h primal/dual g =.5 g = 1 g = / / / /

8 Tab. 7 D F = abs(diag(f)) H/h primal/dual g =.5 g = 1 g = / / / / Tab. 8 D F = diag(f) H/h primal/dual g =.5 g = 1 g = / / / / Příklad 3. V tabulce 9 uvádíme informace o diagonálních vstupech D F = diag(f) = (d ii ). Symboly n, n + označují počet záporných, respektive kladných diagonálních prvků. Jejich extrémní hodnoty jsou označeny takto: d min = min{d ii }, d max = max{d ii }, d max = max{d ii : d ii } a d + min = min{d ii : d ii }. Tab. 9 D F = diag(f) s primal/dual n d min d max n + d + min d max 4(2 2) 972/ (4 4) 3888/ (6 6) 8748/ (8 8) 15552/ (1 1) 243/ ZÁVĚR Pro řešení úlohy Stokesova proudění se skluzovou okrajovou podmínkou jsme použili algoritmus sledování cesty. Vnitřní lineární soustavy jsou řešeny metodou projektovaných sdružených gradientů předpodmíněných šikmým projektorem. Experimentálně jsme ukázali, že vytvoření šikmého projektoru pomocí diagonály duálního Hessiánu vede k nejlepším výsledkům. Jedná se o poměrně překvapivé zjištění, protože diagonála obsahuje záporné prvky.

9 PODĚKOVÁNÍ Tato práce byla podpořena Ministerstvem školství mládeže a tělovýchovy z Národního programu udržitelnosti II (NPU II) v rámci projektu IT4Innovations excellence in science - LQ162 a z podpory Velkých infrastruktur pro výzkum, experimentální vývoj a inovace v rámci projektu IT4Innovations národní superpočítačové centrum - LM2157 a projektem GAČR S Grantové agentury České republiky. LITERATURA 1. C. L. M. H. Navier. Mémoire sur les lois du movement des fluides, Mém. de l Acad. R. Sci. Paris, 1823, 6: I. J. Rao, K. Rajagopal. The effect of the slip boundary condition on the flow of fluids in a channel, Acta Mechanica, Vol. 135(3), 1999, p M. Ayadi, L. Baffico, M. K. Gdoura, T. Sassi. Error estimates for Stokes problem with Tresca friction conditions, ESAIM: Math. Model. Numer. Anal., Vol. 48(5), 214, p D. Arnold, F. Brezzi, M. Fortin. A stable finite element for the stokes equations, Calcolo, 21(4), 1984, p J. Koko. Vectorized Matlab codes for the Stokes problem with P1-bubble/P1 finite element, 212, jkoko/codes/stokesp1bubblep1.pdf [online]. 6. Z. Dostál, D. Horák, R. Kučera. Total FETI - an easier implementable variant of the FETI method for numerical solution of elliptic PDE, Commun. Numer. Methods Eng., Vol. 22(12), 26, p R. Kučera, J. Machalová, H. Netuka, P. Ženčák. An interior point algorithm for the minimization arising from 3D contact problems with friction, Optim. Methods Softw., 6(28), 213, p R. Kučera, V. Šátek, M. Jarošová. Path-following interior point method for QPP with box and equality constraints: theory and applications, in preparation R. Kučera, J. Haslinger, V. Šátek, M. Jarošová. Efficient methods for solving the Stokes problem with slip boundary conditions, Math. Comput. Simul., 1. M. Jarošová, R. Kučera, V. Šátek. A new variant of the path-following algorithm for the parallel solving of the Stokes problem with friction, in P. Iványi, B. H. V. Topping (Editors), Proceedings of the Fourth International Conference on Parallel, Distributed, Grid and Cloud Computing for Engineering. Civil-Comp Press, Paper 11, Stirlingshire, UK, R. Kučera, T. Kozubek, A. Markopoulos. On large-scale generalized inverses in solving two-by-two block linear systems, Linear Algebra Appl., 438(7), 213, p

10 PŘEDPODMÍNĚNÍ ALGORITMU SLEDOVÁNÍ CESTY PRO STOKESOVO PROUDĚNÍ SE SKLUZOVOU PODMÍNKOU Abstrakt: Stokesova úloha se skluzovou podmínkou je řešena smíšenou metodou konečných prvků kombinovanou s TFETI metodou. Výpočet řešení se provádí metodou vnitřních bodů určenou k minimalizaci s oboustraným omezením a rovnostní vazbou. Předpodmíněná projektovaná metoda sdružených gradientů se používá pro řešení vnitřních lineárních soustav. Účinost předpodmiňovačů se testuje experimentálně. Cílem výzkumu je vyvinout efektivní řešiče pro modelování proudění po hydrofobních stěnách, což nachází uplatnění v inženýrských oblastech zahrnujících modelování v biomedicíně nebo při přenosu tekutin. Klíčová slova: Stokesova úloha; skluzová podmínka; metoda vnitřních bodů; TFETI metoda. PRECONDITIONING IN THE PATH-FOLLOWING ALGORITHM FOR THE STOKES FLOW WITH STICK-SLIP CONDITIONS Abstract: The Stokes problem with the stick-slip boundary condition is solved by the mixed finite element method combined with the TFETI method. An interior point method for the minimization subject to box and equality constraints is used. The preconditioned projected conjugate gradient method solves the inner linear systems. The preconditioners are tested experimentally. The aim of our research is to develop efficient solvers for modelling of a flow over hydrophobic walls that exhibits applications in areas including biomedical modelling or transport of fluid. Keywords: Stokes problem; stick-slip condition; interior point method; TFETI method. Datum odeslání článku do redakce: Datum přijetí článku redakcí: Ing. Marta JAROŠOVÁ, Ph.D. VŠB Technická univerzita Ostrava, IT4Innovations 17. listopadu 15/2172, 78 33, Ostrava, Česká republika tel.: , marta.jarosova@vsb.cz doc. RNDr. Radek KUČERA, Ph.D. VŠB Technická univerzita Ostrava Katedra matematiky a deskriptivní geometrie 17. listopadu 15/2172, 78 33, Ostrava, Česká republika tel.: , radek.kucera@vsb.cz

11 Ing. Václav ŠÁTEK, Ph.D. VŠB Technická univerzita Ostrava, IT4Innovations 17. listopadu 15/2172, 78 33, Ostrava, Česká republika tel.: ,