OLYMPIÁDA V INFORMATIKE NA STREDNÝCH ŠKOLÁCH
|
|
|
- Kryštof Kraus
- před 7 lety
- Počet zobrazení:
Transkript
1 OLYMPIÁDA V INFORMATIKE NA STREDNÝCH ŠKOLÁCH Priebeh celoštátneho kola tridsiaty tretí ročník školský rok 2017/2018 Celoštátne kolo 33. ročníka Olympiády v informatike, kategórie A, sa koná v dňoch marca Na riešenie úloh prvého, teoretického dňa majú súťažiaci 4,5 hodiny čistého času. Rôzne úlohy riešia súťažiaci na samostatné listy papiera. Akékoľvek pomôcky okrem písacích potrieb (napr. knihy, výpisy programov, kalkulačky) sú zakázané. Čo má obsahovať riešenie úlohy? Slovne popíšte algoritmus. Slovný popis riešenia musí byť jasný a zrozumiteľný i bez nahliadnutia do samotného algoritmu/programu. Zdôvodnite správnosť vášho algoritmu. Uveďte a zdôvodnite jeho časovú a pamäťovú zložitosť. Podrobne uveďte dôležité časti algoritmu, ideálne vo forme programu v Pascale alebo C/C++. V prípade, že používate vo svojom programovacom jazyku knižnice, ktoré obsahujú implementované dátové štruktúry a algoritmy (napr. STL pre C++), v popise algoritmu stručne vysvetlite, ako by ste napísali program s rovnakou časovou zložitosťou bez použitia knižnice. Hodnotenie riešení prvého (teoretického) dňa Za každú úlohu môžete získať od 0 do 10 bodov. Pokiaľ nie je v zadaní povedané ináč, najdôležitejšie dve kritériá hodnotenia sú v prvom rade správnosť a v druhom rade efektívnosť navrhnutého algoritmu. Na výslednom počte bodov sa môže prejaviť aj kvalita popisu riešenia a zdôvodnenie tvrdení o jeho správnosti a efektívnosti. Efektívnosť algoritmu posudzujeme vypočítaním jeho časovej zložitosti funkcie, ktorá hovorí, ako dlho vykonanie algoritmu trvá v závislosti od veľkosti ných parametrov. Nezávisí pri tom na konštantných faktoroch, len na rádovej rýchlosti rastu tejto funkcie. V zadaní úlohy môžu byť uvedené limity na veľkosť premenných. Tieto môžete použiť na odhad toho, ako dobré vaše riešenie je. Na počítači, ktorý vykoná miliardu inštrukcií za sekundu, vyrieši vzorové riešenie ľubovoľný povolený nanajvýš za niekoľko sekúnd.
2 A-III-1 Kapitánka hľadá posádku Bolo raz jedno dievčatko plné snov. Až jedného dňa vyrástlo, rozhodlo sa, že si jeden aj splní a že sa stane pirátskou kapitánkou. Keď si už zohnala klobúk, pásku cez oko a loď, chýbalo jej už len jediné: spoľahlivá posádka. A tak najprv zakotvila v prístave Port Royal, kde chce nejakú posádku naverbovať. Keď sa rozkríklo, že sa verbuje nová posádka, zišiel sa na móle rad mladých nádejných pirátov, ktorí sa všetci chceli prihlásiť do kapitánkinej posádky. Kapitánka si ich očíslovala od 1 po n v poradí, v ktorom stoja v rade, a o každom z nich si poznačila číslo p i hovoriace, aký je to dobrý pirát (čím väčšia hodnota, tým lepší). Kapitánka vie, že pri výbere posádky sú dôležité dve veci: musia to byť dostatočne dobrí piráti a musia zároveň byť dobrá partia. Naverbovať dobrú partiu je ľahké: piráti, ktorí spolu dobre vychádzajú, určite stoja v rade vedľa seba, takže stačí, keď ako posádku zoberie nejaký neprázdny súvislý úsek uchádzačov. Dobrá partia vám ale námornú bitku nevyhrá a naverbovať dostatočne schopnú posádku vôbec nie je jednoduché. Dôležitá je pri tom tzv. Denisova hranica. Denis je známym archetypom len-tak-tak použiteľného piráta. Nič mu nejde nejak hviezdne, ale všetky podstatné pirátske úlohy nakoniec nejak zvládne. Pri vyhodnotení toho, či je posádka schopná plavby, je dôležitý koncept tzv. stredného piráta: ak by sa všetci piráti usporiadali podľa ich schopností, je to ten, ktorý by stál uprostred. Ak je pirátov párny počet, stredným pirátom je lepší z tých dvoch ktorí sú uprostred poradia. Posádka je plavbyschopná práve vtedy, keď je stredný pirát v nej aspoň takým dobrým pirátom ako je Denis. Súťažná úloha V rade stojí n pirátov, očíslovaných od 1 po n v poradí, v ktorom stoja. Poznáme čísla p 1,..., p n ktoré o každom z nich hovoria, aký je dobrý pirát. Tiež poznáme číslo d hovoriace to isté o Denisovi. (Samotný Denis nepatrí medzi uchádzačov a nedá sa ho naverbovať do posádky.) Kapitánka si chce vybrať neprázdny súvislý úsek uchádzačov, a to tak, aby dostala plavbyschopnú posádku. Inými slovami, stredný pirát vo vybranom úseku musí byť aspoň tak dobrým pirátom ako Denis. Zistite, koľkými spôsobmi si môže Kapitánka vybrať svoju posádku. Formát u a u V prvom riadku u sú celé čísla n a d. V druhom riadku sú celé čísla p 1,..., p n. Na vypíšte počet spôsobov ako vybrať plavbyschopnú posádku ktorá bude dobrou partiou. Obmedzenia a hodnotenie Môžete predpokladať, že d aj všetky p i sa zmestia do bežných celočíselných premenných. Za riešenie, ktoré efektívne vyrieši ľubovoľný s n 500, môžete získať nanajvýš 3 body. Za riešenie, ktoré efektívne vyrieši ľubovoľný s n 5000, môžete získať nanajvýš 5 bodov. Za riešenie, ktoré efektívne vyrieši ľubovoľný s n , môžete získať 8 až 10 bodov podľa jeho presnej asymptotickej časovej zložitosti. Príklad Kapitánka má nasledovné možnosti: zobrať ako posádku len piráta 2, len piráta 4, hociktorých dvoch po sebe idúcich pirátov, pirátov 2+3+4, alebo všetkých štyroch pirátov. Všimnite si, že ak by zobrala pirátov 2+3+4, stredným pirátom v posádke by nebol pirát 3 (ktorý teraz stojí v strede vybraného úseku) ale bol by ním pirát 4. Pirát 4 je taktiež stredným pirátom v prípade, že Kapitánka ako posádku zoberie všetkých štyroch uchádzačov. strana 2 z 7 úloha A-III-1
3 A-III-2 Závažia Jarka našla na povale sadu n exotických závaží. Jednotlivé závažia mali hmotnosti m 1,..., m n. Potešila sa, že si pomocou nich bude môcť vážiť všetko, čo len bude potrebovať. Samozrejme, namiesto jedného závažia vie Jarka použiť aj ľubovoľnú ich podmnožinu a odvážiť tak aj iné hmotnosti. Súťažná úloha Dokopy existuje 2 n podmnožín závaží. Predstavme si, že sme ich všetky zoradili podľa celkovej hmotnosti a očíslovali, začínajúc od jednotky. Ak má viacero podmnožín tú istú hmotnosť, môžeme ich zoradiť ľubovoľne. Pre dané n, jednotlivé hmotnosti závaží a dané relatívne malé číslo k nájdite hmotnosť množiny s číslom k. Formát u a u V prvom riadku u sú kladné celé čísla n a k. V druhom riadku u sú kladné celé čísla m 1,..., m n. Na vypíšte hmotnosť podmnožiny, ktorá vo vyššie definovanom číslovaní dostane číslo k. Obmedzenia a hodnotenie O číslach m i predpokladajte, že sú kladné a ich súčet sa zmestí do bežnej celočíselnej premennej. Tiež môžete predpokladať, že hmotnosti sú usporiadané, teda že platí m 1 m 2 m n. Za riešenie ktoré efektívne vyrieši ľubovoľný s n 20 môžete získať 2 body. Za riešenie ktoré efektívne vyrieši ľubovoľný s n 500 a k 500 môžete získať 5 bodov. Za riešenie ktoré efektívne vyrieši ľubovoľný s n 5000 a k 5000 môžete získať 7 bodov. Za riešenie ktoré efektívne vyrieši ľubovoľný s n a k môžete získať 10 bodov. Príklady Ak si závažia označíme A, B a C, tak máme osem množín závaží: 2, {A}, {B}, {C}, {A, B}, {A, C}, {B, C}, {A, B, C} Ich hmotnosti sú 0, 1, 1, 2, 2, 3, 3, 4, čiže vyššie uvedené poradie je už usporiadané podľa hmotnosti. Poradové číslo k = 5 teda zodpovedá hmotnosti Všimnite si, že dvojprvková množina obsahujúca prvé a druhé závažie je tentokrát ľahšia ako niektoré jednoprvkové množiny strana 3 z 7 úloha A-III-2
4 A-III-3 Stavebnica funkcií Za zadaním súťažnej úlohy nájdete študijný text k nej. Študijný text je identický s textom z krajského kola. Jednotlivé podúlohy súťažnej úlohy môžete riešiť v ľubovoľnom poradí. Každá podúloha je hodnotená zvlášť. Pri riešení konkrétnej podúlohy môžete využívať: Všetky funkcie definované alebo zostrojené v študijnom texte. Konštantné funkcie kb a (kde ka b je funkcia s a mi ktorá vždy vráti hodnotu b). Funkcie z domáceho kola: mul (násobenie), p (predchodca) a sub (odčítanie, ktoré nepodtečie pod nulu). Funkcie z krajského kola: pow (umocnenie), sgn (signum) a geq (predikát väčší alebo rovný ). Funkciu not (logická negácia) zo vzorových riešení krajského kola. Konštrukciu už zostrojených funkcií zbytočne nerozpisujte. Upozorňujeme ale, že konštrukcie využívajúce myšlienku z poslednej podúlohy krajského kola (vetvenie, if ) je potrebné rozpísať. Podúloha A (2 body). Zostrojte binárne funkcie min a max počítajúce minimum a maximum. Podúloha B (2 body). Zostrojte unárnu funkciu last, ktorá vráti poslednú cifru čísla na e. (Formálne, má byť n : last(n) = n mod 10.) Podúloha C (3 body). Zostrojte unárnu funkciu sqrt, ktorá vypočíta dolnú celú časť odmocniny. Dolná celá časť je najväčšie celé číslo neprevyšujúce presný výsledok. Napr. sqrt(99) = 9 a sqrt(100) = 10. Podúloha D (3 body). Fibonacciho čísla sú definované rekurzívne: F 0 = 0, F 1 = 1 a n 2 : F n = F n 1 + F n 2. Zostrojte unárnu funkciu fib, ktorá pre n vráti na e hodnotu F n. Aby sme vám ušetrili prácu, v podúlohe D nemusíte formálne rozpisovať použitia Kompozítora. Presnejšie, vždy, keď chcete nejakú novú funkciu vyrobiť Kompozítorom zo skôr vyrobených funkcií, stačí novú funkciu korektne matematicky definovať. (A samozrejme, naozaj sa danú funkciu musí dať vyrobiť zložením iných funkcií, ktoré už máte vyrobené, nemôžete si len tak vyčarovať úplne nové funkcie.) V riešení tejto podúlohy teda smiete napr. napísať: Z funkcie pow si ľahko vyrobíme funkciu f takú, že n : f(n) = (n + 4) 7. Študijný text: stavebnica funkcií Miška dostala na narodeniny zvláštny darček: stavebnicu funkcií. Keď darček rozbalila, našla v ňom hneď niekoľko rôznych vecí. Ako prvé jej oko padlo na tri sáčky s hotovými funkciami. Každá funkcia je malá škatuľka, ktorá má niekoľko ov a práve jeden. V prvom sáčku bola jediná funkcia. Volala sa z (z anglického zero, čiže nula), nemala žiadne y a na e vracala číslo 0. Aj v druhom sáčku bola len jedna funkcia. Táto sa volala s (z anglického successor, čiže nasledovník). Mala jeden a jeden. Keď na dostala číslo n, vrátila nám na e číslo n + 1. Tretí sáčok bol o čosi plnší bolo v ňom nekonečne veľa funkcií. Pre každé k a n (také, že 1 k n) tam bola funkcia vk n ( vyber k-ty z n ov ), ktorá mala n ov a na vždy vrátila hodnotu, ktorú dostala na k-tom e. strana 4 z 7
5 Na obrázku sú znázornené funkcie z, s a v 4 3. z 0 n s n + 1 v 4 3 Zvyšok balíčka tvorili dva prístroje, ktoré zjavne slúžia na výrobu nových funkcií. Na jednom z nich sa skvel nápis Kompozítor, na druhom zase Cyklovač. Každý z nich funguje tak, že do vnútra v správnom poradí vložíme nejaké funkcie, zatočíme kľukou a vypadne nám nová funkcia. Tá je vhodne poskladaná z funkcií, ktoré sme vložili dovnútra. Ale skôr ako si podrobnejšie popíšeme fungovanie Kompozítora a Cyklovača, potrebujeme si o naších funkciách povedať čosi formálnejšie. V tejto úlohe považujeme nulu za prirodzené číslo. Prirodzené čísla sú teda pre nás množina N = {0, 1, 2, 3,... }. Všetky funkcie, ktoré si budeme vyrábať, budú totálne funkcie na prirodzených číslach. Ako y budeme teda funkcii dávať prirodzené čísla a pre každý možný nám funkcia vráti na jedno prirodzené číslo. Počet ov funkcie sa nazýva arita. Napr. funkcie s jedným om odborne voláme unárne, funkcie s dvoma mi binárne, atď. Funkcia v 7 2 má aritu 7. Funkcia z má aritu 0. Aritu občas budeme explicitne písať ako horný index. Mohli by sme teda napr. hovoriť, že v prvom sáčku bola funkcia z 0 a v druhom zas funkcia s 1. (U vyberacích funkcií v n k aritu musíme uvádzať vždy, keďže napr. v4 1 a v 7 1 sú dve rôzne funkcie.) Akonáhle už nejakú funkciu vyrobíme, máme navždy k dispozícii ľubovoľne veľa jej kópií. Špeciálne platí, že ak funkciu použijeme pri výrobe inej, zložitejšej, nestratíme ju tým. Kompozítor Kompozítor vie funkcie skladať (v bežnom matematickom zmysle tohto slova). Je však trochu háklivý na správne arity. Použitie Kompozítora sa skladá z nasledujúcich krokov: 1. Vyberieme si aritu a 0 funkcie, ktorú chceme vyrobiť. 2. Zvolíme si funkciu g b (čiže funkciu g s nejakou aritou b, možno inou ako a), ktorú použijeme v druhom kroku výpočtu. Hodnota b musí byť kladná. (Inými slovami, funkcia g musí mať aspoň jeden.) 3. Zvolíme si b funkcií f1 a,..., fb a, ktoré použijeme v prvom kroku výpočtu. 4. Zatočíme kľukou na boku Kompozítora. Na e nám vypadne nová funkcia h definovaná nasledujúcim pseudokódom: def h ( x_1,..., x_a ): tmp_1 = f_1 ( x_1,..., x_a ) tmp_2 = f_2 ( x_1,..., x_a )... tmp_b = f_b ( x_1,..., x_a ) return g ( tmp_1,..., tmp_b ) Slovne: Funkcia h zoberie a ov, ktoré dostala. Pomocou funkcií f 1 až f b z nich vypočíta b pomocných hodnôt. No a na záver pomocou funkcie g vypočíta z pomocných hodnôt celej funkcie h. Na obrázku je graficky znázornená funkcia vyrobená Kompozítorom pre a = 3 a b = 2. h K[f 1, f 2, g] f 1 g f 2 strana 5 z 7
6 Cyklovač Cyklovač vie vyrábať for-cykly. Aj on je však trochu háklivý na správne arity funkcií a poradie ich parametrov. Dajte si na ne pozor, keď ho budete kŕmiť. Správne použitie Cyklovača vyzerá nasledovne: 1. Vyberieme si aritu a 1 funkcie, ktorú chceme vytvoriť. Prvý parameter tejto funkcie (označíme ho x) bude špeciálna premenná, ktorá hovorí, koľkokrát sa má for-cyklus vykonať. Ostatné parametre (označíme ich y 1,..., y a 1 ) budú ostávať nezmenené. 2. Zvolíme si funkciu f a 1, ktorou výpočet cyklu začne. 3. Zvolíme si funkciu g a+1, ktorá počíta, čo sa stane počas jednej iterácie cyklu. Funkcia g má až a + 1 ov: všetky premenné, ktoré bude mať aj výsledná funkcia a navyše hodnotu ktorá bola om predchádzajúcej iterácie cyklu. (Ak to nedávalo zmysel, pozri pseudokód uvedený v ďalšom kroku.) 4. Zatočíme kľukou na boku Cyklovača. Na e nám vypadne nová funkcia h definovaná nasledujúcim pseudokódom: Notácia def h ( x, y_1,..., y_{a-1} ): tmp = f ( y_1,..., y_{a-1} ) for i = 0 to x-1: tmp = g ( i, y_1,..., y_{a-1}, tmp ) return tmp Slovne: Výpočet začne tým, že funkciou f vypočítame (z ostatných parametrov) pre x = 0. Z neho potom funkciou g vypočítame pre x = 1, z toho znova funkciou g pre x = 2, a tak ďalej až po požadovanú hodnotu prvého parametra. Rovnosť dvoch funkcií budeme značiť. Zápis f g teda znamená, že funkcie f a g majú rovnakú aritu a na každom e dávajú ten istý. Funkciu ktorá vznikne Kompozítorom z funkcií f 1,..., f b a g budeme značiť K[f 1,..., f b, g]. Funkciu ktorá vznikne Cyklovačom z funkcií f a g budeme značiť C[f, g]. Príklady Uf, to vyzerá komplikovane. Poďme sa preto spolu pozrieť na to, ako si Miška začala vyrábať nejaké nové funkcie. Príklad 1. Čím by sme tak začali? Peknou jednoduchou funkciou je napríklad identita: unárna funkcia i taká, že pre každé n je i(n) = n. Vidíte, ako ju vyrobiť? Toto bola triková otázka. Identitu vyrábať nepotrebujeme, dostali sme ju totiž v treťom sáčku. Identitou je totiž funkcia v 1 1. Môžeme teda písať i v 1 1. Príklad 2. Vyrobme si funkciu j 0 : konštantnú funkciu, ktorá nemá žiadny a na e vracia hodnotu 1. Túto funkciu si vieme vyrobiť Kompozítorom. V prvom kroku použijeme funkciu z, ktorá nemá žiaden a na e vráti 0. Túto 0 potom pošleme ďalej do funkcie s, ktorá ju zväčší na 1. Dostávame teda, že j 0 K[z, s]. Príklad 3. Unárnu funkcia plus3, ktorá svoj jediný zväčší o 3, vieme vyrobiť napríklad ako K[K[s, s], s]. Teda najskôr si vyrobíme funkciu K[s, s], ktorá svoj zväčší o 2, a túto potom opäť vložíme do Kompozítora s ďalšou funkciou s. Príklad 4. Teraz si ukážeme, ako si Miška vie vyrobiť sčítanie teda binárnu funkciu add takú, že x, y : add(x, y) = x + y. Základným pozorovaním je, že sčítanie je vlastne opakované použitie funkcie +1, teda nasledovníka. Výpočet x + y si teda môžeme sformulovať nasledovne: začni s hodnotou y a potom na ňu x-krát použi funkciu s. No a keďže toto vyzerá ako cyklus, na výrobu sčítania budeme chcieť použiť Cyklovač. strana 6 z 7
7 Pozrime sa teda na pseudokód funkcie, ktorú vyrobí Cyklovač (s tým, že si ho už upravíme konkrétne na funkciu s dvoma mi). def add(x,y): tmp = f(y) for i = 0 to x-1: tmp = g(i,y,tmp) return tmp Aké funkcie f a g potrebujeme vhodiť do Cyklovača ak chceme dostať program pre sčítanie? Funkcia f má jednoducho vrátiť hodnotu y, ktorú dostala na e čiže f má byť identita. Funkcia g má v každej iterácii cyklu zobrať starú hodnotu (uloženú v premennej tmp) a inkrementovať ju použitím funkcie s. Potrebujeme teda funkciu s tromi mi, ktorá prvé dva odignoruje, na tretí použije s a vráti výsledok. Takúto funkciu síce ešte nemáme, ale vieme si ju ľahko vyrobiť Kompozítorom: je to funkcia K[v 3 3, s]. Dokopy teda dostávame, že add C[ v 1 1, K[v 3 3, s] ]. Príklad 5. Ďalšou jednoduchou funkciou je unárna konštantná nula, teda funkcia zz 1, ktorá má jeden a na e vždy vracia nulu. (Formálne: n : zz 1 (n) = 0.) Skôr, než si ukážeme, ako zz 1 vyrobiť, podotknime, že zz 1 a z 0 (čo je funkcia z, ktorú sme dostali v prvom sáčku) sú dve rôzne funkcie. Zdalo by sa, že zz 1 musí ísť nejak vyrobiť zo z 0 pomocou Kompozítora. Lenže ako? Ak by sme chceli z 0 použiť v prvom kroku, tak bez ohľadu na to, akú funkciu použijeme v druhom kroku, určite vyrobíme funkciu s aritou 0. No a v druhom kroku z 0 použiť nesmieme, lebo funkcia použitá v druhom kroku musí mať kladnú aritu. Cez Kompozítor teda cesta nevedie. Ukážeme si však, že zz 1 vieme vyrobiť pomocou Cyklovača. Opäť začnime tým, že sa pozrieme, ako to vyzerá, keď chceme pomocou Cyklovača vyrobiť unárnu funkciu. My dodáme funkcie f 0 a g 2 a Cyklovač nám z nich vyrobí funkciu h 1 definovanú nasledovne: def h(x): tmp = f() for i = 0 to x-1: tmp = g(i,tmp) return tmp Ako máme zvoliť funkcie f a g, ak chceme, aby h na každom e vracala nulu? Zjavne musíme zvoliť f z 0, aby bolo h(0) = 0. No a jedna možnosť ako teraz zvoliť funkciu g je jednoducho zobrať g v 2 2. Tým sa z príkazu tmp = g(i,tmp) stane príkaz tmp = tmp, a teda v premennej tmp ostane stále nula, bez ohľadu na hodnotu x. Touto pomerne obskurnou konštrukciou sme si teda ukázali, že funkciu zz 1 vieme zostrojiť ako C[z, v 2 2]. Predikáty. Predikát je odborné meno pre funkciu, ktorej návratová hodnota je logická hodnota: pravda alebo nepravda. Naše funkcie takéto hodnoty síce vracať nevedia, pomôžeme si ale rovnako ako voľakedy napríklad autori programovacieho jazyka C: prehlásime 0 za nepravdu a 1 za pravdu. Funkciu teda budeme volať predikát vtedy, ak: táto funkcia na každom možnom e vráti jednu z hodnôt 0 a 1 chceme zdôrazniť, že na tieto hodnoty sa má zmysel dívať ako na logické hodnoty namiesto číselných Príklady: Funkcia eq(x, y), ktorá vráti 1 ak sa jej y rovnajú a 0 inak, je predikát. Predikátom je aj funkcia isprime(x) ktorá vráti hodnotu 1 ak x je prvočíslo a 0 inak. Na unárnu konštantnú funkciu zz 1 sa môžeme dívať ako na predikát, ktorý vždy vracia hodnotu nepravda. TRIDSIATY TRETÍ ROČNÍK OLYMPIÁDY V INFORMATIKE Príprava úloh: Michal Anderle, Eduard Batmendijn, Michal Forišek, Samuel Gurský, Samuel Sládek, Emanuel Tesař Recenzia: Michal Forišek Slovenská komisia Olympiády v informatike Vydal: IUVENTA Slovenský inštitút mládeže, Bratislava 2018 strana 7 z 7
67. ročník Matematické olympiády 2017/2018
 67. ročník Matematické olympiády 2017/2018 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
67. ročník Matematické olympiády 2017/2018 Úlohy ústředního kola kategorie P 1. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži
67. ročník Matematické olympiády 2017/2018
 67. ročník Matematické olympiády 2017/2018 Úlohy domácího kola kategorie P Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení
67. ročník Matematické olympiády 2017/2018 Úlohy domácího kola kategorie P Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení
67. ročník Matematické olympiády 2017/2018
 67. ročník Matematické olympiády 2017/2018 Úlohy krajského kola kategorie P Krajské kolo 67. ročníku MO kategorie P se koná v úterý 23. 1. 2018 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého
67. ročník Matematické olympiády 2017/2018 Úlohy krajského kola kategorie P Krajské kolo 67. ročníku MO kategorie P se koná v úterý 23. 1. 2018 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Ružové obrázkové slová skladanie slov z písmen
 Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Modré obrázkové slová skladanie slov z písmen
 Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Matematika test. Cesta trvala hodín a minút.
 GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM
 MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
Názov: Osmóza. Vek žiakov: Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút.
 Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Pracovné prostredie MS EXCEL 2003.
 Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Objektovo orientované programovanie v C# ERIK KUČERA METÓDY VÝPOČTOVEJ INTELIGENCIE PREDNÁŠKA 3
 Objektovo orientované programovanie v C# ERIK KUČERA METÓDY VÝPOČTOVEJ INTELIGENCIE PREDNÁŠKA 3 Statické členy Statické členy nie sú takým pilierom OOP ako dedičnosť alebo polymorfizmus, ale sú užitočným
Objektovo orientované programovanie v C# ERIK KUČERA METÓDY VÝPOČTOVEJ INTELIGENCIE PREDNÁŠKA 3 Statické členy Statické členy nie sú takým pilierom OOP ako dedičnosť alebo polymorfizmus, ale sú užitočným
KOMISNÝ PREDAJ. Obr. 1
 KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
ALGORITMY A PROGRAMOVANIE VO VÝVOJOVOM PROSTREDÍ LAZARUS. Vývojové prostredie Lazarus, prvý program
 ALGORITMY A PROGRAMOVANIE VO VÝVOJOVOM PROSTREDÍ LAZARUS Vývojové prostredie Lazarus, prvý program Lazarus si môžete stiahnuť z http://lazarus.freepascal.org 1 Začíname sa učiť programovací jazyk Pascal
ALGORITMY A PROGRAMOVANIE VO VÝVOJOVOM PROSTREDÍ LAZARUS Vývojové prostredie Lazarus, prvý program Lazarus si môžete stiahnuť z http://lazarus.freepascal.org 1 Začíname sa učiť programovací jazyk Pascal
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Ak stlačíme OK, prebehne výpočet a v bunke B1 je výsledok.
 Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Skákalka. Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto.
 Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
TomTom Referenčná príručka
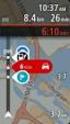 TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Bezdrôtová sieť s názvom EDU po novom
 Bezdrôtová sieť s názvom EDU po novom V priebehu augusta 2011 bolo staré riešenie WiFi (pripojenie k školskej bezdrôtovej sieti cez certifikáty) v plnej miere nahradené novým riešením. Staré riešenie už
Bezdrôtová sieť s názvom EDU po novom V priebehu augusta 2011 bolo staré riešenie WiFi (pripojenie k školskej bezdrôtovej sieti cez certifikáty) v plnej miere nahradené novým riešením. Staré riešenie už
1. Gigabajty si hneď v prvom kroku premeníme na gigabity a postupne premieňame na bity.
 1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
Informačný list 1. Čo je energia? Všetci potrebujeme energiu! Energia doma
 Informačný list 1 Čo je energia? Ľudia potrebujú energiu, aby sa mohli hrať a hýbať. Energiu získajú z jedla. Potrebuješ energiu, aby si mohol rásť. Dokonca aj keď spíš, potrebuješ energiu. Aj zvieratá
Informačný list 1 Čo je energia? Ľudia potrebujú energiu, aby sa mohli hrať a hýbať. Energiu získajú z jedla. Potrebuješ energiu, aby si mohol rásť. Dokonca aj keď spíš, potrebuješ energiu. Aj zvieratá
15. Príkazy vetvenia
 Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešené úlohy Testovania 9/ 2011
 Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Matematika test. 1. Doplň do štvorčeka číslo tak, aby platila rovnosť: (a) 9 + = (b) : 12 = 720. (c) = 151. (d) : 11 = 75 :
 GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
Programovanie I. Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM
 Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Programovanie I 9.10.2007 Úvod do programovania Mgr. Stanislav Horal, Katedra informatiky, FPV, UCM Algoritmus (1) Existuje niekoľko definícií pojmu algoritmus Algoritmus je presná postupnosť krokov a
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Návod na použitie zápisníka jedál
 Návod na použitie zápisníka jedál Sme nesmierne radi, že si sa rozhodla používať tento zápisník jedál. Práve zapisovaním svojho jedálnička ľudia chudnú oveľa rýchlejšie, majú prehľad nad tým, čo zjedia
Návod na použitie zápisníka jedál Sme nesmierne radi, že si sa rozhodla používať tento zápisník jedál. Práve zapisovaním svojho jedálnička ľudia chudnú oveľa rýchlejšie, majú prehľad nad tým, čo zjedia
Obrázok Časový plán projektu, určite kritickú cestu. Obrázok Časový plán projektu, určite kritickú cestu
 Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Začínam so zadaním z NEPOUŽÍVAME ROZSAH POKIAĽ HO MUSÍME PRESKOČIŤ
 Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Príručka pre prostredie Digitálnej autoškoly pre inštruktorov časť elearning
 TVORÍME VEDOMOSTNÚ SPOLOČNOSŤ Riadiaci orgán OPIS Sprostredkovateľský orgán OPIS EURÓPSKA ÚNIA Príručka pre prostredie Digitálnej autoškoly pre inštruktorov časť elearning JISCD-ESD Príručka pre prostredie
TVORÍME VEDOMOSTNÚ SPOLOČNOSŤ Riadiaci orgán OPIS Sprostredkovateľský orgán OPIS EURÓPSKA ÚNIA Príručka pre prostredie Digitálnej autoškoly pre inštruktorov časť elearning JISCD-ESD Príručka pre prostredie
REBRÍČKY. Predaj CD za mesiac 4U2Rock. Počet CD predaných za mesiac. K-Band D. A. R. Metalfolk. Mesiac
 Ukážky uvoľnených úloh z matematickej gramotnosti PISA 2012 REBRÍČKY V januári vyšli nové CD skupín 4U2Rock a K-Band. Vo februári nasledovali CD skupín D.A.R. a Metalfolk. V uvedenom grafe je znázornený
Ukážky uvoľnených úloh z matematickej gramotnosti PISA 2012 REBRÍČKY V januári vyšli nové CD skupín 4U2Rock a K-Band. Vo februári nasledovali CD skupín D.A.R. a Metalfolk. V uvedenom grafe je znázornený
MANUÁL K PROGRAMU MATEMATIKA 2.0 STIAHNUTIE A INŠTALÁCIA PROGRAMU:
 MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Testovanie 5. v školskom roku 2015/2016. Testovanie sa uskutoční 25. novembra 2015 (streda). Žiaci budú testy písať v nasledovnom poradí:
 Testovanie 5 Testovanie žiakov 5. ročníka základných škôl sa uskutoční 25. novembra 2015 (streda) na všetkých základných školách SR z predmetov slovenský jazyk a literatúra, maďarský jazyk a literatúra
Testovanie 5 Testovanie žiakov 5. ročníka základných škôl sa uskutoční 25. novembra 2015 (streda) na všetkých základných školách SR z predmetov slovenský jazyk a literatúra, maďarský jazyk a literatúra
Strojový kód, assembler, emulátor počítača
 Strojový kód, assembler, emulátor počítača Návrh architektúry hypotetického procesora Strojový kód Assemblerový jazyk Programovanie v assemblerovom jazyku: Lineárny program Vetvenie Cyklus Emulátor počítača
Strojový kód, assembler, emulátor počítača Návrh architektúry hypotetického procesora Strojový kód Assemblerový jazyk Programovanie v assemblerovom jazyku: Lineárny program Vetvenie Cyklus Emulátor počítača
AIS2 Hodnotenie študentov po skúške POMÔCKA PRE VYUČUJÚCICH
 AIS2 Hodnotenie študentov po skúške POMÔCKA PRE VYUČUJÚCICH PRIHLÁSENIE SA DO SYSTÉMU Spustite si internetový prehliadač a do riadku pre adresu web-stránky napíšte http://moja.uniba.sk. Kliknite na hypertextový
AIS2 Hodnotenie študentov po skúške POMÔCKA PRE VYUČUJÚCICH PRIHLÁSENIE SA DO SYSTÉMU Spustite si internetový prehliadač a do riadku pre adresu web-stránky napíšte http://moja.uniba.sk. Kliknite na hypertextový
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
KOMBINATORICKÉ PRAVIDLO SÚČINU
 KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST I. ČASŤ TEST
 D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST Počet bodov Podpis 1 Podpis 2 I. ČASŤ TEST 1. Jedna strana trojuholníka meria 4cm a druhá 7cm. Ktoré z uvedených čísel môže byť obvodom tohto trojuholníka?
D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST Počet bodov Podpis 1 Podpis 2 I. ČASŤ TEST 1. Jedna strana trojuholníka meria 4cm a druhá 7cm. Ktoré z uvedených čísel môže byť obvodom tohto trojuholníka?
Téma : Špecifiká marketingu finančných služieb
 Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP.
 POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP. V prípade, že sa rozhodnete použiť ako úložisko kvalifikovaného certifikátu čipovú kartu StarCos2.3, musíte si žiadosť
POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP. V prípade, že sa rozhodnete použiť ako úložisko kvalifikovaného certifikátu čipovú kartu StarCos2.3, musíte si žiadosť
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary.
 Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
DOBROPISY. Dobropisy je potrebné rozlišovať podľa základného rozlíšenia: 1. dodavateľské 2. odberateľské
 DOBROPISY Dobropisy je potrebné rozlišovať podľa základného rozlíšenia: 1. dodavateľské 2. odberateľské 1. DODAVATEĽSKÉ to znamená, že dostanem dobropis od dodávateľa na reklamovaný, alebo nedodaný tovar.
DOBROPISY Dobropisy je potrebné rozlišovať podľa základného rozlíšenia: 1. dodavateľské 2. odberateľské 1. DODAVATEĽSKÉ to znamená, že dostanem dobropis od dodávateľa na reklamovaný, alebo nedodaný tovar.
Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu
 Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu obsah Funkcia Zastavenie a pretočenie obrazu Skôr než začnete Ako používať funkciu Zastavenie a pretočenie obrazu 1. Zastavenie a spustenie
Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu obsah Funkcia Zastavenie a pretočenie obrazu Skôr než začnete Ako používať funkciu Zastavenie a pretočenie obrazu 1. Zastavenie a spustenie
Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut
 Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut V této hře se to hemží kozami a ty jich musíš získat co nejvíce. Ale najednou je jejich počet limitován a ty už žádné kozy nechceš! Nebohá zvířata tedy
Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut V této hře se to hemží kozami a ty jich musíš získat co nejvíce. Ale najednou je jejich počet limitován a ty už žádné kozy nechceš! Nebohá zvířata tedy
Multiplexor a demultiplexor
 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Import Excel Univerzál
 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Vytvorenie používateľov a nastavenie prístupov
 Vytvorenie používateľov a nastavenie prístupov 1. Vytvorenie používateľov Spustite modul Správa systému, prihláste sa ako používateľ sa, z ponuky vyberte Evidencie Používatelia - Zoznam. Pomocou tlačidla
Vytvorenie používateľov a nastavenie prístupov 1. Vytvorenie používateľov Spustite modul Správa systému, prihláste sa ako používateľ sa, z ponuky vyberte Evidencie Používatelia - Zoznam. Pomocou tlačidla
Matematika test. Mesačne zaplatí. Obvod obdĺžnikovej záhrady je. Jedna kniha stojí Súčet
 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť v ľubovoľnom poradí.
1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť v ľubovoľnom poradí.
VYSPORIADANIE PREHRADENÝCH ZÁVÄZKOV A POHĽADÁVOK
 VYSPORIADANIE PREHRADENÝCH ZÁVÄZKOV A POHĽADÁVOK Funkcia Vysporiadanie pohľadávok a záväzkov umožňuje riešiť preplatky pohľadávok a záväzkov, prípady, kedy je úhrada vyššia ako hodnota uvedená na doklade.
VYSPORIADANIE PREHRADENÝCH ZÁVÄZKOV A POHĽADÁVOK Funkcia Vysporiadanie pohľadávok a záväzkov umožňuje riešiť preplatky pohľadávok a záväzkov, prípady, kedy je úhrada vyššia ako hodnota uvedená na doklade.
5.3.3 Vyhlásenie na zdanenie príjmov zo závislej činnosti
 časť 5. diel 3. kapitola 3 str. 1 5.3.3 Vyhlásenie na zdanenie príjmov zo závislej činnosti Výška preddavku na daň závisí od toho, či má zamestnanec u zamestnávateľa podpísané vyhlásenie na zdanenie príjmov
časť 5. diel 3. kapitola 3 str. 1 5.3.3 Vyhlásenie na zdanenie príjmov zo závislej činnosti Výška preddavku na daň závisí od toho, či má zamestnanec u zamestnávateľa podpísané vyhlásenie na zdanenie príjmov
Prijímacie skúšky kritériá pre školský rok 2017/2018
 Prijímacie skúšky kritériá pre školský rok 2017/2018 Študijný odbor 4236 M ekonomika pôdohospodárstva Prihlášky na štúdium v tomto študijnom odbore treba doručiť do 20. 4. 2017 Prijímacie skúšky budú v
Prijímacie skúšky kritériá pre školský rok 2017/2018 Študijný odbor 4236 M ekonomika pôdohospodárstva Prihlášky na štúdium v tomto študijnom odbore treba doručiť do 20. 4. 2017 Prijímacie skúšky budú v
Špecifikácia testu. z matematiky. pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017
 Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017 Bratislava 2016 Test z matematiky pre celoslovenské testovanie je určený žiakom 5. ročníka základných
Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 5. ročníka ZŠ v školskom roku 2016/2017 Bratislava 2016 Test z matematiky pre celoslovenské testovanie je určený žiakom 5. ročníka základných
JCDwin - prechod na EURO
 JCDwin - prechod na EURO Ver. 2 Posledná zmena 1. 1. 2009 www.davidplus.sk Strana:2 Program JCDwin a rok 2009/prechod na menu EUR Vážený užívateľ programu JCDwin. S nastávajúcim rokom 2009 si Vám dovoľujeme
JCDwin - prechod na EURO Ver. 2 Posledná zmena 1. 1. 2009 www.davidplus.sk Strana:2 Program JCDwin a rok 2009/prechod na menu EUR Vážený užívateľ programu JCDwin. S nastávajúcim rokom 2009 si Vám dovoľujeme
Ako funguje stav účtu - prehľad o platbách na zdravotné odvody
 Ako funguje stav účtu - prehľad o platbách na zdravotné odvody Vo svojej Elektronickej pobočke odteraz vidíte nielen svoj stav účtu od roku 2009, ale máte aj možnosť preddavky 1 na poistné alebo dlh zaplatiť
Ako funguje stav účtu - prehľad o platbách na zdravotné odvody Vo svojej Elektronickej pobočke odteraz vidíte nielen svoj stav účtu od roku 2009, ale máte aj možnosť preddavky 1 na poistné alebo dlh zaplatiť
tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač.
 5 tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač. 1. Používanie loga Pri každom použití loga v tlačenej podobe,
5 tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač. 1. Používanie loga Pri každom použití loga v tlačenej podobe,
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami
 11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
Program "Inventúra program.xlsm"
 1 / 14 Program "Inventúra program.xlsm" Program pracuje s reportami, ktoré majú ako zdroj dát tabuľku inventárnych dát. Program je uložený ako VBA projekt v Excel súbore "Inventúra Program.xlsm". Program
1 / 14 Program "Inventúra program.xlsm" Program pracuje s reportami, ktoré majú ako zdroj dát tabuľku inventárnych dát. Program je uložený ako VBA projekt v Excel súbore "Inventúra Program.xlsm". Program
Súťaž Vráťme knihy do škôl je tu už po 5-krát!
 Súťaž Vráťme knihy do škôl je tu už po 5-krát! O súťaži Internetové kníhkupectvo abcknihy.sk v spolupráci s partnermi Bratislavským samosprávnym krajom a vydavateľstvami Ikar, Raabe a vydavateľskou značkou
Súťaž Vráťme knihy do škôl je tu už po 5-krát! O súťaži Internetové kníhkupectvo abcknihy.sk v spolupráci s partnermi Bratislavským samosprávnym krajom a vydavateľstvami Ikar, Raabe a vydavateľskou značkou
Starogrécky filozof Demokritos ( pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov
 STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
Beáta Stehlíková Časové rady, FMFI UK, 2013/2014. CvičenievR-kuI.:ARIMAmodely p.1/15
 Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
Finančný manažment, finančná matematika a účtovníctvo
 MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
Súťaž Vráťme knihy do škôl je tu už po 7-krát!
 Súťaž Vráťme knihy do škôl je tu už po 7-krát! O súťaži Občianske združenie Učenie s úsmevom v spolupráci s partnermi internetové kníhkupectvo abcknihy.sk Bratislavským samosprávnym krajom, vydavateľstvom
Súťaž Vráťme knihy do škôl je tu už po 7-krát! O súťaži Občianske združenie Učenie s úsmevom v spolupráci s partnermi internetové kníhkupectvo abcknihy.sk Bratislavským samosprávnym krajom, vydavateľstvom
Řešení příkladů na procvičení pravděpodobnosti 1
 Řešení příkladů na procvičení pravděpodobnosti 1 1. ŘEŠENÍ Škola: Š...Jakub úspešne dokončí školu Š 3... v komisii sú práve 3 zhovievaví profesori Š 4... v komisii sú práve 4 zhovievaví profesori Š 5...
Řešení příkladů na procvičení pravděpodobnosti 1 1. ŘEŠENÍ Škola: Š...Jakub úspešne dokončí školu Š 3... v komisii sú práve 3 zhovievaví profesori Š 4... v komisii sú práve 4 zhovievaví profesori Š 5...
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ,
 Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Užívateľská príručka systému CEHZ. Základné zostavy Farmy podľa druhu činnosti
 Užívateľská príručka systému CEHZ Základné zostavy Farmy podľa druhu činnosti Užívateľská príručka systému CEHZ... 1 Základné zostavy Farmy podľa druhu činnosti... 1 1.1. Farmy podľa druhu činnosti...
Užívateľská príručka systému CEHZ Základné zostavy Farmy podľa druhu činnosti Užívateľská príručka systému CEHZ... 1 Základné zostavy Farmy podľa druhu činnosti... 1 1.1. Farmy podľa druhu činnosti...
Tlač do PDF a odosielanie dokladov cez . OBSAH
 Tlač do PDF a odosielanie dokladov cez e-mail. OBSAH Úvod... 2 Základné podmienky:... 2 Kde nájdem inštalačný program pre PDF tlačiarne?... 2 Pre aký operačný systém ho môžem použiť?... 2 Inštalácia PDF
Tlač do PDF a odosielanie dokladov cez e-mail. OBSAH Úvod... 2 Základné podmienky:... 2 Kde nájdem inštalačný program pre PDF tlačiarne?... 2 Pre aký operačný systém ho môžem použiť?... 2 Inštalácia PDF
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Elektronické odosielanie výplatných pások
 Elektronické odosielanie výplatných pások Od verzie 11.50 pribudla v programe Olymp možnosť hromadného odosielania zaheslovaných výplatných pások na e-maily jednotlivých pracovníkov. V evidencii Personalistika
Elektronické odosielanie výplatných pások Od verzie 11.50 pribudla v programe Olymp možnosť hromadného odosielania zaheslovaných výplatných pások na e-maily jednotlivých pracovníkov. V evidencii Personalistika
3D origami - tučniak. Postup na prípravu jednotlivých kúskov: A) nastrihanie, alebo natrhanie malých papierikov (tie budeme neskôr skladať)
 3D origami - tučniak Na výrobu 3D tučniaka potrebujeme: 27 bielych kúskov = 2 biele A4 kancelárske papiere, 85 čiernych (resp. inej farby) kúskov = 6 kancelárskych A4 papierov rovnakej farby, 3 oranžové
3D origami - tučniak Na výrobu 3D tučniaka potrebujeme: 27 bielych kúskov = 2 biele A4 kancelárske papiere, 85 čiernych (resp. inej farby) kúskov = 6 kancelárskych A4 papierov rovnakej farby, 3 oranžové
Používateľská príručka k aplikácii na SOČ
 Používateľská príručka k aplikácii na SOČ Aplikácia slúži na podporu procesov pri súťažiach SOČ všetkým zainteresovaným stranám pri všetkých fázach súťaže. Používateľmi sú jednak študenti ako osoby podávajúce
Používateľská príručka k aplikácii na SOČ Aplikácia slúži na podporu procesov pri súťažiach SOČ všetkým zainteresovaným stranám pri všetkých fázach súťaže. Používateľmi sú jednak študenti ako osoby podávajúce
Úroveň strojového kódu procesor Intel Pentium. Adresovanie pamäte
 Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
Finančné riaditeľstvo Slovenskej republiky. Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb
 Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2017 do 3.4.2018 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2017 do 3.4.2018 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
Ako postupovať pri vyplňovaní formulára.
 Ako postupovať pri vyplňovaní formulára. Formulár je dostupný v dvoch verziách a to pre kancelárske balíky Microsoft Office a Open Office. Spôsob vypĺňania formulára sa príliš neodlišuje od bežného písania
Ako postupovať pri vyplňovaní formulára. Formulár je dostupný v dvoch verziách a to pre kancelárske balíky Microsoft Office a Open Office. Spôsob vypĺňania formulára sa príliš neodlišuje od bežného písania
67. ročník Matematické olympiády 2017/2018
 67. ročník Matematické olympiády 2017/2018 Řešení úloh ústředního kola kategorie P 1. soutěžní den P-III-1 Kapitánka hledá posádku Úlohu lze vyřešit tak, že vyzkoušíme všechny možnosti, jak může Kapitánka
67. ročník Matematické olympiády 2017/2018 Řešení úloh ústředního kola kategorie P 1. soutěžní den P-III-1 Kapitánka hledá posádku Úlohu lze vyřešit tak, že vyzkoušíme všechny možnosti, jak může Kapitánka
Želáme Vám veľa úspechov a naďalej veľkú zábavu s matematikou.
 INŠTRUKCIE: Samostatný hárok pre riešenie úloh (hárok pre odpovede) Nezabudnite vyplniť všetky údaje (meno a priezvisko, škola, e-mail atď.). Testy Na vyriešenie otázok máte 4 minút. Správna je vždy len
INŠTRUKCIE: Samostatný hárok pre riešenie úloh (hárok pre odpovede) Nezabudnite vyplniť všetky údaje (meno a priezvisko, škola, e-mail atď.). Testy Na vyriešenie otázok máte 4 minút. Správna je vždy len
