8. Relácia usporiadania
|
|
|
- Přemysl Dvořák
- před 7 lety
- Počet zobrazení:
Transkript
1 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine M sa nazýva relácia ostrého lineárneho usporiadania, ak je: 1. antireflexívna,. antisymetrická,. tranzitívna, 4. súvislá. Relácia R definovaná v množine M sa nazýva relácia lineárneho usporiadania (neostrého), ak je: 1. reflexívna,. antisymetrická,. tranzitívna, 4. súvislá. Relácia R definovaná v množine M sa nazýva relácia ostrého čiastočného usporiadania, ak je: 1. antireflexívna,. antisymetrická,. tranzitívna. Relácia R definovaná v množine M sa nazýva relácia čiastočného usporiadania (neostrého), ak je: 1. reflexívna,. antisymetrická,. tranzitívna. Už na prvý pohľad vidíme, že všetky štyri definície sú si podobné. Vo všetkých štyroch definíciách totiž vyžadujeme, aby relácia R bola antisymetrická a tranzitívna. 146
2 Ako sa daná skutočnosť prejaví na vrcholovom grafe? Pretože relácia R je antisymetrická, jej vrcholový graf neobsahuje žiadne obojsmerné šípky. Pretože relácia R je tranzitívna, v jej vrcholovom grafe nemá zmysel prestupovať. Inými slovami, vždy, keď vrcholový graf obsahuje šípku z x do y a aj z y do z, potom obsahuje aj šípku z x do z. Keď porovnáme prvú a druhú definíciu zistíme, v čom spočíva rozdiel medzi ostrým a neostrým usporiadaním. Kým pri ostrom usporiadaní vyžadujeme, aby relácia R bola antireflexívna, pri neostrom usporiadaní vyžadujeme, aby relácia R bola reflexívna. Vrcholový graf relácie ostrého usporiadania neobsahuje žiadnu slučku. Vrcholový graf relácie neostrého usporiadania má pri každom vrchole slučku. Podobne možno porovnať aj tretiu a štvrtú definíciu. Keď porovnáme prvú a tretiu definíciu zistíme, v čom spočíva rozdiel medzi lineárnym a čiastočným usporiadaním. V definícii lineárneho usporiadania vyžadujeme, aby relácia R bola súvislá. Vo vrcholovom grafe relácie lineárneho usporiadania teda existuje medzi každými dvoma rôznymi vrcholmi nejaká šípka. V definícii čiastočného usporiadania takáto požiadavka nie je obsiahnutá. Podobne možno porovnať aj druhú a štvrtú definíciu. Relácie usporiadania si teraz precvičíme na nasledujúcich príkladoch. Nech množina = { 1,,,4 R = {[ 1,1 ][, 1, ][, 1, ][,, ][,, ][,, ][, 4,4] M a relácia. Vrcholový graf danej 1 4 relácie vidíme na obrázku. Pretože vrcholový graf relácie R neobsahuje obojsmerné šípky, relácia R je antisymetrická. Pretože vo vrcholovom grafe relácie R nemá zmysel prestupovať, relácia R je tranzitívna. Pretože vrcholový graf relácie R obsahuje pri každom vrchole slučku, relácia R je reflexívna. (neostré usporiadanie) Pretože vrcholy 1 a 4 nie sú spojené žiadnou šípkou, relácia R nie je súvislá. (čiastočné usporiadanie) Záver: Relácia R je reláciou neostrého čiastočného usporiadania v množine M. 147
3 Nech množina M = { 1,,,4 a relácia R = {[ 1, ], [ 1,4 ], [,4]. Vrcholový graf danej relácie vidíme na obrázku. Pretože vrcholový graf relácie R neobsahuje obojsmerné šípky, relácia R je antisymetrická. Pretože vo vrcholovom grafe relácie R nemá zmysel prestupovať, relácia R je tranzitívna. Pretože vrcholový graf relácie R neobsahuje žiadnu slučku, relácia R je antireflexívna. (ostré usporiadanie) Pretože vrcholy 1 a nie sú spojené žiadnou šípkou, relácia R nie je súvislá. (čiastočné usporiadanie) 1 4 Záver: Relácia R je reláciou ostrého čiastočného usporiadania v množine M. Nech množina M = { 1,,,4 a relácia = {[ 1,1 ], [ 1, ], [ 1, ], [ 1,4 ], [, ], [, ][,,4 ][,, ][,,4 ][, 4,4] R. Vrcholový graf danej relácie vidíme na obrázku. Pretože vrcholový graf relácie R neobsahuje obojsmerné šípky, relácia R je antisymetrická. Pretože vo vrcholovom grafe relácie R nemá zmysel prestupovať, relácia R je tranzitívna. Pretože vrcholový graf relácie R obsahuje pri každom vrchole slučku, relácia R je reflexívna. (neostré usporiadanie) Pretože každé dva rôzne vrcholy sú spojené šípkou, relácia R je súvislá. (lineárne usporiadanie) Záver: Relácia R je reláciou neostrého lineárneho usporiadania v množine M. 1 4 Nech množina M = { 1,,,4 a relácia R = {[ 1, ], [ 1, ], [ 1,4 ], [, ], [ 4, ], [ 4,]. Vrcholový graf danej relácie vidíme na obrázku. Pretože vrcholový graf relácie R neobsahuje obojsmerné šípky, relácia R je antisymetrická. Pretože vo vrcholovom grafe relácie R nemá zmysel prestupovať, relácia R je tranzitívna. Pretože vrcholový graf relácie R neobsahuje žiadnu slučku, relácia R je antireflexívna. (ostré usporiadanie) Pretože každé dva rôzne vrcholy sú spojené šípkou, relácia R je súvislá. (lineárne usporiadanie) 1 4 Záver: Relácia R je reláciou ostrého lineárneho usporiadania v množine M. 148
4 Nech množina = { 1,,,4 {[ 1,1 ][, 1, ][, 1, ][,,1 ][,, ][,, ][,, ][, 4,4] M a relácia R =. Vrcholový graf danej relácie vidíme na obrázku. Pretože vrcholový graf relácie R obsahuje obojsmernú šípku (z 1 do ), relácia R nie je antisymetrická. Pretože relácia R nie je antisymetrická, nemôže byť reláciou usporiadania (ani ostrého, ani neostrého, ani lineárneho, ani čiastočného). Ďalšie vlastnosti teda ani neurčujeme. 1 4 { Nech množina M = { 1,,,4 a relácia R = [ 1, ],[ 1, 4 ],[, ],[, 4 ],[,1 ],[, 4]. Vrcholový graf danej relácie vidíme na obrázku. Pretože vrcholový graf relácie R neobsahuje obojsmerné šípky, relácia R je antisymetrická. Vrcholový graf relácie R obsahuje šípku z 1 do a aj šípku z do, ale neobsahuje šípku z 1 do. Preto relácia R nie je tranzitívna (vo vrcholovom grafe 1 4 relácie R má zmysel prestupovať, napr. keď cestujeme z 1 do ). Pretože relácia R nie je tranzitívna, nemôže byť reláciou usporiadania (ani ostrého, ani neostrého, ani lineárneho, ani čiastočného. Ďalšie vlastnosti teda ani neurčujeme. Nech množina = { 1,,,4 R = {[ 1, ],[,1 ],[, ],[, 4 ],[ 4,1 ],[ 4,] aby všetky šípky smerovali zľava doprava. Všimnime si, že prvky 1,,, 4 možno Lineárne usporiadaná množina M a relácia ostrého lineárneho usporiadania. Vrcholový graf tejto relácie vieme nakresliť tak, usporiadať do radu 4 1, pričom v relácii lineárneho usporiadania R sú všetky tie usporiadané dvojice prvkov, ktorých prvá zložka sa v rade nachádza vľavo od druhej
5 Nech množina M = { Brno,Senica,Londýn,Trnava,Praha a relácia ostrého lineárneho usporiadania R = {[ xy, ] M M: xmá menej obyvateľov ako y. Aj vrcholový graf tejto relácie vieme nakresliť tak, aby všetky šípky smerovali zľava doprava. Senica Trnava Brno Praha Londýn Prvky množiny M sme opäť usporiadali do radu Senica Trnava Brno Praha Londýn, pričom v relácii lineárneho usporiadania R sú všetky tie usporiadané dvojice prvkov, ktorých prvá zložka sa v rade nachádza vľavo od druhej. Z predchádzajúcich dvoch príkladov vidíme, že: Prvky množiny M, na ktorej je definovaná relácia ostrého lineárneho usporiadania R, vieme vždy zoradiť do reťazca tak, že ak [ x, y] naľavo od y. R, potom x sa nachádza v reťazci Zápis takéhoto reťazca z predchádzajúcich príkladov je 4 1, resp. R R R Senica Trnava Brno Praha Londýn. R R R R Teraz uvedieme definíciu lineárne usporiadanej množiny. Ak na množine M je definovaná relácia lineárneho usporiadania R, tak množinu M usporiadanú touto reláciou označujeme ( M, R ) a nazývame lineárne usporiadaná množina. 150
6 Pod pojmom lineárne usporiadaná množina teda rozumieme dvojicu M, R, kde M je množina objektov a R je relácia lineárneho usporiadania na tejto množine. Príklady lineárne usporiadaných množín sme uviedli v predchádzajúcich dvoch príkladoch. Ďalej uvedieme definíciu prvého a posledného prvku lineárne usporiadanej množiny. Nech ( M, R ) je lineárne usporiadaná množina. Prvok a M nazývame prvým prvkom v množine M vzhľadom na lineárne usporiadanie R, ak platí: x M : x a a x (čítame: pre každý prvok x množiny M platí, že ak x je rôzny od a, R potom a predchádza x v usporiadaní R. Prvok b M nazývame posledným prvkom v množine M vzhľadom na lineárne usporiadanie R, ak platí: x M : x b x b (čítame: pre každý prvok x množiny M platí, že ak x je rôzny od b, R potom x predchádza b v usporiadaní R. Uvedomme si, že zápis a x znamená, že [ ax, ] R, ale [ x, a] R. R V predchádzajúcich príkladoch sme dostali nasledujúce postupnosti prvkov: To znamená, že prvok je prvým prvkom množiny M R R R a prvok 1 je posledným prvkom množiny M. Senica Trnava Brno Praha Londýn... prvok Senica je prvým prvkom množiny M, R R R R prvok Londýn je posledným prvkom množiny M. Pojem lineárne usporiadanej množiny a jej prvého a posledného prvku si vysvetlíme na nasledujúcich príkladoch. 151
7 Nech množina M = { 1,,, 4, 5, 6 a relácia R = {[ xy, ] M M: x y. 1 6 Vrcholový graf relácie R vidíme na obrázku. Z vrcholového grafu vidíme, že relácia R nie je súvislá (neobsahuje žiadnu šípku medzi prvkami a ). Relácia R teda nie je reláciou lineárneho usporiadania na množine M a dvojica ( M, R ) nie je lineárne usporiadanou množinou. 4 5 Nech množina M = { 1,, 4,8,16, a relácia [ ] relácie R vidíme na obrázku. {, : R = xy M M x y. Vrcholový graf Z vrcholového grafu vidíme, že relácia R je reflexívna, antisymetrická, tranzitívna a súvislá. Je teda reláciou neostrého lineárneho usporiadania na množine M. Dvojica ( M, R ) je lineárne usporiadanou množinou. Naviac platí: To znamená, že prvok 1 R R R R R je prvým prvkom množiny M a prvok je posledným prvkom množiny M. 15
8 Test č. 10 V nasledujúcom teste je 0 úloh z oblasti relácie usporiadania a lineárne usporiadanej množiny. Na nich si prakticky precvičíme: - určovanie, či daná relácia je reláciou ostrého lineárneho usporiadania, neostrého lineárneho usporiadania, ostrého čiastočného usporiadania, neostrého čiastočného usporiadania, - určovanie prvého a posledného prvku lineárne usporiadanej množiny. Test č. 10 nájdeme aj v elektronickej verzii v súbore 10.exe. 1. Nech R je binárna relácia v množine M. Označte vlastnosti, ktoré musí mať relácia R, aby bola reláciou ostrého lineárneho a) reflexívna b) antireflexívna c) symetrická d) antisymetrická e) tranzitívna f) súvislá. Nech R je binárna relácia v množine M. Označte vlastnosti, ktoré musí mať relácia R, aby bola reláciou neostrého lineárneho a) reflexívna b) antireflexívna c) symetrická d) antisymetrická e) tranzitívna f) súvislá. Nech R je binárna relácia v množine M. Označte vlastnosti, ktoré musí mať relácia R, aby bola reláciou ostrého čiastočného a) reflexívna b) antireflexívna 15
9 c) symetrická d) antisymetrická e) tranzitívna f) súvislá 4. Nech R je binárna relácia v množine M. Označte vlastnosti, ktoré musí mať relácia R, aby bola reláciou neostrého čiastočného a) reflexívna b) antireflexívna c) symetrická d) antisymetrická e) tranzitívna f) súvislá 5. Daná je relácia R v množine M. M { 1,,, 4, R {[ 1,1 ],[ 1, ],[ 1, ],[ 1, 4 ],[, ],[, ],[, ],[ 4, ],[ 4, ],[ 4, 4] = = Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 6. Daná je relácia R v množine M. M { 1,,, 4, R {[ 1, ],[ 1, ],[ 1, 4 ],[, ],[ 4, ],[ 4, ] = = Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 7. Daná je relácia R v množine M. { 1,,, 4, R {[ 1,1 ],[ 1, ],[ 1, ],[ 1, 4 ],[, ],[, 4 ],[, ],[ 4, 4] M = = 154
10 Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 8. Daná je relácia R v množine M. M { 1,,, 4, R {[ 1, ],[ 1, ],[ 1, 4 ],[, 4] = = Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 9. Daná je relácia R v množine prirodzených čísel. {[, ] : R = xy N N x y Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 10. Daná je relácia R v množine prirodzených čísel. {[, ] : R = xy N N x< y Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 11. Daná je relácia R v množine prirodzených čísel. {[, ] : delí R = xy N N x y 155
11 Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 1. Daná je relácia R v množine prirodzených čísel. {[, ] : delí R = xy N N x y x y Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 1. Na obrázku je vrcholový graf relácie R v množine M = { 1,,, 4, 5, 6. Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 14. Na obrázku je vrcholový graf relácie R v množine M = { 1,,, 4, 5, 6. Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 156
12 15. Na obrázku je vrcholový graf relácie R v množine M = { 1,,, 4, 5, 6. Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 16. Na obrázku je vrcholový graf relácie R v množine M = { 1,,, 4, 5, 6. Vyberte správne tvrdenie. a) Relácia R je reláciou ostrého lineárneho b) Relácia R je reláciou neostrého lineárneho c) Relácia R je reláciou ostrého čiastočného d) Relácia R je reláciou neostrého čiastočného 17. Na obrázku je vrcholový graf relácie ostrého lineárneho usporiadania R v množine M = { 1,,, 4, 5, 6. Prvým prvkom v množine M vzhľadom na ostré lineárne usporiadanie R je a) 1 b) c) d) 4 e) 5 f) 6 157
13 18. Na obrázku je vrcholový graf relácie ostrého lineárneho usporiadania R v množine M = { 1,,, 4, 5, 6. Posledným prvkom v množine M vzhľadom na ostré lineárne usporiadanie R je a) 1 b) c) d) 4 e) 5 f) Na obrázku je vrcholový graf relácie ostrého lineárneho usporiadania R v množine M = { 1,,, 4. Prvým prvkom v množine M vzhľadom na ostré lineárne usporiadanie R je a) 1 b) c) d) 4 0. Na obrázku je vrcholový graf relácie ostrého lineárneho usporiadania R v množine M = { 1,,, 4. Posledným prvkom v množine M vzhľadom na ostré lineárne usporiadanie R je a) 1 b) c) d) 4 Test č. 10 správne riešenia 1. bdef 5. b 9. b 1. c 17. b. adef 6. a 10. a 14. a 18. e. bde 7. d 11. d 15. d 19. d 4. ade 8. c 1. c 16. b 0. c 158
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Aritmetika s didaktikou I.
 Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Teória grafov. Stromy a kostry 1. časť
 Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Obrázok Časový plán projektu, určite kritickú cestu. Obrázok Časový plán projektu, určite kritickú cestu
 Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Ako započítať daňovú licenciu
 Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM
 MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Množina a jej určenie, konečná a nekonečná množina
 Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
INTERNET BANKING. Platby cez Internet banking VŠETKO, ČO JE MOŽNÉ. with.vub.sk, Bank of
 INTERNET BANKING Platby cez Internet banking VŠETKO, ČO JE MOŽNÉ www.vub.sk, with.vub.sk, 0850 123 000 Bank of VYNOVENÝ INTERNET BANKING Nový, moderný dizajn Dostupnosť zo všetkých zariadení Prehľad o
INTERNET BANKING Platby cez Internet banking VŠETKO, ČO JE MOŽNÉ www.vub.sk, with.vub.sk, 0850 123 000 Bank of VYNOVENÝ INTERNET BANKING Nový, moderný dizajn Dostupnosť zo všetkých zariadení Prehľad o
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač.
 5 tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač. 1. Používanie loga Pri každom použití loga v tlačenej podobe,
5 tipov pre kvalitnú tlač Na jednoduchých príkladoch Vám ukážeme ako postupovať a na čo si dávať pozor pri príprave podkladov na kvalitnú tlač. 1. Používanie loga Pri každom použití loga v tlačenej podobe,
KOMBINATORICKÉ PRAVIDLO SÚČINU
 KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV
 CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
AR, MA a ARMA procesy
 Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
je zmena operácie ktorou z nelineárneho systému môže spraviť lineárny. Týmto krokom sme získali signál ktorý môžeme spracovať pomocou LDKI sústavy.
 Homomorfné systémy Homomorfné systémy sú nelineárne systémy, preto pri nich neplatí princíp superpozície a proporcionality tak ako to je pri lineárnych systémoch. A vieme ich takto grafický znázorniť:
Homomorfné systémy Homomorfné systémy sú nelineárne systémy, preto pri nich neplatí princíp superpozície a proporcionality tak ako to je pri lineárnych systémoch. A vieme ich takto grafický znázorniť:
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Test. Ktorý valec by ste použili? A. Jednočinný valec B. Dvojčinný valec. Odpoveď:
 Test Týmto testom môžete zistiť, či sú Vaše základné znalosti o pneumatickom riadení postačujúce pre nadstavbový seminár P121, alebo je pre Vás lepšie absolvovať základný seminár EP111. Test je rýchly,
Test Týmto testom môžete zistiť, či sú Vaše základné znalosti o pneumatickom riadení postačujúce pre nadstavbový seminár P121, alebo je pre Vás lepšie absolvovať základný seminár EP111. Test je rýchly,
Starogrécky filozof Demokritos ( pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov
 STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
Microsoft Project CVIČENIE 6 1
 Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
Kontrola väzieb výkazu Súvaha a Výkaz ziskov a strát Príručka používateľa
 Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Operačný systém Úvodná prednáška
 Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
8. Implikácia. A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna.
 8. Implikácia Implikáciu B A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna. Implikáciu B' A' nazývame obmenou implikácie A B. Implikácia
8. Implikácia Implikáciu B A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna. Implikáciu B' A' nazývame obmenou implikácie A B. Implikácia
Externé zariadenia Používateľská príručka
 Externé zariadenia Používateľská príručka Copyright 2009 Hewlett-Packard Development Company, L.P. Informácie obsiahnuté v tomto dokumente sa môžu zmeniť bez predchádzajúceho upozornenia. Jediné záruky
Externé zariadenia Používateľská príručka Copyright 2009 Hewlett-Packard Development Company, L.P. Informácie obsiahnuté v tomto dokumente sa môžu zmeniť bez predchádzajúceho upozornenia. Jediné záruky
RIZIKO V PODNIKU. Prípadová štúdia 2. Ing. Michal Tkáč, PhD.
 RIZIKO V PODNIKU Prípadová štúdia 2 Ing. Michal Tkáč, PhD. Tento učebný text je venovaný hlavne študentom 1. ročníka II. stupňa Podnikovohospodárskej fakulty, Ekonomickej univerzity v Bratislave. Text
RIZIKO V PODNIKU Prípadová štúdia 2 Ing. Michal Tkáč, PhD. Tento učebný text je venovaný hlavne študentom 1. ročníka II. stupňa Podnikovohospodárskej fakulty, Ekonomickej univerzity v Bratislave. Text
Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin.
 Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin. Cieľom databázy zmlúv, faktúr a objednávok Mesta Martin je zverejnenie uvedených záznamov v zmysle ustanovení zákona č. 211/2000 Z.z.
Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin. Cieľom databázy zmlúv, faktúr a objednávok Mesta Martin je zverejnenie uvedených záznamov v zmysle ustanovení zákona č. 211/2000 Z.z.
TomTom Referenčná príručka
 TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
Užívateľská príručka. Vytvorte 1 medzi stránkami v niekoľkých jednoduchých krokoch
 Užívateľská príručka Vytvorte 1 medzi stránkami v niekoľkých jednoduchých krokoch EXO TECHNOLOGIES spol. s r.o. Garbiarska 3 Stará Ľubovňa 064 01 IČO: 36 485 161 IČ DPH: SK2020004503 support@exohosting.sk
Užívateľská príručka Vytvorte 1 medzi stránkami v niekoľkých jednoduchých krokoch EXO TECHNOLOGIES spol. s r.o. Garbiarska 3 Stará Ľubovňa 064 01 IČO: 36 485 161 IČ DPH: SK2020004503 support@exohosting.sk
Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu
 Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu obsah Funkcia Zastavenie a pretočenie obrazu Skôr než začnete Ako používať funkciu Zastavenie a pretočenie obrazu 1. Zastavenie a spustenie
Užívateľská príručka k funkcii Zastavenie a pretočenie obrazu obsah Funkcia Zastavenie a pretočenie obrazu Skôr než začnete Ako používať funkciu Zastavenie a pretočenie obrazu 1. Zastavenie a spustenie
Návod na nastavenie oprávnení pre oprávnené osoby s udeleným čiastočným prístupom
 Návod na nastavenie oprávnení pre oprávnené osoby s udeleným čiastočným prístupom Dátum zverejnenia: 1. 2. 2014 Verzia: 6 Dátum aktualizácie: 23. 8. 2017 Popis: Tento dokument je určený pre fyzické osoby,
Návod na nastavenie oprávnení pre oprávnené osoby s udeleným čiastočným prístupom Dátum zverejnenia: 1. 2. 2014 Verzia: 6 Dátum aktualizácie: 23. 8. 2017 Popis: Tento dokument je určený pre fyzické osoby,
Začínam so zadaním z NEPOUŽÍVAME ROZSAH POKIAĽ HO MUSÍME PRESKOČIŤ
 Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Matematika (platný od )
 Matematika (platný od 01.09.2016) 1. ročník A variant Obsah vzdelávania: 4 hodiny/týždenne 132 hodín Triedenie predmetov podľa vlastností (množstvo, veľkosť, farba, tvar) Dvojica. Vzťahy rovnako nie rovnako,
Matematika (platný od 01.09.2016) 1. ročník A variant Obsah vzdelávania: 4 hodiny/týždenne 132 hodín Triedenie predmetov podľa vlastností (množstvo, veľkosť, farba, tvar) Dvojica. Vzťahy rovnako nie rovnako,
Postup pri aktivácii elektronickej schránky na doručovanie pre právnické osoby, ktoré nie sú zapísané do obchodného registra
 Postup pri aktivácii elektronickej schránky na doručovanie pre právnické osoby, ktoré nie sú zapísané do obchodného registra Dátum platnosti: 1. 2. 2014 Verzia dokumentu: 9 Dátum zverejnenia: 19. 1. 2017
Postup pri aktivácii elektronickej schránky na doručovanie pre právnické osoby, ktoré nie sú zapísané do obchodného registra Dátum platnosti: 1. 2. 2014 Verzia dokumentu: 9 Dátum zverejnenia: 19. 1. 2017
Metóda 5S. Metóda 5S. Základy štíhleho podniku. Ján Burieta a kolektív
 Metóda 5S Metóda 5S Základy štíhleho podniku Ján Burieta a kolektív Autor Ján Burieta IPA Slovakia, s.r.o. Predmestská 8600/95, 010 01 Žilina www.ipaslovakia.sk www.ipaczech.cz info@ipaslovakia.sk Fotografia
Metóda 5S Metóda 5S Základy štíhleho podniku Ján Burieta a kolektív Autor Ján Burieta IPA Slovakia, s.r.o. Predmestská 8600/95, 010 01 Žilina www.ipaslovakia.sk www.ipaczech.cz info@ipaslovakia.sk Fotografia
Microsoft Outlook. Stručný prehľad základných funkcií. Ing.Anna Grejtáková, SPP DFBERG
 Microsoft Outlook Stručný prehľad základných funkcií Ing.Anna Grejtáková, SPP DFBERG Poslanie Stručne popísať základné funkcie MS Outlook. Upozorniť na problémy, ktoré tu už boli... Odpovedať na Vaše otázky,čo
Microsoft Outlook Stručný prehľad základných funkcií Ing.Anna Grejtáková, SPP DFBERG Poslanie Stručne popísať základné funkcie MS Outlook. Upozorniť na problémy, ktoré tu už boli... Odpovedať na Vaše otázky,čo
Multiplexor a demultiplexor
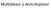 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
INŠTALAČNÝ MANUÁL. TMEgadget
 INŠTALAČNÝ MANUÁL TMEgadget OBSAH 1 KROKY PRED INŠTALÁCIOU... 2 1.1 Kontrola operačného systému a internetového pripojenia... 2 1.2 Príprava inštalačného súboru TMEgadget.exe... 2 2 INŠTALÁCIA... 2 2.1
INŠTALAČNÝ MANUÁL TMEgadget OBSAH 1 KROKY PRED INŠTALÁCIOU... 2 1.1 Kontrola operačného systému a internetového pripojenia... 2 1.2 Príprava inštalačného súboru TMEgadget.exe... 2 2 INŠTALÁCIA... 2 2.1
Automatický timer pre DX7 návod na inštaláciu a manuál
 Automatický timer pre DX7 návod na inštaláciu a manuál Upozornenie: Aj keď je modul pre DX7 obvodovo takmer totožný s modulom pre DX6i, majú niektoré súčiastky odlišnú hodnotu a v procesore je úplne iný
Automatický timer pre DX7 návod na inštaláciu a manuál Upozornenie: Aj keď je modul pre DX7 obvodovo takmer totožný s modulom pre DX6i, majú niektoré súčiastky odlišnú hodnotu a v procesore je úplne iný
Zaciatok programovania na
 Zaciatok programovania na itnc 530 HEIDENHAIN Poznamka : Tento navod bude vytvoreny pomocou virtualnej klávesnice. Jej nastavenie je popisane v navode Instalacia a nastavenie Simulatora. Samozrejme, mozete
Zaciatok programovania na itnc 530 HEIDENHAIN Poznamka : Tento navod bude vytvoreny pomocou virtualnej klávesnice. Jej nastavenie je popisane v navode Instalacia a nastavenie Simulatora. Samozrejme, mozete
Postup pri deaktivácii elektronickej schránky na doručovanie pre fyzické osoby
 Postup pri deaktivácii elektronickej schránky na doručovanie pre fyzické osoby Dátum zverejnenia: 1. 2. 2014 Verzia dokumentu: 4 Dátum aktualizácie: 23. 8. 2017 Popis: Tento dokument je určený pre občanov
Postup pri deaktivácii elektronickej schránky na doručovanie pre fyzické osoby Dátum zverejnenia: 1. 2. 2014 Verzia dokumentu: 4 Dátum aktualizácie: 23. 8. 2017 Popis: Tento dokument je určený pre občanov
Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke Slovenská verzia pravidiel sa pripravuje
 Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
Základné prvky loga OPCHS
 Logo manuál Základné prvky loga OPCHS 1 Základné prvky 1. 1. Logotyp OPCHS 1. 1. 1. Základné prevedenie loga Základný tvar značky je tvorený trojfarebným obdĺžnikom so zaoblenými rohmi, do ktorého je
Logo manuál Základné prvky loga OPCHS 1 Základné prvky 1. 1. Logotyp OPCHS 1. 1. 1. Základné prevedenie loga Základný tvar značky je tvorený trojfarebným obdĺžnikom so zaoblenými rohmi, do ktorého je
Referenčná ponuka na prístup ku káblovodom a infraštruktúre. Príloha 7 Poplatky a ceny
 Príloha 7 Poplatky a ceny Príloha 7: Poplatky a ceny strana 1 z 5 Obsah 1. CENY V RÁMCI DOHODY NDA A RÁMCOVEJ ZMLUVY... 3 2. CENY V RÁMCI ZMLUVY O DUCT SHARING... 3 2.1 CENA ZA POSKYTOVANIE ZÁKLADNEJ SLUŽBY
Príloha 7 Poplatky a ceny Príloha 7: Poplatky a ceny strana 1 z 5 Obsah 1. CENY V RÁMCI DOHODY NDA A RÁMCOVEJ ZMLUVY... 3 2. CENY V RÁMCI ZMLUVY O DUCT SHARING... 3 2.1 CENA ZA POSKYTOVANIE ZÁKLADNEJ SLUŽBY
Imagine. Popis prostredia:
 Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
SKLADOVÁ INVENTÚRA 1 VYTVORENIE INVENTÚRY. 1.1 Nastavenie skladovej inventúry
 SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
Riešenie nelineárnych rovníc I
 Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
Výstupný test projektu KEGA pre 7. roč. ZŠ. Verzia B
 Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia B Meno: Problém U1 U2 Súčet 1 Nehody 2 Zákazka 3 Nákup kozmetiky 4 Štvormiestne kupé 5 Kúpa auta 6 Čokoládové kocky Súčet bodov za test Nehody V minulom
Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia B Meno: Problém U1 U2 Súčet 1 Nehody 2 Zákazka 3 Nákup kozmetiky 4 Štvormiestne kupé 5 Kúpa auta 6 Čokoládové kocky Súčet bodov za test Nehody V minulom
Výstupný test projektu KEGA pre 7. roč. ZŠ. Verzia A
 Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia A Meno: Problém U1 U2 Súčet 1 Zákusky pre hostí 2 Terminovaný vklad 3 Doprava po Ukrajine 4 Preprava nákladu 5 Krémy na tvár výhodne 6 Evidenčné čísla
Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia A Meno: Problém U1 U2 Súčet 1 Zákusky pre hostí 2 Terminovaný vklad 3 Doprava po Ukrajine 4 Preprava nákladu 5 Krémy na tvár výhodne 6 Evidenčné čísla
Ekvia s.r.o EKVIA PREMIUMPRO. Užívateľský manuál
 Ekvia s.r.o EKVIA PREMIUMPRO Užívateľský manuál 1. Prihlásenie sa Pre prihlásenia sa do portálu Ekvia PremiumPro prejdite na adresu: www.ekviapremiumpro.sk Kde po kliknutí na tlačidlo Prihlásenie v pravom
Ekvia s.r.o EKVIA PREMIUMPRO Užívateľský manuál 1. Prihlásenie sa Pre prihlásenia sa do portálu Ekvia PremiumPro prejdite na adresu: www.ekviapremiumpro.sk Kde po kliknutí na tlačidlo Prihlásenie v pravom
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
PROGRAM VZDELÁVACEJ ČINNOSTI. Anotácia predmetu
 PROGRAM VZDELÁVACEJ ČINNOSTI Číslo predmetu : 32131, 2N187 Názov predmetu : Teória grafov Typ predmetu : Povinne voliteľný Študijný odbor: Biomedicinske inžinierstvo, Telekomunikácie, Aplikovaná mechanika
PROGRAM VZDELÁVACEJ ČINNOSTI Číslo predmetu : 32131, 2N187 Názov predmetu : Teória grafov Typ predmetu : Povinne voliteľný Študijný odbor: Biomedicinske inžinierstvo, Telekomunikácie, Aplikovaná mechanika
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL. Algebra a diskrétna matematika
 VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
1. LABORATÓRNE CVIČENIE
 MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
KORUNOVAČNÁ BRATISLAVA MANUÁL LOGA VER. 1/2017
 VER. 1/2017 1. Úvod Tento manuál pojednáva o základných pravidlách použitia loga Korunovačná Bratislava (ďalej KB). Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je súčasťou tohto manuálu.
VER. 1/2017 1. Úvod Tento manuál pojednáva o základných pravidlách použitia loga Korunovačná Bratislava (ďalej KB). Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je súčasťou tohto manuálu.
7.CVIČENIE. Základy HTML
 7.CVIČENIE gajdos@ismpo.sk Základy HTML 1. Štruktúra HTML, XHTML dokumentu 2. Niektoré tagy HTML - Hypertext Markup Language XHTML - Extensible Hypertext Markup Language Webový prehliadač začne čítať web
7.CVIČENIE gajdos@ismpo.sk Základy HTML 1. Štruktúra HTML, XHTML dokumentu 2. Niektoré tagy HTML - Hypertext Markup Language XHTML - Extensible Hypertext Markup Language Webový prehliadač začne čítať web
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary.
 Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
Návod na udelenie oprávnenia na prístup a disponovanie s elektronickou schránkou a jeho zneplatnenie
 Návod na udelenie oprávnenia na prístup a disponovanie s elektronickou schránkou a jeho zneplatnenie Dátum zverejnenia: 1. 2. 2014 Verzia: 7 Dátum aktualizácie: 23. 8. 2016 Popis: Tento dokument je určený
Návod na udelenie oprávnenia na prístup a disponovanie s elektronickou schránkou a jeho zneplatnenie Dátum zverejnenia: 1. 2. 2014 Verzia: 7 Dátum aktualizácie: 23. 8. 2016 Popis: Tento dokument je určený
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Vytvorenie bootovacieho CD
 Vytvorenie bootovacieho CD Obnova Image pomocou bootovacieho CD Image for Linux Je to program, ktorý je kompatibilný s C-Image zálohovaním zakomponovaným v C-Monitor klientovi. Vznikajúce využitie má pri
Vytvorenie bootovacieho CD Obnova Image pomocou bootovacieho CD Image for Linux Je to program, ktorý je kompatibilný s C-Image zálohovaním zakomponovaným v C-Monitor klientovi. Vznikajúce využitie má pri
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI
 Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Fyzika 9. ročník 3. Laboratórna úloha
 Základná škola s materskou školou Chlebnice Fyzika 9. ročník 3. Laboratórna úloha Úloha: Urč pevnú látku, z ktorej je zhotovené teleso, pomocou mernej tepelnej kapacity Príprava: Medzi telesami, ktorých
Základná škola s materskou školou Chlebnice Fyzika 9. ročník 3. Laboratórna úloha Úloha: Urč pevnú látku, z ktorej je zhotovené teleso, pomocou mernej tepelnej kapacity Príprava: Medzi telesami, ktorých
Neplatené voľno / absencia zadanie v programe, oznamovacia povinnosť
 Neplatené voľno / absencia zadanie v programe, oznamovacia povinnosť Ako zadať v programe zamestnancovi rôzne druhy neplateného voľna alebo absencie? Akú má v tejto súvislosti zamestnávateľ oznamovaciu
Neplatené voľno / absencia zadanie v programe, oznamovacia povinnosť Ako zadať v programe zamestnancovi rôzne druhy neplateného voľna alebo absencie? Akú má v tejto súvislosti zamestnávateľ oznamovaciu
Funkcionální řady. January 13, 2016
 Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Názov: Osmóza. Vek žiakov: Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút.
 Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
STRUČNÝ NÁVOD NA OBSLUHU DATALOGERA KIMO KT110 / 150
 STRUČNÝ NÁVOD NA OBSLUHU DATALOGERA KIMO KT110 / 150 1. Inštalácia softvéru KILOG Pre dokončenie inštalácie je potrebné potvrdiť všetky čiastkové inštalácie, ktoré sa budú ponúkať v inštalačnom okne. Strana
STRUČNÝ NÁVOD NA OBSLUHU DATALOGERA KIMO KT110 / 150 1. Inštalácia softvéru KILOG Pre dokončenie inštalácie je potrebné potvrdiť všetky čiastkové inštalácie, ktoré sa budú ponúkať v inštalačnom okne. Strana
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu
 Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ,
 Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Obr. 1 - názov podpísaného súboru/kontajnera v sivej lište
 Zobrazenie dokumentov v elektronickej správe V elektronickej správe sa môžu prenášať autorizované (podpísané/pečatené), ale aj neautorizované súbory, a to buď v hlavnom objekte správy, v prílohách alebo
Zobrazenie dokumentov v elektronickej správe V elektronickej správe sa môžu prenášať autorizované (podpísané/pečatené), ale aj neautorizované súbory, a to buď v hlavnom objekte správy, v prílohách alebo
Pracovné prostredie MS EXCEL 2003.
 Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ. Grafy
 Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Verifikácia a falzifikácia
 Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického poradenstva a prevencie (bývalá KPPP) Banská Bystrica
 Návod 2. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. 24 9. 2016 Prevod textu s obrázkami. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Návod 2. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. 24 9. 2016 Prevod textu s obrázkami. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Školská sieť EDU. Rozdelenie škôl. Obsah: Deleba škôl podľa času zaradenia do projektu: Delba škôl podľa rýchlosti pripojenia:
 Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
Elektronická značka je k dispozícii na stránke etax v záložke Úvod, položka menu Správa Certifikátov.
 OBSAH: 1. ÚVOD 2. Inštalácia klientskej elektronickej značky EP DR SR 3. Inštalácia serverovskej elektronickej značky EP DR SR 4. Kontrola výsledkov inštalácie 5. Používanie elektronickej značky pri podávaní
OBSAH: 1. ÚVOD 2. Inštalácia klientskej elektronickej značky EP DR SR 3. Inštalácia serverovskej elektronickej značky EP DR SR 4. Kontrola výsledkov inštalácie 5. Používanie elektronickej značky pri podávaní
MAGISTRÁT HLAVNÉHO MESTA SLOVENSKEJ REPUBLIKY BRATISLAVY
 MAGISTRÁT HLAVNÉHO MESTA SLOVENSKEJ REPUBLIKY BRATISLAVY Materiál na rokovanie Mestského zastupiteľstva hlavného mesta SR Bratislavy dňa 07. 12. 2017 Návrh na nevyhovenie protestu prokurátora proti uzneseniu
MAGISTRÁT HLAVNÉHO MESTA SLOVENSKEJ REPUBLIKY BRATISLAVY Materiál na rokovanie Mestského zastupiteľstva hlavného mesta SR Bratislavy dňa 07. 12. 2017 Návrh na nevyhovenie protestu prokurátora proti uzneseniu
Krížovka. Hot Potatoes JCross ( červená farba) = vytvorenie krížovky, do ktorej vpisujeme odpovede na zadané otázky. Priradenie
 Krížovka Hot Potatoes JCross ( červená farba) = vytvorenie krížovky, do ktorej vpisujeme odpovede na zadané otázky. Priradenie Hot Potatoes JMatch ( zelený zemiak) = priraďovanie/výber z navolených možností.
Krížovka Hot Potatoes JCross ( červená farba) = vytvorenie krížovky, do ktorej vpisujeme odpovede na zadané otázky. Priradenie Hot Potatoes JMatch ( zelený zemiak) = priraďovanie/výber z navolených možností.
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Skupiny finančných nástrojov a produktov zodpovedajúce typu investora
 Skupiny finančných nástrojov a produktov zodpovedajúce typu investora Obsah Úvod...3 Prehľad č. 1 k retailovému investičnému dotazníku...4 Prehľad č. 2 k investičnému dotazníku oddelenia Predaj...6 2 Úvod
Skupiny finančných nástrojov a produktov zodpovedajúce typu investora Obsah Úvod...3 Prehľad č. 1 k retailovému investičnému dotazníku...4 Prehľad č. 2 k investičnému dotazníku oddelenia Predaj...6 2 Úvod
Logo. Logo je vytvorené z grafickej časti skratka AVF a textovej časti AUDIOVIZUÁLNY FOND. Text je vysádzaný písmom Vafle Mono v reze Mono.
 Logo Logo je vytvorené z grafickej časti skratka AVF a textovej časti AUDIOVIZUÁLNY FOND. Text je vysádzaný písmom Vafle Mono v reze Mono. Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je
Logo Logo je vytvorené z grafickej časti skratka AVF a textovej časti AUDIOVIZUÁLNY FOND. Text je vysádzaný písmom Vafle Mono v reze Mono. Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je
Obchodná akadémia Ružomberok Ing. Igor Rosa
 1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
Beáta Stehlíková Časové rady, FMFI UK, 2013/2014. CvičenievR-kuI.:ARIMAmodely p.1/15
 Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
Cvičenie v R-ku I.: ARIMA modely Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 CvičenievR-kuI.:ARIMAmodely p.1/15 Príklad 1: dáta Použité dáta: Počet používatel ov prihlásených na server, dáta po minútach,
