Řešení příkladů na procvičení pravděpodobnosti 1
|
|
|
- Daniel Havel
- před 6 lety
- Počet zobrazení:
Transkript
1 Řešení příkladů na procvičení pravděpodobnosti 1 1. ŘEŠENÍ Škola: Š...Jakub úspešne dokončí školu Š 3... v komisii sú práve 3 zhovievaví profesori Š 4... v komisii sú práve 4 zhovievaví profesori Š 5... v komisii sú práve 5 zhovievaví profesori Š Š 3 U Š 4 U Š 5 V komisii musia byť aspoň 3 zhovievaví profesori (to znamená 3, 4 alebo 5). m(ω) P(Š) (Š) m(ω) P(Š) F...Jakub založí firmu B...Jakub dostane od banky pôžičku P(F) P(B Š) P(B). P(Š) P(F) 0,5 P(B). P(Š) 0,5 P(B), (Š) P(B), P(B) Musíme teda zistiť, v koľkých bankách musí Jakub požiadať o pôžičku, aby pravdepodobnosť, že mu ju poskytne aspoň 1 z bánk bola aspoň. B i...jakub získa pôžičku v i-tej banke P(B i ) 0,2 B...Jakub získa pôžičku aspoň v jednej z bánk P (U B i ) 1- P(B 1 ).... P(B n) i je od 1 po n P(B) 1-0,8 n 1-0,8 n 1-0,8n 0,8n 1 Příklady vytvořili studenti předmětu BPM_STA1 1
2 ln ln ln 0,8n n. ln 0,8! "!,# n 5,7899 % Jakub musí požiadať o pôžičku aspoň v 6 bankách, aby bola aspoň 50% pravdepodobnosť, že založí firmu. 2. ŘEŠENÍ a) práve v 5 zošitoch je d. úloha alebo práve v 6 zošitoch je d. úloha alebo práve v 7 zošitoch je d.úloha P(A) [( 20 5)*( 10 2)]/( 30 7) + [( 20 6)*( 10 1)]/( 30 7) + ( 20 7)/( 30 7) P(A) 0,34 + 0,19 + 0,04 0,57 Pravdepodobnosť, že aspoň v 5 zošitoch, ktoré učiteľ náhodne vyberie, bude domáca úloha, je 57 %. b) vypočítame pravdepodobnosť, že v žiadnom zošite nie je d. úloha (opačný jav) P(B / ) ( 10 7)/( 30 7) 0,00006 P(B) 1-P(B / ) 1-0, ,99994 Pravdepodobnosť, že aspoň v 1 zošite, ktorý učiteľ náhodne vyberie, bude domáca úloha, je 99,994 %. 3. ŘEŠENÍ A... ČEZ... P(A) 0,85 B...Kofola...P(B) 0,7 C...Fortuna...P(C) 0,65 D...Unipetrol..P(D) 0,5 E...Telefonica...P(E) 0,4 P(I) P(A B C D E) P(I) 0,85*0,7*0,65*0,5*0,4 P(I) 0,07735 P(I) 7,735 % PAN NEOMYLNÝ NEBUDE INVESTOVAT. 4. ŘEŠENÍ m(a ) (74 nad 10) m(ω)(124 nad 10) P(A) 1 P(A ) 1- m(a )/ m(ω)0, ŘEŠENÍ &(' ' ) &(' ) + &(' ) &(' ' ) 0,4 + 0,8 0,9 0,3 2
3 6. ŘEŠENÍ 11tý student pochází ze 790 studentů (800-10) 0,8x m(a) 630 m(ω) 790 P(A) m(a)/m(ω) 630/790 0,7975 (po zaokrouhlení) 7. ŘEŠENÍ Nejprve si musím uvědomit, o jaký typ pravděpodobnosti se jedná. Zadání nám napovídá, že jde o podmíněnou pravděpodobnost, jelikož existuje situace, kdy oba jevy nastanou zároveň. Společné nastoupení obou jevů je dokonce v rámci pokusu pravděpodobnější, než bychom očekávali. Nyní si určím jevy: -A.. firma ALFA zkrachuje P (A) 35% 0,35 -B.. firma BETA zkrachuje P (B) 20% 0,20 -A.. firma ALFA se udrží na trhu (opačný jev k A) P (A ) 1-0,350,65 -B.. firma BETA se udrží na trhu (opačný jev k B) P (B ) 1-0,20 0,80 P (A B) 6% 0,06 Mohu si pro kontrolu ověřit závislost/nezávislost: 3
4 P(A)*P(B)0,35*0,20 0,07, že nastanou oba jevy zároveň, takovýto výsledek by byl u nezávislých jevů, ze zadání víme, že pravděpodobnost nastoupení obou jevů je menší, proto se jedná o závislé jevy a nemohu je tedy mezi sebou násobit. Nyní samotné odpovědi na jednotlivé otázky: a) Jaká je pravděpodobnost, že obě firmy budou fungovat? -spojení obě firmy ze zadání nám napovídají, že se jedná o průnik obou jevů, zde jsou však jako klasické jevy uvedeny situace, kdy podnik krachuje, počítám tedy průnik jevů opačných. Obecně platí: P (A B ) P (A ) + P (B ) P (A B )- podle obecného vzorce sečtu pravděpodobnosti a musím odečíst ještě jejich sjednocení, abych žádný kousek nezapočítala 2x (jsou totiž závislé) P (A B ) 0,65+0,80- P (A B ) P (A B )-dopočítám si, opět mám obecný vzorec pro výpočet: P (A B )1- P (A B) P (A B ) (1-0,06) P (A B )0,94 Nyní jen dosadím od původního vzorce: P (A B ) 0,65+0,80-0,94 P (A B ) 0,51 P (A B ) 51% Odpověď: Pravděpodobnost, že obě firmy budou fungovat, je 51%. b) Jaká je pravděpodobnost, že alespoň jedna firma v tomto pokusu opustí trh? -spojení alespoň jedna firma naznačuje, že se snažím zjistit sjednocení. Obecný vzorec: P (A B) P (A) + P (B) P (A B) P (A B) 0,35+0,20-0,06 P (A B) 0,49 P (A B) 49% Odpověď: Pravděpodobnost, že alespoň jedna firma v pokusu neuspěje a opustí trh, je 49%. 8. ŘEŠENÍ Najskôr vyberieme možné pozície čísel 2 a 4- to môžeme uviesť celkom 4x5 spôsobmi, čiže 20. Na zostávajúce pozície musíme dať čísla 1, 3 a 5- jednotka musí byť ako posledná z týchto troch čísel. Z toho vyplýva, že tieto čísla môžeme uviesť iba v poradí 3,5,1 alebo 5,3,1- celkovo dvomi spôsobmi. Dohromady dostávame 20x2 40 rôznych spôsobov. m(a)40 P(A)40/5!40/1201/3 4
5 9. ŘEŠENÍ Najprv označíme javy: R...Riaditeľ je v práci M...Majster dohliada na robotníkov F...Výrobok je chybný P(R) (počas piatich pracovných dní príde dvakrát) P (R ) 1-P(R) P(M/R) P (M /R) 1- P(M/R) P(M/R ) P (M /R ) 1- P(M/R ) P(F/M R) P(F/M R) P(F/M R ) P(F/M R ) a) P(F)? P(F) P(F M R) + P(F M R ) + P(F M R) + P(F M R ) P(F) P(R). P(M/R). P(F/M R) + P(R ). P(M/R ). P(F/M R ) + P(R). P(M /R). P(F/M R) + P(R ). P(M /R ). P(F/M R ) P(F) ,335 b) P(R/F)? P(R/F) (3 4) (4) P (R 5) P(F M R) +P (F M R) + 0,06 P (F) 0,335 P(R/F) (3 4), 0,1791 (4), Pravdepodobnosť, že výrobok bude chybný je 0,335. Ak je výrobok chybný, pravdepodobnosť, že riaditeľ bol v ten deň v práci je 0, ŘEŠENÍ a) P(A1) (8*7*12+8*12*11+8*7*6+8*12*7)/(20*19*18) 0,4 b) P(A2) (8*7*12+8*12*11+12*8*11+12*11*10)/(20*19*18) 0,6 c) P(A2 Ո A1) P(A1) * P(A2 A1) 0,4*((8*7*12+8*12*11)/(20*19*18)) 0,
6 11. ŘEŠENÍ P(A)(30/32)*(29/31)*(28/30)*(27/29)*(26/28)*(25/27)*(24/26)*(23/25)*(22/24)*(21/23)* (20/22)*(19/21)*(18/20)*(2/19) 9 / ŘEŠENÍ '... připraví se &(' ) 0,75 '...nepřipraví se &(' ) 0, zkoušku složí úspěšně &(7) 0,69 &(7 ' ) 0,9 &(7 ' )? Výpočet přes úplnou pravděpodobnost: &(7) &(7 ' ) &(' ) + &(7 ' ) &(' ) 0,69 0,9 0,75 + 0,25 &(7 ' ) &(7 ' ) 0,06 6% Pravděpodobnost, že nepřipravený student zkoušku udělá je 6%. &(' 7) &(' )&(7 ' ) &(7) 0,25 0,06 0,69 0,0217 Pravděpodobnost, že se náhodně vybraný student neučil, pokud víme, že zkoušku složil je 2,17%. 13. ŘEŠENÍ A... zvládne mikroekonomii... P(A) 368/554 0,66426 B...zvládne makroekonomii...p(b) 254/554 0,45848 P(A B) 0,45848 P(B A) P(A B) / P(A) P(B A) 0,45848/0,66426 P(B A) 0,69021 P(B A) 69 % 6
7 14. ŘEŠENÍ - první volba -> Honza princeznu krásku - druhá volba-> Matěj princeznu ošklivku - hledaná pravděpodobnost Matěj ošklivku za předpokladu, že Honza si vybere krásku Mo Matěj, ošklivka Hk Honza, kráska P(Mo/Hk) 3/6 0,5 15. ŘEŠENÍ Nejprve si musíme ujasnit, o jaký typ pravděpodobnosti se jedná. V tomto případě můžeme vyloučit nezávislost jevů (tím pádem není možné jevy násobit), protože podmínkou je, že jevy platí oba zároveň a my hledáme pravděpodobnost této podmínky. Určení a pojmenování jevů: -A. firma se udrží na trhu 40 let P (A)3 540/ ,3540 -B. firma se udrží na trhu 20 let P (B)7 852/ ,7852 K výpočtu použiji obecný vzorec pro podmíněnou pravděpodobnost: Abych si mohla do vzorce dosadit, potřebuji nejprve znát průnik pravděpodobnosti A s pravděpodobností B, ten je možné si velmi lehce odvodit, jelikož jev B je podmnožinou jevu A (aby se firma mohla udržet na trhu 40 let, musí nejprve překonat 20ti letou životnost, jiný možný scénář je pouze odchod firmy z trhu): P (A B) 0,3540 7
8 Poté jen dosadím do vzorce: P (A/B) 0,3540 / 0,7852 P (A/B) 0,4508 P (A/B) 45 % (po zaokrouhlení) Shrnutí slovy: Počítám, s jakou pravděpodobností nastane jev A za podmínky, že platí jev B. V našem případě s jakou pravděpodobností se tedy společnost udrží na trhu 40 let, za předpokladu, že se na trhu udržela před tím 20 let. Složitost podobných příkladů podle mne není ve výpočtu, ale v samotném uvědomění si, jaká pravidla zde platí. Hned na začátku jsme si ujasnili, že se jedná o jevy závislé, nemohu je tedy mezi sebou násobit. Poté je třeba pochopit, že Jev A je podmnožinou jevu B, jelikož firma má pouze 2 možnosti, prosperovat a udržet se na trhu do námi stanovených hranic 20 nebo 40 let, nebo nesplnit tuto podmínku a odejít u trhu dříve. V tomto nejlépe poslouží obrázek. Odpověď: Pravděpodobnost, že se firma udrží na trhu 40 let, je 45 %. 16. ŘEŠENÍ Jav A: Na modrej kocke padla štvorka. Jav B: Súčet je rovných sedem. Do Javu B by sme mohli zaradiť všetky nasledujúce dvojice: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) P(A B)? Musíme zisdť, ktoré dvojice z B platí, že sú zároveň v A, alebo, že na modrej kocke padla 4. Hodnoty sú napísané v tvare: (Červená, Modrá). Z toho vyplýva, že jediné riešenie, ktoré nám vyhovuje je dvojica (3,4). Z toho vyplýva: P(A/B) P(A B)/P(B) 1/6 8
Jiří Neubauer. Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel
 Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Definice P(A/B) pravděpodobnost nastoupení jevu A za předpokladu, že nastal jev B (P(B) > 0) definujeme vztahem
Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Definice P(A/B) pravděpodobnost nastoupení jevu A za předpokladu, že nastal jev B (P(B) > 0) definujeme vztahem
Matematika I 2a Konečná pravděpodobnost
 Matematika I 2a Konečná pravděpodobnost Jan Slovák Masarykova univerzita Fakulta informatiky 24. 9. 2012 Obsah přednášky 1 Pravděpodobnost 2 Nezávislé jevy 3 Geometrická pravděpodobnost Viděli jsme už
Matematika I 2a Konečná pravděpodobnost Jan Slovák Masarykova univerzita Fakulta informatiky 24. 9. 2012 Obsah přednášky 1 Pravděpodobnost 2 Nezávislé jevy 3 Geometrická pravděpodobnost Viděli jsme už
Intuitivní pojem pravděpodobnosti
 Pravděpodobnost Intuitivní pojem pravděpodobnosti Intuitivní pojem pravděpodobnosti Pravděpodobnost zkoumaného jevu vyjadřuje míru naděje, že tento jev nastane. Řekneme-li, že má nějaký jev pravděpodobnost
Pravděpodobnost Intuitivní pojem pravděpodobnosti Intuitivní pojem pravděpodobnosti Pravděpodobnost zkoumaného jevu vyjadřuje míru naděje, že tento jev nastane. Řekneme-li, že má nějaký jev pravděpodobnost
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Náhodný jev a definice pravděpodobnosti
 Náhodný jev a definice pravděpodobnosti Obsah kapitoly Náhodný jev. Vztahy mezi náhodnými jevy. Pravidla pro počítání s pravděpodobnostmi. Formule úplné pravděpodobnosti a Bayesův vzorec. Studijní cíle
Náhodný jev a definice pravděpodobnosti Obsah kapitoly Náhodný jev. Vztahy mezi náhodnými jevy. Pravidla pro počítání s pravděpodobnostmi. Formule úplné pravděpodobnosti a Bayesův vzorec. Studijní cíle
Náhodné jevy. Teorie pravděpodobnosti. Náhodné jevy. Operace s náhodnými jevy
 Teorie pravděpodobnosti Náhodný pokus skončí jedním z řady možných výsledků předem nevíme, jak skončí (náhoda) příklad: hod kostkou, zítřejší počasí,... Pravděpodobnost zkoumá náhodné jevy (mohou, ale
Teorie pravděpodobnosti Náhodný pokus skončí jedním z řady možných výsledků předem nevíme, jak skončí (náhoda) příklad: hod kostkou, zítřejší počasí,... Pravděpodobnost zkoumá náhodné jevy (mohou, ale
Matematika III. 4. října Vysoká škola báňská - Technická univerzita Ostrava. Matematika III
 Vysoká škola báňská - Technická univerzita Ostrava 4. října 2018 Podmíněná pravděpodobnost Při počítání pravděpodobnosti můžeme k náhodnému pokusu přidat i nějakou dodatečnou podmínku. Podmíněná pravděpodobnost
Vysoká škola báňská - Technická univerzita Ostrava 4. října 2018 Podmíněná pravděpodobnost Při počítání pravděpodobnosti můžeme k náhodnému pokusu přidat i nějakou dodatečnou podmínku. Podmíněná pravděpodobnost
3. Podmíněná pravděpodobnost a Bayesův vzorec
 3. Podmíněná pravděpodobnost a Bayesův vzorec Poznámka: V některých úlohách řešíme situaci, kdy zkoumáme pravděpodobnost náhodného jevu za dalších omezujících podmínek. Nejčastěji má omezující podmínka
3. Podmíněná pravděpodobnost a Bayesův vzorec Poznámka: V některých úlohách řešíme situaci, kdy zkoumáme pravděpodobnost náhodného jevu za dalších omezujících podmínek. Nejčastěji má omezující podmínka
Řešené příklady z pravděpodobnosti:
 Řešené příklady z pravděpodobnosti: 1. Honza se ze šedesáti maturitních otázek 10 nenaučil. Při zkoušce si losuje dvě otázky. a. Určete pravděpodobnost jevu A, že si vylosuje pouze otázky, které se naučil.
Řešené příklady z pravděpodobnosti: 1. Honza se ze šedesáti maturitních otázek 10 nenaučil. Při zkoušce si losuje dvě otázky. a. Určete pravděpodobnost jevu A, že si vylosuje pouze otázky, které se naučil.
Náhodný pokus Náhodným pokusem (stručněji pokusem) rozumíme každé uskutečnění určitého systému podmínek resp. pravidel.
 Základy teorie pravděpodobnosti Náhodný pokus Náhodným pokusem (stručněji pokusem) rozumíme každé uskutečnění určitého systému podmínek resp. pravidel. Poznámka: Výsledek pokusu není předem znám (výsledek
Základy teorie pravděpodobnosti Náhodný pokus Náhodným pokusem (stručněji pokusem) rozumíme každé uskutečnění určitého systému podmínek resp. pravidel. Poznámka: Výsledek pokusu není předem znám (výsledek
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Základy teorie pravděpodobnosti
 Základy teorie pravděpodobnosti Náhodný jev Pravděpodobnost náhodného jevu Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 15. srpna 2012 Statistika
Základy teorie pravděpodobnosti Náhodný jev Pravděpodobnost náhodného jevu Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 15. srpna 2012 Statistika
Pravděpodobnost a její vlastnosti
 Pravděpodobnost a její vlastnosti 1 Pravděpodobnost a její vlastnosti Náhodné jevy Náhodný jev je výsledek pokusu (tj. realizace určitého systému podmínek) a jeho charakteristickým rysem je, že může, ale
Pravděpodobnost a její vlastnosti 1 Pravděpodobnost a její vlastnosti Náhodné jevy Náhodný jev je výsledek pokusu (tj. realizace určitého systému podmínek) a jeho charakteristickým rysem je, že může, ale
( ) ( ) 9.2.7 Nezávislé jevy I. Předpoklady: 9204
 9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
2. přednáška - PRAVDĚPODOBNOST
 2. přednáška - PRAVDĚPODOBNOST NÁHODNÝ POKUS A JEV Každá opakovatelná činnost prováděná za stejných nebo přibližně stejných podmínek, jejíž výsledek je nejistý a závisí na náhodě, se nazývá náhodný pokus.
2. přednáška - PRAVDĚPODOBNOST NÁHODNÝ POKUS A JEV Každá opakovatelná činnost prováděná za stejných nebo přibližně stejných podmínek, jejíž výsledek je nejistý a závisí na náhodě, se nazývá náhodný pokus.
pravděpodobnosti Pravděpodobnost je teorií statistiky a statistika je praxí teorie pravděpodobnosti.
 3.1 Základy teorie pravděpodobnosti Pravděpodobnost je teorií statistiky a statistika je praxí teorie pravděpodobnosti. Co se dozvíte Náhodný pokus a náhodný jev. Pravděpodobnost, počítání s pravděpodobnostmi.
3.1 Základy teorie pravděpodobnosti Pravděpodobnost je teorií statistiky a statistika je praxí teorie pravděpodobnosti. Co se dozvíte Náhodný pokus a náhodný jev. Pravděpodobnost, počítání s pravděpodobnostmi.
pravděpodobnosti a Bayesova věta
 NMUMP0 (Pravděpodobnost a matematická statistika I) Nezávislost, podmíněná pravděpodobnost, věta o úplné pravděpodobnosti a Bayesova věta. Házíme dvěma pravidelnými kostkami. (a) Jaká je pravděpodobnost,
NMUMP0 (Pravděpodobnost a matematická statistika I) Nezávislost, podmíněná pravděpodobnost, věta o úplné pravděpodobnosti a Bayesova věta. Házíme dvěma pravidelnými kostkami. (a) Jaká je pravděpodobnost,
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
MANUÁL K PROGRAMU MATEMATIKA 2.0 STIAHNUTIE A INŠTALÁCIA PROGRAMU:
 MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
Úvod do teorie pravděpodobnosti
 Úvod do teorie pravděpodobnosti Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 33 Obsah 1 Náhodné jevy 2 Pravděpodobnost 3 Podmíněná
Úvod do teorie pravděpodobnosti Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 33 Obsah 1 Náhodné jevy 2 Pravděpodobnost 3 Podmíněná
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol PRAVDĚPODOBNOST
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol PRAVDĚPODOBNOST
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor016 Vypracoval(a),
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor016 Vypracoval(a),
Vzdělávací karetní. Vzdělávací pomůcka. Určeno dětem od 3 do 5 let. volí libovolné otázky případně pořadí dětí, které budou na tahu.
 Vzdělávací karetní BARVY hra Úkolem této hry je naučit děti rozeznávat základní barvy. Princip je založen na komunikaci rodiče nebo pedagoga s dítětem. Hry se může zúčastnit 1 až 6 dětí pod vedením dospělé
Vzdělávací karetní BARVY hra Úkolem této hry je naučit děti rozeznávat základní barvy. Princip je založen na komunikaci rodiče nebo pedagoga s dítětem. Hry se může zúčastnit 1 až 6 dětí pod vedením dospělé
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Informační a znalostní systémy
 Informační a znalostní systémy Teorie pravděpodobnosti není v podstatě nic jiného než vyjádření obecného povědomí počítáním. P. S. de Laplace Pravděpodobnost a relativní četnost Pokusy, výsledky nejsou
Informační a znalostní systémy Teorie pravděpodobnosti není v podstatě nic jiného než vyjádření obecného povědomí počítáním. P. S. de Laplace Pravděpodobnost a relativní četnost Pokusy, výsledky nejsou
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: Název projektu školy: Šablona III/2: CZ.1.07/1.5.00/34.0536 Výuka s ICT na SŠ obchodní České
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: Název projektu školy: Šablona III/2: CZ.1.07/1.5.00/34.0536 Výuka s ICT na SŠ obchodní České
Klasifikačný poriadok pre jednotlivé vyučovacie predmety
 Spojená katolícka škola v Nitre Gymnázium sv. Cyrila a Metoda Klasifikačný poriadok pre jednotlivé vyučovacie predmety V Nitre, 1. októbra 2012 Schválil: Mgr. Ing. Karol Žák, CSc., riaditeľ školy Úvod
Spojená katolícka škola v Nitre Gymnázium sv. Cyrila a Metoda Klasifikačný poriadok pre jednotlivé vyučovacie predmety V Nitre, 1. októbra 2012 Schválil: Mgr. Ing. Karol Žák, CSc., riaditeľ školy Úvod
Pravdepodobnosť. Rozdelenia pravdepodobnosti
 Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Jevy, které za daných podmínek mohou, ale nemusí nastat, nazýváme náhodnými jevy. Příklad: při hodu hrací kostkou padne trojka
 Náhodný jev Mějme určitý soubor podmínek. Provedeme pokus, který budeme chtít zopakovat. Pokud opakování pokusu při zachování nám známých podmínek nevede k jednoznačnému výsledku, můžeme se domnívat, že
Náhodný jev Mějme určitý soubor podmínek. Provedeme pokus, který budeme chtít zopakovat. Pokud opakování pokusu při zachování nám známých podmínek nevede k jednoznačnému výsledku, můžeme se domnívat, že
Obsah. Základy teorie pravděpodobnosti Náhodný jev Pravděpodobnost náhodného jevu Pravděpodobnost. Pravděpodobnost. Děj pokus jev
 Obsah Základy teorie pravděpodobnosti Náhodný jev Pravděpodobnost náhodného jevu Definice pojmů Náhodný jev Pravděpodobnost Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi;-) roman.biskup(at)email.cz
Obsah Základy teorie pravděpodobnosti Náhodný jev Pravděpodobnost náhodného jevu Definice pojmů Náhodný jev Pravděpodobnost Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi;-) roman.biskup(at)email.cz
Inženýrská statistika pak představuje soubor postupů a aplikací teoretických principů v oblasti inženýrské činnosti.
 Přednáška č. 1 Úvod do statistiky a počtu pravděpodobnosti Statistika Statistika je věda a postup jak rozvíjet lidské znalosti použitím empirických dat. Je založena na matematické statistice, která je
Přednáška č. 1 Úvod do statistiky a počtu pravděpodobnosti Statistika Statistika je věda a postup jak rozvíjet lidské znalosti použitím empirických dat. Je založena na matematické statistice, která je
letní semestr Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy Matematická statistika
 Šárka Hudecová Katedra i a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 1 1 Založeno na materiálech doc. Michala Kulicha Organizační pokyny k přednášce přednáškové
Šárka Hudecová Katedra i a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 1 1 Založeno na materiálech doc. Michala Kulicha Organizační pokyny k přednášce přednáškové
AR, MA a ARMA procesy
 Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Diskrétní matematika. DiM /01, zimní semestr 2016/2017
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
KOMBINATORICKÉ PRAVIDLO SÚČINU
 KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
Pravděpodobnost a statistika
 Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
(iv) D - vybíráme 2 koule a ty mají různou barvu.
 2 cvičení - pravděpodobnost 2102018 18cv2tex Definice pojmů a záladní vzorce Vlastnosti pravděpodobnosti Pravděpodobnost P splňuje pro libovolné jevy A a B následující vlastnosti: 1 0, 1 2 P (0) = 0, P
2 cvičení - pravděpodobnost 2102018 18cv2tex Definice pojmů a záladní vzorce Vlastnosti pravděpodobnosti Pravděpodobnost P splňuje pro libovolné jevy A a B následující vlastnosti: 1 0, 1 2 P (0) = 0, P
Lékařská biofyzika, výpočetní technika I. Biostatistika Josef Tvrdík (doc. Ing. CSc.)
 Lékařská biofyzika, výpočetní technika I Biostatistika Josef Tvrdík (doc. Ing. CSc.) Přírodovědecká fakulta, katedra informatiky josef.tvrdik@osu.cz konzultace úterý 14.10 až 15.40 hod. http://www1.osu.cz/~tvrdik
Lékařská biofyzika, výpočetní technika I Biostatistika Josef Tvrdík (doc. Ing. CSc.) Přírodovědecká fakulta, katedra informatiky josef.tvrdik@osu.cz konzultace úterý 14.10 až 15.40 hod. http://www1.osu.cz/~tvrdik
IB112 Základy matematiky
 IB112 Základy matematiky Základy kombinatoriky a kombinatorická pravděpodobnost Jan Strejček Obsah IB112 Základy matematiky: Základy kombinatoriky a kombinatorická pravděpodobnost 2/57 Výběry prvků bez
IB112 Základy matematiky Základy kombinatoriky a kombinatorická pravděpodobnost Jan Strejček Obsah IB112 Základy matematiky: Základy kombinatoriky a kombinatorická pravděpodobnost 2/57 Výběry prvků bez
Statistika (KMI/PSTAT)
 Statistika (KMI/PSTAT) Cvičení šesté aneb Podmíněná pravděpodobnost Statistika (KMI/PSTAT) 1 / 13 Pravděpodobnost náhodných jevů Po dnešní hodině byste měli být schopni: rozumět pojmu podmíněná pravděpodobnost
Statistika (KMI/PSTAT) Cvičení šesté aneb Podmíněná pravděpodobnost Statistika (KMI/PSTAT) 1 / 13 Pravděpodobnost náhodných jevů Po dnešní hodině byste měli být schopni: rozumět pojmu podmíněná pravděpodobnost
Pravděpodobnost a statistika, Biostatistika pro kombinované studium. Jan Kracík
 Pravděpodobnost a statistika, Biostatistika pro kombinované studium Letní semestr 2016/2017 Tutoriál č. 1: Kombinatorika, úvod do teorie pravděpodobnosti Jan Kracík jan.kracik@vsb.cz Kombinatorika Kombinatorika
Pravděpodobnost a statistika, Biostatistika pro kombinované studium Letní semestr 2016/2017 Tutoriál č. 1: Kombinatorika, úvod do teorie pravděpodobnosti Jan Kracík jan.kracik@vsb.cz Kombinatorika Kombinatorika
5.1. Klasická pravděpodobnst
 5. Pravděpodobnost Uvažujme množinu Ω všech možných výsledků náhodného pokusu, například hodu mincí, hodu kostkou, výběru karty z balíčku a podobně. Tato množina se nazývá základní prostor a její prvky
5. Pravděpodobnost Uvažujme množinu Ω všech možných výsledků náhodného pokusu, například hodu mincí, hodu kostkou, výběru karty z balíčku a podobně. Tato množina se nazývá základní prostor a její prvky
Určeno studentům středního vzdělávání s maturitní zkouškou, 4. ročník, okruh Základy počtu pravděpodobnosti
 PRAVDĚPODOBNOST anotace Určeno studentům středního vzdělávání s maturitní zkouškou, 4. ročník, okruh Základy počtu pravděpodobnosti VM vytvořil: Mgr. Marie Zapadlová Období vytvoření VM: září 2013 Klíčová
PRAVDĚPODOBNOST anotace Určeno studentům středního vzdělávání s maturitní zkouškou, 4. ročník, okruh Základy počtu pravděpodobnosti VM vytvořil: Mgr. Marie Zapadlová Období vytvoření VM: září 2013 Klíčová
Diskrétní matematika. DiM /01, zimní semestr 2018/2019
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2018/2019 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Matematika test. Cesta trvala hodín a minút.
 GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
MATEMATIKA III V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA III V PŘÍKLADECH Cvičení 3 Pravděpodobnost jevů Mgr. Petr Otipka Ostrava 2013 Mgr. Petr Otipka Vysoká škola báňská Technická
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA III V PŘÍKLADECH Cvičení 3 Pravděpodobnost jevů Mgr. Petr Otipka Ostrava 2013 Mgr. Petr Otipka Vysoká škola báňská Technická
Tomáš Karel LS 2012/2013
 Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
1. Gigabajty si hneď v prvom kroku premeníme na gigabity a postupne premieňame na bity.
 1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
Imagine. Popis prostredia:
 Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Ak stlačíme OK, prebehne výpočet a v bunke B1 je výsledok.
 Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
nastavenie a realizácia vzájomných zápočtov v Money S4 / Money S5
 VZÁJOMNE ZÁPOČTY nastavenie a realizácia vzájomných zápočtov v Money S4 / Money S5 Aparát vzájomných zápočtov v Money S4/S5 slúži k návrhu vzájomných zápočtov pohľadávok a záväzkov a následne k automatickej
VZÁJOMNE ZÁPOČTY nastavenie a realizácia vzájomných zápočtov v Money S4 / Money S5 Aparát vzájomných zápočtov v Money S4/S5 slúži k návrhu vzájomných zápočtov pohľadávok a záväzkov a následne k automatickej
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ MS EXCEL. 1. Zadáme prvky matice A a B do buniek pracovného hárku zošita MS Excel
 RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
RIEŠENIE NIEKTORÝCH ÚLOH LINEÁRNEJ ALGEBRY V PROSTREDÍ I. VÝPOČET SÚČINU MATÍC Vypočítajme súčin matíc C = A B, ak existuje, pre dané matice A a B. 1. Zadáme prvky matice A a B do buniek pracovného hárku
Import Excel Univerzál
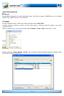 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Školská sieť EDU. Rozdelenie škôl. Obsah: Deleba škôl podľa času zaradenia do projektu: Delba škôl podľa rýchlosti pripojenia:
 Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
cv3.tex. Vzorec pro úplnou pravděpodobnost
 3 cvičení - pravděpodobnost 2102018 18cv3tex n i=1 Vzorec pro úplnou pravděpodobnost Systém náhodných jevů nazýváme úplným, jestliže pro něj platí: B i = 1 a pro i k je B i B k = 0 Jestliže je (Ω, A, P
3 cvičení - pravděpodobnost 2102018 18cv3tex n i=1 Vzorec pro úplnou pravděpodobnost Systém náhodných jevů nazýváme úplným, jestliže pro něj platí: B i = 1 a pro i k je B i B k = 0 Jestliže je (Ω, A, P
Začínam so zadaním z NEPOUŽÍVAME ROZSAH POKIAĽ HO MUSÍME PRESKOČIŤ
 Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
Chcela som urobiť rozumný tútoriál, netuším či to niekomu pomože, pevne verím že aspoň jeden taký sa nájde pretože keď tomu rozumiem ja tak musí aj total magor tomu rozumieť! Začínam so zadaním z 9.11.2010
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
( ) ( ) Binomické rozdělení. Předpoklady: 9209
 9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů b) dá alespoň jeden koš c) dá nejdříve
9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů b) dá alespoň jeden koš c) dá nejdříve
náhodný jev je podmnožinou
 Pravděpodobnost Dovednosti a cíle - Chápat jev A jako podmnožinu množiny, která značí množinu všech výsledků náhodného děje. - Umět zapsat jevy pomocí množinových operací a obráceně umět z množinového
Pravděpodobnost Dovednosti a cíle - Chápat jev A jako podmnožinu množiny, která značí množinu všech výsledků náhodného děje. - Umět zapsat jevy pomocí množinových operací a obráceně umět z množinového
Náhodný jev. Jevy, které za daných podmínek mohou, ale nemusí nastat, nazýváme náhodnými jevy.
 Náhodný jev Mějme určitý soubor podmínek. Provedeme pokus, který budeme chtít zopakovat. Pokud opakování pokusu při zachování nám známých podmínek nevede k jednoznačnému výsledku, můžeme se domnívat, že
Náhodný jev Mějme určitý soubor podmínek. Provedeme pokus, který budeme chtít zopakovat. Pokud opakování pokusu při zachování nám známých podmínek nevede k jednoznačnému výsledku, můžeme se domnívat, že
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
f( x) x x 4.3. Asymptoty funkce Definice lim f( x) =, lim f( x) =, Jestliže nastane alespoň jeden z případů
 3 Výklad Definice 3 Jestliže nastane alespoň jeden z případů lim =, lim =, + + lim =, lim =, kde ( D ), pak říkáme, že přímka = je asymptotou funkce f() v bodě f Jestliže lim ( k q) =, resp lim ( k q)
3 Výklad Definice 3 Jestliže nastane alespoň jeden z případů lim =, lim =, + + lim =, lim =, kde ( D ), pak říkáme, že přímka = je asymptotou funkce f() v bodě f Jestliže lim ( k q) =, resp lim ( k q)
, 1. skupina (16:15-17:45) Jméno: se. Postup je třeba odůvodnit (okomentovat) nebo uvést výpočet. Výsledek bez uvedení jakéhokoliv
 42206, skupina (6:5-7:45) Jméno: Zápočtový test z PSI Nezapomeňte podepsat VŠECHNY papíry, které odevzdáváte Škrtejte zřetelně a stejně zřetelně pište i věci, které platí Co je škrtnuto, nebude bráno v
42206, skupina (6:5-7:45) Jméno: Zápočtový test z PSI Nezapomeňte podepsat VŠECHNY papíry, které odevzdáváte Škrtejte zřetelně a stejně zřetelně pište i věci, které platí Co je škrtnuto, nebude bráno v
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
( ) ( ) 9.2.10 Binomické rozdělení. Předpoklady: 9209
 9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů; b) dá alespoň jeden koš; c) dá nejdříve
9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů; b) dá alespoň jeden koš; c) dá nejdříve
TEORIE PRAVDĚPODOBNOSTI. 2. cvičení
 TEORIE RAVDĚODONOSTI 2. cvičení Základní pojmy Klasická def. Statistická def. Geometrická def. odmíněná prav. ayesův teorém Test Základní pojmy Náhodný pokus - je každý konečný děj, jehož výsledek není
TEORIE RAVDĚODONOSTI 2. cvičení Základní pojmy Klasická def. Statistická def. Geometrická def. odmíněná prav. ayesův teorém Test Základní pojmy Náhodný pokus - je každý konečný děj, jehož výsledek není
Vzorová písemka č. 1 (rok 2015/2016) - řešení
 Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
řešeny numericky 6 Obyčejné diferenciální rovnice řešeny numericky
 řešeny numericky řešeny numericky Břetislav Fajmon, UMAT FEKT, VUT Brno Na minulé přednášce jsme viděli některé klasické metody a přístupy pro řešení diferenciálních rovnic: stručně řečeno, rovnice obsahující
řešeny numericky řešeny numericky Břetislav Fajmon, UMAT FEKT, VUT Brno Na minulé přednášce jsme viděli některé klasické metody a přístupy pro řešení diferenciálních rovnic: stručně řečeno, rovnice obsahující
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Komisionální přezkoušení 1T (druhé pololetí) 2 x. 1) Z dané rovnice vypočtěte neznámou x:. 2) Určete, pro která x R není daný výraz definován:
 1) Z dané rovnice vypočtěte neznámou :. ) Určete, pro která R není daný výraz definován: 3) Určete obor hodnot funkce Komisionální přezkoušení 1T (druhé pololetí) f : y 4 3. 4 8 5 1 4) Vyšetřete vzájemnou
1) Z dané rovnice vypočtěte neznámou :. ) Určete, pro která R není daný výraz definován: 3) Určete obor hodnot funkce Komisionální přezkoušení 1T (druhé pololetí) f : y 4 3. 4 8 5 1 4) Vyšetřete vzájemnou
Populace vs. data. popisná (deskriptivní) popis konkrétních dat. letní semestr 2012 1
 ? Šárka Hudecová Katedra i a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 1? Statistika = věda o získávání, zpracování a interpretaci informace obsažené v
? Šárka Hudecová Katedra i a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy letní semestr 2012 1? Statistika = věda o získávání, zpracování a interpretaci informace obsažené v
Cvičení ze statistiky - 5. Filip Děchtěrenko
 Cvičení ze statistiky - 5 Filip Děchtěrenko Minule bylo.. Začali jsme pravděpodobnost Klasická a statistická definice pravděpodobnosti Náhodný jev Doplněk, průnik, sjednocení Podmíněná pravděpodobnost
Cvičení ze statistiky - 5 Filip Děchtěrenko Minule bylo.. Začali jsme pravděpodobnost Klasická a statistická definice pravděpodobnosti Náhodný jev Doplněk, průnik, sjednocení Podmíněná pravděpodobnost
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
 Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
Dobývání znalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Dobývání znalostí Pravděpodobnost a učení Doc. RNDr. Iveta Mrázová,
RIZIKO V PODNIKU. Prípadová štúdia 2. Ing. Michal Tkáč, PhD.
 RIZIKO V PODNIKU Prípadová štúdia 2 Ing. Michal Tkáč, PhD. Tento učebný text je venovaný hlavne študentom 1. ročníka II. stupňa Podnikovohospodárskej fakulty, Ekonomickej univerzity v Bratislave. Text
RIZIKO V PODNIKU Prípadová štúdia 2 Ing. Michal Tkáč, PhD. Tento učebný text je venovaný hlavne študentom 1. ročníka II. stupňa Podnikovohospodárskej fakulty, Ekonomickej univerzity v Bratislave. Text
5. Na množině R řeš rovnici: 5 x 2 2 x Urči všechna reálná čísla n vyhovující nerovnostem: 3 5
 I 16 VADRO (váha 80) E 1. Na obrázku vpravo je graf funkce g dané předpisem: y = a + b + c. Urči koeficienty a, b, c.. Zapiš definiční obor a obor hodnot funkce f na obrázku vpravo. f: y = 0,5 4 + 3. Na
I 16 VADRO (váha 80) E 1. Na obrázku vpravo je graf funkce g dané předpisem: y = a + b + c. Urči koeficienty a, b, c.. Zapiš definiční obor a obor hodnot funkce f na obrázku vpravo. f: y = 0,5 4 + 3. Na
f(x) = arccotg x 2 x lim f(x). Určete všechny asymptoty grafu x 2 2 =
 Řešení vzorové písemky z předmětu MAR Poznámky: Řešení úloh ze vzorové písemky jsou formulována dosti podrobně podobným způsobem jako u řešených příkladů ve skriptech U zkoušky lze jednotlivé kroky postupu
Řešení vzorové písemky z předmětu MAR Poznámky: Řešení úloh ze vzorové písemky jsou formulována dosti podrobně podobným způsobem jako u řešených příkladů ve skriptech U zkoušky lze jednotlivé kroky postupu
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Práce s daty, kombinatorika a pravděpodobnost Gradovaný řetězec úloh Téma: Pravděpodobnost
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Práce s daty, kombinatorika a pravděpodobnost Gradovaný řetězec úloh Téma: Pravděpodobnost
1.2.9 Usměrňování zlomků
 9 Usměrňování zlomků Předpoklady: 0008 Pedagogická poznámka: Celá hodina by měla být naplňováním jediné myšlenky Při usměrňování rozšiřujeme zlomek tím, co potřebujeme Fakt, že si příklad upravíme, jak
9 Usměrňování zlomků Předpoklady: 0008 Pedagogická poznámka: Celá hodina by měla být naplňováním jediné myšlenky Při usměrňování rozšiřujeme zlomek tím, co potřebujeme Fakt, že si příklad upravíme, jak
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
KOMBINATORIKA. 1. cvičení
 KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
KOMBINATORIKA 1. cvičení Co to je kombinatorika Kombinatorika je vstupní branou do teorie pravděpodobnosti. Zabývá se různými způsoby výběru prvků z daného souboru. 2011 Ing. Janurová Kateřina, FEI VŠB-TU
Pravděpodobnost a aplikovaná statistika
 Pravděpodobnost a aplikovaná statistika MGR. JANA SEKNIČKOVÁ, PH.D. 1. KAPITOLA - PRAVDĚPODOBNOST 2.10.2017 Kontakt Mgr. Jana Sekničková, Ph.D. jana.seknickova@vse.cz Katedra softwarového inženýrství Fakulta
Pravděpodobnost a aplikovaná statistika MGR. JANA SEKNIČKOVÁ, PH.D. 1. KAPITOLA - PRAVDĚPODOBNOST 2.10.2017 Kontakt Mgr. Jana Sekničková, Ph.D. jana.seknickova@vse.cz Katedra softwarového inženýrství Fakulta
Finančné riaditeľstvo Slovenskej republiky
 Finančné riaditeľstvo Slovenskej republiky Informácia k odpočtu daňovej straty v tabuľke D tlačiva daňového priznania k dani z príjmov právnickej osoby Daňovník - právnická osoba so zdaňovacím obdobím
Finančné riaditeľstvo Slovenskej republiky Informácia k odpočtu daňovej straty v tabuľke D tlačiva daňového priznania k dani z príjmov právnickej osoby Daňovník - právnická osoba so zdaňovacím obdobím
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Kombinatorika a úvod do pravděpodobnosti
 Kombinatorika a úvod do pravděpodobnosti Jiří Fišer 27. září 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 27. září 2011 1/ 18 Variacek-tétřídyznprvků: = uspořádanéskupinyokprvcíchvybranýchznprvků. Permutace
Kombinatorika a úvod do pravděpodobnosti Jiří Fišer 27. září 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 27. září 2011 1/ 18 Variacek-tétřídyznprvků: = uspořádanéskupinyokprvcíchvybranýchznprvků. Permutace
Matematika test. 1. Doplň do štvorčeka číslo tak, aby platila rovnosť: (a) 9 + = (b) : 12 = 720. (c) = 151. (d) : 11 = 75 :
 GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
{ 3;4;5;6 } pravděpodobnost je zřejmě 4 = 2.
 9..3 Pravděpodobnosti jevů I Předpoklady: 90 Opět se vrátíme k hodu kostkou. Pokus má šest stejně pravděpodobných náhodných výsledků pravděpodobnost každého z nich je 6. Do domečku nám chybí tři políčka.
9..3 Pravděpodobnosti jevů I Předpoklady: 90 Opět se vrátíme k hodu kostkou. Pokus má šest stejně pravděpodobných náhodných výsledků pravděpodobnost každého z nich je 6. Do domečku nám chybí tři políčka.
Rovnice přímky vypsané příklady. Parametrické vyjádření přímky
 Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
II.7.* Derivace složené funkce. Necht jsou dány diferencovatelné funkce z = f(x,y), x = x(u,v), y = y(u,v). Pak. z u = f. x x. u + f. y y. u, z.
 II.7.* Derivace složené funkce Necht jsou dán diferencovatelné funkce z = f(,), = (u,v), = (u,v). Pak u = u + u, v = v + v. Vpočítejte derivace daných diferencovatelných funkcí. Příklad 0. Jsou dán diferencovatelné
II.7.* Derivace složené funkce Necht jsou dán diferencovatelné funkce z = f(,), = (u,v), = (u,v). Pak u = u + u, v = v + v. Vpočítejte derivace daných diferencovatelných funkcí. Příklad 0. Jsou dán diferencovatelné
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Pravděpodobnost a aplikovaná statistika
 Pravděpodobnost a aplikovaná statistika MGR. JANA SEKNIČKOVÁ, PH.D. 2. KAPITOLA PODMÍNĚNÁ PRAVDĚPODOBNOST 3. KAPITOLA NÁHODNÁ VELIČINA 9.11.2017 Opakování Uveďte příklad aplikace geometrické definice pravděpodobnosti
Pravděpodobnost a aplikovaná statistika MGR. JANA SEKNIČKOVÁ, PH.D. 2. KAPITOLA PODMÍNĚNÁ PRAVDĚPODOBNOST 3. KAPITOLA NÁHODNÁ VELIČINA 9.11.2017 Opakování Uveďte příklad aplikace geometrické definice pravděpodobnosti
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
PRAVDĚPODOBNOST A JEJÍ UŽITÍ
 PRAVDĚPODOBNOST A JEJÍ UŽITÍ Základním pojmem teorie pravděpodobnosti je náhodný jev. náhodný jev : výsledek nějaké činnosti nebo pokusu, o němž má smysl prohlásit že nastal nebo ne. Náhodné jevy se označují
PRAVDĚPODOBNOST A JEJÍ UŽITÍ Základním pojmem teorie pravděpodobnosti je náhodný jev. náhodný jev : výsledek nějaké činnosti nebo pokusu, o němž má smysl prohlásit že nastal nebo ne. Náhodné jevy se označují
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY
 VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY Vektoru můžeme přisoudit velikost. S vektory také můžeme provádět početní operace, které jsme zvyklí provádět s čísly, tzn. že je možné je sčítat, odčítat a
VELIKOST VEKTORU, POČETNÍ OPERACE S VEKTORY Vektoru můžeme přisoudit velikost. S vektory také můžeme provádět početní operace, které jsme zvyklí provádět s čísly, tzn. že je možné je sčítat, odčítat a
