Množiny, relácie, zobrazenia
|
|
|
- Jiří Bílek
- před 7 lety
- Počet zobrazení:
Transkript
1 Množiny, relácie, zobrazenia
2 Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami, považovaných za jeden celok. " Objekty tohto súboru sa nazývajú prvky alebo elementy množiny x A (x je prvkom množiny A) y A (y nepatrí do množiny A) Množiny môže byť daná charakteristickou vlastnosťou vymenovaním jej prvkov Množina B je podmnožinou množina A, ak každý prvok množiny B je zároveň prvkom množiny A, t.j. B A x : x B x A
3 Množina, ktorá neobsahuje žiadny prvok sa nazýva prázdna a označuje sa. Základné operácie s množinami A prienikom B A B je množina, ktorej prvky patria súčasne do A aj B. A zjednotenie B A B je množina, do ktorej patria všetky objekty, ktoré sú prvkami A alebo prvkami B. Rozdiel B a A B A. je množina pozostávajúca zo všetkých objektov, ktoré sú prvkami B, ale nie sú prvkami A. Karteziiánskym súčiinom množín A a B je množina, ktorej prvkami sú usporiadané dvojice [x 1, x 2 ], kde x 1 A, x 2 B a označujeme A B.
4 Množina A sa rovná množine B, ak obe množiny obsahujú tie isté prvky A = B x : x A x B Množina všetkých podmnožin danej množiny A sa nazýva potenčná množina P(A) Množiny A, B sa nazývajú disjunktné, ak A B =. Množina prirodzených čísel je najmenšia podmnožina množiny reálnych čísel R, pre ktorú platí : i ) 1 N ii) Ak množina N obsahuje číslo k, tak obsahuje aj číslo k+1
5 Dôkaz matematickou indukciou : Predpokladajme, že každému prirodzenému číslu n je priradený (pravdivý alebo nepravdivý) výrok P(n ). Ak I. výrok P( 1 ) je pravdivý II. pre každé prirodzenéčíslo k z platnosti výroku P(k )vyplýva platnosť výroku P(k + 1 ), tak výrok P(n ) platí pre každé prirodzenéčíslo Úplna matematická indukcia : Predpokladajme, že každému prirodzenému číslu n je priradený (pravdivý alebo nepravdivý) výrok P(n ). Ak pre každé prirodzenéčíslo k < n z platnosti výroku P(k ) vyplýva platnosť výroku P(n ), tak výrok P(n ) platí pre každé prirodzenéčíslo n.
6 Relácie a zobrazenia Karteziánsky súčin n množín A 1, A 2,..., A n, je A 1 A 2... A n. Prvkom karteziánskeho súčinu A 1 A 2... A n je usporiadaná n-tica [x 1, x 2,..., x n ], kde x i A i, 1 i n Podmnožinu karteziánskeho súčinu A A... A = A n, n N nazývame n-árnou reláciou na množine A. Poznámka : pre n = 1 nazývame unárna relácia, pre n = 2 nazývame binárna relácia, pre n = 3 nazývame ternárna relácia Binárna relácia E na množine A sa nazýva reflexívna, ak pre každé a A platí aea, symetrická, ak z platnosti aeb vyplýva bea, antisymetrická, ak z platnosti aeb a zároveň bea vyplýva a = b, tranzitívna, ak z platnosti aeb a zároveň bec vyplýva aec,
7 Binárna relácia na množine A, ktorá je reflexívna, symetrická a tranzitívna sa nazýva ekvivalencia alebo relácia ekvivalencie na množine A Binárna relácia E A 2, ktorá je reflexívna, antisymetrická a tranzitívna sa nazýva reláciou čiastočného usporiadania na množine A, resp. čiastočným usporiadaním množiny A. Zobrazenie f z množiny A do množiny B chápeme ako určité pravidlo, ktoré každému prvku a z množiny A jednoznačne priradí prvok b z množiny B. T.j. [ a, b1 ] f [ a b2 ] f b1 2 a A, b = b 1, b2 B,, Nech f: A B, g: B C sú zobrazenia. Potom kompozíciu (zložené zobrazenie) f g je zobrazením f g f: A C, kde (f g)(x)=g(f(x)) pre x, ktoré patria do definičného oboru f a f(x) do definičného oboru g(x).
8 Zobrazenie f : A B nazývame : injektívne (prosté) akk pre každé x 1, x 2 A, platí ak x 1 x 2 potom f(x 1 ) f(x 2 )A surjektívne (na) akk ku každému y B existuje aspoň jedno x A také, že y = f(x) bijektívne akk je injektívne a zároveň surjektívne x 1 y 1 x 1 y 1 x 1 y 1 x 1 y 1 x 2 y 2 x 3 y 3 x 2 x 3 y 2 x 2 x 3 y 2 y 3 x 2 y 2 x 3 y 3 nie je prostá nie je na nie je prostá je na je prostá nie je na y4 je prostá je na
9 Zobrazenie f -1 : Y X sa nazýva inverzné zobrazenie k zobrazeniu f : X Y, ak platí f f -1 je rovné identickému zobrazeniu id x. K zobrazeniu f : X Y existuje inverzné zobrazenie f -1 vtedy a len vtedy, ak zobrazenie f je bijektívne. Ne ch n N. Množina A má n prvkov ak existuje bijekcia množiny {1, 2,, n} na A. Prázdna množina má 0 prvkov. Množina A sa nazýva konečná, keď má k prvkov, kde k je prirodzené číslo. Množina, ktorá nie je konečná sa nazýva nekonečná. Množina A sa nazýva spočitateľná, keď má rovnakú alebo menšiu mohutnosť ako množina N ( ak existuje prosté zobrazenie množiny A do množiny prirodzených čísel). Množina, ktorá nie je spočítateľná sa nazýva nespočítateľná. A N,
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Přijímací zkouška - matematika
 Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
 Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Množina a jej určenie, konečná a nekonečná množina
 Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 2016
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 206 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 206 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Množina je nejdůležitější matematický pojem, na kterém stojí veškeré další matematické pojmy.
 1 Teorie množin Základní informace V této výukové jednotce se student seznámí se základními pojmy a algoritmy z teorie množin. Začneme základními operacemi s množinami, seznámíme se s pojmy jako kartézský
1 Teorie množin Základní informace V této výukové jednotce se student seznámí se základními pojmy a algoritmy z teorie množin. Začneme základními operacemi s množinami, seznámíme se s pojmy jako kartézský
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2015
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 05 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 05 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Lineární algebra Kapitola 1 - Základní matematické pojmy
 Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Základy teorie množin
 Základy teorie množin Teorie Výběr základních pojmů: Množina Podmnožina Prázdná množina Označení běžně používaných množin Množinová algebra (sjednocení, průnik, rozdíl) Doplněk množiny Potenční množina
Základy teorie množin Teorie Výběr základních pojmů: Množina Podmnožina Prázdná množina Označení běžně používaných množin Množinová algebra (sjednocení, průnik, rozdíl) Doplněk množiny Potenční množina
KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO ALGEBRA DAGMAR SKALSKÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO ALGEBRA DAGMAR SKALSKÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Olomouc
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO ALGEBRA DAGMAR SKALSKÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Olomouc
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška šestá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Úvod do informatiky přednáška šestá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Cvičení 1. Úvod do teoretické informatiky(2014/2015) cvičení 1 1
 Úvod do teoretické informatiky(2014/2015) cvičení 1 1 Cvičení 1 Příklad 1: Pro každý z následujících formálních zápisů množin uveďte(svými slovy), jaké prvky daná množina obsahuje: a) {1,3,5,7,...} b)
Úvod do teoretické informatiky(2014/2015) cvičení 1 1 Cvičení 1 Příklad 1: Pro každý z následujících formálních zápisů množin uveďte(svými slovy), jaké prvky daná množina obsahuje: a) {1,3,5,7,...} b)
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Relace, zobrazení, algebraické struktury Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Relace, zobrazení, algebraické struktury Michal Botur Přednáška
3 Množiny, Relace a Funkce
 3 Množiny, Relace a Funkce V přehledu matematických formalismů informatiky se v této lekci zaměříme na základní datové typy matematiky, tj. na množiny, relace a funkce. O množinách jste sice zajisté slyšeli
3 Množiny, Relace a Funkce V přehledu matematických formalismů informatiky se v této lekci zaměříme na základní datové typy matematiky, tj. na množiny, relace a funkce. O množinách jste sice zajisté slyšeli
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
 RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
Požiadavky k štátnej bakalárskej skúške (Bc.) pre učiteľstvo matematiky
 Požiadavky k štátnej bakalárskej skúške (Bc.) pre učiteľstvo matematiky Algebra 1. Zobrazenie definícia zobrazenia, injektívne, surjektívne a bijektívne zobrazenie, zložené zobrazenie, identické zobrazenie,
Požiadavky k štátnej bakalárskej skúške (Bc.) pre učiteľstvo matematiky Algebra 1. Zobrazenie definícia zobrazenia, injektívne, surjektívne a bijektívne zobrazenie, zložené zobrazenie, identické zobrazenie,
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Pravdepodobnosť. Rozdelenia pravdepodobnosti
 Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Pravdepodobnosť Rozdelenia pravdepodobnosti Pravdepodobnosť Teória pravdepodobnosti je matematickým základom pre odvodenie štatistických metód. Základné pojmy náhoda náhodný jav náhodná premenná pravdepodobnosť
Množiny, základní číselné množiny, množinové operace
 2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
1. Množiny, zobrazení, relace
 Matematická analýza I přednášky M. Málka cvičení A. Hakové a R. Otáhalové Zimní semestr 2004/05 1. Množiny, zobrazení, relace První kapitola je věnována základním pojmům teorie množin. Pojednává o množinách
Matematická analýza I přednášky M. Málka cvičení A. Hakové a R. Otáhalové Zimní semestr 2004/05 1. Množiny, zobrazení, relace První kapitola je věnována základním pojmům teorie množin. Pojednává o množinách
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 2017
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Kapitola 1. Relace. podle definice podmnožinou každé množiny. 1 Neříkáme už ale, co to je objekt. V tom právě spočívá intuitivnost našeho přístupu.
 Kapitola 1 Relace Úvodní kapitola je věnována důležitému pojmu relace. Protože relace popisují vztahy mezi prvky množin a navíc jsou samy množinami, bude vhodné množiny nejprve krátce připomenout. 1.1
Kapitola 1 Relace Úvodní kapitola je věnována důležitému pojmu relace. Protože relace popisují vztahy mezi prvky množin a navíc jsou samy množinami, bude vhodné množiny nejprve krátce připomenout. 1.1
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Aritmetika s didaktikou I.
 Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 02 Opakování základních pojmů - 2. část O čem budeme hovořit: Binární relace a jejich vlastnosti Speciální typy binárních relací
Entitno - relačný model. Jaroslav Porubän, Miroslav Biňas, Milan Nosáľ (c)
 Entitno - relačný model Jaroslav Porubän, Miroslav Biňas, Milan Nosáľ (c) 2011-2016 Entitno-relačný (ER) model pozor na rozdielnosť pojmov relácia (angl. relation) vzťah, relácia (angl. relationship) konceptuálny
Entitno - relačný model Jaroslav Porubän, Miroslav Biňas, Milan Nosáľ (c) 2011-2016 Entitno-relačný (ER) model pozor na rozdielnosť pojmov relácia (angl. relation) vzťah, relácia (angl. relationship) konceptuálny
NAIVNÍ TEORIE MNOŽIN, okruh č. 5
 NAIVNÍ TEORIE MNOŽIN, okruh č. 5 Definování množiny a jejích prvků Množina je souhrn nějakých věcí. Patří-li věc do množiny X, říkáme, že v ní leží, že je jejím prvkem nebo že množina X tuto věc obsahuje.
NAIVNÍ TEORIE MNOŽIN, okruh č. 5 Definování množiny a jejích prvků Množina je souhrn nějakých věcí. Patří-li věc do množiny X, říkáme, že v ní leží, že je jejím prvkem nebo že množina X tuto věc obsahuje.
Teorie množin. pro fajnšmekry - TeMno. Lenka Macálková BR Solutions Orličky. Lenka (Brkos 2010) TeMno
 Teorie množin pro fajnšmekry - TeMno Lenka Macálková BR Solutions 2010 - Orličky 23.2. 27.2.2010 Lenka (Brkos 2010) TeMno 23.2. 27.2.2010 1 / 42 Bylo nebylo... Starověké Řecko - nekonečnost nepochopená
Teorie množin pro fajnšmekry - TeMno Lenka Macálková BR Solutions 2010 - Orličky 23.2. 27.2.2010 Lenka (Brkos 2010) TeMno 23.2. 27.2.2010 1 / 42 Bylo nebylo... Starověké Řecko - nekonečnost nepochopená
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin.
 1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
MIDTERM D. Příjmení a jméno:
 MIDTERM D Příjmení a jméno: 1 2 3 4 5 6 7 8 9 10 11 12 1 Doplňte místo otazníku ten ze symbolů, aby platil vztah (log n) / (log n 2 ) =?(1/ n): A) o B) O (a současně nelze použít ani o ani Θ) C) Θ D) Ω
MIDTERM D Příjmení a jméno: 1 2 3 4 5 6 7 8 9 10 11 12 1 Doplňte místo otazníku ten ze symbolů, aby platil vztah (log n) / (log n 2 ) =?(1/ n): A) o B) O (a současně nelze použít ani o ani Θ) C) Θ D) Ω
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Zobrazení. prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky BI-ZMA ZS 2009/2010
 Zobrazení prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy 2.
Zobrazení prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy 2.
Marie Duží
 Marie Duží marie.duzi@vsb.cz Co je to množina? Množina je soubor prvků a je svými prvky plně určena; množinu s prvky a, b, c značíme: {a, b, c}. Prvkem množiny může být opět množina, množina nemusí mít
Marie Duží marie.duzi@vsb.cz Co je to množina? Množina je soubor prvků a je svými prvky plně určena; množinu s prvky a, b, c značíme: {a, b, c}. Prvkem množiny může být opět množina, množina nemusí mít
RELACE, OPERACE. Relace
 RELACE, OPERACE Relace Užití: 1. K popisu (evidenci) nějaké množiny objektů či jevů, které lze charakterizovat pomocí jejich vlastnostmi. Entita je popsána pomocí atributů. Ty se vybírají z domén. Různé
RELACE, OPERACE Relace Užití: 1. K popisu (evidenci) nějaké množiny objektů či jevů, které lze charakterizovat pomocí jejich vlastnostmi. Entita je popsána pomocí atributů. Ty se vybírají z domén. Různé
Rozvoj matematických predstáv o číslach
 KATEDRA MATEMATIKY UNIVERZITA KONŠTANTÍNA FILOZOFA V NITRE FAKULTA PRÍRODNÝCH VIED Rozvoj matematických predstáv o číslach Dagmar Markechová - Anna Tirpáková ISBN 978-80-8094-900-6 9 788080 948849 NITRA
KATEDRA MATEMATIKY UNIVERZITA KONŠTANTÍNA FILOZOFA V NITRE FAKULTA PRÍRODNÝCH VIED Rozvoj matematických predstáv o číslach Dagmar Markechová - Anna Tirpáková ISBN 978-80-8094-900-6 9 788080 948849 NITRA
ALGEBRA. Téma 4: Grupy, okruhy a pole
 SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 4: Grupy, okruhy a pole Základní pojmy unární operace, binární operace, asociativita,
SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 4: Grupy, okruhy a pole Základní pojmy unární operace, binární operace, asociativita,
Patří-li do množiny A právě prvky a, b, c, d, budeme zapisovat A = {a, b, c, d}.
 2 Množiny a intervaly lgebraické výrazy 2.1 Množiny Chápání množiny lze shrnout takto: Množinou rozumíme každé shrnutí určitých a navzájem různých předmětů m našeho nazírání nebo myšlení (které nazýváme
2 Množiny a intervaly lgebraické výrazy 2.1 Množiny Chápání množiny lze shrnout takto: Množinou rozumíme každé shrnutí určitých a navzájem různých předmětů m našeho nazírání nebo myšlení (které nazýváme
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Množiny, relace, zobrazení
 Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Kapitola 1. Úvod. 1.1 Značení. 1.2 Výroky - opakování. N... přirozená čísla (1, 2, 3,...). Q... racionální čísla ( p, kde p Z a q N) R...
 Kapitola 1 Úvod 1.1 Značení N... přirozená čísla (1, 2, 3,...). Z... celá čísla ( 3, 2, 1, 0, 1, 2,...). Q... racionální čísla ( p, kde p Z a q N) q R... reálná čísla C... komplexní čísla 1.2 Výroky -
Kapitola 1 Úvod 1.1 Značení N... přirozená čísla (1, 2, 3,...). Z... celá čísla ( 3, 2, 1, 0, 1, 2,...). Q... racionální čísla ( p, kde p Z a q N) q R... reálná čísla C... komplexní čísla 1.2 Výroky -
1. Základy logiky a teorie množin
 1. Základy logiky a teorie množin A. Logika Matematická logika vznikla v 19. století. Jejím zakladatelem byl anglický matematik G. Boole (1815 1864). Boole prosadil algebraické pojetí logiky a zavedl logické
1. Základy logiky a teorie množin A. Logika Matematická logika vznikla v 19. století. Jejím zakladatelem byl anglický matematik G. Boole (1815 1864). Boole prosadil algebraické pojetí logiky a zavedl logické
SKLADOVÁ INVENTÚRA 1 VYTVORENIE INVENTÚRY. 1.1 Nastavenie skladovej inventúry
 SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
3. Algebraické systémy
 Markl: 3.1. Morfismy a kongruence /ras31.doc/ Strana 1 3. Algebraické systémy Na rozdíl od klasické algebry, jejíž ústředním tématem jsou rovnice a potřebný aparát pro jejich řešení /matice, polynomy,.../,
Markl: 3.1. Morfismy a kongruence /ras31.doc/ Strana 1 3. Algebraické systémy Na rozdíl od klasické algebry, jejíž ústředním tématem jsou rovnice a potřebný aparát pro jejich řešení /matice, polynomy,.../,
Princip rozšíření a operace s fuzzy čísly
 Center for Machine Perception presents Princip rozšíření a operace s fuzzy čísly Mirko Navara Center for Machine Perception Faculty of Electrical Engineering Czech Technical University Praha, Czech Republic
Center for Machine Perception presents Princip rozšíření a operace s fuzzy čísly Mirko Navara Center for Machine Perception Faculty of Electrical Engineering Czech Technical University Praha, Czech Republic
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Spracovanie informácií
 2 Spracovanie informácií PC = stroj na spracovanie informácií (nielen výpočty) Spracovanie = Evidovanie (zaznamenávanie, uchovávanie) Selektovanie (výber vhodných údajov) Výstup údajov (napr. na tlačiareň)
2 Spracovanie informácií PC = stroj na spracovanie informácií (nielen výpočty) Spracovanie = Evidovanie (zaznamenávanie, uchovávanie) Selektovanie (výber vhodných údajov) Výstup údajov (napr. na tlačiareň)
MAIS. Verejný portál - kalendárny rozvrh. Používateľská minipríručka pre používateľov systému MAIS. APZ Bratislava
 MAIS Verejný portál - kalendárny rozvrh Používateľská minipríručka pre používateľov systému MAIS APZ Bratislava Rozvrhy nájdete pod URL: https://89.173.153.100/maisportal/ Na úvodnej obrazovke kliknite
MAIS Verejný portál - kalendárny rozvrh Používateľská minipríručka pre používateľov systému MAIS APZ Bratislava Rozvrhy nájdete pod URL: https://89.173.153.100/maisportal/ Na úvodnej obrazovke kliknite
1. Základy matematiky
 1. Základy matematiky 1A. Výroková logika 1. Základy matematiky 1A. Výroková logika Logika se v češtině běžně používá ve smyslu myšlenková cesta, která vede k určitým závěrům. Logika patří k základům matematiky.
1. Základy matematiky 1A. Výroková logika 1. Základy matematiky 1A. Výroková logika Logika se v češtině běžně používá ve smyslu myšlenková cesta, která vede k určitým závěrům. Logika patří k základům matematiky.
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku
 MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
Import Excel Univerzál
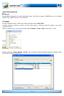 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Vedecký prístup ku koncipovaniu ekonomickej teórie. VET Cvičenie 1.2
 Vedecký prístup ku koncipovaniu ekonomickej teórie VET Cvičenie 1.2 Základné funkcie ekonómie ako vedy 1. poznávacia 2. praktická 3. metodologická Ekonómia má nielen svoj predmet skúmania, ale aj svoje
Vedecký prístup ku koncipovaniu ekonomickej teórie VET Cvičenie 1.2 Základné funkcie ekonómie ako vedy 1. poznávacia 2. praktická 3. metodologická Ekonómia má nielen svoj predmet skúmania, ale aj svoje
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
 Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ
 64 1 TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ OBLASŤ PRIJATIA A ZAMIETNUTIA HYPOTÉZY PRI TESTOVANÍ CHYBY I. A II. DRUHU Chyba I. druhu sa vyskytne vtedy, ak je hypotéza správna, ale napriek tomu je zamietnutá,
64 1 TESTOVANIE ŠTATISTICKÝCH HYPOTÉZ OBLASŤ PRIJATIA A ZAMIETNUTIA HYPOTÉZY PRI TESTOVANÍ CHYBY I. A II. DRUHU Chyba I. druhu sa vyskytne vtedy, ak je hypotéza správna, ale napriek tomu je zamietnutá,
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Úlohy k procvičování textu o svazech
 Úlohy k procvičování textu o svazech Číslo za pomlčkou v označení úlohy je číslo kapitoly textu, která je úlohou procvičovaná. Každá úloha je vyřešena o několik stránek později. Kontrolní otázky - zadání
Úlohy k procvičování textu o svazech Číslo za pomlčkou v označení úlohy je číslo kapitoly textu, která je úlohou procvičovaná. Každá úloha je vyřešena o několik stránek později. Kontrolní otázky - zadání
KOMBINATORICKÉ PRAVIDLO SÚČINU
 KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
Program "Inventúra program.xlsm"
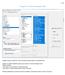 1 / 14 Program "Inventúra program.xlsm" Program pracuje s reportami, ktoré majú ako zdroj dát tabuľku inventárnych dát. Program je uložený ako VBA projekt v Excel súbore "Inventúra Program.xlsm". Program
1 / 14 Program "Inventúra program.xlsm" Program pracuje s reportami, ktoré majú ako zdroj dát tabuľku inventárnych dát. Program je uložený ako VBA projekt v Excel súbore "Inventúra Program.xlsm". Program
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL. Algebra a diskrétna matematika
 VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
VLADIMÍR KVASNIČKA JIŘÍ POSPÍCHAL Algebra a diskrétna matematika Slovenská technická univerzita v Bratislave 2008 prof. Ing. Vladimír Kvasnička, DrSc., prof. RNDr. Jiří Pospíchal, DrSc. Lektori: doc. RNDr.
10. DETERMINANTY " # $!
 10. DETERMINANTY $ V této kapitole zavedeme determinanty čtvercových matic libovolného rozměru nad pevným tělesem, řekneme si jejich základní vlastnosti a naučíme se je vypočítat včetně příkladů jejich
10. DETERMINANTY $ V této kapitole zavedeme determinanty čtvercových matic libovolného rozměru nad pevným tělesem, řekneme si jejich základní vlastnosti a naučíme se je vypočítat včetně příkladů jejich
Obchodná akadémia Ružomberok Ing. Igor Rosa
 1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
Relace. R, S vyjmenovaním prvků. Sestrojte grafy relací R, S. Určete relace
 Relace 1. Nechť A = {n N; n < 10}, B = {m N; m 12}, R = {[m, n] A B; m + 1 = n}, S = {[m, n] A B; m 2 = n}. Zapište relace R, S vyjmenovaním prvků. Sestrojte grafy relací R, S. Určete relace R R, S S,
Relace 1. Nechť A = {n N; n < 10}, B = {m N; m 12}, R = {[m, n] A B; m + 1 = n}, S = {[m, n] A B; m 2 = n}. Zapište relace R, S vyjmenovaním prvků. Sestrojte grafy relací R, S. Určete relace R R, S S,
0.1 Funkce a její vlastnosti
 0.1 Funkce a její vlastnosti Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Příklady veličin: hmotnost (m) čas (t) výše úrokové sazby v bance (i) cena
0.1 Funkce a její vlastnosti Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Příklady veličin: hmotnost (m) čas (t) výše úrokové sazby v bance (i) cena
Predaj cez PC pokladňu
 Predaj cez PC pokladňu PC pokladňa je určená na predaj v hotovosti cez fiškálny modul, ale pracuje so skladom offline, t.j. pri predaji nie je možné zistiť aktuálny stav tovaru na sklade. Pri predaji cez
Predaj cez PC pokladňu PC pokladňa je určená na predaj v hotovosti cez fiškálny modul, ale pracuje so skladom offline, t.j. pri predaji nie je možné zistiť aktuálny stav tovaru na sklade. Pri predaji cez
Matematika (KMI/PMATE)
 Úvod do matematické analýzy Funkce a její vlastnosti Funkce a její vlastnosti Veličina Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Funkce a její
Úvod do matematické analýzy Funkce a její vlastnosti Funkce a její vlastnosti Veličina Veličina - pojem, který popisuje kvantitativní (číselné) vlastnosti reálných i abstraktních objektů. Funkce a její
D.Viewer2 Používateľská príručka
 D.Viewer2 Používateľská príručka Obsah 1. Úvod... 3 2. Inštalácia... 4 Inštalačné predpoklady... 4 3. Práca s aplikáciou... 8 3.1. Práca s podpísanou zložkou... 9 3.2. Menu aplikácie... 11 2 1. Úvod D.Viewer2
D.Viewer2 Používateľská príručka Obsah 1. Úvod... 3 2. Inštalácia... 4 Inštalačné predpoklady... 4 3. Práca s aplikáciou... 8 3.1. Práca s podpísanou zložkou... 9 3.2. Menu aplikácie... 11 2 1. Úvod D.Viewer2
NEINTERAKTÍVNA KOMUNIKÁCIA
 NEINTERAKTÍVNA KOMUNIKÁCIA ICSED3 informatika Gymnázium Kráľovnej pokoja, Žilina Mgr. Miroslav Malacha Komunikácia prostredníctvom IKT Komunikácia: vyvinulo sa z lat. communicare= deliť sa, zverovať, všeobecnosti
NEINTERAKTÍVNA KOMUNIKÁCIA ICSED3 informatika Gymnázium Kráľovnej pokoja, Žilina Mgr. Miroslav Malacha Komunikácia prostredníctvom IKT Komunikácia: vyvinulo sa z lat. communicare= deliť sa, zverovať, všeobecnosti
Teória grafov. Stromy a kostry 1. časť
 Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Účtovná dokumentácia. Obsah a forma účtovného záznamu
 Účtovná dokumentácia Zákon č. 431/2002 Z. z. o účtovníctve: Účtovnú dokumentáciu tvorí súhrn všetkých účtovných záznamov, ktoré sa v účtovnej jednotke vytvárajú v zmysle zákona. Účtovná jednotka je povinná
Účtovná dokumentácia Zákon č. 431/2002 Z. z. o účtovníctve: Účtovnú dokumentáciu tvorí súhrn všetkých účtovných záznamov, ktoré sa v účtovnej jednotke vytvárajú v zmysle zákona. Účtovná jednotka je povinná
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE
 MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
Aplikovaná matematika I, NMAF071
 M. Rokyta, MFF UK: Aplikovaná matematika I kap. 1: Úvod, čísla, zobrazení, posloupnosti 1 Aplikovaná matematika I, NMAF071 M. Rokyta, KMA MFF UK ZS 2013/14 Sylabus = obsah (plán) přednášky [a orientační
M. Rokyta, MFF UK: Aplikovaná matematika I kap. 1: Úvod, čísla, zobrazení, posloupnosti 1 Aplikovaná matematika I, NMAF071 M. Rokyta, KMA MFF UK ZS 2013/14 Sylabus = obsah (plán) přednášky [a orientační
Obsah. Množiny (opakování) Relace a zobrazení (opakování) Relace Binární relace na množině Zobrazení Rozklady, ekvivalence Uspořádání
 Obsah Množiny (opakování) Relace a zobrazení (opakování) Relace Binární relace na množině Zobrazení Rozklady, ekvivalence Uspořádání lgebry lgebry s jednou operací lgebry se dvěma operacemi Svazy 2 Teorie
Obsah Množiny (opakování) Relace a zobrazení (opakování) Relace Binární relace na množině Zobrazení Rozklady, ekvivalence Uspořádání lgebry lgebry s jednou operací lgebry se dvěma operacemi Svazy 2 Teorie
DISKRÉTNÍ MATEMATIKA I
 Fakulta pedagogická, Technická univerzita v Liberci DISKRÉTNÍ MATEMATIKA I Doc. RNDr. Miroslav Koucký, CSc. Prof. RNDr. Bohdan Zelinka, DrSc. Liberec, 4 Obsah Kap. Základní poznatky o množinách 7. Pojem
Fakulta pedagogická, Technická univerzita v Liberci DISKRÉTNÍ MATEMATIKA I Doc. RNDr. Miroslav Koucký, CSc. Prof. RNDr. Bohdan Zelinka, DrSc. Liberec, 4 Obsah Kap. Základní poznatky o množinách 7. Pojem
Naivní teorie množin. Naivní pojem množiny Funkce jako nálepkovací schéma Konečnost, nekonečnost Spočetnost, nespočetnost
 Naivní teorie množin Jiří Velebil: YD01MLO 27. února 2008: Naivní teorie množin 1/16 Definice Množinou A rozumíme souhrn určitých a rozlišitelných objektů x existujících v naší mysli. Těmto objektům říkáme
Naivní teorie množin Jiří Velebil: YD01MLO 27. února 2008: Naivní teorie množin 1/16 Definice Množinou A rozumíme souhrn určitých a rozlišitelných objektů x existujících v naší mysli. Těmto objektům říkáme
Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od
 A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/21 Matematická analýza ve Vesmíru. proměnné - p. 2/21 Definice. Funkcí (přesněji:
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/21 Matematická analýza ve Vesmíru. proměnné - p. 2/21 Definice. Funkcí (přesněji:
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
TomTom Referenčná príručka
 TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
TomTom Referenčná príručka Obsah Rizikové zóny 3 Rizikové zóny vo Francúzsku... 3 Upozornenia na rizikové zóny... 3 Zmena spôsobu upozornenia... 4 tlačidlo Ohlásiť... 4 Nahlásenie novej rizikovej zóny
1. POJMY 1.1. FORMULE VÝROKOVÉHO POČTU
 Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Súhrnný výkaz v roku Ing. Mgr. Martin Tužinký, PhD.
 v roku 2015 Ing. Mgr. Martin Tužinký, PhD. SV je povinný podať platiteľ DPH, ktorý: Dodal tovar oslobodený od dane z tuzemska do IČŠ osobe, ktorá je identifikovaná pre daň v IČŠ ( 43 ods. 1 ZDPH). Premiestnil
v roku 2015 Ing. Mgr. Martin Tužinký, PhD. SV je povinný podať platiteľ DPH, ktorý: Dodal tovar oslobodený od dane z tuzemska do IČŠ osobe, ktorá je identifikovaná pre daň v IČŠ ( 43 ods. 1 ZDPH). Premiestnil
plagát Formát po odrezaní Formát pred odrezaním Spad Vnútorný okraj Formáty súborov Pomoc Sprievodca na prípravu súborov PLAGÁT - A1
 Sprievodca na prípravu súborov PLAGÁT - A1 598 mm (formát pred odrezaním) 594 mm (formát po odrezaní) Formát po odrezaní Plagát bude mať rozmer: 594 x 841 mm. Formát pred odrezaním Správne pripravený súbor
Sprievodca na prípravu súborov PLAGÁT - A1 598 mm (formát pred odrezaním) 594 mm (formát po odrezaní) Formát po odrezaní Plagát bude mať rozmer: 594 x 841 mm. Formát pred odrezaním Správne pripravený súbor
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu
 Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
Pojem struktury z hlediska formální logiky
 let Filosofického časopisu Pojem struktury z hlediska formální logiky Úvodní poznámka Petra Dvořáka Článek je věnován klíčovému pojmu poválečné filosofie, pojmu struktury. V matematice učinil Bourbaki
let Filosofického časopisu Pojem struktury z hlediska formální logiky Úvodní poznámka Petra Dvořáka Článek je věnován klíčovému pojmu poválečné filosofie, pojmu struktury. V matematice učinil Bourbaki
Doporučené příklady k Teorii množin, LS 2018/2019
 Doporučené příklady k Teorii množin, LS 2018/2019 1. přednáška, 21. 2. 2019 1. Napište množina x je prázdná (přesněji množina x nemá žádné prvky ) formulí základního jazyka teorie množin. 2. Dokažte ((x
Doporučené příklady k Teorii množin, LS 2018/2019 1. přednáška, 21. 2. 2019 1. Napište množina x je prázdná (přesněji množina x nemá žádné prvky ) formulí základního jazyka teorie množin. 2. Dokažte ((x
