Mechanika 2 dynamika
|
|
|
- Luboš Procházka
- před 6 lety
- Počet zobrazení:
Transkript
1 České soké učení echncké Pae akula dopaní Mechanka dnaka Te přednášek Přednášející: Pof.Ing. Josef Jía, CSc. Zpacoal: Doc.Ing. Mchal Mcka, CSc. Maek Kříček, Zdeněk Lokaj Paha, posnec
2 . TŘEÍ Va jse uažoal jako úa s dokonale hladký sčný ís a s eakce kolý ke sčný plochá č křká. Ve skuečnos jsou sčná ísa ae íceéně dsná. Vnklé eakce jsou oecně odchýlené od noál sčných ploch (křek). Pasní odpo se pojeují eakce, keé ají ečné složk. V chaakeu ěcho ečných složek olšujee případ. Jeslže jde o ájený poh úaů, oecně luíe o skoé ření. Relaníu kldu přísluší ečné eakce. Všeoecně plaí, že řecí síla (skoé ření) půsoí e sěu a po sslu elaní chlos sýkajících se odů. S pasní odpo se le seka jných foách, jsou o např. odpooé účnk př alení ělesa, př naíjení láken (lan, řeěů). Tření je -časo užečné, e ření nela ožná chůe, ojed a ždění odel, přenos enege řeen - časo škodlé, neoť snžuje ýkonnos sojů, pak se u áníe í, že řecí ploch necháe poáhnou sou přlnaé kapaln (aadla) a í ření enšujee, neoť ření pených láek nahadíe ření kapalnný (enší)... Tření skoé Vnk ečných eakcí u sýkajících se ěles ýá sěloán neonos sčných ploch, keé sý ýsupk ( el nepaný ) do see asahují. Př pohu se usí ěleso přes neonos jednak přenáše a jednak se ýsupk defoují (čás pužně, čás plasck). Tření je je fkálně el složý. Zásí na aeálu, na sau sčných ploch, na síle, keá o ploch přlačuje, na elkos ploch, na eploě. Jné poě jsou a kldu, jné a pohu. Jeslže se ěleso nepohuje, ření ání uedení ělesa do pohu - nasáá ření kldu. Pohuje-l se ěleso, ření se uplaňuje jako síla dící poh - ření pohu. V 8.soleí fouloal fk Coulo epcké ákon o skoé ření.. ákon o skoé ření a kldu Tření skoé kldu neůže přesoup učou hodnou, keá je úěná noáloé složce, jíž jsou ělesa k soě přlačoána. T µ s kde T je elkos řecí složk eakce µ s je součnel ření a kldu je noáloá složka eakce na sku oou ěles sacký součnel ření, ásí přeážně na dsnos ploch. ákon o skoé ření a pohu Tření a pohu ouje ečnou složku eakce, keá je úěná noáloé složce eakce.
3 T µ k kde T je elkos řecí složk eakce µ k je součnel ření a pohu je noáloá složka eakce na sku oou ěles kneacký součnel ření (ásí přeážně na dsnos ploch a neásí na chlos) Plaí: T() µ s > µ k µ s ( planos ahu je oěřena ýsledk epeenů - oáek ) µ k () Úloha..: Těleso na odooné oně, na keé půsoí síla, keá síá s noálou řecí ploch úhel α..a) Je-l ona deálně hladká ěleso je onoáe α poue ehd, je-l síla kolá k oně ( α ). ) Odklonění síl o úhel α se dá ěleso do odooné eakce T snα µ µ µ cosα snα µ cosα s R n ϕ s s R ϕ s R T s s pohu pod účnke hnací síl snα. a) Je-l ona dsná, ůže dooa nejen slá k n kolý, ale ečný slá až do elkos T µ. s () Př půsoení síl odkloněné o úhel α ude ěleso ak dlouho onoáe, pokud ečná složka síl " ude enší než aální hodnoa snα gα µ s cosα čl pokud úhel α ude enší než úhel ϕ s, po keý plaí g ϕ s µ s, kde ϕ s je úhel skoého ření kldu. Udáá kajní poloh nější síl, př nchž aa půsoí. Přesoupí-l úhel α hodnou ϕ s, dá se ěleso do pohu. Hnací slou de ude ýslednce nější síl a eakce edení
4 T snα cosα µ k V éo onc je jž íso µ s součnel µ k a poože se ěleso pohuje je µ k < µ s. Třecí kužel - šafoaná olas e čechoaný hance eený úhle ϕs od sslé os. Pokud papsek síl leží unř řecího kuželu, je ěleso e salní poloe ( kldu ). α > ϕ s R n α ϕ k R α R T a Ekalence: Poože se jedná o poh onoěně chlený, je nuno do ýpoču ahnou seačnou sílu. Pohoá once ělesa ude a T a ( snα µ cosα ) gϕ a sn k gα úhel ϕ k, jehož g ϕ k µ k, se naýá úhel ření a pohu. Poh se ude chloa, pokud plaí gϕ k < gα, klesne-l úhel α pod hodnou ϕ k, ude ěleso žděno a čase se asaí. k Maeál µ s ϕ s µ k ϕ k ocel na ledě,7 o 36,4 48 ocel na ocel, -,3 6 o - 6 o 4,7 -,5 4 o - 4 o ko na dřeě, -,55 o - 9 o, -,5 o - 6 o 3 dřeo na dřeě,43 -,6 3 o - 3 o,9 -,48 o - 5 o Úloha..: Choání ělesa o íe G nakloníe-l onu, na keé leží kád a) G ) ϕ s ϕ s α G α e ření R R G cosα α < ϕs α G snα e pohu, STBILÍ
5 c) řecí kužel d) ϕ ϕ s s α G ϕ s ϕ s α G G cosα α R G cosα G snα α R ϕ k < G snα α α ϕ ( α > ) ϕ s e pohu, ale poh ožný, LBILÍ > POHYB s ϕ k unou a posačující podínkou a ěleso na nakloněné oně lo e salní onoáe, je, a papsek ýslednce nějších půsoících sl (de íha) ležel unř řecího kužele... Tření alé Válec spočíající na dokonale hladké podložce se uede do pohu seeenší odoonou slou. Válec se ude sýka a eakce podložk R ude onoáe s ahou álce, ude sslá a ude pocháe ěžšě G G T a) dokonale hladká podložka ) ření Ve skuečnos sýkání álce po podložce ání ření, podložka koě sslé eakce půsoí slou odoonou, keá ání posunu dokoého odu álce. Teno dokoý od ůsáá na ísě a álec se kole něho očí - alí se. Moen oáčející álec á elkos a elce alá hnací síla ěla sač k uedení álce do pohu. Ve skuečnos klade ěleso odpo po alení. Vsělení: Reakce podložk se poněkud posune před po sěu pohu o jsou délku e (sejně jako u adálního čepu nepřléhající ložsku)
6 G e oenoá podínka onoáh ke sředu e T e T T e T G Váha ělesa hlede ke sředu oáčení půsoí dící oene G e Je se naýá ření alé, délka e je paae ření alého (ačkol ke ření u nedocháí) Tření alé je de faco odpo po alení ělesa. Pakck: Účnek ření alého se podoně jako u ření skoého jadřuje dící slou T, keá je násoke sslého laku. Součoé podínk onoáh T G µ T G - T kde µ je koefcen ření alého, keý je načně enší než u ření skoého. Zjednodušující předpoklad (Coulo) - paae e je neáslý na poloěu álce a jeho ýšce - paae e je neáslý na síle, keou je álec lačen k podkladu G.3. Tření čepech Všeříe oen pořený k překonání odpou čepu..3.. Čep au V Součnel ření kldu je chaakeoán řecí úhle ϕ s a alý odpo paaee alého ření e. Sklon aen V čepu je dán úhle α. V ísě doku kuhoého půřeu a han čepu nkají nenáé eakce R, R, řeí nenáou je elkos oenu. Sesaíe součoé podínk onoáh uhé desk oně e M a M a M a α α G e P B R R B ϕ ϕ e α α p
7 odooné a sslé sěu: ( α ϕ ) R sn( α ϕ ) G R cos( α ϕ ) R cos( α ϕ ) R sn s s s s Řešení oou once dosanee R cos ( α ϕ ) s G sn an ( α ϕ s ) ( α ϕ ) s R cos sn( α ϕ s ) G sn( α ϕ s ) sn ( ) ( α ϕ s ) α ϕ s an( α ϕ ) Výsledk ají ssl, pokud α > ϕ s. Pokud o neplaí, jedná se o úlohu řešící poh kola na nakloněné oně. enáou hodnou oenu počee oenoé ýnk onoáh ke sředu kuhu. M R R ecosϕ snϕ ( )( ) a s s Dosaení a eakce R, R ískáe M k G( ecosϕ s snϕ s ) Pokud l eno oen překonán, ěnl se řecí úhel sacký na kneacký a V čep kladl odpo jádřený oene M G ecosϕ snϕ k ( ) k k s.3.. Válcoý čep Opě udee hleda aální oen, keý ůžee aíž nřní álec čepu. Odpo pohu klade jednak ření alé a jednak ření skoé. Souče ěcho odpoů se naýá ření čepoé a po úhel čepoého ření a kldu ůžee přlžně předpokláda ϕ čs ϕ s ϕ ϕčk ϕk ϕk Sesaíe podínk onoáh álce čepu. Použjee ř neáslé podínk, keé usí splňoa uhá deska oně. Podínk jsou řaen e sěu a oenac nenáých eakcí R n, R Rn G cos ϕ čs R G snϕčs a oenoá podínka onoáh k ose álce M a R Řešení onc pak dosanee Rn G cosϕčs R G snϕčs M a G snϕčs Opě př pohu klade čep odpo jádřený oene M G eϕ k čk.4. Tření lana přes kuhoý álec Lano je edeno přes kuhoý álec, e lane a poche álce je ření. Hledáe nejěší ožný odíl e elkos sl a, a lano doýkající se kuhoého álce délce učené úhle α ( oáek ), nepokloulo. Součnel skoého ření a kldu e aeál lana a álce je µ s.
8 dϕ ϕ ( ϕ dϕ ) R dϕ ( ϕ ) α R n Přeušíe lano ísě dané úhl ϕ a ϕ dϕ a aedee noáloou a ečnou složku eakce shující spolupůsoení e lane a álce úseku d ϕ. Ve sěu nější noál kuhoého půřeu álce poo sesaíe součoou podínk onoáh Rn ( ϕ dϕ ) sn dϕ Rn ( ϕ dϕ ) dϕ Rn ( ϕ ) dϕ ( dϕ ) dϕ ( poože po alý úhel sn d ϕ dϕ ). Zanedáe elčnu duhého řádu a poo R n ( ϕ ) dϕ Podoně ýnka onoáh ísě ϕ e sěu ečn á a ( ϕ dϕ ) cos dϕ ( ϕ ) R ( ϕ dϕ ) ( ϕ ) R ( poože po alý úhel cos d ϕ ) Třecí síla R µ srn µ s ( ϕ ) dϕ. Dosaení do předchoí once a úpaou dosanee ( ϕ dϕ ) ( ϕ ) µ s ( ϕ ) dϕ což předsauje lneání dfeencální onc.řádu d( ϕ ) µ s ( ϕ ). dϕ µ ϕ Řešení once ískáe sílu ( ϕ ) C e s. Inegační konsanu C ískáe okajoé podínk ( ) µ ϕ ( ϕ ) e s, ed Z počeného ahu le odpoědě adání, že aální ožný odíl e sla a je µ e s ϕ. ( ) ( ) a
9 . ZÁKLDY KIEMTIKY Kneaka se aýá popse pohu čásce neo ělesa, anž sleduje příčnné souslos. Jední e ákladních lasnosí pohu je, že jeho pops áleží na olě ažného ělesa. ele louč případ, kd se ažná sousaa souřadnc pohuje... Kneaka honého odu d e e 3 k e j d B Poloha honého odu dána polohoý ekoe. Pops pohu honého odu - jsou-l ná hodno polohoého ekou e šech časoých okažcích. Kaéská souřadncoá sousaa () () () j ( ) k, j, k jednokoé eko kde () () e () e () e3 e, e, e3 áoé eko Roepsáno po jednolé souřadnce () () () [ ] Po elnac času ěcho onc dosááe dáhu ( ajekoe ) - křku, po keé se od pohuje (,, ) } dáha je dána jako půsečnce on,, ( ) Def.... Rchlos je časoá ěna (deace dle času) polohoého ekou d l & & & j & k d d d d - neo e složkách,, [ s ] d d d elkos ekou chlos & & & Sejný ýsledek dosanee, deujee-l dáhu dle času. Důka o elkos ekou chlos: ds d d d d d d d d d d d d & & &
10 Věa... Rchlos je eko a á sě dáh a elkos onou pní deac podle času Důka o sěu d cosα, ds d d d d s s () ds cos β ds ds d ds d d, cosγ ds d cosα d ds d ds se naýá délkou olouku od odu do odu. Olouk s je přípusný paaee křk a její onc le apsa () s a e složkách () s, () s, ( s) ds d d d Odoně d cos β, cosγ Def.... Zchlení je časoá ěna ekou chlos d a & && && && j & k d Složk ekou chlení jsou a & &&, a & &&, a & & Velkos chlení a a a a, [ s - ] Důležé složk ekou chlení Složka do sěu noál k dáe je a n,složka do sěu ečn k dáe a. () e n B e e Z dfeencální geoee plne: V každé odě posooé křk le uč ojhan, keý je popsán ekoe ečn, ekoe noál a ekoe noál. Všechn eko ají jednokoou elkos a plaí, že spolu s uažoaný ode učují ( B, en, ) ( B, e, e )) ( B, e, e e - noáloou onu n - ekfkační onu - oskulační onu
11 a) eko chlos na dáe odu po časoé okažku, ) složk n příůsku chlos do sěu noál a ečn R ϕ s ϕ n Tečné chlení ( ) cos ϕ a l a poože plaí lě cos ϕ d a l & d Věa... Tečné chlení á elkos onou deac elkos chlos podle času oáloé chlení sn ϕ n an l V lě plaí sn ϕ ϕ a o. a) kde R je poloě křos dáh s an l R R s R ϕ ϕ s R Věa..3. oáloé chlení á elkos onou čec chlos dělenéu křosí dáh a sě do sředu křos. oáloá složka chlení se poo naýá chlení dosředé neo cenpeální.... Příočaý poh V oo případě je dáha honého odu příka. Sě chlos je sálý. Zchlení je poue ečné a á sě shodný se sěe chlos Časé jsou případ, kd e sěu někeé os je konsanní chlení neo nuloé. Budee předpokláda, že je o sě os.. Případ a naee poh příočaý onoěný e sěu os. d negací ískáe d kde je negační konsana - počáeční dáha.
12 poh onoěně chlený. Případ a kons. poh onoěně poalený kde ( počáeční dáha ) a (počáeční chlos ) jsou negační konsan. d a d a negací a d a a dojí negací a d Odoné ah plaí po os, Ve lášní případě, kdž poh ačne současně s počáke ěření času nuloé poloh nuloou chlosí plaí s a a a a kons. a s s a Chaakescký příklade pohu onoěně chleného je olný pád, kde ag, j. gaační chlení (neo íhoé chlení g9.8 s -, ění se se eěpsnou šířkou ). Ve sěu odooné je nuloé chlení... Křočaý poh odu a) Zlášní případe křočaého pohu je poh honého odu po kužnc. B ϕ( ) ( R, ϕ() ) ϕ( ) ( ( )) B R, ϕ s Poloha odu ( na o. B, B ) je popsána časoě poěnný úhle ϕ (), dáha kde R je poloě kužnce. s ϕ ( ) ( ) R Veko půodče ( ) ůžee jádř poocí půěů do souřadncoých os R cos ϕ e Rsnϕ e ( ) ( ) () kde jednokoé eko e sěu noál a ečn jsou ( následující oáek ) e e n cos ϕ cos () e snϕ() e ( 9 ϕ() ) e sn( 9 ϕ() ) e sn( 9 ϕ() ) e cos ( 9 ϕ() ) e
13 e R ϕ() Rcosϕ () e Veko okažé chlos d() R snϕ ϕ d R & ϕ() e R () e dϕ Z předchoího ápsu je řejé, že úhloá chlos () d a dále plaí () () R () Rsnϕ e [ e ] () () e R cosϕ() & ϕ() e & R & ϕ() snϕ() e cosϕ() Veko chlení () () () a & e en R & R d Úhloé chlení () () ε & [ ad s d R & R ε 9 & ( ) () e R () en R ε () e R () en - () ] o ϕ( ) Tečná složka chlení a () ( ) oáloá složka chlení R ( ) ( ) ( ) a n ( ) ϕ( ) ϕ e n - [ ad s ] Specální případ - onoěný poh kuhoý, keý je chaakeoán konsanní úhloou chlosí dϕ() ϕ() ϕ poh je peodcký d K poěhnuí kužnce je řea času T - peoda π π ϕ T ϕ T fekence f π f T úhloé chlení ε () je ono.
14 ..3. Šký h e akuu Počáeční podínk - počáeční chlos ( ) ( ) po - eleační úhel α - íhoé chlení a - g o - chlení a o ϕ o o g d ( ) Pohoé once onoěný příočaý poh ( ) () cos α onoěně chlený poh a () g g snα Vloučíe-l čas oou onc dosanee () ( ) ( ) () snα g cos cos α cos Poo once dáh souřadncích, ( (), () ) g gα cos α Učení času dopadu d čásce ( d ) g d d snα d snα g d d ální řešení snα d neální řešení g Dosřel (dole) polohoý eko d α g snα cos d cos g ( ) α d d α
15 Maální dosřel je po eleační úhel α 45 d sn α g.. Kneaka uhého ělesa B a ělese olíe od,b. Poh ělesa popíšee ak, že popíšee polohu odu čase a úhel spojnce B čase ( ), ϕ( ) ϕ skaláně e složkách () ( ) ( ) - jadřuje posunuí "anslac" ělesa ϕ ϕ ϕ ϕ ϕ ϕ - úhl jadřují pooočení podél souřadných () ( ) ( ) Po oecný od ělesa C os, j. oac ělesa ude e šeřoa chlos a chlení ělesa a) Tanslační poh - dáh alespoň 3 odů jsou shodné. Poh šech odů ělesa je sejný,poo je chlos a chlení a od anslačního pohu konsanní a oné chlos a chlení odu. d d d a d d d Polé řešíe jako poh odu o hoě oné hoě celého ělesa. Jeho poloha je učena ekoe () a ) Roační poh - da od ělesa ůsáají sále na sých ísech, poo se nepohují o šechn od ležící na spojnc ěcho dou odů. Těleso se oáčí kole éo spojnce, nasáá oace ělesa kole os. Každý od ělesa konáá kuhoou dáhu o sředu na ose ρ oáčení. O - eko úhloé chlos oáčení áaný na osu oace o, sě je sálý Poo chlos odu C je a chlení d d d d a ( ) d d d d
16 d eko úhloého chlení ε á sě os oáčení d Poo eko ε á sě chlos a naená složku chlení do sěu ečn ke dáe Vjádříe-l asoluních hodnoách, dosanee ρ esp. Veko d d ρ á sě do sředu a předsauje složku chlení dosředého a n ρ ρ a ečné chlení a d d ρ d ρ d d a d c) Poh sfécký - jeden od ůsáá na sé ísě, oáčení ělesa se děje kole odu, dáh šech odů ělesa jsou na sousředných koulích se sřede ono pené odě. d dϕ C ρ polohoý eko oecného odu ělesa k odu d ϕ př pooočení se ěleso pooočí o úhel dϕ e sěu ekou d ϕ ρ ona daná eko ρ (, dϕ ) Zěna poloh odu C pooočení je poo d dϕ a chlos odu C d d Veko úhloé chlos není přede dán a je áslý na čase dϕ & ϕ d a a } n d a & & ε ( d ) d Úhloé chlení je dáno ýae ε & & ϕ d Zchlení odu C je poo a ε ( ) d dϕ d) Oecný poh - olíe od ělesa (např.ěžšě T), k něuž ahujee poh osaních odů. Sečení účnku anslace a oáčení dosááe po loolný od ělesa C:
17 Polohoý eko oecného odu C T C C T C T C Rchlos C T C C d d Zchlení C C T C C a d d a ε Skalání áps po složk chlos ( dosanee cklckou áěnou ndeů ) T T T,,, odoně po složk chlení ( ) ( ) T a a ε ε, upaíe a cklckou áěnou ískáe složk ekou chlení ( ) ( ) ( ) ( ) ( ) ( ) T T T a a a a a a ε ε ε ε ε ε,,,.3. Kneaka desk je lášní případe kneak ělesa, keé konáá poh oně,, n. že ϕ ϕ,, se neění () () ( ) ϕ ϕ ϕ kde, - nepohlý souřadný ssé oně pohu, - pohlý souřadný ssé oně desk s počáke odě. B ϕ ϕ ϕ Souřadnce oecného odu B př pohu desk ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ cos sn cos sn sn cos sn cos
18 deací dah ískáe složk chlos d & ( snϕ cosϕ ) & ϕ d d & ( cosϕ snϕ ) & ϕ d dϕ dosadíe & ϕ d a poo,, ( ) ( ) Def. Okažý sřed oáčení (pól oáčení) je od, keý á čase T nuloou chlos. Souřadnce okažého sředu oáčení, učíe podínk :, odoně ( ) p p p, p, p Def. Spojnc sředů oáčení keslenou pené souřadné sséu, naee pená poloda. Spojnc sředů oáčení keslenou pohlé souřadné sséu, oně desk naee pohlá poloda Polod se použíají po učoání hodného au soukolí. (Použí pncpu uálních pací) ekonečně alý poh desk a časoý okažk okažého sředu oáčení. Dosanee p ϕ p ϕ le ealoa jako oočení desk dle Příklad.3.. Kolo o poloěu se oáčí úhloou chlosí a sřed kola á posunou chlos.n., že kolo pokluuje. Učee penou a pohlou polodu. <,
19 Posuná chlos odu,, Okažý sřed oáčení p p,, Okažý sřed oáčení je sále pod sřede kola (pohlá poloda) < dle adání. p
20 3. ZÁKLDY DYMIKY Dnaka kouá příčnné souslos pohu a je ed důodnění ákonů kneak. K pojů použíaný kneace aádí poje ho a síl. Sacký ýpoče - sousaa se sla a jejch půsoš je kldu, popřípadě onoěné příočaé pohu - nější síl s eakce oří onoážnou sousau sl, keá oláá půřeech hledaná přeoření a napěí; nřní síl učíe ed podínek onoáh Rodíl Dnacký ýpoče - sousau uažujee oecné pohu akže je aížena seačný sla - eakce, přeoření a napěí půřeech učujee áslos na čase a hledáe jejch nejěší hodno; nřní síl usí ués onoáhu s dnacký aížení nejen nější síl, ale seačné síl Dnacký ýpoče se poádí, kdž - konsukce neo její čás se pohuje - půsoící síl ění sou elkos čase (např. peodck) - půsoící síl se pohují po konsukc - aížení ačne půso náhle neo ěhe el káké do ýnaně ění sou elkos 3.. ewono ákon jsou ákladní ákon klascké (ewono) echank. Zákon - Zákon seačnos Těleso seáá kldu neo onoěné příočaé pohu, dokud není donuceno půsoení nější síl eno sa ěn. kons. je - l ( síla ) ewon chaakeoal elkos pohu hnosí. Veko hnos á sě oožný s ekoe chlos. H kde je skalá ho Jnak. ákon Be nějšího půsoení achoáá ěleso soj hnos. Příklad: Ronoěný příočaý poh je chaakeoán hnosí konsanní elkos a sěu.. Zákon - Zákon síl (ákladní ákon dnak) Zěna hnos ůže nasa poue půsoení síl d H d ( ) [ kgs - ] d d d eění-l se př pohu honos a d
21 Def.: Zchlení je přío úěné půsoící síle a nepřío úěné elkos chloané ho. Hoa je ěříke odpou, keý honý od klade po séu chlení č poždění a poo se elčně říká seačná hoa. odpoídá přlžně íe ělesa o honos, kg. 3. Zákon - Zákon akce a eakce Dě ělesa na see půsoí sla, keé jsou sejně elké, leží na sejné papsku a jsou opačně oenoané akce eakce - V kldu a onoěné příočaé pohu se o síl uší a nká lak e ěles - Pokud ěleso ění sou chlos, půsoí po chlující síle odpo seačnos, keý je sejně elký jako chlující síla a a je síla seačná a oo je aložen pncp D'leeů Př. Zdž se pohuje s čloěke a) se chlení (a) hůu př pohu hůu ělo čloěka lačí na podlahu sojí ahou a naíc seačnou eakcí G a celkoá síla na podlahu ) se chlení (-a) dolů G a g a ( g a) Eéní případ - olný pád - a g ( g g) a lak čloěka na podlahu l nuloý. Inecální sousa souřadnc jsou ůč sálcí kldu neo se ůč n pohují onoěně příočaře. ejhodnější SS po naše ýpoč: Za necální udee poažoa sousau souřadnc, keá je asoluní kldu. 3.. Dnaka honého odu 3... Základní poj Podle. ewonoa ákona (ákon síl) le po každý honý od napsa ákladní ewonou pohoou onc, číž le uč poh honého odu a Pohoá once jadřuje ah e elčna pohu (dané chlení a ) a sloý elčna epeenoané ýslednou slou
22 n a a předsauje aeacký odel po šeřoání dnackých poěů uažoaného odu. Pohoá once je once ekooá, keou usíe padla př konkéní řešení oepsa do skaláních onc a () & () && () a () & () && () a () & () && () 3... Vě o hnos H d H d Dle. ákona plaí ( ) násoíe d a oho d( ) d. d d Předpoklad Síla ůže ý čase poěnná, j. půsoí od okažku o do času, přčež honos je konsanní Ipuls síl o dτ () ( ) H () H ( ) I () o o. Věa o hnos Časoá ěna hnos (příůsek hnos), se oná pulsu nější síl. Důsledke. ě o hnos je ákon o achoání hnos epůsoí-l na honý od nější síla, ůsáá jeho hnos konsanní. Př Učee chlos, keou ude í olně padající honý od na konc 5. sekund. Počáeční chlos je nuloá. je íha honého odu g ( ) () dτ ( 5) g dτ g 5 5 g 59,8 & 49 s - 5 ( sonejse oce fk g V echncké pa se sekááe s onoěný oáčení ěles, po keé plaí ákon seačnos (neuažujee ření). Jnak je ou př uchloání oáčého pohu. Podoně jako je defnoán oen síl k odu je aeden oen hnos honého odu k loolnéu odu posou. - H [ kg s ] )
23 deace oenu hnos d d d d d d ( ) a poože a a pak d d d d d d d ( ) M d, poože se jedná o ekooý součn kolneáních ekoů ). ( onc ( ) Přpoeňe s ( oáek ) M M s ϕ d M oen síl k odu je oen časoé deac oenu hnos k éuž odu, d je o oenoá analoge ákona síl. Vnásoíe ah d, j. d M d, a negací dosanee () () ( ) ( ) () ( ) I M () M dτ neol puls oenu. o. Věa o hnos Časoá ěna oenu hnos honého odu k loolnéu odu posou se oná pulsu oenu nější síl k éuž odu. neo Deace dle času oenu hnos se oná oenu nějších sl. Podoně jako ákon o achoání hnos áe ákon o achoání oenu hnos: eoují-l nější síl ůč loolně olenéu odu oen, ůsáá oen hnos konsanní Páce, ýkon, enege d d k Def..3. Skalání součn síl a příůsku dáh naee příůsek páce. dw d [J Joule ] Páce na. Celkoá páce je křkoý negál W d o
24 Po oogonální souřadncoý ssé W o d o d o d Jeslže dáha a síla síají úhel, pak α dw ds cosα W cosα ds ds Def..3. Příůsek páce a jednoku času se naýá ýkon dw d p [J s d d - -W Wa ] Výkon je skalání součn síl a chlos. Po soje se aádí účnnos η, jako podíl ýkonu soje k příkonu (dodáané eneg). Je žd enší než.. ákon - ákon síl a d a dosadíe a a d d d Odoně onc násoíe d d d & d d d d d d d d d le poés úpau d d d d d dosanee sečení d d čl d d d d ( )
25 Def Knecká enege honého odu je defnoána ahe E k Inegujee ýa d d, poo o d E k E k, Věa Knecká enege je schopnos kona pác. Vkonaná páce je ona příůsku knecké enege. Poencální enege Těleso j á důsledku sé poloh. Po eneg poencální neesuje žádný uneální oec, usíe j spočía poocí páce, keou je nuno nalož na o, acho ěleso do jeho poloh dopal Hoogenní gaační pole - po přažlou sílu - íhu plaí W G h g h E p - po případ pužn plaí, neoť síla ěhe slačoání není konsanní k kde k je konsana pužn Plaí W d k d k E p E E E E p p k k neo jné úpaě E p Ek E p Ek kons. Zákon o achoání echancké enege Pohuje-l se honý od poencální sloé pol, pak loolné okažku e šech ísech posou plaí, že souče knecké a poencální enege je konsanní. Půsoí-l na honý od ješě nějaké síl, např. síla oou, ření ap., je enege dodáána neo se ění jnou, docháí ke áá - dspac enege, sousaa se naýá dspaní. Věa Souče knecké a poencální enege se ěší o konanou pác, enší se o spořeoanou pác. Přesože enege je odlšný poje od páce á sejné jednok.
26 Př. Gaační pole je poencální pole. Zdhnee-l ěleso o ýšku h ěší se jeho poencální enege o součn íh a příůsku ýšk. E E celk E p E k celkoá je konsanní klesá lneáně s ýškou s klesající ýškou soupá E k,a Vjádří se ěna enege př olné pádu ýšk h Poencální enege E p honého odu e ýšce h ( síla dáha ) se oná G h g h Př olné pádu chlos ose E k a s poklese ýšk se enšuje enege poencální E p. a e h E p, g. a Dáha h E a g g h g gh h g E p E k k a gh gh E p E p,a Veškeá poencální enege E p se poěnla kneckou eneg E k. h E p g, Př.(Hořejší s. 73, př. V 4) Jeřáoý nosník s řeene Q aěšený na laně dlouhé 6 (hoa lana se anedá) se náhle asaí př chlos 3 s -. Sanoe dálenos, do keé se chýlí řeeno le sé seačnos. ( l h) h( l h) l l l l-h Výšku spočíáe dle ákona o achoání echancké enege gh h g Q T h l g l g g g g 3 469,8 3,3 9,8 4lg
27 3.3. Dnaka sousa honých odů (HB) Sousaa honých odů oří nejoecnější ěleso echanck. a odíl od uhého ělesa se ůže aoě ěn. V sousaě honých odů půsoí síl nější,... (, ) nřní jsou sáán pncpe akce a eakce j j Celkoý sloý oenoý účnek šech nřních sl je nuloý j j j Sousaa olných honých odů á posou s 3 supňů olnos, neol 3 neáslých paaeů učuje jednonačně jejch polohu. j Sousaa honých odů ůže naýa noha podo: a) a sousau honých odů ůžee poažoa honou desku, kde koě nějších sl půsoí na každý od nřní síl, keé jej udžují desce ak, že jejch dálenos se neohou ěn; ) jednolé od na see půsoí poue kolý lak a jnak se ohou po soě posunoa a a sousa je dán nějaký ohančení (spké ho nádoě) Polohu každého -ého odu sousa le defnoa polohoý ekoe a seačné lasnos honého odu jsou chaakeoán jeho honosí a o jeho pohu ohodují šechn síl na něj půsoící. Poh sousa honých odů je učen, le-l u šech jejích odů šeř půěh ( ) po,,..... Pokud každý honých odů sousa ůže aujou posou loolnou polohu, luíe o sousaě olných honých odů.. Je-l poh někeých honých odů ůně oeen, luíe o sousaě áaných honých odů. Snížené pohlos odpoídá nk eakce příslušné aě Těžšě sousa honých odů, ě o pohu ěžšě, hnos Těžšě C je od, e keé á celá sousředěná hoa sousa honých odů sejný sacký oen k počáku souřadnc jako je souče dílčích sackých oenů jednolých honých odů.
28 C Skalání oepsání je e au C C, C, C, Těžšě C j c C c k Všeřuje choání sousa honých odů ěžšťoé sousaě. Po půodče plaí: Plaí c c c c c Sacký oen ěžšťoé sousaě je oen nule. Důka: ( c ) c Hnos sousa honých odů po ěžšťoou souřadncoou sousau Uažujee sousau loolné čase př neěnné honos. Hnos sousa honých odů je ona souču hnosí šech odů: Z kneak plaí () () l c l ( ) ( ) & l, poo c ( ) c ( ) c l [ ] ( ) c ( ) Z oho. c l Věa V ěžšťoé sousaě souřadnc je hnos sousa honých odů nuloá.
29 Z defnce ěžšě d d c c c c ískáe deací podle času.ěa o pohu ěžšě Hnos honos sousa HB sousředěné ěžš se oná souču hnosí jednolých HB sousa. Další deací podle času dosanee dc d a d d a c. ěa o pohu ěžšě Těžšě honých odů se pohuje jen le nějších sl a o jako od o honos oné honos celé sousa, na keý půsoí síla co do elkos a sěu oné ekooéu souču nějších sl půsoících na jednolé honé od. Z. a. ě o pohu plýá Zákon o achoání hnos Je-l sloá složka ýslednce nějších sl půsoících na sousau HB nuloá, je hnos sousa honých odů konsanní. Zákon achoání ěžšě Je-l ěžšě sousa honých odů kldu, pak půsoení poue nřních sl se eno sa neění. Vě o příůsku hnos a ěně oenu hnos plaí po sousau honých odů, neoť nřní síl se podle pncpu akce a eakce uší Enege, páce Plaí odoné ah jako po poh jednoho honého odu. Ek je knecká enege sousa honých odů Jednolé honé od se časoé nealu, posunou poloh učené půodče do poloh. áůs knecké enege od okažku do okažku je dek Ek E k, Celkoá páce př posunu poloh do poloh je
30 W ( e) ( ) W W E E k k ( e) () kde W je páce sl nějších a W je páce sl nřních. Věa o ěně knecké enege Zěna knecké enege sousa honých odů e děa poloha je dána pací nějších a nřních sl e ěo poloha. Jaké ude jednodušení knecké enege po cenální sousau souřadnc sousa honých odů? c C c Půodčů odpoídají chlos c c Knecká enege sousa honých odů Ek c c c c c ( c ) ( c c ) c c Poože hnos po ěžšťoou souřadncoou sousau honých odů, pak í poslední ápsu oa nřní člen a c c c E k c c Věa Köngoa Celkoá knecká enege sousa honých odů je dána souče knecké enege celkoé ho sousředěné ěžš a knecké enege sousa honých odů př elaní pohu kole ohoo odu. Volíe-l př okladu jný efeenční od než ěžšě, neude člen Köngoa neplaí. nuloý a ěa c c Pokud sloé pole je koneaní, n. že ke še sloý polí esují skalání funkce, ak ákon o achoání echancké enege ůsáá planos po sousau honých odů E p E k E p E k kons.
31 Jeslže se sousaa honých odů pohuje poencální sloé pol, pak po loolný časoý okažk plaí e šech ísech posou, že souče poencální a knecké enege je konsanní Dnaka honého uhého ělesa Hnos, oen hnos uhého ělesa Výpoče hnos poedee sousaě souřadnc O, keá konáá sejnou anslac jako ěleso, ale na odíl od něj neouje. Sousaa souřadnc O je necální. Pokud je poh počáku O popsaný chlosí onoěný příočaý, je sousaa O aké necální. Okolí odu o honos d přspíá do hnos ělesa hodnoou e ekooé ápsu d H ( ) d a negací H ( ) d d Přpoenee s ýa o sacké oenu d c d d c d d c d poože sacký oen k ěžš je nuloý d. d H d. oepsáno dosadíe pě do ýau po hnos a dosanee H c. Poože chlos ěžšě je dána chlosí počáku sousa a chlosí její oace c c ed c c, poo ( c c ) c c H Z ýsledku plýá, že sousředíe-l šechnu honos do ěžšě, pak hnos ělesa odpoídá hnos ako nklého honého odu. H c Moen hnos k počáku O sousa popsuje negál O O ( ) d Výa le upa ( Kufne,Kuklík: Saení echanka ) do konečného au po oen hnos k počáku souřadnc O c O I esp. ( dále ) c I O C C Výa se jednoduší po případ oenu hnos po cenální sousau souřadnc (sousaa souřadnc pocháející ěžšě ) C I kde I C I C [ I ] C C je eno seačnos cenální sousaě souřadnc. I D D C C C C C D I D C C C C C D D I C C C C C
32 V acoé ápsu I { C } [ ] { } C Je řea přpoenou, že sejně jako po sousau honých odů plaí po uhé ěleso ákon o achoání hnos, keý říká. Je-l sloá složka ýslednce sl půsoících na uhé ěleso nuloá, poo hnos ělesa je konsanní. Odoně s přpoínáe ákon o achoání oenu hnos, keý říká: Má-l sousaa sl půsoících na uhé ěleso nuloou ýslednc, pak ke še odů posou je oen hnos uhého ělesa konsanní. ( Počíáe-l oen hnos uhého ělesa k jeho ěžš, posačí k ou, a oen hnos l konsanní, poue nuloá hodnoa oenoé čás ýslednce. ) l. pulsoou ěu po uhé ěleso jádříe oncí I () dτ H C () H C ( ) C. pulsoou ěu po uhé ěleso jádříe oncí I M () M dτ C () C ( ) C Knecká enege uhého ělesa kneckou eneg le sano poocí ě Köngo. Po cenální sousau souřadnc kneckou eneg počee jako souče knecké enege celkoé ho sousředěné ěžš, keou ěšíe o kneckou eneg ělesa ůč éo sousaě. Pní sčíanec popsuje příůsek knecké enege le anslačního pohu, duhá čás popsuje příůsek enege osažené oac ělesa. E k kde ( ) ( ) d C C je elkos chlos ěžšě popsuje oac ělesa je polohoý eko nfneálních honosí d ělesa jeho cenální sousaě souřadnc Roedení ápsu a úpaou dosanee onc po kneckou eneg ělesa E k C I C esp. Ek C C Poedou-l se acoé opeace, ůžee kneckou eneg ělesa počía poocí složek jednolých ekoů Ek ( C C C ) ( I C I C I C D D D ) C C C C C C
33 I po uhé ěleso plaí poencální sloé pol ákon o achoání echancké enege. Př Poh álce je dán anslační chlosí ěžšě a oační chlosí kole sředoé os, poo knecká enege álce je dána E k I, kde I je oen seačnos álce k jeho ose.
34 3.5. Sesaoání pohoých onc půsoe ewonoý a půsoe d'leeoý Dnacké úa ůžee nahad jedný honý ode, případě složějšího sousaou honých odů, keou le poažoa a ákladní dnacký odel. Ke kouání pohu honého odu neo sousa honých odů le uží pncp uolňoání. Podle ohoo pncpu se každý honý od sousaě choá sejně jako osaělý honý od po jeho uolnění e sousa, j. po přpojení sloých účnků ae (eakcí) Sesaoání once podle ewonoa půsou Podle. ewonoa ákona (ákon síl) le po každý (uolněný) honý od napsa ákladní ewonou pohoou onc. (, ) a,... přčež k j je ýslednce šech sl půsoících na daný od po jeho uolnění Pohoá once jadřuje ah e elčna pohu (dané chlení j a ) a sloý elčna (dané ýslednou slou ) a předsauje aeacký odel po šeřoání dnackých poěů uažoaného odu. Pohoou onc le ůný půsoe upaoa, např. j násoíe ekooě lea adusekoe příslušného odu. a M o (,,...) M o předsauje oen ýsledné síl půsoící na od k počáku. Uedený ssé onc předsauje sousau pohoých onc oenoé au. To once ůžee oepsa do sséu 6 skaláních pohoých onc. Po onný případ, j. onný poh oně, a a půsoení sl ležících éo oně ude a,. a a ( a a ) M Z hledska úloh geoee sl e sace přpoíná ewonů půso úlohu ekalence Sesaoání once podle d'leeoa půsou Př sesaoání onc le uží d'leeů pncp (3. ákon - ákon akce a eakce). Teno přísup k sesaoání pohoých onc je s ohlede na nalos ískané e sace půhlednější. a Ronc a přepíšee foálně do au a. Součn a á oě síl a poo onačíe uo elčnu jako seačnou sílu D a, keá je oenoána opačné sslu nežl chlení a poo j le sěl jako sílu, keá ání chloání odu a usluje ed o seání odu půodní pohoé sau.
35 Seačná síla D je fkní, neoť o není skuečná síla půsoící na od. Poocí ní dosáá pohoá once anuloaný sa přpoínající onoáhu sl e sace. Ve skuečnos se jedná o dnacký (neonoážný) sa. Poo luíe o. dnacké onoáe (fkce). D'leeů pncp Síl půsoící na honý od jsou onoáe se slou seačnou. k j D pacujee podle padel fouloaných e sace Dosááe ssé onc D ( D ) a upaíe násoíe ekooě polohoý ekoe lea M o M D o D Záě: Pohoé once sesaené ewonoý a d'leeoý půsoe se lší aeackého hledska foálně.
36 4.KMITÁÍ VOLÉ 4. Lneání kání (haoncký oscláo e fce) Vel časný pohe honého odu je kaý poh. Kání ude lneání, jeslže síla, keá př ýchlce ací honý od do onoážné poloh, je úěná ýchlce K (4..) kde konsana úěnos K je péoá konsana, poože uažujee honý od, keý je džen onoážné poloe, např. pé, což jsou pužně poddajné podpo Rolšujee:. nepoddajné a - nedoolující poh. pužně poddajné a - doolují poh koule (jako od) č eknuí Skuečný kaý poh nahaujee hodný jednodušený odele. a) č dokonale uhá - sousaa neá supeň olnos ) č poddajná, nehoná - sousaa á oně supeň olnos, posou supeň olnos (ýchlka odooná oně a odooná kolo k oně) c) koule - uhé ěleso: oně supně olnos (ožnos posunu, oáčení), posou 5 supňů olnos ( posun a oáčení dle šech 3 os) 4. Kání olné neluené asane př chýlení honého odu jeho onoážného sau a ponechání pohu e dalšího uení nější sla. Kání sousa s supně olnos - honý od podepřený pužnou eřešíe naáhání pužn Řešíe půěh ýchlk Vchýlíe-l od do poloh w e sěu os, půsoí po: seačná síla w& a w& odpo pužn Kw w K - péoá konsana [ - ] Kw Podínka onoáh: w&& Kw K (4..) w&& w Zaedee elčnu: lasní (úhloá) kuhoá fekence K (4..) a dosanee hoogenní lneání dfeencální onc. řádu s konsanní koefcen: w& w (4..3)
37 λ Řešení hledáe e au w e ede na chaakesckou onc λ a po kořen λ, ± dosanee řešení w C e C e oou kopleních čísel neo w C sn C cos oou eálných čísel (4..4) C, C jsou negační konsan, keé se učí počáečních podínek. Volíe-l negační konsan e au: C cosϕ C sn ϕ přejde řešení na a: w cos ϕ sn snϕ cos ( cosϕ sn ϕ ) sn cos sn( ϕ ) w ( ϕ ) sn (4..5) kde: - apluda (nejěší ýchlka), ϕ - fáoý posun Ze náé ýchlk ůžee uč chlos pohu a chlení: cos ϕ a w& sn ϕ ( ) ( ) w unkce popsující řešení once (4..3) jsou peodcké, poo defnujee: T - peoda (doa ku) doa, keá je pořená k poěhnuí dáh jednou dokola f - fekence (koče) [H][s - ] udáá kolká a sekundu se celý poh opakuje Plaí T f Po řešení hledáe negační konsan: - apluda, ϕ - fáoý posun oecné řešení: sn ϕ w ( ) cos ( ϕ ) ( ϕ ) w& a w& sn Počáeční podínk w w( ) snϕ přčež w, jsou konkéní hodno po. cosϕ ( ) Upaíe: w snϕ w w. anϕ ϕ acg cosϕ ( w ) w sn ϕ 6447 ( ) ( sn ϕ cos ϕ ) w( ) 448 cos ϕ
38 Gaf ýchlk áslos na čase w α w() (apluda) ϕ T (peoda) K Mohou nasa případ, že pužn jsou řaen do sousa a jejch účnek ůžee nahad ekalenní péoou K K n konsanou: paalelně Síl pužnách K w e n n K w K w e n K w K e n K K K K n ) séoě L w e w e n w n K e n e K K e K e n K 4.3 Kání olné luené př ýchlce w půsoí na honý od: K w a w& Kw ) síla od pea Kw ) seačná síla a 3) odpo posředí úěný chlos Odpo posředí je epeenoán aký článke. Síla jadřující l ohoo článku půsoí po pohu a její elkos je úěná chlos. konsanu úěnos onačujee jako konsanu (lneáního) skóního luení ( např. luče u au ).
39 Sesaení podínek onoáh podle D'leeoa pncpu a Kw (4.3.) w& w& Kw (4.3.) Zaedee elčn: K - lasní kuhoá fekence po kání olné neluené [ s ] (4.3.3) - konsana chaakeující odpo posředí - kuhoá fekence úluu [ s ] (4.3.4) Poo úpaou once (6.3..) dosanee w& w& w, (4.3.5) lneání hoogenní dfeencální onc II.řádu s konsanní koefcen. λ Řešení hledáe e au w e. Chaakescká once á a λ λ (4.3.6) a její kořen λ, ± (4.3.7) nalýa řešení. kcký a nadkcký úlu - jedná se o slné luení, λ je eálné, poh není peodcký onoážnou polohou ůže pojí od nejýše jednou. Poo neajíaé!. p podkcký úlu (4.3.8) V oo případě á chaakescká once řešení oou kopleních čísel, λ ± ( ) ± λ ± aedee (4.3.9), (4.3.) Oecné řešení oou kopleních čísel ( ) ( ) C e e ( C e C e ) w C e Reálné řešení je poo ( ϕ ) w e sn (4.3.) kde, ϕ jsou negační konsan. Rchlos honého odu jádříe dw [ e sn ( ϕ ) e cos ( ϕ )] (4.3.) d Inegační konsan,ϕ učíe počáečních podínek Po čas. w ( ) snϕ Po. ( ) [ snϕ cosϕ] Dělení ískáe: ( ) [ snϕ cosϕ] cosϕ w snϕ snϕ ( ) oho plne:
40 ( ) ( ) w ( ) ( ) ( ) ( ) gϕ cosϕ cosϕ snϕ w snϕ w oho: g ϕ (4.3.3) ( ) w( ) Poo: w( ) snϕ (4.3.4) Plaí-l, že ϕ usíe použí. podínku ( ) snϕ cosϕ (4.3.5) Gaf áslos ýchlk w na čase a ýna negačních konsan,ϕ w gα () α e w() φ - e T (peoda) T pluda se enšuje, doa ku ůsáá sejná π T < (4.3.6) Ze ahu (4.3.) plne, že < a poo se doa ku př luené kání podlužuje opo neluenéu π π T nelu < Tlu Koče (fekence) f T π (4.3.7) Konsan luení neo jsou sáán ahe, nele je přío ěř, ale ůžee ěř po soě jdoucí aální ýchlk, n. ýchlk s časoý odsupe T (doa ku).
41 Věa 4.3. Přoený logaus poěu po soě jdoucích a.ýchlek je konsanní. aýá se logacký dekeen úluu ϑ w() ϑ ln T w( T ) (4.3.8) Jsou-l ná ýchlk, e nž poěhne n ků, plaí oec: w ϑ ln n w n Důka: e sn( ϕ ) e sn( ϕ ) ϑ ln ln e T T sn T ϕ e e sn T ϕ ( ) [ ( ) ] Zkáíe ýae e a dosadíe T π : sn( ϕ ) sn( ϕ ) ϑ ln ln ln T T e [ π ϕ] e sn sn ϕ e sn( α π ) sn α T ϑ ln ln ge T ( součn dou konsan ) T e T [ ] [ ] Voec po ýpoče ϑ T dosadíe π T pak ϑ π π oho kuhoá fekence úluu, konsana luení (4.3.9) 4π ϑ α I Kw K Př Břeeno o honos 4 kg je aěšeno na laně podle o. Kladka á honos 4 kg. Honos lana se anedáá, ale udee uažoa poažení lana na paé saně kladk le osoé síl. Síla k podlouží lano o 4 c. Učee onc pohu př počáeční ýchlce w() c a počáeční chlos (). Př další ku je ýchlka w,6c. Dále učee dou ku a koče. w a w Př ýchlce w se kladka pooočí o úhel ϕ a lano se poáhne o w. Zchlení řeene a je e ahu k úhloéu chlení a kladk přlžně α.
42 3 4 - K,5 w 4 V laně ude ěhe kání síla Kw. Podle d'leeoa pncpu oenoá ýnka ke sředu kladk. a α I kw Dosaení d d w a d w a α d d d I (hooý oen seačnos k ose kladk) dosanee onc e au: w & w&& kw w& Zkáíe : w& w&& w& kw esp. w& w& kw Po dosaení adaných hodno w & w& 5 w esp. w & w& 6,98w 4 Sonání s oncí : Vlasní kuhoá fekence - 6,98 7,8s Konsanu luení učíe poocí logackého dekeenu ϑ : ( ) w, ϑ ln ln,4 w,6 7,8 4π 4π ϑ,4,759 s - 7,8,759 7,85 s π π - Doa ku T,84 s 7,85 Inegační konsan 7,85 / gϕ 8,89 ϕ ϕ,5354 ad ( ),759 w( ), w( ),,, snϕ / sn87 59, f,4 s T,84 Ronc pohu př olné luené kání dosanee dosaení do (4.3.) w,e,759 sn ( 7,85,5354) -
43 Př áa ěu na sožá eleního sílače se opakují po 3 nuách. Doa ku je 6 sekund, úlu je učen logacký dekeene ϑ,4. Učee jak elká je apluda (ýchlka) př příchodu noého náau ěu hlede k počáeční ýchlce. Me náa ěu uplne s 3 ků e náa 6 w w ϑ ϑ ln ϑ ln e w w ϑ apluda (ýchlka) w w e Poo,4 3, w we we, 3w w w
44 5. KMITÁÍ VYUCEÉ 5.. Kání nucené neluené ( ) () w a w& Budící síla ( ) sn kde je kuhoá fekence haonck poěnné síl. Příklade ohou ý á od odla, ěu, účnk necenoané oující čás soje apod. Kw Podínka onoáh á a a Kw ( ) (5..) w& Kw sn le upa w& w sn (5..) Řešení nehoogenní dfeencální once.řádu ískáe kdž k oecnéu řešení once (4..3) přdáe pakulání negál w() C 4 sn 44 C 4 cos 443 sn (5..3) ( ) oecné řešení pakulání řešení Ponáka: Je-l jedná se o případ eonance, n., že ýchlka ose nad šechn ee ; nepřípusné! Řešení hoogenní once: w C sn C cos oecný a. Pakulání řešení once (5..) w& w sn wp w sn w&& p w sn po dosaení w sn w sn sn Zkáíe sn w w w ( ) w w sn p ( ) ( ) Výa dále upaíe: w K Onačíe-l: sackou ýchlku w s K
45 a dnacký součnel nuceného usáleného kání δ K kde, poo apluda nuceného kání w w s δ Výsledný a po ýchlku w př nucené usálené kání je w() sn( ϕ ) sn (5..4) K Je-l j. fekence udící síl je ona lasní fekenc sousa, neoť f π f, docháí k jeu eonance. π Ronc (5..4.) ůžee jádř e au w() sn( ϕ ) w sn (5..5.) a po počáeční podínk w a ( ) pak e au ( ) () w sn sn w. Po není ýchlka defnoána. Hledáe poo lu podle l Hospaloa padla () w l l w () w w s s w w s sn sn cos sn w ( cos sn ) l sn sn K s ( ) cos sn Půěh ýchlk př eonanc je náoněn na oáku po eoěné elčn. Za každou peodu ose apluda o π. s f
46 Reonance Kání nucené, keé je půsoeno haonckou poěnnou slou () sn á po řešení nehoogenní once w& w sn oecný negál: w() sn( ϕ ) W sn, kde: W K Př podoné oou se ukáže, že člen se pakckých případech uluí (řešení olného kání). Poo po analýu nuceného kání je ohodující. člen - keý je uen nější slou, nepřesáá účnke úluu, á ak dlouho, pokud půsoí udící síla. Takoý sa se naýá kání usálené. ekence ohoo pohu je sejná jako u nější síl. pluda usáleného kání áleží: a) na elkos udící síl ) hlaně na poěu fekence udící w síl a lasní fekence sousa Výa W není K w defnoán po, j. apluda s K usáleného kání jde k. Too je případ eonance. f Vah η naýáe f naladění č poěnou fekencí. Záslos e naladění a apludou je eonanční křka. apř. př: 3 je apluda w w 8 př je w 4 3 δ s Reonanční křka
47 ( Plaí po nucené neluené kání s. supně olnos ). Př eonanc nenasáá e skuečnos ýchlka nekonečně elká, nýž účnke pakckého úluu (e ýpoču anedán) poue ýchlka ěšená. Př kání konsukcí se usíe eonanc hnou acho aánl poušení konsukce elký ýchlka. 5. Kání nucené luené () Honý od je okáán pulsující slou, např. á odla, necenoání oující čás soje. K () w a w& Kw Účnk necenoaného oou (le uč přesněj) Těžšě oou se př oáčení pohuje po kužnc o poloěu e, keý naee ecencou oou. Odsředá síla je: e (5..) - úhloá chlos oou se defnuje okle poocí oáček n (j. je adán koče a fekence f ), poče oáček oou a časoou jednoku n[o s - ] πf πn (5..) - honos oou Složka odsředé síl do sěu ýchlk pea je, čas se ěří od okažku, kd je ěžšě oou kolo ke sěu ýchlk pea. D'leeů pncp: w& w& Kw sn (5..3) w& w& w sn (5..4) K lasní kuhoá fekence kání olného nelueného chaakeuje luení Řešení (5..4) dosanee jako oecné řešení once hoogenní doplněné pakulání negále. w w w () () p Leá sana once (5..4) se shoduje s řešení olného lueného kání (4.3.5), poo její oecné řešení je: () e ( ϕ ) w sn (5..5) Paá sana once (5..4) je peodcká funkce se snoý půěhe a poo le í pakulání negál e au: w p sn ( ϕ) (5..6) neo w p ( sn cosϕ cos snϕ) (5..7a) Deací w& p ( cos cosϕ sn snϕ) (5..7) ( sn cosϕ cos ϕ w& p sn ) (5..7c)
48 Dosadíe do once (5..4): cosϕ snϕ ( cosϕ) sn ( ) snϕ cosϕ snϕ cos sn Ronce ůže ý splněna po loolné je ehd plaí-l onos koefcenů u funkcí sn a cos, ed: [( ) cos ϕ snϕ] (5..8) [ ( ) cosϕ cosϕ]. once (5..8.) je po splněna po oho snϕ gϕ ( ) ϕ cos ϕ sn (5..9) cosϕ Poonání čaelů a jenoaelů loku usí ý: sn ϕ cosϕ B B Konsana B se učí podínk: sn ϕ cos ϕ B ( ) ( ) po pěné dosaení: snϕ ( ) ( ) Dosadíe do (5..8) cosϕ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (7..) Oecné řešení once nehoogenní je:. čás ( ϕ ) sn( ϕ w e sn ) (5..) e keé jsou :,ϕ negační konsan, keé se učí počáečních podínek. neo 4π ϑ (po podkcký úlu) nalýa ahu po w( ) (5..).čás se s osoucí čase el chle líží nule, neoť l luení > je e eponenu eponencální funkce. Po její ení ude í ýchlka honého odu podle.čás (5..6) snusoý půěh s konsanní aální ýchlkou dle ahu
49 (5..) se sejnou úhloou chlosí (fekencí) jako udící síla, ale s fáoý posune ϕ daný (5..9). Poo w sn( ϕ) ( ) ( ) Věa: Poě aální dnacké ýchlk ke sacké ýchlce (ýchlka odu a kldu) je oen poěu aální dnacké síl ke sacké síle peu (síla kldu) a naýá se dnacký součnel w d δ d (5..) w s s Důka V onoážné poloe w a w s a.dnacká ýchlka Sacká ýchlka je půsoena sálý nepohlý aížení např. íhou s ws (5..3) K Po učení dnackého součnele ěříe sacké a dnacké ýchlk. oa pooluje počía se aížení sacký násoený dnacký součnele, keý se uádí po jednolé p konsukcí. Dnacký součnel δ se ění dle úhloé chlos udící síl a jeho aální hodnoa je př "kcké úhloé chlos". Veee-l neásle na ude [ ] aální po nální ( ) ( ) Podínka eéu: 4, hledáe ed eé ohoo ýau. ( ) ( )( ) 8 4 ( ) a) Vah je splněn po, což odpoídá a ) k wd ws s K (5..4) kde k je kcká úhloá chlos udící síl, po keou jsou ýchlk a í síl aální. Kcký koče udící síl: f π π (5..5) dosadíe k do a ( ) 4 ( ) Dosaeno (5..4) do (5..)
50 a Odoený ah plaí a předpokladu, že neásí na, např. pulsující síla od odla na osě, od ěu ap. Př haoncké síle nklé odsředou slou neáženého oou ásí úhloé chlos oou a poo eéní apluda je sejná, ale po kcké oáčk: f π na
51 6. ZÁKLDY TEORIE RÁZU 6. Příý á koulí aaí-l pohující se od na překážku, ěhe el káké do se ění ýnaně jeho chlos (např. se ůže sá sejně elkou opačného sslu) Podle ě o ěně hnos napíšee H ( ) H ( ) dτ I ( ) - puls nější síl d, kde je doa ání áu Můžee čísl sřední hodnou síl d ed (6..) Ineal je el káký a poo náaoá síla ůže dosáhnou načných hodno. Př Oceloá koule o íe 5 naaí na uhou desku chlosí,75.s - a odaí se přlžně sejnou chlosí. Doa ání áu la ěřena. -4 s. Učee sílu př náau. Hnos koule před náae 5,75, 383kg s před náae 9,8,383kg s po náau,383, což je 7 ěší než íha koule, Skuečná aální elkos síl ' ( čase poěnná) ude ješě ěší, poože neal je el káký a náaoá síla ůže dosáhnou načných hodno. Př áu nkají načné síl, keé nuně půsoí defoace, poo nesačíe s eoí dokonale uhých ěles.
52 Poue nejjednodušších případech s ůžee uo apoac dool. Jední případů je á koulí, jejchž sřed se před náae po ně pohoal éže příce (příý á) před náae po náau Po ýpoče pořeujee neáslé podínk, acho ohl počía nenáé chlos po náau. Zěnu chlosí půsol náaoé síl e oěa koule. To síl jsou sejně elké a podoně jako sousaě honých odů se naáje uší jako nřní síl. Pak po uo sousau, na keou nepůsoí nější síl, plaí ěa o achoání hnos c čl (6..) Tao once je planá e šech případech příého áu koulí. Jako duhá podínka se aádí ewonoo kolní padlo ; le říc, že další ah ásí už na aeálu koulí ( ) e espeke e (6..3.) Věa 6.. Př příé cenální áu je elaní chlos po áu přío úěná elaní chlos před áe. Konsana úěnos e se naýá součnel esuce Hodnoa e leží nealu e, ) e, á deálně plascký ) e, á deálně pužný ) Koule lák dokonale plascké n., každá jejch defoace ůsane ale a pohují se po áu jako jedno ěleso společnou chlosí ' ( ) Př oo áu došlo ke áě knecké enege o elkos E K ( )
53 keá se spořeoala na přeoření koulí. ) Koule lák dokonale pužné Př náau se koule účnke náaoých sl defoují; ao defoace šak cela pone a přo se koule od see oddělí. eůsane žádná alá defoace. Knecká enege, keá se spořeoala na přeoření koulí se ee ku ění na kneckou eneg př náau koulí do půodního au. Jsou k dspoc once po řešení nenáých chlosí, po náau. Př. 6.. Po deálně pužný á plaí ákon o achoání echancké enege. Dokaže Plaí e () () Přeskupíe () ( ) ( ) (oě san once násoíe sejný čísle) Přeskupíe () Vájeně násoíe ( ) ( ) násoíe celou onc a poo Knecká enege před áe se oná knecké eneg po áu. Př Učee ýšku, do keé se odaí skleněná kulčka, pušěná ýšk na elkou ěžkou skleněnou desku ( e,94) chlos desk (elká a ěžká) před áe po áu ude gh chlos před áe, g chlos po áu, kd kulčka se odaí do ýšk e,94 h, 883,94 g gh h
54 Součnel esuce po někeá ělesa Dojce ěles e ložskoé oceloé kulčk,98 oceloá deska - oceloá koule,93 aooá deska - guoá koule,8 oloěné koule,
2. ZÁKLADY KINEMATIKY
 . ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
. ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
V soustavě N hmotných bodů působí síly. vnější. vnitřní jsou svázány principem akce a reakce
 3.3. naka sousta hotnýh bodů (HB) Soustaa hotnýh bodů toří nejobenější těleso ehank. a odíl od tuhého tělesa se ůže taoě ěnt. V soustaě hotnýh bodů působí síl F nější (,,... ) ntřní jsou sáán pnpe ake
3.3. naka sousta hotnýh bodů (HB) Soustaa hotnýh bodů toří nejobenější těleso ehank. a odíl od tuhého tělesa se ůže taoě ěnt. V soustaě hotnýh bodů působí síl F nější (,,... ) ntřní jsou sáán pnpe ake
Kinematika hmotného bodu
 Kneaka honého bou k j Polohoý eko bou osou Velkos olohoého ekou k j s τ Zěna olohoého ekou s s Dáha τ τ τ s s Rchlos honého bou s Půěná chlos a Zchlení honého bou τ a ečné chlení n R a n Noáloé chlení
Kneaka honého bou k j Polohoý eko bou osou Velkos olohoého ekou k j s τ Zěna olohoého ekou s s Dáha τ τ τ s s Rchlos honého bou s Půěná chlos a Zchlení honého bou τ a ečné chlení n R a n Noáloé chlení
Kinematika a dynamika soustavy těles
 Knemaka a dynamka sousay ěles Vyšeřoání poybu mecansmů Analycké yšeřoání poybu mecansmu le poés pomocí doé funkce j. au me souřadncem popsujícím polou nacío a nanýc členů. Posup je paný níže uedenéo příkladu.
Knemaka a dynamka sousay ěles Vyšeřoání poybu mecansmů Analycké yšeřoání poybu mecansmu le poés pomocí doé funkce j. au me souřadncem popsujícím polou nacío a nanýc členů. Posup je paný níže uedenéo příkladu.
mechanika Statika se zabývá působením sil na tělesa, která jsou v klidu.
 Aplkoná echnk,. přednášk Předě Dnk je součásí ěšího předěu Mechnk. I soný předě Mechnk ůžee cháp šší ác děl jej n echnku nějších sl nebo éž echnku uhých ěles (sk dnk) echnku nřních sl nebol echnku poddjných
Aplkoná echnk,. přednášk Předě Dnk je součásí ěšího předěu Mechnk. I soný předě Mechnk ůžee cháp šší ác děl jej n echnku nějších sl nebo éž echnku uhých ěles (sk dnk) echnku nřních sl nebol echnku poddjných
Hlavní body. Úvod do dynamiky. Dynamika translačních pohybů Dynamika rotačních pohybů
 Mechanka dynaka Hlavní body Úvod do dynaky. Dynaka tanslačních pohybů Dynaka otačních pohybů Úvod do dynaky Mechanka by byla neúplná, kdyby se nezabývala, důvody poč se tělesa dávají do pohybu, zychlují,
Mechanka dynaka Hlavní body Úvod do dynaky. Dynaka tanslačních pohybů Dynaka otačních pohybů Úvod do dynaky Mechanka by byla neúplná, kdyby se nezabývala, důvody poč se tělesa dávají do pohybu, zychlují,
Cvičení č. 14 Vlastní čísla a vlastní vektory. Charakteristický mnohočlen a charakteristická rovnice. Lokalizace spektra. Spektrální rozklad.
 Cičení z lineání algeby 7 Ví Vondák Cičení č 4 Vlasní čísla a lasní ekoy Chaakeisický mnohočlen a chaakeisická onice Lokalizace speka Spekální ozklad Vlasní čísla a lasní ekoy maice Nechť je dána čecoá
Cičení z lineání algeby 7 Ví Vondák Cičení č 4 Vlasní čísla a lasní ekoy Chaakeisický mnohočlen a chaakeisická onice Lokalizace speka Spekální ozklad Vlasní čísla a lasní ekoy maice Nechť je dána čecoá
1. ZÁKLADNÍ POJMY. Základní pojmy v dynamice:
 . ZÁKLADNÍ POJMY je čásí echanky, kerá se zabýá sude pohybů ěles z hledska příčn jejch znku (působení sl, oenů) Základní pojy dynace: Honos [kg] Prosor echancká lasnos honého úaru (ělesa, honého bodu),
. ZÁKLADNÍ POJMY je čásí echanky, kerá se zabýá sude pohybů ěles z hledska příčn jejch znku (působení sl, oenů) Základní pojy dynace: Honos [kg] Prosor echancká lasnos honého úaru (ělesa, honého bodu),
Tlumené kmity. Obr
 1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
FYZIKA I. Pohyb těles po podložce
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHICKÁ UIVERZITA OSTRAVA FAKULTA STROJÍ FYZIKA I Pohyb ěles po podložce Prof. RDr. Vilé Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Ar. Dagar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHICKÁ UIVERZITA OSTRAVA FAKULTA STROJÍ FYZIKA I Pohyb ěles po podložce Prof. RDr. Vilé Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Ar. Dagar Mádrová
asi 1,5 hodiny seznámit studenty se základními zákonitostmi křivočarého pohybu bodu Dynamika I, 3. přednáška Obsah přednášky : Doba studia :
 Dmk I, 3. předášk Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Dmk I, 3. předášk Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Příklad 4 Ohýbaný nosník - napětí
 Příklad 4 Oýaný nosník - napěí Teorie Prosý o, rovinný o Při prosé ou je průře naáán oový oene oáčející kole jedné lavníc os servačnosi průřeu, ovkle os. oen se načí neo jeno. Běžněji je ožné se seka s
Příklad 4 Oýaný nosník - napěí Teorie Prosý o, rovinný o Při prosé ou je průře naáán oový oene oáčející kole jedné lavníc os servačnosi průřeu, ovkle os. oen se načí neo jeno. Běžněji je ožné se seka s
SPECIÁLNÍ TEORIE RELATIVITY
 SPECIÁLNÍ TEORIE RELATIVITY GALILEO GALILEI (6.s.) pohbuje-li se ažná sousaa hlee k jiné onoěný příočaý pohbe, je s ní onoenná (pohb je ájený elainí) neeisuje žáná absoluní ažná sousaa, keou jeinou b ěl
SPECIÁLNÍ TEORIE RELATIVITY GALILEO GALILEI (6.s.) pohbuje-li se ažná sousaa hlee k jiné onoěný příočaý pohbe, je s ní onoenná (pohb je ájený elainí) neeisuje žáná absoluní ažná sousaa, keou jeinou b ěl
Mechanická silová pole
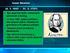 Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
DYNAMIKA časový účinek síly Impuls síly. 2. dráhový účinek síly mechanická práce W (skalární veličina)
 DYNAMIKA 2 Působením síly na čásici se obecně mění její pohybový sav. Síla působí vždy v učiém časovém inevalu a záoveň na učiém úseku ajekoie s. 1. časový účinek síly Impuls síly 2. dáhový účinek síly
DYNAMIKA 2 Působením síly na čásici se obecně mění její pohybový sav. Síla působí vždy v učiém časovém inevalu a záoveň na učiém úseku ajekoie s. 1. časový účinek síly Impuls síly 2. dáhový účinek síly
I. MECHANIKA 4. Soustava hmotných bodů II
 I. CHIK 4. Soustaa hmotných bodů II 1 Obsah Spojté ozložení hmotnost. Počet stupňů olnost. Knematka tuhého tělesa. Zjednodušení popsu otace kolem osy a peného bodu. Chaslesoa ěta. Dynamka tuhého tělesa.
I. CHIK 4. Soustaa hmotných bodů II 1 Obsah Spojté ozložení hmotnost. Počet stupňů olnost. Knematka tuhého tělesa. Zjednodušení popsu otace kolem osy a peného bodu. Chaslesoa ěta. Dynamka tuhého tělesa.
Dynamika hmotných bodů. 3. Hmotný bod o hmotnosti m = 10 kg se pohybuje po kružnici o poloměru r = 2 m,
 Dnik honých bodů 3 Honý bod o honosi kg se ohbuje o kužnici o oloěu 3 3 řičež jeho dáh áisí n čse odle hu s k kde k 5 /s Učee elikos ýsledné síl ůsobící n honý bod úhel α keý síá eko síl s ekoe chlosi
Dnik honých bodů 3 Honý bod o honosi kg se ohbuje o kužnici o oloěu 3 3 řičež jeho dáh áisí n čse odle hu s k kde k 5 /s Učee elikos ýsledné síl ůsobící n honý bod úhel α keý síá eko síl s ekoe chlosi
Dynamika tuhého tělesa. Petr Šidlof
 Dnaika tuhého tělesa Pet Šidlof Dnaika tuhého tělesa Pvní věta ipulsová F dp dt a t Zchlení těžiště Výslednice vnějších sil F A F B F C Celková hbnost soustav p p i Hotnost soustav i těžiště soustav se
Dnaika tuhého tělesa Pet Šidlof Dnaika tuhého tělesa Pvní věta ipulsová F dp dt a t Zchlení těžiště Výslednice vnějších sil F A F B F C Celková hbnost soustav p p i Hotnost soustav i těžiště soustav se
Křivočarý pohyb bodu.
 Křočý pohb bodu. Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Křočý pohb bodu. Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á
 ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
í í ú ř Í ř í á í é é é Í á ý ň ř í š í č í í á í í é í í í á á ó ě Í í ě í í í í í řá ů čč ř č á í í í ě á ě ě í á í š ť Í ě Í ř ě í ě č Í ř é č š ě
 ú ř Í ř á é é é Í á ý ň ř š č á é á á ó Í řá ů čč ř č á á á š ť Í Í ř č Í ř é č š á č ý č é ó á č ř ů á č č š á ů á Í á á é č ú ó ť ý Í ř č é Í č š á ř á é á ř á ř ů ř ř á áž á Í ý é é č ý čů á é é é č
ú ř Í ř á é é é Í á ý ň ř š č á é á á ó Í řá ů čč ř č á á á š ť Í Í ř č Í ř é č š á č ý č é ó á č ř ů á č č š á ů á Í á á é č ú ó ť ý Í ř č é Í č š á ř á é á ř á ř ů ř ř á áž á Í ý é é č ý čů á é é é č
4. KMITÁNÍ VOLNÉ. Rozlišujeme: 1. nepoddajné vazby - nedovolují pohyb 2. pružně poddajné vazby - dovolují pohyb
 4. MITÁNÍ VOLNÉ 4. Lineární kiání (haronický osciláor ve fyzice) Veli časný pohye honého odu je kiavý pohy. iání ude lineární, jesliže síla, kerá při výchylce x vrací honý od do rovnovážné polohy, je úěrná
4. MITÁNÍ VOLNÉ 4. Lineární kiání (haronický osciláor ve fyzice) Veli časný pohye honého odu je kiavý pohy. iání ude lineární, jesliže síla, kerá při výchylce x vrací honý od do rovnovážné polohy, je úěrná
Mechanika kontinua. ) b) každé těleso je spojité (můžeme je chápat jako souvislou množinu M M materiálových bodů B M
 Mechanka konnua moel konnua (moel spoého posřeí: a poso e spoý (souslá množna M G geomeckých boů B G b kažé ěleso e spoé (můžeme e chápa ako souslou množnu M M maeáloých boů B M Aom konnu: V kažém okamžku
Mechanka konnua moel konnua (moel spoého posřeí: a poso e spoý (souslá množna M G geomeckých boů B G b kažé ěleso e spoé (můžeme e chápa ako souslou množnu M M maeáloých boů B M Aom konnu: V kažém okamžku
Mechanismy s konstantním převodem
 Mechanismy s konsanním přeodem Obsah přednášky : eičina - přeod mechanismu, aié soukoí, ozubené soukoí, předohoé a paneoé soukoí, kadkosoje a aiáoy. Doba sudia : asi hodina Cí přednášky : seznámi sudeny
Mechanismy s konsanním přeodem Obsah přednášky : eičina - přeod mechanismu, aié soukoí, ozubené soukoí, předohoé a paneoé soukoí, kadkosoje a aiáoy. Doba sudia : asi hodina Cí přednášky : seznámi sudeny
Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici
 Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Dynamika pohybu po kružnici III
 Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Zada ní 2. Semina rní pra ce z pr edme tu Matematika pro informatiky (KI/MAI)
 Zaa ní. eina ní pa e z p ee u Maeaia po infoai (KI/MAI) Dau zaání. 5. 17 Poín paoání - einání páe se sláá z poaoé čási (ó Malabu) a eoé čási (poool o paoání). - Kažý suen oezáá pái sá za sebe. - uen si
Zaa ní. eina ní pa e z p ee u Maeaia po infoai (KI/MAI) Dau zaání. 5. 17 Poín paoání - einání páe se sláá z poaoé čási (ó Malabu) a eoé čási (poool o paoání). - Kažý suen oezáá pái sá za sebe. - uen si
á í í Č ť ó í íď ý í í íř ý ř ě Í č ť í á š á ý é ů á í ť č Í Í é ď ž é ž ť é éř ů í š ší ý í Í é á É í ě é ř í Í í é í ř ě á ó í í ě š ě ý á ř í á í
 á Č ť ó ď ý ř ý ř ě Í č ť á š á ý é ů á ť č Í Í é ď ž é ž ť é éř ů š š ý Í é á É ě é ř Í é ř ě á ó ě š ě ý á ř á ě é Í Ž ý ť ó ř ý Í ů ů ů š Í ý é ý ý ů é ů š é ů ó Žá Í á Íř ě šř ó ř ě é ě é Ě š č á č
á Č ť ó ď ý ř ý ř ě Í č ť á š á ý é ů á ť č Í Í é ď ž é ž ť é éř ů š š ý Í é á É ě é ř Í é ř ě á ó ě š ě ý á ř á ě é Í Ž ý ť ó ř ý Í ů ů ů š Í ý é ý ý ů é ů š é ů ó Žá Í á Íř ě šř ó ř ě é ě é Ě š č á č
SMR 1. Pavel Padevět
 SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
Dynamika tuhého tělesa
 Dnaika tuhého tělesa Pet Šidlof ECHNCKÁ UNVERZA V LBERC Fakulta echatonik, infoatik a eioboových studií ento ateiál vnikl v áci pojektu ESF CZ..7/../7.47 Reflexe požadavků půslu na výuku v oblasti autoatického
Dnaika tuhého tělesa Pet Šidlof ECHNCKÁ UNVERZA V LBERC Fakulta echatonik, infoatik a eioboových studií ento ateiál vnikl v áci pojektu ESF CZ..7/../7.47 Reflexe požadavků půslu na výuku v oblasti autoatického
1.3.4 Rovnoměrně zrychlený pohyb po kružnici
 34 Rovnoměrně zrychlený pohyb po kružnici Předpoklady: 33 Opakování: K veličinám popisujícím posuvný pohyb exisují analogické veličiny popisující pohyb po kružnici: rovnoměrný pohyb pojíko rovnoměrný pohyb
34 Rovnoměrně zrychlený pohyb po kružnici Předpoklady: 33 Opakování: K veličinám popisujícím posuvný pohyb exisují analogické veličiny popisující pohyb po kružnici: rovnoměrný pohyb pojíko rovnoměrný pohyb
přednáška 3 Základní pojmy - trajektorie, proudnice Trocha matematiky Rovnice kontinuity Pohybové rovnice
 3 HYDROMECHANIKA HYDRODYNAMIKA ákldní once ákon řednášk 3 Leu : Ok Mšoský; HYDROMECHANIKA Jomí Noskeč, MECHANIKA TEKUTIN Fnšek Šob; HYDROMECHANIKA 3 Hdodnmk Úod: Meod osu konnu loo úodem Rodělení oudění
3 HYDROMECHANIKA HYDRODYNAMIKA ákldní once ákon řednášk 3 Leu : Ok Mšoský; HYDROMECHANIKA Jomí Noskeč, MECHANIKA TEKUTIN Fnšek Šob; HYDROMECHANIKA 3 Hdodnmk Úod: Meod osu konnu loo úodem Rodělení oudění
Ý áš á í é ť š í
 ří ď ě ě é ř ý ří ý é úř á ú ě ě ř ář í ší ž í ř í í Í ř ý áš ě ů é í ď Í ř ý řá óš í áš í ý í ř š í á á ř ří ž ě ž ď š ě í í í á žá ý á Í ÍŽ Š Á Ó ř č í Í é ž é ž á í á á Ž ř ě ž ú á á č ě ě í ěž á í
ří ď ě ě é ř ý ří ý é úř á ú ě ě ř ář í ší ž í ř í í Í ř ý áš ě ů é í ď Í ř ý řá óš í áš í ý í ř š í á á ř ří ž ě ž ď š ě í í í á žá ý á Í ÍŽ Š Á Ó ř č í Í é ž é ž á í á á Ž ř ě ž ú á á č ě ě í ěž á í
 č á Č Ě ó č á ů á ě ě é ď Ú č á Č ě ě š č ě í ří á ů š í š í í é ě ů č ě ří č ě ě í ý č á í í á ý á ě í ář š á í á í ň á č é ó í á ě á íč ě á á ě ří č ě í á Č ě á á Ž á ú í ě Č č ý ě ě ď á é á á ě ě
č á Č Ě ó č á ů á ě ě é ď Ú č á Č ě ě š č ě í ří á ů š í š í í é ě ů č ě ří č ě ě í ý č á í í á ý á ě í ář š á í á í ň á č é ó í á ě á íč ě á á ě ří č ě í á Č ě á á Ž á ú í ě Č č ý ě ě ď á é á á ě ě
í é é á š ě í ý ž ď í é žřá čí ř é č í čí á ř á čí é á á á ž ď ř ú ě á í ý ž á ř š í ž ě á š ř ý ř á č í ř á ď ě á á í ě í á ďí é ď ř í č ř ž ř á é č
 ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
č í úř é č úň ž č ň ř č é ř í š ň é č č čí ó ř á é é ů á č é ň é ň á í š ě č áš č ý ř ó š á á á č íó á ň á Ř Á í ří ů á ý á č í í řú ů ě í ě š ř ú á á
 í úř úň ž ň ř ř í š ň í ó ř á ů á ň ň á í š ě áš ý ř ó š á á á íó á ň á Ř Á í ří ů á ý á í í řú ů ě í ě š ř ú á á ž ň í í í á á ň ř á í ú á Č ó Čá Ó í Č É řžňá ř ž ň ý á ň ó á ž ó ř ú ň á á ť ú á ěí ú
í úř úň ž ň ř ř í š ň í ó ř á ů á ň ň á í š ě áš ý ř ó š á á á íó á ň á Ř Á í ří ů á ý á í í řú ů ě í ě š ř ú á á ž ň í í í á á ň ř á í ú á Č ó Čá Ó í Č É řžňá ř ž ň ý á ň ó á ž ó ř ú ň á á ť ú á ěí ú
rovinná soustava sil (paprsky všech sil soustavy leží v jedné rovině) rovinný svazek sil rovinná soustava rovnoběžných sil
 3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
Ý Á Í ŘÁ Č Á
 Ý Á Í ŘÁ Č Á Ř Á úč ř č ě ů Ť é č ě š ř ž š é é š é é Ý ž š é ó ó ť š ž ů é Ť é ž é ů ú š ň ž ě š ž š é é ř š š ě š ó č é ů š ě ř š ť ť é ř ž ó ř š é Ť é ě š ř ě ř š ř ě ó é é ú ů Á ř é é é č š é ř ž ř
Ý Á Í ŘÁ Č Á Ř Á úč ř č ě ů Ť é č ě š ř ž š é é š é é Ý ž š é ó ó ť š ž ů é Ť é ž é ů ú š ň ž ě š ž š é é ř š š ě š ó č é ů š ě ř š ť ť é ř ž ó ř š é Ť é ě š ř ě ř š ř ě ó é é ú ů Á ř é é é č š é ř ž ř
ÚVOD DO DYNAMIKY HMOTNÉHO BODU
 ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
NA POMOC FO. Pád vodivého rámečku v magnetickém poli
 NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
 ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
Kinematika hmotného bodu
 DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
é éž á ó ý ě č ě í ž é é š é í é š ě ě í é í ú úž ú é ž ě ž ď ý ý řě ě ě á š á š ř ý ďá ě ě ě ú Ž ý ť ě ž řěčí ě ž í šě š ž ř ř ěř ďá ó ř š Žá ě í ě ý
 Í Í Ý í í í ě ý á é í á ř č é á ý á ý ň ó š á č ě é ř ř čí é ú č ž é š á é á í á ř č Č á č ě š ě á í ď š á ř é í é ě á í čá ď Í ěč é é ěř é ě ší ě á í é žď á á š ř čí é š ě ž ýš á í é ě á ď ř ě í é á ú
Í Í Ý í í í ě ý á é í á ř č é á ý á ý ň ó š á č ě é ř ř čí é ú č ž é š á é á í á ř č Č á č ě š ě á í ď š á ř é í é ě á í čá ď Í ěč é é ěř é ě ší ě á í é žď á á š ř čí é š ě ž ýš á í é ě á ď ř ě í é á ú
7. SEMINÁŘ Z MECHANIKY
 - 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
- 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
á ě ž ž á íš č Š á š ě ě ř ě í Ú ř č á ť žá á í Í ě ý í á ř ž í í í í á í ň á ý ě á ě ú ě ž á Í á Í í á ě š š á á ěř é á š á ý á ž č ž í é ě á é á ě á
 ě ř é ě ří ž ý ř ý í ž ě ě ž ť č ě ě ž ř á ý á š ě í ů á ě í é á ž š é ě é ů í é řá é í í ě ří č ě é ř é ý ě í ě Í ž á čá í ě ý í á í ě á á í ž š ř á í č ý ž ř ý š ě ó áž ě ý íš á á ší í ě ý ř ě Ž ř ý
ě ř é ě ří ž ý ř ý í ž ě ě ž ť č ě ě ž ř á ý á š ě í ů á ě í é á ž š é ě é ů í é řá é í í ě ří č ě é ř é ý ě í ě Í ž á čá í ě ý í á í ě á á í ž š ř á í č ý ž ř ý š ě ó áž ě ý íš á á ší í ě ý ř ě Ž ř ý
G g. dv dt = M. Energetická rovnováha. Potřebná hnací síla. Celkový jízdní odpor : po dosazení : Potřebný moment motoru : Potřebný výkon motoru :
 TU Lbe aulta stojní Kateda ozdel a otoů Koloé dopaní a anpulační stoje I Enegetá onoáha Celoý jízdní odpo : Enegetá onoáha Potřebná hnaí síla O + O + O + f V O a po dosazení : Gf os α + ρ + G sn α + G
TU Lbe aulta stojní Kateda ozdel a otoů Koloé dopaní a anpulační stoje I Enegetá onoáha Celoý jízdní odpo : Enegetá onoáha Potřebná hnaí síla O + O + O + f V O a po dosazení : Gf os α + ρ + G sn α + G
ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é é řď ú é Á ř é č ř ž ó ř ě ú ů é ě ě ř é č ž é ě ř ě Č ď ř ř č ž ě ě ů ě ř č ě é ž ů ř ó é ř č ř ě ě ř č é é
 Č é Č Í č č Á é č č ě ř ě ř é č č č ř ž ěř č č ř ě č č é ě é ě ž ů č Ý Ť é ř ě é ť ě ů ě é é ť ř ů ě ř ě ů č Š ě ó ó ž ť č ř ž ř ž ě č ž ř Š ž ě ó ž ě ž ě č Šř ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é
Č é Č Í č č Á é č č ě ř ě ř é č č č ř ž ěř č č ř ě č č é ě é ě ž ů č Ý Ť é ř ě é ť ě ů ě é é ť ř ů ě ř ě ů č Š ě ó ó ž ť č ř ž ř ž ě č ž ř Š ž ě ó ž ě ž ě č Šř ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é
Mgr. Zuzana Adamson-Krupičková Docteur de la Sorbonne
 M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. Uá é í www.. U á é í w w w.., U I D : K O S 2 0 3 2 3 2 A á Sě Pí á é A x í M K: K, B, V á L A Txé M K:
M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. Uá é í www.. U á é í w w w.., U I D : K O S 2 0 3 2 3 2 A á Sě Pí á é A x í M K: K, B, V á L A Txé M K:
í ň š ř ú í í ář á í ář ě ě í é é ě é í í ě ě é á é ř í á í ášé ů ž é á á í ě í á ě á ž ě ř é á ý ž í čá á ý í á í é é á ý ě č č ý á á í áš ě é é ě á
 ÚČ É ŘÍ Ě Č Í Č Í Í čá í ř á ý í í á ě ě š é á í á ž é é ě í ří ě ě á í č ž é í á ř íč ů ě á í ě ě ší ý č í í ý í ů í á ý ý í č í ů čá í á ý í í ě í í í ě ř č í ř í á í é ě ě ě ěž ř í š ě á ě í í é ář
ÚČ É ŘÍ Ě Č Í Č Í Í čá í ř á ý í í á ě ě š é á í á ž é é ě í ří ě ě á í č ž é í á ř íč ů ě á í ě ě ší ý č í í ý í ů í á ý ý í č í ů čá í á ý í í ě í í í ě ř č í ř í á í é ě ě ě ěž ř í š ě á ě í í é ář
ř í ší é ě é ří č é č é é š í ě é é á č ý á é ř ě ý ů é é ó ó í ě ěá í ž ě ší ž é á ó ě í ří é é ě ů Ť é ř ý á ě ší ý ž é á í žň á ý é ž í á á ří ž š
 ř í ší é ě é ří č é č é é š í ě é é á č ý á é ř ě ý ů é é ó ó í ě ěá í ž ě ší ž é á ó ě í ří é é ě ů Ť é ř ý á ě ší ý ž é á í žň á ý é ž í á á ří ž š Í ě í š í é í čá í š ý ó ý í ř ě ě ý ř ě ší é ý ý ě
ř í ší é ě é ří č é č é é š í ě é é á č ý á é ř ě ý ů é é ó ó í ě ěá í ž ě ší ž é á ó ě í ří é é ě ů Ť é ř ý á ě ší ý ž é á í žň á ý é ž í á á ří ž š Í ě í š í é í čá í š ý ó ý í ř ě ě ý ř ě ší é ý ý ě
Příklad 4 Ohýbaný nosník napětí
 Příklad 4 Oýaný nosník napěí Zadání Nosník s převislým koncem je aížen spojiým aížení q = 4 kn/m a osamělou silou F = 40 kn. Průře nosníku je ocelový svařovaný proil. Roměr nosníku jsou: L =,6 m L =, m
Příklad 4 Oýaný nosník napěí Zadání Nosník s převislým koncem je aížen spojiým aížení q = 4 kn/m a osamělou silou F = 40 kn. Průře nosníku je ocelový svařovaný proil. Roměr nosníku jsou: L =,6 m L =, m
F1040 Mechanika a molekulová fyzika
 4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ strojní součásti. Přednáška 6
 Faula srojního nženýrsví VUT v Brně Úsav onsruování KONSTRUOVÁNÍ STROJŮ srojní součás řednáša 6 ředepjaé šrouové spoje The greaer our noledge ncreases, he greaer our gnorance unfolds. JOHN F. KENNEDY Osah
Faula srojního nženýrsví VUT v Brně Úsav onsruování KONSTRUOVÁNÍ STROJŮ srojní součás řednáša 6 ředepjaé šrouové spoje The greaer our noledge ncreases, he greaer our gnorance unfolds. JOHN F. KENNEDY Osah
á ý é í č ří Ť á íč é í ž č ř Í é Ť č í ž á ý ý á é č í ý ř ří í ž ř é ř á á í ý ý ů í Í ř ů Ž á á á ž ří š ě Í ž č é ří ř í ř í Ť ý š ý ř í ý ů ří ř
 á ý č ř Ť á č ž č ř Í Ť č ž á ý ý á č ý ř ř ž ř ř á á ý ý ů Í ř ů Ž á á á ž ř š ě Í ž č ř ř ř Ť ý š ý ř ý ů ř ř á š á Í ř ý ý ř ř č ř ř Í š ý Í Ť č ř á Í ó č ř ý ž ý Í ř č ž á ř ž ý ž ří ř š Í É Í ř Í
á ý č ř Ť á č ž č ř Í Ť č ž á ý ý á č ý ř ř ž ř ř á á ý ý ů Í ř ů Ž á á á ž ř š ě Í ž č ř ř ř Ť ý š ý ř ý ů ř ř á š á Í ř ý ý ř ř č ř ř Í š ý Í Ť č ř á Í ó č ř ý ž ý Í ř č ž á ř ž ý ž ří ř š Í É Í ř Í
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 rojek realizoaný na SŠ Noé Měo nad Meují finanční podporou Operační prorau Vzděláání pro konkurencecopno Králoéradeckéo kraje Modul 03 - Tecnické předěy In. Jan Jeelík . Mecanická práce oybuje-li e oný
rojek realizoaný na SŠ Noé Měo nad Meují finanční podporou Operační prorau Vzděláání pro konkurencecopno Králoéradeckéo kraje Modul 03 - Tecnické předěy In. Jan Jeelík . Mecanická práce oybuje-li e oný
Í í É ť ď í é í ř ě ž ří á í í í í ů ě ě é ě É ž ě í á š ý ň á ý ř ů á Í é ž ě ě í á ů á í í ří á ž é ř ě ř á á ř Í č ů í Í ž ří ě ý ě Í ě ří ř ší á í
 Í í É ť ď í é í ř ě ž ří á í í í í ů ě ě é ě É ž ě í á š ýň á ý ř ů á Í é ž ě ě í á ů á í í ří á ž é ř ě ř á á ř Í č ů í Í ž ří ě ý ě Í ě ří ř ší á í Í ď Í ý ší ř Í é ě ř ó Í š ř Í í ň á ú í ř ě ý ě ší
Í í É ť ď í é í ř ě ž ří á í í í í ů ě ě é ě É ž ě í á š ýň á ý ř ů á Í é ž ě ě í á ů á í í ří á ž é ř ě ř á á ř Í č ů í Í ž ří ě ý ě Í ě ří ř ší á í Í ď Í ý ší ř Í é ě ř ó Í š ř Í í ň á ú í ř ě ý ě ší
( ) Kinematika a dynamika bodu. s( t) ( )
 Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
C o r e 4, s p o l. s r. o.
 e L e a r n i n g o v ý s y s t é m s p o l o é n o s t i S L A P o u ž í v a te s k ý m a n u á l Š T U D E N T C o r e 4, s p o l. r. so. S t r a n a 2 O b s a h 1 Ú V O D 3 2 P O P I S 4 2. 1 R e g
e L e a r n i n g o v ý s y s t é m s p o l o é n o s t i S L A P o u ž í v a te s k ý m a n u á l Š T U D E N T C o r e 4, s p o l. r. so. S t r a n a 2 O b s a h 1 Ú V O D 3 2 P O P I S 4 2. 1 R e g
PJS Přednáška číslo 2
 PJS Přednáška číslo Jednoduché elekromagnecké přechodné děje Předpoklady: onsanní rychlos všech očvých srojů (časové konsany delší než u el.-mg. dějů a v důsledku oho frekvence elekrckých velčn. Pops sysému
PJS Přednáška číslo Jednoduché elekromagnecké přechodné děje Předpoklady: onsanní rychlos všech očvých srojů (časové konsany delší než u el.-mg. dějů a v důsledku oho frekvence elekrckých velčn. Pops sysému
í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í
 í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í ů ž á ří ří ž á í í ý é í ž í ě ý č é á ž é á ě á á
í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í ů ž á ří ří ž á í í ý é í ž í ě ý č é á ž é á ě á á
Statika 1. Miroslav Vokáč ČVUT v Praze, Fakulta architektury. Statika 1. M. Vokáč. Plocha.
 Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
ř í ú í ě ě é á í č ěž š ě ř á í ě ú í ž ř í ž č ě č ú í č ě č ě í č č á í í ří í á í ě á é é ě í á í á č é í ě á č ě éř š í ě é á í ě ř ů ů é žň í á
 Ó ě é ě ý á íč á í ě é á í ř ě é ó ž é é á č é ó ě ší íř ář ší í é á é ě ř á č ý ý é á ř ě ř á í í á ě í á í ě š í ř ů ř š ě č í Ž č á ě í á á í ý ý á ý á ý Ž é ší é é ó í í ý ě á í č í ě š é š é é č ě
Ó ě é ě ý á íč á í ě é á í ř ě é ó ž é é á č é ó ě ší íř ář ší í é á é ě ř á č ý ý é á ř ě ř á í í á ě í á í ě š í ř ů ř š ě č í Ž č á ě í á á í ý ý á ý á ý Ž é ší é é ó í í ý ě á í č í ě š é š é é č ě
Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,
 Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
5. SEMINÁŘ Z MECHANIKY
 - 5-5 SEMINÁŘ Z MECHANIKY 5 Osobní auoobi se pohbuje po odoroné dráze se zrhení s a při ronoěrné soupání se zrhení 6 s Určee úhe soupání za předpokadu že ahoá sía ooru a sía ření jsou sáé a F F kons F
- 5-5 SEMINÁŘ Z MECHANIKY 5 Osobní auoobi se pohbuje po odoroné dráze se zrhení s a při ronoěrné soupání se zrhení 6 s Určee úhe soupání za předpokadu že ahoá sía ooru a sía ření jsou sáé a F F kons F
Řešení: uvolnění - volba reakcí, vnitřní síly řešené z levého tělesa: Ekvivalentní varianty prutu: Deformační podmínka: ΔL=0
 Cvičení 4 k procvičení označeno vlevo červeno čaro P/4 až P4/4 osaní D/4 až D4/4, ožný doácí úkol P/4 Dána je soosá příá yč konsanních průřezů =00 s ěžiši T složená z ěděného úsek délky =00 a ocelového
Cvičení 4 k procvičení označeno vlevo červeno čaro P/4 až P4/4 osaní D/4 až D4/4, ožný doácí úkol P/4 Dána je soosá příá yč konsanních průřezů =00 s ěžiši T složená z ěděného úsek délky =00 a ocelového
1.1.18 Rovnoměrně zrychlený pohyb v příkladech IV
 8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
ř ř Ž ž ě á ň ě ě Ž ý ý ú ů ž ý ř š áť ý š ě ž ě ť é šť á š á ž éž á Ž š á ě ý á ý ú Ý š ř á ž áž ě é ř Ž Š ě ž ě á é řá é Í š ř á ř ěř ň é ž ž ě Ú é
 Ž ř á Č ř é ýí ě á ě ř ý ž á ě é Ž ý úř Ú á ž á ř ý ž á á Ť š á Č Íá ř é ě ý ó á š á ř é ž é é á ž á á Ž á ň á ž áš á á ú ů Ž ó ú ů ž á ú ůž á ě á ž á Í Ž ž Í á ř ě ž ř ě Ž Ž š š Íé šť á é áž Í é é ř ě
Ž ř á Č ř é ýí ě á ě ř ý ž á ě é Ž ý úř Ú á ž á ř ý ž á á Ť š á Č Íá ř é ě ý ó á š á ř é ž é é á ž á á Ž á ň á ž áš á á ú ů Ž ó ú ů ž á ú ůž á ě á ž á Í Ž ž Í á ř ě ž ř ě Ž Ž š š Íé šť á é áž Í é é ř ě
é ž ú ú ú ú ý řěč ř ú úč ú š ďá ě č ó ř á úč ě š á žíš řě ě á ó Žíš ě é č é ě ší ěžší ú ě ě ší áč é ž á ý ř š í čě ší č ú ú á é ě é š á ú á á á í ř í
 ář ě ě ý ť Í š ý ýť á í í ň á í č í ý ý ý ý č á č áč í á ť ě ě é á í í ý ř á ší ě ě ší í á ý á ě ší á í č ě é šš č í á í ší ř ě ář Í í ň čá í á ř í é á í ěř š ář í é á á é é ů š á í é ě é ý á ý ú á é á
ář ě ě ý ť Í š ý ýť á í í ň á í č í ý ý ý ý č á č áč í á ť ě ě é á í í ý ř á ší ě ě ší í á ý á ě ší á í č ě é šš č í á í ší ř ě ář Í í ň čá í á ř í é á í ěř š ář í é á á é é ů š á í é ě é ý á ý ú á é á
ř Á Á Í ž Í á í ří ů ž ří ě é é á á í ě ý í á é á ří Á á ř ď ž ó í ěč Í á é á é ě ě ý ží á ý á Á ě č é á ň Í ě ě ří š ě ě ě ří Ú á ě Í á ě č ó Ě ě ř í
 ř Á Á Í ž Í á ř ů ž ř ě é é á á ě ý á é á ř Á á ř ď ž ó ěč Í á é á é ě ě ý ží á ý á Á ě č é á ň Í ě ě ř š ě ě ě ř Ú á ě Í á ě č ó Ě ě ř ěř ě ř ý á á č ě ř ř é ř ó ó ř á á ů á ú ě š á ě ě ě ě ůá ě é ý ř
ř Á Á Í ž Í á ř ů ž ř ě é é á á ě ý á é á ř Á á ř ď ž ó ěč Í á é á é ě ě ý ží á ý á Á ě č é á ň Í ě ě ř š ě ě ě ř Ú á ě Í á ě č ó Ě ě ř ěř ě ř ý á á č ě ř ř é ř ó ó ř á á ů á ú ě š á ě ě ě ě ůá ě é ý ř
2.6.5 Výměny tepla při změnách skupenství
 2.6.5 Výměny epla při změnách skupensí Předpoklady: 2604 Opakoání: Teplo se spořeboáá na da druhy dějů: zyšoání eploy: Q = mc, změna skupensí: Q = mlx. Tepelné konsany ody: c( led ) = 2000 J kg K, l =
2.6.5 Výměny epla při změnách skupensí Předpoklady: 2604 Opakoání: Teplo se spořeboáá na da druhy dějů: zyšoání eploy: Q = mc, změna skupensí: Q = mlx. Tepelné konsany ody: c( led ) = 2000 J kg K, l =
ý í á á š ě é í š íž á á ě š š ě ě á ě é ř é ž čá é ž ř í ř í í á č í š á í š ř í é ě š ž í ý é ě í í í á ř é ě ě ší ž ů ý á ě š é číš ě á ú ě í á í ě
 Í Á Í Ý Á Ú Ř Č Í Í č ř á ý š á ý í í č í í ě í ž ě í č í á í í í í č í í á í ěž ě á í č í ěř í é ýš ý á á ě í í š ů í á í ů č í ž í ž í áš ě ě á é ě á í é š í é ř é á é á í á ě ž áž í ý č á í ž ý ě ší
Í Á Í Ý Á Ú Ř Č Í Í č ř á ý š á ý í í č í í ě í ž ě í č í á í í í í č í í á í ěž ě á í č í ěř í é ýš ý á á ě í í š ů í á í ů č í ž í ž í áš ě ě á é ě á í é š í é ř é á é á í á ě ž áž í ý č á í ž ý ě ší
-Á----Á á-ě-í í ú --ž í ú ----í š é -----š -ě é é í ---é -
 ÁÁ áěí í ú ž í ú í š é š ě é é í é í í ě í č ářž í í í Č á á á í é í í ě í č ářž í í á áč ř Č č í ž ó á áě á č ě řé í ěě ěý í í óů ěí ěš í řů á áž í ě é š ě í é š ě ř ý ř á áá á í ří é í ž á ý ř í Ž é
ÁÁ áěí í ú ž í ú í š é š ě é é í é í í ě í č ářž í í í Č á á á í é í í ě í č ářž í í á áč ř Č č í ž ó á áě á č ě řé í ěě ěý í í óů ěí ěš í řů á áž í ě é š ě í é š ě ř ý ř á áá á í ří é í ž á ý ř í Ž é
ž ě é ú ž é ů á ž ú á š ú Í Ť č é ž ě š ý ěž é řá é é Í č é ž ý Í ě ť ě ě ž é úř ž ř ú ý ř žá ý ý ř ú ý ý ůž ý ř á ě á á ř ě é á á ě ř á ř á é á á é ž
 ň č ý ě ř š ž ř ř é ý á ř é š ě á ú č č ý ě ž é ř á ů á á á ť é ěř ů ť Ť ž č Í úž Ě ě š á é á ě á ř é ř ě ě ž áč ž ě ůž á ž ů á ů é á á á ř é š ě á ž ě š á š é ř áč ý ř ž é ř á ý é ě ž ž ý á ý ů ěř ť ě
ň č ý ě ř š ž ř ř é ý á ř é š ě á ú č č ý ě ž é ř á ů á á á ť é ěř ů ť Ť ž č Í úž Ě ě š á é á ě á ř é ř ě ě ž áč ž ě ůž á ž ů á ů é á á á ř é š ě á ž ě š á š é ř áč ý ř ž é ř á ý é ě ž ž ý á ý ů ěř ť ě
Ě ě é š Á Í ž ě Í á á ž ě š ř ň á ě é á á ě é ř á Í Í é ší á é á ě ť á ě ó á š ě č á č ó ÍÍ á ý á á ář é á é á ě ý ř ý á ř ř ě ó á Á š á á ž á ě ý á ž
 ě ň á ý ř á ší ář š ě ý ť é ě ů ě č č Í ě ž Ů ž é ý řž ý ý Ž ě š ý ů ě ř á ů čí Í Í š Í á á ě á é š ž ů č ř á ó á Í á ší ář Í á á á ě á řž ě řé é ě ů ří ě é Í š ž é ů ě ě ř ší ý á Í ž é á ě š ž ř Ů ě ó
ě ň á ý ř á ší ář š ě ý ť é ě ů ě č č Í ě ž Ů ž é ý řž ý ý Ž ě š ý ů ě ř á ů čí Í Í š Í á á ě á é š ž ů č ř á ó á Í á ší ář Í á á á ě á řž ě řé é ě ů ří ě é Í š ž é ů ě ě ř ší ý á Í ž é á ě š ž ř Ů ě ó
 č š š ř ř Í ů č Ě Á Š ŠÁ Ř Ď É Í Ě Í Í čí ž ě č é č ě ý Ž ř ě č ý ě ý ý ř ě š ý ě ť ý é é ě ě é ě é ř é ř Ť ě š ě ž ě é ě é é ů ě é ř ú ý ý é ěř ý ý š ý ý ž é é š ý š ě ý ř ř ř ě š ý ě ý ý ř ě é Ž é é
č š š ř ř Í ů č Ě Á Š ŠÁ Ř Ď É Í Ě Í Í čí ž ě č é č ě ý Ž ř ě č ý ě ý ý ř ě š ý ě ť ý é é ě ě é ě é ř é ř Ť ě š ě ž ě é ě é é ů ě é ř ú ý ý é ěř ý ý š ý ý ž é é š ý š ě ý ř ř ř ě š ý ě ý ý ř ě é Ž é é
2.2.2 Ú m y sln á u b lížen í n a zd rav í a d alší n á siln é tre stn é čin y N ásiln o sti - les v io le n c e s...
 1. K rim in o lo g ic k á č á s t... 13 1.1 V y m ezen í n á siln é k rim in a lity a so u v isejících p o jm ů... 13 1.1.1 N ásilí a n á siln á k r im in a lita... 14 1.1.2 A grese, k rim in á ln í a
1. K rim in o lo g ic k á č á s t... 13 1.1 V y m ezen í n á siln é k rim in a lity a so u v isejících p o jm ů... 13 1.1.1 N ásilí a n á siln á k r im in a lita... 14 1.1.2 A grese, k rim in á ln í a
 ú ľž ě ý ú ľž č é š Ř ń Ž č ý ú ž č é š ú Ž ľ č ý ú ž č é š ř č é ě č ľ ě ě Š š řč Č Č ą Č č úč Č Č Č Ę ř é ě é Ž č Úč éž č ý ř ř ě č ř ý é č ú Ž č ý č é ú ż č é š ě é ř š č č é č č é ě č č é é Ž Ž ö č
ú ľž ě ý ú ľž č é š Ř ń Ž č ý ú ž č é š ú Ž ľ č ý ú ž č é š ř č é ě č ľ ě ě Š š řč Č Č ą Č č úč Č Č Č Ę ř é ě é Ž č Úč éž č ý ř ř ě č ř ý é č ú Ž č ý č é ú ż č é š ě é ř š č č é č č é ě č č é é Ž Ž ö č
ý Í č ší í ě í ů ý í ě á íó í í á ě í ě í š í ť é ř š ě Í é é Í á í ří í íř í íž í í í í ů ží í ý í ů í ší ěá Í á é á í í ě ě í ó ý ý í í í ť í á ší í
 ý Í č š ě ů ý ě á ó á ě ě š ť é ř š ě Í é é Í á ř ř ž ů ž ý ů š ěá Í á é á ě ě ó ý ý ť á š ě ž é é č Á ž á Í ř Ě ó é ř á ú Í ě ý é ě š č ý Í ě ř ů ě ú ň Í ť é ě ě š Ě ó á ř č ě ó ů ř ř á Íř ží ř ě č ě
ý Í č š ě ů ý ě á ó á ě ě š ť é ř š ě Í é é Í á ř ř ž ů ž ý ů š ěá Í á é á ě ě ó ý ý ť á š ě ž é é č Á ž á Í ř Ě ó é ř á ú Í ě ý é ě š č ý Í ě ř ů ě ú ň Í ť é ě ě š Ě ó á ř č ě ó ů ř ř á Íř ží ř ě č ě
í á ě ý ů ý č ář í š éž á ý š á ě č á ý ý č ě ř ří é ě ší ř í ě í á ž ý č á á é é á í á é ář é č é é ě á š á ř í ě ů á á á ž é ě á ž ý ě ě ů ý š é ř š
 Á Ď é á á ř š ú í á í í ě í é ě š žá é ě ý ý ů ý é í é í ě é á í é ý é áš é š ž í á ý ž á é á řá ý ý ž é í é ě ší š í ě í á á ý í á í ů ž éú é í í á á í ř á í ř á ý ú í á í ú í á á í á ý č í á á á ě ě
Á Ď é á á ř š ú í á í í ě í é ě š žá é ě ý ý ů ý é í é í ě é á í é ý é áš é š ž í á ý ž á é á řá ý ý ž é í é ě ší š í ě í á á ý í á í ů ž éú é í í á á í ř á í ř á ý ú í á í ú í á á í á ý č í á á á ě ě
Á ť ď ť ú é ý ý ý ů é ú Í ě ě ř ě Í é ý ě é š úř ž ýš é é ŕ ů é Í ř ě ř ý ř Ĺ ř Ž š é ý é é é ě š ě š ř ý ů Č ý ě é ě ň š ý ú é ú ů ý ů ý ů ň ř š ý úř
 đ Á ł ř ě é ě Ž é é ä łüł ŕ ł ř ľ ľľ ľľ ľľ Ż ě Ž Í ž ž ý Ž š úř ý é ý ř Í ý ý ý ý ů é ú š ě é ž ú Í ř ě ý ý Í ý ý ů ř ě ř Ž ž ě ř ě ů ý Ž ř ě Ž Ž é Í ý é Í ř ř ě Í é Í é ý ů ř ě ť ž ě é ě é ý ě é šž ř
đ Á ł ř ě é ě Ž é é ä łüł ŕ ł ř ľ ľľ ľľ ľľ Ż ě Ž Í ž ž ý Ž š úř ý é ý ř Í ý ý ý ý ů é ú š ě é ž ú Í ř ě ý ý Í ý ý ů ř ě ř Ž ž ě ř ě ů ý Ž ř ě Ž Ž é Í ý é Í ř ř ě Í é Í é ý ů ř ě ť ž ě é ě é ý ě é šž ř
š í í š ó ý ř Č é ó ěí í č é Č ý í áš ěě ý ý ú í ý ů ý ý ě á ý ď í ž ž á č í á ž ř é í í í ě í í ý á í ý ě á é ř š á ý š í é ů č ú ě ý í ř í í ř í Í ž
 ě áňí š í í š ó ý ř Č é ó ěí í č é Č ý í áš ěě ý ý ú í ý ů ý ý ě á ý ď í ž ž á č í á ž ř é í í í ě í í ý á í ý ě á é ř š á ý š í é ů č ú ě ý í ř í í ř í Í ž ý ý ý ě ší í í ý ě í ěč ý ů ží í í ří í ů ř
ě áňí š í í š ó ý ř Č é ó ěí í č é Č ý í áš ěě ý ý ú í ý ů ý ý ě á ý ď í ž ž á č í á ž ř é í í í ě í í ý á í ý ě á é ř š á ý š í é ů č ú ě ý í ř í í ř í Í ž ý ý ý ě ší í í ý ě í ěč ý ů ží í í ří í ů ř
á í ě ý ďě í í í í í í ř ě á íč ý ů ě ž í ě ý ě ý í ý ě á í í ří ě í í í í ý š í é é á í í á á ě ů á í ě á á í íš é ó ě í í í é í á í č ý ďě ě á á ý ý
 á ě ý ďě ř ě á č ý ů ě ž ě ý ě ý ý ě á ř ě ý š é é á á á ě ů á ě á á š é ó ě é á č ý ďě ě á á ý ý á Í š ě á é Í ř řě ž á ý č é ě á ě ě ůé ý č ů é ž á á ř ž á ň ý á á ě ř ý á ů š č á á ž á é č é ó ě á ů
á ě ý ďě ř ě á č ý ů ě ž ě ý ě ý ý ě á ř ě ý š é é á á á ě ů á ě á á š é ó ě é á č ý ďě ě á á ý ý á Í š ě á é Í ř řě ž á ý č é ě á ě ě ůé ý č ů é ž á á ř ž á ň ý á á ě ř ý á ů š č á á ž á é č é ó ě á ů
= μ. (NB.3.1) L kde bezrozměrný kritický moment μ cr je: Okrajové podmínky při kroucení Krouticí zatížení α β. (volná deplanace) obecné 3,7 1,08
 Kroucení NB. Vniřní síl od kroucení Výsledk jednodušené analý pruů oevřeného průřeu se anedbáním účinku prosého kroucení ve smslu 6..7.(7) le upřesni na ákladě následující modifikované analogie ohbu a
Kroucení NB. Vniřní síl od kroucení Výsledk jednodušené analý pruů oevřeného průřeu se anedbáním účinku prosého kroucení ve smslu 6..7.(7) le upřesni na ákladě následující modifikované analogie ohbu a
č Ú Í ř
 č Ú ř ť á ě á é á ý ě ě é ů ě č ň ě ř é ú ř ž č ě ň ř á ě ě ě ř ů žý č ú ť ě ř ť á š šť č ž ý ů ů ň ě ř ě č é ř á ž ž ž ď š ě ň ů ú Ě é ř á ě ě ř ř ě ř á ý ý ú ř ěž ó ě ý ž ě ý ř ř á ě ě ř š ž š ř ú ý
č Ú ř ť á ě á é á ý ě ě é ů ě č ň ě ř é ú ř ž č ě ň ř á ě ě ě ř ů žý č ú ť ě ř ť á š šť č ž ý ů ů ň ě ř ě č é ř á ž ž ž ď š ě ň ů ú Ě é ř á ě ě ř ř ě ř á ý ý ú ř ěž ó ě ý ž ě ý ř ř á ě ě ř š ž š ř ú ý
ý óň ú Ú Ú ó ř Ú ý ú ú ú Ú ů ú Ó
 ý ř é ě ě č č ý é ó é ž ó é ě é ě ř ě ř ř é š ý ý ž ě ý ž ě ý ř ž é ě ú ř é ě ř ý č š é ý ž ý ž é Ž ě ú é ň ř ř ě ý ý ě ý š ř é ž š é ž ř ý ý š é ě ě ý ě ó é é š ř ř ý é ů ě ě ě ě ě ý č é š ř é ů é ů č
ý ř é ě ě č č ý é ó é ž ó é ě é ě ř ě ř ř é š ý ý ž ě ý ž ě ý ř ž é ě ú ř é ě ř ý č š é ý ž ý ž é Ž ě ú é ň ř ř ě ý ý ě ý š ř é ž š é ž ř ý ý š é ě ě ý ě ó é é š ř ř ý é ů ě ě ě ě ě ý č é š ř é ů é ů č
úč í ář é í áí č ě ě á é č á ě í ů ň é é í áž á á ž í š ě ů ší ý á á Í á š ř í ě ě ěží ě ě í ý ů ě í á ž ý é ě ží ů á é é ř é Č á í á í í é ů ě ý ý é
 í ý č é í á í ř ší ý á ě á ě á í í á í á í ě ý ř š í íž ě á á í ě í í š ý ý é Í ý ý č é á í í í š ě ě í ý ě ý ů ž ů ří ě íš á ý ž á í ěšéá ý á é č ě č ž ý ů í á í é ě á ý é š ě í é ř ř ě í á í ř á č é
í ý č é í á í ř ší ý á ě á ě á í í á í á í ě ý ř š í íž ě á á í ě í í š ý ý é Í ý ý č é á í í í š ě ě í ý ě ý ů ž ů ří ě íš á ý ž á í ěšéá ý á é č ě č ž ý ů í á í é ě á ý é š ě í é ř ř ě í á í ř á č é
ŘÁ ÁŘ Ý ř ú š ř ů ú š ě žď ž ř ě ú ě š ů ž ů ě ř Č ř š ě š ř š ě ž š ě ž ž ž ě ř Č Č š ě ž Č ř ň ů ř š ě Č ě š ě ž ě š šš ř š ě ů š ě Ů ěř ž ů ěř ž ž
 Č ÍŘÁ ě Č ÁŘ Ý ů úř ž ř ů ř ř ž ěú ř Ž ř ě ŘÁ ÁŘ Ý ř ú š ř ů ú š ě žď ž ř ě ú ě š ů ž ů ě ř Č ř š ě š ř š ě ž š ě ž ž ž ě ř Č Č š ě ž Č ř ň ů ř š ě Č ě š ě ž ě š šš ř š ě ů š ě Ů ěř ž ů ěř ž ž ů ů ž ř
Č ÍŘÁ ě Č ÁŘ Ý ů úř ž ř ů ř ř ž ěú ř Ž ř ě ŘÁ ÁŘ Ý ř ú š ř ů ú š ě žď ž ř ě ú ě š ů ž ů ě ř Č ř š ě š ř š ě ž š ě ž ž ž ě ř Č Č š ě ž Č ř ň ů ř š ě Č ě š ě ž ě š šš ř š ě ů š ě Ů ěř ž ů ěř ž ž ů ů ž ř
č Á Á Ú Ě č č č č č ú ř č Ž ů ů Ť ň Ž Ž ř č Ú č š ž š č ň Ě ú č ř š ř č Ž ú č ó ň Ž ůč Ř ň ň Ž Í ů č Íú č ř Ž ř ů ř úč Ú úč Ú ř š ú Í š ú ů ř š č óň É
 Ř ů Ó š č č ř ř Ú Ě ř ř ž ž ň ň ň ř Ž ú ú Ž ú čú Í ů č č Ž č Úč Ú Ú ž úč ž úč č Ú úč č ů č č ň č úř š ú ň Ž Í ú ř č ú ř š ú ů ú ř Ž ž š Ž ř ř ůč ů ů úč Ú Ž š Ž ř ř ůč ů ů ř š ů š č č ř Ž Í č ů š č ř š
Ř ů Ó š č č ř ř Ú Ě ř ř ž ž ň ň ň ř Ž ú ú Ž ú čú Í ů č č Ž č Úč Ú Ú ž úč ž úč č Ú úč č ů č č ň č úř š ú ň Ž Í ú ř č ú ř š ú ů ú ř Ž ž š Ž ř ř ůč ů ů úč Ú Ž š Ž ř ř ůč ů ů ř š ů š č č ř Ž Í č ů š č ř š
á š á á ě ř é ÍŽ ě Ž Ď ě á Ď á á á é Ž š Ď ě Í é š ň á á ě č ě Ů š Í Ý á ě ě á Í Í Í ě š š ěň é Ž á é ě ě é ňí š Í é á ě ě é š č č č á é ě é ě ě Ď á ě
 áě á á Š Á É Ě čá á č é ě ň ě á Í š č é Ž ě é á á Ů ň Í š ě ň ěž ě é ě á Ů á č é á š ě é é ě á ň š š á Í é š ě ň é ě é ě ě é á Ž ň á á č š Í Č č ě ĎÍ ě ěž á é Í á č é é é ě á š ě é š Ž č ě Ž č ě Ž é Ů
áě á á Š Á É Ě čá á č é ě ň ě á Í š č é Ž ě é á á Ů ň Í š ě ň ěž ě é ě á Ů á č é á š ě é é ě á ň š š á Í é š ě ň é ě é ě ě é á Ž ň á á č š Í Č č ě ĎÍ ě ěž á é Í á č é é é ě á š ě é š Ž č ě Ž č ě Ž é Ů
Mgr. Zuzana Adamson-Krupičková Docteur de la Sorbonne
 M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. A á Sě Pí á é A x í M K: K, B, V á L A Txé M K: K, B, V - èq. P áí í. J.-P. M. N é M K, K. é ůé íě áí.
M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. A á Sě Pí á é A x í M K: K, B, V á L A Txé M K: K, B, V - èq. P áí í. J.-P. M. N é M K, K. é ůé íě áí.
Matematika přehled vzorců
 Me přehle zoů. ýz: ýáí: ) (. Mo:... :. o: 4. Ká oe: D 4 D, 5. Kopleí číl: 4 4 5 4 6... Číl opleě žeá:, Zápoý epoe: lgeý opleího číl: Gooeý opleího číl: o 6. Log log log log log log log log log log log
Me přehle zoů. ýz: ýáí: ) (. Mo:... :. o: 4. Ká oe: D 4 D, 5. Kopleí číl: 4 4 5 4 6... Číl opleě žeá:, Zápoý epoe: lgeý opleího číl: Gooeý opleího číl: o 6. Log log log log log log log log log log log
éž á ý š ú ř ž ě ě áž é č é á ž ě á á ě ěž é á č ř é ú č é á ř ý ž ý č á ý ě ý ž Í é é á Í ě Ů ě é ř š š č á ý ž ř ů é é á ě ě ý á ů á ě ě š á é á ě é
 č ý ů ě ý ě ů ř č á ě ý ě ť á ě ě ž ý ě ý ř á Í ů á ý č ý á ě é ě é ůž é á ř š ě ř ě ř č é ř ě ý ě ó ů ě č ž é ě ý ď é á ň á ě ě ě ě ý é č á Í á ě ě é á á ě é ě ř áž á š ě ř ž ř ěó é žč á ž é á ě é ř áž
č ý ů ě ý ě ů ř č á ě ý ě ť á ě ě ž ý ě ý ř á Í ů á ý č ý á ě é ě é ůž é á ř š ě ř ě ř č é ř ě ý ě ó ů ě č ž é ě ý ď é á ň á ě ě ě ě ý é č á Í á ě ě é á á ě é ě ř áž á š ě ř ž ř ěó é žč á ž é á ě é ř áž
Mgr. Zuzana Adamson-Krupičková Docteur de la Sorbonne
 M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. A á Sě Pí á é A x í M K: K, B, V á L A Txé M K: K, B, V - èq. P áí í. J.-P. M. N é M K, K. é ůé íě áí.
M. Z A-Ká D S C: D. Z A-Ká, 2014 P: D. Z A 48. G L: N Ká ISBN 978-80-905352-3-7 A. N w w P, x q w. A á Sě Pí á é A x í M K: K, B, V á L A Txé M K: K, B, V - èq. P áí í. J.-P. M. N é M K, K. é ůé íě áí.
 ž Í ú č č ě ó ě ě é ó ů Ú č Č č ý š ú ě ó š ý ě é ó ý ý ř ž ó č ť Č č ř č é ý é ě ř é é č é ý č é č č ř ě ě ř ě ž č ý ó ž ý č ý š ě é ř ý š š č é č č é ě č Í ó ó ý č ó ý Ž č č é ů ů ř ě ě š ř ě é ř ě
ž Í ú č č ě ó ě ě é ó ů Ú č Č č ý š ú ě ó š ý ě é ó ý ý ř ž ó č ť Č č ř č é ý é ě ř é é č é ý č é č č ř ě ě ř ě ž č ý ó ž ý č ý š ě é ř ý š š č é č č é ě č Í ó ó ý č ó ý Ž č č é ů ů ř ě ě š ř ě é ř ě
é é Ž í á í ů ěž ší á ě ý ý ů ý š é é á ě á é á é á ě ó á Žá é é í é á ý é í á í ě í ů š ř ší ý čá č í š í š ž í á í á ř í š ě í ž ř é ří á í á í č ý
 ří ý ě ší ř é ěř á íč é í ě é á ří š í ě í á ň í š čá á ý ě ý ří íč é ě í é í ř ší í í ť ž í í č é í č í ěř í ž í í ý ě í ý á í ž ů é í í š é ří ří á ě í ř áž ě š é ří č é č í á é á ží ř ř ě é í í ý ř
ří ý ě ší ř é ěř á íč é í ě é á ří š í ě í á ň í š čá á ý ě ý ří íč é ě í é í ř ší í í ť ž í í č é í č í ěř í ž í í ý ě í ý á í ž ů é í í š é ří ří á ě í ř áž ě š é ří č é č í á é á ží ř ř ě é í í ý ř
Ú Úó řá á ě á Ž á á á á É á Ž ř í řáí éž á ě š ů ý š ě Š ýá á á áň ží í ú ýž í ř á ž á á á š á é á ě Ý ú á é í šíř á é á ě š ě íí ě á á á á ě á á é ě
 íúř á áň řáí í á áň á é á í úř á Ž á é Ú Úó řá á ě á Ž á á á á É á Ž ř í řáí éž á ě š ů ý š ě Š ýá á á áň ží í ú ýž í ř á ž á á á š á é á ě Ý ú á é í šíř á é á ě š ě íí ě á á á á ě á á é ě í é í ř é É
íúř á áň řáí í á áň á é á í úř á Ž á é Ú Úó řá á ě á Ž á á á á É á Ž ř í řáí éž á ě š ů ý š ě Š ýá á á áň ží í ú ýž í ř á ž á á á š á é á ě Ý ú á é í šíř á é á ě š ě íí ě á á á á ě á á é ě í é í ř é É
íž ě íž á ť ř ť í ž ě ě á í ň á í á í ů ů íž ď ř ť šíř é ě ě ě ř í ší íř ý ý ů éříš éš ěž ě á í á í ř é šíř ý ěží č ě š é í í ř í á í á í ž ž é ř é í
 Í Ý ČÁ Ú ý ší é č ý ůž í š é á é í ř š ř ů ě í í áří ě ž í á é á ě é í ž ě á á ď ří ě č é í í í í ž ě ý á ý ů č í ý ř ě ž í í í í š í í č í ěž ž ž ř é í á ř í í ě í ž í č ě ží ř ž é ř ě š ě ž á í žší é
Í Ý ČÁ Ú ý ší é č ý ůž í š é á é í ř š ř ů ě í í áří ě ž í á é á ě é í ž ě á á ď ří ě č é í í í í ž ě ý á ý ů č í ý ř ě ž í í í í š í í č í ěž ž ž ř é í á ř í í ě í ž í č ě ží ř ž é ř ě š ě ž á í žší é
Direct emailing na míru Emailing podle kategorií Traffic pro váš web Databáze firem SMS kampaně Propagace přes slevový portál Facebook marketing
 I N T E R N E T O V Ý M A R K E T I N G e f e k t i v n í a c í l e n ý m a r k e t i n g p r o f e s i o n á l n í e m a i l i n g š p i č k o v é t e c h n i c k é z á z e m í p r o p r a c o v a n é
I N T E R N E T O V Ý M A R K E T I N G e f e k t i v n í a c í l e n ý m a r k e t i n g p r o f e s i o n á l n í e m a i l i n g š p i č k o v é t e c h n i c k é z á z e m í p r o p r a c o v a n é
ý é ě é é ž í ř ř í Ž á ř í ž í á ů íč é á ř á í é á ů á Í ří č ýý ř ů ů é ří í ťř č č í á í á ří š í í ř í í é í á í ř ší ý ý ě í ůč ě Í í ě á á š ří
 ďí í ž Íá ý é ří ýč í é í ě í č ý í ý á í ý ř ý á í Ž ž é á é ř ě ě íč ář š č é ý á é í ř ř Í ď ý í ří é š ú í ř é ů čí ů í í č é ěší á ží ý á í é Č é ý é Č á á áč ář á í ž ý č ý í í á á ží á é ří ž š
ďí í ž Íá ý é ří ýč í é í ě í č ý í ý á í ý ř ý á í Ž ž é á é ř ě ě íč ář š č é ý á é í ř ř Í ď ý í ří é š ú í ř é ů čí ů í í č é ěší á ží ý á í é Č é ý é Č á á áč ář á í ž ý č ý í í á á ží á é ří ž š
