Dynamika hmotných bodů. 3. Hmotný bod o hmotnosti m = 10 kg se pohybuje po kružnici o poloměru r = 2 m,
|
|
|
- Jan Netrval
- před 8 lety
- Počet zobrazení:
Transkript
1 Dnik honých bodů 3 Honý bod o honosi kg se ohbuje o kužnici o oloěu 3 3 řičež jeho dáh áisí n čse odle hu s k kde k 5 /s Učee elikos ýsledné síl ůsobící n honý bod úhel α keý síá eko síl s ekoe chlosi úhloou chlos úhloé chlení ε čse s Řešení: Nejdříe učíe chlos noáloé ečné celkoé chlení honého bodu jko ds 3k 9k d 6k n 4 8k 36 6 n 6 k 6 /s Po ýslednou sílu úhloou chlos úhloé chlení honého bodu oé lí 6 N ε 6k - 5 s 3k 75 s Úhel keý síá sě ýsledné síl se sěe chlosi oo očee e hu 6 cosα 58 α 75 o & k - α
2 4 N kldkosoji keý se skládá e dou kldek (iob) isí dě áží o honosech g 5 g Učee hoou sílu T ůsobící lně chlení obou áží Při ýoču neužuje ření ln o kldku honos ln kldek Řešení: Po elikos chlení jednoliých áží ři ohbu lí ájený h Niše si nní ohboé onice o obě áží T g g T Podělení onic ískáe g T T g T T T g g Úou éo onice ůžee jádři sílu T jko 3 g T 4 6 N Dosení T do ohboých onic učíe chlení jednoliých áží T g ( ) g g T ( ) g 5 /s 75 /s 4 4
3 5 Těleso o honosi se ohbuje oině odle onic cos sin kde jsou kldné konsn Učee elikos síl ůsobící n ěleso o jké křice se bude oo ěleso ohbo Řešení: Po olohoý eko eko chlosi eko chlení lí j i sin cos j i cos sin d d j i sin cos d d Velikos chlení je on ) sin ( ) cos ( o ůsobící sílu dosááe Jelikož obecně lí sin cos k se ěleso se řídě ohbuje o elise (iob) cos ϕ sin ϕ ϕ g g ϕ ) ( ϕ ) (
4 6 Učee jké iální chlosi ůže dosáhnou lžř o honosi kg n o shu o sklonu α 3 jesliže se ohbuje říočře dolů e shu koeficien skoého ření lží n sněhu µ odo duchu je úěný čeci chlosi j o k kde koeficien N - k 5 s Vočěe jkou dáhu s ujede lžř dobu s jkou bude í chlos Řešení: žř bude osuně šo sojí chlos ž do jisé ení chlosi keá odoídá su kd bude ýsledná ůsobící síl nuloá j o T g sinα o k T µ µ g cosα O α G T Dosení jednoduchou úou obdžíe o ení chlos g (sinα µ cosα) 85 /s 5 k/h k Níšee-li si nní onici o ohb lžře n shu d o T d k g(sin α µ cosα) bcho ohli co nejjednodušeji řeši uo difeenciální onici řeíšee si ji n d ( ) g(sin α µ cos α) k g (sin α µ cosα)
5 Nní řešíe ředchoí onici eodou sece oěnných s oužií očáečních odínek s j d d d ( ) ( ) ln ln ( ) ( ) ( ) ( ) ( ) Vjádříe-li nní chlos lžře čse dosnee ( ) e ( ) e e e e e e gh( ) 536 /s Po dáhu ískáe inegcí chlosi odle čsu h s e e [ ln( e e )] ln ln[ cosh( ) ] & 574 d
6 7 Rke s očáeční honosí 5 kg se čl klidu ohbo e sislé sěu Výokoá chlos sloných lnů je R 6 /s chlos sloání li je µ 3 kg/s Vočěe jké iální chlosi ke dosáhne do jké iální ýšk h leí jesliže keu sřelíe sisle hůu hoogenní íhoé oli ho li 3 kg Odo osředí nedbááe Řešení: Rkeu budee ožo honý bod s oěnnou honosí Vjádříe-li si hbnos ke čse oo dosnee ( d ) ( d) ( d) ud ( d) ud kde d je ho lnů jež ooušějí keu čs ýsuní skou d d je úbek honosi ke čs es u jsou chlosi ke es odděloné ho (slin) ůči žné ineciální sousě u Dosdíe-li nní ěnu hbnosi do Newono ohboého ákon oo obdžíe ohboou onici R d d d d d ( u ) d R R R d kde R je eliní chlos odlučoné ho ůči keě (ýokoá chlos sloných lnů keá á očný sě nežli chlos ke) R je ekiní síl Po náš říd ohbu ke lí následující ohboá onice d R d G µ R R µ R G g Dosení ískáe difeenciální onici řádu d µ R µ g Dobu keou ke sořebuje šechno lio očee e hu ohboé onice obdžíe o chlos dáhu s čse ( ) / µ Řešení
7 R ln g R ln g R ln g 66 /s µ µ µ R s µ g ln µ µ µ R ( µ ) g ln & 7 µ Po hoření eškeého li se bude ke onoěně olo o dáhu keou ješě uleí než se sí ed lí odle ákon choání enegie ( ) ( ) g 6994 g Po ýšku h nd oche Zeě k ke doleí ed dosnee h & 7 k
8 8 Kulk o honosi 5 g leí odooně chlosí /s ní do blisického kdl o délce honosi M 5 kg uáne ně Učee úhel ϕ o keý se odchýlí áěs kdl od sislého sěu Řešení: Po chlos u kdl ěsně o náu ískáe e ákon choání hbnosi ( M ) u u M ϕ h M Miální ýšku h do keé souí kdlo ůžee uči e ákon choání enegie ( M ) u u ( ) ( M ) gh h g g( M ) Po úhel ϕ ed dosnee h h ( ) o cos ϕ ϕ ccos 369 ( ) g M
9 o 9 Hldký oloužný íček usíe n hldkou nkloněnou oinu se sklone α 3 ýšk h Učee jké odooné dálenosi od ís ního dodu oě dodne íček n nkloněnou oinu Předokládeje že se jedná o nedokonle užný á s koeficiene eisence (užiosi) k 8 Odo osředí nedbeje Řešení: Jedná se o nedokonle užný šiký á koule o desku Vhlede k ou že och jsou dokonle hldké neniknou ei koulí deskou ři náu ečné defoce ed ečná složk chlosi se neění j íco kolá složk bude k Z uedeného obáku je řejé že o úhel dodu íčku lí ε α Úhel odu íčku ε učíe následujících hů g ε o gε gε ε & k k 3k w h ε ε β α u α d Míček dodá n nkloněnou oinu chlosí gh což lne e ákon choání echnické enegie o dodu se odí úhlu β od odooné oin ocháející bode dodu kde o β π/ α ε 4
10 Dále již ůžee šeřo oblé jko šiký h od úhle β chlosí sin ε k cos ε sin ε k cos ε /s Po odoonou es sislou souřdnici odženého íčku čse lí u cosβ w sin β g Dosení onice o u do hu o w ískáe onici křik o keé se bude odžený íček ohbo j gu w u gβ cos β Jesliže nní očee ůsečík éo jekoie (bol) s lochou nkloněné oin w u gα oo dosnee o hlednou dálenos gu (gβ gα) cos β u gα u gβ d u & 5 cos β g
11 Vočěe iální áoou sílu ůsobící n hoolece s lne délk jesliže sdne ýšk h nd ený jišění J n lnou délku ln no á ůžnos ε 5 % o nooé ížení N 8 kn honos hoolece je 8 kg Předokládeje lineání choání nhoného ln Řešení: Předokládáe-li lineání ohoání ln oo elikos síl ůsobící n lno (es hoolece) ůžee jádři jko C k kde k es C je konsn chkeiující užnos ln je ožení ln Konsnu k es C ůžee uči ůžnosi ln jko k N N ε N C N ε Při ádu se ři ožení ln o koná áce H J h C C d d C C k C kde je iální ožení ln ři ádu je iální síl lně Vkonná áce se usí on ěně oenciální enegie E hoolece ři ádu o keou lí H h C E g h ) g( h ) ( c kde h c je celkoá ýšk ádu Dosení do onice E ískáe kdickou onici Cghc g jejíž řešení dosnee o iální áoou sílu g g hc Cg no se ři ádu oáhne o N hc g εg ε / 87 N 697 kn
12 o Učee h o olný ád ěže ýšk h eěisné šířce ϕ 5 jesliže budee užo s ocí Zeě kole sé os úhloou chlosí 77 5 s - (j užuje li Coioliso síl) Vočěe o kolik se odchýlí bod dodu od sislice Odo osředí nedbeje Řešení: Po olný ád ři uážení oáčení Zeě kole sé os ůžee ns ohboou onici d G c g ( ) kde G je íhoá síl c je Coioliso síl g ( g) je íhoé chlení ( ) ( cos ϕ sin ϕ) je eko úhloé chlosi oce Zeě kole sé os Po sndnější řešení nšeho říkldu jse si olili osu souřdného sséu e sěu íhoého chlení osu kolo n oledník dné ísě n ochu Zeě Uedenou ohboou onici ůžee s jko 3 sklání onice d d ( ) d d g d g Inegcí duhé řeí onice (odle es ) oužií očáečních odínek nšeho říkldu ( h ) obdžíe R G ϕ h d es d g dosení do ní onice o souřdnici dosnee d 4( ) g 4( ) 4 gcos ϕ Předchoí onice je občejnou difeenciální onicí duhého řádu s konsnníi koeficien keá á řešení e u
13 C sin C cos ( C cos C sin ) kde C C jsou konsn keé le uči dosení očáečních odínek j C g cos ϕ C 4 Konečné h o olný ád ýšk ed ůžee ísk inegcí onic o odle čsu s uážení očáečních odínek úloh j dosnee g cos ϕ sin cos g sin ϕcosϕ 4 cos h g g cos ϕ 4 Jelikož << hlede k ou že dob ádu je nedbelně lá ůči eiodě oáčení Zeě ůžee oinou funkce sinus kosinus Tloou řdu oei se oue n ní d člen ooje j sin 4 ( 3 3 & cos ( ) ) & Poo obdžíe řibližné h o olný ád h g cos ϕ 3 3 & & h g & Odchlku bodu dodu od sislice učíe k že očee dobu dodu n och Zeě dosdíe-li do hu o Tj oložíe-li oo o dobu olného ádu obdžíe h g o odchlku od sislice dosnee 3 / h & gcosϕ & 4 c 3 g
F1040 Mechanika a molekulová fyzika
 4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
2. ZÁKLADY KINEMATIKY
 . ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
. ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
Kinematika hmotného bodu
 Kneaka honého bou k j Polohoý eko bou osou Velkos olohoého ekou k j s τ Zěna olohoého ekou s s Dáha τ τ τ s s Rchlos honého bou s Půěná chlos a Zchlení honého bou τ a ečné chlení n R a n Noáloé chlení
Kneaka honého bou k j Polohoý eko bou osou Velkos olohoého ekou k j s τ Zěna olohoého ekou s s Dáha τ τ τ s s Rchlos honého bou s Půěná chlos a Zchlení honého bou τ a ečné chlení n R a n Noáloé chlení
Obsah dnešní přednášky : Obecný rovinný pohyb tělesa. Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
přednáška 3 Základní pojmy - trajektorie, proudnice Trocha matematiky Rovnice kontinuity Pohybové rovnice
 3 HYDROMECHANIKA HYDRODYNAMIKA ákldní once ákon řednášk 3 Leu : Ok Mšoský; HYDROMECHANIKA Jomí Noskeč, MECHANIKA TEKUTIN Fnšek Šob; HYDROMECHANIKA 3 Hdodnmk Úod: Meod osu konnu loo úodem Rodělení oudění
3 HYDROMECHANIKA HYDRODYNAMIKA ákldní once ákon řednášk 3 Leu : Ok Mšoský; HYDROMECHANIKA Jomí Noskeč, MECHANIKA TEKUTIN Fnšek Šob; HYDROMECHANIKA 3 Hdodnmk Úod: Meod osu konnu loo úodem Rodělení oudění
mechanika Statika se zabývá působením sil na tělesa, která jsou v klidu.
 Aplkoná echnk,. přednášk Předě Dnk je součásí ěšího předěu Mechnk. I soný předě Mechnk ůžee cháp šší ác děl jej n echnku nějších sl nebo éž echnku uhých ěles (sk dnk) echnku nřních sl nebol echnku poddjných
Aplkoná echnk,. přednášk Předě Dnk je součásí ěšího předěu Mechnk. I soný předě Mechnk ůžee cháp šší ác děl jej n echnku nějších sl nebo éž echnku uhých ěles (sk dnk) echnku nřních sl nebol echnku poddjných
Pohyb po kružnici - shrnutí. ω = Předpoklady:
 .3.3 Pohyb po kružnici - shrnuí Předpokldy: 3 Pomocí dou ě U kruhoého pohybu je ýhodnější měři úhel (kerý je pro šechny body sejný) než dráhu (kerá se pro body s různou zdálenosí od osy liší). Ke kždé
.3.3 Pohyb po kružnici - shrnuí Předpokldy: 3 Pomocí dou ě U kruhoého pohybu je ýhodnější měři úhel (kerý je pro šechny body sejný) než dráhu (kerá se pro body s různou zdálenosí od osy liší). Ke kždé
e en loh 1. kola 44. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh: I. Volf (1), epl (2), J. J r (3 a 7) 1. Cel okruh rozd l me na p t sek podle
 e en loh. kola 44. o n ku fyzik ln olymi dy. Kategoie D Auto i loh: I. Volf (), el (), J. J (3 a 7). Cel okuh ozd l me na t sek odle chaakteu ohybu motocyklisty. Zaedeme ozna en : t = s, t = 40 s, t 3
e en loh. kola 44. o n ku fyzik ln olymi dy. Kategoie D Auto i loh: I. Volf (), el (), J. J (3 a 7). Cel okuh ozd l me na t sek odle chaakteu ohybu motocyklisty. Zaedeme ozna en : t = s, t = 40 s, t 3
Cvičení č. 14 Vlastní čísla a vlastní vektory. Charakteristický mnohočlen a charakteristická rovnice. Lokalizace spektra. Spektrální rozklad.
 Cičení z lineání algeby 7 Ví Vondák Cičení č 4 Vlasní čísla a lasní ekoy Chaakeisický mnohočlen a chaakeisická onice Lokalizace speka Spekální ozklad Vlasní čísla a lasní ekoy maice Nechť je dána čecoá
Cičení z lineání algeby 7 Ví Vondák Cičení č 4 Vlasní čísla a lasní ekoy Chaakeisický mnohočlen a chaakeisická onice Lokalizace speka Spekální ozklad Vlasní čísla a lasní ekoy maice Nechť je dána čecoá
rovinná soustava sil (paprsky všech sil soustavy leží v jedné rovině) rovinný svazek sil rovinná soustava rovnoběžných sil
 3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,
 Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Nakloněná rovina II
 3 Nakloněná rovina II Předoklady: Pedagogická oznáka: Obsah hodiny se za norálních okolnosí saozřejě nedá sihnou, záleží na Vás, co si vyberee Pedagogická oznáka: Na začáku hodiny zadá sudenů říklad Nečeká
3 Nakloněná rovina II Předoklady: Pedagogická oznáka: Obsah hodiny se za norálních okolnosí saozřejě nedá sihnou, záleží na Vás, co si vyberee Pedagogická oznáka: Na začáku hodiny zadá sudenů říklad Nečeká
Mechanická silová pole
 Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Dynamika hmotného bodu - rekapitulace.
 Dnmik hmoného bodu - ekpiulce. Dnmik II,. přednášk Kinemik bodu, ákldní eličin h, lášní přípd pohbu. Křiočý pohb bodu, chlo chlení jko eko, ouřdné ém. Pohb bodu po kužnici. Dnmik hmoného bodu, pohboá onice,
Dnmik hmoného bodu - ekpiulce. Dnmik II,. přednášk Kinemik bodu, ákldní eličin h, lášní přípd pohbu. Křiočý pohb bodu, chlo chlení jko eko, ouřdné ém. Pohb bodu po kužnici. Dnmik hmoného bodu, pohboá onice,
Kinematika hmotného bodu. Petr Šidlof
 et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin
et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin
 ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
Křivočarý pohyb bodu.
 Křočý pohb bodu. Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Křočý pohb bodu. Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Veličiny a jednotky v mechanice
 Veličiny jednoky mechnice Vekory Dokže že úhlopříčky kosočerce jsou n sebe kolmé Řešení Pokládejme srny kosočerce b i jeho úhlopříčky c d z ekory Pro elikosi srn plí b Pro úhlopříčky plí c + b d b Sklární
Veličiny jednoky mechnice Vekory Dokže že úhlopříčky kosočerce jsou n sebe kolmé Řešení Pokládejme srny kosočerce b i jeho úhlopříčky c d z ekory Pro elikosi srn plí b Pro úhlopříčky plí c + b d b Sklární
POHYB BODU V CENTRÁLNÍM POLI SIL
 POHYB BODU V CENTRÁLNÍM POLI SIL SPECIFIKCE PROBLÉMU Centální siloé pole je takoé pole sil, kdy liboolném bodě postou nositelka síly působící na pohybující se bod pochází peným bodem postou (tz centem
POHYB BODU V CENTRÁLNÍM POLI SIL SPECIFIKCE PROBLÉMU Centální siloé pole je takoé pole sil, kdy liboolném bodě postou nositelka síly působící na pohybující se bod pochází peným bodem postou (tz centem
Analýza světla odraženého tenkým kmitajícím zrcadleěm s použitím MATLABu
 Alýz svěl odžeého eký kijící zcdleě s požií MATLAB A.Mikš J.Novák ked fzik Fkl svebí ČVUT v Pze Absk Páce se zbývá eoeicko lýzo vibcí ekého oviého zcdl khového půřez vlive defocí kovéhoo zcdl svělo odžeé
Alýz svěl odžeého eký kijící zcdleě s požií MATLAB A.Mikš J.Novák ked fzik Fkl svebí ČVUT v Pze Absk Páce se zbývá eoeicko lýzo vibcí ekého oviého zcdl khového půřez vlive defocí kovéhoo zcdl svělo odžeé
asi 1,5 hodiny seznámit studenty se základními zákonitostmi křivočarého pohybu bodu Dynamika I, 3. přednáška Obsah přednášky : Doba studia :
 Dmk I, 3. předášk Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
Dmk I, 3. předášk Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í
 GRAVITAČNÍ POLE I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í 1. Newtonů aitační zákon (1687 Newton díle Mateatické pincipy příodní filozofie) aždá dě hotná tělesa na sebe nazáje působí stejně
GRAVITAČNÍ POLE I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í 1. Newtonů aitační zákon (1687 Newton díle Mateatické pincipy příodní filozofie) aždá dě hotná tělesa na sebe nazáje působí stejně
kolmo dolů (její velikost se prakticky nemění) odpor vzduchu F
 .6.4 Sislý r Předpoklady: 6, 6 Pedagogická poznámka: Obsa odpoídá spíše děma yučoacím odinác. Z lediska dalšíc odin je důležié dopočía se k příkladu číslo 7. Hodina paří mezi y, keré záisí na znalosec
.6.4 Sislý r Předpoklady: 6, 6 Pedagogická poznámka: Obsa odpoídá spíše děma yučoacím odinác. Z lediska dalšíc odin je důležié dopočía se k příkladu číslo 7. Hodina paří mezi y, keré záisí na znalosec
Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici
 Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Kinematika hmotného bodu
 DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
Doplňkové kapitoly. dynamika relativního pohybu základy teorie rázu reaktivní pohyb. asi 1 hodina
 Doplňkoé kpitoly Dynik I, 13. přednášk Obsh přednášky : dynik eltiního pohybu zákldy teoie ázu ektiní pohyb Dob studi : si 1 hodin Cíl přednášky : seznáit studenty se způsobe řešení dyniky eltiního pohybu,
Doplňkoé kpitoly Dynik I, 13. přednášk Obsh přednášky : dynik eltiního pohybu zákldy teoie ázu ektiní pohyb Dob studi : si 1 hodin Cíl přednášky : seznáit studenty se způsobe řešení dyniky eltiního pohybu,
Nakloněná rovina I
 1.2.14 Nakloněná rovina I Předoklady: 1213 Pomůcky: kulička, sada na měření řecí síly. Až dosud jsme se u všech říkladů uvažovali ouze vodorovné lochy. Př. 1: Vysvěli, roč jsme u všech dosavadních říkladů
1.2.14 Nakloněná rovina I Předoklady: 1213 Pomůcky: kulička, sada na měření řecí síly. Až dosud jsme se u všech říkladů uvažovali ouze vodorovné lochy. Př. 1: Vysvěli, roč jsme u všech dosavadních říkladů
O s 0 =d s Obr. 2. 1
 3 KINEMATIKA BODU Kinemik jko čás mechniky je nuk o pohybu ěles bez ohledu n síly, keré pohyb způsobily Těles nebudou mí nšich úhách hmonos budou popsán jen sými geomerickými lsnosmi Ty budou během pohybu
3 KINEMATIKA BODU Kinemik jko čás mechniky je nuk o pohybu ěles bez ohledu n síly, keré pohyb způsobily Těles nebudou mí nšich úhách hmonos budou popsán jen sými geomerickými lsnosmi Ty budou během pohybu
FYZIKA I. Mechanická energie. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ TUHÉ TĚLESO
 DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
 ž Í ú č č ě ó ě ě é ó ů Ú č Č č ý š ú ě ó š ý ě é ó ý ý ř ž ó č ť Č č ř č é ý é ě ř é é č é ý č é č č ř ě ě ř ě ž č ý ó ž ý č ý š ě é ř ý š š č é č č é ě č Í ó ó ý č ó ý Ž č č é ů ů ř ě ě š ř ě é ř ě
ž Í ú č č ě ó ě ě é ó ů Ú č Č č ý š ú ě ó š ý ě é ó ý ý ř ž ó č ť Č č ř č é ý é ě ř é é č é ý č é č č ř ě ě ř ě ž č ý ó ž ý č ý š ě é ř ý š š č é č č é ě č Í ó ó ý č ó ý Ž č č é ů ů ř ě ě š ř ě é ř ě
11. cvičení z Matematické analýzy 2
 11. cvičení z Mtemtické nlýzy 1. - 1. prosince 18 11.1 (cylindrické souřdnice) Zpište integrály pomocí cylindrických souřdnic pk je spočítejte: () x x x +y (x + y ) dz dy dx. (b) 1 1 x 1 1 x x y (x + y
11. cvičení z Mtemtické nlýzy 1. - 1. prosince 18 11.1 (cylindrické souřdnice) Zpište integrály pomocí cylindrických souřdnic pk je spočítejte: () x x x +y (x + y ) dz dy dx. (b) 1 1 x 1 1 x x y (x + y
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projek relizoný n SPŠ Noé Měo nd Meují finnční podporou Operční progru Vzděláání pro konkurencechopno Králoéhrdeckého krje Úod do dyniky Ing. Jn Jeelík Dynik je čá echniky, kerá e zbýá pohybe ěle ohlede
Projek relizoný n SPŠ Noé Měo nd Meují finnční podporou Operční progru Vzděláání pro konkurencechopno Králoéhrdeckého krje Úod do dyniky Ing. Jn Jeelík Dynik je čá echniky, kerá e zbýá pohybe ěle ohlede
Tlumené kmity. Obr
 1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
DUM č. 14 v sadě. Ma-2 Příprava k maturitě a PZ geometrie, analytická geometrie, analýza, komlexní čísla
 rojek GML Brno Docen DUM č. 4 dě M- Přír k mriě PZ geomerie, nlická geomerie, nlý, komlení číl 4. or Mgd Krejčoá Dm.08.0 očník mriní ročník noce DUM nlická geomerie roor - d úloh ýledk. Meriál jo rčen
rojek GML Brno Docen DUM č. 4 dě M- Přír k mriě PZ geomerie, nlická geomerie, nlý, komlení číl 4. or Mgd Krejčoá Dm.08.0 očník mriní ročník noce DUM nlická geomerie roor - d úloh ýledk. Meriál jo rčen
Exponenciální funkce, rovnice a nerovnice
 Eonenciální unkce, rovnice a nerovnice Mamut s korovou omáčkou (Eonenciální unkce) a) AN; b) NE; c) NE; d) AN; e) NE; ) NE; g) AN; h) NE a),; b),; c) ; d) ; e) ; ) e + b) - - - D()= R; H ()=( ; ) ; P neeistuje
Eonenciální unkce, rovnice a nerovnice Mamut s korovou omáčkou (Eonenciální unkce) a) AN; b) NE; c) NE; d) AN; e) NE; ) NE; g) AN; h) NE a),; b),; c) ; d) ; e) ; ) e + b) - - - D()= R; H ()=( ; ) ; P neeistuje
cos cos φ ω Převod mechanismu Aplikovaná mechanika, 9. přednáška analytické řešení mechanismu s pravoúhlou kulisou ω, ε φ převod derivace převodu
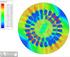 Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
Přijímací zkoušky do navazujícího magisterského studia Učitelství fyziky pro 2. stupeň ZŠ a Učitelství fyziky pro SŠ pro akademický rok 2011/2012
 řijíí ouš do ujíío iseséo sudi čielsí fi po. supeň Š čielsí fi po SŠ po deiý o 0/0 Koouč o poloěu 0 oosi se ůže oáče ole odooé os. N oouči je iuo eé láo. N oi lá isí áží o oosi. ou á oouč úloou los, uí-li
řijíí ouš do ujíío iseséo sudi čielsí fi po. supeň Š čielsí fi po SŠ po deiý o 0/0 Koouč o poloěu 0 oosi se ůže oáče ole odooé os. N oouči je iuo eé láo. N oi lá isí áží o oosi. ou á oouč úloou los, uí-li
SPECIÁLNÍ TEORIE RELATIVITY
 SPECIÁLNÍ TEORIE RELATIVITY GALILEO GALILEI (6.s.) pohbuje-li se ažná sousaa hlee k jiné onoěný příočaý pohbe, je s ní onoenná (pohb je ájený elainí) neeisuje žáná absoluní ažná sousaa, keou jeinou b ěl
SPECIÁLNÍ TEORIE RELATIVITY GALILEO GALILEI (6.s.) pohbuje-li se ažná sousaa hlee k jiné onoěný příočaý pohbe, je s ní onoenná (pohb je ájený elainí) neeisuje žáná absoluní ažná sousaa, keou jeinou b ěl
 Á Ú š ě ý ň šť ž ě Ž ý ě ě ť ý š ě š Í Í ý Í ě ž ý ž š ý Í ý ý š ď š š ž š š š ě ý š ě š š Í š ň ď š ě ě Í š ě Í ď š ě ý ž š ě ý ý ý ě ů ů ů ý ě ů ž ý ě ě ý ů ý ů ý ý Í š š ě ů š ě ě š ě Ú š ě ýš ě ě ý
Á Ú š ě ý ň šť ž ě Ž ý ě ě ť ý š ě š Í Í ý Í ě ž ý ž š ý Í ý ý š ď š š ž š š š ě ý š ě š š Í š ň ď š ě ě Í š ě Í ď š ě ý ž š ě ý ý ý ě ů ů ů ý ě ů ž ý ě ě ý ů ý ů ý ý Í š š ě ů š ě ě š ě Ú š ě ýš ě ě ý
š ž ž ň ž ž ž ší Ťš í Ž Ž Ž ě š ě í Ž š é é ě Ť é ě Ž ě ť Ť šíť ť é í Ž ě š ť í Ž é Ť ě Č ň é í é í í é í Ť ě Ú ě ě ě Ž í Ž ě í Ž ě Ť Ž š é í Ž ší í š
 š É é ě é í ň í ě ě í é ěž í í é í ě Ů ňí é í é é í é í é í í ě é í š Ď ě Ť é ň ě é Ž í é é é í í é ě ě ě í ť Ď é í í šč é é é ňí ě í Ž š ě é é š Ů é é í í é ě é ě é é ň Ť ě í é í š é í ěňí Ž š ť Ť Ž éž
š É é ě é í ň í ě ě í é ěž í í é í ě Ů ňí é í é é í é í é í í ě é í š Ď ě Ť é ň ě é Ž í é é é í í é ě ě ě í ť Ď é í í šč é é é ňí ě í Ž š ě é é š Ů é é í í é ě é ě é é ň Ť ě í é í š é í ěňí Ž š ť Ť Ž éž
š Í í ď í í ŽŮ í Ž Í ň ň ň č ň ň Í í í í č Í Ž č š í Ž č ň Č í Ž í í ť ň č š ň í Ó íč ň í Ť í ňíž ň Ú í í č í Š ň č š ň í Í Ž í í í č Ž ňí í ž ň ň Í š
 í š Č í Á Ů č ÉÁ í í Ž Ť í Ůž Ť í í Ůž í Ž í Ť ž Ť í í Ť ŽÍ Ťí ň ší É Ů í í í Ž í í č í í í ň š Ž č Í š ň Ží ř í í í Í í í í í č í ň í Ž í Ž í ňí č ňí č ň Í í í š í č Ď ňí č í ň ňí í š Í í ď í í ŽŮ í Ž
í š Č í Á Ů č ÉÁ í í Ž Ť í Ůž Ť í í Ůž í Ž í Ť ž Ť í í Ť ŽÍ Ťí ň ší É Ů í í í Ž í í č í í í ň š Ž č Í š ň Ží ř í í í Í í í í í č í ň í Ž í Ž í ňí č ňí č ň Í í í š í č Ď ňí č í ň ňí í š Í í ď í í ŽŮ í Ž
Dynamika pohybu po kružnici III
 Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Dynamika hmotného bodu
 Dynmik hmoného bou Dynmik - obo mechniky, yšeřující zájemné působení ěles, keé ee ke změně pohybu Síl - ekooá eličin, je míou zájemného působení ěles, keé ee ke změnám pohybu nebo efomci ěles Síly mohou
Dynmik hmoného bou Dynmik - obo mechniky, yšeřující zájemné působení ěles, keé ee ke změně pohybu Síl - ekooá eličin, je míou zájemného působení ěles, keé ee ke změnám pohybu nebo efomci ěles Síly mohou
4. SEMINÁŘ Z MECHANIKY
 - 9-4. SEMINÁŘ Z MECHNIKY 4. Čloěk drží jeden konec prkn, jeož druý konec leží n álci. Čloěk zčne posou prkno kupředu k, by se álec lil po odoroné roině bez prokluzoání by ni prkno po álci neklouzlo. Jkou
- 9-4. SEMINÁŘ Z MECHNIKY 4. Čloěk drží jeden konec prkn, jeož druý konec leží n álci. Čloěk zčne posou prkno kupředu k, by se álec lil po odoroné roině bez prokluzoání by ni prkno po álci neklouzlo. Jkou
( ) Kinematika a dynamika bodu. s( t) ( )
 Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
 č á Č Ě ó č á ů á ě ě é ď Ú č á Č ě ě š č ě í ří á ů š í š í í é ě ů č ě ří č ě ě í ý č á í í á ý á ě í ář š á í á í ň á č é ó í á ě á íč ě á á ě ří č ě í á Č ě á á Ž á ú í ě Č č ý ě ě ď á é á á ě ě
č á Č Ě ó č á ů á ě ě é ď Ú č á Č ě ě š č ě í ří á ů š í š í í é ě ů č ě ří č ě ě í ý č á í í á ý á ě í ář š á í á í ň á č é ó í á ě á íč ě á á ě ří č ě í á Č ě á á Ž á ú í ě Č č ý ě ě ď á é á á ě ě
Cvičení 4 (Tenkostěnné a silnostěnné nádoby)
 VŠB Technická univezia Osava akula sojní Kaeda užnosi a evnosi (9) Pužnos a evnos v enegeice (Návod do cvičení) vičení 4 (Tenkosěnné a silnosěnné nádob Auo: Jaoslav ojíček Veze: Osava 9 PPE vičení 4 Tenkosěnné
VŠB Technická univezia Osava akula sojní Kaeda užnosi a evnosi (9) Pužnos a evnos v enegeice (Návod do cvičení) vičení 4 (Tenkosěnné a silnosěnné nádob Auo: Jaoslav ojíček Veze: Osava 9 PPE vičení 4 Tenkosěnné
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
 ě ě ě ň Ž ů ě ř ř É ě ě ď ů ě ě š Ěž ř Ť ňň Á Á É Á ř Č š š ú ď ř ú ě š ř ř ú ř ě ěš ž ě ř ú ř ů Ě ď ř š ě ě ř ů ě š š ú ů ě ě ů ě ě ů ů ř ů ů ř ř ú ř řž ř řž ř řž ř ž ř ř ě ř Ý š ř š ě ř ů š ř Š ž Ň Ú
ě ě ě ň Ž ů ě ř ř É ě ě ď ů ě ě š Ěž ř Ť ňň Á Á É Á ř Č š š ú ď ř ú ě š ř ř ú ř ě ěš ž ě ř ú ř ů Ě ď ř š ě ě ř ů ě š š ú ů ě ě ů ě ě ů ů ř ů ů ř ř ú ř řž ř řž ř řž ř ž ř ř ě ř Ý š ř š ě ř ů š ř Š ž Ň Ú
ÚČ ř Í ů é č ř úč ů ř ř úč ů č Ů Ě Í ÚČ č š ú ú ó é ř é č ž úř ŠĚú Ů é úř ů é Úř ú ř ď Í ú ř ě č Úř ě ě ě ú Č Č úř č Ú ř ř Á č ŘÍ Í ď úč ČÍ úř ř š č ř
 úř úř č č ň č ř ě ú úř úř č č úř ř š úř č é úř ě ě ě ů é ě č ú ú ř ě ě ě ú ě ů ů ě é ě ě é ě ě š ř ů é ě č ř é ě š ř ů ř ž ú ú ž ě Č é ě Č ě Č é ě Č ě Č é ě ř š ě ú č ě úř ě ř š ě é č úř ě ěř ů ě ěř č
úř úř č č ň č ř ě ú úř úř č č úř ř š úř č é úř ě ě ě ů é ě č ú ú ř ě ě ě ú ě ů ů ě é ě ě é ě ě š ř ů é ě č ř é ě š ř ů ř ž ú ú ž ě Č é ě Č ě Č é ě Č ě Č é ě ř š ě ú č ě úř ě ř š ě é č úř ě ěř ů ě ěř č
5.4.2 Objemy a povrchy mnohostěnů I
 5.. Objemy orchy mnohostěnů I Předokldy: 51 Význm slo objem i orch je intuitině jsný. Mtemtická definice musí být oněkud řesnější. Okoání z lnimetrie: Obsh obrzce je kldné číslo, řiřzené obrzci tk, že
5.. Objemy orchy mnohostěnů I Předokldy: 51 Význm slo objem i orch je intuitině jsný. Mtemtická definice musí být oněkud řesnější. Okoání z lnimetrie: Obsh obrzce je kldné číslo, řiřzené obrzci tk, že
 ř ě ě š ř ů ř ěž ú ěž ú ú Č ě Ú š ž ú ž ě ě ř ž ě ú ů ě ř š ž ú ě š ž ě ů š ě ř ě Ú ř ě ř ě ř ě ě ř š ž ž ř ě ť ř ě ů š ř š ě ě ř š ď ů ř ř ž Ž ř ě ž ř ě ř š ř ě ř ř ů ř ž ř ř ř ě ě š ž ř ě ě ž ž ř ž š
ř ě ě š ř ů ř ěž ú ěž ú ú Č ě Ú š ž ú ž ě ě ř ž ě ú ů ě ř š ž ú ě š ž ě ů š ě ř ě Ú ř ě ř ě ř ě ě ř š ž ž ř ě ť ř ě ů š ř š ě ě ř š ď ů ř ř ž Ž ř ě ž ř ě ř š ř ě ř ř ů ř ž ř ř ř ě ě š ž ř ě ě ž ž ř ž š
Nakloněná rovina II
 1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se
1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se
VZÁJEMNÉ SILOVÉ PŮSOBENÍ VODIČŮ S PROUDEM A MAGNETICKÉ POLE
 Příklady: 1A. Jakou silou působí homogenní magnetické pole na přímý vodič o délce 15 cm, kterým prochází proud 4 A, a svírá s vektorem magnetické indukce úhel 60? Velikost vektoru magnetické indukce je
Příklady: 1A. Jakou silou působí homogenní magnetické pole na přímý vodič o délce 15 cm, kterým prochází proud 4 A, a svírá s vektorem magnetické indukce úhel 60? Velikost vektoru magnetické indukce je
Á ť ď ť ú é ý ý ý ů é ú Í ě ě ř ě Í é ý ě é š úř ž ýš é é ŕ ů é Í ř ě ř ý ř Ĺ ř Ž š é ý é é é ě š ě š ř ý ů Č ý ě é ě ň š ý ú é ú ů ý ů ý ů ň ř š ý úř
 đ Á ł ř ě é ě Ž é é ä łüł ŕ ł ř ľ ľľ ľľ ľľ Ż ě Ž Í ž ž ý Ž š úř ý é ý ř Í ý ý ý ý ů é ú š ě é ž ú Í ř ě ý ý Í ý ý ů ř ě ř Ž ž ě ř ě ů ý Ž ř ě Ž Ž é Í ý é Í ř ř ě Í é Í é ý ů ř ě ť ž ě é ě é ý ě é šž ř
đ Á ł ř ě é ě Ž é é ä łüł ŕ ł ř ľ ľľ ľľ ľľ Ż ě Ž Í ž ž ý Ž š úř ý é ý ř Í ý ý ý ý ů é ú š ě é ž ú Í ř ě ý ý Í ý ý ů ř ě ř Ž ž ě ř ě ů ý Ž ř ě Ž Ž é Í ý é Í ř ř ě Í é Í é ý ů ř ě ť ž ě é ě é ý ě é šž ř
7. SEMINÁŘ Z MECHANIKY
 - 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
- 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
 Ť č č ó ó č č č ý č ď ý ď š ě ý ň ě ý ú Ó ý ě č ě č Š ě Ž ý ý ě č č Ú č ý Č ě ě Š ř ěťž ě č É ť Č č ř Ž ě š č č ě ě ú č ó ó č č ů ě ř ě š Ž š ě Ž č š ď č ěž ž č ň š ň ň ř č ň č ý š ě ý Č Ó č É Á Ý Š č
Ť č č ó ó č č č ý č ď ý ď š ě ý ň ě ý ú Ó ý ě č ě č Š ě Ž ý ý ě č č Ú č ý Č ě ě Š ř ěťž ě č É ť Č č ř Ž ě š č č ě ě ú č ó ó č č ů ě ř ě š Ž š ě Ž č š ď č ěž ž č ň š ň ň ř č ň č ý š ě ý Č Ó č É Á Ý Š č
Direct emailing na míru Emailing podle kategorií Traffic pro váš web Databáze firem SMS kampaně Propagace přes slevový portál Facebook marketing
 I N T E R N E T O V Ý M A R K E T I N G e f e k t i v n í a c í l e n ý m a r k e t i n g p r o f e s i o n á l n í e m a i l i n g š p i č k o v é t e c h n i c k é z á z e m í p r o p r a c o v a n é
I N T E R N E T O V Ý M A R K E T I N G e f e k t i v n í a c í l e n ý m a r k e t i n g p r o f e s i o n á l n í e m a i l i n g š p i č k o v é t e c h n i c k é z á z e m í p r o p r a c o v a n é
í í ú ř Í ř í á í é é é Í á ý ň ř í š í č í í á í í é í í í á á ó ě Í í ě í í í í í řá ů čč ř č á í í í ě á ě ě í á í š ť Í ě Í ř ě í ě č Í ř é č š ě
 ú ř Í ř á é é é Í á ý ň ř š č á é á á ó Í řá ů čč ř č á á á š ť Í Í ř č Í ř é č š á č ý č é ó á č ř ů á č č š á ů á Í á á é č ú ó ť ý Í ř č é Í č š á ř á é á ř á ř ů ř ř á áž á Í ý é é č ý čů á é é é č
ú ř Í ř á é é é Í á ý ň ř š č á é á á ó Í řá ů čč ř č á á á š ť Í Í ř č Í ř é č š á č ý č é ó á č ř ů á č č š á ů á Í á á é č ú ó ť ý Í ř č é Í č š á ř á é á ř á ř ů ř ř á áž á Í ý é é č ý čů á é é é č
Matematické metody v kartografii
 Mtetické etod krtorii Přednášk 4 5 Krtorická zkreslení. Délkoé zkreslení lošné zkreslení odínk konorit. Tissoto indiktri. . Mtetická krtorie MK Zýá se: Mtetickýi eoetrickýi retr krtorických děl. Přeode
Mtetické etod krtorii Přednášk 4 5 Krtorická zkreslení. Délkoé zkreslení lošné zkreslení odínk konorit. Tissoto indiktri. . Mtetická krtorie MK Zýá se: Mtetickýi eoetrickýi retr krtorických děl. Přeode
ěř ý ž ů ž ý ž ý ý ě ž č ě ů ř é č ý ú ř é ř ý č ě ÍŽ é č ř é ě ě é é ů č ý ř ě ě č é ý ů ů ř é ě ř Í ůě č é Ž ř ě ž é č ř é ě é é ě ý é ě ř ž é é č ě
 ř č č é ě č č úč ý ů ě č ěř ý ž ů ů ě ž ě é ý ž ý ý č ž č ě ů ř ů é ř é č č ž č č úč ý č Ž ř ř ěř ý ž ů ž ý ž ý ý ě ž č ě ů ř é č ý ú ř é ř ý č ě ÍŽ é č ř é ě ě é é ů č ý ř ě ě č é ý ů ů ř é ě ř Í ůě č
ř č č é ě č č úč ý ů ě č ěř ý ž ů ů ě ž ě é ý ž ý ý č ž č ě ů ř ů é ř é č č ž č č úč ý č Ž ř ř ěř ý ž ů ž ý ž ý ý ě ž č ě ů ř é č ý ú ř é ř ý č ě ÍŽ é č ř é ě ě é é ů č ý ř ě ě č é ý ů ů ř é ě ř Í ůě č
1.3.6 Dynamika pohybu po kružnici II
 .3.6 Dynamika ohybu o kužnici II Pedaoická oznámka: Sočítat šechny uedené říklady jedné hodině není eálné. Př. : Vysětli, oč se čloěk ři jízdě na kole (motocyklu) musí ři ůjezdu zatáčkou naklonit. Podobná
.3.6 Dynamika ohybu o kužnici II Pedaoická oznámka: Sočítat šechny uedené říklady jedné hodině není eálné. Př. : Vysětli, oč se čloěk ři jízdě na kole (motocyklu) musí ři ůjezdu zatáčkou naklonit. Podobná
Vnitřní energie Zhotoveno ve školním roce: 2011/2012 Jméno zhotovitele: Ing. Iva Procházková
 Náze a adesa školy: Střední škola ůysloá a uěleká, Oaa, řísěkoá oganizae, Paskoa 399/8, Oaa, 7460 Náze oeačního ogau: OP zděláání o konkueneshonost, oblast odoy.5 Registační číslo ojektu: CZ..07/.5.00/34.09
Náze a adesa školy: Střední škola ůysloá a uěleká, Oaa, řísěkoá oganizae, Paskoa 399/8, Oaa, 7460 Náze oeačního ogau: OP zděláání o konkueneshonost, oblast odoy.5 Registační číslo ojektu: CZ..07/.5.00/34.09
Předmět studia klasické fyziky
 Přemě sui klsiké fik mehnik, emonmik, elekonmik, opik klsiká fik eoeiká fik epeimenální fik eoie elivi sisiká fik kvnová fik moení fik Přemě sui klsiké fik Fik oeně koumá sukuu hmo její ákon, hování přío
Přemě sui klsiké fik mehnik, emonmik, elekonmik, opik klsiká fik eoeiká fik epeimenální fik eoie elivi sisiká fik kvnová fik moení fik Přemě sui klsiké fik Fik oeně koumá sukuu hmo její ákon, hování přío
ÚVOD DO DYNAMIKY HMOTNÉHO BODU
 ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
Geometrie. RNDr. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Geometie RND. Yett Btákoá Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles komolá těles VY INOVACE_05 9_M Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles A) Komolý jehln - je těleso, kteé znikne půnikem
Geometie RND. Yett Btákoá Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles komolá těles VY INOVACE_05 9_M Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles A) Komolý jehln - je těleso, kteé znikne půnikem
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Nakloněná rovina III
 6 Nakloněná rovina III Předoklady: 4 Pedagogická oznáka: Následující říklady oět atří do kategorie vozíčků Je saozřejě otázkou, zda tyto říklady v takové nožství cvičit Osobně se i líbí, že se studenti
6 Nakloněná rovina III Předoklady: 4 Pedagogická oznáka: Následující říklady oět atří do kategorie vozíčků Je saozřejě otázkou, zda tyto říklady v takové nožství cvičit Osobně se i líbí, že se studenti
Stavba atomu: Elektronový obal
 Svb ou: Elkonový obl Nils Boh 885 96 Bohův ol ou Ewin Schöing 887 96 Schöingov vlnová ovnic Louis Bogli 89 987 uální vlnově-čásicový chk lnáních čásic M Bon 88 97 Bonov pvěpoobnosní inpc vlnové funkc Wn
Svb ou: Elkonový obl Nils Boh 885 96 Bohův ol ou Ewin Schöing 887 96 Schöingov vlnová ovnic Louis Bogli 89 987 uální vlnově-čásicový chk lnáních čásic M Bon 88 97 Bonov pvěpoobnosní inpc vlnové funkc Wn
5. SEMINÁŘ Z MECHANIKY
 - 5-5 SEMINÁŘ Z MECHANIKY 5 Osobní auoobi se pohbuje po odoroné dráze se zrhení s a při ronoěrné soupání se zrhení 6 s Určee úhe soupání za předpokadu že ahoá sía ooru a sía ření jsou sáé a F F kons F
- 5-5 SEMINÁŘ Z MECHANIKY 5 Osobní auoobi se pohbuje po odoroné dráze se zrhení s a při ronoěrné soupání se zrhení 6 s Určee úhe soupání za předpokadu že ahoá sía ooru a sía ření jsou sáé a F F kons F
Gravitační pole. a nepřímo úměrná čtverci vzdáleností r. r r
 Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Goniometrie a trigonometrie
 Goniometrie a trigonometrie Vzorce pro goniometrické funkce Nyní si řekneme něco o velmi důležitých vlastnostech a odvodíme si také některé velmi důležité vzorce pro výpočty s goniometrickými funkcemi.
Goniometrie a trigonometrie Vzorce pro goniometrické funkce Nyní si řekneme něco o velmi důležitých vlastnostech a odvodíme si také některé velmi důležité vzorce pro výpočty s goniometrickými funkcemi.
9. SEMINÁŘ Z MECHANIKY
 - 55-9 SENÁŘ Z ECHNKY 9 Sevční ( = 5 g ) se ozáčí z lidu Z jou dobu dosáne fevence 48 in, působí-li n něj oen síly N ěžišě? = ; ( ) 5 g 3 vzlede ose pocázející jeo () f = ; f = 48 in = 8 s ; = 3 N ; =?
- 55-9 SENÁŘ Z ECHNKY 9 Sevční ( = 5 g ) se ozáčí z lidu Z jou dobu dosáne fevence 48 in, působí-li n něj oen síly N ěžišě? = ; ( ) 5 g 3 vzlede ose pocázející jeo () f = ; f = 48 in = 8 s ; = 3 N ; =?
 ž š ř ú ž ř ž š ř ř ř ř ů š ř ž ř ó ň ó ř š š ž š ř ú ž ú ž ň ř š ř ů ž ž ř ň ř ú ř ř ů ú ú ů ř ú ň ř ž ó ř š ž ž ř ň ř ř ž Ť ó ř ž ú š Á ž ž ř ž ž ž š ž ř š š Á ž ž ž ž ú š ú š ť š ú š ž Š ž ř ž ř š š
ž š ř ú ž ř ž š ř ř ř ř ů š ř ž ř ó ň ó ř š š ž š ř ú ž ú ž ň ř š ř ů ž ž ř ň ř ú ř ř ů ú ú ů ř ú ň ř ž ó ř š ž ž ř ň ř ř ž Ť ó ř ž ú š Á ž ž ř ž ž ž š ž ř š š Á ž ž ž ž ú š ú š ť š ú š ž Š ž ř ž ř š š
Pravoúhlý trojúhelník goniometrické funkce. Výpočet stran pravoúhlého trojúhelníka pomocí goniometrických funkcí
 Prvoúhlý trojúhelník goniometrické funkce V prvoúhlém trojúhelníku ABC jsou definovány funkce úhlu : sin, cos, tg, cotg tkto: sin c cos c tg cot g protilehlá odvěsn ku přeponě přilehlá odvěsn ku přeponě
Prvoúhlý trojúhelník goniometrické funkce V prvoúhlém trojúhelníku ABC jsou definovány funkce úhlu : sin, cos, tg, cotg tkto: sin c cos c tg cot g protilehlá odvěsn ku přeponě přilehlá odvěsn ku přeponě
íž ě íž á ť ř ť í ž ě ě á í ň á í á í ů ů íž ď ř ť šíř é ě ě ě ř í ší íř ý ý ů éříš éš ěž ě á í á í ř é šíř ý ěží č ě š é í í ř í á í á í ž ž é ř é í
 Í Ý ČÁ Ú ý ší é č ý ůž í š é á é í ř š ř ů ě í í áří ě ž í á é á ě é í ž ě á á ď ří ě č é í í í í ž ě ý á ý ů č í ý ř ě ž í í í í š í í č í ěž ž ž ř é í á ř í í ě í ž í č ě ží ř ž é ř ě š ě ž á í žší é
Í Ý ČÁ Ú ý ší é č ý ůž í š é á é í ř š ř ů ě í í áří ě ž í á é á ě é í ž ě á á ď ří ě č é í í í í ž ě ý á ý ů č í ý ř ě ž í í í í š í í č í ěž ž ž ř é í á ř í í ě í ž í č ě ží ř ž é ř ě š ě ž á í žší é
 Ú š šť ž Č Č Č Ž ž š š ž ž š š ď ď Č š š ž š š š Ú š š š š ď š š ď ž š š ď š ů ď ď š Í Ž ů ů ů ů ů š š Ú Í Í ť š š š š ž ů š š š š Ž ž ďš š š Íš Ž š Č š ž Ý ď š Ž š ď ť ž É š š Í š Ž š Č ž ď š Ň ž š óó
Ú š šť ž Č Č Č Ž ž š š ž ž š š ď ď Č š š ž š š š Ú š š š š ď š š ď ž š š ď š ů ď ď š Í Ž ů ů ů ů ů š š Ú Í Í ť š š š š ž ů š š š š Ž ž ďš š š Íš Ž š Č š ž Ý ď š Ž š ď ť ž É š š Í š Ž š Č ž ď š Ň ž š óó
Projekt Odyssea, www.odyssea.cz
 Pojek Odyssea, www.odyssea.cz Přípaa na yučoání s cíli osobnosní a sociální ýchoy (yp B) Téma obooé Vzděláací obo Ročník Časoý ozsah Hlaní obooé cíle (j. cíle ázané na očekáaný ýsup zděláacího obou a na
Pojek Odyssea, www.odyssea.cz Přípaa na yučoání s cíli osobnosní a sociální ýchoy (yp B) Téma obooé Vzděláací obo Ročník Časoý ozsah Hlaní obooé cíle (j. cíle ázané na očekáaný ýsup zděláacího obou a na
Dynamika vozidla, přímá jízda, pohon a brzdění
 Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění lk ntišk : Dynik otooých ozil 0, y 0, z 0 - pný souřný systé, y, z - tělsoý souřný systé s počátk těžišti
Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění lk ntišk : Dynik otooých ozil 0, y 0, z 0 - pný souřný systé, y, z - tělsoý souřný systé s počátk těžišti
Inerciální a neinerciální soustavy
 Inerciální neinerciální soust olný hmotný bod (nepůsobí n něj žádné síl) inerciální soust: souřdnicoá soust ůči které je olný hmotný bod klidu nebo ronoměrném přímočrém pohbu pokud máme tři hmotné bod,
Inerciální neinerciální soust olný hmotný bod (nepůsobí n něj žádné síl) inerciální soust: souřdnicoá soust ůči které je olný hmotný bod klidu nebo ronoměrném přímočrém pohbu pokud máme tři hmotné bod,
Ostrava-Radvanice FTZÚ 02 ATEX 0199U. EEx me 1111 T6
 (1) ES Certifikát o přezkoušení typu (2) Za ř ízen í nebo ochranné systémy určené pro použití v prost ředí s n e b ez p e čím výbuchu podle Směrnice 94/9/EC (NV 23/200 3 Sb.) (3) Číslo ES certifikátu o
(1) ES Certifikát o přezkoušení typu (2) Za ř ízen í nebo ochranné systémy určené pro použití v prost ředí s n e b ez p e čím výbuchu podle Směrnice 94/9/EC (NV 23/200 3 Sb.) (3) Číslo ES certifikátu o
 ř é Ů é ř ž ř é é ř ž ř Ů ř ř ř Ú é Í ř ř ř é Ž é Í ř é Ý ř ř é é é é ř ř ř é é ř é é ř é Ž ř Ý é ří ř Ř é ř ř Ž Ů ř ř ř Š Í ří ř ř řň é ř Ú řň é ř řň é ř Š ř ž é ř Ž ř Ž ř ř ř Ž Á Ž Ž Š ř ř ř ř ř é é
ř é Ů é ř ž ř é é ř ž ř Ů ř ř ř Ú é Í ř ř ř é Ž é Í ř é Ý ř ř é é é é ř ř ř é é ř é é ř é Ž ř Ý é ří ř Ř é ř ř Ž Ů ř ř ř Š Í ří ř ř řň é ř Ú řň é ř řň é ř Š ř ž é ř Ž ř Ž ř ř ř Ž Á Ž Ž Š ř ř ř ř ř é é
= 2888,9 cm -1. Relativní atomové hmotnosti. leží stejný přechod pro molekulu H 37 Cl? Výsledek vyjádřete jako
 Přijímcí zkoušk n nvzující mgisterské studium - 018 Studijní progrm Fyzik - všechny obory kromě Učitelství fyziky-mtemtiky pro střední školy, Vrint A Příkld 1 Určete periodu periodického pohybu těles,
Přijímcí zkoušk n nvzující mgisterské studium - 018 Studijní progrm Fyzik - všechny obory kromě Učitelství fyziky-mtemtiky pro střední školy, Vrint A Příkld 1 Určete periodu periodického pohybu těles,
ěží č ú ú á í í í é ř ě í Ž ž ě á ý ť á í é ž á é š ý ý č ý á č š á ří ú ě ž ěť á Ž ž ž ř ž ř é č ě ť á ří č í á ě ž ú ú í é ě ě ž ř ě š ě ž ť ú é ž é
 ř čí ř í ě ž ú š í ý ť í ž ý š č áš ů ó ří á ž ž ěš í á ě ř ď í á ý š ý ě áž š ě í ř ř ščí áš ě ř ž ř š ě š ě š ž š č č ý č É ř ě ě ě á í ě ř ú ý á í ý ě ú ď í é ř í č ý ďí ě ší á š ř ýš ě ý á ž í Žá č
ř čí ř í ě ž ú š í ý ť í ž ý š č áš ů ó ří á ž ž ěš í á ě ř ď í á ý š ý ě áž š ě í ř ř ščí áš ě ř ž ř š ě š ě š ž š č č ý č É ř ě ě ě á í ě ř ú ý á í ý ě ú ď í é ř í č ý ďí ě ší á š ř ýš ě ý á ž í Žá č
11. cvičení z Matematiky 2
 11. cvičení z Mateatiky. - 6. května 16 11.1 Vypočtěte 1 x + y + z dv, kde : x + y + z 1. Věta o substituci á analogický tva a podínky pouze zanedbatelné nožiny nyní zahnují i plochy, oviny atd.: f dv
11. cvičení z Mateatiky. - 6. května 16 11.1 Vypočtěte 1 x + y + z dv, kde : x + y + z 1. Věta o substituci á analogický tva a podínky pouze zanedbatelné nožiny nyní zahnují i plochy, oviny atd.: f dv
Předmět studia klasické fyziky
 Přemě sui klsiké fik mehnik, emonmik, elekonmik, opik klsiká fik eoeiká fik epeimenální fik eoie elii sisiká fik knoá fik moení fik Přemě sui klsiké fik Fik oeně koumá sukuu hmo její ákon, hoání přío se
Přemě sui klsiké fik mehnik, emonmik, elekonmik, opik klsiká fik eoeiká fik epeimenální fik eoie elii sisiká fik knoá fik moení fik Přemě sui klsiké fik Fik oeně koumá sukuu hmo její ákon, hoání přío se
 š ř Č šť ň ř ž Č Č ř ž š š ď Č Č ť ř ř ž ř ř ž š ř ř ř ř š ř ď š ř š ř ž š š ř š š š š š ď š ď š š ř š ř Ž Á š ř ž ř ů š ř ů ř Ú ř Ú ů ů ň ř ů š ř š Ú ř š ď š š š š ůž ř ň ř ň š š š Č Ú š ž ř ž ř ř š š
š ř Č šť ň ř ž Č Č ř ž š š ď Č Č ť ř ř ž ř ř ž š ř ř ř ř š ř ď š ř š ř ž š š ř š š š š š ď š ď š š ř š ř Ž Á š ř ž ř ů š ř ů ř Ú ř Ú ů ů ň ř ů š ř š Ú ř š ď š š š š ůž ř ň ř ň š š š Č Ú š ž ř ž ř ř š š
 ú Ú ň š Í Š š Š Š š ň ň Á ň ň ň ň Á ň ň ď ú ú š ň ú ú š ď Č Ě Í Í Á Í ŘÍ š Š š š š Š Ť Ú ú š ú ú š š ú Ť ú š š š š ú š š ú ň š š ú š š š š š š š š š š š š š š š š Č úď Ú š š š Š ú ú Ú Ť ú Í š š š š š
ú Ú ň š Í Š š Š Š š ň ň Á ň ň ň ň Á ň ň ď ú ú š ň ú ú š ď Č Ě Í Í Á Í ŘÍ š Š š š š Š Ť Ú ú š ú ú š š ú Ť ú š š š š ú š š ú ň š š ú š š š š š š š š š š š š š š š š Č úď Ú š š š Š ú ú Ú Ť ú Í š š š š š
šš úř ú ý ř é ř ě é ž é Ž ěř ě éř ÓÍ Č ěř ó ěř ó Í é ě Í ě š ě é ě ř ř ó ý Š Ž ě ý Š ř ě é Ž Č é Ó ě Ž ý ří ě ě ý é Ž óí ě ř ř ý
 Ě ř é ř ě é Ž Č é šš úř ú ý ř é ř ě é ž é Ž ěř ě éř ÓÍ Č ěř ó ěř ó Í é ě Í ě š ě é ě ř ř ó ý Š Ž ě ý Š ř ě é Ž Č é Ó ě Ž ý ří ě ě ý é Ž óí ě ř ř ý ž ý ý ů é ý ý ř ů ú ů ý ž úě Í ř é Í ú Í ě Ó ý ří ě ě
Ě ř é ř ě é Ž Č é šš úř ú ý ř é ř ě é ž é Ž ěř ě éř ÓÍ Č ěř ó ěř ó Í é ě Í ě š ě é ě ř ř ó ý Š Ž ě ý Š ř ě é Ž Č é Ó ě Ž ý ří ě ě ý é Ž óí ě ř ř ý ž ý ý ů é ý ý ř ů ú ů ý ž úě Í ř é Í ú Í ě Ó ý ří ě ě
Ě Í Č ŘÍ Ů ň ž óý ó ó ó ú ž ú ú ó ř ů ř É ř ň ř ř ň ř ň ú ň ó ř ř ř ř ó ú ú ř ó ř ř ř ň Á
 Ú š ú ň ú ó ú ř ů Ů ú ů ž ú ú ů ů ů ú Ů ž ů ř ř ř ň óý ó Ó Ě Í Č ŘÍ Ů ň ž óý ó ó ó ú ž ú ú ó ř ů ř É ř ň ř ř ň ř ň ú ň ó ř ř ř ř ó ú ú ř ó ř ř ř ň Á ó ň Ů Ť Ý ú š ó ů Ú Ú ž É ž ž ú ó ž ž š ž ž É ž ž Ď
Ú š ú ň ú ó ú ř ů Ů ú ů ž ú ú ů ů ů ú Ů ž ů ř ř ř ň óý ó Ó Ě Í Č ŘÍ Ů ň ž óý ó ó ó ú ž ú ú ó ř ů ř É ř ň ř ř ň ř ň ú ň ó ř ř ř ř ó ú ú ř ó ř ř ř ň Á ó ň Ů Ť Ý ú š ó ů Ú Ú ž É ž ž ú ó ž ž š ž ž É ž ž Ď
í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í
 í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í ů ž á ří ří ž á í í ý é í ž í ě ý č é á ž é á ě á á
í ě ší ý á í í á ě ě ú í á í é á í ý ů ě ě ší é č ý ří á í čá í í ě í ž é ž ý á ý é ý ž čí ž í ší ř á á č ž ř š é ř č é ží í ě ší ř á č ý ů á ů ý č í ů ž á ří ří ž á í í ý é í ž í ě ý č é á ž é á ě á á
metoda uvolňování metoda redukce G 1 G 2
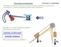 Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
 ú ó ú ó ú ú ó š Í Ť ň ŠÍ Ů ň ú Ů ó š ú ú ň š ú š ť ť ú š š ú ť úť Ď š š ú ú ť ú É ú ó ú ť š É ú ó ú ú ó ú ť ť ó ú ó ť ú ň ú ó ú ú ó ó ó Ý ň ú ú ó ó óé ó ú ó ú ó ó Ó ň ó ó ó ú ú ó ó ó ó ó ó ó ó ú ó ó ú
ú ó ú ó ú ú ó š Í Ť ň ŠÍ Ů ň ú Ů ó š ú ú ň š ú š ť ť ú š š ú ť úť Ď š š ú ú ť ú É ú ó ú ť š É ú ó ú ú ó ú ť ť ó ú ó ť ú ň ú ó ú ú ó ó ó Ý ň ú ú ó ó óé ó ú ó ú ó ó Ó ň ó ó ó ú ú ó ó ó ó ó ó ó ó ú ó ó ú
studentská kopie Př. 9 Složený členěný prut ze dvou úhelníků 15ε = 15 = 15...bezpečně třída 3 (nemusíme redukovat plochu)
 Př. 9 Složený členěný prut e dou úhelníků Stnote únosnost prutu tořeného dojcí ronormenný úhelníků 9x8. Prut toří dgonálu příhrdoého tuždl sstémoá délk prutu je 4 m. Spojk P-8x8 jsou umístěn třetná prutu.
Př. 9 Složený členěný prut e dou úhelníků Stnote únosnost prutu tořeného dojcí ronormenný úhelníků 9x8. Prut toří dgonálu příhrdoého tuždl sstémoá délk prutu je 4 m. Spojk P-8x8 jsou umístěn třetná prutu.
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Pojek ealizoaný na SPŠ Noé Měo nad Meují finanční podpoou Opeačním poamu Vzděláání po konkuencechopno Káloéhadeckého kaje Modul 3 - Technické předměy In. Jan Jemelík - ložený pohyb znikne ložením dou na
Pojek ealizoaný na SPŠ Noé Měo nad Meují finanční podpoou Opeačním poamu Vzděláání po konkuencechopno Káloéhadeckého kaje Modul 3 - Technické předměy In. Jan Jemelík - ložený pohyb znikne ložením dou na
29. OBJEMY A POVRCHY TĚLES
 9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
Výsledky úloh. 1. Úpravy výrazů + x 0, 2x 1 2 2, x Funkce. = f) a 2.8. ( ) ( ) 1.6. , klesající pro a ( 0, ) ), rostoucí pro s (, 1)
 Výsledky úloh. Úpravy výrazů.. +, + R.., a 0, a b.., a ± b, a b a b a +.. + a +, 0, a.., a 0; ± ; n + a.. a + b 9, > 0.7., a ± b a b m n.8., m 0, n 0, m n.9. a, a > 0 m + n.0., ;0; ;;.., k.. tg, k sin.
Výsledky úloh. Úpravy výrazů.. +, + R.., a 0, a b.., a ± b, a b a b a +.. + a +, 0, a.., a 0; ± ; n + a.. a + b 9, > 0.7., a ± b a b m n.8., m 0, n 0, m n.9. a, a > 0 m + n.0., ;0; ;;.., k.. tg, k sin.
ě ě í ý ě á ý ů é á í ů á č š í ř í ó ě é á ž ý í ě ýč ář ř š ě ý ář ý á é á í š ě é í ř áž á á ě í ě á í í í á ý ří ě ý ě ší é á á í í ř ř á á í Í áž
 Á á í ý á í č é é á í í čí í ý á ů í é á í ř ů ý č é é ř í á é é ě ě í ý ě í é ý á í í í ý á í ž í č ý ý á ů ů řá é é á ý á ý ě í ý ě á ř á ř é š í ží í ě é ě é á á í á á ů ě ší ů á í í ů ě í é é ý š š
Á á í ý á í č é é á í í čí í ý á ů í é á í ř ů ý č é é ř í á é é ě ě í ý ě í é ý á í í í ý á í ž í č ý ý á ů ů řá é é á ý á ý ě í ý ě á ř á ř é š í ží í ě é ě é á á í á á ů ě ší ů á í í ů ě í é é ý š š
