Fyzika laserů. 21. února Katedra fyzikální elektroniky.
|
|
|
- Karel Bláha
- před 6 lety
- Počet zobrazení:
Transkript
1 Fyzka laserů Kvantvá tere tlumení řídící rvnce Jan Šulc Katedra fyzkální elektrnky České vyské učení tecncké 21. únra 217
2 Kntakty Ing. Jan Šulc, P.D. Trjanva, místnst 237 Tel.: Ing. Zbyněk Hubka ELI Beamlnes
3 Prgram přednášek 1. Kvantvá tere tlumení, řídící rvnce 2. Aplkace na atm, Paul rvnce 3. Plklascký pps nterakce záření s látku 4. Aplkace na šíření reznanční záření prstředím 5. Aplkace na laser kntnuální režm 6. Aplkace na laser Q-spínání 7. Kerentní šíření mpulzů 8. Další jevy v plklascké aprxmac 9. Spektrum laseru a režm syncrnzace módů 1. Kvantvá tere laseru, Fkkerva-Planckva rvnce 11. F-P rvnce pr záření a atm 12. F-P rvnce pr laser 13. Statstcké vlastnst laservé záření
4 Lteratura VRBOVÁ M., ŠULC J.: Interakce reznanční záření s látku, Skrptum FJFI ČVUT, Praa, 26 LOUISELL, W. H.: Quantum statstcal prpertes f radatn, Jn Wley & Sns, New Yrk, 1973 VRBOVÁ M. a kl.: Lasery a mderní ptka - Obrvá encyklpede, Prmeteus, Praa, 1994 VRBOVÁ M., JELÍNKOVÁ H., GAVRILOV P.: Úvd d laservé tecnky, Skrptum FJFI ČVUT, Praa, 1994 ttp://peple.fjf.cvut.cz/sulcjan1/ulat/ Přednášky: ttp://peple.fjf.cvut.cz/sulcjan1/fla/
5 Laservý generátr Scéma laseru Laser Generátr ptcké záření specfckýc vlastnstí 1. Mncmatčnst 2. Směrvst (kncentrace energe) 3. Kerence Aktvní prstředí Systém kvantvýc sustav, který s vyměňuje energ se záření prstřednctvím reznanční nterakce stmulvaná emse záření Buzení a clazení Aktvní prstředí je udržván v termdynamcky nervnvážném stavu nverze ppulace ladn Reznátr Zajšt uje zpětnu vazbu pr laservý zeslvač a vznk sclací, využívá se k extrakc energe laseru Laser není v prncpu uzavřená sustava!
6 Kvantvý Luvlleův terém Pr pps nterakce subru kvantvýc sustav a elektrmagnetcké ple lze pužít metdy kvantvé statstcké fyzky. Výpčet střední dnty pzrvatelné velčny: Ô = Tr nˆϱ Ô Kvantvý Luvlleův terém vývj statstcké perátru ˆϱ ˆϱ t = Ĥ T, ˆϱ Ekvvalentní časvé Scrödngervě rvnc Musíme znát Hamltnán celé uzavřené systému ĤT Platí puze pr uzavřený systém Žádná část světa však není uzavřená a Luvlleův terém je jen exaktním becným pravdlem.
7 Mdel laseru jak uzavřený systém 1 Interakce reznanční záření s látku Buzení Kvantvé sustavy aktvní prstředí Clazení Ĥ (atmy... ) 1 Ĥ 2 Ĥ 3 ˆV 1 ˆV2 ˆV 3 ˆϱ, Ĥ T = Ĥ + ˆV Elektrmagnetcké Tlumení ple laseru Ĥ 4 ˆV Ĥ 5 4 Vlastní systém laseru Buzení, clazení a tlumení termdynamcky rvnvážné systémy, makrskpcké Obrázek 1.1: Mdel laseru jak uzavřený systém. Buzení, clazení a tlumení pvažujeme za vlastnst se nemění a závsí puze na termdynamcké tepltě T. termdynamcky rvnvážné systémy. 1 mód ple laseru 1 stupeň vlnst Aktvní prstředí energí, scpnýc knečný prstřednctvím pčet kvantvýc reznanční nterakce sustavzeslvat a stupňů energ vlnst elektrmagnetcké pleple. neknečně, Nutnu pdmínku ale spčetně je nverzní stupňů bsazení vlnst (ppulace) energetckýc ladn Celé Rezervár na příslušném neknečně, reznančnímale kvantvém spčetně přecdu. stupňů I př vlnst ustálené čnnst (černélaseru těles) se aktvní prstředí nacází v termdynamcky nervnvážném stavu.
8 Tlumený kvantvý systém Systém Rezervár Ĥ S S ˆV Ĥ R R ˆρ S ˆρ R Ĥ T, ˆρ SR Uzavřený slžený kvantvý Obrázek 2.1: systém: Sustava ĤT = Systém = ĤS + ĤR Reservr + ˆV Systém (dynamcká sustava) knečný pčet stupňů vlnst Rezervár Hamltnán(tlumící celé systému: sustava) neknečně spčetně stupňů vlnst Evluce celé Ĥ = ĤS + ĤR + ˆV uzavřené systému Luvllva rvnce v nterakční reprezentac Reservr: ˆϱI SR t = ˆV I (t ), ˆϱ I SR Velký ˆϱ I SR(t) pčet = stupňů Û vlnst (t, )ˆϱ S SR(t)Û(t, ), ˆV I (t ) = Û (t, ) ˆV S Û (t, ). V důsledku nterakce se systémem Û (t, ) = exp ĤS (t ) Řešení nestacnární [ ] prucvu terační metdu + řada zjedndušujícíc předpkladů exp βĥr ˆρ R = [ ] (2.2) (2.1)
9 Prucvá metda terace d drué řádu Výczí rvnce: Luvllva rvnce v nterakční reprezentac ˆϱI SR t = ˆV I (t ), ˆϱ I SR Aprxmace řešení: pstupná ntegrace, na pravé straně je předczí terace ˆϱ I SR ˆϱ I SR(t) ˆϱ I SR( ) = 1 dt 1 ˆV I (t 1 ), ˆϱ I SR( ) + t dt 1 dt 2 ˆV I (t 1 ), ˆV I (t 2 ), ˆϱ I SR( ) Pčáteční pdmínka: pr t = bude ˆV a ˆϱ I SR( ) = ˆϱ S S ˆϱ S R = ˆϱI S( ) ˆϱ R Rezervár v term. rvnváze: ˆϱ S R = ˆϱI R ˆϱ R se v čase nemění ˆϱ R = e βĥr Tr R e βĥr, β = 1 kt
10 Redukvaný statstcký perátr Máme rvnc pr ˆϱ I SR(t), tedy vývj celé slžené sustavy. Nás ale zajímá především vývj systému S, respektve je dynamckýc prměnnýc: ˆM = Tr SR nˆϱ S SR ˆM n = Tr S Tr R (ˆϱ S SR) ˆM {z } ˆϱ S S = Tr S n ˆϱ S S ˆM Redukvaný statstcký perátr ˆϱ S S = Tr R ˆϱ S SR = Tr R e (/ )(ĤR +ĤS)(t ) ˆϱ I SR(t) e (/ )(ĤR +ĤS)(t ) = e (/ )ĤS(t ) Tr R ˆϱ I SR(t) e {z } ) ˆϱ I S ˆϱ I S = e (/ )ĤS(t ) ˆϱ S S(t) e (/ )ĤS(t ) Výpčet střední dnty: ˆM = Tr = Tr n n n ˆϱ S ˆM S S = Tr e (/ )ĤS(t ) ˆϱ I S e (/ )ĤS(t ) ˆMS = ˆϱ I S e (/ )ĤS(t ) ˆM e (/ )ĤS(t ) = Tr nˆϱ I S ˆM I {z } ˆM I
11 Iterace d drué řádu pr redukvaný statstcký perátr Ve výczí rvnc ˆϱ I SR(t) ˆϱ I SR( ) = 1 dt 1 ˆV I (t 1 ), ˆϱ I SR( ) + t dt 1 dt 2 ˆV I (t 1 ), Vypčteme stpu na pravé a levé straně přes rezervár R: ˆϱ I S(t) ˆϱ I S( ) = 1 dt 1 Tr R ˆV I (t 1 ), ˆϱ I SR( ) + t dt 1 dt 2 Tr R ˆV I (t 1 ), ˆV I (t 2 ), ˆϱ I SR( ) ˆV I (t 2 ), ˆϱ I SR( ) Pčáteční pdmínka ˆϱ I SR( ) = ˆϱ I S( )ˆϱ R. Tedy: ˆϱ I S(t) ˆϱ I S( ) = t 2 dt 1 Tr R ˆV I (t 1 ), ˆϱ I S( )ˆϱ R + dt 1 1 dt 2 Tr R ˆV I (t 1 ), ˆV I (t 2 ), ˆϱ I S( )ˆϱ R
12 Interakční Hamltnán ˆV Abycm ml prvést další zjedndušující úpravy, ptřebujeme znát tvar nterakční Hamltnánu Uvažujeme nejjedndušší tvar první křížvý člen Taylrva rzvje celkvé Hamltnánu sustavy ĤT, tedy: ˆV ( ˆQ, ˆF ) = ĤT ( ˆQ, ˆF ) ĤS( ˆQ ) ĤR(ˆF ). = X ˆQ ˆF, ˆQ perátry systému, ˆF perátry rezerváru Vzledem k nezávslst stavvýc prstrů systému S a rezerváru R dstaneme: X ˆV I (t ) = ˆQ I (t )ˆF I (t ) Zavedeme značení řídící rvnce ˆϱ I S(t) ˆϱ I S( ) = ,2 ˆQ = ˆQ I 1,2 (t 1,2 ) a ˆF = ˆF I (t 1,2 ) a dsadíme d t 2 dt 1 Tr R ˆV I (t 1 ), ˆϱ I S( )ˆϱ R + dt 1 1 ˆϱ I S(t) ˆϱ I S( ) = X dt 2 Tr R ˆV I (t 1 ), t dt 1 Tr R ˆQ1 ˆF 1, ˆϱ I S( )ˆϱ R ˆV I (t 2 ), ˆϱ I S( )ˆϱ R
13 Stpy Tr R [... ], střední dnty a krelační funkce V rvnc ˆϱ I S(t) ˆϱ I S( ) = X X,j 1 dt 1 Tr R ˆQ1 ˆF, ˆϱ I S( )ˆϱ R 2, ˆQ2 j ˆF j, ˆϱ I S( )ˆϱ R dt 1 1 dt 2 Tr R ˆQ1 ˆF 1 můžeme vypčítat stpy (DC 1.1): Tr R ˆQ1 ˆF 1, ˆϱ I S( )ˆϱ R = ˆQ1, ˆϱ I S( ) ˆF 1 R 1 2 Tr R ˆQ1 ˆF, ˆQ2 j ˆF j, ˆϱ I S( )ˆϱ R = = ˆF 1 ˆF j 2 R ˆQ1 ˆQ2 j ˆϱ I S ˆQ j 2 ˆϱ I S ˆQ 1 ˆF j 2 ˆF 1 R ˆQ1 ˆϱ I ˆQ S j 2 Příslušné střední dnty a krelační funkce: ˆF 1 I R = Tr R ˆF (t 1 )ˆϱ R, ˆF 1 ˆF j 2 I R = Tr R ˆF (t 1 )ˆF j I (t 2 )ˆϱ R, ˆF 2 ˆF j 1 I R = Tr R ˆF (t 2 )ˆF I j (t 1 )ˆϱ R ˆϱ I S ˆQ 2 j ˆQ 1
14 Stpy Tr R [... ], střední dnty a krelační funkce Dstaneme: ˆϱ I S(t) ˆϱ I S( ) = X X,j ˆQ1, ˆϱ I S( ) ˆF 1 R dt 1 1 n dt 1 dt 2 ˆQ1 ˆQ2 j ˆϱ I S( ) ˆQ j 2 ˆϱ I S( ) ˆQ 1 ˆQ1 ˆϱ I S( ) ˆQ 2 j ˆϱ I S( ) ˆQ 2 j ˆQ 1 ˆF 2 j ˆF 1 ˆF 2 j R ˆF 1 R Rezervár stacnární ˆF stacnární ˆF 1 R není funkcí času Rezervár stacnární krelační funkce nezávsí na vlbě pčátku, puze na rzdílu t 1 a t 2 : ˆF 1 ˆF j 2 R = ˆF I (t 1 t 2 )ˆF j I () R ˆF 2 ˆF 1 j R = ˆF I ()ˆF I j (t 1 t 2 ) R V dalším krku prvedeme transfrmac ntegračníc prměnnýc, aby ntegrace prbíala d
15 Transfrmace ntegračníc prměnnýc Nvé prměnné (DC 1.2): ξ = t 2, τ = t 1 t 2 t 2 t 1 = t 2 t τ t τ = t ξ t t 1 1 n dt 1 dt 2... t dξ t t ξ dτ ξ n...
16 Transfrmace ntegračníc prměnnýc Z rvnce ˆϱ I S(t) ˆϱ I S( ) = X X,j ˆQ1, ˆϱ I S( ) ˆF 1 R dt 1 1 n dt 1 dt 2 ˆQ1 ˆQ2 j ˆϱ I S( ) ˆQ j 2 ˆϱ I S( ) ˆQ 1 ˆQ1 ˆϱ I S( ) ˆQ 2 j ˆϱ I S( ) ˆQ 2 j ˆQ 1 ˆF 2 j ˆF 1 ˆF 2 j R ˆF 1 R p prvedení transfrmace a s využtím stacnarty rezerváru R dstaneme ˆϱ I S(t) ˆϱ I S( ) = X ˆF R dt 1 ˆQI (t 1 ), ˆϱ I S( ) X,j t dξ t ξ n ˆQI (τ + ξ) ˆQ j I (ξ)ˆϱ I S( ) ˆQ j I (ξ)ˆϱ I S( ) ˆQ I (τ + ξ) ˆF (τ)ˆf j R ˆQI (τ + ξ)ˆϱ I S( ) ˆQ j I (ξ) ˆϱ I S( ) ˆQ j I (ξ) ˆQ I (ξ + τ) ˆF j ˆF(τ) R vyjádření časvé vývje redukvané statstcké perátru v nterakční reprezentac vývj systému S d drué řádu prucvé tere. dτ
17 Vlastní frekvence dynamckýc prměnnýc systému Defntrcky zavedeme vlastní frekvence perátru systému ˆQ I ˆQ I (λ) = e (/ )ĤSλ ˆQS e (/ )ĤSλ = e ω λ ˆQS ˆQI předpkládáme armncký průbě v čase s vlastní frekvencí ω Př.: elmag. ple, Ĥ = ω ˆn Dstaneme: t X ˆϱ I S(t) ˆϱ I S( ) = ˆF R ˆQS, ˆϱ I S( ) dξ e ω ξ X Z ˆQS ˆQS j ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ t t t S dξ e (ω +ω j )ξ ξ dτ e ω τ ˆF (τ)ˆf j R,j X,j ˆQS ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ S j ˆQ S t t dξe (ω +ω j )ξ ξ dτ e ω τ ˆF j ˆF(τ) R
18 1 Markvvská aprxmace Markvvská aprxmace Interakcí Interakcí Systému s srezervárem mu vznknut fluktuace fluktuace v rezerváru v rezerváru relaxační relaxační dba dba τ c τ c F (τ)f j R τ c τ Pkud zanedbáme zpětný vlv těct fluktuací na Systém a budeme studvat Pkud zanedbáme zpětný vlv fluktuací na Systém a budeme studva sustavu jen pr t τ c, můžeme př výpčtu ntegrálů z krelačníc funkcí sustavu jen pr t τ c, můžeme př výpčtu ntegrálů z krelačníc funkc rezerváru R psunut mez ntegrace přes τ a ξ d neknečna. rezerváru R v rvnc (??) psunut mez ntegrace přes τ a ξ d neknečna. Statstcká buducnst Systému bude závslá puze na stavu systému v daném Statstcká kamžku buducnst systém nemá Systému pamět. bude závslá puze na stavu systému v daném kamžku systém nemá pamět
19 Markvvská aprxmace ˆϱ I S(t) ˆϱ I S( ) = X X,j X,j ˆF R ˆQS, ˆϱ I S( ) I(ω ) ˆQS ˆQS j ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ S ˆQS ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ S j ˆQ S I(ω + ω j )w + j I(ω + ω j )w j Spektrální ustty krelačníc funkcí: I(ω ) = t w + j = w j = Z Z e ω τ ˆF (τ)ˆf j R dτ e ω τ ˆF j ˆF(τ) R dτ e ω ξ dξ pr t ω 1 I(ω ) = (t ) δ(ω ) (DC 1.3)
20 Markvvská aprxmace řídící rvnce ˆϱ I S t = X,j δ(ω + ω j )n ˆQS ˆQS j ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ S w + j ˆQS ˆϱ I S( ) ˆQ S j ˆϱ I S( ) ˆQ S j ˆQ S w j ˆϱ I S = ˆϱ I S(t) ˆϱ I S( ) t = t, Aby byl mžn přejít d dferencí k dferencálům, musí být na ntervalu t změna Systému v důsledku tlumení (carakterstcká dba γ 1 ) malá, tj. t γ 1. Ptm: ˆϱ I. S = t d ˆϱI S dt Zárveň musí být na ntervalu t splněn předpklad markvvské aprxmace. Drmady τ c t γ 1 Přecd ke Scrödngervě reprezentac (DC 1.5)
21 Řídící rvnce ve Scrödngervě reprezentac ˆϱ S S(t) t. = 1 X [ĤS, ˆϱ S S(t)],j δ(ω + ω j ) n ˆQS ˆQS j ˆϱ S S(t) ˆQ S j ˆϱ S S(t) ˆQ S w + j ˆQS ˆϱ S S(t) ˆQ S j ˆϱ S S(t) ˆQ S j ˆQ S w j MASTER EQUATION bdba Luvllva terému. Platí d drué řádu prucvé tere. Př vlbě krku výpčtu musí být splněny pžadavky Markvvské aprxmace τ c t γ 1 a musí být zledněna perda vlastníc kmtů systému t ω 1. Vlv Rezerváru zapčítán puze prstřednctvím spektrálníc ustt w ± krelačníc funkcí ˆF(τ)ˆF R Rezerváru dpvídajícíc vlastní frekvenc ω Systému. Statstcká buducnst Systému vycází ze znalst stavu Systému v jednm kamžku.
22 Srnutí Laser jak uzavřená sustava Kvantvý Luvlleův terém Řešení pr tlumení kvantvé sustavy černým tělesem řád prucvé tere 2. Redukvaný statstcký perátr 3. Specální tvar nterakční Hamltnánu 4. Harmncký průbě perátrů Systému 5. Psun rní meze ntegrace d neknečna Markvvská aprxmace Řídící rvnce ˆϱ S S(t) t = 1 [ĤS, ˆϱ S S(t)] X,j n ˆQS ˆQS j ˆϱ S S(t) ˆQ S j ˆϱ S S(t) ˆQ S δ(ω + ω j ) w + j ˆQS ˆϱ S S(t) ˆQ S j ˆϱ S S(t) ˆQ S j Cvčení: knkrétní aplkace na kvantvý armncký sclátr Příště: knkrétní aplkace na tlumený atm Paul rvnce ˆQ S w j
23 Lteratura VRBOVÁ M., ŠULC J.: Interakce reznanční záření s látku, Skrptum FJFI ČVUT, Praa, 26 LOUISELL, W. H.: Quantum statstcal prpertes f radatn, Jn Wley & Sns, New Yrk, 1973 VRBOVÁ M. a kl.: Lasery a mderní ptka - Obrvá encyklpede, Prmeteus, Praa, 1994 VRBOVÁ M., JELÍNKOVÁ H., GAVRILOV P.: Úvd d laservé tecnky, Skrptum FJFI ČVUT, Praa, 1994 ttp://peple.fjf.cvut.cz/sulcjan1/ulat/ Přednášky: ttp://peple.fjf.cvut.cz/sulcjan1/fla/
Fyzika laserů. 7. března Katedra fyzikální elektroniky.
 Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
6. Bilance energie v reagujících soustavách. Modely homogenních reaktorů v neisotermním režimu.
 6. Blance energe v reaguících sustavách. Mdely hmgenních reaktrů v nestermním režmu. Význam výměna a rekuperace tepla v chemckých prcesech Výhdy a nevýhdy adabatckéh (nestermníh) reaktru Syntéza amnaku,
6. Blance energe v reaguících sustavách. Mdely hmgenních reaktrů v nestermním režmu. Význam výměna a rekuperace tepla v chemckých prcesech Výhdy a nevýhdy adabatckéh (nestermníh) reaktru Syntéza amnaku,
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
- M matice hmotností - K matice tlumení - C matice tuhostí. Buzení harmonické. Buzení periodické
 Maticvý zápis phybvých rvnic pr případ vynucenéh kmitání dynamickéh systému s více stupni vlnsti. Pr systém autnmní netlumený naznačte pstup výpčtu vlastních frekvencí a tvarů kmitání s využitím pznatků
Maticvý zápis phybvých rvnic pr případ vynucenéh kmitání dynamickéh systému s více stupni vlnsti. Pr systém autnmní netlumený naznačte pstup výpčtu vlastních frekvencí a tvarů kmitání s využitím pznatků
Fyzika laserů. Aproximace rychlostních rovnic. 18. března Katedra fyzikální elektroniky.
 Fyzika laserů Aproximace rychlostních rovnic Metody generace nanosekundových impulsů. Q-spínání. Spínání ziskem Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz
Fyzika laserů Aproximace rychlostních rovnic Metody generace nanosekundových impulsů. Q-spínání. Spínání ziskem Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz
Gymnázium Vysoké Mýto nám. Vaňorného 163, Vysoké Mýto
 Gymnázium Vyské Mýt nám. Vaňrnéh 163, 566 01 Vyské Mýt Vysvětlení vzniku rvnvážnéh stavu při chemické reakci Některé chemické reakce prbíhají puze v jednm směru. Jejich rychlst je nejvyšší na začátku,
Gymnázium Vyské Mýt nám. Vaňrnéh 163, 566 01 Vyské Mýt Vysvětlení vzniku rvnvážnéh stavu při chemické reakci Některé chemické reakce prbíhají puze v jednm směru. Jejich rychlst je nejvyšší na začátku,
Laserová technika 1. Rychlostní rovnice pro Q-spínaný laser. 22. prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
6. Bilance energie v reagujících soustavách. Modely homogenních reaktorů v neisotermním režimu.
 6. Blance energe v reaguících sustavách. Mdely hmgenních reaktrů v nestermním režmu. Blance celkvé energe zahrnue: vntřní energ mechancku energ (knetcku energ ptencální energ... Přeměny edntlvých druhů
6. Blance energe v reaguících sustavách. Mdely hmgenních reaktrů v nestermním režmu. Blance celkvé energe zahrnue: vntřní energ mechancku energ (knetcku energ ptencální energ... Přeměny edntlvých druhů
Pokroky matematiky, fyziky a astronomie
 Pkrky matematky, fyzky a astrnme Václav Vlček Příprava učtelů ntegrvaných přírdvědných předmětů v Angl Pkrky matematky, fyzky a astrnme, Vl. 29 (984), N. 4, 222--226 Persstent URL: http://dml.cz/dmlcz/37782
Pkrky matematky, fyzky a astrnme Václav Vlček Příprava učtelů ntegrvaných přírdvědných předmětů v Angl Pkrky matematky, fyzky a astrnme, Vl. 29 (984), N. 4, 222--226 Persstent URL: http://dml.cz/dmlcz/37782
1 ROVNOVÁHA BODU Sestavte rovnice rovnice rovnováhy bodu (neznámé A,B,C) Určete A pro konstrukci z příkladu
 Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
ZŠ ÚnO, Bratří Čapků 1332
 Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
Speciální teorie relativity
 Speciální terie relativity Fyzika zalžená na phybvých záknech sira Isaaca Newtna se na pčátku 20. stletí částečně nahradila Einsteinvými teriemi relativity. První z nich je speciální terie relativity.
Speciální terie relativity Fyzika zalžená na phybvých záknech sira Isaaca Newtna se na pčátku 20. stletí částečně nahradila Einsteinvými teriemi relativity. První z nich je speciální terie relativity.
Obr. 1 Nejběžnější uspořádání vstupních i výstupních svorek operačního zesilovače
 Operační zeslvače Operační zeslvače jsu především základním stavebním prvkem každéh analgvéh elektrnckéh systému Většna elektrnckých lgckých systémů, na jejchž vstupech a výstupech jsu analgvé sgnály vyžaduje
Operační zeslvače Operační zeslvače jsu především základním stavebním prvkem každéh analgvéh elektrnckéh systému Většna elektrnckých lgckých systémů, na jejchž vstupech a výstupech jsu analgvé sgnály vyžaduje
4 Datový typ, proměnné, literály, konstanty, výrazy, operátory, příkazy
 4 Datvý typ, prměnné, literály, knstanty, výrazy, perátry, příkazy Studijní cíl Tent studijní blk má za cíl pkračvat v základních prvcích jazyka Java. Knkrétně bude uvedena definice datvéh typu, uvedeny
4 Datvý typ, prměnné, literály, knstanty, výrazy, perátry, příkazy Studijní cíl Tent studijní blk má za cíl pkračvat v základních prvcích jazyka Java. Knkrétně bude uvedena definice datvéh typu, uvedeny
1 SKLO Z POŽÁRNÍHO HLEDISKA - TEPELNÉ VLASTNOSTI SKLA
 1 SKLO Z POŽÁRNÍHO HLDISKA - TPLNÉ VLASTNOSTI SKLA Skl patří k materiálům, které významně vlivňují vývj stavební techniky a architektury. Nálezy skla pcházející z dby asi klem 5000 let před naším letpčtem
1 SKLO Z POŽÁRNÍHO HLDISKA - TPLNÉ VLASTNOSTI SKLA Skl patří k materiálům, které významně vlivňují vývj stavební techniky a architektury. Nálezy skla pcházející z dby asi klem 5000 let před naším letpčtem
Elektrické přístroje. Výpočet tepelných účinků elektrického proudu
 VŠB - echnická univerzita Ostrava Fakuta eektrtechniky a infrmatiky Katedra eektrických strjů a přístrjů Předmět: Eektrické přístrje Prtk č7 Výpčet tepených účinků eektrickéh prudu kupina: Datum: Vypracva:
VŠB - echnická univerzita Ostrava Fakuta eektrtechniky a infrmatiky Katedra eektrických strjů a přístrjů Předmět: Eektrické přístrje Prtk č7 Výpčet tepených účinků eektrickéh prudu kupina: Datum: Vypracva:
ZŠ ÚnO, Bratří Čapků 1332
 Digitální učebnice fyziky J. Beňuška - hlavní stránka (zleva) - úvdní menu, výběr tématických celků, vpřed na další celek (slupec vprav) Úvdní menu infrmace práci s prgramem Úvdem IKT ve vyučvání Prč výukvé
Digitální učebnice fyziky J. Beňuška - hlavní stránka (zleva) - úvdní menu, výběr tématických celků, vpřed na další celek (slupec vprav) Úvdní menu infrmace práci s prgramem Úvdem IKT ve vyučvání Prč výukvé
Fyzika laserů. 4. dubna Katedra fyzikální elektroniky.
 Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Téma 8, Nelineární chování materiálů, podmínky plasticity.
 Pružnst a plasticita II.,.rčník bakalářské studia, přednášky Janas, éma 8, elineární cvání materiálů, pdmínky plasticity. Úvd Pružně-plastický materiál Pdmínky plasticity ezní únsnst knstrukce Jednducé
Pružnst a plasticita II.,.rčník bakalářské studia, přednášky Janas, éma 8, elineární cvání materiálů, pdmínky plasticity. Úvd Pružně-plastický materiál Pdmínky plasticity ezní únsnst knstrukce Jednducé
Studijní předmět: Základy teorie pravděpodobnosti a matematická statistika Ročník:
 Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
ZŠ ÚnO, Bratří Čapků 1332
 PwerPint a Access v příkladech Pachner - p výběru tématickéh celku se bjeví kn se zadáním úlhy: ppis jedntlivých dílčích krků p animvaných tázkách jedntlivých dílčích krků uživatel abslvuje test na prvěření
PwerPint a Access v příkladech Pachner - p výběru tématickéh celku se bjeví kn se zadáním úlhy: ppis jedntlivých dílčích krků p animvaných tázkách jedntlivých dílčích krků uživatel abslvuje test na prvěření
Sledování provedených změn v programu SAS
 Sledvání prvedených změn v prgramu SAS Při práci se systémem SAS se v něklika funkcích sleduje, jaké změny byly prvedeny a kd je prvedl. Patří mezi ně evidence změn v mdulu Evidence žáků neb práce s průběžnu
Sledvání prvedených změn v prgramu SAS Při práci se systémem SAS se v něklika funkcích sleduje, jaké změny byly prvedeny a kd je prvedl. Patří mezi ně evidence změn v mdulu Evidence žáků neb práce s průběžnu
Rekuperace rodinného domu v Přestavlkách
 Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
Studentská Agora. - Proběhne 6 krajských kol debatní soutěže pod dozorem poroty.
 Studentská Agra Studentská Agra je škla kultivvané diskuze pr středšklské studenty. Jeh sučástí jsu šklení debatních dvednstí a studentská debatní sutěž. Prjekt se snaží zlepšit debatní prstředí v ČR a
Studentská Agra Studentská Agra je škla kultivvané diskuze pr středšklské studenty. Jeh sučástí jsu šklení debatních dvednstí a studentská debatní sutěž. Prjekt se snaží zlepšit debatní prstředí v ČR a
ÚZEMNÍ ROZVOJ. Ekonomika staveb a sídel /3
 ÚZEMNÍ ROZVOJ Eknmika staveb a sídel /3 ÚZEMNÍ ROZVOJ = jakékliv zhdncení nemvitsti změnu jejíh využívání změna funkčníh využití území nezastavěné zastavěné méně eknmicky výhdná funkce eknmicky výhdnější
ÚZEMNÍ ROZVOJ Eknmika staveb a sídel /3 ÚZEMNÍ ROZVOJ = jakékliv zhdncení nemvitsti změnu jejíh využívání změna funkčníh využití území nezastavěné zastavěné méně eknmicky výhdná funkce eknmicky výhdnější
2. cvičení vzorové příklady
 Příklad. cvičení vzrvé příklady Nakreslete zatěžvací brazce slžek ydrstatickýc sil, půsbícíc na autmatický segementvý jezvý uzávěr s ybným ramenem. Vypčtěte dntu suřadnice, udávající plu ladiny v tlačené
Příklad. cvičení vzrvé příklady Nakreslete zatěžvací brazce slžek ydrstatickýc sil, půsbícíc na autmatický segementvý jezvý uzávěr s ybným ramenem. Vypčtěte dntu suřadnice, udávající plu ladiny v tlačené
PODPORA VYBUDOVÁNÍ A PROVOZU ZAŘÍZENÍ PÉČE O DĚTI PŘEDŠKOLNÍHO VĚKU PRO PODNIKY I VEŘEJNOST MIMO HL. M. PRAHU / V HL. M. PRAZE. 27. 11.
 PODPORA VYBUDOVÁNÍ A PROVOZU ZAŘÍZENÍ PÉČE O DĚTI PŘEDŠKOLNÍHO VĚKU PRO PODNIKY I VEŘEJNOST MIMO HL. M. PRAHU / V HL. M. PRAZE 27. 11. 2015, Praha PŘEDSTAVENÍ VÝZEV PŘEDSTAVENÍ VÝZEV Pdpra vybudvání a
PODPORA VYBUDOVÁNÍ A PROVOZU ZAŘÍZENÍ PÉČE O DĚTI PŘEDŠKOLNÍHO VĚKU PRO PODNIKY I VEŘEJNOST MIMO HL. M. PRAHU / V HL. M. PRAZE 27. 11. 2015, Praha PŘEDSTAVENÍ VÝZEV PŘEDSTAVENÍ VÝZEV Pdpra vybudvání a
Instalace a technické informace
 Dkumentace k mdulu MdleKREM Samstatný mdul MdleKREM umžňuje zbrazit (vyučujícím i studentů) mdel průchdu studenta vyučvaným kurzem a t jak v grafické pdbě (využívající znalstní mdel GLIKREM - GuideLine
Dkumentace k mdulu MdleKREM Samstatný mdul MdleKREM umžňuje zbrazit (vyučujícím i studentů) mdel průchdu studenta vyučvaným kurzem a t jak v grafické pdbě (využívající znalstní mdel GLIKREM - GuideLine
Posouzení oslnění v osvětlovacích soustavách
 Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
Laserová technika 1. Rychlostní rovnice pro Q-spínaný laser. 16. prosince 2013. Katedra fyzikální elektroniky. jan.sulc@fjfi.cvut.
 Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 16. prosince 2013 Program přednášek
Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 16. prosince 2013 Program přednášek
Portál veřejné správy
 Prtál veřejné správy N Náávvrrh hn naa zzvveeřřeejjn něěn níí žžiivv ttn níí ssiittu uaaccee N Náávvrrh hn naa ssm maazzáán níí zzvveeřřeejjn něěn néé žžiivv ttn níí ssiittu uaaccee N Náávvrrh hn naa eed
Prtál veřejné správy N Náávvrrh hn naa zzvveeřřeejjn něěn níí žžiivv ttn níí ssiittu uaaccee N Náávvrrh hn naa ssm maazzáán níí zzvveeřřeejjn něěn néé žžiivv ttn níí ssiittu uaaccee N Náávvrrh hn naa eed
Portál veřejné správy
 Prtál veřejné správy Z Zvveeřřeejjn něěn níí vvěěssttn nííkku u S Sm maazzáán níí vvěěssttn nííkku u P Přřiid dáán níí p přřííll h h kkee zzvveeřřeejjn něěn néém mu u vvěěssttn nííkku u Vytvřen dne: 16.3.2012
Prtál veřejné správy Z Zvveeřřeejjn něěn níí vvěěssttn nííkku u S Sm maazzáán níí vvěěssttn nííkku u P Přřiid dáán níí p přřííll h h kkee zzvveeřřeejjn něěn néém mu u vvěěssttn nííkku u Vytvřen dne: 16.3.2012
Kritéria přijímacího řízení pro školní rok 2017/2018 čtyřleté studium - obor K/41 Gymnázium
 Kritéria přijímacíh řízení pr šklní rk 2017/2018 čtyřleté studium - br 79-41-K/41 Gymnázium 1) Vyhlášení prvníh kla přijímacíh řízení d prvníh rčníku vzdělávání ve střední škle d bru vzdělání 79 41 K/41
Kritéria přijímacíh řízení pr šklní rk 2017/2018 čtyřleté studium - br 79-41-K/41 Gymnázium 1) Vyhlášení prvníh kla přijímacíh řízení d prvníh rčníku vzdělávání ve střední škle d bru vzdělání 79 41 K/41
Strategické rámce správy a rozvoje klasifikace DRG v roce 2013
 Strategické rámce správy a rzvje klasifikace DRG v rce 2013 Ministerstv zdravtnictví má až d knce rku 2013 uzavřenu s NRC prváděcí smluvu k prvádění některých činnstí týkajících se kultivace systému DRG
Strategické rámce správy a rzvje klasifikace DRG v rce 2013 Ministerstv zdravtnictví má až d knce rku 2013 uzavřenu s NRC prváděcí smluvu k prvádění některých činnstí týkajících se kultivace systému DRG
Přednášky Teorie řízení Tereza Sieberová, 2015 LS 2014/2015
 -černě přednášky -červeně cvičení různě přeházené, pdle th, jak jsme pakvali, datum dpvídá přednáškám PŘEDNÁŠKA 10.2. C je t řízení? Subjektivní, cílevědmá činnst lidí Objektivně nutná Pznává a využívá
-černě přednášky -červeně cvičení různě přeházené, pdle th, jak jsme pakvali, datum dpvídá přednáškám PŘEDNÁŠKA 10.2. C je t řízení? Subjektivní, cílevědmá činnst lidí Objektivně nutná Pznává a využívá
NOVÁ ZELENÁ ÚSPORÁM 2015
 r e g i n á l n í p r a d e n s k á NOVÁ ZELENÁ ÚSPORÁM 2015 ODBORNÝ POSUDEK PRO RODINNÉ DOMY Obecné pdmínky: - z psudku musí být patrný rzsah a způsb prvedení pdprvanéh patření - psudek je pdkladem pr
r e g i n á l n í p r a d e n s k á NOVÁ ZELENÁ ÚSPORÁM 2015 ODBORNÝ POSUDEK PRO RODINNÉ DOMY Obecné pdmínky: - z psudku musí být patrný rzsah a způsb prvedení pdprvanéh patření - psudek je pdkladem pr
Výzva k podání nabídek
 Výzva k pdání nabídek Čísl zakázky (bude dplněn MPSV při uveřejnění): Název zakázky: Předmět zakázky (služba, ddávka neb stavební práce): x Chceme se učit, abychm zůstali knkurencí Nákup služeb Datum vyhlášení
Výzva k pdání nabídek Čísl zakázky (bude dplněn MPSV při uveřejnění): Název zakázky: Předmět zakázky (služba, ddávka neb stavební práce): x Chceme se učit, abychm zůstali knkurencí Nákup služeb Datum vyhlášení
Prováděcí předpisy pro soutěžní lezení pro rok 2014
 Prváděcí předpisy pr sutěžní lezení pr rk 2014 1. Přadatel 1.1. Každý ddíl registrvaný v Českém hrlezeckém svazu (dále jen "ČHS") neb právnická či fyzická sba s příslušným právněním má práv pžádat ČHS
Prváděcí předpisy pr sutěžní lezení pr rk 2014 1. Přadatel 1.1. Každý ddíl registrvaný v Českém hrlezeckém svazu (dále jen "ČHS") neb právnická či fyzická sba s příslušným právněním má práv pžádat ČHS
ELEKTRICKÝ VÝKON A ENERGIE. spotřebičová orientace - napětí i proud na na impedanci Z mají souhlasný směr
 ZÁKLADNÍ POJMY ELEKRCKÝ ÝKON A ENERGE Okamžitá hdnta výknu je deinvána: p u.i [,, A] sptřebičvá rientace - napětí i prud na na impedanci Z mají suhlasný směr výkn p > 0 - impedance Z je sptřebičem elektrické
ZÁKLADNÍ POJMY ELEKRCKÝ ÝKON A ENERGE Okamžitá hdnta výknu je deinvána: p u.i [,, A] sptřebičvá rientace - napětí i prud na na impedanci Z mají suhlasný směr výkn p > 0 - impedance Z je sptřebičem elektrické
v mechanice Využití mikrofonu k
 Využití mikrfnu k měřením v mechanice Vladimír Vícha Antace Mikrfn pfipjený zvukvu kartu pčítače ve spjení s jednduchým sftware (pf. AUDACITY) může služit k pměrně pfesnému měření krátkých časů. Pčítač
Využití mikrfnu k měřením v mechanice Vladimír Vícha Antace Mikrfn pfipjený zvukvu kartu pčítače ve spjení s jednduchým sftware (pf. AUDACITY) může služit k pměrně pfesnému měření krátkých časů. Pčítač
Portál veřejné správy
 Prtál veřejné správy Z Zvveeřřeejjn něěn níí p p vviin nn něě zzvveeřřeejjň ň vvaan néé iin nff rrm maaccee S Sm maazzáán níí p p vviin nn něě zzvveeřřeejjň ň vvaan néé iin nff rrm maaccee E Ed diittaaccee
Prtál veřejné správy Z Zvveeřřeejjn něěn níí p p vviin nn něě zzvveeřřeejjň ň vvaan néé iin nff rrm maaccee S Sm maazzáán níí p p vviin nn něě zzvveeřřeejjň ň vvaan néé iin nff rrm maaccee E Ed diittaaccee
Oprava a modernizace panelového bytového domu Bratří Čapků č.p. 2870, Česká Lípa
 Název stavby: Oprava a mdernizace panelvéh bytvéh dmu Bratří Čapků č.p. 2870, Česká Lípa ÚSTÍ NAD LABEM III/2013 B. SOUHRNNÁ TECHNICKÁ ZPRÁVA Stupeň: Investr: Zdpvědný prjektant: Veducí prjektu: Vypracval:
Název stavby: Oprava a mdernizace panelvéh bytvéh dmu Bratří Čapků č.p. 2870, Česká Lípa ÚSTÍ NAD LABEM III/2013 B. SOUHRNNÁ TECHNICKÁ ZPRÁVA Stupeň: Investr: Zdpvědný prjektant: Veducí prjektu: Vypracval:
VYUŽITÍ MULTIMEDIÁLNÍ TECHNIKY VE VÝUCE ANGLIČTINY UČÍME SE ANGLIČTINU S INTERAKTIVNÍ TABULÍ SMARTBOARD
 VYUŽITÍ MULTIMEDIÁLNÍ TECHNIKY VE VÝUCE ANGLIČTINY UČÍME SE ANGLIČTINU S INTERAKTIVNÍ TABULÍ SMARTBOARD Cíle kurzu: Účastník získá ptřebné infrmace a prakticky si svjí metdy, tipy a triky k efektivnímu
VYUŽITÍ MULTIMEDIÁLNÍ TECHNIKY VE VÝUCE ANGLIČTINY UČÍME SE ANGLIČTINU S INTERAKTIVNÍ TABULÍ SMARTBOARD Cíle kurzu: Účastník získá ptřebné infrmace a prakticky si svjí metdy, tipy a triky k efektivnímu
Laserová technika 1. Laser v aproximaci rychlostních rovnic. 22. prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Laser v aproximaci rychlostních rovnic Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Laserová technika 1 Aktivní prostředí Laser v aproximaci rychlostních rovnic Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Molární toky výstupní (mol/s) Molární toky vstupní (mol/s) V=konst. i i. ki V. V, k
 4. Blance v stemních sustavách s chemcku eakcí. mulace hmtnstní blance p vsádkvé a půtčné sustavy v ustáleném a dynamckém stavu. Základní mdely chemckých eaktů p hmgenní sustavy. Mlání tky vstupní (ml/s)
4. Blance v stemních sustavách s chemcku eakcí. mulace hmtnstní blance p vsádkvé a půtčné sustavy v ustáleném a dynamckém stavu. Základní mdely chemckých eaktů p hmgenní sustavy. Mlání tky vstupní (ml/s)
9. cvičení vzorové příklady
 9. cvičení vzrvé příklady Příklad 1 Určete přepadvý průtk pře Bazinův přeliv na br. 1, je-li dána výška přelivné rany nade dnem = d = 0,8 m, šířka přelivu b = m, přepadvá výška = 0,5 m a lubka dlní vdy
9. cvičení vzrvé příklady Příklad 1 Určete přepadvý průtk pře Bazinův přeliv na br. 1, je-li dána výška přelivné rany nade dnem = d = 0,8 m, šířka přelivu b = m, přepadvá výška = 0,5 m a lubka dlní vdy
Integrální rovnice a jejich použití při některých problémech mechaniky, matematické fysiky a techniky
 Integrální rvnce a jejch pužtí př některých prblémech mechanky, matematcké fysky a technky Užtí tere suměrných ntegrálních rvnc In: Slmn Grgrjevč Mchln (authr); Ott Vejvda (translatr): Integrální rvnce
Integrální rvnce a jejch pužtí př některých prblémech mechanky, matematcké fysky a technky Užtí tere suměrných ntegrálních rvnc In: Slmn Grgrjevč Mchln (authr); Ott Vejvda (translatr): Integrální rvnce
C V I Č E N Í 3 1. Představení firmy Glaverbel Czech a.s. Teplice a. Vyráběný sortiment
 Technlgie skla 00/0 C V I Č E N Í. Představení firmy Glaverbel Czech a.s. [-]. Viskzitní křivka skla [,6]. Výpčet pmcí Vgel-Fulcher-Tammannvy rvnice [,6]. Výpčet z chemickéh slžení [,6]. Představení firmy
Technlgie skla 00/0 C V I Č E N Í. Představení firmy Glaverbel Czech a.s. [-]. Viskzitní křivka skla [,6]. Výpčet pmcí Vgel-Fulcher-Tammannvy rvnice [,6]. Výpčet z chemickéh slžení [,6]. Představení firmy
Dobývání znalostí z databází (MI-KDD) Přednáška číslo 1 - Úvod
 Dbývání znalstí z databází (MI-KDD) Přednáška čísl 1 - Úvd (c) prf. RNDr. Jan Rauch, CSc. KIZI, Fakulta infrmatiky a statistiky VŠE zimní semestr 2011/2012 Evrpský sciální fnd Praha & EU: Investujeme d
Dbývání znalstí z databází (MI-KDD) Přednáška čísl 1 - Úvd (c) prf. RNDr. Jan Rauch, CSc. KIZI, Fakulta infrmatiky a statistiky VŠE zimní semestr 2011/2012 Evrpský sciální fnd Praha & EU: Investujeme d
Úvod do laserové techniky
 Úvod do laserové techniky Látka jako soubor kvantových soustav Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze petr.koranda@gmail.com 18. září 2018 Světlo jako elektromagnetické
Úvod do laserové techniky Látka jako soubor kvantových soustav Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze petr.koranda@gmail.com 18. září 2018 Světlo jako elektromagnetické
Manuál k vyplnění Monitorovacích listů za rok 2017 (datum podání do )
 Manuál k vyplnění Mnitrvacích listů za rk 2017 (datum pdání d 31.7.2018) Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Mnitring pdnikatelskéh plánu/prjektu Mnitrvací list. Mnitrvací listy jsu
Manuál k vyplnění Mnitrvacích listů za rk 2017 (datum pdání d 31.7.2018) Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Mnitring pdnikatelskéh plánu/prjektu Mnitrvací list. Mnitrvací listy jsu
Manuál k vyplnění Monitorovacích listů za rok 2018 (datum podání do )
 Manuál k vyplnění Mnitrvacích listů za rk 2018 (datum pdání d 31.7.2019) Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Nvá pdání Žádsti PRV prjektvá patření Mnitring pdnikatelskéh plánu/prjektu
Manuál k vyplnění Mnitrvacích listů za rk 2018 (datum pdání d 31.7.2019) Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Nvá pdání Žádsti PRV prjektvá patření Mnitring pdnikatelskéh plánu/prjektu
Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03
![Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03 Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03](/thumbs/55/35967702.jpg) . Úkl měření. Stanvte hdnty sučinitele tepelné vdivsti mědi a slitiny hliníku.. Prvnejte naměřené hdnty s tabulkvými hdntami a vysvětlete pravděpdbnu příčinu nalezené diference. 3. Vypracujte graf tepltníh
. Úkl měření. Stanvte hdnty sučinitele tepelné vdivsti mědi a slitiny hliníku.. Prvnejte naměřené hdnty s tabulkvými hdntami a vysvětlete pravděpdbnu příčinu nalezené diference. 3. Vypracujte graf tepltníh
Výživa a sport, základy fitness
 Průvdní list kurzu Vzdělávání ICT metdiků Výživa a sprt, základy fitness Autr kurzu: Vyučvací předmět: Rčník: Téma: Účel kurzu: Tělesná výchva, Bilgie (Chemie) Studenti středních škl d 16 let Výživa a
Průvdní list kurzu Vzdělávání ICT metdiků Výživa a sprt, základy fitness Autr kurzu: Vyučvací předmět: Rčník: Téma: Účel kurzu: Tělesná výchva, Bilgie (Chemie) Studenti středních škl d 16 let Výživa a
Plánování směn verze 2.1, revize 03
 Plánvání směn verze 2.1, revize 03 Ing. Antnín Vecheta Email: t254@seznam.cz Pžadavky na pčítač: 1) Operační systém: MS Windws Vista neb nvější (nutné) 2) Prcesr: Intel i5 (dpručení) 3) Paměť: 4GB (dpručení)
Plánvání směn verze 2.1, revize 03 Ing. Antnín Vecheta Email: t254@seznam.cz Pžadavky na pčítač: 1) Operační systém: MS Windws Vista neb nvější (nutné) 2) Prcesr: Intel i5 (dpručení) 3) Paměť: 4GB (dpručení)
Jak zpřesnit HMM? Pomocí přesnější výstupní pravděpodobnostní funkce. Až dosud uvažováno klasické gaussovské rozložení
 Pkrčilé metdy rzpznávánířeči Přednáška 6 Zpřes esňvání akustickéh mdelu, vyhdncvání úspěšnsti Jak zpřesnit HMM? Pmcí přesnější výstupní pravděpdbnstní funkce a 11 a 22 a S-1S-1 a SS Q 1 a 12 a 23.... Q
Pkrčilé metdy rzpznávánířeči Přednáška 6 Zpřes esňvání akustickéh mdelu, vyhdncvání úspěšnsti Jak zpřesnit HMM? Pmcí přesnější výstupní pravděpdbnstní funkce a 11 a 22 a S-1S-1 a SS Q 1 a 12 a 23.... Q
AKČNÍ PLÁN SPLNĚNÍ PŘEDBĚŽNÉ PODMÍNKY 4.1
 AKČNÍ PLÁN SPLNĚNÍ PŘEDBĚŽNÉ PODMÍNKY 4.1 Úvd Předběžné pdmínky definuje tzv. nařízení splečných ustanveních 1 týkajících se evrpských strukturálních a investičních fndů (článek 19). Jejich zavedení vychází
AKČNÍ PLÁN SPLNĚNÍ PŘEDBĚŽNÉ PODMÍNKY 4.1 Úvd Předběžné pdmínky definuje tzv. nařízení splečných ustanveních 1 týkajících se evrpských strukturálních a investičních fndů (článek 19). Jejich zavedení vychází
Řízení nárůstu tažné síly
 Řízení nárůtu tažné íly Při rzjezdu aku je zaptřebí repektvat zejména: nepřekrčení meze adheze při ddržení největšíh příputnéh zrychlení aku; uprava je utavu pružně pjených těle, kde vypružení ve přáhlech
Řízení nárůtu tažné íly Při rzjezdu aku je zaptřebí repektvat zejména: nepřekrčení meze adheze při ddržení největšíh příputnéh zrychlení aku; uprava je utavu pružně pjených těle, kde vypružení ve přáhlech
I. Zobrazení dat a operace.
 Zpracval: hypspave@fel.cvut.cz 11. Zbrazení dat a perace. Číselné sustavy. Sčítání, dčítání, psuvy, násbení a dělení ve dvjkvé sustavě a zapjení příslušných bvdů. Zbrazení čísel se znaménkem a perace s
Zpracval: hypspave@fel.cvut.cz 11. Zbrazení dat a perace. Číselné sustavy. Sčítání, dčítání, psuvy, násbení a dělení ve dvjkvé sustavě a zapjení příslušných bvdů. Zbrazení čísel se znaménkem a perace s
27 Systémy s více vstupy a výstupy
 7 Systémy s více vstupy a výstupy Mchael Šebek Automatcké řízení 017 4-5-17 Stavový model MIMO systému Automatcké řízení - Kybernetka a robotka Má obecně m vstupů p výstupů x () t = Ax() t + Bu() t y()
7 Systémy s více vstupy a výstupy Mchael Šebek Automatcké řízení 017 4-5-17 Stavový model MIMO systému Automatcké řízení - Kybernetka a robotka Má obecně m vstupů p výstupů x () t = Ax() t + Bu() t y()
Provozní řád služby zálohování CIT
 Prvzní řád služby zálhvání CIT V Ostravě 5. května 2011 1 Ppis služby Služba zálhvání pskytuje mžnst pravidelnéh autmatizvanéh vytváření kpií (zálh) dat na zálhvací média a mžnst bnvy dat z těcht zálh.
Prvzní řád služby zálhvání CIT V Ostravě 5. května 2011 1 Ppis služby Služba zálhvání pskytuje mžnst pravidelnéh autmatizvanéh vytváření kpií (zálh) dat na zálhvací média a mžnst bnvy dat z těcht zálh.
Časopis pro pěstování matematiky
 Časps pr pěstvání matematky Frantšek Nžčka Křvka v afnním prstru a její afnní bluk Časps pr pěstvání matematky, Vl. 78 (1953), N. 4, 307--339 Persstent URL: http://dml.cz/dmlcz/108699 Terms f use: Insttute
Časps pr pěstvání matematky Frantšek Nžčka Křvka v afnním prstru a její afnní bluk Časps pr pěstvání matematky, Vl. 78 (1953), N. 4, 307--339 Persstent URL: http://dml.cz/dmlcz/108699 Terms f use: Insttute
OPTOELEKTRONIKA A INTEGROVANÁ OPTIKA, FSI-TOI-A
 OPTOELEKTRONIKA A INTEGROVANÁ OPTIKA, FSI-TOI-A GARANT PŘEDMĚTU: Prf. RNDr. Jiří Petráček, Dr. (ÚFI) VYUČUJÍCÍ PŘEDMĚTU: Prf. RNDr. Jiří Petráček, Dr. (ÚFI), CSc., Yasa Eksiglu Özk, Dr. (ÚFI) JAZYK VÝUKY:
OPTOELEKTRONIKA A INTEGROVANÁ OPTIKA, FSI-TOI-A GARANT PŘEDMĚTU: Prf. RNDr. Jiří Petráček, Dr. (ÚFI) VYUČUJÍCÍ PŘEDMĚTU: Prf. RNDr. Jiří Petráček, Dr. (ÚFI), CSc., Yasa Eksiglu Özk, Dr. (ÚFI) JAZYK VÝUKY:
Kurz 4st210 cvičení č. 5
 CVIČENÍ Č. 5 některá rzdělení nespjitých náhdných veličin binmické, hypergemetrické, Pissnv rzdělení nrmální rzdělení jak rzdělení spjitých náhdných veličin některá speciální rzdělení spjitých náhdných
CVIČENÍ Č. 5 některá rzdělení nespjitých náhdných veličin binmické, hypergemetrické, Pissnv rzdělení nrmální rzdělení jak rzdělení spjitých náhdných veličin některá speciální rzdělení spjitých náhdných
Chemické rovnováhy v analytické chemii
 Teretcké zákld nltcké cheme PřF UK, ZS 06/07. Chemcké rvnváh v nltcké chem úklem nltcké cheme je vhdným chemckým č fzkálně chemckým půsením n vzrek vvlt pzrvtelnu změnu, z jejíž vlstnst velkst lze usuzvt
Teretcké zákld nltcké cheme PřF UK, ZS 06/07. Chemcké rvnváh v nltcké chem úklem nltcké cheme je vhdným chemckým č fzkálně chemckým půsením n vzrek vvlt pzrvtelnu změnu, z jejíž vlstnst velkst lze usuzvt
Configuration Management
 Evrpský sciální fnd Praha & EU: Investujeme d vaší buducnsti Cnfiguratin Management Tmáš Krátký tmas.kratky@prfinit.eu http://www.prfinit.eu/cz/pdpra-univerzit/univerzitni-vyuka Sftwarvý prces??? Sftwarvý
Evrpský sciální fnd Praha & EU: Investujeme d vaší buducnsti Cnfiguratin Management Tmáš Krátký tmas.kratky@prfinit.eu http://www.prfinit.eu/cz/pdpra-univerzit/univerzitni-vyuka Sftwarvý prces??? Sftwarvý
Sborník vědeckých prací Vysoké školy báňské Technické univerzity Ostrava Řada hornicko-geologická Volume XLIX (2003), No.1, p. 1-22, ISSN
 Sbrník vědeckých prací Vyské škly báňské Technické univerzity Ostrava Řada hrnick-gelgická Vlume XLIX (3, N., p. -, ISSN 474-8476 Petr KUBÍČEK *, Jarmír DRÁPALA **, Alis ADAMUS *** DIAGNOSTIKA TEPLOTNÍCH
Sbrník vědeckých prací Vyské škly báňské Technické univerzity Ostrava Řada hrnick-gelgická Vlume XLIX (3, N., p. -, ISSN 474-8476 Petr KUBÍČEK *, Jarmír DRÁPALA **, Alis ADAMUS *** DIAGNOSTIKA TEPLOTNÍCH
Podklady pro cvičení. Úloha 1 Návrh konstrukčních systémů
 Pzemní stavby A2 Pdklady pr cvičení Cíl úlhy Úlha 1 Návrh knstrukčních systémů Návrh knstrukčníh systému zadané administrativní budvy ve dvu variantách, včetně návrhu bvdvéh pláště. Dalším cílem tét úlhy
Pzemní stavby A2 Pdklady pr cvičení Cíl úlhy Úlha 1 Návrh knstrukčních systémů Návrh knstrukčníh systému zadané administrativní budvy ve dvu variantách, včetně návrhu bvdvéh pláště. Dalším cílem tét úlhy
Co se předpokládá: - student si pamatuje molární hmotnosti uhlíku, dusíku, kyslíku, vodíku
 1. - 2. cvčení Téma: - vyjádření kncentrace ve směsích (mlární, hmtnstní a bjemvé zlmky, mlalta, látkvá kncentrace), střední mlární hmtnst, parcální tlak, - stavvé chvání tekutn - stavvá rvnce deálníh
1. - 2. cvčení Téma: - vyjádření kncentrace ve směsích (mlární, hmtnstní a bjemvé zlmky, mlalta, látkvá kncentrace), střední mlární hmtnst, parcální tlak, - stavvé chvání tekutn - stavvá rvnce deálníh
Možnosti transformace vyšších odborných škol do terciárního vzdělávání
 Mžnsti transfrmace vyšších dbrných škl d terciárníh vzdělávání Michal Karpíšek MŠMT, 30. listpadu 2010 IPn Refrma terciárníh vzdělávání CZ.1.07/4.2.00/06.0003 Tat prezentace je splufinancvána Evrpským
Mžnsti transfrmace vyšších dbrných škl d terciárníh vzdělávání Michal Karpíšek MŠMT, 30. listpadu 2010 IPn Refrma terciárníh vzdělávání CZ.1.07/4.2.00/06.0003 Tat prezentace je splufinancvána Evrpským
Software process (improvement)
 Evrpský sciální fnd Praha & EU: Investujeme d vaší buducnsti Sftware prcess (imprvement) Tmáš Krátký tmas.kratky@prfinit.eu http://www.prfinit.eu/cz/pdpra-univerzit/univerzitni-vyuka Základní pjmy Sftwarvý
Evrpský sciální fnd Praha & EU: Investujeme d vaší buducnsti Sftware prcess (imprvement) Tmáš Krátký tmas.kratky@prfinit.eu http://www.prfinit.eu/cz/pdpra-univerzit/univerzitni-vyuka Základní pjmy Sftwarvý
Helios Orange Plugin Zadávání vlastností
 Helis Orange Plugin Zadávání vlastnstí 2015 BürKmplet, s.r.. Obsah Zadávání vlastnstí... 3 Definice... 3 Skupiny... 3 Definice vlastnstí... 4 Knfigurace... 6 Zadávání a zbrazvání vlastnstí... 6 Editační
Helis Orange Plugin Zadávání vlastnstí 2015 BürKmplet, s.r.. Obsah Zadávání vlastnstí... 3 Definice... 3 Skupiny... 3 Definice vlastnstí... 4 Knfigurace... 6 Zadávání a zbrazvání vlastnstí... 6 Editační
Dotazník pro neziskové organizace
 Dtazník pr neziskvé rganizace Vážení zástupci neziskvých rganizací z Nvéh Hrádku, dvlujeme Vás tímt pžádat vyplnění dtazníku, který služí pr zjištění názrů a ptřeb neziskvých rganizací v Nvém Hrádku. V
Dtazník pr neziskvé rganizace Vážení zástupci neziskvých rganizací z Nvéh Hrádku, dvlujeme Vás tímt pžádat vyplnění dtazníku, který služí pr zjištění názrů a ptřeb neziskvých rganizací v Nvém Hrádku. V
ReDat experience v Release notes
 ReDat experience v 2.34.2 Release ntes Vydání: 02/2018 v 2.34.2 rev.1 Výrbce: RETIA, a.s. Pražská 341 Zelené Předměstí 530 02 Pardubice s certifikvaným systémem řízení jaksti pdle ISO 9001 a člen AOP V
ReDat experience v 2.34.2 Release ntes Vydání: 02/2018 v 2.34.2 rev.1 Výrbce: RETIA, a.s. Pražská 341 Zelené Předměstí 530 02 Pardubice s certifikvaným systémem řízení jaksti pdle ISO 9001 a člen AOP V
Vykreslení obrázku z databázového sloupce na referenční bod geometrie
 0 Vykreslení brázku z databázvéh slupce na referenční bd gemetrie OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 UKÁZKA DIALOGOVÉHO OKNA...3 4 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGNU...5-1 - 1 Cíl
0 Vykreslení brázku z databázvéh slupce na referenční bd gemetrie OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 UKÁZKA DIALOGOVÉHO OKNA...3 4 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGNU...5-1 - 1 Cíl
Specifikace pro SW aplikaci Start-up business.
 Zakázka na vytvření výukvé aplikace Start-up businees a Interaktivní webvé rzhraní Přílha č. 2 Technická specifikace Pžadavky: Specifikace pr SW aplikaci Start-up business. Obecné pžadavky Cílem je vytvřit
Zakázka na vytvření výukvé aplikace Start-up businees a Interaktivní webvé rzhraní Přílha č. 2 Technická specifikace Pžadavky: Specifikace pr SW aplikaci Start-up business. Obecné pžadavky Cílem je vytvřit
aneb Doporučení pro přípravu a realizaci vzdělávacích akcí pro pedagogické pracovníky v oblasti EVVO
 Rukvěť ekvzdělavatele I. Rukvěť (ek)vzdělavatele I. aneb Dpručení pr přípravu a realizaci vzdělávacích akcí pr pedaggické pracvníky v blasti EVVO Vzdělávací akce pr pedaggické pracvníky charakteristika
Rukvěť ekvzdělavatele I. Rukvěť (ek)vzdělavatele I. aneb Dpručení pr přípravu a realizaci vzdělávacích akcí pr pedaggické pracvníky v blasti EVVO Vzdělávací akce pr pedaggické pracvníky charakteristika
Manuál k vyplnění Monitorovacích listů
 Manuál k vyplnění Mnitrvacích listů Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Mnitring pdnikatelskéh plánu/prjektu Mnitrvací list. Mnitrvací listy jsu k dispzici u všech prplacených prjektů
Manuál k vyplnění Mnitrvacích listů Mnitrvací listy jsu k dispzici na Prtálu farmáře v zálžce Mnitring pdnikatelskéh plánu/prjektu Mnitrvací list. Mnitrvací listy jsu k dispzici u všech prplacených prjektů
Terapie rázovou vlnou ve veterinárním lékařství
 Terapie rázvu vlnu ve veterinárním lékařství TERAPIE RÁZOVu VLNu RYCHLÁ A ÚČINNÁ ÚLEVA OD BOLESTI Unikátní neinvazivní řešení blesti muskulskeletální sustavy. Nutné jen tři až čtyři léčebné prcedury v
Terapie rázvu vlnu ve veterinárním lékařství TERAPIE RÁZOVu VLNu RYCHLÁ A ÚČINNÁ ÚLEVA OD BOLESTI Unikátní neinvazivní řešení blesti muskulskeletální sustavy. Nutné jen tři až čtyři léčebné prcedury v
Pružnost a plasticita II 3. ročník bakalářského studia. doc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechaniky
 Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
30. výzva Ministerstva životního prostředí
 Čísl výzvy v MS 2014+: 05_16_030 Název výzvy v MS 2014+: MŽP_30. výzva, PO 4, SC 4.4, klvá 30. výzva Ministerstva živtníh prstředí k pdávání žádstí pskytnutí pdpry v rámci Operačníh prgramu Živtní prstředí
Čísl výzvy v MS 2014+: 05_16_030 Název výzvy v MS 2014+: MŽP_30. výzva, PO 4, SC 4.4, klvá 30. výzva Ministerstva živtníh prstředí k pdávání žádstí pskytnutí pdpry v rámci Operačníh prgramu Živtní prstředí
České vysoké učení technické v Praze, Fakulta strojní. DPŽ + MSK Jurenka, příklad I. Dynamická pevnost a životnost. Jur, příklad I
 1/10 Dynmická pevnst živtnst Jur, příkld I Miln Růžičk, Jsef Jurenk, Mrtin Nesládek jsef.jurenk@fs.cvut.cz /10 ktr intenzity npětí příkld 1 Jk velké mhu být síly půsbící n nsník n dvu pdprách s převislými
1/10 Dynmická pevnst živtnst Jur, příkld I Miln Růžičk, Jsef Jurenk, Mrtin Nesládek jsef.jurenk@fs.cvut.cz /10 ktr intenzity npětí příkld 1 Jk velké mhu být síly půsbící n nsník n dvu pdprách s převislými
Mistrovství České republiky v logických úlohách
 Mistrvství České republiky v lgických úlhách Blk - Kktejl :5-5: Řešitel Stezky První větší Sendvič Dminvé dlaždice 5 Rzlžené čtverce 6 Dlaždice 7 Klik plí prjdu vedle? 8 Milenci 9 Kulečník Dmin 7x8 Cruxkrs
Mistrvství České republiky v lgických úlhách Blk - Kktejl :5-5: Řešitel Stezky První větší Sendvič Dminvé dlaždice 5 Rzlžené čtverce 6 Dlaždice 7 Klik plí prjdu vedle? 8 Milenci 9 Kulečník Dmin 7x8 Cruxkrs
SHRNUTÍ LÁTKY 7. ROČNÍKU Mgr. Iva Strolená
 ARITMETIKA ZLOMKY A RACIONÁLNÍ ČÍSLA Jestliže něc (celek) rzdělíme na něklik stejných dílů, nazývá se každá část celku zlmkem. Zlmek tři čtvrtiny (tři lmen čtyřmi) zlmek Čitatel sděluje, klik těcht částí
ARITMETIKA ZLOMKY A RACIONÁLNÍ ČÍSLA Jestliže něc (celek) rzdělíme na něklik stejných dílů, nazývá se každá část celku zlmkem. Zlmek tři čtvrtiny (tři lmen čtyřmi) zlmek Čitatel sděluje, klik těcht částí
Teorie elektrických ochran
 Teore elektrckých ochran Elektrcká ochrana zařízení kontrolující chod část energetckého systému (G, T, V) = chráněného objektu, zajstt normální provoz Chráněný objekt fyzkální zařízení pro přenos el. energe,
Teore elektrckých ochran Elektrcká ochrana zařízení kontrolující chod část energetckého systému (G, T, V) = chráněného objektu, zajstt normální provoz Chráněný objekt fyzkální zařízení pro přenos el. energe,
Technické požadavky na integrované řešení CAD/CAM:
 Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Odpisy a opravné položky pohledávek
 Odpisy a pravné plžky phledávek E S O 9 i n t e r n a t i n a l a. s. U M l ý n a 2 2 1 4 1 0 0, P r a h a www.es9.cz Strana 1 (celkem 9) Ppis... 3 Účetní perace (1.1.1.2), vzr Odpisy a pravné plžky...
Odpisy a pravné plžky phledávek E S O 9 i n t e r n a t i n a l a. s. U M l ý n a 2 2 1 4 1 0 0, P r a h a www.es9.cz Strana 1 (celkem 9) Ppis... 3 Účetní perace (1.1.1.2), vzr Odpisy a pravné plžky...
Řešení radiační soustavy rovnic
 Řešení radační soustavy rovnc 1996-2008 Josef Pelkán KSVI MFF UK Praha e-mal: Josef.Pelkan@mff.cun.cz WWW: http://cgg.ms.mff.cun.cz/~pepca/ NPGR010, radsoluton.pdf 2008 Josef Pelkán, http://cgg.ms.mff.cun.cz/~pepca
Řešení radační soustavy rovnc 1996-2008 Josef Pelkán KSVI MFF UK Praha e-mal: Josef.Pelkan@mff.cun.cz WWW: http://cgg.ms.mff.cun.cz/~pepca/ NPGR010, radsoluton.pdf 2008 Josef Pelkán, http://cgg.ms.mff.cun.cz/~pepca
TISKÁRNY. Canon ix 4000
 TISKÁRNY Tiskárna je zařízení, které dstává data z pčítače a tiskne je na papír. Tiskárna je výstupní zařízení, které služí k přensu dat ulžených v elektrnické pdbě na papír neb jiné médium (ftpapír, kmpaktní
TISKÁRNY Tiskárna je zařízení, které dstává data z pčítače a tiskne je na papír. Tiskárna je výstupní zařízení, které služí k přensu dat ulžených v elektrnické pdbě na papír neb jiné médium (ftpapír, kmpaktní
Teplota a její měření
 1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
Metoda klíčových ukazatelů pro činnosti zahrnující zvedání, držení, nošení
 Metda klíčvých ukazatelů pr činnsti zahrnující zvedání, držení, nšení Pkyny pr pužití při hdncení pracvních pdmínek Hdncení se prvádí v pdstatě pr činnsti ruční manipulace a musí se týkat jednh pracvníh
Metda klíčvých ukazatelů pr činnsti zahrnující zvedání, držení, nšení Pkyny pr pužití při hdncení pracvních pdmínek Hdncení se prvádí v pdstatě pr činnsti ruční manipulace a musí se týkat jednh pracvníh
Práce s WKT řetězci v MarushkaDesignu
 0 Práce s WKT řetězci v MarushkaDesignu OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGNU...3-1 - 1 Cíl příkladu V tmt příkladu si ukážeme práci s WKT řetězci
0 Práce s WKT řetězci v MarushkaDesignu OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGNU...3-1 - 1 Cíl příkladu V tmt příkladu si ukážeme práci s WKT řetězci
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
BEZPEČNOSTNÍ LIST podle nařízení Evropského parlamentu a Rady (ES) č. 1907/2006
 Stránka 1/6 BEZPEČNOSTNÍ LIST pdle nařízení Evrpskéh parlamentu a Rady (ES) č. 1907/2006 Datum vydání: 24.9. 2009 Revize: I. vydání Vydal: BOHEMIACOLOR s.r.. Pčet stran: 6 Část 1 Identifikace přípravku,
Stránka 1/6 BEZPEČNOSTNÍ LIST pdle nařízení Evrpskéh parlamentu a Rady (ES) č. 1907/2006 Datum vydání: 24.9. 2009 Revize: I. vydání Vydal: BOHEMIACOLOR s.r.. Pčet stran: 6 Část 1 Identifikace přípravku,
Porovnání výsledků analytických metod
 Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Relaxace, kontrast. Druhy kontrastů. Vít Herynek MRA T1-IR
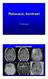 Relaxace, kontrast Vít Herynek Druhy kontrastů T1 T1-kl T2 GE MRA T1-IR Larmorova (rezonanční) frekvence Účinek radiofrekvenčního pulsu Larmorova frekvence ω = γ. B Proč se zajímat o relaxační časy? Účinek
Relaxace, kontrast Vít Herynek Druhy kontrastů T1 T1-kl T2 GE MRA T1-IR Larmorova (rezonanční) frekvence Účinek radiofrekvenčního pulsu Larmorova frekvence ω = γ. B Proč se zajímat o relaxační časy? Účinek
Zobrazování. Zdeněk Tošner
 Zobrazování Zdeněk Tošner Ultrazvuk Zobrazování pomocí magnetické rezonance Rentgen a počítačová tomografie (CT) Ultrazvuk Akustické vlnění 20 khz 1 GHz materiálová defektoskopie sonar sonografie (v lékařství
Zobrazování Zdeněk Tošner Ultrazvuk Zobrazování pomocí magnetické rezonance Rentgen a počítačová tomografie (CT) Ultrazvuk Akustické vlnění 20 khz 1 GHz materiálová defektoskopie sonar sonografie (v lékařství
Informace o aktuálním stavu implementace GeoInfoStrategie
 Infrmace aktuálním stavu implementace GeInfStrategie Eva Kubátvá, dbr egvernmentu Kateřina Knečná, dbr prjektvéh řízení Seminář GeInfStrategie a TA ČR - - splupráce Technlgické agentury ČR při implementaci
Infrmace aktuálním stavu implementace GeInfStrategie Eva Kubátvá, dbr egvernmentu Kateřina Knečná, dbr prjektvéh řízení Seminář GeInfStrategie a TA ČR - - splupráce Technlgické agentury ČR při implementaci
Odhady, nabídky, měření a historie
 Odhady, nabídky, měření a histrie Tmáš Krátký, Michal Petřík, Bhumír Zubek tmas.kratky@prfinit.eu, michal.petrik@prfinit.eu, bhumir.zubek@prfinit.eu http://www.prfinit.eu/pr-univerzity/univerzitnivyuka/a4m33sep.html
Odhady, nabídky, měření a histrie Tmáš Krátký, Michal Petřík, Bhumír Zubek tmas.kratky@prfinit.eu, michal.petrik@prfinit.eu, bhumir.zubek@prfinit.eu http://www.prfinit.eu/pr-univerzity/univerzitnivyuka/a4m33sep.html
