IV.7. Potenciální vektorové pole
|
|
|
- Vlasta Němcová
- před 9 lety
- Počet zobrazení:
Transkript
1 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 IV.7. Poteniální vektorové pole Vektorové pole f (U,V,W se nazývá poteniální pole v oblasti G E 3, jestliže eistuje skalární funke ϕ taková, že f gradϕ v oblasti G. Podobně pro vektorové pole f (U,V v oblasti G E. Skalární funki ϕ nazýváme poteniálem vektorového pole f v G. Platí následujíí tvrzení (podrobněji ve skriptu Matematika II od J. Neustup: Věta. Neht f je poteniální a spojité vektorové pole s poteniálem ϕ v oblasti G E3 (resp. E. Neht je orientovaná křivka v G s počátečním bodem A a s konovým bodem B. Pak f d s ϕ(b ϕ(a. Poznámka.Protože pro poteniální vektorové pole f závisí hodnota křivkového integrálu f d s pouze na počátečním a konovém bodě, lze v tomto případě psát B f d s f d s. A Věta. Neht f je spojité vektorové pole v oblasti G E3 (resp. E. Pak následujíí tři výrok jsou ekvivalentní: a f je poteniální pole v G. b Křivkový integrál f d s nezávisí v oblasti G na integrační estě. Cirkulae pole f po libovolné uzavřené křive v G je nulová. V dalším tetu se soustředíme především na vektorové pole v E. Věta. (Postačujíí podmínka poteniálnosti v E. Neht a G je jednoduše souvislá oblast v E a b f (U,V je vektorové pole, jehož souřadniové funke U(,,V(, mají v oblasti G spojité pariální derivae a funke U,V splňují podmínku V v G. Pak f je poteniální vektorové pole v G. Při výpočtu poteniálu zpravidla nejprve ověříme podle postačujíí podmínk, že dané vektorové pole je poteniální v oblasti G. Pro výpočet poteniálu v E pak máme několik možností. 1. metoda.poteniálurčímezdefiniepoteniálu,tzn. f gradϕ ve.takdostáváme rovnie (1 U, ( V. metoda. Poteniál určíme výpočtem křivkového integrálu. Z výše uvedené vět vplývá, že poteniál ϕ(, f d s, kde je vhodně zvolená křivka v G se zvoleným počátečním bodem, ] a konovým bodem,]. Příklad 554. Určete největší možnou oblast(i, na níž je dané vektorové pole poteniální. a f ( sin, +, b f (,
2 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 Řešení: a Souřadniové funke U, V daného pole mají spojité pariální derivae v oblasteh D 1 a D, kde D 1 {,] E ; > }, D {,] E ; < }. Vpočteme pariální derivae: V, zatímo os. Není ted splněna nutná podmínka, ab vektorové pole blo poteniální, tj. podmínka V. b Dané vektorové pole má spojité pariální derivae v oblasti D 1 a v oblasti D z úloh a. Každá z těhto oblastí je jednoduše souvislá a platí V,. Zadané vektorové pole ted splňuje výše uvedenou postačujíí podmínku a proto je poteniální v každé z oblastí D 1, D. Příklad 555. a Ověřte, že vektorové pole f (3+, 3 je poteniální v oblasti E. b Určete poteniál tohoto vektorového pole. Vpočítejte křivkový integrál f d s, kde je úsečka od bodu A 1,3] do bodu B,1]. Řešení: a Souřadniové funke U, V jsou polnom. Mají ted spojité pariální derivae v množině E, ož je oblast jednoduše souvislá. Výpočtem V, vidíme, že dané pole je poteniální v oblasti E. b Při výpočtu poteniálu podle 1. metod vjdeme ze dvou podmínek (1 3+, ( 3 Integrováním podle vpočítáme z podmínk (1: ϕ(, (3+d 3+ +K(. Takto vpočtená funke ϕ(, obsahuje neznámou funki K(. Po dosazení za ϕ do podmínk ( získáme rovnii (, ve které už nebude proměnná. To je kontrolní místo výpočtu. Derivai funke K zapíšeme ve tvaru dk d, nebot K je funke jedné proměnné. ( + dk d 3 dk d 3. Funki K( pak získáme integrováním: K( 3 d 3 +C. Po dosazení za K( obdržíme výsledný tvar poteniálu ϕ(, C,,] E, C je libovolné reálné číslo. Zadaný křivkový integrál lze vpočítat pomoí parametrizae dané úsečk. Protože však dané pole je poteniální v E, lze křivkový integrál vpočítat pomoí poteniálu: (3+, 3 d s ϕ(b ϕ(a ϕ(,1 ϕ(1,
3 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 Příklad 556. a Ověřte, že jsou splněn postačujíí podmínk poteniálnosti pro dané vektorové pole f v oblasti G E. b Určete jeho poteniál výpočtem křivkového integrálu, tj.. metodou. Vpočtěte B A (3 3, 3 6 d s, je-li A 1,3],B,1]. Řešení: a Funke U a V jsou spojité a diferenovatelné v elém E. G E je jednoduše souvislá oblast, Pak k ověření, že f je poteniální v G, stačí zjistit, zda V : V 3 6, 3 6. Ano, pole f je poteniální v E. b f ( gradϕ,,], ] f d s,], ] d+ d,],], ] dϕ ϕ (, ϕ (,. Zvolíme, ],] : ϕ(, (3 3 d+( 3 6d (,] víme, že integrál nezávisí na estě, proto zvolíme,] lomenou čáru,],],] :,],] :,d,],] : konst.,d,],],],] (3 3 d+( 3 6d + d+,1] 1,3],],] ( 3 6d 3 3 ϕ(, 3 3 +C, (3 3 d+( 3 6d f d s ϕ(,1 ϕ(1,3 (8 6 ( Příklad 557. Je dáno vektorové pole f (3, 3 +. Napište postačujíí podmínk pro to, ab křivkový integrál vektorové funke f d s nezávisel v oblasti D E na estě. Určete poteniál ϕ a užijte jej k výpočtu křivkového integrálu vektorové funke f po dané křive. a 1 je úsečka z bodu A,4] do bodu B 1,1]. b je záporně orientovaná hranie množin M {,] : +( 3 8, }. Řešení: U(, 3, V(, 3 +. Ověřte si, že pariální derivae jsou spojité a v oblasti D {,] E ; > }, která je jednoduše souvislá platí rovnost V. Výpočet poteniálu ϕ: Podmínk (1 a ( mají tvar: 118
4 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 (1 3, ( 3 + Z podmínk (1 vpočítáme ϕ(, 3 d 3 +K(. Po dosazení do (: 3 + dk d 3 +. Po úpravě získáme rovnii dk d, d ze které určíme K( 3 +C. 3 Hledaný poteniál v D je ϕ(, C. a b B A 1 M f d s (3, 3 + d s 1 1 ϕ(1,1] ϕ(,4] 17/3. Daná křivka je uzavřená. Je to obvod půlkruhu M, který leží v oblasti D, v níž je dané vektorové pole f poteniální. Z vlastnosti poteniálu pak vplývá, že irkulae daného vektorového pole f podél této křivk je rovna nule. Příklad 558. Je dáno vektorové pole f (os, sin. a Ověřte, že je pole poteniální v E. b Určete jeho poteniál ϕ. Vpočtěte f d s, kde je křivka s počátečním bodem A,] a konovým bodem B 4,π/]. Řešení: a Oblast E je jednoduše souvislá oblast a platí sin, V sin f je poteniální v E. b os ϕ(, osd os +K( sin ( sin+ dk d sin dk d K( C ϕ(, os +C. f d s ϕ(4,π/ ϕ(, 16os π 4os 4. Příklad559.Určete oblasti G E, v nihž je pole f ( 1 + 5, poteniální a stanovte jeho poteniál ϕ(,, který splňuje podmínku ϕ(,. 119
5 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 Řešení: G 1 {,] E ; >, > }, G {,] E ; <, > }, G 3 {,] E ; >, < }, G 4 {,] E ; <, < }. Platí V 1 1 +, ted je f poteniální v G i,i 1,,3,4. Výpočet poteniálu ϕ : ϕ(, 1 + 5d K( dk d K( 11+C ϕ(, C; Z podmínk ϕ(, vpočteme konstantu C: C C ϕ(, pro,] G. Příklad 56. Určete největší možnou oblast G E, v níž je vektorová funke ( f,4 spojitá a rozhodněte, zda f d s nezávisí na integrační estě v G. Pokud tato oblast eistuje, vpočtěte 4, ] 1,] f d s. Řešení: G {,] E, > } je polorovina, a ted je jednodušše souvislá oblast v E. f d s nezávisí na estě, protože pariální derivae souřadniovýh funkí U, V jsou spojité v G a platí 4, ] 1,] V eistuje poteniál ϕ. ϕ(, d +K( 4 + dk d 4 K( C f d s 4, ] 1,] ϕ(, +C (,4 d s ϕ(4, ϕ(1, 8 Příklad561.Je dána funke ϕ(, 3 +. Určete a silové pole f, jehož poteniálem je funke ϕ(,; b prái síl f při pohbu z bodu M 1,1] do bodu N,3]; prái síl f podél křivk {,] E ; +4 4}, která je orientována kladně. Řešení: a f gradϕ f (3 +, 3 + ; 1
6 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 b W N M f d s (integrál nezávisí na estě ϕ(n ϕ(m ( 4+36 (1+1 1; W f d s. Příklad56.Je dáno vektorové pole f (,+ v G E + \{,]}. a Ověřte, že platí V vg. b Výpočtem integrálu f d s, kde je záporně orientovaná kružnie S, ], r, se přesvědčte, že pole není poteniální v G. Řešení: a V + ( + (,+ b Cirkulae f d s d s + P(t ost,sint], t,π P(t ( sint,ost křivka je nesouhlasně orientovaná s parametrizaí π (ost sint,(ost+sint ( sint,ostdt 4 1 π ( 4(ost sintsint+4(ost+sintost dt 4 Pole f není poteniální, protože f d s. π 1dt π Poznámka: K výpočtu tohoto integrálu nelze použít Greenovu větu, jelikož bod,] int {,] E ; + < 4} nepatří do D( f. Příklad 563. Vpočtěte N M f d s, kde M 1,,e], N, 1,e ], víte-li, že pole f je poteniální v oblasti E 3 a jeho poteniál je funke ϕ(,,z lnz. Určete největší možnou oblast G, v níž je ϕ poteniálem pole f. Řešení: G {,,z] E 3 ;z > }; N M f d s ϕ(n ϕ(m lne 4. Je dáno vektorové pole f. Ověřte, že je pole poteniální v G E, resp. E 3, stanovte jeho poteniál a vpočtěte B A f d s : Příklad564.* f (3 z +z, 3 +z 3, z ++5, A,1,1], B 3,,], G E 3 Řešení: a K ověření stačí: 1 spojitost pariálníh derivaí funkí U(,,z, V(,,z, W(,,z v oblasti G, která je jednodušše souvislá v E 3, 11
7 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 rot f v G. i j k rot f z 3 z +z 3 +z 3 z ++5 (, z ++z,3 3 f je poteniální v E 3.,,z],,],,],,] b ϕ(,,z (3 z +zd+( 3 +z 3d +( z ++5dz z,,],,z],,z] f d s+ f d s+ f d s,,],,],,],,] :,d,z,dz,,],,] : d,z,dz,,],,z] : d,d d+ ( 3 3d + z z z +z +5z +C, 3,,],1,1] ( z ++5dz f d s ϕ(3,, ϕ(,1, f (e,( +1e, A 1,], B 3,1],,],,],,] ϕ 1 ] ( +1e +C; 5e f (3, 3, A 1,1], B, 1] ϕ 3 +C; 1] 567. f (os + +, sin +, A,7], B 1,] ϕ + +os + +C; 3] 568.* f ( z, z,z, A,,3], B 3,3,] ϕ 1 ] 3 ( z 3 z +C; * f ( +z,+1,z +, A,1,1 ],B 3,,] 57.* f ( + +1, ϕ + +z +z +C; 13] + +1,z, A 1,,], B,1,1] ϕ 1 ] ln( + +1+z +C; Ověřte, že pole f (, je poteniální v E. Stanovte poteniál ϕ(,, splňujíí ϕ( 4,3 9. ϕ +7] 57.* Stanovte poteniál pole f ( z, z +,z na G E z 3 : >, z >. ϕ + z +z +C ] 1
8 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II ( Najděte prái silového pole f, jehož poteniálem je funke ϕ(, artg při pohbu a z bodu M 1, 3] do bodu N, ] ; b podél křivk {,] E ; ( + 1} v kladném směru. a π ] 1, b Vpočtěte : ,],1] π/6,1] π/4,] d d sind+(1 osd 3, integrál nezávisí na estě ] 3 ] 576. (+d+(+d, : + a ] Určete oblasti G, v nihž je vektorové pole f poteniální a stanovte poteniál : 577. f ( 3 +, + 4 G, f není poteniální] 578. f 579.* f (ln e e, + ( z, z,ln( + 1 z G 1 E : >, > G E : >, < ϕ e +ln +C G E 3 : >, z > ϕ zln( + z +C ] Je dáno vektorové pole f (U,V a křivka. a Pomoí křivkového integrálu vektorové funke vpočítejte prái, kterou vkoná síla f působením po křive. b Ověřte, že vektorové pole f (U,V je poteniální v E. Určete poteniál ϕ tohoto pole a pomoí něho ověřte výsledek z úloh a. 58. f (+3, 3, jeorientovanáúsečkaspočátečnímbodema,1]akonovým] bodem B 1,3] a19/ ϕ(, /+3 +C 581. f (,, je část parabol s počátečním bodem A,] a konovým] bodem B,4] 58. f (,3, {,] E ; 1} od bodu 1;] do bodu 5; ] a3 ϕ(, +C a38 ϕ(, +3 +C 583. f (,, {,] E ; + 4} od bodu A,] do bodu B,] a a Vsvětlete, o to znamená, že integrál ϕ(, /+ /+C f d s nezávisí v oblasti G E na integrační estě. b Zdůvodněte, zda ( sin, os ds nezávisí v E na integrační estě. Eistuje-lipoteniálpole f ( sin, os ve,najdětejejavpočítejte ] ] 13
9 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (16 křivkový integrál tohoto pole po křive s počátečním bodem A,] a konovým bodem B,π]. ] bověřte splnění postačujíí podmínk, ϕ(, / os+c, π / π Je dána skalární funke ϕ(,,z, která je poteniálem nějakého vektorového pole f. a Určete největší oblast v E 3, ve které má ϕ spojité pariální derivae a vjádřete v této oblasti pole f. b Je-li ještě nějaká jiná funke poteniálem f v této oblasti, pak ji uved te. Vpočítejte křivkový integrál f d s pro danou křivku ϕ(,,z 1 ln( + +z ; je křivka v G s počátečním bodem 1,,] a konovým bodem,1,1] ϕ(,,z +z+z; } pro t,4 ag {,,z] E 3; + > } b f(,,z ( +, +, z 1 {,,z] : 1+t, + t, z os ( tπ 4 ae 3, funkeϕ+c b f ( +z, +z, +, Je dáno vektorové pole f (U,V, oblast D a křivka. a Napište postačujíí podmínk pro to, ab vektorové pole f (U,V blo poteniální v oblasti D E. b Ověřte, že postačujíí podmínk poteniálnosti jsou splněn pro dané vektorové pole f a danou oblast D (není-li oblast D dána, uved te největší možnou. Určete poteniál a užijte jej k výpočtu křivkového integrálu vektorové funke f po dané křive f ( +,, D {,] E + ; >, > }, je úsečka AB s počátečním bodem A,4] a konovým bodem B 1,] ϕ(, f ( +,, D {,] E + ; > }, je kladně orientovaná ln( + +C; ln ] ϕ(, artg +C; ] kružnie ( 1 +( f (, + 1, D {,] E ; > }, je křivka s poč. bodem A,1] a kon. bodem B 1,] 59. f ( +, ln os, je křivka s počátečním bodem A 1,π/4] a konovým bodem B ;] ϕ(, + +C; ] ϕ(, 3 /3+ ln sin/+c; 17/6 ] 14
(k 1)x k + 1. pro k 1 a x = 0 pro k = 1.
 . Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
. Funkce dvou a více proměnných. Úvod. Určete definiční obor funkce a proveďte klasifikaci bodů z R vzhledem k a rozhodněte zda je množina uzavřená či otevřená. Určete a načrtněte vrstevnice grafu funkce
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Výrazy lze též zavést v nečíselných oborech, pak konstanty označuji jeden určitý prvek a obor proměnné není množina čísel.
 Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Lineární algebra. Vektorové prostory
 Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
Definice 6.2.1. z = f(x,y) vázané podmínkou g(x,y) = 0 jsou z geometrického hlediska lokálními extrémy prostorové křivky k, Obr. 6.2.1. Obr. 6.2.
 Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
U dx+v dy = y. f = (2x+3y,5x y 4) po obvodu ABC ve směru A B C, kde A = [1,0],B = [1, 3], C = [ 3,0].
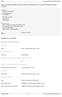
![U dx+v dy = y. f = (2x+3y,5x y 4) po obvodu ABC ve směru A B C, kde A = [1,0],B = [1, 3], C = [ 3,0]. U dx+v dy = y. f = (2x+3y,5x y 4) po obvodu ABC ve směru A B C, kde A = [1,0],B = [1, 3], C = [ 3,0].](/thumbs/49/25334309.jpg) E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (6) IV.6. Greenova věta Křivkový integrál vektorového pole po uzavřené křive nazýváme irkulaí vektorového pole f po křive a zapisujeme
E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (6) IV.6. Greenova věta Křivkový integrál vektorového pole po uzavřené křive nazýváme irkulaí vektorového pole f po křive a zapisujeme
Rostislav Horčík. 13. října 2006
 3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
Numerická integrace. 6. listopadu 2012
 Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
Numerická integrace Michal Čihák 6. listopadu 2012 Výpočty integrálů v praxi V přednáškách z matematické analýzy jste se seznámili s mnoha metodami výpočtu integrálů. V praxi se ale poměrně často můžeme
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY
 Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Gymnázium, Praha 10, Voděradská 2 Projekt OBZORY INDIVIDUÁLNÍ VÝUKA Matematika METODIKA Soustavy rovnic Mgr. Marie Souchová květen 2011 Tato část učiva následuje po kapitole Rovnice. Je rozdělena do částí
Analytická geometrie (3. - 4. lekce)
 Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
Analytická geometrie (3. - 4. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 16. června 2011 Příklad 1 Příklad 1. Algebraicky
1 Měření kapacity kondenzátorů
 . Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
. Zadání úlohy a) Změřte kapacitu kondenzátorů, 2 a 3 LR můstkem. b) Vypočítejte výslednou kapacitu jejich sériového a paralelního zapojení. Hodnoty kapacit těchto zapojení změř LR můstkem. c) Změřte kapacitu
Věty o pravoúhlém trojúhelníku. Vztahy pro výpočet obvodu a obsahu. Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu
 Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
Jan Březina. Technical University of Liberec. 17. března 2015
 TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
Hra a hry. Václav Vopravil. Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována R },
 Hra a hry Václav Vopravil Úvod 1 Kombinatorické hry Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována pomocí jednodušších her, tj. jako uspořádaná dvojice množin her.
Hra a hry Václav Vopravil Úvod 1 Kombinatorické hry Teorie kombinatorických her se zabývá abstraktními hrami dvou hráčů. Hra je definována pomocí jednodušších her, tj. jako uspořádaná dvojice množin her.
10.1.13 Asymptoty grafu funkce
 .. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
.. Asmptot grafu funkce Předpoklad:, Asmptot grafu už známe kreslili jsme si je jako přímk, ke kterým se graf funkce přibližuje. Nakreslení asmptot, pak umožňuje přesnější kreslení grafu. Například u hperbol
2.3.19 Grafické řešení soustav lineárních rovnic a nerovnic
 .3.19 Grafické řešení soustav lineárních rovnic a nerovnic Předpoklad: 307, 311 Př. 1: Vřeš soustavu rovnic + =. Pokud se také o grafické řešení. = 5 Tak jednoduchou soustavu už jsme dlouho neměli: + =
.3.19 Grafické řešení soustav lineárních rovnic a nerovnic Předpoklad: 307, 311 Př. 1: Vřeš soustavu rovnic + =. Pokud se také o grafické řešení. = 5 Tak jednoduchou soustavu už jsme dlouho neměli: + =
IRACIONÁLNÍ ROVNICE. x /() 2 (umocnění obou stran rovnice na druhou) 2x 4 9 /(-4) (ekvivalentní úpravy) Motivace: Teorie: Řešené úlohy:
 IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
IRACIONÁNÍ ROVNICE Motivace: V řadě matematických úloh je nutno ovládat práci s odmocninami a rovnicemi, které obsahují neznámou pod odmocninou, mj. při vyjádření neznámé z technických vzorců. Znalosti
Konzultace z předmětu MATEMATIKA pro první ročník dálkového studia
 - - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
- - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
Goniometrie trigonometrie
 Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
Goniometrie trigonometrie Goniometrie se zabývá funkcemi sinus, kosinus, tangens, kotangens (goniometrické funkce). V tomto článku se budeme zabývat trigonometrií (součást goniometrie) používáním goniometrických
7. Silně zakřivený prut
 7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
7. Silně zakřivený prut 2011/2012 Zadání Zjistěte rozložení napětí v průřezu silně zakřiveného prutu namáhaného ohybem analyticky a experimentálně. Výsledky ověřte numerickým výpočtem. Rozbor Pruty, které
2.6.4 Lineární lomené funkce s absolutní hodnotou
 .6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
.6. Lineární lomené funkce s absolutní hodnotou Předpoklady: 60, 603 Pedagogická poznámka: Hlavním cílem hodiny je nácvik volby odpovídajícího postupu. Proto je dobré nechat studentům chvíli, aby si metody
Orientovaná úseka. Vektory. Souadnice vektor
 Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení)
 KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
KVADRATICKÉ ROVNICE A NEROVNICE (početní a grafická řešení) KVADRATICKÉ ROVNICE (početně) Teorie: Kvadratická rovnice o jedné neznámé se nazývá každá taková rovnice, kterou lze ekvivalentními úpravami
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Druhá mocnina. Druhá odmocnina. 2.8.5 Druhá odmocnina. Předpoklady: 020804. V této hodině jsou kalkulačky zakázány.
 .8.5 Druhá odmocnina Předpoklady: 0080 V této hodině jsou kalkulačky zakázány. Druhá mocnina nám umožňuje určit z délky strany plochu čtverce. Druhá mocnina 1 1 9 11 81 11 délky stran čtverců obsahy čtverců
.8.5 Druhá odmocnina Předpoklady: 0080 V této hodině jsou kalkulačky zakázány. Druhá mocnina nám umožňuje určit z délky strany plochu čtverce. Druhá mocnina 1 1 9 11 81 11 délky stran čtverců obsahy čtverců
MODEL MOSTU. Ing.Jiřina Strnadová. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti. Předmět:Fyzika
 MODEL MOSTU Ing.Jiřina Strnadová Předmět:Fyzika Praha a EU Investujeme do vaší budoucnosti Model mostu Teoretický úvod: Příhradové nosníky (prutové soustavy) jsou složené z prutů, které jsou vzájemně spojené
MODEL MOSTU Ing.Jiřina Strnadová Předmět:Fyzika Praha a EU Investujeme do vaší budoucnosti Model mostu Teoretický úvod: Příhradové nosníky (prutové soustavy) jsou složené z prutů, které jsou vzájemně spojené
Pokusy s kolem na hřídeli (experimenty s výpočty)
 Zvyšování kvality výuky v přírodních a technických oblastech CZ.1.07/1.1.28/02.0055 Pokusy s kolem na hřídeli (experimenty s výpočty) Označení: EU-Inovace-F-7-08 Předmět: fyzika Cílová skupina: 7. třída
Zvyšování kvality výuky v přírodních a technických oblastech CZ.1.07/1.1.28/02.0055 Pokusy s kolem na hřídeli (experimenty s výpočty) Označení: EU-Inovace-F-7-08 Předmět: fyzika Cílová skupina: 7. třída
SMĚŠOVACÍ KALORIMETR -tepelně izolovaná nádoba s míchačkou a teploměrem, která je naplněná kapalinou
 KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
KALORIMETRIE Kalorimetr slouží k měření tepla, tepelné kapacity, případně měrné tepelné kapacity Kalorimetrická rovnice vyjadřuje energetickou bilanci při tepelné výměně mezi kalorimetrem a tělesy v kalorimetru.
Kružnice. Kruh. Kruh K(S; r) je množina všech bodů roviny, které mají. od zadaného bodu S, vzdálenost r. Bod S je střed, r je poloměr kružnice.
 Kružnice Kružnice k(s; r) je množina všech bodů roviny, které mají d od zadaného bodu S, vzdálenost r. Bod S je střed, r je poloměr kružnice. S r Délka spojnice dvou bodů kružnice, která prochází středem
Kružnice Kružnice k(s; r) je množina všech bodů roviny, které mají d od zadaného bodu S, vzdálenost r. Bod S je střed, r je poloměr kružnice. S r Délka spojnice dvou bodů kružnice, která prochází středem
Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu.
 Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Svarové spoje Posouzení únosnosti svaru se provádí podle zásad pružnosti a pevnosti v nebezpečném průřezu. Vybrané druhy svarů a jejich posouzení dle EN ČSN 1993-1-8. Koutový svar -T-spoj - přeplátovaný
Digitální učební materiál
 Digitální učební materiál Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.057 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
Digitální učební materiál Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.057 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
( ) ( ) 7.2.2 Sčítání vektorů. Předpoklady: 7201
 7.. Sčítání ektorů Předpoklady: 70 Pedagogická poznámka: Stdenti ětšino necítí potřeb postpoat při definici sčítání ektorů (obecně při zaádění jakékoli operace) tak striktně, jak yžadje matematika. Upozorňji
7.. Sčítání ektorů Předpoklady: 70 Pedagogická poznámka: Stdenti ětšino necítí potřeb postpoat při definici sčítání ektorů (obecně při zaádění jakékoli operace) tak striktně, jak yžadje matematika. Upozorňji
( x ) 2 ( ) 2.5.4 Další úlohy s kvadratickými funkcemi. Předpoklady: 2501, 2502
 .5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
.5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor013 Vypracoval(a),
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu CZ.1.07/1.5.00/34.0218 Šablona III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Hor013 Vypracoval(a),
Novinky v programu Majetek 2.06
 Novinky v programu Majetek 2.06 Možnost použít zvětšené formuláře program Majetek 2.06 je dodávám s ovládacím programem ProVIS 1.58, který umožňuje nastavit tzv. Zvětšené formuláře. Znamená to, že se formuláře
Novinky v programu Majetek 2.06 Možnost použít zvětšené formuláře program Majetek 2.06 je dodávám s ovládacím programem ProVIS 1.58, který umožňuje nastavit tzv. Zvětšené formuláře. Znamená to, že se formuláře
EHLED OSV za rok 2015 vykonávajících pouze hlavní SV
 Zadání pro programátory ehled o p íjmech a výdajích OSV za rok 2015 N_OSVC lokální aplikace ehled o p íjmech a výdajích OSV za rok 2015 Údaje P ehledu 2015 Dle FU(kont): Oznámil da. p.: M l podat na FU:
Zadání pro programátory ehled o p íjmech a výdajích OSV za rok 2015 N_OSVC lokální aplikace ehled o p íjmech a výdajích OSV za rok 2015 Údaje P ehledu 2015 Dle FU(kont): Oznámil da. p.: M l podat na FU:
4 Soustavy lineárních rovnic
 4 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic, to znamená několika lineárními rovnicemi, které musí být současně splněny. 4.1 Základní pojmy Definice Soustavu
4 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic, to znamená několika lineárními rovnicemi, které musí být současně splněny. 4.1 Základní pojmy Definice Soustavu
2.7.15 Rovnice s neznámou pod odmocninou I
 .7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte můžete obětovat hodiny dvě a nechat
.7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte můžete obětovat hodiny dvě a nechat
1) Určete ohniskové vzdálenosti čoček, jsou-li jejich optické mohutnosti 2 D, 16 D, - 4 D, - 12 D.
 ČOČKY ) Určete ohniskové vzdálenosti čoček, jsou-li jejich optické mohutnosti 2 D, 6 D, - 4 D, - 2 D. φ = 2 D φ 2 = 6 D φ = 4 D φ = 2 D f 4 =? (m) Optická mohutnost je převrácená hodnota ohniskové vzdálenosti
ČOČKY ) Určete ohniskové vzdálenosti čoček, jsou-li jejich optické mohutnosti 2 D, 6 D, - 4 D, - 2 D. φ = 2 D φ 2 = 6 D φ = 4 D φ = 2 D f 4 =? (m) Optická mohutnost je převrácená hodnota ohniskové vzdálenosti
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE
 MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
MS Word 2007 REVIZE DOKUMENTU A KOMENTÁŘE 1 ZAPNUTÍ SLEDOVÁNÍ ZMĚN Pokud zapnete funkci Sledování změn, aplikace Word vloží značky tam, kde provedete mazání, vkládání a změny formátu. Na kartě Revize klepněte
Moravské gymnázium Brno s.r.o. Mgr. Věra Jeřábková, Mgr. Marie Chadimová. Matematika, Mnohoúhelníky, pokračování
 Číslo projektu CZ.1.07/1.5.00/34.0743 Název školy Moravské gymnázium Brno s.r.o. Autor Mgr. Věra Jeřábková, Mgr. Marie Chadimová Tematická oblast Matematika, Mnohoúhelníky, pokračování Ročník 2. Datum
Číslo projektu CZ.1.07/1.5.00/34.0743 Název školy Moravské gymnázium Brno s.r.o. Autor Mgr. Věra Jeřábková, Mgr. Marie Chadimová Tematická oblast Matematika, Mnohoúhelníky, pokračování Ročník 2. Datum
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
Příklad 1.3: Mocnina matice
 Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
3.1.4 Trojúhelník. Předpoklady: 3103. Každé tři různé body neležící v přímce určují trojúhelník. C. Co to je, víme. Jak ho definovat?
 3..4 Trojúhelní Předpolady: 303 Každé tři různé body neležící v přímce určují trojúhelní. o to je, víme. Ja ho definovat? Př. : Definuj trojúhelní jao průni polorovin. Trojúhelní je průni polorovin, a.
3..4 Trojúhelní Předpolady: 303 Každé tři různé body neležící v přímce určují trojúhelní. o to je, víme. Ja ho definovat? Př. : Definuj trojúhelní jao průni polorovin. Trojúhelní je průni polorovin, a.
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem
 souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
souřadné systémy geometrické určení polohy pevně spojené se vztažným tělesem kartézský souřadný systém Z Y X kartézský souřadný systém Z Y X kartézský souřadný systém Z x y Y X kartézský souřadný systém
Funkce Vypracovala: Mgr. Zuzana Kopečková
 Funkce Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů OP
Funkce Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů OP
Fyzikální praktikum 3 - úloha 7
 Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
Fyzikální praktikum 3 - úloha 7 Operační zesilovač, jeho vlastnosti a využití Teorie: Operační zesilovač je elektronická součástka využívaná v měřící, regulační a výpočetní technice. Ideální model má nekonečně
Řešení lineárních a kvadratických funkcí v prostředí programu GeoGebra
 Řešení lineárních a kvadratických funkcí v prostředí programu GeoGebra Lineární a kvadratické rovnice jsou součástí velké množiny rovnic. Jejich uplatnění je často velmi praktické, a proto je pojmu rovnice
Řešení lineárních a kvadratických funkcí v prostředí programu GeoGebra Lineární a kvadratické rovnice jsou součástí velké množiny rovnic. Jejich uplatnění je často velmi praktické, a proto je pojmu rovnice
Měřidla. Existují dva druhy měření:
 V této kapitole se seznámíte s většinou klasických druhů měřidel a se způsobem jejich použití. A co že má dělat měření na prvním místě mezi kapitolami o ručním obrábění kovu? Je to jednoduché - proto,
V této kapitole se seznámíte s většinou klasických druhů měřidel a se způsobem jejich použití. A co že má dělat měření na prvním místě mezi kapitolami o ručním obrábění kovu? Je to jednoduché - proto,
matematika vás má it naupravidl
 VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
2.8.8 Kvadratické nerovnice s parametrem
 .8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
.8.8 Kvadratické nerovnice s arametrem Předoklady: 806 Pedagogická oznámka: Z hlediska orientace v tom, co studenti očítají, atří tato hodina určitě mezi nejtěžší během celého středoškolského studia. Proto
Provozní deník jakosti vody
 Provozní deník jakosti vody Pro zdroje tepla z hliníku Pro odbornou firmu Logamax plus GB162 Logano plus GB202 Logano plus GB312 Logano plus GB402 Před montáží a údržbou pečlivě pročtěte. 6 720 642 944
Provozní deník jakosti vody Pro zdroje tepla z hliníku Pro odbornou firmu Logamax plus GB162 Logano plus GB202 Logano plus GB312 Logano plus GB402 Před montáží a údržbou pečlivě pročtěte. 6 720 642 944
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_3_12 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_3_12 ŠVP Podnikání RVP 64-41-L/51
Univerzita Tomáše Bati ve Zlíně
 Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ ELEKTROTECHNIKY A PRŮMYSLOVÉ ELEKTRONIKY Název úlohy: pracovali: Měření činného výkonu střídavého proudu v jednofázové síti wattmetrem Petr Luzar, Josef
Měření základních vlastností OZ
 Měření základních vlastností OZ. Zadání: A. Na operačním zesilovači typu MAA 74 a MAC 55 změřte: a) Vstupní zbytkové napětí U D0 b) Amplitudovou frekvenční charakteristiku napěťového přenosu OZ v invertujícím
Měření základních vlastností OZ. Zadání: A. Na operačním zesilovači typu MAA 74 a MAC 55 změřte: a) Vstupní zbytkové napětí U D0 b) Amplitudovou frekvenční charakteristiku napěťového přenosu OZ v invertujícím
Úloha 2 Tepelný odpor a vrstvená konstrukce
 SF Podklady pro cvičení Úloha Tepelný odpor a vrstvená konstrukce Ing. Kamil Staněk 10/010 kamil.stanek@fsv.cvut.cz 1 Tepelný odpor 1.1 Tepelný odpor materiálové vrstvy Tepelný odpor materiálové vrstvy
SF Podklady pro cvičení Úloha Tepelný odpor a vrstvená konstrukce Ing. Kamil Staněk 10/010 kamil.stanek@fsv.cvut.cz 1 Tepelný odpor 1.1 Tepelný odpor materiálové vrstvy Tepelný odpor materiálové vrstvy
1. LINEÁRNÍ APLIKACE OPERAČNÍCH ZESILOVAČŮ
 1. LNEÁNÍ APLKACE OPEAČNÍCH ZESLOVAČŮ 1.1 ÚVOD Cílem laboratorní úlohy je seznámit se se základními vlastnostmi a zapojeními operačních zesilovačů. Pro získání teoretických znalostí k úloze je možno doporučit
1. LNEÁNÍ APLKACE OPEAČNÍCH ZESLOVAČŮ 1.1 ÚVOD Cílem laboratorní úlohy je seznámit se se základními vlastnostmi a zapojeními operačních zesilovačů. Pro získání teoretických znalostí k úloze je možno doporučit
M - Příprava na čtvrtletní písemnou práci
 M - Příprava na čtvrtletní písemnou práci Určeno pro třídu 1ODK. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na čtvrtletní písemnou práci Určeno pro třídu 1ODK. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
Nerovnosti s podmínkou
 Nerovnosti s podmínkou Michael Majkl Bílý ØÖ ØºMnohonerovnostímáusebeještětakzvanouomezujícípodmínku.Příspěvek se zabývá metodami řešení právě takových nerovností od těch základních až po některé pokročilé.
Nerovnosti s podmínkou Michael Majkl Bílý ØÖ ØºMnohonerovnostímáusebeještětakzvanouomezujícípodmínku.Příspěvek se zabývá metodami řešení právě takových nerovností od těch základních až po některé pokročilé.
Technický popis koncovky výfukového systému vozu Mercedes Econic 1833LL:
 Všeobecný popis: Cílem je vyřešit provedení odsávacího systému na stanicích HZS MSK opravou stávajícího stavu, v souladu s aktuálními požadavky na tento systém celkem pro 5 ks používaných vozidel CAS 20
Všeobecný popis: Cílem je vyřešit provedení odsávacího systému na stanicích HZS MSK opravou stávajícího stavu, v souladu s aktuálními požadavky na tento systém celkem pro 5 ks používaných vozidel CAS 20
Algoritmizace a programování
 Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
M-10. AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km. V následující tabulce je závislost doby
 M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
M-10 Jméno a příjmení holka nebo kluk * Třída Datum Škola AU = astronomická jednotka = vzdálenost Země-Slunce = přibližně 150 mil. km V následující tabulce je závislost doby a/au T/rok oběhu planety (okolo
Zadávací dokumentace dle ustanovení 44 zákona č. 137/2006 Sb., o veřejných zakázkách (dále jen zákon )
 Vyřizuje: Milena Pecnová Telefon: 267 994 541 Fax: 272 936 383 E-mail: milena.pecnova@sfzp.cz Zadávací dokumentace dle ustanovení 44 zákona č. 137/2006 Sb., o veřejných zakázkách (dále jen zákon ) Název
Vyřizuje: Milena Pecnová Telefon: 267 994 541 Fax: 272 936 383 E-mail: milena.pecnova@sfzp.cz Zadávací dokumentace dle ustanovení 44 zákona č. 137/2006 Sb., o veřejných zakázkách (dále jen zákon ) Název
Lokální a globální extrémy funkcí jedné reálné proměnné
 Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
Téma 9 Těžiště Těžiště rovinných čar Těžiště jednoduchých rovinných obrazců Těžiště složených rovinných obrazců
 Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO POHYBY TUHÉHO TĚLESA
 Předmět: Ročník: Vytvořil: Datum: YZIKA PRVNÍ MGR. JÜTTNEROVÁ 29. 0. 202 Název zpracovaného celku: MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO Budeme uvažovat takové pohyby tělesa, při nichž nelze zanedbat
Předmět: Ročník: Vytvořil: Datum: YZIKA PRVNÍ MGR. JÜTTNEROVÁ 29. 0. 202 Název zpracovaného celku: MECHANIKA TUHÉHO TĚLESA POJEM TUHÉ TĚLESO Budeme uvažovat takové pohyby tělesa, při nichž nelze zanedbat
Vítězslav Bártl. prosinec 2013
 VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
VY_32_INOVACE_VB09_ČaP Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, vzdělávací obor, tematický okruh, téma Anotace Vítězslav
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1. Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Uživatelská nastavení parametrických modelářů, využití
Komora auditorů České republiky. Opletalova 55, 110 00 Praha 1. volební řád sněmu
 Komora auditorů České republiky Opletalova 55, 110 00 Praha 1 volební řád sněmu Komory auditorů České republiky Praha, prosinec 2015 Komora auditorů ČR prosinec 2015 VOLEBNÍ ŘÁD SNĚMU KOMORY AUDITORŮ ČESKÉ
Komora auditorů České republiky Opletalova 55, 110 00 Praha 1 volební řád sněmu Komory auditorů České republiky Praha, prosinec 2015 Komora auditorů ČR prosinec 2015 VOLEBNÍ ŘÁD SNĚMU KOMORY AUDITORŮ ČESKÉ
1.4.1 Výroky. Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pravdivé
 1.4.1 Výroky Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pradié Číslo π je iracionální. pradiý ýrok Ach jo, zase matika. není ýrok V rozrhu máme deset hodin matematiky týdně.
1.4.1 Výroky Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pradié Číslo π je iracionální. pradiý ýrok Ach jo, zase matika. není ýrok V rozrhu máme deset hodin matematiky týdně.
( ) ( ) 9.2.12 Podmíněné pravděpodobnosti I. Předpoklady: 9207
 9.. Podmíněné pravděpodobnosti I Předpoklady: 907 Pedagogická poznámka: Podmíněné pravděpodobnosti se často vynechávají jako velmi těžké a nepochopitelné učivo. Moje zkušenosti ukazují, že situace není
9.. Podmíněné pravděpodobnosti I Předpoklady: 907 Pedagogická poznámka: Podmíněné pravděpodobnosti se často vynechávají jako velmi těžké a nepochopitelné učivo. Moje zkušenosti ukazují, že situace není
Základní škola Fr. Kupky, ul. Fr. Kupky 350, 518 01 Dobruška 5.2 MATEMATIKA A JEJÍ APLIKACE - 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 9.
 5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 9. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M9101 provádí početní operace
5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 9. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M9101 provádí početní operace
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: Název projektu školy: Šablona III/2: CZ.1.07/1.5.00/34.0536 Výuka s ICT na SŠ obchodní České
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: Název projektu školy: Šablona III/2: CZ.1.07/1.5.00/34.0536 Výuka s ICT na SŠ obchodní České
Matematika pro 9. ročník základní školy
 Matematika pro 9. ročník základní školy Řešení Ćíselné výrazy 1. Prvočíslo je přirozené číslo, které je beze zbytku dělitelné právě dvěma různými přirozenými čísly, a to číslem jedna a sebou samým (tedy
Matematika pro 9. ročník základní školy Řešení Ćíselné výrazy 1. Prvočíslo je přirozené číslo, které je beze zbytku dělitelné právě dvěma různými přirozenými čísly, a to číslem jedna a sebou samým (tedy
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu
MATEMATIKA DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. Časový limit pro řešení didaktického testu
1) Vypočítej A) 32 B) 44 C) 48 D) 56. 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 A) 12 B) 13 C) 14 D) 15
 Varianta A 4 4 4 4 4 4 4 4 1) Vypočítej A) 32 B) 44 C) 48 D) 56 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 20 120 A. A) 12 B) 13 C) 14 D) 15 3) Najdi největší a nejmenší trojciferné číslo skládající
Varianta A 4 4 4 4 4 4 4 4 1) Vypočítej A) 32 B) 44 C) 48 D) 56 2) Urči číslo, které se skrývá za A ve výpočtu: 8 5 20 120 A. A) 12 B) 13 C) 14 D) 15 3) Najdi největší a nejmenší trojciferné číslo skládající
5.2.3 Kolmost přímek a rovin I
 5.2.3 Kolmost římek rovin I ředokldy: 5202 vě římky jsou k soě kolmé rávě tehdy, když jejich odchylk je 90. Nvzájem kolmé mohou ýt i mimoěžky. vě úsečky jsou kolmé, rávě když leží n kolmých římkách. íšeme:
5.2.3 Kolmost římek rovin I ředokldy: 5202 vě římky jsou k soě kolmé rávě tehdy, když jejich odchylk je 90. Nvzájem kolmé mohou ýt i mimoěžky. vě úsečky jsou kolmé, rávě když leží n kolmých římkách. íšeme:
ZADÁVACÍ DOKUMENTACE
 ZADÁVACÍ DOKUMENTACE dle Pravidel, kterými se stanovují podmínky pro poskytování dotace na projekty PRV ČR na období 2007-2013, Opatření IV.1.2 Realizace místní rozvojové strategie Název veřejné zakázky
ZADÁVACÍ DOKUMENTACE dle Pravidel, kterými se stanovují podmínky pro poskytování dotace na projekty PRV ČR na období 2007-2013, Opatření IV.1.2 Realizace místní rozvojové strategie Název veřejné zakázky
Komentář k datovému standardu a automatizovaným kontrolám obsahu F_ODPRZ_BAT
 Komentář k datovému standardu a automatizovaným kontrolám obsahu F_ODPRZ_BAT Ohlašovací povinnost: Roční zpráva zpětného odběru baterií a akumulátorů Formulář: F_ ODPRZ_BAT Dle příslušné legislativy: Příloha
Komentář k datovému standardu a automatizovaným kontrolám obsahu F_ODPRZ_BAT Ohlašovací povinnost: Roční zpráva zpětného odběru baterií a akumulátorů Formulář: F_ ODPRZ_BAT Dle příslušné legislativy: Příloha
B Kvantitativní test. Semestrální práce TUR. Novotný Michal novotm60@fel.cvut.cz
 B Kvantitativní test Semestrální práce TUR Novotný Michal novotm60@fel.cvut.cz OBSAH 1. Úvod... 2 1.1. Předmět testování... 2 1.2. Cílová skupina... 2 2. Testování... 2 2.1. Nulová hypotéza... 2 2.2. Metoda
B Kvantitativní test Semestrální práce TUR Novotný Michal novotm60@fel.cvut.cz OBSAH 1. Úvod... 2 1.1. Předmět testování... 2 1.2. Cílová skupina... 2 2. Testování... 2 2.1. Nulová hypotéza... 2 2.2. Metoda
Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace:
 Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace: 1. na str. 3 požadujete: Volání a SMS mezi zaměstnanci zadavatele zdarma bez paušálního poplatku za tuto službu. Tento požadavek
Dne 12. 7. 2010 obdržel zadavatel tyto dotazy týkající se zadávací dokumentace: 1. na str. 3 požadujete: Volání a SMS mezi zaměstnanci zadavatele zdarma bez paušálního poplatku za tuto službu. Tento požadavek
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Průniky rotačních ploch
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Průniky rotačních ploch Vypracoval: Vojtěch Trnka Třída: 8. M Školní rok: 2012/2013 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Průniky rotačních ploch Vypracoval: Vojtěch Trnka Třída: 8. M Školní rok: 2012/2013 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
Výzva k podání nabídky včetně zadávací dokumentace na veřejnou zakázku malého rozsahu
 Výzva k podání nabídky včetně zadávací dokumentace na veřejnou zakázku malého rozsahu Zadavatel Úřední název zadavatele: Česká školní inspekce IČO: 00638994 Sídlo/místo podnikání: Fráni Šrámka 37 150 21
Výzva k podání nabídky včetně zadávací dokumentace na veřejnou zakázku malého rozsahu Zadavatel Úřední název zadavatele: Česká školní inspekce IČO: 00638994 Sídlo/místo podnikání: Fráni Šrámka 37 150 21
Výzva k podání cenové nabídky
 Město Oslavany náměstí 13. prosince 2 664 12 Oslavany IČ: 00282286 Výzva k podání cenové nabídky Město Oslavany ve smyslu 18 odst. 3 zákona č. 137/2006 Sb. o veřejných zakázkách, Vás za účelem zjištění
Město Oslavany náměstí 13. prosince 2 664 12 Oslavany IČ: 00282286 Výzva k podání cenové nabídky Město Oslavany ve smyslu 18 odst. 3 zákona č. 137/2006 Sb. o veřejných zakázkách, Vás za účelem zjištění
Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X se nazývá obraz.
 7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
1.2.5 Reálná čísla I. Předpoklady: 010204
 .2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
.2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
Kótování na strojnických výkresech 1.část
 Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
10 je 0,1; nebo taky, že 256
 LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
Řeší parametry kaskády (obvodu složeného ze sériově řazených bloků)
 Kaskádní syntéza Kaskádní syntéza Řeší parametry kaskády (obvodu složeného ze sériově řazených bloků) Šumové číslo (N) Dynamický rozsah (I) Bod zahrazeni produkty třetího řádu Dynamický rozsah bez produktů
Kaskádní syntéza Kaskádní syntéza Řeší parametry kaskády (obvodu složeného ze sériově řazených bloků) Šumové číslo (N) Dynamický rozsah (I) Bod zahrazeni produkty třetího řádu Dynamický rozsah bez produktů
VY_62_INOVACE_VK53. Datum (období), ve kterém byl VM vytvořen Květen 2012 Ročník, pro který je VM určen
 VY_62_INOVACE_VK53 Jméno autora výukového materiálu Věra Keselicová Datum (období), ve kterém byl VM vytvořen Květen 2012 Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace 9. ročník
VY_62_INOVACE_VK53 Jméno autora výukového materiálu Věra Keselicová Datum (období), ve kterém byl VM vytvořen Květen 2012 Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace 9. ročník
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ mechanismy. Přednáška 8
 Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ mechanismy Přednáška 8 Převody s korigovanými ozubenými koly Obsah Převody s korigovanými ozubenými koly Výroba ozubení odvalováním
Novinky verze ArCon 14 Small Business
 Novinky verze ArCon 14 Small Business Windows 7 Struktura souborů ArCon 14 Small Business je již optimalizována pro operační systém Windows 7 a nové typy procesorů Intel. Uživatelské prostředí Uživatelské
Novinky verze ArCon 14 Small Business Windows 7 Struktura souborů ArCon 14 Small Business je již optimalizována pro operační systém Windows 7 a nové typy procesorů Intel. Uživatelské prostředí Uživatelské
ZEMNÍ ODPOR ZEMNIČE REZISTIVITA PŮDY
 Katedra elektrotechniky Fakulta elektrotechniky a informatiky, VŠB TU Ostrava ZEMNÍ ODPOR ZEMNIČE REZISTIVITA PŮDY Návody do měření Září 2009 Ing. Tomáš Mlčák, Ph.D. Měření zemního odporu zemniče Úkol
Katedra elektrotechniky Fakulta elektrotechniky a informatiky, VŠB TU Ostrava ZEMNÍ ODPOR ZEMNIČE REZISTIVITA PŮDY Návody do měření Září 2009 Ing. Tomáš Mlčák, Ph.D. Měření zemního odporu zemniče Úkol
ZADÁNÍ: ÚVOD: SCHÉMA:
 ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
ZADÁNÍ: ) U daného síťového transformátoru vyhodnoťte osciloskopickou metodou ze zobrazení hysterezní smyčky hlavní magnetické vlastnosti jádra - H MAX,H 0,B r při B MAX T. 2) Ze zjištěného průběhu hysterezní
KOMPLEXNÍ ČÍSLA (druhá část)
 KOMPLEXNÍ ČÍSLA (druhá část) V prví kaptole jsme se seáml s algebrackým tvarem komplexího čísla. Některé výpočty s komplexím čísly je však lépe provádět ve tvaru goometrckém. Po. V ásledujícím textu předpokládám
KOMPLEXNÍ ČÍSLA (druhá část) V prví kaptole jsme se seáml s algebrackým tvarem komplexího čísla. Některé výpočty s komplexím čísly je však lépe provádět ve tvaru goometrckém. Po. V ásledujícím textu předpokládám
