Úvod do molekulové dynamiky simulace proteinů. Eva Fadrná
|
|
|
- Vratislav Vítek
- před 9 lety
- Počet zobrazení:
Transkript
1 Úvod do molekulové dynamiky simulace proteinů Eva Fadrná
2 Molekulová mechanika = metoda silového pole = force field Energie vypočtená řešením Schrodingerovy rovnice Energie vypočtená z_empirických konstant pnutí pružin a z_atomových nábojů
3 AMBER software Assisted Model Building with Energy Refinement Amber 9 50 modulů stavba modelu, MD, free energy, TI, analýza, sander, gibbs, XleaP, mmpbsa, nmode, ptraj, Tutoriály: simulace DNA, simulace HIV-I, streptavidin-biotin komplex, Fees: Academic/non-profit/government: $400
4 Rovnice silového pole energie pnutí vazeb energie rotace vazeb (torze) energie deformace vazebných úhlů vdw energie elektrostatická energie nevazebné interakce
5 Parametry silového pole AMBER - parm94.dat (W. Cornell et all. 1995) definice atomových typů vazby úhly torze vdw poloměry
6 Hyperplocha potenciální energie = Potential Energy (hyper)surface (PES) Globální minimum tranzitní stav Lokální minimum Energie = funkce struktury Energie reakční bariéra Vzdálenost atomů A a B
7 1D plocha: E = f(torze) Hyperplocha potenciální energie (PES) 17 Energie úhel 180
8 Dimethylfosfát Energie = f (souřadnice) x souřadnice (torze) y souřadnice (torze) z... energie
9 Minimum funkce z Funkce 2 proměnných: 1. derivace v bodě x i = 0 2. derivace v bodě x i > 0 x i y x Funkce více proměnných: gradient v bodě x i... vektor 1. derivací Hessian v bodě x i... matice 2. parc. derivací
10 Minimalizace na PES Spádové metody: metoda největšího spádu (steepest descent) směr negativního gradientu v bodě x i iterativní proces: startovní bod směr pohybu? prohledání regionu konvergenční kritéria? nový bod Energie konvergence? minimum strukturní parametr
11 Konvergenční kritéria Rozdíl mezi 2 po sobě následujícími kroky: Energie rozdíl energie rozdíl ve struktuře strukturní parametr
12 Metody minimalizace derivační: metoda největšího spádu konjugované gradienty Newton-Raphsonova metoda daleko od minima blízko minima pro malé molekuly nederivační: simplexová metoda
13 Problém lokálních minim sedlový bod Globální minimum Energie Lokální minima PES
14 Hledání minim na PES lokální metody = minimalizace (hledání lokálních minim) globální metody = hledání všech lokálních minim + globální minimum systematické prohledávání (grid) MD a odvozené techniky (simulované žíhání, LES, FEP) Monte Carlo CICADA
15 Restraints X Constraints (restraint = omezení, nátlak; constraint = donucení, přesné vymezení) restraints = měkké vazné podmínky zvýšení silové konstanty K constraints = tvrdé vazné podmínky silová konstanta K r 0 r 0
16 Dlouhodosahové elektrostatické interakce Systém N-částic: nejnáročnější část minimalizace = výpočet dlouhodosahových interakcí (Coulomb síly) N 2 výpočtů elektrostatická energie
17 Nevazebné interakce vdw elektrostat
18 Dielektrický model solventu E(r) = 1 q i q j 4πε 0 r vakuum ε =ε 0 ε r prostředí o relativní permitivitě ε r
19 Explicitní solvent sledování specifických interakcí s molekulami H 2 O značná výpočetní náročnost peptid (330 atomů) molekul H 2 O
20 Periodic Boundary Conditions (PBC) Hraniční podmínky
21 Výpočet elektrostatických interakcí v PBC odříznutí interakcí o vzdálenosti > cutoff původní funkce funkce při použití cutoffu Energie problém vyšších cutoffů vzdálenost
22 Ewaldova sumace Periodický box E(r) = 1 q i q j 4πε 0 r E(r) = n=0 1 q i q j 4πε 0 r+ n n... násobek délky hrany boxu L Ewald (1921): reálný prostor reciproký prostor E = f (L) E = f (1/L)
23 Particle Mesh bodové náboje model kontinuálního solventu Poissonova rovnice: 2 φ = ρ (x) elektrický potenciál nábojová hustota umístění nábojů na mřížku výpočet E pomocí P. rovnice interpolace E mezi body mřížky
24 Particle Mesh Ewald (PME) explicitní solvent cutoff dielektrikum
25 Molekulová dynamika
26 Historie molekulové dynamiky 1. MD simulace: 1957 hard-sphere model kolize pevných částic pohybujících se konstantní rychlostí, sledování srážek částic Energie E(vzdálenost) = pro vzdál. < σ 0 pro vzdál. > σ vzdálenost
27 dark ages před. r. 1995: Historie MD MD simulace nukleových kyselin (vysoce nabité systémy, nutno správně pracovat s dlouhodosahovými elektrostatickými interakcemi) - nestabilní (zkroucení duplexu, zlomení párů bazí). Nedostatek výpočetní síly: Pro výpočet dlouhodosahových elektrostatických interakcí je užíván cutoff - useknutí interakcí - nestabilita. Neužívá se PME (známo od r. 1993) Pomalý vývoj silových polí - nemožnost kvalitních QM výpočtů Krátké simulace < 200ps
28 Historie MD zvýšená počítačová síla (superpočítače) korektní zacházení s dlouhodosahovými nevazebnými interakcemi (elektrostatika, vdw) - PME kvalitní QM výpočty na vyšší úrovni silové pole 2. generace - např. AMBER parm94.dat (W. Cornell) stabilní trajektorie přesná interpretace krystalových struktur Př.: MD simulace nukleových kyselin - DNA (duplex,..., kvadruplex), RNA (hairpin, ribozymy), modifikovaná DNA, RNA, protein/na interakce
29 Historie MD přesná interpretace struktur + G Př.: MD simulace nukleových kyselin + výpočty volné energie komplexů molekul. Omezení: nedostatky silových polí nezahrnutí polarizace
30 Molekulová dynamika integrace Newtonových pohybových rovnic t F i = m i a i stav 1 stav 2 r i 1 r i 1a r i r i 2b r i 2a r i 2 r i 1b Termodynamika: Kinetika: jaké stavy jsou možné? jak (a jak rychle) stavy interkonvertují?
31 Molekulová dynamika de dr i F i = m i a i dv i dt de dr i = m i d 2 r i dt 2 dr i dt
32 Molekulová dynamika t < 0.5 ; 2 fs > stav 1 stav 2 r i 1 r i 2 t MD trajektorie
33 Molekulová dynamika leap-frog algoritmus t t+ t t r(t) r(t+ t) r(t+ t) = r(t) + t. v(t + 1/2 t) v(t-1/2 t) v(t+1/2 t) v(t+1/2 t) = v(t-1/2 t) + t. a(t) a(t)
34 Časový krok v MD příliš malý - MD pokrývá jen omezenou část konformačního prostoru příliš velký - nestabilita trajektorie, vysoká E Správný časový krok t : 1/10 nejkratšího vibračního pohybu Př.: C H vazba vibruje s periodou 10fs integrační krok t = 1 fs Př.: constraints na vazby obsahující H (SHAKE algoritmus) integrační krok t = 2 fs
35 Počáteční konfigurace pro MD z experimentu (strukturní databáze ) úprava (dostavění) struktury přiřazení počátečních rychlostí - náhodně podle Maxwell - Boltzman distribuce (Gaussova distribuce) relaxace dostavěných částí Generátor (pseudo)náhodných čísel: produkuje čísla <0, 1 > rovnoměrně přepočet na čísla odpovídající gaussovské distribuci
36 Algoritmus MD Síla působící na částici = vektorový součet interakcí s ostatními částicemi zrychlení F = m. a rychlost pozice v čase t + t
37 Algoritmus MD Síla působící na částici = vektorový součet interakcí s ostatními částicemi Aplikace termostatu: přeškálování rychlostí vzhledem k tepelné lázni nová pozice v čase t + t
38 Termostat napodobuje působení teploty na systém - působení makroskopických vibračních modů na dynamiku jednotlivých atomů = násobení každé rychlosti atomu faktorem, který tvoří požadovanou teplotu (každý krok nebo periodicky každých X kroků)
39 Moduly AMBERu stavba systému Xleap výpočty volné energie GIBBS simulace MD sander vizualizace VMD, Chimera, GRASP, RasMol, MOLMOL, analýza ptraj (anal, carnal) MM-PBSA Delphi, CMIP
40 Příprava systému - XLeap PDB souřadnice struktury - soubor.pdb Přidání solventu Přidání iontů XLeap databáze parametrů souřadnice - soubor.crd topologie + PARAMETRY soubor.top sander
41 Příprava systému - XLeap
42 SANDER modul soubor.in minimalizace nebo dynamika? soubor.crd soubor.top SANDER soubor.out human readable soubor.traj soubor.rst soubor.pdb soubor.ene
43 Vstup/výstupní soubory vystupni_soubor.out vstupni_soubor.in
44 Postup MD volba vstupní struktury (např. z RTG), úprava (doplnění chybějících residuí, vodíků) - Xleap optimalizace doplněných částí - sander přidání iontů (neutralizace systému), solvatace - přidání molekul vody (solvatační box) - Xleap ekvilibrace systému - minimalizace vody a iontů - sander krátká MD vody a iontů - sander postupné uvolňování proteinu (= snižování restrains) - sander zahřívání na simulační teplotu - sander produkční MD - sander
45 Ekvilibrace systému Minimalizace a dynamika solventu a iontů constraints na molekulu peptidu
46 Několikastupňová minimalizace s postupným uvolňováním peptidu restraints na molekulu peptidu (25 kcal/mol/a, 20, 15, 10, 5, 0)
47 Zahřívání systému Teplota 0 ps 2 ps Čas 20 ps Zahřívání 100 K 300 K během 20 ps start produkční fáze MD
48 Kontrola ekvilibrace
49 Produkční fáze MD 1 krok MD = ps = 2 fs Frekvence ukládání snímků = 500 kroků 0ps 1ps 2ps... Čas 2ns 500 kroků 500 kroků... 1 snímek 1 snímek... MD trajektorie = soubor snímků
50 Molekulová dynamika termostat
51 Výpočet MD
52 1600 ps 1800 ps Trajektorie - snímky 0ps 200 ps 400 ps 600 ps 800 ps 1000 ps 1200 ps 1400 ps
53 MD trajektorie
54 Analýza - modul PTRAJ soubor.in autor T. E. Cheatham III. trajektorie = soubor snímků soubor.top PTRAJ modifikovaná trajektorie (imaging, center, strip, closest, ) jednotl. snímky vzdálenosti, úhly, torze, rmsd gridy, b-faktory
55 Průměrná struktura z poslední fáze MD (např. 0.5 ns)...
56 Analýza trajektorie celková energie potenciální energie kinetická energie
57 RMS RMS odchylka (root-mean-square deviation)
58 Geometrické parametry vzdálenosti torzní úhly
59 Změny ve struktuře
60 Vody a ionty
61 Elektrostat. potenciál
62 Vyhodnocení dat srovnání s experimentem mutace klíčových míst ve struktuře a následná MD termodynamická analýza vývoj lepšího modelu
63 Simulované žíhání Energie zahřátí na vysokou teplotu pomalé ochlazování snímky Quenched dynamics minimalizace nalezená minima Energie
64 Vázaná MD = MD s užitím restraints Restraints (vazné podmínky)... získány z NMR přiřazení signálů MD + restraints NMR vzdálenosti 3D struktura
65 Problémy simulací Energie? časová škála: cíl: µs - ms realita: ps - ns kvalita reprezentace: cíl: komplexní systém realita: molekulová mechanika
66 SGI Power Challenge SGI Onyx vt 100 PC clusters SGI Origin2000
PLOCHA POTENCIÁLNÍ ENERGIE
 PLOCHA POTENCIÁLNÍ ENERGIE Zero point energy - Energie nulového bodu Molekula o určitou část své energie nikdy nemůže přijít Tzv. Zbytková energie (ZPE) vnitřní energie molekuly, která je přítomna vždy
PLOCHA POTENCIÁLNÍ ENERGIE Zero point energy - Energie nulového bodu Molekula o určitou část své energie nikdy nemůže přijít Tzv. Zbytková energie (ZPE) vnitřní energie molekuly, která je přítomna vždy
Computing structural chemistry and biology
 Computing structural chemistry and biology Chemistry and biology with computers http://www.nobel.se/chemistry/laureates/1998/illpres/index.html Why computing chemistry Snížené náklady na laboratorní experimenty
Computing structural chemistry and biology Chemistry and biology with computers http://www.nobel.se/chemistry/laureates/1998/illpres/index.html Why computing chemistry Snížené náklady na laboratorní experimenty
Počítačová chemie. výpočetně náročné simulace chemických a biomolekulárních systémů. Zora Střelcová
 Počítačová chemie výpočetně náročné simulace chemických a biomolekulárních systémů Zora Střelcová Národní centrum pro výzkum biomolekul, Masarykova univerzita, Kotlářská 2, 611 37 Brno, Česká Republika
Počítačová chemie výpočetně náročné simulace chemických a biomolekulárních systémů Zora Střelcová Národní centrum pro výzkum biomolekul, Masarykova univerzita, Kotlářská 2, 611 37 Brno, Česká Republika
KAM SE UBIRA POČÍTAČOVÁ CHEMIE - ZAOSTŘENO NA MODELOVÁNÍ VĚTŠÍCH MOLEKUL
 Chem. Listy 92, 101-113 (1998) KAM SE UBIRA POČÍTAČOVÁ CHEMIE - ZAOSTŘENO NA MODELOVÁNÍ VĚTŠÍCH MOLEKUL JAROSLAV KOCA Katedra organické chemie a Laboratoř struktury a dynamiky biomolekul, Přírodovědecká
Chem. Listy 92, 101-113 (1998) KAM SE UBIRA POČÍTAČOVÁ CHEMIE - ZAOSTŘENO NA MODELOVÁNÍ VĚTŠÍCH MOLEKUL JAROSLAV KOCA Katedra organické chemie a Laboratoř struktury a dynamiky biomolekul, Přírodovědecká
POŽADAVKY KE STÁTNÍ ZÁVĚREČNÉ ZKOUŠCE MAGISTERSKÉ STUDIUM POČÍTAČOVÉ MODELOVÁNÍ VE VĚDĚ A TECHNICE (NAVAZUJÍCÍ STUDIUM I DOBÍHAJÍCÍ 5-LETÉ STUDIUM)
 POŽADAVKY KE STÁTNÍ ZÁVĚREČNÉ ZKOUŠCE MAGISTERSKÉ STUDIUM POČÍTAČOVÉ MODELOVÁNÍ VE VĚDĚ A TECHNICE (NAVAZUJÍCÍ STUDIUM I DOBÍHAJÍCÍ 5-LETÉ STUDIUM) Organizace zkoušky Zkouška je ústní a má čtyři části:
POŽADAVKY KE STÁTNÍ ZÁVĚREČNÉ ZKOUŠCE MAGISTERSKÉ STUDIUM POČÍTAČOVÉ MODELOVÁNÍ VE VĚDĚ A TECHNICE (NAVAZUJÍCÍ STUDIUM I DOBÍHAJÍCÍ 5-LETÉ STUDIUM) Organizace zkoušky Zkouška je ústní a má čtyři části:
Vedení tepla v MKP. Konstantní tepelné toky. Analogické úlohám statiky v mechanice kontinua
 Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
NMR biomakromolekul RCSB PDB. Progr. NMR
 NMR biomakromolekul Typy biomakromolekul a možnosti studia pomocí NMR proteiny a peptidy rozmanité složení, omezení jen velikostí molekul nukleové kyseliny (RNA, DNA) a oligonukleotidy omezení malou rozmanitostí
NMR biomakromolekul Typy biomakromolekul a možnosti studia pomocí NMR proteiny a peptidy rozmanité složení, omezení jen velikostí molekul nukleové kyseliny (RNA, DNA) a oligonukleotidy omezení malou rozmanitostí
Elektrický náboj, Elektrické pole Elektrický potenciál a elektrické napětí Kapacita vodiče
 Elektrické pole Elektrický náboj, Elektrické pole Elektrický potenciál a elektrické napětí Kapacita vodiče Elektrický náboj Elektrování těles: a) třením b) přímým dotykem jevy = elektrické příčinou - elektrický
Elektrické pole Elektrický náboj, Elektrické pole Elektrický potenciál a elektrické napětí Kapacita vodiče Elektrický náboj Elektrování těles: a) třením b) přímým dotykem jevy = elektrické příčinou - elektrický
VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY
 VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY A VLASTNOSTÍ MOLEKUL Michal Čajan Katedra anorganické chemie PřF UP v Olomouci MOLEKULOVÉ MODELOVÁNÍ V CHEMII MOLEKULOVÉ MODELOVÁNÍ aplikace zobrazení a analýza strukturních
VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY A VLASTNOSTÍ MOLEKUL Michal Čajan Katedra anorganické chemie PřF UP v Olomouci MOLEKULOVÉ MODELOVÁNÍ V CHEMII MOLEKULOVÉ MODELOVÁNÍ aplikace zobrazení a analýza strukturních
Struktura atomů a molekul
 Struktura atomů a molekul Obrazová příloha Michal Otyepka tento text byl vysázen systémem L A TEX2 ε ii Úvod Dokument obsahuje všechny obrázky tak, jak jsou uvedeny ve druhém vydání skript Struktura atomů
Struktura atomů a molekul Obrazová příloha Michal Otyepka tento text byl vysázen systémem L A TEX2 ε ii Úvod Dokument obsahuje všechny obrázky tak, jak jsou uvedeny ve druhém vydání skript Struktura atomů
Mezimolekulové interakce
 Mezimolekulové interakce, od teorie po interakce biomolekul s grafenem Pavel Banáš Mezimolekulové interakce slabé mezimolekulové interakce fyzikální původ mezimolekulárních interakcí poruchová teorie mezimolekulárních
Mezimolekulové interakce, od teorie po interakce biomolekul s grafenem Pavel Banáš Mezimolekulové interakce slabé mezimolekulové interakce fyzikální původ mezimolekulárních interakcí poruchová teorie mezimolekulárních
The Economist, reporting on the work of the 1998 Chemistry Nobel Prize Awardees
 MOLEKULOVÁ DYNAMIKA In the real world, this could eventually mean that most chemical experiments are conducted inside the silicon of chips instead of the glassware of laboratories. Turn off that Bunsen
MOLEKULOVÁ DYNAMIKA In the real world, this could eventually mean that most chemical experiments are conducted inside the silicon of chips instead of the glassware of laboratories. Turn off that Bunsen
Pro zředěné roztoky za konstantní teploty T je osmotický tlak úměrný molární koncentraci
 TRANSPORTNÍ MECHANISMY Transport látek z vnějšího prostředí do buňky a naopak se může uskutečňovat dvěma cestami - aktivním a pasivním transportem. Pasivním transportem rozumíme přenos látek ve směru energetického
TRANSPORTNÍ MECHANISMY Transport látek z vnějšího prostředí do buňky a naopak se může uskutečňovat dvěma cestami - aktivním a pasivním transportem. Pasivním transportem rozumíme přenos látek ve směru energetického
FYZIKÁLNÍ CHEMIE I: 2. ČÁST
 Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
2. RBF neuronové sítě
 2. RBF neuronové sítě Kapitola pojednává o neuronových sítích typu RBF. V kapitole je popsána základní struktura tohoto typu neuronové sítě. Poté následuje definice a charakteristika jednotlivých radiálně
2. RBF neuronové sítě Kapitola pojednává o neuronových sítích typu RBF. V kapitole je popsána základní struktura tohoto typu neuronové sítě. Poté následuje definice a charakteristika jednotlivých radiálně
Molekulární dynamika vody a alkoholů
 Molekulární dynamika vody a alkoholů Pavel Petrus Katedra fyziky, Univerzita J. E. Purkyně, Ústí nad Labem 10. týden 22.4.2010 Modely vody SPC SPC/E TIP4P TIP5P Modely alkoholů OPLS TraPPE Radiální distribuční
Molekulární dynamika vody a alkoholů Pavel Petrus Katedra fyziky, Univerzita J. E. Purkyně, Ústí nad Labem 10. týden 22.4.2010 Modely vody SPC SPC/E TIP4P TIP5P Modely alkoholů OPLS TraPPE Radiální distribuční
Lekce 4 Statistická termodynamika
 Lekce 4 Statistická termodynamika Osnova 1. Co je statistická termodynamika 2. Mikrostav, makrostav a Gibbsův soubor 3. Příklady Gibbsových souborů 4. Souborové střední hodnoty 5. Časové střední hodnoty
Lekce 4 Statistická termodynamika Osnova 1. Co je statistická termodynamika 2. Mikrostav, makrostav a Gibbsův soubor 3. Příklady Gibbsových souborů 4. Souborové střední hodnoty 5. Časové střední hodnoty
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I. Mechanika hmotného bodu
 Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Nekovalentní interakce
 Nekovalentní interakce Jan Řezáč UOCHB AV ČR 3. listopadu 2016 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 3. listopadu 2016 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii
Nekovalentní interakce Jan Řezáč UOCHB AV ČR 3. listopadu 2016 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 3. listopadu 2016 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii
Nekovalentní interakce
 Nekovalentní interakce Jan Řezáč UOCHB AV ČR 31. října 2017 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 31. října 2017 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii 4 Výpočty
Nekovalentní interakce Jan Řezáč UOCHB AV ČR 31. října 2017 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 31. října 2017 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii 4 Výpočty
Analýza směsí, kvantitativní NMR spektroskopie a využití NMR spektroskopie ve forenzní analýze
 Analýza směsí, kvantitativní NMR spektroskopie a využití NMR spektroskopie ve forenzní analýze Analýza směsí a kvantitativní NMR NMR spektrum čisté látky je lineární kombinací spekter jejích jednotlivých
Analýza směsí, kvantitativní NMR spektroskopie a využití NMR spektroskopie ve forenzní analýze Analýza směsí a kvantitativní NMR NMR spektrum čisté látky je lineární kombinací spekter jejích jednotlivých
Řešené úlohy ze statistické fyziky a termodynamiky
 Řešené úlohy ze statistické fyziky a termodynamiky Statistická fyzika. Uvažujme dvouhladinový systém, např. atom s celkovým momentem hybnosti h v magnetickém ) ) poli. Bázové stavy označme = a =, první
Řešené úlohy ze statistické fyziky a termodynamiky Statistická fyzika. Uvažujme dvouhladinový systém, např. atom s celkovým momentem hybnosti h v magnetickém ) ) poli. Bázové stavy označme = a =, první
Projekty do předmětu MF
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
Kapitoly z fyzikální chemie KFC/KFCH. VII. Spektroskopie a fotochemie
 Kapitoly z fyzikální chemie KFC/KFCH VII. Spektroskopie a fotochemie Karel Berka Univerzita Palackého v Olomouci Katedra Fyzikální chemie karel.berka@upol.cz Spektroskopie Analýza světla Excitované Absorbované
Kapitoly z fyzikální chemie KFC/KFCH VII. Spektroskopie a fotochemie Karel Berka Univerzita Palackého v Olomouci Katedra Fyzikální chemie karel.berka@upol.cz Spektroskopie Analýza světla Excitované Absorbované
Elektřina a magnetismus UF/01100. Základy elektřiny a magnetismu UF/PA112
 Elektřina a magnetismus UF/01100 Rozsah: 4/2 Forma výuky: přednáška Zakončení: zkouška Kreditů: 9 Dop. ročník: 1 Dop. semestr: letní Základy elektřiny a magnetismu UF/PA112 Rozsah: 3/2 Forma výuky: přednáška
Elektřina a magnetismus UF/01100 Rozsah: 4/2 Forma výuky: přednáška Zakončení: zkouška Kreditů: 9 Dop. ročník: 1 Dop. semestr: letní Základy elektřiny a magnetismu UF/PA112 Rozsah: 3/2 Forma výuky: přednáška
Měřicí a řídicí technika Bakalářské studium 2007/2008. odezva. odhad chování procesu. formální matematický vztah s neznámými parametry
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
Molekulová mechanika. empirické potenciály silová pole. Michal Otyepka, PřF UP Olomouc
 Molekulová mechanika empirické potenciály silová pole Michal Otyepka, PřF UP Olomouc Proč, když máme QM? běžná malá molekula kvantový chemik jásá středně velká molekula kvantovému chemikovi tuhnou rysy
Molekulová mechanika empirické potenciály silová pole Michal Otyepka, PřF UP Olomouc Proč, když máme QM? běžná malá molekula kvantový chemik jásá středně velká molekula kvantovému chemikovi tuhnou rysy
ELEKTROSTATICKÉ POLE V LÁTKÁCH
 LKTROSTATIKÉ POL V LÁTKÁH A) LKTROSTATIKÉ POL V VODIČÍH VODIČ látka obsahující volné elektrické náboje náboje se po vložení látky do pole budou pohybovat až do vytvoření ustáleného stavu, kdy je uvnitř
LKTROSTATIKÉ POL V LÁTKÁH A) LKTROSTATIKÉ POL V VODIČÍH VODIČ látka obsahující volné elektrické náboje náboje se po vložení látky do pole budou pohybovat až do vytvoření ustáleného stavu, kdy je uvnitř
Analýzy vlivu cholesterolu na vlastnosti biomembrán pomocí molekulového modelování
 STŘEDOŠKOLSKÁ ODBORNÁ ČINNOST Analýzy vlivu cholesterolu na vlastnosti biomembrán pomocí molekulového modelování Michaela Kajšová Zlín 2014 GYMNÁZIUM ZLÍN- LESNÍ ČTVRŤ STŘEDOŠKOLSKÁ ODBORNÁ ČINNOST Obor
STŘEDOŠKOLSKÁ ODBORNÁ ČINNOST Analýzy vlivu cholesterolu na vlastnosti biomembrán pomocí molekulového modelování Michaela Kajšová Zlín 2014 GYMNÁZIUM ZLÍN- LESNÍ ČTVRŤ STŘEDOŠKOLSKÁ ODBORNÁ ČINNOST Obor
Obr. 141: První tři Bernsteinovy iontové módy. Na vodorovné ose je bezrozměrný vlnový vektor a na svislé ose reálná část bezrozměrné frekvence.
 Mikronestability 33 m Re( ) ( m1) m1,,3, (5.18) ci Imaginární část frekvence, která je zodpovědná za útlum, razantně roste, pokud se vlny nešíří kolmo na magnetické pole. Útlum také roste s číslem módu
Mikronestability 33 m Re( ) ( m1) m1,,3, (5.18) ci Imaginární část frekvence, která je zodpovědná za útlum, razantně roste, pokud se vlny nešíří kolmo na magnetické pole. Útlum také roste s číslem módu
Oddělení fyziky vrstev a povrchů makromolekulárních struktur
 Oddělení fyziky vrstev a povrchů makromolekulárních struktur Témata diplomových prací 2014/2015 Studium změn elektrické vodivosti emeraldinových solí vystavených pokojovým a mírně zvýšeným teplotám klíčová
Oddělení fyziky vrstev a povrchů makromolekulárních struktur Témata diplomových prací 2014/2015 Studium změn elektrické vodivosti emeraldinových solí vystavených pokojovým a mírně zvýšeným teplotám klíčová
(Auto)korelační funkce. 2. 11. 2015 Statistické vyhodnocování exp. dat M. Čada www.fzu.cz/ ~ cada
 (Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
(Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie
 Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie Základním předmětem výzkumu prováděného ústavem je chemická termodynamika a její aplikace pro popis vybraných vlastností chemických systémů
Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie Základním předmětem výzkumu prováděného ústavem je chemická termodynamika a její aplikace pro popis vybraných vlastností chemických systémů
MODUL 3. ELEKTROMAGNETICKÉ POLE
 MODUL 3. ELEKTROMAGNETICKÉ POLE 3.1. ELEKTROSTATIKA 3.1.1. ELEKTRICKÝ NÁBOJ SHRNUTÍ Stavební jednotkou látky je atom. Skládá se z protonů, elektronů a neutronů. Elektrony a protony jsou nositeli elementárního
MODUL 3. ELEKTROMAGNETICKÉ POLE 3.1. ELEKTROSTATIKA 3.1.1. ELEKTRICKÝ NÁBOJ SHRNUTÍ Stavební jednotkou látky je atom. Skládá se z protonů, elektronů a neutronů. Elektrony a protony jsou nositeli elementárního
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie
 Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Euklidovský prostor Stručnější verze
 [1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
[1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
Kapacita. Gaussův zákon elektrostatiky
 Kapacita Dosud jsme se zabývali vztahy mezi náboji ve vakuu. Prostředí mezi náboji jsme charakterizovali permitivitou ε a uvedli jsme, že ve vakuu je ε = 8,854.1-1 C.V -1.m -1. V této kapitole se budeme
Kapacita Dosud jsme se zabývali vztahy mezi náboji ve vakuu. Prostředí mezi náboji jsme charakterizovali permitivitou ε a uvedli jsme, že ve vakuu je ε = 8,854.1-1 C.V -1.m -1. V této kapitole se budeme
Mechanika s Inventorem
 Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Studie rozložení teplotních polí v dielektricky ohřívaných kaučucích. Bc. Jan Kartousek
 Studie rozložení teplotních polí v dielektricky ohřívaných kaučucích Bc. Jan Kartousek Diplomová práce 2008 ABSTRAKT Diplomová práce se zabývá studiem rozložení teplotních polí uvnitř dielektricky ohřívaných
Studie rozložení teplotních polí v dielektricky ohřívaných kaučucích Bc. Jan Kartousek Diplomová práce 2008 ABSTRAKT Diplomová práce se zabývá studiem rozložení teplotních polí uvnitř dielektricky ohřívaných
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Obsah PŘEDMLUVA 11 ÚVOD 13 1 Základní pojmy a zákony teorie elektromagnetického pole 23
 Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
Neuropočítače. podnět. vnímání (senzory)
 Neuropočítače Princip inteligentního systému vnímání (senzory) podnět akce (efektory) poznání plánování usuzování komunikace Typické vlastnosti inteligentního systému: schopnost vnímat podněty z okolního
Neuropočítače Princip inteligentního systému vnímání (senzory) podnět akce (efektory) poznání plánování usuzování komunikace Typické vlastnosti inteligentního systému: schopnost vnímat podněty z okolního
Elektrotechnická fakulta
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
Maturitní okruhy Fyzika 2015-2016
 Maturitní okruhy Fyzika 2015-2016 Mgr. Ladislav Zemánek 1. Fyzikální veličiny a jejich jednotky. Měření fyzikálních veličin. Zpracování výsledků měření. - fyzikální veličiny a jejich jednotky - mezinárodní
Maturitní okruhy Fyzika 2015-2016 Mgr. Ladislav Zemánek 1. Fyzikální veličiny a jejich jednotky. Měření fyzikálních veličin. Zpracování výsledků měření. - fyzikální veličiny a jejich jednotky - mezinárodní
Studium enzymatické reakce metodami výpočetní chemie
 Studium enzymatické reakce metodami výpočetní chemie 2. kolo Petr Kulhánek, Zora Střelcová kulhanek@chemi.muni.cz CEITEC - Středoevropský technologický institut Masarykova univerzita, Kamenice 5, 625 00
Studium enzymatické reakce metodami výpočetní chemie 2. kolo Petr Kulhánek, Zora Střelcová kulhanek@chemi.muni.cz CEITEC - Středoevropský technologický institut Masarykova univerzita, Kamenice 5, 625 00
MATURITNÍ TÉMATA - CHEMIE. Školní rok 2012 / 2013 Třídy 4. a oktáva
 MATURITNÍ TÉMATA - CHEMIE Školní rok 2012 / 2013 Třídy 4. a oktáva 1. Stavba atomu Modely atomu. Stavba atomového jádra, protonové a nukleonové číslo, izotop, izobar, nuklid, stabilita atomového jádra,
MATURITNÍ TÉMATA - CHEMIE Školní rok 2012 / 2013 Třídy 4. a oktáva 1. Stavba atomu Modely atomu. Stavba atomového jádra, protonové a nukleonové číslo, izotop, izobar, nuklid, stabilita atomového jádra,
2 MECHANICKÉ VLASTNOSTI SKLA
 2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
Numerické metody a programování. Lekce 8
 Numerické metody a programování Lekce 8 Optimalizace hledáme bod x, ve kterém funkce jedné nebo více proměnných f x má minimum (maximum) maximalizace f x je totéž jako minimalizace f x Minimum funkce lokální:
Numerické metody a programování Lekce 8 Optimalizace hledáme bod x, ve kterém funkce jedné nebo více proměnných f x má minimum (maximum) maximalizace f x je totéž jako minimalizace f x Minimum funkce lokální:
Využití strojového učení k identifikaci protein-ligand aktivních míst
 Využití strojového učení k identifikaci protein-ligand aktivních míst David Hoksza, Radoslav Krivák SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita
Využití strojového učení k identifikaci protein-ligand aktivních míst David Hoksza, Radoslav Krivák SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita
Národní centrum pro výzkum biomolekul & MetaCentrum
 Masarykova Univerzita Národní centrum pro výzkum biomolekul Národní centrum pro výzkum biomolekul & Petr Kulhánek kulhanek@chemi.muni.cz Národní centrum pro výzkum biomolekul, Masarykova Univerzita Přírodovědecká
Masarykova Univerzita Národní centrum pro výzkum biomolekul Národní centrum pro výzkum biomolekul & Petr Kulhánek kulhanek@chemi.muni.cz Národní centrum pro výzkum biomolekul, Masarykova Univerzita Přírodovědecká
Počítačové simulace a statistická mechanika
 Počítačové simulace a statistická mechanika Model = soubor aproximaci přijatých za účelem popisu určitého systému okrajové podmínky mezimolekulové interakce Statistické zpracování průměrování ve fázovém
Počítačové simulace a statistická mechanika Model = soubor aproximaci přijatých za účelem popisu určitého systému okrajové podmínky mezimolekulové interakce Statistické zpracování průměrování ve fázovém
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
I. Statické elektrické pole ve vakuu
 I. Statické elektické pole ve vakuu Osnova:. Náboj a jeho vlastnosti 2. Coulombův zákon 3. Intenzita elektostatického pole 4. Gaussova věta elektostatiky 5. Potenciál elektického pole 6. Pole vodiče ve
I. Statické elektické pole ve vakuu Osnova:. Náboj a jeho vlastnosti 2. Coulombův zákon 3. Intenzita elektostatického pole 4. Gaussova věta elektostatiky 5. Potenciál elektického pole 6. Pole vodiče ve
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
Elektrická impedanční tomografie
 Biofyzikální ústav LF MU Projekt FRVŠ 911/2013 Je neinvazivní lékařská technika využívající nízkofrekvenční elektrické proudy pro zobrazení elektrických vlastností tkaní a vnitřních struktur těla. Různé
Biofyzikální ústav LF MU Projekt FRVŠ 911/2013 Je neinvazivní lékařská technika využívající nízkofrekvenční elektrické proudy pro zobrazení elektrických vlastností tkaní a vnitřních struktur těla. Různé
Návrhy elektromagnetických zení
 Návrhy elektromagnetických součástek stek a zařízen zení Zuzana Záhorová zuzanaz@humusoft.cz Karel Bittner bittner@humusoft.cz www.humusoft.cz www.comsol comsol.com tel.: 284 011 730 fax: 284 011 740 Program
Návrhy elektromagnetických součástek stek a zařízen zení Zuzana Záhorová zuzanaz@humusoft.cz Karel Bittner bittner@humusoft.cz www.humusoft.cz www.comsol comsol.com tel.: 284 011 730 fax: 284 011 740 Program
Pružnost. Pružné deformace (pružiny, podložky) Tuhost systému (nežádoucí průhyb) Kmitání systému (vlastní frekvence)
 Pružnost Pružné deformace (pružiny, podložky) Tuhost systému (nežádoucí průhyb) Kmitání systému (vlastní frekvence) R. Hook: ut tensio, sic vis (1676) 1 2 3 Pružnost 1) Modul pružnosti 2) Vazby mezi atomy
Pružnost Pružné deformace (pružiny, podložky) Tuhost systému (nežádoucí průhyb) Kmitání systému (vlastní frekvence) R. Hook: ut tensio, sic vis (1676) 1 2 3 Pružnost 1) Modul pružnosti 2) Vazby mezi atomy
MM/PBSA a MM/GBSA analýzy
 MM/PBSA a MM/GBSA analýzy TEORIE: Při realistickém modelování biomolekul musí být brán v potaz vliv solventního prostředí. V MD simulacích velkých molekul je vzhledem k výpočetní náročnosti častější implicitní
MM/PBSA a MM/GBSA analýzy TEORIE: Při realistickém modelování biomolekul musí být brán v potaz vliv solventního prostředí. V MD simulacích velkých molekul je vzhledem k výpočetní náročnosti častější implicitní
LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015
 LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015 1 LBP 1 LBP Tato metoda, publikovaná roku 1996, byla vyvinuta za účelem sestrojení jednoduchého a výpočetně rychlého nástroje pro
LBP, HoG Ing. Marek Hrúz Ph.D. Plzeň Katedra kybernetiky 29. října 2015 1 LBP 1 LBP Tato metoda, publikovaná roku 1996, byla vyvinuta za účelem sestrojení jednoduchého a výpočetně rychlého nástroje pro
1. Úvod do genetických algoritmů (GA)
 Obsah 1. Úvod do genetických algoritmů (GA)... 2 1.1 Základní informace... 2 1.2 Výstupy z učení... 2 1.3 Základní pomy genetických algoritmů... 2 1.3.1 Úvod... 2 1.3.2 Základní pomy... 2 1.3.3 Operátor
Obsah 1. Úvod do genetických algoritmů (GA)... 2 1.1 Základní informace... 2 1.2 Výstupy z učení... 2 1.3 Základní pomy genetických algoritmů... 2 1.3.1 Úvod... 2 1.3.2 Základní pomy... 2 1.3.3 Operátor
Základy matematické statistiky
 r- MATEMATICKO-FYZIKÁLNí FAKULTA UNIVERZITY KARLOVY V PRAZE Jifí Andel Základy matematické statistiky matfyzpress PRAHA 2011 r I Obsah Predmluva. 11 1 Náhodné veličiny 1.1 Základní pojmy 1.2 Príklady diskrétních
r- MATEMATICKO-FYZIKÁLNí FAKULTA UNIVERZITY KARLOVY V PRAZE Jifí Andel Základy matematické statistiky matfyzpress PRAHA 2011 r I Obsah Predmluva. 11 1 Náhodné veličiny 1.1 Základní pojmy 1.2 Príklady diskrétních
O symetrii tokamaku. Vtomto článku opustíme tematiku konkrétních. Jan Mlynář. 50 let UFP AV ČR
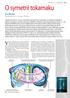 č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
č. 4 Čs. čas. fyz. 59 (2009) 207 O symetrii tokamaku Jan Mlynář Ústav fyziky plazmatu AV ČR, v. v. i., Za Slovankou 3, 182 00 Praha 8 Loňské čtvrté číslo Čs. čas. fyz. se podrobně věnovalo historii tokamaků
Přepočet provozních stavů sítě daných: Výpočet ztrát a kapacitních proudů v síti: Výpočet zkratových poměrů v síti:
 Přepočet provozních stavů sítě daných: změnou topologie sítě (nová přípojnice, transformátor, vedení resp. kabel v síti) změnou zapojení sítě (změna provozu přípojnic resp. směrů napájení sítě) změnou
Přepočet provozních stavů sítě daných: změnou topologie sítě (nová přípojnice, transformátor, vedení resp. kabel v síti) změnou zapojení sítě (změna provozu přípojnic resp. směrů napájení sítě) změnou
Světlo v multimódových optických vláknech
 Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
Jak se matematika poučila v biologii
 Jak se matematika poučila v biologii René Kalus IT4Innovations, VŠB TUO Role matematiky v (nejen) přírodních vědách Matematika inspirující a sloužící jazyk pro komunikaci s přírodou V 4 3 r 3 Matematika
Jak se matematika poučila v biologii René Kalus IT4Innovations, VŠB TUO Role matematiky v (nejen) přírodních vědách Matematika inspirující a sloužící jazyk pro komunikaci s přírodou V 4 3 r 3 Matematika
Část 3. Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA
 HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
Petr Chvosta. vlevo, bude pravděpodobnost toho, že se tyč na počátku intervalu τ B nachází nad vpravo
 MOLEKULÁRNÍ MOTORY Petr Chvosta. Automobil v krupobití aneb brzděním k pohybu Uvažme automobil stojící na mírném svahu a bombardovaný rovnoměrně ze všech stran obrovskými kroupami. Svah stoupá směrem doprava
MOLEKULÁRNÍ MOTORY Petr Chvosta. Automobil v krupobití aneb brzděním k pohybu Uvažme automobil stojící na mírném svahu a bombardovaný rovnoměrně ze všech stran obrovskými kroupami. Svah stoupá směrem doprava
CHEMICKÁ ENERGETIKA. Celá termodynamika je logicky odvozena ze tří základních principů, které mají axiomatický charakter.
 CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
ZÁKLADNÍ EXPERIMENTÁLNÍ
 Kurz praktické NMR spektroskopie 10. - 12. říjen 2011, Praha ZÁKLADNÍ EXPERIMENTÁLNÍ POSTUPY NMR ROZTOKŮ A KAPALIN Jana Svobodová Ústav Makromolekulární chemie AV ČR, v.v.i. Bruker 600 Avance III PŘÍSTROJOVÉ
Kurz praktické NMR spektroskopie 10. - 12. říjen 2011, Praha ZÁKLADNÍ EXPERIMENTÁLNÍ POSTUPY NMR ROZTOKŮ A KAPALIN Jana Svobodová Ústav Makromolekulární chemie AV ČR, v.v.i. Bruker 600 Avance III PŘÍSTROJOVÉ
ELEKTROMAGNETISMUS ELEKTRO MAGNETISMUS
 ELEKTROMAGNETISMUS ELEKTRO MAGNETISMUS úvodní poznámky klasický elektromagnetismus: ve smyslu nekvantový, tj. všechny veličiny měřitelné s libovolnou přesností klasická teorie měla dnešní podobu již před
ELEKTROMAGNETISMUS ELEKTRO MAGNETISMUS úvodní poznámky klasický elektromagnetismus: ve smyslu nekvantový, tj. všechny veličiny měřitelné s libovolnou přesností klasická teorie měla dnešní podobu již před
Národní gridová infrastruktura MetaCentrum & související služby pro akademickou obec
 Národní gridová infrastruktura MetaCentrum & související služby pro akademickou obec Tomáš Rebok MetaCentrum, CESNET z.s.p.o. CERIT-SC, Masarykova univerzita (rebok@ics.muni.cz) MetaCentrum @ CESNET aktivita
Národní gridová infrastruktura MetaCentrum & související služby pro akademickou obec Tomáš Rebok MetaCentrum, CESNET z.s.p.o. CERIT-SC, Masarykova univerzita (rebok@ics.muni.cz) MetaCentrum @ CESNET aktivita
FYZIKA I KOMBINOVANÉ STUDIUM, FBI. Radim Uhlář
 FYZIKA I KOMBINOVANÉ STUDIUM, FBI Radim Uhlář 1 FYZIKA I ÚVOD Postavení fyziky ve vědě a její členění Slovo fyzika pochází z řeckého slova fysis = příroda. V antice byla fyzika chápána jako filozofie přírody
FYZIKA I KOMBINOVANÉ STUDIUM, FBI Radim Uhlář 1 FYZIKA I ÚVOD Postavení fyziky ve vědě a její členění Slovo fyzika pochází z řeckého slova fysis = příroda. V antice byla fyzika chápána jako filozofie přírody
Breviář fyzikální chemie
 Breviář fyzikální chemie Anatol Malijevský Josef P. Novák Stanislav Labík Ivona Malijevská Připomínky k elektronické verzi posílejte na adresu: labik@vscht.cz 24. ledna 2001 Strana 1 z 519 Úvod Milí přátelé,
Breviář fyzikální chemie Anatol Malijevský Josef P. Novák Stanislav Labík Ivona Malijevská Připomínky k elektronické verzi posílejte na adresu: labik@vscht.cz 24. ledna 2001 Strana 1 z 519 Úvod Milí přátelé,
CREATION OF THE STABLE ELASTIC LOOP
 National Conference with International Participation ENGINEERING MECHANICS 2006 Svratka, Czech Republic, May 15 18, 2006 paper no. 122 CREATION OF THE STABLE ELASTIC LOOP P. Frantík 1 Summary: Paper deals
National Conference with International Participation ENGINEERING MECHANICS 2006 Svratka, Czech Republic, May 15 18, 2006 paper no. 122 CREATION OF THE STABLE ELASTIC LOOP P. Frantík 1 Summary: Paper deals
Metropolis Hastings MC: Nesymetrická matice α + 1/21
 Metropolis Hastings MC: Nesymetrická matice α + 1/21 Co když α j = α j? α j je-li π j α j π α j W j = π j α j α j π α j 1 k, k = p přij = min W k je-li π j α j < π α j pro = j 1, α j exp( βδu) α j Toto
Metropolis Hastings MC: Nesymetrická matice α + 1/21 Co když α j = α j? α j je-li π j α j π α j W j = π j α j α j π α j 1 k, k = p přij = min W k je-li π j α j < π α j pro = j 1, α j exp( βδu) α j Toto
I Mechanika a molekulová fyzika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Mechanika a molekulová fyzika Úloha č.: XVII Název: Studium otáčení tuhého tělesa Pracoval: Pavel Brožek stud. skup. 12
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Mechanika a molekulová fyzika Úloha č.: XVII Název: Studium otáčení tuhého tělesa Pracoval: Pavel Brožek stud. skup. 12
Podle skupenského stavu stýkajících se objemových fází: kapalina / plyn (l/g) - povrch kapalina / kapalina (l/l) tuhá látka / plyn (s/g) - povrch
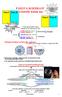 Fáze I Fáze II FÁZOVÁ ROZHRANÍ a koloidy kolem nás z mikroskopického, molekulárního hlediska Fáze I Fáze II z makroskopického hlediska Podle skupenského stavu stýkajících se objemových fází: kapalina /
Fáze I Fáze II FÁZOVÁ ROZHRANÍ a koloidy kolem nás z mikroskopického, molekulárního hlediska Fáze I Fáze II z makroskopického hlediska Podle skupenského stavu stýkajících se objemových fází: kapalina /
Rotující kotouče Drahomír Rychecký Drahomír Rychecký Rotující kotouče
 Nabídka Kotouče bez otvoru Obecná úloha zde Volný kotouč zde Kotouč zatížený tahovým napětím na vnějším poloměru zde Kotouče s otvorem Obecná úloha zde Volný kotouč zde Kotouč zatížený tahovým napětím
Nabídka Kotouče bez otvoru Obecná úloha zde Volný kotouč zde Kotouč zatížený tahovým napětím na vnějším poloměru zde Kotouče s otvorem Obecná úloha zde Volný kotouč zde Kotouč zatížený tahovým napětím
Matematické symboly a značky
 Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Počítačové modelování interakcí molekul s minerálními povrchy
 Jihočeská univerzita v Českých Budějovicích Přírodovědecká fakulta Počítačové modelování interakcí molekul s minerálními povrchy Bakalářská práce Hana Barvíková Školitel: RNDr. Milan Předota, Ph.D. České
Jihočeská univerzita v Českých Budějovicích Přírodovědecká fakulta Počítačové modelování interakcí molekul s minerálními povrchy Bakalářská práce Hana Barvíková Školitel: RNDr. Milan Předota, Ph.D. České
Název: Měření rychlosti zvuku různými metodami
 Název: Měření rychlosti zvuku různými metodami Autor: Doc. RNDr. Milan Rojko, CSc. Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět, mezipředmětové vztahy: fyzika, biologie Ročník: 4.
Název: Měření rychlosti zvuku různými metodami Autor: Doc. RNDr. Milan Rojko, CSc. Název školy: Gymnázium Jana Nerudy, škola hl. města Prahy Předmět, mezipředmětové vztahy: fyzika, biologie Ročník: 4.
Zpracování informací a vizualizace v chemii (C2150) 1. Úvod, databáze molekul
 Zpracování informací a vizualizace v chemii (C2150) 1. Úvod, databáze molekul Organizační pokyny Přednášející: Martin Prokop Email: martinp@chemi.muni.cz Pracovna: INBIT/2.10 (v dubnu/květnu přesun do
Zpracování informací a vizualizace v chemii (C2150) 1. Úvod, databáze molekul Organizační pokyny Přednášející: Martin Prokop Email: martinp@chemi.muni.cz Pracovna: INBIT/2.10 (v dubnu/květnu přesun do
Osvětlování a stínování
 Osvětlování a stínování Pavel Strachota FJFI ČVUT v Praze 21. dubna 2010 Obsah 1 Vlastnosti osvětlovacích modelů 2 Světelné zdroje a stíny 3 Phongův osvětlovací model 4 Stínování 5 Mlha Obsah 1 Vlastnosti
Osvětlování a stínování Pavel Strachota FJFI ČVUT v Praze 21. dubna 2010 Obsah 1 Vlastnosti osvětlovacích modelů 2 Světelné zdroje a stíny 3 Phongův osvětlovací model 4 Stínování 5 Mlha Obsah 1 Vlastnosti
Některé zákony rozdělení pravděpodobnosti. 1. Binomické rozdělení
 Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
Obsah PŘEDMLUVA...9 ÚVOD TEORETICKÁ MECHANIKA...15
 Obsah PŘEDMLUVA...9 ÚVOD...11 1. TEORETICKÁ MECHANIKA...15 1.1 INTEGRÁLNÍ PRINCIPY MECHANIKY... 16 1.1.1 Základní pojmy z mechaniky... 16 1.1.2 Integrální principy... 18 1.1.3 Hamiltonův princip nejmenší
Obsah PŘEDMLUVA...9 ÚVOD...11 1. TEORETICKÁ MECHANIKA...15 1.1 INTEGRÁLNÍ PRINCIPY MECHANIKY... 16 1.1.1 Základní pojmy z mechaniky... 16 1.1.2 Integrální principy... 18 1.1.3 Hamiltonův princip nejmenší
Mechanika - kinematika
 Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
nano.tul.cz Inovace a rozvoj studia nanomateriálů na TUL
 Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci 9. Návody na cvičení
Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci 9. Návody na cvičení
PRINCIPY ZAŘÍZENÍ PRO FYZIKÁLNÍ TECHNOLOGIE (FSI-TPZ-A)
 PRINCIPY ZAŘÍZENÍ PRO FYZIKÁLNÍ TECHNOLOGIE (FSI-TPZ-A) GARANT PŘEDMĚTU: Prof. RNDr. Tomáš Šikola, CSc. (ÚFI) VYUČUJÍCÍ PŘEDMĚTU: Prof. RNDr. Tomáš Šikola, CSc., Ing. Stanislav Voborný, Ph.D. (ÚFI) JAZYK
PRINCIPY ZAŘÍZENÍ PRO FYZIKÁLNÍ TECHNOLOGIE (FSI-TPZ-A) GARANT PŘEDMĚTU: Prof. RNDr. Tomáš Šikola, CSc. (ÚFI) VYUČUJÍCÍ PŘEDMĚTU: Prof. RNDr. Tomáš Šikola, CSc., Ing. Stanislav Voborný, Ph.D. (ÚFI) JAZYK
Základy rádiové navigace
 Základy rádiové navigace Obsah Definice pojmů Způsoby navigace Principy rádiové navigace Pozemské navigační systémy Družicové navigační systémy Definice pojmů Navigace Vedení prostředku po stanovené trati
Základy rádiové navigace Obsah Definice pojmů Způsoby navigace Principy rádiové navigace Pozemské navigační systémy Družicové navigační systémy Definice pojmů Navigace Vedení prostředku po stanovené trati
Ideální krystalová mřížka periodický potenciál v krystalu. pásová struktura polovodiče
 Cvičení 3 Ideální krystalová mřížka periodický potenciál v krystalu Aplikace kvantové mechaniky pásová struktura polovodiče Nosiče náboje v polovodiči hustota stavů obsazovací funkce, Fermiho hladina koncentrace
Cvičení 3 Ideální krystalová mřížka periodický potenciál v krystalu Aplikace kvantové mechaniky pásová struktura polovodiče Nosiče náboje v polovodiči hustota stavů obsazovací funkce, Fermiho hladina koncentrace
Měření kinematické a dynamické viskozity kapalin
 Úloha č. 2 Měření kinematické a dynamické viskozity kapalin Úkoly měření: 1. Určete dynamickou viskozitu z měření doby pádu kuličky v kapalině (glycerinu, roztoku polysacharidu ve vodě) při laboratorní
Úloha č. 2 Měření kinematické a dynamické viskozity kapalin Úkoly měření: 1. Určete dynamickou viskozitu z měření doby pádu kuličky v kapalině (glycerinu, roztoku polysacharidu ve vodě) při laboratorní
Základní spádové metody
 Základní spádové metody Petr Tichý 23. října 2013 1 Metody typu line search Problém Idea metod min f(x), f : x R Rn R. n Dána počáteční aproximace x 0. Iterační proces (krok k): (a) zvol směr d k, (b)
Základní spádové metody Petr Tichý 23. října 2013 1 Metody typu line search Problém Idea metod min f(x), f : x R Rn R. n Dána počáteční aproximace x 0. Iterační proces (krok k): (a) zvol směr d k, (b)
Využití metod strojového učení v bioinformatice David Hoksza
 Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Základy magnetohydrodynamiky. aneb MHD v jedné přednášce?! To si snad děláte legraci!
 Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
Základy magnetohydrodynamiky aneb MHD v jedné přednášce?! To si snad děláte legraci! Osnova Magnetohydrodynamika Maxwellovy rovnice Aplikace pinče, MHD generátory, geofyzika, astrofyzika... Magnetohydrodynamika
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P01 KINEMATIKA HMOTNÉHO BODU
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. Ing. Bohumil Koktavý,CSc. FYZIKA PRŮVODCE GB01-P01 KINEMATIKA HMOTNÉHO BODU STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA 2 OBSAH
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. Ing. Bohumil Koktavý,CSc. FYZIKA PRŮVODCE GB01-P01 KINEMATIKA HMOTNÉHO BODU STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA 2 OBSAH
Plastická deformace a pevnost
 Plastická deformace a pevnost Anelasticita vnitřní útlum Zkoušky základních mechanických charakteristik konstrukčních materiálů (kovy, plasty, keramiky, kompozity) Fyzikální podstata pevnosti Skutečný
Plastická deformace a pevnost Anelasticita vnitřní útlum Zkoušky základních mechanických charakteristik konstrukčních materiálů (kovy, plasty, keramiky, kompozity) Fyzikální podstata pevnosti Skutečný
Neideální plyny. Z e dr dr dr. Integrace přes hybnosti. Neideální chování
 eideální plyny b H Q(, V, T )... e dp 3... dpdr... dr! h Integrace přes hybnosti QVT (,, ) pmkt! h 3 / e dr dr dr /... U kt... eideální chování p kt r B ( T) r B ( T) r 3 3 Vyšší koeficinety velice složité
eideální plyny b H Q(, V, T )... e dp 3... dpdr... dr! h Integrace přes hybnosti QVT (,, ) pmkt! h 3 / e dr dr dr /... U kt... eideální chování p kt r B ( T) r B ( T) r 3 3 Vyšší koeficinety velice složité
Experimentální metody EVF II.: Mikrovlnná
 Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
Matematicko-fyzikální model vozidla
 12. listopadu 2012 Obsah 1 2 3 Reprezentace trasy Řízení vozidla Motivace Motivace Simulátor se snaží přibĺıžit charakteristikám vozu Škoda Octavia Combi 2.0TDI Podpůrný nástroj pro vývoj regulátoru EcoDrive
12. listopadu 2012 Obsah 1 2 3 Reprezentace trasy Řízení vozidla Motivace Motivace Simulátor se snaží přibĺıžit charakteristikám vozu Škoda Octavia Combi 2.0TDI Podpůrný nástroj pro vývoj regulátoru EcoDrive
Fyzika biopolymerů. Struktura a vlastnosti vody, vodíková vazba
 Fyzika biopolymerů Struktura a vlastnosti vody, vodíková vazba Pět základních podmínek pro život na Zemi přítomnost uhlíku a dalších důležitých prvků tvořících biomolekuly voda v blízkosti povrchu vhodná
Fyzika biopolymerů Struktura a vlastnosti vody, vodíková vazba Pět základních podmínek pro život na Zemi přítomnost uhlíku a dalších důležitých prvků tvořících biomolekuly voda v blízkosti povrchu vhodná
