Množina a jej určenie, konečná a nekonečná množina
|
|
|
- Jindřiška Zemanová
- před 6 lety
- Počet zobrazení:
Transkript
1 Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina je súbor (súhrn, skupina) predmetov, ľudí, čísel, atď. vecí - objektov dobre rozlíšiteľných našou mysľou alebo intuíciou, pričom tento súbor chápeme ako nový objekt nášho myslenia. (Georg Cantor , nemecký matematik a logik, zakladateľ teórie množín.): Russellov paradox alebo Russellova antinómia: Označme S množinu všetkých množín, ktoré nie sú svojím vlastným prvkom (tj. množín, ktoré neobsahujú samých seba). Táto množina je v Cantorovom systému dobre definovaná, tzn. teraz by malo byť pre ľubovoľnú množinu M možno rozhodnúť, či táto množina M je alebo nie je prvkom množiny S. Toto však sa nedá rozhodnúť v prípade samotnej množiny S. Obe možnosti totiž vedú k sporu s ich definíciou. (Ak S nie je svojim vlastným prvkom, mala by podľa definície do S patriť; ak však S je svojim vlastným prvkom, potom podľa definície do S by patriť nemala.) Z pohľadu matematiky ide o to, že nemôže existovať množina, ktorej prvkami by boli všetky množiny, ktoré nie sú prvkami samej seba. Bertrand Russel ( ) anglický filozof a matematik: Paradox holiča: V malom meste je jediný holič, ktorý holí práve tých mužov v meste, ktorí sa neholia sami. Také mesto (množina) však nemôže existovať, lebo tu opäť dochádza ku sporu: 1
2 Holí holič sám seba? Sám seba má holiť práve vtedy, kedy sám seba holiť nebude. Napr. množina všetkých prirodzených čísel, množina všetkých celých čísel menších ako 7, množina všetkých žiakov vašej školy nosiacich okuliare,... Množiny sa väčšinou označujú veľkými písmenami, napr. A, B, N a ich obsah (objekty) sa zapisujú do zložených zátvoriek. Napr. množinu A obsahujúcu práve dva objekty a, b zapíšeme A = {a, b}. Objekty, ktoré patria do danej množiny nazývame prvky množiny. Obvykle ich označujeme malými písmenami x, y, c,... Množinu môžeme považovať za určenú jedine vtedy, ak o každom objekte vieme jednoznačne povedať, či do danej množiny patrí alebo nie. Príklad: Pozorne si prečítajte nasledovné vety. Prvky množiny A sú čísla 2, 3, 4. Prvky množiny A sú práve čísla 2, 3, 4. Môžeme v oboch prípadoch hovoriť, že množina A je jednoznačne určená? Nie. Pýtate sa prečo? V prvom prípade hovoríme, že Prvky množiny A sú čísla 2, 3, 4. Ale... čo ak množina A = {1,2,3,4,5} alebo {1,2,3,4,5,7} alebo {2,3,4,5,...} alebo... stále platí, že prvkami množiny A sú čísla 2, 3, 4, čiže v tomto prípade množina A nie je jednoznačne určená. V druhom prípade sme použili slovíčko práve, ktoré spôsobilo, že do množiny A patria práve a jedine čísla 2, 3, 4, čiže množina je jednoznačne určená. Ak chceme vyjadriť, že prvok x je prvkom množiny M, tak zapíšeme x M a čítame: x je prvkom množiny M alebo x patrí množine M. Ak d nie je prvkom množiny B, tak zapíšeme d B. Každá množina je určená buď vymenovaním všetkých jej prvkov: B = {a, b, c, d}, alebo určením charakteristických vlastností prvkov, ktoré do danej množiny patria. Napr.: B = {x Z; 3 x} je zápis množiny B, ktorej prvky sú celé čísla deliteľné číslom 3. Množina, ktorá neobsahuje žiadny prvok, sa nazýva prázdna množina. Jej obsah sa vyjadruje znakom alebo {}, v žiadnom prípade však nie { }. Napr.: množina všetkých prirodzených čísel menších ako nula. 2
3 Množiny obsahujúce aspoň jeden prvok nazývame neprázdne množiny. Každú množinu, ktorá obsahuje konečný počet prvkov nazývame konečnou množinou. Konečný počet prvkov je daný prirodzených číslom resp. nulou, čiže i prázdna množina je konečnou množinou. Napr.: množina všetkých prirodzených čísel menších ako 7; množina všetkých celých čísel, ktorých druhá mocnina je rovná 25;... Množinu, ktorá nie je konečná, nazývame nekonečnou množinou. Napr.: množina všetkých prirodzených čísel väčších ako 18; množina všetkých celých čísel, ktorých tretia mocnina je väčšia ako 49;... Príklad 1: Určte množinu A všetkých celých čísel, ktoré sú väčšie ako 2 a menšie než 3 a) vymenovaním prvkov b) charakteristickou vlastnosťou. a) Väčšie ako -2 a menšie ako 3 sú celé čísla -1, 0, 1, 2. Teda množinu A zapíšeme: A = {-1, 0, 1, 2} b) Charakteristickou vlastnosťou danú množinu zapíšeme nasledovne: A = {x Z; -2<x<3} Príklad 2: Určte množinu B všetkých prirodzených čísel, ktoré sú deliteľné číslom 3 a zároveň sú menšie než 13 a) vymenovaním prvkov b) charakteristickou vlastnosťou. a) Deliteľné číslom 3 a zároveň menšie než 13 sú prirodzené čísla 3, 6, 9, 12. Teda množinu B zapíšeme: B = {3, 6, 9, 12} b) Charakteristickou vlastnosťou danú množinu zapíšeme nasledovne: B = {x N; 3 x x<13} Úlohy: 1/ Vymenujte všetky prvky nasledujúcich množín: 3
4 Vzťahy medzi množinami, operácie s množinami Rovnosť množín: Množiny A a B sa rovnajú, keď každý prvok množiny A patrí množine B a každý prvok množiny B patrí množine A. Zapisujeme: A = B Rovnosť množín je: reflexívna: A = A symetrická: A = B B = A tranzitívna: (A = B B = C) A = C A = B ( x: x A x B) Príklad 1: Zistite či sa rovnajú množiny A = {2; 4; 6; 8} a B = {x Z + ; 2 x x<10}. Množina A je zapísaná vymenovaním prvkov a množina B charakteristickou vlastnosťou. Zapíšeme i množinu B vymenovaním prvkov. Označenie množiny Z + predstavuje kladné celé čísla, pre ktoré platí 2 x (sú deliteľné dvomi) (a zároveň) x<10 (sú menšie ako 10). Obe podmienky spĺňajú len čísla 2, 4, 6, 8, teda množinu B môžeme zapísať vymenovaním prvkov nasledovne: B = {2; 4; 6; 8}. Vidíme, že množiny A a B obsahujú tie isté prvky a teda sa rovnajú. Inklúzia množín: Množina A je podmnožinou množiny B práve vtedy, ak všetky prvky množiny A patria zároveň aj množine B. Zapisujeme: A B Vlastnosti inklúzie množín: A B ( x: x A x B) reflexívnosť: A A tranzitívnosť: (A B B C) A C prázdna množina je podmnožinou každej množiny 4
5 Príklad 2: Zistite či množina C = {3; 4; 5} je podmnožinou množiny B = {x Z; -3<x 5}. Množinu B zapíšeme vymenovaním prvkov nasledovne: B={-2; -1; 0; 1; 2; 3; 4; 5} Všetky prvky množiny C patria aj množine B (sú prvkami aj množiny B), preto množina C podmnožinou množiny B. Príklad 3: Napíšte všetky podmnožiny týchto množín: A = :... počet = 1 alebo 2 0 B = {1} :, {1}... počet = 2 alebo 2 1 C = {1; 2} :, {1}, {2}, {1; 2}... počet = 4 alebo 2 2 D = {1; 2; 3} :, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}... počet = 8 alebo 2 3 E = {1; 2; 3; 4} :, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3}, {1; 2; 4}, {1; 3; 4}, {2; 3; 4}, {1; 2; 3; 4}... počet = 16 alebo 2 4 Vo všeobecnosti platí, že n - prvková množina má 2 n podmnožín. Príklad 4: Čo môžeme povedať o množinách A = {a; b; c}, B = {b; a; c} z pohľadu rovnosti množín a ich inklúzie? A = B alebo A B a zároveň B A Z definície rovnosti množín a podmnožiny vidíme, že ( A = B ) [ (A B) (B A) ] t.j. množiny A, B sa rovnajú, ak množina A je podmnožinou množiny B a zároveň množina B je podmnožinou množiny A. Na základe vzťahu ( A = B ) [ (A B) (B A) ] sa dokazuje rovnosť dvoch množín A, B tak, že dokážeme, že: 1. každý prvok z množiny A patrí do množiny B, 2. každý prvok z množiny B patrí do množiny A. Zjednotenie množín: Zjednotením množín A a B nazývame množinu A B, ktorá obsahuje prvky patriace aspoň do jednej z množín A, B, teda obsahuje prvky, ktoré patria do množiny A alebo do množiny B a okrem nich neobsahuje žiadne iné prvky. Zapisujeme: A B x A B (x A x B) 5
6 Vlastnosti zjednotenia množín: A A = A A B = B A A = A A (B C) = (A B) C A B A B = B... komutatívnosť (... nezáleží na poradí )... asociatívnosť (... nezáleží na poradí ) Príklad 5: Zapíšte prvky, ktoré patria zjednoteniu množín E = {x N; 2 x<6}, F = {x Z;x 2 =9}. Množinu E zapíšeme vymenovaním prvkov nasledovne: E={ 2; 3; 4; 5} Množinu F zapíšeme vymenovaním prvkov nasledovne: F={-3; 3} Zjednotenie množín E, F zapíšeme: E F = {-3; 2; 3; 4; 5 } Prienik množín: Prienikom množín A a B nazývame množinu A B, ktorá obsahuje všetky prvky patriace súčasne do oboch množín A, B. Zapisujeme: A B x A B (x A x B) Ak je prienikom množín A, B prázdna množina ( A B= ), nazývame množiny A, B disjunktnými ( nemajú žiadne spoločné prvky). Vlastnosti prieniku množín: A A = A A B = B A A = A (B C) = (A B) C A B A B = A... komutatívnosť (... nezáleží na poradí )... asociatívnosť (... nezáleží na poradí ) Príklad 6: Zapíšte prvky, ktoré patria prieniku množín G, H, kde G je množina všetkých nepárnych prirodzených čísel menších ako 10 a H = {-1,1,3,5,7}. Množinu G zapíšeme vymenovaním prvkov nasledovne: G ={1; 3; 5; 7; 9} 6
7 Prienik množín G, H zapíšeme: G H = {1; 3; 5; 7} Rozdiel množín: Rozdielom množín A a B nazývame množinu A B ( A \ B ), ktorá obsahuje tie prvky množiny A, ktoré súčasne nepatria do množiny B. Zapisujeme: A B alebo A \ B x A - B (x A x B) Vlastnosti rozdielu množín: A A = A = A A = (A B) A ak A B, tak A B B A A B = A B... operácia rozdielu nie je komutatívna Príklad 7: Zapíšte prvky, ktoré patria rozdielu množín I, J, kde I je množina všetkých prirodzených čísel menších ako 100, ktorých odmocnina je prirodzené číslo väčšie ako 2 a J = {4,5,6,7,8,9}. Množinu I zapíšeme vymenovaním prvkov nasledovne: I ={9; 16; 25; 36;... ; 81} Rozdiel množín I, J zapíšeme: I J = {16; 25; 36;... ; 81 } Úlohy: 1/ Dané sú množiny: 2/ Dané sú množiny: 7
8 3/ Dané sú množiny: Doplnok (komplement) množiny: Ak A B, tak množinu U A = A' U nazývame Doplnok (komplement) množiny A vzhľadom na množinu U. Množina A' U je množina všetkých prvkov množiny U, ktoré nepatria do množiny A. (... ktoré dopĺňajú množinu A na množinu U) Zapisujeme: A' U = U - A Vlastnosti rozdielu množín: A' U = U - A A A = A A = U (A ) = A De Morganove pravidelá: (A B) = A B (A B) = A B x A' U (x U x A) Príklad 8: Dané sú množiny K = {1,2,3,4,5,6,7,8,9}, L = {-4,-3,5,6,7,11,12}, M = {2,3,4,5}. Určte M' K L. Zjednotenie množín K, L zapíšeme vymenovaním prvkov nasledovne: K L={-4; -3; 1; 2; 3; 4; 5; 6; 7; 8; 9; 11; 12} Doplnok množiny M na množine K L zapíšeme: M' K L ={-4; -3; 1; 6; 7; 8; 9; 11; 12 } 8
9 Symetrický rozdiel množín: Symetrický rozdiel množín A, B tvoria všetky prvky množín A, B, ktoré patria práve jednej z nich (patria do A alebo do B, nie však do A aj B). Zapisujeme: A B A B = (A-B) (B-A) Príklad 9: Dané sú množiny: A={2,3,5,7}, B={1,2,3,4}. Zapíšte prvky, ktoré patria do symetrického rozdielu množín A a B. A B={1,4,5,7} - vynecháme spoločné prvky množín A a B Niektoré vlastnosti základných operácií na množinách: Operácia Popis, poznámky A A Každá množina je súčasne podmnožinou samej seba. A Prázdna množina je podmnožinou každej ľubovoľnej množiny. A A=A Zjednotenie tých istých množín je tá istá množina (idempotentnosť). A =A Prázdna množina je neutrálny prvok vzhľadom na zjednotenie. A B=B A Operácia zjednotenie množín je komutatívna. A (B C)=(A B) C Operácia zjednotenie množín je asociatívna. A A=A Prienik tých istých množín je opäť tá istá množina (idempotentnosť). A = Prienikom ľubovoľnej množiny s prázdnou množinou je prázdna mn. A B=B A Operácia prienik množín je komutatívna. A (B C)=(A B) C Operácia prienik množín je asociatívna. A (B C)=(A B) (A C) Distributívne zákony. A (B C)=(A B) (A C) (A')'=A Dvojitý doplnok. (A B)'=A' B' (A B)'=A' B' De Morganove pravidlá. A-B=A B' 9
10 Princíp inklúzie a exklúzie Počet prvkov konečnej množiny A označujeme n(a) alebo A. Na výpočet počtu prvkov sa často používa princíp inklúzie (zapojenia) a exklúzie (vypojenia). Pre 2 množiny: n(a B) = n(a) + n(b) n(a B) Pre disjunktné množiny platí: n(a B) = n(a) + n(b Pre 3 množiny: n(a B C ) = n(a) + n(b) + n(c) n(a B) n(a C) n(b C) + n(a B C) Pre 4 množiny: n(a B C D ) = n(a) + n(b) + n(c) + n(d) n(a B) n(a C) n(a D) n(b C) n(b D) n(c D) + n(a B C) + n(a B D) + n(a C D) + n(b C D) - n(a B C D) Úlohy: 1/ Na recepcii na vyslanectve každý ovláda aspoň jeden cudzí jazyk, 15 ľudí hovorí po anglicky, 12 po nemecky a 7 obidvoma jazykmi. Z koľkých ľudí sa skladá táto spoločnosť, ak v spoločnosti nikto iný jazyk neovláda? 2/ Z 35 žiakov odoberá denník SME 8 žiakov, Pravdu 10 žiakov, 21 žiakov neodoberá žiadne z týchto novín. Koľko žiakov odoberá obidvoje noviny. 3/ Za jeden deň opravili v autodielni na 46 autách 24 chýb na brzdách a 36 chýb na motore. Koľko áut malo chybu len na brzdách a koľko len na motore? 4/ Prieskum čitateľských záujmov ukázal, že 60% žiakov číta časopis A, 50% časopis B, 50% časopis C, 30% časopis A aj B, 20% časopis B aj C, 30% časopis A aj C a 10% všetky tri časopisy. Koľko % žiakov číta práve dva časopisy a koľko % nečíta ani jeden z týchto časopisov? 10
11 Grafické znázornenie množín, dôkazy množinových rovností Na názornú predstavu množín, množinových vzťahov a operácií medzi množinami sa používajú ich grafické znázornenia v rovine, tzv. množinové diagramy. Základná množina U (alebo Z) sa znázorňuje spravidla obdĺžnikom a jej podmnožiny A, B,... ako kruhy alebo iné zvyčajne oválne obrazce vnútri obdĺžnika. Tieto grafické znázornenia sa nazývajú Vennove diagramy. K znázorneniu množín reálnych čísel sa zvyčajne používa číselná os. Vennov diagram pre jednu množinu A: alebo Vennov diagram pre dve množiny A a B: Vennov diagram pre tri množiny A, B a C: alebo alebo 11
12 Vennov diagram pre štyri množiny A, B, C a D: Príklad 1: Daná je základná množina Z = {1,2,3,...,9} a jej podmnožiny A = {1,2,3,4,5} a B = {3,6,9}. Znázornite pomocou Vennovych diagramov a zapíšte vymenovaním prvkov nasledovné množiny: a) doplnok množiny A vzhľadom k množine Z, t.j. A Z b) A B ; c) A B ; d) A - B a) Doplnok množiny A vzhľadom k množine Z tvoria všetky prvky patriace množine Z a zároveň nepatriace množine A, čiže: A' Z ={6,7,8,9} b) A B={ } c) A B={3} d) A - B={ } 12
13 Príklad 2: Dané sú množiny A, B. Pomocou Vennovych diagramov zobrazte: a) A = B b) A B c) A B d) A B e) A B f) A U g) A B Pri používaní Vennovych diagramov je dobré používať šrafovanie rôznymi farbami alebo v prípade prieniku dva rôzne smery a v prípade zjednotenia ten istý smer šrafovania. A = B : A B : A B : A B : A B : A U : A B : 13
14 Príklad 3: Pomocou Vennových diagramov znázornite množiny: Príklad 4: Dané sú množiny A, B, C. Pomocou Vennovych diagramov zistite, či platia nasledovné rovnosti: a) A B = A B b) (A B)'=A' B' c) (A - B) C = (A B) - C A B : A B : = 14
15 (A B)' : A' B' : = (A - B) C : (A B) C : Zapisovanie množiny reálnych čísel pomocou intervalov V článku Množina a jej určenie, konečná a nekonečná množina sme si hovorili o dvoch možnostiach zápisu množín - vymenovaním prvkov alebo určením charakteristických vlastností prvkov. Pozrime sa teraz spoločne na nasledovné dve zadania: Príklad 1: Dané sú dve množiny: A = {x N; 2<x<7}, B = {x R; 2<x<7}. Zapíšte tieto množiny vymenovaním prvkov. Množinu A viete určite všetci zapísať vymenovaním prvkov bez zaváhania. Teda A = {3; 4; 5; 6}. Čo ale spravíme s množinou B? Bude to tiež množina {3; 4; 5; 6}? Určite nie, pretože by sme museli zapísať i číslo 2,1 alebo 2,23 alebo 2,2346 alebo 2,007 atď. pretože všetko sú to reálne čísla väčšie ako 2 a zároveň menšie ako 7. Správne uvažujete, že vymenovaním prvkov sa nám množinu B nepodarí zapísať. Vždy by sme našli ďalšie a ďalšie čísla, ktoré by neboli zapísané. A riešenie? Množina B patrí medzi tie množiny reálnych čísel, ktoré je možné zobraziť na číselnej osi úsečkou, polpriamkou alebo priamkou, pričom krajné body tejto úsečky alebo začiatočný bod polpriamky môžu, ale nemusia patriť k týmto množinám. Takéto podmnožiny množiny R nazývame intervaly. 15
16 Ohraničené intervaly sú intervaly, ktoré je možné na číselnej osi zobraziť pomocou úsečky. Podľa toho, či tejto úsečke patria 2, 1 alebo žiadny z krajných bodov rozlišujeme intervaly: ohraničené, uzavreté, polouzavreté a otvorené. Interval Množina Znázornenie na číselnej osi Zápis uzavretý {x R; a x b} <a, b> (zľava uzavretý, sprava otvorený) {x R; a x<b} <a, b) polouzavretý (zľava otvorený, sprava uzavretý) {x R; a<x b} (a, b> otvorený {x R; a<x<b} (a, b) A teraz môžeme zapísať množinu B z príkladu 1 ako interval (2; 7). Pri zápise neohraničených intervalov používame znak + alebo. Znázornenie na Interval Množina Zápis číselnej osi sprava neohraničený {x R; x a} <a, ) {x R; x>a} (a, ) zľava neohraničený {x R; x a} (-, a> {x R; x<a} (-, a) obojstranne neohraničený R (-, ) Keďže intervaly sú množiny, tak môžeme určovať zjednotenie, prienik, rozdiel intervalov i doplnok intervalu vzhľadom na množinu R. Príklad 2: Dané sú intervaly A = < 2, 3), B = ( 1, 5>, C = (3, ). Určte a) A B a) A B c) C B d) B' R a) A B = <-2; 5> b) A B = (-1; 3) 16
17 c) C - B = (5; ) d) B' R = (- ; -1> (5; ) Úlohy: 1/ Dané množiny zapíšte ako intervaly: 2/ Dané sú intervaly: Úlohy súhrn: 1) Určte množinu všetkých päťciferných prirodzených čísel, ktorých ciferný súčet je 3. 2) Určte vzťahy medzi množinami A, B, C, D. Množiny a vzťahy medzi nimi znázornite pomocou Vennovych diagramov. A = {1, 2, 3, 4, 5}, B = {2, 4, 6}, C = {2, 5}, D = {6, 2, 4} 3) Daná je množina M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Zapíšte nasledujúce podmnožiny množiny M: a) podmnožinu T všetkých násobkov 3, b) podmnožinu H všetkých násobkov 10, c) podmnožinu D všetkých násobkov dvojciferných čísel, d) podmnožinu J všetkých čísel, ktorých zápis začína číslicou 1 Množinu M i jej podmnožiny T, H, D, J znázornite graficky. 17
18 4) Overte pomocou Vennovych diagramov, že pre ľubovoľné podmnožiny A, B danej základnej množiny platí: a) (A B) = A B b) (A B) = A B 5) Určte vymenovaním dvojice všetkých podmnožín X, Y, ktoré spĺňajú jednotlivé trojice podmienok: a) X {1, 2, 3, 5, 6, 9}, Y {2, 3, 4, 5, 8}, X Y = {5} b) X Y = {3, 5, 6, 8}, X {4, 6, 8} =, Y {1, 3, 5, 7} = {3, 5} c) X Y =, X Y = {3, 5, 7}, X Y = {2, 4, 6, 8} d) X Y = {2, 6, 7}, X {5}, Y {1, 3, 4, 6, 7} 6) V triede je 38 žiakov, 16 z nich pretekalo v behu, 20 v plávaní. Žiadneho z týchto pretekov sa nezúčastnilo 10 žiakov. Koľko žiakov behalo aj plávalo? 7) Všetky uvedené rovnosti s výnimkou jednej platia pre ľubovoľné neprázdne množiny K, L, M. Ktorá z uvedených rovností neplatí? A: K = K B: K (L M) = (K L) M C: (K L) L = L D: K (L ) = K L E: (K L) M = L (M K) 8) Dané sú množiny: A = {x Z; x 2 < 10}, B = {x N; 3 x x < 17}, C = {x Z; x 2 = 1 2. x < 5}. Vymenovaním prvkov určte množiny A, B, C, A B, B C, C A. 9) A, B sú dve podmnožiny množiny M, pričom A je nekonečná množina a B je konečná množina. Ktorý z nasledujúcich výrokov je potom nepravdivý? A: A B je nekonečná množina B: A B je konečná množina C: A M = M D: A M = M 18
19 E: A B M je nekonečná množina 10) Čo najjednoduchšie zapíšte množiny: a) (2, 6) <4, > b) (2, 6) (10, ) c) (2, 6) <4, ) d) (, 3) (0, ) e) (, 2) (6, ) f) doplnok intervalu (, 3> v množine R g) zjednotenie doplnku intervalu (5, ) v množine R s intervalom <0, 10> h) prienik doplnku intervalu <1, 5> v množine R s intervalom <2, 10> i) prienik zjednotenia intervalov (, 3), <0, 5> v množine R. 11) Pomocou intervalov zapíšte množinu: a) A = {x R; x 2}, b) B = {x R; 3x 8 5x < 29}, c) C = {x R; x 2 < 3}, d) D = {x R; x 1 4}. 12) Charakteristickou vlastnosťou zapíšte množinu: a) A = (, 5, b) B = ( 2, 7, c) C = (, 1 (3, + ), d) D = { 2, 1, 0, 1, 2}. 13) Dané sú množiny A = 2, 7, B = (0, 10, C = {x R; x > 2}. Pomocou intervalov zapíšte množiny: A B, A B, A C, B C, A R, C R. 19
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
KOMBINATORICKÉ PRAVIDLO SÚČINU
 KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
KOMBINATORIKA MODERNÉ VZDELÁVANIE PRE VEDOMOSTNÚ SPOLOČNOSŤ/ PROJEKT JE SPOLUFINANCOVANÝ ZO ZDROJOV EÚ KÓD ITMS PROJEKTU: 26110130645 UČIŤ MODERNE, INOVATÍVNE, KREATÍVNE ZNAMENÁ OTVÁRAŤ BRÁNU DO SVETA
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Matematika pre tretiakov. Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp
 Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
MOCNINY A ODMOCNINY Eva Zummerová
 MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
 Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
Patří-li do množiny A právě prvky a, b, c, d, budeme zapisovat A = {a, b, c, d}.
 2 Množiny a intervaly lgebraické výrazy 2.1 Množiny Chápání množiny lze shrnout takto: Množinou rozumíme každé shrnutí určitých a navzájem různých předmětů m našeho nazírání nebo myšlení (které nazýváme
2 Množiny a intervaly lgebraické výrazy 2.1 Množiny Chápání množiny lze shrnout takto: Množinou rozumíme každé shrnutí určitých a navzájem různých předmětů m našeho nazírání nebo myšlení (které nazýváme
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI
 Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
B i n á r n í r e l a c e. Patrik Kavecký, Radomír Hamřík
 B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
Matice. Matica typu m x n je tabuľka s m riadkami a n stĺpcami amn. a ij. prvok matice, i j udáva pozíciu prvku
 Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Starogrécky filozof Demokritos ( pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov
 STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
STAVBA ATÓMU Starogrécky filozof Demokritos (450-420 pred n.l) Látky sú zložené z veľmi malých, ďalej nerozdeliteľných častíc - atómov Starogrécky filozof Aristoteles (384-322 pred n.l) Látky možno neobmedzene
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Ružové obrázkové slová skladanie slov z písmen
 Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin.
 1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
Modré obrázkové slová skladanie slov z písmen
 Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Množiny, základní číselné množiny, množinové operace
 2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Kontrola väzieb výkazu Súvaha a Výkaz ziskov a strát Príručka používateľa
 Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06)
 C 189/16 Úradný vestník Európskej únie 29.6.2011 Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06) Podľa článku 9 ods. 1 písm. a) druhej zarážky nariadenia Rady (EHS) č. 2658/87 z
C 189/16 Úradný vestník Európskej únie 29.6.2011 Vysvetlivky ku kombinovanej nomenklatúre Európskej únie (2011/C 189/06) Podľa článku 9 ods. 1 písm. a) druhej zarážky nariadenia Rady (EHS) č. 2658/87 z
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE
 MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
MATURITA 2016 ZÁKLADNÉ INFORMÁCIE Organizáciu MS upravuje zákon č. 245/2008 Z. z. o výchove a vzdelávaní (školský zákon) a o zmene a doplnení niektorých zákonov v znení neskorších predpisov a vyhláška
Microsoft Project CVIČENIE 6 1
 Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
AR, MA a ARMA procesy
 Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku
 MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
Šifrovanie, kódovanie, bit a byte, digitálne informácie. Kódovanie informácií v PC binárna (dvojková) číselná sústava
 Šifrovanie, kódovanie, bit a byte, digitálne informácie Šifry šifrovanie sa používa všade tam, kde treba utajiť obsah komunikácie. Existuje veľmi veľa metód na tajné šifrovanie (a protimetód na dešifrovanie).
Šifrovanie, kódovanie, bit a byte, digitálne informácie Šifry šifrovanie sa používa všade tam, kde treba utajiť obsah komunikácie. Existuje veľmi veľa metód na tajné šifrovanie (a protimetód na dešifrovanie).
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
DIZAJN MANUÁL KULT MINOR LOGO MANUÁL. Fond na podporu kultúry národnostných menšín
 LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava A. 2 B. 6 C. 9 D. 14 A. 21 B. 36 C. 24 D. 33
 V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
NEINTERAKTÍVNA KOMUNIKÁCIA
 NEINTERAKTÍVNA KOMUNIKÁCIA ICSED3 informatika Gymnázium Kráľovnej pokoja, Žilina Mgr. Miroslav Malacha Komunikácia prostredníctvom IKT Komunikácia: vyvinulo sa z lat. communicare= deliť sa, zverovať, všeobecnosti
NEINTERAKTÍVNA KOMUNIKÁCIA ICSED3 informatika Gymnázium Kráľovnej pokoja, Žilina Mgr. Miroslav Malacha Komunikácia prostredníctvom IKT Komunikácia: vyvinulo sa z lat. communicare= deliť sa, zverovať, všeobecnosti
(Text s významom pre EHP)
 29.9.2015 L 252/49 VYKONÁVACIE ROZHODNUTIE KOMISIE (EÚ) 2015/1735 z 24. septembra 2015 o presnom umiestnení všeobecného varovania a informačného odkazu na tabaku na vlastnoručné zhotovenie cigariet predávanom
29.9.2015 L 252/49 VYKONÁVACIE ROZHODNUTIE KOMISIE (EÚ) 2015/1735 z 24. septembra 2015 o presnom umiestnení všeobecného varovania a informačného odkazu na tabaku na vlastnoručné zhotovenie cigariet predávanom
Všeobecne záväzné nariadenie Mesta Trenčianske Teplice č. x/2016 o používaní pyrotechnických výrobkov na území mesta Trenčianske Teplice
 Dôvodová správa S účinnosťou k 2.12.2015 došlo k zmene zákona č. 58/2014 Z. z. o výbušninách, výbušných predmetoch a munícii a o zmene a doplnení niektorých zákonov v znení neskorších predpisov, ktorý
Dôvodová správa S účinnosťou k 2.12.2015 došlo k zmene zákona č. 58/2014 Z. z. o výbušninách, výbušných predmetoch a munícii a o zmene a doplnení niektorých zákonov v znení neskorších predpisov, ktorý
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami
 11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
Reálná čísla. Sjednocením množiny racionálních a iracionálních čísel vzniká množina
 Reálná čísla Iracionální číslo je číslo vyjádřené ve tvaru nekonečného desetinného rozvoje, ve kterém se nevyskytuje žádná perioda. Při počítání je potřeba iracionální číslo vyjádřit zaokrouhlené na určitý
Reálná čísla Iracionální číslo je číslo vyjádřené ve tvaru nekonečného desetinného rozvoje, ve kterém se nevyskytuje žádná perioda. Při počítání je potřeba iracionální číslo vyjádřit zaokrouhlené na určitý
Funkcionální řady. January 13, 2016
 Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Naformátuj to. Naformátuj to. pre samoukov
 Naformátuj to pre samoukov PREDHOVOR Publikácia je praktickou príručkou pre každého, kto hľadá jednoduché a ucelené vysvetlenie MS Word z oblasti formátovania dokumentu. Príručka obsahuje jednoduché a
Naformátuj to pre samoukov PREDHOVOR Publikácia je praktickou príručkou pre každého, kto hľadá jednoduché a ucelené vysvetlenie MS Word z oblasti formátovania dokumentu. Príručka obsahuje jednoduché a
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Technická univerzita v Košiciach
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut
 Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut V této hře se to hemží kozami a ty jich musíš získat co nejvíce. Ale najednou je jejich počet limitován a ty už žádné kozy nechceš! Nebohá zvířata tedy
Počet hráčů: 3 6 Věk: 8+ Hrací doba: cca 15 minut V této hře se to hemží kozami a ty jich musíš získat co nejvíce. Ale najednou je jejich počet limitován a ty už žádné kozy nechceš! Nebohá zvířata tedy
KOMISNÝ PREDAJ. Obr. 1
 KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
Obchodná akadémia Ružomberok Ing. Igor Rosa
 1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
1 Komunikácia: vyvinulo sa z lat. communicare = deliť sa, zverovať, vo všeobecnosti znamená komunikácia rozhovor, v sociálnej komunikácii poznáme tri druhy komunikácie: verbálna, neverbálna, komunikácia
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ. Grafy
 Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Obsah. Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie.
 Obsah Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie. Reprezentácia údajov v počítači. Počítač je stroj, ktorý na kódovanie údajov (čísla,
Obsah Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie. Reprezentácia údajov v počítači. Počítač je stroj, ktorý na kódovanie údajov (čísla,
Základy štatistiky. Charakteristiky štatistického znaku
 Základy štatistiky Základy štatistiky Úvod Základné pojmy Popisná štatistika Triedenie Tabuľky rozdelenia početností Grafické znázornenie Charakteristiky štatistického znaku charakteristiky polohy (priemer,
Základy štatistiky Základy štatistiky Úvod Základné pojmy Popisná štatistika Triedenie Tabuľky rozdelenia početností Grafické znázornenie Charakteristiky štatistického znaku charakteristiky polohy (priemer,
Na aute vyfarbi celé predné koleso na zeleno a pneumatiku zadného kolesa vyfarbi na červeno.
 Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
MATEMATICKA OLYMPIADA
 SK MTEMTIK OLYMPI 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z8 1. Martin má na papieri napísané päťciferné číslo s piatimi rôznymi ciframi a nasledujúcimi vlastnosťami: škrtnutím druhej
SK MTEMTIK OLYMPI 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z8 1. Martin má na papieri napísané päťciferné číslo s piatimi rôznymi ciframi a nasledujúcimi vlastnosťami: škrtnutím druhej
Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke
 Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke Všeobecne, platí pre každú kontrolu: Ak nie je status po overení údajov dávky Bez chýb zobrazí sa k danej chybe príslušný
Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke Všeobecne, platí pre každú kontrolu: Ak nie je status po overení údajov dávky Bez chýb zobrazí sa k danej chybe príslušný
Názov: Osmóza. Vek žiakov: Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút.
 Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Lineární algebra Kapitola 1 - Základní matematické pojmy
 Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Nová maturita - zmeny v maturite 2013
 Nová maturita - zmeny v maturite 2013 Sprísnenie maturitnej skúšky POZOR ZMENA! Od školského roku 2012/2013 (Maturita 2013) dochádza k sprísneniu MS, lebo sa určujú predpoklady na úspešné vykonanie MS
Nová maturita - zmeny v maturite 2013 Sprísnenie maturitnej skúšky POZOR ZMENA! Od školského roku 2012/2013 (Maturita 2013) dochádza k sprísneniu MS, lebo sa určujú predpoklady na úspešné vykonanie MS
Operačný systém Úvodná prednáška
 Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Finančný manažment, finančná matematika a účtovníctvo
 MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od
 A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
Špecifikácia testu. z matematiky. pre celoslovenské testovanie žiakov 9. ročníka ZŠ v školskom roku 2017/2018
 Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 9. ročníka ZŠ v školskom roku 2017/2018 Bratislava jún 2017 Test z matematiky pre celoslovenské testovanie je určený žiakom 9. ročníka
Špecifikácia testu z matematiky pre celoslovenské testovanie žiakov 9. ročníka ZŠ v školskom roku 2017/2018 Bratislava jún 2017 Test z matematiky pre celoslovenské testovanie je určený žiakom 9. ročníka
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV
 CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Riešené úlohy Testovania 9/ 2011
 Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
P O D M I E N K Y V Ý M E N Y E U R P A L I E T
 P O D M I E N K Y V Ý M E N Y E U R P A L I E T KEMA Stavebné materiály, s.r.o. KEMA Stavebné materiály, s.r.o. Zavarská 10/H Trnava 917 01 objednavky@kema-sk.sk +421 (0)33 5936 805 Firma KEMA Stavebné
P O D M I E N K Y V Ý M E N Y E U R P A L I E T KEMA Stavebné materiály, s.r.o. KEMA Stavebné materiály, s.r.o. Zavarská 10/H Trnava 917 01 objednavky@kema-sk.sk +421 (0)33 5936 805 Firma KEMA Stavebné
Základné prvky loga OPCHS
 Logo manuál Základné prvky loga OPCHS 1 Základné prvky 1. 1. Logotyp OPCHS 1. 1. 1. Základné prevedenie loga Základný tvar značky je tvorený trojfarebným obdĺžnikom so zaoblenými rohmi, do ktorého je
Logo manuál Základné prvky loga OPCHS 1 Základné prvky 1. 1. Logotyp OPCHS 1. 1. 1. Základné prevedenie loga Základný tvar značky je tvorený trojfarebným obdĺžnikom so zaoblenými rohmi, do ktorého je
Matematika test. 1. Doplň do štvorčeka číslo tak, aby platila rovnosť: (a) 9 + = (b) : 12 = 720. (c) = 151. (d) : 11 = 75 :
 GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti
 Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti Na overenie trénovanosti hráčov sa o.i. vykonávajú testy všeobecnej pohybovej výkonnosti. Z hľadiska vyhodnotenia je potrebné
Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti Na overenie trénovanosti hráčov sa o.i. vykonávajú testy všeobecnej pohybovej výkonnosti. Z hľadiska vyhodnotenia je potrebné
Súradnice bodov na priamke a v rovine
 Analytická geometria lineárnych útvarov Za zakladateľa analytickej geometrie je považovaný René Descartes, ktorý publikoval základné metódy analytickej geometrie v roku 637. Analytická geometria skúma
Analytická geometria lineárnych útvarov Za zakladateľa analytickej geometrie je považovaný René Descartes, ktorý publikoval základné metódy analytickej geometrie v roku 637. Analytická geometria skúma
Multiplexor a demultiplexor
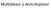 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
 RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP.
 POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP. V prípade, že sa rozhodnete použiť ako úložisko kvalifikovaného certifikátu čipovú kartu StarCos2.3, musíte si žiadosť
POSTUP GENEROVANIA ŽIADOSTI O KVALIFIKOVANÝ CERTIFIKÁT POMOCOU PROGRAMU COMFORTCHIP. V prípade, že sa rozhodnete použiť ako úložisko kvalifikovaného certifikátu čipovú kartu StarCos2.3, musíte si žiadosť
Matematika test. Cesta trvala hodín a minút.
 GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
MATEMATIKA v reálnom živote. Soňa Čeretková Katedra matematiky FPV UKF Nitra
 MATEMATIKA v reálnom živote Soňa Čeretková Katedra matematiky FPV UKF Nitra Ciele a obsah predmetu...vyučovanie by malo viesť k budovaniu vzťahu medzi matematikou a realitou, k získavaniu skúseností s
MATEMATIKA v reálnom živote Soňa Čeretková Katedra matematiky FPV UKF Nitra Ciele a obsah predmetu...vyučovanie by malo viesť k budovaniu vzťahu medzi matematikou a realitou, k získavaniu skúseností s
PRIEMYSELNÁ INFORMATIKA DISKRÉTNE LINEÁRNE RIADENIE
 e(k 1) e(k) e(k) e(k 1) PRIEMYSELNÁ INFORMATIKA 5.5. Číslicové regulátory Od číslicového regulátora budeme očakávať rovnakú funkciu ako od spojitého regulátora a tou je vstupujúcu regulačnú odchýlku zosilňovať,
e(k 1) e(k) e(k) e(k 1) PRIEMYSELNÁ INFORMATIKA 5.5. Číslicové regulátory Od číslicového regulátora budeme očakávať rovnakú funkciu ako od spojitého regulátora a tou je vstupujúcu regulačnú odchýlku zosilňovať,
Školská sieť EDU. Rozdelenie škôl. Obsah: Deleba škôl podľa času zaradenia do projektu: Delba škôl podľa rýchlosti pripojenia:
 Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
Obsah: Rozdelenie škôl Zariadenia dodané v rámci projektu Typy zapojenia zariadení Služby poskytovane na ASA Školská sieť EDU Rozdelenie škôl Deleba škôl podľa času zaradenia do projektu: 1. 2. školy ktoré
A... B... C... D E. Ak sa parazit na postihnutom strome dá použiť, napíšte na čo...
 Biologická olympiáda - kategória F 51. ročník Okresné kolo - školský rok 2016/2017 Test starší žiaci I. časť 1. Na obrázkoch sú predpísané druhy kvitnúcich ihličnatých stromov a šišky jedného z nich. Vašou
Biologická olympiáda - kategória F 51. ročník Okresné kolo - školský rok 2016/2017 Test starší žiaci I. časť 1. Na obrázkoch sú predpísané druhy kvitnúcich ihličnatých stromov a šišky jedného z nich. Vašou
Zápis predmetov do AiSu na aktuálny akademický rok
 Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
 Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Pracovnoprávny vzťah závislá práca
 časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
Téma : Špecifiká marketingu finančných služieb
 Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
Téma : Špecifiká marketingu finančných služieb Marketing predstavuje komplex činností, ktorý zahrňuje všetky činnosti od nápadu až po uvedenie produktu na trh. Cieľom marketingu je potom predať: správny
Elektronické odosielanie výplatných pások
 Elektronické odosielanie výplatných pások Od verzie 11.50 pribudla v programe Olymp možnosť hromadného odosielania zaheslovaných výplatných pások na e-maily jednotlivých pracovníkov. V evidencii Personalistika
Elektronické odosielanie výplatných pások Od verzie 11.50 pribudla v programe Olymp možnosť hromadného odosielania zaheslovaných výplatných pások na e-maily jednotlivých pracovníkov. V evidencii Personalistika
2. Množiny, funkce. Poznámka: Prvky množiny mohou být opět množiny. Takovou množinu, pak nazýváme systém množin, značí se
 MNOŽIN, ZÁKLDNÍ POJMY Pojem množiny patří v matematice ke stěžejním. Nelze jej zavést ve formě definice pomocí primitivních pojmů; považuje se totiž rovněž za pojem primitivní. Představa o pojmu množina
MNOŽIN, ZÁKLDNÍ POJMY Pojem množiny patří v matematice ke stěžejním. Nelze jej zavést ve formě definice pomocí primitivních pojmů; považuje se totiž rovněž za pojem primitivní. Představa o pojmu množina
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
