8. Implikácia. A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna.
|
|
|
- Jaroslava Sedláčková
- před 8 lety
- Počet zobrazení:
Transkript
1 8. Implikácia Implikáciu B A nazývame obrátenou implikáciou k implikácii A B. Pravdivostná hodnota implikácie a obrátenej implikácie je rôzna. Implikáciu B' A' nazývame obmenou implikácie A B. Implikácia má rovnakú pravdivostnú hodnotu ako jej obmena. Pravdivostné hodnoty implikácie, obrátenej implikácie a obmeny implikácie nájdeme v nasledujúcej tabuľke pravdivostných hodnôt. implikácia obmena implikácie obrátená implikácia A B A B A B B ' A' B A Implikácia: Ak je dnes utorok, potom máme školu až do šiestej. Obmena: Ak nemáme školu až do šiestej, potom nie je dnes utorok. Obrátená implikácia: Ak máme školu až do šiestej, potom je dnes utorok. Implikácia: Ak 3 delí 9, potom 6 delí 5. Obmena: Ak 6 nedelí 5, potom 3 nedelí 9. Obrátená implikácia: Ak 6 delí 5, potom 3 delí 9. Implikácia: Ak nosím okuliare, potom som ďalekozraký. Obmena: Ak nie som ďalekozraký, potom nenosím okuliare. Obrátená implikácia: Ak som ďalekozraký, potom nosím okuliare. Implikácia: Ak Dunaj tečie cez Bratislavu, potom tvorí časť hranice s Maďarskom. Obmena: Ak Dunaj netvorí časť hranice s Maďarskom, potom netečie cez Bratislavu. Obrátená implikácia: Ak Dunaj tvorí časť hranice s Maďarskom, potom tečie cez Bratislavu. 40
2 9. Tautológie a kontradikcie Tautológiou nazývame každú formulu zloženú zo znakov p, q,... a logických spojok, ktorá sa zmení na pravdivý výrok, keď za p, q,... dosadíme akýkoľvek výrok (pravdivý alebo nepravdivý. Kontradikciou nazývame každú formulu zloženú zo znakov p, q,... a logických spojok, ktorá sa zmení na nepravdivý výrok, keď za p, q,... dosadíme akýkoľvek výrok (pravdivý alebo nepravdivý. Formulu zloženú zo znakov p, q,... a logických spojok nazývame splniteľnou, ak sa zmení na pravdivý výrok pri vhodnom dosadení výrokov za p, q,.... Teda každá takáto formula, ktorá nie je kontradikciou, je splniteľná. Nech p, q, r sú ľubovoľné výroky. Potom nasledujúce formuly sú tautológie. 1. ( p q ( q p ( komutatívny zákon,. ( p q ( q p ( komutatívny zákon, p q r p q r ( asociatívny zákon, 3. ( ( p q r p q r ( asociatívny zákon, 4. ( ( 5. p ( q r ( p q ( p r ( distributívny zákon, 6. p p ' ( platí výrok alebo jeho negácia, 7. ( p p' 0 ( výrok a jeho negácia neplatia zároveň, 8. ( p q ' ( p' q' 9. ( p q ' ( p' q' (de Morganovo pravidlo pravidlo pre negáciu konjunkcie, (de Morganovo pravidlo pravidlo pre negáciu disjunkcie, 10. ( p q ( q r ( p r ( tranzitívnosť implikácie, 11. ( p q ( q' p' ( obmena implikácie, 1. ( p q ( p' q (implikácia je pravdivá, ak neplatí predpoklad alebo platí tvrdenie, 13. ( p q ' ( p q' (pravidlo pre negáciu implikácie, 14. ( p q ( p q ( q p ( zápis ekvivalencie ako dvojitej implikácie, 41
3 15. ( p q ' ( p q' ( p' q (pravidlo pre negáciu ekvivalencie, Okrem týchto formúl existuje ešte mnoho iných tautológií. To, či formula ( p q ( q p je tautológiou, môžeme overiť pomocou tabuľky pravdivostných hodnôt. p q p q q p ( p q ( q p Z vytieňovaného stĺpca vidíme, že bez ohľadu na pravdivosť výrokov p, q je formula ( p q ( q p vždy pravdivá. Teda formula ( p q ( q p je tautológiou. Nech p, q sú ľubovoľné výroky. Potom nasledujúce formuly sú kontradikcie. 1. p p ' (výrok a jeho negácia nemôže platiť zároveň,. ( p p' 0, 3. ( p q ( p' q' 4. ( p q ( p' q',. Okrem týchto formúl existuje ešte mnoho iných kontradikcií. To, či formula ( p q ( p' q' je kontradikciou, môžeme overiť pomocou tabuľky pravdivostných hodnôt. p q p q p q p ' q ' ( p q ( p' q' Z vytieňovaného stĺpca vidíme, že bez ohľadu na pravdivosť výrokov p, q je formula ( p q ( p' q' vždy nepravdivá. Teda formula ( p q ( p' q' je kontradikciou. 4
4 10. Dôkazy Matematika sa líši od mnohých iných vied najmä tým, že všetky svoje tvrdenia vždy podrobne dokazuje. Nezaoberá sa iba otázkou Ako?, ale najmä otázkou Prečo?. Na rozdiel od niektorých iných vied, nič nepovažuje za samozrejmé alebo očividné. Pri budovaní matematickej teórie si na začiatku zvolíme tvrdenia, ktorých platnosť nedokazujeme. Tieto tvrdenia nazývame axiómy. Príkladom axiómy v geometrii je napríklad výrok Danými dvoma rôznymi bodmi prechádza práve jedna priamka.. Okrem toho si na začiatku zvolíme určitú množinu základných pojmov - v geometrii je to napríklad bod. Z axióm potom postupne vybudujeme celú matematickú teóriu. Vytvoríme definície, ktoré pomenovávajú určité objekty alebo ich vlastnosti a vety, ktoré charakterizujú vzťahy medzi objektmi a ich vlastnosťami. Všetky matematické vety, ktoré v teórii vytvoríme, musíme dokázať pomocou axióm a už predtým dokázaných viet. Matematické vety by sme mohli rozdeliť do dvoch skupín: 1. Jednoduché výroky napríklad Uhlopriečky v štvorci sú navzájom kolmé.,. Výroky v tvare implikácie či ekvivalencie napríklad Ak je ciferný súčet prirodzeného čísla deliteľný tromi, potom toto číslo je deliteľné tromi Priamy dôkaz Priamy dôkaz matematického výroku spočíva v tom, že z už dokázaných výrokov (viet a axióm dokážeme tento výrok po konečnom počte korektných úsudkov. Príklad na priamy dôkaz nájdeme v nasledujúcich dvoch úlohách. Úloha: Dokážte, že Riešenie: 1 3 < = = = = ( Pretože Teda 3 <, dostaneme 1 3 < = + < + = + =. 43
5 Úloha: Ak 3 delí n, potom 9 delí n 3. Dokážte! Riešenie: Ak 3 delí n, potom existuje také celé číslo k, pre ktoré platí n= 3. k Potom n 3 ( 3k 3 7k 3 9 ( 3k 3 = = =, z čoho vyplýva, že 9 delí n Nepriamy dôkaz Nepriamy dôkaz jednoduchého výroku T vychádza z predpokladu, že výrok T je nepravdivý, z čoho odvodíme očividne nepravdivé tvrdenie. Pretože odvodené tvrdenie je nepravdivé, musí byť nepravdivý aj pôvodný predpoklad o nepravdivosti tvrdenia T. Teda tvrdenie T je pravdivé. Nepriamy dôkaz implikácie A B uskutočníme tak, že priamym spôsobom dokážeme obmenu implikácie B ' A'. Pretože táto obmena má rovnakú pravdivostnú hodnotu ako implikácia A B, je pravdivá nielen obmena, ale aj implikácia A B. Príklad na nepriamy dôkaz nájdeme v nasledujúcej úlohe. Úloha: Dokážte, že pre všetky prirodzené čísla n platí: Ak 5 nedelí n. Riešenie: Vytvoríme obmenu implikácie: Ak 5 delí n, potom 5 delí Túto obmenu dokážeme priamo. n. Ak 5 delí n, potom existuje také celé číslo k, pre ktoré platí n= 5. k n = 5k = 5 k, z čoho vyplýva, že 5 delí n. Potom ( Pretože obmena implikácie je pravdivá, je pravdivá aj pôvodná implikácia. Teda pre všetky prirodzené čísla n platí: Ak 5 nedelí n, potom 5 nedelí n. n, potom 5 nedelí 10.3 Iné spôsoby používané pri dôkazoch Všeobecný alebo existenčný výrok možno vyvrátiť už jedným jediným príkladom. Takýto príklad nazývame protipríklad. 44
6 Napríklad francúzsky matematik A. Legendre ( sa domnieval, že neexistujú také 3 3 p r prirodzené čísla p, q, r, s, pre ktoré platí + = 6. q s Túto hypotézu vyvrátil protipríkladom anglický matematik H. Dudeney ( , ktorý zistil, že + = n ( P. Fermat ( sa domnieval, že všetky čísla tvaru + 1 sú prvočísla. Avšak L. Euler ( našiel ako protipríklad rozklad čísla 5 ( = + 1 = = Jeden z najstarších existenčných dôkazov poznal už Euklides. Vedel dokázať, že prvočísel je nekonečne veľa. Úloha: Dokážte, že prvočísel je nekonečne veľa. Riešenie: Použijeme nepriamy dôkaz. Budeme preto vychádzať z tvrdenia, že prvočísel je konečne veľa. Sú to p1, p, p3,..., p n. Ukážeme, že za tohto predpokladu by aj číslo p1 p... 1 p3 p n + bolo prvočíslo. Číslo p1 p... 1 p3 p n + očividne nie je deliteľné žiadnym z čísel p1, p, p3,..., p n, pretože po delení týmito číslami dáva zvyšok 1. Teda číslo p1 p... 1 p3 p n + je prvočíslom, čo je v spore s predpokladom, že všetky prvočísla sú p1, p, p3,..., p n. Nakoľko negácia výroku neplatí, platí výrok Prvočísel je nekonečne veľa. Uvedomme si, že predchádzajúci dôkaz dokazuje iba to, že prvočísel je nekonečne veľa, ale nedáva nám návod na vytvorenie ľubovoľne veľkého prvočísla. Napríklad číslo = 30031, ktoré vznikne súčinom prvých 6 prvočísel zväčšeným o 1, nie je prvočíslo, pretože sa dá zapísať v tvare = Dirichletov princíp nám hovorí, že ak máme utriediť n objektov do m tried, pričom n>m, potom exuistuje taká trieda, v ktorej sú aspoň dva objekty. 45
7 Úloha: Dokážte, že ak je v miestnosti s rozmermi 10 x 10 metrov 30 osôb, potom aspoň dve osoby sú od seba vzdialené menej ako 3 metre. Riešenie: Miestnosť s rozmermi 10x10 metrov rozdelíme na štvorce so stranou dĺžky metre. Týchto štvorcov je 5. Pretože osôb je 30, musia sa aspoň dve osoby nachádzať v jednom štvorci, a teda ich vzdialenosť je menšia ako uhlopriečka štvorca so stranou metre. Podľa Pytagorovej vety pre uhlopriečku štvorca so stranou metre platí u u u u = + = 8 = 8,83 metra. Teda v miestnosti skutočne existujú aspoň dve osoby, ktoré sú od seba vzdialené menej ako 3 metre. Uvedomme si, že predchádzajúci dôkaz nám nevraví, ktoré sú to osoby. Dokazuje iba to, že taká dvojica existuje Dôkaz matematickou indukciou Matematickou indukciou dokazujeme výroky typu Pre každé prirodzené číslo n N platí výrok V ( n. Pri dôkaze matematickou indukciou používame nasledujúci postup: 1. Dokážeme, že platí V ( 1, teda že výrok V je pravdivý pre n = 1.. Dokážeme, že k N : V ( k V ( k+ 1, teda ak platí V ( k, potom platí aj ( 1 V k+. 3. Vyslovíme záver n N : V( n, teda pre každé prirodzené číslo n platí výrok ( V n. Úloha: Dokážte, že pre súčet prvých n nepárnych čísel platí (n 1 = n. Riešenie: Použijeme dôkaz matematickou indukciou. 1. Nech n=1. Potom 1= 1. Teda tvrdenie platí pre n=1.. Predpokladajme, že tvrdenie platí pre n=k, teda že (k 1 = k. 46
8 Dokážeme, že potom platí tvrdenie aj pre n=k+1, teda že ( k+ 1 1 = ( k+ 1 Najprv upravíme ľavú stranu:. ( k ( k ( k ( k = = Použijeme predpoklad, podľa ktorého (k 1 = k. ( k ( k k ( k k k ( k = = + + 1= + 1 Teda ( k+ 1 1 = ( k Pre súčet prvých n nepárnych čísel platí (n 1 = n. Test č. 4 V nasledujúcom teste je 30 úloh z oblasti implikácií, tautológií, kontradikcií a dôkazov v matematike. Na nich si prakticky precvičíme: - implikácie, obrátené implikácie, obmeny implikácií, - určovanie, či daná výroková forma je tautológiou, kontradikciou, či splniteľnou, - rozdiel medzi definíciou a vetou v matematike, - základné metódy dokazovania v matematike. Test č. 4 nájdeme aj v elektronickej verzii v súbore 4.exe. 1. Z daných zápisov vyberte ten, ktorý predstavuje obmenu implikácie A B. a B' A' b B A c A B ' d A B '. Z daných zápisov vyberte ten, ktorý predstavuje negáciu implikácie A B. a B' A' b B A c A B ' d A B ' 47
9 3. Z daných zápisov vyberte ten, ktorý predstavuje obrátenú implikáciu k implikácii A B. a B' A' b B A c A B ' d A B ' 4. Z daných zápisov vyberte ten, ktorý predstavuje obmenu implikácie B A. a A' B ' b A B c A B ' d A' B 5. Z daných zápisov vyberte ten, ktorý predstavuje negáciu implikácie B A. a A' B ' b A B c A B ' d A' B 6. Z daných zápisov vyberte ten, ktorý predstavuje obrátenú implikáciu k implikácii B A. a A' B ' b A B c A B ' d A' B 7. Priraďte implikácie k ich negáciám. a A B ' 1. A B b A' B '. B' A c A' B 3. A' B ' d A B 4. A B ' 8. Priraďte k sebe implikácie s rovnakou pravdivostnou hodnotou. a B' A' 1. A B 48
10 b A' B. B' A c B A 3. A B ' d B A' 4. A' B ' 9. Priraďte formuly k ich vzťahu k implikácii B A. a obmena 1. A B ' b negácia. A B c obrátená implikácia 3. B A' d negácia obrátenej implikácie 4. A' B ' 10. Priraďte implikácie k ich negáciám. a Bude pekne a nepôjdem hrať tenis. 1. Ak bude pekne, nepôjdem hrať tenis. b Nebude pekne a pôjdem hrať tenis.. Ak bude pekne, pôjdem hrať tenis. c Bude pekne a pôjdem hrať tenis. 3. Ak nepôjdem hrať tenis, bude pekne. d Nebude pekne a nepôjdem hrať tenis. 4. Ak nebude pekne, nepôjdem hrať tenis. 11. Priraďte k sebe implikácie s rovnakou pravdivostnou hodnotou. a Ak nebude pekne, pôjdem hrať tenis. 1. Ak bude pekne, pôjdem hrať tenis. b Ak pôjdem hrať tenis, nebude pekne.. Ak nebude pekne, nepôjdem hrať tenis. c Ak pôjdem hrať tenis, bude pekne. 3. Ak bude pekne, nepôjdem hrať tenis. d Ak nepôjdem hrať tenis, nebude pekne. 4. Ak nepôjdem hrať tenis, bude pekne. 1. Priraďte formuly podľa ich vzťahu k implikácii Ak budeš dobrý, dostaneš cukríky. a obrátená implikácia 1. Budeš dobrý a nedostaneš cukríky. b negácia. Ak dostaneš cukríky, budeš dobrý. c negácia obrátenej implikácie 3. Nebudeš dobrý a dostaneš cukríky. d obmena 4. Ak nedostaneš cukríky, nebudeš dobrý. 13. Priraďte formuly podľa ich vzťahu k implikácii Ak nebudeš dobrý, zostaneš doma. a obmena 1. Budeš dobrý a zostaneš doma. b negácia. Ak nezostaneš doma, budeš dobrý. c obrátená implikácia 3. Nebudeš dobrý a nezostaneš doma. d negácia obrátenej implikácie 4. Ak zostaneš doma, nebudeš dobrý. 49
11 14. Pomocou tabuľky pravdivostných hodnôt overte, či formula ( p q ( q p je tautológiou. Doplňte prázdny stĺpec tabuľky. 15. Pomocou tabuľky pravdivostných hodnôt overte, či formula ( p q' ( p' q' je tautológiou. Doplňte prázdny stĺpec tabuľky. 16. Pomocou tabuľky pravdivostných hodnôt overte, či formula ( p q ' ( p' q' je tautológiou. Doplňte prázdny stĺpec tabuľky. 17. Pomocou tabuľky pravdivostných hodnôt overte, či formula ( p q'' ( p q je tautológiou. Doplňte prázdny stĺpec tabuľky. 18. Pomocou tabuľky pravdivostných hodnôt overte, či formula (( p q ( p r ( q r je tautológiou. Doplňte prázdny stĺpec tabuľky. 19. Pomocou tabuľky pravdivostných hodnôt overte, či formula ( p ( q r ( q r je tautológiou. Doplňte prázdny stĺpec tabuľky. 0. Označte matematické tvrdenia, ktoré majú tvar implikácie či ekvivalencie. a Číslo 1 má práve šesť deliteľov. b Súčet veľkostí uhlov v päťuholníku je 540. c Ak je trojuholník pravouhlý, potom pre dĺžky jeho strán platí Pytagorova veta. 50
12 d Prirodzené číslo je deliteľné dvoma, ak končí číslicou 0,, 4, 6, Označte matematické tvrdenia, ktoré majú tvar implikácie či ekvivalencie. a Štvoruholník je štvorec práve vtedy, ak má všetky strany rovnakej dĺžky. b Štvoruholník je štvorec práve vtedy, ak má všetky uhly pravé. c Kocka má práve 1 hrán. d Dĺžka telesovej uhlopriečky v kocke je väčšia ako dĺžka jej stenovej uhlopriečky.. Označte tie výroky, ktoré môžu predstavovať definície. a Štvorec je štvoruholník, ktorý má všetky strany rovnakej dĺžky a všetky vnútorné uhly pravé. b Aritmetická postupnosť je taká postupnosť, pri ktorej rozdiel ľubovoľných dvoch po sebe nasledujúcich členov je konštantný. c Číslo 1 má práve šesť rôznych kladných deliteľov. d Všetky prvočísla sú párne. 3. Označte tie výroky, ktoré môžu predstavovať definície. a Binárna relácia z A do B je ľubovoľná podmnožina karteziánskeho súčinu AxB. b Pravidelný štvorboký ihlan má osem hrán. c Číslo 1 je zložené číslo. d Prvočíslo je také prirodzené číslo, ktoré má práve dva rôzne kladné delitele. 4. Na obrázku je dôkaz jedného matematického výroku. Určte, o aký typ dôkazu ide. a priamy dôkaz b nepriamy dôkaz c dôkaz sporom d dôkaz matematickou indukciou 51
13 5. Na obrázku je dôkaz jedného matematického výroku. Určte, o aký typ dôkazu ide. a priamy dôkaz b nepriamy dôkaz c dôkaz sporom d dôkaz matematickou indukciou 6. Na obrázku je dôkaz jedného matematického výroku. Určte, o aký typ dôkazu ide. a priamy dôkaz b nepriamy dôkaz c dôkaz sporom d dôkaz matematickou indukciou 7. Na obrázku je dôkaz jedného matematického výroku. Určte, o aký typ dôkazu ide. 5
14 a priamy dôkaz b nepriamy dôkaz c dôkaz sporom d dôkaz matematickou indukciou 8. Označte pravdivé tvrdenie. a Kontrapríklady možno využiť pri dôkaze algebraických tvrdení, ale nie geometrických. b Kontrapríklad predstavuje prvý krok pri dôkaze matematickou indukciou. c Pomocou kontrapríkladu dokazujeme platnosť všeobecných výrokov. d Pomocou kontrapríkladu možno vyvrátiť platnosť všeobecného výroku. 9. Označte tvrdenia, pri dôkaze ktorých je výhodné využiť Dirichletov princíp. a V Bratislave žijú aspoň dvaja ľudia, ktorí sa narodili v ten istý deň. b Ak je trojuholník pravouhlý, potom obsah štvorca zostrojeného nad jeho preponou sa rovná súčtu obsahu štvorcov zostrojených nad jeho odvesnami. c Ak v telocvični s rozmermi 30 x 30 metrov cvičí 91 ľudí, tak vzdialenosť aspoň dvoch z nich je menej ako 1,5 metra. d Prvočíselných dvojčiat je nekonečne veľa. 30. Ak by sme dokázali, že žiadne dve prvočíselné dvojčatá nie sú väčšie ako číslo ( , znamenalo by to, že: a neexistujú žiadne prvočíselné dvojčatá, b prvočíselných dvojčiat je konečne veľa, c existujú iba dve prvočíselné dvojčatá, d prvočíselných dvojčiat je nekonečne veľa. 1. a. d 3. b 4. a 5. d 6. b Test č. 4 správne riešenia 7. a1,b,c3,d4 13. a,b3,c4,d a1,b,c4,d cd 9. a4,b3,c,d ab 10. a,b4,c1,d ab 11. a4,b3,c,d ad 1. a,b1,c3,d a 5. b 6. c 7. d 8. d 9. ac 30. b 53
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
1. Pojem výroku. Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť.
 LOGIKA 1. Pojem výroku Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť. Pravdivosť (správnosť) výroku chápeme aj intuitívne. Príklady výrokov: 1.
LOGIKA 1. Pojem výroku Výrok je nejaké tvrdenie v tvare oznamovacej vety, o pravdivosti (správnosti) ktorého má zmysel hovoriť. Pravdivosť (správnosť) výroku chápeme aj intuitívne. Príklady výrokov: 1.
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
2. Vyslovte negáciu nasledujúcich výrokov, určte pravdivostnú hodnotu pôvodných výrokov aj negácií: a. Súčin dvoch kladných reálnych čísel je kladný.
 Banka úloh 1 1. ročník 1. Rozhodnite, ktoré z nasledujúcich viet môžeme považovať za výroky. Pri výrokoch uveďte ich pravdivostnú hodnotu: a. Uhlopriečky obdĺžnika nie sú navzájom kolmé. b. Existuje rovnoramenný
Banka úloh 1 1. ročník 1. Rozhodnite, ktoré z nasledujúcich viet môžeme považovať za výroky. Pri výrokoch uveďte ich pravdivostnú hodnotu: a. Uhlopriečky obdĺžnika nie sú navzájom kolmé. b. Existuje rovnoramenný
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Matematika pre tretiakov. Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp
 Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Riešené úlohy Testovania 9/ 2011
 Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
MATEMATICKA OLYMPIADA
 SK MTEMTIK OLYMPI 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z8 1. Martin má na papieri napísané päťciferné číslo s piatimi rôznymi ciframi a nasledujúcimi vlastnosťami: škrtnutím druhej
SK MTEMTIK OLYMPI 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z8 1. Martin má na papieri napísané päťciferné číslo s piatimi rôznymi ciframi a nasledujúcimi vlastnosťami: škrtnutím druhej
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Obrázok Časový plán projektu, určite kritickú cestu. Obrázok Časový plán projektu, určite kritickú cestu
 Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Matematika (platný od )
 Matematika (platný od 01.09.2016) 1. ročník A variant Obsah vzdelávania: 4 hodiny/týždenne 132 hodín Triedenie predmetov podľa vlastností (množstvo, veľkosť, farba, tvar) Dvojica. Vzťahy rovnako nie rovnako,
Matematika (platný od 01.09.2016) 1. ročník A variant Obsah vzdelávania: 4 hodiny/týždenne 132 hodín Triedenie predmetov podľa vlastností (množstvo, veľkosť, farba, tvar) Dvojica. Vzťahy rovnako nie rovnako,
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
1. ZÁKLADNÉ VZORCE, POUČKY A VLASTNOSTI ÚTVAROV MATEMATIKY ZÁKLADNÝCH ŠKÔL
 1. ZÁKLADNÉ VZORCE, POUČKY A VLASTNOSTI ÚTVAROV MATEMATIKY ZÁKLADNÝCH ŠKÔL ROZDELENIE ČÍSEL : Reálne ( 4; -2,85; log7; 8 ) Racionálne Iracionálne (2; -6,2; 5,33; 7/8) (3;-log5; 15 ) Celé Necelé (zlomky,
1. ZÁKLADNÉ VZORCE, POUČKY A VLASTNOSTI ÚTVAROV MATEMATIKY ZÁKLADNÝCH ŠKÔL ROZDELENIE ČÍSEL : Reálne ( 4; -2,85; log7; 8 ) Racionálne Iracionálne (2; -6,2; 5,33; 7/8) (3;-log5; 15 ) Celé Necelé (zlomky,
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Na aute vyfarbi celé predné koleso na zeleno a pneumatiku zadného kolesa vyfarbi na červeno.
 Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
AR, MA a ARMA procesy
 Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Beáta Stehlíková FMFI UK Bratislava Overovanie stacionarity a invertovateľnosti Opakovanie - stacionarita AR procesu Zistite, či je proces x t = 1.2x t 1 + 0.5x t 2 + 0.3x t 3 + u t stacionárny. Napíšte
Markéta Tajtáková. semestrální úkol zimní semestr Platónske a Archimedovské telesá
 Markéta Tajtáková semestrální úkol zimní semestr 2013 Platónske a Archimedovské telesá zadání semestrální úkol/klauzura letní/zimní semestr 2013 hlavní téma: Platónske a Archimedovské telesá čím se zabýváme:
Markéta Tajtáková semestrální úkol zimní semestr 2013 Platónske a Archimedovské telesá zadání semestrální úkol/klauzura letní/zimní semestr 2013 hlavní téma: Platónske a Archimedovské telesá čím se zabýváme:
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
Obvod štvorca a obdĺžnika
 Obvod štvorca a obdĺžnika 1. Vypočítaj obvod štvorca, ktorého strana je: a) a = 5 cm c) a = 39 dm b) a = 14 mm d) a = 104 m e) a = 24 cm f) a = 48 dm g) a = 1 037 mm h) a = 59 m 2. Vypočítaj obvod obdĺžnika,
Obvod štvorca a obdĺžnika 1. Vypočítaj obvod štvorca, ktorého strana je: a) a = 5 cm c) a = 39 dm b) a = 14 mm d) a = 104 m e) a = 24 cm f) a = 48 dm g) a = 1 037 mm h) a = 59 m 2. Vypočítaj obvod obdĺžnika,
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
VÝROKY VÝROK, PRAVDIVOSTNÁ HODNOTA
 VÝROKY Obsah Výroky... 1 Výrok, pravdivostná hodnota... 1 Konkrétne kvantifikátory... 1 Všeobecný a existenčný kvantifikátor... 2 Negácia výrokov S existenčným alebo všeobecným kvantifikátorom... 3 Zložené
VÝROKY Obsah Výroky... 1 Výrok, pravdivostná hodnota... 1 Konkrétne kvantifikátory... 1 Všeobecný a existenčný kvantifikátor... 2 Negácia výrokov S existenčným alebo všeobecným kvantifikátorom... 3 Zložené
1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava A. 2 B. 6 C. 9 D. 14 A. 21 B. 36 C. 24 D. 33
 V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
V úlohách s výberom odpovede je vždy len jedna správna možnosť. Vyber a zakrúžkuj ju. 1. Vypočítaj: 24 :4 8 A. 2 B. 6 C. 9 D. 14 2. Vypočítaj: 3 5 1 2 A. 21 B. 36 C. 24 D. 33 3. Súčet dvoch za sebou idúcich
Matematika test. 1. Doplň do štvorčeka číslo tak, aby platila rovnosť: (a) 9 + = (b) : 12 = 720. (c) = 151. (d) : 11 = 75 :
 GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
GJH-Prima 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Test-13 Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Ako započítať daňovú licenciu
 Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Premeňte a doplňte správne jednotky : a) 18 dm = m d) 5 m = 50... 195 l = m e) m 15 dm =...l c) 5,6 hl = dm f) 756 l = 7,56.... Vypočítajte : 1 1 1 a) + 1 0,
1. písomná práca z matematiky Skupina A 1. Premeňte a doplňte správne jednotky : a) 18 dm = m d) 5 m = 50... 195 l = m e) m 15 dm =...l c) 5,6 hl = dm f) 756 l = 7,56.... Vypočítajte : 1 1 1 a) + 1 0,
Skákalka. Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto.
 Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
MATEMATIKA v reálnom živote. Soňa Čeretková Katedra matematiky FPV UKF Nitra
 MATEMATIKA v reálnom živote Soňa Čeretková Katedra matematiky FPV UKF Nitra Ciele a obsah predmetu...vyučovanie by malo viesť k budovaniu vzťahu medzi matematikou a realitou, k získavaniu skúseností s
MATEMATIKA v reálnom živote Soňa Čeretková Katedra matematiky FPV UKF Nitra Ciele a obsah predmetu...vyučovanie by malo viesť k budovaniu vzťahu medzi matematikou a realitou, k získavaniu skúseností s
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST I. ČASŤ TEST
 D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST Počet bodov Podpis 1 Podpis 2 I. ČASŤ TEST 1. Jedna strana trojuholníka meria 4cm a druhá 7cm. Ktoré z uvedených čísel môže byť obvodom tohto trojuholníka?
D- 1.strana D- 2.strana D- 3.strana D. - SPOLU TEST Počet bodov Podpis 1 Podpis 2 I. ČASŤ TEST 1. Jedna strana trojuholníka meria 4cm a druhá 7cm. Ktoré z uvedených čísel môže byť obvodom tohto trojuholníka?
1 Úvod do matematické logiky
 1 Úvod do matematické logiky Logikou v běžném slova smyslu rozumíme myšlenkovou cestu, která vede k určitým závěrům. Logika je také formální věda, která zkoumá způsob vyvozování závěrů. Za zakladatele
1 Úvod do matematické logiky Logikou v běžném slova smyslu rozumíme myšlenkovou cestu, která vede k určitým závěrům. Logika je také formální věda, která zkoumá způsob vyvozování závěrů. Za zakladatele
Množina a jej určenie, konečná a nekonečná množina
 Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
Množina a jej určenie, konečná a nekonečná množina Pojem množina je jeden zo základných pojmov modernej matematiky. Pojem množiny nemožno definovať klasickým spôsobom. Približne možno povedať, že množina
Verifikácia a falzifikácia
 Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
2. cvičný test - riešenia
 2. cvičný test - riešenia 01. Veľké akvárium tvaru kvádra je postavené na zemi a zaberá plochu 30m 2. Hoci je vysoké 3m, voda siaha len do 2/3 výšky. Koľko hl vody je v akváriu? výška vody: 2/3 z 3m =
2. cvičný test - riešenia 01. Veľké akvárium tvaru kvádra je postavené na zemi a zaberá plochu 30m 2. Hoci je vysoké 3m, voda siaha len do 2/3 výšky. Koľko hl vody je v akváriu? výška vody: 2/3 z 3m =
Zápis predmetov do AiSu na aktuálny akademický rok
 Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického poradenstva a prevencie (bývalá KPPP) Banská Bystrica
 Návod 2. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. 24 9. 2016 Prevod textu s obrázkami. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Návod 2. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. 24 9. 2016 Prevod textu s obrázkami. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke
 Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke Všeobecne, platí pre každú kontrolu: Ak nie je status po overení údajov dávky Bez chýb zobrazí sa k danej chybe príslušný
Popis kontrol vykonávaných pri OVEROVANÍ zúčtovacích dávok na Elektronickej pobočke Všeobecne, platí pre každú kontrolu: Ak nie je status po overení údajov dávky Bez chýb zobrazí sa k danej chybe príslušný
MAT I. Logika, množiny 6. Finančná matematika 4. Geometria 8. Planimetria 14. Výrazy 18. Funkcie Függvények 4
 MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
MAT I Logika, množiny 6 1. Výrok, pravdivostná hodnota výroku, výroková forma 2. Logické spojky. Kvantifikované výroky 3. Pravdivostná hodnota zložených výrokov 4. Množina, prvok, množina prázdna, konečná,
Názov: Osmóza. Vek žiakov: Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút.
 Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického poradenstva a prevencie (bývalá KPPP) Banská Bystrica
 Návod 1. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. Jednoduchý. 25. 9. 2016 Prevod jednoduchého textu. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Návod 1. Prevod tlačeného textu na písané písmo fontu Abeceda.ttf. Jednoduchý. 25. 9. 2016 Prevod jednoduchého textu. Príklad. Mgr. Stanislav Fila, psychológ CPPPaP Banská Bystrica Centrum pedagogicko-psychologického
Finančné riaditeľstvo Slovenskej republiky
 Finančné riaditeľstvo Slovenskej republiky Informácia k odpočtu daňovej straty v tabuľke D tlačiva daňového priznania k dani z príjmov právnickej osoby Daňovník - právnická osoba so zdaňovacím obdobím
Finančné riaditeľstvo Slovenskej republiky Informácia k odpočtu daňovej straty v tabuľke D tlačiva daňového priznania k dani z príjmov právnickej osoby Daňovník - právnická osoba so zdaňovacím obdobím
Kontrola väzieb výkazu Súvaha a Výkaz ziskov a strát Príručka používateľa
 Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Kontrola Príručka používateľa úroveň: Klient Štátnej pokladnice Verzia 1.0 Január 2013 Autor: Michal Pikus FocusPM Page 1 of 5 Obsah Obsah... 2 1. Úvod... 3 2. Logika porovnania... 3 3. Vykonanie kontroly...
Finančné riaditeľstvo Slovenskej republiky
 Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu preddavkov na daň z príjmov FO Výška preddavkov na daň v preddavkovom období od 1.4.2015 do 31.3.2016 sa vyčísli z poslednej známej daňovej
Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu preddavkov na daň z príjmov FO Výška preddavkov na daň v preddavkovom období od 1.4.2015 do 31.3.2016 sa vyčísli z poslednej známej daňovej
15. Príkazy vetvenia
 Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Príkaz vetvenia je zložený riadiaci príkaz. Používame ho vtedy, keď potrebujeme, aby sa určitý príkaz alebo príkazy vykonal/vykonali iba vtedy, keď je splnená nejaká podmienka. V programe sa vykoná iba
Matematika test. Cesta trvala hodín a minút.
 GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
- rysovať rovnobežky, rôznobežky, kolmice; Uč.I.str.36/1; str.38/12; str.41/2 - rysovať obdĺžnik, štvorec a trojuholník. Uč.I.str.
 Tézy z matematiky - 5. ročník I. Sčítanie a odčítanie prirodzených čísel - sčítať a odčítať prirodzené čísla; Uč.II.str. 42/2,3,4; str.48/4 - sčítať aj viacej sčítancov; Uč.II. str.44/7; str.51/3, - riešiť
Tézy z matematiky - 5. ročník I. Sčítanie a odčítanie prirodzených čísel - sčítať a odčítať prirodzené čísla; Uč.II.str. 42/2,3,4; str.48/4 - sčítať aj viacej sčítancov; Uč.II. str.44/7; str.51/3, - riešiť
Doplňte na vyznačené miesta chýbajúce číslice a desatinné čiarky tak, aby boli rovnosti správne. a) 3, 2 = 3, 2
 1 3 4 5 6 7 8 9 10 Napíšte slovne, ako sa správne prečítajú čísla.,03 104,007 34,00 6 Doplňte na vyznačené miesta chýbajúce číslice a desatinné čiarky tak, aby boli rovnosti správne. a) 3, = 3, b) 5 0,
1 3 4 5 6 7 8 9 10 Napíšte slovne, ako sa správne prečítajú čísla.,03 104,007 34,00 6 Doplňte na vyznačené miesta chýbajúce číslice a desatinné čiarky tak, aby boli rovnosti správne. a) 3, = 3, b) 5 0,
Finančné riaditeľstvo Slovenskej republiky. Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb
 Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2017 do 3.4.2018 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2017 do 3.4.2018 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
Ružové obrázkové slová skladanie slov z písmen
 Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
DIZAJN MANUÁL KULT MINOR LOGO MANUÁL. Fond na podporu kultúry národnostných menšín
 LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
LOGO MANUÁL 1 1.1 Explikácia Základným prvkom vizuálnej identity je logo. Logo abstraktým, geometrickým spôsobom zobrazuje zástúpenie menšín na Slovensku. Z dvoch typov geometrických tvarov, kruhu a štvorca
ZÁKLADY TEÓRIE GRAFOV
 ZÁKLAY EÓRIE GRAFOV PRÍKLA : Minimálna kostra grafu v zadanom grafe určite minimálnu kostru grafu 9 Riešenie: Kostra grafu je taký podgraf, ktorý obsahuje všetky vrcholy pôvodného grafu a neobsahuje uzavretý
ZÁKLAY EÓRIE GRAFOV PRÍKLA : Minimálna kostra grafu v zadanom grafe určite minimálnu kostru grafu 9 Riešenie: Kostra grafu je taký podgraf, ktorý obsahuje všetky vrcholy pôvodného grafu a neobsahuje uzavretý
Import cenových akcií FRESH
 Návod obsahuje podrobný popis nastavenia a použitia importu cenových akcií reťazca FRESH, druhá časť popisuje ako využiť elektronické faktúry firmy Labaš pre automatické vytvorenie príjemky. Import cenových
Návod obsahuje podrobný popis nastavenia a použitia importu cenových akcií reťazca FRESH, druhá časť popisuje ako využiť elektronické faktúry firmy Labaš pre automatické vytvorenie príjemky. Import cenových
Želáme Vám veľa úspechov a naďalej veľkú zábavu s matematikou.
 INŠTRUKCIE: Samostatný hárok pre riešenie úloh (hárok pre odpovede) Nezabudnite vyplniť všetky údaje (meno a priezvisko, škola, e-mail atď.). Testy Na vyriešenie otázok máte 4 minút. Správna je vždy len
INŠTRUKCIE: Samostatný hárok pre riešenie úloh (hárok pre odpovede) Nezabudnite vyplniť všetky údaje (meno a priezvisko, škola, e-mail atď.). Testy Na vyriešenie otázok máte 4 minút. Správna je vždy len
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Matematika pre 4. ročník ZŠ 1.časť
 Matematika pre 4. ročník ZŠ 1.časť Rozvíjanie numerických zručností žiakov. Využitie individuálnych metód získavania nových Rozvíjať logické a kritické myslenie. Výpočty spamäti, písomne, kalkulačkou.
Matematika pre 4. ročník ZŠ 1.časť Rozvíjanie numerických zručností žiakov. Využitie individuálnych metód získavania nových Rozvíjať logické a kritické myslenie. Výpočty spamäti, písomne, kalkulačkou.
Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia
 Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia v školskom roku 2014/2015 Skupina A Kód žiaka: dátum: 12. máj 2014 1. Barborka si kupuje v obchode pečivo za centov, dva jogurty
Test z matematiky na prijímacie skúšky do 1. ročníka osemročného štúdia v školskom roku 2014/2015 Skupina A Kód žiaka: dátum: 12. máj 2014 1. Barborka si kupuje v obchode pečivo za centov, dva jogurty
Finančné riaditeľstvo Slovenskej republiky. Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb
 Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb Výška preddavkov na daň v preddavkovom období od 4.4.2018 do 1.4.2019 sa vyčísli z poslednej známej
Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb Výška preddavkov na daň v preddavkovom období od 4.4.2018 do 1.4.2019 sa vyčísli z poslednej známej
Modré obrázkové slová skladanie slov z písmen
 Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
NOVÝ POMOCNÍK Z MATEMATIKY 9, 1.časť
 Tematický výchovno-vzdelávací plán k pracovnému zošitu NOVÝ POMOCNÍK Z MATEMATIKY 9, 1.časť Stupeň vzdelávania: ISCED 2 - nižšie sekundárne vzdelávanie Vzdelávacia oblasť: Matematika a práca s informáciami
Tematický výchovno-vzdelávací plán k pracovnému zošitu NOVÝ POMOCNÍK Z MATEMATIKY 9, 1.časť Stupeň vzdelávania: ISCED 2 - nižšie sekundárne vzdelávanie Vzdelávacia oblasť: Matematika a práca s informáciami
Tematický výchovno vzdelávací plán Matematika
 Tematický výchovno vzdelávací plán Matematika Vypracovaný podľa Štátneho vzdelávacieho programu ISCED 1 a Školského vzdelávacieho programu ŠTVORLÍSTOK, schválený MZ dňa 30.8.2012 Ročník: štvrtý Šk. rok
Tematický výchovno vzdelávací plán Matematika Vypracovaný podľa Štátneho vzdelávacieho programu ISCED 1 a Školského vzdelávacieho programu ŠTVORLÍSTOK, schválený MZ dňa 30.8.2012 Ročník: štvrtý Šk. rok
OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE
 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE júl 2017 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY
OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY PRE FIRMY EURÓPSKEJ ÚNIE ZHRNUTIE júl 2017 OCHRANA INOVÁCIÍ PROSTREDNÍCTVOM OBCHODNÝCH TAJOMSTIEV A PATENTOV: DETERMINANTY
3D origami - tučniak. Postup na prípravu jednotlivých kúskov: A) nastrihanie, alebo natrhanie malých papierikov (tie budeme neskôr skladať)
 3D origami - tučniak Na výrobu 3D tučniaka potrebujeme: 27 bielych kúskov = 2 biele A4 kancelárske papiere, 85 čiernych (resp. inej farby) kúskov = 6 kancelárskych A4 papierov rovnakej farby, 3 oranžové
3D origami - tučniak Na výrobu 3D tučniaka potrebujeme: 27 bielych kúskov = 2 biele A4 kancelárske papiere, 85 čiernych (resp. inej farby) kúskov = 6 kancelárskych A4 papierov rovnakej farby, 3 oranžové
Matematika test. Mesačne zaplatí. Obvod obdĺžnikovej záhrady je. Jedna kniha stojí Súčet
 1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť v ľubovoľnom poradí.
1 2 3 4 5 6 7 8 9 10 11 12 13 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 13 úloh a má 4 strany. Úlohy môžeš riešiť v ľubovoľnom poradí.
Vážení používatelia programu WISP.
 Vážení používatelia programu WISP. V súvislosti s Kontrolným výkazom DPH (ďalej iba KV) sme doplnili od verzie IS WISP 165.3633 a DB 165.1414 údaje potrebné pre ďalšie spracovanie a vyhotovenie súboru
Vážení používatelia programu WISP. V súvislosti s Kontrolným výkazom DPH (ďalej iba KV) sme doplnili od verzie IS WISP 165.3633 a DB 165.1414 údaje potrebné pre ďalšie spracovanie a vyhotovenie súboru
 Matematika VI. ročník Tematický výchovno-vzdelávací plán bol vypracovaný podľa učebných osnov Štátneho vzdelávacieho programu a upravený podľa Školského vzdelávacieho programu Štvorlístok. Schválené PK
Matematika VI. ročník Tematický výchovno-vzdelávací plán bol vypracovaný podľa učebných osnov Štátneho vzdelávacieho programu a upravený podľa Školského vzdelávacieho programu Štvorlístok. Schválené PK
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI
 Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Imagine. Popis prostredia:
 Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Multiplexor a demultiplexor
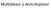 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Pracovné prostredie MS EXCEL 2003.
 Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke Slovenská verzia pravidiel sa pripravuje
 Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
Referenčná ponuka na prístup ku káblovodom a infraštruktúre. Príloha 7 Poplatky a ceny
 Príloha 7 Poplatky a ceny Príloha 7: Poplatky a ceny strana 1 z 5 Obsah 1. CENY V RÁMCI DOHODY NDA A RÁMCOVEJ ZMLUVY... 3 2. CENY V RÁMCI ZMLUVY O DUCT SHARING... 3 2.1 CENA ZA POSKYTOVANIE ZÁKLADNEJ SLUŽBY
Príloha 7 Poplatky a ceny Príloha 7: Poplatky a ceny strana 1 z 5 Obsah 1. CENY V RÁMCI DOHODY NDA A RÁMCOVEJ ZMLUVY... 3 2. CENY V RÁMCI ZMLUVY O DUCT SHARING... 3 2.1 CENA ZA POSKYTOVANIE ZÁKLADNEJ SLUŽBY
Ďalší spôsob, akým je možné vygenerovať maticu je použitie zabudovaných funkcií na generovanie elementárnych matíc.
 MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od
 A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
Deliteľnosť v obore prirodzených čísel
 JKTc04-T List 1 Deliteľnosť v obore prirodzených čísel Mgr. Jana Králiková U: Čo vieš o deliteľnosti v obore prirodzených čísel? Ž: Poznám len pojmy delenie a deliteľ. Delenie je operácia, ktorú môžem
JKTc04-T List 1 Deliteľnosť v obore prirodzených čísel Mgr. Jana Králiková U: Čo vieš o deliteľnosti v obore prirodzených čísel? Ž: Poznám len pojmy delenie a deliteľ. Delenie je operácia, ktorú môžem
1. LABORATÓRNE CVIČENIE
 MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
MENO: ROČNÍK A TRIEDA: 1. LABORATÓRNE CVIČENIE ROVNOMERNÝ POHYB - ZÁVISLOSŤ POLOHY OD ČASU Cieľ: Naučiť sa pracovať so senzorom polohy a ako sú rôzne druhy pohybu prezentované na grafe závislosti polohy
Súbor úloh z matematiky
 Súbor úloh z matematiky 01. Vyber číslo, ktoré má na mieste stoviek nulu. Zapíš ho do rámčeka. 4 278 3 560 9 078 1 409 02. Ktoré číslo má byť na číselnej osi na obrázku pod machuľou? 558 566 574 03. Doplň
Súbor úloh z matematiky 01. Vyber číslo, ktoré má na mieste stoviek nulu. Zapíš ho do rámčeka. 4 278 3 560 9 078 1 409 02. Ktoré číslo má byť na číselnej osi na obrázku pod machuľou? 558 566 574 03. Doplň
Matice. Matica typu m x n je tabuľka s m riadkami a n stĺpcami amn. a ij. prvok matice, i j udáva pozíciu prvku
 Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Logotyp NADÁCIA ZSE Logotyp NADÁCIA ZSE
 01. 09. 2016 1 Obsah 1.1 3 1.2 Popis logotypu 4 1.3 Práca s veľkosťou logotypu 5 1.4 Odsadenia v layoute 6 1.5 vo vzťahu k logám tretích strán 7 1.6 Farebnosť pozitív 8 1.7 Farebnosť negatív 9 1.8 Piktogram
01. 09. 2016 1 Obsah 1.1 3 1.2 Popis logotypu 4 1.3 Práca s veľkosťou logotypu 5 1.4 Odsadenia v layoute 6 1.5 vo vzťahu k logám tretích strán 7 1.6 Farebnosť pozitív 8 1.7 Farebnosť negatív 9 1.8 Piktogram
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Úplný zápis každého desiatkového čísla môžeme zapísať pomocou polynómu:
 1 ČÍSELNÉ SÚSTAVY Systém zobrazeia ľubovoľého čísla pomocou určitého počtu zakov sa azýva číselá sústava. Podľa počtu použitých zakov rozozávame rôze číselé sústavy. V bežom živote sa pri výpočtoch ajčastejšie
1 ČÍSELNÉ SÚSTAVY Systém zobrazeia ľubovoľého čísla pomocou určitého počtu zakov sa azýva číselá sústava. Podľa počtu použitých zakov rozozávame rôze číselé sústavy. V bežom živote sa pri výpočtoch ajčastejšie
Finančné riaditeľstvo Slovenskej republiky. Informácia k výpočtu preddavkov na daň z príjmov fyzických osôb
 Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2016 do 31.3.2017 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
Finančné riaditeľstvo Slovenskej republiky Informácia k výpočtu na daň z príjmov fyzických osôb Výška na daň v om období od 1.4.2016 do 31.3.2017 sa vyčísli z poslednej známej daňovej povinnosti vypočítanej
Dodanie tovaru a reťazové obchody Miesto dodania tovaru - 13/1
 Dodanie u a reťazové obchody Miesto dodania u - 13/1 ak je dodanie u spojené s odoslaním alebo prepravou u - kde sa nachádza v čase, keď sa odoslanie alebo preprava u osobe, ktorej má byť dodaný, začína
Dodanie u a reťazové obchody Miesto dodania u - 13/1 ak je dodanie u spojené s odoslaním alebo prepravou u - kde sa nachádza v čase, keď sa odoslanie alebo preprava u osobe, ktorej má byť dodaný, začína
