Úvodní info. Studium
|
|
|
- Milada Doležalová
- před 6 lety
- Počet zobrazení:
Transkript
1 [mozilla le:/home/jiri/www/fch/cz/pomucky/kolafa/n4316.html] 1/16 Úvodní info Jiøí Kolafa Ústav fyzikální chemie V CHT Praha budova A, místnost 325 (zadním vchodem) jiri.kolafa@vscht.cz Web pøedmìtu: : fyzikální a koloidní chemie Studium Bakaláøské pøedmìty Fyzikální a koloidní chemie literatura a pøedná¹ky
2 Chemická kinetika rychlost reakcí a závislost na podmínkách výpoèet slo¾ení v závislosti na èase reakèní mechanismy 2/16 credit: people.bath.ac.uk/ch3mw/photo3.gif
3 Chemická kinetika Klasikace reakcí podle poètu fází: homogenní heterogenní enzymatické provedení: vsádkový (jednorázový) nástøikový (otevøený) kontinuální (prùtokový) podmínek: izotermický { adiabatický izobarický { izochorický Zpùsob aktivace: [show show/ardioxin -S35 -x-2 -Ii% -q] 3/16 katalyzátor (zvy¹uje rychlost pøímé i zpìtné reakce, nemìní rovnová¾nou konstantu) tepelná, jiná reakce, mikrovlny svìtlo (VIS, UV, X), ultrazvuk,...
4 Reakèní rychlost 4/16 i ν i A i Rychlost reakce (ξ = rozsah reakce, [ξ] = mol): J = dξ = 1 dn i ν i Obvykle vzta¾ena na objem (intenzivní velièina): r závisí na zápisu reakce: r = J V = 1 ν i dc i r(2 A A 2 ) = 1 2 r(a 1 2 A 2) výchozí látky (reaktanty) : ν i < produkty: ν i > koncentrace: c i = [A i ] = n i /V rozmìr: mol dm 3 = mol/l = M bezrozmìrná (relativní) koncentrace: c rel i = {A i } = c i /c st, té¾ nepøesnì [A i ]
5 Kinetická (rychlostní) rovnice 5/16 Jednoduchá reakce je dána jednou reakcí a jednou kinetickou rovnicí (která nemusí odpovídat molekularitì) Obecnì: Èasto vyhovuje: k(t) = rychlostní konstanta r = f(c A, c B,..., T) r = k(t) c α A cβ B α, β = dílèí øády (celá èísla pro elementární reakce) n = α + β = (celkový) øád reakce Rozmìr(k) = (mol dm 3 ) 1 n s 1 Èasto se pou¾ívají bezrozmìrné c rel i = c i /c st, pak rozmìr(k) = s 1 Poloèas reakce: c A (zvolené látky) klesne na polovinu c A ( 1/2 ) = c A() 2
6 Formální kinetika homogenních reakcí: bilance 6/16 i ν i A i Konstantní objem: bilance v koncentracích (x = x() = ξ/v): c i = c i, + ν i x Stupeò pøemìny, (stupeò) konverze (k = klíèová slo¾ka ν k < ): Platí α 1 α = c k, c k c k, = ν k x c k, Pøíklad. Nitryl uorid vzniká v plynné fázi reakcí 2 NO 2 (g) + F 2 (g) 2 NO 2 F(g) Reakce je prvního øádu vzhledem k NO 2 i F 2. Napi¹te kinetickou rovnici, probíhá-li reakce za konstantního objemu a znáte-li obì poèáteèní koncentrace, [NO 2 ] a [F 2 ], a rychlostní konstantu, k. dx = d[f 2] = 1 2 d[no2] = 1 2 d[no2f] = k([no2] 2x)([F2] x)
7 Reakce A P Kinetická rovnice: dc A = kc n A pro c A > = pro c A = c A [plot/kinnd.sh] 7/16 Poèáteèní podmínka: c A () = c A Øe¹ení (integrovaný tvar): n= n=1 n=2 n c A () kdy 1/2 c A k < c A /k c A c A /k 2k 1 c A e k ln 2/k 2 1 1/c A +k (1, ) [c 1 n A (, 1) [c 1 n (1 n)k]1/(1 n) A (1 n)k]1/(1 n) < ca 1 n c 1 n A /[(1 n)k] /[(1 n)k] 1 kc A 2 n 1 1 (n 1)k c1 n A
8 Kinetická mìøení 8/16 Integrální data: známe hodnoty koncentrací pro øadu èasù, ( 1, c A,1 ), ( 2, c A,2 ),..., ( N, c A,N ) þ ÿ þje úmìrnýÿ Diferenciální data: známe rychlosti pro øadu èasù, ( 1, r 1 ), ( 2, r 2 ),... { v prùtoèném reaktoru v ustáleném stavu r i c in i c out i { poèáteèní reakèní rychlost (necháme zreagovat málo) Sledování slo¾ení { odebírání vzorkù a analýza, pøíp. po prudkém zchlazení Sledování slo¾ení { pomocí vhodné velièiny (kontinuálnì): mechanické velièiny: (g): manometrie (p), volumetrie (V) (l): dilatometrie ( V), densitometrie (ρ) (s/g): gravimetrie (m) (l/g): tlak nasycených par optické: spektrofotometrie, refraktometrie (index lomu), polarimetrie (optická otáèivost) elektrické: konduktometrie (vodivost), potenciometrie (napìtí), polarograe (napìtí/proud), hmotnostní spektrograe, chromatograe
9 Urèování øádu a rychlostní konstanty Pøíklad pro reakci A P øídící se rovnicí dc/ = kc n Fitování (korelace, regrese): data prolo¾íme metodou nejmen- ¹ích ètvercù køivkou integrované kinetické rovnice c A = c A (c A, k, n; ) Minimalizujeme souèet ètvercù pøes 3 neznámé parametry c A, k, n Matematická formulace: s 2 1 N [ ca (c = min A, k, n; ) c i c A,k,n N 3 i=1 kde σ i je standardní chyba a konc. c A,i (její odhad); pro velká N pak pak s 2 = 1. Neznáme-li σ i, obv. pøedpokládáme, ¾e v¹echny chyby jsou stejné a urèíme je z podmínky s = 1. a þchybaÿ je termín matematické statistiky, v metrologii se pou¾ívá termín þnejistotaÿ σ i ] 2 [plot/kint.sh] 9/16 min c mol L 1 min c mol L 1 min c mol L 1 min c mol L c() = [c 1-n A +(n-1)k] 1/(1-n) 2 k =.977(13) n = 1.5(3) c A = 2.44(3) c A
10 Nemáme-li poèítaè se softwarem... Integrální metoda zkusmo: Pro rùzné øády n vypoèteme rychlostní konstantu z dvojic c( 1 ), c( 2 ), pro rovnici A P: k = c 1 n A1 c1 n A2 (n 1)( 1 2 ) n 1 ln(c A1/c A2 ) 1 2 n = 1 Diferenciální metoda: známe rychlosti ve dvou èasech (nebo pro rùzná poè. slo¾ení) n = ln(r 1/r 2 ) ln(c A1 /c A2 ) Izolaèní metoda (Ostwald): r = kc α A cβ B : c B c A (pøebytek B) r = k c α A Pøíklad (pøedchozí data): 1/ n = 1 n = 2 n = v nouzi { derivace pøibli¾nì: r(.2) [c() c(.4)]/.4 min = 2.32 mol L 1 min 1 r(1.2) [c(.8) c(1.6)]/.8 min =.64 mol L 1 min 1 n ln(2.32/.64) ln(1.779/.675) = 1.39
11 Následné reakce 1. øádu A k 1 Kinetické rovnice: dc A dc B dc C B = k 1 c A k 2 C = k 1 c A k 2 c B = k 2 c B Poèáteèní podmínky: c A () = c A, c B () =, c C () = Øe¹ení: c A = c A e k 1 c B = k 1 k 2 k 1 c A [ e k 1 e k 2 ] pro k 1 k 2 = k 1 c A e k 1 pro k 1 = k 2 c C = c A c A c B c A max B [plot/naslr.sh] 11/16 C k 1 = k 2 Max. koncentrace: max = ln(k 1/k 2 ) pro k k 1 k 1 k 2 2 = 1/k 1 pro k 1 = k 2 radioaktivní rozpad farmakokinetika: k 1 = absorpèní konst. k 2 = eliminaèní konst. Poloèas: 1/2 = ln(2)/k prùchod ¾aludkem 1/2 1 2 h
12 Pou¾ití ve farmakokinetice 12/16 Distribuèní objem V d je objem vody, ve kterém by se muselo léèivo rozpustit, aby bylo dosa¾eno jeho stejné koncentrace jako v krevní plazmì. V d = hmotnost léku hm. konc. v plazmì objem V d /(L kg 1 ) Èasto se udává na kg hmotnosti pacienta: hmotnost léku V d = (hm. konc. v plazmì) (hm. pacienta) voda celkem.6 dìti více, starci ménì z toho intracelulární.4 extracelulární.2 krev celkem.8 z toho plazma.4{.5 Lék dobøe rozpustný ve vodì + proniká bunìènými stìnami + na nic se nevá¾e V d.6 L kg 1. Vá¾e-li se lék na nìco, mù¾e se V d li¹it (mù¾e být i vìt¹í ne¾.6 L kg 1 ) Pokud lék pomalu proniká napø. bunìènou membránou, nutno zlep¹it model (více kompartmentù)
13 Pou¾ití ve farmakokinetice Zjednodu¹ení: jeden kompartment, vstøebávání s absorpèní konstantou k 1, eliminace s eliminaèní konstantou k 2 kinetiky 1. øádu (jiné mo¾nosti:. øád, Michaelis{ {Mentenová) Poèáteèní hm. konc.: c A = hmotnost léku hmotnost pacienta V d Jednorázové podání viz þnásledné reakceÿ Opakované podání k-krát v intervalu a (v èasech, a, 2 a,... (k 1) a ) koncentrace leku v krvi / c a opakovane a jednorazove [pic/farmakokin.sh] 13/16 k 1 =.4/hod k 2 =.1/hod a = 8 hod c = davka/v d k 1c A k 2 k 1 /hod 1 /hod Po mnoha cyklech ( øada) pro 1 = (k 1) a = èas od posl. podání: [ ] e k 1 1 c B = 1 e k e k a 1 e k 2 a = k 1c A e k e k 1 a [ + ae k 1 a 1 e k 1 a ], k 1 k 2, k 1 = k 2
14 Boèní (paralelní) reakce Pøíklad. Rozvìtvená reakce, obì reakce prvního øádu [plot/bocni.sh] 14/16 Kinetické rovnice: dc A dc B dc C A A k 1 k 2 B C = k 1 c A k 2 c A = k 1 c A = k 2 c A Øe¹ení pro c A () = c A, c B () =, c C () = : c A = c A exp[ (k 1 + k 2 )] c B = c A k 1 k 1 + k 2 { 1 exp[ (k1 + k 2 )] } c C = c A k 2 k 1 + k 2 { 1 exp[ (k1 + k 2 )] } Varianty: konkurenèní (A + B, A + C ) jsou-li obì rovnice stejného øádu, platí Wegscheiderùv princip c A c C c B = k 2 k 1 B C k 2 /k 1 = 2
15 Vratné (protismìrné) reakce [plot/vratne.sh] 15/16 Pøíklad. Obì reakce prvního øádu: A k 1 k 1 Kinetická rovnice: dc A = k 1c A + k 1 c B Bilance pro c A () = c A, c B () = : B c A B k 1 :k -1 = 1:2 k 1 :k -1 = 3:2 Øe¹ení: Rovnováha: c A = c A + c B = c A c [ ] A k k 1 + k 1 e (k 1+k ) 1 + k 1 1 lim c A = Rovnová¾ná konstanta: c B( ) c A ( ) = k 1 k 1 = K k 1 k 1 + k 1 c A pro racemizaci (1 opticky aktivní uhlík) K = 1
16 Zákon pùsobení aktivních hmot Guldberg{Waage: Nech» obì reakce v 16/16 A + B k 1 k 1 C + D jsou 1. øádu vzhledem ke ka¾dé slo¾ce (resp. jsou elementární { viz dále). Kinetická rovnice: dc A = k 1c A c B + k 1 c C c D Rovnováha: dc A = èili c C c D c A c B = k 1 k 1 = K kde K je rovnová¾ná konstanta credit: Wikipedia Pro A + B k 1 k 1 C se správným rozmìrem: c Ccst c A c B = k 1c st k 1 = K
Úvodní info. Studium
 [mozilla le:///home/jiri/www/fh/z/pomuky/kolafa/n4341.html] 1/16 Úvodní info Jiøí Kolafa Ústav fyzikální hemie V CHT Praha budova A, místnost 325 (zadním vhodem) jiri.kolafa@vsht.z 2244 4257 Web pøedmìtu:
[mozilla le:///home/jiri/www/fh/z/pomuky/kolafa/n4341.html] 1/16 Úvodní info Jiøí Kolafa Ústav fyzikální hemie V CHT Praha budova A, místnost 325 (zadním vhodem) jiri.kolafa@vsht.z 2244 4257 Web pøedmìtu:
Stanislav Labík. Ústav fyzikální chemie V CHT Praha budova A, 3. patro u zadního vchodu, místnost
 Stanislav Labík Ústav fyzikální chemie V CHT Praha budova A, 3. patro u zadního vchodu, místnost 325 labik@vscht.cz 220 444 257 http://www.vscht.cz/fch/ Výuka Letní semestr N403032 Základy fyzikální chemie
Stanislav Labík Ústav fyzikální chemie V CHT Praha budova A, 3. patro u zadního vchodu, místnost 325 labik@vscht.cz 220 444 257 http://www.vscht.cz/fch/ Výuka Letní semestr N403032 Základy fyzikální chemie
Klasická termodynamika (aneb pøehled FCH I)
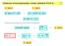 Klasická termodynamika (aneb pøehled FCH I) 1/16 0. zákon 1. zákon id. plyn: pv = nrt pv κ = konst (id., ad.) id. plyn: U = U(T) }{{} Carnotùv cyklus dq T = 0 2. zákon rg, K,... lim S = 0 T 0 S, ds = dq
Klasická termodynamika (aneb pøehled FCH I) 1/16 0. zákon 1. zákon id. plyn: pv = nrt pv κ = konst (id., ad.) id. plyn: U = U(T) }{{} Carnotùv cyklus dq T = 0 2. zákon rg, K,... lim S = 0 T 0 S, ds = dq
Viriálová stavová rovnice 1 + s.1
 Viriálová stavová rovnice 1 + s.1 (Mírnì nestandardní odvození Prùmìrná energie molekul okolo vybrané molekuly (β = 1/(k B T : 0 u(r e βu(r 4πr 2 dr Energie souboru N molekul: U = f 2 k B T + N 2 2V Tlak
Viriálová stavová rovnice 1 + s.1 (Mírnì nestandardní odvození Prùmìrná energie molekul okolo vybrané molekuly (β = 1/(k B T : 0 u(r e βu(r 4πr 2 dr Energie souboru N molekul: U = f 2 k B T + N 2 2V Tlak
Opakování: Standardní stav þ ÿ
 Opakování: Standardní stav þ ÿ s.1 12. øíjna 215 Standardní stav þ ÿ = èistá slo¾ka ve stavu ideálního plynu za teploty soustavy T a standardního tlaku = 1 kpa, døíve 11,325 kpa. Èistá látka: Pøibli¾nì:
Opakování: Standardní stav þ ÿ s.1 12. øíjna 215 Standardní stav þ ÿ = èistá slo¾ka ve stavu ideálního plynu za teploty soustavy T a standardního tlaku = 1 kpa, døíve 11,325 kpa. Èistá látka: Pøibli¾nì:
Matematika II Lineární diferenciální rovnice
 Matematika II Lineární diferenciální rovnice RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Lineární diferenciální rovnice Denice
Matematika II Lineární diferenciální rovnice RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Lineární diferenciální rovnice Denice
Elementární reakce. stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. ) 2 NO 2 ; radioak-
 Elementární reakce 1/15 stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. ) 2 NO 2 ; radioak- reakce monomolekulární (rozpad molekuly: N 2 O 4 tivní rozpad; izomerizace) reakce bimolekulární
Elementární reakce 1/15 stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. ) 2 NO 2 ; radioak- reakce monomolekulární (rozpad molekuly: N 2 O 4 tivní rozpad; izomerizace) reakce bimolekulární
2.4 Stavové chování směsí plynů Ideální směs Ideální směs reálných plynů Stavové rovnice pro plynné směsi
 1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
Matematika II Aplikace derivací
 Matematika II Aplikace derivací RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Derivace slo¾ené funkce Vìta o derivaci slo¾ené funkce.
Matematika II Aplikace derivací RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Derivace slo¾ené funkce Vìta o derivaci slo¾ené funkce.
Aproximace funkcí. Chceme þvzoreèekÿ. Známe: celý prùbìh funkce
 Aproximace funkcí 1/13 Známe: celý prùbìh funkce Chceme þvzoreèekÿ hodnoty ve vybraných bodech, pøíp. i derivace Kvalita údajù: známe pøesnì (máme algoritmus) známe pøibli¾nì (experiment èi simulace) {
Aproximace funkcí 1/13 Známe: celý prùbìh funkce Chceme þvzoreèekÿ hodnoty ve vybraných bodech, pøíp. i derivace Kvalita údajù: známe pøesnì (máme algoritmus) známe pøibli¾nì (experiment èi simulace) {
Fyzikální chemie Úvod do studia, základní pojmy
 Fyzikální chemie Úvod do studia, základní pojmy HMOTA A JEJÍ VLASTNOSTI POSTAVENÍ FYZIKÁLNÍ CHEMIE V PŘÍRODNÍCH VĚDÁCH HISTORIE FYZIKÁLNÍ CHEMIE ZÁKLADNÍ POJMY DEFINICE FORMY HMOTY Formy a nositelé hmoty
Fyzikální chemie Úvod do studia, základní pojmy HMOTA A JEJÍ VLASTNOSTI POSTAVENÍ FYZIKÁLNÍ CHEMIE V PŘÍRODNÍCH VĚDÁCH HISTORIE FYZIKÁLNÍ CHEMIE ZÁKLADNÍ POJMY DEFINICE FORMY HMOTY Formy a nositelé hmoty
Fyzikální chemie. Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302. 14. února 2013
 Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
Termochemie { práce. Práce: W = s F nebo W = F ds. Objemová práce (p vn = vnìj¹í tlak): W = p vn dv. Vratný dìj: p = p vn (ze stavové rovnice) W =
 Termochemie { práce Práce: W = s F nebo W = Objemová práce (p vn = vnìj¹í tlak): W = V2 V 1 p vn dv s2 Vratný dìj: p = p vn (ze stavové rovnice) W = V2 V 1 p dv s 1 F ds s.1 Diferenciální tvar: dw = pdv
Termochemie { práce Práce: W = s F nebo W = Objemová práce (p vn = vnìj¹í tlak): W = V2 V 1 p vn dv s2 Vratný dìj: p = p vn (ze stavové rovnice) W = V2 V 1 p dv s 1 F ds s.1 Diferenciální tvar: dw = pdv
Mol. fyz. a termodynamika
 Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Rovnováha kapalina{pára u binárních systémù
 Rovnováha kapalina{pára u binárních systémù 1 Pøedpoklad: 1 kapalná fáze Oznaèení: molární zlomky v kapalné fázi: x i molární zlomky v plynné fázi: y i Poèet stupòù volnosti: v = k f + 2 = 2 stav smìsi
Rovnováha kapalina{pára u binárních systémù 1 Pøedpoklad: 1 kapalná fáze Oznaèení: molární zlomky v kapalné fázi: x i molární zlomky v plynné fázi: y i Poèet stupòù volnosti: v = k f + 2 = 2 stav smìsi
Matematika II Urèitý integrál
 Matematika II Urèitý integrál RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Motivace Je dána funkce f(x) = 2 + x2 x 4. Urèete co
Matematika II Urèitý integrál RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Motivace Je dána funkce f(x) = 2 + x2 x 4. Urèete co
Exponenciální rozdìlení
 Exponenciální rozdìlení Ing. Michael Rost, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích Katedra aplikované matematiky a informatiky Exponenciální rozdìlení Exp(A, λ) "Rozdìlení bez pamìti" Exponenciální
Exponenciální rozdìlení Ing. Michael Rost, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích Katedra aplikované matematiky a informatiky Exponenciální rozdìlení Exp(A, λ) "Rozdìlení bez pamìti" Exponenciální
9. Chemické reakce Kinetika
 Základní pojmy Kinetické rovnice pro celistvé řády Katalýza Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti reakční mechanismus elementární reakce a molekularita reakce reakční rychlost
Základní pojmy Kinetické rovnice pro celistvé řády Katalýza Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti reakční mechanismus elementární reakce a molekularita reakce reakční rychlost
Matematika II Limita a spojitost funkce, derivace
 Matematika II Limita a spojitost funkce, derivace RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Prstencové a kruhové okolí bodu
Matematika II Limita a spojitost funkce, derivace RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Prstencové a kruhové okolí bodu
Elektrochemie. Pøedmìt elektrochemie: disociace (roztoky elektrolytù, taveniny solí) vodivost jevy na rozhraní s/l (elektrolýza, èlánky)
 Elektrochemie 1 Pøedmìt elektrochemie: disociace (roztoky elektrolytù, taveniny solí) vodivost jevy na rozhraní s/l (elektrolýza, èlánky) Vodièe: I. tøídy { vodivost zpùsobena pohybem elektronù uvnitø
Elektrochemie 1 Pøedmìt elektrochemie: disociace (roztoky elektrolytù, taveniny solí) vodivost jevy na rozhraní s/l (elektrolýza, èlánky) Vodièe: I. tøídy { vodivost zpùsobena pohybem elektronù uvnitø
Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C;
![Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C;](/thumbs/56/39180690.jpg) Rychlost chemické reakce A B time rychlost = - [A] t rychlost = [B] t Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; 1 1 R A = RB = R 2 3 C Př.: Určete rychlost rozkladu HI v následující
Rychlost chemické reakce A B time rychlost = - [A] t rychlost = [B] t Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; 1 1 R A = RB = R 2 3 C Př.: Určete rychlost rozkladu HI v následující
Chemická kinetika. Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky)
 Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost průběhu
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost průběhu
Vybrané kapitoly z fyzikální chemie
 Vybrané kapitoly z fyzikální chemie c Jiří Kolafa (4. ledna 2013, 23. dubna 2018) mujweb.cz/kolafa Ústav Fyzikální chemie, VŠCHT Praha Tato skripta jsou uceleným učebním textem pro předměty Fyzikální a
Vybrané kapitoly z fyzikální chemie c Jiří Kolafa (4. ledna 2013, 23. dubna 2018) mujweb.cz/kolafa Ústav Fyzikální chemie, VŠCHT Praha Tato skripta jsou uceleným učebním textem pro předměty Fyzikální a
5. CHEMICKÉ REAKTORY
 5. CHEMICÉ REAORY 5.1 IZOERMNÍ REAORY... 5.1.1 Diskontinuální reaktory... 5.1. Průtočné reaktory... 5.1..1 Průtočné reaktory s pístovým tokem... 5.1.. Průtočné reaktory s dokonale promíchávaným obsahem...4
5. CHEMICÉ REAORY 5.1 IZOERMNÍ REAORY... 5.1.1 Diskontinuální reaktory... 5.1. Průtočné reaktory... 5.1..1 Průtočné reaktory s pístovým tokem... 5.1.. Průtočné reaktory s dokonale promíchávaným obsahem...4
Reakční kinetika. Nauka zabývající se rychlostí chemických reakcí a ovlivněním rychlosti těchto reakcí
 Nauka zabývající se rychlostí chemických reakcí a ovlivněním rychlosti těchto reakcí Vymezení pojmů : chemická reakce je děj, při kterém zanikají výchozí látky a vznikají látky nové reakční mechanismus
Nauka zabývající se rychlostí chemických reakcí a ovlivněním rychlosti těchto reakcí Vymezení pojmů : chemická reakce je děj, při kterém zanikají výchozí látky a vznikají látky nové reakční mechanismus
Vybrané kapitoly z fyzikální chemie
 Vybrané kapitoly z fyzikální chemie c Jiří Kolafa (4. ledna 2013, 23. dubna 2018) mujweb.cz/kolafa Ústav Fyzikální chemie, VŠCHT Praha Tato skripta jsou uceleným učebním textem pro předměty Fyzikální a
Vybrané kapitoly z fyzikální chemie c Jiří Kolafa (4. ledna 2013, 23. dubna 2018) mujweb.cz/kolafa Ústav Fyzikální chemie, VŠCHT Praha Tato skripta jsou uceleným učebním textem pro předměty Fyzikální a
2. KINETICKÁ ANALÝZA HOMOGENNÍCH REAKCÍ
 2. KINETICKÁ ANALÝZA HOMOGENNÍCH REAKCÍ Úloha 2-1 Řád reakce a rychlostní konstanta integrální metodou stupeň přeměny... 2 Úloha 2-2 Řád reakce a rychlostní konstanta integrální metodou... 2 Úloha 2-3
2. KINETICKÁ ANALÝZA HOMOGENNÍCH REAKCÍ Úloha 2-1 Řád reakce a rychlostní konstanta integrální metodou stupeň přeměny... 2 Úloha 2-2 Řád reakce a rychlostní konstanta integrální metodou... 2 Úloha 2-3
kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ]
![kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ] kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ]](/thumbs/98/135866737.jpg) KINETIKA JEDNODUCHÝCH REAKCÍ Různé vyjádření reakční rychlosti a rychlostní konstanty 1 Rychlost reakce, rychlosti přírůstku a úbytku jednotlivých složek Rozklad kyseliny dusité je popsán stechiometrickou
KINETIKA JEDNODUCHÝCH REAKCÍ Různé vyjádření reakční rychlosti a rychlostní konstanty 1 Rychlost reakce, rychlosti přírůstku a úbytku jednotlivých složek Rozklad kyseliny dusité je popsán stechiometrickou
Termodynamické zákony
 Termodynamické zákony Makroskopická práce termodynamické soustavy Již jsme uvedli, že změna vnitřní energie soustavy je obecně vyvolána dvěma ději: tepelnou výměnou mezi soustavou a okolím a konáním práce
Termodynamické zákony Makroskopická práce termodynamické soustavy Již jsme uvedli, že změna vnitřní energie soustavy je obecně vyvolána dvěma ději: tepelnou výměnou mezi soustavou a okolím a konáním práce
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru. Petr Svačina
 Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Molekulová fyzika a termika. Přehled základních pojmů
 Molekulová fyzika a termika Přehled základních pojmů Kinetická teorie látek Vychází ze tří experimentálně ověřených poznatků: 1) Látky se skládají z částic - molekul, atomů nebo iontů, mezi nimiž jsou
Molekulová fyzika a termika Přehled základních pojmů Kinetická teorie látek Vychází ze tří experimentálně ověřených poznatků: 1) Látky se skládají z částic - molekul, atomů nebo iontů, mezi nimiž jsou
Elementární reakce. stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. )
 Elementární reakce /27 stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. ) 2 NO 2 ; radioak- reakce monomolekulární (rozpad molekuly: N 2 O 4 tivní rozpad; izomerizace) reakce bimolekulární
Elementární reakce /27 stechiometrický zápis vystihuje mechanismus (Cl. + H 2 HCl + H. ) 2 NO 2 ; radioak- reakce monomolekulární (rozpad molekuly: N 2 O 4 tivní rozpad; izomerizace) reakce bimolekulární
IDEÁLNÍ PLYN. Stavová rovnice
 IDEÁLNÍ PLYN Stavová rovnice Ideální plyn ) rozměry molekul jsou zanedbatelné vzhledem k jejich vzdálenostem 2) molekuly plynu na sebe působí jen při vzájemných srážkách 3) všechny srážky jsou dokonale
IDEÁLNÍ PLYN Stavová rovnice Ideální plyn ) rozměry molekul jsou zanedbatelné vzhledem k jejich vzdálenostem 2) molekuly plynu na sebe působí jen při vzájemných srážkách 3) všechny srážky jsou dokonale
Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Farmakokinetická analýza
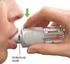 Farmakokinetická analýza Doc. PharmDr. František Štaud, Ph.D. Katedra farmakologie a toxikologie Univerzita Karlova v Praze Farmaceutická fakulta v Hradci Králové PK analýza Vliv organismu na lék Vliv
Farmakokinetická analýza Doc. PharmDr. František Štaud, Ph.D. Katedra farmakologie a toxikologie Univerzita Karlova v Praze Farmaceutická fakulta v Hradci Králové PK analýza Vliv organismu na lék Vliv
FARMAKOKINETIKA PODÁNÍ LÉČIVA (JEDNORÁZOVÉ, OPAKOVANÉ) Pavel Jeřábek
 FARMAKOKINETIKA PODÁNÍ LÉČIVA (JEDNORÁZOVÉ, OPAKOVANÉ) Pavel Jeřábek METABOLIZACE ZPŮSOBY APLIKACE Sublingvální nitroglycerin ph ionizace, lipofilita, ochrana před prvním průchodem játry, rychlá resorpce
FARMAKOKINETIKA PODÁNÍ LÉČIVA (JEDNORÁZOVÉ, OPAKOVANÉ) Pavel Jeřábek METABOLIZACE ZPŮSOBY APLIKACE Sublingvální nitroglycerin ph ionizace, lipofilita, ochrana před prvním průchodem játry, rychlá resorpce
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky)
 Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch H + O, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch H + O, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost
Přírodní vědy - Chemie vymezení zájmu
 Přírodní vědy - Chemie vymezení zájmu Hmota Hmota má dualistický, korpuskulárně (částicově) vlnový charakter. Převládající charakter: korpuskulární (částicový) - látku vlnový - pole. Látka se skládá z
Přírodní vědy - Chemie vymezení zájmu Hmota Hmota má dualistický, korpuskulárně (částicově) vlnový charakter. Převládající charakter: korpuskulární (částicový) - látku vlnový - pole. Látka se skládá z
Rychlost chemické reakce
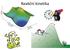 Reakční kinetika Rychlost chemické reakce A B energeticky minimální reakční cesta Rare event vznik/zánik vazeb ~1-10 fs Náhodnost reakce ~ms až roky P R Rychlost chemické reakce A B energeticky minimální
Reakční kinetika Rychlost chemické reakce A B energeticky minimální reakční cesta Rare event vznik/zánik vazeb ~1-10 fs Náhodnost reakce ~ms až roky P R Rychlost chemické reakce A B energeticky minimální
Fyzikální chemie. 1.2 Termodynamika
 Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 12
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 2 Termodynamika reálných plynů část 2 Hana Charvátová, Dagmar Janáčová Zlín 203 Tento studijní
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY VYBRANÉ STATĚ Z PROCESNÍHO INŢENÝRSTVÍ cvičení 2 Termodynamika reálných plynů část 2 Hana Charvátová, Dagmar Janáčová Zlín 203 Tento studijní
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Fyzikální chemie. ochrana životního prostředí analytická chemie chemická technologie denní. Platnost: od 1. 9. 2009 do 31. 8. 2013
 Učební osnova předmětu Fyzikální chemie Studijní obor: Aplikovaná chemie Zaměření: Forma vzdělávání: Celkový počet vyučovacích hodin za studium: Analytická chemie Chemická technologie Ochrana životního
Učební osnova předmětu Fyzikální chemie Studijní obor: Aplikovaná chemie Zaměření: Forma vzdělávání: Celkový počet vyučovacích hodin za studium: Analytická chemie Chemická technologie Ochrana životního
Teorie Pøíèné vlny se ¹íøí v napjaté strunì pøibli¾nì rychlostí. v =
 24. roèník, úloha V. E... strunatci (8 bodù; prùmìr 4,80; øe¹ilo 5 studentù) Vytvoøte si zaøízení, na kterém bude moci být upevnìna struna (èi gumièka) s promìnlivou délkou tak, ¾e bude napínána stále
24. roèník, úloha V. E... strunatci (8 bodù; prùmìr 4,80; øe¹ilo 5 studentù) Vytvoøte si zaøízení, na kterém bude moci být upevnìna struna (èi gumièka) s promìnlivou délkou tak, ¾e bude napínána stále
v trojúhelníku P QC sestrojíme vý¹ky na základnu a jedno rameno, patu vý¹ky na rameno oznaèíme R a patu na základnu S
 Øe¹ení 5. série IV. roèníku kategorie JUNIOR RS-IV-5-1 Pro na¹e úvahy bude vhodné upravit si na¹í rovnici do tvaru 3 jx 1 4 j+2 = 5 + 4 sin 2x: Budeme uva¾ovat o funkci na pravé stranì na¹í rovnice, tj.
Øe¹ení 5. série IV. roèníku kategorie JUNIOR RS-IV-5-1 Pro na¹e úvahy bude vhodné upravit si na¹í rovnici do tvaru 3 jx 1 4 j+2 = 5 + 4 sin 2x: Budeme uva¾ovat o funkci na pravé stranì na¹í rovnice, tj.
5. PRŮTOČNÉ HOMOGENNÍ REAKTORY
 5. PRŮTOČNÉ HOMOGENNÍ REAKTORY Úloha 5-1 Diskontinuální a průtočný reaktor s pístovým tokem... 2 Úloha 5-2 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 5-3 Protisměrné reakce
5. PRŮTOČNÉ HOMOGENNÍ REAKTORY Úloha 5-1 Diskontinuální a průtočný reaktor s pístovým tokem... 2 Úloha 5-2 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 5-3 Protisměrné reakce
a) Jaká je hodnota polytropického exponentu? ( 1,5257 )
 Ponorka se potopí do 50 m. Na dně ponorky je výstupní tunel o průměru 70 cm a délce, m. Tunel je napojen na uzavřenou komoru o objemu 4 m. Po otevření vnějšího poklopu vnikne z části voda tunelem do komory.
Ponorka se potopí do 50 m. Na dně ponorky je výstupní tunel o průměru 70 cm a délce, m. Tunel je napojen na uzavřenou komoru o objemu 4 m. Po otevření vnějšího poklopu vnikne z části voda tunelem do komory.
Adsorpce. molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth{Fajans výmìnná iontová adsorpce, protionty v aluminosilikátech
 Adsorpce molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth{Fajans výmìnná iontová adsorpce, protionty v aluminosilikátech 1/16 Ar na gratu adsorpce: na povrch/rozhraní absorpce: dovnitø
Adsorpce molekulární adsorpce: (g) (s), (l) (s)/(l),... iontová adsorpce Paneth{Fajans výmìnná iontová adsorpce, protionty v aluminosilikátech 1/16 Ar na gratu adsorpce: na povrch/rozhraní absorpce: dovnitø
TERMOMECHANIKA 1. Základní pojmy
 1 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 1. Základní pojmy OSNOVA 1. KAPITOLY Termodynamická soustava Energie, teplo,
1 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 1. Základní pojmy OSNOVA 1. KAPITOLY Termodynamická soustava Energie, teplo,
J., HÁJEK B., VOTINSKÝ J.
 Kontakty a materiály J. Šedlbauer e-mail: josef.sedlbauer@tul.cz tel.: 48-535-3375 informace a materiály k Obecné chemii: www.fp.tul.cz/kch/sedlbauer (odkaz na předmět) konzultace: úterý odpoledne nebo
Kontakty a materiály J. Šedlbauer e-mail: josef.sedlbauer@tul.cz tel.: 48-535-3375 informace a materiály k Obecné chemii: www.fp.tul.cz/kch/sedlbauer (odkaz na předmět) konzultace: úterý odpoledne nebo
Matematika I Ètvercové matice - determinanty
 Matematika I Ètvercové matice - determinanty RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Co u¾ známe? vektory - základní operace
Matematika I Ètvercové matice - determinanty RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Co u¾ známe? vektory - základní operace
Výroba tablet. Inženýrství chemicko-farmaceutických výrob. Lisování tablet. POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY
 Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
Lisování tablet Výroba tablet GRANULÁT POMOCNÉ LÁTKY (kluzné látky, rozvolňovadla) LÉČIVÉ LÁTKY POMOCNÉ LÁTKY plniva, suchá pojiva, kluzné látky, rozvolňovadla tabletování z granulátu homogenizace TABLETOVINA
Rozpustnost s. Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku.
 Rozpustnost 1 Rozpustnost s Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku. NASYCENÝ = při určité t a p se již více látky
Rozpustnost 1 Rozpustnost s Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku. NASYCENÝ = při určité t a p se již více látky
Termodynamika a živé systémy. Helena Uhrová
 Termodynamika a živé systémy Helena Uhrová Základní pojmy termodynamiky soustava izolovaná otevřená okolí vlastnosti soustavy znaky popisující soustavu stav rovnováhy tok m či E =0 funkce stavu - soubor
Termodynamika a živé systémy Helena Uhrová Základní pojmy termodynamiky soustava izolovaná otevřená okolí vlastnosti soustavy znaky popisující soustavu stav rovnováhy tok m či E =0 funkce stavu - soubor
Chemická kinetika. Reakce 1. řádu rychlost přímo úměrná koncentraci složky
 Chemická kinetika Chemická kinetika Reakce 0. řádu reakční rychlost nezávisí na čase a probíhá konstantní rychlostí v = k (rychlost se rovná rychlostní konstantě) velmi pomalé reakce (prakticky se nemění
Chemická kinetika Chemická kinetika Reakce 0. řádu reakční rychlost nezávisí na čase a probíhá konstantní rychlostí v = k (rychlost se rovná rychlostní konstantě) velmi pomalé reakce (prakticky se nemění
Chemická kinetika. Chemické změny probíhající na úrovni atomárně molekulové nazýváme reakční mechanismus.
 Chemická kinetika Chemická reakce: děj mezi jednotlivými atomy a molekulami, při kterých zanikají některé vazby v molekulách výchozích látek a jsou nahrazovány vazbami v molekulách nově vznikajících látek.
Chemická kinetika Chemická reakce: děj mezi jednotlivými atomy a molekulami, při kterých zanikají některé vazby v molekulách výchozích látek a jsou nahrazovány vazbami v molekulách nově vznikajících látek.
CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL.
 CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL. Látkové množství Značka: n Jednotka: mol Definice: Jeden mol je množina, která má stejný počet prvků, jako je atomů ve 12 g nuklidu
CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL. Látkové množství Značka: n Jednotka: mol Definice: Jeden mol je množina, která má stejný počet prvků, jako je atomů ve 12 g nuklidu
10. Chemické reaktory
 10. Chemické reaktory V každé chemické technologii je základní/nejvýznamnější zařízení pro provedení chemické reakce chemický reaktor. Celý technologický proces se skládá v podstatě ze tří typů zařízení:
10. Chemické reaktory V každé chemické technologii je základní/nejvýznamnější zařízení pro provedení chemické reakce chemický reaktor. Celý technologický proces se skládá v podstatě ze tří typů zařízení:
h nadmořská výška [m]
![h nadmořská výška [m] h nadmořská výška [m]](/thumbs/92/109475205.jpg) Katedra prostředí staveb a TZB KLIMATIZACE, VĚTRÁNÍ Cvičení pro navazující magisterské studium studijního oboru Prostředí staveb Cvičení č. 1 Zpracoval: Ing. Zdeněk GALDA Nové výukové moduly vznikly za
Katedra prostředí staveb a TZB KLIMATIZACE, VĚTRÁNÍ Cvičení pro navazující magisterské studium studijního oboru Prostředí staveb Cvičení č. 1 Zpracoval: Ing. Zdeněk GALDA Nové výukové moduly vznikly za
pevná látka tekutina (kapalina, plyn) (skripta str )
 Reakce v heterogenních soustavách pevná látka tekutina (kapalina, plyn) (skripta str. 90-03) Rozpouštění pevných látek s chemickou reakcí (např. Mg 3(s) + HN 3(l) ) CVD - Chemical Vapor Deposition (SiH
Reakce v heterogenních soustavách pevná látka tekutina (kapalina, plyn) (skripta str. 90-03) Rozpouštění pevných látek s chemickou reakcí (např. Mg 3(s) + HN 3(l) ) CVD - Chemical Vapor Deposition (SiH
Model dokonalého spalování pevných a kapalných paliv Teoretické základy spalování. Teoretické základy spalování
 Spalování je fyzikálně chemický pochod, při kterém probíhá organizovaná příprava hořlavé směsi paliva s okysličovadlem a jejich slučování (hoření) za intenzivního uvolňování tepla, což způsobuje prudké
Spalování je fyzikálně chemický pochod, při kterém probíhá organizovaná příprava hořlavé směsi paliva s okysličovadlem a jejich slučování (hoření) za intenzivního uvolňování tepla, což způsobuje prudké
3 Základní modely reaktorů
 3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
Úloha 1-39 Teplotní závislost rychlostní konstanty, reakce druhého řádu... 11
 1. ZÁKLADNÍ POJMY Úloha 1-1 Různé vyjádření reakční rychlosti rychlosti přírůstku a úbytku jednotlivých složek... 2 Úloha 1-2 Různé vyjádření reakční rychlosti změna celkového látkového množství... 2 Úloha
1. ZÁKLADNÍ POJMY Úloha 1-1 Různé vyjádření reakční rychlosti rychlosti přírůstku a úbytku jednotlivých složek... 2 Úloha 1-2 Různé vyjádření reakční rychlosti změna celkového látkového množství... 2 Úloha
STRUKTURA A VLASTNOSTI PLYNŮ POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D09_Z_OPAK_T_Plyny_T Člověk a příroda Fyzika Struktura a vlastnosti plynů Opakování
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D09_Z_OPAK_T_Plyny_T Člověk a příroda Fyzika Struktura a vlastnosti plynů Opakování
Fyzika. 7. Motor o příkonu 5 kw pracuje s účinností 80 %. Pracuje-li 1 hodinu, vykoná práci: a) 14, J b) Wh c) 4 kwh d) kj
 Fyzika 1. Která veličina je bezrozměrná? a) permitivita prostředí b) relativní permeabilita prostředí c) zvětšení čočky d) absolutní index lomu prostředí 2. Do odměrného válce o vnitřním průměru 50 mm
Fyzika 1. Která veličina je bezrozměrná? a) permitivita prostředí b) relativní permeabilita prostředí c) zvětšení čočky d) absolutní index lomu prostředí 2. Do odměrného válce o vnitřním průměru 50 mm
Příklady k opakování TERMOMECHANIKY
 Příklady k opakování TERMOMECHANIKY P1) Jaký teoretický výkon musí mít elektrický vařič, aby se 12,5 litrů vody o teplotě 14 C za 15 minuty ohřálo na teplotu 65 C, jestliže hustota vody je 1000 kg.m -3
Příklady k opakování TERMOMECHANIKY P1) Jaký teoretický výkon musí mít elektrický vařič, aby se 12,5 litrů vody o teplotě 14 C za 15 minuty ohřálo na teplotu 65 C, jestliže hustota vody je 1000 kg.m -3
Poznámky k cvičením z termomechaniky Cvičení 3.
 Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
Základem molekulové fyziky je kinetická teorie látek. Vychází ze tří pouček:
 Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
LOGO. Struktura a vlastnosti plynů Ideální plyn
 Struktura a vlastnosti plynů Ideální plyn Ideální plyn Protože popsat chování plynů je nad naše možnosti, zavádíme zjednodušený model tzv. ideálního plynu, který má tyto vlastnosti: Částice ideálního plynu
Struktura a vlastnosti plynů Ideální plyn Ideální plyn Protože popsat chování plynů je nad naše možnosti, zavádíme zjednodušený model tzv. ideálního plynu, který má tyto vlastnosti: Částice ideálního plynu
Termodynamika 2. UJOP Hostivař 2014
 Termodynamika 2 UJOP Hostivař 2014 Skupenské teplo tání/tuhnutí je (celkové) teplo, které přijme pevná látka při přechodu na kapalinu během tání nebo naopak Značka Veličina Lt J Nedochází při něm ke změně
Termodynamika 2 UJOP Hostivař 2014 Skupenské teplo tání/tuhnutí je (celkové) teplo, které přijme pevná látka při přechodu na kapalinu během tání nebo naopak Značka Veličina Lt J Nedochází při něm ke změně
PROTOLYTICKÉ ROVNOVÁHY
 PROTOLYTICKÉ ROVNOVÁHY Protolytické rovnováhy - úvod Obecná chemická reakce a A + b B c C + d D Veličina Symbol, jednotka Definice rovnovážná konstanta reakce K K = ac C a d D a a A a b B aktivita a a
PROTOLYTICKÉ ROVNOVÁHY Protolytické rovnováhy - úvod Obecná chemická reakce a A + b B c C + d D Veličina Symbol, jednotka Definice rovnovážná konstanta reakce K K = ac C a d D a a A a b B aktivita a a
Hydrochemie koncentrace látek (výpočty)
 1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
MODELOVÁNÍ. Základní pojmy. Obecný postup vytváření induktivních modelů. Měřicí a řídicí technika magisterské studium FTOP - přednášky ZS 2009/10
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
Zákony ideálního plynu
 5.2Zákony ideálního plynu 5.1.1 Ideální plyn 5.1.2 Avogadrův zákon 5.1.3 Normální podmínky 5.1.4 Boyleův-Mariottův zákon Izoterma 5.1.5 Gay-Lussacův zákon 5.1.6 Charlesův zákon 5.1.7 Poissonův zákon 5.1.8
5.2Zákony ideálního plynu 5.1.1 Ideální plyn 5.1.2 Avogadrův zákon 5.1.3 Normální podmínky 5.1.4 Boyleův-Mariottův zákon Izoterma 5.1.5 Gay-Lussacův zákon 5.1.6 Charlesův zákon 5.1.7 Poissonův zákon 5.1.8
Teplota a její měření
 Teplota a její měření Teplota a její měření Číslo DUM v digitálním archivu školy VY_32_INOVACE_07_03_01 Teplota, Celsiova a Kelvinova teplotní stupnice, převodní vztahy, příklady. Tepelná výměna, měrná
Teplota a její měření Teplota a její měření Číslo DUM v digitálním archivu školy VY_32_INOVACE_07_03_01 Teplota, Celsiova a Kelvinova teplotní stupnice, převodní vztahy, příklady. Tepelná výměna, měrná
Termodynamické potenciály
 Kapitola 1 Termodynamické potenciály 11 Vnitřní energie a U-formulace Fyzikání význam vnitřní energie: v průběhu adiabatického děje je vykonaná práce rovna úbytku vnitřní energie Platí pro vratné i pro
Kapitola 1 Termodynamické potenciály 11 Vnitřní energie a U-formulace Fyzikání význam vnitřní energie: v průběhu adiabatického děje je vykonaná práce rovna úbytku vnitřní energie Platí pro vratné i pro
VLASTNOSTI PARAMETRY SVÍTIDLA VÝHODY NA PØÁNÍ
 PARAMETRY SVÍTIDLA Krytí optické èásti: Krytí elektrické èásti: Odolnost proti nárazu (sklo): Napájecí napìtí: El. tøída izolace: Hmotnost: TECEO 1 TECEO 2 Instalaèní výška: TECEO 1 TECEO 2 VÝHODY NA PØÁNÍ
PARAMETRY SVÍTIDLA Krytí optické èásti: Krytí elektrické èásti: Odolnost proti nárazu (sklo): Napájecí napìtí: El. tøída izolace: Hmotnost: TECEO 1 TECEO 2 Instalaèní výška: TECEO 1 TECEO 2 VÝHODY NA PØÁNÍ
část 6, díl 5, kapitola 1, str. 1 prosinec 2002
 S R O J N IC K Á P Ř ÍR U Č K A část 6, díl 5, kapitola 1, str 1 6/51 E M P IR IC K É Z Á K O N Y Předmětem zájmu termodynamiky jsou především děje probíhající v látkách ve skupenství plynném a děje související
S R O J N IC K Á P Ř ÍR U Č K A část 6, díl 5, kapitola 1, str 1 6/51 E M P IR IC K É Z Á K O N Y Předmětem zájmu termodynamiky jsou především děje probíhající v látkách ve skupenství plynném a děje související
na stabilitu adsorbovaného komplexu
 Vliv velikosti částic aktivního kovu na stabilitu adsorbovaného komplexu Jiří Švrček Ing. Petr Kačer, Ph.D. Ing. David Karhánek Ústav organické technologie VŠCHT Praha Hydrogenace Základní proces chemického
Vliv velikosti částic aktivního kovu na stabilitu adsorbovaného komplexu Jiří Švrček Ing. Petr Kačer, Ph.D. Ing. David Karhánek Ústav organické technologie VŠCHT Praha Hydrogenace Základní proces chemického
Základní chemické výpočty I
 Základní chemické výpočty I Tomáš Kučera tomas.kucera@lfmotol.cuni.cz Ústav lékařské chemie a klinické biochemie 2. lékařská fakulta, Univerzita Karlova v Praze a Fakultní nemocnice v Motole 2017 Relativní
Základní chemické výpočty I Tomáš Kučera tomas.kucera@lfmotol.cuni.cz Ústav lékařské chemie a klinické biochemie 2. lékařská fakulta, Univerzita Karlova v Praze a Fakultní nemocnice v Motole 2017 Relativní
1. Látkové soustavy, složení soustav
 , složení soustav 1 , složení soustav 1. Základní pojmy 1.1 Hmota 1.2 Látky 1.3 Pole 1.4 Soustava 1.5 Fáze a fázové přeměny 1.6 Stavové veličiny 1.7 Složka 2. Hmotnost a látkové množství 3. Složení látkových
, složení soustav 1 , složení soustav 1. Základní pojmy 1.1 Hmota 1.2 Látky 1.3 Pole 1.4 Soustava 1.5 Fáze a fázové přeměny 1.6 Stavové veličiny 1.7 Složka 2. Hmotnost a látkové množství 3. Složení látkových
Numerická derivace a kvadratura
 Numerická derivce kvdrtur 1/7 kvdrtur = výpoèet urèitého integrálu jednodimenzionální Dt prolo¾it vhodnou funkcí tu pk derivovt/integrovt. Vhodné, jsou-li dt ztí¾en chybmi. Pøíkld: Shomteov rovnice C pm(t)
Numerická derivce kvdrtur 1/7 kvdrtur = výpoèet urèitého integrálu jednodimenzionální Dt prolo¾it vhodnou funkcí tu pk derivovt/integrovt. Vhodné, jsou-li dt ztí¾en chybmi. Pøíkld: Shomteov rovnice C pm(t)
Vícefázové reaktory. Probublávaný reaktor plyn kapalina katalyzátor. Zuzana Tomešová
 Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
Vícefázové reaktory Probublávaný reaktor plyn kapalina katalyzátor Zuzana Tomešová 2008 Probublávaný reaktor plyn - kapalina - katalyzátor Hydrogenace méně těkavých látek za vyššího tlaku Kolony naplněné
9. Struktura a vlastnosti plynů
 9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
Stanovení optimálních teplot výpalu vápenců z různých lokalit a jejich souvislostí s fyzikálními vlastnostmi vápenců
 Stanovení optimálních teplot výpalu vápenců z různých lokalit a jejich souvislostí s fyzikálními vlastnostmi vápenců Ing. Radovan Nečas, Ing. Dana Kubátová, Ph.D., Ing. Jiří Junek, Ing. Vladimír Těhník
Stanovení optimálních teplot výpalu vápenců z různých lokalit a jejich souvislostí s fyzikálními vlastnostmi vápenců Ing. Radovan Nečas, Ing. Dana Kubátová, Ph.D., Ing. Jiří Junek, Ing. Vladimír Těhník
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP. Termodynamika. Příklad 10
 Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
Biofyzika laboratorní cvičení
 Biofyzika laboratorní cvičení Cvičení z biofyziky 1. A) Stanovení koncentrace glukosy polarimetricky B) Mutarotace glukosy C) Refraktometrie 2. A) Potenciometrické stanovení disociační konstanty B) Kapacita
Biofyzika laboratorní cvičení Cvičení z biofyziky 1. A) Stanovení koncentrace glukosy polarimetricky B) Mutarotace glukosy C) Refraktometrie 2. A) Potenciometrické stanovení disociační konstanty B) Kapacita
TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY.
 TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY. T.Lederer 10.1.2013 OBSAH Obsah... 2 Stručný popis ČOV... 3 Instalace rámů s nanovlákenným nosičem do aktivační nádrže AN 2 a
TECHNOLOGIE ČIŠTĚNÍ ODPADNÍCH VOD S VYUŢITÍM NANOVLÁKENNÉHO NOSIČE BIOMASY. T.Lederer 10.1.2013 OBSAH Obsah... 2 Stručný popis ČOV... 3 Instalace rámů s nanovlákenným nosičem do aktivační nádrže AN 2 a
Bezpečnost chemických výrob N111001
 Bezpečnost chemických výrob N111001 Petr Zámostný místnost: A-72a tel.: 4222 e-mail: petr.zamostny@vscht.cz Specifická rizika chemických reakcí Reaktivita látek Laboratorní měření reaktivity Reaktory s
Bezpečnost chemických výrob N111001 Petr Zámostný místnost: A-72a tel.: 4222 e-mail: petr.zamostny@vscht.cz Specifická rizika chemických reakcí Reaktivita látek Laboratorní měření reaktivity Reaktory s
Fluktuace termodynamických veličin
 Kvantová a statistická fyzika (Termodynamika a statistická fyzika Fluktuace termodynamických veličin Fluktuace jsou odchylky hodnot fyzikálních veličin od svých středních (rovnovážných hodnot. Mají původ
Kvantová a statistická fyzika (Termodynamika a statistická fyzika Fluktuace termodynamických veličin Fluktuace jsou odchylky hodnot fyzikálních veličin od svých středních (rovnovážných hodnot. Mají původ
Pravdìpodobnostní popis
 Pravdìpodobnostní popis 1/19 klasická mechanika { stav = { r 1,..., r N, p 1,..., p N } stavù je { hustota pravdìpodobnosti stavù ρ( r 1,..., r N, p 1,..., p N ) kvantové mechaniky { stav = stavù je koneènì
Pravdìpodobnostní popis 1/19 klasická mechanika { stav = { r 1,..., r N, p 1,..., p N } stavù je { hustota pravdìpodobnosti stavù ρ( r 1,..., r N, p 1,..., p N ) kvantové mechaniky { stav = stavù je koneènì
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
ČVUT v Praze, fakulta stavební katedra hydrauliky a hydrologie (K4) Přednáškové slidy předmětu 4 HYA (Hydraulika) verze: 09/008 K4 Fv ČVUT Tato webová stránka nabízí k nahlédnutí/stažení řadu pdf souborů
Matematická statistika
 Matematická statistika 1/30 Náhodná/stochastická promìnná pøiøazuje pravdìpodobnost/hustotu pravdìpodobnosti mo¾nému diskrétnímu/spojitému jevu z diskrétní/spojité mno¾iny jevù. diskrétní pøíklad: hod
Matematická statistika 1/30 Náhodná/stochastická promìnná pøiøazuje pravdìpodobnost/hustotu pravdìpodobnosti mo¾nému diskrétnímu/spojitému jevu z diskrétní/spojité mno¾iny jevù. diskrétní pøíklad: hod
VÝPO C TY. Tomáš Kuc era & Karel Kotaška
 ZÁKLADNÍ CHEMICKÉ VÝPO C TY I Tomáš Kuc era & Karel Kotaška tomas.kucera@lfmotol.cuni.cz Ústav lékar ské chemie a klinické biochemie 2. lékar ská fakulta, Univerzita Karlova v Praze a Fakultní nemocnice
ZÁKLADNÍ CHEMICKÉ VÝPO C TY I Tomáš Kuc era & Karel Kotaška tomas.kucera@lfmotol.cuni.cz Ústav lékar ské chemie a klinické biochemie 2. lékar ská fakulta, Univerzita Karlova v Praze a Fakultní nemocnice
Osnova pro předmět Fyzikální chemie II magisterský kurz
 Osnova pro předmět Fyzikální chemie II magisterský kurz Časový a obsahový program přednášek Týden Obsahová náplň přednášky Pozn. Stavové chování tekutin 1,2a 1, 2a Molekulární přístup kinetická teorie
Osnova pro předmět Fyzikální chemie II magisterský kurz Časový a obsahový program přednášek Týden Obsahová náplň přednášky Pozn. Stavové chování tekutin 1,2a 1, 2a Molekulární přístup kinetická teorie
Elektrické jevy na membránách
 Elektrické jevy na membránách Polopropustná (semipermeabilní) membrána; frita, diafragma propou¹tí ionty, vzniká el. napìtí rùzné koncentrace iontù na obou stranách rùzná propustnost/difuzivita pro rùzné
Elektrické jevy na membránách Polopropustná (semipermeabilní) membrána; frita, diafragma propou¹tí ionty, vzniká el. napìtí rùzné koncentrace iontù na obou stranách rùzná propustnost/difuzivita pro rùzné
Potenciometrie. Obr.1 Schema základního uspořádání elektrochemické cely pro potenciometrická měření
 Potenciometrie 1.Definice Rovnovážná potenciometrie je analytickou metodou, při níž se analyt stanovuje ze změřeného napětí elektrochemického článku, tvořeného indikační elektrodou ponořenou do analyzovaného
Potenciometrie 1.Definice Rovnovážná potenciometrie je analytickou metodou, při níž se analyt stanovuje ze změřeného napětí elektrochemického článku, tvořeného indikační elektrodou ponořenou do analyzovaného
