Digitální učební materiál
|
|
|
- Marcela Šimková
- před 6 lety
- Počet zobrazení:
Transkript
1 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/ Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_158_IVT Autor: Ing. Pavel Bezděk Tematický okruh: Algoritmy Datum tvorby: září 2013 Ročník: 4. ročník a oktáva Anotace: Algoritmus XVIII. Algoritmus interpolačních polynomů I. Lagrangeův polynom Metodický pokyn: Při výuce nutno postupovat individuálně. Pokud není uvedeno jinak, je použitý materiál z vlastních zdrojů autora DUM.
2 Autor Ing. Pavel Bezděk Vytvořeno dne Odpilotováno dne ve třídě 4.A Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Klíčová slova Informatika a informační a komunikační technologie Informatika a výpočetní technika Algoritmus Algoritmus XVIII. - Algoritmus interpolačních polynomů I. - Lagrangeův polynom Algoritmus, Lagrangeův interpolační polynom Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Pavel Bezděk. Dostupné z Metodického portálu ; ISSN Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání pedagogických pracovníků (NÚV).
3 Lagrangeův interpolační polynom
4 Interpolace x extrapolace Interpolace je přibližný výpočet hodnot funkce v bodě, které leží uvnitř daného intervalu int(x 0,x 1,x 2, x n ). Extrapolace je přibližný výpočet hodnot funkce v bodě, které leží vně intervalu int(x 0,x 1,x 2, x n ) z hodnot funkce v krajních bodech x 0 a x n, popř. i z hodnot funkce v některých vnitřních bodech intervalu int(x 0,x 1,x 2, x n ). Chyba výpočtu může být velká. Ale pro x velmi blízká koncovým bodům intervalu int(x 0,x 1,x 2, x n ), lze dostat dobré výsledky.
5 Interpolace x extrapolace Vypočteme bod funkce. mezi známými body funkce. Vypočteme bod funkce.mimo známé body funkce.
6 Interpolační podmínky Předpokládejme nyní, že funkce f je dána pouze svou hodnotou v n+1 bodech x 0, x 1, x 2,..x n a že chceme najít aproximaci ϕ takovou, která napodobuje chování funkce f v okolí všech těchto bodů. Např. funkce zadané tabulkou. O tabulkových bodech x i i=0, 1, 2, n, v nichž jsou zadané hodnoty f(x i ), budeme předpokládat, že jsou navzájem různé. Budeme se při interpolaci snažit volit funkci ϕ tak, aby platilo ϕ(x i )= f(x i ) i= 0,1,2.n (interpolační podmínky) tj. aby přesně nabývala zadaných funkčních hodnot. Existuje takový interpolační polynom pro funkci f v bodech x 0, x 1, x 2,.. x n a budeme ho značit L n a nazývat Lagrangeův interpolační polynom. Tabulkovým bodům x 0, x 1, x 2,.. x n budeme říkat uzly interpolace. Lagrangeův interpolační polynom
7 Lagrangeův interpolační polynom (Polynom n-tého stupně: P n (x)=p 0 +p 1 x+p 2 x 2 + p 3 x p n x n nejvyšší mocnina x je n-tá x n a p n 0) kde l i jsou polynomy n- tého stupně takové, že platí l i (x k ) = 0 pro k i l i (x k ) = 1 pro k=i (x i jsou navzájem různé, i=0,1,2, n) i, k = 0,1,2, n Polynom l i má tedy kořeny x 0,x 1,..x i-1, x i+1,..x n a můžeme jej zapsat ve tvaru:
8 Výpočet Lagrangeova polynomu Funkce f dána svými hodnotami v bodech x 0 =0, x 1 =1, x 2 =-1, x 3 =3, f(0)=1, f(1)=2, f(-1)=2, f(3)=0. Vypočítáme přibližnou hodnotu f(2) pomocí Lagrangeova interpolačního polynomu l o (x) = ((x-1)(x+1)(x-3))/((0-1)(0+1)(0-3)) = 1/3(x-1)(x+1)(x-3) l o (2) =-1 l 1 (x) = ((x-0)(x+1)(x-3))/((1-0)(1+1)(1-3)) = (1/(-4))x(x+1)(x-3) l 1 (2) = 3/2 l 2 (x) = ((x-0)(x-1)(x-3))/((-1-0)(-1-1)(-1-3)) = (1/(-8))x(x-1)(x-3) l 2 (2) = 1/4 l 3 (x) = ((x-0)(x-1)(x+1))/((3-0)(3-1)(3+1)) = (1/24)x(x+1)(x-3) l 3 (2) = 1/4 L 3 (2) = 1. (-1)+2. 3/2+2. 1/4+0. 1/4 = 5/2 f(2) Lagrangeův polynom: L 3 = 1. l o (x) +2. l 1 (x) +2. l 2 (x) +0. l 3 (x) L 3 = (1/3)(x-1)(x+1)(x-3)-(1/2)x(x+1)(x-3) (1/4)x(x-1)(x-3) L 3 (2) = -(5/12)x 3 + x 2 + (5/12)x +1
9 Lineární a kvadratická interpolace Lineární interpolace n=1, máme známé 2 body funkce, aproximujeme polynomem 1.stupně P 1 = p 0 +p 1 x jeho grafem je přímka spojující 2 známé body funkce, vypočtený bod tedy leží na této přímce. Používáme třeba při práci s tabulkami. Kvadratická interpolace n=2, máme známé 3 body funkce, aproximujeme polynomem 2.stupně P 2 = p 0 +p 1 x +p 2 x 2 jeho grafem je parabola spojující 3 známé body funkce, vypočtený bod tedy leží na této parabole. Kvadratická interpolace je přesnější než lineární interpolace (kromě případů, když funkce f je lineární).
10 Výpočet lineární a kvadratické interpolace Tabulka hodnot funkce f(x)=sin(x), máme dopočítat hodnotu sin z hodnot v bodech x 0 =20, x 1 =21,x 2 =22. x =20,3 sin (x) 0, , ,37461 Lineární interpolace: L 1 (x) = f(x 0 ) (x-x 1 )/(x 0 -x 1 ) + f(x 1 ) (x-x 0 )/(x 1 -x 0 ) sin ,34202(20,3-21)/(20-21) + 0,35837 (20,3-20)/(21-20)= =0, ,34693 Kvadratická interpolace: L 2 (x) = f(x 0 )((x-x 1 )(x-x 2 ))/((x 0 -x 1 ) (x 0 -x 2 ) +f(x 1 )((x-x 0 )(x-x 2 ))/((x 1 -x 0 )(x 1 -x 2 )) + f(x 2 ) ((x-x 0 )(x-x 1 ))/((x 2 -x 0 )(x 2 -x 1 )) sin ,34202 ((20,3-21)(20,3-22))/((20-21)(20-22)) +0,35837((20,3-20) (20,3-22))/((21-20)(21-22)) +0,37461 ((20,3-20)(20,3-21))/((22-20)(22-21)) = 0, ,34694 Přesná hodnota sin = 0, , Vidíme, že kvadratická interpolace je přesnější, ale v tomto případě přesnost lineární interpolace byla dostačující.
11 program Lagrange; uses crt; const n=10; type pole=array[1..n] of real; var xx,yy: pole; x,y: real; i,k,l,mm:byte; procedure nacti(m:byte;var aa,bb:pole); var d:byte; g,gg:real; begin end; for d:=1 to m do begin writeln(' Zadej souradnice ',d,'. bodu:'); write(' x='); readln(g); aa[d]:=g; write(' y='); procedure tisk(m:byte;aa,bb:pole); var t:byte; readln(gg); bb[d]:=gg; end; begin writeln; for t:=1 to m do write(' f(',aa[t]:5:3,')=',bb[t]:5:3,' '); writeln; end; Lagrangeova interpolace Pascal
12 procedure lagran(m:byte; a:real; aa,bb:pole; var ss:real); var q,qq:byte; s,j,z:real; begin ss:=0; for q:=1 to m do begin s:=1; j:=1; z:=0; if q=1 then for qq:=2 to m do begin s:=s*(a-aa[qq]); j:=j*(aa[q]-aa[qq]) end else if q<m then begin for qq:=1 to q-1 do begin s:=s*(a-aa[qq]); j:=j*(aa[q]-aa[qq]) end; for qq:=q+1 to m do begin s:=s*(a-aa[qq]); j:=j*(aa[q]-aa[qq]) end end else for qq:=1 to m-1 do begin s:=s*(a-aa[qq]); j:=j*(aa[q]-aa[qq]) end; z:=((s/j)*bb[q]); write(' f(x',q,')*l',q,'=',z:5:3,' '); ss:=ss+z; end; writeln; end;
13 begin clrscr; writeln(' Zadej pocet bodu: Maximum = ',n); read(mm); writeln(' Zadej x-souradnici hledaneho bodu: '); readln(x); writeln; nacti(mm,xx,yy); writeln; lagran(mm,x,xx,yy,y); writeln; writeln(' Zadane body : '); tisk(mm,xx,yy); writeln; writeln( ' Hodnota Lagrangeova polynomu L',mm,'(',x:3:2,') =',y:10:3); repeat until keypressed; end.
14 // Lagrangeuv interpolacni polynom #include <iostream> #include <stdlib.h> //#include <conio.h> const int N=50; using namespace std; Lagrangeuv interpolační polynom C++ int main() { double x[n],y[n]; // tabulka funkce double x0,fx0,cit,jm; // x0 -> bod, v nemz urcujeme funkcni hodnotu int i,n,p; cout<<endl<<" Lagrangeuv interpolacni polynom."<<endl; cout <<endl<< " Zadejte pocet vstupnich bodu (max. 50):"<<endl; cout<<" Pocet bodu: "; cin >> n; cout<<endl; cout << " Zadejte tabulku:"<<endl; for(i=0;i<n;i++) {cout<<" x["<<i<<"]= "; cin >>x[i]; cout<<" y["<<i<<"]= "; cin >>y[i];} Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Pavel Bezděk. Dostupné z Metodického portálu ; ISSN Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání pedagogických pracovníků (NÚV).
15 cout << endl<<" Zadejte hodnotu x0, pro niz chceme urcit y=f(x0)"<<endl; cout<<" x0 = "; cin >> x0; cout<<endl; for (i=0;i<n;i++) {cout<<" x["<<i<<"]="<<x[i]<<" y["<<i<<"]="<<y[i]<<endl;} fx0=0; for( int i=0; i<n; i++) { cit=1; jm= 1; if (i==0) {for ( p=1; p<n;p++) {cit *=(x0-x[p]); jm *=(x[i] - x[p]); } } else if (i<(n-1)) { for ( p=0; p<(i);p++) {cit *=(x0-x[p]); jm *=(x[i] - x[p]); } for(p=(i+1); p<n;p++) {cit *=(x0-x[p]); jm *=(x[i] - x[p]); } } else { for(p=0; p<(n-1);p++) {cit *=(x0-x[p]); jm *=(x[i] - x[p]); } } fx0 +=((cit/jm)*y[i]); } cout<<endl<<" f("<<x0<<") = "<<fx0<<endl; return 0; } Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Pavel Bezděk. Dostupné z Metodického portálu ; ISSN Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání pedagogických pracovníků (NÚV).
16 Použité zdroje PŘIKRYL, Petr. Numerické metody analýzy. Praha: Státní nakladatelství technické literatury, MATEMATIKA PRO VYSOKÉ ŠKOLY TECHNICKÉ, sešit XXIV.
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_156_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_156_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_144_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_144_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_149_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_149_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_145_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_145_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_154_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_154_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_147_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_147_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_142_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_142_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_150_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_150_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_143_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_143_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_148_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_148_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_153_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_153_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_146_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_146_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení
 Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Aproximace funkcí. x je systém m 1 jednoduchých, LN a dostatečně hladkých funkcí. x c m. g 1. g m. a 1. x a 2. x 2 a k. x k b 1. x b 2.
 Aproximace funkcí Aproximace je výpočet funkčních hodnot funkce z nějaké třídy funkcí, která je v určitém smyslu nejbližší funkci nebo datům, která chceme aproximovat. Třída funkcí, ze které volíme aproximace
Aproximace funkcí Aproximace je výpočet funkčních hodnot funkce z nějaké třídy funkcí, která je v určitém smyslu nejbližší funkci nebo datům, která chceme aproximovat. Třída funkcí, ze které volíme aproximace
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_141_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_141_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL
 APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
Aplikovaná matematika I
 Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Interpolace, aproximace
 11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice. sin x + x 2 2 = 0.
 A 9 vzorové řešení Př. 1. Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice Počítejte v radiánech, ne ve stupních! sin x + x 2 2 = 0. Rovnici lze upravit na sin
A 9 vzorové řešení Př. 1. Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice Počítejte v radiánech, ne ve stupních! sin x + x 2 2 = 0. Rovnici lze upravit na sin
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
3. Derivace funkce Definice 3.1. Nechť f : R R je definována na nějakém okolí U(a) bodu a R. Pokud existuje limita f(a + h) f(a) lim
 3 a b s = (a + b) 2 f(s) 3,46 4,680 3,93-2,9422 3,93 4,680 4,2962-2,034 4,2962 4,680 4,4886-0,0954 4,4886 4,680 4,5848 3,2095 4,4886 4,5848 4,5367,0963 4,4886 4,5367 4,526 0,427 4,4886 4,526 4,5006 0,508
3 a b s = (a + b) 2 f(s) 3,46 4,680 3,93-2,9422 3,93 4,680 4,2962-2,034 4,2962 4,680 4,4886-0,0954 4,4886 4,680 4,5848 3,2095 4,4886 4,5848 4,5367,0963 4,4886 4,5367 4,526 0,427 4,4886 4,526 4,5006 0,508
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
 Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Martin Flusser. Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague. October 17, 2016
 ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
ZPRO cvičení 2 Martin Flusser Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague October 17, 2016 Outline I 1 Outline 2 Proměnné 3 Proměnné - cvičení 4 Funkce 5 Funkce
Aproximace funkcí. Numerické metody 6. května FJFI ČVUT v Praze
 Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Lineární a polynomická regrese, interpolace, hledání v tabulce
 co byste měli umět po dnešní lekci: proložit body přímku, parabolu,... a určit chyby parametrů (u přímky) interpolovat mezi hodnotami v tabulce hledat v tabulce (1D) prokládání (fitování) křivek metoda
co byste měli umět po dnešní lekci: proložit body přímku, parabolu,... a určit chyby parametrů (u přímky) interpolovat mezi hodnotami v tabulce hledat v tabulce (1D) prokládání (fitování) křivek metoda
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_141_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_141_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
úloh pro ODR jednokrokové metody
 Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Numerické řešení diferenciálních rovnic
 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Čebyševovy aproximace
 Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
4 Numerické derivování a integrace
 Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
Numerická matematika Banka řešených příkladů
 Numerická matematika Banka řešených příkladů Radek Kučera, Pavel Ludvík, Zuzana Morávková Katedra matematiky a deskriptivní geometrie Vysoká škola báňská Technická Univerzita Ostrava K D M G ISBN 978-80-48-894-6
Numerická matematika Banka řešených příkladů Radek Kučera, Pavel Ludvík, Zuzana Morávková Katedra matematiky a deskriptivní geometrie Vysoká škola báňská Technická Univerzita Ostrava K D M G ISBN 978-80-48-894-6
5. Interpolace a aproximace funkcí
 5. Interpolace a aproximace funkcí Průvodce studiem Často je potřeba složitou funkci f nahradit funkcí jednodušší. V této kapitole budeme předpokládat, že u funkce f známe její funkční hodnoty f i = f(x
5. Interpolace a aproximace funkcí Průvodce studiem Často je potřeba složitou funkci f nahradit funkcí jednodušší. V této kapitole budeme předpokládat, že u funkce f známe její funkční hodnoty f i = f(x
Numerické algoritmy KAPITOLA 11. Vyhledávání nulových bodů funkcí
 Numerické algoritmy KAPITOLA 11 V této kapitole: Vyhledávání nulových bodů funkcí Iterativní výpočet hodnot funkce Interpolace funkcí Lagrangeovou metodou Derivování funkcí Integrování funkcí Simpsonovou
Numerické algoritmy KAPITOLA 11 V této kapitole: Vyhledávání nulových bodů funkcí Iterativní výpočet hodnot funkce Interpolace funkcí Lagrangeovou metodou Derivování funkcí Integrování funkcí Simpsonovou
Interpolace Lagrangeovy polynomy. 29. října 2012
 Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Přijímací zkouška z informatiky Dz
 Přijímací zkouška z informatiky Dz Každý příklad je hodnocen osmi body. Je dovoleno používat počítací stroje a není dovoleno používat matematické tabulky. Hodnotí se nejen výsledek, ale i postup. 1. Určete
Přijímací zkouška z informatiky Dz Každý příklad je hodnocen osmi body. Je dovoleno používat počítací stroje a není dovoleno používat matematické tabulky. Hodnotí se nejen výsledek, ale i postup. 1. Určete
Typy příkladů na písemnou část zkoušky 2NU a vzorová řešení (doc. Martišek 2017)
 Typy příkladů na písemnou část zkoušky NU a vzorová řešení (doc. Martišek 07). Vhodnou iterační metodou (tj. metodou se zaručenou konvergencí) řešte soustavu: x +x +4x 3 = 3.5 x 3x +x 3 =.5 x +x +x 3 =.5
Typy příkladů na písemnou část zkoušky NU a vzorová řešení (doc. Martišek 07). Vhodnou iterační metodou (tj. metodou se zaručenou konvergencí) řešte soustavu: x +x +4x 3 = 3.5 x 3x +x 3 =.5 x +x +x 3 =.5
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/ Anotace. Diferenciální počet VY_32_INOVACE_M0216.
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace pomocí splajnu
 Interpolace pomocí splajnu Interpolace pomocí splajnu Připomenutí U interpolace požadujeme, aby graf aproximující funkce procházel všemi uzlovými body. Interpolační polynom aproximující funkce je polynom
Interpolace pomocí splajnu Interpolace pomocí splajnu Připomenutí U interpolace požadujeme, aby graf aproximující funkce procházel všemi uzlovými body. Interpolační polynom aproximující funkce je polynom
VÝUKOVÝ MATERIÁL. Bratislavská 2166, Varnsdorf, IČO: tel Číslo projektu
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
APROXIMACE FUNKCÍ V MA TLABU ' Část 3. - Lazran eův inter olační 01 mom v Matlabu
 APROXIMACE FUKCÍ V MA TLABU ' Část 3. - Lazran eův inter olační 0 mom v Matlabu I Jiří Kulička Umverzna Pardubice, Dopravru fakulta Jana Pcrnera. Katedra Informatiky v dopravě University oj Pardubice.
APROXIMACE FUKCÍ V MA TLABU ' Část 3. - Lazran eův inter olační 0 mom v Matlabu I Jiří Kulička Umverzna Pardubice, Dopravru fakulta Jana Pcrnera. Katedra Informatiky v dopravě University oj Pardubice.
Numerické metody a statistika
 Numerické metody a statistika Radek Kučera VŠB-TU Ostrava 016-017 ( ) Numerické metody a statistika 016-017 1 / Numerické integrování ( ) Numerické metody a statistika 016-017 / Geometrický význam integrálu
Numerické metody a statistika Radek Kučera VŠB-TU Ostrava 016-017 ( ) Numerické metody a statistika 016-017 1 / Numerické integrování ( ) Numerické metody a statistika 016-017 / Geometrický význam integrálu
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Optické vlastnosti oka Číslo DUM: III/2/FY/2/3/17 Vzdělávací předmět: Fyzika Tematická oblast:
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Optické vlastnosti oka Číslo DUM: III/2/FY/2/3/17 Vzdělávací předmět: Fyzika Tematická oblast: Optika Autor: Ing. Markéta Střelcová Anotace: Žák se seznámí
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Optické vlastnosti oka Číslo DUM: III/2/FY/2/3/17 Vzdělávací předmět: Fyzika Tematická oblast: Optika Autor: Ing. Markéta Střelcová Anotace: Žák se seznámí
Obsah. Metodický list Metodický list Metodický list Metodický list
 METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
PRÁVNÍ ZÁKLADY STÁTU- ÚSTAVA
 PRÁVNÍ ZÁKLADY STÁTU- ÚSTAVA Dostupné z Metodického portálu www.rvp.cz ; ISSN 1802-4785. Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání pedagogických
PRÁVNÍ ZÁKLADY STÁTU- ÚSTAVA Dostupné z Metodického portálu www.rvp.cz ; ISSN 1802-4785. Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání pedagogických
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Hustota Číslo DUM: III/2/FY/2/1/9 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Hustota Číslo DUM: III/2/FY/2/1/9 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Hustota Číslo DUM: III/2/FY/2/1/9 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Sada 1 - Základy programování
 S třední škola stavební Jihlava Sada 1 - Základy programování 14. Strukturované datové typy - pole, záznam, množina Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 1 - Základy programování 14. Strukturované datové typy - pole, záznam, množina Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/ Anotace. Diferenciální počet VY_32_INOVACE_M0217.
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Několik příkladů v Turbo Pascalu
 Kapitola 5 Několik příkladů v Turbo Pascalu V literatuře [3] se student mohl seznámit s podprogramy standardních jednotek Turbo Pascalu. V následujících dvou částech uvedeme ukázku několika příkladů využívajících
Kapitola 5 Několik příkladů v Turbo Pascalu V literatuře [3] se student mohl seznámit s podprogramy standardních jednotek Turbo Pascalu. V následujících dvou částech uvedeme ukázku několika příkladů využívajících
Integrace funkcí více proměnných, numerické metody
 Matematika III 6. přednáška Integrace funkcí více proměnných, numerické metody Michal Bulant Masarykova univerzita Fakulta informatiky 27. 10. 2010 Obsah přednášky 1 Literatura 2 Integrální počet více
Matematika III 6. přednáška Integrace funkcí více proměnných, numerické metody Michal Bulant Masarykova univerzita Fakulta informatiky 27. 10. 2010 Obsah přednášky 1 Literatura 2 Integrální počet více
Střední odborná škola a Střední odborné učiliště, Hořovice
 Kód DUM : VY_32_INOVACE_DYN.1.07 Název materiálu: Anotace Autor Jazyk Očekávaný výstup 07 Vytvoření šablony webové stránky pro výuku PHP DUM dává žákům k dispozici jednotnou výukovou šablonu pro psaní
Kód DUM : VY_32_INOVACE_DYN.1.07 Název materiálu: Anotace Autor Jazyk Očekávaný výstup 07 Vytvoření šablony webové stránky pro výuku PHP DUM dává žákům k dispozici jednotnou výukovou šablonu pro psaní
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Skládání a rozkládání sil Číslo DUM: III/2/FY/2/1/17 Vzdělávací předmět: Fyzika Tematická oblast:
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Skládání a rozkládání sil Číslo DUM: III/2/FY/2/1/17 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Skládání a rozkládání sil Číslo DUM: III/2/FY/2/1/17 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra
INTERPOLAČNÍ POLYNOM. F (x)... hledaná funkce (polynom nebo funkce vytvořená z polynomů), pro kterou platí
 8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace Kateřina Konečná/1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení:
8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace Kateřina Konečná/1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení:
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Výpočty s hustotou Číslo DUM: III/2/FY/2/1/10 Vzdělávací předmět: Fyzika Tematická oblast:
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Výpočty s hustotou Číslo DUM: III/2/FY/2/1/10 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Výpočty s hustotou Číslo DUM: III/2/FY/2/1/10 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Číslo projektu: CZ.1.07/1.4.00/ Název DUM: Lom světla II.část Číslo DUM: III/2/FY/2/3/18 Vzdělávací předmět: Fyzika Tematická oblast: Optika
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Lom světla II.část Číslo DUM: III/2/FY/2/3/18 Vzdělávací předmět: Fyzika Tematická oblast: Optika Autor: Ing. Markéta Střelcová Anotace: Žák se seznámí
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Lom světla II.část Číslo DUM: III/2/FY/2/3/18 Vzdělávací předmět: Fyzika Tematická oblast: Optika Autor: Ing. Markéta Střelcová Anotace: Žák se seznámí
Numerická matematika Písemky
 Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
A 9. Počítejte v radiánech, ne ve stupních!
 A 9 Př.. Je dána rovnice sin + 2 = 0. Najděte interval délky, v němž leží kořen rovnice. Metodou půlení intervalů tento interval zužte až na interval délky 0,25. Pak kořen najděte s přesností ε = 0,00
A 9 Př.. Je dána rovnice sin + 2 = 0. Najděte interval délky, v němž leží kořen rovnice. Metodou půlení intervalů tento interval zužte až na interval délky 0,25. Pak kořen najděte s přesností ε = 0,00
Programovací jazyk Pascal
 Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí.
 NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, Radovan.Potucek@unob.cz, tel. 443056 -----
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, Radovan.Potucek@unob.cz, tel. 443056 -----
Diferenciál a Taylorův polynom
 Diferenciál a Taylorův polynom Základy vyšší matematiky lesnictví LDF MENDELU c Simona Fišnarová (MENDELU) Diferenciál a Taylorův polynom ZVMT lesnictví 1 / 11 Aproximace funkce v okoĺı bodu Danou funkci
Diferenciál a Taylorův polynom Základy vyšší matematiky lesnictví LDF MENDELU c Simona Fišnarová (MENDELU) Diferenciál a Taylorův polynom ZVMT lesnictví 1 / 11 Aproximace funkce v okoĺı bodu Danou funkci
Přijímací zkoušky z matematiky pro akademický rok 2016/17 NMgr. studium Učitelství matematiky ZŠ, SŠ
 Přijímací zkoušky z matematiky pro akademický rok 6/7 NMgr. studium Učitelství matematiky ZŠ, SŠ Datum zkoušky: Varianta Registrační číslo uchazeče: Příklad 3 5 Celkem Body Ke každému příkladu uved te
Přijímací zkoušky z matematiky pro akademický rok 6/7 NMgr. studium Učitelství matematiky ZŠ, SŠ Datum zkoušky: Varianta Registrační číslo uchazeče: Příklad 3 5 Celkem Body Ke každému příkladu uved te
Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková. Výukový materiál
 1 Výukový materiál Identifikační údaje škol Všší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 07 7 Varnsdorf, IČO: 1838387 www.vosassvdf.cz, tel. +2012372632 Číslo
1 Výukový materiál Identifikační údaje škol Všší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 07 7 Varnsdorf, IČO: 1838387 www.vosassvdf.cz, tel. +2012372632 Číslo
Klasický podprogram, který nazýváme procedura. Jedná se v podstatě o příkaz. 1
 Kapitola 3 Podprogramy Jak již název napovídá, podprogram je část programu ( malý program), která může být kdykoliv v příkazové části programu (hlavního, velkého programu) aktivována. V jazyce Pascalu
Kapitola 3 Podprogramy Jak již název napovídá, podprogram je část programu ( malý program), která může být kdykoliv v příkazové části programu (hlavního, velkého programu) aktivována. V jazyce Pascalu
Podprogramy; procedury a funkce
 Kapitola 2 Podprogramy; procedury a funkce Jak již víme, program je v Pascalu blok, který označujeme jménem uvedeným v hlavičce programu Hlavička programu i blok jsou syntakticky definované kategorie Pascalu,
Kapitola 2 Podprogramy; procedury a funkce Jak již víme, program je v Pascalu blok, který označujeme jménem uvedeným v hlavičce programu Hlavička programu i blok jsou syntakticky definované kategorie Pascalu,
1. Chyby vstupních dat metody převedení úlohy na numerickou (řád použité metody) zaokrouhlovací reprezentace čísel v počítači
 1. Chyby vstupních dat metody převedení úlohy na numerickou (řád použité metody) zaokrouhlovací reprezentace čísel v počítači 2. Reprezentace čísel v Pascalu celá čísla Typ Rozsah Formát shortint 128..127
1. Chyby vstupních dat metody převedení úlohy na numerickou (řád použité metody) zaokrouhlovací reprezentace čísel v počítači 2. Reprezentace čísel v Pascalu celá čísla Typ Rozsah Formát shortint 128..127
Funkce. Mocninné funkce. Mgr. Tomáš Pavlica, Ph.D. Digitální učební materiály, Gymnázium Uherské Hradiště.
 Funkce Mocninné funkce Mgr. Tomáš Pavlica, Ph.D. Gymnázium Uherské Hradiště Digitální učební materiály, 2012-14 Obsah Mocninné funkce 1 Mocninné funkce mocninné funkce s celým kladným mocnitelem mocninné
Funkce Mocninné funkce Mgr. Tomáš Pavlica, Ph.D. Gymnázium Uherské Hradiště Digitální učební materiály, 2012-14 Obsah Mocninné funkce 1 Mocninné funkce mocninné funkce s celým kladným mocnitelem mocninné
C++ Akademie SH. 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory. Michal Kvasni ka. 20. b ezna Za áte níci C++
 C++ Akademie SH 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory Za áte níci C++ 20. b ezna 2011 Obsah 1 Prom nné - primitivní typy Celá ísla ƒísla s pohyblivou desetinnou árkou, typ bool 2 Podmínka
C++ Akademie SH 2. Prom nné, podmínky, cykly, funkce, rekurze, operátory Za áte níci C++ 20. b ezna 2011 Obsah 1 Prom nné - primitivní typy Celá ísla ƒísla s pohyblivou desetinnou árkou, typ bool 2 Podmínka
Zlín, 23. října 2011
 (. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
(. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
Numerická matematika 1
 Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/ Anotace. Integrální počet. Substituce v určitém integrálu VY_32_INOVACE_M0311
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..7/.5./. Zlepšení podmínek pro výuku
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..7/.5./. Zlepšení podmínek pro výuku
Břetislav Fajmon, UMAT FEKT, VUT Brno. Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu.
 Břetislav Fajmon, UMAT FEKT, VUT Brno Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu. Na jiných příkladech je téma podrobně zpracováno ve skriptech
Břetislav Fajmon, UMAT FEKT, VUT Brno Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu. Na jiných příkladech je téma podrobně zpracováno ve skriptech
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 1 / 40 regula Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague regula 1 2 3 4 5 regula 6 7 8 2 / 40 2 / 40 regula Iterační pro nelineární e Bud f reálná funkce
1 / 40 regula Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague regula 1 2 3 4 5 regula 6 7 8 2 / 40 2 / 40 regula Iterační pro nelineární e Bud f reálná funkce
Úvod do programování
 Úvod do programování Základní literatura Töpfer, P.: Algoritmy a programovací techniky, Prometheus, Praha učebnice algoritmů, nikoli jazyka pokrývá velkou část probíraných algoritmů Satrapa, P.: Pascal
Úvod do programování Základní literatura Töpfer, P.: Algoritmy a programovací techniky, Prometheus, Praha učebnice algoritmů, nikoli jazyka pokrývá velkou část probíraných algoritmů Satrapa, P.: Pascal
Téma je podrobně zpracováno ve skriptech [1], kapitola
![Téma je podrobně zpracováno ve skriptech [1], kapitola Téma je podrobně zpracováno ve skriptech [1], kapitola](/thumbs/39/19231280.jpg) Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 6. Základní aproximační úlohu lze popsat následovně: Jsou dány body [x 0, y 0 ], [x 1, y 1 ],..., [x n, y n
Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 6. Základní aproximační úlohu lze popsat následovně: Jsou dány body [x 0, y 0 ], [x 1, y 1 ],..., [x n, y n
Aproximace a interpolace
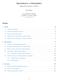 Aproximace a interpolace Matematické algoritmy (11MAG) Jan Přikryl 12. přednáška 11MAG pondělí 15. prosince 2014 verze:2014-12-15 11:10 Obsah 1 Úlohy 2 1.1 Aproximace funkcí...................................
Aproximace a interpolace Matematické algoritmy (11MAG) Jan Přikryl 12. přednáška 11MAG pondělí 15. prosince 2014 verze:2014-12-15 11:10 Obsah 1 Úlohy 2 1.1 Aproximace funkcí...................................
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření teploty Číslo DUM: III/2/FY/2/1/14 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření teploty Číslo DUM: III/2/FY/2/1/14 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření teploty Číslo DUM: III/2/FY/2/1/14 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Hledání extrémů funkcí
 Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
INTERPOLAČNÍ POLYNOM.... hledaná funkce (polynom nebo funkce vytvořená z polynomů), pro kterou platí
 8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace 1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení: P (n) množina všech
8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace 1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení: P (n) množina všech
Cvičení 9 - Monitory. monitor m; var proměnné... procedure p; begin... end; begin inicializace; end;
 Cvičení 9 - Monitory na rozdíl od semaforů je monitor jazyková konstrukce monitor = Pascalský blok podobný proceduře nebo fci uvnitř monitoru jsou definovány proměnné, procedury a fce proměnné monitoru
Cvičení 9 - Monitory na rozdíl od semaforů je monitor jazyková konstrukce monitor = Pascalský blok podobný proceduře nebo fci uvnitř monitoru jsou definovány proměnné, procedury a fce proměnné monitoru
2.1 Podmínka typu case Cykly Cyklus s podmínkou na začátku Cyklus s podmínkou na konci... 5
 Obsah Obsah 1 Řídicí struktury 1 2 Podmínka 1 2.1 Podmínka typu case......................... 2 3 Příkaz skoku 3 4 Cykly 4 4.1 Cyklus s podmínkou na začátku................... 4 4.2 Cyklus s podmínkou
Obsah Obsah 1 Řídicí struktury 1 2 Podmínka 1 2.1 Podmínka typu case......................... 2 3 Příkaz skoku 3 4 Cykly 4 4.1 Cyklus s podmínkou na začátku................... 4 4.2 Cyklus s podmínkou
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 2018 Řešení příkladů pečlivě odůvodněte. Příklad 1 (2 bodů) Studijní program: Studijní obory: Varianta A Matematika MMUI Navrhněte deterministický konečný
Přijímací zkouška na navazující magisterské studium 2018 Řešení příkladů pečlivě odůvodněte. Příklad 1 (2 bodů) Studijní program: Studijní obory: Varianta A Matematika MMUI Navrhněte deterministický konečný
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/ Mgr. Jakub Novák. Datum: Ročník: 9.
 Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/1.581 VY_4_INOVACE_1NOV40 Autor: Mgr. Jakub Novák Datum: 10. 3. 013 Ročník: 9. Vzdělávací oblast: Matematika a její aplikace
Projekt: Zlepšení výuky na ZŠ Schulzovy sady registrační číslo: CZ.1.07./1.4.00/1.581 VY_4_INOVACE_1NOV40 Autor: Mgr. Jakub Novák Datum: 10. 3. 013 Ročník: 9. Vzdělávací oblast: Matematika a její aplikace
4.3.3 Goniometrické nerovnice I
 4 Goniometrické nerovnice I Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
4 Goniometrické nerovnice I Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
NPRG030 Programování I, 2018/19 1 / :25:37
 NPRG030 Programování I, 2018/19 1 / 26 24. 9. 2018 10:25:37 Čísla v algoritmech a programech 10 26 Poloměr vesmíru 2651 studujících studentů MFF UK 3.142857... Ludolfovo číslo 10 16 stáří vesmíru v sekundách!!!
NPRG030 Programování I, 2018/19 1 / 26 24. 9. 2018 10:25:37 Čísla v algoritmech a programech 10 26 Poloměr vesmíru 2651 studujících studentů MFF UK 3.142857... Ludolfovo číslo 10 16 stáří vesmíru v sekundách!!!
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření délky Číslo DUM: III/2/FY/2/1/2 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření délky Číslo DUM: III/2/FY/2/1/2 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Měření délky Číslo DUM: III/2/FY/2/1/2 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
1 Diference a diferenční rovnice
 1 Diference a diferenční rovnice Nechť je dána ekvidistantní síť uzlů x 0, x 1,..., x n tj. h R, h > 0 takové, že x i = x 0 + ih, i = 0, 1,..., n. Číslo h se nazývá krok. Někdy můžeme uvažovat i nekonečnou
1 Diference a diferenční rovnice Nechť je dána ekvidistantní síť uzlů x 0, x 1,..., x n tj. h R, h > 0 takové, že x i = x 0 + ih, i = 0, 1,..., n. Číslo h se nazývá krok. Někdy můžeme uvažovat i nekonečnou
Numerické řešení rovnice f(x) = 0
 Numerické řešení rovnice f(x) = 0 Přemysl Vihan 9.10.2003 Katedra fyziky, Pedagogická fakulta Univerzity J.E. Purkyně v Ústí n.l. 2. ročník, PMVT-mag. Abstrakt Seminární práce se zabývá numerickým řešením
Numerické řešení rovnice f(x) = 0 Přemysl Vihan 9.10.2003 Katedra fyziky, Pedagogická fakulta Univerzity J.E. Purkyně v Ústí n.l. 2. ročník, PMVT-mag. Abstrakt Seminární práce se zabývá numerickým řešením
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
Závěrečná zkouška z informatiky 2011
 Závěrečná zkouška z informatiky 2011 1) Číslo A je v dvojkové soustavě a má hodnotu 1101011. Číslo B je v šestnáctkové soustavě a má hodnotu FF3. Vypočítejte : A * B a výsledek napište v desítkové soustavě.
Závěrečná zkouška z informatiky 2011 1) Číslo A je v dvojkové soustavě a má hodnotu 1101011. Číslo B je v šestnáctkové soustavě a má hodnotu FF3. Vypočítejte : A * B a výsledek napište v desítkové soustavě.
Přehled funkcí. Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo. přehled fcí.
 Přehled funkcí Martina Hetmerová Gymnázium Přípotoční 1337 Praha 10 Vlastnosti funkcí Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo Zapisujeme: f:y=f(x)
Přehled funkcí Martina Hetmerová Gymnázium Přípotoční 1337 Praha 10 Vlastnosti funkcí Funkce na množině D R je předpis, který každému číslu z množiny D přiřazuje právě jedno reálné číslo Zapisujeme: f:y=f(x)
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
VÝUKOVÝ MATERIÁL. Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632 Číslo projektu
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
VÝUKOVÝ MATERIÁL Identifikační údaje školy Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková organizace Bratislavská 2166, 407 47 Varnsdorf, IČO: 18383874 www.vosassvdf.cz, tel. +420412372632
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
1 PRVOCISLA: KRATKY UKAZKOVY PRIKLAD NA DEMONSTRACI BALIKU WEB 1
 1 PRVOCISLA: KRATKY UKAZKOVY PRIKLAD NA DEMONSTRACI BALIKU WEB 1 1. Prvocisla: Kratky ukazkovy priklad na demonstraci baliku WEB. Nasledujici program slouzi pouze jako ukazka nekterych moznosti a sluzeb,
1 PRVOCISLA: KRATKY UKAZKOVY PRIKLAD NA DEMONSTRACI BALIKU WEB 1 1. Prvocisla: Kratky ukazkovy priklad na demonstraci baliku WEB. Nasledujici program slouzi pouze jako ukazka nekterych moznosti a sluzeb,
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Teplota Číslo DUM: III/2/FY/2/1/13 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny
 Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Teplota Číslo DUM: III/2/FY/2/1/13 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
Číslo projektu: CZ.1.07/1.4.00/21.3811 Název DUM: Teplota Číslo DUM: III/2/FY/2/1/13 Vzdělávací předmět: Fyzika Tematická oblast: Fyzikální veličiny a jejich měření Autor: Mgr. Petra Kejkrtová Anotace:
