NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí.

Transkript

1 NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, tel

2 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Základní literatura: 1. Jevický, J., Kovařík, P. : Vybrané numerické metody. S vyd., Brno: Vojenská akademie v Brně, Jevický, J., Kovařík, P. : Numerické metody algebry. S vyd., Brno: Vojenská akademie Antonína Zápotockého, Jevický, J., Kovařík, P. :. Numerické metody analýzy. S vyd., Brno: Vojenská akademie Antonína Zápotockého, Doporučená literatura: 4. Jevický, J.: Fourierovy řady, Fourierova transformace. S vyd., Brno: Vojenská akademie v Brně, Míka, S.: Numerické metody algebry. S-670/4. Praha, SNTL, Přikryl, P.: Numerické metody matematické analýzy. S-670/4. Praha, SNTL, Další odkazy a materiály: 7. Čermák, L., Hlavička, R.: Numerické metody Aproximace funkcí. FSI VUT v Brně, 006. Matematika online. Dostupné z:

3 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 NUMERICKÉ METODY A. Problematika numerického řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. B. Řešení nelineárních rovnic. Numerické řešení obyčejných diferenciálních rovnic 1. řádu a jejich soustav. C. Numerické metody užití systému počítačové algebry Mathcad. Zadání sady D.ú. (1 příkladů) z numerických metod:

4 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Z historie numerické matematiky Jednou z nejstarších památek numerické matematiky je babylonská hliněná destička (cca př.n.l.) obsahující aproximace čísel a 1 čtyřmi a třemi ciframi v šedesátkové soustavě: = 1, ( = 1, ) = 0, (1 = 0, ) Za důležité milníky v numerické matematiky lze považovat vývoj a zavedení těchto metod: 63 - Gaussova eliminace (Liu, Lagrange, Gauss, Jacobi) Newtonova metoda (Newton, Simpson) Metoda nejmenších čtverců (Gauss, Legendre) Rungova Kuttova metoda (Runge, Heun, Kutta) Metoda konečných prvků (Courant, Feng) Simplexový algoritmus (Kantorovich, Dantzig) Rychlá Fourierova transformace (Cooley, Tukey) Rozklad funkce vlnkovou transformací (wavelety)

5 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Problematika numerického řešení úloh Numerická matematika se zabývá řešením numerických úloh a problémů a tvoří jeden z mostů mezi teorií a praxí matematiky. Ve skutečnosti lze jen málo problémů vzniklých matematizací reálných situací vyřešit přesně i tehdy, jsou-li přesně zadána vstupní data, což také často není splněno. Pak je třeba užít numerické matematiky. Numerická matematika zahrnuje následující základní oblasti a metody: Numerické řešení soustav lineárních rovnic, interpolace a aproximace funkcí, metoda nejmenších čtverců, numerická derivace a integrace, numerické řešení nelineárních rovnic a jejich soustav, numerické řešení obyčejných a parciálních diferenciálních rovnic, Numerické řešení dané úlohy probíhá podle schématu Algoritmem je jasný a jednoznačný popis konečné posloupnosti aritmetických a logických operací realizovatelných na PC, jejichž prostřednictvím se vstupním datům přiřadí výstupní data. Výsledek numerického řešení dané úlohy není prakticky nikdy zcela přesný. Během řešení vznikají chyby, které se mohou kumulovat a výrazně tak zkreslit požadovaný výsledek.

6 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Chyby a jejich druhy 1. Chyby vstupních dat vznikají měřením a zaokrouhlováním hodnot vstupních veličin.. Chyby metody vznikají, když danou metodu nahradíme úlohou aproximující, kterou umíme řešit. Výchozí úloha a její matematický model reálného problému většinou zjednodušuje skutečnost (tzv. chyba úlohy). Při řešení matematické úlohy často nahrazujeme spojité problémy diskrétními nebo nekonečné procesy konečnými (tzv. zbytkové chyby). 3. Chyby zaokrouhlovací vznikají tak, že v počítači lze zaznamenávat reálná čísla jen pomocí konečného počtu cifer, takže např. čísla 1 3, 3, π nahrazujeme přibližnými hodnotami. Celkovou chybu řešení lze zmenšit na zanedbatelnou nebo alespoň přijatelnou míru přesnějším měřením vstupních dat, volbou vhodné metody a výběrem vhodného PC a softwaru. Kromě výše uvedených chyb, tedy nepřesností (nikoliv hrubých chyb), kterých se dopustíme, užíváme pojmy absolutní a relativní chyba. Označme x přesnou hodnotu čísla a x jeho přibližnou hodnotu. Absolutní chybou přibližného čísla x nazýváme číslo x = x x a odhadem absolutní hodnoty číslo ε x. Relativní chybou nazýváme číslo x x, x 0, a odhadem relativní chyby číslo δ. x x

7 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Numerické aspekty řešené úlohy a užitého algoritmu Při řešení dané úlohy numerické matematiky nás zajímají tyto vlastnosti úlohy: 1. Existence a jednoznačnost řešení tj. zda úloha má řešení nebo nemá řešení, a pokud řešení má, zda existuje jediné řešení nebo více řešení.. Podmíněnost úlohy tj. zda úloha je dobře podmíněná nebo špatně podmíněná, přičemž u špatně podmíněné úlohy malé změny ve vstupních datech vyvolají velké změny v řešení, tj. ve výstupních datech. Např. řešením soustavy x 1 + 4,001x = 0, x 1 + x = 1 je vektor x = (4001, 000) T, avšak řešením soustavy x 1 + 3,999x = 0, x 1 + x = 1 je vektor x = ( 3999, 000) T. 3. Stabilita nestabilní algoritmy, na rozdíl od stabilních, jsou citlivé na zaokrouhlovací chyby, které mohou vést k velké chybě v konečném výsledku. 4. Rychlost tj. zda je algoritmus rychlý nebo pomalý, měříme zpravidla počtem pouze aritmetických operací, potřebných k řešení úlohy, případně dobou výpočtu na počítači. 5. Složitost logická stavba algoritmu může být jednoduchá nebo složitá. Při výběru algoritmu často neexistuje nejlepší algoritmus pro širší třídu úloh. Rychlé algoritmy bývají méně stabilní a stabilní algoritmy bývají pomalejší a stabilnější, takže je třeba při volbě algoritmu používat kompromisy.

8 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Aproximace funkcí Při řešení různých úloh často nahrazujeme danou funkci f jinou jednodušší funkcí φ. Zpravidla požadujeme, aby se nová funkce φ snadněji matematicky zpracovávala (vyčíslovala, derivovala, integrovala) nebo modelovala na počítači. Funkci φ nazýváme aproximací (přiblížením) funkce f a píšeme f φ. Při výběru aproximace postupujeme takto: Nejprve zvolíme systém jednoduchých základních funkcí φ 0, φ 1,, φ n. Danou funkci f pak aproximujeme lineární kombinací φ těchto funkcí φ t = c 0 φ 0 t + c 1 φ 1 t + + c n φ n t. Úloha aproximace je převedena na úlohu vhodně vybrat koeficienty c 0, c 1,, c n. Za základní funkce nejčastěji volíme mocniny, goniometrické a exponenciální funkce: 1, t, t,, t n, resp. 1, t t 0, t t 0,, t t 0 n, 1, cos π p t, sin π p t, cos π p t, sin π p t, cos L π p t, sin L π p t, p > 0 je perioda, n = L, 1, e jπ p t e jπ p t,, e jnπ p t, p > 0. První dva systémy jsou polynomy (nejvýše) n-tého stupně, další dva systémy jsou tzv. trigonometrické polynomy.

9 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Chybou aproximace f t φ t, t a, b, nazýváme funkci ε t = f t φ t, t a, b. Při výběru aproximační funkce φ(t), tedy při výběru koeficientů c 0, c 1,, c n, se snažíme minimalizovat chybu aproximace ε(t). Pro výběr aproximace φ lze stanovit i další kritéria, která definují čtyři základní typy aproximací: 1. Aproximace Taylorovým polynomem funkce f(t) a aproximující polynom φ(t) mají ve zvoleném bodě t 0 stejnou funkční hodnotu a stejné hodnoty prvních n derivací: φ t = f t 0 + f (t 0) 1! t t 0 + f (t 0)! (t t 0 ) + + f n (t 0 ) n! (t t 0 ) n.. Interpolace funkce f(t) a aproximace φ(t) mají v pevně zvolených bodech t 0, t 1,, t n stejné funkční hodnoty (případně i hodnoty některých derivací). 3. Aproximace metodou nejmenších čtverců aproximaci φ vybíráme tak, aby měla ze všech funkcí φ t = c 0 φ 0 t + c 1 φ 1 t + + c n φ n t, t a, b, nejmenší velikost (normu) chyby aproximace, která je ve spojitém případě tvaru b f φ = f t φ(t) dt a,

10 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 a v diskrétním případě, kdy je funkce f(t) dána tabulkou funkčních hodnot v bodech t 0, t 1,, t N, veličinou N f φ = f t i φ(t i ) i=0. 4. Čebyševova aproximace funkci φ vybíráme tak, abychom minimalizovali maximální chybu, tj. minimalizujeme veličinu f φ = max t a,b f t φ(t), resp. f φ = max i=0,1,,n f t i φ(t i ). Volba typu aproximace: Je-li funkce f dána tabulkou s přesnými hodnotami, volíme interpolaci, jsou-li tabulkové hodnoty zatíženy chybami, volíme metodu nejmenších čtverců. Je-li funkce dána analyticky, volíme metodu nejmenších čtverců, případně Čebyševovu aproximaci.

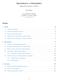
11 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Aproximace polynomem 1. stupně φ pro jednotlivé typy aproximace znázorňuje následující obrázek:

12 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Interpolace funkcí Předpokládejme, že známe n + 1 funkčních hodnot funkce f(t) v bodech (uzlech) t 0, t 1,, t n, které jsou navzájem různé. Máme tedy k dispozici tabulku t t 0 t 1 t n f(t) f 0 f 1 f n Funkce φ se nazývá interpolační funkcí funkce f, rovnají-li se funkční hodnoty φ(t) a f(t) v uzlech t 0, t 1,, t n, tj. platí-li interpolační podmínky φ t i = f t i, i = 0,1,, n. Pro interpolační funkci φ ve tvaru φ t = c 0 φ 0 t + c 1 φ 1 t + + c n φ n t dostáváme z interpol. podmínek soustavu n + 1 lin. algebr. rovnic o n + 1 neznámých c 0, c 1,, c n : c 0 φ 0 t 0 + c 1 φ 1 t c n φ n t 0 = f 0 c 0 φ 0 t 1 + c 1 φ 1 t c n φ n t 1 = f 1 c 0 φ 0 t n + c 1 φ 1 t n + + c n φ n t n = f n Tato soustava má jediné řešení, je-li matice soustavy regulární, tj. má-li nenul. determinant. To nastane právě tehdy, když sloupce matice, tj. jsou-li vektory funkčních hodnot φ 0 t 0, φ 0 t 1,, φ 0 t n T,, φ n t 0, φ n t 1,, φ n t n T lin. nezáv. v R n+1 (C n+1 ).

13 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Mezi nejpoužívanější interpolační polynomy φ t patří Lagrangeův interpolační vzorec který je po rozepsání tvaru n φ t = f k k=0 n i=0 i k t t i t k t i = c 0 + c 1 t + c t + + c n t n φ t = f 0 t t 1 t t t t n t 0 t 1 t 0 t t 0 t n + f 1 t t 0 t t t t n t 1 t 0 t 1 t t 1 t n + + f n t t 0 t t 1 t t n 1 t n t 0 t n t 1 t n t n 1. Příklad: Určete interpolační polynom φ(t) pro funkci f(t) danou tabulkou t f t 3 6, φ t = 3 t 1 t t 0 t t 0 t , odkud φ t = t 1 t 3 t t 3 + t t 1 = 3 t + t a mj. f = 3.

14 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Metoda nejmenších čtverců Předpokládejme, že známe N + 1 funkčních hodnot funkce f(t) v bodech t 0, t 1,, t N, které jsou navzájem různé a dané tabulkou Funkci f(t) budeme aproximovat metodou nejmenších čtverců funkcí φ(t) tvaru φ t = c 0 φ 0 t + c 1 φ 1 t + + c n φ n t, n N. Budeme přitom pracovat s (N + 1)-rozměrnými vektory funkčních hodnot zvolených bázových funkcí φ k (t), k = 0,1,, n a s vektorem hodnot funkce f: φ 0 = φ 0 (t 0 ) φ 0 (t 1 ) φ 0 (t N ), φ 1 = t t 0 t 1 t N f(t) f 0 f 1 f N φ 1 (t 0 ) φ 1 (t 1 ) φ 1 (t N ),, φ n = φ n t 0 φ n t 1, f = φ n t N f t 0 f t 1 f t N. Vynásobíme-li aproximační vektorovou rovnici f = c 0 φ 0 + c 1 φ c n φ n postupně skalárně vektory φ 0, φ 1,, φ n, obdržíme soustavu n + 1 rovnic o n + 1 neznámých koeficientech c 0, c 1,, c n.

15 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Tato soustava se nazývá normální soustava rovnic a je tvaru c 0 φ 0, φ 0 + c 1 φ 1, φ c n φ n, φ 0 = f, φ 0 c 0 φ 0, φ 1 + c 1 φ 1, φ c n φ n, φ 1 = f, φ 1 c 0 φ 0, φ n + c 1 φ 1, φ n + + c n φ n, φ n = f, φ n Soustava má právě jedno řešení, pokud jsou vektory φ 0, φ 1,, φ n lin. nezávislé. Velikost chyby aproximace je v tomto diskrétním případě (tabulka hodnot) N f φ = f t i φ t i i=0. Ve spojitém případě, tj. v případě funkce f t, t a, b, dané nikoliv tabulkou, ale analytickým předpisem, je skalární součin funkcí g(t) a h(t), t a, b, dán určitým integrálem b g(t), h(t) = g(t) h t dt. a

16 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Příklad: Aproximujte funkci f t = t, t 0,, polynomem 1. stupně metodou nejm. čtverců. Hledáme aproximaci ve tvaru f t φ t = c c 1 t, takže bázovými funkcemi (vektory) jsou funkce φ 0 t = 1 a φ 1 t = t. Normální soustava rovnic je tvaru c 0 φ 0 (t), φ 0 (t) + c 1 φ 1 (t), φ 0 (t) = f(t), φ 0 (t) c 0 φ 0 (t), φ 1 (t) + c 1 φ 1 (t), φ 1 (t) = f(t), φ 1 (t). Vypočteme skalární součiny funkcí a dostaneme soustavu s neznámými koeficienty c 0 a c 1, kterou vyřešíme a obdržíme tak hledanou aproximaci: φ 0 t, φ 0 (t) = 1 1dt = t 0 = 0, φ 1 t, φ 1 (t) = t tdt = t3 3 φ 1 t, φ 0 (t) = φ 0 t, φ 1 (t) = 1 tdt = t f t, φ 0 (t) = t 1dt = t3 3 0 normální soustava je (po vynásobení rovnic číslem 3) tvaru =, 0 = 8, f t, φ 3 1 (t) = t tdt = t4 4 6c 0 + 6c 1 = 8 6c 0 + 8c 1 = 1, odkud c 0 = /3, c 1 =, takže hledaná aproximace t 0,667 + t, t 0,. 0 0 = 8, 3 0 = 4,

17 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 Příklad: Funkci f(t), která je zadána tabulkou, aproximujte a) polynomem φ t = c c 1 t + c t, b) exponenciální funkcí φ t = c 0 e c 1t. a) Vektory funkčních hodnot bázových funkcí φ 0 t = 1, φ 1 t = t, φ t = t a funkce f(t) jsou: φ 0 =, φ 1 1 =, φ 3 =, f = Normální soustava je tvaru c 0 φ 0, φ 0 + c 1 φ 1, φ 0 + c φ, φ 0 = f, φ 0 c 0 φ 0, φ 1 + c 1 φ 1, φ 1 + c φ, φ 1 = f, φ 1 c 0 φ 0, φ + c 1 φ 1, φ + c φ, φ = f, φ. Protože skalární součiny vektorů jsou: φ 0, φ 0 = 4, φ 1, φ 0 = φ 0, φ 1 = 10, φ, φ 0 = φ 0, φ = 30, φ, φ 1 = φ 1, φ = 100, φ 1, φ 1 = 30, φ, φ = 354, f, φ 0 = 17, f, φ 1 = 5, f, φ = 178, je normální soustava tvaru 4c c c = 17 takže f t 3,5 1,85t + 0,75t. t f(t) c c c = 5 30c c c = 178,

18 ----- M4B-K Problematika numerického řešení úloh, aproximace funkcí /18 b) Aproximační funkci φ t = c 0 e c 1t nejprve zlinearizujeme tak, že ji, stejně jako tabulkové hodnoty zadané funkce zlogaritmujeme. Dostaneme tak funkci ln φ t = ln c 0 + c 1 t, tj. funkci Φ t = a1 + bt, kde a = ln c 0, b = c 1. K tabulce připojíme řádek se zlogaritmovanými funkčními hodnotami: t f(t) ln f(t) ln ln 3 ln 3 ln Vektory funkčních hodnot bázových funkcí φ 0 t = 1, φ 1 t = t a funkce F t = ln f(t) jsou: φ 0 = , φ 1 = 1 3 4, F = ln ln 3 ln 3 ln Normální soustava je tvaru a φ 0, φ 0 + b φ 1, φ 0 = F, φ 0 a φ 0, φ 1 + b φ 1, φ 1 = F, φ 1. Protože skalární součiny vektorů jsou: φ 0, φ 0 = 4, φ 1, φ 0 = φ 0, φ 1 = 10, φ 1, φ 1 = 30, F, φ 0 = 6 ln + ln 3, F, φ 1 = 19 ln + ln 3, je normální soustava tvaru 4a + 10b = 5,575 10a + 30b = 15,3670, tedy Φ t = 0, ,44465t, odkud c 0 = 1,48, takže hledaná funkce je tvaru φ t = 1,48e 0,44465t..