APROXIMACE FUNKCÍ V MA TLABU ' Část 3. - Lazran eův inter olační 01 mom v Matlabu
|
|
|
- Adam Ovčačík
- před 8 lety
- Počet zobrazení:
Transkript
1 APROXIMACE FUKCÍ V MA TLABU ' Část 3. - Lazran eův inter olační 0 mom v Matlabu I Jiří Kulička Umverzna Pardubice, Dopravru fakulta Jana Pcrnera. Katedra Informatiky v dopravě University oj Pardubice. Jan Perner Transport Fakulty, Department oj informatics in transport Univerzita Hradec Králové, Pedagogická fakulta, Katedra informatiky University oj Hradec Králové. Fakult)' ofeducation, Department aj lnformatics Resumé: Článek se zabývá odvozením, algoritmizací a popisem konstrukce Lagrangeova interpolačního polynomu. Jsou zde popsány a vysvětleny základní výpočetní postupy týkající se této problematiky, nejprve je vždy proveden teoretický rozbor, pak následuje řešený příklad a výpisy funkcí v Matlabu s vysvětlujícím komentářem. Summary: The article deals with deriving, algorithm design and description of the Lagrange interpolation polynomial. There are described and explained the basic computational procedures regarding this issue, the first one is always a theoretical analysis, followed by solved examples and extracts functions in Matlab with explanatory commentary. ÚVOD umerické (obecně matematické) metody jsou nezbytnou součástí výuky technicky orientovaných předmětů nejen na školách vysokých, ale (samozřejmě s daleko menšími nároky) i na školách středních. Zejména pro vysokoškolské studenty bývají numerické metody a matematika obecně, obtížnými pasážemi studia. Počítače přinesly do technické praxe výraznou podporu právě u numerických metod, od zrychlení a zpřesnění výpočtů matematických modelů až po výpočty metodou konečných prvků. Interpolovat znamená odhadnout chybějící funkční hodnoty pomocí váženého průměru známých funkčních hodnot v sousedních bodech. LIEÁRÍ ITERPOLACE Lineární interpolace používá přímku procházející dvěma body. y y Xa Xl-)(n B y t- yo Obrázek Lineární interpolace Sklon přímky je: k = tgep = YI - Yo. Dosazením do směrnicového tvaru rovnice přímky dostáváme: XI -xo ávrat na obsah Media4u Magazine 2/200 32
2 -===-====-===-=== ( ) y, - y=k x-xo+yo= Yo,x-xo+Yo ( ) X, -xo Tento vztah upravíme na tvar, který odvodil Joseph Louis Lagrange (736-83): () y, - Yo () () x - Xo x - Xo x - Xo Y = P x =. x - Xo + Yo = Yo + y, - Yo. = Yo + y,. - Yo. = ~-~ ~-~ ~-~ ~-~ Poslední část výrazu v této úpravě nazýváme interpolační polynom prvního stupně (přímka). () v () jsou lineární faktory a nazýváme je Lagrangeovými polynomickými a Xl' Dosazením bodů A a B do lineárních faktorů dostáváme: koeficienty založenými na pólech Xo a proto polynom P l (x) prochází body A, B. Výsledný tvar interpolačního polynomu prvního stupně můžeme zapsat:, ~(x)= LYk.L"k(xL r, =f(xk) ZOBECĚÍ POlynomPn(x) stupně nejvýše, který prochází + body [xo; YoL [x,; yd,..., [X,' Y] je určen předpisem: Pn(x) = LYk.L,k(X), kde L,k (x) jsou Lagrangeovy polynomické koeficienty dané uzly x o, Xl... r x a jsou určeny výrazem: (2) IT(x-xJ j=o,}-*k IT(Xk j=o,j"#-k - Xj) Lagrangeovy polynomické koeficienty mají tyto vlastnosti: L,k (x j) = I, když j == k a L, k (x j ) = O, když j *' k. Polynom prochází všemi danými body, což je vidět z následující rovnice dosazením za x = x j : P(Xj)= YO' L,O(Xj ) Y j. L,j(X j ) Y. L,(Xj)= Yo(O)+... y j(i) Y(O) = Y j' ávrat na obsah Media4u Magazine 2/200 33
3 a obrázku 2 vidíme názorně konstrukci výsledného interpolačního polynomu P(x) druhého stupně pomocí funkčních hodnot vynásobených Lagrangeovými polynomickými koeficienty v jednotlivých pólech 2, 4, P(x) --L(x) --L2(x) L3(x) / _2L-----L-----~----~-----L----~----~ Obr.2 Interpolační polynom a Lagrangeovy polynomické koeficienty druhého řádu LAGRAGEŮVITERPOLAČÍVZOREC Funkci r(x) aproximujeme polynomem Pn (x) (2), který nabývá ve známých uzlech stejných hodnot, jako daná funkce r(x). f{x)= LYk 'L,k{X)+E{x)=Pn{x)+E{x), kde Pn (x) je aproximace funkce f(x) a E(x) chyba aproximace. Jestliže Pn (x) je použito k aproximaci r(x) v intervalu < xo/ x >, nazýváme daný proces jako interpolace, mimo daný interval extrapolace. PŘÍKLADY LAGRAGEOVÝCH POLYOMŮ Kvadratický LagrangeElv polynom, který prochází body [xo/ Yo], [XI/ yd a [xv' Y2] je: Kubický l.aqranqeův polynom, který prochází body [xo; Yo], [Xl/ h], [X2; Y2] a [X3/' Y3] je: (x - xo) (x - xd (x - X3) (x - xo) (x - xd (x - X2) + Y2' (X2 -XO)'(X2 -Xd'(X2 -X3r Y3' (X3 -XO)'(X3 -Xl)'(X3 -X2) ávrat na obsah Media4u Magazine 2/200 34
4 Příklad ahradíme funkci y = In(x) v intervalu x E < ; 2,2 > Lagrangeovými polynomy druhého a třetího stupně. Zobrazíme také chyby, kterých se dopouštíme. Y = t(x) = ln x, x E< ;2,2 > Kvadratický Lagrangeův polynom Xo =,xl =,6,x2 =2,2 Yo = In = O, Yl = ln,6 = 0,470004, Y2 = ln 2,2 = 0, L2,O(x) = (( -,6~. ~x - 2,V =, x 2-5, x + 4, ,6. - 2,2 (x-).(x-22) 2 L 2 () X = ( ) ( ') = -2, x + 8, x - 6,,,6 -.,6-2,2 L22(X) = ( (x -~. i x -,6) ) =, x 2-3,6 x + 2,222222, 2,2 -. 2,2 -,6 = 0-, (x 2-3,2x + 2,2)+, (x 2-2,6x +,6) = = -0,20488 x 2 +, x -, ~ "'~»>: -----o O+ ----~------~---~~-~~~--~----~L----~~ Obr.3 Kvadratický Lagrangeův interpolačni polynom (odchylky P2(X) od y = In(x) jsou červeně a desetkrát zvětšeny) ávrat na obsah Media4u Magazine 2/200 35
5 KubkkýLagrangeůvpolynom L3 o (x) = (x -,4). (x -,8). (x - 2,2) = -2, x3 + 4,0625. x2-24, x + 4,4375, (-,4). (-,8). (- 2,2) (x-l).(x-l,8).(x-2,2) 3 2 (),,4 -.,4 -,8.,4-2,2 L3x =( ) ( ) ( )=7,825.X -39,0625 x +62,875 x+30,9375 (x-l).(x-l,4).(x-2,2) 3 2 L32 () X = ( ) ( ) ( )=-7,825.X +35,9375 x -52,875 x+24,0625,,8-.,8-,4.,8-2,2 L (x) = (x -). (X -,4). (x -,8) = x x x ,3 (2,2-).(2,2-,4).(2,2-,8)',,, P3(X) = O L3,0(X)+ 0, L3,l (x)+ 0, L3,2(x) + 0, L3,3(X) = = 0, x 3-0,64366 x 2 +,99398 x -, / r '.,. O : / ~ '-o Obr.4 Kubický Lagrangeův interpolační polynom (odchylky P3(X) od y = In(x) jsou červeně a padesátkrát zvětšeny) m-soubor Matlab Určení Lagrangeova polynomu P(x) = I Yk. L, k (x) daného + body [x k; Yk] I k = 0,,...,. v ukázce m-souboru z Matlabu jsou za znakem % uvedeny vysvětlující komentáře. ávrat na obsah Media4u Magazine 2/200 36
6 tunction fc,l]=/agrange(x, Y) % vstup X je vektor x-ových souřadnic bodu Xk % Yje vektor y-ových souřadnic bodu Xk %výstup Cje matice výsledných koeficientů Lagrangeova polynomu % Lje matice koeficientů u mocnin x u Lagrangeových polynomů w=length(x)/ n=w-l; L =zeros/w: w)/' % výpočet koeficientů mocnin x u Lagrangeových polynomů for k=l:w v=i: for j=l:w If k-v=] V=conv(V,poly(XÚ)))/(X(k)-XU))/ end end L(k,:)=V,' end % výpočet koeficientů Lagrangeova interpolačn/ho polynomu C=Y*L,' pnkaz: fc,l]=/agrange(x, Y) ZÁVĚR Pro určení interpolačního polynomu existuje více postupu, všechny ale určí stejný polynom. Lagrangeova interpolace patří k těm nejstarším, nejznámějším a nejjednodušším. Její nevýhoda ovšem spočívá v tom, že postup nelze vyjádřit rekurentně a je velmi náročný na počet výpočtů. Proto při přidání dalšího uzlu, musíme celý polynom znovu přepočítat. Komentované výpisy funkcí v Matlabu jsou používány ve výuce předmětu umerické metody na DF UPCE. (v pňstim pokračováni ewtonúv Interpolačni polynom) Použité zdroje MATHEWS. J. - FIK. K. umerical Methods Using MATLAB. Pearson Prentice Hall 2004, fourth edition. ISB RALSTO, A. Základy numerické matematiky. Academia Praha 978 VIT ÁSEK. E. umerické metody. STL 987 KARBA. P. výpočty a simulace v programech Matlab a Simulink. Computer Press ISB Kontaktni adresa Mgr. Jiři Kulička Univerzita Pardubice Dopravni fakulta Jana Pernera Studentská Pardubice 2 jiri.kulicka@upce.cz ávrat na obsah Media4u Magazine 2/200 37
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL
 APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
APROXIMACE KŘIVEK V MATLABU TRIGONOMETRICKÉ POLYNOMY CURVE FITTING IN MATLAB TRIGONOMETRIC POLYNOMIAL
 APROXIMACE KŘIVEK V MATLABU TRIGONOMETRICKÉ POLYNOMY CURVE FITTING IN MATLAB TRIGONOMETRIC POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce trigonometrického
APROXIMACE KŘIVEK V MATLABU TRIGONOMETRICKÉ POLYNOMY CURVE FITTING IN MATLAB TRIGONOMETRIC POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce trigonometrického
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení
 Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Polynomy a interpolace text neobsahuje přesné matematické definice, pouze jejich vysvětlení Polynom nad R = zobrazení f : R R f(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, kde a i R jsou pevně daná
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_158_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_158_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
VÝUKA ZÁKLADNÍCH NUMERICKÝCH ALGORITMŮ V MATLABU APROXIMACE KUBICKÝMI SPLAJNY
 VÝUKA ZÁKLADNÍCH NUMERICKÝCH ALGORITMŮ V MATLABU APROXIMACE KUBICKÝMI SPLAJNY Jiří Kulička Mgr Jiří Kulička, University of Pardubice, Jan Perner Transport Faculty, Department of Informatics in Transport,
VÝUKA ZÁKLADNÍCH NUMERICKÝCH ALGORITMŮ V MATLABU APROXIMACE KUBICKÝMI SPLAJNY Jiří Kulička Mgr Jiří Kulička, University of Pardubice, Jan Perner Transport Faculty, Department of Informatics in Transport,
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace, aproximace
 11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
11 Interpolace, aproximace Metoda nejmenších čtverců 11.1 Interpolace Mějme body [x i,y i ], i =0, 1,...,n 1. Cílem interpolace je najít funkci f(x), jejíž graf prochází všemi těmito body, tj. f(x i )=y
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
Interpolace pomocí splajnu
 Interpolace pomocí splajnu Interpolace pomocí splajnu Připomenutí U interpolace požadujeme, aby graf aproximující funkce procházel všemi uzlovými body. Interpolační polynom aproximující funkce je polynom
Interpolace pomocí splajnu Interpolace pomocí splajnu Připomenutí U interpolace požadujeme, aby graf aproximující funkce procházel všemi uzlovými body. Interpolační polynom aproximující funkce je polynom
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Aproximace funkcí. x je systém m 1 jednoduchých, LN a dostatečně hladkých funkcí. x c m. g 1. g m. a 1. x a 2. x 2 a k. x k b 1. x b 2.
 Aproximace funkcí Aproximace je výpočet funkčních hodnot funkce z nějaké třídy funkcí, která je v určitém smyslu nejbližší funkci nebo datům, která chceme aproximovat. Třída funkcí, ze které volíme aproximace
Aproximace funkcí Aproximace je výpočet funkčních hodnot funkce z nějaké třídy funkcí, která je v určitém smyslu nejbližší funkci nebo datům, která chceme aproximovat. Třída funkcí, ze které volíme aproximace
Čebyševovy aproximace
 Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
INTERPOLAČNÍ POLYNOM.... hledaná funkce (polynom nebo funkce vytvořená z polynomů), pro kterou platí
 8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace 1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení: P (n) množina všech
8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace 1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení: P (n) množina všech
INTERPOLAČNÍ POLYNOM. F (x)... hledaná funkce (polynom nebo funkce vytvořená z polynomů), pro kterou platí
 8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace Kateřina Konečná/1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení:
8 Řešení Lagrangeovy a Hermiteovy úlohy interpolace Kateřina Konečná/1 INTERPOLAČNÍ POLYNOM aproximace zadaných hodnot nebo hledané funkce f funkcí F (x) (polynomem) F musí být k f co nejblíže značení:
Numerická matematika Písemky
 Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
Numerická matematika Písemky Bodování Každá písemka je bodována maximálně 20 body. Celkem student může získat za písemky až 40 bodů, pro udělení zápočtu musí získat minimálně 20 bodů. Písemka č. 1 Dva
Aplikovaná matematika I
 Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Metoda nejmenších čtverců Aplikovaná matematika I Dana Říhová Mendelu Brno c Dana Říhová (Mendelu Brno) Metoda nejmenších čtverců 1 / 8 Obsah 1 Formulace problému 2 Princip metody nejmenších čtverců 3
Numerické řešení diferenciálních rovnic
 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice. sin x + x 2 2 = 0.
 A 9 vzorové řešení Př. 1. Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice Počítejte v radiánech, ne ve stupních! sin x + x 2 2 = 0. Rovnici lze upravit na sin
A 9 vzorové řešení Př. 1. Libovolnou z probraných metod najděte s přesností na 3 desetinná místa kladný kořen rovnice Počítejte v radiánech, ne ve stupních! sin x + x 2 2 = 0. Rovnici lze upravit na sin
REGRESNÍ ANALÝZA V PROSTŘEDÍ MATLAB
 62 REGRESNÍ ANALÝZA V PROSTŘEDÍ MATLAB BEZOUŠKA VLADISLAV Abstrakt: Text se zabývá jednoduchým řešením metody nejmenších čtverců v prostředí Matlab pro obecné víceparametrové aproximační funkce. Celý postup
62 REGRESNÍ ANALÝZA V PROSTŘEDÍ MATLAB BEZOUŠKA VLADISLAV Abstrakt: Text se zabývá jednoduchým řešením metody nejmenších čtverců v prostředí Matlab pro obecné víceparametrové aproximační funkce. Celý postup
Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy
![Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy](/thumbs/97/130835283.jpg) Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
UNIVERZITA PARDUBICE. 4.4 Aproximace křivek a vyhlazování křivek
 UNIVERZITA PARDUBICE Licenční Studium Archimedes Statistické zpracování dat a informatika 4.4 Aproximace křivek a vyhlazování křivek Mgr. Jana Kubátová Endokrinologický ústav V Praze, leden 2012 Obsah
UNIVERZITA PARDUBICE Licenční Studium Archimedes Statistické zpracování dat a informatika 4.4 Aproximace křivek a vyhlazování křivek Mgr. Jana Kubátová Endokrinologický ústav V Praze, leden 2012 Obsah
Matematika III přednáška Aplikace vytvořujících funkcí - další úlohy
 S Matematika III - 14. přednáška Aplikace vytvořujících funkcí - další úlohy Michal Bulant Masarykova univerzita Fakulta informatiky 18. 12. 2007 Obsah přednášky Řešení rekurencí Q Exponenciální vytvořující
S Matematika III - 14. přednáška Aplikace vytvořujících funkcí - další úlohy Michal Bulant Masarykova univerzita Fakulta informatiky 18. 12. 2007 Obsah přednášky Řešení rekurencí Q Exponenciální vytvořující
Lineární a polynomická regrese, interpolace, hledání v tabulce
 co byste měli umět po dnešní lekci: proložit body přímku, parabolu,... a určit chyby parametrů (u přímky) interpolovat mezi hodnotami v tabulce hledat v tabulce (1D) prokládání (fitování) křivek metoda
co byste měli umět po dnešní lekci: proložit body přímku, parabolu,... a určit chyby parametrů (u přímky) interpolovat mezi hodnotami v tabulce hledat v tabulce (1D) prokládání (fitování) křivek metoda
4 Numerické derivování a integrace
 Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
úloh pro ODR jednokrokové metody
 Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Numerické metody pro řešení počátečních úloh pro ODR jednokrokové metody Formulace: Hledáme řešení y = y() rovnice () s počáteční podmínkou () y () = f(, y()) () y( ) = y. () Smysl: Analyticky lze spočítat
Pozn. 1. Při návrhu aproximace bychom měli aproximační funkci vybírat tak, aby vektory ϕ (i) byly lineárně
 9. Řešení typických úloh diskrétní metodou nejmenších čtverců. DISKRÉTNÍ METODA NEJMENŠÍCH ČTVERCŮ použití: v případech, kdy je nevhodná interpolace využití: prokládání dat křivkami, řešení přeurčených
9. Řešení typických úloh diskrétní metodou nejmenších čtverců. DISKRÉTNÍ METODA NEJMENŠÍCH ČTVERCŮ použití: v případech, kdy je nevhodná interpolace využití: prokládání dat křivkami, řešení přeurčených
Interpolace Lagrangeovy polynomy. 29. října 2012
 Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Interpolace Lagrangeovy polynomy Michal Čihák 29. října 2012 Problematika interpolace V praxi máme často k dispozici údaje z různých měření tzv. data. Data mohou mít například podobu n uspořádaných dvojic
Typy příkladů na písemnou část zkoušky 2NU a vzorová řešení (doc. Martišek 2017)
 Typy příkladů na písemnou část zkoušky NU a vzorová řešení (doc. Martišek 07). Vhodnou iterační metodou (tj. metodou se zaručenou konvergencí) řešte soustavu: x +x +4x 3 = 3.5 x 3x +x 3 =.5 x +x +x 3 =.5
Typy příkladů na písemnou část zkoušky NU a vzorová řešení (doc. Martišek 07). Vhodnou iterační metodou (tj. metodou se zaručenou konvergencí) řešte soustavu: x +x +4x 3 = 3.5 x 3x +x 3 =.5 x +x +x 3 =.5
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
 Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
ALGEBRA. 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = , b =
 ALGEBRA 1 Úkol na 13. 11. 2018 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = 353 623, b = 244 571. 2. Připomeňte si, že pro ε = cos 2π 3 + i sin
ALGEBRA 1 Úkol na 13. 11. 2018 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = 353 623, b = 244 571. 2. Připomeňte si, že pro ε = cos 2π 3 + i sin
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
5. Interpolace a aproximace funkcí
 5. Interpolace a aproximace funkcí Průvodce studiem Často je potřeba složitou funkci f nahradit funkcí jednodušší. V této kapitole budeme předpokládat, že u funkce f známe její funkční hodnoty f i = f(x
5. Interpolace a aproximace funkcí Průvodce studiem Často je potřeba složitou funkci f nahradit funkcí jednodušší. V této kapitole budeme předpokládat, že u funkce f známe její funkční hodnoty f i = f(x
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Numerická matematika. Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou
 Numerická matematika Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou Václav Bubník, xbubni01, sk. 60 FIT VUT v Brně, 2004 Obsah Numerická matematika...1 1. Teorie... 3 1.1 Diferenciální
Numerická matematika Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou Václav Bubník, xbubni01, sk. 60 FIT VUT v Brně, 2004 Obsah Numerická matematika...1 1. Teorie... 3 1.1 Diferenciální
Aproximace a interpolace
 Aproximace a interpolace Aproximace dat = náhrada nearitmetické veličiny (resp. složité funkce) pomocí aritmetických veličin. Nejčastěji jde o náhradu hodnot složité funkce g(x) nebo funkce zadané pouze
Aproximace a interpolace Aproximace dat = náhrada nearitmetické veličiny (resp. složité funkce) pomocí aritmetických veličin. Nejčastěji jde o náhradu hodnot složité funkce g(x) nebo funkce zadané pouze
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ
 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LII 6 Číslo 3, 2004 Gasser-Müllerův odhad J. Poměnková Došlo: 8.
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LII 6 Číslo 3, 2004 Gasser-Müllerův odhad J. Poměnková Došlo: 8.
a a
 1.. Cíle V této kapitole se naučíme určovat zejména celočíselné kořeny některých polynomů. Výklad Při výpočtu hodnoty polynomu n k p( x) = ak x n-tého stupně n 1 v bodě x 0 C k = 0 musíme provést ( n 1)
1.. Cíle V této kapitole se naučíme určovat zejména celočíselné kořeny některých polynomů. Výklad Při výpočtu hodnoty polynomu n k p( x) = ak x n-tého stupně n 1 v bodě x 0 C k = 0 musíme provést ( n 1)
Numerická matematika Banka řešených příkladů
 Numerická matematika Banka řešených příkladů Radek Kučera, Pavel Ludvík, Zuzana Morávková Katedra matematiky a deskriptivní geometrie Vysoká škola báňská Technická Univerzita Ostrava K D M G ISBN 978-80-48-894-6
Numerická matematika Banka řešených příkladů Radek Kučera, Pavel Ludvík, Zuzana Morávková Katedra matematiky a deskriptivní geometrie Vysoká škola báňská Technická Univerzita Ostrava K D M G ISBN 978-80-48-894-6
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Pseudospektrální metody
 Pseudospektrální metody Obecně: založeny na rozvoji do bázových funkcí s globálním nosičem řešení diferenciální rovnice aproximuje sumou kde jsou např. Čebyševovy polynomy nebo trigonometrické funkce tyto
Pseudospektrální metody Obecně: založeny na rozvoji do bázových funkcí s globálním nosičem řešení diferenciální rovnice aproximuje sumou kde jsou např. Čebyševovy polynomy nebo trigonometrické funkce tyto
Citlivost kořenů polynomů
 Citlivost kořenů polynomů Michal Šmerek Univerzita obrany v Brně, Fakulta ekonomiky a managementu, Katedra ekonometrie Abstrakt Článek se zabývá studiem citlivosti kořenů na malou změnu polynomu. Je všeobecně
Citlivost kořenů polynomů Michal Šmerek Univerzita obrany v Brně, Fakulta ekonomiky a managementu, Katedra ekonometrie Abstrakt Článek se zabývá studiem citlivosti kořenů na malou změnu polynomu. Je všeobecně
Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012
 Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012 Metoda nejmenších čtverců Matematicko-statistická metoda používaná zejména při zpracování nepřesných dat (typicky experimentálních empirických
Metoda nejmenších čtverců Michal Čihák 26. listopadu 2012 Metoda nejmenších čtverců Matematicko-statistická metoda používaná zejména při zpracování nepřesných dat (typicky experimentálních empirických
VÝUKA MOŽNOSTÍ MATLABU
 VÝUKA MOŽNOSTÍ MATLABU Miroslav Olehla Technická univerzita v Liberci, Fakulta strojní, Katedra aplikované kybernetiky V následujícím příspěvku jsou uvedeny některé oblasti MATLABU ve výuce. Vychází se
VÝUKA MOŽNOSTÍ MATLABU Miroslav Olehla Technická univerzita v Liberci, Fakulta strojní, Katedra aplikované kybernetiky V následujícím příspěvku jsou uvedeny některé oblasti MATLABU ve výuce. Vychází se
Opakovací test. Komlexní čísla A, B
 VY_32_INOVACE_MAT_195 Opakovací test Komlexní čísla A, B Mgr. Radka Mlázovská Období vytvoření: září 2012 Ročník: čtvrtý Tematická oblast: matematické vzdělávání Předmět: matematika, příprava k maturitě,
VY_32_INOVACE_MAT_195 Opakovací test Komlexní čísla A, B Mgr. Radka Mlázovská Období vytvoření: září 2012 Ročník: čtvrtý Tematická oblast: matematické vzdělávání Předmět: matematika, příprava k maturitě,
5. Aproximace funkcí. Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita. Hana Hladíková
 5 Aproximace funkcí Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Hana Hladíková V praxi je často potřeba složitou funkci f nahradit funkcí jednodušší, která v nějakém vhodném
5 Aproximace funkcí Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Hana Hladíková V praxi je často potřeba složitou funkci f nahradit funkcí jednodušší, která v nějakém vhodném
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Vektorové prostory R ( n 1,2,3)
 n Vektorové prostory R ( n 1,2,) (Velikonoční doplněk ke cvičení LAG) Prvky kartézské mocniny R RR R jsou uspořádané trojice reálných čísel, které spolu s operacemi ( a1, a2, a) ( b1, b2, b) ( a1b1, a2
n Vektorové prostory R ( n 1,2,) (Velikonoční doplněk ke cvičení LAG) Prvky kartézské mocniny R RR R jsou uspořádané trojice reálných čísel, které spolu s operacemi ( a1, a2, a) ( b1, b2, b) ( a1b1, a2
Obsah Obyčejné diferenciální rovnice
 Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
PREDIKCE DÉLKY KOLONY V KŘIŽOVATCE PREDICTION OF THE LENGTH OF THE COLUMN IN THE INTERSECTION
 PREDIKCE DÉLKY KOLONY V KŘIŽOVATCE PREDICTION OF THE LENGTH OF THE COLUMN IN THE INTERSECTION Lucie Váňová 1 Anotace: Článek pojednává o předpovídání délky kolony v křižovatce. Tato úloha je řešena v programu
PREDIKCE DÉLKY KOLONY V KŘIŽOVATCE PREDICTION OF THE LENGTH OF THE COLUMN IN THE INTERSECTION Lucie Váňová 1 Anotace: Článek pojednává o předpovídání délky kolony v křižovatce. Tato úloha je řešena v programu
Numerické řešení obyčejných diferenciálních rovnic
 Numerické řešení obyčejných diferenciálních rovnic Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Numerické řešení obyčejných diferenciálních rovnic Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Matematika (KMI/PMATE)
 Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí.
 NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, Radovan.Potucek@unob.cz, tel. 443056 -----
NUMERICKÉ METODY. Problematika num. řešení úloh, chyby, podmíněnost, stabilita algoritmů. Aproximace funkcí. RNDr. Radovan Potůček, Ph.D., K-15, FVT UO, KŠ 5B/11, Radovan.Potucek@unob.cz, tel. 443056 -----
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál
 Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál Jan Slovák Masarykova univerzita Fakulta informatiky 16. 9. 2008 Obsah přednášky 1 Literatura 2 Funkce a
Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál Jan Slovák Masarykova univerzita Fakulta informatiky 16. 9. 2008 Obsah přednášky 1 Literatura 2 Funkce a
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Mathematical Assistant on Web
 Mathematical Assistant on Web Robert Mařík Mendelova zemědělská a lesnická univerzita v Brně Mathematical Asistant on Web MAW) Jak se rodila myšlenka na vytvoření aplikace Vláda ČR a EU podporují celoživotní
Mathematical Assistant on Web Robert Mařík Mendelova zemědělská a lesnická univerzita v Brně Mathematical Asistant on Web MAW) Jak se rodila myšlenka na vytvoření aplikace Vláda ČR a EU podporují celoživotní
SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování
 KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
Numerické metody a programování. Lekce 7
 Numerické metody a programování Lekce 7 Řešení nelineárních rovnic hledáme řešení x problému f x = 0 strategie: odhad řešení iterační proces postupného zpřesňování řešení výpočet skončen pokud je splněno
Numerické metody a programování Lekce 7 Řešení nelineárních rovnic hledáme řešení x problému f x = 0 strategie: odhad řešení iterační proces postupného zpřesňování řešení výpočet skončen pokud je splněno
Aplikovaná numerická matematika - ANM
 Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté
 Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté polynomy pro případ dvou uzlových bodů ξ 1 = 1 a ξ 2 = 4. Experimentální body jsou x = [0.2 0.4 0.6 1.5 2.0 3.0
Úloha 1. Napište matici pro případ lineárního regresního spline vyjádřeného přes useknuté polynomy pro případ dvou uzlových bodů ξ 1 = 1 a ξ 2 = 4. Experimentální body jsou x = [0.2 0.4 0.6 1.5 2.0 3.0
Aproximace funkcí. Numerické metody 6. května FJFI ČVUT v Praze
 Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Ukázka možností interpolace dat v softwaru Matlab
 Ukázka možností interpolace dat v softwaru Matla Ing. Stanislav Olivík Anotace: V následujícím tetu ude čtenář seznámen s několika základními funkcemi softwaru Matla, pomocí nichž může interpolovat data
Ukázka možností interpolace dat v softwaru Matla Ing. Stanislav Olivík Anotace: V následujícím tetu ude čtenář seznámen s několika základními funkcemi softwaru Matla, pomocí nichž může interpolovat data
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
Robustní odhady statistických parametrů
 Robustní odhady statistických parametrů ěkdy pracují dobře, jinde ne. Typická data - pozorování BL Lac 100 mag 40 0 0.41 0.40 JD date 0.39 0.38 0.38223-1.586 0.017 0.40550-1.530 0.019 0.39453-1.610 0.024
Robustní odhady statistických parametrů ěkdy pracují dobře, jinde ne. Typická data - pozorování BL Lac 100 mag 40 0 0.41 0.40 JD date 0.39 0.38 0.38223-1.586 0.017 0.40550-1.530 0.019 0.39453-1.610 0.024
Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci)
 2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
5. Plochy v počítačové grafice. (Bézier, Coons)
 5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
Matematika 1 sbírka příkladů
 Matematika 1 sbírka příkladů RNDr. Rudolf SCHWARZ, CSc. Brno 2012 1. Poznámka Výsledky jednotlivých příkladů mají tuto barvu. 2. Poznámka Pokud je v hranatých závorkách uvedeno písmeno, označuje, ze které
Matematika 1 sbírka příkladů RNDr. Rudolf SCHWARZ, CSc. Brno 2012 1. Poznámka Výsledky jednotlivých příkladů mají tuto barvu. 2. Poznámka Pokud je v hranatých závorkách uvedeno písmeno, označuje, ze které
Aproximace a interpolace
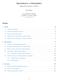 Aproximace a interpolace Matematické algoritmy (11MAG) Jan Přikryl 12. přednáška 11MAG pondělí 15. prosince 2014 verze:2014-12-15 11:10 Obsah 1 Úlohy 2 1.1 Aproximace funkcí...................................
Aproximace a interpolace Matematické algoritmy (11MAG) Jan Přikryl 12. přednáška 11MAG pondělí 15. prosince 2014 verze:2014-12-15 11:10 Obsah 1 Úlohy 2 1.1 Aproximace funkcí...................................
POLYNOMICKÁ REGRESE. Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými.
 POLYNOMICKÁ REGRESE Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými. y = b 0 + b 1 x + b 2 x 2 + + b n x n kde b i jsou neznámé parametry,
POLYNOMICKÁ REGRESE Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými. y = b 0 + b 1 x + b 2 x 2 + + b n x n kde b i jsou neznámé parametry,
Q(y) dy = P(x) dx + C.
 Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Lineární rovnice pro učební obory
 Variace 1 Lineární rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Rovnice Co je rovnice
Variace 1 Lineární rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Rovnice Co je rovnice
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Variace. Lineární rovnice
 Variace 1 Lineární rovnice Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Rovnice Co je rovnice Rovnice je
Variace 1 Lineární rovnice Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Rovnice Co je rovnice Rovnice je
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
4. Diferenciál a Taylorova věta
 4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
Hledání extrémů funkcí
 Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení.
 @083 6 Polynomické funkce Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení. Definice: Polynomická funkce n-tého stupně (n N) je dána předpisem n n 1 2 f : y a x
@083 6 Polynomické funkce Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení. Definice: Polynomická funkce n-tého stupně (n N) je dána předpisem n n 1 2 f : y a x
Základy numerické matematiky. Interpolace a aproximace funkcí
 Základy numerické matematiky Interpolace a aproximace funkcí Nejdříve se podíváme na interpolaci. Lagrangeovu interpolaci počítá Maple pomocí funkce interp. Jejími parametry jsou - soubor uzlů, funkčních
Základy numerické matematiky Interpolace a aproximace funkcí Nejdříve se podíváme na interpolaci. Lagrangeovu interpolaci počítá Maple pomocí funkce interp. Jejími parametry jsou - soubor uzlů, funkčních
Interpolace a aproximace dat.
 Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
Digitální učební materiál
 Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_143_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
Digitální učební materiál Číslo projektu: CZ.1.07/1.5.00/34.0548 Název školy: Gymnázium, Trutnov, Jiráskovo náměstí 325 Název materiálu: VY_32_INOVACE_143_IVT Autor: Ing. Pavel Bezděk Tematický okruh:
0.1 Úvod do matematické analýzy
 Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
1 Polynomiální interpolace
 Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ
 MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
AVDAT Náhodný vektor, mnohorozměrné rozdělení
 AVDAT Náhodný vektor, mnohorozměrné rozdělení Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Opakování, náhodná veličina, rozdělení Náhodná veličina zobrazuje elementární
AVDAT Náhodný vektor, mnohorozměrné rozdělení Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Opakování, náhodná veličina, rozdělení Náhodná veličina zobrazuje elementární
Aproximace funkcí. Polynom Φ m (x) = c 0 + c 1 x + c 2 x c m x m. Φ m (x) = c 0 g 0 (x) + c 1 g 1 (x) + c 2 g 2 (x) +...
 Aproximace funkcí 1 Úvod Aproximace funkce - výpočet funkčních hodnot nejbližší (v nějakém smyslu) funkce v určité třídě funkcí (funkce s nějakými neznámými parametry) Příklady funkcí používaných pro aproximaci
Aproximace funkcí 1 Úvod Aproximace funkce - výpočet funkčních hodnot nejbližší (v nějakém smyslu) funkce v určité třídě funkcí (funkce s nějakými neznámými parametry) Příklady funkcí používaných pro aproximaci
3 Lineární kombinace vektorů. Lineární závislost a nezávislost
 3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
----- Studijní obory. z matematiky. z matematiky. * Aplikovaná matematika * Matematické metody v ekonomice
 Minimum Maximum Minimum Maximum Studijní obory z matematiky z matematiky z matematiky z matematiky * Aplikovaná matematika * Matematické metody v ekonomice * Obecná matematika Navazující magisterský studijní
Minimum Maximum Minimum Maximum Studijní obory z matematiky z matematiky z matematiky z matematiky * Aplikovaná matematika * Matematické metody v ekonomice * Obecná matematika Navazující magisterský studijní
Bézierovy křivky Bohumír Bastl KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26
 Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
