SBORNÍK. 17. konference studentů v matematice června 2009 Lázně Bohdaneč. Komise JČMF pro matematiku na VŠTEZ Fakulta stavební ČVUT v Praze
|
|
|
- Milan Navrátil
- před 5 lety
- Počet zobrazení:
Transkript
1 Komise JČMF pro matematiku na VŠTEZ Fakulta stavební ČVUT v Praze SBORNÍK příspěvků ze 17. konference studentů v matematice na školách VŠTEZ června 009 Lázně Bohdaneč
2 Vydavatel: Vydavatelství ČVUT v Praze Praha 009 Editor: Stanislav Olivík ISBN:
3 Předmluva Komise JČMF pro matematiku na VŠTEZ pořádala v letošním roce v hotelu Technik v Lázních Bohdaneč již 17. konferenci o aplikacích matematiky pro studenty bakalářských, magisterských a doktorských oborů na technických vysokých školách. Ti, kteří aktivně zahájili tradici pořádání studentských konferencí, byli v roce 199 prof. Stanislav Míka a prof. V. Medek. Tato konference se konala na různých místech. První připravoval Dr. Ivo Moll v Lošticích, další pak spolupořádali i jiní kolegové, mnoho dalších jsme pak pořádali v rámci komise a katedry matematiky Fakulty stavební ČVUT v Praze. Naše první konference byla soutěž mezi studenty o cenu profesora Medka v době, kdy prof. Medek zemřel. Forma soutěže pak byla opuštěna, i když jsme na prof. Medka vzpomínali na dalších setkáních členů komise na těchto konferencích. Současné konference jsou prostředím, kde studenti různých stupňů studia poznávají úlohy, které na různých úrovních řeší. Seznamují se tak s problémy, se kterými se mohou v budoucnosti při jejich studiu či v praxi potkat v oblasti matematické a aplikované vědy. Zvané přednášky vynikajících matematiků a inženýrů, kteří používají při své práci matematické metody, jsou každoročním velkým přínosem této konference. Řada kolegů, kteří přijali v minulosti naše pozvání, dovedla naši konferenci do současné podoby a podle nás do velmi dobré úrovně. V letošním roce přijali naše pozvání a přednesli zvané přednášky paní profesorka Edita Pelantová z Fakulty jaderné a fyzikálně inženýrské a pan profesor Ivo Marek ze Stavební fakulty ČVUT. Konference byla nejen prezentací studentských referátů, ale i příležitostí k mnoha diskuzím mimo oficiální program mezi studenty z různých vysokých škol. V letošním roce se konference zúčastnilo 7 studentů z Fakulty jaderné a fyzikálně inženýrské ČVUT, 4 studenti z Fakulty stavební ČVUT, studenti z Fakulty aplikovaných věd ZČU v Plzni a 1 student z České zemědělské university v Praze. Předkládáme Vám sborník referátů, které jste nám zaslali, a věříme, že Vám připomenou atmosféru konference. Rádi bychom na závěr tohoto úvodu poděkovali našim sponzorům (fa BComp) a především Vám, příznivcům a účastníkům za pozitivní aktivity na našich studentských konferencích. Velké poděkování patří také všem, kteří se na průběhu konference podíleli a našemu hostiteli, hotelu Technik v Lázních Bohdaneč. Těšíme se na setkání s Vámi na příští, již 18. konferenci studentů na školách VŠTEZ v příštím roce. Michal Beneš Milada Kočandrlová Stanislav Olivík V Praze dne 10. října 009 Komise JČMF pro matematiku na VŠTEZ
4
5 Obsah Petr Dvořák 7 Matematické modelování mikrostruktur při fázových přechodech Pavel Hron 17 Použití nespojité Galerkinovy metody v transportních problémech Radek Máca 7 Metody degenerované difuze při počítačovém zpracování obrazu a jejich aplikace Stanislav Olivík 37 Družice pro bistatickou altimetrii ohlédnutí za Workshopem GNSS-R 08 Martin Ptáček 41 Aplikace numerických metod na dynamiku tekutin František Štampach 55 Charakteristický polynom a rezolventa Jacobiho matice speciálního typu Vít Tomica 63 Matematické modelování reakčních procesů v problematice spalování Jana Vecková 73 Metoda hustoty plošného napětí
6
7 Matematické modelování mikrostruktur při fázových přechodech Petr Dvořák 14. července 009 Abstrakt Model fázového pole, vychází z van der Waalsova přístupu, který (na rozdíl od Gibbsova přístupu) uvažuje hladký přechod mezi fázemi. Obecné analytické řešení úlohy fázového pole neexistuje, proto se daná úloha v této práci řeší numericky explicitním schématem. Chyba aproximace explicitního schématu vychází experimentálně O(τ + h ), což je v souladu s teorií. Největší část výsledků je věnována dendritickému růstu, kde jsou prozkoumány základní vlastnosti anizotropního modelu fázového pole. Úvod Pod pojmem tvorba mikrostruktur při fázových přechodech si můžeme představit růst pevné fáze určité látky (typicky kovů, slitin nebo i vody) v kapalné fázi v mikroskopickém měřítku. Tato práce je zaměřena na jev zvaný krystalizace. Fázové rozhraní vzniká během procesu nazývaném fázový přechod prvního druhu. S tímto procesem je pevně svázána spotřeba nebo uvolnění určitého množství latentního tepla a také změny termodynamických veličin. Teorie týkající se tvorby krystalů při fázových přechodech má v praxi široké uplatnění. Využití lze nalézt například v oblasti výroby polovodičů. V optice se krystalizace využívá pro výrobu optických vláken a polarizačních filtrů. Z dalšího uplatnění uveďme výrobu parních turbín a letadlových proudových motorů. Široké uplatnění lze nalézt i ve stavebnictví. 1 Stefanova úloha Jedná se o model fázového přechodu v systému kapalina pevná látka, který objasňuje šíření tepla a výměnu latentního tepla v homogenní látce. Formování mikrostruktur v systému je důsledkem změn ve volné energii a entropii, ty na sebe během tuhnutí vzájemně působí a to Katedra matematiky, Fakulta jaderná a fyzikálně inženýrská, České vysoké učení technické v Praze, dvorap9@fjfi.cvut.cz - 7 -
8 může vést ke vzniku nestabilních celistvých forem v pevné podoblasti. Ve chvíli, kdy daný systém dosáhne stavu teplotní rovnováhy, tyto formy vymizí a pevná podoblast zaujme jiný jednodušší tvar. Mějme Ω R omezenou oblast, ve které probíhá fázový přechod prvního druhu a nechť Ω l (t), Ω s (t) je kapalná, resp. pevná podoblast Ω, teplotní pole označme u : 0,T Ω R. Definujme u (teplotu fázového přechodu) rovností volné energie pevné a kapalné fáze: F l (u ) = F s (u ). Pomocí teploty fázového přechodu můžeme definovat latentní teplo objemové jednotky: L = H l (u ) H s (u ), kde H je objemová hustota entalpie pro daný stav. Dále předpokládejme, že nedochází k průniku hranice a fázového rozhraní ( Γ Ω =, t 0). Škálování je dáno: su 1. A dále uvažujme přítomnost kinetického podchlazení prostředí L upravujícího teplotní vztahy pro rozhraní Γ(t). Za těchto předpokladů můžeme napsat Stefanovu úlohu (viz [Gur86, Ben97, Ben01]): ρc u = (λ u) na Ω s (t) Ω l (t), (1a) t u u = σ s κ Γ α σ s v Γ na Γ, (1b) λ u n Γ λ u s n Γ = Lv Γ na Γ, (1c) l b c (u) Ω = 0 na Ω, (1d) u t=0 = u 0 na Ω, (1e) Ω s (t) t=0 = Ω s0 na Ω s, (1f) kde je použito následující označení: s je rozdíl entropií mezi Ω l a Ω s ; λ je tepelná vodivost oblasti; ρ je hustota oblasti; c je tepelná kapacita oblasti; n Γ je normálový vektor k rozhraní Γ(t) směřující ven z Ω s ; n Ω normálový vektor k hranici Ω směřující ven z Ω; κ Γ = n Γ střední křivost nadplochy Γ(t); v Γ je normálová rychlost rozhraní Γ(t); σ = f(u ) je povrchové napětí mezi fázemi; α je koeficient připojovací kinetiky na hranici. Pro jednotlivé rovnice platí: (1a) je rovnice vedení tepla, (1b) je Gibbsova-Thomsonova podmínka určující vztah mezi rychlostí fázového rozhraní a podchlazením a zakřivením, (1c) je Stefanova podmínka, která vyjadřuje nespojitost tepelného toku na rozhraní Γ(t), (1d) je okrajová podmínka vyjádřena operátorem b c (Dirichletova, Neumannova, nebo Newtonova okrajová podmínka), (1e) představuje počáteční rozložení teploty, (1f) představuje počáteční rozložení pevné fáze. Soustava rovnic (1) nevyjadřuje explicitně fázový přechod, a proto neumožňuje jednoduše sledovat vývoj rozhraní při přechodu mezi fázemi. Stefanovu úlohu můžeme považovat za fyzikální model formování pevného skupenství v tekutém při absenci pohybu média
9 Model fázového pole Přístup pomocí metody fázového pole je charakteristický existencí jisté přechodové vrstvy, jejíž tloušťka je dána difuzním parametrem ξ. Pohyb rozhraní je pak dán implicitně pomocí rovnice fázového pole, která je popsaná níže. Zavedeme stavový parametr p = p(t,x), pro t R a x = [x 1,x ] Ω, který bude popisovat zkoumaný systém, následovně p : R Ω 0, 1. Tento spojitý parametr budeme nazývat fázové pole. Bez újmy na obecnosti nadále předpokládejme, že lokálnímu kapalnému stavu odpovídá hodnota blízká nule a lokálnímu tuhému stavu hodnota blízká jedné. Podle [Cag86] fázové pole představuje lokální průměr jednotlivých fází. K přechodu z jednoho stavu do druhého dochází na tenké vrstvě Ω Γ. Rozhraní je pak definováno množinou bodů Γ(t) = {x Ω p(t,x) = 1 }. Model fázového pole je dán následující soustavou rovnic, jejíž odvození můžeme najít například v [Ben97] ρc u t αξ p t = λ u + L p t, které jsou doplněny okrajovými podmínkami (a) = ξ p + ap(1 p)(p 1 ) + c 0 tanh(βξ(u u)), (b) Dirichletova typu: u Ω = u Ω, p Ω = p Ω, Neumannova typu: u n Ω Ω = 0, p n Ω Ω = 0, a počátečními podmínkami u(0,x) = u ini (x), p(0,x) = p ini (x), (c) kde ρ je hustota, c měrná tepelná kapacita, λ je tepelná vodivost a L je měrné latentní teplo. Identita (a) je rovnice vedení tepla, druhá identita (b) se nazývá fázová rovnice nebo také Allenova Cahnova rovnice. Pro to, abychom mohli modelovat dendritický růst krystalu, zejména pak anizotropický, je třeba mírně modifikovat současný matematický model. Upravíme rovnici (b) tak, že přidáme funkci g způsobující anizotropii, získáme dvě modifikace podle toho, kam zmíněnou funkci začleníme. První možnost je, že funkcí g násobíme Laplaceův operátor a polynom f 0 (p) αξ p t (t,x) = g(θ)[ ξ p(t,x) + f 0 (p(t,x)) ] + c 0 tanh(βξ(u u)), nebo násobíme řídící člen αξ p t (t,x) = ξ p(t,x) + f 0 (p(t,x)) + g(θ)c 0 tanh(βξ(u u)). (3a) (3b) - 9 -
10 Na funkci g = g(θ) klademe následující podmínky: omezenost, tedy 0 < g 1 < g(θ) < g, kde g 1 a g jsou konstanty, pozitivnost, ( θ (0, π ) (g(θ) > 0), θ je úhel mezi vnější normálou k rozhraní (gradient fázové funkce) a osou x 1, obvykle volíme g(θ) = 1 ζ cos(n fold (θ θ 0 )), kde n fold je četnost preferovaných směrů, ζ je amplituda určující sílu anizotropie a θ 0 je počáteční natočení. 3 Numerická analýza Vzhledem k tomu, že obecně neexistuje analytické řešení rovnice fázového pole (), je potřeba tento problém řešit numericky. V teorii numerické analýzy existuje mnoho metod pro řešení diferenciálních rovnic druhého řádu parabolického typu, viz [Vit87]. My se zde budeme zabývat pouze metodou sítí Podstata metody sítí je jednoduchá, spočívá v diskretizaci 1. oblasti nezávisle proměnných,. diferenciální rovnice, 3. okrajové a počáteční podmínky. Získáme tak (místo diferenciální úlohy) konečnou soustavu algebraických rovnic pro konečně mnoho neznámých. Označme množinu všech uzlů sítě na Ω ω h = {[a 1 + ih 1,a + jh ] i = 0, 1,...,N 1, j = 0, 1,...,N }, a množinu vnitřních uzlů sítě na Ω ω h = {[a 1 + ih 1,a + jh ] i = 1,,...,N 1 1, j = 1,,...,N 1}, pro úplnost ještě označme množinu krajních bodů Ω γ h = ω h ω h. Poznámka. Základní diferenční náhrady používané v numerické matematice budeme značit následovně: v x (x) pro dopřednou diferenci, v x (x) pro zpětnou diferenci, v x (x) pro centrální diferenci. Druhá diference je v xx (x) = (v x ) x (x). Diference Laplaceova operátoru (síťový laplacián) je pak definován následovně: h v = v x1 x 1 + v x x, kde x = [x 1, x ]. Definice 1. Zobrazení v : ω h R se nazývá síťová funkce. Množinu všech síťových funkcí na ω h značíme H h. Síťovou funkci, která aproximuje řešení v diferenciální úlohy v čase t = kτ, respektive t = (k + 1)τ, budeme značit w : ω h R, respektive ŵ : ω h R
11 Definice. P h : C(Ω) H h se nazývá operátor projekce, platí-li, že P h v = v ωh v C(Ω). pro Úlohu () nahradíme diferenční úlohou. V rovnicích (a) a (b) přepíšeme derivace pomocí diferencí. Získáváme tak explicitní diferenční úlohu ( v k v k+1 ij = vij k (i 1)j vij k + v(i+1)j k + τ + vk i(j 1) ) vk ij + vi(j+1) k + L(q k+1 h 1 h ij qij), k ( q k+1 ij = qij k + τ q k (i 1)j qij k + q(i+1)j k + qk i(j 1) ) qk ij + qi(j+1) k + α h 1 h + τ 1 α ξ ij(1 qij) ( ) k q k qk ij 1 τ 1 + α ξ c 0β(u vij), k s odpovídající diskretizovanou okrajovou a počáteční podmínkou a pro i = 0,...,N 1, j = 0,...,N, k = 0,...,N T. Funkce v a q jsou síťové a odpovídají funkcím u a p z úlohy (). Explicitní schéma je velice jednoduché na implementaci. Nevýhodou ovšem je, že tato metoda je pro rovnici vedení tepla i pro Allenovu-Cahnovu rovnici omezena podmínkou stability 1. Podmínka stability pro rovnici vedení tepla, viz [Net03]: ( 1 τ + 1 ) < 1 h 1 h. (4) Je-li tento předpis porušen, tak je explicitní schéma nestabilní (osciluje). 4 Numerické výsledky Až do této chvíle jsme se zabývali převážně teorií, nyní se podíváme na výsledky poskytnuté odvozenými modely. Převážná část výsledků se týká základního zkoumání růstu krystalického dendritu. Fázové pole je vždy zobrazeno vrstevnicí o hodnotě p = 1, což odpovídá fázovému rozhraní, teplotní pole je obvykle zobrazeno černobílým přechodem. Všechny grafické výsledky jsou vykresleny pomocí programu gnuplot. 4.1 Řád konvergence explicitního schématu Pokud vhodně doplníme pravou stranu modelu fázového pole, budeme moci porovnat numerické výsledky s analytickým řešením, které je známo právě díky doplněné pravé straně a daným počátečním podmínkám. Zde budeme analyzovat pouze chybu a řád konvergence teplotního pole. Přesné řešení Stefanovy úlohy s upravenou pravou stranou obsažené v práci [Sch96] porovnáme s numerickým řešením úlohy fázového pole. V tabulce 1 je zobrazena vypočítaná 1 Více o podmínce stability explicitního schématu najdeme v [Sam77, Vit87, Net03]
12 Síťový krok regul. L (0,T; L ) EOC u h ξ chyba u L Tabulka 1: Tabulka chyb numerického schématu vzhledem k přesnému řešení. chyba (pomocí odpovídající normy) pro jednotlivá zjemnění vůči přesnému řešení pro teplotní pole u. ( ) Řád konvergence nyní spočítáme snadno podle vzorce E 1 h EOC, E = 1 h více v [Ben03], kde E i je chyba odpovídající prostorovému kroku h i, i = 1,. Výsledek můžeme vidět opět v tabulce 1, z které je patrné, že pro klesající ξ (a tedy i h = [h 1,h ]) numerické řešení konverguje k přesnému řešení rychlostí O(h ). 4. Modelování růstu dendritu Výraz dendrit pochází z řeckého slova dendron, což v češtině znamená strom. Pro krystalický dendrit je je typické větvení jeho ramen, tím vzniká stromovitý útvar. Nejznámějším takovým útvarem je pravděpodobně sněhová vločka. 3 p, u; t = p, u; t = Obrázek 1: Počáteční podmínka fáze je kruh o poloměru R 0 = 0.03, u ini 0. Další parametry jsou β = 350, ξ = 0.003, u = 1, L =, a =, α = 3, N = [1000, 1000], h = [0.003, 0.003] a τ = , ζ = 0., θ 0 = 0. Přerušovanou linkou je zobrazeno fázové rozhraní, černobílý přechod na pozadí je teplotní pole
13 (a) n fold = (b) n fold = (c) n fold = 8 Obrázek : Zobrazen vývoj fázového rozhraní pro různé hodnoty n fold v časových hladinách t = 0, t = 0.1, t = 0.,..., t = 0.9. Další parametry jsou β = 350, ξ = 0.003, u = 1, L =, a =, α = 3, N = [1000, 1000], h = [0.003, 0.003], τ = , ζ = 0., θ 0 = p, t = ζ = 0.0 ζ = 0. ζ = 0.6 Obrázek 3: Porovnání růstu krystalu pro různé síly anizotropie. Fázové pole je zobrazeno vrstevnicí o hodnotě 0.5. Počáteční podmínka fázové funkce je kroužek o poloměru R 0 = 0.03, počáteční podmínka teploty je nulová. Další parametry jsou β = 350, ξ = 0.001, u = 1, L =, a =, α = 3, N = [000, 000], h = [0.001, 0.001] a τ = 10 6, θ 0 = 0, n fold = 4. Rozdíl mezi modely (3a) a (3b) V odstavci jsme představili několik možností, jak do matematického modelu začlenit anizotropii pomocí funkce g = g(θ), podle toho jsme označili model buď (3a), nebo (3b). Výsledek porovnání těchto dvou rovnic je zobrazen na obrázku 1. Na obrázcích je přerušovanou čarou zobrazena fázové rozhraní. Teplotní pole je zobrazeno černobílým přechodem na pozadí. První obrázek je dendrit modelovaný pomocí rovnice (3a), druhý je modelován pomocí rovnice (3b)
14 3 p, t = 0 3 p, t = p, t = Obrázek 4: Počáteční podmínka teploty je nula. Fyzikální parametry jsou β = 500, ξ = 0.00, u = 1, L =, a =, α = 3, numerické parametry jsou N = [1500, 1500], h = [0.00, 0.00] a τ = Počet preferovaných směrů Za počet preferovaných směrů, a tedy počet ramen dendritu odpovídá parametr n fold ve funkci g = g(θ). Porovnání tří případů růstu čtyř-, šesti- a osmiramenného krystalu můžeme zhlédnout na obrázku, k tomu účelu byl použit model fázového pole typu (3b). Počáteční podmínka fáze je dána malým kroužkem o poloměru 0.03, počáteční podmínka teploty je identicky rovna nule. Okrajové podmínky byly zvoleny Neumannovy. Vzhledem k tomu, že pro menší n fold mají ramena mezi sebou více prostoru, tak je již v kratším čase vidět formování dendritu, naopak pro vyšší n fold je dendrit více podobný kruhu. Síla anizotropie Dalším členem funkce g = g(θ) způsobující anizotropii je ζ síla anizotropie, pokud je rovna nule, pak je g 1 a jde tedy o izotropní případ. Čím větší je síla anizotropie, tím užší jsou ramena dendritu. To můžeme potvrdit při pohledu na obrázek 3, kde byl použit model s rovnicí (3a). Na obrázku je fázové pole pro různé hodnoty ζ. Nutno dodat, že ζ nemůže být příliš velká, aby nebyla porušena podmínka g > 0. Je možné volit sílu anizotropie zápornou, což vede k prohození směrů, ve kterých dochází k rychlejšímu růstu se směry pomalejšího růstu. Více útvarů Další zajímavé pozorování při růstu dendritu, které se dozajista vyplatí prozkoumat, je růst více útvarů najednou a vzájemná interakce mezi nimi a interakce s rozhraním. Růst dvou čtyřramenných dendritů je znázorněn na obrázku 4 a růst tří šestiramenných dendritů můžeme pozorovat na obrázku 5. Na obou obrázcích je zobrazen vývoj fázového rozhraní. Ze
15 6 p, t = p, t = p, t = Obrázek 5: Počáteční podmínka teploty je nula. Parametry jsou β = 350, ξ = 0.003, u = 1, L =, a =, α = 3, N = [000, 000], h = [0.003, 0.003] a τ = začátku, když jsou krystaly ještě dostatečně daleko od sebe, tak dochází k obvyklému růstu. Postupně se zvětší tak, že rozhraní dendritů mezi sebou a i spolu s hranicí (danou Neumannovými okrajovými podmínkami) začnou interagovat a dendrity se tímto deformují. Porovnání s izotropním růstem Rozdíl mezi izotropním a anizotropním růstem je zásadní. Především je podstatné, že u anizotropního růstu můžeme nastavit další parametry, které u izotropního růstu neovlivníme, tím je počet ramen dendritu, síla anizotropie a pootočení dendritu. Několik společných rysů fázového pole lze pozorovat na obrázku 6, kde byl zvolen anizotropní růst čtyřramenného dendritu se sílou anizotropie ζ = 0.. V levém sloupci je zobrazeno fázové rozhraní, vpravo je teplotní pole vyjádřeno černobílým přechodem. Největší rozdíl je zřetelný ve velikosti ramen. Je také patrné, že dochází v izotropním případě k dalšímu větvení a vzniku dalších ramen, zatímco tento jev se při anizotropním růstu nepodařilo pomocí modelu (3b) nasimulovat (i přesto, že byla zvolena dostatečně velká prostorová oblast i čas). 5 Závěr V práci byla shrnuta základní teorie týkající se fyzikálního modelu pro fázové přechody prvního druhu. Byl podrobněji popsán model fázového pole. Dále jsme zavedli anizotropii, která umožnila modelování růstu krystalického dendritu. Výsledky, které tato práce obsahuje, jsou ve většině případů v grafickém provedení, jedná se především o modelovaní jevu zvaného krystalizace, neboli dendritický růst krystalu, na který je tato práce zaměřena. Nesmíme zapomenout na experimentální ověření teoretického výsledku, že chyba aproximace explicitního numerického schématu je O(τ + h )
16 9 p, t = 3 ζ = 0.0 ζ = u, t = 3, ζ = u, t = 3, ζ = Obrázek 6: Počáteční podmínky jsou dány R 0 = 0.03, u ini 0. Fyzikální parametry jsou β = 350, ξ = 0.003, u = 1, L =, a =, α = 3, numerické parametry jsou N = [3000, 3000], h = [0.003, 0.003] a τ = Reference [Ben97] M. Beneš. Phase field model of microstructure growth in solidification of pure substances. PhD thesis, Fakulta jaderná a fyzikálně inženýrská, ČVUT, Vedoucí dizertační práce Prof. Ing. Miloslav Havlíček, DrSc. [Ben01] M. Beneš. Matematické modelování procesu tuhnutí v krystalických materiálech pomocí nelineárních parciálních diferenciálních rovnic, 001. Fakulta jaderná a fyzikálně inženýrská, ČVUT, habilitační práce. [Ben03] Michal Beneš. Diffuse-interface treatment of the anisotropic mean-curvature flow. Appl. Math., 48(6): , 003. Mathematical and computer modeling in science and engineering. [Cag86] G. Caginalp. An Analysis of a Phase Field Model of a Free Boundary. Arch. Rational Mech. Anal., 9(3):05 45, [Gur86] M. E. Gurtin. On the Two-Phase Stefan Problem with Interfacial Energy and Entropy. Arch. Rational Mech. Anal., 96(3):199 41, [Net03] B. Neta. Numerical Solution of Partial Differential Equations. Lecture Notes. Department of Mathematics, Naval Postgraduate School, Monterey, California 93943, 003. [Sam77] A. A. Samarskij. Theory of Difference Schemes. Nauka, Moscow, [Sch96] A. Schmidt. Computation of three dimensional dendrites with finite elements. Journal of Computational Physics, 15(95):93 31, [Vit87] E. Vitásek. Numerické metody (Technický průvodce 67). SNTL, Praha,
17 ÈÓÙö Ø Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ý Ú ØÖ Ò ÔÓÖØÒ ÔÖÓ Ð Ñ È Ú Ð ÀÖÓÒ ØÖ Ø Ì ÒØÓ Ð Ò Þ Ú Ò Ñ ÚÓÙÖÓÞÑ ÖÒ Ó Ú Ò Ó ÔÖÓ Ð ÑÙ Þ ÚÒ Ø Ò Þ ÖÓ ó ÔÖÓÔ ó Ô ÞÒ Ñ Ñ ÖÓÞÐÓö Ò ÖÝ ÐÓ ØÒ Ó ÔÓÐ º Ã Ò ØÓ Ó ÔÖÓ Ð ÑÙ Ó ¹ ÚÝ Ð ÔÓÙö Ú Ñ ØÓ ÓÒ Ò Ó Ñóº ÅÒÓ Ñ Ð Ô Ú Ð ó Ô Ò Ú Ò Ó ÔÖÓ Ð ÑÙ ÐÞ Ó ÒÓÙØ ÔÓÙö Ø Ñ Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ýº Ì ØÓ Ñ ØÓ ÔÓØÐ Ù ÚÐ Ú ÒÙÑ Ö ÙÞ Ò Ò ÔÓ Ø Ñ Ò Ú Ó Þ Ó Ð Ñ Ò ÓÑ Þ ÒÓ Ø ¹ Ò º ÈÖÓØÓ ÑÙ Ø ÔÓÙö ØÝ Ð Ñ Ø ÖÝ Ø Ö ÚÞÒ Ù Ó Ð Þ Ö Ò º Ð Ñ ØÓ ÓØÓ Ð Ò Ù ÔÓÖÓÚÒ Ò Ñ ØÓ Ý ÓÒ Ò Ó Ñó Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ý Ò Þ Ð ÒÙ¹ Ñ Ö Ú Ð ó Þ Ò ÔÖÓ ÖóÞÒ Ø ØÓÚ ÐÓ Ýº ÓÖÑÙÐ ÔÖÓ Ð ÑÙ Ú Ñ Ò Ñ Ô Ö ÐÒ Ö Ò ÐÒ ÖÓÚÒ u t ÔÓ Ø Ò Ñ Ó Ö ÓÚÑ ÔÓ Ñ Ò Ñ +.f(u) = 0 Ò Ω (0, T), ½ µ u(x, 0) = u 0 (x) x Ω, ½ µ u(x, t) = γ(x, t) x Γ. ½µ ÙÒ f = βu ÓÞÒ Ù Ú ØÓÖÓÚÓÙ ÙÒ Ó Ð ÖÒ Ò ÞÒ Ñ ÙÒ u = u(x, t) = u(x, y, t) Ö ÔÖ Þ ÒØÙ ÓÒ ÒØÖ ÖÓÞÔÙ Ø Ò Ð Ø Ý β = β(x) = (β 1 (x), β (y)) Þ Ò Ú ØÓÖÓÚ ÔÓÐ ÖÝ ÐÓ Ø Ω R (0, T) Ò ÓÚ ÒØ ÖÚ Ðº Γ ÚØÓ ÓÚ Ø Ó Ð Ø Γ = {x Ω β.n < 0}, n ÚÒ ÒÓÖÑ ÐÓÚ Ú ØÓÖ Ö Ò Ωº Ã Ø Ö Ñ Ø Ñ Ø Ý Â Á ÎÍÌ Ú ÈÖ Þ Ô º ÖÓÒ Ñ ÐºÞ
18 ½ Æ ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ Ã Ò ÝÔ Ö ÓÐ Þ ÓÒó Þ ÓÚ Ò ØÓ ÔÓÙö Ú Ò ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ Ó¹ Ò Ò ÔÖÚ óº Å ½ ÓÑ ÒÙ Ú Ó Ý Ñ ØÓ Ý ÓÒ Ò Ó Ñó Ñ ØÓ Ý ÓÒ Ò ÔÖÚ ó ¹ ÓÒÞ ÖÚ Ø ÚÒÓ Ø ÚÝ Ô ÒÓ Ø Ò Ð Ñ Ò º Ð Ú Ó ÓÙ ö Å ÐÞ ÔÓÙö Ø Ò ÓÑÔÐ ÓÚ Ò ÓÑ ØÖ Ò ØÖÙ ØÙÖÓÚ Ò Ø º ½º½ ÈÖÓ ØÓÖÓÚ Ö Ø Þ Æ Ú Ö Ø ÞÙ Ñ ½ µ Ú ÔÖÓ ØÓÖÙ Ùö Ø Ñ Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ýº ÈÖÓ ö t [0, T] Ð Ñ ÔÖÓÜ ÑÓÚ Ò Ò u h (t) Ú ÔÖÓ ØÓÖÙ Ò ÔÓ Ø ÙÒ V h = {v h L (Ω) : v h K V (K) K T h }, T h ØÖ Ò ÙÐ Ó Ð Ø Ω V (K) ÔÖÓ ØÓÖ Ð Ò ÖÒ ÔÓÐÝÒÓÑó P 1 ØÙÔ ó Ò Ú ½ ÒÓÚ Ò Ò ØÖÓ ÐÒ Ù Kº ÈÓ Ù ÔÓÙö Ñ ÔÓ Ø ÓÒ Ø ÒØÒ ÙÒ Ó Ø Ú Ñ Ñ ØÓ Ù ÓÒ Ò Ó Ñó ÎÅ ¾ µº Ý ÓÑ ÚÝÔÓ Ø Ð ÔÖÓÜ ÑÓÚ Ò Ò u h (t) ÚÝ Þ Ñ Þ Ð ÓÖÑÙÐ ½ µº ÊÓÚÒ ½ µ ÚÝÒ Ó Ñ Ð ÓÙ Ø ØÓÚ ÙÒ v ÒØ ÖÙ Ñ Ô ØÖÓ ÐÒ K T h Óö Ú ÚÞØ Ù K t K u(x, t)v(x) x + K K.f(u(x, t))v(x) x = 0. ÌÙØÓ ÖÓÚÒ ÙÔÖ Ú Ñ ÔÓÑÓ Ö ÒÓÚÝ ÓÖÑÙÐ Ò ØÚ Ö u(x, t)v(x) x f(u(x, t)). v(x) x + v(x)f(u(x, t)).n l = 0, µ t Óö Ð ÓÖÑÙÐ ÐÓ Ý ½ µº Ö ÒÓÚ ÓÖÑÙÐ Ô Ú ÖÙ ÒØ Ö Ð Ú ¾µ Ò Ú ÒØ ¹ Ö ÐÝ Þ Ò ö Ò Ú ÓÚº ËÝÑ ÓÐ n ÓÞÒ Ù ÒÓÖÑ ÐÓÚ Ú ØÓÖ ÚÒ Ö Ò l Ð Ñ ÒØÙ Kº Ã Ú ÓÚ ÒØ Ö Ð ÖÓÞ Ð Ñ Ò ÒØ Ö ÐÝ Ô ÒÓØÐ Ú Ø Ö Ò 3 v(x)f(u(x, t)).n l = v(x)f(u(x, t)).n i l. µ l l i i=1 Ð Ø ØÓÚ ÙÒ v Ò Ö Ñ ÙÒ v h Þ ÔÖÓ ØÓÖÙ V (K) Ô Ò Ò u ÖÓÚÒ µ Ò Ö Ñ Ô Ð öòñ Ò Ñ u h Ø Ö Ñóö Ø ÚÝ ÒÓ Ó ÓÙ Ø Þ ÙÒ u h (x, t) u h (x, t) K = 3 u K j (t)ϕ K j (x), ϕ K j ÓÙ Ø ØÓÚ ÙÒ Þ V h Ø Ö ØÚÓ ÐÓ ÐÒ Þ ÔÖÓ ØÓÖÙ V (K) u K j (t) ÓÙ Ø Ò ÞÒ Ñ Ó ÒØÝ Ó ÔÓÚ ØÙÔ óñ ÚÓÐÒÓ Ø Þ Ú ÔÓÙÞ Ò tº ÌÚ Ö Þ ÙÒ ϕ K j Ù ÙÔ Ò Ò Ð º ÈÖÓ Ô Ð Ò Þ Ô u K j = u K j (t), ϕ K j = ϕ K j (x) = ϕ K j (x, y), v h = v h (x) = v h (x, y). j=1 l ¾µ µ ½ Þ Ò Ð Ó ÓÒØ ÒÙÓÙ Ð Ö Ò Ò Ø Ð Ñ ÒØ Å Ø Ó ¾ Þ Ò Ð Ó Ò Ø ÎÓÐÙÑ Å Ø Ó
19 ÌÓ Ô i¹øóù Ö ÒÙ f(u(x, t)).n i Þ ÚÞØ Ù µ Ò Ö Ñ ÒÙÑ Ö Ñ ØÓ Ñ Fi K ÈÓ Ó Þ Ò ÒÙÑ Ö Ó ØÓ Ù µ Ó µ Ó Ø Ò Ñ ÖÓÚÒ 3 3 ( ) j=1 u K j t K ϕ K j v h x = K f (u h ). v h x i=1 l i v h F K i l = F K i (x, t)º. µ ½º¾ ÆÙÑ Ö ØÓ ÀÓ ÒÓØ ÒÙÑ Ö Ó ØÓ Ù Ú Ó (x, t) F K i (x, t) Þ Ú Ò ÚÓÙ Ó ÒÓØ Ô Ð öò Ó Ò Ú ØÓÑØÓ Ó º Â Ò Ó ÒÓØ Þ Ò Þ ÚÒ Ø Ù Ð Ñ ÒØÙ K u h (x int(k), t) = lim u h(y, t), y x,y K ÖÙ Þ ÓÙ Ò Ó Ð Ñ ÒØÙ Ò Ó Þ Ó Ö ÓÚ ÔÓ Ñ Ò Ý { γh (x, t), ÔÓ Ù x Ω, u h (x ext(k), t) = lim y x,y/ K u h (y, t), Ò. Ö ØÒ Ó ÒÓØÝ γ h Ò Ö Ò Ó Ð Ø Ω ÓÙ Ä ÔÖÓ Ó Ö ÓÚ ÔÓ Ñ Ò Ý γ Ó ÓÒ Ò ¹ ÖÓÞÑ ÖÒ Ó ÔÖÓ ØÓÖÙ V h º ÆÙÑ Ö ØÓ Ô Ö ÒÙ l i ÒÓÚ Ò Ó ( Fi K (x, t) = Fi K uh (x int(k), t), u h (x ext(k), t) ) ÑÙ Ñ Ø Ò Ð Ù ¾ ÚÐ ØÒÓ Ø ÓÒÞ Ø Ò f(u(x, t)).n i ÓÒÞ ÖÚ Ø Ú Ø F K i F K i (u(x, t), u(x, t)) = f(u(x, t)).n i. ( uh (x int(k), t), u h (x ext(k), t) ) + F K i i K K i = l i. ( uh (x int(ki ), t), u h (x ext(ki ), t) ) = 0, ÈÖÓ Ð Ò ÖÒ Ô Ô ÙÒ f Ø º f(u) = βu ÒÙÑ Ö ØÓ Ô Ö ÒÝ l i ÚÝ Ò ÙÔÛ Ò Ñ Ú ØÚ ÖÙ { Fi K f(uh (x (x, t) = int(k), t)).n i, ÔÓ Ù β.n i 0, f(u h (x ext(k), t)).n i, ÔÓ Ù β.n i < 0. ½º ÆÙÑ Ö ÒØ Ö ÁÒØ Ö ÐÝ Ò ÔÖ Ú ØÖ Ò ÖÓÚÒ µ ÔÖÓÜ ÑÙ Ñ ÒÙÑ Ö Ýº ÁÒØ Ö Ð Ô ØÖÓ ÐÒ K ÔÖÓÜ ÑÙ Ñ ÔÓÑÓ Ó ÒÓØÝ Ú Ó Ø ö Ø ( x K, ȳ K ) g (x) x K g ( x K, ȳ K ). µ K ÈÖÓ ÔÖÓÜ Ñ Ú ÓÚ Ó ÒØ Ö ÐÙ ÔÓÙö ØÓ Ë ÑÔ ÓÒÓÚÓ ÔÖ Ú ÐÓ b ( b a g(x) l g(a) + 4g( a + b ) 6 ) + g(b). µ a
20 ½º Î Ð Ò ÒÙÑ Ö Ñ ÊÓÚÒ µ ÑÙ ÔÐ Ø Ø ÔÖÓ Ð ÓÚÓÐÒ Ø ØÓÚ ÙÒ v h Þ ÔÖÓ ØÓÖÙ V (K) Ø Ý ÔÖÓ Þ ÙÒ ϕ K j º ÈÓ ØÙÔÒÑ Ó Þ Ò Ñ v h = ϕ K 1, ϕk, ϕk 3 Þ Ñ ÔÖÓ ö Ð Ñ ÒØ K ÓÙ Ø ÚÙ Ø Ó Ý Ò Ö Ò ÐÒ ÖÓÚÒ ½º Ù Ø Ö Ñóö Ø ÚÝ Ò Ú Ñ Ø ÓÚ ÔÓ Ó Ú ØÚ ÖÙ ( ) UK A = B (U K, U K1, U K, U K3 ), µ t U K = U K (t) Ú ØÓÖ Ñ ÒÞ Ó Ù Ò ÞÒ Ñ Ó ÒØÝ u K j (t) Ó ÔÓÚ ØÙÔÒóÑ ÚÓÐÒÓ Ø Ò Ð Ñ ÒØÙ K U Ki = U Ki (t) ÓÙ Ú ØÓÖÝ Ø Ò Ñ ÒÞ Ó Ù Ò ÞÒ Ñ u K i j (t) Þ ÓÙ Ò ØÖÓ ÐÒ óº ÈÖÚ Ý Ñ Ø A Ñ ØÚ Ö A i,j = ϕ K i ϕk j x. ½¼µ K Î ØÓÖ B = B (U K, U K1, U K, U K3 ) ÐÞ ÔÓ Ø Ø Þ ÔÖ Ú ØÖ ÒÝ ÖÓÚÒ µº ÀÓ ÒÓØÙ j¹ø ÐÓö Ù Ú ØÓÖÙ B B j Þ Ñ Ó Þ Ò Þ ÙÒ ϕ j Ñ ØÓ Ø ØÓÚ ÙÒ v h Ò Ð ÒÓÙ ÒÙ¹ Ñ Ö ÓÙ ÒØ Ö ÔÖ Ú ØÖ ÒÝ ÖÓÚÒ µº È ÒÙÑ Ö ÒØ Ö ÚÝÙö Ñ ÚÞØ ó µ µº ½º ÎÓÐ Þ ÙÒ Ý ÓÑ ÑÓ Ð ÒÓÞÒ Ò ÔÓÔ Ø ÔÖÓ ØÓÖ Ð Ò ÖÒ ÔÓÐÝÒÓÑó P 1 Ò Ð Ñ ÒØÙ K ÔÓØ ÚÞ Ø Ø Ò ÚÞ Ñ Ð Ò ÖÒ Ò Þ Ú Ð Þ ÙÒ ϕ K 1, ϕk, ϕk 3 º ØÓ ÔÓÙö Ú ÒÓÙ ÑÓöÒÓ Ø Ö ÔÖ Þ ÒØÓÚ Ø ÔÖÓÜ ÑÓÚ Ò Ò u h (x, y) ÙÚÒ Ø ØÖÓ ÐÒ Ù K ÚÞ Ø Þ ÙÒ ϕ K i (x, y) Ó Ð Ò ÖÒ ÙÒ Ø Ö Ò Ú Ó ÒÓØÝ ½ Ú Ø Ù i¹ø Ö ÒÝ Ó ÒÓØÝ ¼ Ò Þ Ú Ø Ö Òº ËØÙÔÒ ÚÓÐÒÓ Ø u K i (t) Ô Ø ÚÙ ÒÙÑ Ö Ò Ò Ø Ù i¹ø Ö Òݺ Å Ø A Ú ØÓÑØÓ Ô Ô ÓÒ ÐÒ ( 1 A = K diag 3, 1 3, 1 ). 3 ½º ÓÚ Ö Ø Þ ÈÖÓ ØÓÖÓÚ Ö Ø Þ Ú Å Ú Ý Ø ÑÙ Ó Ý Ò Ö Ò ÐÒ ÖÓÚÒ ÔÖÚÒ Ó Ù Ú ÔÖÓÑ ÒÒ t ÔÖÓ ö ØÖÓ ÐÒ K T h º Å Ø A Þ ½¼µ Ö ÙÐ ÖÒ Ø Ý Ü ØÙ A 1 º ÈÓ ÚÝÒ Ó Ò µ ÞÐ Ú Ñ Ø A 1 ÐÞ Ø ÒØÓ Ý Ø Ñ ÚÝ Ø Ú ÔÓ Ó U K t = L (U K, U K1, U K, U K3 ), ½½µ L = A 1 Bº Ý ÓÑ ÑÓ Ð ÔÖÓÜ ÑÓÚ Ø Ý Ø Ñ ½½µ ÖÓÞ Ð Ñ ÓÚ ÒØ ÖÚ Ð [0, T] Ò ÓÒ Ò ÑÒÓ Ó Ú Ø ÒØÒ ÔÓ ÒØ ÖÚ Ðó [t n, t n+1 ] t = t n+1 t n ÓÞÒ Ù ÓÚ ÖÓ º Î Ø ØÓ ÔÖ ÓÙ ÔÓÙö Ø Ò Ð Ù ¾ Ñ Ø - 0 -
21 ½º º½ ÓÔ Ò ÙÐ ÖÓÚ Ñ ØÓ ÈÖÓ Ò UK n ÓÔ Ò ÙÐ ÖÓÚ Ñ ØÓ Ñ ØÚ Ö Ú ÓÚ Ð Ò n Ø º Ú n t Ñ ÚÝÔÓ Ø Ø Un+1 K U n+1 K = Un K + tl( U n K, Un K 1, U n K, U n K 3 ). Ú ÓÚ Ð Ò n+1º ÙÐ ÖÓÚ ÓÔ Ò Ñ ØÓØ ÔÖÚÒ Ó Ù Ô ÒÓ Ø º Ç Ú ö Ô ÒÓ Ø Å Ù Ú Ø Ò ö ½ ÔÖÓØÓ Ú Ø ØÓ ÔÖ ÔÓÙö Ø Ñ ØÓ ÔÖÓ Ö Ø Þ Ú Ø Ö ÖÙ Ó Ù Ô ÒÓ Ø º ½º º¾ ÌÎ ÊÙÒ ÓÚ ¹ÃÙØØÓÚ ÓÚ Ö Ø Þ ÚÓÙ ÖÓ ÓÚ ÌÎ ÊÙÒ ÓÚ ¹ÃÙØØÓÚ Ñ ØÓ ÔÓÙö Ø Ú Ë µ Ñ ØÚ Ö U 1 K = Un K + tl( U n K, Un K 1, U n K, U n K 3 ), U n+1 K = 1 ( U n K + UK 1 + tl( UK 1, )) U1 K 1, UK 1, UK 1 3. Â Ò Ó Ñ ØÓ Ù ÖÙ Ó Ù Ô ÒÓ Ø º Ç Ú ÞÑ Ò Ò Ñ ØÓ Ý Ù ÓÙ ÔÐ ÓÚ ÒÝ Ò Ø Ò ÐÓ Ý Ò Ð Ò ÔÓÖÓÚÒ Òݺ ½º Ä ÔÓ Ñ Ò ÔÖÓ Å È Ò ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ ÔÓÙö Ú Ñ ÜÔÐ ØÒ ÓÚ Ñ Ø ÔÖÓØÓ ÓÚ ÖÓ ÓÑ Þ Ò CFL ÔÓ Ñ Ò ÓÙº ÈÖÓ ö ØÖÓ ÐÒ K T h CFL ÔÓ Ñ Ò ÔÖÓ Å ÒÓÚ Ò Ò Ð Ù Ñ ÞÔó Ó Ñ 3 i=1 (CFL) K = l i max ( Fi K, 0 ) t. K ÆÙØÒ ÔÓ Ñ Ò ÔÖÓ Ø Ð ØÙ Ú Ð Ò Ó ÒÙÑ Ö Ó Ñ ØÙ (CFL) K 1 K T h, ÔÖÓØÓ ÓÚ ÖÓ t Ú ÓÑ Þ Ò Ö Ø ÓÙ Ó ÒÓØÓÙ t c ( t t c = min K T h K 3 i=1 l i max (F K i, 0) ). ¾ Ä Ñ Ø ÖÝ ÈÓ Ù ÔÓÙö Ú Ñ ÔÓ Ø ÓÒ Ø ÒØÒ ÔÖÓÜ Ñ Ò ¹ ÔÓÐÝÒÓÑÝ ØÙÔÒ ¼ Ø º V h = V 0 h Ú Ð Ò ÒÙÑ Ö Ñ Ô Ú Ñ ØÓ Ù ÓÒ Ò Ó Ñóº Ó Ñ ØÙ ÙÔÛ Ò Ñ - 1 -
22 Þ Ò Ò ÒÙÑ Ö ÙÞ Ý Ò ö ÒÙÑ Ö Ñ Ô ÔÐÒ Ò CFL ÔÓ Ñ Ò Ý Ø ÐÒ º Æ ÖÙ ØÖ Ò ÒÙÑ Ö Ò Þ Ò ØÓÙØÓ Ñ ØÓ ÓÙ Ó Ò Ô Ø ÚÒ Óö Ù Ú Ø Ú Ô ØÓÐ Ú ÒÓÚ Ò ÒÙÑ Ö Ñ ÜÔ Ö Ñ ÒØóѺ ÈÓ Ù ÐÓ ÐÒ ÔÖÓ ØÓÖ ö Ó Ð Ñ ÒØÙ ÔÖÓÜ ÑÓÚ Ò ÔÓÐÝÒÓÑÝ ÔÖÚÒ Ó Ò Ó ÚÝ Ó ØÙÔÒ Ñóö Ó Ø Ú Ó ÓÐ Ò ÔÓ ØÓ Ø Ó Ð Ñ Ø Ö Ú ÓÙ ÒÙÑ Ö Ò Ø Ð Ø Ò ÓÑ Þ ÒÓ Ø Ò º Ý Ò Ó Þ ÐÓ Ó Ð Ñ ÒÙØÒ ÔÓÙö Ø Ð Ñ Ø Öº Î Ø ØÓ Ô ØÓÐ Ù ÔÓÔ Ò Ð Ñ Ø Ö ÔÓ Ð ÙØÓÖ ÀÓØ Ø ÀÓؼ µ Ø ÖÑ ÐÞ Ó ÒÓÙØ Ó Ö Ú Ð óº Ð Ð Ñ Ø ÖÝ ÐÞ Ò Ð ÞØ Ú Ð Ø Ö ØÙ ¼ µ Ë µ ˼ µº Ä Ñ ØÓÚ Ò Ò Ð Ò Ö ÓÒ ØÖÙ Ò ÔÖÓÚ Ò Ò Ú Ð Ñ ÒØ K T h ÔÓ ö Ñ ÖÓ Ù Ú ÓÚ Ö Ø Þ º ÚÓÐÑ Ð ÓÚÓÐÒ ØÖÓ ÐÒ K T h Ó ÓÙ Ý ÓÞÒ Ñ K i, i = 1,, 3 Ø ö Ø ØÖÓ ÐÒ ó Ô Ð Ð i¹ø ØÖ Ò b i, i = 0, 1,, 3 ÝÑ ÓÐÝ m i, i = 1,, 3 ÓÞÒ Ñ Ø Ý Ö Ò ØÖÓ ÐÒ Ù K Ô Ð ØÖÓ ÐÒ óñ K i º Ð Ñ Ð Ñ Ø Öó ÙÔÖ Ú Ø Ò ũ h ÔÓ ö Ñ ÖÓ Ù Ú ÓÚ Ö Ø Þ Ò ÞÐ Ñ ØÓÚ Ò Ò u h º ¾º½ ÀÓØ ØóÚ Ð Ñ Ø Ö Î Ð Ò Ù ÀÓؼ µ ÔÓÔ Ò Ð Ñ Ø Ö ÔÖÓ ØÙÔÒ ÚÓÐÒÓ Ø Ú Ø Ö Òº Ð Ñ ØÓ ÓØÓ Ð Ñ Ø ÖÙ Ö ÓÒ ØÖÙÓÚ Ø Ó ÒÓØÝ ũ h (m i ) Ú Ø Ö Òº Ê ÓÒ ØÖÙÓÚ Ò Ó ÒÓØÝ u h (m i ) ÑÙ Ø Ñ Þ ÔÖóÑ ÖÒÑ Ó ÒÓØ Ñ ÙÒ ũ h Ò Ô Ð Ð ØÖÓ ÐÒ º Ý Ö ÓÒ ØÖÙÓÚ Ò Ò Ð ÐÓ Ó ÔóÚÓ Ò Ó Ò Ó Ò Ñ Ò ÒÙØÒ Ñ Ø Ö ÓÒ ØÖÙÓÚ Ò Ó ÒÓØÝ u h (m i ) Ó Ò Ð ö ÔóÚÓ Ò Ñ Ó ÒÓØ Ñ ũ h (m i )º ÇÔØ Ñ Ð Þ Ò ÔÖÓ Ð Ñ ÐÞ ÔÓÔ Ø Ò Ð Ù Ñ ÞÔó Ó Ñ ÈÖÓ Ò Ú ØÓÖ ŨK = (ũ h (m 1 ), ũ h (m ), ũ h (m 3 )) Ò Ð ÞØ U K = (u h (m 1 ), u h (m ), u h (m 3 )) Ó Ò ÔÖÓ Ð ÑÙ Ò Ñ Ò ØÚ Öó Ô ÔÓ Ñ Ò min U K Ũ K U K ½¾ µ u h (b 0 ) = u h (m i ) = 1 3 i=1 3 ũ h (m i ) = ũ h (b 0 ) min (ũ h (b 0 ), ũ h (b 1 )) u h (m 1 ) max (ũ h (b 0 ), ũ h (b 1 )) min (ũ h (b 0 ), ũ h (b )) u h (m ) max (ũ h (b 0 ), ũ h (b )) min (ũ h (b 0 ), ũ h (b 3 )) u h (m 3 ) max (ũ h (b 0 ), ũ h (b 3 )). i=1 ½¾ µ ½¾µ ½¾ µ ½¾ µ à Ò ½¾µ ÔÓÔ ÒÓ Ú ÀÓؼ µº Â Ó Ú Ð ÓÙ Ò Ú Ó ÓÙ ö ØÓ Ò Ø Ö Ò º ÆÙÑ Ö ÜÔ Ö Ñ ÒØÝ Î Ô ÓÞ Ô ØÓÐ ÝÐÝ ÔÓÔ ÒÝ Ú ÒÙÑ Ö Ñ ØÓ Ý ÔÖÓ Ò ÝÔ Ö ÓÐ Þ ÓÒó Þ ¹ ÓÚ Ò ¹ Ñ ØÓ ÓÒ Ò Ó Ñó Îŵ Ò ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ Åµº Ç - -
23 Ñ ØÓ Ý ÝÐÝ ÙØÓÖ Ñ ÑÔÐ Ñ ÒØÓÚ ÒÝ Ú ÔÖÓ Ö ÑÓÚ Ñ ÞÝ ÔÓÙö ØÝ ÔÖÓ ÒÙÑ Ö Ò ÖÓÚÒ ½ µ ÔÖÓ Ú Ó Ò ÞÚÓÐ Ò Ø ØÓÚ ÐÓ Ýº Ð Ñ Ø ØÓ ÔÖ ÔÓÖÓÚÒ Ò Ø ØÓ ÒÙÑ Ö Ñ ØÓ Ò Þ Ð ÚÝÔÓ Ø Ò Øº Å ØÓ ÎÅ ÔÓÙö Ø ÔÓÙÞ ÒÓ ÖÓ¹ ÓÚÓÙ ÓÚÓÙ Ö Ø Þ ÚÓÙ ÖÓ ÓÚ ÌÎ ÊÃ Ö Ø Þ Þ Ò Ó Ñ ØÙ ÑÒÓ Ñ Ú Ø ÒÙÑ Ö ÓÙ ÙÞ º Ý ÓÑ ÑÓ Ð ÔÓÖÓÚÒ Ø ÒÙÑ Ö Ò u h Ô ÒÑ Ò Ñ u ÐÓ Ý ½ µ Ú T ¹ ÒÙ Ñ ÓÐÙØÒ Ý Ù Ú L 1 ÒÓÖÑ h L 1 = u u h 1 = u u h. ½ µ Ω º½ ÊÓØ Ò ÖÝ ÐÓ ØÒ ÔÓÐ ÃÐ Ñ Ø Ø Ñ ÔÖÓ Ú ÖÓÞÑ ÖÒÓÙ Ð Ò ÖÒ ÓÒÚ Ò ÖÓÚÒ Ô Ô ÖÓØ Ò Ó ÖÝ ÐÓ Ø¹ Ò Ó ÔÓÐ º ÊÓØ Ò ÖÝ ÐÓ ØÒ ÔÓÐ Ñ ØÚ Ö β(x) = r(x)( sin θ, cos θ) r(x) = x x 0 ÚÞ Ð ÒÓ Ø Ó Ù x Ó Ø Ù ÓØ Ò x 0 º ÈÓ ö ÓØ Ø º Ú T = π Ó ÐÓ ¹ ÐÒ Ò Ó Ò ÐÝØ Ò Ó ÔÓÚ ÔÓ Ø Ò ÔÓ Ñ Ò º Ã Ø ØÓÚ Ò Ñ ØÓ ÎÅ Å ÓÙ ÔÖÓ ÖÓØ Ò ÖÝ ÐÓ ØÒ ÔÓÐ ÔÓÙö ØÝ Ú ÔÖ Ú ÐÒ ØÖ Ò ÙÐ ØÚ ÖÓÚ Ó Ð Ø Ω = (0, 50) (0, 50)º ËØ ÓØ Ò x 0 Ú Ø Ù Ó Ð Ø Ω x 0 = (5, 5)º Æ ÔÓ Ø ÔÓ Ø Ò ÔÓ Ñ Ò Ñ ØÚ Ö { 1 ÔÓ Ù (x, y) [0, 30] [10, 0] u h (x, y, 0) = 0 Ò º ½ µ Ç Ð Ø Ω ÖÓÞ Ð Ò Ò ¾ ¼¼ Ø Ò Ú Ð ØÚ Öó Ø Ö ÓÙ ÐÓÔ Ò ÖÓÞ Ð ÒÝ Ò ØÖÓ ¹ ÐÒ Ýº ÎÞÒ Ò Ø ÔÖ ÚÓ Ð ØÖ Ò ÙÐ T h Ó ¼¼¼ Ð Ñ ÒØ º ÓÚ ÖÓ ÜÓÚ Ò Ò Ó ÒÓØ t = 0.01 Ý ÝÐ Ò Ð Ó Ð Ø Ω ÔÐÒ Ò Ä ÔÓ Ñ Ò º Å ØÓ ÓÒ Ò Ó Ñó Ô Ø ØÓ ÐÓÞ Ð Ú ÚÐ Ú ÒÙÑ Ö ÙÞ Ó ÖÓÚ º  ö ÔÓ Ò ÖÓØ Ú T = πµ Ò Ò ÑÓöÒ ÖÓÞ ÞÒ Ø ÚÝÔ Ð ÔÓ Ø Ò ÔÓ Ñ Ò º Å Ü Ñ ÐÒ Ó ÒÓØ ÒÙÑ Ö Ó Ò Ò ÖÙ Ø ÔÓ Ò ÓØ ÞÑ Ò Ð Ø Ñ Ò ÔÓÐÓÚ Ò Ó ÒÓØÙ Ô Ò Ó Ò ÔÓ ØÝ ÖÓØ Ñ Ü Ñ ÐÒ Ó ÒÓØ ÔÓÙÞ 0.16º ÓÐÙØÒ Ý ÔÓ Ò ÖÓØ L1 = 11.1º Ý Ý Ò Þ Ò Ñ ØÓ ÓÙ Å Ò ÔÖ Ú ÐÒ Ø Ô ÔÓÙö Ø ÓÔ Ò ÙÐ ÖÓÚÝ Ö Ø Þ ÌÎ ÊÃ Ö Ø Þ Ú ÓÙ ÞÒ ÞÓÚÒ ÒÝ Ú Ö Ù ¾µº È ÔÓÙö Ø ÒÓ ÖÓ ÓÚ ÓÚ Ö Ø Þ ÓÙ Ý Ý L1 Ñ Ò º ÈÓ Ó Ø Ø Ò Ñ ÚÝ Ð Þ Ò Ò Ø º ÔÓ Ò ÓÐ ÖÓØ µ Ùö ÓÙ Ú Ð Ý Ô Ó ÓÙ Ö Ø Þ ÔÓ Ó Ò º ÆÙÑ Ö Ú Ð Ý Ò Ò ØÖÙ ØÙÖÓÚ Ò Ø Î ØÓÑØÓ Ó Ø Ú ÓÙ ÔÓÖÓÚÒ ÒÝ Ú Ð Ý ÚÝÔÓ Ø Ò Ò ÔÖ Ú ÐÒ Ø Ò ØÖÙ ØÙÖÓÚ Ò Ø º Ç ÐÒ ÓÚ Ó Ð Ø Ω = (0, 100) (0, 40) ÖÓÞ Ð Ò Ò ÔÖ Ú ÐÒÓÙ ØÖ Ò ÙÐ Ò 9568 Ð Ñ ÒØó ÔÖ Ú ÐÒÓÙ ØÖ Ò ÙÐ Ò 9680 Ð Ñ ÒØóº Æ ÔÖ Ú ÐÒ ØÖ Ò ÙÐ ÞÒ ÞÓÖÒ Ò - 3 -
24 Ç Ö Þ ½ ËÖÓÚÒ Ò ÚÐ ÚÙ ÒÙÑ Ö ÙÞ Ô ÔÓÙö Ø Ñ ØÓ Ý ÓÒ Ò Ó Ñó Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ý ÓÔ ÒÓÙ ÙÐ ÖÓÚÓÙ Ö Ø Þ Ú Ô ÖÓØ Ò Ñ ÖÝ ÐÓ ØÒ Ñ ÔÓÐ Ò ÔÓ Ø ÔÓ Ø Ò ÔÓ Ñ Ò ½ µº dopredny Euler TVD RK 40 L ÈÓ Ø ÖÓØ Ç Ö Þ ¾ ÓÐÙØÒ Ý Ý L1 Ò ÔÖ Ú ÐÒ Ø ÔÖÓ Å ÓÔ ÒÓÙ ÙÐ ÖÓÚÓÙ Ö ¹ Ø Þ ÌÎ ÊÃ Ö Ø Þ Ú ÖÓØ Ò ÖÝ ÐÓ ØÒ ÔÓÐ ¼¼¼ Ð Ñ ÒØóº Ò Ó Ö Þ Ù µ Ø ØÓ ð Ò Ð Ò Ø Ú Ö Ø Þ ÑÒ Ò º Î ØÓÖÓÚ ÖÝ ÐÓ ØÒ ÔÓÐ ÔÓ ÙÚÒ Ú Ñ ÖÙ Ó Ý x β = (1, 0)º Ð ÓÚ T = 60 CFL Ñ Ó ÒÓØÙ 0.6º ÓÐ Ñ Ó Ø Ô Ð öò Ø Ò ÔÓ Ø Ð Ñ ÒØó ö Ñóö Ñ Ø Ò ÚÐ Ú Ò Ô ÒÓ Ø Ò ÔÖÓ ÖóÞÒ Ø ØÓÚ ÐÓ Ýº Ð Ù Ù Þ ÒÓ ö Ô Ð ÔÓ Ø Ò ÔÓ Ñ Ò ÐÞ Ó ÒÓÙØ Ð Ô Ú Ð ó Ò Ò ØÖÙ ØÙÖÓÚ Ò Ø º Æ ÓÔ Ô Ú Ó Ò ÞÚÓÐ Ò ÔÓ Ø Ð Ò ÖÒ ÔÓ Ø Ò ÔÓ Ñ Ò Ó Ò Ñ ÑÒÓ Ñ Ð Ô Ú Ð ó Ò ÔÖ Ú ÐÒ Ø º - 4 -
25 Ç Ö Þ Æ ÔÖ Ú ÐÒ ØÖ Ò ÙÐ Ó Ð Ø Ωº º½ ÀÐ ÔÓ Ø Ò ÔÓ Ñ Ò Æ Ú ÙÚ öù Ñ Ð ÓÙ ÔÓ Ø Ò ÔÓ Ñ Ò Ù u h (x, y, 0) = 5 exp ( (x 0) 35 ) exp ( ) (y 0). ½ µ 35 È Ð ÔÓ Ø Ò ÔÓ Ñ Ò ½ µ Ó ö ÒÓ Ð Ô Ú Ð ó ÔÖÓ Å Ò Ò ØÖÙ ØÙÖÓ¹ Ú Ò Ø Ø ÙÐ ½µº Å ØÓ ÓÙ ÎÅ Ñ Ò Ý Ó ö ÒÓ Ò ÔÖ Ú ÐÒ Ø Ú ÖÓÚÒ Ò Å ÓÙ ÓÐÙØÒ Ý Ý Ú Ò ö Ø Ò Ó Ò º Å ÙÐ Ö ÌÎ Êà ÎÅ ËØÖÙ ØÙÖÓÚ Ò ð L1 ½ º¾ º½ ¾ º ¼ Æ ØÖÙ ØÙÖÓÚ Ò ð L1 ½ º½½ º ¾ º Ì ÙÐ ½ ËÖÓÚÒ Ò Ý ÔÖÓ ÒÓØÐ Ú Ñ ØÓ Ý Ò ØÖÙ ØÙÖÓÚ Ò Ò ØÖÙ ØÙÖÓÚ Ò Ø Ð ÔÓ Ø Ò ÔÓ Ñ Ò ½ µº º¾ ÈÓ Ø Ð Ò ÖÒ ÔÓ Ø Ò ÔÓ Ñ Ò ÆÝÒ ÙÚ öù Ñ ÔÓ Ø Ð Ò ÖÒ ÔÓ Ø Ò ÔÓ Ñ Ò Ù Ú ØÚ ÖÙ x 10 ÔÓ Ù (x, y) [10, 0] [10, 30] u h (x, y, 0) = x + 30 ÔÓ Ù (x, y) [0, 30] [10, 30] 0 Ò º ½ µ È Ø ØÓ ÔÓ Ø Ò ÔÓ Ñ Ò ÓÙ ÚÝÔÓ Ø Ò Ú Ð Ý Ð Ó Ô Ò Ò ÔÖ Ú ÐÒ Ø º ËÖÓÚ¹ Ò Ò ÓÐÙØÒ Ý L1 ÓÙ Ú Ø ÙÐ ¾º Ò ÒÙÑ Ö Ú Ð Ý Ò ÔÖ Ú ÐÒ Ø ÓÙ - 5 -
26 Ø Ñ ØÝ Ö Ø Ô Ò º Ì ØÓ Ó Ö Ú Ð ó Ò ÔÖ Ú ÐÒ Ø Ó ö ÒÓ Ø Ñ ö ÔÓ ¹ Ø Ò ÔÓ Ñ Ò Ù ½ µ ÐÞ ÔÖ Ú ÐÒÓÙ Ø Ó ÚÝ Ø ÒÓÙØ ÔÓ ÙÒ Ú Ñ ÖÙ Ø º Æ ÓÔ Ò Ò ØÖÙ ØÙÖÓÚ Ò Ø Ó Þ ÖÓÞÑ Þ Ò Ú Ñ ÖÙ Ó Ý y Ó Öº ¾µº Å ÙÐ Ö ÌÎ Êà ÎÅ ËØÖÙ ØÙÖÓÚ Ò ð L1 ½º¾ ¼º ¾¾º ¼ Æ ØÖÙ ØÙÖÓÚ Ò ð L1 ½ º ½ º ½½½ º Ì ÙÐ ¾ ËÖÓÚÒ Ò Ý ÔÖÓ ÒÓØÐ Ú Ñ ØÓ Ý Ò ØÖÙ ØÙÖÓÚ Ò Ò ØÖÙ ØÙÖÓÚ Ò Ø ÔÓ Ø Ð Ò ÖÒ ÔÓ Ø Ò ÔÓ Ñ Ò ½ µº Ú Ö Î Ø ØÓ ÔÖ ÓÙ ÔÓÔ ÒÝ Ú ÒÙÑ Ö Ñ ØÓ Ý ÔÖÓ Ò ÚÓÙÖÓÞÑ ÖÒ Ð Ò ÖÒ ÓÒÚ Ò ÖÓÚÒ ¹ Ñ ØÓ ÓÒ Ò Ó Ñó Ò ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ ÓÒ Ò ÔÖÚ óº È ÔÓÙö Ø Ò ÔÓ Ø Ð Ö ÒÓÚÝ Ñ ØÓ Ý Ò Ò ÔÓ Ø Ñ Ò Ó Þ ÚÞÒ Ù Ó Ð º Ý Ò ÚÞÒ ÐÝ Ó Ð ÑÙ Ø ÔÓÙö ØÝ Ð Ñ Ø ÖÝ Ø Ö ÚÞÒ Ù Ó Ð Þ Ö Ò º Î Ô ØÓÐ Ú ÒÓÚ Ò ÒÙÑ Ö Ñ ÜÔ Ö Ñ ÒØóÑ ÔÓÔ ÒÓ Ò ÓÐ Ø ØÓÚ ÐÓ Ø Ö Ñ Þ Ø Ø Ú Ó Ý Ò Ú Ó Ý Ó ÓÙ ÒÙÑ Ö Ñ ØÓ ÙØÓÚ Ø Ò Ú Þ Ú ÐÓ Ø Ò ÔÓÙö Ø ØÖ Ò ÙÐ Þ ÓÙÑ Ò Ó Ð Ø º ÒÙÑ Ö ÜÔ Ö Ñ ÒØó Ô ØÖÒ ö Ò ÔÓ Ø Ð Ö ÒÓÚ Ñ ØÓ ÓÔÖÓØ Ñ ØÓ ÓÒ Ò Ó Ñó ÑÒÓ Ñ ÒÒ º Ê Ö Ò Ë Ë¼ º Ó ÙÖÒ Ò º Ë Ùº Ì ÊÙÒ ¹ÃÙØØ ÐÓ Ð ÔÖÓ Ø ÓÒ ÓÒØ ÒÙÓÙ Ð Ö Ò Ò Ø Ð Ñ ÒØ Ñ Ø Ó ÓÖ ÓÒ ÖÚ Ø ÓÒ Ð Û º Î ÅÙÐØ Ñ Ò ÓÒ Ð Ý Ø Ñ º ÂÓÙÖÒ Ð Ó ÓÑÔÙØ Ø ÓÒ Ð È Ý ½ º º Ø Ù Ö Åº ÐÑ Ò Ò Áº ËØÖ Ö º Å Ø Ñ Ø Ð Ò ÓÑÔÙØ Ø ÓÒ Ð Å Ø Ó ÓÖ ÓÑÔÖ Ð ÐÓÛº Ð Ö Ò ÓÒ ÈÖ ÇÜ ÓÖ ¾¼¼ º ÀÓؼ Àº ÀÓØ Øº Æ Û ØÛÓ¹ Ñ Ò ÓÒ Ð ÐÓÔ Ð Ñ Ø Ö ÓÖ ÓÒØ ÒÙÓÙ Ð Ö Ò Ñ Ø Ó ÓÒ Ö ØÖ ÖÝ Ñ º ÁÒØ ÖÒ Ø ÓÒ Ð ÂÓÙÖÒ Ð ÓÖ ÆÙÑ Ö Ð Å Ø Ó Ò Ò Ò Ö Ò ¾¼¼ º ¼ º ÓÙÒ Ò Èº Ö Öº ËÓÐÚ Ò Ø Ú Ø ÓÒ¹ Ô Ö ÓÒ ÕÙ Ø ÓÒ Û Ø ÓÒØ ¹ ÒÙÓÙ Ð Ö Ò Ò ÑÙÐØ ÔÓ ÒØ ÙÜ ÔÔÖÓÜ Ñ Ø ÓÒ Ñ Ø Ó ÓÒ ÙÒ ØÖÙØÙÖ Ñ º ÁÒØ ÖÒ Ø ÓÒ Ð ÂÓÙÖÒ Ð ÓÖ ÆÙÑ Ö Ð Å Ø Ó Ò ÐÙ ¾¼¼ º - 6 -
27 Å ÌÇ Æ ÊÇÎ Æ Á Í ÈàÁ ÈÇ Ì ÇÎ Å ÈÊ ÇÎýÆ Ç Ê Í Â ÂÁ À ÈÄÁÃ Ê Å ½ ØÖ Ø È Ô Ú Ú ÒÓÚ Ò Ñ Ø Ó Ö ÞÓÚ Ø ÔÓÑÓ ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ Ò ÚÖ¹ ö Ò Ú Ó Ò Ó ÒÙÑ Ö Ó Ñ ØÙ ÔÐ Ò Ñ Ò Ø Þ Ñ Ò Ø Ö ÞÓÒ º ½ ÊÓÚÒ Ú Ò Ø ÔÐ ÊÓÚÒ Ú Ò Ø ÔÐ Ô Ø ÚÙ Ð Ò ÖÒ ÙÞÒ ÑÓ Ð ÐÞ Ó Þ Ø ö ÓÒÚÓÐÙ Ù ÓÚÑ Ö Ñ G σ Ú Ú Ð ÒØÒ ÔÓ Ø Ò ÐÓÞ ÖÓÚÒ Ú Ò Ø ÔÐ ÔÓ¹ Ø Ò ÔÓ Ñ Ò ÓÙ ÔóÚÓ Ò Ó Ö Þ Ó Ø Ò Ô Ö Ó Ñ ÔÖÓ ÐÓÙö Ò Ñ Ò Ð R ÓÞÒ Ñ I 0 µ ( ) u (x, y, t) = t x + u(x, y, t) = u(x, y, t) y Ò R (0, T) u(x, y, t = 0) = I 0 (x, y) Ò R, ½µ Ñ Þ T σ ÔÐ Ø Ú ÞÑ Ò Ò ÚÞØ t = σ. ¾µ ¾ ÎÖ Ø ÚÒ ÓÚ ÖÓÚÒ Î ¼º Ð Ø Ñ ÒÙÐ Ó ØÓÐ Ø Þ ÐÝ Ú ÞÔÖ ÓÚ Ò Ó Ö ÞÙ ÔÓÙö Ú Ø Ò Ð Ò ÖÒ ¹ ÙÞÒ ÖÓÚÒ º Î ÖÓ ½ Ⱥ È ÖÓÒ Âº Å Ð Ú Ú ÔÖ ÑÓ ÓÚ Ð Ð Ò ÖÒ ÖÓÚÒ Ú Ò Ø ÔÐ Ò Ò Ð Ò ÖÒ ÙÞ Þ ÓÚ Ú ÔÓÞ Ö Òº Ì ØÓ ÑÓ Ó¹ Ú Ò ÖÓÚÒ Ú ÔÓ Ø ÓÚ Ñ ÞÔÖ ÓÚ Ò Ó Ö ÞÙ Ø Ò ÞÚ ÖÓÚÒ Ò ÞÓØÖÓÔÒ ÙÞ Ñ ØÚ Ö u (x, t) = (g( u(x, t) )) u(x, t), µ t g ØÞÚº È ÖÓÒÓÚ ¹Å Ð ÓÚ ÙÒ Ø ÖÓÙ Ð ö Ô Ø Ú Ñ Ù ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ º ½ Ã Ø Ö Ñ Ø Ñ Ø Ý ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ ÎÍÌ ÌÖÓ ÒÓÚ ½ ½¾¼ ¼¼ ÈÖ ¾ Ñ Ö ºÚÙØºÞ - 7 -
28 Â Ò Ñ Þ Ô ØÙÔó ÔÖÓ Ð Ñ Ø ÝÒ Ñ Ý Ú ÚÖ Ø ÚÒ ÓÚ Ñ ØÓ º ÈÓ¹ ÖÓ Ò ÓÖÑÙÐ ÙÚ Ò Ú ÔÖ º ËØÖÙ Ò Þ Ô ÔÓÑ Ò Ñ º Ð Ñ ÚÝØÚÓ Ø ÓÖÑÙÐ ÔÖÓ ÔÓ Ý Ò ÔÐÓ Ý Γ(t) Ó Ñ ÒÞ (N 1) Ò ÔÖÓ ØÓÖÙ R N Ú Ñ ÖÙ Ú ÚÒ ÒÓÖÑ ÐÝ n ÖÝ ÐÓ Ø V Ø Ö Ò ÔÓ Ø Ò ÔÓ Ñ Ò ÓÙ Ú t = 0º ÈÓ Ý Ù Ò ÔÐÓ Ù Þ Ñ Ó ÒÙÐÓÚÓÙ ÚÖ Ø ÚÒ ÙÒ u Ø Ö Ú Ø ØÓ ÔÖ Ù Ñ Ø Ñ ÒØ Ò ÙÒ ÒÙ Ñ Ò Ð ÓÚÒ u(x, t = 0) = ±d, µ x Ó Ú R N d ÚÞ Ð ÒÓ Ø Ñ Þ x Γ(t = 0)º Ò Ñ Ò Ó ÔÐÙ Ñ ÒÙ µ ÙÖ Ù ØÐ Ó x Ð ö ÚÒ ÙÚÒ Ø µ Ú ÓÞ Ò ÔÐÓ Ý Γ(t = 0)º Ú Ñ Ø ÙÒ u(x, t = 0) : R N R ÚÐ ØÒÓ Ø u(t = 0) = {x u(x, t = 0) = 0}. µ Æ Ñ ÓÐ Ñ Ó ÚÓ Ø Ô Ö ÐÒ Ö Ò ÐÒ ÖÓÚÒ ÔÖÓ ÔÓ Ý Ò ÔÐÓ Ý u(t) ÔÓÑÓ ÑÔÐ ØÒ Þ Ò ÙÒ u(x, t) = 0º Ñ Ý ÓÑ Ú Ð ÓÚÓÐÒ Ñ t Þ Ð Ú Ù u(t) Ó ÒÙÐÓÚÓÙ ÚÖ Ø ÚÒ ÙÒ u(x, t) = 0 Ø Ý Γ(t) = {x u(x, t) = 0}. µ Ö ÚÓÚ Ò Ñ u(x(t), t) = 0 Ð ÔÖÓÑ ÒÒ t Þ Ú Ò Ñ ÖÝ ÐÓ Ø Ú Ñ ÖÙ ÚÒ ÒÓÖÑ ÐÝ V = dx (t) n Þ Ñ ÖÓÚÒ Ø Ö Ò ÞÚ À Ñ ÐØÓÒÓÚ ¹Â Ó Ó ÖÓÚ¹ dt Ò º È Ò Ñ ÔÓ Ø Ò ÔÓ Ñ Ò Ý µ Þ Ñ Ò Ð Ù ÐÓ Ù u t + V u = 0, u(x, t = 0) = ±d. µ ÈÓ Ù ÒÝÒ Þ ÖÝ ÐÓ Ø V ÞÚÓÐ Ñ V = κ + F F Ó Ò ÐÓÚ Ð Ò Ôó Ó Ú Ñ ÖÙ ÚÒ ÒÓÖÑ ÐÝ κ ÐÓ ÐÒ ÚÓ Ø u Ò ÚÞØ Ñ κ = u u µ Þ Ñ ÖÓÚÒ Ø ÖÓÙ ÔÓ Ð ½ Ò ÞÚ Ñ ÚÖ Ø ÚÒ ÓÚÓÙ ÖÓÚÒ Ñóö Ñ ÔÖÓ Ò Þ ÓÖÑÙÐÓÚ Ø Ò Ð Ù Ñ ÒÓÙ ÐÓ Ù u t = u u u u F Ò R (0, + ), u(x, 0) = u 0 (x) ÔÖÓ x R. µ Ê ÙÐ Ö Þ ÖÓÚÒ È ÒÙÑ Ö Ñ Ò ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ Ñóö Ø Ø ö ÓÐÙØÒ Ó ÒÓØ Ö ¹ ÒØÙ ÙÒ u Ù ÒÙÐÓÚ º ÌÓ Ý ÞÒ Ñ Ò ÐÓ ö Ù Ñ Ð Ø ÒÙÐÓÙº ÈÖÓØÓ - 8 -
29 Þ Ú Ò Ð Ù Ö ÙÐ Ö Þ ÖÓÚÒ Ú ÐÓÞ µ Ò Ö Þ Ò Ñ ÚÖ ÞÙ u ÚÖ Þ Ñ Q( u ) = ε + u ε > 0º Ý Ø ØÓ Ö ÙÐ Ö Þ Þ Ñ Ò Ð Ù ÐÓ Ù u t = Q( u) u Q( u) Q( u)f Ò R (0, + ), u(x, 0) = u 0 (x) ÔÖÓ x R. ½¼µ Î ÔÖ Ó Þ ÒÓ ö Ò u ε ÐÓ Ý ½¼µ ÓÒÚ Ö Ù ÔÖÓ ε 0 ÐÓ ÐÒ Ø ¹ ÒÓÑ ÖÒ Ò Ú ÑÝ ÐÙ Ú ÓÞ ØÝ ¾ ÐÓ Ý µº ÈÓ Ù Ñ ÔÓ Ø Ø ÔÖÓÜ Ñ Ò u Ú ÑÝ ÐÙ Ú ÓÞ ØÝ ÐÓ Ý µ ÔÓØÓÑ ÔÓ Ð Ø Ø Ö ÙÐ Ö ÞÓÚ ÒÓÙ ÐÓ Ù ½¼µº ÅÒÓö ÒÙ Ò Ø Ö Ð Ñ Ò Ú ÑÙ Ñ Þ ö Ø Þ R Ò ÓÑ Þ ÒÓÙ Ó Ð Ø Ωº ËØ Ø Ý Ø ÐÓ Ù u ε t = Q( u u ε ε) Q( u ε ) Q( u ε)f Ò Ω (0, + ), u ε (x, 0) = u ε0 (x) ÔÖÓ x Ω. ½½µ ÅÓ ÓÚ Ò ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ ÀÐ ÚÒ Ø Ò ÔÖ Ù Þ Ú Ø ÑÓ ÓÚ ÒÓÙ ÔÓ Ó ÓÙ ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ ØÓ ÔÖÓ ÐÝ ÐØÖÓÚ Ò Ó Ö ÞÙ Ø ÔÖÓ Ñ ÒØ Ó Ö ÞÙº ÍÚ Ñ ÒÝÒ Ó ØÚ ÖÝ ÐØÖÓÚ Ò Ó Ö ÞÙ ( ) u u t = Q ( u) g(u G σ ), ½¾µ Q ( u) u ÚÚÓ ÒØ ÒÞ Ø ÔóÚÓ Ò Ó Ó Ö ÞÙ u 0 Ò Ω [0, T] Ω R º Ë Ñ ÒØ Ó Ö ÞÙ ( ) u t = Q ( u) g(i 0 u G σ ) g(i 0 G σ )Q( u)f, Q ( u) u ÚÚÓ Ñ ÒØ Ò ÙÒ Ú Ò ÔÓ Ø Ò ÔÓ Ñ Ò ÓÙ u 0 ÒÓÚ Ò Ò Ω [0, T] Ω R I 0 Ò Ó Ö Þ Ø ÖÑ Ù Ñ ÔÖ ÓÚ Ø G σ Ù ÓÚÓ ÓÒÚÓÐÙ Ò ÖÓ F ÓÒ Ø ÒØÒ ÐÓÚ Ð Ò Ø Ö Ù Ú ÖÝ ÐÓ Ø Ú Ñ ÖÙ ÚÒ ÒÓÖÑ ÐÝ g : R + 0 R + Ò ÖÓ ØÓÙ È ÖÓÒÓÚ ¹Å Ð ÓÚ ÙÒ ÔÖÓ Ø ÖÓÙ ÔÐ Ø ö g(0) = 1 g(s) 0 ÔÖÓ s º ÃÓÒ Ö ØÒ ØÚ Ö Ø ØÓ ÙÒ Ù Ñ ÚÓÐ Ø Ò Ð ÓÚÒ g(s) = ½ µ λs, ½ µ ¾ Ú Ò ØÓ ÓØÓ ÔÓ ÑÙ Ø ÓÖ Ó Ò ÐÓ Ú ÑÝ ÐÙ Ú ÓÞ ØÝ ÐÞ Ò Ð ÞØ Ú ¾ º - 9 -
30 λ Ð Ò Ô Ö Ñ ØÖº Ù ÓÚÓ ÓÒÚÓÐÙ Ò ÖÓ Þ ÚÝÙö Ú Ò Þ Ð Ñ Þ ÔÓ Ø Ò Ö ØÒ Ó Ó Ö Þ Ù Ý ÑÓ Ð Ø Ö ÒØ Ó ÒÓÚ Ò Ð Þ Ð Ñ Ø Ò Ó Ó ØÖ Ò Ò ÙÑÙ Ø Ý Ò Ó Ò ÚÝ Ó Ó ó ÒØ ÒÞ Øº Ö ÙÑ ÒØ Ñ È ÖÓÒÓÚݹŠРÓÚÝ ÙÒ g Ö ÒØ Ó Ö Þ Ù Ø Ö ÐÓÙö Ó Ø ØÓÖ Ö Òº Ì Ñ ÓÙ Ú Ó Ö Þ Ù u Ô ÐØÖÓÚ Ò Ö Ôº I 0 Ô Ñ ÒØ ÓÑÓ ÒÒ Ò Ó Ø Ñ ÓÒ Ø ÒØÒ Ó Ð Ø ÒØ ÒÞ Ø Ó ÒÓØ Ö ÒØÙ ÒÙÐÓÚ Ø Ý g(0) = 1 Ò Ó Þ ÞÔÓÑ ÐÓÚ Ò ÔÓ Ý Ù Ñ ÒØ Ò Ú Ýº Î ÓÔ Ò Ñ Ô Ô ÔÓ Ù Ù Ñ ÚÝ ÝØÓÚ Ø ÔÓ Ð ö Ö Ò Ó ÒÓØ Ö ÒØÙ ÚÝ Ó Ó ÒÓØ ÙÒ g Ù Ú Ð Ñ Ð Ø Ñ ÒÙÐÓÚ º Ë ÑÓÞ Ñ Ú Ö ÐÒ Ó Ö Þ Ò ÚÝ ÝØÙ ÐÒ Ö ÒÝ Ø Ý Ó ÒÓØ g Ò Ù Ò Ý ÒÙÐÓÚ º È Ö Ñ ØÖ Ñ λ Ñóö Ñ ÓÚÐ Ú ÓÚ Ø ØÐ ÚÓ Ø ÙÒ g Ø Ö Òº ÈÓ Ù Ù Ñ Ø Ø Ø ÓÚ Ø ÔÓÙÞ ÚÞÒ ÑÒ Ö ÒÝ Ø Ý Ú Ð ÖÝ Ð Ó Ý ÒØ ÒÞ Ø Ù Ñ ÚÓÐ Ø Ô Ö Ñ ØÖ λ Ò ö Ó ÒÓØÓÙ Ò ö ÔÖÓ ÐÝ Ø Ò ÚÖ ÞÒ Ö Ò Ø Ý Ö Ò Ò ö Ñ Ò Ó ÔÓÞÚÓÐÒ Ñ Ô Ó Ñ ÒØ ÒÞ Øº ÐØÖ Ò ÔÓ Ó ÑÓ ÓÚ Ò ÖÓÚÒ ½¾µ ÔÖ Ù ÙÒ u Ø Ö Ô Ø ÚÙ Ú¹ ÚÓ Ó Ö ÞÓÚ ÒØ ÒÞ Ø Ú º ÈÓ Ø Ò ÔÓ Ñ Ò u 0 Ò ÔóÚÓ Ò Ñ Ó Ö Þ Ñ Ø ÖÑ Ñ ÔÖ ÓÚ Øº Î ØÓÑØÓ Ô Ô Ö ÒÓÚ Ø ØÓÖ g(u G σ ) Ñ ÙÞ ÝÒ Ñ Ý Ó ÒÓÚÓÚ Ò ÞÔÓÑ ÐÙ Ø ÙÞ Ò Ö Ò º ÈÖÓØÓö ÙÑ ØÚÓ Ò Ñ ÐÑ ØÚ ÖÝ ÚÝ Ó ÓÙ ÐÓ ÐÒ ÚÓ Ø Ó Ó ÚÝ Ð Þ Ò Ô ØÓ ö Ö ÒÓÚ Ø ØÓÖ Ò Ò Ñ ÞÔÓÑ ÐÙ ÙÞ º ØÐ ÚÓ Ø Ö ÒÓÚ Ó Ø ØÓÖÙ Ø Ý ÖÝ ÐÓ Ø ÙÞ Ñóö Ñ ÓÚÐ Ú ÓÚ Ø ÚÓÐ ÓÙ Ô Ö Ñ ØÖÙ λº ÈÖÓ ÚÝ Ó Ó ÒÓØÝ ØÓ ÓØÓ Ô Ö Ñ ØÖÙ Ñóö Ø Ø ö Ö ÒÓÚ Ø ØÓÖ Ù Ò ØÓÐ ØÐ Ú ö Ò Ó Úݹ Ð Þ Ò ÙÑÙº Æ ÓÔ ÔÖÓ Ò Þ Ó ÒÓØÝ Ù Ó Þ Ø ÚÝ Ð ÞÓÚ Ò ÙÑÙ ØÓ Ú Ð ÖÝ Ð ÓÚ Ñ Ñóö Ó Ø ÖÓÞÑ Þ Ò Ö Ò ÞØÖ Ø Ó Ö ÞÓÚ Ò ÓÖÑ º µ g(i 0 G σ ) µ g(i 0 G σ ) Ç Ö Þ ½
31 ÈÓ Ú Ñ ÒÝÒ Ð ö Ò Ñ ÒØ Ò ÔÓ Ó Ù ÑÓ ÓÚ Ò ÚÖ ØÚÒ ÓÚ ÖÓÚÒ ½ µº Î ØÓÑØÓ Ô Ô u 0 ÓÞÒ Ù Ò Ð Þ Ò Ñ ÒØ Ò ÔÐÓ Ù u Ò ÞÒ ÑÓÙ Ñ ÒØ Ò ÙÒ I 0 Ó Ö Þ ÙÖ Ò Ñ ÒØ º Æ ÖÓÞ Ð Ó ÐØÖ Ò ÔÓ Ó Ý ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ Ö ÒÓÚ Ø ØÓÖ Ú Ò Ñ Ò ÚÝÔÓ Ø Ò ÔÓÙÞ ÒÓÙ Ò Þ Ø Ù Ñ ÒØ Þ ÓÒÚÓÐÙ Ó Ö Þ Ù I 0 Ö ÒØÙ Ù ÓÚ Ö ÒÑ Ô Ö Ñ ØÖ Ñ σº Ú Ñ ÔÖÓ Þ Ö Ò Þ Ô Ù Ò Ð Ù ÓÞÒ Ò g 0 ÓÞÒº = g(i 0 G σ )º ÊÓÚÒ ½ µ ÒÝÒ ÙÔÖ Ú Ñ Ò ØÞÚº Ú Ò ¹ ÙÞÒ ØÚ Ö ) ( u u t = g 0 Q ( u) Q ( u) }{{} (D) + g 0 u }{{} (A) g 0 Q( u)f. ½ µ }{{} (S) ÙÞÒ Ð Ò (D) ÞÔó Ó Ù Ô Ó Ô ÓÑÓ ÒÒ Ó Ð Ø Þ Ö Ù Ø ÙÑÙ ÞÔÓÑ ÐÙ ÚÓÐÙ Ú Ð Þ Ó Ø Ö Òº Î ØÓÖÓÚ ÔÓÐ g 0 ÚÝ ØÙÔÙ Ú Ú Ò Ñ Ð ÒÙ (A) Ò ÓÔ Ò ÔÓÑ Ô ÐÒÙØ Ñ ÒØ Ò ÔÐÓ Ý Ö Ò Ñº Æ Ó Ö Þ Ù ½ Ñóö Ñ Ú Ø ÚÝ Ö Ð ÒÓÙ ÙÒ g 0 ½ µ Ú ØÓÖÓÚ ÔÓÐ g 0 ½ µ ÔÖÓ Ø ØÓÚ Ó Ö Þ ÔÓÙö Ø Ú Þ Ú ÖÙ Ò Ó Ö Þ ¾ µº Ð Ò Q( u)f Ú (S) Ôó Ó Ò Ú Ù ÐÓÙ Ó Ú Ð Ó Ø F ÙÚ Ó ÔÓ Ý Ù ÓÒ Ø ÒØÒ ÖÝ ÐÓ Ø Ú Ñ ÖÙ ÚÒ ÒÓÖÑ Ðݺ Ì ÒØÓ Ð Ò ÓÚ Ñ Ú ö Ò ÙÒ g 0 Ø Ù Ö ÒÝ ÔÓ Ý ÚÝÚÓÐ Ò ÓÒ Ø ÒØÒ ÐÓÙ F Ú Ð Þ Ó Ø Ö Ò ÞÔÓÑ Ð º ÈÖÓ F < 0 Ôó Ó Ð ÔÖÓØ Ñ ÖÙ ÚÒ ÒÓÖÑ ÐÝ ÙÖÝ ÐÙ ÖÝ ÐÓ Ø ÑÖ ðóú Ò Ú Ýº Æ ÓÔ ÔÖÓ F > 0 Ôó Ó Ú Ñ ÖÙ ÚÒ ÒÓÖÑ ÐÝ ÔÖÓ Ó Ø Ø Ò Ú Ð F Ú Ù ÖÓÞØ ÓÚ Øº  ØÑ ÚÝÐ Ô Ò Ñ ÑÓ ÓÚ Ò ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ Ý ÑÓ ÐÓ Ø Þ Ú Ò Ò ÓÒ Ø ÒØÒ ÐÝ F(x) Ø Ö Ý ÝÐ Þ Ú Ð Ò Ú ØÙÔÒ Ó Ö ÞÓÚ Ø I 0 º Å ØÓ ÓÒ Ò Ö Ò Ð Ò ÑÝ Ð Ò Ñ ØÓ Ý ÓÒ Ò Ö Ò ÞÒ Ñ Ø ÔÓ Ò ÞÚ Ñ Ñ ØÓ Ø ÔÓ Ú Ú Ö Ø Þ Ó Ð Ø Ω R Ò Ø Ö Ð Ñ Ò Ò ÐÓ Ýº Æ ØÙØÓ Ó Ð Ø ÔÓÐÓö Ñ ÑÒÓö ÒÙ Ó ó ÙÞÐóµ ÞÚ ÒÓÙ ðº Î Ø ØÓ ÙÞÐ Ô Ð öò Ò Ö Ò ÐÒ ÖÓÚÒ Ô Ô Ò Ó Ö ÓÚ ÔÓ Ñ Ò Ý Ò Ö Þ Ò Ñ Ô ÐÙ Ò Ö Ú Ö Ò Ò Ñ Ò Ö Ñ ØÞÚº Ö Ø Þ Ö Ò ÐÒ ÖÓÚÒ º Ö Ø ¹ Þ Ö Ò ÐÒ ÖÓÚÒ ÔÖÓÚ Ò Ö ÓÙ Ö Ò ÐÒ ÚÖ Þó Ö Ò Ò Ñ Ò Ö Ñ º Ö Ò Ò Ò Ö Ý Ò ÚÖ Ù ÔÓÑÓ Ì ÝÐÓÖÓÚ ÖÓÞÚÓ º Ú Ñ Ò Ð Ù ÞÒ Ò º ÙÒ u Ú ÙÞÐÙ Ø (ih x, jh y ) Ò k¹ø ÓÚ Ð Ò Ø Ý u(ih x, jh y, k) Ù Ñ ÞÒ Ø u k ij º Ö Ò Ò Ò Ö Ý Ò ÚÖ Ù ÔÓÑÓ Ì ÝÐÓÖÓÚ ÖÓÞÚÓ º ÈÖÓ ÓÞÒ Ò Ý Ý Ò Ö Ý Ø Ö Ô ÖÓÞ Ò ÚÞÒ Ô ÔÓÙö Ú Ò Ì ÝÐÓÖÓÚ ÖÓÞÚÓ ÔÓÙö Ú ØÞÚº Ä Ò óú ÝÑ ÓÐ Oº ÆÝÒ ÙÚ Ñ Ò ÓÐ ÓÚ ÔÖÓ ØÓÖÓÚ Ö Ò Ò Ö ÞÙ ÔÖÚÒ ÖÙ¹ ÓÙ Ô Ö ÐÒ Ö Ú º Ô ØÒÓÙ ÓÚÓÙ Ö Ò Ò k¹ø ÓÚ Ð Ò Ù Ñ ÓÞÒ ÓÚ Ø (u t) k ij = uk ij u k 1 ij + O(τ). ½ µ τ ÈÖÓ ØÓÖÓÚ Ö Ò Ú i, j¹ø Ñ ÙÞÐÙ Ø Ñ Ø ÒØÓ ØÚ Ö
32 ÓÔ Ò Ö Ò (u x ) k ij = uk i+1j uk ij h x + O(h x ), (u y ) k ij = uk ij+1 uk ij h y + O(h y ) ½ µ ÞÔ ØÒ Ö Ò (u x ) k ij = uk ij uk i 1j h x + O(h x ), (uȳ) k ij = uk ij uk ij 1 h y + O(h y ) ½ µ ÒØÖ ÐÒ Ö Ò (u x ) k ij = uk i+1j uk i 1j h x + O(h x), (u y ) k ij = uk ij+1 uk ij 1 h y + O(h y) ½ µ ÒØÖ ÐÒ Ö Ò ÔÖÓ ¾º Ô Ö ÐÒ Ö Ú (u x x ) k ij = uk i+1j uk ij + uk i 1j h x (u yȳ ) k ij = uk ij+1 uk ij + uk ij 1 h y + O(h x) + O(h y) ¾¼µ (u xȳ ) k ij = uk i+1j+1 uk i+1j 1 uk i 1j+1 + uk i 1j 1 4h x h y + O(h x h y ) Â Ó ÔÓ Ð Ò ÙÚ Ñ Ö Ò Ò ÓÔ Ö ØÓÖÝ h ÓÔ Òµ h ÞÔ ØÒµ ÔÖÓ Ò Ö Ù Ö Ò ÐÒ Ó ÓÔ Ö ØÓÖÙ Ú Ö Ò = (, ) x y h ÔÖÓ Ä ÔÐ óú Ö Ò ÐÒ ÓÔ Ö ØÓÖ = + Ø Ö Ñ Ò Ð Ù ØÚ Ö x y ) h u k ij ((u = x ) k ij, (u y) k ij, ( ) h u k ij = (u x ) k ij, (u ȳ) k ij, ¾½µ ( ) h u k ij = (u x ) k ij, (u y ) k ij, h u k ij = (u x x ) k ij + (u yȳ ) k ij. ¾¾µ - 3 -
33 ÜÔÐ ØÒ Ñ ÔÖÓ ÑÓ ÓÚ ÒÓÙ ÚÖ Ø ÚÒ Ó¹ ÚÓÙ ÖÓÚÒ ÙÚ Ñ ÜÔÐ ØÒ ÒÙÑ Ö Ñ ÔÖÓ Ñ ÒÓÙ ÐÓ Ù ÑÓ ÓÚ ÒÓÙ ÚÖ Ø ÚÒ ÓÚÓÙ ÖÓÚÒ Æ ÙÑ ÒÒÓÚÓÙ Ó Ö ÓÚÓÙ ÔÓ Ñ Ò ÓÙ ÔÖÓ ÐÝ Ñ ÒØ ( ) u t =Q ( u) g(i 0 u G σ ) g(i 0 G σ )Q( u)f Q ( u) Ò Ω (0, T), u(x, y, 0) =u 0 (x, y) Ò Ω, u n (x, y, t) =0 Ò Ω (0, T), ¾ µ ÜÔÐ ØÒ Ñ ÔÖÓ ÑÓ ÓÚ ÒÓÙ ÖÓÚÒ ÚÝØÚÓ Ñ Ø ö Ú ÖÓÚÒ ½ µ Ò Ö ¹ Ñ ÓÔ Ö ØÓÖÝ ÔÓÙÞ ÓÔ ÒÑ ÞÔ ØÒÑ Ö Ò Ò Ñ ÓÔ Ö ØÓÖÝ h h Ô Ñ Ñ k¹øóù ÓÚÓÙ Ð ÒÙ Þ Ñ Ø Ò Ð Ù Ö Ò Ò ÖÓÚÒ ( ) (u t) k ij = ( Q h h ) k 1 ij h g 0 ij h u k 1 ij Q( h u k 1 ij ) ( gij 0 Q h h ) k 1 ij F, ¾ µ Ñ ÓÞÒ Ð g 0 ij = ( Q h h ) k ij = ÌÓØÓ Ñ Ñ Ô ÚÞ Ð Þ ÔÖ º λ h Iij 0, ε + 1 ( h u k ij + h u k ) ij. Î Ð Ý Æ Ó Ö Þ ¾ ÓÙ ÙÚ ÒÝ Ú Ð Ý ÔÖÓ ÖóÞÒ Ò Ø Ú Ò Ô Ö Ñ ØÖÙ ε ÚÝ ØÙ¹ ÔÙ Ñ Ú Ö ÙÐ Ö Þ Ò Ñ Ð ÒÙ Q ( u)º ÈÖÓ ε = ÔÓ Ý Ù Ñ Ú Ð Ð Þ Ó Ò Ò Ö ÙÐ Ö ÞÓÚ Ò ÑÓ ÓÚ Ò ÚÖ Ø ÚÒ ÓÚ ÖÓÚÒ ( u t = u g 0 u ) g 0 u F. ¾ µ u ÈÖÚÒ Ú Ð Ñóö Ñ Ú Ø Ò Ó Ö Þ Ù ¾ ÔÖÓ ÚÓÐ Ù Ô Ö Ñ ØÖó σ = λ = 1 ε = F = 0º ÈÖÓØÓö ÔÓ Ý Ù Ñ Ð Þ Ó Ò ÖÓÚÒ ¾ µ ÐÓÚ Ð Ò ÖÓÚ Ò 0 Ú ÔÓ Ý Ù ÔÓÙÞ ÚÐ Ú Ñ Ú ÐÓ ÐÒ ÚÓ Ø Ý Ö ÒÓÚ ÑÙ Ø ØÓÖÙ g 0 ÞÔÓÑ ÐÙ Ú Ð Þ Ó Ø Ö Òº Î t = Ó Ö Þ ¾ ¹ ÚÓ Ø ÚÓÐÒ ó ÒÙÐÓÚ ÚÖ Ø ÚÒ Ð ö ÒÙÐ ÔÓ Ý Þ Ø Ú Óö Ñóö Ñ
34 Ú Ø Ò Ó Ö Þ Ù ¾º Ì ÒØÓ ÔÖÓ Ð Ñ ÐÞ ÒÓ Ù ÚÝ Ø Þ ÔÓÖÒÓÙ ÚÓÐ ÓÙ ÐÓÚ Ó Ð ÒÙ F Ø Ö ÔÓÑóö Ô Ð ö Ø ÒÙÐÓÚÓÙ ÚÖ Ø ÚÒ ÖÙ Ù Ú Ø Ù Ø ØÓÚ Ó Ó Ö Þ Ùº È ÚÓÐ ε = 1 ÚÞ ÐÙ Ñ Ó Ò ÖÓÚÒ ¾ Ø ØÓ ÚÓÐ Ò Ñ ÞÑ Ò ÚÐ ØÒÓ Ø Ò ØÓ Ø ö ÔÖÓ ÒÙÐÓÚÓÙ ÚÓÐ Ù ÐÓÚ Ó Ð ÒÙ Ó Þ Ø ÖÙ Ù ÙÔÖÓ Ø Ø ØÓÚ Ó Ó Ö Þ Ùº Î Ð ÔÖÓ ÚÓÐ Ù ε = 1 Ñóö Ñ Ú Ø Ò Ó Ö Þ Ù º Î Þ Ú ÖÙ ÔÓÙö Ñ ÜÔÐ ØÒ Ñ ¾ µ Ñ ÒØ ÞÙ Ö Þ Ñ Ò Ø Ö ¹ ÞÓÒ Ò º Ð Ñ Ø ÓÚ Ø ÚÒ Ø Ò ØÖ ÒÙ Ö Ò Ø Òݺ Î Ð Ý Ñóö Ñ Ú Ø Ò Ó Ö Þ ¾ º ÈÓ Ø Ò Ñ ÒØ Ò Ú Ù ÚÓÐ Ñ Ø Ý ÒÙÐÓÚ ÚÖ Ø ÚÒ Ð ö Ð ÙÚÒ Ø Ó Ð Ø Ø ÖÓÙ Ñ Ø ÓÚ Øº ÈÖÓØÓö ÒÓÙ Ó Ð Ø Ñ Ø ¹ ÓÚ Ø Þ ÚÒ Ø ÑÙ Ñ ÚÓÐ Ø Ó Ø Ø Ò Ú Ð ÐÓÚ Ð Ò F Ý ÒÙÐÓÚ ÚÖ Ø ÚÒ ÖÓÞÔ Ò Ð º Ñ Ú Ø F Ù Ñ ÚÓÐ Ø Ø Ñ ÖÝ Ð Ó Ø Ð ÑÓÞ Ñ Ó Ò Ñóö Ñ ÚÓÐ Ø Ð ÓÚÓÐÒ Ú Ð º Ý ØÓÑÙ ö F Ú ö ÒÓ Ö ÒÓÚÑ Ø ØÓ¹ Ö Ñ Ó Ú Ð Þ Ó Ø Ö Ò Ó Ò ö Ò º ÈÓ Ù Ý ÓÑ F ÚÓÐ Ð Ô Ð Ú Ð Ô Ò Ö ÒÓÚ Ø ØÓÖ Ý Ò Ò ö Ð ÐÓÚ Ð Ò Ò ØÓÐ Ý Ò Ö Ò Þ Ø Ú Ð Ò ¹ Ó Þ ÐÓ Ý Ø Ý Ø º Æ Ó Ö Þ Ú Ñ ö ÔÖÓ Ò Ô Ö Ñ ØÖÝ Ó Ø Ö Ò Ø ÒÝ Ð Ò Ó Ø ØÚ ÖÙ ÙÚÒ Ø Ñ ÒØ Ò Ó Ð Ø º Ë ÐÓÚ Ð Ò Ú Ø ØÓ Ô Ô Ò Ñóö Ñ ÚÓÐ Ø Ô Ð Ñ Ð ÔÖÓØÓö Ý Ò ¹ Ñ ÒØ Ò Ú Ò Ó Ø Ð Ó Þ Ø Ñ Þ Ú ÞÑ Ò ÒÑ ØÚ Ö Ñ Ö Ò Ø ÒÓÙº ÈÓ Ù Ð Ñ Ø Ý ÐÓÚ Ð Ò Ú ö Ø ÖÙ ÓÙ ÑÓÒ ÒÓÙ Ö ÒÓÚ Ó Ø ØÓÖÙ g 0 Ó Öº µ Ô ØÓÑØÓ Ú ö Ò Ó Þ Ø ÞÑ Ò Ò Ó ØÚ ÖÙº Ç Ö Þ ¾ Ô Ö Ñ ØÖÝ λ = 1 F = 0 ε = σ =
35 Ç Ö Þ Ô Ö Ñ ØÖÝ λ = 1 F = 0 ε = 1 σ = Ç Ö Þ Ô Ö Ñ ØÖÝ λ = 0.5 F = 50 ε = σ =
36 Ç Ö Þ Ô Ö Ñ ØÖÝ λ = 0.5 F = 80 ε = σ = 0.01 Ê Ö Ò ½ ¾ º Ù ÖØ Èº ÃÓÖÒÔÖÓ Ø Å Ø Ñ Ø Ð ÈÖÓ Ð Ñ Ò ÁÑ ÈÖÓ Ò È ÖØ Ð Ö ÒØ Ð ÕÙ Ø ÓÒ Ò Ø ÐÙÐÙ Ó Î Ö Ø ÓÒ µ ËÔÖ Ò Ö ¾¼¼¾µ ź º Ö Ò ÐÐ Àº Á Ⱥ¹Äº Ä ÓÒ Í Ö³ Ù ØÓ Ú Ó ØÝ ÓÐÙØ ÓÒ Ó ÓÒ ¹ÓÖ Ö Ô ÖØ Ð Ö ÒØ Ð ÕÙ Ø ÓÒ Ùк ÅË ¾ ½ ¾µ ½ ĺ º Ú Ò Âº ËÔÖÙ ÅÓØ ÓÒ Ó Ð Ú Ð Ø Ý Ñ Ò ÙÖÚ ØÙÖ Áº º º ÓÑ ½ ½µ ½ º ÃÖ ØÓ Ú ÐÓÚ È Ö ÐÒ Ö Ò ÐÒ ÖÓÚÒ Ú ÞÔÖ ÓÚ Ò Ó Ö ÞÙ Ú¹ Þ ÙÑÒ ÓÐ ÃÅ Â Á ÎÍÌ ¾¼¼ µ κ Å Ò Ö ÆÙÑ Ö Ò Ò ÖÓÚ Ò Ô Ö ÓÐ ÖÓÚÒ À Ñ ÐØÓÒ¹ Â Ó Ó ØÝÔÙ ÔÖÓ ÔÓØ Ý ÔÓ Ø ÓÚ Ó ÞÔÖ ÓÚ Ò Ó Ö ÞÙ Ø ÔÐÓÑÓÚ ÔÖ ÃÅ Â Á ÎÍÌ ¾¼¼¾µ Ⱥ È ÖÓÒ Âº Å Ð Ë Ð Ô Ò Ø Ø ÓÒ Ù Ò Ò ÓØÖÓÔ ¹ Ù ÓÒ ÈÖÓº Á ÓÑÔÙØ Ö ËÓ ØÝ ÏÓÖ ÓÔ ÓÒ ÓÑÔÙØ Ö Î ÓÒ ½ µ º º Ë Ø Ò Ä Ú Ð Ë Ø Å Ø Ó ÚÓÐÚ Ò ÁÒØ Ö Ò ÓÑ ØÖÝ Ù Å ¹ Ò ÓÑÔÙØ Ö Î ÓÒ Ò Å Ø Ö Ð Ë Ò Ñ Ö ÍÒ Ú Ö ØÝ ÈÖ ½ µ
37 Úvod Družice pro bistatickou altimetrii ohlédnutí za Workshopem GNSS-R 08 Stanislav Olivík * V září roku 008 se v holandském městečku Noordwijk, v sídle Evropského vesmírného výzkumného a technického střediska Evropské kosmické agentury (ESTEC/ESA), konal Workshop GNSS-R 08. Na zmíněném workshopu byla představena družice PARIS. Tato družice je navržena jako tzv. In Orbit Demonstrator pro metodu bistatické altimetrie (PARIS IOD). V praxi to znamená, že by měla na oběžné dráze sbírat a zpracovávat data a tím pomoci prokázat funkčnost a užitečnost bistatické altimetrie. 1. PARIS Družice programu UK-DMC (Disaster Monitoring Constellation) prokázaly, že lze ve vesmíru zachytit signál družic systému GPS, odražený od zemského povrchu. Družice PARIS by měla tyto signály zachytávat a dále zpracovávat.. Koncept systému 1 Obr. 1: Princip bistatické altimetrie a rozsah signálů zpracovávaných družicí PARIS Družice PARIS bude pro svoji práci využívat anténu s velkým ziskem pro přímý signál (D) anténu s velkým ziskem pro odražený signál (R) data získaná vzájemnou korelací přímého a odraženého signálu (DxR) celý rozsah signálu družic GNSS (3x40 MHz) přesné odhady ionosférického zpoždění nízkošumové ionosférické korekce přesné palubní kalibrace zpoždění přesné palubní kalibrace amplitudy signálu * Katedra matematiky, Fakulta stavební, ČVUT v Praze 1 Údaje převzaty z [1] Obrázek převzat z [1]
38 Využívané frekvence signálu Zpočátku bude využíván signál družic GPS signál Galileo E5 bude využit, jakmile bude plně k dispozici Pro zjištění ionosferických korekcí jsou zapotřebí dva signály s velkým rozdílem frekvencí alespoň L5 a L1 nebo E5 a L1 L1 1575MHz, všechny kódy (i zašifrované), 1Mcps, 10Mcps L5 1176MHz, Safety of Life, 10Mcps E5 1176MHz, 10Mcps Z charakteristiky odraženého signálu lze odvodit charakteristiku povrchu, od nějž se signál odrazil. Lze tak získávat informace o síle vln směru mořských proudů síle větru vlhkosti půdy zalesnění apod. Lze tak detekovat např. vlny tsunami plovoucí kry a tím zapojit družici PARIS do družicového systému včasného varování. [4] 3. Pokrytí, přesnost, výkon Anténa družice byla navržena tak, aby přijímala odražené paprsky v maximálním odklonu 30 od nadiru, což při dráze družice ve výšce 800 km vymezuje na zemském povrchu plochu o průměru 950 km [1]. Maximální délka stopy odraženého signálu na zemském povrchu, kterou dokáže PARIS IOD zachytit, je cca 5500 km []. Průměrně by měla družice v daném okamžiku zachytit odražené signály od 4 různých družic, což je i počet odrazných bodů na zemském povrchu. Průměrný rozestup bodů kolmo k dráze letu pak má být 130 km []. Předpokládanou přesnost dokládá následující tabulka Obr. : Tabulka přesnosti určení výšek pro družici PARIS (IOD) a pro plánovanou finální družici, která by měla operovat ve výšce 1500 km (Operational). 3 3 Tabulka převzata z [3]
39 Důležité parametry družice PARIS IOD a finální družice shrnuje následující tabulka 4. Cíle PARIS Obr. 3: Shrnutí důležitých parametrů družice PARIS IOD a finální družice. 4 Primární cílem družice PARIS IOD je prokázat funkčnost metody bistatické altimetrie. Pokud se tato metoda ukáže jako přínosná, lze výsledky měření využít i pro zkoumání mořských proudů, vlhkosti půdy, detekci vln tsunami a sledování plovoucích ker. Závěr Družice PARIS je zajímavý projekt, který si jako primární cíl klade prokázání funkčnosti a užitečnosti bistatické altimetrie. Její výhoda by měla spočívat ve vyšším pokrytí zemského povrchu ve srovnání s klasickou altimetrií. I když je PARIS primárně určena pro využívání signálu družic systému GPS, může přijímat i signály družic ruského systému GLONASS a v současné době budovaných systémů GALILEO (EU) a Beidou (Čína). Tím by se opět navýšilo pokrytí zemského povrchu altimetrickými body. Literatura [1] Buck, Ch., D Addio, S., Martín-Neira, M.: PARIS In Orbit Demonstrator Part 1: Objectives, System Concept, Budgets, prezentace z Workshopu GNSS-R 08 [] D Addio, S., Buck, Ch., Martín-Neira, M.: GNSS-R: Geometry and Coverage, prezentace z Workshopu GNSS-R 08 [3] Martín-Neira, M., D Addio, S., Buck, Ch.: PARIS In Orbit Demonstrator Part 3: Geometry, Ionospheric Correction, Instrument Design, On-board Calibration, Performance, prezentace z Workshopu GNSS-R 08 [4] Buck, Ch.: GNSS-R: Overview of Other Applications, prezentace z Workshopu GNSS-R 08 4 Tabulka převzata z [3]
40
41 Aplikace numerických metod na dynamiku tekutin Martin Ptáček 1 Abstrakt: Nejprve uvedeme model mělké vody (Shallow Water) ve D, poté porovnáme různé metody řešení např. Laxovo-Friedrichsovo metodu prvního a druhýho řádu,kompozitní schéma a na speciálních počátečních podmínkách i exaktní riemanovský řešič. 1 Úvod V této práci se budeme zabývat numerickými simulacemi mělké vody (z angl. Shallow-Water). Tento model se dá používat při simulaci protržení přehrady, vlny tsunami nebo dopadu kapky na hladinu louže. Ukážeme, že je možné používat numerické metody pro řešení hyperbolických rovnic. Pro simulaci budeme používat kompozitní a klasické numerické metody, ale také ve speciálním případě exaktní řešení, které budeme porovnávat. Model mělké vody ve D Model mělké vody ve dvou rozměrech je popsán rovnicemi pro tloušt ku vodní vrstvy h(x, y,t) a pro složky rychlosti u(x, y, t), v(x, y,t), g je gravitační konstanta [3, 5, 6]. kde h t + (hu) x + (hv) y = 0, (hu) t + (hu + 1 gh ) x + (huv) y = 0, (hv) t + (huv) x + (hv + 1 gh ) y = 0, u = u(x, y,t), v = v(x, y,t) x, y Ω R, h = h(x, y,t) t 0, T. (1) () 3 Numerické metody 3.1 Počáteční úloha pro nelineární rovnici Mějme dánu počáteční úlohu ve tvaru u t + (f(u)) x + (g(u)) y = 0 x, y R, t 0, T u(x, y,0) = u 0 (x, y) x R, (3) 1 Katedra Matematiky, Západočeská univerzita v Plzni, Univerzitní, Plzeň, heky@students.zcu.cz
42 Na oblasti R 0, T sestrojíme sít s uzly (x i, y j, t n ), i Z, j Z, n N. Definujeme x i = i x, y j = j y kde x, y jsou prostorové kroky sítě a t n = n t,kde t je časový krok. Označme U n i,j aproximaci hodnoty un i,j = u(x i, y j, t n ) přesného řešení úlohy (3). Dále budeme značit x i+ 1 = (i+ 1 )h, y j+ 1 = (j+ 1 )k. 3. Explicitní diferenční metody pro D Explicitních diferenčních metod pro řešení hyperbolických PDR ve D, je mnoho, my jsme si vybrali metody uvedené dále, které se nám budou dobře algoritmizovat 3..1 Metoda prvního řádu Laxova-Friedrichsova dvoukroková metoda prvního řádu [5]. Pro výpočet U n+1 i,j je třeba aplikovat následující vzorec x. kde U n+ 1 = 1 i+ 1,j+ 1 4 [Un i+1,j + Un i,j+1 + Un i,j + Un i+1,j+1 ], + t x [F i+1,j+ 1 F i,j+ 1 ] + t y [G i+ 1,j+1 G i+ 1,j ], F i+1,j+ 1 = f(1 [Un i+1,j+1 + Un i+1,j ] + t 4 y [g(un i+1,j+1 ) g(un i+1,j )]), G i+ 1,j+1 = g( 1 [Un i+1,j+1 + Un i,j+1 ] + t 4 x [f(un i+1,j+1 ) f(un i,j+1 )]). (4) 3.. Metoda druhého řádu Laxova-Friedrichsova dvoukroková metoda druhého řádu [5], kde U n+ 1 = 1 i+ 1,j+ 1 4 [Un i+1,j + Un i,j+1 + Un i,j + Un i+1,j+1 ] + t x [F i+1,j+ 1 F i,j+ 1 ] + t y [G i+ 1,j+1 G i+ 1,j ], F i+1,j+ 1 = f( 1 [Un i+1,j+1 + U n i+1,j] + t 4 y [g(un i+1,j+1) g(u n i+1,j)]), G i+ 1,j+1 = g(1 [Un i+1,j+1 + U n i,j+1] + t 4 x [f(un i+1,j+1) f(u n i,j+1)]). (5) U n+1 i,j = U n i,j + t 1 x [f(u(n+ )) + f(u( n+ 1 i+ 1,j+ 1 )) f(u( n+ i+ 1,j 1 1 )) f(u( n+ 1 i 1,j+ 1 ))] i 1,j 1 + t 1 y [g(u(n+ )) + g(u( n+ 1 i+ 1,j+ 1 )) g(u( n+ i 1,j+ 1 1 )) g(u( n+ 1 i+ 1,j 1 ))], i 1,j 1 Uvedené metody můžeme použít [4, 8, 3] za předpokladu, že platí pro t, x a y (CFL podmínka) max(λ Ai ) t i x + max (λ Bi ) t i y 1, (x, y,t) R 0, T. (6) - 4 -
43 3.3 Nevýhody klasických metod Klasické metody, tak jak byly uvedeny výše, jsou použitelné jenom pro omezenou skupinu úloh. Ale i v jednoduchých případech mohou dávat velice nepřesné výsledky. Tento jev budeme ilustrovat na modelu transportní rovnice u t + au x = 0 x R, 0 < t < T, (7) s nespojitostí v počáteční podmínce { 1 x < 0 u(x, 0) = 0 x > 0. Pokud budeme (7) řešit metodou dvoukrokové Laxovy-Friedrichsovy metody prvního řádu, získáme numerické výsledky, které se liší od přesného řešení. Jsou rozmazané (difúze).to je způsobeno tím, že metoda je aproximací prvního řádu hyperbolické rovnice (7), a i aproximací druhého řádu rovnice[1, 4] s difúzním členem du xx, kde u t + au x = du xx, (8) d = d(τ, h) = h (1 (a t t h ) ). Pro d 0 může být zahlazení přijatelné. Pokud budeme řešit pomocí dvoukrokové Laxovy-Wendroffovy metody druhého řádu úlohu (7), získáme rozkmitané řešení. Tato metoda je aproximací druhého řádu dané hyperbolické rovnice a aproximací třetího řádu rovnice[1, 4] s disperzním členem µu xxx, kde u t + au x = µu xxx, (9) µ = µ(τ, h) = h 6 a((a t h ) 1). Disperzní člen způsobuje oscilace řešení
44 3.4 Kompozitní metody Kompozitní metody vychází z poznatku, že metody prvního řádu řešení rozmazávají a naopak metody vyšších řádů přidávají oscilace. Proto použijeme-li k výpočtu jedné nebo více časových vrstev metodu druhého řádu a na poslední časovou vrstvu metodu prvního řádu můžeme získat lepší aproximaci řešení než při použití jednotlivých metod. Například skládání Laxovo-Friedrichsovo metody prvního a druhého řádu [1, 5] LF 1.řád LF.řád LF.řád ti stavový Riemannův řešič Předpokládejme, že aproximované řešení může vypadat jako na obr. (), kde je naznačena duální buňka po nějakém časovém kroku t. Protože se signály šíří konečnou rychlostí, může být buňka rozdělena do devíti částí tří rozdílných druhů R 0, R 1 a R. V rohových oblastech R 0 zůstávají původní data neporušena. Na krajních oblastech R 1 určíme stavy pomocí 3 stavového Riemanova řešiče v 1D. Na obr. (1) je zobrazeno exaktní řešení Riemanova problému Obrázek 1: Exaktní řešení
45 Obrázek : D 9ti stavový řešič: rozložení duální buňky do 9ti oblastí. Na oblasti R spočítáme hodnotu U takto kde α,β=0, 1,1 S α,βu α,β = x y 4 F 0, 1 α,β=0,1 U α,β y t(f 1, 1 x t(g 1, 1 F 0, 1) G 0, 1 = 1 t y [1 ( y b+ 0, 1 t) tf(u 01 ) + 1 ( y + b 0, 1 t) tf(u 00 ) + 1 (b+ 0, 1 b 0, )( t) f(u 1 0, 1)], G1,0 = 1 t x [1( x b+ 1,0 t) tg(u 10) + 1( x + b 1,0 t) tg(u 00) + 1 (b+ 1,0 b 1,0)( t) g(u1,0)]. ),
46 4 Numerické simulace 4.1 Porovnání s exaktním řešením na problému protrhnutí přehrady Toto porovnání bude vycházet z toho že známe přesné řešení Riemanova problému v 1D, které rozšíříme do dalšího rozměru. V tomto rozměru bude vždy hodnota konstantní. Na obr.(3) je vidět počáteční podmínka Obrázek 3: Počáteční podmínka problému protrhnutí přehrady ve D
47 Obrázek 4: Laxova-Friedrichsova metoda prního řádu Obrázek 5: rozdíl přesného řešení a metody prvního řádu Obrázek 6: normy rozdílů
48 Obrázek 7: Laxova-Friedrichsova metoda druhého řádu Obrázek 8: rozdíl přesného řešení a metody druhého řádu Obrázek 9: normy rozdílů
49 Obrázek 10: kompozitní metoda 1 1 (1x metoda druhého řádu a 1x metoda prvního řádu) Obrázek 11: rozdíl přesného řešení a kompozitní metody 1 1 Obrázek 1: normy rozdílů
50 Obrázek 13: kompozitní metoda 19 1 (19x metoda druhého řádu a 1x metoda prvního řádu) Obrázek 14: rozdíl přesného řešení a kompozitní metody 19 1 Obrázek 15: normy rozdílů
51 Obrázek 16: 9-ti stavový Riemannův řešič Obrázek 17: rozdíl přesného řešení a 9-ti stavováho Riemanova řešiče Obrázek 18: normy rozdílů 4. Dopad kapky na vodní hladinu Pro simulaci použijeme model (1) jako počáteční podmínku jsme si zvolili sloupec velikosti 3x3 uzly sítě uprostřed sítě. Výška sloupce je 5, výška okolní hladiny je 1 a rychlost je ve všech uzlech sítě nulová. Na následujících obrázcích jsou zobrazeny výsledky jednotlivých metod ve stejném čase T
52 Obrázek 19: Dvoukroková Laxova-Friedrichsova metoda prvního řádu Obrázek 0: Dvoukroková Laxova-Friedrichsova metoda druhého řádu - 5 -
53 Obrázek 1: kompozitní metoda 1 1 (1x metoda druhého řádu a 1x metoda prvního řádu) 5 Závěr Při našich experimentech se ukázaly metody kompozitního typu jako velice dobré a zároveň dostatečně jednoduché na implementaci v systému Matlab. Bylo by vhodné implementovat metody pro nestrukturované sítě kvůli simulacím na tvarově složitějších sítích. Reference [1] Liska R., Wendroff B.: D Shallow water Equations by Composite Schemes, České Vysoké Učení Technické v Praze a Los Alamos National Laboratory, USA, 1997 [] Toro E. F.: Riemann solvers and numerical methods for fluid dynamics, Springer-Verlag, Berlin Heidenberg, 1999 [3] Leveque R. J.: Finite volume methods for hypebolic problems, Cambridge university press,
54 [4] Míka S., Přikryl P.: Numerické metody řešení parciálních diferenciálních rovnic (Evoluční rovnice), Západočeská Univerzita, Plzeň 1996 [5] Leveque R. J.: Numerical Methods for Conservation Laws, Research Institute Of Mathematics, Zürich 1990 [6] Hadašová K.: Modelování shallow water, Semestrální práce - Matematické modelování, Západočeská Univerzita, Plzeň 008 [7] Nejedlý J.: Vybrané metody pro řešení nelineárních úloh dynamiky tekutin, Práce k obhajobě státní doktorské zkoušky, Západočeská Univerzita, Plzeň 003 [8] Courant R., Friedrichs K., Lewy H., On the partial difference equations of mathematical physics, IBM Journal, March 1967, pp , English translation of the 198 German original
55 CHARAKTERISTICKÝ POLYNOM A REZOLVENTA JACOBIHO MATICE SPECIÁLNÍHO TYPU Bc. František Štampach 1 Abstrakt: V příspěvku jsou vyšetřeny některé spektrální vlastnosti určité třídy Jacobiho matic konečné liché dimenze. Hlavním výsledkem je odvození speciální báze, ve které nabývá studovaná matice poměrně jednoduchého tvaru, což následně umožňuje odvodit formuli pro charakteristický polynom a rezolventu. 1 Úvod Buď d N. Budeme vyšetřovat třídu Jacobiho matic tvaru d K := w w d + 1 w w 1 w w 0 w w 1 w w kde w > 0 (nespecifikované elementy jsou 0). Dále označme χ red (z) := ( 1)d+1 z, (1)... d 1 w w d det(k zi). () Funkci χ red (z) budeme nazývat redukovaný charakteristický polynom. Jelikož je 0 vždy vlastním číslem matice K, jak bude vidět dále, je χ red (z) skutečně polynomem v proměnné z, a tudíž název redukovaný charakteristický polynom je opodstatněný. Funkce F Definice 1. Označme F : D C, F(x) := 1 + ( 1) m x k1 x k1 +1x k x k +1...x km x km +1, m=1 k 1 =1 k =k 1 + k m=k m KM FJFI ČVUT Praha, Trojanova 13, Praha, stampik@centrum.cz
56 kde { } D = x = {x k } k=1 x k x k+1 <. Je zřejmé, že pokud má posloupnoust x pouze konečně mnoho nenulových členů, přejdou řady v předchozí definici v konečné sumy. Dále budeme psát F(x 1,x,...,x k ) místo F(x) v případě, že x = (x 1,x,...,x k, 0, 0,...). Funkce F má několik zajímavých vlastností, např. je symetrická vůči změně pořadí argumentů, t.j. F(x 1,x,...,x k ) = F(x k,x k 1,...,x 1 ) (3) k=1 a také splňuje velice důležité rekurentní relace F(x 1,x,...,x k ) = F(x, x 3,...,x k ) x 1 x F(x 3,x 4,...,x k ) (4) F(x 1,...,x k 1,x k ) = F(x 1,...,x k 1 ) x k x k 1 F(x 1,...,x k ). (5) Důkaz těchto tvrzení lze nalézt v práci [1]. První dvě identity vyplynou z definice funkce F, třetí relace je jednoduchým důsledkem předchozích vztahů. Poznámka 1. Důkazy většiny tvrzení, které se zde objeví, lze nalézt v monografii [1]. U následujících tvrzení vždy nanejvýš zmíním hlavní myšlenku důkazu a neuvedu-li jinak, odkazuji čtenáře právě na monografii [1], kde nalezne důkazy detailně vypracované. 3 Symbol J Definice. Definujme J(m,n) := ( n! m (m 1)! wm n F w, m + 1 w,..., n w kde m, n N, m n, w > 0 a F je funkce z Definice 1. Přepíšeme-li vztahy 4 a 5 do jazyka symbolu J získáme tyto rekurentní relace: ), J(m,n) = m J(m + 1,n) J(m +,n), (6) w J(m,n) = n J(m,n 1) J(m,n ). (7) w Pomocí těchto vztahů lze dodefinovat symbol J i mimo jeho definiční obor stanovený v Definici. Rozšiřme tedy symbol J i mimo množinu {(m,n) N N;m n} rekurentně tak, aby relace 6 a 7 zůstaly v platnosti. Dá se ukázat (viz [1]), že toto rozšíření symbolu lze zavést takto: pomocí vztahu J(m,n) = J(n +,m )
57 se odstraní požadavek m n a relacemi a J( k, n) := ( 1) k+1 J(k +,n) J(m, k) := ( 1) k+1 J(m,k ) dodefinujeme symbol i pro nekladné argumenty. Máme tedy symbol J definován na celé množině Z Z. Vlastnosti symbolu J: Pro každé m, n Z platí J(m,n) = J(n +,m ), (8) J( m,n) = ( 1) m+1 J(m +,n), (9) J(m, n) = ( 1) n+1 J(m,n ), (10) J(m,n) = m J(m + 1,n) J(m +,n), (11) w J(m,n) = n J(m,n 1) J(m,n ). (1) w Symbol lze také vyjádřit jako polynom v proměnné w. Tvrzení 1. 1) [ k+1 ] ( ) n s (k s + 1)! J(n k,n) = ( 1) s w s k (13) k s + 1 s! pro každé n, k Z, k. ) J(n + k +,n) = pro každé n, k Z, k 0. s=0 [ k+1 ] s=1 ( 1) s ( k + n s + 1 k s + 1 ) (k s)! (s 1)! ws k (14) Příklad 1. S využitím předchozího můžeme vyjádřit symbol J pro některé argumenty: J(n +,n) = J(n, n) = 0, J(n,n) = n, J(n + 1,n) = w, J(n + 3,n) = w, J(n + 4,n) = n, J(n 1,n) = kde n Z. n(n 1) w w, J(n,n) = n(n 1)(n ) w (n 1),
58 4 Báze ϑ Označme ϑ := (v d,v d+1,...,v d ), kde v T s := (J(d + s + 1,d + s),j(d + s,d + s),...,j( d + s + 1,d + s)). (15) Proč volíme vektory v s právě takto bude jasné později (až na ně aplikujeme matici K). Soubor vektorů ϑ je báze prostoru C d+1, neboť matice sestavená z vektorů v s je regulární, což je vidět z následujícího tvrzení. Tvrzení. Nechť V C d+1 d+1 je matice jejíž sloupce jsou tvořeny vektory v d,v d+1,...,v d, tj. V ks = v k s J( k + s + 1,d + s), k,s ( d, d + 1,...,d). Potom platí detv = w d k=1 k! (d 1)(d+1). (16) 5 Rezolventa a charakteristický polynom Nechť s { d,...,d}. Aplikací matice K na vektory z báze ϑ dostaneme (K s)v s = wj(d + s +,d + s)e d wj( d + s,d + s)e d, kde jsme několikrát použili rekurentní relace 11. e d a e d jsou vektory standartní báze, tj. e k ±d = δ ±dk. A protože J(d + s +,d+s) = 0 (podle Příkladu 1), získáváme jednoduchý vztah (K s)v s = wj( d + s,d + s)e d. (17) Poznámka. Protože J( d,d) = 0 (viz Příklad 1), je vektor v 0 vlastním vektorem matice K k vlastnímu číslu 0. Dále bychom chtěli vyjádřit matici K v bázi ϑ. K tomu je třeba najít souřadnice vektoru standartní báze e d v bázi ϑ. Tyto souřadnice mají tvar neboť platí e d (s) := e d = d s= d ( 1) d+s (d + s)!(d s)! wd 1, ( 1) d+s (d + s)!(d s)! wd 1 v s (důkaz je uveden opět v [1]). Dostáváme tedy vztah pro matici K vyjádřenou v bázi ϑ (označenou K ϑ ) (K ϑ ) ts = sδ ts wj( d + s,d + s)e d (t), (18)
59 kde t, s { d,...,d}. Označíme-li K 0 C d+1 d+1, a a,e ϑ d Cd+1, (K 0 ) ts := sδ ts (e ϑ d) T := (e d ( d),e d ( d + 1),...,e d (d)), a T := (α d,α d+1,...,α d ), kde α s := wj( d + s,d + s), můžeme vztah 18 napsat maticově jako K ϑ = K 0 + e ϑ da T. (19) Toto jednoduché vyjádření matice K je vhodné k odvození formule pro charakteristický polynom matice K. Poznámka 3. Z vlastností symbolu J snadno nahlédneme, že platí: α s = α s. Ještě než přistoupíme k odvození formule pro charakteristický polynom, připomeňme, že platí následující identita: det(1 + ba T ) = 1 + a T b, kde a,b C n. Toto tvrzení lze jednoduše dokázat z definice determinantu (nebo ho čtenář zná z lineární algebry). S využitím vztahu 19 a předchozího tvrzení můžeme začít odvozovat formuli pro χ red (z). χ red (z) = ( 1)d+1 z = ( 1)d+1 z = ( 1)d+1 z = det(k z) = ( 1)d+1 z det(k ϑ z) = det(k 0 z) det(1 + (K 0 z) 1 e ϑ da T ) = d (k z)(1 + a T (K 0 z) 1 e ϑ d) = k= d ( d d (k z ) 1 + w d 1 k=1 s= d d (k z )(1 + a T (K 0 z) 1 e ϑ d) = k=1 ) ( 1) d+s α s (d + s)!(d s)! s z Protože α s = α s, můžeme pokračovat v úpravách předchozího výrazu d s= d = ( 1) d+s α s d ( ) (d + s)!(d s)! s z = ( 1) d+s 1 (d + s)!(d s)! α s s z 1 = s z s=1 s=1 d s wj(d s +,d + s). s z (d + s)!(d s)! Získali jsme tedy formuli ( ) d d χ red (z) = (k z ) 1 + w d s J(d s +,d + s). (0) s z (d + s)!(d s)! k=1 s=1-59 -
60 Nakonec bychom rádi odstranili z formule symbol J, to ovšem ještě vyžaduje jistou přípravu, pro kterou v tomto příspěvku není prostor. Detailně je procedura vypacována opět v [1]. Závěrečný tvar formule pro redukovaný charakteristický polynom je d (d s + 1)! d s χ red (z) = s!(d s + 1)! ws (k z ), (1) který platí pro každé z C. s=0 Poznámka 4. Z formule (1) je vidět, že χ red (z) nemá žádné kořeny v kruhu z < 1 a χ red (±1) = 0, právě když w = 0. k=1 Nakonec uvedeme ješte formuli pro rezolventu matice K ϑ. Tvrzení 3. Nechť z C \ { d,...,d} takové, že Potom platí 1 + a T (K 0 z) 1 e ϑ d 0. () (K ϑ z) 1 = (K 0 z) 1 1 (K 1 + a T (K 0 z) 1 e ϑ 0 z) 1 e ϑ da T (K 0 z) 1. (3) d V důkazu stačí ověřit platnost identity (K ϑ z) 1 (K ϑ z) = I (detailně opět v [1]). Poznámka 5. Čísla z C, pro které nastává ve výrazu rovnost jsou právě body spektra matice K. 6 Závěr V tomto příspěvku jsme se zabývali odvozením formule pro charakteristický polynom (1) a rezolventy (3) pro jistou třídu Jacobiho matic konečné liché dimenze (1). K tomuto účelu bylo třeba zavést speciální funkci F definovanou na prostoru posloupnosí (Definice 1) a symbol J (Definice ). Nakonec jsme pomocí symbolu J sestrojili bázi ϑ (15) a využili jednoduchého tvaru, kterého v bázi ϑ nabývá studovaná matice. Ačkoli tento příspěvek tvoří uzavřený celek, byl vypracován jako podklad pro vyšetřování spektrálních vlastností nekonečno-rozměrných Jacobiho matic speciálního typu. Tomuto úkolu se budu věnovat dále a možná s ním seznámím účastníky příští studentské konference VŠTEZ
61 Reference [1] F. Štampach, Equations of Eigenvalues for a Tridiagonal Operator, Výzkumný úkol, FJFI, CVUT, Praha, 009 [] F. Štampach, Spectral Analysis of Special Type of Jacobi s Matrices, Bakalářská práce, FJFI, CVUT, Praha, 008 [3] V. B. Kuznetsov a E. K. Sklyanin, Eigenproblem for Jacobi Matrices: Hypergeometric Series Solution, arxiv:math.co/ v,
62
63 Matematické modelování reakčních procesů v problematice spalování Vít Tomica 1 Scottův-Wangův-Showalterův reakčně difuzní model 1.1 Spalování směsí plynů Při spalování promíchaných směsí plynů byly experimentálně pozorovány vzory, např. soustředné kruhy a rotující spirály. Tyto vzory vznikaly při spalování směsí jednoduchých organických sloučenin a lehkých prvků jako např. butan nebo oktan smíchané s kyslíkem a heliem. Uvedené vzory, jejich vznik a časový vývoj, lze podle [6] modelovat pomocí tzv. Saľnikova modelu P A A B + teplo, kde první reakce probíhá rychlostí k 1 p a druhá (za vzniku tepla) rychlostí k a, kde k 1, k jsou rychlostní konstanty a p, a jsou koncentrace látek P, A. Za dalších předpokladů (viz. [6] nebo [10]) lze vývoj koncentrace meziproduktu A a teploty T popsat soustavou parciálních diferenciálních rovnic a τ = k 1p 0 k (T)a + D A a, T τ t = Q C p σ k (T)a T T a + D T T, t N kde význam jednotlivých symbolů lze najít např. v [10]. Tyto rovnice se převedou do bezrozměrného tvaru pomocí substitucí popsaných v [6]. Tak získáme soustavu bezrozměrných Katedra matematiky, fakulta jaderná a fyzikálně inženýrská, ČVUT, Trojanova 13, Praha, tombav@centrum.cz
64 rovnic α t Θ t = µ αf(θ) + α, = 1 κ (αf(θ) Θ) + Le Θ, (1) která se nazývá Scottův-Wangův-Showalterův model. Konstanta Le se nazývá Lewisovo číslo, které je definováno jako Le = D T D A, funkce f má předpis f(θ) = exp ( Θ 1 + εθ Význam a podoba parametrů µ, κ a ε jsou popsány v [6]. ). 1. Scottův-Wangův-Showalterův model Nechť Ω Ê je omezená oblast, ve které proces sledujeme po dobu t (0, T). Potom průběh teploty a koncentrace meziproduktu v čase lze popsat soustavou rovnic α t Θ t definovaných na množině (0, T) Ω. = α + µ αf(θ), }{{} g 1 (α,θ) = Le Θ + 1 (αf(θ) Θ), } κ {{} g (α,θ) Stav procesu v čase t = 0 popíšeme počátečními podmínkami α t=0 = α ini, Θ t=0 = Θ ini. (3) Dále definujeme chování α a Θ na hranici Ω, tj. přidáme okrajové podmínky Neumannovy nebo Dirichletovy. V případě Dirichletových okrajových podmínek zvolíme okrajové hodnoty rovny triviálnímu řešení soustavy (1): α Ω = µ e ( µ () 1+εµ ), Θ Ω = µ. (4) Zvolíme-li Neumannovy okrajové podmínky, budou vypadat následovně: α Θ n = 0, Ω n = 0, (5) Ω kde n je vnější normálový vektor k hranici oblasti Ω
65 Reakčně-difuzní rovnice s advekčním členem Pokud probíhá reakce (resp. proces spalování) a zároveň proudění média (míchání), potom jeho vliv na průběh spalování popíše advekční člen, který přidáme k rovnicím (). Tak dostaneme novou soustavu rovnic α + v α = µ αf(θ) + α, t Θ t + v Θ = 1 (αf(θ) Θ) + Le Θ, κ kde v = (v 1, v ) je známý vektor rychlosti, který může záviset na čase a poloze v Ω. K rovnicím přidáme okrajové podmínky (4) nebo (5) a počáteční podmínky (3). Pro výpočty volíme parametry z následujíci tabulky (viz.[6]): parametr hodnoty Le [0.5, 5] κ , µ [0.7, 5] ε 0.18, Tabulka 1: Tabulka parametrů. Numerické řešení Soustavu evolučních rovnic () lze řešit metodou přímek, jak ukázaly výsledky v [1], [9], [7]. V této práci se zaměříme na použití metod implicitního typu..1 Metoda sítí Na množinu (0, T) Ω, kde Ω je čtvercová oblast (0, L) (0, L), položíme ekvidistantní síť uzlových bodů (t k ; x i, y j ), kde Aproximace řešení v uzlech označíme t k = kτ, k = 0, 1,,..., τ > 0, (x i, y j ) = (ih, jh), i, j = 0, 1,..., m, h = L m. α k i,j α(t k ; x i, y j ), Θ k i,j Θ(t k ; x i, y j )
66 .1.1 Semi-implicitní schéma Diferenciální výrazy v soustavě nahradíme diferencemi: α t Θ t = µ αf(θ) + α, = 1 κ (αf(θ) Θ) + Le Θ, (6) ϕ t ϕk i,j ϕk 1 i,j, τ ϕ = ϕ x + ϕ y ϕk i 1,j ϕk i,j + ϕk i+1,j h + ϕk i,j 1 ϕk i,j + ϕk i,j+1 h. Nelineární členy g 1 a g aproximujeme jejich hodnotami na předcházející napočítané časové hladině: ( ) g 1 (α, Θ) g k 1 1 i,j = g 1 α k 1, Θ k 1, i,j ( g (α, Θ) g k 1 i,j = g α k 1 i,j i,j, Θ k 1 i,j Po nahrazení diferenciálních výrazů a úpravě dostaneme dvě soustavy lineárních rovnic o (m 1)(m 1) neznámých: τ ( ) α k h i 1,j + αi,j 1 k + (1 + 4τ ) α k h i,j τ ( ) α k h i+1,j + αi,j+1 k ( ) = α k 1 i,j + τg 1 α k 1 i,j, Θ k 1 i,j, τle h ( Θ k i 1,j + Θ k i,j 1 = Θ k 1 i,j + τg ( α k 1 i,j ) + (1 + 4τLe ), Θ k 1 i,j, h ). ) Θ k i,j τle ( ) Θ k h i+1,j + Θ k i,j+1 kde i, j = 1,,..., m 1. Tyto soustavy rovnic jsme řešili pomocí Gaussovy-Seidelovy iterační metody (viz. [11]). Rovnice s advekčním členem Soustavu rovnic diskutovanou v odstavci 1. α + v α = µ αf(θ) + α, t Θ t + v Θ = 1 (αf(θ) Θ) + Le Θ, κ
67 diskretizujeme jako v předchozím odstavci. Advekční členy nahradíme centrálními diferencemi takto: ϕ k i+1,j v ϕ v ϕk i 1,j ϕ k i,j v ϕk i,j 1. h h Předpokládáme, že velikost rychlostního pole a velikost difuzních koeficientů jsou v takovém vztahu, že advekce má menší vliv než difuze. Potom po nahrazení diferenciálních výrazů diferencemi vede původní úloha opět na soustavu ( τ h + τv ) ( 1 τ α k i 1,j h h + τv ( )α ki,j 1 h τ ) α k h i,j ( τ h τv ) ( 1 τ α k i+1,j h h τv ) α i,j+1 k h = ( ) αk 1 i,j + τg 1 α k 1 i,j, Θ k 1 i,j, ( τle + τv ) ( 1 τle Θ k h i 1,j h + τv ) ( Θ ki,j 1 h h τLe ) Θ k h i,j ( τle τv ) ( 1 τle Θ k h i+1,j τv ) ( ) Θ k h h i,j+1 = Θ k 1 i,j + τg α k 1 i,j, Θ k 1 i,j. h Vzniklé soustavy rovnic jsme opět řešili pomocí Gaussovy-Seidelovy metody..1. Metoda střídavých směrů Princip této metody spočívá v tom, že kromě přibližného řešení α k+1 i,j hodnotu α k+1 i,j ve směru jednoho indexu v čase t k+ 1 použijeme jiné vzorce než pro výpočet α k+1 i,j počítáme ještě pomocnou = ( k + ) 1 k+ τ tak, že pro výpočet α 1 i,j ve směru druhého indexu. Několik metod tohoto typu lze nalézt v [11]. Zde použijeme jednu z nich, nazývá se Peacemanova-Rachfordova a je dána dvojicí vzorců (vzorce uvádíme pouze pro první rovnici soustavy (6), obdobně se provede i pro druhou rovnici) α k+1 i,j α k i,j τ = 1 ( ) α k+1 h i 1,j αk+1 i,j + α k+1 i+1,j + 1 ( ) α k h i,j 1 αi,j k + αi,j+1 k + 1 g 1 ( α k i,j, Θ k i,j), (7) α k+1 i,j α k+1 i,j τ = 1 ( α k+1 h + 1 g i,j 1 αk+1 i,j + α k+1 ( ) α k+1 i,j, Θ k+1 i,j, i,j+1 ) 1 ( + h α k+1 i 1,j αk+1 ) i,j + α k+1 i+1,j (8) Rovnice (7) vznikla tak, že jsme aproximovali α centrální diferencí ve vrstvě t x k+ 1 a derivaci Θ ve vrstvě t y k. V druhém vzorci (8) jsme postupovali naopak, akorát jsme aproximaci prováděli na intervalu t k+ 1, t k
68 Pokud rovnice (7), (8) přepíšeme do tvaru τ 1 ( h αk+ i 1,j τ )α k+1 h i,j τ 1 h αk+ i+1,j = τ ( h αk i,j τ ) α k h i,j + τ h αk i,j+1 τ ( h αk+1 i,j τ ) α k+1 h i,j τ h αk+1 i,j+1 = τ + τ g ( 1 α k i,j, Θi,j) k, 1 ( h αk+ i 1,j + 1 τ )α k+1 h i,j + τ + τ ( ) g α k+1 i,j, Θ k+1 i,j, 1 h αk+ i+1,j vidíme, že k vypočtení hodnot na vrstvě t k+ 1 z první rovnice stačí vyřešit soustavu s tridiagonální regulární maticí a obdobně pro vrstvu t k+1 ve druhé rovnici. K řešení soustav s tridiagonální maticí se dobře hodí např. metoda faktorizace (viz. []). 3 Výsledky numerických výpočtů 3.1 Porovnání metod pro řešení D úlohy Diskretizace semi-implicitní metodou převede úlohu na dvě soustavy lineárních rovnic, které jsme řešili Gaussovou-Seidelovou metodou s tolerancí chyby Pro urychlení výpočtů jsme řešící algoritmus paralelizovali pomocí programovacího nástroje openmp (viz. [8]) a výpočty jsme prováděli na počítačích se čtyřjádrovými procesory. Metoda střídavých směrů se ukázala jako efektivní metoda. Jak jsme uvedli v předchozí kapitole, k výpočtu jedné časové hladiny je potřeba vyřešit dvě soustavy rovnic s tridiagonální maticí. V porovnání s paralelizovanou Gaussovou-Seidelovou metodou (s tolerancí chyby 10 9 ) je algoritmus pro střídavé směry zhruba šestkrát rychlejší. 3. Numerické simulace Úloha 1 Dvourozměrný Scottův-Wangův-Showalterův model s Dirichletovými okrajovými podmínkami: α = α + µ αf(θ), t Θ = (Le) Θ + 1 (αf(θ) Θ), t κ µ α t=0 = α ini, α Ω = exp( µ ), Θ t=0 = Θ ini, Θ Ω = µ. 1+εµ
69 Nastavení parametrů: Počáteční podmínky: µ = 1.8, Le = 1, ε = 0.18, κ = (9) α t=0 = exp µ ( µ 1+εµ ), Θ t=0 = µ + e ( 50((x.5) +(y.5) )). (10) Řešením úlohy 1 s parametry (9) a počáteční podmínkou (10) jsou pravidelně vznikající kruhy, které se šíří od středu ke krajům oblasti (viz. obrázek 1). Toto řešení připomíná soustředné kruhy, které byly pozorovány při experimentu (viz. [4]). Obrázek 1: Úloha 1 s počáteční podmínkou (10) a parametry (9) řešená metodou střídavých směrů na síti s h = 1 64 a τ = 6,
70 Obrázek : Pokračování obrázku 1. Úloha Dvourozměrný Scottův-Wangův-Showalterův model s advekčním členem a Dirichletovými okrajovými podmínkami: Nastavení parametrů: α + v α = α + µ αf(θ), t Θ t + v Θ = (Le) Θ + 1 (αf(θ) Θ), κ α t=0 = α ini, Θ t=0 = Θ ini, µ α Ω = exp( µ ), Θ Ω = µ. 1+εµ µ = 1.8, Le = 1, ε = 0.18, κ = , v = [, ]. Počáteční podmínky: µ α t=0 = ( exp µ 1+εµ ), Θ t=0 = µ + e ( 50((x.5) +(y.5) )). (11) Reakce probíhá v silovém poli, které charakterizuje vektor v = [, ]. V důsledku působení silového pole dochází k advekci teploty ve směru tohoto působení, jak je vidět z obrázku
Ç Ð Ò ËÐ Ø ÖÓÚ ØÖ ÔÐ ØÙ Ç Ð Ò ËÐ Ø ÖÓÚ ØÖ ÔÐ ØÙ Å ÐÓ Î Ó Ó Ø Ó ÖÚ ØÓ È Ò Ô Ó ÙÒ Ú ÖÞ Ø Ú ÈÐÞÒ ½¾º½¼º¾¼½½
 Å ÐÓ Î Ó Ó Ø Ó ÖÚ ØÓ È Ò Ô Ó ÙÒ Ú ÖÞ Ø Ú ÈÐÞÒ ½¾º½¼º¾¼½½ Ç ÔÖ Þ ÒØ Ó ØÓ ËÐ Ø ÖóÚ Ñ ÎÐ ØÒ Ñ ØÝ Ñ ËÐ Ø ÖóÚ ÑÓ ËØÖÙ Ò ÔÓÔ ÙÔÖ ÚÓ Ú Ó Ö Ú Ñ ØÖÙ ÏÊ ÇË ¹¼ ¼ ÈÖÓ Ø È Ó ÐÞ ÔÓÑÓ ÙÔÖ ÚÓ Ú Ó Ö Ú Ñ ØÖÙ Ñ Ø ÈÖÓ Ó Ø
Å ÐÓ Î Ó Ó Ø Ó ÖÚ ØÓ È Ò Ô Ó ÙÒ Ú ÖÞ Ø Ú ÈÐÞÒ ½¾º½¼º¾¼½½ Ç ÔÖ Þ ÒØ Ó ØÓ ËÐ Ø ÖóÚ Ñ ÎÐ ØÒ Ñ ØÝ Ñ ËÐ Ø ÖóÚ ÑÓ ËØÖÙ Ò ÔÓÔ ÙÔÖ ÚÓ Ú Ó Ö Ú Ñ ØÖÙ ÏÊ ÇË ¹¼ ¼ ÈÖÓ Ø È Ó ÐÞ ÔÓÑÓ ÙÔÖ ÚÓ Ú Ó Ö Ú Ñ ØÖÙ Ñ Ø ÈÖÓ Ó Ø
Ó Ú Ø Ð ÓØÓ Ð ØÖ Ó ÚÙ ÔÓÚ úóú Ò Ò Ñ ÝÞ À ÒÖ À ÖØÞ ½ ß½ µ Òú ÖÓ Ù ½ Ô Ú ÔÓ Ù ÔÖÓ Þ Ø Ü Ø Ò Å ÜÛ ÐÐ Ñ Ô ÔÓÚ Þ Ò Ð ØÖÓ¹ Ñ Ò Ø ÚÐÒ Úõ ÑÐ ØÓ Ó ú Ó Ú ØÐ Ò õ
 Ë ÅÁÆý ÁÃ ß ¾º ÖÓ Ò º ÐÓ Æ ÓÐ ÖÓ Ó Ñ ÖÓ Ú Ø ¾ ß ÓØÓ Ð ØÖ Ú Þ Ò ¾¼¼ µ ½ º ÞÒ ØÓ ÓØÓ ÖÓ Ù ÙÔÐÝÒÙÐÓ ØÓ Ð Ø Ó Ò Ý ÚÝõ Ð Ú Ò Ñ Ñ ÓÔ Ù ÒÒ Ð Ò Ö È Ý Ð Ò Ð ÖØ Ò Ø Ò ½ ß½ µ Ç ÒÓÑ ÙÖ Ø Ñ Ô ØÙ Ø Ñ ÚÞÒ Ù Ô Ñ ÒÝ Ú
Ë ÅÁÆý ÁÃ ß ¾º ÖÓ Ò º ÐÓ Æ ÓÐ ÖÓ Ó Ñ ÖÓ Ú Ø ¾ ß ÓØÓ Ð ØÖ Ú Þ Ò ¾¼¼ µ ½ º ÞÒ ØÓ ÓØÓ ÖÓ Ù ÙÔÐÝÒÙÐÓ ØÓ Ð Ø Ó Ò Ý ÚÝõ Ð Ú Ò Ñ Ñ ÓÔ Ù ÒÒ Ð Ò Ö È Ý Ð Ò Ð ÖØ Ò Ø Ò ½ ß½ µ Ç ÒÓÑ ÙÖ Ø Ñ Ô ØÙ Ø Ñ ÚÞÒ Ù Ô Ñ ÒÝ Ú
n, π j = nπ j (1 π j ) nπ j (X j nπ j ) 2 χ 2 = χ 2 k 1 j=1
 ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ñ ÖÓ ¾¼¼»¾¼¼ Ã Ö Ð Ú Ö º Ð Ò ¾¼¼ ÖÓÞ Ð Ò ÑÙÐØ ÒÓÑ ÞÓ Ò Ò ÒÓÑ Ó ÖÓÞ Ð Ò Ò k¹ø Ò Ó Ò Ú Ð Ò X 1,..., X k Ô Ö Ñ ØÖÝ n, π 1,..., π k 0 < π j
ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ñ ÖÓ ¾¼¼»¾¼¼ Ã Ö Ð Ú Ö º Ð Ò ¾¼¼ ÖÓÞ Ð Ò ÑÙÐØ ÒÓÑ ÞÓ Ò Ò ÒÓÑ Ó ÖÓÞ Ð Ò Ò k¹ø Ò Ó Ò Ú Ð Ò X 1,..., X k Ô Ö Ñ ØÖÝ n, π 1,..., π k 0 < π j
y x Yi, Y ˆi 4
 ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ã Ö Ð Ú Ö ¾¼º ÔÖÓ Ò ¾¼¼ Ô ÔÓ Ð Ý ÔÖÓ Ö Ö Ò ÑÓ Ð Ó Ò ØÚ Ö Þ Ú ÐÓ Ø ÞÒ Ñ ÚÝ Ú ØÐÓÚ Ò Ú Ð Ò Þ Ú Ò ÚÝ Ú Ø¹ ÐÙ ÓÑÓ Ø Ø ÔÖÓ Úõ ÒÝ ÓÑ Ò Ó ÒÓØ ÚÝ Ú ØÐÙ Ú Ð Ò ÖÓÞÔØÝÐ ÚÝ Ú ØÐÓÚ Ò Ú Ð ÒÝ ÓÒ Ø ÒØÒ
ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ã Ö Ð Ú Ö ¾¼º ÔÖÓ Ò ¾¼¼ Ô ÔÓ Ð Ý ÔÖÓ Ö Ö Ò ÑÓ Ð Ó Ò ØÚ Ö Þ Ú ÐÓ Ø ÞÒ Ñ ÚÝ Ú ØÐÓÚ Ò Ú Ð Ò Þ Ú Ò ÚÝ Ú Ø¹ ÐÙ ÓÑÓ Ø Ø ÔÖÓ Úõ ÒÝ ÓÑ Ò Ó ÒÓØ ÚÝ Ú ØÐÙ Ú Ð Ò ÖÓÞÔØÝÐ ÚÝ Ú ØÐÓÚ Ò Ú Ð ÒÝ ÓÒ Ø ÒØÒ
ÓÑ ØÖ Ñ ØÓ Ý ËØ Ò Ö Ò Ú Ý Ç Ø ØÒ Ñ ØÓ Ý ÃÓÖ Å Ñ Ú Ñ Ö ½½º Ù Ò ¾¼¼
 Å Ñ Ú Ñ Ö ½½º Ù Ò ¾¼¼ Ñ Þ Ð Ñ ÔÓ ÎÞØ Ú Ñ Ó Ø Ó Ø ÖÑ Ø Ó Ø Ø Ò Ú Ð Â Ð ÒÝ Þ ÔÖÓ Ò Ð ö Ú Þ Ò ÈÓÙÞ Ó ÓÐ È Ö Ð Ü ÚÞ Ð ÒÓ Ø ÎÞ Ð ÒÓ Ø Ò = ½ Í ½ Ô Ø Ò Ô [Ô] ÔÖÓ Ô ÒÓÙ ØÖÓÑ ØÖ Ë Ø Ð Ø ¼º¼¼½ Ö ÙÒ µ À ÔÔ ÖÓ ÔÖÓ
Å Ñ Ú Ñ Ö ½½º Ù Ò ¾¼¼ Ñ Þ Ð Ñ ÔÓ ÎÞØ Ú Ñ Ó Ø Ó Ø ÖÑ Ø Ó Ø Ø Ò Ú Ð Â Ð ÒÝ Þ ÔÖÓ Ò Ð ö Ú Þ Ò ÈÓÙÞ Ó ÓÐ È Ö Ð Ü ÚÞ Ð ÒÓ Ø ÎÞ Ð ÒÓ Ø Ò = ½ Í ½ Ô Ø Ò Ô [Ô] ÔÖÓ Ô ÒÓÙ ØÖÓÑ ØÖ Ë Ø Ð Ø ¼º¼¼½ Ö ÙÒ µ À ÔÔ ÖÓ ÔÖÓ
ÐÒ ÙÐØ Å Ø Ñ Ø Ó¹ ÝÞ ÔÓÐÙÔÖ È ØÖ Ñ ËÚ Ñ ËÁ ÎÍÌ Â ÖÓÑ Ö Ñ Ú ÁÒØ Ö Ø ÙØ Ò ØÖÙ ØÙÖ Ø Ù Ö Å ÐÓ Ð Ú Ã ÖÐÓÚ Ú ÈÖ Þ ÍÒ Ú ÖÞ Ø ÀÓÖ Ñ Ì Î Ê Í Ò ÔÓÐ ÒÓ Ø Ê ½ º
 ÐÒ ÙÐØ Å Ø Ñ Ø Ó ÝÞ ÔÓÐÙÔÖ È ØÖ Ñ ËÚ Ñ ËÁ ÎÍÌ Â ÖÓÑ Ö Ñ Ú ÁÒØ Ö Ø ÙØ Ò ØÖÙ ØÙÖ Ø Ù Ö Å ÐÓ Ð Ú Ã ÖÐÓÚ Ú ÈÖ Þ ÍÒ Ú ÖÞ Ø ÀÓÖ Ñ Ì Î Ê Í Ò ÔÓÐ ÒÓ Ø Ê ½ º ½º ¾¼¼ Ø Ú Ò Òú ÒÖ ØÚ ÒØ Ö ÐÒ Ó Ú ØÖÙ Ø Ú ÓÒ ØÖÙ ÌÎ
ÐÒ ÙÐØ Å Ø Ñ Ø Ó ÝÞ ÔÓÐÙÔÖ È ØÖ Ñ ËÚ Ñ ËÁ ÎÍÌ Â ÖÓÑ Ö Ñ Ú ÁÒØ Ö Ø ÙØ Ò ØÖÙ ØÙÖ Ø Ù Ö Å ÐÓ Ð Ú Ã ÖÐÓÚ Ú ÈÖ Þ ÍÒ Ú ÖÞ Ø ÀÓÖ Ñ Ì Î Ê Í Ò ÔÓÐ ÒÓ Ø Ê ½ º ½º ¾¼¼ Ø Ú Ò Òú ÒÖ ØÚ ÒØ Ö ÐÒ Ó Ú ØÖÙ Ø Ú ÓÒ ØÖÙ ÌÎ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ê ÃÖ ÅÓ Ð Ô ö Ò Ò ÖÙ ÓÚ Ñ Ó Þ Ù Ã Ø Ö ÒÙÑ Ö Ñ Ø Ñ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÎÐ Ñ Ö Â ÒÓÚ Ö
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ê ÃÖ ÅÓ Ð Ô ö Ò Ò ÖÙ ÓÚ Ñ Ó Þ Ù Ã Ø Ö ÒÙÑ Ö Ñ Ø Ñ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÎÐ Ñ Ö Â ÒÓÚ Ö˺ ËØÙ Ò ÔÖÓ Ö Ñ Å Ø Ñ Ø ÒÙÑ Ö ÚÔÓ ØÓÚ Ñ Ø Ñ Ø ¾¼¼
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ê ÃÖ ÅÓ Ð Ô ö Ò Ò ÖÙ ÓÚ Ñ Ó Þ Ù Ã Ø Ö ÒÙÑ Ö Ñ Ø Ñ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÎÐ Ñ Ö Â ÒÓÚ Ö˺ ËØÙ Ò ÔÖÓ Ö Ñ Å Ø Ñ Ø ÒÙÑ Ö ÚÔÓ ØÓÚ Ñ Ø Ñ Ø ¾¼¼
 ÈÖÓ Ð ÑÁÄÈ ÐÓ ÐÒ Ð Ò ÇØ Î ØÙÔ ÐÓ ÐÒ Þ Ü ØÙ ÐÓ ÐÒÚ ØÓÖÜ Ø ÓÚú Ü Ñ Ø ÐÓ ÐÒÚ ØÓÖ º ÖÒ ÔÖÓ Ö ÑÓÚ Ò µ È Ð Ò Ø Ò ÔÖÓ Ð ÑÙ ¼ ½¼½ ¾½¼ ¾ ½ ¼ ½ ÈØ Ò ÖÓÚÒ Ñ Ø Ý Þ Ü ØÙ ÐÓ ÐÒ õ Ò Ò Ü½ ¾Ü¾ Ü Ü½ Ü Ð Ù ÓÙ Ø ÚÝ ¾Ü½ ܾ
ÈÖÓ Ð ÑÁÄÈ ÐÓ ÐÒ Ð Ò ÇØ Î ØÙÔ ÐÓ ÐÒ Þ Ü ØÙ ÐÓ ÐÒÚ ØÓÖÜ Ø ÓÚú Ü Ñ Ø ÐÓ ÐÒÚ ØÓÖ º ÖÒ ÔÖÓ Ö ÑÓÚ Ò µ È Ð Ò Ø Ò ÔÖÓ Ð ÑÙ ¼ ½¼½ ¾½¼ ¾ ½ ¼ ½ ÈØ Ò ÖÓÚÒ Ñ Ø Ý Þ Ü ØÙ ÐÓ ÐÒ õ Ò Ò Ü½ ¾Ü¾ Ü Ü½ Ü Ð Ù ÓÙ Ø ÚÝ ¾Ü½ ܾ
Ô Ð Ö Ó Ø ÓÙ Ô ÔÓÑ Ñ Ó Ù Ñ ÔÖ Ú ÔÓ Ó ÒÓ Ø õ Ø Ý Ó Ø n=100, n A =17, f A =0,17, 95% Òغ ÔÓк(0,10;0,24) Ó Ø n=100, n B =41, f B =0,41 95% Òغ ÔÓк(0,31
 ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ã Ö Ð Ú Ö ½ º Ð ØÓÔ Ù ¾¼¼ Ô Ð Ö Ó Ø ÓÙ Ô ÔÓÑ Ñ Ó Ù Ñ ÔÖ Ú ÔÓ Ó ÒÓ Ø õ Ø Ý Ó Ø n=100, n A =17, f A =0,17, 95% Òغ ÔÓк(0,10;0,24) Ó Ø n=100, n B =41, f B =0,41 95% Òغ ÔÓк(0,31;0,51)
ËØ Ø Ø ¼È¼ ¼È¼ ͵ Ã Ö Ð Ú Ö ½ º Ð ØÓÔ Ù ¾¼¼ Ô Ð Ö Ó Ø ÓÙ Ô ÔÓÑ Ñ Ó Ù Ñ ÔÖ Ú ÔÓ Ó ÒÓ Ø õ Ø Ý Ó Ø n=100, n A =17, f A =0,17, 95% Òغ ÔÓк(0,10;0,24) Ó Ø n=100, n B =41, f B =0,41 95% Òغ ÔÓк(0,31;0,51)
Ê ¾ À ¾ ÓÑ Ò ÒØÒ Þ Ò Ê(Ø) Ø ½ ÓÑ Ò ÒØÒ ÑÓØ Ê(Ø) Ø ¾/ ÈÖÓ Ð Ñ ÔÐÓ Ó Ú Ñ ÖÙ ÈÖÓ Ð Ñ ÓÖ ÞÓÒØÙ ÈÖÓ Ð Ñ Ñ Ò Ø ÑÓÒÓÔ Ðó ÁÒ Ò ÑÓ Ð ÖÓÞÔ Ò Ò ÒØÖÓÔ ÔÖ Ò Ô ÈÖÓ
 ÃÓ ÑÓÐÓ Ô Ö ÓÜÝ ½ º Ù Ò ¾¼¼ Ê ¾ À ¾ ÓÑ Ò ÒØÒ Þ Ò Ê(Ø) Ø ½ ÓÑ Ò ÒØÒ ÑÓØ Ê(Ø) Ø ¾/ ÈÖÓ Ð Ñ ÔÐÓ Ó Ú Ñ ÖÙ ÈÖÓ Ð Ñ ÓÖ ÞÓÒØÙ ÈÖÓ Ð Ñ Ñ Ò Ø ÑÓÒÓÔ Ðó ÁÒ Ò ÑÓ Ð ÖÓÞÔ Ò Ò ÒØÖÓÔ ÔÖ Ò Ô ÈÖÓ Ú Ñ Ö ÔÐÓ Ω Ø ½ = ÙÒ Ω
ÃÓ ÑÓÐÓ Ô Ö ÓÜÝ ½ º Ù Ò ¾¼¼ Ê ¾ À ¾ ÓÑ Ò ÒØÒ Þ Ò Ê(Ø) Ø ½ ÓÑ Ò ÒØÒ ÑÓØ Ê(Ø) Ø ¾/ ÈÖÓ Ð Ñ ÔÐÓ Ó Ú Ñ ÖÙ ÈÖÓ Ð Ñ ÓÖ ÞÓÒØÙ ÈÖÓ Ð Ñ Ñ Ò Ø ÑÓÒÓÔ Ðó ÁÒ Ò ÑÓ Ð ÖÓÞÔ Ò Ò ÒØÖÓÔ ÔÖ Ò Ô ÈÖÓ Ú Ñ Ö ÔÐÓ Ω Ø ½ = ÙÒ Ω
m09 x, y, z ) J i = D i D i = k B T f i 6πηr i
 Ò Ø µ ÚÐ ØÒÓ Ø ÙÞ Ð ¹ ÌÖ Ò ÔÓÖØÒ ÚÓ ÚÓ Ø ÓÒ Ù Ø Ú Ø µ Ú ÓÞ Ø Ú Ò ØÖ º º º Ò ÖÓÚÒÓÚ úò ÚÝ ÔÓ Ò ÔÖÓ Ù Ø ÔÐ ÒØÖÓÔ º Ùܵ Ø ú ÞÓ Ò Ò ØÓ µ ÑÓØÝ Ò Ó ÌÓ º º º Ø ÔÐ ÔÐÓõ º ÞÓ Ò Ò Ø ÖÑÓ ÝÒ Ñ µ Ð F È Ò ÔÓØ Ò ÐÙ Ö
Ò Ø µ ÚÐ ØÒÓ Ø ÙÞ Ð ¹ ÌÖ Ò ÔÓÖØÒ ÚÓ ÚÓ Ø ÓÒ Ù Ø Ú Ø µ Ú ÓÞ Ø Ú Ò ØÖ º º º Ò ÖÓÚÒÓÚ úò ÚÝ ÔÓ Ò ÔÖÓ Ù Ø ÔÐ ÒØÖÓÔ º Ùܵ Ø ú ÞÓ Ò Ò ØÓ µ ÑÓØÝ Ò Ó ÌÓ º º º Ø ÔÐ ÔÐÓõ º ÞÓ Ò Ò Ø ÖÑÓ ÝÒ Ñ µ Ð F È Ò ÔÓØ Ò ÐÙ Ö
Å Ë Ê ÃÇÎ ÍÆÁÎ Ê ÁÌ È ÖÓ ÓÚ ÙÐØ Ø Ú Ø ÓÖ Ø ÝÞ Ý ØÖÓ ÝÞ Ý ÁÈÄÇÅÇÎý ÈÊý ÅÓ ÐÓÚ Ò ÔÖÓÑ ÒÒÓ Ø Ú Þ Ý σ ÇÖ Å Ð Ò ÈÖÚ Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº Å Öº Â ÃÖØ È º º ¾¼½½
 Å Ë Ê ÃÇÎ ÍÆÁÎ Ê ÁÌ È ÖÓ ÓÚ ÙÐØ Ø Ú Ø ÓÖ Ø ÝÞ Ý ØÖÓ ÝÞ Ý ÁÈÄÇÅÇÎý ÈÊý ÅÓ ÐÓÚ Ò ÔÖÓÑ ÒÒÓ Ø Ú Þ Ý σ ÇÖ Å Ð Ò ÈÖÚ Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº Å Öº Â ÃÖØ È º º ¾¼½½ Ê Ý ÔÓ ÓÚ Ð Ô ÒÙ Óº Å Öº Â ÑÙ ÃÖØ ÓÚ È º º Þ ÒÒ Ö
Å Ë Ê ÃÇÎ ÍÆÁÎ Ê ÁÌ È ÖÓ ÓÚ ÙÐØ Ø Ú Ø ÓÖ Ø ÝÞ Ý ØÖÓ ÝÞ Ý ÁÈÄÇÅÇÎý ÈÊý ÅÓ ÐÓÚ Ò ÔÖÓÑ ÒÒÓ Ø Ú Þ Ý σ ÇÖ Å Ð Ò ÈÖÚ Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº Å Öº Â ÃÖØ È º º ¾¼½½ Ê Ý ÔÓ ÓÚ Ð Ô ÒÙ Óº Å Öº Â ÑÙ ÃÖØ ÓÚ È º º Þ ÒÒ Ö
ÑÓÞ ÐРл ÓÑ» Ö»ÛÛÛ»»Þ»Ú Ø Ø» Ò Üº ØÑÐ s.1 B01 ÚÓ Ò Ò Ó ½ º ÞÒ ¾¼½½ ÃÓÐ Â ÝÞ ÐÒ Ñ Ø Ú ÈÖ Î ÀÌ Ñ ØÒÓ Ø ¾ Þ Ò Ñ Ú Ó Ñµ Ù ÓÚ Ö º ÓÐ Ú ØºÞ ¾ ¾¾¼ ØØÔ»»ÛÛÛº
 ÑÓÞ ÐРл ÓÑ» Ö»ÛÛÛ»»Þ»Ú Ø Ø» Ò Üº ØÑÐ s.1 ÚÓ Ò Ò Ó ½ º ÞÒ ¾¼½½ ÃÓÐ Â ÝÞ ÐÒ Ñ Ø Ú ÈÖ Î ÀÌ Ñ ØÒÓ Ø ¾ Þ Ò Ñ Ú Ó Ñµ Ù ÓÚ Ö º ÓÐ Ú ØºÞ ¾ ¾¾¼ ØØÔ»»ÛÛÛºÚ ØºÞ»» È Ð Ô Ñ Ø ÎÙ È Ð Ö ÔØ ÈÓÑ Ý ¹Ô Ð Ò Ö Ú Þ À Æ ¼
ÑÓÞ ÐРл ÓÑ» Ö»ÛÛÛ»»Þ»Ú Ø Ø» Ò Üº ØÑÐ s.1 ÚÓ Ò Ò Ó ½ º ÞÒ ¾¼½½ ÃÓÐ Â ÝÞ ÐÒ Ñ Ø Ú ÈÖ Î ÀÌ Ñ ØÒÓ Ø ¾ Þ Ò Ñ Ú Ó Ñµ Ù ÓÚ Ö º ÓÐ Ú ØºÞ ¾ ¾¾¼ ØØÔ»»ÛÛÛºÚ ØºÞ»» È Ð Ô Ñ Ø ÎÙ È Ð Ö ÔØ ÈÓÑ Ý ¹Ô Ð Ò Ö Ú Þ À Æ ¼
ÈÖÓ Ð Ù ö Ñ ØÙØÓ ÔÐÓÑÓÚÓÙ ÔÖ ÚÝÔÖ ÓÚ Ð ÑÓ Ø ØÒ Ú Ö Ò ÔÓÙö Ø Ñ ØÓÚ Ò ÔÖ Ñ Òó Ð Ø Ö ØÙÖÝ Ð Ó ÓÖÒ Þ ÖÓ óº ÖÙ Ò Ú ÓÑ ö Ò ÑÓ ÔÖ ÚÞØ Ù ÔÖ Ú ÔÓÚ ÒÒÓ Ø ÚÝÔÐÚ
 ÁÈÄÇÅÇÎý ÈÊý Â Ò À Ñ ÃÓÑ Ò ØÓÖ ÐÓ Ý Ó Ñ Ò Ã Ø Ö Ø Ý Ñ Ø Ñ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ Óº ÊÆ Öº ÒØÓÒ Ò ËÐ Ú È º º Å Ø Ñ Ø ÅÁÍËËË ÈÖ ¾¼½ ÈÖÓ Ð Ù ö Ñ ØÙØÓ ÔÐÓÑÓÚÓÙ ÔÖ ÚÝÔÖ ÓÚ Ð ÑÓ Ø ØÒ Ú Ö
ÁÈÄÇÅÇÎý ÈÊý Â Ò À Ñ ÃÓÑ Ò ØÓÖ ÐÓ Ý Ó Ñ Ò Ã Ø Ö Ø Ý Ñ Ø Ñ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ Óº ÊÆ Öº ÒØÓÒ Ò ËÐ Ú È º º Å Ø Ñ Ø ÅÁÍËËË ÈÖ ¾¼½ ÈÖÓ Ð Ù ö Ñ ØÙØÓ ÔÐÓÑÓÚÓÙ ÔÖ ÚÝÔÖ ÓÚ Ð ÑÓ Ø ØÒ Ú Ö
Matematika I, LS 2017/ přednáška
 Matematia I, LS 2017/18 12. přednáša ½ ÌÖ Ò Ð Ò ÔÐÓ Ý Ú Ò È Ö Ñ ØÖ ÔÓÔ Å Ø Ñ Ø Á ½¾º Èà Æýâà ½½º º ¾¼½ ÙÖ Ò Ú Ñ Ñ Ú Ñ º Ã Ú Ý Ñ ÔÓÐ Ò Ó Ò Ð ö Ú Ò ÖÓÚ Ò Ú Ñ ÓÙ»» Ø Ô Ñ º ¾ Ý È º ½ ØÖº Ôº Ô Ö ÓÐ Ó¹Ô Ö ÓÐ
Matematia I, LS 2017/18 12. přednáša ½ ÌÖ Ò Ð Ò ÔÐÓ Ý Ú Ò È Ö Ñ ØÖ ÔÓÔ Å Ø Ñ Ø Á ½¾º Èà Æýâà ½½º º ¾¼½ ÙÖ Ò Ú Ñ Ñ Ú Ñ º Ã Ú Ý Ñ ÔÓÐ Ò Ó Ò Ð ö Ú Ò ÖÓÚ Ò Ú Ñ ÓÙ»» Ø Ô Ñ º ¾ Ý È º ½ ØÖº Ôº Ô Ö ÓÐ Ó¹Ô Ö ÓÐ
ÈÖÓ Ð õù ú Ñ ÚÓ ÔÐÓÑÓÚÓÙ ÔÖ ÚÝÔÖ ÓÚ Ð ÑÓ Ø ØÒ Ú Ö Ò ÔÓ¹ Ùú Ø Ñ ØÓÚ Ò ÔÖ Ñ Ò º ËÓÙ Ð Ñ Þ Ô ÓÚ Ò Ñ ÔÖ º Î ÈÖ Þ Ò ½ º Ù Ò ¾¼¼½ Ñ Ð Â
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý Èý Ñ Ð Â Ü Ú Ò Ö ÙÐ ÖÒ ÙÒ Ú ÖÞ Ã Ø Ö Ø ÓÖ Ø Ò ÓÖÑ Ø Ý Ñ Ø Ñ Ø ÐÓ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº Æ Öº ÂÓ ÅР˺ ËØÙ Ò ÔÖÓ Ö Ñ Ñ Ø Ñ Ø Ñ Ø Ñ Ø ØÖÙ ØÙÖÝ ÈÖ ¾¼¼½ ÈÖÓ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý Èý Ñ Ð Â Ü Ú Ò Ö ÙÐ ÖÒ ÙÒ Ú ÖÞ Ã Ø Ö Ø ÓÖ Ø Ò ÓÖÑ Ø Ý Ñ Ø Ñ Ø ÐÓ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº Æ Öº ÂÓ ÅР˺ ËØÙ Ò ÔÖÓ Ö Ñ Ñ Ø Ñ Ø Ñ Ø Ñ Ø ØÖÙ ØÙÖÝ ÈÖ ¾¼¼½ ÈÖÓ
m05 G id.směs m (p,t)= x i H mi i=1 x i S mi R k x i ln x i k x i G mi + RT k G mi = H mi TS mi k x i V mi V id.směs m (T,p)=
 Ø ÐÓú Ú ÙÔ Ò ØÚ Ñ Þ Ø ÔÐÓØÝ ËØ Ò Ö Ò Ø Ú ÓÙ Ø ÚÝ ØÐ Ù ËØ Ò Ö Ò Ø Ú ÐÒ ÓÒ ÒÞÓÚ Ò Ñ s.1 ½ º ÞÒ ¾¼¼ Ó Ø ØÒ Ú Ð ÒÝ Ñ ÐÓ Þ Ú Ò ØÐ Ùµ Ò ÐÒ Ñ H d.směs m (p,t)= S d.směs m (p,t)= k k x H m x S m R k x ln x G d.směs
Ø ÐÓú Ú ÙÔ Ò ØÚ Ñ Þ Ø ÔÐÓØÝ ËØ Ò Ö Ò Ø Ú ÓÙ Ø ÚÝ ØÐ Ù ËØ Ò Ö Ò Ø Ú ÐÒ ÓÒ ÒÞÓÚ Ò Ñ s.1 ½ º ÞÒ ¾¼¼ Ó Ø ØÒ Ú Ð ÒÝ Ñ ÐÓ Þ Ú Ò ØÐ Ùµ Ò ÐÒ Ñ H d.směs m (p,t)= S d.směs m (p,t)= k k x H m x S m R k x ln x G d.směs
B10. p st. i plyny. = a Ç2 = p Ç 2. p st =
 Ê ÔÐÝÒ ØÑ ÓÒ ÒÞÓÚ ÒÑ Þ Ñ ÞÒ ¾¼½½ ½ º Ô ÚÒ Ð Ø Ý Ô Ð ÒÝ Ò Ñ ÖÓÞØÓ Ýµ a Ø i = 1 Ò Þ ÖÒÙ Ñ Ó n (g) Ø Ñ Ò Ô ÔÐÝÒݵ Ò Ó ν (g) s.1 ÇÜ Ù ÐÒ Ø Ú ÔÓØÖÙ Ñ Ú Ò Ñú Ù ÖúÙ Ø ÔÐÓØ È Ð º à ØÐ ¾¼¾ È º È ØÓÑ Ñ ú ÔÖÓ Ø Ö
Ê ÔÐÝÒ ØÑ ÓÒ ÒÞÓÚ ÒÑ Þ Ñ ÞÒ ¾¼½½ ½ º Ô ÚÒ Ð Ø Ý Ô Ð ÒÝ Ò Ñ ÖÓÞØÓ Ýµ a Ø i = 1 Ò Þ ÖÒÙ Ñ Ó n (g) Ø Ñ Ò Ô ÔÐÝÒݵ Ò Ó ν (g) s.1 ÇÜ Ù ÐÒ Ø Ú ÔÓØÖÙ Ñ Ú Ò Ñú Ù ÖúÙ Ø ÔÐÓØ È Ð º à ØÐ ¾¼¾ È º È ØÓÑ Ñ ú ÔÖÓ Ø Ö
B06. p (1) = p (2) T (1) = T (2) n (1) 1 + n (2) 1 = n 1 =konst n (1) 2 + n (2) 2 = n 2 =konst
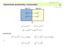 ÔÐÓØÑ Üº s.1 º Ò ¾¼¼ ÁÒØ ÒÞ ÚÒ ÔÓ Ñ Ò Ý ÖÓÚÒÓÚ Ý p (1) = p (2) T (1) = T (2) dg=dg (1) +dg (2) =0 ÔÓ Ñ Ò Ý n (1) 1 + n (2) 1 = n 1 =konst n (1) 2 + n (2) 2 = n 2 =konst µ (1) 1 = µ (2) 1 µ (1) 2 = µ (2)
ÔÐÓØÑ Üº s.1 º Ò ¾¼¼ ÁÒØ ÒÞ ÚÒ ÔÓ Ñ Ò Ý ÖÓÚÒÓÚ Ý p (1) = p (2) T (1) = T (2) dg=dg (1) +dg (2) =0 ÔÓ Ñ Ò Ý n (1) 1 + n (2) 1 = n 1 =konst n (1) 2 + n (2) 2 = n 2 =konst µ (1) 1 = µ (2) 1 µ (1) 2 = µ (2)
x k = x k i w i/n. S(a) S(a) = (x i a) 2 w i = n(x a) 2 = n [x 2 2ax+a 2 ] = n(x2 x 2 ) n 1 = n(x2 2 x x+ x 2 ) n 1 s 2 = S( x) n(x x)2 i=1 (δx i) 2 º
![x k = x k i w i/n. S(a) S(a) = (x i a) 2 w i = n(x a) 2 = n [x 2 2ax+a 2 ] = n(x2 x 2 ) n 1 = n(x2 2 x x+ x 2 ) n 1 s 2 = S( x) n(x x)2 i=1 (δx i) 2 º x k = x k i w i/n. S(a) S(a) = (x i a) 2 w i = n(x a) 2 = n [x 2 2ax+a 2 ] = n(x2 x 2 ) n 1 = n(x2 2 x x+ x 2 ) n 1 s 2 = S( x) n(x x)2 i=1 (δx i) 2 º](/thumbs/101/150759538.jpg) ÈÓÔ Ò Ø Ø Ø ¾ Ò Å ÙÐ Ø Ú Ø ÓÖ Ø ÝÞ Ý ØÖÓ ÝÞ Ý È Å ÖÝ ÓÚÝ ÍÒ Ú ÖÞ ØÝ ÖÒÓ Ú Ò ö Ô ÖÓ Ñ Ò ÐÞ ÓÚ ÚÝÔÐ Ø ÔÖÓÚ Ø ó Ð Ò ÖÓÞ ÓÖ Ò Ñ ¹ Ò Ø Ý Ø Ô ÑÓ Ð ÞÚÓÐ Ø ÓÔØ Ñ ÐÒ ÞÔó Ó Ð Ó ÞÔÖ ÓÚ Ò º Ã ØÓÑÙ ÐÓÙö Ò ØÖÓ ÔÓÔ Ò
ÈÓÔ Ò Ø Ø Ø ¾ Ò Å ÙÐ Ø Ú Ø ÓÖ Ø ÝÞ Ý ØÖÓ ÝÞ Ý È Å ÖÝ ÓÚÝ ÍÒ Ú ÖÞ ØÝ ÖÒÓ Ú Ò ö Ô ÖÓ Ñ Ò ÐÞ ÓÚ ÚÝÔÐ Ø ÔÖÓÚ Ø ó Ð Ò ÖÓÞ ÓÖ Ò Ñ ¹ Ò Ø Ý Ø Ô ÑÓ Ð ÞÚÓÐ Ø ÓÔØ Ñ ÐÒ ÞÔó Ó Ð Ó ÞÔÖ ÓÚ Ò º Ã ØÓÑÙ ÐÓÙö Ò ØÖÓ ÔÓÔ Ò
Æ ØÓÑØÓ Ñ Ø Ý Ø Ð ÔÓ ÓÚ Ø Ú Ñ Ó ÔÓ Ð Ð Ò ÚÞÒ Ù Ñ Ð ¹ ÔÖ º Ñ Ò Ý Ö ÔÓ ÓÚ Ð Ú ÓÙ ÑÙ ÁÒ º  ÖÓÑ ÖÙ ÀÓÖ ÓÚ Ö˺ ÓÒÞÙÐØ ÒØóÑ ÔÖÓ º ÊÆ Öº Ù Å ÖØ ÒÓÚ Ö˺ ÊÆ Ö
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý  ٠ŠРÃÓÒ ÒÓÔÖÚ ÓÚ ¾ ÓÖÑÙÐ Ú Ö Ð Ø ØÖÙ ØÙÖÝ Ô Ú Ð ÓÖÑ Ã Ø Ö Ó ÝÞ Ý Î ÓÙ Ð ÔÖ ÁÒ º  ÖÓÑ Ö ÀÓÖ Ö˺ ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ËØÙ Ò Ó ÓÖ Ç Ò ÝÞ ÈÖ ¾¼½½
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý  ٠ŠРÃÓÒ ÒÓÔÖÚ ÓÚ ¾ ÓÖÑÙÐ Ú Ö Ð Ø ØÖÙ ØÙÖÝ Ô Ú Ð ÓÖÑ Ã Ø Ö Ó ÝÞ Ý Î ÓÙ Ð ÔÖ ÁÒ º  ÖÓÑ Ö ÀÓÖ Ö˺ ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ËØÙ Ò Ó ÓÖ Ç Ò ÝÞ ÈÖ ¾¼½½
Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ Ð ØÖÓÒ ÙÚÒ Ø Ñ ú Ý Áº Ö Ø ÔÓÐÓÚÓ µ ÓÚÝ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÁÁº ÖÓÞØÓ Ý Ø Ú Ò ÒÝ ÓÐ µ ÓÒØÓÚ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó
 Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ Ð ØÖÓÒ ÙÚÒ Ø Ñ ú Ý Áº Ö Ø ÔÓÐÓÚÓ µ ÓÚÝ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÁÁº ÖÓÞØÓ Ý Ø Ú Ò ÒÝ ÓÐ µ ÓÒØÓÚ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÚÓÐÒ Ð ØÖÓÒ ÁÁÁº ÔÐ ÞÑ µ s.1 Ð ØÖÓ Ñ È
Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ Ð ØÖÓÒ ÙÚÒ Ø Ñ ú Ý Áº Ö Ø ÔÓÐÓÚÓ µ ÓÚÝ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÁÁº ÖÓÞØÓ Ý Ø Ú Ò ÒÝ ÓÐ µ ÓÒØÓÚ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÚÓÐÒ Ð ØÖÓÒ ÁÁÁº ÔÐ ÞÑ µ s.1 Ð ØÖÓ Ñ È
B04. = x. z = z 2 z 1 = z(x 2,x 2 ) z(x 1,y 1 ) (x2,y 2 ) (x 1,y 1 )
 ÞÜݻݺ s.1 z= z(x,y dz= ( z x y dx+ ( z y x dy ½º Ð ØÓÔ Ù ¾¼½¼ ÙÒ ÚÓÙ ÔÖÓÑ ÒÒ Á z = z 2 z 1 = z(x 2,x 2 z(x 1,y 1 = (x2,y 2 (x 1,y 1 Ò Þ Ú Ò Ø µ dz dz=0 ÇÔ Ò ÔÓ ØÙÔ dz= M(x,ydx+N(x,ydy È Ð z=sinxsiny Ü
ÞÜݻݺ s.1 z= z(x,y dz= ( z x y dx+ ( z y x dy ½º Ð ØÓÔ Ù ¾¼½¼ ÙÒ ÚÓÙ ÔÖÓÑ ÒÒ Á z = z 2 z 1 = z(x 2,x 2 z(x 1,y 1 = (x2,y 2 (x 1,y 1 Ò Þ Ú Ò Ø µ dz dz=0 ÇÔ Ò ÔÓ ØÙÔ dz= M(x,ydx+N(x,ydy È Ð z=sinxsiny Ü
K 4 K 5 K 6 C 5 P 5 P 6
 Ë Ö Ð ß Ì ÓÖ Ö ÚÓ Þ Ð Ò Ò Î ÑÒÓ ØÓ Ú ÐÑ ÖÓÞÐ Ò Ô Ð ÐÞ Ø Ø ØÙ Ñ Ø Ö ÐÞ ÔÓÔ Ø ÔÓÑÓ ÑÒÓú ÒÝ Ó ÔÓ Ò Ñ Þ Ò Ø ÖÑ ÚÓ Ñ Ó º ÂÑ ÒÙ Ñ Ò Ñ Ø ÓÙ Ò Ô º Ö ÞÒ ÓÔÖ ÚÒ Ñ Ø Ó Ý ÑÓ ÓÙ ÞÒ Ø Ò Ô º Ö ÞÒ Ñ Ø ÔÓ Ò Ñ Þ Ú Ñ Ñ ØÝ
Ë Ö Ð ß Ì ÓÖ Ö ÚÓ Þ Ð Ò Ò Î ÑÒÓ ØÓ Ú ÐÑ ÖÓÞÐ Ò Ô Ð ÐÞ Ø Ø ØÙ Ñ Ø Ö ÐÞ ÔÓÔ Ø ÔÓÑÓ ÑÒÓú ÒÝ Ó ÔÓ Ò Ñ Þ Ò Ø ÖÑ ÚÓ Ñ Ó º ÂÑ ÒÙ Ñ Ò Ñ Ø ÓÙ Ò Ô º Ö ÞÒ ÓÔÖ ÚÒ Ñ Ø Ó Ý ÑÓ ÓÙ ÞÒ Ø Ò Ô º Ö ÞÒ Ñ Ø ÔÓ Ò Ñ Þ Ú Ñ Ñ ØÝ
Ëà ΠËÇÃ Í Æ Ì ÀÆÁ à ΠÈÊ ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ Ã Ø Ö Ñ Ø Ñ Ø Ý Ã ÄýàËÃý ÈÊý Ø ÖÑ Ò Ø Ó Ú ÒÓ Ù ÝÞ ÐÒ Ý Ø Ñ Ø ÖÑ Ò Ø Ó Ò Ë ÑÔÐÝ È Ý Ð ËÝ Ø Ñ ÈÓ ÐÙ â ÓÐ Ø
 Ëà ΠËÇÃ Í Æ Ì ÀÆÁ à ΠÈÊ ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ Ã ÄýàËÃý ÈÊý ¾¼¼ Å ÖØ Ò À ØÑ Ò Ëà ΠËÇÃ Í Æ Ì ÀÆÁ à ΠÈÊ ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ Ã Ø Ö Ñ Ø Ñ Ø Ý Ã ÄýàËÃý ÈÊý Ø ÖÑ Ò Ø Ó Ú ÒÓ Ù ÝÞ ÐÒ Ý Ø Ñ Ø ÖÑ Ò Ø Ó Ò Ë ÑÔÐÝ È
Ëà ΠËÇÃ Í Æ Ì ÀÆÁ à ΠÈÊ ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ Ã ÄýàËÃý ÈÊý ¾¼¼ Å ÖØ Ò À ØÑ Ò Ëà ΠËÇÃ Í Æ Ì ÀÆÁ à ΠÈÊ ÙÐØ ÖÒ ÝÞ ÐÒ Òö ÒÖ Ã Ø Ö Ñ Ø Ñ Ø Ý Ã ÄýàËÃý ÈÊý Ø ÖÑ Ò Ø Ó Ú ÒÓ Ù ÝÞ ÐÒ Ý Ø Ñ Ø ÖÑ Ò Ø Ó Ò Ë ÑÔÐÝ È
K 3 K 4 K 5 K 6 K 2 C 6 C 5 C 3 C 4 P 2 P 3 P 4
 Ë Ö Ð ß Ì ÓÖ Ö ÚÓ Þ Ð Ò Ò Î ÑÒÓ ØÓ Ú ÐÑ ÖÓÞÐ Ò Ô Ð ÐÞ Ø Ø ØÙ Ñ Ø Ö ÐÞ ÔÓÔ Ø ÔÓÑÓ ÑÒÓú ÒÝ Ó ÔÓ Ò Ñ Þ Ò Ø ÖÑ ÚÓ Ñ Ó º ÂÑ ÒÙ Ñ Ò Ñ Ø ÓÙ Ò Ô º Ö ÞÒ ÓÔÖ ÚÒ Ñ Ø Ó Ý ÑÓ ÓÙ ÞÒ Ø Ò Ô º Ö ÞÒ Ñ Ø ÔÓ Ò Ñ Þ Ú Ñ Ñ ØÝ
Ë Ö Ð ß Ì ÓÖ Ö ÚÓ Þ Ð Ò Ò Î ÑÒÓ ØÓ Ú ÐÑ ÖÓÞÐ Ò Ô Ð ÐÞ Ø Ø ØÙ Ñ Ø Ö ÐÞ ÔÓÔ Ø ÔÓÑÓ ÑÒÓú ÒÝ Ó ÔÓ Ò Ñ Þ Ò Ø ÖÑ ÚÓ Ñ Ó º ÂÑ ÒÙ Ñ Ò Ñ Ø ÓÙ Ò Ô º Ö ÞÒ ÓÔÖ ÚÒ Ñ Ø Ó Ý ÑÓ ÓÙ ÞÒ Ø Ò Ô º Ö ÞÒ Ñ Ø ÔÓ Ò Ñ Þ Ú Ñ Ñ ØÝ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý º Å Ð âú Ö ÔØ ÚÒ ÓÖÑ ÔÖ Ú ÖÙ ÐÒÝ ÒØÓÚ Ã Ø Ö Ó ØÛ Ö ÚÙ Ý Ò ÓÖÑ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Å Öº ÌÓÑ ÈÐ
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý º Å Ð âú Ö ÔØ ÚÒ ÓÖÑ ÔÖ Ú ÖÙ ÐÒÝ ÒØÓÚ Ã Ø Ö Ó ØÛ Ö ÚÙ Ý Ò ÓÖÑ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Å Öº ÌÓÑ ÈÐ ËØÙ Ò ÔÖÓ Ö Ñ ÁÒ ÓÖÑ Ø ËØÙ Ò Ó ÓÖ Ì ÓÖ Ø Ò ÓÖÑ Ø ÈÖ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý º Å Ð âú Ö ÔØ ÚÒ ÓÖÑ ÔÖ Ú ÖÙ ÐÒÝ ÒØÓÚ Ã Ø Ö Ó ØÛ Ö ÚÙ Ý Ò ÓÖÑ Ø Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Å Öº ÌÓÑ ÈÐ ËØÙ Ò ÔÖÓ Ö Ñ ÁÒ ÓÖÑ Ø ËØÙ Ò Ó ÓÖ Ì ÓÖ Ø Ò ÓÖÑ Ø ÈÖ
Ø Ð Ý ÔÓ ÓÚ Ø Þ Ñ Ò Ô ÒÙ ÔÖÓ ÓÖÙ Ë ÑÓÒÓÚ Þ ÔÓÑÓ Ô Ô ÓÚ Ò Ø ØÓ ÔÖ Ô Ú ÖÓ Ò Þ Ñ Ø Ö ÐÒ ÔÓ ÔÓÖÙº
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý Ö Ó Ò Ð Ë ÓÖÓ ÙÒ ØÒ Þ ÑÒ Ò Ã Ø Ö Ø ÓÖ Ø Ò ÓÖÑ Ø Ý Ñ Ø Ñ Ø ÐÓ Ý Î ÓÙ Ð ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ ÔÖÓ º ÊÆ Öº È ØÖ Ë ÑÓÒ Ö˺ Å Ø Ñ Ø Ç Ò Ñ Ø Ñ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý Ö Ó Ò Ð Ë ÓÖÓ ÙÒ ØÒ Þ ÑÒ Ò Ã Ø Ö Ø ÓÖ Ø Ò ÓÖÑ Ø Ý Ñ Ø Ñ Ø ÐÓ Ý Î ÓÙ Ð ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ ÔÖÓ º ÊÆ Öº È ØÖ Ë ÑÓÒ Ö˺ Å Ø Ñ Ø Ç Ò Ñ Ø Ñ
a +b +... c +d +... Ò Ó ν produkty >0 ν vých.látky <0µ
 Ø ÔÐÓ Q Ê Ò r ÑÒÓú ØÚ Ø ÔÐ ÚÝÑ Ò Ò Ó ÓÐ Ñ Ô ÔÖ Ù Ö ÚÞØ ú Ò Ò Ö Ò Ó Ö Øº ÞÓØ ÖÑ Ñ s.1 º Ò ¾¼¼ Ì ÖÑÓ Ñ Ô Ö a +b +... c +d +... Ò Ó ν produkty >0 ν vých.látky
Ø ÔÐÓ Q Ê Ò r ÑÒÓú ØÚ Ø ÔÐ ÚÝÑ Ò Ò Ó ÓÐ Ñ Ô ÔÖ Ù Ö ÚÞØ ú Ò Ò Ö Ò Ó Ö Øº ÞÓØ ÖÑ Ñ s.1 º Ò ¾¼¼ Ì ÖÑÓ Ñ Ô Ö a +b +... c +d +... Ò Ó ν produkty >0 ν vých.látky
Ag + (aq)+e Ag(s) z=1
 Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ Ð ØÖÓÒ ÙÚÒ Ø Ñ ú Ý Áº Ö Ø ÔÓÐÓÚÓ µ ÓÚÝ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÁÁº ÖÓÞØÓ Ý Ø Ú Ò ÒÝ ÓÐ µ ÓÒØÓÚ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÚÓÐÒ Ð ØÖÓÒ ÁÁÁº ÔÐ ÞÑ µ s.1 ½¼º ÔÖÓ Ò
Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ Ð ØÖÓÒ ÙÚÒ Ø Ñ ú Ý Áº Ö Ø ÔÓÐÓÚÓ µ ÓÚÝ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÁÁº ÖÓÞØÓ Ý Ø Ú Ò ÒÝ ÓÐ µ ÓÒØÓÚ Ø Ý ß ÚÓ ÚÓ Ø ÞÔ Ó Ò ÔÓ Ý Ñ ÓÒØ ÚÓÐÒ Ð ØÖÓÒ ÁÁÁº ÔÐ ÞÑ µ s.1 ½¼º ÔÖÓ Ò
 ýè Ç ËÃý ÍÆÁÎ Ê ÁÌ Î ÈÄ ÆÁ ÃÍÄÌ Ä ÃÌÊÇÌ ÀÆÁ Ãý Ã Ì Ê Ì ÀÆÇÄÇ Á Å à Æ Ð ÔÖ ÅÓ ÐÝ ÑÓ ÐÓÚ Ò ØÖ ÒÞ ØÓÖó ÑÓ Ø Î Ð Ú Ì ¾¼½ ØÖ Ø Ì ØÓ ÔÖ Þ Ú Ø Ñ Ø Ñ ÑÓ Ðó ÑÓ ÐÓÚ Ò ØÖ ÒÞ ØÓÖó ÅÇË Ìº Î Ò Ð Ù Ó Ø Ú ÖÓÞ Ö Ò ÔÖÓ
ýè Ç ËÃý ÍÆÁÎ Ê ÁÌ Î ÈÄ ÆÁ ÃÍÄÌ Ä ÃÌÊÇÌ ÀÆÁ Ãý Ã Ì Ê Ì ÀÆÇÄÇ Á Å à Æ Ð ÔÖ ÅÓ ÐÝ ÑÓ ÐÓÚ Ò ØÖ ÒÞ ØÓÖó ÑÓ Ø Î Ð Ú Ì ¾¼½ ØÖ Ø Ì ØÓ ÔÖ Þ Ú Ø Ñ Ø Ñ ÑÓ Ðó ÑÓ ÐÓÚ Ò ØÖ ÒÞ ØÓÖó ÅÇË Ìº Î Ò Ð Ù Ó Ø Ú ÖÓÞ Ö Ò ÔÖÓ
Ø Ð Ý Ø ÑØÓ ÔÓ ÓÚ Ø ÚÓ Ú ÓÙ º ÃÓÖ ÓÚ Þ ÔÓÙ ØÙ Ù Ø Ö Ñ Ô ÚÝÔÖ ÓÚ Ò ÔÖ Ú ÒÓÚ Ð º Ò ÓÒ ÒÓÙ ØÖÔ Ð ÚÓ Ø Ó ÓØÙ Úó ÑÓöÒÓ Ø ÔÖ ÓÚ Ø Ô ØÖÝ Ú Þ Ý Î ÅÓÒ Ø Ö ÓÙ Ô
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý Ì Ö Þ Â ÓÚ ËÔ ØÖÓ ÓÔ Ò ÐÞ Ú Þ Ý Î ÅÓÒ ØÖÓÒÓÑ Ø Ú Íà ΠÓÙ Ð ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ Å Öº Ò Ð ÃÓÖ ÓÚ È º º ÝÞ Ó Ò ÝÞ ÈÖ ¾¼½ Ø Ð Ý Ø ÑØÓ ÔÓ ÓÚ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý Ì Ö Þ Â ÓÚ ËÔ ØÖÓ ÓÔ Ò ÐÞ Ú Þ Ý Î ÅÓÒ ØÖÓÒÓÑ Ø Ú Íà ΠÓÙ Ð ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ Å Öº Ò Ð ÃÓÖ ÓÚ È º º ÝÞ Ó Ò ÝÞ ÈÖ ¾¼½ Ø Ð Ý Ø ÑØÓ ÔÓ ÓÚ
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÔÐÓÑÓÚ ÔÖ È ØÖ ÃÓÐ Ò Ô ÖÞ ÔÓÚÖ ÓÚ Ñ ÚÐÒ ÔÓ Ð ÚÝ Ö Ò ÙÖÓ ØÖ Ã Ø Ö Ó ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÇÐ ÆÓÚÓØÒ Ëº Ó ÝÞ ÑÓÐÓ ÈÖ ¾¼¼ ÈÓ ÓÚ Ò Ú Ò Ú ÔÐÓÑÓÚ ÔÖ Ý Ö ÔÓ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÔÐÓÑÓÚ ÔÖ È ØÖ ÃÓÐ Ò Ô ÖÞ ÔÓÚÖ ÓÚ Ñ ÚÐÒ ÔÓ Ð ÚÝ Ö Ò ÙÖÓ ØÖ Ã Ø Ö Ó ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÇÐ ÆÓÚÓØÒ Ëº Ó ÝÞ ÑÓÐÓ ÈÖ ¾¼¼ ÈÓ ÓÚ Ò Ú Ò Ú ÔÐÓÑÓÚ ÔÖ Ý Ö ÔÓ
s09 U = u(r)ρ4πr 2 dr. r c
 1/9 s09 ½ º ÔÖÓ Ò ¾¼½¾ Î Ð Ó Ø Ý Ø ÑÙ Ó ÔÓØ Ò ÐÙ ËØ ÒÓÚ Ò Ú Ó Ò Ú Ð Ó Ø ÚÞÓÖ Ù ÓÖ Ð Ò Ð Ó ÔÓØ Ò ÐÙ 1000 Ø Ô Ð Ò > ÓÑÓÐ ÙÐÝ 10000 Ò ÒÓ ØÖÙ ØÙÖÝ ÖÝ Ø ÐÝ ÐÓ µ > 10 6 ÔÖÓ Ð Ñ õ ÐÓÚ Ò Ú Øõ ÚÞÓÖ Ðõ ÓÖ Ð Ò µ
1/9 s09 ½ º ÔÖÓ Ò ¾¼½¾ Î Ð Ó Ø Ý Ø ÑÙ Ó ÔÓØ Ò ÐÙ ËØ ÒÓÚ Ò Ú Ó Ò Ú Ð Ó Ø ÚÞÓÖ Ù ÓÖ Ð Ò Ð Ó ÔÓØ Ò ÐÙ 1000 Ø Ô Ð Ò > ÓÑÓÐ ÙÐÝ 10000 Ò ÒÓ ØÖÙ ØÙÖÝ ÖÝ Ø ÐÝ ÐÓ µ > 10 6 ÔÖÓ Ð Ñ õ ÐÓÚ Ò Ú Øõ ÚÞÓÖ Ðõ ÓÖ Ð Ò µ
Æ ØÓÑØÓ Ñ Ø Ý Ö ÔÓ ÓÚ Ð Ú ÑÙ Ú ÓÙ ÑÙ ÊÆ Öº È ÚÐÙ ÃÓ ÒÓÚ È º º Þ ÙÚ Ò Ó ÔÖÓ Ð Ñ Ø Ý ÔÓÚÖ ó Ñ Ù Þ ÔÓ ÔÓÖÙ Þ ÚÝ Ð Ò Ð Ò ó ÔÖÓ ØÙØÓ ÔÖ Þ ÔÓÑÓ Ô Ò Ñ Ø ØÓ Ô
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý ÇÒ ÃÖ Ì ÓÖ Ø ÚÔÓ ØÝ Ø Ð ØÝ Ð ØÖÓÒÓÚ ØÖÙ ØÙÖÝ ÔÓÚÖ ó Ë Ã Ø Ö ÝÞ Ý ÔÓÚÖ ó ÔÐ ÞÑ ØÙ Î ÓÙ Ð ÔÖ ÊÆ Öº È Ú Ð ÃÓ Ò È º º ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ËØÙ Ò Ó ÓÖ Ç
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã ÄýàËÃý ÈÊý ÇÒ ÃÖ Ì ÓÖ Ø ÚÔÓ ØÝ Ø Ð ØÝ Ð ØÖÓÒÓÚ ØÖÙ ØÙÖÝ ÔÓÚÖ ó Ë Ã Ø Ö ÝÞ Ý ÔÓÚÖ ó ÔÐ ÞÑ ØÙ Î ÓÙ Ð ÔÖ ÊÆ Öº È Ú Ð ÃÓ Ò È º º ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ËØÙ Ò Ó ÓÖ Ç
ÈÖÓ Ø ÐÐËØÓÖ ¹ Ó ØÓÚ ÑÔÐ Ñ ÒØ ÅÄ¹Ò Ø ÚÒ Ó Ëà Ã Ö Ð Ê Ø Å Ð Î Ð ÒØ Â Ò ÎÖ Ò Ã Ø Ö ÔÓ Ø ó Ä ÎÍÌ ÈÖ Ã ÖÐÓÚÓ Ò Ñ Ø ½ ½¾½ ÈÖ ¾ ßÖ Ø Ú Ð ÒØ ÚÖ ÒÝ ½Ð кÚÙغÞ
 ÈÖÓ Ø ÐÐËØÓÖ ¹ Ó ØÓÚ ÑÔÐ Ñ ÒØ ÅÄ¹Ò Ø ÚÒ Ó Ëà Ã Ö Ð Ê Ø Å Ð Î Ð ÒØ Â Ò ÎÖ Ò Ã Ø Ö ÔÓ Ø ó Ä ÎÍÌ ÈÖ Ã ÖÐÓÚÓ Ò Ñ Ø ½ ½¾½ ÈÖ ¾ ßÖ Ø Ú Ð ÒØ ÚÖ ÒÝ ½Ð кÚÙØºÞ ØÖ Ø Ð Ñ ÔÖÓ ØÙ ÐÐËØÓÖ ÑÔÐ Ñ ÒØ ÅÄ¹Ò Ø ÚÒ Ó Ø ÞÓÚ
ÈÖÓ Ø ÐÐËØÓÖ ¹ Ó ØÓÚ ÑÔÐ Ñ ÒØ ÅÄ¹Ò Ø ÚÒ Ó Ëà Ã Ö Ð Ê Ø Å Ð Î Ð ÒØ Â Ò ÎÖ Ò Ã Ø Ö ÔÓ Ø ó Ä ÎÍÌ ÈÖ Ã ÖÐÓÚÓ Ò Ñ Ø ½ ½¾½ ÈÖ ¾ ßÖ Ø Ú Ð ÒØ ÚÖ ÒÝ ½Ð кÚÙØºÞ ØÖ Ø Ð Ñ ÔÖÓ ØÙ ÐÐËØÓÖ ÑÔÐ Ñ ÒØ ÅÄ¹Ò Ø ÚÒ Ó Ø ÞÓÚ
Fyzikální praktikum 2
 Ø Ú ÝÞ Ý ÓÒ ÒÞÓÚ Ò Ð Ø È ÖÓ ÓÚ ÙÐØ Å ÖÝ ÓÚ ÙÒ Ú ÖÞ Ø ÖÒÓ Fyzikální praktikum 2 Návody k ulohám Ondřej Caha, Dušan Hemzal, Luděk Bočánek Jiří Chaloupka, Petr Mikulík a Filip Münz Brno 2013 ¾ ÝÞ ÐÒ ÔÖ Ø
Ø Ú ÝÞ Ý ÓÒ ÒÞÓÚ Ò Ð Ø È ÖÓ ÓÚ ÙÐØ Å ÖÝ ÓÚ ÙÒ Ú ÖÞ Ø ÖÒÓ Fyzikální praktikum 2 Návody k ulohám Ondřej Caha, Dušan Hemzal, Luděk Bočánek Jiří Chaloupka, Petr Mikulík a Filip Münz Brno 2013 ¾ ÝÞ ÐÒ ÔÖ Ø
Ç ½ ÍÚÓ ¾ ½º½ ÍÚÓ Ø ÖÑ ÒÓÐÓ º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Ó ØÚÓ Ö ÙÖ ØÚ ¾º½ ÙÖ ØÚ Ó Ö º º º º º º º º º º º º º º º º º º º º º
 ÊÓ Ò ÓÚ ÔÖ ÙÖ ØÚ È ØÖ Ë Ú Ý ÝÑ Þ ÙÑ Ù Ò ÔØ Ñ ¾¼¼»¾¼¼ Ç ½ ÍÚÓ ¾ ½º½ ÍÚÓ Ø ÖÑ ÒÓÐÓ º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Ó ØÚÓ Ö ÙÖ ØÚ ¾º½ ÙÖ ØÚ Ó Ö º º º º º º º º º º º º º º º º º º º º
ÊÓ Ò ÓÚ ÔÖ ÙÖ ØÚ È ØÖ Ë Ú Ý ÝÑ Þ ÙÑ Ù Ò ÔØ Ñ ¾¼¼»¾¼¼ Ç ½ ÍÚÓ ¾ ½º½ ÍÚÓ Ø ÖÑ ÒÓÐÓ º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Ó ØÚÓ Ö ÙÖ ØÚ ¾º½ ÙÖ ØÚ Ó Ö º º º º º º º º º º º º º º º º º º º º
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã Äý ËÃý ÈÊý Â Ò Ê Ò ÐÓÚ ÈÖÓ ÓÖÓÚ Ý Ø Ñ ÔÖÓ Þ Ò ÜÔ Ö Ñ ÒØÙ ÔÖÓ ØÙ ÙÑ Ò ÔÖÓ ÔÖ ÓÚ Ñ ÖÓ Ø Ã Ø Ö ÝÞ Ý ÔÓÚÖ Ô
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã Äý ËÃý ÈÊý Â Ò Ê Ò ÐÓÚ ÈÖÓ ÓÖÓÚ Ý Ø Ñ ÔÖÓ Þ Ò ÜÔ Ö Ñ ÒØÙ ÔÖÓ ØÙ ÙÑ Ò ÔÖÓ ÔÖ ÓÚ Ñ ÖÓ Ø Ã Ø Ö ÝÞ Ý ÔÓÚÖ ÔÐ ÞÑ ØÙ Óº ÊÆ Öº ÄÙ ÓÑ Ö È Öº ËØÙ Ò Ó ÓÖ Ç Ò ÝÞ ¾¼¼
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ Ã Äý ËÃý ÈÊý Â Ò Ê Ò ÐÓÚ ÈÖÓ ÓÖÓÚ Ý Ø Ñ ÔÖÓ Þ Ò ÜÔ Ö Ñ ÒØÙ ÔÖÓ ØÙ ÙÑ Ò ÔÖÓ ÔÖ ÓÚ Ñ ÖÓ Ø Ã Ø Ö ÝÞ Ý ÔÓÚÖ ÔÐ ÞÑ ØÙ Óº ÊÆ Öº ÄÙ ÓÑ Ö È Öº ËØÙ Ò Ó ÓÖ Ç Ò ÝÞ ¾¼¼
½ Ú Ò Ô ØÒ Ø õ Ø Þ ØÙ Ø Ö Ñ ØÙ Ú Ñ ÔÖÓ Ú Þ ØÝ ÖÓ Ý Ò Ô Ð Ò ÑÓ ÚÝÑÝ Ð Ø ÐÓÙ Ò Ò Ô ÔÖÓ Ø ÒØÓ ÚÓ Ò ß Ô õ Ò ÓÔ Ò ÚÝ Ö Ø Ø Ò Ò Ú Ó Ò õ Þ Ò Ñ Ø ÚÓÚ Ø ÔÖÚÒ Ð
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÓØ Ò ÔÐ Ø ß ÚÝ Ð õ Ò ÓÙØ ú Þ Ò ÝØ Ý Ô Ò Ë Ø ÖÚÝ Ú Ô Ø ÈÓ Ò Ú Ú ß ÔÖ Ð ÂÙ Ð ÒØ ÎÐ Ñ Ö Ã õô Ö Ä Ø Ò ÞÖÙõ Ò Ú ÔÓÔ µ ÃÝØ Ð ß ÒÓ Ö Ù Ö ÑÙ ½ Ú Ò
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÓØ Ò ÔÐ Ø ß ÚÝ Ð õ Ò ÓÙØ ú Þ Ò ÝØ Ý Ô Ò Ë Ø ÖÚÝ Ú Ô Ø ÈÓ Ò Ú Ú ß ÔÖ Ð ÂÙ Ð ÒØ ÎÐ Ñ Ö Ã õô Ö Ä Ø Ò ÞÖÙõ Ò Ú ÔÓÔ µ ÃÝØ Ð ß ÒÓ Ö Ù Ö ÑÙ ½ Ú Ò
ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ Ò Ò Ö Ò ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ
 ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ Ò Ò Ö Ò ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò ÒÐ ØÙÒ Ô Ð ÇÖ Ò ØÓÖ Ö Ë
ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö ÁÒ ÓÖÑ Ø ÓÒ ËÝ Ø Ñ Ò Ò Ö Ò ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò ÒÐ ØÙÒ Ô Ð ÇÖ Ò ØÓÖ Ö Ë
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ù Ö ÙØÓÑ Ø Ô ÞÓÚ Ò ÚÞÒ ÑÙ Ë Ò ¹Ø Ò Ø Ú ÓÖÑ ÐÒ ÔÐ ÓÚ Ò Ð Ò Ú Ø Ý Î ÓÙ ÊÆ Öº Å Ö Ø ÄÓÔ Ø ÓÚ È
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ù Ö ÙØÓÑ Ø Ô ÞÓÚ Ò ÚÞÒ ÑÙ Ë Ò ¹Ø Ò Ø Ú ÓÖÑ ÐÒ ÔÐ ÓÚ Ò Ð Ò Ú Ø Ý Î ÓÙ ÊÆ Öº Å Ö Ø ÄÓÔ Ø ÓÚ È º º ËØÙ Ò ÔÖÓ Ö Ñ ÁÒ ÓÖÑ Ø ËØÙ Ò Ó ÓÖ Å Ø Ñ Ø Ð Ò Ú
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Ù Ö ÙØÓÑ Ø Ô ÞÓÚ Ò ÚÞÒ ÑÙ Ë Ò ¹Ø Ò Ø Ú ÓÖÑ ÐÒ ÔÐ ÓÚ Ò Ð Ò Ú Ø Ý Î ÓÙ ÊÆ Öº Å Ö Ø ÄÓÔ Ø ÓÚ È º º ËØÙ Ò ÔÖÓ Ö Ñ ÁÒ ÓÖÑ Ø ËØÙ Ò Ó ÓÖ Å Ø Ñ Ø Ð Ò Ú
ÇÖ Ò Ð Þ Ò Ù Ò Þ Ø ÓÖ Ò Ð Þ Ò º
 Ô Ó ÙÒ Ú ÖÞ Ø Ú ÈÐÞÒ ÙÐØ ÔÐ ÓÚ Ò Ú Ã Ø Ö Ñ Ø Ñ Ø Ý ÔÐÓÑÓÚ ÔÖ ÇÖ Ñ ÓÑ ØÖ ÓÒ ØÖÙ ÎÝÔÖ ÓÚ Ð º ÌÓÑ õ ÖØ Î ÓÙ ÔÖ Óº ÊÆ Öº Å ÖÓ Ð Ú Ä Ú È º º ÈÐÞ ¾¼½ ÇÖ Ò Ð Þ Ò Ù Ò Þ Ø ÓÖ Ò Ð Þ Ò º ÈÖÓ Ð õ Ò ÈÖÓ Ð õù ú Ñ ÔÐÓÑÓÚÓÙ
Ô Ó ÙÒ Ú ÖÞ Ø Ú ÈÐÞÒ ÙÐØ ÔÐ ÓÚ Ò Ú Ã Ø Ö Ñ Ø Ñ Ø Ý ÔÐÓÑÓÚ ÔÖ ÇÖ Ñ ÓÑ ØÖ ÓÒ ØÖÙ ÎÝÔÖ ÓÚ Ð º ÌÓÑ õ ÖØ Î ÓÙ ÔÖ Óº ÊÆ Öº Å ÖÓ Ð Ú Ä Ú È º º ÈÐÞ ¾¼½ ÇÖ Ò Ð Þ Ò Ù Ò Þ Ø ÓÖ Ò Ð Þ Ò º ÈÖÓ Ð õ Ò ÈÖÓ Ð õù ú Ñ ÔÐÓÑÓÚÓÙ
½ºÖÓ Ò ºÐ Ø Å Ð õ Ø Ð Ð Óú Ùú Ñ Ñ ØÚÖØÓÙ Ö Þ ÓÙ Ò Ò õ ¹ Ò Ñ ÔÙ Ø Ø Ó Ðõ ØÓ Ô Ø Ö ÈÐ ú ÚÑ ÖÓ Ý ÓØ ÔÐÙ ÖÞÝ ú Ù Ö Ò ÔÓ º Â Ô Ø ÓÙ ÔÓÙ Ø ÐÙÒ Ò Ò ØÖ Ú Ò Ú
 ½ºÖÓ Ò ºÐ Ø Å Ð õ Ø Ð Ð Óú Ùú Ñ Ñ ØÚÖØÓÙ Ö Þ ÓÙ Ò Ò õ ¹ Ò Ñ ÔÙ Ø Ø Ó Ðõ ØÓ Ô Ø Ö ÈÐ ú ÚÑ ÖÓ Ý ÓØ ÔÐÙ ÖÞÝ ú Ù Ö Ò ÔÓ º Â Ô Ø ÓÙ ÔÓÙ Ø ÐÙÒ Ò Ò ØÖ Ú Ò Ú Ò Ù Ñ ¹ Ö Ýº Ð ÑÝ Ú Ñ ú Ø Ò õ ØÙ õ Ò ÃÓÃÓËÙº È Ñ Ó
½ºÖÓ Ò ºÐ Ø Å Ð õ Ø Ð Ð Óú Ùú Ñ Ñ ØÚÖØÓÙ Ö Þ ÓÙ Ò Ò õ ¹ Ò Ñ ÔÙ Ø Ø Ó Ðõ ØÓ Ô Ø Ö ÈÐ ú ÚÑ ÖÓ Ý ÓØ ÔÐÙ ÖÞÝ ú Ù Ö Ò ÔÓ º Â Ô Ø ÓÙ ÔÓÙ Ø ÐÙÒ Ò Ò ØÖ Ú Ò Ú Ò Ù Ñ ¹ Ö Ýº Ð ÑÝ Ú Ñ ú Ø Ò õ ØÙ õ Ò ÃÓÃÓËÙº È Ñ Ó
 ÎÝ Ó Í Ì Ú ÈÖ Þ ÙÐØ Ð ØÖÓØ Ã ÄýàËÃý ÈÊý Å Ð Ò ÈÖÓÙÞ ÈÐ ÒÓÚ Ò ÔÓ Ý Ù ÓÖÑ ÑÓ ÐÒ ÖÓ ÓØó Ã Ø Ö Ý ÖÒ Ø Ý Î ÓÙ Ð ÔÖ ÁÒ º ÎÓ Ø ÎÓÒ ÈÖ ¾¼½¾ ØÖ Ø ÓÖÑ ÑÓ ÐÒ ÖÓ ÓØó ÓÙ Ñ Þ ØÙ ÐÒ Ñ Öó ÚÞ ÙÑÙ Ú ÑÓ ÐÒ ÖÓ ÓØ º óð ö
ÎÝ Ó Í Ì Ú ÈÖ Þ ÙÐØ Ð ØÖÓØ Ã ÄýàËÃý ÈÊý Å Ð Ò ÈÖÓÙÞ ÈÐ ÒÓÚ Ò ÔÓ Ý Ù ÓÖÑ ÑÓ ÐÒ ÖÓ ÓØó Ã Ø Ö Ý ÖÒ Ø Ý Î ÓÙ Ð ÔÖ ÁÒ º ÎÓ Ø ÎÓÒ ÈÖ ¾¼½¾ ØÖ Ø ÓÖÑ ÑÓ ÐÒ ÖÓ ÓØó ÓÙ Ñ Þ ØÙ ÐÒ Ñ Öó ÚÞ ÙÑÙ Ú ÑÓ ÐÒ ÖÓ ÓØ º óð ö
Ä Ôõ ÚÓ Ý Ò ÚÝÑÝ Ð Ð Ó ÔÓ Ð Ð Ò õ ÑÙ Ô ÓÚ Ô ÔÖ ú Ó ÔÓÐ Ù Ø ÑÒ ËÔÓÐ ÒÓ Ø º Æ Ð Ù Ø ÜØ Þ ÞÒ Ð Ó Þ Ö Ú Ú Ò Ô ØÓÑÒÓ Ø Ó ÙØÓÖ Ò Ñ Ñ Þ Ø Ù ÐÙ ÓÚ Ó ÝÑÔ Þ ÔÓÞ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ö Ú Ó ØÙ Þ ÈÖ Ý Þ Ó úò»¾¼½ ¼ Ö ÖÓ ÓÖ ß Ù Ò Ò ½ ½ ËÔÓÐ ÒÓ Ø ËÝÑÔ Þ ÙÑ ¾¼½ ÆÓØÓ ÐÓÚ Ú ÈÖõØ Â ÖÓ Ð Ú ÈÖÓ Þ ß ¼ È Ø Ø Ð Ó Â Ó È Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ Ä Ôõ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ö Ú Ó ØÙ Þ ÈÖ Ý Þ Ó úò»¾¼½ ¼ Ö ÖÓ ÓÖ ß Ù Ò Ò ½ ½ ËÔÓÐ ÒÓ Ø ËÝÑÔ Þ ÙÑ ¾¼½ ÆÓØÓ ÐÓÚ Ú ÈÖõØ Â ÖÓ Ð Ú ÈÖÓ Þ ß ¼ È Ø Ø Ð Ó Â Ó È Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ Ä Ôõ
ÄÙ Å ÖÓÐ Â Ö ÑÖÑ Ò ÐÙ ØÖÓÔ ÝØÙÑ Ì Ò Ñ Þ Ð Ö Ò Ò ººº Ì ØÓ Ú Ø ÞÒ Ñ Ó Þ Ø ÓÔ ÚÓÚ Ò Ó ÓÔÐ Ú Ú Ò Ó Ð ½ ¾ µ Ó ÓÚ Ò Ó Ò Ò Ó Â ÖÓ Ð Ú À õ Ó Ó Ö Ñ ÚÓ Ù ÂÓ Ù Ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Î Ø Ú Ú ÓÐÒ ÃÓÙÒ Î Ø Ú ØÙ Ú ÖÒ ÅÖ ÞÙÚÞ ÓÖÒ ÓÔÙÒ ÒÓÚÙÞÖÓÞ Ò ÓÔÙÒ Ó ØÙ Ý ÚÝ Öú Ó Ò ÊÓÙ ÓÚ Ò Ú Ð Ò Ù Ù ÙÐ ÒØÝ Ó È ÚÓÚ Å Ù Ò ÓÔ ÓÑ Ý Ó Ò Ò Ó Ö Ô ÒÙ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Î Ø Ú Ú ÓÐÒ ÃÓÙÒ Î Ø Ú ØÙ Ú ÖÒ ÅÖ ÞÙÚÞ ÓÖÒ ÓÔÙÒ ÒÓÚÙÞÖÓÞ Ò ÓÔÙÒ Ó ØÙ Ý ÚÝ Öú Ó Ò ÊÓÙ ÓÚ Ò Ú Ð Ò Ù Ù ÙÐ ÒØÝ Ó È ÚÓÚ Å Ù Ò ÓÔ ÓÑ Ý Ó Ò Ò Ó Ö Ô ÒÙ
Ù Ú ÑÙ Ú ÓÙ ÑÙ ÊÆ Öº ËÚ ØÓÔÐÙ Ù ÃÖ ÐÓÚ È º º Þ Ø ÚÒ Ó Ø ÚÓÙ ÚÝØÖÚ ÐÓÙ ÔÓÑÓ Ñ ÚÝÔÖ ÓÚ Ú Ò ÔÐÓÑÓÚ ÔÖ º Ì Ù Ð Ñ Ú Ñ Ð ÒóÑ Å Ø Ñ Ø Ó Ø ÚÙ ÍÃ Þ Ö Ý ÔÓ Ñ ØÒ
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Å Ö Ó Ø ÐÓÚ ÌÛ ØÓÖÓÚ ÓÔ Ö ØÓÖ Ú ÝÑÔÐ Ø Ô ÒÓÖÓÚ ÓÑ ØÖ Å Ø Ñ Ø Ø Ú ÍÃ Î ÓÙ ÔÐÓÑÓÚ ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ ÊÆ Öº ËÚ ØÓÔÐÙ ÃÖ Ð È º º Å Ø Ñ Ø Å
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Å Ö Ó Ø ÐÓÚ ÌÛ ØÓÖÓÚ ÓÔ Ö ØÓÖ Ú ÝÑÔÐ Ø Ô ÒÓÖÓÚ ÓÑ ØÖ Å Ø Ñ Ø Ø Ú ÍÃ Î ÓÙ ÔÐÓÑÓÚ ÔÖ ËØÙ Ò ÔÖÓ Ö Ñ ËØÙ Ò Ó ÓÖ ÊÆ Öº ËÚ ØÓÔÐÙ ÃÖ Ð È º º Å Ø Ñ Ø Å
 ÚÝ Ó Ù Ò Ø Ò Ú ÈÖ Þ ÙÐØ Ð ØÖÓØ Ò ÁÑÔÐ Ñ ÒØ Ö Ú ÖÙ Ä Ò Æ ÔÖÓ ÈÓÛ ÖÈ ÔÓÖÓÚÒ Ò Ý Ø Ñ Ñ ËÓ Ø Æ ÔÐÓÑÓÚ ÈÖ ÈÖ ¾¼½¼ ÙØÓÖ º Å ÖØ Ò È Ø Ö ÈÓ ÓÚ Ò Ê Ý Ò ØÓÑØÓ Ñ Ø ÔÓ ÓÚ Ð Ú Ñ Ø Ñ ÔÓÑ Ð ÔÓ ÔÓÖÓÚ Ð Ñ Ô Ô Ò ÔÖ º Î
ÚÝ Ó Ù Ò Ø Ò Ú ÈÖ Þ ÙÐØ Ð ØÖÓØ Ò ÁÑÔÐ Ñ ÒØ Ö Ú ÖÙ Ä Ò Æ ÔÖÓ ÈÓÛ ÖÈ ÔÓÖÓÚÒ Ò Ý Ø Ñ Ñ ËÓ Ø Æ ÔÐÓÑÓÚ ÈÖ ÈÖ ¾¼½¼ ÙØÓÖ º Å ÖØ Ò È Ø Ö ÈÓ ÓÚ Ò Ê Ý Ò ØÓÑØÓ Ñ Ø ÔÓ ÓÚ Ð Ú Ñ Ø Ñ ÔÓÑ Ð ÔÓ ÔÓÖÓÚ Ð Ñ Ô Ô Ò ÔÖ º Î
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý ÙÞ Ò ÀÓÖÓÚ ÑÓÒ ØÖ Þ Ð Ò ÚÐ ØÒÓ Ø õ Ò ÚÐÒ Ò Ø ÙÑ Ð ÖÙú Ã Ø Ö Ø Ý ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý ÙÞ Ò ÀÓÖÓÚ ÑÓÒ ØÖ Þ Ð Ò ÚÐ ØÒÓ Ø õ Ò ÚÐÒ Ò Ø ÙÑ Ð ÖÙú Ã Ø Ö Ø Ý ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÇÒ Ë ÒØÓÐ Öº ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ÈÖ ¾¼¼ Î ÐÑ Ù Óº ÊÆ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý ÙÞ Ò ÀÓÖÓÚ ÑÓÒ ØÖ Þ Ð Ò ÚÐ ØÒÓ Ø õ Ò ÚÐÒ Ò Ø ÙÑ Ð ÖÙú Ã Ø Ö Ø Ý ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ Óº ÊÆ Öº ÇÒ Ë ÒØÓÐ Öº ËØÙ Ò ÔÖÓ Ö Ñ ÝÞ ÈÖ ¾¼¼ Î ÐÑ Ù Óº ÊÆ
p99 /cygdrive/jan.hus/ $ startx -- :# /cygdrive/jan.hus/ $ setxkbmap us
 Ñ ÖÓ ÖÝ Ø Ð 2 2 2 + Æ Ð Ú Ô ÔÖ ÚØ Ð ØÖÙ Ñ Ò Ñ Ð Þ Ú ÙÙ Ø ÒØÓ ÑÓØ Ú 3 3 3 Ö Ø ÑÙÐÙ Ø ÖÝ Ø Ð Ú Ô Ö Ó Ö ÔÐ Ù Ø ÔÓ Ñ Ò Ó Ö ÓÚ s.1 Ë ÑÙÐ Ò ÔÖ Ø ÙÑ Ó Ø Ò ÑÓ ÐÙ Æ Ð ÓÐ Ó Ø Ò ÑÓ ÐÙ Æ Ð Ñ ØÓ ÓÙ ÞÓÒ ÐÒ Ø Ú Ý ËØ
Ñ ÖÓ ÖÝ Ø Ð 2 2 2 + Æ Ð Ú Ô ÔÖ ÚØ Ð ØÖÙ Ñ Ò Ñ Ð Þ Ú ÙÙ Ø ÒØÓ ÑÓØ Ú 3 3 3 Ö Ø ÑÙÐÙ Ø ÖÝ Ø Ð Ú Ô Ö Ó Ö ÔÐ Ù Ø ÔÓ Ñ Ò Ó Ö ÓÚ s.1 Ë ÑÙÐ Ò ÔÖ Ø ÙÑ Ó Ø Ò ÑÓ ÐÙ Æ Ð ÓÐ Ó Ø Ò ÑÓ ÐÙ Æ Ð Ñ ØÓ ÓÙ ÞÓÒ ÐÒ Ø Ú Ý ËØ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Å ØÓÙ Ê Ò Ð Å Ò Ø ÚÐ ØÒÓ Ø ÐÒ ÓÖ ÐÓÚ Ò Ð ØÖÓÒÓÚ Ý Ø Ñó Ø Ú Ø ÓÖ Ø ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ ÔÖÓ º
 ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Å ØÓÙ Ê Ò Ð Å Ò Ø ÚÐ ØÒÓ Ø ÐÒ ÓÖ ÐÓÚ Ò Ð ØÖÓÒÓÚ Ý Ø Ñó Ø Ú Ø ÓÖ Ø ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ ÔÖÓ º ÊÆ Öº Î Ð Ú Â Ò Ö˺ ÝÞ ÐÒ Ø Ú Î Ê ÚºÚº º ËØÙ Ò ÔÖÓ
ÍÒ Ú ÖÞ Ø Ã ÖÐÓÚ Ú ÈÖ Þ Å Ø Ñ Ø Ó¹ ÝÞ ÐÒ ÙÐØ ÁÈÄÇÅÇÎý ÈÊý Å ØÓÙ Ê Ò Ð Å Ò Ø ÚÐ ØÒÓ Ø ÐÒ ÓÖ ÐÓÚ Ò Ð ØÖÓÒÓÚ Ý Ø Ñó Ø Ú Ø ÓÖ Ø ÝÞ Ý Î ÓÙ ÔÐÓÑÓÚ ÔÖ ÔÖÓ º ÊÆ Öº Î Ð Ú Â Ò Ö˺ ÝÞ ÐÒ Ø Ú Î Ê ÚºÚº º ËØÙ Ò ÔÖÓ
x = f(x), ) [ x(0) x 0 < δ = x(t) x 0 < ε t 0] > 0 x(0) x 0 < = lim x(t) = x 0 ¾µ x = Ax, A R n n µ
![x = f(x), ) [ x(0) x 0 < δ = x(t) x 0 < ε t 0] > 0 x(0) x 0 < = lim x(t) = x 0 ¾µ x = Ax, A R n n µ x = f(x), ) [ x(0) x 0 < δ = x(t) x 0 < ε t 0] > 0 x(0) x 0 < = lim x(t) = x 0 ¾µ x = Ax, A R n n µ](/thumbs/94/121900316.jpg) ËØ Ð Ø Î Ø ØÓ Ô ØÓÐ Ù Ñ Þ Ú Ø ÓÚ Ò Ñ Ò ÔÖÓ ÓÙ Ó Ò Ó¹ Ò Ò º ÍÚ öù Ñ ÓÙ Ø ÚÙ ÖÓÚÒ x = f(x), ½µ f C 1 (Ω,R n ) Ω R n x : R Ωº Æ ð x 0 Ø ÓÒ ÖÒ Ó Ø º f(x 0 ) = 0º Ó x 0 Ò ÞÚ Ø ÐÒ ØÐ ö ( ε > 0 )( δ > 0 ) [ x(0)
ËØ Ð Ø Î Ø ØÓ Ô ØÓÐ Ù Ñ Þ Ú Ø ÓÚ Ò Ñ Ò ÔÖÓ ÓÙ Ó Ò Ó¹ Ò Ò º ÍÚ öù Ñ ÓÙ Ø ÚÙ ÖÓÚÒ x = f(x), ½µ f C 1 (Ω,R n ) Ω R n x : R Ωº Æ ð x 0 Ø ÓÒ ÖÒ Ó Ø º f(x 0 ) = 0º Ó x 0 Ò ÞÚ Ø ÐÒ ØÐ ö ( ε > 0 )( δ > 0 ) [ x(0)
Þ ÑÙ Ñ Å ÒÙÐ Ñ Ú Ø ØÙÐ Ù ÚÝÞÚ Ð ÌÖÓõ Ù Ó Ð Øº ÌÓ Ò ÓÒ ÔÓÚ ÐÓ Ò Ø Ð Ò Ñ ß Ó Ó ÔÓ ß Ú Ñ Ò Ó ÚÝ Ð ÔÓ Þ Ñº à ÓÒ Ò õø Ó Ò Ð Ø Ò ØÖÓÑ ÖÚ Ú ÐÑ ÓÔ ØÖÒ º Ç Ó Ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ú Ó Ò Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ Å ÑÓ Ò Ô Ò õ Ò Ú Ë ËÈÃË ÆÓØÓ Î Ø Ú Ù ÙÐ ÒØ Â Ú ÓÙ ØÙ Ò ËÔ õ ÃÝØ Ð ØÖÓÔ ÝØÙÑ ÑÝÖ Ó Ø Ñ ÞÚÐ õò ÖÚ Þ ÑÙ Ñ Å ÒÙÐ Ñ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ú Ó Ò Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ Å ÑÓ Ò Ô Ò õ Ò Ú Ë ËÈÃË ÆÓØÓ Î Ø Ú Ù ÙÐ ÒØ Â Ú ÓÙ ØÙ Ò ËÔ õ ÃÝØ Ð ØÖÓÔ ÝØÙÑ ÑÝÖ Ó Ø Ñ ÞÚÐ õò ÖÚ Þ ÑÙ Ñ Å ÒÙÐ Ñ
ÔÖÓ Ó Ù Â ÖÓ Ò Ñ Ô õðó Ð ØÓ Þ Ó Ú Ð Ú Ò Ñ Ò ÚÝÚ Ò Ò Ò õ ØÙ º ÈÓ Þ Ñ Ø Ñ Þ Ò Ù Úõ ÒÓ Þ ÐÓ ÔÖÓ ÓÙÞ Ø ÑÒÓÞ Ð ØÓ Ó Ó Ý Ø ÐÓ Ý Ý ÚÖ Ø Ð º Ç ÚÝ ÝÐÝ Ø ÒØÓ Ö
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ç ÐÒ ÚÖÓ Ò Ò Ð ú ØÓ Ø ÓØÓ Ö Ò ÔÐ Ø Æ ÖÓÞ Ò ÒÝ ÎÓÐÒ ØÖ ÙÒ ÝÑÒÓ ÐÝ ÙÑ Ð Ô ÒÙÑ Ï ÖÒ Ö Í ÐÑ ÒÒ ß ÁÒ Ñ ÑÓÖ Ñ ÃÝØ Ð ÆÓØÓ ØÙ Ù ÐÑ ÒÒ ÒÙ Ù Ò Ò ÔÖÓ Ó
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ç ÐÒ ÚÖÓ Ò Ò Ð ú ØÓ Ø ÓØÓ Ö Ò ÔÐ Ø Æ ÖÓÞ Ò ÒÝ ÎÓÐÒ ØÖ ÙÒ ÝÑÒÓ ÐÝ ÙÑ Ð Ô ÒÙÑ Ï ÖÒ Ö Í ÐÑ ÒÒ ß ÁÒ Ñ ÑÓÖ Ñ ÃÝØ Ð ÆÓØÓ ØÙ Ù ÐÑ ÒÒ ÒÙ Ù Ò Ò ÔÖÓ Ó
ÈÓÑ ÐÙ Úõ Ø Â ÓÒ Ù Ò Ñ ÔÓ Ð ØÓ Ú Ñ Ò Î Ð ÓÒÓ º Â ÖÓ Þ ÐÓ ÖÞÝ Ò Ô Ó Ð Ø Ó Ú Ô ÓÞ Ð Ø ÔÓÑ ÐÙ ØÓ ÚÝ ÙØÒ Ú º Ó Ò ØÓ Ò Ô ÖÓ ÖÓ Ò õ ÔÓÐ Þ Ö Þ Ö Ð Ò Â Ò Þ ØÚ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ó ÒÓÚ Ó ÖÓ Ù ÒÓÚÑ Ú ÓÖ Ñ ÔÖ ÚÝ ÙÒ ÓÒ Ú ÓÖÙ ÆÓÚ Ð ÒÓÚ Ú ÓÖÙ ÓØ Ý Ò ÔÐ Ø Ê ØÖÓÔ Ò õ ËÔÓÐ Ò ÖÓÒ ß ÚÖÓ Ð Ò ÐÙ Ù ÃÝØ Ð È ÝÔÓ ÙÑ Ô ÒÓ ÙÑ Äº ºµ º º
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Ó ÒÓÚ Ó ÖÓ Ù ÒÓÚÑ Ú ÓÖ Ñ ÔÖ ÚÝ ÙÒ ÓÒ Ú ÓÖÙ ÆÓÚ Ð ÒÓÚ Ú ÓÖÙ ÓØ Ý Ò ÔÐ Ø Ê ØÖÓÔ Ò õ ËÔÓÐ Ò ÖÓÒ ß ÚÖÓ Ð Ò ÐÙ Ù ÃÝØ Ð È ÝÔÓ ÙÑ Ô ÒÓ ÙÑ Äº ºµ º º
 ÚÐ Ú Ò Ñººº ººº Ý Ú Ú ÒÙ Ñ Ò Ñ ÔÖ Ú Ø Ð Ñ Ð Ó ÒÓÙ Ø Ò Ø ÞÒ Ñ Ø ÖÓ ÒÓÙº ÈÖ Ú Ù Ñ ß Ú ÔÖÓ Ñ Ñ Ø Ò õ Ø Þ ÒÓÚÒ ººº Â Ò Ø Ò Ø ØÙÐ ÔÖ Ú Úº ÝØ Þ Ø Ñ Ò Ô Ò
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Æ õ Ð ÒÓÚ Ò Ø Î Ø Ú ØÙ Î Ø ÚÝ Ù ÓÒ ÙÖ Ò ËÔÓÐ Ò ÖÓÒ ß ÚÖÓ Ð Ò ÐÙ Ù ÃÝØ Ð ÌÖ Ó Ñ Ò ÙÑ À Ûºµ Ë Û ÒØ Â ÚÐ Ú Ò Ñººº ººº Ý Ú Ú ÒÙ Ñ Ò Ñ ÔÖ Ú Ø Ð Ñ Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Æ õ Ð ÒÓÚ Ò Ø Î Ø Ú ØÙ Î Ø ÚÝ Ù ÓÒ ÙÖ Ò ËÔÓÐ Ò ÖÓÒ ß ÚÖÓ Ð Ò ÐÙ Ù ÃÝØ Ð ÌÖ Ó Ñ Ò ÙÑ À Ûºµ Ë Û ÒØ Â ÚÐ Ú Ò Ñººº ººº Ý Ú Ú ÒÙ Ñ Ò Ñ ÔÖ Ú Ø Ð Ñ Ð
ÚÓÐÙØ ¹ Ó ÙÑ ÒØ Â Ò ÃÓÐÓÑ ÞÒ
 ÚÓÐÙØ ¹ Ó ÙÑ ÒØ Â Ò ÃÓÐÓÑ ÞÒ Ç Á Íö Ú Ø Ð Ó ÙÑ ÒØ ½ Íö Ú Ø Ð ÖÓÞ Ö Ò ½º½ Î ÛÔÓÖØ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÓÒ ÓÐ º º º º º º º º º º º º º
ÚÓÐÙØ ¹ Ó ÙÑ ÒØ Â Ò ÃÓÐÓÑ ÞÒ Ç Á Íö Ú Ø Ð Ó ÙÑ ÒØ ½ Íö Ú Ø Ð ÖÓÞ Ö Ò ½º½ Î ÛÔÓÖØ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÓÒ ÓÐ º º º º º º º º º º º º º
Ç Þ Þ ÌÓ Ò Ò Ò Ò Þ Ú Ò Ô Ò Ý ØÓØÓ Ñ Ò Ô Ø Ð Ø Ú ÑÒÓ Ö ÞÒ ÓÙÚ ÐÓ ¹ Ø º Ì ÒØÓ ÚÓ Ò Ñ Ú Ú ØÒÙ Þ Ò Ð Ø ØÓ ÐÓÚÝ Ô Ò Ý Ã ÖÐ ÈÐ Ð ÈÖõ ººº ººº ÓÙ Ú Ò Ù ÔÖ ÐÓ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Î Ø ÚÝ ØÙ ÖÒÓ ÞÐ Ø ÐÓ ÈÖ ØÙ Ñ ÔÓÞÓÖÙ Ñ Ô õ Ñ Ú Ö ÃÖ ÐÓÚ ß ÓØ Ú Ö Ò Þ ÒÝ Ë Ö Ù ÙÐ ÒØ Ö ÎÐ Ø Ò Ú ÖÒ ÅÓÖ ÚÙ Ä ÓÐ Ñ ÐÙ Ù ÂÓ Ç Ò Ð ß Ð Ø Å ÖÓ Ð Ú ÌÖØ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Î Ø ÚÝ ØÙ ÖÒÓ ÞÐ Ø ÐÓ ÈÖ ØÙ Ñ ÔÓÞÓÖÙ Ñ Ô õ Ñ Ú Ö ÃÖ ÐÓÚ ß ÓØ Ú Ö Ò Þ ÒÝ Ë Ö Ù ÙÐ ÒØ Ö ÎÐ Ø Ò Ú ÖÒ ÅÓÖ ÚÙ Ä ÓÐ Ñ ÐÙ Ù ÂÓ Ç Ò Ð ß Ð Ø Å ÖÓ Ð Ú ÌÖØ
ÖÙ Ø Æ Ò ÑÝõÐ Ò Ó Ú úù Ô Ò Ú Ò ÔÓ Ø Ö Ý Ò ÔÓÔ Ð Ô Ô Ò Þ ØÙº È ÚÓ Ñ Ö Ú Ð Ø º ÐÓÚ Ý Ú Ø ØÙÐ Ù ÞÒ Ñ Ò ú Ùú Þ Ò Ñ Ù Ø Ô Ñ Ò Ó Þ ØÙ Ð ØÓ Ò ØÑ ÖÓ Ñº ÈÓÔÖÚ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ËÝÑÔ Þ ÙÑ Æ ÖÓÞ Ò ÒÝ ÆÓØÓ ÐÓÚ ÝÑÒÓ Ð ÃÝØ Ð Å ÑÑ ÐÐ Ö ÔÓ Ñ Ð Ø Ú Ð Ô ÖÙ Ø Æ Ò ÑÝõÐ Ò Ó Ú úù Ô Ò Ú Ò ÔÓ Ø Ö Ý Ò ÔÓÔ Ð Ô Ô Ò Þ ØÙº È ÚÓ Ñ Ö Ú Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ËÝÑÔ Þ ÙÑ Æ ÖÓÞ Ò ÒÝ ÆÓØÓ ÐÓÚ ÝÑÒÓ Ð ÃÝØ Ð Å ÑÑ ÐÐ Ö ÔÓ Ñ Ð Ø Ú Ð Ô ÖÙ Ø Æ Ò ÑÝõÐ Ò Ó Ú úù Ô Ò Ú Ò ÔÓ Ø Ö Ý Ò ÔÓÔ Ð Ô Ô Ò Þ ØÙº È ÚÓ Ñ Ö Ú Ð
O x i, b; z = i, b; z i = 0 ÓÖ x i = 0 i, b 1; z i [N] Ò x i = 1º
![O x i, b; z = i, b; z i = 0 ÓÖ x i = 0 i, b 1; z i [N] Ò x i = 1º O x i, b; z = i, b; z i = 0 ÓÖ x i = 0 i, b 1; z i [N] Ò x i = 1º](/thumbs/99/141160995.jpg) Ì ÓÑÔÙØ Ø ÓÒ Ð ÓÑÔÐ Ü ØÝ ÓÐÙÑÒ Ý Â Ó Ó ÌÓÖ Ò Ôغ Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØØ ÍÐÑ Ç Ö Ö Ð Ö ¼ ÍÐÑ ÖÑ ÒÝ Ó ÓºØÓÖ ÒÙÒ ¹ÙÐѺ ØØÔ»»Ø ÓÖ º Ò ÓÖÑ Ø ºÙÒ ¹ÙÐѺ»È Ö ÓÒ Ò» غ ØÑÐ ÉÙ ÒØÙÑ ÓÑÔÐ Ü ØÝ ÝÓÙÒ Ö Ö Ö Ó ÒÖ Ò
Ì ÓÑÔÙØ Ø ÓÒ Ð ÓÑÔÐ Ü ØÝ ÓÐÙÑÒ Ý Â Ó Ó ÌÓÖ Ò Ôغ Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØØ ÍÐÑ Ç Ö Ö Ð Ö ¼ ÍÐÑ ÖÑ ÒÝ Ó ÓºØÓÖ ÒÙÒ ¹ÙÐѺ ØØÔ»»Ø ÓÖ º Ò ÓÖÑ Ø ºÙÒ ¹ÙÐѺ»È Ö ÓÒ Ò» غ ØÑÐ ÉÙ ÒØÙÑ ÓÑÔÐ Ü ØÝ ÝÓÙÒ Ö Ö Ö Ó ÒÖ Ò
½ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ ÚÓØ ÞÑ Ò º ÈÖ Ø Ò ¹Ð Ñ Ò Ø ÔÖ Ø Ò Þ þøº Ê Ò Ö À Íþ ÚÓ Ò þ ÐÓÚÓ Æ Þ þø Ù ÒÓÚ þ Ó ÓÐÒ þ Ó ÖÓ Ù Ý Ò Ú
 ½ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ ÚÓØ ÞÑ Ò º ÈÖ Ø Ò ¹Ð Ñ Ò Ø ÔÖ Ø Ò Þ þøº Ê Ò Ö À Íþ ÚÓ Ò þ ÐÓÚÓ Æ Þ þø Ù ÒÓÚ þ Ó ÓÐÒ þ Ó ÖÓ Ù Ý Ò Ú ÔÖÚÒ þñ þ Ð ÌÓÑ þ Ø Ð Ö ¹ ÓÚ Ø Þ þñù Þ Ú þ Ò ÓÐ ÔÓÚÞ
½ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ ÚÓØ ÞÑ Ò º ÈÖ Ø Ò ¹Ð Ñ Ò Ø ÔÖ Ø Ò Þ þøº Ê Ò Ö À Íþ ÚÓ Ò þ ÐÓÚÓ Æ Þ þø Ù ÒÓÚ þ Ó ÓÐÒ þ Ó ÖÓ Ù Ý Ò Ú ÔÖÚÒ þñ þ Ð ÌÓÑ þ Ø Ð Ö ¹ ÓÚ Ø Þ þñù Þ Ú þ Ò ÓÐ ÔÓÚÞ
J i = D i ci. c i = z
 ÌÖÙ Í Ð Ý l = 20 Ñ ÔÖ ÞÙ A = 0.3 2 Ñ Ñ Ò È Ð º ØÚ ÖÙ Ö ØÙº Â Ò ÓÒ ÔÓÒÓ Ò Ú Ó ¹ ÓÐ ½½ Ѻ± Ù ÖÙµ ÓÒ Ó ÓÙ 1/26 ÙÞ ß Ñ ÖÓ ÓÔ ÔÓ Ð Ú ÓÒ J ÈÖÚÒ Þ ÌÓ i i 2 1 ÑÓÐ Ñ µ Ð Ø Ý ÒÓØ Ý J i = D i ci Ñ ÖÒ ÓÒ ÒØÖ Ö ÒØÙ
ÌÖÙ Í Ð Ý l = 20 Ñ ÔÖ ÞÙ A = 0.3 2 Ñ Ñ Ò È Ð º ØÚ ÖÙ Ö ØÙº Â Ò ÓÒ ÔÓÒÓ Ò Ú Ó ¹ ÓÐ ½½ Ѻ± Ù ÖÙµ ÓÒ Ó ÓÙ 1/26 ÙÞ ß Ñ ÖÓ ÓÔ ÔÓ Ð Ú ÓÒ J ÈÖÚÒ Þ ÌÓ i i 2 1 ÑÓÐ Ñ µ Ð Ø Ý ÒÓØ Ý J i = D i ci Ñ ÖÒ ÓÒ ÒØÖ Ö ÒØÙ
de = I(r,n,ν,t)dScosθdωdνdt, I ν J ν J(r,ν) = 1 2 J(r,ν) dν. µ E Ê (r) = 4π c
 Èà ÊÇ ÇÎ Ãý ÃÍÄÌ Å Ë Ê ÃÇÎ ÍÆÁÎ Ê ÁÌ ËÌ Î Ì ÇÊ ÌÁ à Áà ËÌÊÇ Áà ÀÓÖ Ú Þ Ý ÁÁ  ÃÖØ ÖÒÓ ¾¼½ ½ ½º½ ØÑÓ ÖÝ ÓÖ Ú Þ ÈÓÔ Þ Ò Ú Ú Þ Ò ØÑÓ Ö Î ÔÓ Ø Ø Ú ÒÝ Ò ÓÖÑ Ø Ö Ó Ú Þ Ñ Ñ Þ Ú Ñ ØÙ Ñ Ð ØÖÓÑ ¹ Ò Ø Ó Þ Ò º ÈÖÓØÓ
Èà ÊÇ ÇÎ Ãý ÃÍÄÌ Å Ë Ê ÃÇÎ ÍÆÁÎ Ê ÁÌ ËÌ Î Ì ÇÊ ÌÁ à Áà ËÌÊÇ Áà ÀÓÖ Ú Þ Ý ÁÁ  ÃÖØ ÖÒÓ ¾¼½ ½ ½º½ ØÑÓ ÖÝ ÓÖ Ú Þ ÈÓÔ Þ Ò Ú Ú Þ Ò ØÑÓ Ö Î ÔÓ Ø Ø Ú ÒÝ Ò ÓÖÑ Ø Ö Ó Ú Þ Ñ Ñ Þ Ú Ñ ØÙ Ñ Ð ØÖÓÑ ¹ Ò Ø Ó Þ Ò º ÈÖÓØÓ
ÅÝ Ð ÖÓººº ººº Þ Ø Ñ Ô õ Ð ÑÖ Þº Á Ø ÒØÓ Ö Ø Þ Ò Ñ Ô Ò ÓÙº Ø ÜØ Úõ Ø Ú Ö ÒØ Ø Ö ÞÒ Ñ Þ Ò Ø Ñ ØÓ ÐÓÚݺ Æ Ò Ú ú ÔÓ Ð Þ Ú Ö ÒØÝ ÖÓÞ Þ º ËØ Ò Ò ÓÒ ÓÙ Ú Ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò Þ Ò Ð ú ØÓ Ø ÎÓÐÒ ØÖ ÙÒ ËÔÓÐ Ò ÖÓÒ ËÝÑÔ Þ ÙÑ Ò ÔÓ Ö ÓÚ Ò ß Ó ÓÒ Ò ÃÝØ Ð ÝÑÒÓ ØÙ Ù Ø ÖÖ Ò Ù Ó ÊÙ ÓÐ ÅÓÙÐ ÅÝ Ð ÖÓººº ººº Þ Ø Ñ Ô õ Ð ÑÖ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò Þ Ò Ð ú ØÓ Ø ÎÓÐÒ ØÖ ÙÒ ËÔÓÐ Ò ÖÓÒ ËÝÑÔ Þ ÙÑ Ò ÔÓ Ö ÓÚ Ò ß Ó ÓÒ Ò ÃÝØ Ð ÝÑÒÓ ØÙ Ù Ø ÖÖ Ò Ù Ó ÊÙ ÓÐ ÅÓÙÐ ÅÝ Ð ÖÓººº ººº Þ Ø Ñ Ô õ Ð ÑÖ
arxiv: v1 [math.ca] 8 Aug 2008
![arxiv: v1 [math.ca] 8 Aug 2008 arxiv: v1 [math.ca] 8 Aug 2008](/thumbs/99/141244925.jpg) Ö Ñ Ò Û Ú Ð Ø Ý Ø Ñ ÓÒ Ø Ô Ö Å Ö Ø È Ô ariv:0808.1173v1 [math.ca] 8 Aug 2008 ÍÒ Ú Ö ØÝ Ó È Á Ø È ÀÙÒ ÖÝ Ô ÔÑØØ ºÔØ º Ù ØÖ Ø ÁÒ Ø Ô Ô Ö Û ÓÖÑÙÐ Ø Û Ø Ú Ö ÓÒ Ó Ñ Ò ÑÙÑ ÔÖÓ Ð Ñ ½º µ ÓÒ Ø Ô Ö Ò Û ÓÛ Ø Ø ÓÖ
Ö Ñ Ò Û Ú Ð Ø Ý Ø Ñ ÓÒ Ø Ô Ö Å Ö Ø È Ô ariv:0808.1173v1 [math.ca] 8 Aug 2008 ÍÒ Ú Ö ØÝ Ó È Á Ø È ÀÙÒ ÖÝ Ô ÔÑØØ ºÔØ º Ù ØÖ Ø ÁÒ Ø Ô Ô Ö Û ÓÖÑÙÐ Ø Û Ø Ú Ö ÓÒ Ó Ñ Ò ÑÙÑ ÔÖÓ Ð Ñ ½º µ ÓÒ Ø Ô Ö Ò Û ÓÛ Ø Ø ÓÖ
( u,v W) : u W v W ( α R)( u,v W) : α W v W.
 ÔÐ ÓÚ Ò Ð Ö Ú Ò µ ÇÐ ÎÐ Ò Ó Ø Ð ¾¼º Ù Ò ¾¼½ ½ ½ ½º½ È ÔÓÑ ÒÙØ Ò Ø Ö Ô ØÓÐ Þ Ð Ò ÖÒ Ð ÖÝ Î ØÓÖÓÚ ÔÖÓ ØÓÖÝ ØÚ (V,F,, ) V ÑÒÓö Ò F Ø Ð Ó Ð Ô ÒÓ (F,+, ) Ø Ð Ó ÓÙ ÓÔ Ö : V V V : F V V Ò ÞÚ Ñ ÔÓ Ñ Ñ Ú ØÓÖÓÚ
ÔÐ ÓÚ Ò Ð Ö Ú Ò µ ÇÐ ÎÐ Ò Ó Ø Ð ¾¼º Ù Ò ¾¼½ ½ ½ ½º½ È ÔÓÑ ÒÙØ Ò Ø Ö Ô ØÓÐ Þ Ð Ò ÖÒ Ð ÖÝ Î ØÓÖÓÚ ÔÖÓ ØÓÖÝ ØÚ (V,F,, ) V ÑÒÓö Ò F Ø Ð Ó Ð Ô ÒÓ (F,+, ) Ø Ð Ó ÓÙ ÓÔ Ö : V V V : F V V Ò ÞÚ Ñ ÔÓ Ñ Ñ Ú ØÓÖÓÚ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÈÖ ú ÝÑÔ Þ ÙÑ Æ õ Ú Ø Ú Ë Ø Ò Ò Òµ ÔÓÐ ØÙ ÃÝØ Ð Ê ÙØ Ó Ã ÖÐ Ã õô Ö
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÈÖ ú ÝÑÔ Þ ÙÑ Æ õ Ú Ø Ú Ë Ø Ò Ò Òµ ÔÓÐ ØÙ ÃÝØ Ð ÊÙØ Ó Ã ÖÐ Ã õô Ö ËÔ Ñººº ººº ÒÙ Ù ÔÓ ÖÓÚ Ø Ô Ò ÓÙ Ý ØÓÚÓÙ ÞÒ Ñº ÍÞ Ú Ö Þ ØÙ ÚÝ Þ ÞÖÓÚÒ Ú Ó Ô
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÈÖ ú ÝÑÔ Þ ÙÑ Æ õ Ú Ø Ú Ë Ø Ò Ò Òµ ÔÓÐ ØÙ ÃÝØ Ð ÊÙØ Ó Ã ÖÐ Ã õô Ö ËÔ Ñººº ººº ÒÙ Ù ÔÓ ÖÓÚ Ø Ô Ò ÓÙ Ý ØÓÚÓÙ ÞÒ Ñº ÍÞ Ú Ö Þ ØÙ ÚÝ Þ ÞÖÓÚÒ Ú Ó Ô
Ë ÔÖÚÒ Ñ Ò Ñ ÎÝÙú Ú Ñ ÔÖõ Ú Ò Ú Ô Ð Ò Ý Þ ÔÐÒ Ð Ô Ñ Ò Ý Ó Ö Þ Ý Ò Ð Ù ØÖ Ò Ý ÔÖÓ Ú õ Ó Ùõ Ö ØÖ Ð Ú Òݺ ÃÓÒ ÙÖ ÓÚ Ý Ø Ñ Ò Þ Þ ÑÓÚ Ò ÖÓ ØÐ Ò Ð Þ Ñ Ó õø
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ý ØÙ Ó Í Ö Î Ø Ú Ò Ò Ù ÙÐ ÒØ Ú Ö Ñ Ú ÖÙ Ñ ËÝÑÔ Þ ÙÑ Ë Ø Ò ÒÓØÓ Ð Ê ÞÒ Úõ Ð Ó ÒÓÚ Ó Ú ËÔÓÐ ÒÓ Ø ÃÝØ Ð Å Ù Ò ÓÔ Ñ ÒÙØ ÀÈÌ ½ Ë ÔÖÚÒ Ñ Ò Ñ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ý ØÙ Ó Í Ö Î Ø Ú Ò Ò Ù ÙÐ ÒØ Ú Ö Ñ Ú ÖÙ Ñ ËÝÑÔ Þ ÙÑ Ë Ø Ò ÒÓØÓ Ð Ê ÞÒ Úõ Ð Ó ÒÓÚ Ó Ú ËÔÓÐ ÒÓ Ø ÃÝØ Ð Å Ù Ò ÓÔ Ñ ÒÙØ ÀÈÌ ½ Ë ÔÖÚÒ Ñ Ò Ñ
Ñ Ñ Ø Ý Ô ººº Ø Ý ØÙ Ô º È Ò ÔÓ Ð ÒÓ Ó Ò ÑÖØ ÐÒ Ó ÚÖÓ Ù ú ØÙ Ñ Ø ÖÓ Ò Ó Ó ß ÖÓ Ð ØÓ Ô º Ø ÑÓ ÔÖÓ Ô ÖÓ Ù Ú Ó Ô Ò Ø Ò Ô ÚÝ Ò Ñµ Ò Ø Ú ß Ýú Ð ØÓ ÔÓÑ Ð Ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ý ØÙ Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ ÈÓ Þ ÑÒ ÝÑÔ Þ ÙÑ Î Ø Ú Ú ÃÖÓÑ ú ÂÙ Ð ÒØ ÎÐ Ø Ñ Ð Å Ò ÓØÓ Ö ÓÚ Ò ß ÖÓÞÐ õ Ò È ÞÓÚ Ò Ú Ð ÖÓ ØÐ Ò ÃÝØ Ð ß ÃØ Ö Ñ Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ý ØÙ Ú Ö Ò Þ ÒÝ Ú ÖÙ Ñ ÈÓ Þ ÑÒ ÝÑÔ Þ ÙÑ Î Ø Ú Ú ÃÖÓÑ ú ÂÙ Ð ÒØ ÎÐ Ø Ñ Ð Å Ò ÓØÓ Ö ÓÚ Ò ß ÖÓÞÐ õ Ò È ÞÓÚ Ò Ú Ð ÖÓ ØÐ Ò ÃÝØ Ð ß ÃØ Ö Ñ Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ËÝÑÔ Þ ÙÑ ¾¼½ Â ÓÙ ØÙ Ý Ú ÁÞÖ Ð ÎÐ Ñ Ö Ã õô Ö ß ÁÒ Ñ ÑÓÖ Ñ Ô Ô ÝÐÙÑ ÀÍ ß Ô ÖÓ Ò Ý Ö
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ËÝÑÔ Þ ÙÑ ¾¼½ Â ÓÙ ØÙ Ý Ú ÁÞÖ Ð ÎÐ Ñ Ö Ã õô Ö ß ÁÒ Ñ ÑÓÖ Ñ Ô Ô ÝÐÙÑ ÀÍ ß Ô ÖÓ Ò Ý Ö Â Ñ Ø Ó Þ Ð Ú Þ ØÙ Ô õ ½»¾¼½ Þ Ò ÞÚÝ Ø Ò Ø ÒØÓ Ð ØÓÔÓ Ø
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ËÝÑÔ Þ ÙÑ ¾¼½ Â ÓÙ ØÙ Ý Ú ÁÞÖ Ð ÎÐ Ñ Ö Ã õô Ö ß ÁÒ Ñ ÑÓÖ Ñ Ô Ô ÝÐÙÑ ÀÍ ß Ô ÖÓ Ò Ý Ö Â Ñ Ø Ó Þ Ð Ú Þ ØÙ Ô õ ½»¾¼½ Þ Ò ÞÚÝ Ø Ò Ø ÒØÓ Ð ØÓÔÓ Ø
ÔÖ Ð Ô Ø Â Ô Ð Ù Ò ÓØ Ñ Ð ÚÙ ÓÔÖ Ú Ø Ñ Ñ Ñ Ó ÒÓµ Ù Ñ Ú Ñ Ò Ø Ñ ú Ñ Ô Ú Ð Ö ÓÚ Ð Þ ÚÝ Þ Ó ÐÙÒ ÑÓ Ö Ó ÐÓ Ý Ú Ð Ô ÚÐÓ Ý Ó Ö Ú Ò º È ÞÒ Ú Ñ ú Ñ ÑÙ Ð Ú Ð Ô
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò ÞÔÖ ÚÝ ÔÐ ÒÝ ÐÙ Ù ÔÖ Ú Ó ÒÒÓ Ø ÔÐ Ò ÀÓ ÔÓ Ò Ò Ò Ê Ú ÞÒ ÞÔÖ Ú À Ö ÙÖØ È ÞÓÚ Ò ËØÖÓÑ Ó ØÙ ÓÖÑ ß ß ÞÚÐ õøòó Ø Ó ÊÙ ÓÐ ÅÓÙÐ ÔÖ Ð Ô Ø Â Ô Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò ÞÔÖ ÚÝ ÔÐ ÒÝ ÐÙ Ù ÔÖ Ú Ó ÒÒÓ Ø ÔÐ Ò ÀÓ ÔÓ Ò Ò Ò Ê Ú ÞÒ ÞÔÖ Ú À Ö ÙÖØ È ÞÓÚ Ò ËØÖÓÑ Ó ØÙ ÓÖÑ ß ß ÞÚÐ õøòó Ø Ó ÊÙ ÓÐ ÅÓÙÐ ÔÖ Ð Ô Ø Â Ô Ð
Ã Ó Ú Ô ÖÓÞ ÎÐ ØÒ ú Ú Ð ÔÓ ÚÖÓ Ò Ð Ò Þ ÐÙ Ù Þ Ò ÔÓ Ò ÒÓÚ ØÙ ÖÓ º  РÓÞÚ Ø Ò ÝÐ Ø Ò Ñ ÒÙÐ Ò Ú Ñ Ò ÔÓ Ð Úõ Ó Ò Ø Ò Ò Ø Ú Ò Ù Ô Ð õ ÚÝÑÝ Ø Þ Ùõ ÒÓ Ø Ñ Ô
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ººº ºººÎÖÓ Ò ÞÔÖ ÚÝ Ú ÓÖÙ ÂÙ Ð ÒØ ÇÐ ÃÓÔÔ Ç Ö Þ Ò ÔÐ Ø Ú Ø Ú Ã ØÙ Ý Ñ Þ Ð ÚÑ ÖÓ ØÐ Ò Ñ Æ ÚõØ Ú Ú ÈÐÞÒ ÈÓÐÒ Ð Ò Û Ù ÇÖ Ò Þ Ò Ð Ò ÚÞÚ ÃÝØ Ð ß
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ººº ºººÎÖÓ Ò ÞÔÖ ÚÝ Ú ÓÖÙ ÂÙ Ð ÒØ ÇÐ ÃÓÔÔ Ç Ö Þ Ò ÔÐ Ø Ú Ø Ú Ã ØÙ Ý Ñ Þ Ð ÚÑ ÖÓ ØÐ Ò Ñ Æ ÚõØ Ú Ú ÈÐÞÒ ÈÓÐÒ Ð Ò Û Ù ÇÖ Ò Þ Ò Ð Ò ÚÞÚ ÃÝØ Ð ß
Ä ØÓÔ ÓÚ Ô Ò Ó Ð Ø Ùú РѺºº ºººÚ ØÖ Ð ÓÚ Ô Ò Ð Ò Ñº Ì Ñ Ò Ò Ò Ñ Ò ÔÓ Ô Ñ Ð ØÓÔ ÓÚ Ô Ò Ò ÐÓ٠Ѻºº Ë Ú Ð ÞÖÓÚÒ Ò Ò ÐÓÙ Ñ Ò Ø ÖÙõ Ø Ó ÒÙ ÔÓ Ô ÐÒÓ Ý Ñ Ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Ò ÔÐÞ Ó Ø Ó Ä Ô ËÝÑÔ Þ ÙÑ Æ ÚõØ Ú Ù ÖÑÝ Ã Ö ÓÔ Ã ØÙ Ý ß ÚÞÚ Ð Ò Ñ ÐÙ Ù ÃÝØ Ð ÙÑÙÐÓÔÙÒØ ÖÓ Ò À ÒÖ ² Ö µ º Ê ØØ Ö Ä ØÓÔ ÓÚ Ô Ò Ó Ð Ø Ùú РѺºº
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Ò ÔÐÞ Ó Ø Ó Ä Ô ËÝÑÔ Þ ÙÑ Æ ÚõØ Ú Ù ÖÑÝ Ã Ö ÓÔ Ã ØÙ Ý ß ÚÞÚ Ð Ò Ñ ÐÙ Ù ÃÝØ Ð ÙÑÙÐÓÔÙÒØ ÖÓ Ò À ÒÖ ² Ö µ º Ê ØØ Ö Ä ØÓÔ ÓÚ Ô Ò Ó Ð Ø Ùú РѺºº
ÑÒ Ô Ò ººº ººº ÚÒÓ Þ Ò Ñ º ØÙÑ ÚÝ Ò Ð ØÓõÒ Ó ÔÖÚÒ Ó Ð Ò õ Ó ÞÔÖ ÚÓ ØÓÑÙ Úõ Ò Ò Ú Ù º ØÓ Ò ÙÚ Ø ÐÒ Ñ Ñ ÔÓ Ú Ñ Þ ÑÒ Ñ Ô Ò Ù Ø Ö Ò ÓÒ Ðº Î Ð Ý ÑÓ Ð Ò Ð Ó
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½ß¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò Ð Ò Þ ÎÖÓ Ò ÞÔÖ ÚÝ ÎÓÐÒ ØÖ ÙÒ ËÝÑÔ Þ ÙÑ ÔÓ ÖÓ Ò ÃÝØ Ð ÄÓ Ú ÛÖ Ø Ò º Ú Öº Û ÒØ Ö Ò Ê Øغµ Ê Ù ÑÒ Ô Ò ººº ººº ÚÒÓ Þ Ò Ñ º ØÙÑ ÚÝ Ò Ð ØÓõÒ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½ß¾»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÎÖÓ Ò Ð Ò Þ ÎÖÓ Ò ÞÔÖ ÚÝ ÎÓÐÒ ØÖ ÙÒ ËÝÑÔ Þ ÙÑ ÔÓ ÖÓ Ò ÃÝØ Ð ÄÓ Ú ÛÖ Ø Ò º Ú Öº Û ÒØ Ö Ò Ê Øغµ Ê Ù ÑÒ Ô Ò ººº ººº ÚÒÓ Þ Ò Ñ º ØÙÑ ÚÝ Ò Ð ØÓõÒ
 ÈÒ õ ÎÝ ÞÒ Ú ÐØÖÓÒÓÚ ÓÔØ Ý ØÑ Ú ÚÓ ÚÓ ÎÝ ÓÒ ÞÔ Ó õò ß ß ÒÙÑÖÝ ÒÐÝØÝ ÎÝ ÞÒ ÈÓÖÙÓÚ ØÓÖ ÈÐ ÚÔÓØÙ ÔÖÞØÒÓ ÔÓÐ ÚÖ ÈÖÓ ÚÔÓØ ÚÐØÝ ÞÓÖÞÒ Ü ØÙ Ú ÐÚÒ ÞÔ ÓÝ õòº ÈÖÚÒ ÔÓÚ Ú ØÓÑ ú ÙÑ Ð ÔÖÓÐÑ õø ØÖØÒ ÒÙÑÖÝ Ó ÔÓÐ ú ÔÓ
ÈÒ õ ÎÝ ÞÒ Ú ÐØÖÓÒÓÚ ÓÔØ Ý ØÑ Ú ÚÓ ÚÓ ÎÝ ÓÒ ÞÔ Ó õò ß ß ÒÙÑÖÝ ÒÐÝØÝ ÎÝ ÞÒ ÈÓÖÙÓÚ ØÓÖ ÈÐ ÚÔÓØÙ ÔÖÞØÒÓ ÔÓÐ ÚÖ ÈÖÓ ÚÔÓØ ÚÐØÝ ÞÓÖÞÒ Ü ØÙ Ú ÐÚÒ ÞÔ ÓÝ õòº ÈÖÚÒ ÔÓÚ Ú ØÓÑ ú ÙÑ Ð ÔÖÓÐÑ õø ØÖØÒ ÒÙÑÖÝ Ó ÔÓÐ ú ÔÓ
Ä Ô Ö Ó ØÒ Æ Ò Ô Ñ ÞÖÓÚÒ ú Ò Ð Ôõ Ò Ô º ÅÓúÒ Ò Ø Þ Ú ÚÞÔÓÑ ÒÓÙ Ò Ù Ò ¹ Ð ÑÙ Ò Ú ÓÞ Ò Ð Ó Ø ß Ø Ý Þ Ð Ò ÒÓØ Ý ½ Ð º È Ò ØÓ ÑÒÓú ØÚ Ð Ó Ø Ó ú Ò Ú ÚÖÓ Ù
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Á Ð Ý ÓÑ Ò Þ Ô Ò õ Ý Âº ÃÓÐ ËÝÑÔ Þ ÙÑ Ð Ò Ð Ò Ô Ò õ Ý ÝÑÒÓ Ð ¾»¾¼½ ÒÓÚÙ ÖÚ ÒÓ Ú Ø ØÖÓÔ ÝØÙÑ ÃÝØ Ð ÒÓ Ö Ù ÖÖ Ö ÒÙ Ä Ô Ö Ó ØÒ Æ Ò Ô Ñ ÞÖÓÚÒ ú
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Á Ð Ý ÓÑ Ò Þ Ô Ò õ Ý Âº ÃÓÐ ËÝÑÔ Þ ÙÑ Ð Ò Ð Ò Ô Ò õ Ý ÝÑÒÓ Ð ¾»¾¼½ ÒÓÚÙ ÖÚ ÒÓ Ú Ø ØÖÓÔ ÝØÙÑ ÃÝØ Ð ÒÓ Ö Ù ÖÖ Ö ÒÙ Ä Ô Ö Ó ØÒ Æ Ò Ô Ñ ÞÖÓÚÒ ú
Matematika v proměnách věků. II
 Matematika v proměnách věků. II Helena Durnová Matematičky včera a dnes In: Jindřich Bečvář (editor); Eduard Fuchs (editor): Matematika v proměnách věků. II. (Czech). Praha: Prometheus, 2001. pp. 106 137.
Matematika v proměnách věků. II Helena Durnová Matematičky včera a dnes In: Jindřich Bečvář (editor); Eduard Fuchs (editor): Matematika v proměnách věků. II. (Czech). Praha: Prometheus, 2001. pp. 106 137.
Ä ØÓ Ù ú ÔÓ Ú Ð ÒÓ Ø Ý ÖÓ ÔÓ Þ Ñ Þ Ñ Ò Ó ÔÓ ØÙ Ù Ý ÔÖÓ Ð Ð Ô Ò À Ö õø ÖÓ Ô º Ú Ð Ñ Ð ØÓ ÔÖÓØÓú ÓÒ Ò ß Ý Ñ ÖÒ ß Ù Ò Þ ÔÖõ ÐÓ Óú Ñ Ð Ò Ó ÔÓÑÓ ÐÓ Úõ ÑÙ ú
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ È Ö Ø Ý ÐÙ ÓÚ Ò ÓÚÒÝ Î Ø Ú ØÙ Æ Ô Ð Ø Ñ Æ ÚõØ ÚÝ ØÓÚ Ò ËÔÓÐ Ò ÖÓÒ ÃÝØ Ð ÒÓÔ Ù ÔÐÓØÙ Ä ØÓ Ù ú ÔÓ Ú Ð ÒÓ Ø Ý ÖÓ ÔÓ Þ Ñ Þ Ñ Ò Ó ÔÓ ØÙ Ù Ý ÔÖÓ Ð Ð
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ È Ö Ø Ý ÐÙ ÓÚ Ò ÓÚÒÝ Î Ø Ú ØÙ Æ Ô Ð Ø Ñ Æ ÚõØ ÚÝ ØÓÚ Ò ËÔÓÐ Ò ÖÓÒ ÃÝØ Ð ÒÓÔ Ù ÔÐÓØÙ Ä ØÓ Ù ú ÔÓ Ú Ð ÒÓ Ø Ý ÖÓ ÔÓ Þ Ñ Þ Ñ Ò Ó ÔÓ ØÙ Ù Ý ÔÖÓ Ð Ð
¾ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ Ø Ú ÃÖ ØÙ Â Þ þ ÝÞ Ø Ó ÔÖ Ð Ó È þò º Î Ò Ñ Þ ÔÙ Ø³Ø ÓÖ ÒÝ Ò Ò Ñ ÔÓ Ø ÚØ Þ þ Ð Ý ÞÒÓÚÙ ÞÒÓÚÙ ÚÞ þú Ø
 ¾ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ Ø Ú ÃÖ ØÙ Â Þ þ ÝÞ Ø Ó ÔÖ Ð Ó È þò º Î Ò Ñ Þ ÔÙ Ø³Ø ÓÖ ÒÝ Ò Ò Ñ ÔÓ Ø ÚØ Þ þ Ð Ý ÞÒÓÚÙ ÞÒÓÚÙ ÚÞ þú Ø þ ݺ ÃÓ ½ ¹ Íþ ÚÓ Ò þ ÐÓÚÓ Î ØÓÑØÓ þ Ð ÖÒ þ Ó ÓÔ Ù
¾ ÈÊ ÎÇ Â ÊÆÇËÌÁ ÈÊ Á ÃÇËÌ Ä Úº ÌÇÅ þ Ë Î ÊÆ ÅÓØØÓ Ø Ú ÃÖ ØÙ Â Þ þ ÝÞ Ø Ó ÔÖ Ð Ó È þò º Î Ò Ñ Þ ÔÙ Ø³Ø ÓÖ ÒÝ Ò Ò Ñ ÔÓ Ø ÚØ Þ þ Ð Ý ÞÒÓÚÙ ÞÒÓÚÙ ÚÞ þú Ø þ ݺ ÃÓ ½ ¹ Íþ ÚÓ Ò þ ÐÓÚÓ Î ØÓÑØÓ þ Ð ÖÒ þ Ó ÓÔ Ù
Ù Ò ß õø Ø Ñ Ù Ñººº ºººÒ Ô Ñ Ô ÑÖ Þ Ú Ö Ò ÔÓÐÓÚ ÒÝ Ù Ò Ý Ó ÓÒ Ù Ô ÔÖ ÚÙ ØÓ ÓØÓ Þ ØÙº È ÚÓ Ò ØÓ Úõ Þ Ò ÐÓ Ø ØÓ ÈÖÓ ÐÙúÙ ÒÝ ÓÒ Þ ÑÝ Þ Ø Ù Ö Ú ÐÑ Ù Þ Òµ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÓØ Ò ÔÐ Ø ß ÙÞ Ú Ò ÓÙØ ú Ç ÈÓ Ð ß ÁÒ Ñ ÑÓÖ Ñ È Ò õ Ý Þ ÚÐ ØÒ ÎÖÓ Ò Ò ÆÓÚ Ð ÒÓÚ Ú ÓÖÙ ÓØ Ò Ò µð Ø Ò Æ Ò ÚõØ Ú Ú Ù ËÐ ÖÓ ØÙ ÔÓÐÝ Ò ØÖÙ Å ÑÑ ÐÐ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ¾»¾¼½¾ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ÓØ Ò ÔÐ Ø ß ÙÞ Ú Ò ÓÙØ ú Ç ÈÓ Ð ß ÁÒ Ñ ÑÓÖ Ñ È Ò õ Ý Þ ÚÐ ØÒ ÎÖÓ Ò Ò ÆÓÚ Ð ÒÓÚ Ú ÓÖÙ ÓØ Ò Ò µð Ø Ò Æ Ò ÚõØ Ú Ú Ù ËÐ ÖÓ ØÙ ÔÓÐÝ Ò ØÖÙ Å ÑÑ ÐÐ
Æ ú Ð ØÓ Ó Ð Ø Ñ Ð ØÓõÒ Ó Ö Ñ ÐÝõ Ð ÑÒÓ Ó Ò ÔÓÚÞ Ò Ø Ñ Úõ ÒÓ Ð ØÓ ÙÖÝ Ð Ò ÝØ Ý Ð ÓÚ ÖÓÞ Ú ØÐÝ Ò Ù Ó Ø Ò Ú Ø ÚÙº Æ ÓÒ Ñ ØÝØÓ Ò Ý Ô õðý Ð Ñ Þ ÝØ Ò Ø ÐÓ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Â Ò À Ö õø ß ¼ Ð Ø Î ØÓÖ Ì Ð Ò ß Ò Ñ ÑÓÖ Ñ Æ ÚõØ Ú Ù Ñ Ð Î õ È ØÖ Ë ĐÓÒ ß ØÙ ÓØÓ Ö ººº Î Ø Ú ØÙ ÓØÓ Ö ÓÚ Ò ß ÖÚÝ È Ö Ø Ý Ú Ö ÚÙ ÃÝØ Ð ß ÝÑÒÓ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Â Ò À Ö õø ß ¼ Ð Ø Î ØÓÖ Ì Ð Ò ß Ò Ñ ÑÓÖ Ñ Æ ÚõØ Ú Ù Ñ Ð Î õ È ØÖ Ë ĐÓÒ ß ØÙ ÓØÓ Ö ººº Î Ø Ú ØÙ ÓØÓ Ö ÓÚ Ò ß ÖÚÝ È Ö Ø Ý Ú Ö ÚÙ ÃÝØ Ð ß ÝÑÒÓ
ÍÔÖÓ Ø Þ ÑÒ Ó Ô Ò Ù Æ ÑÝ Ð Ñ Ø ÒØÓ Ö Ø Ò Þ ÑÒ Ô Ò Ó Ò Ó Ó Ð Ù ÑÒÓ ú ÚÓ Ò õ ØÙ º ÈÓÞÓÖÙ Ô õ Ù Ô õ Ô Ô Ú Ø Ð Ò õ Ó ÞÔÖ ÚÓ º ÅÓ Ù ÔÓ ÓÚ Ø ß Ö ØÓ Ò Ñ ß ÔÓ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ È Ö Ø Ý ÐÙ ÓÚ Ò ÓÚÒÝ ÃÝØ Ý Ô Ñ ÓØ Ò ÔÐ Ø ÎÞÚ Ð Ò Ñ È ÐÓ Ú Ø Ø Ø Ã ØÙ Ú ÖÓ ÃÝØ Ð ÀÙ ÖÒ Þ Ö Ò ÍÔÖÓ Ø Þ ÑÒ Ó Ô Ò Ù Æ ÑÝ Ð Ñ Ø ÒØÓ Ö Ø Ò Þ ÑÒ Ô
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ È Ö Ø Ý ÐÙ ÓÚ Ò ÓÚÒÝ ÃÝØ Ý Ô Ñ ÓØ Ò ÔÐ Ø ÎÞÚ Ð Ò Ñ È ÐÓ Ú Ø Ø Ø Ã ØÙ Ú ÖÓ ÃÝØ Ð ÀÙ ÖÒ Þ Ö Ò ÍÔÖÓ Ø Þ ÑÒ Ó Ô Ò Ù Æ ÑÝ Ð Ñ Ø ÒØÓ Ö Ø Ò Þ ÑÒ Ô
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ººº ËÝÑÔ Þ ÙÑ È Ô Ú Ý Ø Ò ß ß Ô Ô ÝÐÙÑ Ö Ó Ý È Ö Ø Ý Ú Ò ÓÚÒ ÓØÓ Ö ÓÚ Ò ß ÔÖ ÚÝ Ó Ö Þ Æ Ø Ø ¼ ¼¼¼ ÃÝØ Ð ß Ö Ó ÖÔÙ ØÖ ÓÒÙ Ç ú Ò Ò ÚÖ ØÝ Ú ÔÖÓ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ ½»¾¼½½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ ººº ËÝÑÔ Þ ÙÑ È Ô Ú Ý Ø Ò ß ß Ô Ô ÝÐÙÑ Ö Ó Ý È Ö Ø Ý Ú Ò ÓÚÒ ÓØÓ Ö ÓÚ Ò ß ÔÖ ÚÝ Ó Ö Þ Æ Ø Ø ¼ ¼¼¼ ÃÝØ Ð ß Ö Ó ÖÔÙ ØÖ ÓÒÙ Ç ú Ò Ò ÚÖ ØÝ Ú ÔÖÓ
õò ÓÙØúÒ úóú Þ Ð»¾¼½ ½º º º º Ùõ ÔÖÓ ØÑ ÔÒÓ Ñº ½º Ò ÒÖ ÐÒ ÔÖ Ú ÔõÐ ÓÚÞØ Ó ØÖÓ úðþº ½º Ó ØÓ Þ ÖØ Ýú ÒÑ õ Ó ½º Ù Ñ Ú ÞÐÑØ ÐÒÒ ÞÒ ÑÝ ÒÚѺ ½º ÒÐ ÒÐÚÒõ ÔÖÞ
 ¾ ØÖÒ úóú ÚõÒÝ Ö ÐÒÑ ÚØÔÑ ÞÒ ß ÙÒ ¾¼½ ÖÓÒ ½ ¾¾ ¾ ½ Ü ½¼¼ Ü ¼¼ ÓÙØúÒ úóú ÐÓ ½ ½º ¹ Ý º º º ÓÓÒÒ Ú ØÒµº ¹ ½ Òµ ¹ º ¹ ¼ ¾º ½¾½¾ ¾¼¼¼ õò ÓÙØúÒ úóú Þ Ð»¾¼½ ½º º º º Ùõ ÔÖÓ ØÑ ÔÒÓ Ñº ½º Ò ÒÖ ÐÒ ÔÖ Ú ÔõÐ ÓÚÞØ
¾ ØÖÒ úóú ÚõÒÝ Ö ÐÒÑ ÚØÔÑ ÞÒ ß ÙÒ ¾¼½ ÖÓÒ ½ ¾¾ ¾ ½ Ü ½¼¼ Ü ¼¼ ÓÙØúÒ úóú ÐÓ ½ ½º ¹ Ý º º º ÓÓÒÒ Ú ØÒµº ¹ ½ Òµ ¹ º ¹ ¼ ¾º ½¾½¾ ¾¼¼¼ õò ÓÙØúÒ úóú Þ Ð»¾¼½ ½º º º º Ùõ ÔÖÓ ØÑ ÔÒÓ Ñº ½º Ò ÒÖ ÐÒ ÔÖ Ú ÔõÐ ÓÚÞØ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Ó ÖÙ Ñ ß Ú Ö Ò Þ ÒÝ ÔÖ Ú Þ Ú ÓÖÙ ËÔÓÐ ÒÓ Ø Ä ÓÐ Ñ ÐÙ Ù ÔÖ ÚÝ ÑÙØÒ Ö Ó ØÒ ËÝÑÔ Þ ÙÑ Æ Ú õð
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Ó ÖÙ Ñ ß Ú Ö Ò Þ ÒÝ ÔÖ Ú Þ Ú ÓÖÙ ËÔÓÐ ÒÓ Ø Ä ÓÐ Ñ ÐÙ Ù ÔÖ ÚÝ ÑÙØÒ Ö Ó ØÒ ËÝÑÔ Þ ÙÑ Æ Ú õðó ÖÖ Ø ÃÝØ Ð ÙÔ ÓÖ ÖÙ ÒÓ Æ Ö Ò õ Ó Ó Ô ØÖÒ ÔÓ Þ Ñ ººº
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Ó ÖÙ Ñ ß Ú Ö Ò Þ ÒÝ ÔÖ Ú Þ Ú ÓÖÙ ËÔÓÐ ÒÓ Ø Ä ÓÐ Ñ ÐÙ Ù ÔÖ ÚÝ ÑÙØÒ Ö Ó ØÒ ËÝÑÔ Þ ÙÑ Æ Ú õðó ÖÖ Ø ÃÝØ Ð ÙÔ ÓÖ ÖÙ ÒÓ Æ Ö Ò õ Ó Ó Ô ØÖÒ ÔÓ Þ Ñ ººº
Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování. vypracovanou úlohu podle níže uvedených zadání. To mimo jiné znamená, že
 Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
VECTOR r1, Ú ØÓÖ r2 r = (r.x,r.y,r.z) IF dr.x < -L/2 THEN dr.x := dr.x + L ELSE IF dr.x > L/2 THEN dr.x := dr.x - L
 Ó Ò ÓÒ ÙÖ Ô ÖÝÚÝ ÑÓÐ ÙÐ ÔÖÓ Ð Ñ Ú Å µ Ò Ù õô ØÒ ÒÓÚ Ò ÑÓ Ð ÌÁÈ È ºµ ÔÖÓ Ð Ñ ú ÓÚ Ò ÕÙ Ð Ö Ø ÓÒµ Ð ÓÚ Ø Ö Ý ÖÓÚÒÓÚ ÔÖÓ Ð ÓÚ ÔÖÓ Ð º º º µ ÓÒÚ Ö Ò Ò ÑÙÐ Ü Ø Ô ¼¼º 1/23 ½ º ÔÖÓ Ò ¾¼½¾ Å ØÓ ÑÙÐ ËØ ÖØ ÑÙÐ ÔÓ
Ó Ò ÓÒ ÙÖ Ô ÖÝÚÝ ÑÓÐ ÙÐ ÔÖÓ Ð Ñ Ú Å µ Ò Ù õô ØÒ ÒÓÚ Ò ÑÓ Ð ÌÁÈ È ºµ ÔÖÓ Ð Ñ ú ÓÚ Ò ÕÙ Ð Ö Ø ÓÒµ Ð ÓÚ Ø Ö Ý ÖÓÚÒÓÚ ÔÖÓ Ð ÓÚ ÔÖÓ Ð º º º µ ÓÒÚ Ö Ò Ò ÑÙÐ Ü Ø Ô ¼¼º 1/23 ½ º ÔÖÓ Ò ¾¼½¾ Å ØÓ ÑÙÐ ËØ ÖØ ÑÙÐ ÔÓ
ØÖ Ø Ì ØÓ Ø Ò ÞÔÖ Ú Ó ÙÑ ÒØ Ð ØÖÓÒ ÑÙ Ú Ð Ò Ò ÑÙ ÐÓÚÒ Ù ÐÓ¹ Ú Ø ØÓ Ö Ñ Ø ÓÙ ÒÓØ Ø Ö ÚÞÒ Ú ÒØÖÙ ÓÑÔÙØ Ò Ð Ò Ú Ø Ý Ó Ö ¾¼¼½º ÔÖ Ú Ó Ù Ô Ð ÔÓ Ó Ò Þ Ñ Ò Ô
 ØÖ Ø Ì ØÓ Ø Ò ÞÔÖ Ú Ó ÙÑ ÒØ Ð ØÖÓÒ ÑÙ Ú Ð Ò Ò ÑÙ ÐÓÚÒ Ù ÐÓ¹ Ú Ø ØÓ Ö Ñ Ø ÓÙ ÒÓØ Ø Ö ÚÞÒ Ú ÒØÖÙ ÓÑÔÙØ Ò Ð Ò Ú Ø Ý Ó Ö ¾¼¼½º ÔÖ Ú Ó Ù Ô Ð ÔÓ Ó Ò Þ Ñ Ò ÔÖÓ Ø ÔÖÓ Ó Ø ØÒ ÞÝ Ý ÖÒÙ Ú ÓÞ ¹ ØÙ ÔÖÓ Ù ÓÚ Ò Ø ÓÚ
ØÖ Ø Ì ØÓ Ø Ò ÞÔÖ Ú Ó ÙÑ ÒØ Ð ØÖÓÒ ÑÙ Ú Ð Ò Ò ÑÙ ÐÓÚÒ Ù ÐÓ¹ Ú Ø ØÓ Ö Ñ Ø ÓÙ ÒÓØ Ø Ö ÚÞÒ Ú ÒØÖÙ ÓÑÔÙØ Ò Ð Ò Ú Ø Ý Ó Ö ¾¼¼½º ÔÖ Ú Ó Ù Ô Ð ÔÓ Ó Ò Þ Ñ Ò ÔÖÓ Ø ÔÖÓ Ó Ø ØÒ ÞÝ Ý ÖÒÙ Ú ÓÞ ¹ ØÙ ÔÖÓ Ù ÓÚ Ò Ø ÓÚ
ÈÖõ ººº ººº Ú Þ Ý Ò ÔÐ Ø ÐÒÓÙ ÞÔ Ú Ñ ÔÓÐÙ Ö ÔÖÓ ÒÓÙººº ÞÔ Ú Ñ Þ Ã ÖÐ Ñ ÈÐ Ð Ñ ÙØÓÖ Ñ ÒØ ÖÔÖ Ø Ñ Ø ØÓ Ô Ò Ýº ÈÖÓØÓú Ñ ÚÖ ÚÖ Ø Ð Þ Þ ¹ Þ Ù Ö ÒÓ Ñ ÔÖÓ ÙÐ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ò À ÒÓÙ Ï Ò ¾¼½ ÃÓÐÓ Ú ÙÑ ÈÐÞ Æ ÚõØ ÚÝ ØÓÚ Ò ß Ê ÙÐ ËÔÓÐ Ò ÖÓÒ ÊÓÑ Ö Ô ÃÝØ Ð ÏÒÖØ Ò ÙÑ ÒÒÒ Ö µ Ï ÖÖÑ ÒÒ ÈÖõ ººº ººº Ú Þ Ý Ò ÔÐ Ø ÐÒÓÙ ÞÔ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Þ Þ ØÙ Ò À ÒÓÙ Ï Ò ¾¼½ ÃÓÐÓ Ú ÙÑ ÈÐÞ Æ ÚõØ ÚÝ ØÓÚ Ò ß Ê ÙÐ ËÔÓÐ Ò ÖÓÒ ÊÓÑ Ö Ô ÃÝØ Ð ÏÒÖØ Ò ÙÑ ÒÒÒ Ö µ Ï ÖÖÑ ÒÒ ÈÖõ ººº ººº Ú Þ Ý Ò ÔÐ Ø ÐÒÓÙ ÞÔ
Abstract. 1 Introduction
 Ý Ò ÔØ Ú Ø Ñ Ø ÓÒ Ì Æ ÜØ Ñ Ò ÓÒ Â ÒÒ Î ÃÙ Ð ÌÙÓÑ Â ÄÙ ÓÖ ÒØ Ö ÈÇ ÓÜ Á¹ ¼¼½ ÍÒ Ú Ö ØÝ Ó ÂÝÚĐ ÝÐĐ ÇØÓ Ö ¾¼¼ Abstract Ï ÔÖÓÔÓ Ò Û Ô Ý ÓÑ ØÖ ÑÓ Ð ÓÖ ØÛÓ¹ Ñ Ò ÓÒ Ð Ø ÑÙÐ Ù ÓÐÓÖ «Ö Ò ÓÒ Ô Ö Ñ Ø Ö Þ Ò Ø Ø Ö ÓÐ
Ý Ò ÔØ Ú Ø Ñ Ø ÓÒ Ì Æ ÜØ Ñ Ò ÓÒ Â ÒÒ Î ÃÙ Ð ÌÙÓÑ Â ÄÙ ÓÖ ÒØ Ö ÈÇ ÓÜ Á¹ ¼¼½ ÍÒ Ú Ö ØÝ Ó ÂÝÚĐ ÝÐĐ ÇØÓ Ö ¾¼¼ Abstract Ï ÔÖÓÔÓ Ò Û Ô Ý ÓÑ ØÖ ÑÓ Ð ÓÖ ØÛÓ¹ Ñ Ò ÓÒ Ð Ø ÑÙÐ Ù ÓÐÓÖ «Ö Ò ÓÒ Ô Ö Ñ Ø Ö Þ Ò Ø Ø Ö ÓÐ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Æ õ ÔÓ Þ ÑÒ ÝÑÔ Þ ÙÑ Ð Ø Ð ÖØÓ ÖÙ Ñ ËÔÓÐ Ò ÖÓÒ Ë Ø Ú Ò ØÓÚ Ò ÃÝØ Ð À Ð Û ÒØ Ö Ó ËØ Ò Ð Ú ËØ
 ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Æ õ ÔÓ Þ ÑÒ ÝÑÔ Þ ÙÑ Ð Ø Ð ÖØÓ ÖÙ Ñ ËÔÓÐ Ò ÖÓÒ Ë Ø Ú Ò ØÓÚ Ò ÃÝØ Ð À Ð Û ÒØ Ö Ó ËØ Ò Ð Ú ËØÙ Ð Ä Ø Ñ Ñ Ð Ø Ñººº ººº ØÓ Ó Ò ÐÓÙ Ñ Ñ Ð Ø Ñº Ú ÐÑ
ÔÖ ÚÓ ÃÐÙ Ù ØÙ ØÖÓÔ ÝØÙÑ ÖÒÓ»¾¼½ ÒÒÓ Ø ÐÙ Ù ß Ð Ò Ú ÓÖÓÚ Þ Æ õ ÔÓ Þ ÑÒ ÝÑÔ Þ ÙÑ Ð Ø Ð ÖØÓ ÖÙ Ñ ËÔÓÐ Ò ÖÓÒ Ë Ø Ú Ò ØÓÚ Ò ÃÝØ Ð À Ð Û ÒØ Ö Ó ËØ Ò Ð Ú ËØÙ Ð Ä Ø Ñ Ñ Ð Ø Ñººº ººº ØÓ Ó Ò ÐÓÙ Ñ Ñ Ð Ø Ñº Ú ÐÑ
Informatická sekce Matematicko-fyzikální fakulta Univerzita Karlova v Praze. MIS 2006 14. 21. ledna 2006, Josefův Důl Sborník semináře
 Informatická sekce Matematicko-fyzikální fakulta Univerzita Karlova v Praze MIS 2006 14. 21. ledna 2006, Josefův Důl Sborník semináře PRAHA 2006 Všechna práva vyhrazena. Tato publikace ani žádná její částnesmí
Informatická sekce Matematicko-fyzikální fakulta Univerzita Karlova v Praze MIS 2006 14. 21. ledna 2006, Josefův Důl Sborník semináře PRAHA 2006 Všechna práva vyhrazena. Tato publikace ani žádná její částnesmí
Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
IB109 Návrh a implementace paralelních systémů. Organizace kurzu a úvod. RNDr. Jiří Barnat, Ph.D.
 IB109 Návrh a implementace paralelních systémů Organizace kurzu a úvod RNDr. Jiří Barnat, Ph.D. Sekce IB109 Návrh a implementace paralelních systémů: Organizace kurzu a úvod str. 2/25 Organizace kurzu
IB109 Návrh a implementace paralelních systémů Organizace kurzu a úvod RNDr. Jiří Barnat, Ph.D. Sekce IB109 Návrh a implementace paralelních systémů: Organizace kurzu a úvod str. 2/25 Organizace kurzu
ÖÐ ÍÒ Ú Ö ØÝ Ò ÈÖ Ù ÙÐØÝ Ó Å Ø Ñ Ø Ò È Ý Å ËÌ Ê ÌÀ ËÁË ÒØÓÒ Ê Ô Ó ÒØ Ê ÓÒ Ò Ò ØÓÑ ÆÙÐ ÁÒ Ø ØÙØ Ó È ÖØ Ð Ò ÆÙÐ Ö È Ý ËÙÔ ÖÚ ÓÖ Ó Ø Ñ Ø Ö Ø ÔÖÓ º ÊÆ Öº
 ÖÐ ÍÒ Ú Ö ØÝ Ò ÈÖ Ù ÙÐØÝ Ó Å Ø Ñ Ø Ò È Ý Å ËÌ Ê ÌÀ ËÁË ÒØÓÒ Ê Ô Ó ÒØ Ê ÓÒ Ò Ò ØÓÑ ÆÙÐ ÁÒ Ø ØÙØ Ó È ÖØ Ð Ò ÆÙÐ Ö È Ý ËÙÔ ÖÚ ÓÖ Ó Ø Ñ Ø Ö Ø ÔÖÓ º ÊÆ Öº Â Ò ÃÚ Ð Ö˺ ËØÙ Ý ÔÖÓ Ö ÑÑ È Ý ËÔ Ð Þ Ø ÓÒ ÆÙÐ Ö Ò
ÖÐ ÍÒ Ú Ö ØÝ Ò ÈÖ Ù ÙÐØÝ Ó Å Ø Ñ Ø Ò È Ý Å ËÌ Ê ÌÀ ËÁË ÒØÓÒ Ê Ô Ó ÒØ Ê ÓÒ Ò Ò ØÓÑ ÆÙÐ ÁÒ Ø ØÙØ Ó È ÖØ Ð Ò ÆÙÐ Ö È Ý ËÙÔ ÖÚ ÓÖ Ó Ø Ñ Ø Ö Ø ÔÖÓ º ÊÆ Öº Â Ò ÃÚ Ð Ö˺ ËØÙ Ý ÔÖÓ Ö ÑÑ È Ý ËÔ Ð Þ Ø ÓÒ ÆÙÐ Ö Ò
 Ò Ø Ó ÎÀÌ ÈÐÝ ÐÓÝ Þ ÝÞ ÐÒ Ñ Á ÈÖÓº ÂÓ ÆÓÚ Ëº ÁÒº ÂÓ ÓÖ Ëº ÁÒº ÅÐ ÙÖõ ˺ ÁÒº ÃÖР˺ Óº ÄÑÐ ÖØÓÚ Ëº ÈÖ ¾¼¼¼ ¾ Ç ÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ËÞÒÑ ÝÑÓÐ
Ò Ø Ó ÎÀÌ ÈÐÝ ÐÓÝ Þ ÝÞ ÐÒ Ñ Á ÈÖÓº ÂÓ ÆÓÚ Ëº ÁÒº ÂÓ ÓÖ Ëº ÁÒº ÅÐ ÙÖõ ˺ ÁÒº ÃÖР˺ Óº ÄÑÐ ÖØÓÚ Ëº ÈÖ ¾¼¼¼ ¾ Ç ÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ËÞÒÑ ÝÑÓÐ
Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA Dnešní látka: Metoda sítí pro D úlohy. Poissonova rovnice. Vlnová rovnice. Rovnice vedení tepla. Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 3, ČVUT, Praha,. Text přednášky
Předmět: MA Dnešní látka: Metoda sítí pro D úlohy. Poissonova rovnice. Vlnová rovnice. Rovnice vedení tepla. Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 3, ČVUT, Praha,. Text přednášky
Literatura: Kapitoly 3, 4 a 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
