Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
|
|
|
- Josef Švec
- před 6 lety
- Počet zobrazení:
Transkript
1 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx y u yy = 0, převed te i do kanonického tvaru a načrtněte reálné charakteristiky. 2. Určete typ parciální diferenciální rovnice x u xx 2 xy u xy + y u yy u y = 0, x, y > 0, a převed te i do kanonického tvaru. 3. Převed te parciální diferenciální rovnici 2 u xx + 2 u xy + u yy + 4 u x + 4 u y + u = 0 na neednodušší kanonický tvar. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce tří a více proměnných 4. Určete kanonický tvar a typ rovnice u xx + 2 u xy 2 u xz + 2 u yy + 6 u zz = 0, u = u(x, y, z). 5. Určete kanonický tvar a typ rovnice 4 u xx 4 u xy 2 u yz + u y + u z = 0, u = u(x, y, z). 6. Určete kanonický tvar a typ rovnice u xy u xz + u x + u y u z = 0, u = u(x, y, z). 7. Určete kanonický tvar a typ rovnice u xx + 2 u xy + 2 u yy + 2 u yz + 2 u yt + 2 u zz + 3 u tt = 0, u = u(x, y, z, t). 1
2 8. Určete kanonický tvar a typ rovnice u x1 x n u xk x k 2 k=2 n 1 k=1 u xk x k+1 = 0, u = u(x 1,..., x n ). 9. Určete kanonický tvar a typ rovnice u x1 x n ( 1) k u xk 1 x k = 0, u = u(x 1,..., x n ). k=2 3 Řešení Cauchyových úloh pro lineární PDR 2. řádu metodou charakteristik 10. Necht u C 2 (R 2 ) e řešením rovnice a u xx + 2 b u xy + c u yy = 0, a 0, kde a, b, c sou reálná čísla. Dokažte, že e-li tato rovnice parabolická, pak existuí funkce F, G C 2 (R) takové, že kde m = b/a. 11. Nalezněte řešení Cauchyovy úlohy u(x, y) = F (m x + y) + x G(m x + y), 4 y 2 u xx + 2 (1 y 2 ) u xy u yy 2 y 1 + y 2 (2 u x u y ) = 0 v R 2, u(x, 0) = f(x), u y (x, 0) = g(x), x R, kde f C 2 (R) a g C 1 (R) sou zadané funkce. 12. Nalezněte řešení Cauchyovy úlohy u xx 2 (sin x) u xy (3 + cos 2 x) u yy + u x + (2 sin x cos x) u y = 0 v R 2, u(x, cos x) = 0, u y (x, cos x) = e x 2 cos x, x R. 13. Nalezněte řešení Cauchyovy úlohy u xx + 2 (cos x) u xy (sin 2 x) u yy (sin x) u y = 0 v R 2, u(x, sin x) = x + cos x, u y (x, sin x) = sin x, x R. 2
3 14. Nalezněte řešení Cauchyovy úlohy (1 cos y) u xx + (cos y) u xy u yy sin y 2 cos y (u x u y ) = 0 v R 2, u(x, 0) = 2 x, u y (x, 0) = 1, x R. 15. Nalezněte řešení Cauchyovy úlohy 2 u xx + 2 u xy 4 u yy 3 u x + 3 u y = 0 v R 2, u(x, 0) = 2 e x 2, uy (x, 0) = 0, x R. 4 Základní vztahy metody konečných diferencí 16. Dokažte, že pro libovolnou funkci v C 2 (R) platí vztahy + v h = v + O(h), v h = v + O(h), 0 v h = v + O(h), δ v h = v + O(h). 17. Dokažte, že pro libovolnou funkci v C 3 (R) platí vztahy 0 v h = v + O(h 2 ), δ v h = v + O(h 2 ). Dále ukažte, že pokud funkce v C 3 (R) pro dané x R a α > 0 splňue pak v (x) = 0. + v h (x) = v (x) + O(h 1+α ) nebo v h (x) = v (x) + O(h 1+α ), 18. Dokažte, že pro libovolnou funkci v C 4 (R) platí vztah δ 2 v h 2 = v + O(h 2 ). 19. Dokažte, že pro libovolnou funkci v C 6 (R) platí vztah δ 4 v h 4 = v (4) + O(h 2 ). 20. Ověřte platnost vztahu δ 2 = + = +. 3
4 5 Lineární a kvazilineární PDR 1. řádu 21. Nalezněte charakteristiky a řešení Cauchyovy úlohy u t +a u x = 0 v R 2, u(x, 0) = sin x pro x R (a 0). 22. Odvod te řešení Cauchyovy úlohy u t + a u x = 0 v R 2, u(x, 0) = u 0 (x) pro x R (a 0) iným způsobem než metodou charakteristik. Návod: zaved te nové proměnné ξ = x at, η = x + at. 23. Nalezněte charakteristiky a řešení Cauchyovy úlohy kde u 0 C 1 (R). u x = 6 x 2 u y v R 2, u(x, 0) = u 0 (x), x R, 24. Nalezněte charakteristiky a řešení Cauchyovy úlohy kde u 0 C 1 (R). u t + x u x = 0 v R 2, u(x, 0) = u 0 (x), x R, 25. Nalezněte charakteristiky a řešení Cauchyovy úlohy u t + x u x + t u = 0 v R 2, u(x, 0) = sin x, x R. 26. Nalezněte charakteristiky a řešení úlohy u x + y u y = 0 v R R +, u(0, y) = 1 y, y > Nalezněte charakteristiky a řešení Cauchyovy úlohy u t + u u x = 0 v R R +, u(x, 0) = u 0 (x), x R, kde 1. u 0 (x) = 0 pro x 0, u 0 (x) = x pro x > 0, 2. u 0 (x) = x pro x 0, u 0 (x) = 0 pro x > 0, 3. u 0 (x) = 0 pro x 0, u 0 (x) = 1 pro x 1, u 0 e spoitá na R a afinní na [0, 1], 4. u 0 (x) = 1 pro x 0, u 0 (x) = 0 pro x 1, u 0 e spoitá na R a afinní na [0, 1], 5. u 0 (x) = sin x. 28. Nalezněte charakteristiky a řešení úlohy (z + y x) u x + (z + x y) u y + z u z = 0 pro x, y R, z > 0, u(x, y, 1) = u 0 (x, y) pro x, y R, kde u 0 C 1 (R 2 ). 4
5 6 Numerické řešení transportní rovnice Ve všech úlohách, v nichž e požadováno vyšetření stability, e tím míněna von Neumannova analýza (t. analýza stability pomocí Fourierovy metody). Rychlost a e ve všech úlohách konstantní. 29. Vyšetřete chybu diskretizace a stabilitu Laxova Friedrichsova schématu pro rovnici u t + a u x = 0, t. schématu 1 2 (U n +1 + U n 1) + a U n +1 U n 1 2 h = Uvažume schéma Ũ n+1 = U n ν 2 (U n +1 U n 1), = 1 n+1 (Ũ Ũ n+1 + Ũ n+1 1 ) pro rovnici u t + a u x = 0. Vyšetřete chybu diskretizace a stabilitu. 31. Uvažume schéma tvaru = α U n + β U n +1 a ukažte, že = Co z toho plyne pro stabilitu schématu U n 2 ( α + β ) 2n = U 0 2. pro řešení rovnice u t + a u x = 0? U n + a U n +1 U n h = Ukažte, že schéma tvaru = α U+1 n + β U 1 n e stabilní pro α + β 1. Co z toho plyne pro Laxovo Friedrichsovo schéma? 33. Uvažume leapfrog scheme přenásobení členem = + U n 1 U n 1 + ν (U+1 n U 1) n = 0. Ukažte, že po a sečtení přes Z získáme { U n U n 2 + ν ( U n U n ) } = = { U n 2 + U n ν (U n U n 1 +1 U +1 n U n 1 ) }. Ukažte, že z toho plyne stabilita schématu pro ν < 1. 5
6 34. Uvažume implicitní schéma U n + a h = 0 pro rovnici u t + a u x = 0. Vyšetřete chybu diskretizace a stabilitu. 35. Uvažume implicitní schéma U n + a 1 h pro rovnici u t + a u x = 0, kde a > 0. Vyšetřete chybu diskretizace a stabilitu. 36. Uvažume implicitní schéma U n + a +1 h = 0 = 0 pro rovnici u t + a u x = 0. Vyšetřete chybu diskretizace a stabilitu. 37. Ukažte, že pro = h 2 e schéma U n stabilní a konzistentní s rovnicí u t + a u x = 0. + a U n +1 U n 1 2 h = Vyšetřete stabilitu a konzistenci následuícího schématu pro rovnici u t + a u x = f: U n+ 1 2 = U n ν 2 (U n +1 U n 1) + f n, = U n ν 2 (U n U n ) + f n Ukažte, že MacCormackovo schéma Ũ n+1 = U n ν (U n +1 U n ) + f n, = 1 2 { } U n + Ũ n+1 ν (Ũ n+1 Ũ n+1 1 ) + fn+1 e schéma druhého řádu přesnosti pro rovnici u t + a u x = f. Ukažte, že pro f = 0 e identické s Laxovým Wendroffovým schématem U n + a U n +1 U n 1 2 h a2 2 U+1 n 2 U n + U 1 n = 0. h Vypočítete fázovou chybu Laxova Wendroffova schématu pro rovnici u t + a u x = 0. 6
7 41. Ukažte, že box scheme 1 2 [ (U n ) (U n + U+1) ] n + a [ (U n h ) + (U+1 n U n ) ] = 1 ( f n f n+1 + f+1 n + f n e aproximace rovnice u t + a u x = f, která e 2. řádu přesnosti a stabilní pro všechna ν R. 42. Uvažume nasleduící variantu leapfrog scheme U n 1 2 ( ) + a 1 δ2 x U n +1 U 1 n 6 2 h = f n. Které uzly pro U schéma spoue? Vyšetřete chybu diskretizace při aproximaci rovnice u t + au x = f a zistěte za akých podmínek e schéma stabilní. 43. Uvažume modifikované schéma Crankovo Nicolsonové ) U n + a U +1 n U 1 n + ε 4 h ( ) 4 δx U n = 1 ( ) f n+1 + f n 2 2 pro numerické řešení rovnice u t + a u x = f. Ukažte, že toto schéma e druhého řádu přesnosti, disipativní řádu 4 pro ε (0, 2) a vyšetřete, kdy e stabilní. 44. Uvažume schéma U n + a U +1 n U n = 0 h pro numerické řešení rovnice u t + a u x = 0. Vypočítete fázovou chybu a zistěte, kdy e splněn princip maxima. 45. Uvažume schéma 1 2 (U n +1 + U n 1) + a U n +1 U n 1 2 h pro numerické řešení rovnice u t + a u x = 0. Vypočítete fázovou chybu a zistěte, kdy e splněn princip maxima. = 0 7
8 7 Rovnice struny (ednorozměrná vlnová rovnice) 46. Necht Ω R 2 e konvexní oblast a necht u C 2 (Ω) splňue rovnici u tt a 2 u xx = 0 v Ω, kde a e kladná konstanta. Metodou charakteristik dokažte, že pak existuí funkce P a Q třídy C 2 takové, že u(x, t) = P (x at) + Q(x + at) pro všechna (x, t) Ω. 47. Uvažume Cauchyovu úlohu (1) u tt a 2 u xx = 0 v R 2, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x R, kde a e kladná konstanta a ϕ C 2 (R), ψ C 1 (R) sou dané funkce. Dokažte, že tato úloha má ednoznačné řešení u C 2 (R 2 ) tím, že pro ně odvodíte vzorec. 48. Necht funkce ϕ C 2 (R), ψ C 1 (R) sou liché vzhledem k bodu x 0 R (t. pro x R platí ϕ(x 0 + x) = ϕ(x 0 x), ψ(x 0 + x) = ψ(x 0 x)). Dokažte, že pak řešení u úlohy (1) e též liché vzhledem k bodu x 0. Speciálně potom platí, že u(x 0, t) = 0 pro všechna t R. 49. Necht funkce ϕ C 2 (R), ψ C 1 (R) sou sudé vzhledem k bodu x 0 R (t. pro x R platí ϕ(x 0 + x) = ϕ(x 0 x), ψ(x 0 + x) = ψ(x 0 x)). Dokažte, že pak řešení u úlohy (1) e též sudé vzhledem k bodu x 0. Speciálně potom platí, že u x (x 0, t) = 0 pro všechna t R. 50. Uvažume Cauchyovu úlohu (2) u tt a 2 u xx = f v R 2, u(x, 0) = u t (x, 0) = 0 x R, kde a e kladná konstanta a f C 1 (R 2 ) e daná funkce. Dokažte, že tato úloha má ednoznačné řešení u C 2 (R 2 ) tím, že pro ně odvodíte vzorec. 51. Necht funkce f C 1 (R 2 ) e lichá vzhledem k bodu x 0 R. Dokažte, že pak řešení úlohy (2) e též liché vzhledem k bodu x 0. Speciálně e u(x 0, t) = 0 pro všechna t R. 52. Necht funkce f C 1 (R 2 ) e sudá vzhledem k bodu x 0 R. Dokažte, že pak řešení úlohy (2) e též sudé vzhledem k bodu x 0. Speciálně e u x (x 0, t) = 0 pro všechna t R. 53. Naděte řešení u úlohy (2) s f(x, t) = x. Ukažte, že u C 2 (R 2 ), ale u C 3 (R 2 ). 54. Ukažte, že Cauchyova úloha (2) s pravou stranou f splňuící f(x, t) = at pro x at a f(x, t) = x pro x > at nemá řešení u C 2 (R 2 ). 55. Necht f : R 2 R a 1 f : R 2 R sou spoité. Pak d dt t 56. Necht f C 1 (R 2 ) a a > 0. Bud 0 f(t, ) d = f(t, t) + t 0 f t (t, ) d. u(x, t) = 1 2 a t x+a(t ) 0 x a(t ) f(σ, ) dσ d. 8
9 Ukažte, že u C 2 (R 2 ) a že u e řešením Cauchyovy úlohy (2). 57. Bud l > 0 a necht ϕ C 1 ([0, l]), ϕ(0) = ϕ(l) = 0. Ukažte, že pak existue ednoznačně určené rozšíření ϕ funkce ϕ definované na R, které e liché vzhledem k bodu 0 a 2l periodické. Navíc platí ϕ C 1 (R) a ϕ e liché vzhledem k bodu l. Je-li ϕ C 2 ([0, l]) a ϕ (0) = ϕ (l) = 0, ukažte, že e též ϕ C 2 (R). 58. Uvažume okraovou úlohu u tt a 2 u xx = 0 pro (x, t) R + R, u(0, t) = 0 t R, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x R +, kde a e kladná konstanta a ϕ C 2 (R + 0 ), ψ C 1 (R + 0 ) sou dané funkce splňuící ϕ(0) = ψ(0) = ϕ (0) = 0. Dokažte, že tato úloha má ednoznačné řešení u C 2 (R + 0 R) a odvod te pro ně vzorec. 59. Uvažume okraovou úlohu u tt a 2 u xx = 0 pro (x, t) R + R, u x (0, t) = 0 t R, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x R +, kde a e kladná konstanta a ϕ C 2 (R + 0 ), ψ C 1 (R + 0 ) sou dané funkce splňuící ϕ (0) = ψ (0) = 0. Dokažte, že tato úloha má ednoznačné řešení u C 2 (R + 0 R) a odvod te pro ně vzorec. 60. Naděte všechna λ R a w C 2 ([0, l]) splňuící w(0) = 0, w(l) = 0 a rovnici w = λ w v (0, l). 61. Naděte všechna λ R a w C 2 ([0, l]) splňuící w(0) = 0, w (l) = 0 a rovnici w = λ w v (0, l). 62. Naděte všechna λ R a w C 2 ([0, l]) splňuící w (0) = 0, w(l) = 0 a rovnici w = λ w v (0, l). 63. Naděte všechna λ R a w C 2 ([0, l]) splňuící w (0) = 0, w (l) = 0 a rovnici w = λ w v (0, l). 64. Řešte Fourierovou metodou úlohu u tt a 2 u xx = 0 v (0, l) R +, u(0, t) = u x (l, t) = 0 t R +, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x (0, l). Určete, za akých předpokladů na funkce ϕ, ψ Fourierova řada stenoměrně konvergue ke klasickému řešení, a sečtěte i. Jaké sou nutné a postačuící podmínky pro existenci 9
10 klasického řešení? 65. Pomocí Duhamelova principu řešte úlohu u tt a 2 u xx = f v (0, l) R, u(0, t) = u x (l, t) = 0 t R, u(x, 0) = u t (x, 0) = 0 x (0, l). Jaké sou postačuící podmínky na funkci f pro existenci klasického řešení? 66. Uvažume úlohu u tt a 2 u xx = 0 v (0, l) R, u(0, t) = µ 1 (t), u x (l, t) = µ 2 (t) t R, u(x, 0) = u t (x, 0) = 0 x (0, l). Jaké sou postačuící podmínky na funkce µ 1 a µ 2 pro existenci klasického řešení? 67. Řešte úlohu u tt a 2 u xx = 0 v (0, l) R +, u(0, t) = µ 1 (t), u(l, t) = µ 2 (t) t R +, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x (0, l), kde ϕ C 2 ([0, l]), ψ C 1 ([0, l]) a µ 1, µ 2 C 2 (R + 0 ). Proved te homogenizaci okraových podmínek a použite Fourierovu metodu. 68. Řešte Fourierovou metodou úlohu u tt a 2 u xx = 0 v (0, l) R +, u x (0, t) = u x (l, t) = 0 t R +, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x (0, l). 8 Rovnice vedení tepla Řešte Fourierovou metodou úlohu Řešte Fourierovou metodou úlohu u t a 2 u xx = 0 v (0, l) R +, u(0, t) = u(l, t) = 0 t R +, { x x (0, l 2 u(x, 0) = ], l x x ( l, l). 2 u t a 2 u xx = 0 v (0, l) R +, u x (0, t) = u x (l, t) = 0 t R +, u(x, 0) = x x (0, l). 10
11 71. Řešte Fourierovou metodou úlohu u t a 2 u xx = 0 v (0, l) R +, u(0, t) = 0, u x (l, t) = 0 t R +, { x x (0, l 2 u(x, 0) = ], l x ( l, l) Řešte Fourierovou metodou úlohu u t a 2 u xx = 0 v (0, l) R +, u x (0, t) = 0, u(l, t) = 0 t R +, u(x, 0) = x 2 l 2 x (0, l). 73. Řešte Fourierovou metodou úlohu u t a 2 u xx = 0 v (0, l) R +, u x (0, t) = 0, K 1 u x (l, t) + K 2 u(l, t) = 0 t R +, u(x, 0) = u 0 (x) x (0, l), kde K 1 K 2 > 0 a u 0 e daná funkce. 74. Řešte Fourierovou metodou úlohu u t a 2 u = 0 v G R +, G = (0, l 1 ) (0, l 2 ), u(x, y, t) = 0 (x, y) G, t R +, u(x, y, 0) = u 0 (x, y) (x, y) G. 75. Naděte pomocí Duhamelova principu řešení úlohy u t a 2 u xx = f v Ω = R R +, u(x, 0) = 0 x R, kde f C 2 (Ω) L (Ω). 9 Vlnová rovnice v R n 76. Ukažte, že řešení u rovnice u tt a 2 u = 0 v R 3 R +, které e sféricky symetrické vzhledem k počátku, má tvar P (r a t) + Q(r + a t) u(x, t) =, r (x, t) R 3 R +, r = x, kde P, Q sou vhodné funkce. 11
12 77. Uvažume úlohu z předchozího cvičení s počátečními daty u(x, 0) = 0, u t (x, 0) = g(r) x R 3. Dodefinume funkci g sudě na R. Ukažte, že pak u(x, t) = 1 2 a r r+a t r a t s g(s) ds. 78. Necht v Cauchyově úloze z předchozích dvou cvičení e { 1 pro 0 r R, g(r) = 0 pro r > R. Pomocí vzorce odvozeného v předchozím cvičení určete explicitně řešení u v ednotlivých oblastech omezených kuželovými plochami typu r = ±R ± a t. Ukažte, že u e nespoité v bodě (0, R/a). (Je to důsledkem toho, že nespoitost u t pro t = 0 a x = R se soustředí v bodě (0, R/a).) 79. Uvažume Cauchyovu úlohu u tt a 2 u = 0 v R 5 R +, Pro x R 5, r R a t R + 0 označme M u (x, r, t) = 1 u(x + r ξ, t) dσ ξ, Ω 5 u(x, 0) = f(x), u t (x, 0) = g(x) x R 5. ξ =1 N(x, r, t) = r 2 M u r (x, r, t) + 3 r M u(x, r, t). Ukažte, že N(x, r, t) e řešením rovnice N tt a 2 N rr = 0 a nalezněte N pomocí eho počátečních dat vyádřených užitím M f a M g. Ukažte, že ( N(x, r, t) 1 u(x, t) = lim = ) r 0 3 r 3 t2 t + t M g (x, a t) + ( 1 ) t 3 t2 t + t M f (x, a t). Návod: použite vztahy ( 2 x M u = r r a sudost M f a M g vzhledem k r. 80. Uvažume Cauchyovu úlohu ) M u, r u tt a 2 u xx = 0 v R R +, x M u = 1 a 2 2 M u t 2 u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x R, kde ϕ C 2 (R), ψ C 1 (R). Odvod te řešení této úlohy metodou sestupu s využitím vzorce pro řešení Cauchyovy úlohy pro vlnovou rovnici v R 3 R Odvod te řešení Cauchyovy úlohy z předchozího cvičení metodou sestupu s využitím vzorce pro řešení Cauchyovy úlohy pro vlnovou rovnici v R 2 R +. 12
13 82. Necht ϕ 1, ϕ 2 C 2 (R), ψ 1, ψ 2 C 1 (R) sou dané funkce. Nalezněte řešení Cauchyovy úlohy u tt a 2 (u xx + u yy ) = 0 v R 2 R +, u(x, y, 0) = ϕ 1 (x) + ϕ 2 (y), u t (x, y, 0) = ψ 1 (x) + ψ 2 (y) x, y R. 10 Distribuce 83. Vypočítete fundamentální řešení Laplaceovy rovnice v R n. Návod: Určete neprve obecný tvar radiálně symetrického řešení Laplaceovy rovnice. 84. Vypočítete fundamentální řešení rovnice vedení tepla v 1D s a = 1, t. rovnice u t = u xx. Návod: Hledete u ve tvaru u(x, t) = v(x/ t). Tím získáte funkci u, pro níž e u(x, 0) konstantní pro x < 0 i pro x > 0. Vhodný násobek derivace u x e hledané fundamentální řešení. 85. Uvažume Cauchyovu úlohu u t a 2 u = 0 v R n R +, u(x, 0) = u 0 (x) x R n, kde u 0 C 0 (R n ) (spoitá funkce s kompaktním nosičem). Pomocí výsledku předchozího cvičení nalezněte klasické řešení této úlohy. 86. Ukažte, že funkce { 1 pro x < t, 2 G(x, t) = 0 pro x t definovaná na R R + 0 e fundamentální řešení rovnice u tt = u xx. 87. Uvažume temperovanou distribuci δ x =R (ϕ) = x =R ϕ(x) dσ (zdro rovnoměrně rozložený na sféře o poloměru R kolem počátku v R n ). Ukažte, že Fourierova transformace této distribuce e (3) (2 π) n 2 e i ξ x dσ x. 88. Vypočítete integrál v (3) pro n = 3. x =R 89. Pomocí Fourierovy transformace a výsledků předchozích dvou cvičení vypočítete fundamentální řešení vlnové rovnice v R Metodou sestupu vypočítete z fundamentálního řešení odvozeného v předchozím cvičení fundamentální řešení vlnové rovnice v R 2. 13
14 91. Necht G e fundamentální řešení rovnice u t (x, t) = L u(x, t), x R n, t > 0, kde L e lineární diferenciální operátor s konstantními koeficienty neobsahuící derivace podle t. To znamená, že G : R + 0 D (R n ) e spoitě diferencovatelné na R + 0, G t (t) = L G(t) a G(0) = δ. Necht f : R + 0 D (R n ), u 0 D (R n ) a f i u 0 maí kompaktní nosiče. Ověřte, že u(t) = G(t) u 0 + t 0 G(t s) f(s) ds e zobrazení R + 0 D (R n ) splňuící u t (t) = (L u)(t) + f(t) a u(0) = u Necht L e lineární diferenciální operátor s konstantními koeficienty na R n a necht G : R + 0 D (R n ) e fundamentální řešení rovnice u t = L u. Ukažte, že funkcionál F (ϕ) = 0 G(t), ϕ(t) dt, ϕ D(R n+1 ), e distribuce na R n+1 a že F t L F = δ, kde δ D (R n+1 ). 93. Pomocí fundamentálního řešení odvod te Kirchhoffův vzorec pro řešení vlnové rovnice v R Pomocí fundamentálního řešení odvod te Poissonův vzorec pro řešení vlnové rovnice v R Pomocí fundamentálního řešení nalezněte řešení u rovnice u tt a 2 u = 0 v R 3 R + s počátečními podmínkami kde g L 1 (R + ). u(x, 0) = 0, u t (x, 0) = g( x ) x R 3, 96. Necht P L 1,loc (R) a pro x R 3 a t R položme u(x, t) = P (r a t) P ( r a t) r Dokažte, že pak u tt a 2 u = 0 v D (R 3 R). 97. Necht, r = x. { 1 pro x1 > ξ 1, x 2 > ξ 2, u(x 1, x 2 ) = 0 inde, kde ξ = (ξ 1, ξ 2 ) e zvolený bod v R 2. Dokažte, že u e fundamentální řešení s pólem ξ pro operátor L = 2 x 1 x 2, t. že L u = δ ξ. 14
15 98. Dokažte, že pro n = 2 e funkce v = 1 8 π r2 ln r, kde r = x, fundamentální řešení pro operátor 2. Návod: Dokažte neprve, že v = 1 1 (1 + ln r). Uvědomte si, že ln r e 2 π 2 π fundamentální řešení Laplaceovy rovnice. 99. Uvažume úlohu (4) (5) (6) u tt a 2 u xx = 0 v Ω = (0, l) R +, u(0, t) = u(l, t) = 0 t R +, u(x, 0) = ϕ(x), u t (x, 0) = ψ(x) x (0, l), kde ϕ, ψ C([0, l]). Ukažte, že funkce u získaná formální aplikací Fourierovy metody e vždy řešením rovnice (4) ve smyslu distribucí na Ω Uvažume úlohu (4) (6), kde ϕ, ψ L 2 (0, l). Formální aplikací Fourierovy metody získáme [ u(x, t) = α n cos n π a t l + β n l n π a sin n π a t ] sin n π x, l l kde α n = 2 l l 0 n=1 ϕ(x) sin n π x l dx, β n = 2 l l 0 ψ(x) sin n π x l Na funkci u se můžeme dívat ako na zobrazení u : R + 0 D ((0, l)). Dokažte, že u e nekonečně hladké na R + 0 a že splňue diferenciální rovnici a počáteční podmínky u(0) = ϕ, u t (0) = ψ Necht n=1 X n T n e řada získaná Fourierovou metodou akožto řešení parciální diferenciální rovnice u t a 2 u xx = 0 v Ω = (0, l) (0, T ) s vhodnými okraovými a počátečními podmínkami. Předpokládeme, že řada konvergue v L 2 (Ω). Dokažte, že součet řady e řešením uvedené diferenciální rovnice v D (Ω). dx Řešte Fourierovou metodou úlohu u t a 2 u xx = 0 v (0, l) R +, u(0, t) = u(l, t) = 0 t R +, u(x, 0) = u 0 (x) x (0, l), kde u 0 L 2 (0, l). Ukažte, že součet u Fourierovy řady řeší uvedenou úlohu ve smyslu distribucí akožto funkce u : R + 0 D ((0, l)). 11 Numerické řešení rovnice vedení tepla 103. Uvažume soustavu rovnic X α X + X 1 = 0, = 1,..., N 1, X 0 = X N = 0. Zistěte, pro které hodnoty α R má tato úloha netriviální řešení, a tato řešení vypočítete. 15
24. Parciální diferenciální rovnice
 24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
22 Základní vlastnosti distribucí
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
Parciální diferenciální rovnice
 Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Matematika 5 FSV UK, ZS Miroslav Zelený
 Matematika 5 FSV UK, ZS 2018-19 Miroslav Zelený 1. Stabilita řešení soustav diferenciálních rovnic 2. Úvod do variačního počtu 3. Globální extrémy 4. Teorie optimálního řízení 5. Různé 1. Stabilita řešení
Matematika 5 FSV UK, ZS 2018-19 Miroslav Zelený 1. Stabilita řešení soustav diferenciálních rovnic 2. Úvod do variačního počtu 3. Globální extrémy 4. Teorie optimálního řízení 5. Různé 1. Stabilita řešení
Diferenˇcní rovnice Diferenciální rovnice Matematika IV Matematika IV Program
 Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Příklady pro cvičení 22. dubna 2015
 Úvod Předběžná verze (015) 1 1 Normy vektorů a matic, vlastnosti matic Příklad 1.1 Pro dané vektory x = ( 1; ; 1) T, y = (; 3; 1) T určete x =? x =? x 1 =? y =? y =? y 1 =? Příklad 1. Je dán vektor x =
Úvod Předběžná verze (015) 1 1 Normy vektorů a matic, vlastnosti matic Příklad 1.1 Pro dané vektory x = ( 1; ; 1) T, y = (; 3; 1) T určete x =? x =? x 1 =? y =? y =? y 1 =? Příklad 1. Je dán vektor x =
Rovnice matematické fyziky
 Rovnice matematické fyziky cvičení 1 Rovnice matematické fyziky cvičení Michael Krbek Obsah Opakování ze známé matematické analýzy Parciální diferenciální rovnice metoda charakteristik Okrajová úloha pro
Rovnice matematické fyziky cvičení 1 Rovnice matematické fyziky cvičení Michael Krbek Obsah Opakování ze známé matematické analýzy Parciální diferenciální rovnice metoda charakteristik Okrajová úloha pro
Co jsme udělali: Au = f, u D(A)
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
21. Úvod do teorie parciálních diferenciálních rovnic
 21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
18 Fourierovy řady Úvod, základní pojmy
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
NMAF063 Matematika pro fyziky III Zápočtová písemná práce B Termín pro odevzdání 4. ledna 2019
 Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
MKI Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0.
 MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
Kapitola 7: Integrál.
 Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Otázky k ústní zkoušce, přehled témat A. Číselné řady
 Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
9. přednáška 26. listopadu f(a)h < 0 a pro h (0, δ) máme f(a 1 + h, a 2,..., a m ) f(a) > 1 2 x 1
 9 přednáška 6 listopadu 007 Věta 11 Nechť f C U, kde U R m je otevřená množina, a a U je bod Pokud fa 0, nemá f v a ani neostrý lokální extrém Pokud fa = 0 a H f a je pozitivně negativně definitní, potom
9 přednáška 6 listopadu 007 Věta 11 Nechť f C U, kde U R m je otevřená množina, a a U je bod Pokud fa 0, nemá f v a ani neostrý lokální extrém Pokud fa = 0 a H f a je pozitivně negativně definitní, potom
12 Obyčejné diferenciální rovnice a jejich soustavy
 12 Obyčejné diferenciální rovnice a jejich soustavy 121 Úvod - opakování Opakování z 1 ročníku (z kapitoly 5) Definice 121 Rovnice se separovanými proměnnými je rovnice tvaru Návod k řešení: Pokud g(c)
12 Obyčejné diferenciální rovnice a jejich soustavy 121 Úvod - opakování Opakování z 1 ročníku (z kapitoly 5) Definice 121 Rovnice se separovanými proměnnými je rovnice tvaru Návod k řešení: Pokud g(c)
Matematika 4 FSV UK, LS Miroslav Zelený
 Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
2. Určte hromadné body, limitu superior a limitu inferior posloupností: 2, b n = n. n n n.
 Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK. Matematika pro fyziky III
 ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
OBECNOSTI KONVERGENCE V R N
 FUNKCE VÍCE PROMĚNNÝCH V reálných situacích závisejí děje obvykle na více proměnných než jen na jedné (např. na teplotě i na tlaku), závislost na jedné proměnné je spíše výjimkou. OBECNOSTI Reálná funkce
FUNKCE VÍCE PROMĚNNÝCH V reálných situacích závisejí děje obvykle na více proměnných než jen na jedné (např. na teplotě i na tlaku), závislost na jedné proměnné je spíše výjimkou. OBECNOSTI Reálná funkce
Uzavřené a otevřené množiny
 Teorie: Uzavřené a otevřené množiny 2. cvičení DEFINICE Nechť M R n. Bod x M nazveme vnitřním bodem množiny M, pokud existuje r > 0 tak, že B(x, r) M. Množinu všech vnitřních bodů značíme Int M. Dále,
Teorie: Uzavřené a otevřené množiny 2. cvičení DEFINICE Nechť M R n. Bod x M nazveme vnitřním bodem množiny M, pokud existuje r > 0 tak, že B(x, r) M. Množinu všech vnitřních bodů značíme Int M. Dále,
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Kapitola 7: Neurčitý integrál. 1/14
 Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
em do konce semestru. Obsah Vetknutý nosník, str. 8 Problém č.8: Průhyb nosníku - Ritzova metoda
 Zápočtové problémy Na následujících stránkách naleznete druhou sérii zápočtových problémů věnovanou nosníkům. Ti, co ještě nemají žádný problém přidělený, si mohou vybrat libovolný z nich. Řešení můžete
Zápočtové problémy Na následujících stránkách naleznete druhou sérii zápočtových problémů věnovanou nosníkům. Ti, co ještě nemají žádný problém přidělený, si mohou vybrat libovolný z nich. Řešení můžete
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Obsah Obyčejné diferenciální rovnice
 Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
0 = 2e 1 (z 3 1)dz + 3z. z=0 z 3 4z 2 + 3z + rez. 4. Napište Fourierův rozvoj vzhledem k trigonometrickému systému periodickému
 2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
Občas se používá značení f x (x 0, y 0 ), resp. f y (x 0, y 0 ). Parciální derivace f. rovnoběžného s osou y a z:
 PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
ALGEBRA. Téma 5: Vektorové prostory
 SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
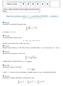 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápo tová písemná práce. 1 z p edm tu 01RMF varianta A
 Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
které charakterizují danou fyzikální situaci. souvislostí). Může být formulován jako soustava rovnic a nerovnic.
 1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
I. 7. Diferenciál funkce a Taylorova věta
 I. 7. Diferenciál funkce a Taylorova věta 343 I. 7. Diferenciál funkce a Taylorova věta Věta 26. Funkce f má v bodě x 0 diferenciál (je diferencovatelná v x 0 ) právě tehdy, když existuje vlastní derivace
I. 7. Diferenciál funkce a Taylorova věta 343 I. 7. Diferenciál funkce a Taylorova věta Věta 26. Funkce f má v bodě x 0 diferenciál (je diferencovatelná v x 0 ) právě tehdy, když existuje vlastní derivace
+ 2y y = nf ; x 0. závisí pouze na vzdálenosti bodu (x, y) od počátku, vyhovuje rovnici. y F x x F y = 0. x y. x x + y F. y = F
 Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE
 PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE Základní pojmy Řešení rovnice je hledání neznámé, která po dosazení do této rovnice vytvoří rovnost. V případě ODR byla neznámou funkce jedné proměnné obvykle ji označujeme
PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE Základní pojmy Řešení rovnice je hledání neznámé, která po dosazení do této rovnice vytvoří rovnost. V případě ODR byla neznámou funkce jedné proměnné obvykle ji označujeme
Literatura: Kapitoly 3, 4 a 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1
![Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1 Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1](/thumbs/103/161289080.jpg) 9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Příklady pro předmět Aplikovaná matematika (AMA) část 1
 Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
Separovatelné diferenciální rovnice
 Matematika 2, příklady na procvičení (Josef Tkadlec, 8. 6. 2009) Separovatelné diferenciální rovnice. Řešte diferenciální rovnici s počáteční podmínkou x = e x t, x() = 0. 2. Řešte diferenciální rovnici
Matematika 2, příklady na procvičení (Josef Tkadlec, 8. 6. 2009) Separovatelné diferenciální rovnice. Řešte diferenciální rovnici s počáteční podmínkou x = e x t, x() = 0. 2. Řešte diferenciální rovnici
1 Topologie roviny a prostoru
 1 Topologie roviny a prostoru 1.1 Základní pojmy množin Intervaly a okolí Intervaly v rovině nebo prostoru jsou obdélníky nebo hranoly se stranami rovnoběžnými s osami souřadnic. Podmnožiny intervalů se
1 Topologie roviny a prostoru 1.1 Základní pojmy množin Intervaly a okolí Intervaly v rovině nebo prostoru jsou obdélníky nebo hranoly se stranami rovnoběžnými s osami souřadnic. Podmnožiny intervalů se
Kapitola 7: Integrál. 1/17
 Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Matematika pro chemické inženýry
 Matematika pro chemické inženýry Drahoslava Janovská Parciální diferenciální rovnice Přednášky ZS 2016-2017 Sponzorováno grantem VŠCHT Praha, PIGA 413-17-6642, 2016 Povinná látka. Bude v písemkách a bude
Matematika pro chemické inženýry Drahoslava Janovská Parciální diferenciální rovnice Přednášky ZS 2016-2017 Sponzorováno grantem VŠCHT Praha, PIGA 413-17-6642, 2016 Povinná látka. Bude v písemkách a bude
Komplexní analýza. Laplaceova transformace. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
Obsah. 1 Lineární prostory 2
 Obsah 1 Lineární prostory 2 2 Úplné prostory 2 2.1 Metrické prostory.................................... 2 2.2 Banachovy prostory................................... 3 2.3 Lineární funkcionály..................................
Obsah 1 Lineární prostory 2 2 Úplné prostory 2 2.1 Metrické prostory.................................... 2 2.2 Banachovy prostory................................... 3 2.3 Lineární funkcionály..................................
Diferenciální rovnice
 Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Potenciál vektorového pole
 Kapitola 12 Potenciál vektorového pole 1 Definice a výpočet Důležitým typem vektorového pole je pole F, pro které existuje spojitě diferencovatelná funkce f tak, že F je pole gradientů funkce f, tedy F
Kapitola 12 Potenciál vektorového pole 1 Definice a výpočet Důležitým typem vektorového pole je pole F, pro které existuje spojitě diferencovatelná funkce f tak, že F je pole gradientů funkce f, tedy F
10 Funkce více proměnných
 M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
VI. Derivace složené funkce.
 VI. Derivace složené funkce. 17. Parciální derivace složené funkce Budeme uvažovat složenou funkci F = f(g, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce,
VI. Derivace složené funkce. 17. Parciální derivace složené funkce Budeme uvažovat složenou funkci F = f(g, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce,
Řešení. Označme po řadě F (z) Odtud plyne, že
 Úloha Nechť ~ R(, ) a Y = Jinak řečeno, Y je odmocnina čísla vybraného zcela náhodně z intervalu (, ) Popište rozdělení veličiny Y a určete jeho modus, medián, střední hodnotu a rozptyl Řešení Označme
Úloha Nechť ~ R(, ) a Y = Jinak řečeno, Y je odmocnina čísla vybraného zcela náhodně z intervalu (, ) Popište rozdělení veličiny Y a určete jeho modus, medián, střední hodnotu a rozptyl Řešení Označme
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
 Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
8.4. Shrnutí ke kapitolám 7 a 8
 8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb
 Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb Jan Slovák Masarykova univerzita Fakulta informatiky 23. 10. 2006 Obsah
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb Jan Slovák Masarykova univerzita Fakulta informatiky 23. 10. 2006 Obsah
16 Fourierovy řady Úvod, základní pojmy
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 16: Fourierovy řady 1 16 Fourierovy řady 16.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 16: Fourierovy řady 1 16 Fourierovy řady 16.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA Dnešní látka: Metoda sítí pro D úlohy. Poissonova rovnice. Vlnová rovnice. Rovnice vedení tepla. Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 3, ČVUT, Praha,. Text přednášky
Předmět: MA Dnešní látka: Metoda sítí pro D úlohy. Poissonova rovnice. Vlnová rovnice. Rovnice vedení tepla. Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 3, ČVUT, Praha,. Text přednášky
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
9.5. Soustavy diferenciálních rovnic
 Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
Numerické řešení diferenciálních rovnic
 Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
Numerické řešení diferenciálních rovnic Omezení: obyčejné (nikoli parciální) diferenciální rovnice, Cauchyho počáteční úloha, pouze jedna diferenciální rovnice 1. řádu 1/1 Numerické řešení diferenciálních
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu 1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg) [M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
8.2. Exaktní rovnice. F(x, y) x. dy. df = dx + y. Nyní budeme hledat odpověd na otázku, zda a jak lze od této diferenciální formule
 Cíle Ve výkladu o funkcích dvou proměnných jsme se seznámili také s jejich diferenciálem prvního řádu, který je pro funkci F(x, y) vyjádřen výrazem df dx + dy. Nyní budeme hledat odpověd na otázku, zda
Cíle Ve výkladu o funkcích dvou proměnných jsme se seznámili také s jejich diferenciálem prvního řádu, který je pro funkci F(x, y) vyjádřen výrazem df dx + dy. Nyní budeme hledat odpověd na otázku, zda
MATEMATIKA 2. Sbírka úloh. RNDr. Edita Kolářová, Ph.D. ÚSTAV MATEMATIKY
 MATEMATIKA Sbírka úloh RNDr. Edita Kolářová, Ph.D. ÚSTAV MATEMATIKY MATEMATIKA Sbírka úloh Úvod Dostali jste do rukou sbírku příkladů k přednášce Matematika. Tato sbírka je doplněním textu Matematika.
MATEMATIKA Sbírka úloh RNDr. Edita Kolářová, Ph.D. ÚSTAV MATEMATIKY MATEMATIKA Sbírka úloh Úvod Dostali jste do rukou sbírku příkladů k přednášce Matematika. Tato sbírka je doplněním textu Matematika.
V této kapitole si ukážeme, jak lze řešit některé nelineární autonomní soustavy rovnic. Uvažujme soustavu X = F (X), (1)
 Nelineární systémy V této kapitole si ukážeme, jak lze řešit některé nelineární autonomní soustavy rovnic. Uvažujme soustavu X = F (X), () kde X : (a, b) R R n je neznámá funkce a F : Ω R n R n je spojitá
Nelineární systémy V této kapitole si ukážeme, jak lze řešit některé nelineární autonomní soustavy rovnic. Uvažujme soustavu X = F (X), () kde X : (a, b) R R n je neznámá funkce a F : Ω R n R n je spojitá
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Požadavky ke zkoušce
 Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 2 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 2 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Téma 22. Ondřej Nývlt
 Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
K oddílu I.1 základní pojmy, normy, normované prostory
 ÚVOD DO FUNKCIONÁLNÍ ANALÝZY PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2015/2016 PŘÍKLADY KE KAPITOLE I K oddílu I1 základní pojmy, normy, normované prostory Příklad 1 Necht X je reálný vektorový prostor a : X
ÚVOD DO FUNKCIONÁLNÍ ANALÝZY PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2015/2016 PŘÍKLADY KE KAPITOLE I K oddílu I1 základní pojmy, normy, normované prostory Příklad 1 Necht X je reálný vektorový prostor a : X
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých
 Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Implicitní funkce. 2 + arcsin(x + y2 ) = arccos(y + x 2 ), [0, 0] , 5] stacionární bod?
![Implicitní funkce. 2 + arcsin(x + y2 ) = arccos(y + x 2 ), [0, 0] , 5] stacionární bod? Implicitní funkce. 2 + arcsin(x + y2 ) = arccos(y + x 2 ), [0, 0] , 5] stacionární bod?](/thumbs/102/152847714.jpg) Implicitní funkce V následujících úlohách ukažte, že uvedená rovnice určuje v jistém okolí daného bodu [ 0, y 0 ] implicitně zadanou funkci proměnné. Spočtěte první a druhou derivaci této funkce v bodě
Implicitní funkce V následujících úlohách ukažte, že uvedená rovnice určuje v jistém okolí daného bodu [ 0, y 0 ] implicitně zadanou funkci proměnné. Spočtěte první a druhou derivaci této funkce v bodě
5. cvičení z Matematiky 2
 5. cvičení z Matematiky 2 21.-25. března 2016 5.1 Nalezněte úhel, který v bodě 1, 0, 0 svírají grafy funkcí fx, y ln x 2 + y 2 a gx, y sinxy. Úhel, který svírají grafy funkcí je dán jako úhel mezi jednotlivými
5. cvičení z Matematiky 2 21.-25. března 2016 5.1 Nalezněte úhel, který v bodě 1, 0, 0 svírají grafy funkcí fx, y ln x 2 + y 2 a gx, y sinxy. Úhel, který svírají grafy funkcí je dán jako úhel mezi jednotlivými
Derivace funkce DERIVACE A SPOJITOST DERIVACE A KONSTRUKCE FUNKCÍ. Aritmetické operace
 Derivace funkce Derivace je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako
Derivace funkce Derivace je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako
4. Diferenciál a Taylorova věta
 4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
Diskretizace. 29. dubna 2015
 MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
Diferenciální rovnice a jejich aplikace. (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36
 Diferenciální rovnice a jejich aplikace Zdeněk Kadeřábek (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36 Obsah 1 Co to je derivace? 2 Diferenciální rovnice 3 Systémy diferenciálních rovnic
Diferenciální rovnice a jejich aplikace Zdeněk Kadeřábek (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36 Obsah 1 Co to je derivace? 2 Diferenciální rovnice 3 Systémy diferenciálních rovnic
Lineární rovnice prvního řádu. Máme řešit nehomogenní lineární diferenciální rovnici prvního řádu. Funkce h(t) = 2
 Cvičení Lineární rovnice prvního řádu. Najděte řešení Cauchyovy úlohy x + x tg t = cos t, které vyhovuje podmínce xπ =. Máme nehomogenní lineární diferenciální rovnici prvního řádu. Funkce ht = tg t a
Cvičení Lineární rovnice prvního řádu. Najděte řešení Cauchyovy úlohy x + x tg t = cos t, které vyhovuje podmínce xπ =. Máme nehomogenní lineární diferenciální rovnici prvního řádu. Funkce ht = tg t a
z Matematické statistiky 1 1 Konvergence posloupnosti náhodných veličin
 Příklady k procvičení z Matematické statistiky Poslední úprava. listopadu 207. Konvergence posloupnosti náhodných veličin. Necht X, X 2... jsou nezávislé veličiny s rovnoměrným rozdělením na [0, ]. Definujme
Příklady k procvičení z Matematické statistiky Poslední úprava. listopadu 207. Konvergence posloupnosti náhodných veličin. Necht X, X 2... jsou nezávislé veličiny s rovnoměrným rozdělením na [0, ]. Definujme
Sbírka příkladů z matematické analýzy II. Petr Tomiczek
 Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah Diferenciální rovnice. řádu 3. Separace proměnných......................... 3. Přechod k separaci.......................... 4.3 Variace konstant...........................
Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah Diferenciální rovnice. řádu 3. Separace proměnných......................... 3. Přechod k separaci.......................... 4.3 Variace konstant...........................
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
