1 Sémantika a její vztah k syntaxi
|
|
|
- Danuše Kučerová
- před 5 lety
- Počet zobrazení:
Transkript
1 1 Sémantika a její vztah k syntaxi Mjme formální jazyk L T nad abecedou T. Tento formální jazyk je vymezen popisem syntaxe, která stanoví množinu všech syntakticky správných etzc jazyka. V dalším textu pedpokládáme, že podmnožina L je rozhodnutelná, tj. pro každý etzec x T* umíme na základ popisu syntaxe rozhodnout, zda patí do formálního jazyka L, i nikoliv. Píklad Jako píklad uveme jazyk binárních zápis pirozených ísel. Abecedou je množina T 1 ={0,1} binárních íslic. Syntaxe jazyka íká, že správn vytvoený binární zápis je libovolný neprázdný etzec nad abecedou T 1, tj. L 1 = T 1 * - {ε}. Nap. etzce , 110, 0, jsou správn vytvoené binární zápisy pirozených ísel. Popisem syntaxe jsou však pouze vymezeny správné etzce znak, které zatím nemají pisouzen žádný význam. Nevíme tedy, jaké pirozené íslo daný etzec oznauje - neumíme urit jeho význam (z definice formálního jazyka L 1 ). Definice Uvažme neprázdnou množinu M, kterou nazveme model význam jazykových konstrukcí. Binární relaci sem mezi etzci x L a prvky y M, tj.: sem L x M, takovou, že L tvoí defininí obor relace sem, nazýváme sémantická interpretace etzc z L v modelu M. Prvky množiny M nazýváme možné významy. Protože L tvoí defininí obor relace sem, je každý etzec jazyka L v relaci nejmén s jedním prvkem množiny M. Obrácené tvrzení obecn neplatí, nebo obecn nemusí být obor hodnot relace sem shodný s množinou M, tj. ne každý prvek množiny M musí nutn modelovat význam nkteré syntaktické konstrukce. Množinu M nkdy též nazýváme univerzum význam pro formální jazyk L. Univerzum význam M spolu se sémantickou interpretací sem pedstavuje definici sémantiky jazyka, jehož syntaxe je vymezena specifikací formálního jazyka L. Sémantická interpretace definuje vztah mezi syntaktickými objekty formálního jazyka a prvky sémantického univerza. Abychom striktn oddlili syntaktické konstrukce popisovaného jazyka od metajazykových prostedk vlastní definice, použijeme pro jejich vyznaení dvojitých závorek [,]. Pokud je x L a y 1,...,y n y i M, 1 i n jsou všechny prvky modelu M takové, že x sem y i, pak místo obvyklého zápisu "sem(x) = {y 1,...,y n }" píšeme "sem[x] = {y 1,...,y n }". V ad pípad má sémantická interpretace charakter zobrazení, tj. sem: L M. Aplikaci zobrazení sem na argument x zapisujeme namísto sem[x] = {y} zkrácen sem[x] = y. Pokud sem[x] = {y} (píp. sem[x] = y) íkáme, že etzec x interpretujeme v dané sémantice jako oznaení objektu y, píp. že význam x modelujeme objektem y. Píklad V pedchozím píkladu jsme zavedli formální jazyk L 1 binárních zápis pirozených Karel Richta 1
2 ísel. Ozname Nat matematickou strukturu pirozených ísel, tj. množinu všech pirozených ísel spolu s bžnými operacemi na pirozených íslech. Abychom odlišili binární zápisy ísel od prvk Nat, budeme prvky Nat zapisovat ve slovním vyjádení. Sémantiku jazyka binárních zápis pirozených ísel mžeme definovat pomocí zobrazení int 1 : L 1 Nat, kterým popíšeme, jak interpretovat binární zápis x L 1 jako pirozené íslo int 1 [x] Nat. Pirozená interpretace nap. je int 1 [0] = nula, int 1 [1] = jedna, int 1 [2] = dv,.... Binární zápis 10 interpretujeme pak jako oznaení pirozeného ísla dv. Jediný problém, na který zde pi definici interpretace narážíme, je nekonenost množiny L Definice sémantické interpretace Pro konený formální jazyk L, který obsahuje dostaten málo etzc, lze definici sémantické interpretace zapsat ve form tabulky dvojic (etzec,význam). Obvykle je však poet prvk L píliš velký - asto se jedná o nekonenou (by samozejm spoetnou) množinu. K vyjádení definice sémantické interpretace musíme proto použít silnjší vyjadovací prostedek, který umožní konené vyjádení nekonené tabulky. Vhodným nástrojem bude syntaxí ízená forma induktivní definice. Popisem syntaxe formálního jazyka L máme definovánu syntaktickou strukturu etzc jazyka. Syntaktickou analýzu etzce x A* nelze chápat pouze jako realizaci charakteristické funkce podmnožiny L A*. Rozhodnutí, zda x patí do L i nikoliv, je provedeno na základ rozboru syntaktické struktury etzce x. Pokud struktura etzce x vyhovuje definici syntaxe jazyka, získáme krom kladného rozhodnutí ješt informaci o jeho syntaktické struktue. Tuto informaci pak mžeme využít pro zjištní významu x, na základ syntaxí ízené definice interpretace. P.: Jazyk binárních zápis pirozených ísel Syntaxi jazyka L 1 binárních zápis pirozených ísel lze popsat následující gramatikou G 1. G 1 = ( {Bin}, {0,1}, P 1, Bin ), kde P 1 = { p 1 : Bin 0, p 2 : Bin 1, p 3 : Bin Bin 0, p 4 : Bin Bin 1 }. Zejm platí L 1 = L(G 1 ). Pi definici sémantické interpretace se budeme ídit možnou syntaktickou strukturou etzc z L 1. Podle pravidel gramatiky G 1 má každý etzec x L 1 práv jeden ze ty možných tvar - bu se jedná o samostatný symbol 0 i 1, nebo je struktura etzce x taková, že koní symbolem 0 i 1 a po oddlení posledního symbolu dostáváme opt binární zápis ísla (který má opt jeden ze ty možných tvar, atd.). To nás vede k závru, že pro popis významu libovolného etzce, postaí urit zpsob, jak zjistit význam všech pravých stran pravidel z P 1. Pesnji, pro popis významu etzce, který lze odvodit z neterminálního symbolu Bin, je nutno urit význam pravých stran pravidel, která mají na levé stran symbol Bin. Následující induktivní definice sémantické interpretace binárních zápis ilustruje výše uvedenou myšlenku. int 1 : L 1 Nat Karel Richta 2
3 r p1 : int 1 [ 0 ] = nula r p2 : int 1 [ 1 ] = jedna r p3 : int 1 [ Bin 0 ] = dv * int 1 [ Bin ] r p4 : int 1 [ Bin 1 ] = dv * int 1 [ Bin ] + jedna Defininí rovnosti jsou pro pehlednost oznaeny dle pravidel gramatiky, tj. pravidlu p i P odpovídá rovnost r pi. Uvážíme-li nap. etzec L 1, existuje jeho derivace v gramatice G 1 (šipky jsou oznaeny použitým pravidlem): Bin =>p 4 Bin 1 =>p 3 Bin 01 =>p 4 Bin 101 =>p 3 Bin 0101 =>p Sémantickou interpretaci etzce získáme postupnou aplikací defininích rovností podle syntaktické struktury vyjadující derivaci etzce (po pravé stran jsou pro názornost uvedeny odkazy na použité defininí rovnosti). int 1 [10101] = (r p4 ) = dv* int 1 [1010]+jedna = (r p3 ) = dv*(dv* int 1 [101])+jedna = (r p4 ) = dv*(dv*(dv* int 1 [10]+jedna))+jedna = (r p3 ) = dv*(dv*(dv*(dv* int 1 [1])+jedna))+jedna = (r p2 ) = dv*(dv*(dv*(dv*jedna)+jedna))+jedna = = dvacetjedna Abychom ješt více zpesnili formální vyjádení interpretace, zavedeme pojem lineární zápis derivaního stromu, kterým zachytíme syntaktickou strukturu etzce. Syntaktická struktura je popsána derivací etzce podle pravidel gramatiky. Postup aplikace pravidel zachytíme lineárním zápisem derivaního stromu. Lineární zápisy derivaních strom budeme explicitn zapisovat pomocí výraz, složených z oznaení pravidel gramatiky a dalších pomocných symbol. 1.2 Lineární zápisy derivaních strom Bu G = (N,T,P,S) bezkontextová gramatika, kde P = {p 1 : A 1 α 1,..., p n : A n α n }. Jednotlivá pravidla jsou oznaena symboly p 1 až p n a ozname OP(G) množinu všech oznaení pravidel gramatiky G, tj. OP(G) = {p 1,...,p n }. Nech X = {X A, A N} je soubor nejvýše spoetných množin X A symbol promnných pro každý neterminální symbol A N. Lineární zápisy derivaních strom etzc jazyka L(G) definujeme jako soubor D(G,X) = {D(G,X) A, A N}, kde len D(G,X) A nazýváme množina lineárních zápis odvozených z neterminálního symbolu A a definujeme jako nejmenší podmnožinu množiny (OP(G) {(,)} X)*, která spluje následující podmínky. a) X A D(G,X) A (každý symbol promnné je lineární zápis); b) jestliže p OP(G) je oznaení pravidla gramatiky G, které má tvar p: A α, kde A N, α T, pak p je lineární zápis derivaního stromu, tj. p D(G,X) A ; c) jestliže p OP(G) je oznaení pravidla gramatiky G, které má tvar p: A α 1 A 1 α 2 A 2... A n α n+1, kde A N, A i N, i <1,n>, α j T, j <1,n+1> a nech t 1,...,t n jsou lineární zápisy derivaních strom takové, že t i D(G,X) Ai, pak i zápis Karel Richta 3
4 p(t 1,...,t n ) je lineární zápis derivaního stromu, tj. p(t 1,...,t n ) D(G,X) A. V dalším textu budeme pro zjednodušení používat zkratky derivaní strom namísto úplného oznaení lineární zápis derivaního stromu. Derivaní stromy, které neobsahují promnné budeme nazývat konstantní zápisy. Soubor konstantních zápis znaíme zjednodušen D(G). P.: Jazyk binárních zápis pirozených ísel Pro pípad gramatiky G 1 dostáváme množinu konstantních zápis D(G 1 ) Bin, jejíž nkteré prvky jsou uvedeny v následující tabulce. Pro každý derivaní strom souasn uvádíme i derivaci etzce, kterou reprezentuje. Strom p 1 Bin =>p 1 0 p 2 Bin =>p 2 1 Odpovídající etzec a jeho derivace p 3 (p 1 ) Bin =>p 3 Bin 0 =>p 1 00 p 3 (p 2 ) Bin =>p 3 Bin 0 =>p 2 10 p 4 (p 1 ) Bin =>p 4 Bin 1 =>p 1 01 p 4 (p 2 ) Bin =>p 4 Bin 1 =>p 2 11 p 3 (p 3 (p 1 )) Bin =>p 3 Bin 0 =>p 3 Bin 00 =>p p 3 (p 3 (p 2 )) Bin =>p 3 Bin 0 =>p 3 Bin 00 =>p Konstantní zápisy reprezentují jednotlivé etzce. Derivaní stromy, které obsahují promnné, zastupují celé množiny etzc. Nap. derivaní strom p 3 (x), kde x X Bin, zastupuje množinu derivací všech etzc, které jsou ukoneny symbolem 0 a obsahují více než jeden symbol. Reprezentace derivací tchto etzc lze z derivaního stromu p 3 (x) získat tak, že nahradíme symbol promnné x libovolným konstantním zápisem odpovídající kategorie, tj. prvkem D(G 1 ) Bin. Nap. nahradíme-li x konstantním zápisem p 4 (p 2 ), dostáváme jednu možnou derivaci p 3 (p 4 (p 2 )) (v tomto pípad etzce 110). Zápisem {p 3 (x): x D(G 1 ) Bin } oznaíme množinu etzc, které zastupuje derivaní strom p3(x). Zejm platí: {p 3 (x): x D(G 1 ) Bin } D(G 1 ) Bin. Pomocí derivaních strom mžeme opt zpesnit zpsob definice sémantické interpretace. Syntaktickou analýzu budeme chápat jako relaci anal z L(G) do D(G), tj. anal L(G) D(G). Pokud <q,t> anal, pak derivaní strom t D(G) reprezentuje (jednu z možných) derivací etzce q L(G) v gramatice G. Sémantickou interpretaci definujeme pro derivaní stromy z D(G) jako relaci int z D(G) do M, tj. int D(G) x M. Karel Richta 4
5 Obecn, máme-li formální jazyk L(G) a univerzum význam M, definujeme sémantickou interpretaci derivaních strom z D(G) získaných syntaktickou analýzou etzc z L v modelu M pomocí syntaxí ízené sady sémantických rovností. Jestliže bezkontextová gramatika G obsahuje pravidlo p: A α, pak do definice interpretace musí být zahrnuta sémantická rovnost r p tvaru: r p : int A [ α ] = f p, kde f p je výraz popisující zpsob nalezení významu α v sémantickém modelu M. Pokud pravá strana α pravidla p neobsahuje neterminální symbol, oznauje konstantní zápis p pímo derivaci etzce α T* a defininí rovností r p je pímo uren objekt sémantického modelu, tj. f p je výraz oznaující objekt modelu M. Obsahuje-li pravá strana α pravidla p neterminální symboly A 1,...,A n, pak derivaní strom p(x 1,...,x n ), kde x i X Ai (1 i n), oznauje množinu derivací, které lze v gramatice G generovat z neterminálního symbolu A použitím pravidla p. Jednotlivé derivace lze z p(x 1,...,x n ) získat náhradou promnných x i konstantními zápisy odpovídající kategorie. Sémantickou rovností r p pak musí být popsán postup, jak získáme oznaený objekt na základ znalosti významu syntaktických podstruktur x 1,...,x n. Pesnjší zápis sémantické rovnosti proto bude mít tvar: int A [ p(x 1,...x n ) ] = f p (int[x 1 ],...,int[x n ]). Použití promnných v defininích sémantických rovnostech a induktivní charakter rovností umožují konenou prezentaci interpretace i pro nekonenou množinu L. 1.3 Formální popis sémantiky jazyka Formální popis sémantiky jazyka L je trojice (G,M,R), kde G = (N,T,P,S) je bezkontextová gramatika taková, že platí L = L(G), M = {M A, A N} je matematická struktura tvoící sémantické univerzum jazyka a R je soubor R = {R A, A N} množin sémantických rovností. len M A souboru M pedstavuje matematický model syntaktických konstrukcí, které lze vygenerovat z neterminálního symbolu A. len R A souboru R je množina sémantických rovností pro neterminální symbol A N. Bu P = {p 1 : A 1 α 1,..., p k : A k αk} množina pravidel gramatiky G. Nech dále X = {X A, A N} je soubor nejvýše spoetných množin X A symbol promnných pro každý neterminální symbol A N. Množina R A obsahuje pro každé pravidlo p: A α P, na jehož levé stran je neterminální symbol A, práv jednu sémantickou rovnost r p. Jestliže má pravidlo p tvar: p: A α 1 A 1 α 2 A 2... A n α n+1, kde A i N, 1 i n, α j T, 1 j n+1, pak R A obsahuje sémantickou rovnost r p : r p : int A [α 1 x 1 α 2 x 2... x n α n+1 ] = f p (int A1 [x 1 ],...,int An [x n ]), kde x i X Ai (1 i n) jsou promnné a f p je funkce typu f p : M A1,...,M An M A, která popisuje, jak získáme význam syntaktické konstrukce α 1 x 1 α 2 x 2... x n α n+1 na základ význam int A1 [x 1 ],..., int An [x n ] podstruktur x 1,...,x n. P.: Jazyk binárních zápis pirozených ísel Karel Richta 5
6 Opt použijeme píklad jazyka L 1 binárních zápis pirozených ísel. Formální popis sémantiky jazyka L 1 je trojice (G 1,M 1,R 1 ), kde L 1 = L(G 1 ). Sémantickým modelem M 1 je zde struktura pirozených ísel, tj. M 1 = M 1Bin = Nat. Formální jazyk L 1 generovaný gramatikou G 1 lze nahradit (po syntaktické analýze) množinou derivaních strom D(G 1 ) = D(G 1 ) Bin. Pitom platí: D(G 1 ) = {p 1 } {p 2 } {p 3 (x): x D(G 1 ) Bin } {p 4 (x): x D(G 1 ) Bin }, kde x X Bin. D(G 1 ) lze tedy rozložit na podmnožiny odpovídající množinám derivací, které zaínají pravidly p 1 až p 4. Pro n pak definujeme sémantické rovnosti R 1 = R 1Bin = {r p1,r p2,r p3,r p4 }. r p1 : int 1 [ p 1 ] = nula r p2 : int 1 [ p 2 ] = jedna r p3 : int 1 [ p 3 (x) ] = dv * int 1 [ x ] r p4 : int 1 [ p 4 (x) ] = dv * int 1 [ x ] + jedna 1.4 Sémantická interpretace Bu (G,M,R) formální popis sémantiky jazyka. Sémantická interpretace derivaních strom z D(G) je soubor: int = {int A : D(G) A -> M A, A N}, zobrazení popsaných souborem sémantických rovností R. Pokud má derivaní strom q D(G) A tvar p OP(G), pak využijeme rovnosti r p a definujeme: int A [q] = int A [p] = f p. Pokud má derivaní strom q tvar p(p 1,...,p n ), opt využijeme rovnosti r p a definujeme: int A [q] = int A [p(p 1,...p n )] = f p (int A1 [p 1 ],...,int An [p a ]), kde hodnoty int Ai [p i ] získáme stejným zpsobem. Formální definice sémantiky popisuje peklad z množiny etzc L(G) do výraz zastupujících objekty univerza M. Na základ znalosti sémantické interpretace derivaních strom int: D(G) M a syntaktické analýzy anal L(G) x D(G) mžeme stanovit význam etzc jazyka L(G) jako relaci sem z L(G) do M, tj. sem L(G) x M, kterou získáme složením relací anal a int, tj.: sem = anal int Pokud je gramatika G jednoznaná, je syntaktická analýza zobrazení: anal: L(G) D(G). Rovnž význam etzc jazyka L(G) pak bude zobrazení: sem: L(G) M, sem[x] = int[anal[x]]. P.: Jazyk binárních zápis pirozených ísel Sémantickými rovnostmi R 1 z pedchozího píkladu je ureno zobrazení Karel Richta 6
7 int 1 : D(G 1 ) Nat, které popisuje sémantickou interpretaci derivaních strom z D(G 1 ). etzec L(G 1 ) má v gramatice G 1 derivaci, kterou reprezentuje derivaní strom p 4 (p 3 (p 4 (p 3 (p 2 )))). Význam etezce proto získáme následujícím postupem: sem[10101] = int 1 [anal[10101]] = = int 1 [p 4 (p 3 (p 4 (p 3 (p 2 ))))] = = dv*int 1 [p 3 (p 4 (p 3 (p 2 )))]+jedna = = dv*(dv*int 1 [p 4 (p 3 (p 2 ))])+jedna = = dv*(dv*(dv*int 1 [p 3 (p 2 )]+jedna))+jedna = = dv*(dv*(dv*(dv*int 1 [p 2 ])+jedna))+jedna = = dv*(dv*(dv*(dv*jedna)+jedna))+jedna = = dvacetjedna Pestože je zápis sémantických rovností pomocí derivaních strom pesnjší, budeme kvli pehlednosti a srozumitelnosti rovností používat v zápisu tvar s pravou stranou pravidla, tj. nap. namísto pesnjšího zápisu: int 1 [ p 3 (x) ] = dv * int 1 [ x ], x X Bin použijeme ilustrativnjší zápis: int 1 [ Bin 0 ] = dv * int 1 [ Bin ]. Pedpokládáme pi tom, že pechod k pesnjšímu zápisu je vždy možný. V píkladu jazyka binárních zápis pirozených ísel jsme jako sémantický model použili strukturu pirozených ísel. V sémantických rovnostech jsme pak použili pímo bžných zápis složených z oznaení pirozených ísel a odpovídajících operátor. Ne vždy však je definice sémantického modelu takto jednoduchá. Pro pípad definice sémantiky programovacího jazyka je nutno vybudovat sémantický model význam program a vhodné znaení tchto význam. Touto problematikou se budeme zabývat v následujících odstavcích. 1.5 Sémantické modely programovacích jazyk Rzné definice sémantiky se liší pedevším v použitém sémantickém modelu. Dva základní pístupy jsou: interpretan orientovaná sémantika (nkdy též matematická sémantika), kdy jako univerzum slouží njaká matematická struktura, kompilan orientovaná sémantika, kdy jako univerzum slouží njaký jiný (díve definovaný) jazyk. Dlení na kompilan a interpretan orientovanou sémantiku má smysl spíše z hlediska používaných metod popisu. Pro definici kompilan orientované sémantiky se obvykle využívá atributových i atributových pekladových gramatik. Z hlediska sémantiky pedstavuje peklad relaci: komp L 1 x L 2, kde L 1 je zdrojový jazyk a L 2 je cílový jazyk. Známe-li sémantiku cílového jazyka, známe sémantický model M a relaci sem 2 L 2 M. Na základ této znalosti a s pomocí relace komp mžeme definovat sémantiku zdrojového jazyka jako souin relací, tj. Karel Richta 7
8 sem 1 L 1 M, sem 1 = komp sem 2 Zde se budeme vnovat zejména interpretan orientované sémantice. Interpretaní sémantika vychází z pedstavy, že program je pedpisem pro innost výpoetního automatu - interpretu jazyka. Výpoetní automat obsahuje jistou sadu výpoetních prostedk - procesor, pamtí a vnjších zaízení. Stavem výpoetního automatu rozumíme souhrn hodnot všech pamových prostedk. Do stavu tedy zahrneme aktuální hodnoty všech promnných (vetn stavu vnjších pamtí) a stav všech vnjších zaízení. Pitom vstupní zaízení mžeme považovat za pam urenou pouze pro tení, výstupní zaízení za pam urenou pouze pro zápis. Nap. tiskárnu lze modelovat posloupností již vytištných znak. Pi formálním popisu abstrahujeme od nepodstatných rys výpoetních prostedk a stav automatu reprezentujeme pomocí njakého matematického modelu. innost výpoetního automatu se projevuje zmnou stavu. Pedpokládejme, že máme vytvoen matematický model stavu výpoetních prostedk a ozname si S množinu všech takových možných stav. Nachází-li se automat v njakém (poátením) stavu s 1 S, a pedložíme-li mu syntakticky správný program p L k provedení, zahájí automat innost pedepsanou programem p, která se projevuje zmnami stavu prostedk. Tuto innost nazýváme výpoetní proces probíhající podle programu p z poáteního stavu s 1. Mohou pi tom nastat dva pípady: po uritém potu krok (zmn stavu) se výpoetní proces zastaví v njakém (koncovém) stavu s 2 S; výpoetní proces probíhá nepetržitou adou zmn stav (což nemusí být sémanticky špatn - uvažme napíklad program pro ízení nepetržitého provozu). V obou pípadech lze ze sémantického hlediska považovat za význam programu posloupnost stav (pípadn prázdnou nebo nekonenou) - jakousi posloupnost snímk z innosti modelu. Metody interpretaní sémantiky založené na této pedstav nazýváme obvykle metodami operaní sémantiky. Jejich použití je nutné zejména tehdy, zajímáme-li se o to, jak výpoet podle daného programu probíhá. Dva programy považujeme pi tomto pístupu za ekvivalentní pouze tehdy, pokud jim odpovídající výpoetní procesy probíhají stejnými stavy. asto nás však nezajímají jednotlivé mezistavy, kterými výpoet probíhá, ale za dležité považujeme pouze poátení a koncový stav výpoetního procesu - zajímá nás co program poítá. Otázku, zda výpoetní proces skoní a má-li tedy vbec smysl o koncovém stavu mluvit, ešíme obvykle oddlen. V takovém pípad lze chápat význam programu p jako (parciální) binární relaci rsem na množin všech stav, tj. rsem S S. Pitom <s 1,s 2 > rsem práv tehdy, když s 2 je koncovým stavem výpoetního procesu probíhajícího podle programu p z poáteního stavu s 1, za pedpokladu, že výpoet skoní (relace rsem je parciální, nebo v pípad, že výpoet nekoní, není koncový stav definován). Sémantickým univerzem je tedy matematická struktura všech binárních relací na množin všech stav S a mluvíme o relaním modelu sémantiky. V ad pípad požadujeme, aby výpoet byl deterministický - tzn. aby koncový stav Karel Richta 8
9 (pokud existuje) byl nejvýše jeden pro každý poátení stav. Sémantickým univerzem je pak struktura všech (parciálních) funkcí nad množinou S a mluvíme o funkcionálním modelu sémantiky. interpretan orientovaná sémantika /! \ operaní funkcionální relaní sémantika sémantika sémantika 1.6 Interpreten orientované metody popisu Funkcionální sémantiku použijeme pro definici sémantiky jazyka PL0. Následující odstavec proto vnujeme funkcionálnímu sémantickému modelu. 1.7 Funkcionální model Základní myšlenkou funkcionální sémantiky je interpretovat význam programu jako funkci zobrazující vstupní data na výstupní. Aby bylo možno významy program zapisovat, musíme mít k dispozici vhodný aparát, umožující s funkcemi pracovat (oznaovat je, konstruovat, skládat a pod.). Pimeným kandidátem je aparát λ kalkulu, jehož základy vybudoval Alonzo Church [Church,A.: The Calculi of Lambda- Conversion. Annals of Mathemetics Studies No.6, Princeton University Press 1941]. Mezi rznými modifikacemi λ kalkulu si vybereme tzv. typovaný Karel Richta 9
10 λ kalkul, variantu, která nejvíce vyhovuje našim potebám [Glaser,H., Hankin,Ch., Till,D.: Principles of Functional Programming. Prentice Hall 1984]. Karel Richta 10
11 λ kalkul Základem každého systému pro znaení funkcí musí být dv konstrukce: konstrukce pro definici nové funkce tak, že zadáme pravidlo pro výpoet funkní hodnoty a konstrukce umožující oznaení aplikace funkce na njaké argumenty. Bžná matematická symbolika nedovoluje dostaten pesný zápis. Uvažme napíklad výraz x+y. Není pesn zejmé, zda se jedná o oznaení hodnoty soutu promnných x a y, i o oznaení funkce sítání. Abychom tento rozdíl explicitn zdraznili, použijeme pro oznaení aplikace operace sítání na argumenty 2 a 3 zápis (x+y)(2,3), zastupující hodnotu 5. Jakou hodnotu však zastupuje zápis (x-y)(2,3)? Zde se mže hodnota lišit podle poadí vazby argument (2-3 nebo 3-2). Tomu lze pedejít explicitním vyznaením argument a poadí jejich vazby, tzv. abstrakcí λxy.x+y. Poadím promnných v zápisu abstrakce je ureno poadí vazby argument. Zejm pak (λxy.x-y)(2,3) = 2-3 = -1, nebo první argument (2) se váže na x a druhý (3) na y. V dosud zavedeném zápisu abstrakce λxy.x+y pipouštíme možnost aplikace operace + na libovolný typ argument. Uvažme však výraz λxy.x/y, oznaující funkci dlení prvního argumentu druhým. Funkní hodnota bude jist záviset na typu operace dlení, kterou použijeme. Napíklad zápis (λxy.x/y)(5,2) mže oznaovat hodnotu 2 nebo 2.5 podle toho, zda uvažujeme celoíselné dlení i dlení reálných ísel. Zápis abstrakce proto zpesníme tak, že explicitn vyjádíme požadovaný typ argument. Pak bude nap. platit: (λxy:integer.x/y)(5,2) = 2 a (λxy:real.x/y)(5,2) = 2.5. Výrazy nerespektující typové požadavky prohlásíme za chybn vytvoené. Nap. výraz (λx:integer.x+1)(2.5) prohlásíme za chybný, nebo skutený typ argumentu neodpovídá typu požadovanému. Uvažme dále výraz λy:real.1/y oznaující funkci, jejíž hodnotou je pevrácená hodnota argumentu. Funkní hodnota této funkce bude stejná, jako hodnota funkce Karel Richta 11
12 λxy:real.x/y kde za prvý argument dosadíme vždy hodnotu 1, tj. (λy:real.1/y)(z) = (λxy:real.x/y)(1,z), pro všechna z:real. Zápis λxy:real.x/y budeme proto chápat jako zkratku podrobnjšího zápisu Karel Richta 12
13 λx:integer.(λy:integer.x/y). To nám umožní chápat výraz (λx:real.(λy:real.x/y))(1) jako speciální pípad funkce x/y, když x=1, tj. funkci oznaenou λy:real.1/y. Pak také podrobnji: (λxy:real.x/y)(5,2) = = (λx:real.(λy:real.x/y))(5,2) = = ((λx:real.(λy:real.x/y))(5))(2) = = (λy:real.5/y)(2) = 5/2 = 2.5. Uvedená diskuse je pouze ilustrativní. tenáe, kterého problematika kalkulu pro znaení funkcí zaujala, doporuujeme podrobnjší studium literatury. Zde uvedeme pouze základní definice, potebné pro další výklad. Pro pesnjší definici výraz oznaujících funkce musíme zavést typy a symboly primitivních operací, ze kterých ostatní funkce vytváíme. 1.8 Typy Mjme konenou neprázdnou množinu symbol B = {B 1,...,B n }, kterou nazveme báze. Prvky množiny B budeme nazývat bázové typy. Množinu T(B) všech typ nad bází B definujeme induktivním pedpisem. 1) Každý bázový typ je typ, tj. B T(B). 2) Jsou-li A,B typy, pak i (A B) je typ (tzv. souin typ), (A B) je typ (tzv. sjednocení typ) a (A B) je typ (tzv. funkní typ). Píklad Pro bázi B 1 = {Bool,Int}, kde symboly Bool a Nat zastupují bázové typy logických hodnot a pirozených ísel, bude množina T(B 1 ) všech typ nad bází B 1 obsahovat nap. následující typy (v závorkách je uveden intuitivní význam typu): Bool (typ logických hodnot), Int (typ celých ísel), (Int Int) (typ dvojic celých ísel), (Int Bool) (typ jehož obor hodnot zahrnuje jak celá ísla, tak i logické hodnoty, tj. sjednocení Int a Bool), (Int Bool) (typ vlastností celých ísel), ((Int Int) Bool) (typ charakteristických funkcí binárních relací na celých íslech). 1.9 Signatura Bu B báze. Soubor F = {F A : A T(B)} konených množin F A symbol nazveme signatura nad bází B. Symboly z množiny F A nazýváme konstanty typu A. Pro každý symbol konstanty máme signaturou uren jeho typ. Fakt, že konstanta f je typu A, tj. Karel Richta 13
14 f F A zapisujeme f:a. Pozn. Bez újmy na obecnosti mžeme pedpokládat, že leny F jsou až na konený poet prázdné (existuje jen konen mnoho symbol). Dále pedpokládáme, že pro všechny bázové typy jsou odpovídající leny neprázdné (každý druh má nejmén jednu konstantu - generátor). Píklad Pro bázový typ celých ísel mže být signatura nad bází B={Int} tvoena nap. následujícími symboly konstant. Pedevším zavedeme primitivní symboly oznaující základní dekadické konstanty. 0,1,2,..., 9: Int. Další dekadické zápisy ísel lze vytváet s využitím unárních operací: _0,_1,_2,..., _9: (Int Int). Dekadický zápis 123 pak chápeme jako zkratku zápisu ((1)2)3. Mimo to lze pro celá ísla použít bžné aritmetické operace: +: (Int (Int Int))... celoíselné sítání, -: (Int (Int Int))... celoíselné odítání, *: (Int (Int Int))... celoíselné násobení, div: (Int (Int Int))... celoíselné dlení, mod: (Int (Int Int))... zbytek po dlení. asto používáme zkrácený zapis, nap. +: Integer,Integer Integer λ výrazy Mjme dánu bázi B={B 1,...,B n } a soubor X={X A : A T(B)} nejvýše spoetných množin symbol promnných pro každý typ nad bází B. Bu dále F = {F A : A T(B)} signatura nad bází B. Pak soubor všech λ výraz (nad bází B) definujeme: 1. Každá konstanta f F A nebo promnná x X A je λ výraz typu A. 2. Je-li x promnná typu A 1 a t λ výraz typu A 2, pak (λx:a 1.t) je λ výraz typu (A 1 A 2 ) (abstrakce). 3. Je-li x λ výraz typu (A 1 A 2 ) a y λ výraz typu A 1, pak x(y) je λ výraz typu A 2 (aplikace). 4. Je-li x λ výraz typu A 1 a y λ výraz typu A 2, pak <x,y> je λ výraz typu (A 1 A 2 ) (konstrukce). 5. Je-li x λ výraz typu (A 1 A 2 ), pak x.1 je λ výraz typu A 1 a x.2 je λ výraz typu A 2 (selekce). 6. Je-li x λ výraz typu A 1 a y λ výraz typu A 2, pak in-a 1 -to-a 1 A 2 (x) a in-a 2 -to-a 1 A 2 (y) jsou λ výrazy typu (A 1 A 2 ) (inspekce). 7. Je-li x λ výraz typu (A 1 A 2 ), pak (A 1 )(x) je λ výraz typu A 1 a (A 2 )(x) je λ výraz typu A 2 (projekce). Zápisem t:a zvýrazujeme, že λ výraz t je typu A. Pokud nemže dojít k nedorozumní, Karel Richta 14
15 budeme v zápise λ výraz vynechávat nadbytené závorky, nap. místo pesného zápisu: (λx:int.(λy:int.+(x)(y))), použijeme zkrácený tvar: λx:int.λy:int.+(x,y). asto též využijeme infixovou, postfixovou, nebo komplikovanjší notaci zápisu aplikace, nap. λx:int.λy:int.x+y. Použitou notaci lze vyznait pímo deklarací v rámci signatury pomocí znaku "_" uvedeného v míst dosazení argument, nap. deklarací: _+_: Int Int Int, stanovíme infixovou notaci pro operátor +. Deklaraci not: Bool Bool pak lze považovat za zkratku podrobnjší deklarace not(_): Bool Bool. Rovnž povolíme spojování abstrakcí, výsledný zkrácený tvar pak bude: λxy:int.x+y. Soubor všech dobe vytvoených λ výraz má jako generátory jednak konstanty ze signatury, jednak jistý soubor symbol promnných. Ve funkcionální sémantice využijeme λ výrazy jako prostedek pro vyjádení funkcí, které jsou významem syntaktických konstrukcí. Otázkou, kterou funkci daný λ výraz oznauje, se budeme zabývat v následujícím odstavci. Píklad Uvažme bázi B = {Bool,Nat} a signaturu F 1 = {true: Bool, false: Bool, not: Bool Bool, _and_: Bool Bool Bool, _or_: Bool Bool Bool, 0: Nat, _+_: Nat Nat Nat}. Pak nap. λ-výraz λx:nat.x oznauje identickou funkci na pirozených íslech, λ-výraz λx:nat.0 oznauje konstantní funkci, která nabývá pro libovolný argument typu Nat hodnoty 0. λ- výraz λx:nat.<x,0> oznauje funkci, která argumentu typu Nat piadí objekt typu (Nat Nat). Funkce λy:nat Nat.(y.1) naopak argumentu typu (Nat Nat) piadí hodnotu typu Nat. Karel Richta 15
1 Píklady popisu typických konstrukcí
 1 Píklady popisu typických konstrukcí V tomto odstavci se pokusíme ilustrovat denotaní popis sémantiky ve funkcionálním modelu pro typické píklady jazykových konstrukcí. Popisované konstrukce budou fragmenty
1 Píklady popisu typických konstrukcí V tomto odstavci se pokusíme ilustrovat denotaní popis sémantiky ve funkcionálním modelu pro typické píklady jazykových konstrukcí. Popisované konstrukce budou fragmenty
Programovací jazyky, syntaxe, sémantika, zpsoby popisu
 Sémantika programovacích jazyk: Syntaxe a sémantika Syntaxe a sémantika Programovací jazyky, syntaxe, sémantika, zpsoby popisu Ti hlavní charakteristiky jazyka (sémiotika) jsou: - syntax, sémantika a pragmatika
Sémantika programovacích jazyk: Syntaxe a sémantika Syntaxe a sémantika Programovací jazyky, syntaxe, sémantika, zpsoby popisu Ti hlavní charakteristiky jazyka (sémiotika) jsou: - syntax, sémantika a pragmatika
Každý datový objekt Pythonu má minimáln ti vlastnosti. Identitu, datový typ a hodnotu.
 Datový objekt [citováno z http://wraith.iglu.cz/python/index.php] Každý datový objekt Pythonu má minimáln ti vlastnosti. Identitu, datový typ a hodnotu. Identita Identita datového objektu je jedinený a
Datový objekt [citováno z http://wraith.iglu.cz/python/index.php] Každý datový objekt Pythonu má minimáln ti vlastnosti. Identitu, datový typ a hodnotu. Identita Identita datového objektu je jedinený a
Rzné algoritmy mají rznou složitost
 X36DSA 25 / 3 DSA Rzné algoritmy mají rznou složitost X36DSA 25 2 / 3 DSA The complexity of different algorithms varies X36DSA 25 3 / 3 Abeceda Jazyk Abeceda konená (neprázdná) množina symbol A mohutnost
X36DSA 25 / 3 DSA Rzné algoritmy mají rznou složitost X36DSA 25 2 / 3 DSA The complexity of different algorithms varies X36DSA 25 3 / 3 Abeceda Jazyk Abeceda konená (neprázdná) množina symbol A mohutnost
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
1. Signatura datového typu
 1. Signatura datového typu a) popisuje vlastnosti operací datového typu b) popisuje sémantiku datového typu c) popisuje jména druh a operací a druhy argument a výsledku d) je grafickým vyjádením implementace
1. Signatura datového typu a) popisuje vlastnosti operací datového typu b) popisuje sémantiku datového typu c) popisuje jména druh a operací a druhy argument a výsledku d) je grafickým vyjádením implementace
Cykly Intermezzo. FOR cyklus
 Cykly Intermezzo Rozhodl jsem se zaadit do série nkolika lánk o základech programování v Delphi/Pascalu malou vsuvku, která nám pomže pochopit principy a zásady pi používání tzv. cykl. Mnoho ástí i jednoduchých
Cykly Intermezzo Rozhodl jsem se zaadit do série nkolika lánk o základech programování v Delphi/Pascalu malou vsuvku, která nám pomže pochopit principy a zásady pi používání tzv. cykl. Mnoho ástí i jednoduchých
Správa obsahu ízené dokumentace v aplikaci SPM Vema
 Správa obsahu ízené dokumentace v aplikaci SPM Vema Jaroslav Šmarda, smarda@vema.cz Vema, a. s., www.vema.cz Abstrakt Spolenost Vema patí mezi pední dodavatele informaních systém v eské a Slovenské republice.
Správa obsahu ízené dokumentace v aplikaci SPM Vema Jaroslav Šmarda, smarda@vema.cz Vema, a. s., www.vema.cz Abstrakt Spolenost Vema patí mezi pední dodavatele informaních systém v eské a Slovenské republice.
Automaty a gramatiky(bi-aag) Formální překlady. 5. Překladové konečné automaty. h(ε) = ε, h(xa) = h(x)h(a), x, x T, a T.
 BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 2/41 Formální překlady BI-AAG (2011/2012) J. Holub: 5. Překladové konečné automaty p. 4/41 Automaty a gramatiky(bi-aag) 5. Překladové konečné
Formální jazyky a gramatiky Teorie programovacích jazyků
 Formální jazyky a gramatiky Teorie programovacích jazyků doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Připomenutí základních pojmů ABECEDA jazyk je libovolná podmnožina
Formální jazyky a gramatiky Teorie programovacích jazyků doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Připomenutí základních pojmů ABECEDA jazyk je libovolná podmnožina
PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY
 PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY YAMACO SOFTWARE 2006 1. ÚVODEM Nové verze produkt spolenosti YAMACO Software pinášejí mimo jiné ujednocený pístup k použití urité množiny funkcí, která
PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY YAMACO SOFTWARE 2006 1. ÚVODEM Nové verze produkt spolenosti YAMACO Software pinášejí mimo jiné ujednocený pístup k použití urité množiny funkcí, která
Množinu všech slov nad abecedou Σ značíme Σ * Množinu všech neprázdných slov Σ + Jazyk nad abecedou Σ je libovolná množina slov nad Σ
 Abecedou se rozumí libovolná konečná množina Σ. Prvky abecedy nazýváme znaky (symboly) Slovo (řetězec) v nad abecedou Σ je libovolná konečná posloupnost znaků této abecedy. Prázdné posloupnosti znaků odpovídá
Abecedou se rozumí libovolná konečná množina Σ. Prvky abecedy nazýváme znaky (symboly) Slovo (řetězec) v nad abecedou Σ je libovolná konečná posloupnost znaků této abecedy. Prázdné posloupnosti znaků odpovídá
2 Formální jazyky a gramatiky
 2 Formální jazyky a gramatiky 2.1 Úvod Teorie formálních gramatik a jazyků je důležitou součástí informatiky. Její využití je hlavně v oblasti tvorby překladačů, kompilátorů. Vznik teorie se datuje přibližně
2 Formální jazyky a gramatiky 2.1 Úvod Teorie formálních gramatik a jazyků je důležitou součástí informatiky. Její využití je hlavně v oblasti tvorby překladačů, kompilátorů. Vznik teorie se datuje přibližně
1. MODELY A MODELOVÁNÍ. as ke studiu: 30 minut. Cíl: Po prostudování této kapitoly budete umt: Výklad. 1.1. Model
 1. MODELY A MODELOVÁNÍ as ke studiu: 30 minut Cíl: Po prostudování této kapitoly budete umt: charakterizovat model jako nástroj pro zobrazení skutenosti popsat proces modelování provést klasifikaci základních
1. MODELY A MODELOVÁNÍ as ke studiu: 30 minut Cíl: Po prostudování této kapitoly budete umt: charakterizovat model jako nástroj pro zobrazení skutenosti popsat proces modelování provést klasifikaci základních
4. Lineární diferenciální rovnice rovnice 1. ádu
 4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
VYTVÁENÍ VÝBROVÝCH DOTAZ
 VYTVÁENÍ VÝBROVÝCH DOTAZ V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - VYTVÁENÍ VÝBROVÝCH SESTAV YAMACO SOFTWARE 2003-2004 1. ÚVODEM Standardní souástí všech produkt Yamaco Software jsou prostedky
VYTVÁENÍ VÝBROVÝCH DOTAZ V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - VYTVÁENÍ VÝBROVÝCH SESTAV YAMACO SOFTWARE 2003-2004 1. ÚVODEM Standardní souástí všech produkt Yamaco Software jsou prostedky
4 - Architektura poítae a základní principy jeho innosti
 4 - Architektura poítae a základní principy jeho innosti Z koncepního hlediska je mikropoíta takové uspoádání logických obvod umožující provádní logických i aritmetických operací podle posloupnosti povel
4 - Architektura poítae a základní principy jeho innosti Z koncepního hlediska je mikropoíta takové uspoádání logických obvod umožující provádní logických i aritmetických operací podle posloupnosti povel
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
 28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
IMPORT DAT Z TABULEK MICROSOFT EXCEL
 IMPORT DAT Z TABULEK MICROSOFT EXCEL V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - IMPORTU DAT DO PÍSLUŠNÉ EVIDENCE YAMACO SOFTWARE 2005 1. ÚVODEM Všechny produkty spolenosti YAMACO Software
IMPORT DAT Z TABULEK MICROSOFT EXCEL V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - IMPORTU DAT DO PÍSLUŠNÉ EVIDENCE YAMACO SOFTWARE 2005 1. ÚVODEM Všechny produkty spolenosti YAMACO Software
Automaty a gramatiky(bi-aag) Motivace. 1. Základní pojmy. 2 domácí úkoly po 6 bodech 3 testy za bodů celkem 40 bodů
 BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 2/29 Hodnocení předmětu BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 4/29 Automaty a gramatiky(bi-aag) 1. Základní pojmy Jan Holub Katedra teoretické
BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 2/29 Hodnocení předmětu BI-AAG (2011/2012) J. Holub: 1. Základní pojmy p. 4/29 Automaty a gramatiky(bi-aag) 1. Základní pojmy Jan Holub Katedra teoretické
3 NÁHODNÁ VELIINA. as ke studiu kapitoly: 80 minut. Cíl: Po prostudování tohoto odstavce budete umt
 NÁHODNÁ VELIINA as ke studiu kapitoly: 8 minut Cíl: Po prostudování tohoto odstavce budete umt obecn popsat náhodnou veliinu pomocí distribuní funkce charakterizovat diskrétní i spojitou náhodnou veliinu
NÁHODNÁ VELIINA as ke studiu kapitoly: 8 minut Cíl: Po prostudování tohoto odstavce budete umt obecn popsat náhodnou veliinu pomocí distribuní funkce charakterizovat diskrétní i spojitou náhodnou veliinu
KUSOVNÍK Zásady vyplování
 KUSOVNÍK Zásady vyplování Kusovník je základním dokumentem ve výrob nábytku a je souástí výkresové dokumentace. Každý výrobek má svj kusovník. Je prvotním dokladem ke zpracování THN, objednávek, ceny,
KUSOVNÍK Zásady vyplování Kusovník je základním dokumentem ve výrob nábytku a je souástí výkresové dokumentace. Každý výrobek má svj kusovník. Je prvotním dokladem ke zpracování THN, objednávek, ceny,
1 KOMBINATORIKA, KLASICKÁ PRAVDPODOBNOST
 1 KOMBINATORIKA, KLASICKÁ PRAVDPODOBNOST Kombinatorické pravidlo o souinu Poet všech uspoádaných k-tic, jejichž první len lze vybrat n 1 zpsoby, druhý len po výbru prvního lenu n 2 zpsoby atd. až k-tý
1 KOMBINATORIKA, KLASICKÁ PRAVDPODOBNOST Kombinatorické pravidlo o souinu Poet všech uspoádaných k-tic, jejichž první len lze vybrat n 1 zpsoby, druhý len po výbru prvního lenu n 2 zpsoby atd. až k-tý
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Programovací jazyk Pascal
 Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Programovací jazyk Pascal Syntaktická pravidla (syntaxe jazyka) přesná pravidla pro zápis příkazů Sémantická pravidla (sémantika jazyka) pravidla, která každému příkazu přiřadí přesný význam Všechny konstrukce
Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly.
 Výkaz rozvaha Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly. Po spuštní modulu se zobrazí základní okno výkazu: V tabulce se zobrazují sloupce výkazu. Ve
Výkaz rozvaha Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly. Po spuštní modulu se zobrazí základní okno výkazu: V tabulce se zobrazují sloupce výkazu. Ve
Ing. Jaroslav Halva. UDS Fakturace
 UDS Fakturace Modul fakturace výrazn posiluje funknost informaního systému UDS a umožuje bilancování jednotlivých zakázek s ohledem na hodnotu skutených náklad. Navíc optimalizuje vlastní proces fakturace
UDS Fakturace Modul fakturace výrazn posiluje funknost informaního systému UDS a umožuje bilancování jednotlivých zakázek s ohledem na hodnotu skutených náklad. Navíc optimalizuje vlastní proces fakturace
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
1. Exponenciální rst. 1.1. Spojitý pípad. Rstový zákon je vyjáden diferenciální rovnicí
 V tomto lánku na dvou modelech rstu - exponenciálním a logistickém - ukážeme nkteré rozdíly mezi chováním spojitých a diskrétních systém. Exponenciální model lze považovat za základní rstový model v neomezeném
V tomto lánku na dvou modelech rstu - exponenciálním a logistickém - ukážeme nkteré rozdíly mezi chováním spojitých a diskrétních systém. Exponenciální model lze považovat za základní rstový model v neomezeném
POPIS TESTOVACÍHO PROSTEDÍ 1 ZÁLOŽKA PARSER
 POPIS TESTOVACÍHO PROSTEDÍ Testovací prostedí je navrženo jako tízáložková aplikace, každá záložka obsahuje logicky související funkce. Testovací prostedí obsahuje následující ti záložky: Analýza Gramatiky
POPIS TESTOVACÍHO PROSTEDÍ Testovací prostedí je navrženo jako tízáložková aplikace, každá záložka obsahuje logicky související funkce. Testovací prostedí obsahuje následující ti záložky: Analýza Gramatiky
Naproti tomu gramatika je vlastně soupis pravidel, jak
 1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
1 Kapitola 1 Úvod V přednášce se zaměříme hlavně na konečný popis obecně nekonečných množin řetězců symbolů dané množiny A. Prvkům množiny A budeme říkat písmena, řetězcům (konečným posloupnostem) písmen
Promnné. [citováno z
 Promnné [citováno z http://wraith.iglu.cz/python/index.php] Abychom s datovým objektem mohli v programu njak rozumn pracovat, potebujeme se na nj njakým zpsobem odkázat. Potebujeme Pythonu íct, aby napíklad
Promnné [citováno z http://wraith.iglu.cz/python/index.php] Abychom s datovým objektem mohli v programu njak rozumn pracovat, potebujeme se na nj njakým zpsobem odkázat. Potebujeme Pythonu íct, aby napíklad
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Splajny a metoda nejmenších tverc
 Splajny a metoda nejmenších tverc 1. píklad a) Najdte pirozený kubický splajn pro funkci na intervalu Za uzly zvolte body Na interpolaci pomocí kubického splajnu použijeme píkaz Spline(ydata,, endpts).
Splajny a metoda nejmenších tverc 1. píklad a) Najdte pirozený kubický splajn pro funkci na intervalu Za uzly zvolte body Na interpolaci pomocí kubického splajnu použijeme píkaz Spline(ydata,, endpts).
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE
 GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Tabulkový procesor Excel
 Tabulkový procesor Excel Excel 1 SIPVZ-modul-P0 OBSAH OBSAH...2 ZÁKLADNÍ POJMY...4 K EMU JE EXCEL... 4 UKÁZKA TABULKOVÉHO DOKUMENTU... 5 PRACOVNÍ PLOCHA... 6 OPERACE SE SOUBOREM...7 OTEVENÍ EXISTUJÍCÍHO
Tabulkový procesor Excel Excel 1 SIPVZ-modul-P0 OBSAH OBSAH...2 ZÁKLADNÍ POJMY...4 K EMU JE EXCEL... 4 UKÁZKA TABULKOVÉHO DOKUMENTU... 5 PRACOVNÍ PLOCHA... 6 OPERACE SE SOUBOREM...7 OTEVENÍ EXISTUJÍCÍHO
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
 RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
OCR (optical character recognition) - rozpoznávání textu v obraze
 OCR (optical character recognition) - rozpoznávání textu v obraze Martin Koníek, I46 programová dokumentace 1. Úvod Tento projekt vznikl na MFF UK a jeho cílem bylo vytvoit algoritmus schopný rozpoznávat
OCR (optical character recognition) - rozpoznávání textu v obraze Martin Koníek, I46 programová dokumentace 1. Úvod Tento projekt vznikl na MFF UK a jeho cílem bylo vytvoit algoritmus schopný rozpoznávat
DUM. Databáze - úvod
 DUM Název projektu íslo projektu íslo a název šablony klíové aktivity Tematická oblast - téma Oznaení materiálu (pílohy) Inovace ŠVP na OA a JŠ Tebí CZ.1.07/1.5.00/34.0143 III/2 Inovace a zkvalitnní výuky
DUM Název projektu íslo projektu íslo a název šablony klíové aktivity Tematická oblast - téma Oznaení materiálu (pílohy) Inovace ŠVP na OA a JŠ Tebí CZ.1.07/1.5.00/34.0143 III/2 Inovace a zkvalitnní výuky
Efektivní uení. Žádná zpráva dobrá zpráva. (Structured training) Schopnost pracovat nezávisí od IQ. Marc Gold
 Efektivní uení (Structured training) Schopnost pracovat nezávisí od IQ. Marc Gold Žádná zpráva dobrá zpráva 1 ásti efektivního uení Stanovení cíle (+ kritéria) Analýza úkolu Použití pimené podpory Volba
Efektivní uení (Structured training) Schopnost pracovat nezávisí od IQ. Marc Gold Žádná zpráva dobrá zpráva 1 ásti efektivního uení Stanovení cíle (+ kritéria) Analýza úkolu Použití pimené podpory Volba
Fuzzy množiny, Fuzzy inference system. Libor Žák
 Fuzzy množiny, Fuzzy inference system Proč právě fuzzy množiny V řadě případů jsou parametry, které vstupují a ovlivňují vlastnosti procesu, popsané pomocí přibližných nebo zjednodušených pojmů. Tedy
Fuzzy množiny, Fuzzy inference system Proč právě fuzzy množiny V řadě případů jsou parametry, které vstupují a ovlivňují vlastnosti procesu, popsané pomocí přibližných nebo zjednodušených pojmů. Tedy
Obsah...1 1. Úvod...2 Slovníek pojm...2 2. Popis instalace...3 Nároky na hardware a software...3 Instalace a spouštní...3 Vstupní soubory...3 3.
 Obsah...1 1. Úvod...2 Slovníek pojm...2 2. Popis instalace...3 Nároky na hardware a software...3 Instalace a spouštní...3 Vstupní soubory...3 3. Popis prostedí...4 3.1 Hlavní okno...4 3.1.1 Adresáový strom...4
Obsah...1 1. Úvod...2 Slovníek pojm...2 2. Popis instalace...3 Nároky na hardware a software...3 Instalace a spouštní...3 Vstupní soubory...3 3. Popis prostedí...4 3.1 Hlavní okno...4 3.1.1 Adresáový strom...4
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
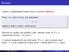 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Základní pojmy klasického sudoku hlavolamu. Techniky odkrývání bunk. Technika Naked Single. Technika Hidden Single
 Základní pojmy klasického sudoku hlavolamu Sudoku hlavolam (puzzle) obsahuje celkem 81 bunk (cells), devt vodorovných ádk (rows), devt svislých sloupc (columns) a devt skupin po 3 3 bukách nazývaných bloky
Základní pojmy klasického sudoku hlavolamu Sudoku hlavolam (puzzle) obsahuje celkem 81 bunk (cells), devt vodorovných ádk (rows), devt svislých sloupc (columns) a devt skupin po 3 3 bukách nazývaných bloky
1. Predikátová logika jako prostedek reprezentace znalostí
 1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
1. Predikátová logika jako prostedek reprezentace znalostí 1.1 Historie výrokové logiky Problém explicitních znalostí a údaj, kterých je obrovské množství, vedl ke vzniku výrokové logiky. lovk si obecn
Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i,
 [161014-1204 ] 11 2.1.35 Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i, kde i = 0, 1,..., takto: p 0 q právě tehdy, když bud p, q F nebo p, q F. Dokud i+1 i konstruujeme p
[161014-1204 ] 11 2.1.35 Konstrukce relace. Postupně konstruujeme na množině všech stavů Q relace i, kde i = 0, 1,..., takto: p 0 q právě tehdy, když bud p, q F nebo p, q F. Dokud i+1 i konstruujeme p
Základní pojmy teorie množin Vektorové prostory
 Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
Turingovy stroje. Teoretická informatika Tomáš Foltýnek
 Turingovy stroje Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Jaké znáte algebraické struktury s jednou operací? Co je to okruh,
Turingovy stroje Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Jaké znáte algebraické struktury s jednou operací? Co je to okruh,
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
9.3. Úplná lineární rovnice s konstantními koeficienty
 Úplná lineární rovnice s konstantními koeficienty Cíle Nyní přejdeme k řešení úplné lineární rovnice druhého řádu. I v tomto případě si nejprve ujasníme, v jakém tvaru můžeme očekávat řešení, poté se zaměříme
Úplná lineární rovnice s konstantními koeficienty Cíle Nyní přejdeme k řešení úplné lineární rovnice druhého řádu. I v tomto případě si nejprve ujasníme, v jakém tvaru můžeme očekávat řešení, poté se zaměříme
Množiny, relace, zobrazení
 Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
2. PÍKLAD DÍLÍ ÁSTI SOUSTAVY - DÍLÍ ÁST SDÍLENÍ TEPLA
 2. PÍKLAD DÍLÍ ÁSTI SOUSTAVY - DÍLÍ ÁST SDÍLENÍ TEPLA 2.1. OBECN Tepelné požadavky na dílí ást sdílení tepla zahrnují mimoádné ztráty pláštm budovy zpsobené: nerovnomrnou vnitní teplotou v každé tepelné
2. PÍKLAD DÍLÍ ÁSTI SOUSTAVY - DÍLÍ ÁST SDÍLENÍ TEPLA 2.1. OBECN Tepelné požadavky na dílí ást sdílení tepla zahrnují mimoádné ztráty pláštm budovy zpsobené: nerovnomrnou vnitní teplotou v každé tepelné
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
Množiny, základní číselné množiny, množinové operace
 2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
2 Množiny, základní číselné množiny, množinové operace Pokud kliknete na některý odkaz uvnitř textu kromě prezentace, zobrazí se odpovídající příklad nebo tabulka. Levý Alt+šipka doleva nebo ikona Vás
Úvodní studie (pokraov
 Úvodní studie (pokraov ování) Model jednání a kontext Model jednání (use case model) slouží pro evidenci aktér a služeb systému. Kontextový diagram slouží pro evidenci aktér a datových tok. Oba modely
Úvodní studie (pokraov ování) Model jednání a kontext Model jednání (use case model) slouží pro evidenci aktér a služeb systému. Kontextový diagram slouží pro evidenci aktér a datových tok. Oba modely
Limita a spojitost funkce a zobrazení jedné reálné proměnné
 Přednáška 4 Limita a spojitost funkce a zobrazení jedné reálné proměnné V několika následujících přednáškách budeme studovat zobrazení jedné reálné proměnné f : X Y, kde X R a Y R k. Protože pro každé
Přednáška 4 Limita a spojitost funkce a zobrazení jedné reálné proměnné V několika následujících přednáškách budeme studovat zobrazení jedné reálné proměnné f : X Y, kde X R a Y R k. Protože pro každé
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Datový typ POLE. Jednorozmrné pole - vektor
 Datový typ POLE Vodítkem pro tento kurz Delphi zabývající se pedevším konzolovými aplikacemi a základy programování pro mne byl semestr na vysoké škole. Studenti nyní pipravují semestrální práce pedevším
Datový typ POLE Vodítkem pro tento kurz Delphi zabývající se pedevším konzolovými aplikacemi a základy programování pro mne byl semestr na vysoké škole. Studenti nyní pipravují semestrální práce pedevším
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Zbytky zákaznického materiálu
 Autoi: V Plzni 31.08.2010 Obsah ZBYTKOVÝ MATERIÁL... 3 1.1 Materiálová žádanka na peskladnní zbytk... 3 1.2 Skenování zbytk... 7 1.3 Vývozy zbytk ze skladu/makulatura... 7 2 1 Zbytkový materiál V souvislosti
Autoi: V Plzni 31.08.2010 Obsah ZBYTKOVÝ MATERIÁL... 3 1.1 Materiálová žádanka na peskladnní zbytk... 3 1.2 Skenování zbytk... 7 1.3 Vývozy zbytk ze skladu/makulatura... 7 2 1 Zbytkový materiál V souvislosti
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Texty k přednáškám z MMAN3: 4. Funkce a zobrazení v euklidovských prostorech
 Texty k přednáškám z MMAN3: 4. Funkce a zobrazení v euklidovských prostorech 1. července 2008 1 Funkce v R n Definice 1 Necht n N a D R n. Reálnou funkcí v R n (reálnou funkcí n proměnných) rozumíme zobrazení
Texty k přednáškám z MMAN3: 4. Funkce a zobrazení v euklidovských prostorech 1. července 2008 1 Funkce v R n Definice 1 Necht n N a D R n. Reálnou funkcí v R n (reálnou funkcí n proměnných) rozumíme zobrazení
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
 Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Grafy. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 13.
 Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Negativní informace. Petr Štěpánek. S použitím materiálu M.Gelfonda a V. Lifschitze. Logické programování 15 1
 Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Negativní informace Petr Štěpánek S použitím materiálu M.Gelfonda a V. Lifschitze 2009 Logické programování 15 1 Negace jako neúspěch Motivace: Tvrzení p (atomická formule) neplatí, jestliže nelze odvodit
Lineární algebra Petriho sítí
 ) Notace Lineární algebra Petriho sítí Definice: Neznaená PN je taková tveice Q = P Pre Post kde P = {P P n } je množina míst (konená nenulová) = { m } je množina pechod (konená nenulová) Pre: P {} vstupní
) Notace Lineární algebra Petriho sítí Definice: Neznaená PN je taková tveice Q = P Pre Post kde P = {P P n } je množina míst (konená nenulová) = { m } je množina pechod (konená nenulová) Pre: P {} vstupní
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Relace, zobrazení, algebraické struktury Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Relace, zobrazení, algebraické struktury Michal Botur Přednáška
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Bezkontextové jazyky. Bezkontextové jazyky 1 p.1/39
 Bezkontextové jazyky Bezkontextové jazyky 1 p.1/39 Jazyky typu 2 Definice 4.1 Gramatika G = (N, Σ, P, S) si nazývá bezkontextovou gramatikou, jestliže všechna pravidla z P mají tvar A α, A N, α (N Σ) Lemma
Bezkontextové jazyky Bezkontextové jazyky 1 p.1/39 Jazyky typu 2 Definice 4.1 Gramatika G = (N, Σ, P, S) si nazývá bezkontextovou gramatikou, jestliže všechna pravidla z P mají tvar A α, A N, α (N Σ) Lemma
Kapitola 6. LL gramatiky. 6.1 Definice LL(k) gramatik. Definice 6.3. Necht G = (N, Σ, P, S) je CFG, k 1 je celé číslo.
 Kapitola 6 LL gramatiky 6.1 Definice LL(k) gramatik Definice 6.1. Necht G = (N, Σ, P, S) je CFG, k 1 je celé číslo. Definujme funkci FIRST G k : (N Σ) + P({w Σ w k}) předpisem FIRST G k (α) = {w Σ (α w
Kapitola 6 LL gramatiky 6.1 Definice LL(k) gramatik Definice 6.1. Necht G = (N, Σ, P, S) je CFG, k 1 je celé číslo. Definujme funkci FIRST G k : (N Σ) + P({w Σ w k}) předpisem FIRST G k (α) = {w Σ (α w
Efektivní hodnota proudu a nap tí
 Peter Žilavý: Efektivní hodnota proudu a naptí Efektivní hodnota proudu a naptí Peter Žilavý Katedra didaktiky fyziky MFF K Praha Abstrakt Píspvek experimentáln objasuje pojem efektivní hodnota stídavého
Peter Žilavý: Efektivní hodnota proudu a naptí Efektivní hodnota proudu a naptí Peter Žilavý Katedra didaktiky fyziky MFF K Praha Abstrakt Píspvek experimentáln objasuje pojem efektivní hodnota stídavého
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Kapitola 1. Úvod. 1.1 Značení. 1.2 Výroky - opakování. N... přirozená čísla (1, 2, 3,...). Q... racionální čísla ( p, kde p Z a q N) R...
 Kapitola 1 Úvod 1.1 Značení N... přirozená čísla (1, 2, 3,...). Z... celá čísla ( 3, 2, 1, 0, 1, 2,...). Q... racionální čísla ( p, kde p Z a q N) q R... reálná čísla C... komplexní čísla 1.2 Výroky -
Kapitola 1 Úvod 1.1 Značení N... přirozená čísla (1, 2, 3,...). Z... celá čísla ( 3, 2, 1, 0, 1, 2,...). Q... racionální čísla ( p, kde p Z a q N) q R... reálná čísla C... komplexní čísla 1.2 Výroky -
METODY OCEOVÁNÍ PODNIKU DEFINICE PODNIKU. Obchodní zákoník 5:
 METODY OCEOVÁNÍ PODNIKU DEFINICE PODNIKU Obchodní zákoník 5: soubor hmotných, jakož i osobních a nehmotných složek podnikání. K podniku náleží vci, práva a jiné majetkové hodnoty, které patí podnikateli
METODY OCEOVÁNÍ PODNIKU DEFINICE PODNIKU Obchodní zákoník 5: soubor hmotných, jakož i osobních a nehmotných složek podnikání. K podniku náleží vci, práva a jiné majetkové hodnoty, které patí podnikateli
Základy MIDI komunikace
 Propojení nástroje a poítae Základy MIDI komunikace MIDI IN, OUT, THRU Možností, jak pipojit klávesy k poítai je hned nkolik. Stále nejrozšíenjší porty pro MIDI komunikaci u kláves jsou klasické MIDI IN
Propojení nástroje a poítae Základy MIDI komunikace MIDI IN, OUT, THRU Možností, jak pipojit klávesy k poítai je hned nkolik. Stále nejrozšíenjší porty pro MIDI komunikaci u kláves jsou klasické MIDI IN
IV. CVIENÍ ZE STATISTIKY
 IV. CVIENÍ ZE STATISTIKY Vážení studenti, úkolem dnešního cviení je nauit se analyzovat data kvantitativní povahy. K tomuto budeme opt používat program Excel 2007 MS Office. 1. Jak mžeme analyzovat kvantitativní
IV. CVIENÍ ZE STATISTIKY Vážení studenti, úkolem dnešního cviení je nauit se analyzovat data kvantitativní povahy. K tomuto budeme opt používat program Excel 2007 MS Office. 1. Jak mžeme analyzovat kvantitativní
PŘEDNÁŠKA 2 POSLOUPNOSTI
 PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin.
 1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
1.2. Cíle Cílem kapitoly je opakování a rozšíření středoškolských znalostí v oblasti teorie množin. Průvodce studiem Množina je jedním ze základních pojmů moderní matematiky. Teorii množin je možno budovat
Související ustanovení ObZ: 66, 290, 1116 až 1157, 1158 a násl., 1223 až 1235, 1694, 1868 odst. 1, 2719, 2721, 2746, 2994, 3055, 3062, 3063,
 Pídatné spoluvlastnictví Obecná ustanovení 1223 (1) Vc náležící spolen nkolika vlastníkm samostatných vcí urených k takovému užívání, že tyto vci vytváejí místn i úelem vymezený celek, a která slouží spolenému
Pídatné spoluvlastnictví Obecná ustanovení 1223 (1) Vc náležící spolen nkolika vlastníkm samostatných vcí urených k takovému užívání, že tyto vci vytváejí místn i úelem vymezený celek, a která slouží spolenému
Lineární prostory. - vektorové veličiny(síla, rychlost, zrychlení,...), skládání, násobení reálným číslem
 Lineární prostory - vektorové veličiny(síla, rychlost, zrychlení,...), skládání, násobení reálným číslem - volné vektory a operace s nimi(sčítání, násobení reálným číslem) -ve 2 nebove 3 vázanévektorysespolečnýmpočátkem
Lineární prostory - vektorové veličiny(síla, rychlost, zrychlení,...), skládání, násobení reálným číslem - volné vektory a operace s nimi(sčítání, násobení reálným číslem) -ve 2 nebove 3 vázanévektorysespolečnýmpočátkem
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Lineární algebra : Lineární prostor
 Lineární algebra : Lineární prostor (3. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. dubna 2014, 14:43 1 2 3.1 Aximotické zavedení lineárního prostoru Číselné těleso Celou lineární
Lineární algebra : Lineární prostor (3. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. dubna 2014, 14:43 1 2 3.1 Aximotické zavedení lineárního prostoru Číselné těleso Celou lineární
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
3 Množiny, Relace a Funkce
 3 Množiny, Relace a Funkce V přehledu matematických formalismů informatiky se v této lekci zaměříme na základní datové typy matematiky, tj. na množiny, relace a funkce. O množinách jste sice zajisté slyšeli
3 Množiny, Relace a Funkce V přehledu matematických formalismů informatiky se v této lekci zaměříme na základní datové typy matematiky, tj. na množiny, relace a funkce. O množinách jste sice zajisté slyšeli
Úvod do programovacích jazyků (Java)
 Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
Úvod do programovacích jazyků (Java) Michal Krátký Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programovacích jazyků (Java), 2007/2008 c 2006 2008 Michal Krátký Úvod do programovacích
Virtuální počítač. Uživatelský program Překladač programovacího jazyka Operační systém Interpret makroinstrukcí Procesor. PGS K.
 Virtuální počítač Uživatelský program Překladač programovacího jazyka Operační systém Interpret makroinstrukcí Procesor Virtuální počítač Překladač Překladač : Zdrojový jazyk Cílový jazyk Analytická část:
Virtuální počítač Uživatelský program Překladač programovacího jazyka Operační systém Interpret makroinstrukcí Procesor Virtuální počítač Překladač Překladač : Zdrojový jazyk Cílový jazyk Analytická část:
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Programovací jazyk Python. Objektov orientovaný. [citováno z http://wraith.iglu.cz/python/index.php]
![Programovací jazyk Python. Objektov orientovaný. [citováno z http://wraith.iglu.cz/python/index.php] Programovací jazyk Python. Objektov orientovaný. [citováno z http://wraith.iglu.cz/python/index.php]](/thumbs/27/12237219.jpg) Programovací jazyk Python [citováno z http://wraith.iglu.cz/python/index.php] Python je jazyk objektov orientovaný, interpretovaný, dynamický a siln typovaný, multiplatformní, s jednoduchou a itelnou syntaxí,
Programovací jazyk Python [citováno z http://wraith.iglu.cz/python/index.php] Python je jazyk objektov orientovaný, interpretovaný, dynamický a siln typovaný, multiplatformní, s jednoduchou a itelnou syntaxí,
