SVM - Support Vector Machines

Transkript

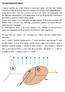
1 SVM - Support Vector Machines Menu: QCExpert SVM Modu Support Vector Machines (SVM, do češtiny se někdy překádá jako metoda podpůrných vektorů) nabízí vemi progresivní a novou metodu z obasti strojového učení, kterou rozpracova koncem 0. a začátkem 1. stoetí Vadimir Naumovič Vapnik a Aexej Jakovevič Červoněnkis (Akademie věd SSSR, Stanford University, Roya Hooway Coege London, AT&T Be Labs New Jersey, NEC Labs Princeton, Coumbia University New York). Této metody ze využít především pro kasifikační úohy, rovněž ae nachází upatnění v regresním modeování a neparametrických odhadech hustoty. Modey SVM využívají teorii empirického risku R a Vapnik-Chervonenkisovy (VC) dimenze modeu h. S pravděpodobností 1 patí nerovnost R R n h 1 n 4 h emp, ( 0-1) 1 kde R y f x, px, ydx dy je risk (skutečná střední chyba modeu), je počet 1 dat, parametry modeu, Remp yi f x, je empirický risk a h je nezáporná i1 ceočísená VC-dimenze modeu. Posední čen na pravé straně (ceá odmocnina) se nazývá VC-confidence. SVM-C Kasifikační modey SVM Vastní modey SVM pak minimaizují vhodně definovanou chybu (např. miskasifikaci u kasifikačních modeů, chybu v nějaké metrice u regrese). Napříkad v úoze ineární separabiní kasifikace ve dvou dimenzích (dvě čísené nezávise proměnné) se hedá přímka, která rozděuje (diskriminuje) obě třídy tak, že zachová maximání vzdáenost od experimentáních dat a tím za poměrně obecných předpokadů minimaizuje riziko miskasifikace v predikci z nových dat, viz Obrázek 1. Mode SVM pak může mimo jiné soužit k tomu, abychom na zákadě nových hodnot nezávise proměnné uměi odhadnout (včetně pravděpodobností) do které třídy přísušný objekt patří. Obrázek 1 SVM, separabiní data, ineární mode

2 V neseparabiním případě se hedá přímka, která minimaizuje přešapy nesprávně kasifikovaných dat. Příkad uvádí Obrázek, kde jsou minimaizovány komé vzdáenosti jednoho nesprávně kasifikovaného bodu B a jednoho nesprávně kasifikovaného bodu A od separační přímky při současném požadavku maximání separace ostatních dat. Tím je zajištěna vysoká účinnost kasifikačního modeu. Obrázek SVM, ineárně neseparabiní data, ineární mode V případě separabiních dat s binární odezvou (y i = 1 nebo 1) se minimaizuje déka normáy w separační přímky (obecně nadroviny) f x w i i 1 0, 1,..., za omezující podmínky y wx b i, v případě neseparabiních dat se k optimaizovanému kritériu přidá ještě čen penaizace za přešap s uživateem definovaným parametrem C, který ze chápat jako cenu (cost) za chybnou kasifikaci w f x Ci za podmínky i1 wx 1, 1,..., yi i b i i. ( 0-) 0, i1,..., i Geometrickou interpretaci v případě neseparabiních dat iustruje Obrázek 3, souřadnice bodů (odpovídající řádek nezávise proměnných), o které se opírají separační meze H 1 a H (na obrázku označeny kroužkem), se nazývají support vectors (česky se překádají jako podpůrné vektory).

3 Obrázek 3 Schéma separace SVM-nadrovinou H pro neseparabiní data Aternativně ze použít kriteriání podmínku obsahující místo ztrátového koeficientu C zomek ν (0 < ν < 1), který přibižně odpovídá očekávanému maximánímu podíu miskasifikací (chybných kasifikací). f x w 1 i za podmínky i1 wx, 1,..., yi i b i i. ( 0-3) 0, i1,..., ; 0 SVM-R Regresní modey SVM Podobně ze zapsat anaogické kritérium pro SVM regresi, které definuje přijatenou chybu modeu, mimo tuto chybu je mode opět penaizován ineární funkcí se ztrátovým koeficientem C>0. Odhad ineárního modeu se získá minimaizací i w i i za podmínky i1 C wx b y, i 1,..., i i i y wx b, i 1,..., i i i ( 0-4) Obrázek 4 Schéma SVM regrese (SVM-R) Koeficienty w zde odpovídají regresním koeficientům ineárního modeu, b je absoutní čen. Parametr ε je poošířka pásu, v němž očekáváme správné hodnoty y i, ze tedy ε

4 chápat jako nejvyšší přípustnou absoutní chybu. Takto definované regresní kritérium vede mimochodem i k nastavitené robustnosti regresního modeu, který se snaží dostat co nejvíce dat do pásu f(x), proto je SVM regrese vhodná také pro data znečištěná hrubými chybami měření, odehými hodnotami y a podobně. Čím je vyšší koeficient ztráty C, tím vyšší je penaizace za překročení absoutní odchyky, případně podíu ν, jak iustruje Obrázek 5. Podobně jako v předchozím odstavci ze rovněž zavést aternativní vyjádření kritéria SVM-R s parametrem ν (0<ν<1), který přibižně odpovídá očekávanému maximánímu podíu korektních bodů, tedy dat, která odpovídají očekávanému modeu, který se získá vázanou minimaizací vzhedem k w, b, ξ, ξ *, ε výrazu w f x C 1 * i i i1 za podmínek y i b yi i * b wx w x ( 0-5) i i i * i, i 0, i1,..., ; 0 Regresní mode SVM ze pak využít také pro predikci očekávané hodnoty závise proměnné pro nové známé hodnoty nezávise proměnných. Na rozdí od kasické regrese nemá tento odhad nutně charakter odhadu střední hodnoty ve smysu statistického momentu. Regresní přímka SVM-R, ν=0.01, nebo =5 Regresní přímka SVM-R, ν=0.1, nebo = Regresní přímka SVM-R, ν=0.5, nebo =1 Regresní přímka SVM-R, ν=0.95, nebo =0.1 Obrázek 5 Viv ztrátového koeficientu na robustnost modeu SVM-R při C = 1 SVM-OneCass Hustota rozděení Pro naezení hranice rozděení vícerozměrné náhodné veičiny s ibovoným rozděením ze minimaizovat kritérium (B. Schoekopf et a., 001)

5 w 1 wxi i, i1,..., C i za podmínky 0, i1,..., i1 i ( 0-6) Takto získaná hranice je opět ineární hyperpocha v x a odpovídá přibižně ν-kvantiu rozděení. Koeficient ν, 0 1 tedy odpovídá maximu podíu dat, které chceme odděit od jádra rozděení, což ze interpretovat jako (1 ν) kvanti rozděení, ae s výhodou také jako maximání očekávaný podí vybočujících bodů, které do rozděení nepatří. Řešením uvedených podmínek je hyperpocha, která ohraničuje vnitřní (1 ν).100% část rozděení. Výsedná hranice pak identifikuje vybočující body a ze jí použít i k predikci, zda nově naměřená data patří do natrénovaného vícerozměrného rozděení. Takové interpretace ze s výhodou využít napříkad pro detekci změn ve sožitých vícerozměrných procesech s ibovoným rozděením. SVM-jádrové transformace Uvedené modey a kritéria vedou jen na ineární funkce (diskriminační, regresní) typu w x a nebyy by příiš praktické. Jedním ze zásadních přínosů SVM je transformace - rozměrného prostoru x na prostor definovaný systémem neineárních funkcí φx, jehož dimenze n nesouvisí s dimenzí x, často bývá větší a může být až nekonenčná. V tomto prostoru se teprve vytvoří přísušný ineární SVM-mode. Protože se však mode vytváří na neineárně transformovaném prostoru φx, je i samotný mode neineární v prostoru původních proměnných x. Tím získávají SVM neobvykou fexibinost. Definují-i se T transformace ve formě kvadratické formy K i, j i j x x φ x φ x, (kde funkce K se nazývá jádrová), ze úohu naezení modeu formuovat jako kvadratickou vázanou optimaizaci, pro níž ze v kombinaci s metodou Lagrangeových mutipikátorů naézt poměrně ryché a stabiní derivační agoritmy. Nejčastěji používaná jádra jsou typu RBF (Radia Base Functions) definovaná jako K i, j exp i j x x x x ( 0-7) Mezi daší, méně používané jádrové transformace patří: Poynomické jádro T d Kxi x j xi x j r T Sigmoida Kxi, x j tanh xi x j r Lineární (bez transformace) K,, exp ; 0 T i j i j x x x x Parametry γ a d zadává uživate, r se počítá. Parametr γ má význam strmosti jádra, vyšší hodnoty γ vedou k podrobnějším, někdy i méně stabiním modeům. Zavedením takové neineární transformace je pak možné v kasifikaci separovat ibovoné neineární útvary v - rozměrném prostoru, v regresi vytvářet ibovoné neineární regresní funkce a v modeování rozděení naézt nejepší hranici rozděení, přesněji naézt neineární hyperpochu, která ohraničuje minimání objem v prostoru dat R, který obsahuje aespoň 100(1 ν)% dat. Příkady

6 Zde uvádíme někoik jednoduchých iustračních příkadů pro snadnější orientaci v metodách SVM a rychou referenci pro nastavení a smys parametrů metod SVM. Přestože metody SVM jsou určeny pro větší množství vysvětujících proměnných x (prediktorů), pro účey epší iustrace se omezíme převážně na dvourozměrné, snáze pochopitené příkady (jeden nebo dva soupce x). Pro vícerozměrné modey se nicméně SVM chovají anaogicky. Příkad 1 Kasifikace Pro hodnoty spojitých prediktorů X a Y jsou známy kategorie A, B, C, D. Tyto kategorie mohou být napříkad výsedky experimentů při podmínkách x i, y i, nebo předem známé kategorie, u nichž jsou známy hodnoty X a Y. Výskyty různých úrovní kategorie se překrývají nejsou zřejmě zcea separovatené v rovině X, Y. Pro tato (trénovací) data se vytvoří mode SVM-C. Násedující grafy ukazují chování modeu SVM nejprve bez transformace (ineární jádro) a pak s RBF transformací s různými hodnotami strmosti (nebo neinearity) γ od γ=0.01 do γ=10. U výsedných modeů jsou uvedeny i počty miskasifikací (miscass), tedy chybných kasifikací. Vobou vhodného γ chceme získat takový mode, který bude nejépe předpovídat kategorii pro nové hodnoty x a y bez ohedu na náhodné umístění trénovacích dat. Proto posední ( přetrénovaný ) mode s nejmenším počtem miskasifikací nebude zřejmě nejepší. Kvaitu modeu ze posoudit cross-vaidací, kdy odstraníme část z trénovacích dat (obvyke 10-30%) a tuto část pak použijeme pro predikci kategorie. Podí správně predikovaných kategorií pak může být mírou úspěšnosti zvoeného modeu. Ukázka tabuky dat Lineární, Miscass=15 RBF, γ=0.01, Miscass=14 RBF, γ=0.1, Miscass=8 RBF, γ=1, Miscass=5 RBF, γ=10, Micass=1 Příkad Kasifikace Násedující tři grafy ukazují ineárně neseparovatená data s binární odezvou (A,B), kdy ineární mode SVM-C, a částečně i poynomické jádro. stupně je geometricky nevhodné a sehává. Transformace s RBF jádrem naopak vemi dobře separuje obě kategorie.

7 Lineární jádro Kvadratické jádro (stupeň=) RBF jádro Příkad 3 Robustní regrese Nastavením parametru ε v rovnici ( 0-4) na str. 3 se určuje šířka pásu koem modeu, v němž má ežet co nejvíce dat, viz Obrázek 4, str. 3. Zmenšováním hodnoty tohoto parametru ze dosáhnout obdoby robustnosti u kasických regresních modeů. Data mimo interva f x ; f x se v SVM regresi považují za data, která jsou mimo interva přípustných chyb a tedy neodpovídají modeu. Na násedujících grafech je iustrováno chování ineárního SVM-regresního modeu v porovnání s kasickou ineární regresí metodou nejmenších čtverců (A) a iterativní robustní metodou bounded infuence regression (B). Na obrázcích (C) až (F) jsou přímky pro různě široké přípustné meze ±ε. Z iustrace je zřejmé, že se mode snaží nacpat do zadaného pásu co nejvíce dat. Tím ze dosáhnout pynuho zvyšování robustnosti modeu vůči odehým datům. Povaha této robustnosti je však značně odišná od robustních metod v kasické regresi. (A) Kasická regrese, metoda nejmenších čtverců (B) Kasická regrese, robustní metoda BIR

8 (C) SVM-R, ε = 3 (D) SVM-R, ε = 1.5 (E) SVM-R, ε = 1 (F) SVM-R, ε = 0.5 (A) RBF kerne, ε=; γ=0.5 (B) RBF kerne, ε=1; γ=0.5

9 (C) RBF kerne, ε=0.5; γ=5 (D) RBF kerne, ε=0.1; γ=5 Příkad 4 Adekvátnost regresního modeu Data odpovídající regresnímu modeu se řídí vztahem y i = f(x i ) + e i, úkoem regrese je odhad f(x) a tím i veikosti chyb e i a jejich rozptyu. Díky značné fexibiitě modeů SVM je snadné mode přeurčit. Takový mode pak nereprezentuje střední hodnotu, ae spíše šum v datech a není použitený jako popis sedované závisosti. Vhodná diagnostika, která pomůže indikovat přeurčení modeu je (mimo standardních cross-vaidačních technik) koncentrace výskytu residuí na hranici ± ε. Grafy na předcházející straně iustrují čtyři modey na stejných datech, z nichž pouze první (A) zřejmě správně modeuje hadkou křivku skutečné závisosti (zda je modeem křivka (RBF, poynom, sigmoida), či přímka, je vobou uživatee). Křivost ostatních modeů je ovivněna náhodnými chybami v datech. Koncentrace reziduí na nastavených hranicích indikující příiš vekou hodnotu γ v rov. ( 0-7), případně i C v rov. ( 0-5) je zváště patrná na grafech (B) a (D). Mode (D) iustruje mezní možnost, kdy mode kopíruje pouze náhodné chyby a je zcea nepoužitený. Násedující příkad iustruje postup cross-vaidace, kdy se mode vytvoří z podmnožiny původních dat (obvyke náhodně vybraných 70-90% trénovacích dat) avšak predikce se počítá ze všech (100%) dat. Zobrazení vynechaných testovacích dat v grafu predikce pomůže posoudit predikční schopnost modeu. Modey SVM mohou být tak fexibiní, že dokonae prooží i zcea náhodná data (A), takový mode je však nepoužitený, má nuovou predikční schopnost (světejší predikovaná data v grafu predikce jsou zcea mimo dokonaý fit). V grafu (B) má sice mode 50x větší chyby, než (A), avšak tento mode má vemi dobrou predikční schopnost, světejší testovací data prakticky spývají s trénovacími.

10 (A) Neadekvátní mode s nereáným požadavkem na chyby(ε = 0.0), a příiš vekým γ (B) Adekvátní mode pro daná data Příkad 5 Viv γ a ν na mode rozděení Násedující tabuka grafů iustruje viv voitených parametrů na tvar hranice hustoty rozděení na příkadu jádra RBF. Parametr γ ovivňuje tuhost rozděení, parametr ν odpovídá podíu rozděení mimo hranici. Uvedených 16 grafů znázorňuje tvar vypočítané hranice pro rostoucí podí ν při konstantním γ a pro rostoucí γ při konstantním ν. γ = 0.1, ν = 0.1 γ = 0.1, ν = 0. γ = 0.1, ν = 0.3 γ = 0.1, ν = 0.4 γ = 0.1, ν = 0.5 γ = 0.1, ν = 0.6 γ = 0.1, ν = 0.8 γ = 0.1, ν = 0.9 γ = 0., ν = 0.9 γ = 0.3, ν = 0.9 γ = 0.4, ν = 0.9 γ = 0.5, ν = 0.9

11 γ = 0.6, ν = 0.9 γ = 0.7, ν = 0.9 γ = 0.8, ν = 0.9 γ = 0.9, ν = 0.9 Impementace Support Vector Machines je zaožena na kódu LIB-SVM (c) Chih-Chung Chang and Chih-Jen Lin vyvíjeného na Nationa Taiwan University, viz např. Chih-Chung Chang and Chih-Jen Lin: Library for Support Vector Machines Doporučená iteratura Vapnik, V.: The Nature of Statistica Learning Theory. New York, Springer-Verag (1995). Vapnik, V.: Statistica earning theory. New York, John Wiey (1998). Vapnik, V., & Chervonenkis, A.: Theory of pattern recognition. Nauka, Moscow (1974). [In Russian] B. Schoekopf, J. C. Patt, J. Shawe-Tayor, A. J. Smoa, and R. C. Wiiamson: Estimating the support of a high-dimensiona distribution. Neura Computation, 13(7): , (001). Christopher J.C. Burges: A Tutoria on Support Vector Machines for Pattern Recognition, Data Mining and Knowedge Discovery, , Kuwer Academic Pubishers, (1998) SVM Kasifikace Menu: QCExpert SVM SVM-Kasifikace Data a parametry Data jsou uspořádána do jednoho nebo více soupce nezávise proměnných a jednoho soupce s úrovněmi faktoru. Nezávise proměnné jsou čísené hodnoty, faktor musí mít aespoň rozdíné úrovně. Úrovně faktoru mohou být čísa (např. 1,, 3), nebo text (napříkad ANO, NE). Každý řádek musí obsahovat patné hodnoty ve všech soupcích. Neúpné řádky nejsou použity. V diaogovém paneu (Obrázek 6 A) se označí jeden nebo více soupců nezávise proměnné a soupec faktoru. Chceme-i počítat predikci, označíme ještě poíčko a vybereme soupce, pro něž chceme predikovat hodnotu (přesněji: úroveň) faktoru. Stiskem tačítka Dopň X ze označit soupce odpovídající vybraným nezávise proměnným a predikce se pak počítá pro táž data, z nichž se vytvoři mode. Ve skupině Data se zvoí chceme-i pro výpočet použít jen nějakou podmnožinu dat, či všechna data. Ve skupině Typ SVM zvoíme, zda se má použít varianta Cost se ztrátovým koeficientem C, nebo Nu se zadáním koeficientu ν. Zaškrtneme-i poíčko Zobrazit Support Vectors, vypíší se do protokou všechny support vektory modeu a rovněž se označí v grafu křížkem, pokud se graf konstruuje. To má obvyke orientační význam havně u ineárních modeů. V poíčku Popis ze vybrat soupec, který se pak použije k identifikaci jednotivých bodů (řádků) v grafech. Dáe se zvoí jádro pro transformaci z možností Lineární: (xi*xj) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r) a parametry výpočtu: Stupeň (pouze u poynomického jádra), hodnotu parametru γ Gamma, který souvisí se strmostí jádra a tím s neinearitou modeu, tento parametr není nutno zadávat

12 impicitně se použije hodnota 1/n, ztrátový koeficient C Cost, podí ν Nu a parametr jádra R. Zvoíme, zda chceme provést závěrečnou korekci modeu po výpočtu (Shrinking, většinou nemá na výsedek viv) a zda chceme pro predikované úrovně vypočítat pravděpodobnosti (poe Pravděpodobnosti). Tačítkem Nastavit váhy vyvoáme diaogový pane pro zadání vah (Obrázek 6 B). Zde můžeme přiřadit každé úrovni faktoru váhu, kterou můžeme chápat také jako poměr škod při chybné predikci jednotivých úrovní. Impicitně se váhy nepoužívají, resp. jsou rovny jedné. Po stisku OK se zahájí výpočet. (A) Obrázek 6 Diaogový pane SVM Kasifikace (B) Obrázek 7 Příkad typických dat pro SVM-kasifikaci (zkrácená tabuka) Protoko Název úohy Nezávise proměnná Závise proměnná Typ SVM Zadaný název úohy Seznam použitých nezávise proměnných Název soupce s faktorem Soupce použité pro predikci Zvoený typ SVM kasifikace, pomocí zadaného ztrátového

13 Jádro Stupeň Gamma Cost R Nu Shrinking Pravděpodobnosti Primání parametry koeficientu C Kasifikace - Cost, nebo pode předpokádaného podíu chybných kasifikací Kasifikace - Nu Zvoený typ jádra: Lineární: (xi*xj) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r) Požadovaný stupeň poynomického jádra (je-i použito) Zadaný parametr jádra γ Zadaný ztrátový koeficient pro optimaizaci C (pouze pro zvoený typ C) Zadaný parametr jádra R Zadaný parametr ν (pouze pro zvoený typ Nu) Zvoená možnost dodatečné stabiizace modeu pomocí techniky Shrinking Voba, zda se mají počítat predikované pravděpodobnosti kasifikace (Ano / Ne) Počítají se pouze v případě ineární kasifikace. Hodnoty parametrů ineární hranice w T x + β = w 1 x 1 + w x + w m x m + β = 0 mezi všemi dvojicemi úrovní faktoru v prostoru prediktorů X. Ve soupci Beta je absoutní čen β, v daších soupcích jsou koeficienty k jednotivým soupcům prediktoru. Řádky tabuky jsou označeny dvojicemi hodnot (úrovní) faktoru, napříkad A B. Vyjde-i po dosazení nějakých hodnot prediktorů kadné číso, eží tento bod na straně první z dvojice úrovní (v tomto příkadu A ), vyjde-i záporné číso, eží tento bod na straně druhé z dvojice úrovní. V níže uvedeném příkadu bude bod (x=5; y=4) hodnota w T x = 5*( ) + 4*( 0.445) = 1.60, tedy pro bod (5,4) predikujeme úroveň A. Tabuka Souhrnný počet správně a chybně kasifikovaných dat (Správně,

14 miskasifikací Chybně) a kontingenční tabuka miskasifikací, která uvádí počty správně a chybně kasifikovaných dat pro všechny úrovně faktoru. Ve spodním řádku tabuky jsou skutečné počty výskytů jednotivých úrovní, v pravém soupci jsou predikované počty výskytů jednotivých úrovní. Jednotivé hodnoty v tabuce pak vyjadřují počty predikovaných úrovní. Napříkad hodnota 9 v násedující iustraci znamená, že SVM-mode predikuje 9-krát úroveň B pro řádek, který má ve skutečnosti úroveň A. Efektivita kasifikace Tato tabuka uvádí pro každou úroveň faktoru podí chybných kasifikací do dané úrovně (fase positives, FP), podí správných kasifikací do dané úrovně (true positives, TP) a pochu pod bodem přísušné úrovně v grafu ROC (Reciever Operating Characteristic area under curve, ROC AUC), tedy (TP*(1 FP)+1/*(TP*FP+(1 TP)*(1 FP)) Support Vectors Index Data Rezidua Pravd. úrovně Pokud bya možnost vybrána v diaogovém paneu, vypíší se všechny použité support vektory. Tabuka predikovaných hodnot pro trénovací (původní zadaná) data. Pořadové číso Predikovaná úroveň z modeu Skutečná pozorovaná úroveň z dat 0 v případě správné kasifikace, 1 v případě chybné kasifikace Pravděpodobnost každé z úrovní faktoru pro dané hodnoty nezávise proměnných. Má-i faktor napříkad tři úrovně, ze snadno zkonstruovat (pomocí moduu Grafy / 3D Spine) rozožení pravděpodobnosti výskytu dané úrovně pro zvoenou dvojici nezávise proměnné, jak ukazuje iustrace:

15 pravděpodobnost A pravděpodobnost B pravděpodobnost C Index (nezávise proměnné) Pravd. úrovně Grafy Pokud bya zvoena v diaogovém paneu, obsahuje tato tabuka predikované úrovně faktoru pro zadané hodnoty nezávise proměnné včetně vypočítaných pravděpodobností. Jako predikce je vždy uvedena úroveň, která má nejvyšší pravděpodobnost (při více úrovních faktoru to může být i pravděpodobnost mnohem menší než 0.5) Pořadové číso predikce Hodnoty zadaných nezávise proměnných Predikovaná (nejpravděpodobnější) úroveň faktoru Predikované pravděpodobnosti jednotivých úrovní faktoru Pokud je nezávise proměnná dvourozměrná (má dva soupce), konstruuje se graf predikčních obastí pro jednotivé úrovně. Každá barva reprezentuje obast, v níž očekáváme výskyt přísušné úrovně faktoru častěji, než výskyt kterékoiv jiné úrovně. Je-i napříkad počet úrovní faktoru Y={ A, B, C, D } m = 4, je v obasti predikované hodnoty A pravděpodobnost výsedku A aespoň 1/m, tedy 0.5. Graf hranice predikčních obastí je tvarově totožná s předchozím grafem, vyznačuje v případě dvourozměrné nezávise proměnné hranice, na nichž jsou pravděpodobnosti sousedících úrovní stejné. Graf predikce vyznačuje v případě dvourozměrné nezávise proměnné nové zadané hodnoty nezávise proměnné pro predikci v grafu, pokud bya zvoena v diaogovém paneu.

16 (A) Body ROC (Reciever Operating Characteristic) pro posouzení efektivity kasifikačního modeu pro každou úroveň faktoru. Na ose Y je podí správných kasifikací do dané úrovně (true positives, TP), na ose X je podí chybných kasifikací do dané úrovně (fase positives, FP). Čím jsou body bíže evému hornímu rohu trojúheníka (bodu [0, 1]), tím epší je rozišení této úrovně daným modeem, obr (A). jsou-i body bízko úhopříčce, je rozišovací schopnost modeu špatná, obr. (B), body mimo trojúheník, viz obr. (C), představují predikci horší, než náhodné hádání, mode je zcea nepoužitený. Je dobré mít na paměti, že špatné rozišení nemusí vždy znamenat chybu v modeu, někdy úroveň faktoru na zvoených nezávise proměnných prostě nezávisí, nebo ji rozišit neze. (B) (C) SVM Regrese Menu: QCExpert SVM SVM-Regrese Data a parametry Data jsou uspořádána do soupců nezávise proměnných a jednoho soupce s hodnotami závise proměnné. Nezávise proměnné i závise proměnná musí být čísené hodnoty. Každý řádek musí obsahovat patné hodnoty ve všech soupcích. Neúpné řádky nejsou ve výpočtu použity. V diaogovém paneu (Obrázek 8) se označí jeden nebo více soupců nezávise proměnné a jeden soupec závise proměnné. Chceme-i počítat predikci, označíme ještě poíčko a vybereme soupce, pro něž chceme predikovat hodnotu závise proměnné. Stiskem tačítka Dopň X ze označit soupce odpovídající vybraným

17 nezávise proměnným a predikce se pak počítá pro táž data, z nichž se vytvoři mode. Ve skupině Data se zvoí chceme-i pro výpočet použít jen nějakou podmnožinu dat, či všechna data. Ve skupině Typ SVM zvoíme, zda se má použít varianta Epsion se zadáním veikosti očekávané maximání chyby ε, nebo Nu se zadáním koeficientu ν. Zaškrtneme-i poíčko Zobrazit Support Vectors, vypíší se do protokou všechny support vektory modeu a rovněž se označí v grafu křížkem, pokud se graf konstruuje. To má obvyke orientační význam havně u ineárních modeů. V poíčku Popis ze vybrat soupec, který se pak použije k identifikaci jednotivých bodů (řádků) v grafech. Dáe se zvoí jádro pro transformaci z možností Lineární: (xi*xj) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r) a parametry výpočtu: Stupeň (pouze u poynomického jádra), hodnotu parametru γ Gamma, který souvisí se strmostí jádra a tím i s neinearitou modeu, tento parametr není nutno zadávat impicitně se použije hodnota 1/n, ztrátový koeficient C Cost, očekávaný podí vybočujících hodnot ν Nu, očekávaná maximání chyba ε v poi Epsion a parametr jádra R. Zvoíme, zda chceme provést závěrečnou korekci modeu po výpočtu (Shrinking, většinou nemá na výsedek veký viv). Po stisku OK se zahájí výpočet. Obrázek 8 Diaogový pane SVM - Regrese Protoko Název úohy Nezávise proměnná Závise proměnná Typ SVM Jádro Zadaný název úohy Seznam použitých nezávise proměnných Název soupce se závise proměnnou Soupce použité pro predikci Zvoený typ SVM regrese, Regrese pomocí zadaného Epsion pode rov. ( 0-4), nebo Regrese pode podíu chybných dat Nu pode ( 0-5) Zvoený typ jádra: Lineární: (xi*xj)

18 Stupeň Gamma Cost Epsion R Nu Shrinking Support Vectors Index Data Rezidua Index (nezávise proměnné) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r) Požadovaný stupeň poynomického jádra Zadaný parametr jádra γ Zadaný ztrátový koeficient pro optimaizaci C Zadaná hodnota maximání chyby ε (pouze pro Typ SVM = Epsion) Zadaný parametr jádra R (pouze pro poynom a tanh) Zadaný parametr ν (pouze pro Typ SVM = Nu) Zvoená možnost dodatečné stabiizace modeu pomocí techniky Shrinking Pokud bya tato možnost vybrána v diaogovém paneu, vypíší se všechny použité support vektory. Tabuka predikovaných hodnot pro trénovací data. Pořadové číso Predikovaná hodnota závise proměnné z modeu Skutečná pozorovaná hodnota závise proměnné z tabuky dat Pokud bya zvoena v diaogovém paneu, obsahuje tato tabuka predikované hodnoty závise proměnné pro zadané hodnoty nezávise proměnné. Pořadové číso predikce Hodnoty zadaných nezávise proměnných Predikovaná hodnota závise proměnné z modeu Grafy Graf predikce SVM Regrese vynáší na vodorovnou osu vypočtenou (predikovanou) hodnotu Y-Vyp závise proměnné, na svisou osu skutečnou hodnotu Y-Data z datové tabuky. Čím bíže k přímce eží body, tím těsněji se mode přibižuje k datům. Graf reziduí, svisé vzdáenosti od přímky v předchozím grafu, rozdí mezi skutečnou a predikovanou hodnotou závise proměnné. Tvary a interpretace tohoto grafu jsou iustrovány v odst. 0 Příkady.

19 Pokud je nezávise proměnná jednorozměrná (jeden soupec), zobrazí se regresní funkce, tedy skutečný SVM-regresní mode a data. SVM Hustota rozděení Menu: QCExpert SVM SVM-Hustota Data a parametry Data jsou uspořádána do jednoho nebo více soupců proměnných. Proměnné jsou čísené hodnoty. Každý řádek musí obsahovat patné hodnoty ve všech soupcích. Neúpné řádky nejsou použity. V diaogovém paneu (Obrázek 9) se označí jeden nebo více soupců proměnné. Chceme-i počítat predikci, označíme ještě poíčko a vybereme soupce, pro něž chceme predikovat přísušnost k rozděení. Stiskem tačítka Dopň X ze označit soupce odpovídající vybraným proměnným a predikce se pak počítá pro táž data, z nichž se vytvoři mode. Ve skupině Data se zvoí chceme-i pro výpočet použít jen nějakou podmnožinu dat, či všechna data. Zaškrtneme-i poíčko Zobrazit Support Vectors, vypíší se do protokou všechny support vektory modeu a rovněž se označí v grafu křížkem, pokud se graf konstruuje. V poíčku Popis ze vybrat soupec, který se pak použije k identifikaci jednotivých bodů (řádků) v grafech. Dáe se zvoí jádro pro transformaci z možností Lineární: (xi*xj) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r)

20 Obrázek 9 Diaogový pane SVM Hustota rozděení a parametry výpočtu: Stupeň (pouze u poynomického jádra), hodnotu parametru γ Gamma, který souvisí se strmostí jádra a tím s neinearitou modeu, tento parametr není nutno zadávat impicitně se použije hodnota 1/n, podí dat mimo rozděení ν Nu a parametr jádra R. Zvoíme, zda chceme provést závěrečnou korekci modeu po výpočtu (Shrinking, většinou nemá na výsedek viv. Po stisku OK se zahájí výpočet. Protoko Název úohy Nezávise proměnná Typ SVM Jádro Stupeň Gamma Nu R Shrinking Support Vectors Zadaný název úohy Seznam použitých nezávise proměnných Soupce použité pro predikci Zvoený typ SVM kasifikace, pomocí zadaného ztrátového koeficientu C Kasifikace - Cost, nebo pode předpokádaného podíu chybných kasifikací Kasifikace - Nu Zvoený typ jádra: Lineární: (xi*xj) Poynomické: (-gamma*(xi*xj)+r)^d Radia Base Function: exp(-gamma* xi-xj ^) Sigmoida: tanh(gamma*(xi*xj)+r) Požadovaný stupeň poynomického jádra (je-i použito) Zadaný parametr jádra γ Zadaný parametr ν (pouze pro zvoený typ Nu) Zadaný parametr jádra R Zvoená možnost dodatečné stabiizace modeu pomocí techniky Shrinking Pokud bya vybrána tato možnost v diaogovém paneu, vypíší se všechny použité support vektory.

21 Predikovaná přísušnost trénovacích (původních) dat k rozděení při daném ν (Nu) Index Pořadové číso Přísušnost k rozděení při daném ν (Nu), 1 = uvnitř rozděení, -1 = vně rozděení. Index proměnné Pokud bya zvoena v diaogovém paneu, obsahuje tato tabuka predikované přísušnosti zadaných hodnot proměnné k rozděení při daném ν (Nu), 1 = uvnitř rozděení, -1 = vně rozděení. Pořadové číso Zadané hodnoty proměnné přísušnosti k rozděení při daném ν (Nu) Grafy Graf obasti přísušnosti k rozděení při daném ν (Nu), tento graf se konstruuje pouze pro -rozměrnou proměnnou. Graf hranice obasti přísušnosti k rozděení při daném ν (Nu), tento graf se konstruuje pouze pro -rozměrnou proměnnou.